- 1Dipartimento di Ingegneria Strutturale e Geotecnica, Sapienza Università di Roma, Rome, Italy
- 2Joint Research Centre, European Commission, Ispra, Italy
This study focuses on multi-hazard analysis for bridges, following a two-tier approach. First, it identifies relevant open issues and recent literature developments in the field, presenting data in a meaningful manner, with specific focus on the issues related with the analysis of hazard chain scenario treated as low probability–high consequence events. Second, it describes a practically useful and sufficiently generic approach for efficient computational investigation of hazard chain scenarios in highway bridges. Following that, the applicability of the approach is exemplified in an appealing and commonly encountered in real-life hazard chain scenario, in which a multilevel modeling strategy is adopted to assess the structural response under hazard chain scenarios of a highway viaduct. Among the considered scenarios is the impact of a heavy vehicle (tank truck) on the bridge pier, and the fire spread following the collision due to the presence of inflammable materials. The bridge structure is a typical 189-m-long multi-span composite highway viaduct. The impact is modeled with a non-linear transient dynamic analysis that accounts the inertial effect of the global structure, while the fire modeling is performed with non-linear quasi static dynamic analysis focusing on local behavior with a substructured model. Then different impact and fire scenarios are considered, including different impact velocities of the truck.
Introduction and Open Issues in Hazard Chain Structural Analysis
Multi-hazard events involving bridge structures are more frequent nowadays, as a consequence to man-made events and climate change. These include natural events that trigger technological accidents (“Natech” accidents), such as the release of hazardous material, fires, and explosion (Krausmann et al., 2019). Events involving “hazard chains” at the dawn of the new millennium highlight this issue, with more notable examples such as those following the Hurricane Katrina in 2005 (with flooding loads followed by impact of debris) and the 2011 Tohoku earthquake in Japan (with coastal structures and bridges exposed to the chained action of the tsunami and fire following an earthquake).
As a follow-up to these events, the scientific community focused on approaches accounting for multi-hazard exposures in the design of structures (Ellingwood, 2010). In addition to academic research, an effort is ongoing also to bridge research and policy (Collins et al., 2017), supporting the actions of the Sendai Framework for Disaster Risk Reduction 2015–2030 (United Nations International Strategy for Disaster Reduction [UNISDR], 2015).
Focusing on the scientific dimension of the problem, and in particular civil engineering structures and infrastructures, research on the topic thrived in the last years. Li et al. (2012) provide a literature review and state of practice of multiple hazard assessment, design, and mitigation. Bruneau et al. (2017) provide a snapshot of multi-hazard state of art in engineering in the form of selected examples, highlighting considerations for achieving robustness against multiple hazards in bridges.
As reported in Petrini and Palmeri (2012), five open key issues emerge when the structural problem is addressed in a multi-hazard context, in order to define real multi-hazard assessment and design approach. These key issues can now be re-shaped and adapted to the current state advancement of the research as follows:
(1) The methodological approaches and computational tools used in different fields (analysis under different hazards) need to be combined within a unified risk assessment/design framework (“unified framework problem”).
(2) The interaction between different hazards is intrinsically difficult to model due to the lack of data and the unavailability of concurrent hazard models (“hazard interaction problem”).
(3) The consideration of rare multi-hazard scenarios located in the tails of the probabilistic hazard distributions/curves needs to be codified and coherently accounted for in the hazard characterization (“probabilistic tails problem”).
(4) The design and assessment need to consider consistent safety levels to different hazards and different multi-hazard scenarios (“risk consistency problem”).
(5) The design philosophies for different hazards lead often to conflicting strategies for bridge structures, e.g., either reducing or increasing the flexibility and/or the redundancy (“conflicting design strategies problem”).
These five main problems have been addressed from time to time in scientific literature, mainly in the context of risk assessment and referring to pairs of concurrent hazards (e.g., flooding and wind, and wind and earthquakes). A key contribution in clarifying the abovementioned hazard interaction problem has been given in Zaghi et al. (2016), in which the authors identify site effects and physical impacts of numerous hazards.
The so-called “hazard chain” interaction scenario, can occur when a first hazard is followed by (or triggers) a second one, and the intensities or the effects of these chained hazards are somewhat correlated. As introduced by Barbato et al. (2013), the hazard chain differs from the “concurrent-hazard” scenario, in which different hazard simultaneously act on the structural system and interact each other. Under the definitions provided in Zaghi et al. (2016), the hazard chain interaction can occur both at hazard-nature level (the first hazard influences the intensity of the second one) and at the level of the hazard effects on the structure (the preceding hazard influences the fragility of the structural system to the following hazard).
Apart from the qualitative definition of these two interaction levels for chained hazards, considerable issues arise in their correct treatment due to the fact that the hazard chain scenario is often related with the so-called low probability–high consequence (LP-HC) events (or intensities), for which:
(A) The probabilistic correlation of the chained hazard (or of their effect) is challenging because such LP (-HC) scenarios are located in the tails of the probabilistic distributions, something that dramatically reduces the reliability and the consistency of traditional probabilistic approaches and methods (Taleb, 2020), also in structural reliability. The issue is easily understood by relevant examples:
(a) earthquake triggering blast or fire events (it is a hazard-nature level interaction that occurs during high intensity–low probability earthquakes);
(b) scour followed by earthquake (it is an interaction at the induced effects level, due to long-run scour actions).
Such LP-HC scenarios can be tackled by assessing the ability of a critical transport infrastructure to maintain a certain level of functionality under unfavorable conditions, by means of stress tests (Argyroudis et al., 2019).
(B) The numerical analyses required for a reliable evaluation of the structural response and of the (LP-) HC due to the high intensity of the chained hazards are strongly non-linear, characterized by the presence of structural damage or degradation and, often, must be carried out in the time dynamic field in order to take into account specific interaction effects (e.g., impulsive load, resonating effects, and damage-induced dynamic amplifications).
Considering the above, this study focuses on point (B), with specific reference to the analysis of a highway viaduct under a hazard chain scenario, which implies the impact of a heavy vehicle (tank truck) on a bridge reinforced concrete pier, and the fire spread following the collision due to the presence of inflammable material acting on the steel bridge deck. Bridges have a critical role, especially in the immediate aftermath of natural disasters or in case of LP-HC scenarios, and thus, their safety level has to be evaluated by appropriate numerical models, which are able to provide the structural response in quite a rigorous manner. The proposed multilevel numerical strategy adopts different finite element (FE) models for the two chained hazards of the considered case. Multilevel modeling strategies are often necessary in hazard chain analyses for the sake of efficiency due to the fact that each hazard of the chain requires specific peculiarities of the numerical model (e.g., beam vs. shell FEs, transient vs. quasi static analysis, and geometric vs. material non-linearity).
The aim of this paper is multifold. First, we provide an overview of recent development in the field of multi-hazard analysis, focusing on bridge structures, presenting them in a meaningful manner that can be of interest to both researchers and practitioners in bridge engineering. To this aim, the methodology developed for the European Commission’s Transport Research and Innovation Monitoring and Information System (TRIMIS) using Scopus data is implemented (Tsakalidis et al., 2018). Following that, we present a practical and sufficiently generic approach for the efficient computational investigation of hazard chain scenarios in highway bridges, focusing on the structural behavior of a highway viaduct, a structure of strategic importance, under different hazard scenarios that include fire after impact hazard chains. Finally, we highlight issues related with the numerical structural modeling of bridges under hazard chains and how these can be approached by a multi-scale finite element method (FEM) strategy.
The paper is organized in the following manner. Bridge Multiple Hazard Research provides a concise overview of multi-hazard research in bridges in the last 10 years. Numerical Analyses for the Assessment of a Highway Viaduct Under Hazard Chains provides the performed analyses. Finally, conclusions are drawn in Conclusions.
Bridge Multiple Hazard Research
Bridges Collapse Statistics and Vulnerabilities
A faithful investigation of multi-hazard effects on bridges should start from bridge collapse statistics. By analyzing the collapses, as a first step, it is useful to identify what is the main collapse-triggering hazard (the one that has been identified as the collapse cause), which provides an indication of the vulnerability of bridges to this kind of hazard. As second step, it is useful to identify potential cases of occurrence of multi-hazard interactions. Starting from three independent collapses surveys reported in literature (Harik et al., 1990; Wardhana and Hadiprionio, 2003; Payá-Zaforteza and Garlock, 2012), a tentative connection to the different hazards to some occurrence of damages or collapses in bridges in last 30 years is carried out (Figure 1). The different hazards here are classified as follows: (i) “natural,” which is intended as hydraulic (flooding, scouring, tsunami, etc.) earthquake or wind hazards; (ii) “accidental” (or human induced), which is intended as fire, blast or impact hazards; and (iii) “other,” intended as any other cause that has been considered to lead collapses (e.g., fatigue, corrosion/deterioration, construction, or design errors or overload), while the numbers inside the pie portions indicate the number of collapsed/damaged bridges reported in the three abovementioned literature sources. A first consideration emerging from Figure 1 is that natural and accidental are two main causes for bridge collapse, while “other” scenarios (which globally also represent a significant portion of the statistics) are the ones that should be focused on the location of multi-hazard scenarios as a minor contribution to the statistics. It has to be also specified that, under the multi-hazard view, there is a chance that some of the cases cataloged in “accident” should be better identified as hazard chains (e.g., the scenario in which a fire follows an impact as the one considered in the application of this paper). It can be then said that a significant portion of collapses are worth investigating as potential multi-hazard-triggered collapses.

Figure 1. Tentative connection of occurrence of bridge damages or collapses to hazards (source: left, Harik et al., 1990; middle, Wardhana and Hadiprionio, 2003; right, Payá-Zaforteza and Garlock, 2012).
The numbers reported in the figure are destined to rise due to climate change (Yang and Frangopol, 2019), deficiencies in maintenance funding (European Commission, 2019; Gkoumas et al., 2019), and the further increase of traffic loads (Casas, 2015).
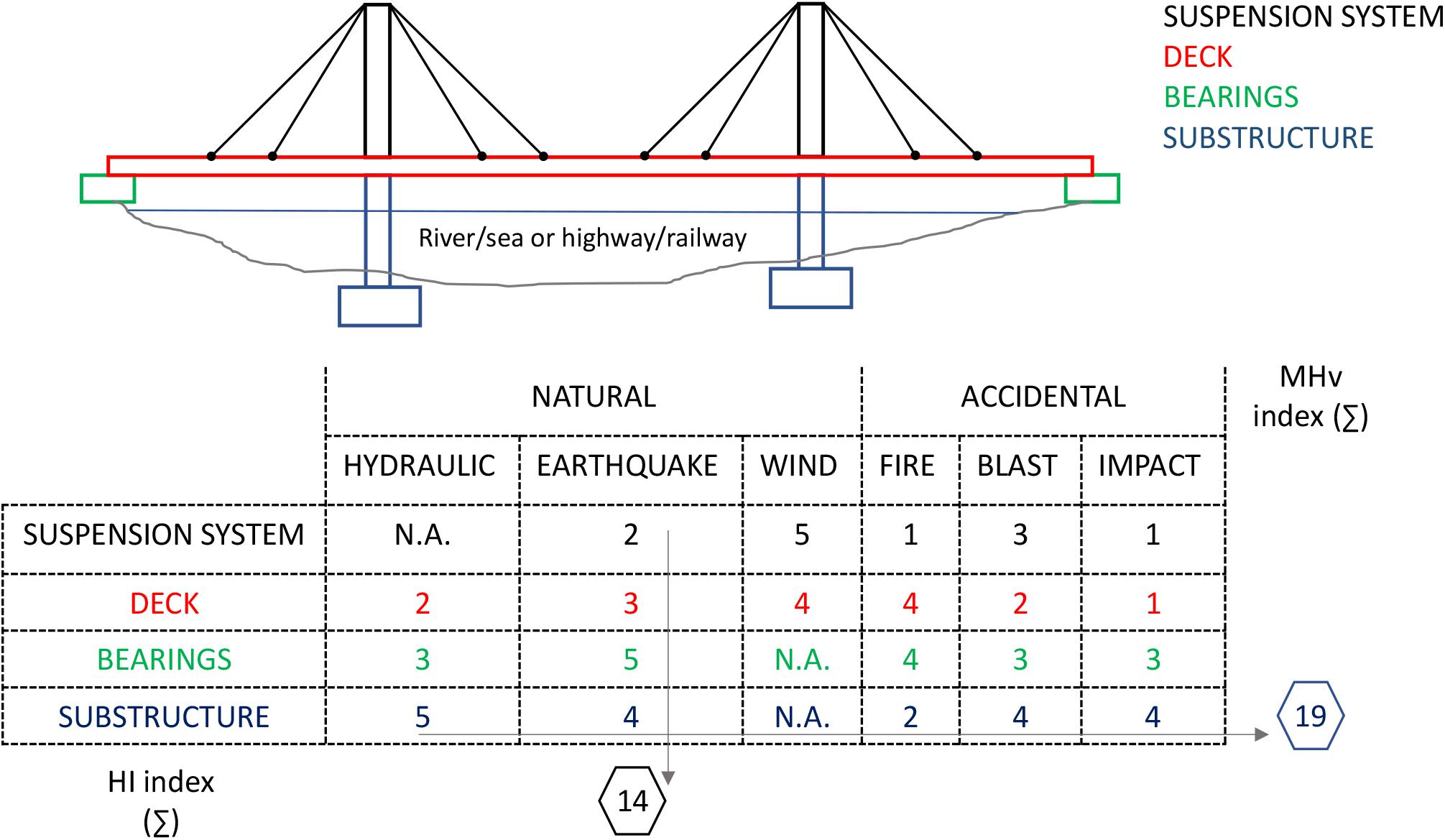
A classification of the vulnerability of different components to different hazards is the starting step of a thorough multi-hazard analysis of bridges. To this purpose, in Figure 2, a bridge schematic composed of a number of typical sub-assemblies/components (suspension system, deck, bearings, and substructure) is represented, together with a qualitative indication of the vulnerabilities of such structural parts to the different hazards potentially acting on them. The adopted vulnerability index ranges from 1 (low) to 5 (high), including 2 (moderate), 3 (medium), and 4 (consistent). The schematization aims to be as generic as possible: the bridge is represented with a mixed supporting system (suspended and simply supported), and it crosses either a highway or a sea/river, something that allows considering a wide range of active hazards. As for the previous figure, the hazards are grouped into two main typologies, i.e., “natural” and “accidental,” while, hazards classified in the “other” class are not represented because they are assumed to potentially act on several parts of the bridge, as perfectly understandable for corrosion and overload hazards. The vulnerability levels are coherently assigned as a result of exposure and typical fragilities of the components to different hazards. For example, the suspension system in a bridge can be assumed to have the highest level of vulnerability with respect to wind hazard, while it is assumed as not vulnerable or has low level of vulnerability to hydraulic or fire hazards. Summing the index in a column (i.e., the vulnerabilities assigned to different bridge components for a fixed hazard), a “hazard importance” (HI) index is obtained, while alignments of vulnerabilities for a component indicate potential multi-hazard vulnerability (MHv) for that component. Following that, the sum of the indexes assigned in a row (i.e., vulnerabilities indexed assigned to a specific component for different hazards) can be interpreted as a “MHv” index.
Multi-hazard events affecting more than one bridge component need to be also considered, like those involving frequently two adjacent components. This is the case of the hazard chain scenario considered in the second part of this study, involving an impact on the substructure and the consequent fire on the deck.
Regarding the type of multi-hazard interactions that can occur when the MHv index is high, they can be of the “concurrent” or of the “chain” typology. In this sense, while hazard chains are possible inside each hazard main group (e.g., earthquake could be chained to scouring, and blast can be chained to impact), chain interactions in bridges are rare between “natural” and “accidental” hazards. For example, it is rare that blast is chained to earthquake in bridges (while it is more frequent in buildings).
Finally, “other” hazards surely interact as chained with both “natural” and “accidental” hazards, for example, when the presence of corrosion in a component increases its vulnerability to earthquake or to impact.
From the provided analysis, it is clear that the HI index is maximum for earthquakes, while the MHv index is maximum for the substructure sub-assembly of bridges.
The hazard actions on bridges can be further detailed, by providing additional levels in the hazard taxonomy of Figure 2. Under natural hazards, hydraulic hazards, for example, may include scouring (foundation), hydraulic forces (at piers or on the deck), and debris accumulation (at foundation, piers, or deck). In a similar manner, the taxonomy of the other natural hazards (earthquake and wind) and accidental hazards can be expanded.
Literature in Multi-Hazard Design and Assessment of Bridges
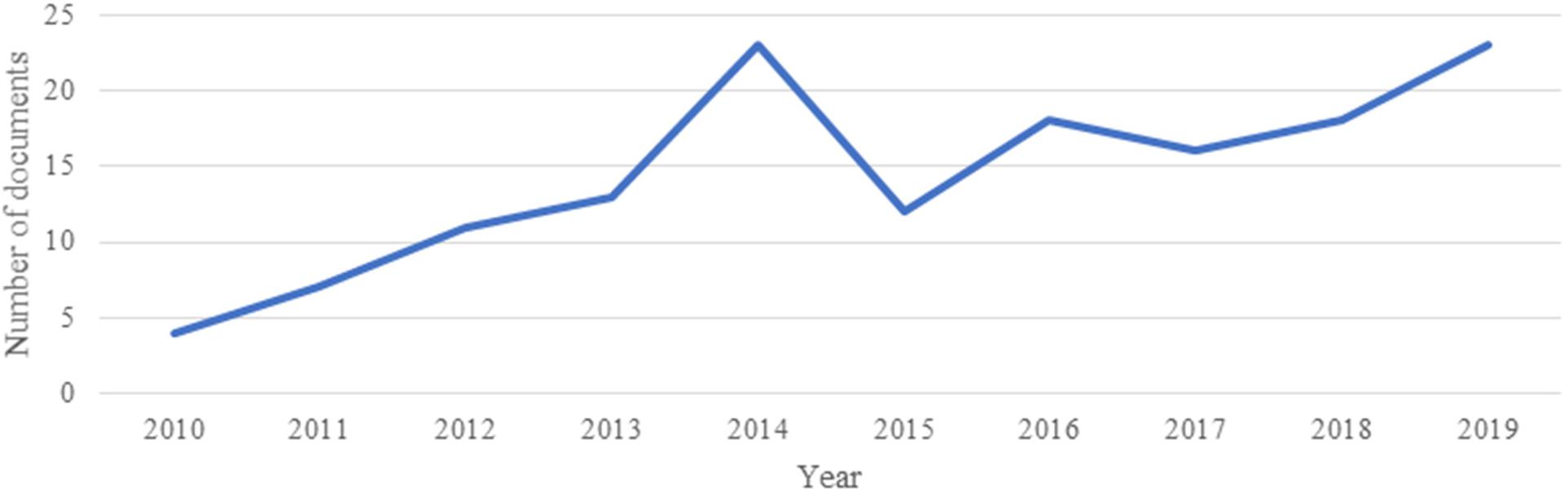
A bibliometric research is performed using the Scopus database. The research was performed on June 2020 using query that includes the words “bridge” and “multi-hazard” (including derivatives) on the title, abstracts, and keywords. A first finding is that research begun to be more consistent after 2010 with 166 results for the 10-year period (2010–2019), while in 2020 (not shown in the figure), nine documents appear, but the number is destined to grow. A thorough manual check eliminated 19 documents, thus leaving 154 relevant documents. Figure 3 shows the evolution of the research.
As can be seen, the research peaked in 2014 with 23 documents. This can be linked in large part, considering also the delay in publications, to the 2011 Tohoku earthquake and tsunami events and aftermath (Chian et al., 2019).
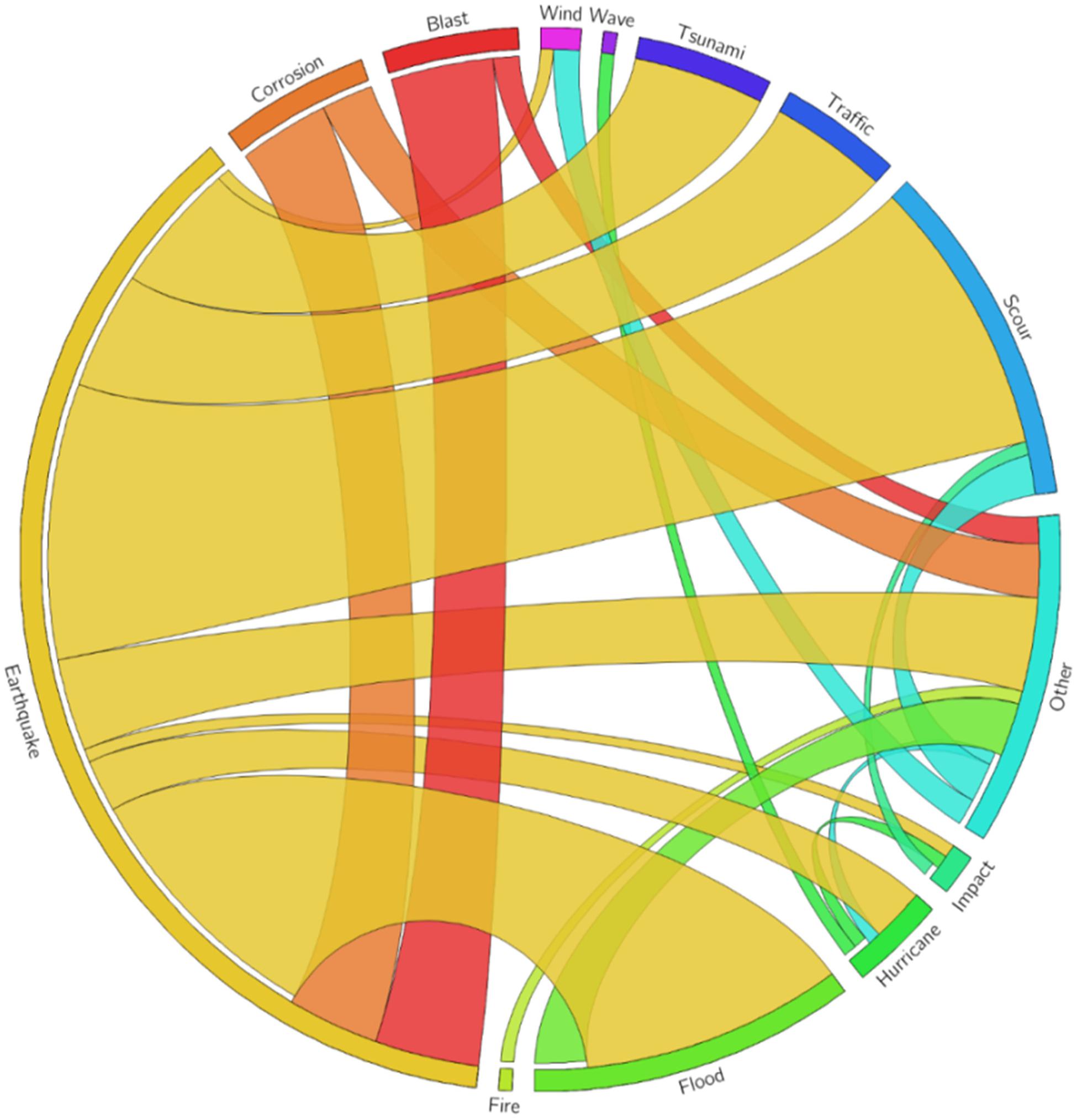
An additional analysis focuses on the hazards that have been researched. Excluding 46 more documents that focus either on literature review or general multi-hazard methodology, an effort has been made to identify principal hazards researched, as well as hazard chains (pairs of hazards). These are depicted in the chord diagram of Figure 4, which suggests that earthquake hazard has been the dominant research issue in a multi-hazard environment (71 cases out of the 108), followed by blast (10) and corrosion (10). Principal hazard chains with earthquake in literature are scour (21) and flooding (19): in the first case (scour), the count includes those cases that focus on scour independently from the cause (Pizarro et al., 2020), while in the latter (flooding), the count includes often flooding-induced scour.
A second literature analysis focuses on qualitative aspects of multi-hazard research for bridges, concentrating mostly on peer-reviewed journal papers, including documents from 2020.
Multi-hazard analysis and design methods for bridges have been studied under different perspectives and focusing on different aspects: risk analysis (Decò and Frangopol, 2011; Andriæ and Lu, 2016), influence of aging parameters (Padgett et al., 2010; Zhong et al., 2012; Capacci and Biondini, 2020), bridge design (Lee, 2010), bridge pier structural stability (Fioklou and Alipour, 2019), and intervention strategies (Nikellis and Sett, 2020). Research includes aspects focusing on the concatenated actions of surge and wave (Ataei et al., 2010); earthquake and hurricane (Kameshwar and Padgett, 2014); earthquakes and extreme wind (Martin et al., 2019); earthquake and scouring (Wang et al., 2014); earthquake and flood (Gehl and D’Ayala, 2016; Yilmaz et al., 2018); earthquake, tsunami, and corrosion (Akiyama et al., 2020); and earthquake and scouring (Prasad and Banerjee, 2013; Markogiannaki, 2019; Pizarro and Tubaldi, 2019), also in a infrastructural resilience perspective (Argyroudis et al., 2020), scouring and impact (Kameshwar and Padgett, 2018) and earthquake and blast (Fujikura and Bruneau, 2012).
Table 1 provides a snapshot and a timeline of principal research, including the hazards they address, the principal methods used, and the indication (last column) of which key issue they contributed to address referring to the list provided in the introduction of this paper.
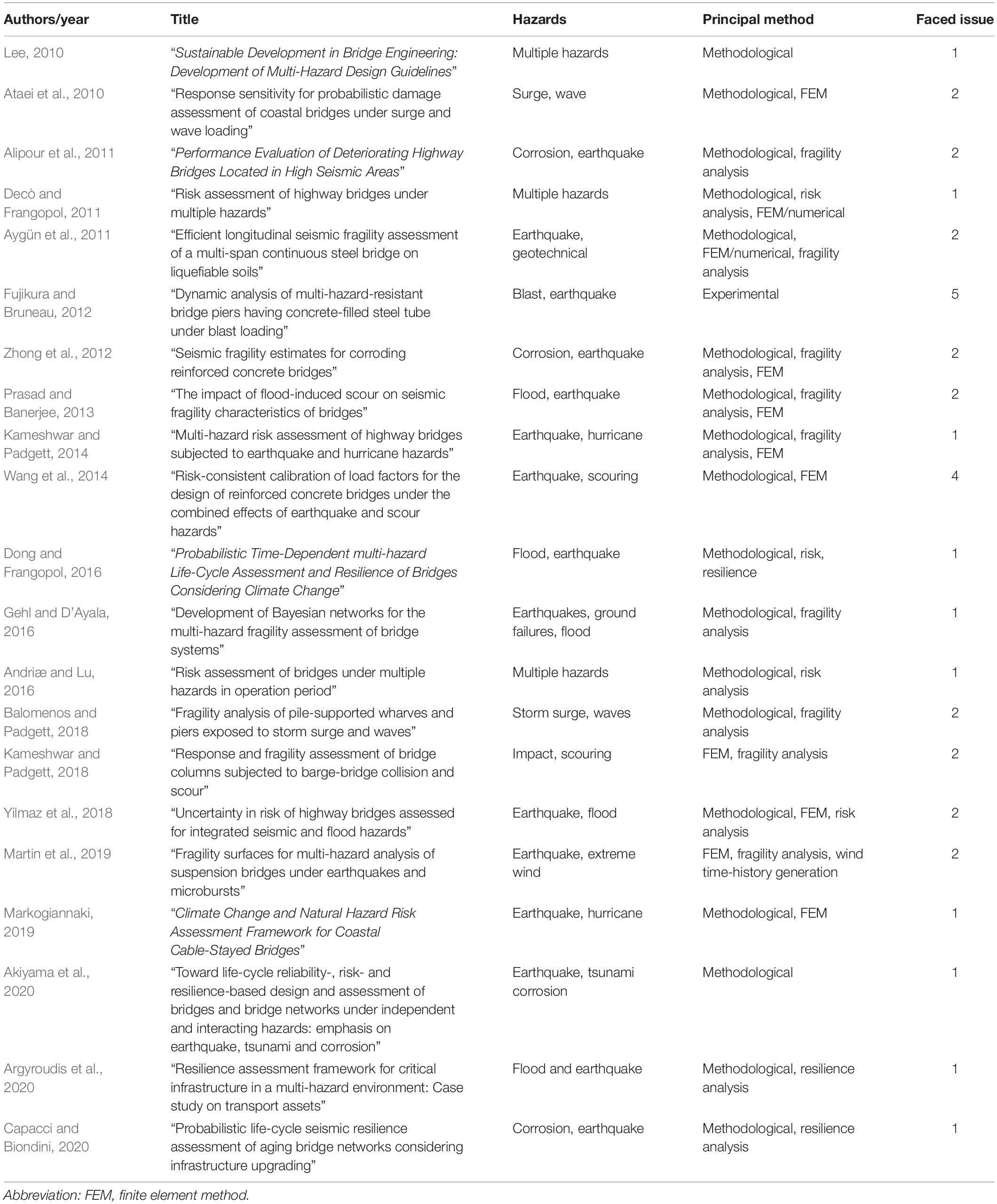
Table 1. Principal multi-hazard research timeline on bridges since 2010 (last column: 1 = unified framework; 2 = hazards interaction; 3 = probabilistic tails; 4 = risk consistency; 5 = conflicting design strategies).
As can be seen, research has focused on several hazards, using a variety of methods and providing in most cases case studies to support them. Much of the research is on the concatenated effect of multiple hazards, focusing on modeling aspects and in particular the creation of fragility curves and surfaces.
Even though the problems of a vehicle impacting a bridge (see, for example, Auyeung et al., 2019) and fire loading on bridges (see, for example, Zhu et al., 2020) have been thoroughly studied in literature individually, there is lack of research on the concurrent problem of fire after impact. The next paragraph focuses on the multi-hazard assessment of a highway viaduct under the combined effect of impact and fire.
Numerical Analyses for the Assessment of a Highway Viaduct Under Hazard Chains
In this section, an example of hazard chain analysis is presented in order to outline some aspects related with the hazard chain scenario analysis treated as LP-HC event (point B in the introduction of the paper).
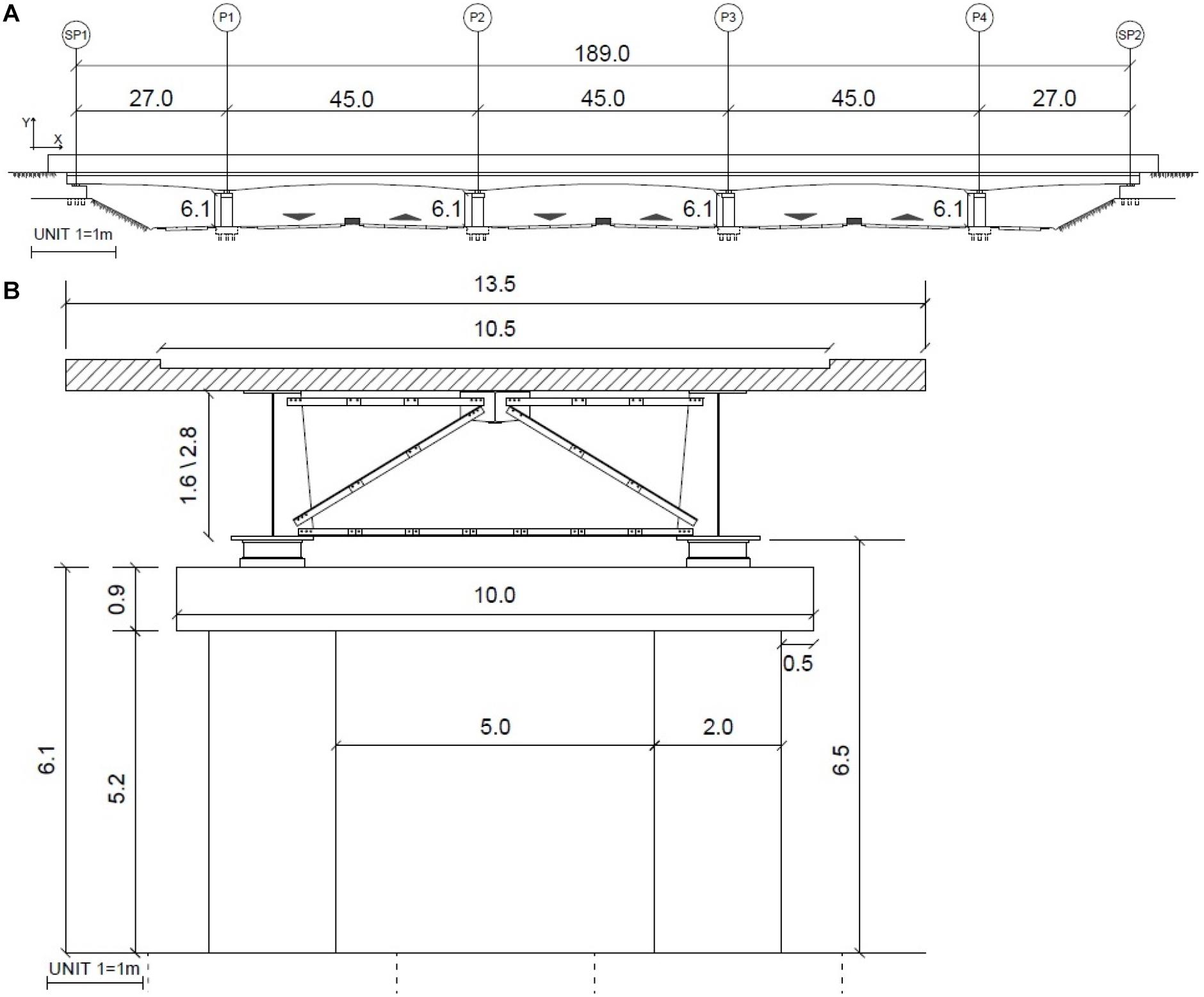
The case study viaduct consists in a multi-span continuous beam deck developed over five spans with individual lengths between 27 and 45 m (Figure 5A), the total length is 189 m. The deck comprises two principal steel beam girders with a variable section, a composite slab, and a horizontal steel bracing system. The reinforced concrete slab is 13.50 m wide, including 10.50 m driveways with a thickness of 0.35 m and 3.00-m sidewalks with a thickness of 0.50 m. The viaduct cross section is reinforced in correspondence to the piers with a 2.8-m-high deck transversal I-girder (Figure 5B).
A transversal bracing system is developed along the viaduct axis. The substructure is composed of two reinforced hollow concrete piers with a 2-m external diameter and 1-m internal diameter in axis with the two main beam girders. The deck is simply supported on the piers by means of seismic isolators. The bridge is provided with back-wall type abutments having an appropriate expansion joint for the deck in the longitudinal direction. Both the abutments and the piers are based on pile foundations.
Multilevel Finite Element Modeling of the Viaduct
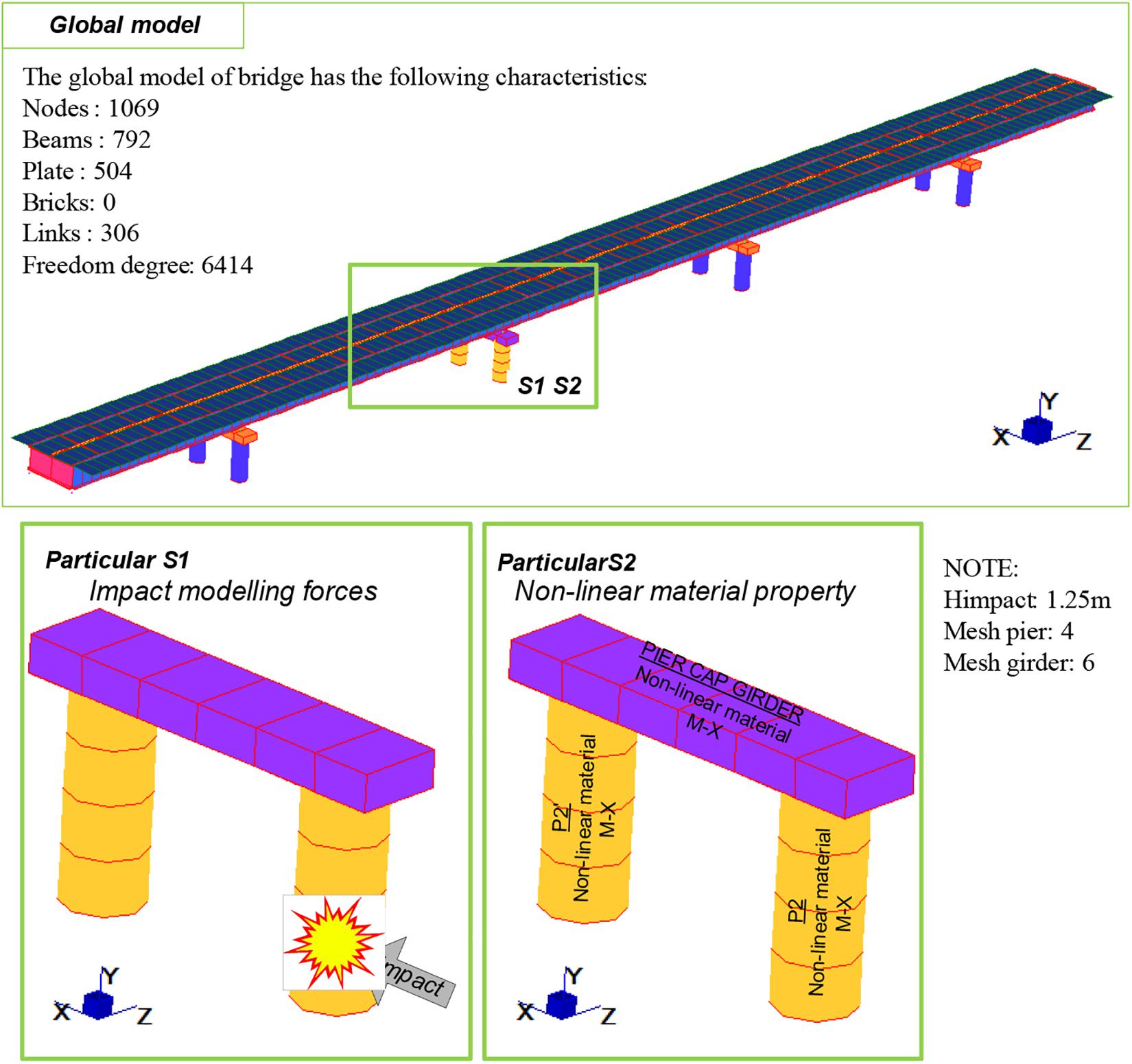
A suitable strategy to address the numerical modeling issues in multi-hazard non-linear analysis of bridges is the adoption of a multilevel modeling strategy (Petrini et al., 2010). For the modeling of the viaduct, the entire structural system (macrolevel) is hierarchically divided in substructures (mesolevel) and single structural elements and connections (microlevel). In the same way, the structural problem and the relevant aspects are hierarchically organized in several levels of detail, which can be individually dealt with, yet they are interconnected (Sgambi et al., 2012). This approach is particularly convenient is case of analysis of multi-hazard scenarios involving different parts of the structure, as, for example, the considered case of the impact (on a pier of the bridge) of a tank truck, with consequent fire acting mainly on the deck.
The macrolevel (global) model is necessary to evaluate the global dynamics of the structural system under the impact force and to extract the forces exchanged between the different structural parts, which will be used to calibrate the boundary conditions in the models at other scales. In this view, the macrolevel global model can be built by adopting simplified geometries/details, something that will be refined in the mesolevels and microlevels. Another operative aspect of the multilevel modeling regards the type of FEs used: beam elements are often used at the macrolevel, while plane and brick models are usually introduced at the mesolevels and microlevels, respectively, with the goal of increasing the abovementioned level of detail in describing the geometry and the results. In this study, the global model of the viaduct is developed by the commercial code Strand7®1, and it is shown in Figure 6.
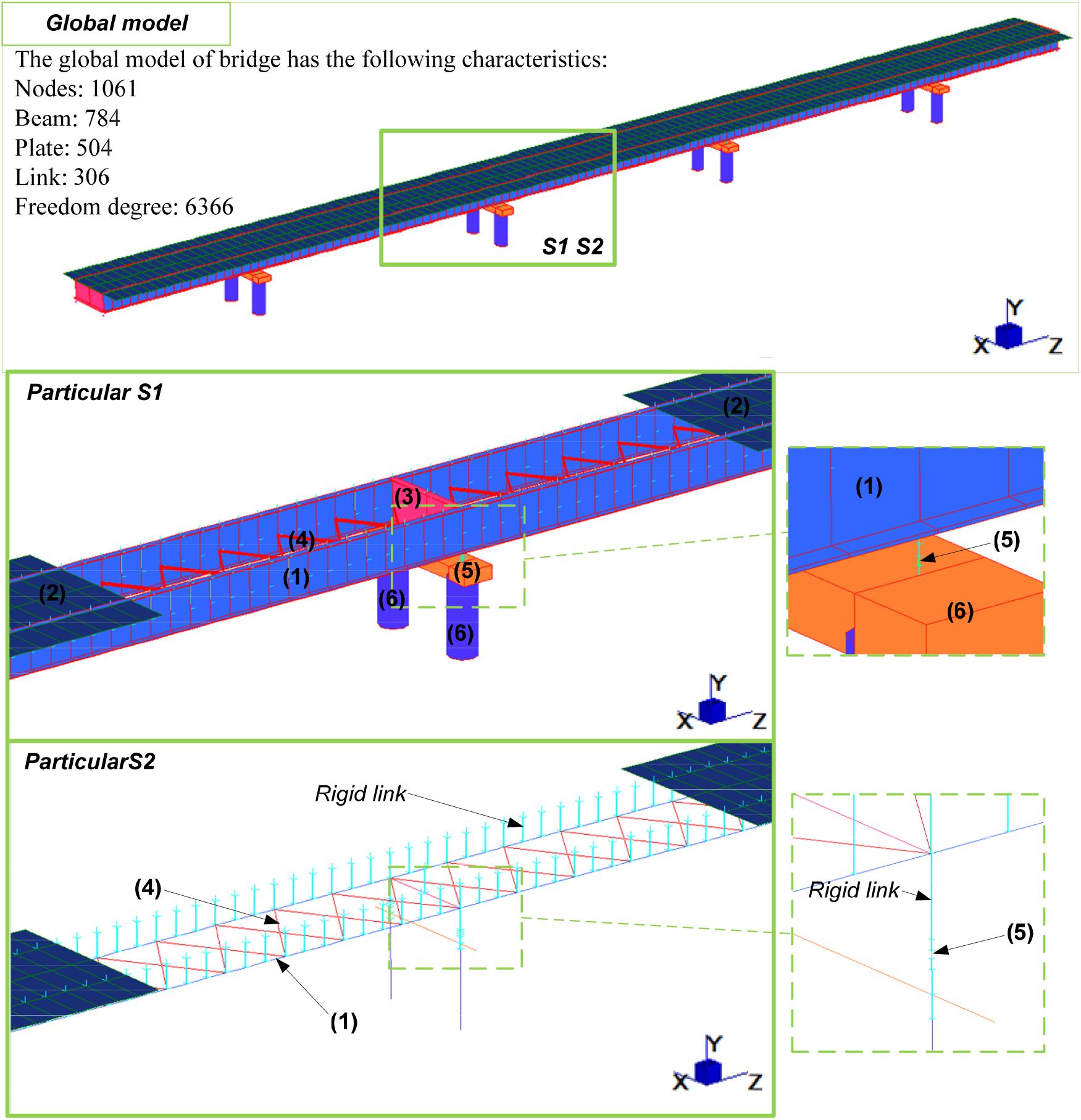
Figure 6. Global model of the viaduct: (1) main longitudinal girders; (2) concrete deck; (3) horizontal diaphragm; (4) horizontal bracing system; (5) Nelson headed shear connectors; (6) pier cap girder.
The two main girders with a variable section have been modeled with beam elements with a constant cross section height of 2.8 m. This is considered acceptable also because the first global mode of vibration is only translation and rotation in the horizontal plane, since the deck is supported by seismic isolators, and also since the first mode is not influenced by the vertical stiffness of the girder. The concrete slab is modeled with plate elements with thickness equal to 0.35 m. The slab is connected with the main girder through Nelson headed shear connectors, which are explicitly modeled as rigid links. The deck transversal girder, the horizontal diaphragms, and the horizontal bracing systems are modeled with beam elements. Likewise, the modeling of reinforced concrete piers and girders pier is done with beam elements, while the seismic isolators are modeled with spring/damper elements that allow to set the axial stiffness, lateral stiffness, and viscous damping. A non-linear moment–curvature relationship has been assigned to the piers and to the pier cap girder in the region of the impact, while isolators have been modeled as linear with a secant stiffness. Non-linear time domain analyses are carried out to simulate the impact scenario by the global model.
For the sake of simplicity, the foundation is not modeled, and the piers are fully restrained at the bottom. Abutments are not explicitly modeled, but the final nodes of the deck are simply supported and/or pinned depending on the degree of freedom (DOF) direction.
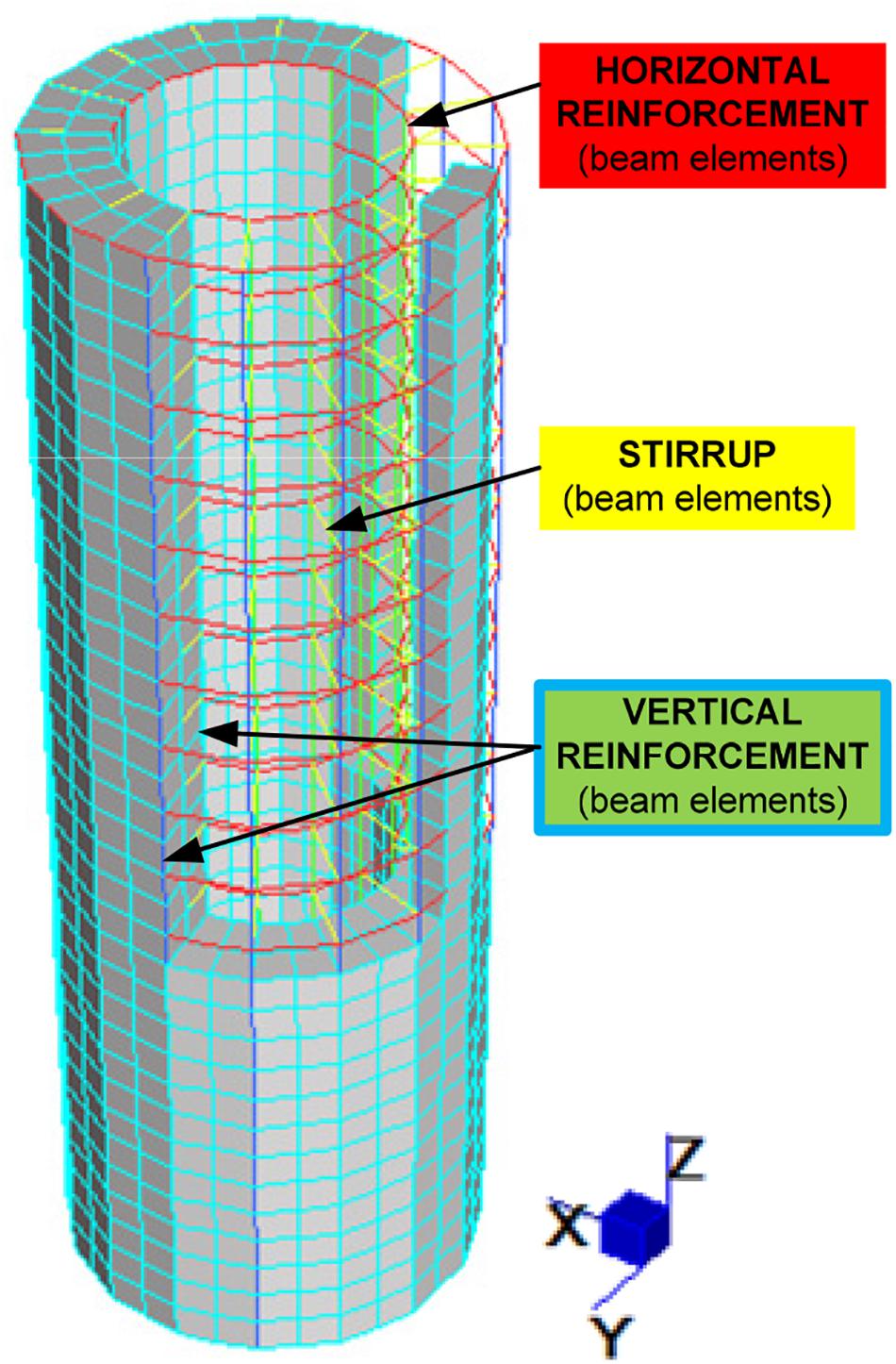
Nevertheless, this simplified global model does not account for some effects occurring in the pier (i.e., cross-sectional ovalization, cracking, and loss of concrete portions during the impact phases). To study in detail these effects during the impact analysis, a microlevel model of the pier subjected to the impact has been developed using brick and beam elements (Figure 7). The longitudinal and transverse reinforcement bars have been explicitly modeled using beam elements, connected at nodes with the brick elements used for modeling the concrete and constrained to have the same translational response. A birth and death response technique has been implemented for concrete in tension: when the stress in a concrete brick element is larger than the tensional stress, it is eliminated from the model for the evaluation of the response, while an axial stress bilinear relationship has been assigned to the reinforcements in order to model their plastic behavior. The DOFs of the nodes have been fully restrained at the bottom cross section, while rotations were constrained at the top, where horizontal x and y axis translational stiffness is assigned to the nodes for modeling the reactions from the isolation bearings. Finally, z translation is allowed at the top, where a vertical force representing the weight of the deck is applied. The impact scenario is analyzed by mean of a force-controlled multistep non-linear static analysis in order to follow the evolution of the damage in the pier at increased lateral forces and deformations.
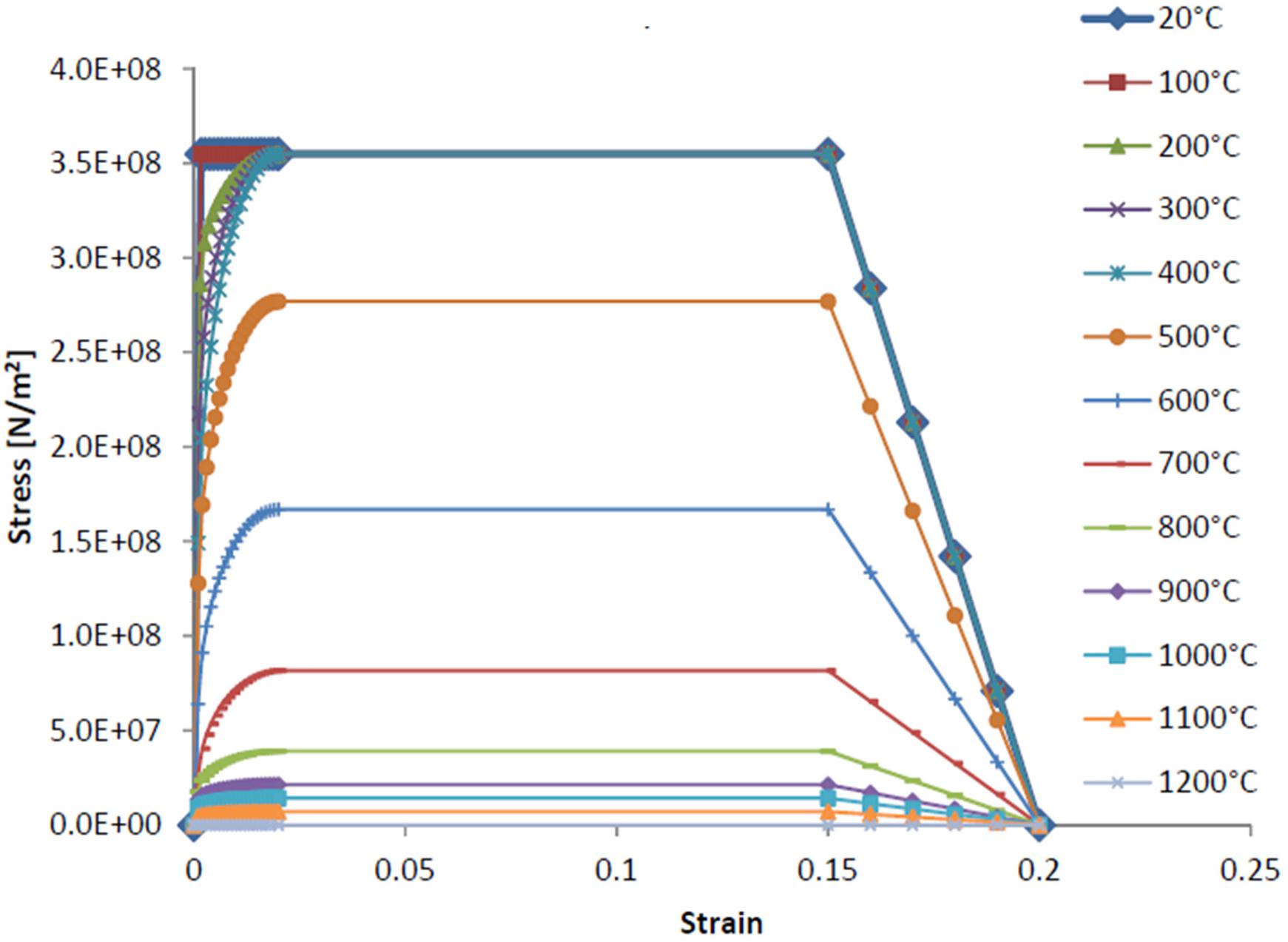
A mesolevel structural model developed in the Abaqus® commercial code2 has been also built for analyzing the detailed response to the fire scenario occurring in consequence of the impact of the tank truck to the pier. Figure 8 provides an overview of the FEM model. Following also what was discussed in literature (Payá-Zaforteza and Garlock, 2012; Kodur et al., 2013), and coherent with the vulnerability indexes assigned in Figure 2 to the various bridge components with respect to the fire hazard, it can be said that the most vulnerable part of the bridge is the deck, i.e., the steel main girders collaborating with the concrete slab. Thus, for the fire analysis, the viaduct model is limited to this part of the bridge. All parts of the bridge are modeled using shell elements, taking into account the real variability of the cross-sectional height of the steel main girder along the bridge’s longitudinal axis. The supports of the bridge deck are modeled by linear springs in horizontal directions, simulating the secant stiffness of the bearings, while the nodes at the supports are restrained to the vertical translation and rotations. In case the pier is considered as collapsed after the impact damage, the restrains and springs at the support are removed. Non-linear quasi static dynamic analyses are carried out in the Abaqus FEM, with the steel having the non-linear behavior degrading with the temperature shown in Figure 9 (steel class fyk = 355 MPa), and concrete of the slab is modeled by a Drucker–Prager constitutive law.
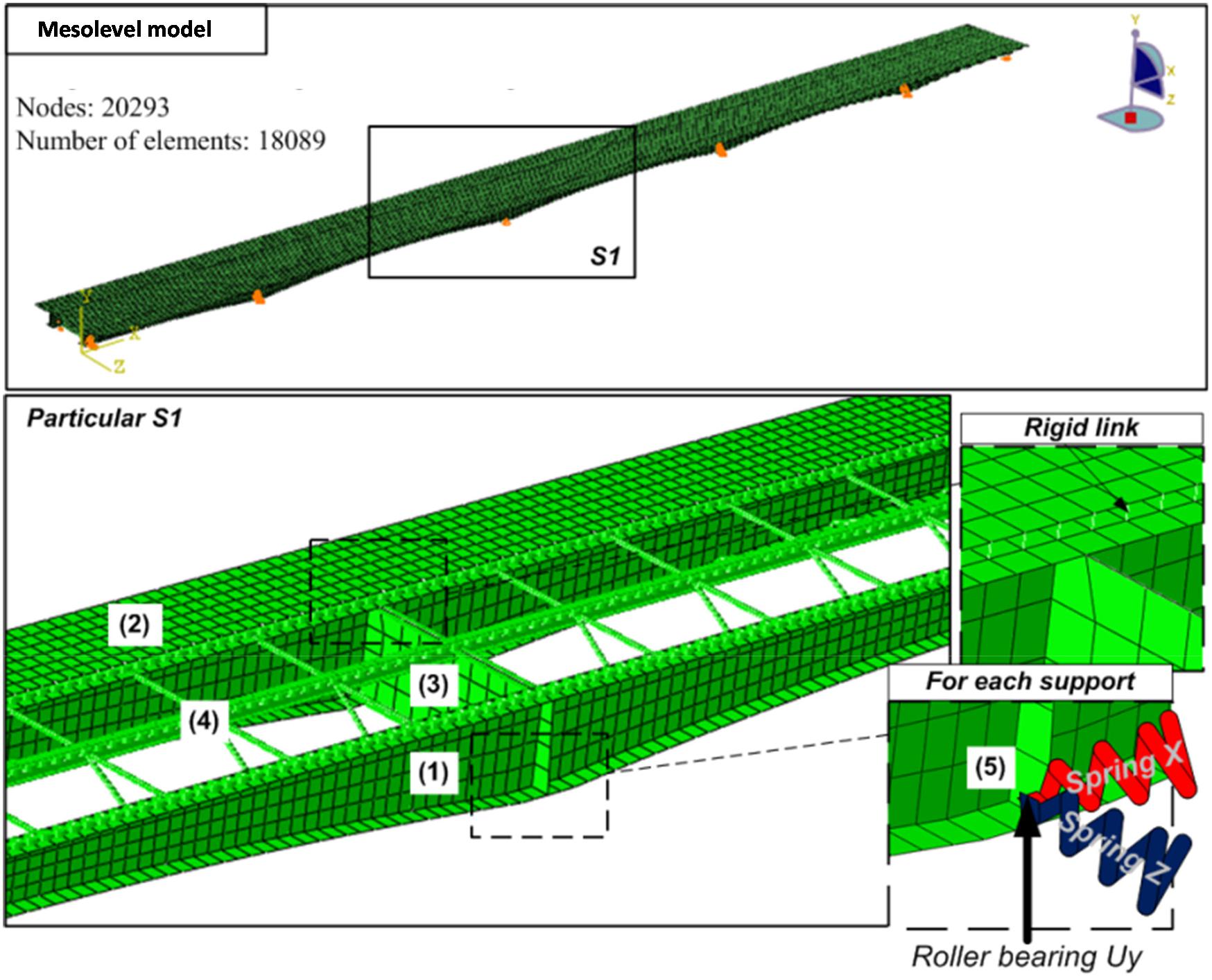
Figure 8. Bridge superstructure finite element method (FEM) model: (1) main longitudinal girders; (2) concrete deck; (3) horizontal diaphragm; (4) horizontal bracing system; (5) boundary conditions at the supports.
The three-level modeling strategy used in hazard chain scenario is summarized in Table 2 where, together with the “modeled parts” and the “FE used” for each model, the “type (and goal) of the analyses carried out” with each model level is also specified. Furthermore, the “analysis order” column in the table specifies the order of the analyses when run in sequence for assessing the response of the bridge in a hazard chain scenario. To this regard, while the macrolevel and mesolevel models are used to assess the bridge response (demand) under impact and fire scenarios, respectively, the microlevel model is used for evaluating the capacity of the pier under truck impact force scenario. As explained in the following section, this capacity is used to calibrate the stiffness of the spring to be set in the mesolevel model. Following that, the order of the analyses carried out is as follows: (1) macrolevel; (2) microlevel, and (3) mesolevel analyses.
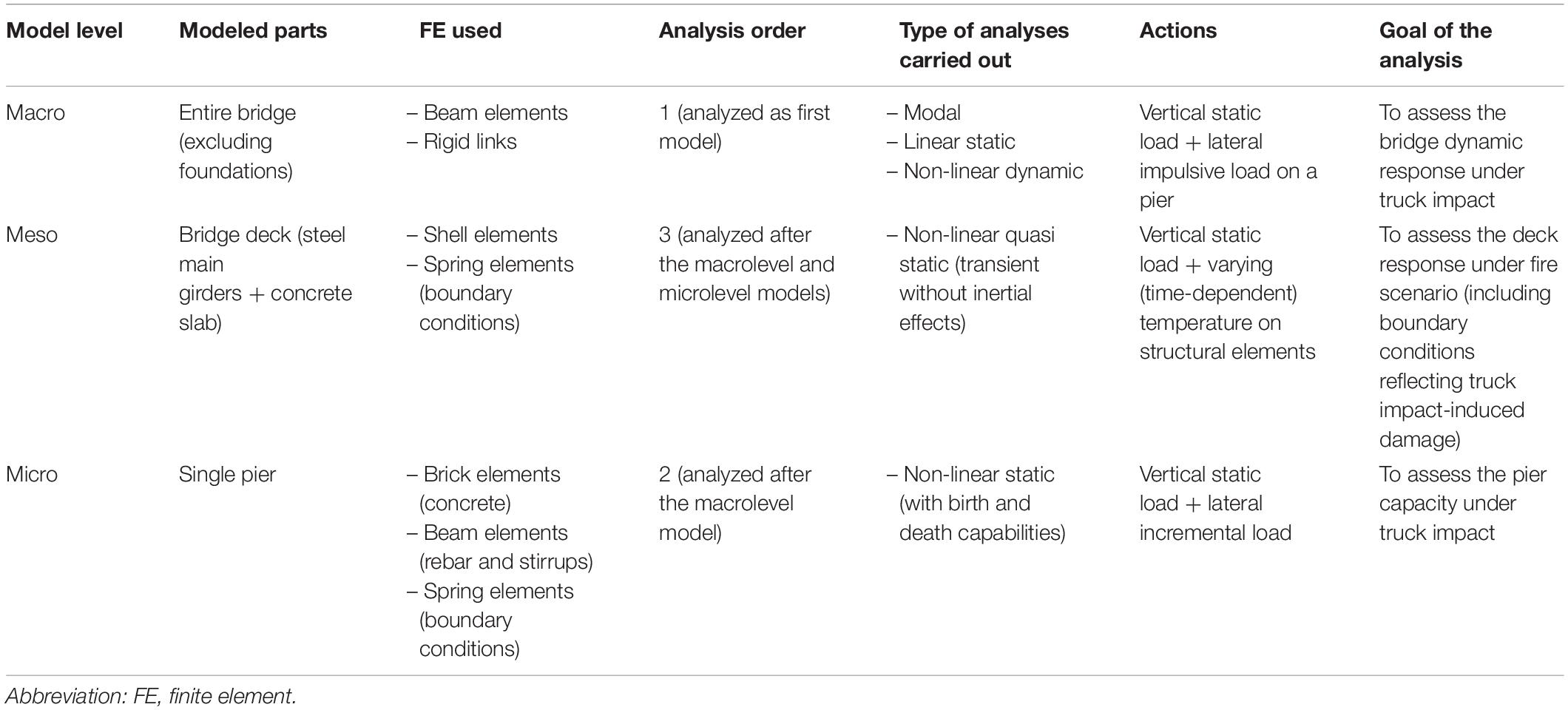
Table 2. Overview of the characteristics of the models and of the analyses in the adopted three-level strategy.
Impact Scenario
A first scenario considers the potential collision of a tank truck on one of the piers of the viaduct. For this scenario, non-linear FEM transient dynamic analyses are carried out using the global model.
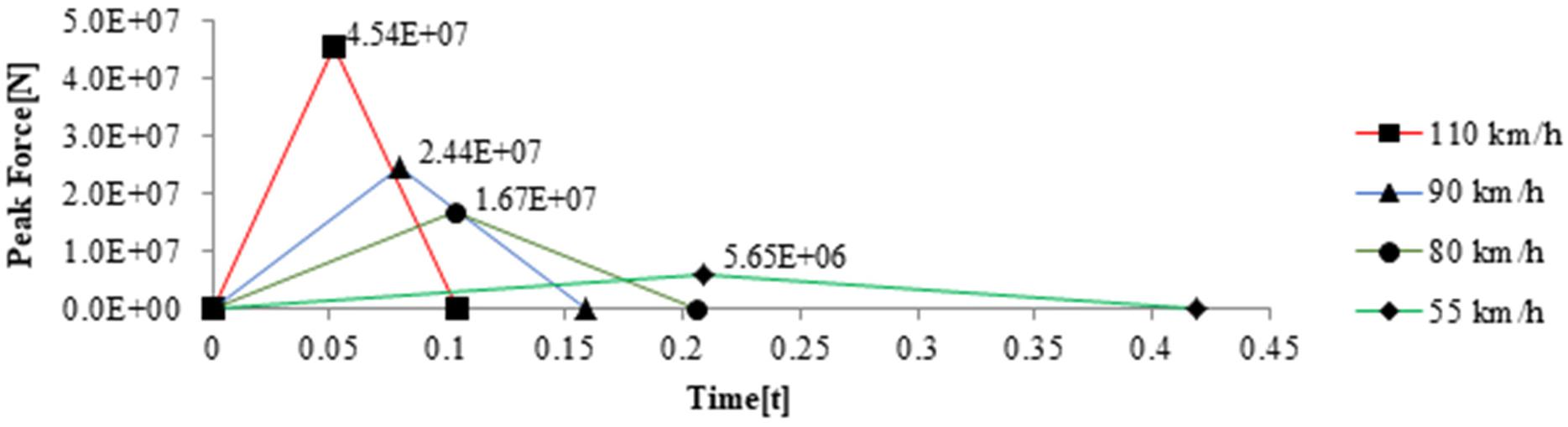
The impact action has been modeled as an impulsive force punctually applied on the bridge pier at a height H = 1.25 m from the base of the carriageway. Even though the maximum speed for a heavy truck on the most European highways is limited to 80 km/h, four different vehicle velocities are considered in this study: 110, 90, 80, and 55 km/h.
Figure 10 shows the bridge model for the vehicle impact scenario.
The time-history impact force is shown in Figure 11, considering that:
– The vehicle mass is m = 40 t;
– The diameter of the cross section is D = 2 m.
All the cases where the curvature registered during the dynamic analysis in the impacted pier exceeds the ultimate curvature, and it is assumed that the element is collapsed. The pier collapse causes a change to the structural configuration of the entire viaduct, since the latter lacks the support from the substructure. Following an analysis based on the moment–curvature relationship monitored at the impacted pier, Table 3 provides an overview of the four different cases.
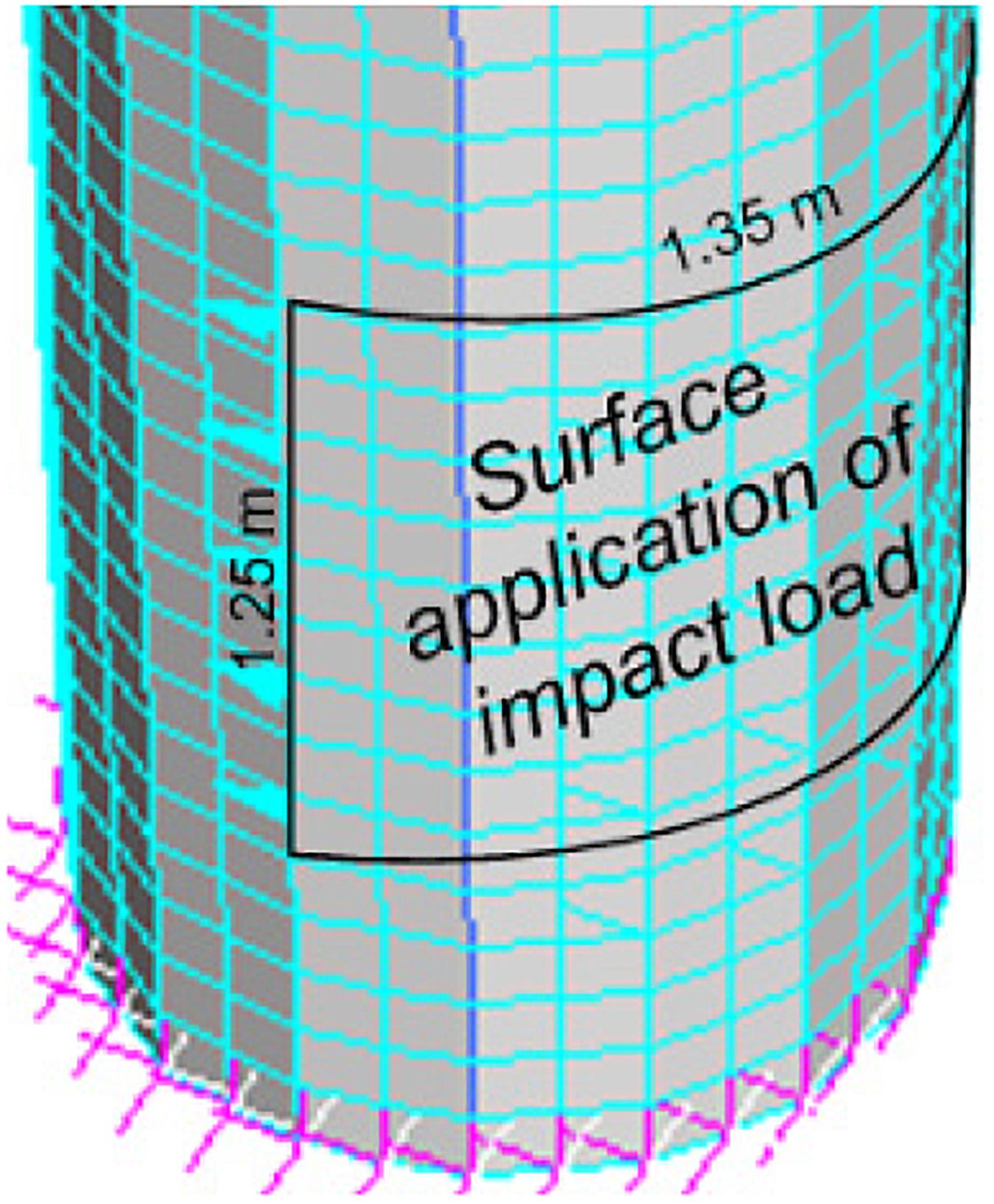
As already stated, the impact scenario has been analyzed also by the above-introduced microlevel model of the pier. The final goal of the microlevel analysis is to calculate the collapse load of the pier, compare it the result obtained with the global model, and eventually refine the moment–curvature diagram assigned to the piers in the global model. In the microlevel model, the impact is modeled by a force that is uniformly distributed and applied on the external exposed surface of the hollow section. The application area of load is A = 1.69 m2, which corresponds to the contact surface between the tank truck and the pier (Figure 12).
The resultant of the impact force at the initial step is F0 = 1.3634 107 N, corresponding to the activation of the plastic hinge in the previously analyzed global model. Starting from F0, the force increases using a multistep non-linear analysis until the collapse of pier. The dead load exerted to the pier by the deck is applied as initial condition of the analysis. As already said, a multistep non-linear analysis is conducted until the applied force reaches the maximum value of the pertinent impact scenario.
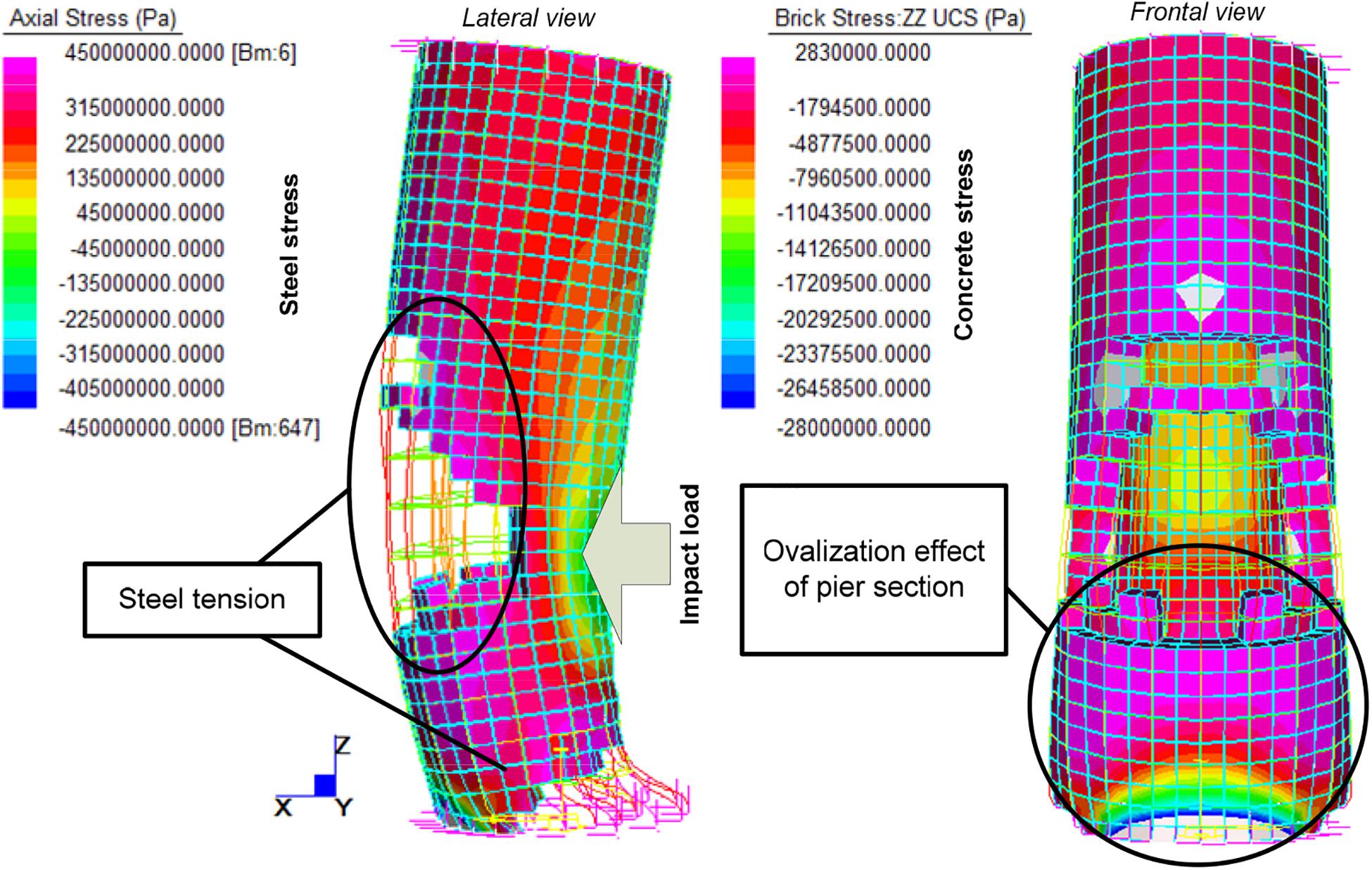
Figure 13 shows the final model in its deformed configuration (amplified by a factor of 2). The collapse load for the pier is FU = 1.72⋅107 N, which confirms the results obtained by the global model, where all the impact intensities that do not reach this value are classified as not leading to the collapse of the pier. Thus, the collapse occurs only in the cases where the impact speed is higher than 80 km/h.
Focusing on the results of the microlevel model, it can be seen that the horizontal impact force generates zones of tension and compression in the steel and concrete parts. By considering the behavior of concrete only as elastic, it is not possible to account for its actual tensile strength. For this reason, as already stated, the concrete elements that exceed the tension limit (set here equal to 2.8 MPa) are eliminated from the model. The process is iterative and finishes with a final model where the parts in traction are minimized.
The results of the analysis show that the vertical most-stressed bars are those at the base of the pier and on the opposite side with respect to the impact. At the pier base, there are numerous yielding bars in tension and compression. The shear reinforcement is the most stressed at the pier bottom and in the section area of ovalization. During the last step, the concrete at the base of the pier exceeds the limit of resistance in compression.
After-Impact Fire Chained Scenarios
This section focuses on fire scenarios developed as a consequence of the truck impacting the bridge pier. The analysis is carried out by the mesolevel model described above, and it consists in a quasi static non-linear analysis in a large displacement regime.
The fire scenario analysis consists in the application of the temperature–time history to the parts of the bridge involved in the fire, while the vertical loads are maintained as constant. The boundary conditions (stiffness of the springs supporting the deck at the location of the column, which is involved in the truck impact) are calibrated to represent the real residual stiffness of the damaged pier and the vertical displacements of the deck before the fire. Such stiffness is linear and independent from the temperature due to the large thermal inertia of the concrete pier with respect to the steel deck.
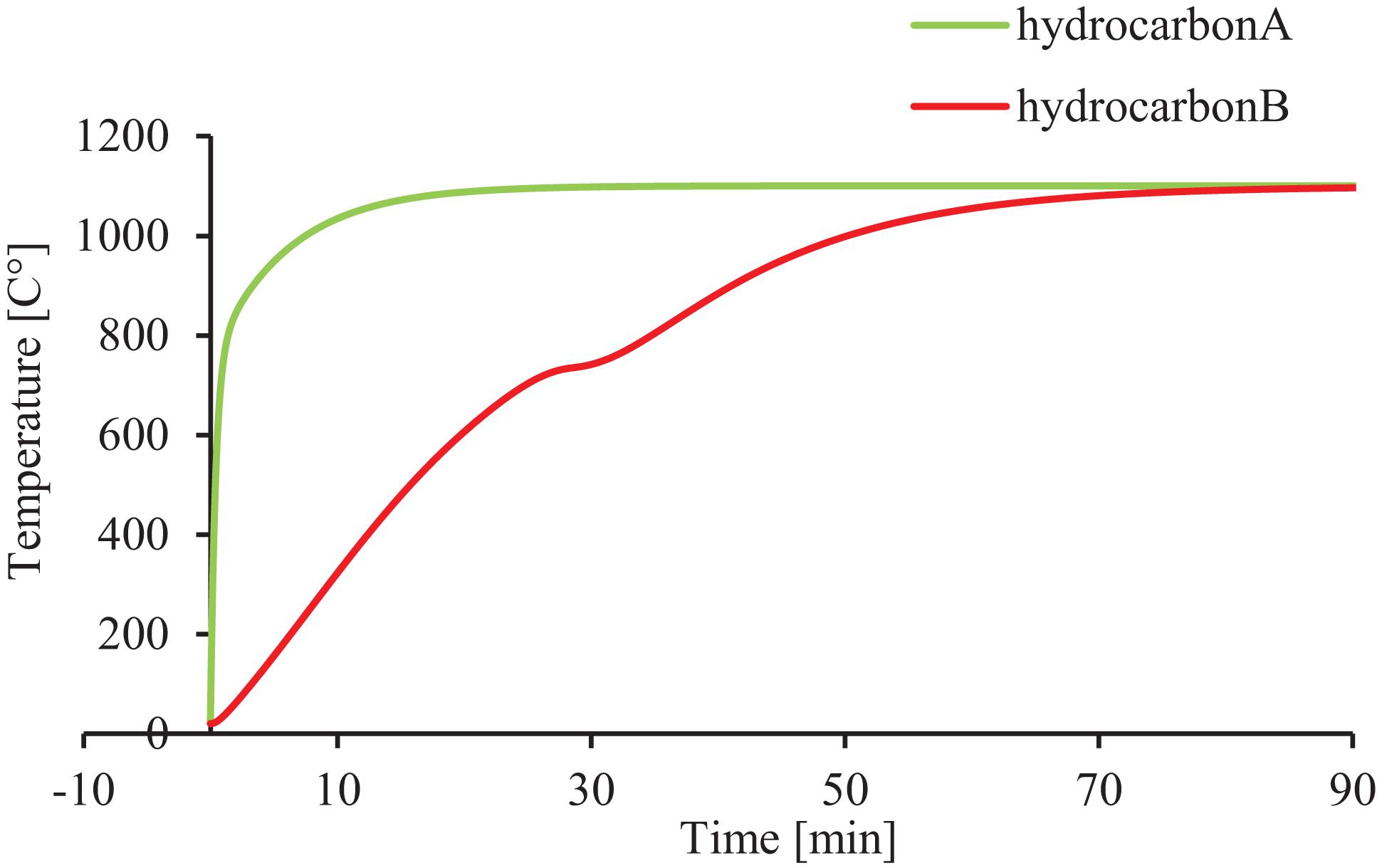
One of the critical aspects in fire response structural analyses is the model of the temperature force applied to the structural elements involved by fire. In this study, the hydrocarbon curve is applied to the steel elements of the structures (Figure 14).
In Figure 14, “hydrocarbon A” refers to the hydrocarbon curve, while “hydrocarbon B” refers to the hydrocarbon curve with the effect of the temperature distribution in the steel members. It is straightforward to observe that the temperature development within the section (thermal response of the steel members) proceeds more slowly with respect to the hydrocarbon curve.
Some additional assumptions are made:
– The effect of the heat on the concrete part of the structure (concrete slab and piers) is not considered. This assumption can be assumed as valid since concrete has a much higher thermal inertia than steel.
– The temperature–time curve that identifies the fire load is uniformly applied on the entire height of the section.
– The heat source is extinguished after t = 90 min from the beginning of fire ignition.
– The propagation of heat and flames depends also on the environmental conditions (wind and environmental temperature) and on the actual propagation of the hydrocarbon oil following the truck impact. This part is not treated in the model.
– The seismic isolators in the region under fire lose the lateral stiffness during the fire scenario as a consequence of the heat. For this reason, it is decided to attribute a lateral stiffness of zero value at the temperature of 900°C.
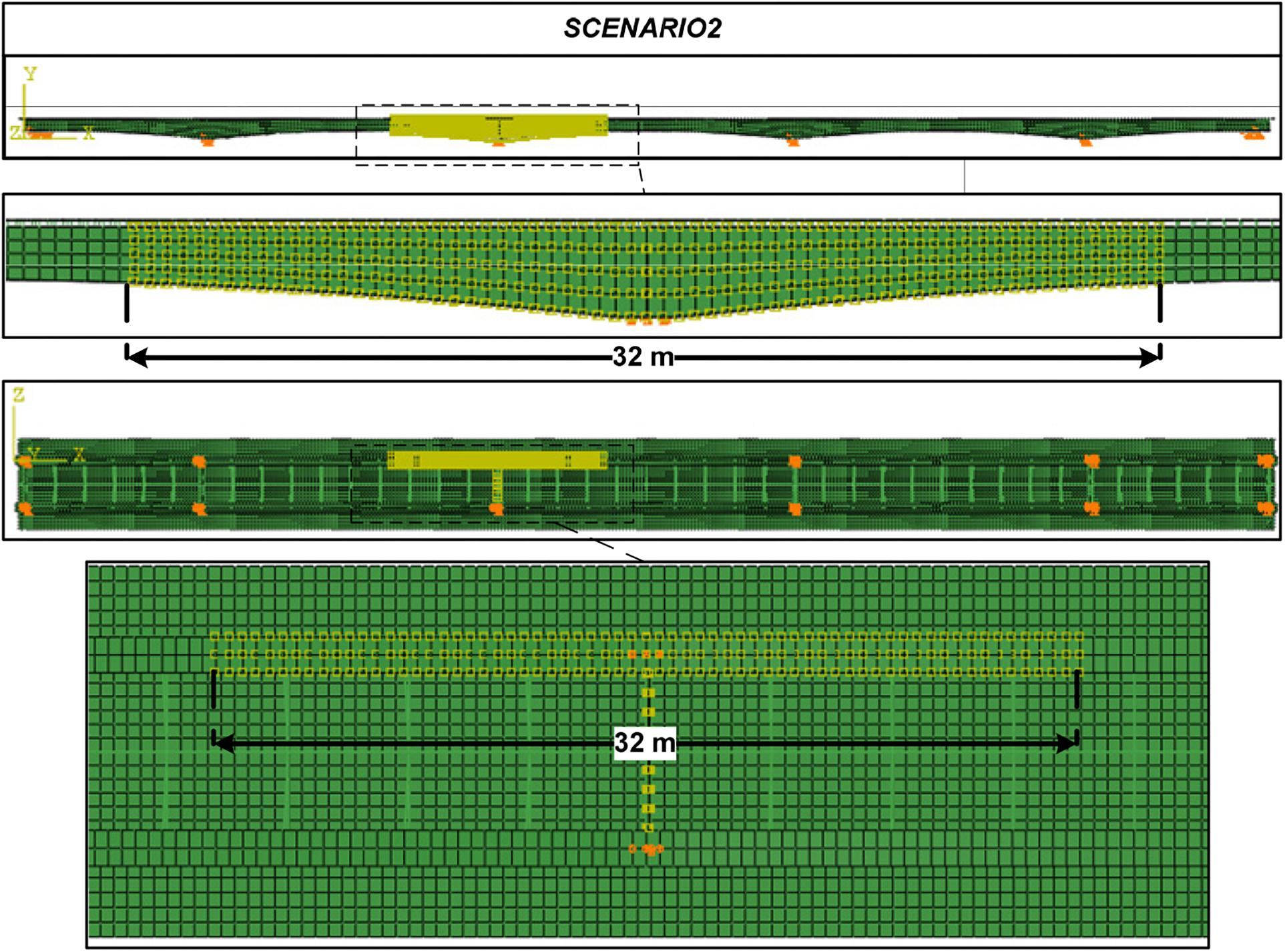
The fire load is not symmetrical with respect to the bridge axis on the two main girders, because the damage is localized near the pier involved in the impact (Figure 15).
Two sub-cases are considered:
– The fire load is applied to the substructure with the pier damaged from the impact but not collapsed.
– The fire load is applied to the substructure after the vehicle impact has caused the pier to collapse.
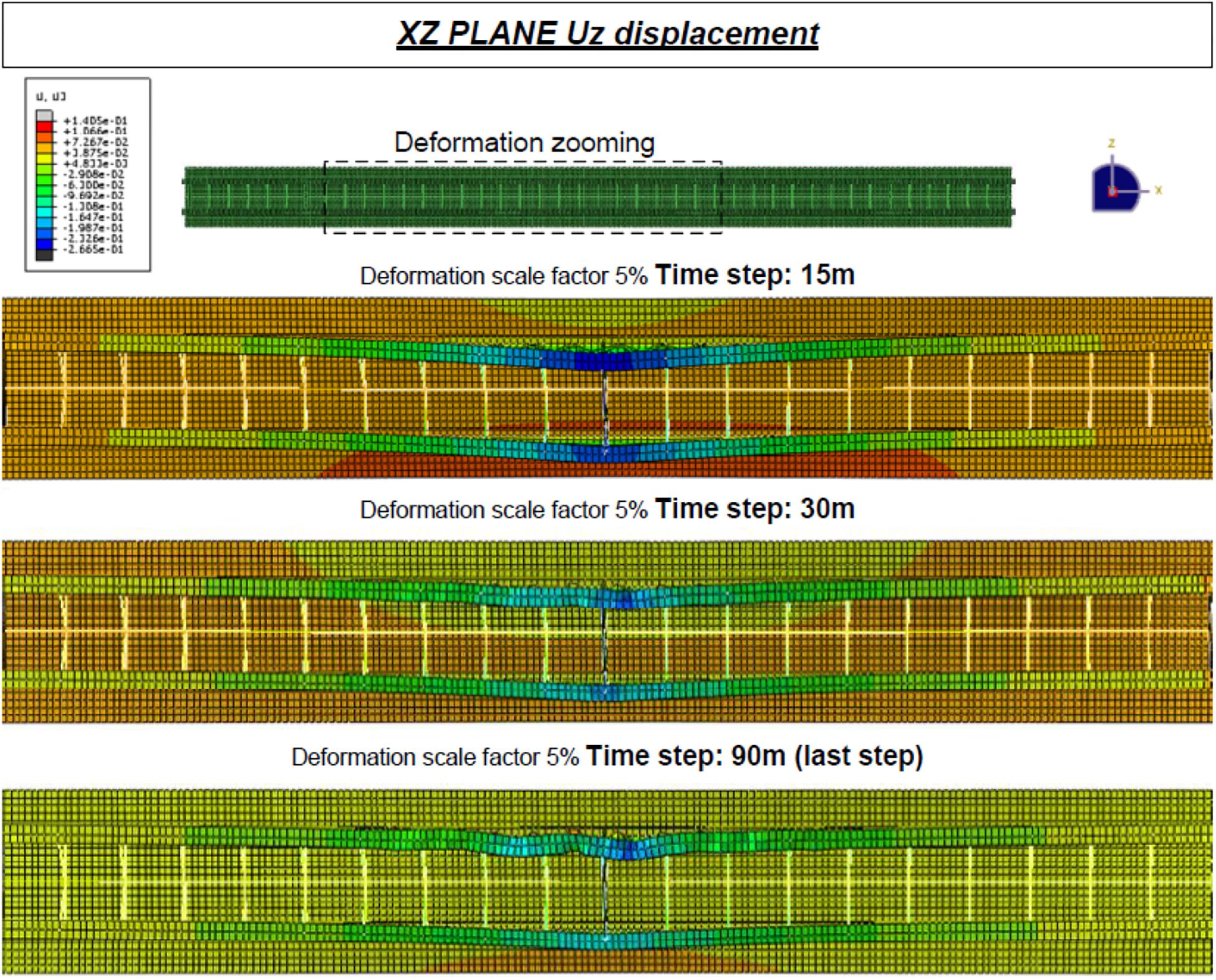
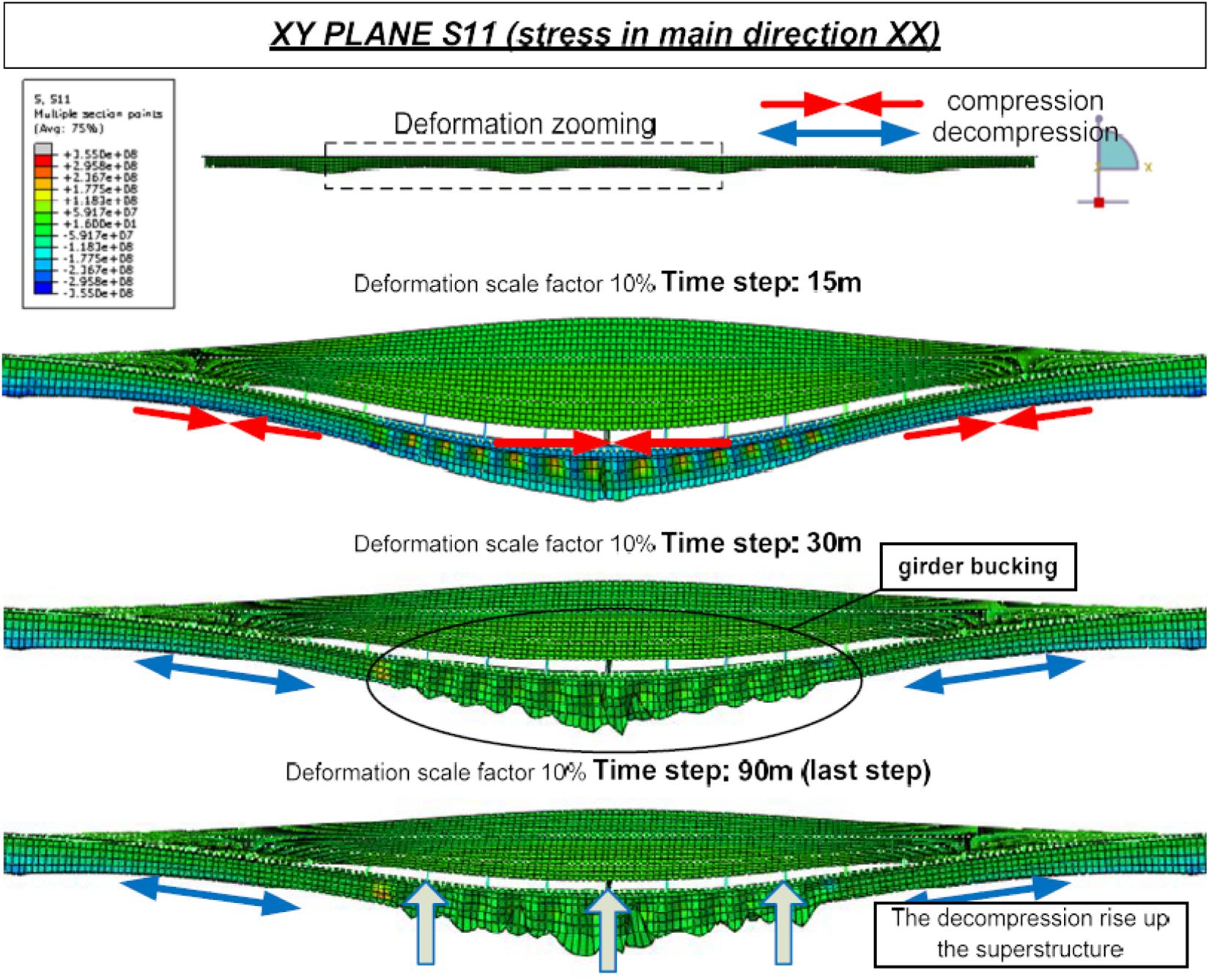
Figures 16, 17 show a set of typical results obtained from the analyses at different time steps for the second sub-case, in which the fire load is applied to the deck after an impact that leads to the collapse of the pier. It is shown how local buckling phenomena occur in the main steel girder under fire and how these buckling effects propagate along all the regions under fire. Figure 16 shows that the buckling-induced lateral displacement of the girder is restrained only by the horizontal diaphragm, which is present on the top of the pier at the impact/fire location. When the pier under the fire-affected region is lost due to the previous impact, a complex structural behavior occurs in the bridge (Figure 17). Up to the time step of 15 min, the vertical displacements of the bottom girder flange continue to increase due to the elongation of the heated portion, which is contrasted by the compression occurring in the parts outside the fire area. When the girder starts to experiment local buckling in the fire-subjected area, a decompression of the two lateral parts outside the fire area occurs, leading to the superstructure rising, an effect that continues until the end of the analysis due to the progressive softening of the steel portion under fire. It is important to observe that this particular behavior of the structure does not occur when the pier is present (also if damaged by the impact), as the pier is able to contrast the vertical displacements both in the increasing phase (something that is less evident) and in the rising phase (that completely disappears from the resulting behavior). This is important because, depending on the intensity, the effect of the impact is able to change the physical behavior of the bridge under the chained fire hazard, clearly highlighting that this kind of hazard chain interaction cannot be treated by separate analyses of the two hazards.
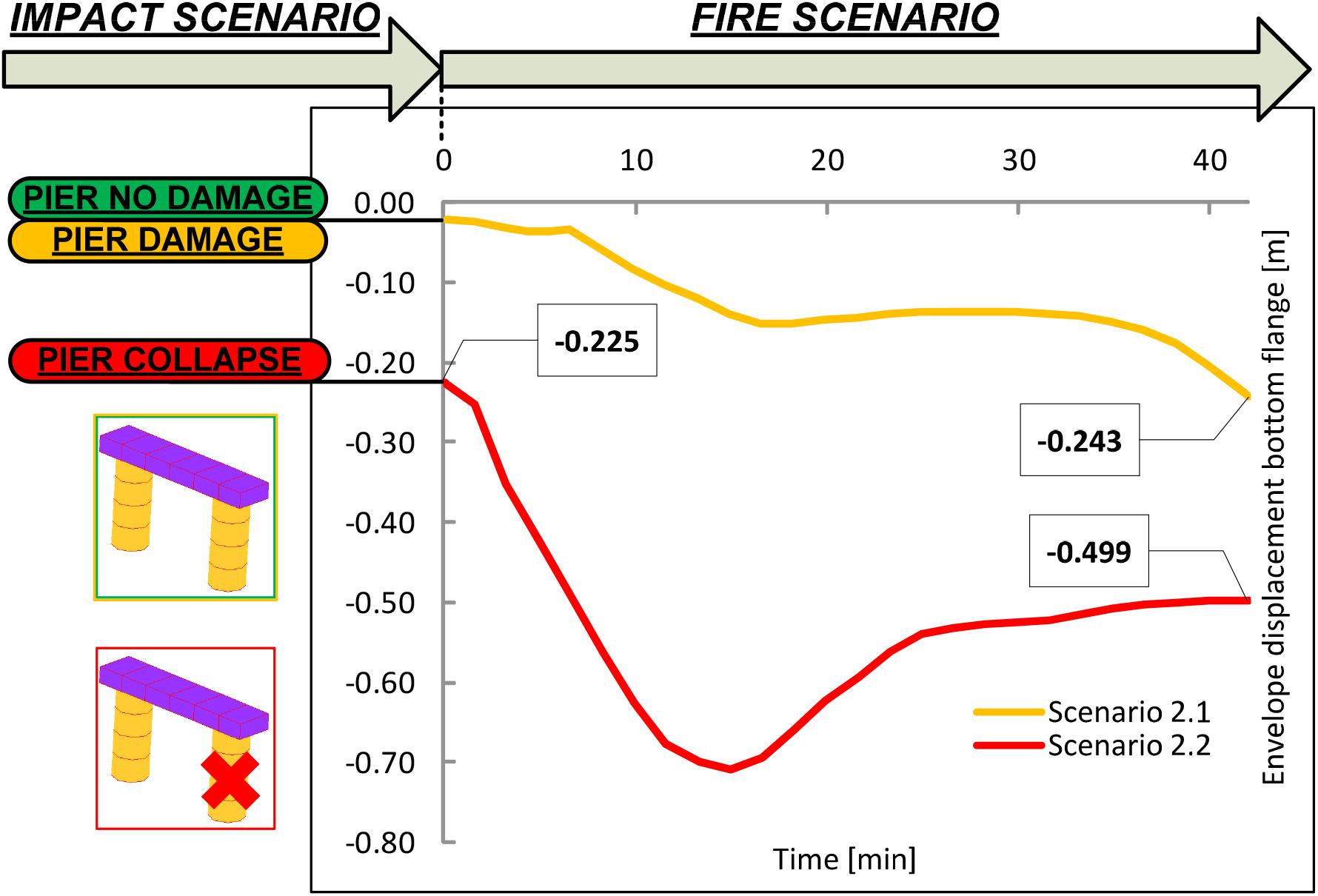
As a final assessment for the multi-hazard scenario involving fire after impact, the vertical displacement of the bottom flange of the main girder can be considered a metric for the estimation of the damage. Figure 18 shows the two abovementioned scenarios where the fire is applied after the impact-induced pier damage or pier collapse. As can be seen, the damage is already substantial for the structure following the pier collapse (Scenario 2.2, red line) with an initial vertical displacement of 0.225 m. In addition to a vertical displacement (up to 0.5 m), there is also a strong plasticization caused by the decrease of the mechanical performance in the structural parts susceptible to fire, at the extent of the steel girder of 32 m. Furthermore, according to the assumptions, the heat source also causes loss of functionality to the seismic isolation system. The high temperatures during the fire scenario can lead to the collapse of parts of the structure affected by the heat flow.
Conclusion
After having introduced and analyzed research issues that need to be addressed in order to move toward true multi-hazard assessment of bridges and after providing a concise state of the art of the research in the topic, this paper focuses on specific issues related to the assessment of bridges under hazard chain scenarios.
The multi-hazard analysis of bridges under hazard chain is a complex issue that requires i) a robust and clear framework for classifying the different hazard chain interaction and the probabilistic occurrence of hazard chains, which can be treated as LP-HC events; ii) advanced tools and sophisticated numerical models for correctly analyzing the structural damaged state, which is expected to be severely affected especially in the hazard chain scenarios, due both to the typical intensity of the triggering hazard and to the combination of the effects of the two chained hazards.
To this end, this study proposes an effective strategy for dealing with multi-hazard analysis in bridges, including the identification of the vulnerability to single hazard and hazard chain events, and the establishment of a multiscale FE modeling strategy for capturing the abovementioned complex structural behavior.
The proposed strategy is applied to the assessment of the structural behavior of bridge under impact and fire chained hazards scenario. A three-level modeling strategy is put in place for the case study, and the damage under the hazard chain scenario is evaluated as a function of the intensity of the first hazard. The results obtained in the case study bridge highlight the importance of carrying out a multi-hazard analysis. In general, the results obtained from the analysis under fire load show a high vulnerability of bridges with the deck being the most vulnerable part. The results presented here are limited since many analyses have been omitted for the sake of brevity. However, the substructuring of the structural problem to account for the different steps of the multi-hazard analysis (i.e., first impact and then fire) is an important step for the truthful implementation and assessment of multi-hazard scenarios.
Data Availability Statement
The raw data supporting the conclusions of this article are available on request to the corresponding author, to any qualified researcher.
Author Contributions
FP and FB contributed to the conception and design of the study. KG and FP wrote the first draft of the manuscript. CR and FP performed the numerical analyses. All authors contributed to manuscript revision and read and approved the submitted version.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Parts of this study are derived from the Master Thesis “Multi-hazard analysis of a viaduct subjected to impact and fire” by Mr. Claudio Rossi, defended at the Sapienza University of Rome. The thesis was co-advised by two of the authors, together with Dr. Alessandro Palmeri (Loughborough University), who is acknowledged. The views expressed here are purely those of the authors and may not, under any circumstances, be regarded as an official position of the European Commission.
Footnotes
References
Akiyama, M., Frangopol, D. M., and Ishibashi, H. (2020). Toward life-cycle reliability-, risk- and resilience-based design and assessment of bridges and bridge networks under independent and interacting hazards: emphasis on earthquake, tsunami and corrosion. Struct. Infrastruct. Eng. 16, 26–50. doi: 10.1080/15732479.2019.1604770
Alipour, A., Shafei, B., and Shinozuka, M. (2011). Performance evaluation of deteriorating highway bridges located in high seismic areas. J. Bridge Eng. 16, 597–611. doi: 10.1061/(ASCE)BE.1943-5592.0000197
Andriæ, J. M., and Lu, D. G. (2016). Risk assessment of bridges under multiple hazards in operation period. Saf. Sci. 83, 80–92. doi: 10.1016/J.SSCI.2015.11.001
Argyroudis, S. A., Fotopoulou, S., Karafagka, S., Pitilakis, K., Selva, J., Salzano, E., et al. (2019). A risk-based multi-level stress test methodology: application to six critical non-nuclear infrastructures in Europe. Nat. Hazards 100, 595–633. doi: 10.1007/s11069-019-03828-5
Argyroudis, S. A., Mitoulis, S. A., Hofer, L., Zanini, M. A., Tubaldi, E., and Frangopol, D. M. (2020). Resilience assessment framework for critical infrastructure in a multi-hazard environment: case study on transport assets. Sci. Total Environ. 714:136854. doi: 10.1016/j.scitotenv.2020.136854
Ataei, N., Stearns, M., and Padgett, J. E. (2010). Response sensitivity for probabilistic damage assessment of coastal bridges under surge and wave loading. Transport. Res. Rec. 2202, 93–101. doi: 10.3141/2202-12
Auyeung, S., Alipour, A., and Saini, D. (2019). Performance-based design of bridge piers under vehicle collision. Eng. Struct. 191, 752–765. doi: 10.1016/j.engstruct.2019.03.005
Aygün, B., Duẽas-Osorio, L., Padgett, J. E., and Desroches, R. (2011). Efficient longitudinal seismic fragility assessment of a multispan continuous steel bridge on liquefiable soils. J. Bridge Eng. 16, 93–107. doi: 10.1061/(ASCE)BE.1943-5592.0000131
Balomenos, G. P., and Padgett, J. E. (2018). Fragility analysis of pile-supported wharves and piers exposed to storm surge and waves. J. Waterway Port Coast. Ocean Eng. 144:4017046. doi: 10.1061/(ASCE)WW.1943-5460.0000436
Barbato, M., Petrini, F., Unnikrishnan, V. U., and Ciampoli, M. (2013). Performance-based hurricane engineering (PBHE) framework. Struct. Saf. 45, 24–35. doi: 10.1016/j.strusafe.2013.07.002
Bruneau, M., Barbato, M., Padgett, J. E., Zaghi, A. E., Mitrani-Reiser, J., and Li, Y. (2017). State of the art of multi-hazard design. J. Struct. Eng. 143, 1–25. doi: 10.1061/(ASCE)ST.1943-541X.0001893
Capacci, L., and Biondini, F. (2020). Probabilistic life-cycle seismic resilience assessment of aging bridge networks considering infrastructure upgrading. Struct. Infrastruct. Eng. 16, 659–675. doi: 10.1080/15732479.2020.1716258
Casas, J. R. (2015). The bridges of the future or the future of bridges? Front. Built Environ. 1:3. doi: 10.3389/fbuil.2015.00003
Chian, S. C., Wilkinson, S. M., Whittle, J. K., Mulyani, R., Alarcon, J. E., Pomonis, A., et al. (2019). Lessons learnt from the 2009 Padang Indonesia, 2011 Tohoku Japan and 2016 muisne ecuador earthquakes. Front. Built Environ. 5:73. doi: 10.3389/fbuil.2019.00073
Collins, A., Tatano, H., James, W., Wannous, C., Takara, K., Murray, V., et al. (2017). The 3rd global summit of research institutes for disaster risk reduction: expanding the platform for bridging science and policy making. Int. J. Disaster Risk. Sci. 8, 224–230. doi: 10.1007/s13753-017-0123-z
Decò, A., and Frangopol, D. M. (2011). Risk assessment of highway bridges under multiple hazards. J. Risk Res. 14, 1057–1089. doi: 10.1080/13669877.2011.571789
Dong, Y., and Frangopol, D. M. (2016). Probabilistic time-dependent multihazard life-cycle assessment and resilience of bridges considering climate change. J. Perform. Constr. Facil. 30:04016034.
Ellingwood, B. R. (2010). “Performance-based engineering for multiple hazards: Role of risk assessment,” in Proceedings of the Keynote Lecture, International Symposium on Reliability Engineering and Risk Management (ISRERM2010), Shanghai.
European Commission (2019). “Directorate-general for internal market, industry, entrepreneurship and SMEs,” in Paper Presented at the State of Infrastructure Maintenance Discussion Paper, Brussels.
Fioklou, A., and Alipour, A. (2019). Significance of non-uniform scour on the seismic performance of bridges. Struct. Infrastruct. Eng. 15, 822–836. doi: 10.1080/15732479.2019.1584226
Fujikura, S., and Bruneau, M. (2012). Dynamic analysis of multihazard-resistant bridge piers having concrete-filled steel tube under blast loading. J. Bridge Eng. 17, 249–258. doi: 10.1061/(ASCE)BE.1943-5592.0000270
Gehl, P., and D’Ayala, D. (2016). Development of bayesian networks for the multi-hazard fragility assessment of bridge systems. Struct. Saf. 60, 37–46. doi: 10.1016/j.strusafe.2016.01.006
Gkoumas, K., Marques Dos Santos, F. L., van Balen, M., Tsakalidis, A., Ortega Hortelano, A., Grosso, M., et al. (2019). Research and Innovation in Bridge Maintenance, Inspection and Monitoring - A European Perspective Based on the Transport Research and Innovation Monitoring and Information System (TRIMIS), EUR 29650 EN. Luxembourg: Publications Office of the European Union.
Harik, I. E., Shanaban, A. M., Gesund, H., Vali, J. Y. S., and Wang, S. T. (1990). United States Bridge Failures,1951-1988. J. Perform. Construct. Facilit. 4, 272–277.
Kameshwar, S., and Padgett, J. E. (2014). Multi-hazard risk assessment of highway bridges subjected to earthquake and hurricane hazards. Eng. Struct. 78, 154–166. doi: 10.1016/J.ENGSTRUCT.2014.05.016
Kameshwar, S., and Padgett, J. E. (2018). Response and fragility assessment of bridge columns subjected to bargebridge collision and scour. Eng. Struct. 168, 308–319.
Kodur, V., Aziz, E., and Dwaikat, M. (2013). Evaluating fire resistance of steel girders in bridges. J. Bridge Eng. 18:412. doi: 10.1061/(ASCE)BE.1943-5592.0000412
Krausmann, E., Girgin, S., and Necci, A. (2019). Natural hazard impacts on industry and critical infrastructure: natech risk drivers and risk management performance indicators. Intern. J. Disaster Risk Reduct. 40:101163. doi: 10.1016/j.ijdrr.2019.101163
Lee, G. C. (2010). Sustainable development in bridge engineering: development of multi - hazard design guidelines. Time 716, 3307–3307.
Li, Y., Ahuja, A., and Padgett, J. E. (2012). Review of methods to assess, design for, and mitigate multiple hazards. J. Perform. Construct. Facilit. 26, 104–117. doi: 10.1061/(ASCE)CF.1943-5509.0000279
Markogiannaki, O. (2019). Climate change and natural hazard risk assessment framework for coastal cable-stayed bridges. Front. Built Environ. 5:116. doi: 10.3389/fbuil.2019.00116
Martin, J., Alipour, A., and Sarkar, P. (2019). Fragility surfaces for multi-hazard analysis of suspension bridges under earthquakes and microbursts. Eng. Struct. 197:11. doi: 10.1016/j.engstruct.2019.05.011
Nikellis, A., and Sett, K. (2020). Multihazard risk assessment and cost-benefit analysis of a bridge-roadway-levee system. J. Struct. Eng. 146:2579. doi: 10.1061/(ASCE)ST.1943-541X.0002579
Padgett, J. E., Ghosh, J., and Ataei, N. (2010). “Sensitivity of dynamic response of bridges under multiple hazards to aging parameters,” in Proceedings of the 19th Analysis and Computation Specialty Conference, Reston, VA.
Payá-Zaforteza, I., and Garlock, M. E. M. (2012). A numerical investigation on the fire response of a steel girder bridge. J. Construct. Steel Res. 75, 93–103. doi: 10.1016/j.jcsr.2012.03.012
Petrini, F., Manenti, S., Gkoumas, K., and Bontempi, F. (2010). Structural design and analysis of offshore wind turbines from a system point of view. Wind Eng. 34, 85–108.
Petrini, F., and Palmeri, A. (2012). “Performance-based design of bridge structures subjected to multiple hazards: a review,” in Proceedings of the Sixth International Conference on Bridge Maintenance, Safety and Management - Bridge Maintenance, Safety, Management, Resilience and Sustainability -, Lake Maggiore, Italy, 8-12 July 2012, eds F. Biondini and D. M. Frangopol (Rotterdam: Balkema), doi: 10.1201/b12352-303
Pizarro, A., Manfreda, S., and Tubaldi, E. (2020). The science behind scour at bridge foundations: a review. Water 12:374.
Pizarro, A., and Tubaldi, E. (2019). Quantification of modelling uncertainties in bridge scour risk assessment under multiple flood events. Geosciences 9:445. doi: 10.3390/geosciences9100445
Prasad, G. G., and Banerjee, S. (2013). The impact of flood-induced scour on seismic fragility characteristics of bridges. J. Earthq. Eng. 17, 803–828. doi: 10.1080/13632469.2013.771593
Sgambi, L., Gkoumas, K., and Bontempi, F. (2012). Genetic algorithms for the dependability assurance in the design of a long-span suspension bridge. Comput. Aided Civil Infrastruct. Eng. 27, 655–675. doi: 10.1111/j.1467-8667.2012.00780.x
Tsakalidis, A., van Balen, M., Gkoumas, K., Grosso, M., Haq, G., and Pekar, F. (2018). Towards an Integrated Monitoring and Assessment Framework for the Strategic Transport Research and Innovation Agenda: Using TRIMIS as a Policy Support Mechanism. Luxembourg: Office of the European Union.
United Nations International Strategy for Disaster Reduction [UNISDR] (2015). Sendai Framework for Disaster Risk Reduction 2015-2030. Geneva: UNISDR.
Wang, Z., Padgett, J. E., and Dueñas-Osorio, L. (2014). Risk-consistent calibration of load factors for the design of reinforced concrete bridges under the combined effects of earthquake and scour hazards. Eng. Structur. 79, 86–95. doi: 10.1016/J.ENGSTRUCT.2014.07.005
Wardhana, K., and Hadiprionio, F. C. (2003). Analysis of recent bridge failures in the United States. J. Perform. Construct. Facilit. 17, 144–150.
Yang, D. Y., and Frangopol, D. M. (2019). Physics-based assessment of climate change impact on long-term regional bridge scour risk using hydrologic modeling: application to lehigh river watershed. J. Bridge Eng. 24:04019099. doi: 10.1061/(ASCE)BE.1943-5592.0001462
Yilmaz, T., Banerjee, S., and Johnson, P. A. (2018). Uncertainty in risk of highway bridges assessed for integrated seismic and flood hazards. Struct. Infrastruct. Eng. 14, 1182–1196. doi: 10.1080/15732479.2017.1402065
Zaghi, E. A., Padgett, J. E., Bruneau, M., Barbato, M., Li, Y., Mitrani-Reiser, J., et al. (2016). Establishing common nomenclature, characterizing the problem, and identifying future opportunities in multihazard design. Forum Pap. J. Struct. Eng. 142:H2516001.
Zhong, J., Gardoni, P., and Rosowsky, D. (2012). Seismic fragility estimates for corroding reinforced concrete bridges. Struct. Infrastruct. Eng. 8, 55–69. doi: 10.1080/15732470903241881
Keywords: multi-hazard analysis, bridge, modeling, impact, fire
Citation: Petrini F, Gkoumas K, Rossi C and Bontempi F (2020) Multi-Hazard Assessment of Bridges in Case of Hazard Chain: State of Play and Application to Vehicle-Pier Collision Followed by Fire. Front. Built Environ. 6:580854. doi: 10.3389/fbuil.2020.580854
Received: 07 July 2020; Accepted: 14 August 2020;
Published: 15 September 2020.
Edited by:
Luca Sgambi, Catholic University of Leuven, BelgiumReviewed by:
Sotirios Argyroudis, Aristotle University of Thessaloniki, GreeceAgathoklis Giaralis, City, University of London, United Kingdom
Copyright © 2020 Petrini, Gkoumas, Rossi and Bontempi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Konstantinos Gkoumas, a29uc3RhbnRpbm9zLmdrb3VtYXNAZWMuZXVyb3BhLmV1
 Francesco Petrini
Francesco Petrini Konstantinos Gkoumas
Konstantinos Gkoumas Claudio Rossi1
Claudio Rossi1