- 1Department of Engineering and Applied Sciences, University of Bergamo, Dalmine, Italy
- 2European Centre for Training and Research in Earthquake Engineering, Pavia, Italy
- 3University School for Advanced Studies (IUSS), Pavia, Italy
This research evaluates the influence of different modelling assumptions on the global and local seismic risk assessment of code-conforming precast reinforced concrete buildings, specifically single-story industrial buildings. In particular the modelling of the system mass, the overhead crane, the beam-to-column and roof-to-beam connections and the cladding system are investigated. For this purpose, a case study resembling a new industrial building designed in accordance with the current Italian building code was selected. Typical dowel beam-to-column connections were considered and the influence of various modelling strategies investigated: perfect hinges, linear elastic connections and non-linear connections with a degrading hysteretic force-displacement model which was calibrated from available data on experimental tests. Three different types of roof-to-beam connections were investigated removing the assumption of rigid diaphragm, namely hot-rolled, cold-formed and socket welded connections. Initially, simplified planar models of single frames were considered to evaluate the influence of the different modelling strategies, then 3D models of the entire building were analyzed. Multiple-stripe non-linear dynamic time history analyses allowed to evaluate displacements, drifts, deformations and ultimate curvatures of the main elements and connections for various intensity measure levels. The seismic risk was assessed in terms of failure rate considering the collapse of both the columns and of the connections. The results show that the beam-to-column connections fail right after reaching yielding due to their low displacement ductility, leading to the loss of support of the beam and therefore increasing the collapse rate of the investigated structural typology.
Introduction
The last earthquakes in Italy, particularly the ones that struck Emilia Romagna region (Northern Italy) in 2012, highlighted major vulnerabilities in reinforced concrete (RC) precast industrial buildings designed before the entry into force of modern anti-seismic provisions and accurate seismic zonation of the Italian territory (Belleri et al., 2015a; Belleri et al., 2015b; Ercolino et al., 2016; Bournas et al., 2014; Magliulo et al., 2014; Minghini et al., 2016; Nastri et al., 2017; Palanci et al., 2017; Savoia et al., 2012; Toniolo and Colombo, 2012). The main collapses observed were due to failure of the RC fork supporting the beams, the development of short columns due to ribbon glazing, or to the loss of support of the main structural elements due to under-designed or friction-based connections (Brunesi et al., 2015; Casotto et al., 2015; Demartino et al., 2018; Titi et al., 2018; Bosio et al., 2020). On the beam-to-column faying surface, a neoprene bearing pad is generally included both for spreading the vertical load and to allow for thermal expansions; the neoprene pads lead to a reduction of the coefficient of friction from 0.5, typical of concrete-to-concrete contact, to values also in the order of 0.1 (Magliulo et al., 2011), therefore facilitating relative displacements during earthquakes. Another observed failure is the fall of perimetral cladding elements, generally RC precast panels, due to the failure of their mechanical connections, which were under-designed to sustain the in-plane deformation demand and the out-of-plane loads arising in the system as the results of flexible diaphragms (Scotta et al., 2015; Belleri et al., 2016; Belleri et al., 2017a; Dal Lago et al., 2018).
In Italy, in the field of industrial buildings, RC precast buildings are broadly employed given their capability of covering large spaces, the high-quality standards on materials and elements, and the reduction of construction time if compared with ordinary RC buildings. Precast industrial structures are also characterized by a low displacement ductility if compared with typical RC buildings due to the higher inter-story height. They are commonly built following simple structural schemes, with columns fixed at the base and behaving as cantilever beams placed into socket foundations or connected to the foundation through mechanical devices (Belleri and Riva, 2012; Dal Lago et al., 2016). In modern precast buildings, the beams are generally simply supported and dowel connections are employed (Clementi at al., 2016; Magliulo et al., 2014; Zoubek et al., 2015; Kremmyda et al., 2017). In general, one or two dowels are embedded in the upper part of the column and inserted in pass-through holes, filled with mortar, within the beam. The adopted connections play a crucial role in the seismic response of precast buildings (Bressanelli et al., 2019; Cimmino et al., 2020): beam-to-column connections, in particular, influence the global response of the structure, altering substantially its behavior in terms of deformability and ductility.
The present work aims to assess the influence of different finite element modelling approaches on the probability of failure of precast industrial buildings. At this regard, a case study resembling a typical precast industrial building was selected and a multiple-stripe analysis was carried out. The current research is part of an Italian national project, namely RINTC (Bracchi et al., 2019; Cantisani and Della Corte, 2019; Iervolino et al., 2019; Magliulo et al., 2019; Ragni et al., 2019; Ricci et al., 2019), aiming at assessing the failure rate of various construction typologies designed in accordance with modern anti-seismic regulations (specifically the Italian building code, NTC18, 2018), therefore estimating the implicit risk of code-conforming buildings. Specifically, the comparison of the collapse rates of the investigated comprehensive 3D model with models accounting for simplified assumptions (such as those used in the RINTC project) allows validating the simplifying assumptions, such as in the case of the dowel beam-to-column connections, in order to obtain good estimates of the structural failure rate while reducing the computational effort.
Starting from the work of Bressanelli et al. (2019) and Magliulo et al. (2018), this research moves further by: investigating two different hysteretic models for the beam-to-column connections, such as the hysteretic uniaxial material model (Sousa et al., 2020) and the Modified Ibarra-Medina-Krawinkler Deterioration model (Lignos and Krawinkler, 2011); explicitly modelling the cladding panels in a pendulum configuration; removing the hypothesis of rigid diaphragm by introducing the roof elements and three types of beam-to-roof connections, namely hot-rolled, cold-formed and welded; explicitly modelling the overhead crane and the oscillating payload. The building collapse rates obtained from the comprehensive 3D model allowed to validate the collapse rates obtained from previous simplified analyses.
Considered Case Study
The considered case study is a single-story four-bay precast RC industrial building supposed located at L’Aquila (Italy). The span length along the transverse x-direction and the longitudinal y-direction are 15 and 6 m, respectively (Figure 1). The structural elements have been designed according with the Italian building code (NTC18, 2018). For further structural verifications, not available or not fully addressed in the Italian building code, Eurocode 2 (CEN, 2004), Eurocode 3 (CEN, 2004), CNR 10018/99 and CNR 10025/98 provisions were considered, particularly in respect to dowel capacity. Other details regarding the geometry of the selected case study may be found in Magliulo et al. (2019).
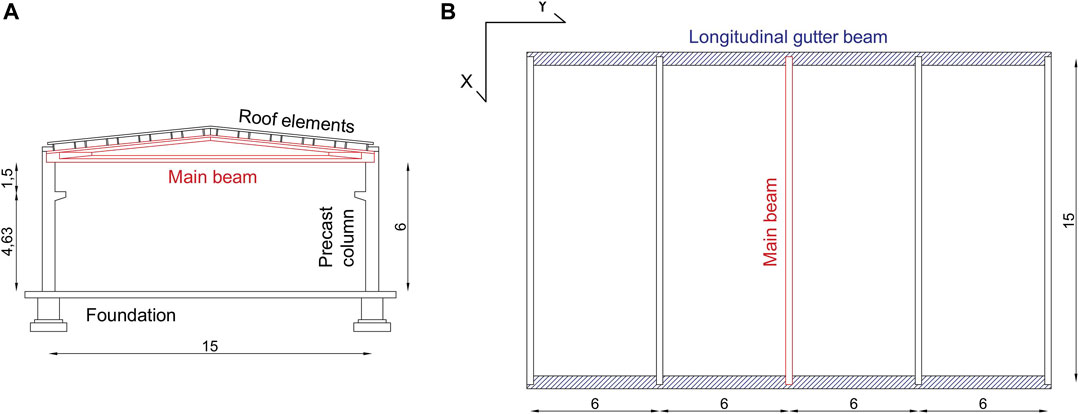
FIGURE 1. Building cross section (A) and plan view (B). Note: the dimensions are expressed in meters.
The lateral force resisting system is constituted by precast RC square columns (60 × 60 cm) fixed at the base. The concrete grade is C45/55 (characteristic cylindrical strength at 28 days equal to 55 MPa) and the steel grade is B450C (characteristic yield stress equal to 450 MPa). The columns have a longitudinal reinforcement ratio equal to 2.5% and are connected through dowels to double-tapered prestressed beams. The dowel connection is considered effective only in the transverse direction due to the presence of a RC fork at the top of the column inhibiting the beam movements in the longitudinal direction. The height of the column is 6 m, a corbel supporting the overhead crane is located at height equal to 4.5 m. The beams are double-tapered with 10% slope and they are characterized by a I-shaped cross-section with varying web dimensions. The longitudinal gutter beams, hatched in Figure 1B, have a rectangular cross section (0.3 × 0.5 m) and provide a support to the cladding system. The roof is made by precast double-tee elements. A cast in place RC topping (5 cm thickness) is considered when evaluating the influence of a rigid diaphragm. The cladding system consists of vertical precast panels connected to the longitudinal girder beams; the panel weight per unit surface is 4 kN/m2. An overhead-crane with a pay load equal to 80 kN is also considered with HE400A runway beams. For this structural typology, the structural behavior factor considered in the design is equal to 2.5 for “low ductility class” (NTC18, 2018).
Modelling and Analysis
Numerical models were created in the OpenSees software (McKenna et al., 2000). Initially a planar frame was taken as reference and simplified models were developed to preliminary evaluate the seismic influence of modelling assumptions, such as the mass location, i.e. distributed or lumped in a single point at the centre of the plane diaphragm, the beam-to-column connection, i.e. perfectly hinged or with a non-linear hysteresis, and the presence of an overhead crane.
Subsequently, 3D models were created to validate the results of the planar models and to investigate additional aspects such as the roof-to-beam connections and the precast cladding system; the latter was considered both as lumped masses at the panel-to-structure connections or explicitly modelled. For all the analyses a tangent stiffness Rayleigh damping was adopted with 5% relative damping at 0.5 and 2s. No damping was applied at the connection level which were modelled as zero-length elements.
2D Simplified Models
Nine simplified numerical models representative of a portal frame were developed for preliminary multiple-stripe analyses:
− Model SA1: non-linear beam-to-column connections and distributed masses;
− Model SA2: hinged beam-to-column connections and distributed masses;
− Model SA3: non-linear beam-to-column connections with Coulomb friction and distributed masses;
− Model SA4: non-linear beam-to-column connections and lumped mass;
− Model SA5: hinged beam-to-column connections and lumped mass;
− Model SA6: non-linear beam-to-column connections, distributed masses and crane model;
− Model SA7: non-linear beam-to-column connections with Coulomb friction, distributed masses and crane model;
− Model SA8: elastic-perfectly-plastic beam-to-column connections and distributed masses;
− Model SA9: linear elastic beam-to-column connections and distributed masses.
The columns were fixed at the base. The main beams and the girders were modelled with elastic elements; a constant cross section was assigned to the double-tapered beams as the mean value of the variable height and width. The cladding panels were only included in terms of mass and gravity loads applied to the main structure. This is in accordance with the hypothesis that the cladding panels are connected to the structure with an isostatic pendulum connection arrangement (Toniolo and Dal Lago, 2017). The non-linear behavior of the structural elements was modelled considering a lumped plasticity approach with plastic hinges at the column bases and elastic column elements. The column curvature and the yielding moment were obtained from a fiber analysis of the column cross-section. The plastic hinge was modelled with a zero-length element considering the Modified Ibarra-Medina-Krawinkler Deterioration Model with peak-oriented hysteretic response (Fischinger et al., 2008): effective yield moment My equal to 1256 kNm, effective stiffness Ke equal to 4.37∙104 kN/m and cyclic deterioration parameter λ equal to 2.734.
The seismic masses were lumped at the centre of the roof diaphragm or distributed to the various elements. In the first case, the lumped mass (MC) was equal to 44.6 kN/g and 35.6 kN/g in the horizontal and vertical direction, respectively. The lower value in the vertical direction was due to the absence of the cladding panel mass which does not participate in the seismic response in this direction. In the second case, two sets (MD and MT) of distributed masses were defined: the mass MD (1.329 kN/g), placed at each corbel, corresponds to an equal distribution among the columns of the crane mass (5 kN/g) and of 80% of the crane payload; the mass MT, placed at the top of each column, is the mass of the roof system equal to 28.9 kN/g and 37.90 kN/g in the vertical and horizontal direction, respectively. In the case of explicit modelling of the overhead crane, the crane payload (ME) was set equal to 8 kN/g.
The influence of the overhead crane modelling was assessed in two ways: in the first case, the crane was modelled only in terms of mass (MD in the case of model with distributed masses or as part of MC in the case of model with lumped mass in the diaphragm centroid); in the second case, the overhead crane was modelled with an elastic element with adequate stiffness connected to the runway beams, while the mass ME of the payload was connected to the middle of the overhead crane through an elastic spring with stiffness equal to ME·g/R (Belleri et al., 2017b). R is the assumed length of the cable, equal to half the column height (i.e. 3 m). The simplified models are represented in Figure 2.
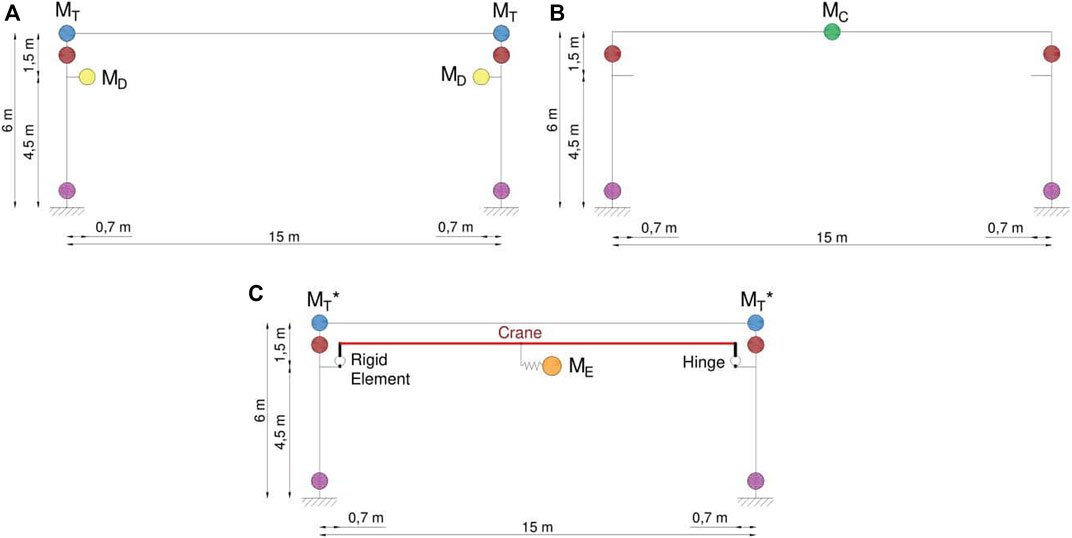
FIGURE 2. Simplified models with distributed masses (A), lumped mass at the centre of the roof (B) and distributed masses and crane load (C). Note: The purple circle represents the plastic hinge at the base of the column, the red circle indicates the position of the beam-to-column connection, the yellow circle represents the mass MD at the corbel position, the green circle represents the lumped mass MC, the orange circle represents the mass of the payload crane ME and the blue circle indicates the roof mass MT (in the model (C) the blue circle represents the mass MT minus the mass of the crane, indicated as MT*).
Beam-to-Column Connection
Different types of beam-to-column connection modelling were considered (Kramar et al., 2010; Soroushian, 1987; Zoubek et al., 2014; Capozzi et al., 2011): hinged, elastic, elastic-perfectly plastic and non-linear hysteresis (Figure 3). All types of connections have been modelled as zero-length elements at the top of the column. The non-linear beam-to-column connections were designed following a shear demand resulting from capacity design and a shear strength resulting from the following formulation (Tassios and Vintzeleou, 1987; Psycharis and Mouzakis, 2012; Kremmyda et al., 2017):
where n represents the number of dowels, db the dowel diameter, fym is the mean yielding value of the dowels, fcm is the concrete mean compression strength and α is a reduction factor (Magliulo et al., 2014; Zoubek et al., 2015). For this specific case, fym is equal to 816 MPa and fcm is equal to 60 MPa. The connections have been designed with a coefficient α equal to 1.6 according to CNR10018 (1999) and CNR10025 (1998) and have been checked against failure with the formulation provided in the design guidelines of the Safecast project (Negro and Toniolo, 2012) with a coefficient α equal to 0.9. The design process led to two steel dowels with 24 mm diameter for each joint. The stiffness of the beam-to-column dowel’s connection was derived according to Ferreira and El Debs (2000):
where the subscripts n, cls, and g indicate neoprene, concrete and grout, respectively. The yield displacement was computed as:
with Fy derived from Equation 1 (i.e., VRm). The resulting yield displacement of the considered beam-to-column connection is 2.8 mm.
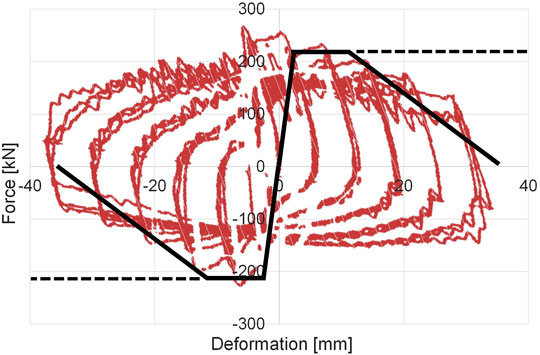
FIGURE 3. Comparison of the analytical and experimental force-displacement diagrams of the dowel connection. Note: the red dots indicate the experimental results (Kremmyda et al., 2014), the black lines indicate the analytical model used in the finite element analysis.
The beam-to-column connection hysteresis was defined in accordance with the experimental results of cyclic tests reported in Kremmyda et al. (2014): the capping displacement was conservatively assumed equal to half the dowel diameter, i.e. 12 mm, while the ultimate displacement capacity equal of 1.5 times the dowel diameter, i.e. 36 mm. The OpenSees hysteretic uniaxial material model according with Sousa et al. (2020) and the Modified Ibarra-Medina-Krawinkler Deterioration model (Lignos and Krawinkler, 2011) were adopted and compared. For the hysteretic uniaxial material model, the following parameters were considered (according to Fischinger et al., 2013): damage1 equal to 0, damage 2 equal to 0.06, pinchX and pinchY equals to 0.5 and beta equal to 0. Such parameters allow adjusting the strength degradation, pinching effects and unloading stiffness of the constitutive model. Figure 3 shows the comparison of the analytical and experimental force-displacement diagrams of the dowel connection.
Finally, the possible presence of friction in the beam-to-column connection was considered using a Coulomb model with friction coefficient µ equal to 0.1337 and initial stiffness kinit equal to 490 kN/m, corresponding to the lateral stiffness of the neoprene pad.
3D Complete Models
3D models of the entire reference building were developed. As for the simplified models, the beams (both the transversal main beams and the longitudinal secondary beams) were modeled as elastic elements. The columns were modeled following the same lumped plasticity approach of the planar models with the same parameters of the “Krawinkler-Ibarra-Medina Deterioration Model with Peak-Oriented Hysteretic Response” (Fischinger et al., 2008). The seismic masses were lumped at the centre of the roof diaphragm or distributed to the various elements as before. In the first case, the lumped mass (MC) was equal to 425.3 and 287.5 kN/g in the horizontal and vertical direction, respectively. The lower value in the vertical direction was due to the absence of the cladding panel mass which were considered directly supported by the ground. In the second case, a distributed masses approach was adopted with the same mass values of the planar model previously described.
The beam-to-column connection was modeled in three different ways: perfectly hinged, linear elastic and non-linear hysteresis connections. The Krawinkler-Ibarra-Medina Deterioration hysteretic model was selected in the 3D models on the basis of the results obtained from the planar frame analyses. The presence of the overhead crane was considered either only in terms of masses (models MA1, MA2, MB1, MB2, MC1, and MC2) or with an explicit modeling (models MA3, MB3, MC3, and ME1). Figure 4 shows the model of the overhead crane with the same parameters adopted in the simplified models.
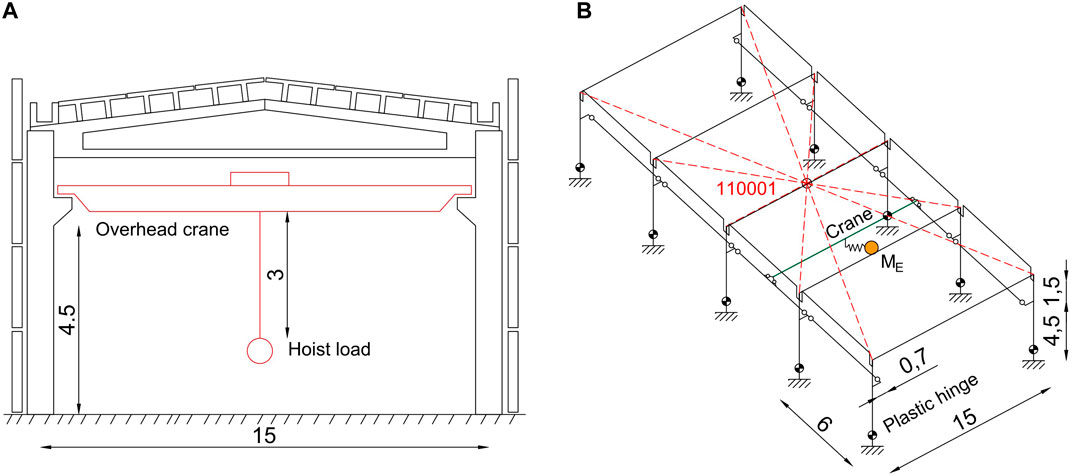
FIGURE 4. Building section drawing with overhead crane (A) and schematic view of models MA3, MB3 and MC3 (B). Note: in the right figure, the empty dots indicate the position of the hinges in the modelled structure with OpenSees and the number 110001 in the centre indicates the degree of constraints of the diaphragm floor, i.e. no relative displacements in the horizontal plane.
The precast cladding system was modelled either in terms of lumped masses or by two explicit modeling approaches. In the first explicit modelling approach (MC4 model), the whole cladding system was modelled by placing a single beam element with 15 subdivisions (12 and 19.2 kN/g·m mass per unit length in the transverse and longitudinal direction, respectively) hinged connected to the ground and to the roof centroid. In the second explicit modelling approach, model ME1 in Figure 5, the cladding panels of each bay were modelled by a single element hinged connected at the ground and at the center line of each span, similarly to what carried out in the first explicit modelling approach. The related distributed mass per unit length was in accordance with a RC panel thickness of 12 cm.
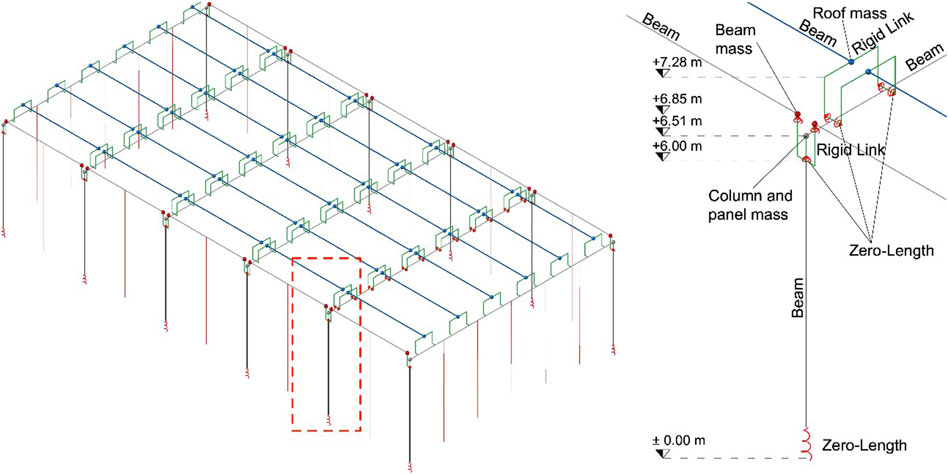
FIGURE 5. Schematic view of models ME1 and detail of the connections (close-up on the dashed red box). Note: in the left-side figure the red vertical lines indicate the position of the elements introduced to capture the seismic effects of the cladding system.
The considered models are:
− Model MA1: hinged beam-to-column connections and distributed masses;
− Model MA2: hinged beam-to-column connections and lumped mass;
− Model MA3: hinged beam-to-column connections, distributed masses and explicit modeling of the overhead crane;
− Model MB1: elastic beam-to-column connections and distributed masses;
− Model MB2: elastic beam-to-column connections and lumped mass;
− Model MB3: elastic beam-to-column connections, distributed masses and explicit modeling of the overhead crane;
− Model MC1: non-linear beam-to-column connections and distributed masses;
− Model MC2: non-linear beam-to-column connections and lumped mass;
− Model MC3: non-linear beam-to-column connections, distributed masses and overhead crane;
− Model MC4: non-linear beam-to-column connections, distributed masses, overhead crane and cladding panels;
− Model MD1: hot rolled beam-to-roof element connections and distributed masses;
− Model MD2: cold formed beam-to-roof element connections and distributed masses;
− Model MD3: welded beam-to-roof element connections and distributed masses;
− Model MD4: rigid beam-to-roof element connections and distributed masses;
− Model ME1: non-linear beam-to-column connections, distributed masses, hot-rolled beam-to-roof element connections and cladding panels.
Roof Element-to-Beam Connections
Two possible roof modeling methods were considered: a rigid diaphragm approach and the explicit modeling of the roof elements and of their connections (Dotreppe et al., 2006; Felicetti et al., 2008a; Beconcini et al., 2008; Felicetti et al., 2008b; Beconcini et al., 2009; Dal Lago et al., 2012). In the latter case, the double-tee roof elements were modeled as beams connected to the main beam by means of rigid links (Figure 6A) which behaves as a cylindrical hinge in the vertical plane and a rigid connection in the horizontal plane. The in-plane stiffness of the roof is associated with the torque that is transferred to the base of the links, which represent the ribs of the double-tee roof elements; such stiffness is directly related to the stiffness of the roof element-to-beam connections. This modelling approach is able to capture the real in-plane stiffness of the roof for both new and existing buildings.
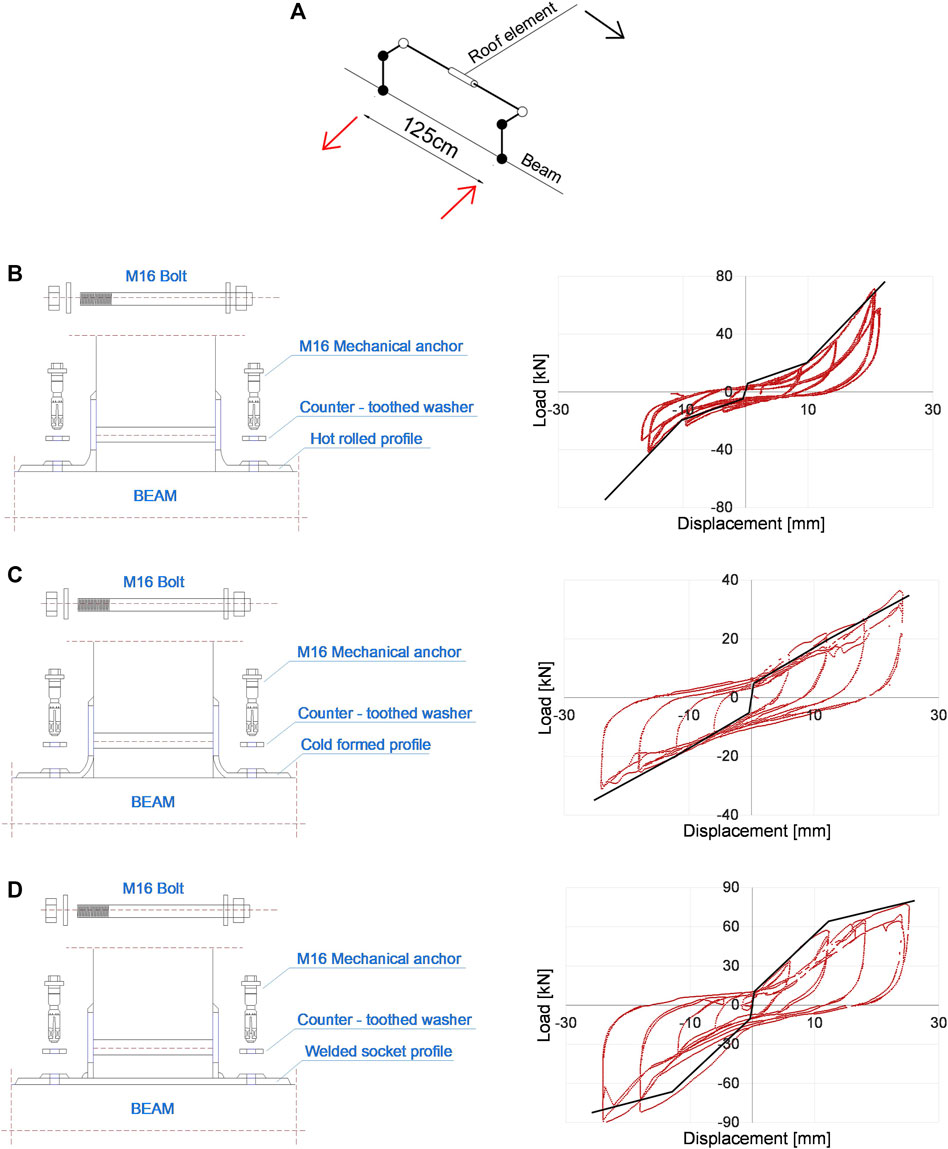
FIGURE 6. (A) Rigid link arrangement for the connection of the roof double-tee beam element to the supporting beam; the empty dots indicate the position of the hinges, the full dots indicate the position of the rigid connections and the thick lines indicate the rigid link in the modelled structure with OpenSees.Considered connections: hot-rolled (B), cold-formed (C) and socket welded (D).
The connection between the double-tee roof element and the beam is made by two steel angle profiles located at the base of each rib of the roof element. Three types of connections were considered (Dal Lago and Ferrara, 2018): hot rolled, cold formed and welded socket with M16 anchor bolts. The hysteresis of the connections was analytically reproduced using the non-linear OpenSees solver combined with Matlab (Matlab, 2019) (Figure 6). The connections were modeled in OpenSees through a MultiLinear Material in terms of load and relative displacement.
The connection failure occurs when the maximum displacement recorded in the experimental tests is reached. The roof element remains connected to the beam after the collapse, but with a connection stiffness equal to zero. At this regard, the relative displacement of the two nodes of the connection was checked in a step-by-step basis during the analysis: if such displacement exceeds the allowable displacement, the zero-length element associated with the connection is removed and a new zero-length elastic element with stiffness approximately equal to zero is placed between the two nodes.
Regarding the connection modelling, zero-length elements are placed at the base of the vertical rigid links of the roof elements (Figure 6A). In the longitudinal direction, i.e. along the roof element, the hysteresis depicted in Figure 6 was considered, while in the transverse direction an elastic behaviour with high stiffness was implemented.
Definition of the Seismic Input
The multiple-stripe analysis (MSA) method (Jalayer, 2003; Jalayer and Cornell, 2009) was adopted herein among the available approaches used to retrieve fragility curves and associated collapse probabilities. Within MSA, a number of nonlinear dynamic analyses were carried out with records scaled at ten increasing levels (i.e., the stripes) of Sa(T1) [0.011; 0.026; 0.049; 0.08; 0.124; 0.184; 0.27; 0.379; 0.572; 1.077] g, corresponding to return periods Tr [10; 50; 100; 250; 500; 1,000; 2,500; 5,000; 10,000; 100,000] years, respectively. The fundamental period of the considered precast structure is T1 = 2s. Hazard-consistent record selection was employed. In particular, at each stripe, both horizontal components of 20 records were selected through disaggregation of seismic hazard and matched with target spectra conditioned on the ten intensity measure (IM) levels, using the Conditional Spectrum method (Baker, 2011).
Figure 7 shows the time-histories and response spectra of both components of the 20 records selected at the 6th stripe (i.e., intensity measure level, IML, 6), related to a 1,000-years return period, scaled at Sa(T1) = 0.184 g. The considered values of Sa(T1) are those related to the site of L’Aquila, with soil type C and topographic category T1, according to the Italian code (NTC18, 2018). These values, as well as the ones related to other Italian sites and soil types considered within the RINTC project (RINTC Workgroup, 2018), can be found in the work by Cimmino et al. (2020). The selected records were extracted from the Italian accelerometric archive (Luzi et al., 2008) and from the NGAwest2 database (Ancheta et al., 2014).
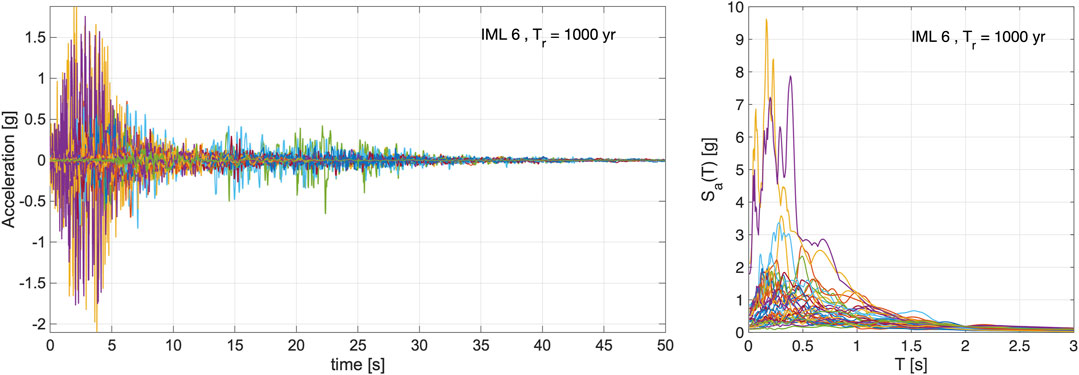
FIGURE 7. Selected scaled records (both components) for the stripe at Tr = 1,000 years, in terms of (left) time histories and (right) response spectra.
Numerical Results
2D Simplified Models
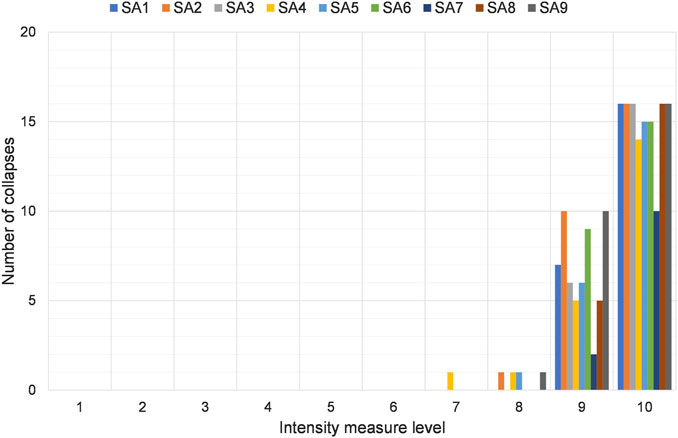
The failure rate of the building could be associated with both local collapses (i.e. related to the loss of support of the beam) and global collapse. Considering local collapses, different assumptions apply based on the type of the beam-to-column connection modelling. For non-linear modeling, the failure is considered related to the achievement of the maximum relative displacement of the connection, set herein equal to 1.5·db (where db is the diameter of the dowel), i.e. 36 mm. As it will be highlighted in the following, it is worth to note that the beam displacement increases in such a way to lead to the loss of support after the failure of the connection. For linear modelling, the failure is considered when reaching the shear capacity, equal to 230 kN (Vmax). Regarding the global collapse, the failure was considered related to a lateral displacement corresponding to a 50% reduction of the total base shear, obtained from a non-linear static analysis. Depending on these considerations, Figure 8 shows the number of analyses leading to a local collapse for each seismic intensity and for each model.
The models with non-linear beam-to-column connections shown in Figure 8 refer to modelling with the Krawinkler-Ibarra-Medina deterioration model. The use of the hysteretic uniaxial material model, in place of the aforementioned degradation model, causes a limited increase in the number of collapses in the case of lumped masses due to the increased stress in the dowels (model SA4). The other models are characterized by a similar number of collapses. For this reason, the Krawinkler-Ibarra-Medina deterioration model was used in the analyses of the 3D models. Two possible failure conditions have been considered when the beam-to-column connection hysteresis is accounted for: the relative displacement corresponding to the loss of support of the beam, and the failure of the beam-to-column connection. It is observed that the only difference among these two types of failure conditions occurs only for the seismic intensity level 9 in Model SA3 (i.e. Krawinkler-Ibarra-Medina deterioration model for the beam-to-column connection, Coulomb’s friction and distributed masses), where seven collapses are recorded instead of six. These results show that the connections move directly from the elastic stage (or yield stage) to its failure by developing high relative displacements leading to the loss of support of the beam. It is also noted that there are no cases in which the beam-to-column connection is in the softening zone. This was also observed by introducing a strain hardening in the post-yield range.
The results of two different models of the beam-to-column connection are showed on the left side of Figure 9, a non-linear (a) and an elastic (b) connection, respectively. The same figure, on the right side, shows the corresponding moment-rotation curves of the plastic hinges at the base of the column. In the case with elastic beam-to-column connection (a), the demand on the column is greater than in the case with a non-linear connection (b) because in such model the connection can reach higher values (exceeding its capacity 230 kN).
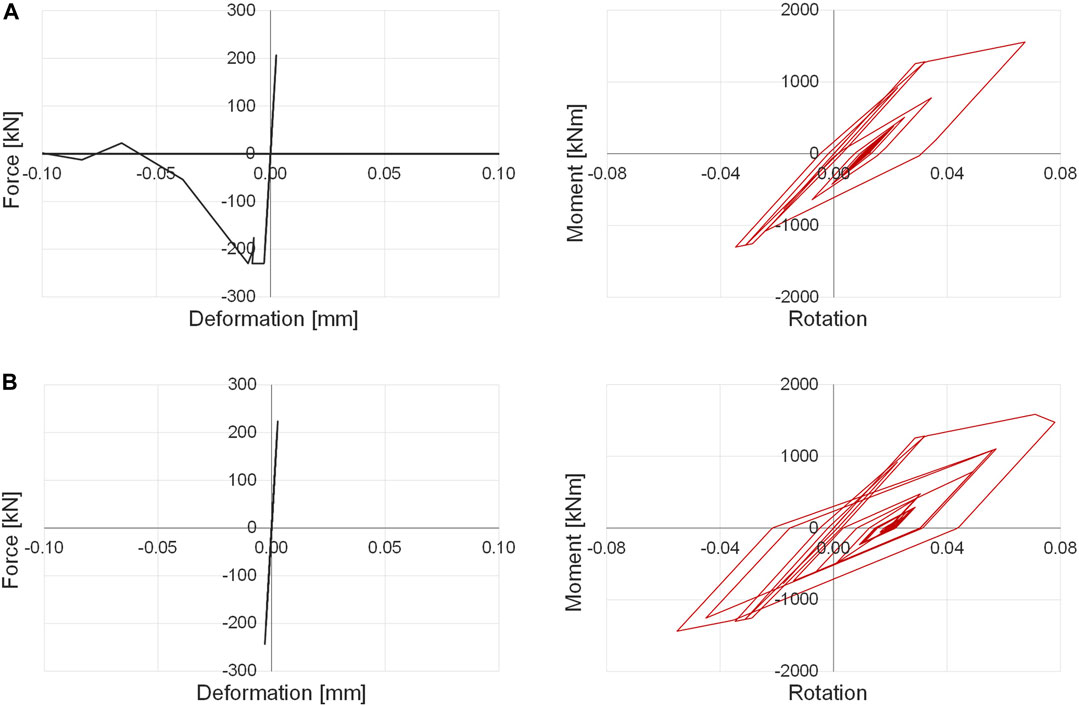
FIGURE 9. Time history results in the case of elastic (A) and non-linear (B) beam-to-column connection. The left-side refers to the beam-to-column connection hysteresis, while the right side refers to the base column plastic hinge.
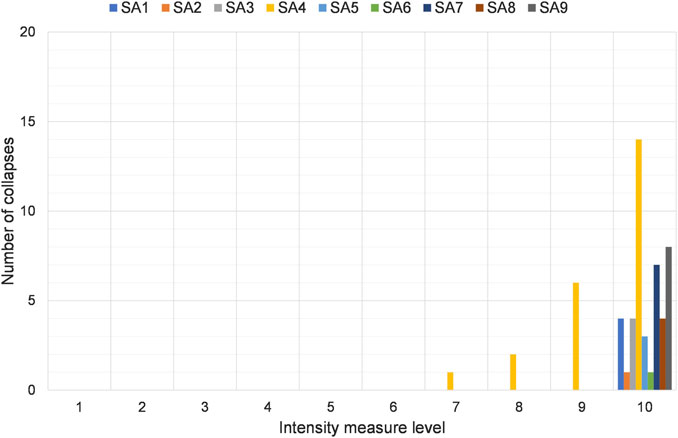
Figure 10 shows the number of analyses leading to global failure for each seismic intensity and for each model. The global results for the models SA2, SA5, SA8, and SA9 are not significant because they are characterized by beam-to-column connections modelled with hinged, elastic-plastic or perfectly elastic models. In general, global collapses occur only at the highest seismic intensity. An exception is observed for Model SA4 (non-linear beam-to-column connections, lumped masses at the centre of the roof), where the lumping of the mass at the roof center caused an increase of the demand both in local and global terms.
3D Complete Models
Initial evaluations were carried out on models MA, MB and MC. Non-linear static analyses were performed with a lateral load distribution according to the fundamental mode of vibration in each of the principal directions. Figure 11 shows the capacity curves of the 3D complete models. In Figure 11B (corresponding to a capacity curve for a loading direction perpendicular to the main beams) a lower initial stiffness is observed in the lumped mass models (A2, B2 and C2) as a result of the different height of the lateral loads. This difference is not observed in the transverse direction.
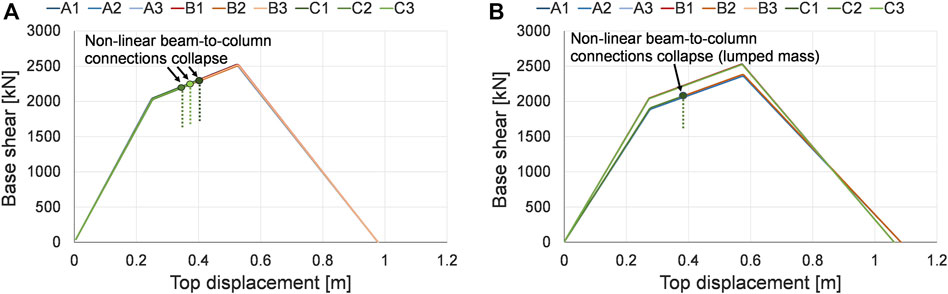
FIGURE 11. Capacity curves of the 3D complete models in the transverse (A) and longitudinal (B) direction.
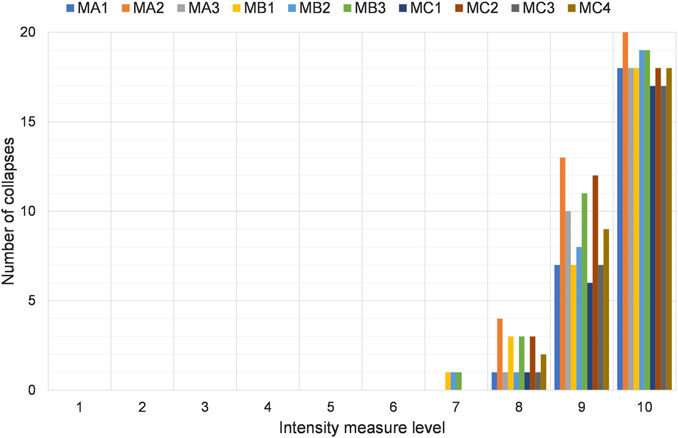
Figure 12 shows the number of analyses leading to a local collapse for each seismic intensity and for each model. The same local failure assumptions made in the previous section were considered.
For the higher seismic intensities, it is possible to observe a clear correlation, in terms of number of local collapses, between the various models. In general, the number of collapses increases for models with lumped masses (MA2, MB2, MC2) compared with models with distributed masses (MA1, MB1, MC1). This trend is even more significant at the seismic intensity level 9 with Sa(T1) equal to 0.572 g. For the lower seismic intensities, the local behavior of the connections is generally similar among the various models. The models with elastic beam-to-column connections are the only ones showing collapses at seismic intensity level 7, where Sa(T1) is equal to 0.27 g.
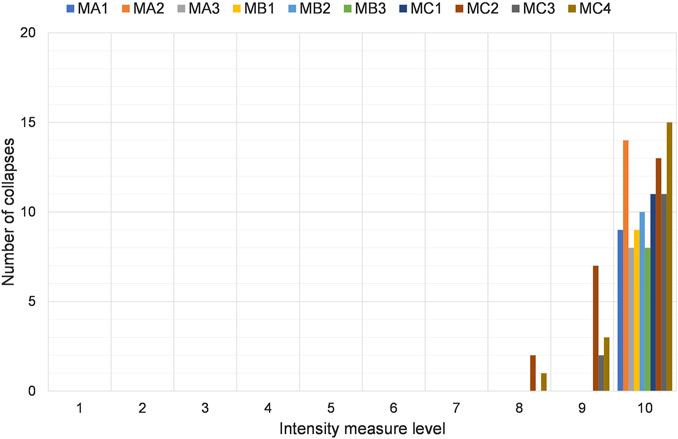
Considering global collapses (Figure 13), the models are characterized by similar results. The collapses are slightly higher in models characterized by a lumped mass at the centre of the roof diaphragm (MA2, MB2, MC2). Models with non-linear beam-to-column connections and lumped masses, i.e. MC2, or distributed masses and overhead crane load, i.e. MC3, are the only ones with global collapses for lower seismic intensities. The results obtained from the analysis of 3D models confirm the results previously obtained for the simplified planar models.
As well as for simplified models, also for the complete 3D models there is a direct transition of the beam-to-column connections from the elastic field to failure. To highlight this aspect, the non-linear behavior of the beam-to-column connection has been divided into four fields (Figure 14A): elastic (A), plastic (B), softening (C) and failure (D). For the three highest seismic intensities, the number of cases falling inside these fields are reported in Figure 14B. The results clearly show that the beam-to-column connections moves directly from the elastic (A) or plastic (B) field to failure (D).
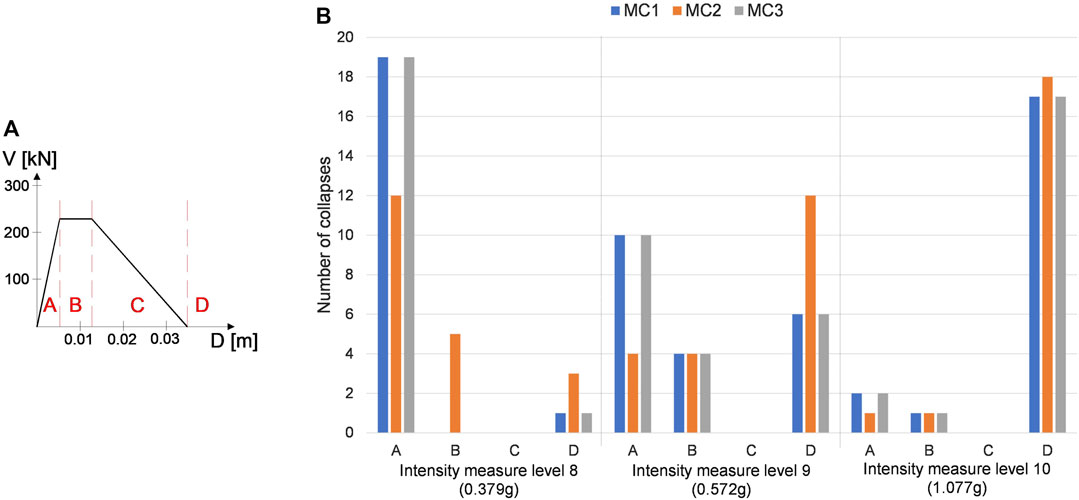
FIGURE 14. Subdivision of the Krawinkler-Ibarra-Medina deterioration model of the beam-to-column dowel’s connection (A) and evolution of the number of collapses for the dowel’s connection in the tri-dimensional complete models (B).
With regard to the modelling of the beam-to-roof connection, i.e. MD models, the obtained results are reported in Figure 15. Figure 15A indicates the number of local collapses of the beam-to-roof connection. MD4 is not represented because it is characterized by rigid roof element-to-beam connections. Figure 15B indicates the number of global collapses of columns in the x-direction, i.e. the transverse direction. For the global assessment, the maximum displacement capacity is that corresponding to a 50% reduction of the shear at the base of the column (0.818 m). For the local assessment, the maximum capacity is that corresponding to the maximum relative displacement of the roof-to-beam connections, herein assumed equal to 24 mm. When the relative displacement between the roof element and the supporting beam exceeds the support length, the double-tee unit is considered collapsed and the analysis is stopped. In terms of number of collapses, it is observed that for the present case study there is no significant difference between flexible or rigid diaphragm and that failure at the column base generally foregoes failure at the roof element-to-beam connections.
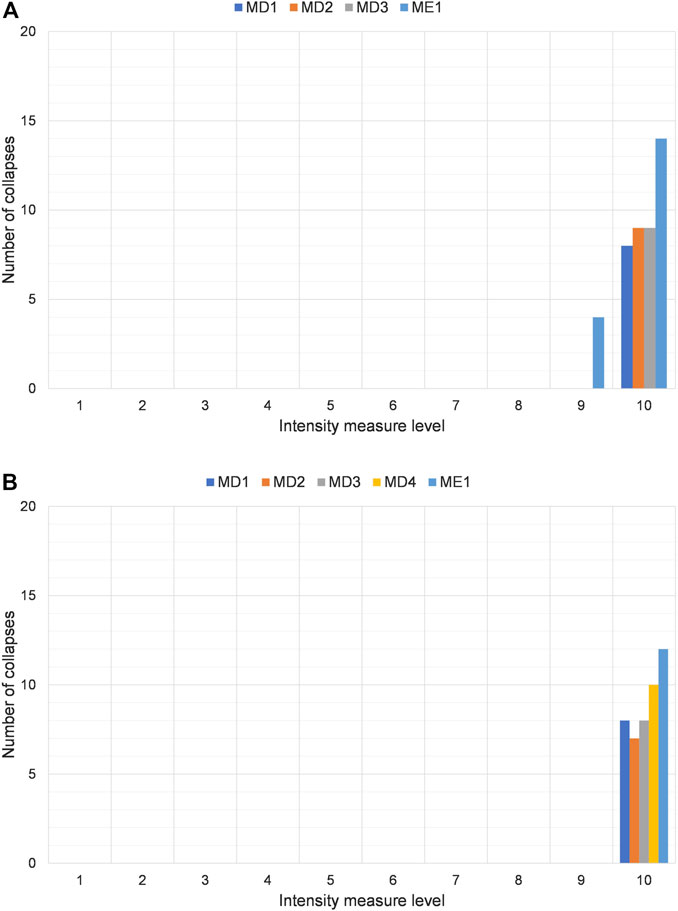
FIGURE 15. Total number of analyses leading to a local (A) and global (B) collapse for models MD1, MD2, MD3, MD4 and ME1 (20 ground motions were considered for each intensity measure level).
The last considered model (ME1) is characterized by the simultaneous presence of: beam-to-column connections modelled with the Ibarra-Medina-Krawinkler deterioration model; roof-to-beam connections modelled with a multilinear model; distributed masses at the top of the columns; precast cladding system located along the perimeter of the structure. The results of the analyses are reported in Figure 15. The models with the roof elements show collapses for seismic intensities 9 and 10 with Sa(T1) equal to or greater than 0.572 g. Therefore, the modelling of the cladding system along the perimeter of the structure has led to global and local collapses (at the roof-to-beam connections) for the intensity measure level 9, unlike the MD models where the only collapses occurred for intensity level 10. The analyses also showed that the roof-to-beam connections adopted are effective both in terms of capacity and stiffness, because there are collapses in these connections only for the highest intensity levels.
Finally, the rate of collapses associated with the most comprehensive model (ME1) is obtained from the following equation (Suzuki and Iervolino, 2019):
where the addition of 10-5 is due to the lack of information in the hazard curve beyond 100,000 years; therefore, this formulation leads to a conservative estimate. The fragility parameters of the intensity measure were derived through the R2R_EU software (Baraschino et al., 2020) using the maximum likelihood estimation. The obtained failure rate λf is equal to 6.9 × 10-5 in the case of global collapse and 1.1 × 10-4 in the case of collapse of the connections, the corresponding values obtained from previous research with simplified 3D models are 5.8 × 10-5 (Suzuki and Iervolino, 2019) and 1.7 × 10-4 (Iervolino et al., 2018). Therefore, the collapse rate estimation considering local collapse is slightly overestimated compared to the results obtained from detailed models, while the collapse rate estimation considering global collapse is slightly underestimated. It is worth noting that these differences are reasonable and in the same order of magnitude. Therefore, the previous formulation of the building models is suitable for the collapse rate evaluation. The main advantage of detailed 3D models is related to the possibility of detecting local damages in a more comprehensive way suitable, for instance, for a detailed loss assessment (Bosio et al., 2020).
Conclusion
The present paper investigated the influence of finite element modelling in the evaluation of the collapse rate of precast industrial buildings, referring in particular to beam-to-column and beam-to-roof connections. A single-story precast industrial building was selected as reference structure and modelled in OpenSees with different assumptions: the overhead crane (modelled explicitly or present only in terms of masses) and the distribution of the overhead crane mass (i.e. equally distributed on each column corbel and with or without accounting for the payload); the beam-to-column connections (i.e. elastic, hinged or dowel connection with a non-linear model); the masses acting on the structure (distributed or lumped at the center of the roof diaphragm); the beam-to-roof connections (i.e. hot-rolled, cold-formed and socket welded). Non-linear dynamic analyses with increasing intensity were carried out for Sa(T1) ranging from 0.011 to 1.077 g. Each intensity level consists of twenty pairs of ground motions acting in both horizontal directions. Simplified planar models and complete three-dimensional models were considered.
The analyses showed that the complete three-dimensional models reflect the results of the simplified planar models as regards the different modelling of the mass, the beam-to-column connections and the overhead crane. In the case of beam-to-column connections with non-linear hysteresis, it was observed a direct transition of the connections from the elastic or plastic range to the collapse, with no cases in the softening range.
Moving from models with distributed masses toward models with a lumped mass at the roof diaphragm centroid causes a slight increase in the number of collapses, both in global and local terms. The explicit model of the payload of the overhead crane provided limited influence on the results.
The beam-to-roof connections modelling allowed to capture the actual in-plane stiffness of the diaphragm and it is suitable for both existing and new buildings models. The results showed that in the present case study the different types of beam-to-roof connections considered did not affect the results and that the collapse of the connections was generally anticipated by the collapse of the columns.
Regarding beam-to-column connections, various collapses were observed for high intensity levels. The analyses of the model with linear elastic beam-to-column connections and distributed masses showed collapses of several connections for Sa(T1) equal or higher than 0.379 g. While, in the case of non-linear beam-to-column connections, a high number of collapses is observed only in the case of a lumped mass at the roof level, which causes an increase of the connections demand. It is worth observing that, despite capacity design was used for the design of these connections, various collapses were recorded. This result reflects the fact that the design formulation for the connections was taken from an aged Italian co-normative document while the actual capacity used in the analyses was obtained from a stricter formulation taken from a more recent European design guideline report.
Finally, the collapse rate for the most representative three-dimensional model was provided considering both for global and local collapses. The obtained values allowed to validate the collapse rate previously obtained with simplified models. The comprehensive model formulation is also suitable to detect local vulnerabilities and to assess losses in a more detailed manner.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, upon reasonable requests.
Author Contributions
MB: Conceptualization, Methodology, Formal analysis, Visualization, Investigation, Validation, Writing - original draft, Writing - review and editing. DB: Conceptualization, Methodology, Formal analysis, Investigation, Writing - review and editing. AB: Conceptualization, Methodology, Formal analysis, Visualization, Investigation, Writing - review and editing, Supervision. FC: Conceptualization, Methodology, Formal analysis, Investigation, Writing - review and editing. PR: Conceptualization, Methodology, Writing - review and editing. RN: Conceptualization, Methodology, Writing - review and editing.
Funding
This research study has been funded by the Italian Department of Civil Protection, in the framework of the national project DPC-ReLUIS-EUCENTRE WP3 (RINTC) 2019–2021; however, opinions and conclusions do not necessarily reflect those of the funding entity.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Ancheta, T. D., Darragh, R. B., Stewart, J. P., Seyhan, E., Silva, W. J., Chiou, B. S. J., et al. (2014). NGA-West2 database. Earthqua. Spectra. 30 (3), 989. doi:10.1193/070913EQS197M
Baker, J. W. (2011). Conditional mean spectrum: tool for ground-motion selection. J. Struct. Eng. 137 (3). doi:10.1061/(ASCE)ST.1943-541X.0000215
Baraschino, R., Baltzopoulos, G., and Iervolino, I. (2020). R2R-EU: software for fragility fitting and evaluation of estimation uncertainty in seismic risk analysis. Soil Dyn. Earthqu. Eng. 132, 106093. doi:10.1016/j.soildyn.2020.106093
Beconcini, M. L., Croce, P., Del Corso, R., Formichi, P., Previdero, M., and Taccola, R. (2009). “Analisi sperimentale del comportamento statico e ciclico di connessioni tegolo-trave di strutture prefabbricate,” in 25° Convegno nazionale AICAP, Pisa.
Beconcini, M. L., Croce, P., and Formichi, P. (2008). “Comportamento sismico di connessioni tegolo-trave in strutture prefabbricate.” in 17° Convegno CTE, Roma.
Belleri, A., Brunesi, E., Nascimbene, R., Pagani, M., and Riva, P. (2015a). Seismic performance of precast industrial facilities following major earthquakes in the Italian territory. J. Perform. Construct. Facil. 29 (5). doi:10.1061/(ASCE)CF.1943-5509.0000617
Belleri, A., Torquati, M., Riva, P., and Nascimbene, R. (2015b). Vulnerability assessment and retrofit solutions of precast industrial structures. Earthqua. Struct. 8 (3), 801. doi:10.12989/eas.2015.8.3.801
Belleri, A., Cornali, F., Passoni, C., Marini, A., and Riva, P. (2017a). Evaluation of out-of-plane seismic performance of column-to-column precast concrete cladding panels in one-storey industrial buildings. Earthquake Engng Struct. Dyn. 47, 397. doi:10.1002/eqe.2956
Belleri, A., Labò, S., Marini, A., and Riva, P. (2017b). The influence of Overhead cranes in the seismic Performance of industrial Buildings. Front. Built Environ. 3. doi:10.3389/fbuil.2017.00064
Belleri, A., and Riva, P. (2012). Seismic performance and retrofit of precast concrete grouted sleeve connections. PCI J. 57 (1), 97. doi:10.15554/pcij.01012012.97.109
Belleri, A., Torquati, M., Marini, A., and Riva, P. (2016). Horizontal cladding panels: in-plane seismic performance in precast concrete buildings. Bull. Earthqu. Eng. 14, 1103. doi:10.1007/s10518-015-9861-8
Bosio, M., Belleri, A., Riva, P., and Marini, A. (2020). Displacement-based simplified seismic loss assessment of Italian precast buildings. J. Earthqu. Eng. 24 (Suppl. 1), 60. doi:10.1080/13632469.2020.1724215
Bournas, D. A., Negro, P., and Taucer, F. F. (2014). Performance of industrial buildings during the Emilia earthquakes in Northern Italy and recommendations for their strengthening. Bull. Earthquake Eng. 12 (5), 2383–2404. doi:10.1007/s10518-013-9466-z
Bracchi, S., Cattari, S., Degli Abbati, S., Lagomarsino, S., Magenes, G., Mandirola, M., et al. (2019). “RINTC-e project: towards the seismic risk of retrofitted existing Italian URM buildings.” in 7th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Crete, Greese, 24–26 June 2019
Bressanelli, M. E., Belleri, A., Riva, P., Magliulo, G., Bellotti, D., and Dal Lago, B. (2019). “Effects of modeling assumptions on the evaluation of the local seismic response for RC precast industrial buildings.” in 7th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering Methods in Structural Dynamics and Earthquake Engineering – COMPDYN, Crete, Greece, 24–26 June 2019, 182–195.
Brunesi, E., Nascimbene, R., Bolognini, D., and Bellotti, D. (2015). Experimental investigation of the cyclic response of reinforced precast concrete framed structures. PCI J. 60 (2), 57. doi:10.15554/pcij.03012015.57.79
Cantisani, G., and Della Corte, G. (2019). “RINTC-e: seismic risk of pre-code single-story non-residential steel buildings in Italy.”in 7th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering. Crete, Greece, 24–26 June 2019, doi:10.7712/120119.7323.19971
Capozzi, V., Magliulo, G., and Manfredi, G. (2011). “Prove a taglio su connessioni trave pilastro spinottate nelle strutture prefabbricate.” in 14° Convegno ANIDIS.
Casotto, C., Silva, V., Crowley, H., Nascimbene, R., and Pinho, R. (2015). Seismic fragility of Italian RC precast industrial structures. Eng. Structures 94, 122. doi:10.1016/j.engstruct.2015.02.034
CEN, 2004 (2004). Eurocode 2, Design of concrete structures - Part 1-1: general rules and rules for buildings. European Standard. Brussels, Belgium.
Cimmino, M., Magliulo, G., and Manfredi, G. (2020). Seismic collapse assessment of new European single-story RC precast buildings with weak connections. Bull. Earthqu. Eng. 18, 6661–6686. doi:10.1007/s10518-020-00952-7
Cimmino, M., Magliulo, G., and Manfredi, G. (2020). Seismic collapse assessment of new European single-story RC precast buildings with weak connections. Bull. Earthquake Eng. 1–26. doi:10.1007/s10518-020-00952-7
Clementi, F., Scalbi, A., and Lenci, S. (2016). Seismic performance of precast reinforced concrete buildings with dowel pin connections. J. Building Eng. 7, 224. doi:10.1016/j.jobe.2016.06.013
CNR 10025 (1998). Istruzioni per il progetto, l'esecuzione ed il controllo delle strutture prefabbricate in calcestruzzo. Bollettino Ufficiale Del. CNR.
Dal Lago, B., and Ferrara, L. (2018). Efficacy of roof-to-beam mechanical connections on the diaphragm behaviour of precast decks with spaced roof elements. Eng. Struct. 176, 681–696. doi:10.1016/j.engstruct.2018.09.027
Dal Lago, B., Lamperti, M., and Toniolo, G. (2012). “Comportamento a strappo di estremità di tegoli prefabbricati con connessioni meccaniche.” in 19° Congresso CTE.
Dal Lago, B., Negro, P., and Dal Lago, A. (2018). Seismic design and performance of dry-assembled precast structures with adaptable joints. Soil Dyn. Earthqu. Eng. 106, 182. doi:10.1016/j.soildyn.2017.12.016
Dal Lago, B., Toniolo, G., and Lamperti, M. (2016). Influence of different mechanical column foundation connection devices on the seismic behaviour of precast structures. Bull. Earthqu. Eng. 14 (12), 3485–3508. doi:10.1007/s10518-016-0010-9
Demartino, C., Vanzi, I., Monti, G., and Sulpizio, C. (2018). Precast industrial buildings in Southern Europe: loss of support at frictional beam-to-column connections under seismic actions. Bull. Earthqu. Eng. 16, 259–294. doi:10.1007/s10518-017-0196-5
Dotreppe, J. C., Colinet, G., and Kaiser, F. (2006). “Influence of the deformability of connections in the analysis of precast concrete frames.” in Fédération Internationale du Béton, Proceedings of the 2nd fib congress, Naples, Italy.
Ercolino, M., Magliulo, G., and Manfredi, G. (2016). Failure of a precast RC building due to Emilia-Romagna earthquakes. Eng. Struct. 118, 262–273. doi:10.1016/j.engstruct.2016.03.054
Felicetti, R., Lamperti, M., Toniolo, G., and Zenti, C. L. (2008). “Analisi sperimentale del comportamento sismico di connessioni tegolo-trave di strutture prefabbricate.“ in 17° Convegno CTE, Roma.
Felicetti, R., Toniolo, G., and Zenti, C. L. (2008). Amsterdam. “Experimental investigation on the seismic behaviour of connections in precast structures.” in Proceedings of the International FIB symposium
Ferreira, A., and El Debs, M. K. (2000). “Deformability of a beam-column connection with elastomeric cushion and dowel bar to beam axial force.” in The Second International Symposium on Prefabrication, Helsinki, Finland.
Fischinger, M., Kramar, M., and Isaković, T. (2008). Cyclic response of slender RC columns typical of precast industrial buildings. Bull. Earthqu. Eng. 6, 519–534. doi:10.1007/s10518-008-9064-7
Fischinger, M., Zoubek, B., and Isakovic, T. (2013). “Seismic behaviour of the beam-to-column dowel connections: macro modelling.” in 4th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering.
Iervolino, I., Spillatura, A., and Bazzurro, P. (2019). “RINTC-e project: towards the assessment of the seismic risk of existing buildings in Italy, RINTC-e: towards seismic risk assessment of existing residential reinforced concrete buildings in Italy.” in 7th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering.
Iervolino, I., Spillatura, A., and Bazzurro, P. (2018). Seismic reliability of code-conforming Italian buildings. J. Earthqu. Eng. 22 (S2), 5–27. doi:10.1080/13632469.2018.1540372
Jalayer, F., and Cornell, C. A. (2009). Alternative non-linear demand estimation methods for probability-based seismic assessments. Earthqu. Eng. Struct. Dyn. 38 (8), 951. doi:10.1002/eqe.876
Jalayer, F. (2003). Direct probabilistic seismic analysis: implementing non-linear dynamic assessments. [Ph.D. Dissertation]: Stanford University.
Kramar, M., Isakovic, T., and Fischinger, M. (2010). “Experimental investigation of “pinned” beam-to-column connections in precast industrial buildings. ” in Proceedings of the Fourteenth European Conference on Earthquake Engineering. Ohrid, Republic of Macedonia, 30 August–3 September 2010 Republic of Macedonia.
Kremmyda, G. D., Fahjan, Y. M., Psycharis, I. N., and Tsoukantas, S. G. (2017). Numerical investigation of the resistance of precast RC pinned beam-to-column connections under shear loading. Earthqu. Engng Struct. Dyn. 46 (9), 1511–1529. doi:10.1002/eqe.2868
Kremmyda, G. D., Fahjan, Y. M., and Tsoukantas, S. G. (2014). Nonlinear FE analysis of precast RC pinned beam-to-column connections under monotonic and cyclic shear loading. Bull. Earthqu. Eng. 12, 1615–1638. doi:10.7712/120113.4611.c1443
Lignos, D. G., and Krawinkler, H. (2011). Deterioration modeling of steel components in support of collapse prediction of steel moment frames under earthquake loading. J. Struct. Eng. 137 (11), 1291–1302. doi:10.1061/(asce)st.1943-541x.0000376
Luzi, L., Hailemikael, S., Bindi, D., Pacor, F., Mele, F., and Sabetta, F. (2008). ITACA (Italian ACcelerometric Archive): a web portal for the dissemination of Italian strong-motion data. Seismological Res. Lett. 79 (5), 716–722. doi:10.1785/gssrl.79.5.716
Magliulo, G., Bellotti, D., Cimmino, M., and Nascimbene, R. (2018). Modeling and seismic response analysis of RC precast Italian code-conforming buildings. J. Earthquake Eng. 22, 140–167. doi:10.1080/13632469.2018.1531093
Magliulo, G., Bellotti, D., Di Salvatore, C., and Cavalieri, F. (2019). “RINTC-e project: towards the seismic risk of low and pre-code single-story RC precast buildings in Italy.” in 7th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering. Crete, Greece. doi:10.7712/120119.7110.20034
Magliulo, G., Capozzi, V., Fabbrocino, G., and Manfredi, G. (2011). Neoprene-concrete friction relationships for seismic assessment of existing precast buildings. Eng. Struct. 33 (2), 532. doi:10.1016/j.engstruct.2010.11.011
Magliulo, G., Ercolino, M., Petrone, C., Coppola, O., and Manfredi, G. (2014). The Emilia earthquake: seismic performance of precast reinforced concrete buildings. Earthqua. Spectra 30 (2), 891. doi:10.1193/091012EQS285M
Magliulo, G., Ercolino, M., Petrone, C., Coppola, O., and Manfredi, G. (2014). The Emilia earthquake: seismic performance of precast reinforced concrete buildings. Earthqua. Spectra 30 (2). doi:10.1193/091012eqs285m
McKenna, F., Fenves, G. L., Scott, M. H., and Jeremic, B. (2000). OpenSees: open system for earthquake engineering simulation. Berkeley: Pacific earthquake engineering research center, University of CaliforniaAvailable at: http://opensees.berkeley.edu (Accessed April 8, 2021).
Minghini, F., Ongaretto, E., Ligabue, V., Savoia, M., and Tullini, N. (2016). Observational failure analysis of precast buildings after the 2012 Emilia earthquakes. Earthqua. Struct. 11 (2), 327–346. doi:10.12989/eas.2016.11.2.327
Nastri, E., Vergato, M., and Latour, M. (2017). Performance evaluation of a seismic retrofitted R.C. precast industrial building. Earthqua. Struct. 12 (1), 13. doi:10.12989/eas.2017.12.1.013
Negro, P., and Toniolo, G. (2012). Design guidelines for connections of precast structures under seismic actions. JRC Scientific Pol. Rep. doi:10.2777/37605
NTC08 (2008). Norme tecniche per le costruzioni.Decreto Ministeriale del 14/01/2008Suppl. ord. n. 30 alla G.U. n. 29 del 04/02/2008
NTC18. (2018). Aggiornamento delle “Norme tecniche per le costruzioni”. Decreto Ministeriale del 17/01/2018. Suppl. ord. n. 8 alla G.U. n. 42 del 20/02/2018.
Palanci, M., Senel, S. M., and Kalkan, A. (2017). Assessment of one story existing precast industrial buildings in Turkey based on fragility curves. Bull. Earthquake Eng. 15 (1), 271–289. doi:10.1007/s10518-016-9956-x
Psycharis, I. N., and Mouzakis, H. P. (2012). Shear resistance of pinned connections of precast members to monotonic and cyclic loading. Eng. Structures 41, 413. doi:10.1016/j.engstruct.2012.03.051
Ragni, L., Cardone, D., Conte, N., Dall'Asta, A., Di Cesare, A., Flora, A., et al. (2019). “RINTC-e project: the seismic risk of existing Italian RC buildings retrofitted with seismic isolation.”in 7th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering.
Ricci, P., Manfredi, V., Noto, F., Terrenzi, M., De Risi, M. T., Di Domenico, M., et al. (2019). “RINTC-e: towards seismic risk assessment of existing residential reinforced concrete buildings in Italy.” in 7th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering.
RINTC Workgroup (2018). Results of the 2015-2017 Implicit seismic risk of code-conforming structures in Italy (RINTC) project. ReLUIS report, Rete dei Laboratori Universitari di Ingegneria Sismica (ReLUIS). Naples, Italy. doi:10.1080/13632469.2018.1543697
Savoia, M., Mazzotti, C., Buratti, N., Ferracuti, B., Bovo, M., Ligabue, V., et al. (2012). Damages and collapses in industrial precast buildings after the Emilia earthquake. Ingegne. Sismi. 29, 120–131.
Scotta, R., De Stefani, L., and Vitaliani, R. (2015). Passive control of precast building response using cladding panels as dissipative shear walls. Bull. Earthqu. Eng. 13, 3527–3552. doi:10.1007/s10518-015-9763-9
Soroushian, P. (1987). Behavior of bars in dowel action against concrete cover. Struct. J. 84 (2), 170–176.
Sousa, R., Batalha, N., and Rodrigues, H. (2020). Numerical simulation of beam-to-column connections in precast reinforced concrete buildings using fibre-based frame models. Eng. Struct. 203, 109845. doi:10.1016/j.engstruct.2019.109845
Suzuki, A., and Iervolino, I. (2019). Seismic fragility of code-conforming Italian buildings based on SDoF approximation. J. Earthqu. Eng., 1. doi:10.1080/13632469.2019.1657989
Tassios, T. P., and Vintzeleou, E. N. (1987). Behavior of dowels under cyclic Deformations. Aci Struct. J. 84 (1), 18–30. doi:10.14359/2749
Titi, A., Biondini, F., and Toniolo, G. (2018). Seismic assessment of existing precast structures with dry-friction beam-to-column joints. Bull. Earthqu. Eng. 16, 2067–2086. doi:10.1007/s10518-017-0271-y
Toniolo, G., and Colombo, A. (2012). Precast concrete structures: the lessons learned from the L'Aquila earthquake. Struct. Concrete 13 (2), 73. doi:10.1002/suco.201100052
Toniolo, G., and Dal Lago, B. (2017). Conceptual design and full-scale experimentation of cladding panel connection systems of precast buildings. Earthqu. Eng. Struct. Dyn. 46 (14), 2565. doi:10.1002/eqe.2918
Zoubek, B., Fahjan, Y., Fischinger, M., and Isaković, T. (2014). Nonlinear finite element modelling of centric dowel connections in precast buildings. Eng. structures 14 (4), 463–477. doi:10.12989/cac.2014.14.4.463
Keywords: precast industrial buildings, modelling assumptions, seismic risk, beam-to-column connections, dowel connections, overhead crane
Citation: Bressanelli ME, Bellotti D, Belleri A, Cavalieri F, Riva P and Nascimbene R (2021) Influence of Modelling Assumptions on the Seismic Risk of Industrial Precast Concrete Structures. Front. Built Environ. 7:629956. doi: 10.3389/fbuil.2021.629956
Received: 16 November 2020; Accepted: 18 February 2021;
Published: 20 April 2021.
Edited by:
Massimo Latour, University of Salerno, ItalyReviewed by:
Alessia Monaco, Polytechnic University of Turin, ItalySaverio Spadea, University of Dundee, United Kingdom
Copyright © 2021 Bressanelli, Bellotti, Belleri, Cavalieri, Riva and Nascimbene. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Andrea Belleri, YW5kcmVhLmJlbGxlcmlAdW5pYmcuaXQ=
 Michele Egidio Bressanelli
Michele Egidio Bressanelli Davide Bellotti
Davide Bellotti Andrea Belleri
Andrea Belleri Francesco Cavalieri
Francesco Cavalieri Paolo Riva
Paolo Riva Roberto Nascimbene
Roberto Nascimbene