- Department of Civil and Environmental Engineering, Politecnico di Milano, Milan, Italy
In precast concrete buildings, connections play a key role. Among them and especially in industrial buildings, the ability to transfer a shear force from the beam to the column is often left to steel bars (often a single one) that act as dowels. Despite several research studies carried out in recent years, there is still a lack of agreement regarding the applicability of Eurocode 2 rules for fastening in concrete to such specific design case. More specifically, the role of the edge reinforcement and the effectiveness of multiple reinforcement layers in the proximity of the steel bar do not find a unique interpretation. The present paper aims to review existing design methods, both in codes and in literature, for such connections, aiming to propose a common interpretation of the load-transfer mechanism.
Introduction
Steel dowel connections are universally used to transfer shear forces acting transversal to their axes between two separate elements in reinforced concrete structures. The maximum capacity of the connection is directly linked to the shear resistance of the single shear plane at the joint location between the two connected members.
However, when the dowel is located close to a free edge, the stress field induced in the narrow member is such that the brittle response of the concrete may become dominant.
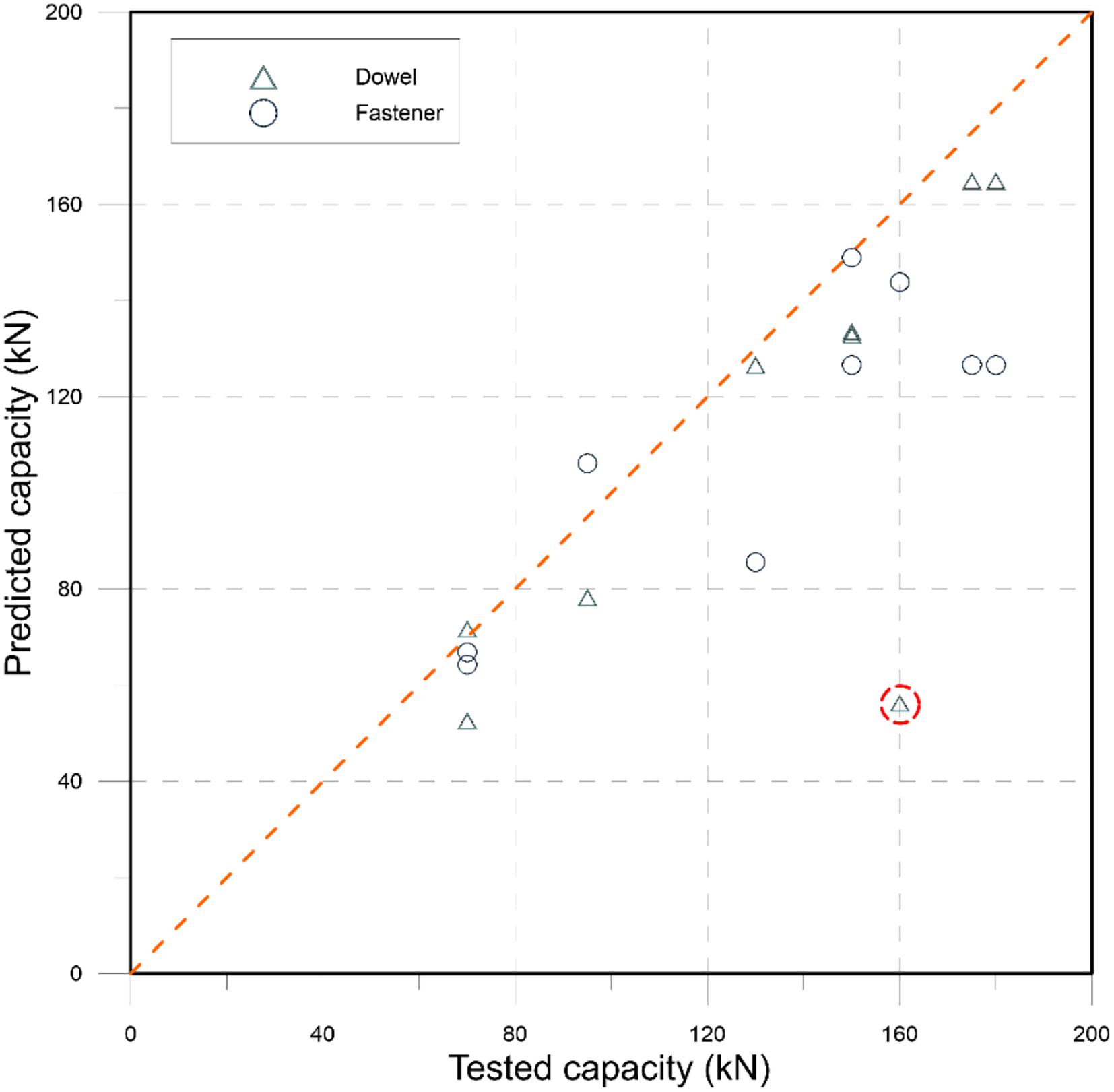
Such effect was carefully investigated by Vintzeleou and Tassios (1987) in the eighties, who predicted the conditions corresponding to side or bottom splitting of the concrete member. At the same time, due to the local crushing of the concrete in front of the dowel, they capped the dowel capacity by the force generating a plastic hinge in the dowel located within its portion embedded in the concrete. Additionally, the proposed model also accounted for strength degradation due to cyclic loading. In the end, such model indicates that the capacity of the connection is the minimum between the capacity associated with contemporary yielding of the bar and crushing of the concrete and the capacity associated with (side or bottom) splitting of the concrete member (Figure 1).
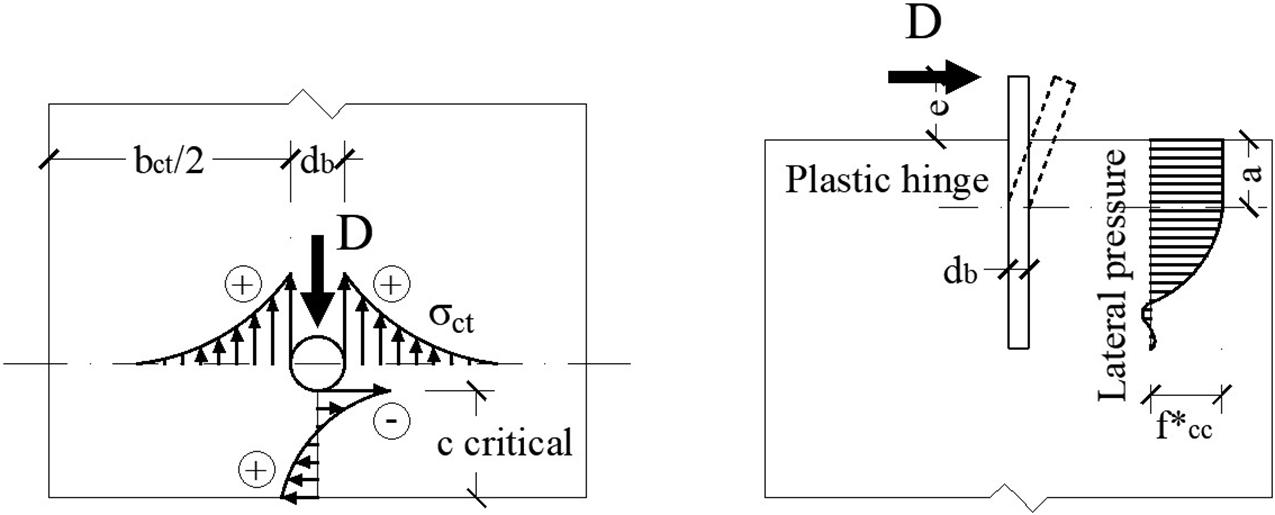
Figure 1. Stress state induced by the dowel in the concrete as regards splitting failure (left) and front crushing (right). Adapted from Vintzeleou and Tassios (1987).
Approximately 10 years later, the concrete capacity design (CCD) approach was proposed (Fuchs et al., 1995) to evaluate the capacity of single or groups of precast or post-installed fasteners in concrete subjected to tension, shear, or their interaction. In shear, the model derives semi-empirically the capacity of the concrete in front of the fastener assuming a failure surface equal to a half-cone (idealized as a half-pyramid for design easiness) and accounting for the effect of the concrete member size (Figure 2). The capacity of the connection is evaluated as the minimum between the capacity given by the cone mechanism and the simple capacity in shear of the steel element section at the concrete surface.
Figure 2. Idealized half-pyramid failure surface for individual fastener in shear. Adapted from Fuchs et al. (1995).
Such model was the basis for the initial provisions of ETAG 001 Annex C (1998), which, after some refinements (CEN/TS 1992-4-2:2009, 2009), represents the basis for the current design model of EN 1992-4 (2018).
None of the methods, at least in their original formulation, accounted for the effects of additional reinforcement in the proximity of the dowel/fastener.
EN 1992-4 (2018) currently considers the beneficial effect of the so-called “anchor reinforcement” in preventing concrete edge breakout to be decisive, while a different design model was developed by Zoubek et al. (2015) on the basis of the one proposed by Vintzeleou and Tassios (1987) for dowel connections in heavily reinforced elements subjected to cyclic loading. Such model was rapidly adopted in the design of precast industrial buildings in the presence of seismic actions.
The present paper compares the provisions provided by the two methods with respect to test results available in literature, aiming to address the inconsistencies between the two approaches and finally suggesting possible improvements and additions. To the author’s knowledge, the test results accounted in this paper are the only available ones such as to allow a direct comparison of such methods.
Accounted Design Models in Presence of Additional Reinforcement in Shear
Eurocode 2 Model
The Eurocode 2 model (EN 1992-4, 2018) accounts for the possibility that the reinforcement can entirely take up shear load if placed according to a simplified strut and tie model under some given conditions (see Figure 3). From a physical point of view, it is assumed that the reinforcement is activated after the concrete fails, according to the model previously discussed. This implies that only the reinforcement within the concrete edge breakout body, and if placed at a transversal distance no larger than 0.75 the edge distance, is activated. Additionally, it is required that (i) inside the breakout body, non-welded straight bars are anchored at least 10 times the bar diameter (and four times in the other cases) and (ii) the bars are properly anchored outside the breakout body according to “standard” Eurocode 2 prescriptions.
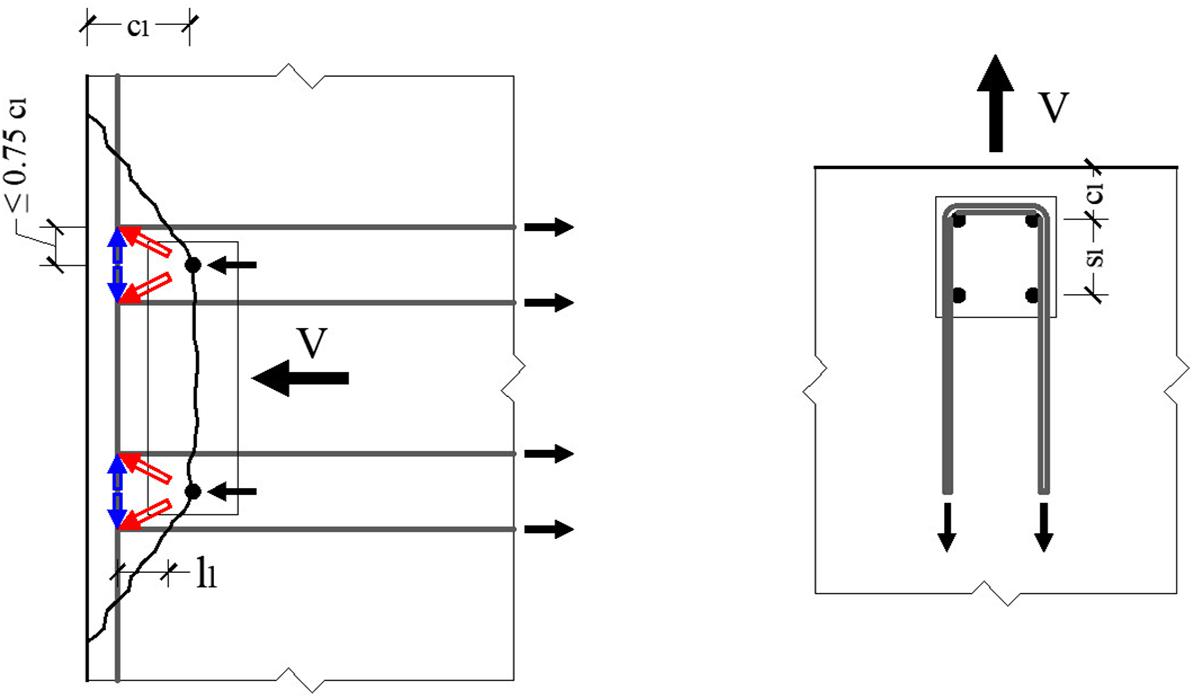
Figure 3. Surface reinforcement to take up shear forces with simplified strut and tie model to design edge reinforcement. Adapted from EN 1992-4 (2018).
Against such detailed requirements on the bars parallel to the shear direction, the model is quite vague regarding the verification of the horizontal tie. Even if in the case of stirrups, due to the limitation regarding the transversal “activation band,” the verification of the tie is automatically satisfied, in the case of single bars (whether straight or not), there is the need of accounting on surface reinforcement to guarantee the equilibrium. Such requirement is often overlooked when this model is applied, assuming that the existing surface reinforcement is sufficient to prevent any splitting action.
Finally, no specification is given with respect to the concrete strut beside the assumption of a 45° angle of the same strut.
The Zoubek, Fischinger, and Isakovic Model
Relatively recently, Zoubek et al. (2015) developed a model to predict the capacity of beam-to-column dowel connections under cyclic actions. The model was developed on the basis of experimental results obtained in the FP7 SAFECAST project (Toniolo, 2012), and it is currently adopted in the precast industry, such that it will be probably introduced or accounted in the next generation of Eurocodes.
The model distinguishes between “local” and “global” failure modes.
The local failure mode is heavily based on the previously described Vintzeleou and Tassios (1987) model, assuming a fixed position of the plastic hinge in the dowel (at a distance from the surface equal to 2.5 times the dowel diameter) and limiting the maximum contact pressure in front of the dowel to three times the concrete uniaxial compressive strength. The resistance of the dowel Rdu associated with such failure mode results as follows:
where dd is the dowel diameter, fc is the concrete cylindrical compressive strength, and fsy is the steel yield strength.
The global failure mode is a strut-and-tie model (Figure 4), which accounts for the presence of multiple layers of closed stirrups, in line with the principle designed such as to avoid the occurrence of concrete brittle failure, where (i) the strut varies its inclination, which is always determined by the relative position between the dowel and the bend of the hook, and (ii) the reinforcement layers below the surface one are also activated, if located within a critical region hcrit, with an effectiveness that decreases as a function of the depth.
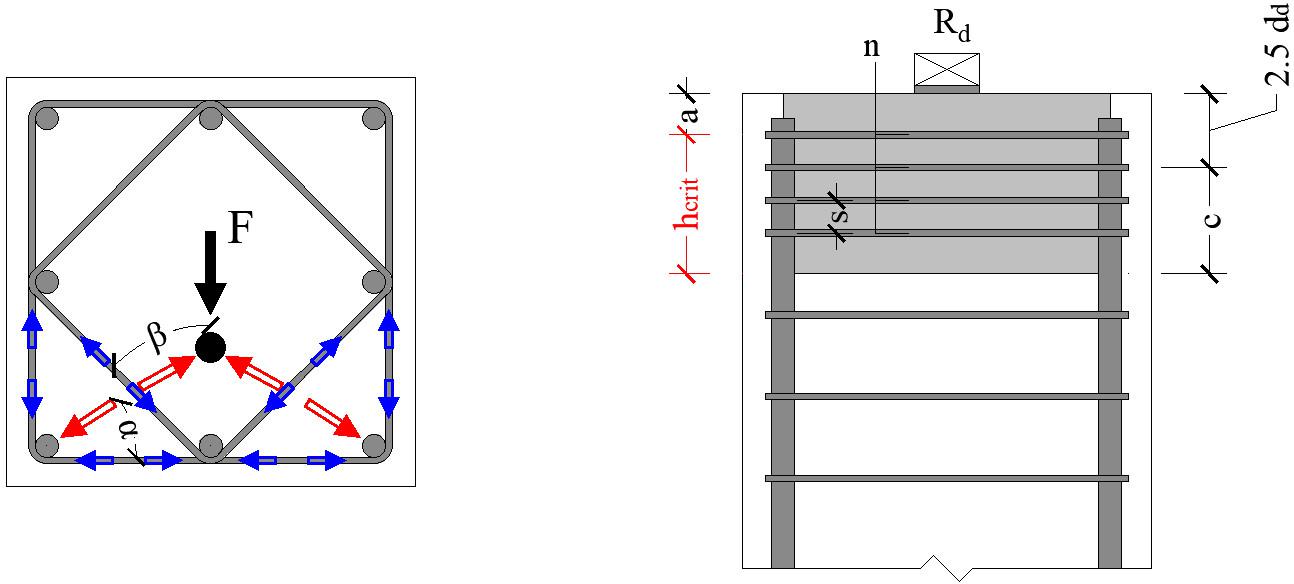
Figure 4. Zoubek et al. model: strut and tie model for a connection with a single dowel (left and center) and schematic representation of the activated stirrups (right). Adapted from Zoubek et al. (2015).
The number of the engaged stirrups n is defined as
where s is the vertical spacing between the stirrups and hcrit is defined as
with c equal to the distance between the dowel axis and the stirrup axis and a equal to the vertical concrete cover of the outermost stirrup.
In such a model, the strength of the dowel connection is defined as the force that is applied to the dowel when yielding of the first layer of stirrups occurs, while stresses in the other stirrups in the critical region are linearly reduced. As a matter of fact, from a purely computational perspective, such an assumption is equivalent to assume a number of stirrups at yielding equal to n/2.
It is remarked that an explicit evaluation of the concrete strut is not accounted by the author.
Finally, it is interesting to notice that, even though the model was developed to predict the dowel capacity under cyclic actions, it does not account for any degradation of the strength of the materials or any impact on force redistribution as potential effects of the load cycling. In particular, as for the local failure mode, this represents a significant difference with respect to the Vintzeleou and Tassios (1987) model, where the influence of cyclic loading on the dowel capacity was estimated in a 50% reduction of the capacity under monotonic loading. Such inconsistency may be solved considering that, if sufficient confinement is provided to concrete along the dowel embedment depth, concrete crushing is not dominant and dowel yielding in shear is attained (Tullini and Minghini, 2016).
Besides, it is the author’s opinion that some of the simplified assumptions in the local equilibrium in the Zoubek et al. (2015) model compensate the absence of an explicit reduction factor.
Comparison Between the Described Models
The main features of the previously described models are summarized in Table 1. For simplicity, the Eurocode model and the Zoubek et al. models are hereinafter labeled as “fastener” and “dowel,” respectively.
It can be noticed how:
(a) both models account for local steel failure, even if in the “dowel” model it is assumed that a plastic hinge develops in the connector within the embedded part contemporary to local concrete crushing;
(b) the “fastener” model does not account for local concrete crushing but for a possible engagement of a wider concrete portion resulting in a half-cone edge breakout;
(c) both models account for the possibility of reinforcement to take up shear load, even if its effectiveness strongly depends on its spatial arrangement;
(d) even though the local concrete crushing in the “dowel” model accounts for a bearing resistance in front of the connector, none of the two models explicitly evaluates the capacity of the concrete strut.
Regarding the last item, it is also noticed that the assumption of a bearing resistance equal to three times the concrete uniaxial compressive strength in the “dowel” model may be unconservative in the case of small edge distances or conservative in the opposite case.
In particular, the way the two models account for the reinforcement effectiveness is discussed with respect to the graphical representation reported in Figure 5, based on a typical detailing of reinforcement in precast concrete column (as reported in the same Zoubek et al., 2015).
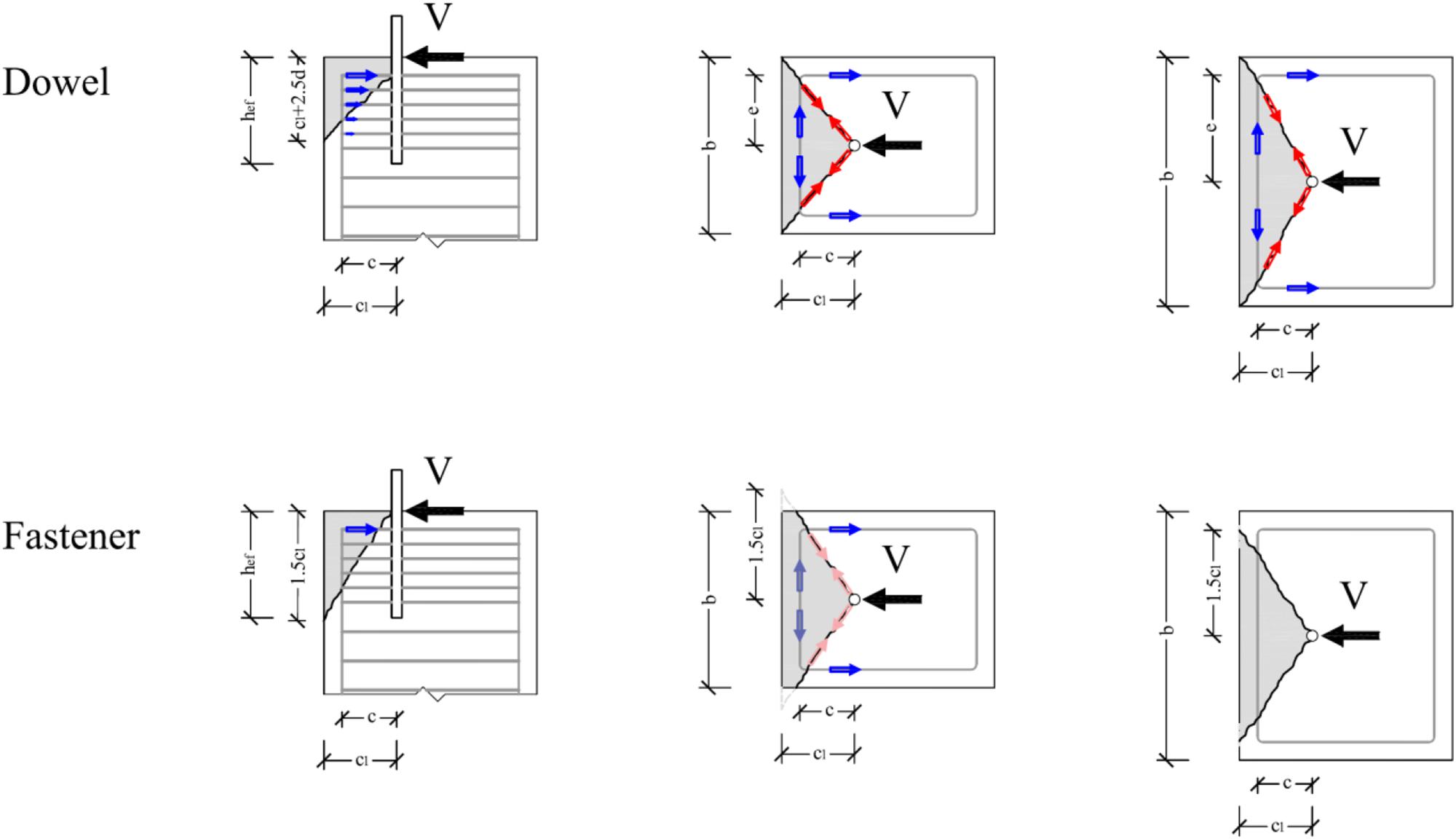
Figure 5. Engagement of reinforcement according to the “dowel” and “fastener” models (blue, tensioned ties; red, compressed struts).
As it can be seen, both models account for a portion of concrete in front of the connector, which is engaged, but while in the “dowel” model, such portion is defined only to the scope of defining the number of activated stirrups (over a depth equal to the edge distance c1 + 2.5 times the diameter d of the connector), and in the “fastener” model, such portion, as previously mentioned, is assumed to provide a resistance to the breakout actions carried out by the connector.
Additionally, a fundamental difference exists with regards the possibility of engaging the stirrups with respect to the in-plan geometry.
In fact, according to the “fastener” model, the stirrups may be engaged only if they “bend” within the concrete breakout cone (Figure 5, bottom center), whose geometry is defined uniquely as a function of the edge distance. If, for the same edge distance, the stirrup corner is located outside of the concrete cone (Figure 5, bottom right), then the stirrups are considered as ineffective in resisting the external action.
On the contrary, the “dowel” model simply sets the inclination of the concrete strut as a function of the stirrups corners, starting from the assumption that they are always engaged.
As previously mentioned, none of the models accounts for an explicit verification of the concrete compressive strut. It is the author’s opinion that the capacity related to such mechanism cannot be assumed to be automatically accounted by estimating the capacity of other concrete-related failure modes, especially in the case of heavily reinforced elements. However, very few investigations were dedicated to evaluate the strut capacity in this type of connections, as will be discussed later.
Evaluation With Respect to Existing Literature Results
When presenting their “dowel” model, Zoubek et al. (2015) compared its prediction and the ones provided by the “fastener” model (in the version of CEN/TS 1992-4-2:2009, 2009) with existing literature results on precast beam-to-column dowel connections (Fischinger et al., 2012; Psycharis and Mouzakis, 2012) obtained from the University of Ljubljana (UL) and the National Technical University of Athens (NTUA), respectively.
The same results are taken as reference in the comparison that will follow. The reason lies in the fact that Zoubek et al. (2015), when carrying out their comparison, did not account for the following items:
– The capacity related to the concrete edge breakout model should be carried out with respect not to its characteristic value (corresponding to the Eurocode 2 formulation) but rather to its mean values, which can be derived by Hofmann (2005). The ratio between such mean and characteristic values is equal to 1.8.;
– The Eurocode 2 model assumes that the reinforcement may activate after the concrete edge breaks out. However, for low amounts of reinforcement and great edge distances, the capacity provided by the edge breakout mechanism may be higher than the one provided by the reinforcement. Hence, the biggest between the two has to be considered.
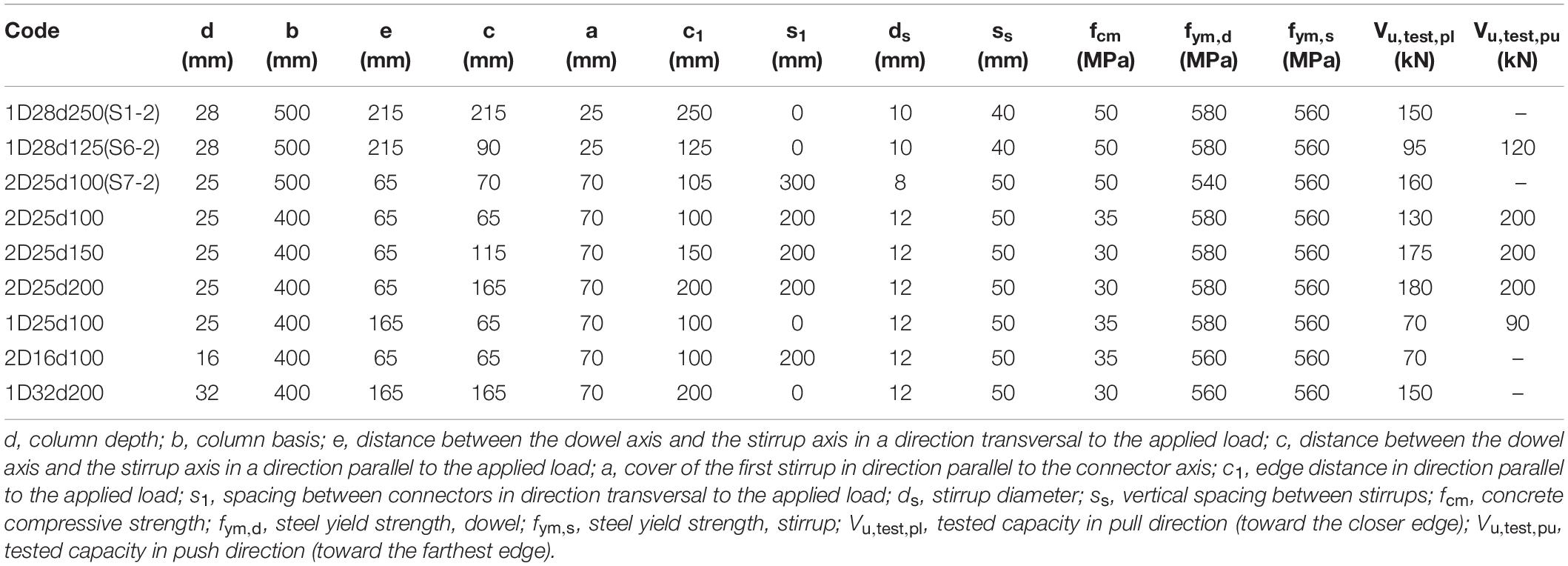
The main geometrical parameter and the experimental capacity for the evaluated tests are reported in Table 2.
By adopting such refined approach and considering, as for the test results, only the direction for which the lower capacity was detected (which is always the “pull” one, being the connector closer to the edge), the connection capacities are evaluated according to the two approaches. It is recalled that:
– as for the “dowel” model, the capacity is given by the minimum between the “local” (concrete crushing + dowel bending) and the “global” (failure of the tie represented by the reinforcement) mechanisms;
– as for the “fastener” model, the capacity is given by the maximum between the concrete edge breakout and the reinforcement (when considered to be activated) failures.
With respect to the effects of cyclic loading, it is remarked that:
– The “dowel model,” as discussed in The Zoubek, Fischinger, and Isakovic Model section, does not provide any specific material strength reduction factor;
– The “fastener” model, as formulated in EN 1992-4 (2018), generally accounts for a capacity reduction factor under cyclic (seismic) loading. As for the failure modes relevant in the evaluated tests (concrete edge failure and steel failure of the reinforcement), assuming that both the dowel and the reinforcement have adequate ductility, such factor is taken as unitary, except in the case of concrete edge group failure, where such factor is estimated as 0.85. However, such factor mainly accounts for the effects of uneven crack distribution, which, in the author’s opinion, is not applicable to the considered case, given both the compact geometry and the dense reinforcement. Consequently, to the scopes of the current comparison, no reduction is accounted.
The comparison between the predicted and tested capacities is reported in Figure 6.
It can be noticed how the predictions of the two models, globally, are not dramatically different. The mean value and the coefficient of variation (CoV) for the tested vs. predicted ratio are equal to (1.18, 18%) and (1.31, 45%) for the fastener and dowel models, respectively. The dowel model seems to provide a bigger scatter (CoV equal to 45%); this is probably due to the very low predicted capacity associated with the specimen 2D25d100(S7-2) (marked by a circle in Figure 6), which was characterized by the presence of ø8 stirrups (instead of ø10 or ø12 as in the other cases). If such specimen is not included, the model prediction significantly improves (1.12 mean and 10% CoV). However, such result stresses one critical aspect of the model, which consists in taking the minimum of the capacity associated with the “local” and “global” failure modes and of not considering any mechanism related to a global concrete failure.
It is remarked that, according to the fastener model, in specimens 1D28d125(S6-2) and 1D25d100, the stirrups are not active, since their bend is located outside of the potential concrete edge cone. Additionally, it is remarked that the dowel model is a better predictor when multiple rows are engaged, as for the specimens 2D25d150 and 2D25d200.
Enhanced Fastener Model
On the basis of the final remark of the previous section, a modification of the fastener model can be proposed to account for a number of engaged stirrups rows higher than one, as considered in its original formulation.
It is noticed that the possibility of activating all the rows within the critical region, as accounted in the dowel model, strongly accounts for a significant redistribution capacity along the depth, which may be impaired by the limited displacement associated with the local failure of the connector.
Consequently, it is proposed to limit the maximum number of activated rows to three, while still adopting a linear decrease of stresses along the depth. Such an assumption is equivalent to consider a maximum increase with respect to the full capacity provided by the first layer equal to 50%.
With reference to the test results reported in Table 2, the capacity predicted according to such model is reported in Figure 7, jointly with the predictions provided by the standard fastener model.
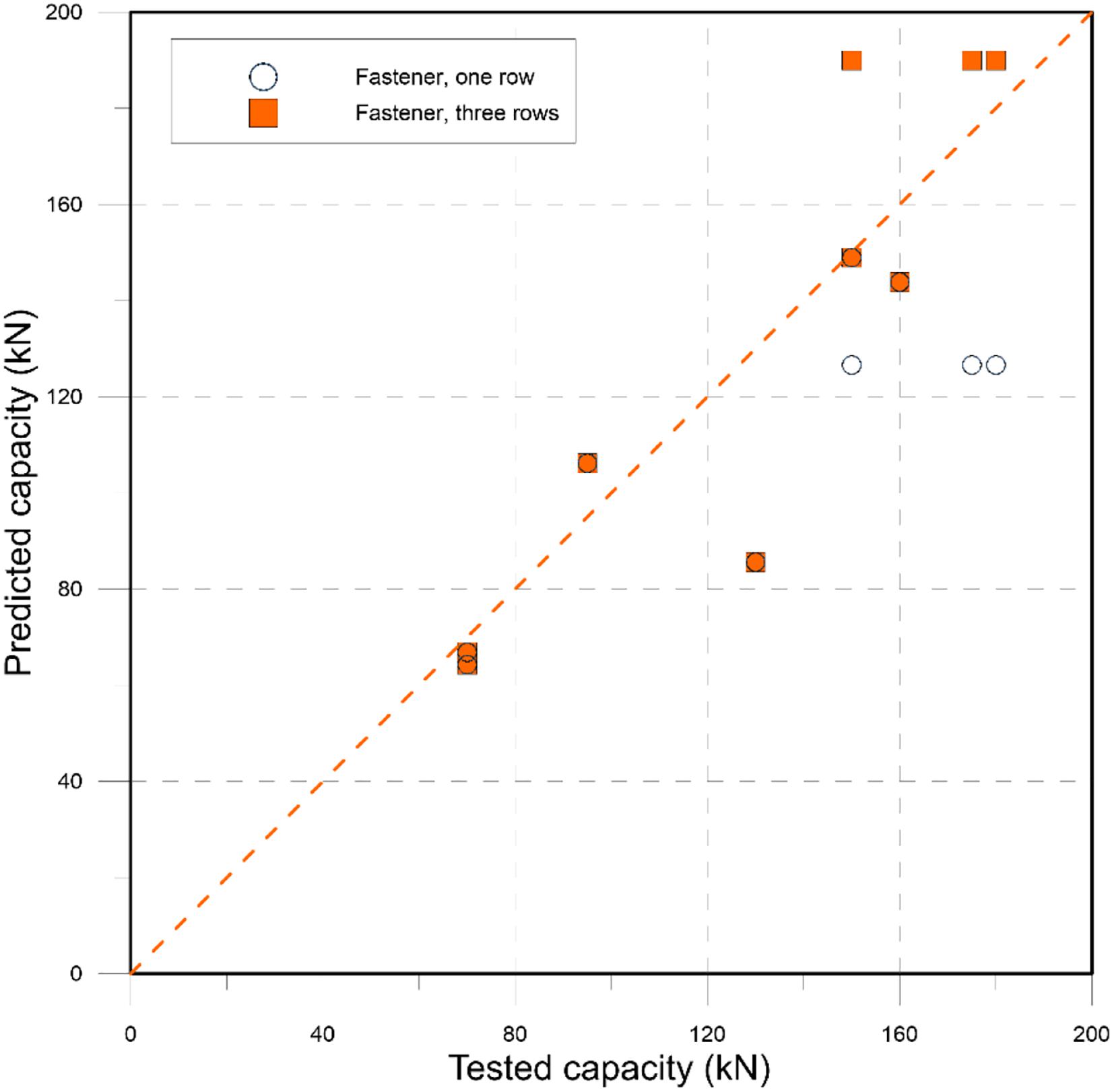
Figure 7. Predicted capacity vs. tested capacity for the “fastener” model accounting for different numbers of engaged rows.
A better agreement of the enhanced model with respect to the considered test results is provided, with a mean value and the coefficient of variation for the tested vs. predicted ratio equal to 1.04 and 18%, respectively.
Additionally, the following modifications are proposed.
As previously discussed, the fastener model does not account for a contribution of the stirrups where these ones bend outside of the edge breakout cone. However, in such case, at least the contribution of the stirrup related to their shear capacity (i.e., a “dowel effect” across the cone crack plane) should be considered.
With respect to the analyzed experimental cases, such contribution is not significant (out of two affected cases, only in one of them the predicted capacity is closer to the tested one). However, it cannot be excluded that such modification can be relevant in other cases.
Finally, it is recalled that none of the discussed models explicitly accounts for a verification of the concrete strut. Relatively recently, Eligehausen et al. (2018) showed how this failure mode may be decisive when dealing with fastener reinforcement, and they proposed an evaluation of the capacity of the concrete strut, which is basically evaluated as a Ψstrut multiplier of the edge breakout capacity:
where e and c1 are consistent with the definitions adopted in Table 2.
Such opportunity should be considered, especially when considering multiple rows of stirrups engaged, which implies a higher force acting in the strut.
It is remarked that the evaluation according to the model proposed by Eligehausen et al. (2018) is carried out for the tests previously discussed, and it is found to be never decisive. However, it would be prudent to account for it in a robust design model.
Finally, it is noticed that the current comparison is carried out for rectangular stirrups only. In the presence of additional reinforcement layers placed in non-rectangular shapes (for instance, “diamond stirrups”), an additional contribution to the reinforcement capacity may be accounted, directly proportional to the sum of the reinforcement resistance components parallel to the applied shear.
Conclusion
The paper reviews the main features of two existing models used to predict the lateral capacity of dowel-type steel connections in precast reinforced concrete elements, namely, the EN 1992-4 (2018) and the Zoubek et al. (2015) models, referred to as “fastener” and “dowel” model, respectively.
It is noticed how the two models, even if they both account for a potential strut-and-tie force transfer mechanism, significantly differ in the way they consider concrete-related failure modes and the capacity associated with the additional reinforcement.
By also comparing the predictions based on the models with existing test results for cases with stirrups arranged in rectangular shapes, as main critical issues, it is noticed how the “fastener” model (i) does not allow to consider multiple rows of stirrups along the member depth and (ii) does not consider any contribution of the stirrup where their corners are located outside of the edge breakout area. On the other side, the “dowel” model, assuming that sufficient confinement is provided along the dowel embedment depth, does not consider any contribution provided by a global failure mechanism in the concrete element (as the “edge breakout failure”), being conservative in the cases where a low reinforcement is present. Additionally, none of the models accounts for an explicit verification of the concrete strut.
However, with respect to the considered test results, no remarkable differences are detected for elements that are not lightly reinforced.
To overcome such potential conflict, it is proposed to enhance the “fastener” model by (i) accounting for a possible increase of the reinforcement capacity in the case of multiple rows up to 50% of the capacity of the most engaged row, (ii) accounting for the capacity associated with “dowel effect” in shear for cases where the stirrup corners are not internal to the volume of the edge concrete cone, and (iii) introducing an explicit verification for the concrete strut.
A validation of the proposed enhancement on a wider test results database is preferred, perhaps involving different shapes and layout of stirrups and building specimens (fullscale or not); however, to the author’s knowledge, no additional test results for dowel-type connections in narrow concrete member with multiple layers of closed stirrups are currently available.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
CEN/TS 1992-4-2:2009 (2009). Design of Fastenings for Use in Concrete—Part 4–2: Headed Fasteners. Brussels: CEN.
Eligehausen, R., Asmus, J., and Sharma, A. (2018). Neue Versuche erlauben ein wesentlich verbessertes Modell für die Berechnung des Tragverhaltens und die Bemessung. Der. Prüfingenieur. 52, 54–67.
EN 1992-4 (2018). Eurocode 2–Design of Concrete Structures–Part 4: Design of Fastenings for Use in Concrete. Brussels: CEN.
ETAG 001 Annex C (1998). European Technical Approval Guidelines 001 “Metal anchors for use in concrete”, Annex C “Design Methods for Anchorages. Brussels: EOTA.
Fischinger, M., Zoubek, B., Kramar, M., and Isakovic, T. (2012). “Cyclic response of dowel connections in precast structures,” in Proceedings of the 15th World Conference on Earthquake Engineering (Lisbon), 24–28.
Fuchs, W., Eligehausen, R., and Breen, J. E. (1995). Concrete Capacity Design (CCD) approach for fastening to concrete. ACI Struct. J. 92, 73–94. doi: 10.14359/1533
Hofmann, J. E. (2005). Tragverhalten Und Bemessung von Befestigungen Unter Beliebiger Querbelastung in Ungerissenem Beton. PhD Dissertation, University of Stuttgart, Stuttgart.
Psycharis, I. N., and Mouzakis, H. P. (2012). Shear resistance of pinned connections of precast members to monotonic and cyclic loading. Eng. Struct. 41, 413–427. doi: 10.1016/j.engstruct.2012.03.051
Toniolo, G. (2012). “SAFECAST Project: European research on seismic behavior of the connections of precast structures,” in Proceedings of the 15th World Conference on Earthquake Engineering (Lisbon), 24–28.
Tullini, N., and Minghini, F. (2016). Grouted sleeve connections used in precast reinforced concrete construction–experimental investigation of a column-to-column joint. Eng. Struct. 127, 784–803. doi: 10.1016/j.engstruct.2016.09.021
Vintzeleou, E. N., and Tassios, T. P. (1987). Behavior of dowels under cyclic deformations. ACI Struct. J. 84, 18–30. doi: 10.14359/2749
Keywords: anchorage, fastener, dowel, shear, supplementary reinforcement
Citation: Muciaccia G (2021) Design Approach for Lateral Capacity of Dowel-Type Steel Connections in Precast Reinforced Concrete Elements. Front. Built Environ. 7:640189. doi: 10.3389/fbuil.2021.640189
Received: 10 December 2020; Accepted: 03 March 2021;
Published: 29 April 2021.
Edited by:
Bruno Dal Lago, University of Insubria, ItalyReviewed by:
Fabio Minghini, University of Ferrara, ItalyEmanuele Brunesi, Fondazione Eucentre, Italy
Tatjana Isakovic, University of Ljubljana, Slovenia
Copyright © 2021 Muciaccia. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Giovanni Muciaccia, Z2lvdmFubmkubXVjaWFjY2lhQHBvbGltaS5pdA==
 Giovanni Muciaccia
Giovanni Muciaccia