Fragility Assessment of Beam-Slab Connections for Informing Earthquake-Induced Repairs in Composite-Steel Moment Resisting Frames

Introduction

In composite-steel moment-resisting frames (MRFs) seismic loads are transmitted to the MRF through bearing on the column flanges, friction and the shear stud connectors between steel beams and the concrete slab. Past experimental studies (E.g., Civjan et al., 2001; Ricles et al., 2004; Cheng and Chen, 2005) have demonstrated that structural damage in the steel beam-slab connection could lead to extensive cracking and crushing of concrete and even complete loss of composite action. Severe concrete spalling may also occur (Cordova and Deierlein, 2005). Accordingly, in full and partial-composite steel MRFs it is essential to ensure that the integrity of the shear stud connectors is maintained during an earthquake. Current seismic provisions (CEN, 2004b; AISC, 2016a) impose a 25% reduction in the shear capacity of stud connectors in order to diminish the consequences associated with uncertainty in shear stud hysteretic behavior during earthquake shaking. While this reduction aims at preventing loss of composite action, there is no quantitative information regarding the extent of potential earthquake-induced damage in the steel beam-slab connection to inform post-earthquake repair actions.

Advancements in performance-based seismic design within the framework established in the Pacific Earthquake Engineering Research Center (Cornell and Krawinkler, 2000; FEMA, 2012) necessitates the use of fragility functions to express damage in a probabilistic manner (Porter et al., 2007). For this purpose, several researchers have developed fragility functions for non-structural elements (Taghavi and Miranda, 2003; Ruiz-García and Negrete, 2009; Retamales et al., 2013) as well as steel and reinforced concrete members and their connections (Gardoni et al., 2002; Aslani and Miranda, 2005; Lignos et al., 2010; Gulec et al., 2011; Roeder et al., 2012; Lignos and Karamanci, 2013; Elkady et al., 2018). Similar efforts have been conducted for masonry infill walls (E.g., Cardone and Perrone, 2015). As yet, no means for the estimation of damage in steel beam-slab connections exists. However, this would entail the consideration of local engineering demand parameter (EDP) indicators to relate with various damage states of the steel beam-slab connection. Recent advancements in building-specific loss estimation (Elkady et al., 2020) suggests that local EDPs may be key for reliable post-earthquake decisions regarding repairs of a building. However, the significant majority of available fragility functions in the literature (E.g., FEMA, 2012) are usually expressed as a function of a story-based EDP, such as the story drift ratio (SDR).

The objective of this paper is to develop fragility functions that permit the estimation of the level of damage in steel beam-slab connections in composite floor systems as a function of the imposed local slip demands on the headed shear stud connectors. This is achieved by assembling an experimental dataset of 42 cyclic push-out tests. Four sets of fragility functions for four different damage states seen in steel beam-slab connections are developed. The first set consists of all the assembled cyclic push-out tests, whereas the remaining ones account for the stress state (i.e. tension or compression) in the slab (Suzuki and Kimura, 2019) as well as the slab type. Finally, the use of the proposed fragility functions to facilitate performance-based seismic design of buildings is demonstrated through an application to a six-story prototype building with composite-steel MRFs.

Definition of Damage States

Beam-slab connections in composite-steel MRFs constitute welded headed shear stud connectors as well as the surrounding concrete in which the studs are embedded. Since damage at specific shear stud slip demands occurs in both components of the steel beam-slab connection, thereafter, these are not separated in seismic assessment of steel beam-slab connections. Four discrete damage states (DS) of steel beam-slab connections are defined. Figure 1A depicts a schematic representation of a composite-steel beam-to-column connection along with the geometric characteristics of the shear stud and the concrete slab. The definition of damage states is based on a typical hysteretic response of steel beam-slab connections as shown in Figure 1B in terms of shear force, $Q$ vs. slip, ${\Delta }_s$. Figures 1C–F depict schematically the observed state of a steel beam-slab connection at each DS. While in a typical cyclic push-out test, damage occurs at both sides of the headed stud connectors, for illustration purposes damage states are only shown for one loading direction.

FIGURE 1

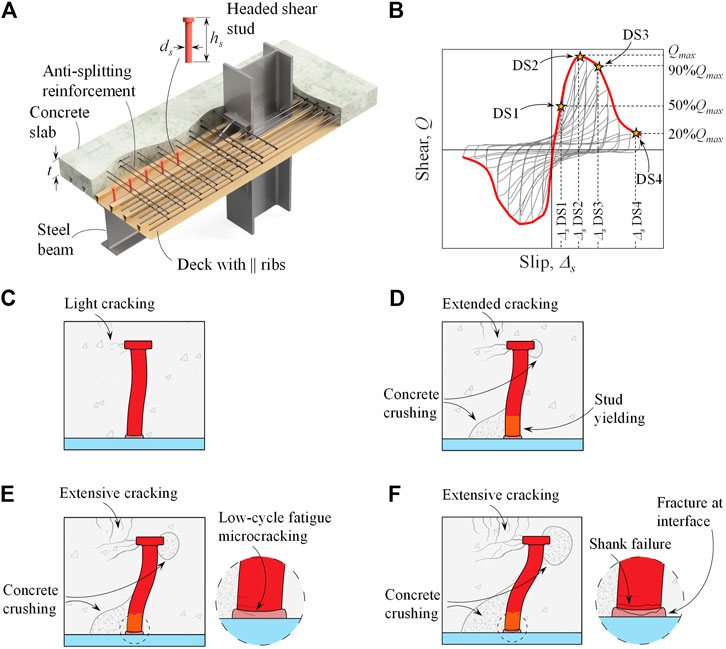
FIGURE 1. (A) Typical beam-slab connection in a composite steel MRF (B) definition of damage states from a cyclic push-out test; schematic view of the four damage states considered for steel beam-slab connections (C) DS1 (D) DS2 (E) DS3; and (F) DS4.

DS1 Light Cracking

Light cracking corresponds to crack widths less than 0.3 mm (An and Cederwall, 1996; Aslani and Miranda, 2005) that initiate in highly stressed areas near the shear stud head and may propagate to the surface of the slab. Steel beam-slab connections with higher concrete strength can sustain larger slip values before light cracking becomes visible. These cracks do not affect the structural integrity of concrete and typically require either no or cosmetic repairs as shown in Figure 1C. Hence, the shear capacity of the steel beam-slab connection is maintained.

A decrease in the initial stiffness of the steel beam-slab connection occurs at DS1. Nevertheless, the change in initial stiffness cannot be accurately determined. Saari et al. (1999) found that appreciable deviation from the initial stiffness occurs at 50% of the ultimate shear strength of the studs. Accordingly, DS1 is deduced from the cyclic envelope at 50% of the ultimate shear strength of the steel beam-slab connection as shown in Figure 1B.

DS2 Extended Cracking/Stud Yielding and Concrete Crushing Near the Base of the Shear Studs

This damage state involves visible cracks with widths between 0.3 and 2 mm (Aslani and Miranda, 2005) as well as stud yielding and crushing of concrete at the base of the shear studs. Both flexural (Bursi and Gramola, 1999; Suzuki and Kimura, 2019) and shear yielding of the studs (Zandonini and Bursi, 2000) have been reported in past push-out tests. Civjan and Singh (2003) employed finite element analysis and found that the main contributors to the Von Mises stresses at the base of shear studs are normal stresses due to bending followed by shear stresses. Past monotonic push-out tests have shown that extended cracking is observed in the slab once the peak shear, $Q_{max}$, is reached (E.g., Ollgaard et al., 1971; An and Cederwall, 1996). Herein, it is assumed that this behavior applies to cyclic push-out tests as well. Within such a context, DS2 corresponds to the slip demand at the peak shear capacity of the studs (see Figure 1B). Figures 1D, 2A illustrate the slab state at DS2. The latter shows the crack pattern, obtained using digital image correlation (DIC), from a recently conducted cyclic push-out test (El Jisr et al., 2021). The measured crack widths were found to be greater than 0.3 mm.

FIGURE 2

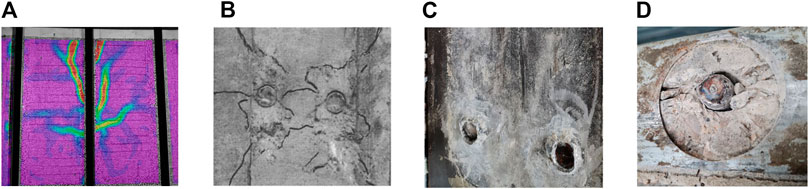
FIGURE 2. Observed damage in cyclic push-out tests (A) DS2: Extended cracking in the slab measured using digital image correlation (DIC) (El Jisr et al., 2021) (B) DS3: Extensive cracking in the slab (image from Zandonini and Bursi, 2000) (C) DS4: Loss of shear load carrying capacity/fracture of weld collar (El Jisr et al., 2021) (D) DS4: Loss of shear load carrying capacity/shearing of headed studs (El Jisr et al., 2021).

The extent of steel beam-slab connection damage is influenced by the material properties of the shear stud connectors and the surrounding concrete. Depending on the concrete compressive strength and the ultimate tensile strength of the shear studs, their ultimate shear capacity may be governed by either i) stud yielding; and/or ii) concrete crushing at the stud base (Lam and El-Lobody, 2005). The current design provisions (CEN, 2004a; AISC, 2016b) acknowledge this difference in the equations used to calculate the ultimate shear strength of a steel beam-slab connection. Generally speaking, for concrete compressive strength values of 20–40 MPa, stud yielding is dominant but a high compressive stress concentration at the base of the shear studs may result in some concrete crushing (Zandonini and Bursi, 2000). Additionally, about 90% of the collected cyclic push-out tests were governed by stud yielding as per EN 1994-1-1 (CEN, 2004a).

DS3 Low-Cycle Fatigue Microcracking in the Shear Studs/Extensive Cracking

This damage state corresponds to microcracking in the shear studs due to ultra-low-cycle fatigue (Zandonini and Bursi, 2000; Civjan and Singh, 2003). Unlike monotonic push-out tests in which the reduction in the shear strength of the steel beam-slab connection is mainly attributed to concrete crushing, ultra-low-cycle fatigue cracking in cyclic push-out tests results in rapid cyclic degradation of the connection’s shear strength and stiffness. The quality of shear stud welds on the steel beam’s top flange strongly influences DS3. Weld defects and/or out-of-straightness in the shear studs may result in early crack initiation at the tension side of the shear studs (Civjan and Singh, 2003) as shown in Figure 1E. This is usually accompanied by extensive slab cracking as shown in Figure 2B.

Referring to Figure 1B, the slip at DS3 is derived from the first cycle envelope at 10% drop in peak shear capacity of the shear studs. This corresponds to the permissible characteristic slip capacity as per EN 1994-1-1 (CEN, 2004a).

DS4 Loss of Shear Load Carrying Capacity

The last damage state is associated with the loss of shear load carrying capacity of the steel beam-slab connection. According to Cordova and Deierlein (2005), loss of force transfer in the steel beam-slab connection is detrimental and could lead to other types of failure as the slab attempts to drag the inertia forces into the MRF. Damage state DS4 is characterized by shank failure and/or fracture at the weld-collar/shank interface (Zandonini and Bursi, 2000) as schematically depicted in Figure 1F. Moreover, Figures 2C,D show typical examples of fracture at the weld-collar/shank interface in the steel beam-slab connection. Concrete cracking and crushing around the base of the shear studs are also prevalent (Zandonini and Bursi, 2000; Civjan et al., 2001; Civjan and Singh, 2003).

Zandonini and Bursi (2000) reported shear failures of the studs when their shear resistance reached 20% of their peak shear strength; hence, DS4 is deduced from the cyclic envelope curve at this shear strength level as shown in Figure 1B.

Description of Dataset of Cyclic Push-Out Experiments

Data from past cyclic push-out tests are used to establish different sets of slip demands at which DS1 to DS4 occur. For this purpose, a dataset consisting of 42 symmetric cyclic push-out tests from 11 prior test programs (Hawkins and Mitchell, 1984; Aribert and Lachal, 2000; Zandonini and Bursi, 2000; Civjan and Singh, 2003; Nakajima et al., 2003; Saari et al., 2004; Ciutina and Stratan, 2008; Fan and Liu, 2014; Zhai et al., 2018; Sun et al., 2019; Suzuki and Kimura, 2019) is assembled. Tests in which brittle failures of the shear studs occurred (E.g., rib shear or concrete pull-out failure) are not included as these are not deemed to be representative in capacity-designed composite steel MRFs. Unlike conventional push-out tests, thirteen specimens (Suzuki and Kimura, 2019) accounted for the stress state (tensile or compressive) depending on the direction of the loading excursion. This was achieved with a customized test setup that featured two steel beams sandwiched between the slabs. The slip demand was applied by either pulling the two beams away from each other or by pushing them towards each other. This setup has the advantage of alternating the stress state in the slab between tension and compression depending on the loading direction. Accordingly, test specimens from Suzuki and Kimura (2019) provide a more realistic representation of the shear stud behavior in composite steel beams.

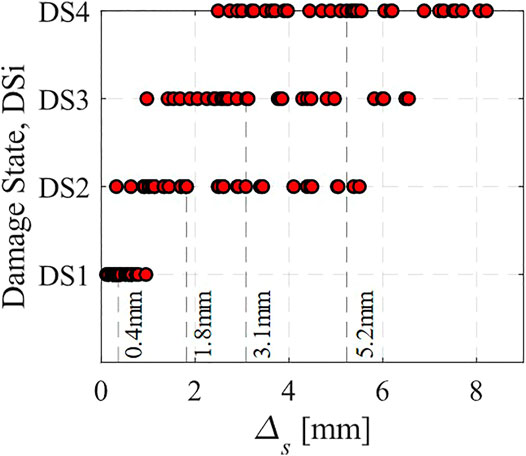
The assembled dataset features test specimens with various geometric and material properties. In brief, the dataset covers shear stud diameters between 13 and 22 mm, floor slab thicknesses between 102 and 300 mm, as well three different floor slab configurations. Particularly, i) 29 tests with a solid slab (SS) with no steel deck; ii) 12 tests with a slab with steel deck featuring ribs parallel (||) to the loading direction; and iii) one test with a slab with steel deck ribs perpendicular (⊥) to the loading direction. While the nominal ultimate tensile strength of shear studs was 450 MPa in all cases, their reported ultimate tensile strength ranges between 414 and 535 MPa. The reported concrete compressive strength ranges between 21 and 53 MPa. These correspond to a characteristic normal strength (C25/30 to C40/50) concrete. Specimen-to-specimen variability also includes the type of shear stud welds (stud gun welding vs. shield metal arc welding) as well the degree of imperfections in the welds. Figure 3 demonstrates the corresponding slip demand, on the steel beam-slab connections per damage state. The results indicate that the specimen-to-specimen variability necessitates the development of fragility functions that can estimate the probability of reaching or exceeding DS1 to DS4 in steel beam-slab connections. Note that the associated variability in slip demands increases considerably for DS2 to DS4 compared to DS1. The slip demands at each of the four damage states are summarized in Table 1. Slip demand values that are available but not reported in the respective experimental program are labeled as “NR”, whereas those not available due to early termination of the tests are labeled as not applicable, “NA”.

FIGURE 3

FIGURE 3. Distribution of slip demands, ${\Delta }_s$, corresponding to the four damage states.

TABLE 1

TABLE 1. Dataset of cyclic push-out tests.

Slip-Based Fragility Functions

In order to estimate the likelihood of damage in steel beam-slab connections, slip-based fragility functions are developed based on the assembled dataset of Table 1. These provide the probability of reaching or exceeding a damage state as a function of the peak slip demands on headed shear stud connectors.

The employed methodology to derive the fragility functions has already been successfully implemented in prior related work (Aslani and Miranda, 2005; Ruiz-García and Negrete, 2009; Lignos et al., 2010; Gulec et al., 2011; Ramirez et al., 2012; Elkady et al., 2018). In brief, the slip values at each damage state are sorted in ascending order. The empirical cumulative probability is then calculated as $p_i=i/n$, in which $n$ is the total number of data points for each damage state (see Table 2), and $i$ is the position of the slip value within the sorted data. If needed, outlier data points are excluded as per Chauvenet’s criterion (Taylor, 1997). For a given damage state, the calculated $p_i$ is plotted at its corresponding slip value in order to obtain the empirically derived cumulative distribution function (CDF). Four different CDFs (lognormal, gamma, Weibull, and Gumbel) are fitted to the empirically derived CDFs using the maximum likelihood approach (Venables and Ripley, 2013). The Kolmogorov-Smirnov (K-S) goodness-of-fit test (Benjamin and Cornell, 1970) is conducted at a 5% significance level in order to assess which of the four CDFs provides the best fit to the empirical CDF. A goodness-of-fit is assumed if the K-S test fails to reject the null hypothesis at 5% significance level; that is, the K-S statistic defined as the largest absolute difference between the theoretical and empirical CDF is less than the critical value at 5% significance level, $D_{crit,5\%}$. The K-S test is shown in Figure 4 for DS1. The hypothesis that the lognormal CDF fits the empirically derived CDF holds true if all data points lie between the upper and lower bounds represented by the dashed lines. It is found that both the lognormal (see Figure 4A) and the gamma (see Figure 4B) CDFs provide a relatively good fit for the empirical CDF because they yielded the highest p-value of K-S test.

TABLE 2

TABLE 2. Statistical parameters of the lognormal distributions for each damage state.

FIGURE 4

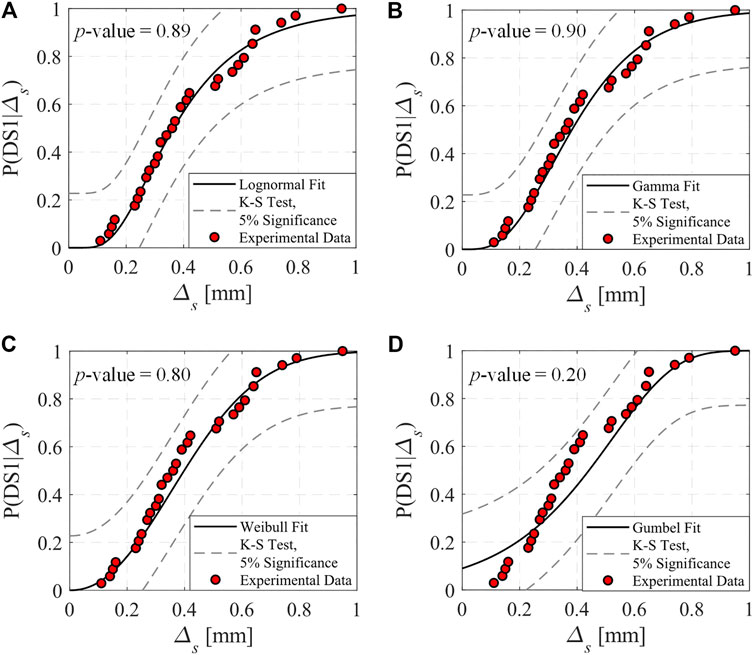
FIGURE 4. Comparison of four theoretical CDFs fitted to the empirically derived CDF for damage state DS1 (A) lognormal (B) gamma (C) Weibull and (D) Gumbel.

The lognormal distribution is selected hereinafter due to its ease of implementation and for consistency with available fragility functions defined in FEMA P-58-1 (FEMA, 2012) as well as other related studies. The lognormal CDF is defined as follows:

$\begin{array}{c}P\left(\text{DS}\ge {\text{ds}}_i\text{|}{\Delta }_s={\delta }_s\right)=\Phi \left[\frac{\ln {\Delta }_s-\ln {\mu }_{{\Delta }_s}}{{\sigma }_{\ln {\Delta }_s}}\right]\end{array}(1)$

in which $\text{P}\left(\text{DS}\ge {\text{ds}}_i\text{|}{\Delta }_s={\delta }_s\right)$ is the conditional probability of reaching or exceeding damage state $i$ in the steel beam-slab connection at a specified slip value ${\delta }_s$; ${\mu }_{{\Delta }_s}$ is the counted median of slip values at damage state $i$; ${\sigma }_{\ln {\Delta }_s}$ is the standard deviation of the natural logarithm of the slip values at damage state $i$; and $\text{Φ}$ is the cumulative standard normal distribution. Figure 5 shows that the lognormal CDF fits the empirically derived CDF fairly well for all four damage states.

FIGURE 5

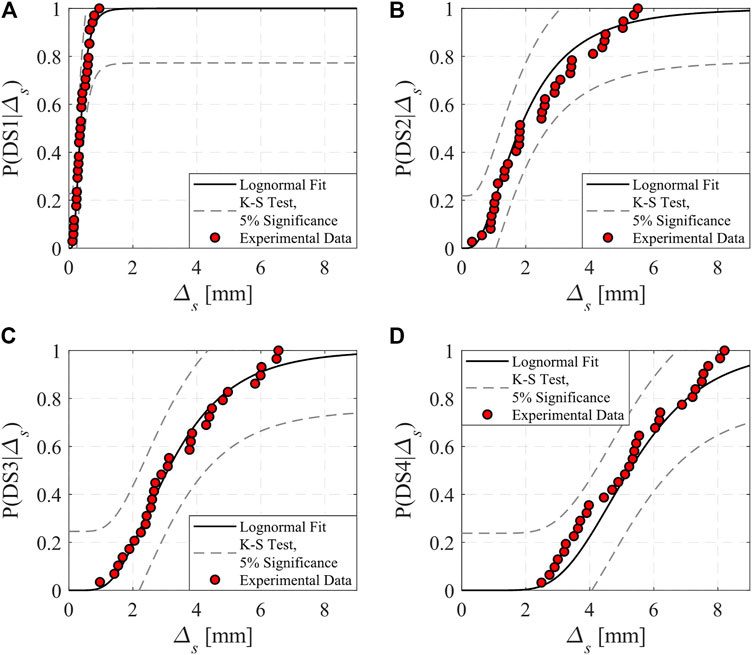
FIGURE 5. Slip-based fragility functions corresponding to the four damage states in steel beam-slab connections. (A) DS1 (B) DS2 (C) DS3 and (D) DS4.

Influence of Epistemic Uncertainty

The developed fragility functions incorporate the specimen-to-specimen uncertainty as discussed earlier. Nevertheless, the epistemic uncertainty arising from the finiteness of the dataset is not accounted for. This finite sample uncertainty can be considered by estimating confidence intervals (CI) of the peak slip demands for each damage state (Crow et al., 1960; Benjamin and Cornell, 1970). The confidence intervals of the median and logarithmic standard deviation of a lognormal CDF is computed using Eqs. 2, 3 respectively (Crow et al., 1960):

$\begin{array}{c}{\mu }_{{\Delta }_s}\cdot \exp \left[\pm z_{a/2}\cdot \frac{{\sigma }_{\ln {\Delta }_s}}{\sqrt{n}}\right]\end{array}(2)$

$\begin{array}{c}\sqrt{\frac{n-1}{{\chi }_{a/2,n-1}^2}}\cdot {\sigma }_{\ln {\Delta }_s}and\sqrt{\frac{n-1}{{\chi }_{1-a/2,n-1}^2}}\cdot {\sigma }_{\ln {\Delta }_s}\end{array}(3)$

in which, $z_{a/2}$ is the value of the standard normal deviation such that the probability of a random deviation numerically greater than $z_{a/2}$ is $a$ ; ${\chi }_{a/2,n-1}^2$ and ${\chi }_{1-a/2,n-1}^2$ are the inverse of the distribution with $n-1$ degrees of freedom and a probability of occurrence $a/2$ and $1-a/2$, respectively. Table 2 summarizes the 10 and 90% confidence intervals of the median, ${\mu }_{{\Delta }_s}$, and the logarithmic standard deviation, ${\sigma }_{\ln {\Delta }_s}$, for each damage state. The effects of the epistemic uncertainty are depicted through the uncertainty envelopes in Figure 6. This provides the upper- and lower-bound probability of reaching or exceeding each damage state from local slip demands. For instance, according to EN 1994-1-1 (CEN, 2004a), the characteristic slip capacity, ${\delta }_{uk}$, shall be greater than or equal to 6 mm at DS3. Figure 6C shows that the probability of reaching or exceeding DS3 at a slip demand of 6 mm varies between 80 and 95%; that is, the probability that the shear stud connectors in the steel beam-slab connection are ductile (CEN, 2004a) is low (5–20%). While it is true that shear studs subjected to cyclic loading may have a lower characteristic slip capacity than that recommended by EN 1994-1-1, continuum finite element analyses (El Jisr et al., 2020) and system-level nonlinear response history analysis conducted hereinafter on composite-steel MRFs with shallow beams (depth of 500 mm or less), have shown that the shear stud demands are considerably lower than ${\delta }_{uk}$. In fact, at design basis earthquake events, the probability of DS2 at slip demands of 0.5 mm (see Performance-based Assessment of a Composite Steel MRF) varies between 1 and 10%. Even if the slip demands were to be twice as high (i.e., 1 mm), the upper bound probability of DS2 remains below 30% and repairs due to extended cracking in the slab are highly unlikely.

FIGURE 6

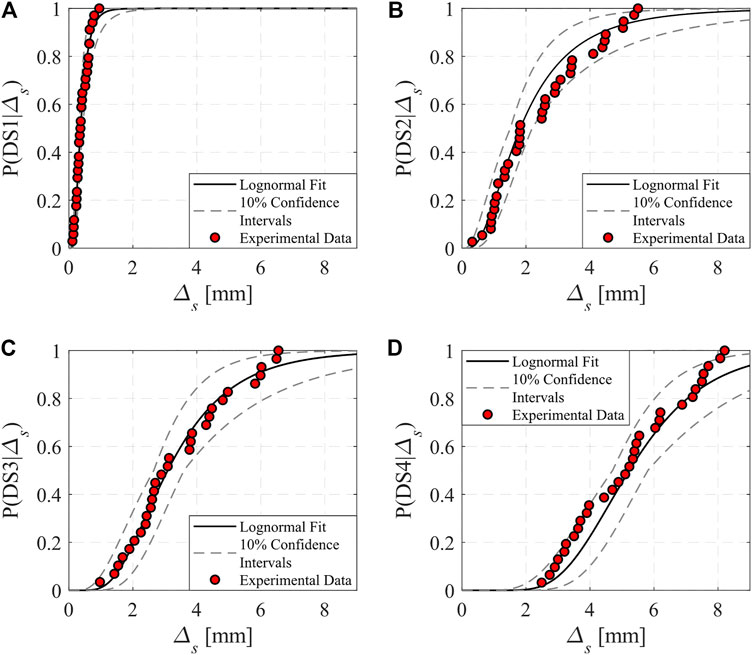
FIGURE 6. Envelope of epistemic uncertainties on fragility functions of steel beam-slab connections derived from the full dataset. (A) DS1 (B) DS2 (C) DS3 and (D) DS4.

Effect of the Stress State in the Slab

The effect of the slab stress state on the steel beam-slab connection behavior has been investigated in a recent experimental program conducted by Suzuki and Kimura (2019). In composite steel MRFs, the slab is subjected to compressive stresses under sagging bending and tensile stresses under hogging bending depending on the direction of lateral loading. These tests better emulate the steel beam-slab connection in composite steel MRFs since the stress state in the floor slab is taken into consideration. Table 1 suggests that the dataset of Suzuki and Kimura (2019) achieves appreciably higher slip demands than those from conventional push-out tests prior to reaching DS2 to DS4.

Albeit the limited available data at this point, a separate subset consisting of 13 cyclic push-out tests from Suzuki and Kimura (2019) is used to derive four complementary fragility functions at each damage state to comprehend the differences at the achieved slip demands between the two datasets. The statistical parameters of the fitted lognormal CDFs, derived with the same methodology discussed earlier, are summarized in Table 2. The reported logarithmic standard deviations from the smaller subset demonstrate a lower variability in slip demands compared to those from the full dataset, regardless of the DS under consideration. Figure 7A suggests that the effect of the slab stress state on the slip demands at DS1 (light cracking) is minimal. Conversely, DS2 to DS4 are significantly influenced by the stress state in the slab as shown in Figures 7B–D, respectively.

FIGURE 7

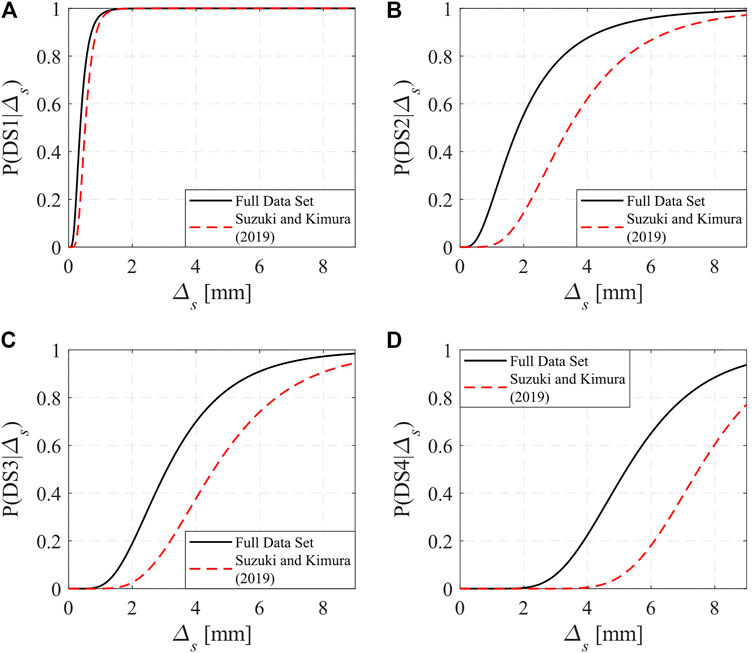
FIGURE 7. Comparison between fragility functions of steel beam-slab connections derived from the full dataset and those derived from Suzuki and Kimura (2019) subset. (A) DS1 (B) DS2 (C) DS3 and (D) DS4.

A possible explanation of the observed discrepancy is the fact that the shear studs in conventional push-out tests are subjected to fairly similar demands in both loading directions, while those in Suzuki and Kimura (2019) are asymmetric. The cyclic push-out tests showed that normal strains due to bending at the base of the shear studs are more than 10 times lower when the slab is in tension than when it is in compression. On the other hand, in conventional cyclic push-out tests, the strain demands at the base of the shear studs are nearly the same in both loading directions, thereby leading to crack initiation due to low-cycle fatigue. This often causes fracture as depicted in Figure 7D. Particularly, the probability of being or exceeding DS4 (i.e., loss of shear load carrying capacity) at 6 mm slip is more than 65% based on the full dataset, whereas when the effect of stress state in the slab is considered, the probability of being or exceeding DS4 is less than 20%. In prior work (El Jisr et al., 2020), the influence of loading history on the shear stud demands has been stressed. While physical data is not available to examine this issue, the fragility functions presented herein are considered to be a conservative estimate of the observed damage seen in beam-slab connections of composite steel MRFs under earthquake loading.

Effect of Slab Type

In composite construction practice, a steel deck is typically present as part of the composite floor system. Nevertheless, a large portion (about 70%) of the cyclic push-out tests available in the literature consist of a solid slab with no steel deck. Referring to Table 2, the dispersion measured by the logarithmic standard deviation, ${\sigma }_{\ln {\Delta }_s}$, is fairly high in the full dataset for DS1 to DS3. This dispersion is due to specimen-to-specimen variability, which comprises differences in geometry, material properties as well as the loading protocol. In order to examine how the aleatoric uncertainty is influenced by the presence of a steel deck, the full dataset is divided into two additional subsets with: i) solid slab test specimens (29) and ii) test specimens that consist of a steel deck with ribs parallel to the beam (12). Subsequently, fragility functions at DS1 to DS4 are derived for each subset. Referring to Figure 8, it is evident that specimens with a solid slab have a higher slip capacity at DS2 and DS3 damage states. At DS1, the difference between the two types of fragility functions is negligible because damage is mostly associated with fairly light slab cracking. Moreover, at DS4, loss of shear load carrying capacity due to fracture of the shear stud is not practically influenced by the slab type.

FIGURE 8

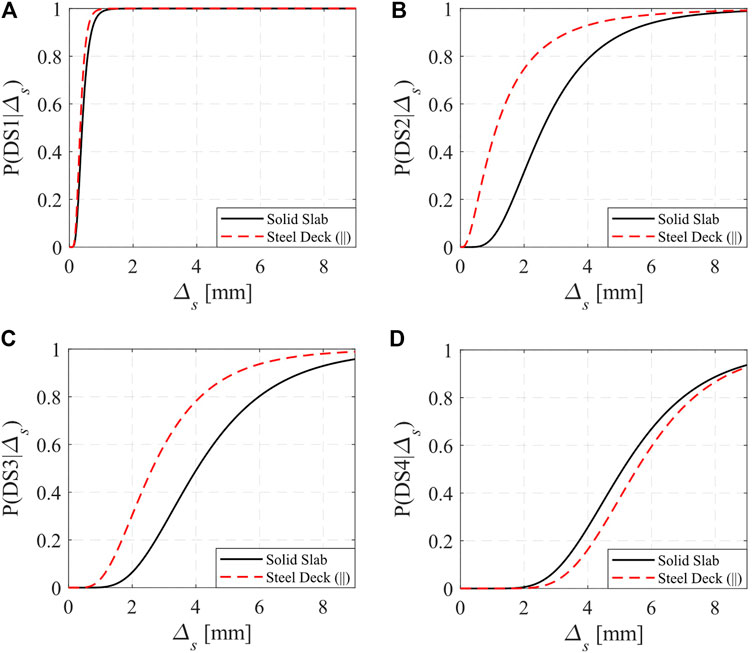
FIGURE 8. Comparison between fragility functions of steel beam-slab connections derived for solid slabs and those derived for slabs consisting of a steel deck with ribs parallel to the steel beam. (A) DS1 (B) DS2 (C) DS3 and (D) DS4.

Table 2 shows that ${\sigma }_{\ln {\Delta }_s}$ in the solid slab subset is lower at DS2 (21%) and DS3 (8%) than that in the full dataset. In contrast, for the subset with the steel deck, ${\sigma }_{\ln {\Delta }_s}$ is 26% higher at DS2 and 9% higher at DS3. The reason for the higher dispersion in the subset with the steel deck is the fact that damage in these specimens is also dependent on the deck geometry (i.e., rib height and width). Additionally, the number of data points is relatively small (12) and most of the data points are obtained from Zandonini and Bursi (2000) in which the stud dimensions, concrete compressive strength, and loading protocol were varied. In solid slabs, the studs are fully confined with the surrounding concrete, whereas in slabs consisting of a steel deck, the level of confinement is dependent on the rib dimensions. Since the slip values at DS2 and DS3 are influenced by concrete crushing, the effect of concrete compressive strength on ${\Delta }_s$ is more evident in slabs with a steel deck where less confinement is present. In the assembled dataset, the slip at DS2 and DS3, in test specimens with a steel deck present, exhibits an increasing trend with respect to the concrete compressive strength (see Table 1). Nevertheless, this dependency is inconclusive because of the limited data available. In the collected test specimens with a solid slab, the slip demand is not found to be statistically significant with respect to the concrete compressive strength.

Performance-Based Assessment of a Composite Steel Moment Resisting Frame

In this section, an application of the proposed fragility functions is demonstrated for a six-story prototype building designed according to current European design provisions (CEN 2004a; CEN, 2004b; CEN, 2005a; CEN, 2005b) for a site in Sion, Switzerland. The aim is to assess the integrity of beam-slab connections in composite-steel MRFs with shallow steel beams (depth of 500 mm or less) and partial degree composite action. The latter can be used in the design of composite-steel MRFs to effectively target a lower number of shear stud connectors, thereby leading to appreciable cost savings in composite construction.

The main seismic design parameters of the prototype building are: i) building importance class II; ii) reference peak ground acceleration, $a_{gR}=0.22g$; iii) a behavior factor, $q=$3 [i.e., strength reduction factor, R according to the United States provisions (AISC, 2016a)] and iv) soil Type D. Referring to Figure 9A, the building consists of space composite-steel MRFs in the E-W loading direction. The elevation view of the building is shown in Figure 9B. Headed shear studs ($h_s=$ 100 mm, $d_s=$16 mm) connect the MRF girders to a 125 mm thick floor slab with a 56 mm steel deck. The ribs of the deck are parallel to the girders. An 80% degree of composite action (defined as the ratio of the actual number of shear studs to that required for full composite action) is achieved in the seismic design. This corresponds to the minimum value permitted by EN-1998-1 (CEN, 2004b). However, the 25% reduction in shear stud capacity is intentionally waived. Recent findings (El Jisr et al., 2020) have shown that slip demands in composite-steel beams with depths of less than 500 mm are fairly minimal and they should not affect the integrity of the steel beam-slab connection.

FIGURE 9

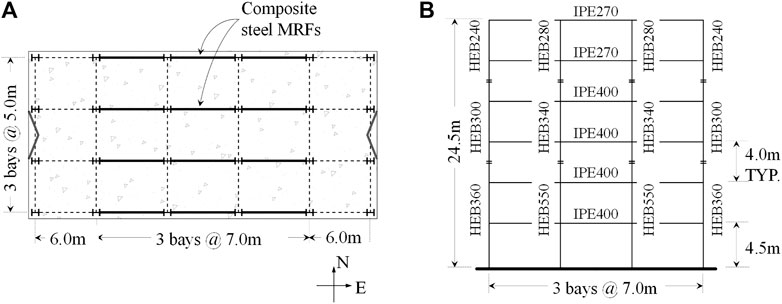
FIGURE 9. Typical plan (A) and elevation (B) view of the six-story building with composite steel MRFs.

Half of the prototype building is modelled in 2-dimensions (2-D) in the open-source simulation platform OpenSEES (McKenna, 1997). Particularly, two of the composite steel MRFs are modelled in series including a leaning column to properly represent i) the lateral strength and stiffness of the building in the E-W direction; and ii) de-stabilizing effects due to gravity loading (i.e., P-Delta). The composite beam-to-column joints are modeled by using a validated macro-model that features several nonlinear zero length elements as shown in Figure 10A. The macro-model can explicitly simulate slab-column interaction through the two force transfer mechanisms in EN-1998-1 (CEN, 2004b). The first mechanism consists of slab bearing on the column flange (noted as mechanism 1), whereas the second one is a strut-and-tie mechanism (noted mechanism 2). Slip demands on the steel beam-slab connection are captured by lumping the shear studs into a single translational zero length element. A similar approach has been implemented in past studies for partial-strength beam-to-column connections (Rassati et al., 2004; Braconi et al., 2007; Amadio et al., 2008). Flexural strength and stiffness deterioration of composite-steel beams as well as composite beam-to-column web panel zone joints are simulated according to the procedures discussed in Elkady and Lignos (2014), El Jisr et al. (2019). Figure 10B illustrates a comparison between the simulated and experimentally obtained moment-rotation relation of a fully-composite steel beam of 400 mm (Yamada et al., 2009). Moreover, as expected, the shear force, $Q$, vs. slip demand, ${\Delta }_s$, relation in the steel beam-slab connection is elastic as shown in Figure 10C. The modeling approach is deemed to be rational as it represents the hysteretic response of the composite steel beam reasonably well and can also capture slip demands on the steel beam-slab connection.

FIGURE 10

FIGURE 10. Modeling approach implemented for the system-level response history analysis of the 6-story composite steel building (A) macro-model (B) model validation with Yamada et al. (2009)(C) shear-slip response of the beam-slab connection.

Nonlinear response history analysis is conducted on the composite steel MRF at two different seismic intensities: the design basis earthquake (DBE) with a return period $T_R=$475 years and the maximum considered earthquake (MCE) with a return period $T_R=$2475 years. The earthquake records at each seismic intensity are selected to target the conditional mean spectrum (CMS) obtained from the mean magnitude and distance from rupture for each $T_R$ (Baker, 2011; Lin et al., 2013; Kohrangi et al., 2017). Figure 11 shows the two sets of 40 ground motions that were obtained by conducting probabilistic seismic hazard analysis for Sion for average spectral acceleration values, $Sa$, over a period range of 0.4–4.4 s.

FIGURE 11

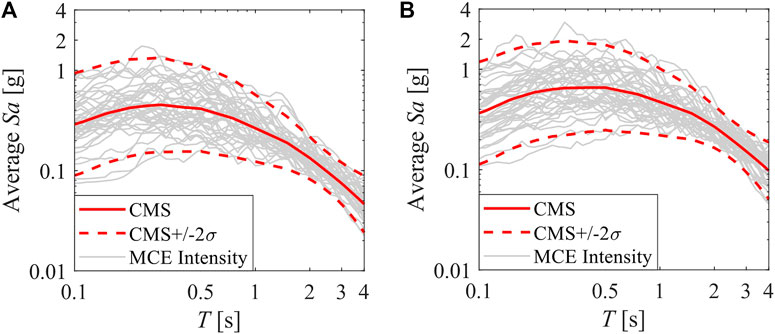
FIGURE 11. Selected ground motion records for Sion in Switzerland for two different return periods (A) 475 years (B) 2475 years.

The peak slip demands on the steel beam-slab connections are obtained along the height of the building through nonlinear response history analyses and plotted together with the median, 16th and 84th percentiles. Referring to Figure 12, the median peak slip demand values at DBE and MCE are 0.5 and 1.8 mm, respectively. Based on these values, the potential damage in the steel beam-slab connection is captured by using the developed fragility functions.

FIGURE 12

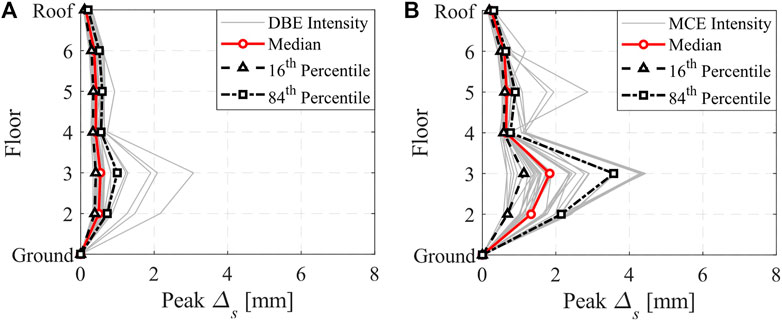
FIGURE 12. Peak ${\mathit{\Delta }}_{\mathit{s}}$ profile for the prototype composite steel MRF at (A) DBE seismic intensity and (B) MCE seismic intensity.

Figure 13Ashows the likelihood of occurrence of each damage state based on the fragility functions that were derived from the full dataset. The largest damage in the steel beam-slab connections occurs at the third floor where the demand on the composite steel beams is the highest. At DBE, the probability of attaining or exceeding DS2 (i.e., extended cracking/shear stud yielding and crushing of concrete) is less than 5%. Hence, most of the damage in the slab is attributed to light cracking, which corresponds to DS1. The probability of reaching DS1 varies between 3% at the roof to 73% at the third floor. Waiving the 25% reduction in the capacity of the shear stud connectors does not practically affect the integrity of steel beam-slab connections at seismic intensities associated with DBE. At seismic events with a low probability of occurrence, i.e., MCE, there is a 50% chance that DS2 is attained. Nevertheless, the probability of low-cycle fatigue microcracking (DS3) and therefore severe degradation in the steel beam-slab connection strength is less than 15%. Furthermore, the probability of complete loss of composite action (DS4) is negligible. Noteworthy stating that the aforementioned values are fairly conservative as they do not account for the stress state in the slab. Within such a context, the simulation results demonstrate that the 25% reduction in the shear resistance of the stud connectors may be potentially waived in seismic designs with beam depths less than 500 mm. Particularly, Figure 13B depicts the probability of being or exceeding in DS1 to DS4 according to the fragility functions that were derived based on the Suzuki and Kimura (2019) subset. Interestingly, the probability of exceeding DS1 at DBE becomes negligible and that of attaining DS2 at MCE drops to nearly 10%. The results convey the importance of the developed fragility functions for performance-based seismic design of frame buildings with composite-steel MRFs.

FIGURE 13

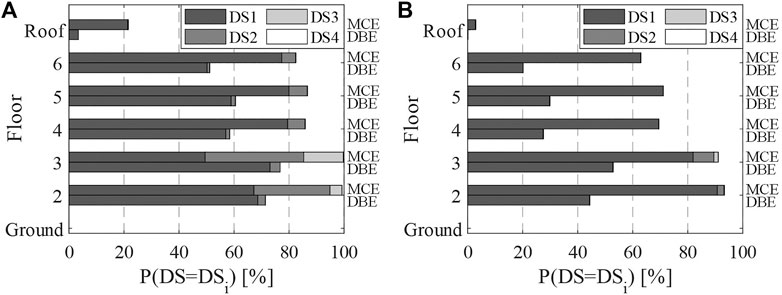
FIGURE 13. Probability of attaining each damage state along the height of the composite steel MRF; at DBE and MCE seismic intensities. (A) Full dataset (B)Suzuki and Kimura (2019) subset

Summary and Conclusion

This paper proposes slip-based fragility functions that permit the estimation of damage in steel beam-slab connections as part of composite-steel MRFs. The proposed fragility functions provide the probability of reaching or exceeding four discrete damage states as a function of the local slip demands on the steel beam-slab connections. To this end, an experimental dataset of 42 cyclic push-out tests is assembled. The four damage states include light to extensive cracking and crushing of the concrete slab, shear stud connector yielding, low-cycle fatigue microcracking in the shear studs and ultimately fracture of the steel beam-slab connection.

The fragility functions incorporate uncertainty due to specimen-to-specimen variability as well as epistemic uncertainty associated with the finite number of the collected tests. The latter is accounted for through confidence band intervals. Moreover, the dependency of the steel beam-slab connection damage on the slab stress state (tension or compression) is acknowledged through four complementary fragility functions that are derived from a subset of 13 cyclic tests (Suzuki and Kimura, 2019). These complementary fragility functions are considered more representative to describe, in a probabilistic manner, the damage of steel beam-slab connections in composite-steel MRFs. It is shown that the fragility functions derived from the full dataset provide conservative estimates of the anticipated damage in the steel beam-slab connections. Separate fragility functions are also derived for the two predominant slab types in the dataset: i) solid slab and ii) slab consisting of a steel deck with ribs parallel to the beam. The results suggest that higher damage is experienced at DS2 and DS3 if a steel deck is present. Furthermore, damage states DS2 and DS3 in specimens with a steel deck parallel to the beam are more dependent on the compressive strength of concrete than those with a solid slab.

A six-story prototype building with composite-steel MRFs is used to illustrate the potential benefits of the proposed fragility functions. The building is located in Sion, Switzerland and it is designed according to the current European seismic provisions with 80% degree of composite action. Nevertheless, the code-required 25% reduction in the shear capacity of the stud connectors is intentionally neglected. Nonlinear response history analysis is conducted at two seismic intensities, namely DBE and MCE. It is found that, at DBE, there is at least 50% to 70% chance for the slab to exhibit only minor cracking depending on the employed fragility function type. At seismic intensities associated with a low probability of exceedance, i.e., MCE, the probability of shear studs in steel beam-slab connections to exhibit low-cycle fatigue drops from about 35% to less than 10% when considering the stress state of the steel beam-slab connection in the seismic performance assessment of the building. Interestingly, the loss of the shear capacity of the steel beam-slab connections is negligible, at the same seismic intensity, regardless of the employed fragility function type. In that sense, disregarding the 25% reduction in the shear strength of the stud connectors of the examined composite steel MRF seems rational.

Data Availability Statement

The datasets presented in this study can be found in online repositories: doi:10.5281/zenodo.4660271 (El Jisr and Lignos, 2021). The names of the repository/repositories and accession number(s) can be found in the article/Supplementary Material.

Author Contributions

HE contributed in assembling the experimental data, deriving the fragility functions, and conducting the performance-based assessment of the composite-steel MRF. DL contributed in developing the methodology for developing the fragility functions, supervising HE and co-writing the article.

Funding

This study is based on work supported by the Swiss National Science Foundation (Project No. 200021_169248 and Project No. CRSK-2_190535).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The financial support is gratefully acknowledged. Any opinions expressed in the paper are those of the authors and do not necessarily reflect the views of sponsors.

References

AISC (2016a). Seismic Provisions for Structural Steel Buildings, ANSI/AISC 341-16. Chicago, IL: American Institute of Steel Construction.

AISC (2016b). Specification for Structural Steel Buildings, ANSI/AISC 360-16. Chicago, IL: American Institute of Steel Construction.

Amadio, C., Clemente, I., Macorini, L., and Fragiacomo, M. (2008). Seismic Behaviour of Hybrid Systems Made of PR Composite Frames Coupled with Dissipative Bracings. Earthquake Engng Struct. Dyn. 37, 861–879. doi:10.1002/eqe.790

CrossRef Full Text | Google Scholar

An, L., and Cederwall, K. (1996). Push-out Tests on Studs in High Strength and normal Strength concrete. J. Constructional Steel Res. 36, 15–29. doi:10.1016/0143-974X(94)00036-H

CrossRef Full Text | Google Scholar

Aribert, J. M., and Lachal, A. (2000). Cyclic Behaviour of the Shear Connection Component in Composite Joints. Behaviour of Steel Structures in Seismic Area, 105–112. (Montreal: CanadaBalkema).

Aslani, H., and Miranda, E. (2005). Fragility Assessment of Slab-Column Connections in Existing Non-ductile Reinforced concrete Buildings. J. Earthquake Eng. 9, 777–804. doi:10.1080/13632460509350566

CrossRef Full Text | Google Scholar

Baker, J. W. (2011). Conditional Mean Spectrum: Tool for Ground-Motion Selection. J. Struct. Eng. 137, 322–331. doi:10.1061/(ASCE)ST.1943-541X.0000215

CrossRef Full Text | Google Scholar

Benjamin, J. R., and Cornell, C. A. (1970). Probability, Statistics, and Decision for Civil Engineers. New York: McGraw-Hill.

Braconi, A., Salvatore, W., Tremblay, R., and Bursi, O. S. (2007). Behaviour and Modelling of Partial-Strength Beam-To-Column Composite Joints for Seismic Applications. Earthquake Engng Struct. Dyn. 36, 142–161. doi:10.1002/eqe.629

CrossRef Full Text | Google Scholar

Bursi, O. S., and Gramola, G. (1999). Behaviour of Headed Stud Shear Connectors under Lowcycle High Amplitude Displacements. Mat. Struct. 32, 290–297. doi:10.1007/BF02479599

CrossRef Full Text | Google Scholar

Cardone, D., and Perrone, G. (2015). Developing Fragility Curves and Loss Functions for Masonry Infill walls. Earthquakes and Structures 9, 257–279. doi:10.12989/eas.2015.9.1.00010.12989/eas.2015.9.1.257

CrossRef Full Text | Google Scholar

Cen, (2005a). EN 1993-1-1: Eurocode 3: Design of Steel Structures – Part 1-1: General Rules and Rules for Buildings. Brussels, Belgium: European Committee for Standardization.

Cen, (2005b). EN 1993-1-8: Eurocode 3: Design of Steel Structures – Part 1-8: Design of Joints. Brussels, Belgium: European Committee for Standardization.

Cen, (2004a). EN 1994-1-1: Eurocode 4: Design of Composite Steel and concrete Structures – Part 1-1: General Rules and Rules for Buildings. Brussels, Belgium: European Committee for Standardization.

Cen, (2004b). EN 1998-1: Eurocode 8: Design of Structures for Earthquake Resistance – Part 1: General Rules, Seismic Actions and Rules for Buildings. Brussels, Belgium: European Committee for Standardization.

Cheng, C.-T., and Chen, C.-C. (2005). Seismic Behavior of Steel Beam and Reinforced concrete Column Connections. J. Constructional Steel Res. 61, 587–606. doi:10.1016/j.jcsr.2004.09.003

CrossRef Full Text | Google Scholar

Ciutina, A. L., and Stratan, A. (2008). Cyclic Performances of Shear Connectors. Int. Conf. Compos. Construction Steel Concrete (Asce), 52–64. doi:10.1061/41142(396)5

CrossRef Full Text | Google Scholar

Civjan, S. A., Engelhardt, M. D., and Gross, J. L. (2001). Slab Effects in SMRF Retrofit Connection Tests. J. Struct. Eng. 127, 230–237. doi:10.1061/(ASCE)0733-944510.1061/(asce)0733-9445(2001)127:3(230)

CrossRef Full Text | Google Scholar

Civjan, S. A., and Singh, P. (2003). Behavior of Shear Studs Subjected to Fully Reversed Cyclic Loading. J. Struct. Eng. 129, 1466–1474. doi:10.1061/(ASCE)0733-944510.1061/(asce)0733-9445(2003)129:11(1466)

CrossRef Full Text | Google Scholar

Cordova, P. P., and Deierlein, G. G. (2005). in Validation of the Seismic Performance of Composite RCS Frames: Full-Scale Testing, Analytical Modeling, and Seismic designThe John A. Blume Earthquake Engineering Center (Stanford, CA: Stanford University).

Cornell, C. A., and Krawinkler, H. (2000). Progress and Challenges in Seismic Performance Assessment. Berkeley, CA: PEER.

Crow, E. L., Davis, F. A., Maxfield, M. W., and Davis, F. R. (1960). Statistics Manual: With Examples Taken from Ordnance Development. Courier Corporation, Dover, New York.

El Jisr, H., Elkady, A., and Lignos, D. G. (2019). Composite Steel Beam Database for Seismic Design and Performance Assessment of Composite-Steel Moment-Resisting Frame Systems. Bull. Earthquake Eng. 17, 3015–3039. doi:10.1007/s10518-019-00564-w

CrossRef Full Text | Google Scholar

El Jisr, H., Elkady, A., and Lignos, D. G. (2020). Hysteretic Behavior of Moment-Resisting Frames Considering Slab Restraint and Framing Action. J. Struct. Eng. 146, 04020145. ST. doi:10.1061/(ASCE10.1061/(asce)st.1943-541x.0002696

CrossRef Full Text | Google Scholar

El Jisr, H., Kempter, N., and Lignos, D. G. (2021). Full-scale Testing of a 2-Bay Composite Moment Resisting Frame under Lateral Cyclic Loading - Design and Setup Description. 9th International Conference on Composite Construction in Steel and Concrete. Stromberg, Germany: RUHR-Universität Bochum.

Google Scholar

El Jisr, H., and Lignos, D. (2021). Cyclic Push-Out Tests Dataset. Zenodo. doi:10.5281/zenodo.4660271

CrossRef Full Text | Google Scholar

Elkady, A., Ghimire, S., and Lignos, D. G. (2018). Fragility Curves for Wide-Flange Steel Columns and Implications for Building-specific Earthquake-Induced Loss Assessment. Earthquake Spectra 34, 1405–1429. doi:10.1193/122017EQS260M

CrossRef Full Text | Google Scholar

Elkady, A., Güell, G., and Lignos, D. G. (2020). Proposed Methodology for Building‐specific Earthquake Loss Assessment Including Column Residual Axial Shortening. Earthquake Engng Struct. Dyn. 49, 339–355. doi:10.1002/eqe.3242

CrossRef Full Text | Google Scholar

Elkady, A., and Lignos, D. G. (2014). Modeling of the Composite Action in Fully Restrained Beam-To-Column Connections: Implications in the Seismic Design and Collapse Capacity of Steel Special Moment Frames. Earthquake Engng Struct. Dyn. 43, 1935–1954. doi:10.1002/eqe.2430

CrossRef Full Text | Google Scholar

Fan, J. S., and Liu, W. (2014). Tests on Shear Studs Using Profiled Steel Sheeting Subjected to Cyclic Loading. Amm 578-579, 196–200. doi:10.4028/www.scientific.net/AMM.578-579.196

CrossRef Full Text | Google Scholar

Fema, (2012). Seismic Performance Assessment of Buildings. Washington, D.C., USA: Federal Emergency Management Agency.

Gardoni, P., Der Kiureghian, A., and Mosalam, K. M. (2002). Probabilistic Capacity Models and Fragility Estimates for Reinforced concrete Columns Based on Experimental Observations. J. Eng. Mech. 128, 1024–1038. doi:10.1061/(ASCE)0733-939910.1061/(asce)0733-9399(2002)128:10(1024)

CrossRef Full Text | Google Scholar

Gulec, C. K., Gibbons, B., Chen, A., and Whittaker, A. S. (2011). Damage States and Fragility Functions for Link Beams in Eccentrically Braced Frames. J. Constructional Steel Res. 67, 1299–1309. doi:10.1016/j.jcsr.2011.03.014

CrossRef Full Text | Google Scholar

Hawkins, N. M., and Mitchell, D. (1984). Seismic Response of Composite Shear Connections. J. Struct. Eng. 110, 2120–2136. doi:10.1061/(ASCE)0733-944510.1061/(asce)0733-9445(1984)110:9(2120)

CrossRef Full Text | Google Scholar

Kohrangi, M., Bazzurro, P., Vamvatsikos, D., and Spillatura, A. (2017). Conditional Spectrum-Based Ground Motion Record Selection Using Average Spectral Acceleration. Earthquake Engng Struct. Dyn. 46, 1667–1685. doi:10.1002/eqe.2876

CrossRef Full Text | Google Scholar

Lam, D., and El-Lobody, E. (2005). Behavior of Headed Stud Shear Connectors in Composite Beam. J. Struct. Eng. 131, 96–107. doi:10.1061/(ASCE)0733-944510.1061/(asce)0733-9445(2005)131:1(96)

CrossRef Full Text | Google Scholar

Lignos, D. G., and Karamanci, E. (2013). Drift-based and Dual-Parameter Fragility Curves for Concentrically Braced Frames in Seismic Regions. J. Constructional Steel Res. 90, 209–220. doi:10.1016/j.jcsr.2013.07.034

CrossRef Full Text | Google Scholar

Lignos, D. G., Kolios, D., and Miranda, E. (2010). Fragility Assessment of Reduced Beam Section Moment Connections. J. Struct. Eng. 136, 1140–1150. doi:10.1061/(ASCE)ST.1943-541X.0000214

CrossRef Full Text | Google Scholar

Lin, T., Harmsen, S. C., Baker, J. W., and Luco, N. (2013). Conditional Spectrum Computation Incorporating Multiple Causal Earthquakes and Ground-Motion Prediction Models. Bull. Seismological Soc. America 103, 1103–1116. doi:10.1785/0120110293

CrossRef Full Text | Google Scholar

McKenna, F. (1997). “Object Oriented Finite Element Programming Frameworks for Analysis, Algorithms and Parallel Computing”. Ph.D. Thesis, University of California, Berkeley, Berkeley, CA.

Nakajima, A., Saiki, I., Kokai, M., Doi, K., Takabayashi, Y., and Ooe, H. (2003). Cyclic Shear Force-Slip Behavior of Studs under Alternating and Pulsating Load Condition. Eng. Structures 25, 537–545. doi:10.1016/S0141-0296(02)00165-7

CrossRef Full Text | Google Scholar

Ollgaard, J., Roger, R., and Fisher, J. (1971). Shear Strength of Stud Connectors in Lightweight and normal-weight concrete. Bethlehem, PA: Lehigh University.

Porter, K., Kennedy, R., and Bachman, R. (2007). Creating Fragility Functions for Performance-Based Earthquake Engineering. Earthquake Spectra 23, 471–489. doi:10.1193/1.2720892

CrossRef Full Text | Google Scholar

Ramirez, C. M., Lignos, D. G., Miranda, E., and Kolios, D. (2012). Fragility Functions for Pre-Northridge Welded Steel Moment-Resisting Beam-To-Column Connections. Eng. Structures 45, 574–584. doi:10.1016/j.engstruct.2012.07.007

CrossRef Full Text | Google Scholar

Rassati, G. A., Leon, R. T., and Noè, S. (2004). Component Modeling of Partially Restrained Composite Joints under Cyclic and Dynamic Loading. J. Struct. Eng. 130, 343–351. doi:10.1061/(ASCE)0733-944510.1061/(asce)0733-9445(2004)130:2(343)

CrossRef Full Text | Google Scholar

Retamales, R., Davies, R., Mosqueda, G., and Filiatrault, A. (2013). Experimental Seismic Fragility of Cold-Formed Steel Framed gypsum Partition walls. J. Struct. Eng. 139, 1285–1293. doi:10.1061/(ASCE)ST.1943-541X.0000657

CrossRef Full Text | Google Scholar

Ricles, J. M., Zhang, X., Lu, L.-W., and Fisher, J. W. (2004). Development of Seismic Guidelines for Deep-Column Steel Moment Connections. Bethlehem, PA, USA: Lehigh University.

Roeder, C. W., Lumpkin, E. J., and Lehman, D. E. (2012). Seismic Performance Assessment of Concentrically Braced Steel Frames. Earthquake Spectra 28, 709–727. doi:10.1193/1.4000006

CrossRef Full Text | Google Scholar

Ruiz-García, J., and Negrete, M. (2009). Drift-based Fragility Assessment of Confined Masonry walls in Seismic Zones. Eng. Structures 31, 170–181. doi:10.1016/j.engstruct.2008.08.010

CrossRef Full Text | Google Scholar

Saari, W. K., Hajjar, J. F., Schultz, A. E., and Shield, C. K. (2004). Behavior of Shear Studs in Steel Frames with Reinforced concrete Infill walls. J. Constructional Steel Res. 60, 1453–1480. doi:10.1016/j.jcsr.2004.03.003

CrossRef Full Text | Google Scholar

Saari, W. K., Schultz, A. E., Hajjar, J. F., and Shield, C. K. (1999). Behavior of Shear Connectors in Steel Frames with Reinforced concrete Infill walls. Minneapolis, Minnesota 55455: University of Minnesota.

Sun, Q., Nie, X., Denavit, M. D., Fan, J., and Liu, W. (2019). Monotonic and Cyclic Behavior of Headed Steel Stud Anchors Welded through Profiled Steel Deck. J. Constructional Steel Res. 157, 121–131. doi:10.1016/j.jcsr.2019.01.022

CrossRef Full Text | Google Scholar

Suzuki, A., and Kimura, Y. (2019). Cyclic Behavior of Component Model of Composite Beam Subjected to Fully Reversed Cyclic Loading. J. Struct. Eng. 145. 04019015. ST. doi:10.1061/(ASCE10.1061/(asce)st.1943-541x.0002294

CrossRef Full Text | Google Scholar

Taghavi, S., and Miranda, E. (2003). Response Assessment of Nonstructural Building Elements. Berkeley, CA: Pacific Earthquake Engineering Research (PEER) Center.

Taylor, J. R. (1997). An Introduction to Error Analysis. University Science Books, Sausalito, California. 166–168.

Venables, W. N., and Ripley, B. D. (2013). Modern Applied Statistics with S-PLUS. Springer Science & Business Media, New York.

Yamada, S., Satsukawa, K., Kishiki, S., Shimada, Y., Matsuoka, Y., and Suita, K. (2009). Elasto-plastic Behavior of Panel Zone in Beam to External Column Connection with concrete SlabNihon Kenchiku Gakkai Kozokei Ronbunshu 74, 1841–1849. doi:10.3130/aijs.74.1841

CrossRef Full Text | Google Scholar

Zandonini, R., and Bursi, O. S. (2000). Cyclic Behavior of Headed Stud Shear Connectors. American Society of Civil Engineers, 470–482. doi:10.1061/40616(281)41

CrossRef Full Text | Google Scholar

Zhai, C., Lu, B., Wen, W., Ji, D., and Xie, L. (2018). Experimental Study on Shear Behavior of Studs under Monotonic and Cyclic Loadings. J. Constructional Steel Res. 151, 1–11. doi:10.1016/j.jcsr.2018.07.029

CrossRef Full Text | Google Scholar