A Screening Methodology for the Identification of Critical Units in Major-Hazard Facilities Under Seismic Loading

The complexity of process industry and the consequences that Na-Tech events could produce in terms of damage to equipment, release of dangerous substances (flammable, toxic, or explosive), and environmental consequences have prompted the scientific community to focus on the development of efficient methodologies for Quantitative Seismic Risk Analysis (QsRA) of process plants. Several analytical and numerical methods have been proposed and validated through representative case studies. Nevertheless, the complexity of this matter makes their applicability difficult, especially when a rapid identification of the critical components of a plant is required, which may induce hazardous material release and thus severe consequences for the environment and the community. Accordingly, in this paper, a screening methodology is proposed for rapid identification of the most critical components of a major-hazard plant under seismic loading. It is based on a closed-form assessment of the probability of damage for all components, derived by using analytical representations of the seismic hazard curve and the fragility functions of the equipment involved. For this purpose, fragility curves currently available in the literature or derived by using low-fidelity models could be used for simplicity, whereas the parameters of the seismic hazard curve are estimated based on the regional seismicity. The representative damage states (DS) for each equipment typology are selected based on specific damage states/loss of containment (DS/LOC) matrices, which are used to individuate the most probable LOC events. The risk is then assessed based on the potential consequences of a LOC event, using a classical consequence analysis, typically adopted in risk analysis of hazardous plants. For this purpose, specific probability classes will be used. Finally, by associating the Probability Class Index (PI) with Consequence Index (CI), a Global Risk Index (GRI) is derived, which provides the severity of the scenario. This allows us to build a ranking of the most hazardous components of a process plant by using a proper risk matrix. The applicability of the method is shown through a representative case study.

1 Introduction

The process industry is composed of a large number of types of equipment; a seismic event could cause the simultaneous damage of several units and the consequent release of dangerous substances, as well as the development of multiple accidental chains. The classical consequence-based methods for risk assessment, largely employed for the evaluation of the risk of process industries (Uijt De Haag, 2005), well fit the conditions in which events that imply the release of material and the relevant consequences are generated by failure and malfunctioning of single equipment, during service conditions. Quantitative Risk Analysis (QRA) of major-hazard process plants is a well-recognized group of techniques devoted to the risk assessment of existing facilities with a high level of potential consequences on people and the environment. These methods typically account for single events characterized by the release of content to evaluate physical effects, like overpressure, toxic dispersions, or thermal radiation able to cause injuries and environmental consequences. The frequency of these events is also predefined, so that, based on selected event trees, the frequency of the physical effects can be quantified and, using specific Probit functions, the consequence on human beings and the environment can be determined (TNO, 1992). Moreover, it is not necessary to assess the risk of all installation of an industrial facility; a selection is made based on the type of installation, the position, the amount, and the hazardousness of substances present in the installation and on the process conditions.

In the presence of Na-Tech events (technological accidents triggered by natural hazard as earthquakes), damage and loss of containment (LOC) depend on the structural behavior of the equipment; seismic events could induce structural damage that is not known a priori as well as the frequency of occurrence. Consequently, it is not possible to predetermine the worst release conditions and evaluate their consequences. In this case, classical methods lose their applicability because of additional complexities as the simultaneous damage of more units or the different frequencies of occurrence of the seismic damage, the different structural damage conditions, and LOC, as well as the development of multiple accidental chains (Young et al., 2004; Caputo, 2015). Several attempts to modify the classical QRA methods to account for these aspects are available in the literature, but without converging toward a unified approach (Fabbrocino et al., 2005; Antonioni et al., 2007).

A new probabilistic method for the seismic risk assessment in the process industry, based on the Monte Carlo simulations technique, has been recently proposed by Alessandri et al. (2018). This methodology, beyond the advantage of automatically generating all possible damage scenarios, appears very flexible because it can be easily adapted to different necessities, including economic loss evaluation, business continuity, and fatality risk analysis. This methodology can also be very useful as a starting point of a resilience computation of process plant under Na-Tech events because it allows us to identify the main starting damage scenarios (Kalemi et al., 2016). The procedure is based on a multilevel approach (Caputo, 2015; Caputo, 2016). Each propagation level includes a series of process units directly damaged by the units belonging to the previous level. The analysis starts with the “level 0,” in which only units directly damaged by the seismic event are considered. The physical effects generated by LOC are used for the damage propagation (domino effects) by means of Probit functions (TNO, 1992). One of the main results of this procedure is a list of all possible seismic damage scenarios ordered based on their annual probability of occurrence.

Despite the numerous advantages previously mentioned, this methodology requires a large amount of data and a high computational cost. Processing time increases with the amount of the equipment because it grows the number of possible initial seismic damage scenarios. Generally, it is quite prohibitive to expect that the plant manager might include in the risk analysis the individuation of seismic starting damage scenarios with their probability of occurrence and the domino effects, mainly because of the large time necessary for the data elaboration and the recognized complexity of these operations, due to the high uncertainty of the models and the interpretation of the results. Therefore, it is usually required to assess only the risk of the single equipment with respect to DS that generate LOC events. Since the total number of installations in hazardous facilities can be very large and not all installations contribute significantly to the risk, it is not worthwhile to include all types of equipment in a quantitative seismic risk assessment. Therefore, a preliminary selection method appears necessary.

Accordingly, in this paper, a screening methodology for the identification of the most critical units for seismic risk analysis of major-hazard facilities is proposed. This methodology has a double advantage: it responds to the needs of plant managers and increases the efficiency of a Quantitative Seismic Risk Analysis (QsRA) by reducing the amount of relevant equipment and the computational time.

2 Main Issues in Seismic Risk Assessment of Major-Hazard Industrial Facilities

A critical analysis of QsRA methodologies and some relevant issues can be found in (Caputo et al., 2018). The authors identified the most critical aspects of a QsRA, including hazard analysis, seismic vulnerability of the plant units, and the risk assessment in the presence of seismic loading and escalation phenomena. Estimation of site-specific seismic hazard is the first logical step of any seismic risk assessment procedure. Seismic hazard analysis and the definition of seismic input are a delicate matter that for major-hazard plants becomes more and more crucial because of the high potential consequences that seismic damage could generate. Usually, Probabilistic Seismic Hazard Analysis (PSHA) is used, which is based on full probabilistic approaches incorporating site effects and proper ranges of frequencies (Cornell, 1968).

Nevertheless, several issues are still under discussion. For example, the definition of nominal life is a controversial point that should be analyzed with the due attention because of the extremely harsh conditions in which the equipment of a process plant usually works. Typically, an important factor is adopted to account for the criticalities of these structures, even though this does not favor the harmonization of the uniform risk conditions required by the codes (Koller and Kolz, 2015). The return period of the seismic action is another issue related to the seismic design and the assessment of the process plant. Bursi et al., 2016, tried to clarify this aspect, defining two different limit states (LS) called Operating Basis Earthquake (OBE) and Safe Shutdown Earthquake (SSE); the first one is associated with significant damage LS and the second one with the near-collapse (NC) conditions (CEN, 1998). This approach, which has been borrowed by the well-known performance-based approach, needs more clarification concerning the meaning of the LS in terms of consequences. Actually, the new generation of Eurocodes contains an explicit reference to consequence classes, even though their definition is still too vague to be applied for risk analysis (Labbè, 2018).

Fragility Analysis of industrial equipment and relevant LOC conditions is crucial for a credible risk and consequence-based analysis of process plants. A large number of methodologies for deriving fragility curves, especially for the most diffused equipment like storage tanks, can be found in the literature (Salzano et al., 2003; HAZUS, 2001; Campedel et al., 2008; Buratti and Tavano, 2014; Bakalis et al., 2015; Iervolino et al., 2004; Paolacci et al., 2015; Phan et al., 2016; Kaynia, 2013; Paolacci et al., 2018). Nevertheless, few contributions focused on the possible LOC events and potential consequences (Kalemi et al., 2016; Campedel et al., 2008). Therefore, the definition of proper damage states/loss of containment (DS/LOC) relationship is still an open issue. For example, Alessandri et al., 2018; Alessandri et al., 2017, proposed the adoption of specific DS/LOC matrices. This is crucial in consequence analysis, which strongly depends on the amount of released material and the generated physical effects (TNO, 1992).

Finally, the risk analysis of a process plant can be quantified by combining seismic hazard, vulnerability, and consequence analyses. In addition, given that the seismic action could generate a multiplicity of damage conditions, the mutual interaction should also be accounted for, including the possible domino effects (Alessandri et al., 2018; Caputo, 2016). A QsRA methodology, accounting for, in a realistic manner, all these steps is not yet available, despite many years of research. In fact, while the literature about seismic risk assessment of process plants is scarce, as compared to other sectors (O’Reilly and Calvi, 2021), recently, the attention toward this issue increased, as demonstrated by the funding of dedicated international research projects (LESSLOSS, 2004; Tsionis et al., 2016; Karamanos et al., 2013; Bursi and Reza, 2018a; Bursi and Reza, 2018b). All the above-mentioned aspects clearly show the complexity of this matter and the need to simplify the approach for practical applications. Since the total number of installations may be very large, a QsRA would require a very long and unrealistic data processing time.

Consequently, in what follows, a short-cut methodology for a decision-making analysis implying the selection of critical equipment of major-hazard industries is proposed and applied to a realistic case study. The selection method here allows us to assess also the risk of the single equipment with respect to DS that generate LOC events.

3 A Methodology for the Identification of Critical Units in Major-Hazard Industrial Plants Under Seismic Loading

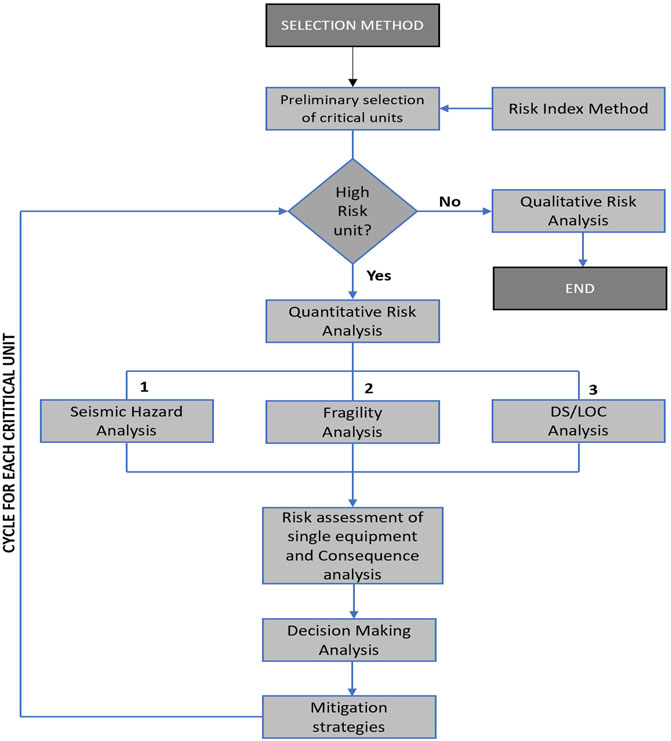
In this section, a screening methodology for the identification of the most critical units in major-hazard industrial plants under seismic loading is proposed and described. The method is based on the following main steps:

1. Preliminary identification of the critical units of the industrial plant.

2. Estimation of site-specific seismic hazard.

3. Fragility analysis of each critical unit previously selected.

4. LOC events identification with DS/LOC correlation matrices.

5. Evaluation of the mean annual frequency of LOC events.

6. Decision-making analysis and ranking of scenarios.

In the first step, a preliminary selection of the units is performed through the use of an index method, which is based on the idea of using synthetic indexes to account for seismic hazard, vulnerability, and exposition (consequences). A ranking of all possible critical equipment is then built, which allows the preliminary identification of the most critical units. Subsequently, the seismic hazard analysis and the fragility analysis of each critical unit previously identified can be performed; the mean annual frequency of their most relevant DS is then calculated using a closed-form solution for seismic hazard and vulnerability. Based on the identification of a DS-LOC matrix, it is possible to evaluate LOC events and quantify the consequence class to which the analyzed equipment belongs. Starting from the mean annual frequency of the damage of each unit, a ranking of the most critical units can be drawn up, and consequently, the seismic risk conditions can be managed through a decision-making analysis and the selection of proper seismic mitigation strategies. Figure 1 shows the flowchart of the proposed screening methodology, whose single steps will be analyzed and discussed in detail in the next sections.

FIGURE 1

FIGURE 1. Flowchart of the selection method of critical units in major-hazard plants.

3.1 Preliminary Identification of the Critical Units

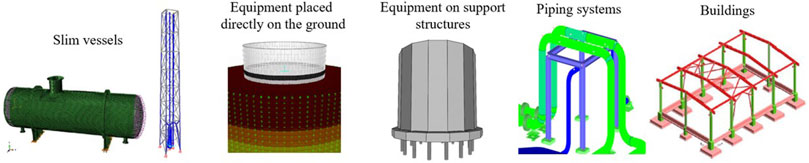
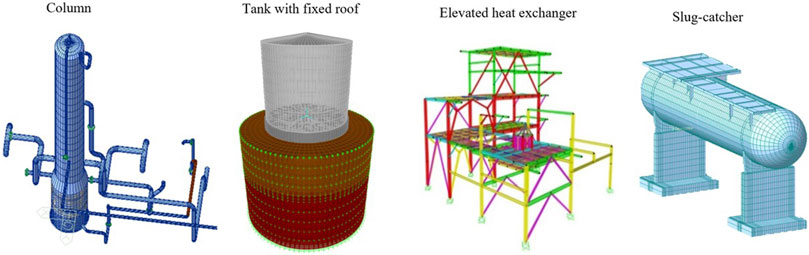
Since the total number of installations in the major-hazard industrial plant can be very large, a preliminary selection of critical components is a very important task of the methodology because it allows the selection of the most critical units, decreasing the amount of equipment to be considered in the following steps and drastically reducing the computational time. According to (Paolacci et al., 2013), the main equipment of a process plant can be classified into a restricted number of categories (Figure 2):

• Slim vessels: cylindrical equipment with a large height-to-diameter ratio (usually from 5 to 30). They can be vertical elements anchored to the foundation, both free and restrained along the height, or horizontal vessels on saddle supports. Columns, stacks, reactors, and horizontal vessels are also included.

• Equipment directly placed on the ground: this category consists of equipment characterized by comparable dimensions in the three directions and high masses. The most important category is represented by storage tanks.

• Equipment on support structures: this category includes equipment supported by columns (furnaces, spherical tanks, compressors, tanks on legs, air-cooler, etc.\enleadertwodots) or elevated equipment placed on metallic frames.

• Piping systems.

• Buildings: in this paper, this category will be excluded since the risk assessment methods are well established in the literature.

FIGURE 2

FIGURE 2. Structural typologies of a process plant.

Special attention should be paid to elements that have no direct consequences because, for example, they contain nonhazardous material but are crucial for the safety of the plant (e.g., firefighting water tank), or they represent secondary structural elements. In the first case, they should be clearly included in the ranking list, discussed in Section 3.6. In the second case, a specific structural analysis should be performed only in the further levels of analysis to account for the eventual influence on the seismic response of the main equipment. A special case is represented by nonhazardous equipment, whose collapse may induce failure in some surrounding elements, generating in turn accidents and triggering domino effects (Kikic et al., 1999).

The identification of the most critical equipment of a major-hazard industrial plant depends on several factors: 1) level of expected seismic hazard, 2) seismic design and vulnerability of the equipment, 3) conservation and maintenance status of the equipment, 4) physical effects related to the dangerousness of the stored material, 5) exposition to the external zones, and 6) domino effects.

A reasonable selection criterion should necessarily integrate all these aspects in a rational manner. At this end, the international literature provides at least three methods (Caputo et al., 2018):

• Preliminary calculation of the damage probability for each equipment, evaluation of the relevant consequences, and risk recomposition (Girgin and Krausmann, 2013).

• Use of vulnerability curves.

• Risk Index methods (Giannelli et al., 2020; Cruz and Okada, 2008).

The first two methods require a high level of information and analysis that generally is not suitable in this step for quick screening of numerous equipment. For this reason, a model based on risk indices appears more reasonable. Sometimes equipment design and other pieces of information are not available, especially in an older process plant, so that the choice of a simplified method such as Risk Index methods becomes mandatory. Starting from the definition of seismic risk, whose main ingredients are hazard, vulnerability, and exposure, a synthetic I_R index can be defined, which can be expressed in a conventional manner as follows:

$I_R=I_H\times I_V\times I_E(1)$

where

I_R is the Risk Index;

I_H is the Seismic Hazard Index;

I_V is the Seismic Vulnerability Index;

I_E is the Exposure Index.

Usually, the Seismic Hazard Index I_H should be used to characterize and compare the risk of different seismic zones. In the presence of a plant placed in a specific seismic zone, it becomes meaningless and can be omitted. Instead, in the case of very large industrial plants, which include areas with different seismic hazard conditions, the definition of a Hazard Index (I_H) is recommended. I_H can be defined by assigning to the index a value between one and the maximum number of zones with different seismic hazards identified in the industrial site. This value should be assigned to each equipment based on the area where it is located.

The Seismic Vulnerability Index I_V depends on aspects of different nature, such as

• equipment typology;

• state of preservation;

• degradation phenomena;

• typical DS.

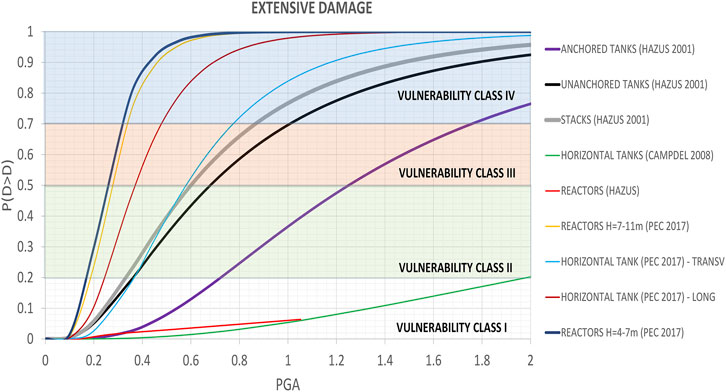
The most direct way to define I_V is to identify vulnerability classes. Different from civil structures, for which the EMS-98 scale is available, which relates vulnerability classes to structural typologies, for industrial equipment, seismic vulnerability classes are not defined yet (Musson et al., 1998). For this reason, a simple method based on fragility curves is herein proposed. A fragility curve describes the probability of exceeding different damage LS given a certain level of ground motion intensity. Different methods can be employed to develop fragility curves in the field of earthquake engineering. When you need a very quick analysis or do not have much information about the equipment, the use of empirical curves or expert opinion-based curves is suggested. Empirical curves are based on observation of actual damage and postseismic surveys, while expert opinion-based curves are directly estimated by experts or based on Vulnerability Index models that use expert judgment. Both solutions are available in the literature for the different structural categories (HAZUS, 2001; Campedel et al., 2008; PEC, 2017).

Because the significant DS for the risk analysis of a process plant are those associable with a material release (LOC), it is reasonable to adopt fragility curves related to an “extensive DS” that could reasonably generate a LOC (HAZUS, 2001). If the plant manager can provide design material and other documentations, the fragility curves of the main equipment like tanks, columns, or horizontal vessels can be analytically evaluated with static or dynamic seismic analysis performed on lumped masses models with a few degrees of freedom. Whenever possible, a careful inspection of the equipment in an industrial plant is strongly recommended, even at this level. This allows us to directly observe some critical issues and to modify the Vulnerability Indexes if necessary, including the units deemed critical through an expert judgment. The vulnerability classes of equipment typologies could be related to fragility curves by simply setting limits on the probability of damage. In this respect, the damage frequency defined by EMS-98 can be adopted. Consequently, the first vulnerability class can be defined by a damage probability between 0 and 20%, while the second class is defined by a damage probability between 20 and 50%. The third and fourth classes are defined by the damage probability ranging from 50 to 70% and 70 to 100%, respectively. This latter differentiation, which is not included in the EMS-98, is here introduced to better distinguish the seismic vulnerability.

For each unit, the vulnerability class and the corresponding Vulnerability Index (I_V), which assumes values between I_V = 1 and I_V = 4, are assigned by identifying, on the fragility curve, the range of damage probability measured at the peak ground acceleration (PGA), corresponding to the considered damage LS.

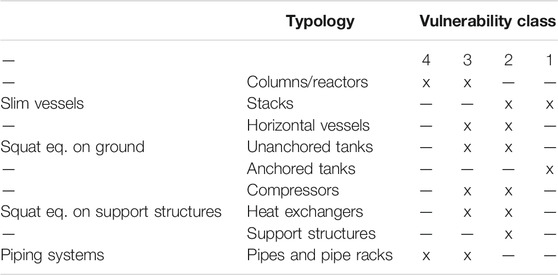
According to Figure 3, which represents some fragility curves of industrial equipment available in the literature, Table 1 proposes the association between structural categories and the seismic vulnerably class, considering a PGA range, whose lower and upper bounds correspond to the OBE and SSE damage LS, with values related to the seismic zone. According to past seismic damage surveys (Krausmann et al., 2017), reasonable values for the lower and upper limits can be assumed to be 0.3 and 0.8 g, respectively.

FIGURE 3

FIGURE 3. Fragility functions of plant equipment.

TABLE 1

TABLE 1. Vulnerability classes of process plant equipment.

The highest class represents structures with the highest seismic vulnerability. Given that each structural category could be characterized by a certain geometrical and mechanical variability, it has been deemed necessary to individuate, for each structural category, adjacent vulnerability classes. For example, the highest columns are typically more vulnerable than the other (PEC, 2017).

Finally, the Exposure Index I_E is defined in such a way to account for the criteria related to the standard major-hazard accidental conditions. The Seveso III European directive on the Control of Major-Accident Hazards Involving Dangerous Substances (Directive 2012/18/EU, S. I, 2012) suggests a preliminary screening based on the standard safety report of the major-hazard plants. Consequently, I_E can be determined using standard technological accidental conditions. For events with limited impact on the surrounding area, it can be assumed that I_E = 1 and I_E = 2 are assigned to events confined in the reference area of the units (distance D $<$ 50 m), I_E = 3 is assigned to events with impact on large zones of the plant (distance D $>$ 50 m), and finally, I_E = 4 is assigned to events with consequences on the surrounding community.

In order to identify and complete the preliminary identification of the most critical units, the Risk Index values of Table 2 are proposed. Once the equipment with medium/high-risk level is selected, the quantitative evaluation of their seismic risk is performed to recognize structural and nonstructural deficiencies that could generate severe consequences. In this paper, such evaluation is confined to structures that can be directly damaged by the earthquake, neglecting eventual damage propagation effects (Kalemi et al., 2016).

TABLE 2

TABLE 2. Risk Index and risk level for process plant equipment.

3.2 Estimation of Site-Specific Seismic Hazard

The seismic hazard of a site is usually derived through a full PSHA, which is expressed as a mean annual frequency of exceeding a certain intensity measure (IM) (Cornell, 1968). In addition, local seismic analyses are often performed to better characterize soil class and thus account for possible amplification phenomena. In this respect, OpenQuake, an open-source software developed by the Global Earthquake Model Foundation, can be profitably used (Pagani et al., 2014). In the present work, the Matlab script MatHazard, developed by the research group of the Roma Tre University, has been adopted, whose typical interface is illustrated in Figure 4A. As a matter of fact, an example of a hazard curve for the city of Viggiano (Italy) located in the Basilicata Region is shown in Figure 4B, which has been built for soil class C. In this case, the seismogenic zones 926 and 927 have been used, which are identified in the Italian zonation ZS9 (INGV, 2014).

FIGURE 4

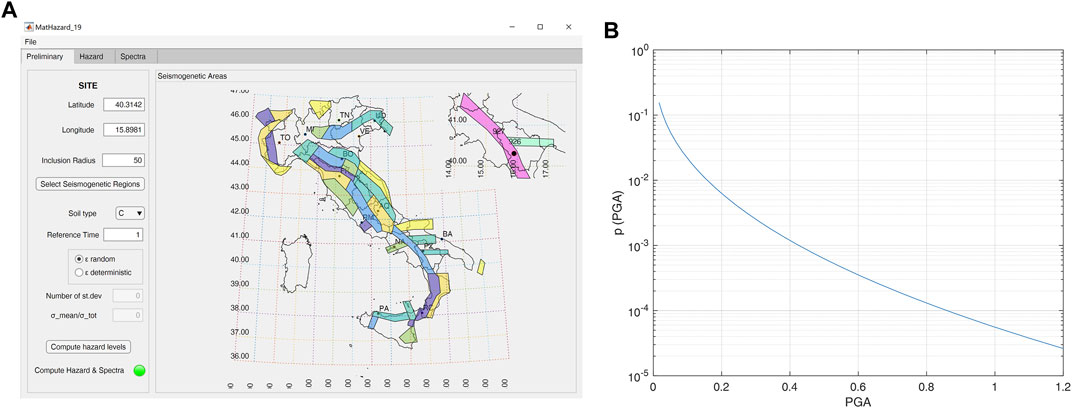
FIGURE 4. (A) MatHazard software interface for PSHA; (B) seismic hazard curve of Viggiano city (Italy).

As a simplified alternative, many technical codes, as the Italian one (NTC 2018, 2018) or the Eurocodes (CEN, 1998), provide, for different LS, the return period of the earthquake and thus the mean annual frequency of exceeding the PGA. Consequently, a simplified linear piece-wise seismic hazard curve representation can be used. However, in the light of the risk assessment method that will be illustrated inSection 3.5, it is convenient to linearize the hazard curve in the log-log plane, whose equation in the ordinary plan can be expressed as (Jalayer and Cornell, 2003)

$\lambda (PGA)=k_{0}PG{A}^{-k}(2)$

where k₀ and k are the regression line parameters in the log-log plane. According to (Jalayer and Cornell, 2003), the lower and upper bound of the seismic intensity, to perform the linearization, should correspond to the Design Basis Earthquake (DBE) and Maximum Credible Earthquake (MCE) intensity levels, with 10 and 2% probabilities of exceedance in 50 years, respectively, whereas Cornell, 1968, suggests fitting between two points: one equal to the targeted mean annual frequency (MAF) and one with a MAF ten times higher. Both suggestions appear reasonable as investigated in (Gkimprixis et al., 2019). However, given that OBE and DBE are comparable LS as well as SSE and MCE, adopting OBE and SSE as the lower and upper bound is herein suggested.

A crucial aspect is the local seismic response that could strongly affect the risk assessment. Consequently, the local seismic response should be always conducted, including the soil effects. This is possible by adopting a frequency-dependent amplification factor or directly integrating the site effects into PSHA (Aristizábal et al., 2018). The code-compliant approach is instead simplified because a constant amplification factor is applied to all IM. Such an approach is suitable for a rapid risk assessment, where the resources are limited.

3.3 Fragility Analysis of Critical Equipment

The seismic vulnerability of a process plant equipment can be effectively quantified using the fragility curves. Fragility functions provide the probability of exceeding a certain LS, given a ground-shaking intensity. For this type of structure, the PGA is usually considered an efficient and sufficient IM (Kaynia, 2013; Phan and Paolacci, 2016), fully consistent with the seismic hazard analysis. One of the most diffused techniques for fragility functions analysis, which conjugate reduced computational effort and easiness, is the so-called “Cloud Analysis” (Mackie and Stojadinovic, 2005). This technique utilizes the results of proper numerical models to build a probabilistic model based on a regression analysis. Usually, a lognormal distribution is adopted so that the probability of exceeding a specific LS; i.e., the probability that an engineering demand parameter (EDP) exceeds LS, given that IM = x, can be estimated adopting a normal standard cumulative distribution function:

$P(D_{EDP}>LS|IM=x)=1-\varphi \frac{\mathit{ln}(L{S}_m)-\mathit{ln}(D_m)}{\sqrt{({\beta }_{D|IM}^2+{\beta }_{LS}^2)}}(3)$

where ϕ is the standard normal distribution function;

LS_m is the median value of the LS;

D_m is the median value of the demand;

β_D|IM is the std. dev of the response;

β_LS is the std. dev of the capacity.

Static or dynamic seismic analysis carried out with proper low-fidelity or high-fidelity models can be used to build fragility curves. For a given number of return periods, consistent with the expected damage, a minimum number of seven accelerograms (CEN, 1998) should be selected and used to derive the parameters of the linear regression in the log-log plane as follows:

$D_m=aI{M}^b(4)$

${\beta }_{D|IM}=\sqrt{\frac{{\sum }_{i=1}^n{[\mathit{ln}(d_i)-\mathit{ln}(D_m)]}^2}{n-2}}(5)$

where a and b represent the linear regression coefficients evaluated by recording the maximum values of a certain EDP, produced by each accelerogram. The LS of the different equipment have been defined according to both the structural behavior and the possible loss of hazardous containment in the several pipe-equipment connections. Concerning the first ones, particular attention should be paid to the collapse LS, which could lead to a catastrophic failure of the equipment and therefore the instantaneous release of the full content (liquid or gas).

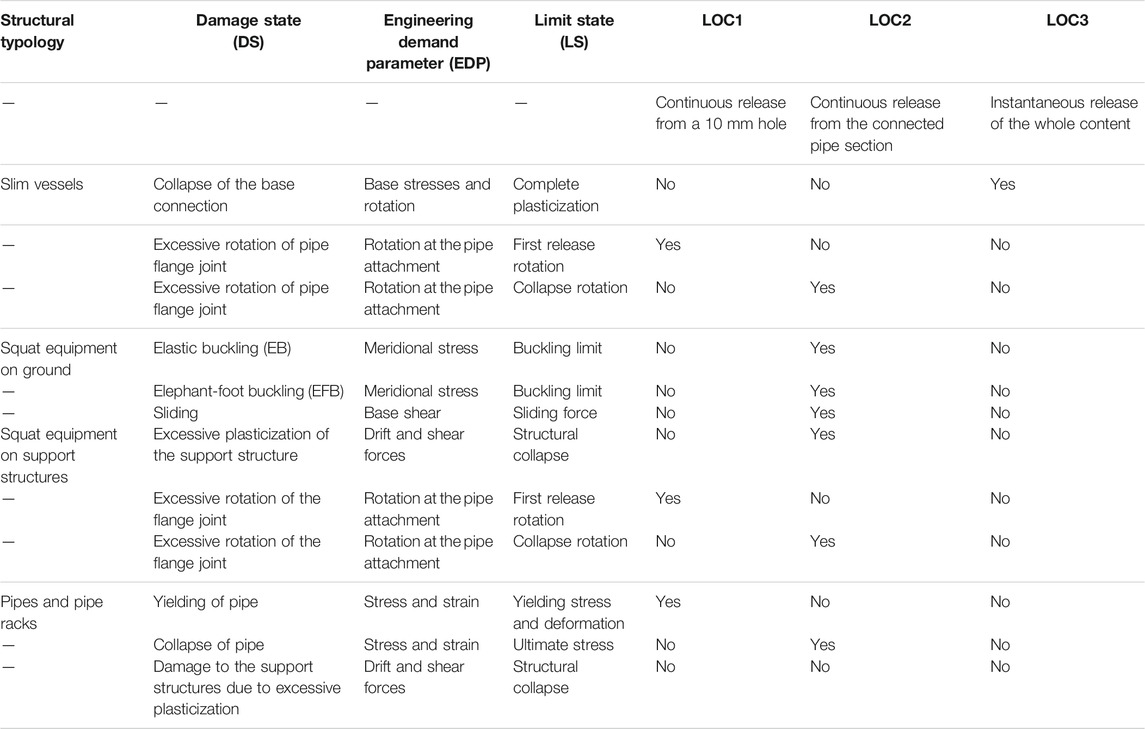
The collapse condition, as defined in the codes, refers to conditions that potentially could cause a structural collapse. Specific collapse fragility curves have been introduced recently, which are based on models able to follow step-by-step the structural collapse. Therefore, the term “collapse” must be intended as a condition of potential collapse. This conservative choice guarantees appropriate margins with respect to phenomena considered more disastrous of the mere collapse, being involved in potentially catastrophic consequences with the release of hazardous material. The collapse LS for each category of equipment are listed in Table 3. In the same table, the EDP, through which each LS can be analytically evaluated, is also individuated.

TABLE 3

TABLE 3. Vulnerability classes of process plant equipment.

Concerning the LS associated with the failure of pipes connected to the equipment and coming from other units, literature definitions have been adopted, which are associated with standard LOC conditions often used in the QRA of process industries. Three different LOC events are herein adopted, whose definition is reported in Table 4. The first level (LOC1) is associated with the plasticization of the pipe flange joint at the connection to the equipment, able to produce a moderate loss from a small break. A serious loss (LOC2) is associated with the excessive rotation of the flanged joints of pipes connected to the equipment. Finally, the instantaneous release of full content, here identified as LOC3, is associated with the collapse of LS.

TABLE 4

TABLE 4. Definition of LOC events in process plant equipment.

For the definition of LOC events from pipes, the results of experimental tests can be used; for example, in (Karamanos et al., 2013), different types of flange joints have been tested to identify the levels of damage corresponding to LOC. Accordingly, the rotation of pipes with a large diameter (8–14 inches), corresponding to the first release of materials, is around 0.01 rad, while the complete breaking of the joint occurs for 0.03 rad. These values can be considered rather conservative because of the high dispersion of the results. These values are referred to conditions in which the pipes are considered rigidly connected to equipment. In different conditions, these limits should be appropriately increased.

3.4 DS/LOC Correlation Matrix

In case of process plants, the risk calculation necessary involves the effects of the content release from a critical unit (tank, pipe, etc.\enleadertwodots), which can cause important effects on the surrounding equipment and community. Thus, only DS involving the release of dangerous substances (toxic, flammable, explosive, or polluting) or critical equipment for emergency phases (e.g., firefighting water tanks) are important in seismic risk analysis, while the other DS can be neglected. As stated before, nonhazardous equipment, whose collapse may induce failure in some surrounding elements, should be included in the list of elements at risk.

The aim of this part of the framework is to use a reasonable criterion to correlate seismic DS and LOC resulting from the structural damage analysis for different categories of industrial equipment. In this respect, the probability of LOC for a given level of seismic damage should be calculated. Nevertheless, the contributions in this direction have been particularly limited. The few contributions present in literature are typically based on empirical approaches (Fabbrocino et al., 2005), in which the relationship between LOC and seismic damage is defined on accident databases and is generally considered as deterministic. A probabilistic approach for the assessment of LOC event in steel storage tanks under seismic loading has been proposed in (Paolacci et al., 2018). Since further developments in this regard are necessary, only deterministic DS/LOC correlation matrices are herein considered, leaving more refined approaches to future investigations. In this respect, Table 3 collects all possible DS/LOC correlations for the structural typologies defined in (Paolacci et al., 2013).

In case of slim vessels category, LOC may occur due to the excessive rotation of bolted flange joints or to the failure of the anchorage; the first one is caused by the structure deformation and the plasticization of the base plate and/or of the skirt, while the second one is due to the excessive rotation and stresses in the anchorage systems. Squat equipment placed on the ground is mainly represented by storage tanks. For this kind of equipment, LOC may occur due to the following DS: elastic buckling (EB), elephant-foot buckling (EFB), sliding, and overturning. The first three DS can cause the pipes’ detachment, while the overturning DS can generate a complete release of the full content. For the equipment on support structures, the DS mainly related to the LOC are the excessive rotation of pipe connection and the failure of the support structure, with following overturning and loss of the whole content.

The definition of DS for pipe racks is carried out in terms of lateral deformation (Paolacci et al., 2011), considering the maximum drift as a reference parameter, in accordance with the provisions of the codes. The LS can be defined assuming the reference values in the FEMA-356, 2000, standard.

3.5 Evaluation of the MAF of Exceeding LOC Events

The MAF of exceeding a given DS can be performed by applying the total probability theorem, combining the seismic hazard curve with the fragility curves. The general equation is as follows:

${\lambda }_{DS}=P[DS>d]=\int P[D>d|PGA=PG{A}_0]d\lambda (PGA)(6)$

where λ_DS is the MAF of exceeding the damage d, P (D > d|PGA = PGA₀) is the fragility curve, and dλ is the differential of the seismic hazard curve. Considering that the fragility curve can be expressed analytically using the Cloud Analysis, as well as the hazard curve using Eq. 2, the previous integral assumes the following closed form, as suggested by (Jalayer and Cornell, 2003):

${\lambda }_{DS}(d)=\lambda (PG{A}_{50\%})e^{\frac{1}{2}k{\beta }_{ED}^2}(7)$

where λ (PGA50%) represents the hazard corresponding to a probability of 50% of exceeding the damage d, which is derived by the fragility curves, whereas k represents the slope of the linearized seismic hazard curve. β_ED represents the logarithmic standard deviation of the response due to the seismic action. This latter can be increased to account for epistemic uncertainty β_U (e.g., model imprecision). The total standard deviation β_TOT becomes

${\beta }_{TOT}=\sqrt{{\beta }_{ED}^2+{\beta }_U^2}(8)$

Consequently, the risk calculation can be estimated using the following formula:

${\lambda }_{DS}(d)=\lambda (PG{A}_{50\%})e^{\frac{1}{2}{\beta }_{TOT}^2}(9)$

Thus, the calculation of the MAF of exceeding the damage can be immediately derived. Finally, by means of the above-mentioned DS/LOC matrices, it is possible to obtain the annual frequency of exceeding the LOC events (LOC1, LOC2, and LOC3) and thus to evaluate the degree of exposure of the equipment.

3.6 Decision-Making Analysis and Ranking of Scenarios

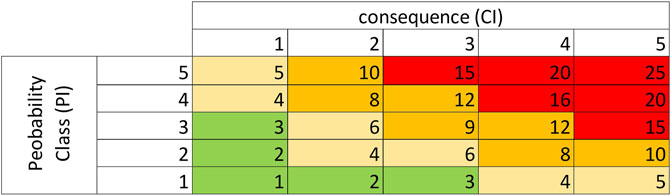
From the calculation of the MAF of exceeding the LOCs, it is possible to derive the ranking of the most critical components, identifying the ones for which it may be necessary to intervene with appropriate mitigation systems. The reference values of the LOC probability are not easily identifiable from the literature. In the present work, it is suggested to evaluate the consequences of a given LOC event through the correlated event tree. Once the frequency of the different scenarios is known, it is possible to evaluate a consequence-based risk level. For this purpose, it may refer to the probability classes characterized by the Probability Class Index (PI) shown in Table 5 (CPS, 1992).

TABLE 5

TABLE 5. Probability classes (PI) (CPS, 1992).

By associating each PI with a Consequence Index (CI), it is possible to derive a Global Risk Index (GRI) product of the first two, which provides a measure of the severity of the scenario. The definition of the CI is provided in Table 6 in terms of damage thresholds and accidental scenarios Table 5 (TNO, 1992). Since each LOC event is associated with different possible (mutually exclusive) events, a total GRI can be defined as the sum of the indexes of each of the scenarios. This index can be used to derive a ranking of events with decreasing level of risk and draw up a list of priorities. These priorities can be further refined by identifying some additional parameters, for example, the impact of the intervention, including implementation time and plant shutdown, leading to the calculation of the plant resilience as well.

TABLE 6

TABLE 6. Damage thresholds and Consequence Index (CI).

The ranking and the related priorities can be established in the form of a risk matrix (Duijm, 2015). In the present paper, the following one is proposed, where the likelihood is represented by the PI and the consequence by the CI, whose product represents the already defined GRI. Observing the probability classes, we defined, according to Table 5, the likelihood as limited when PI ≤ 2, moderate when 2 $<$ PI ≤ 3, and high when PI ≥ 4. Analogously, the consequence, according to Table 6, is deemed limited when CI ≤ 2, moderate when 2 $<$ CI ≤ 3, and high when CI ≥ 4. Consequently, the risk matrix illustrated in Figure 5 can be profitably employed for the decision-making analysis and thus for the selection of the proper mitigation measures.

FIGURE 5

FIGURE 5. Risk matrix for decision-making analysis.

4 Application to a Representative Case Study

The proposed selection method of critical units and their risk assessment have been carried out for an idealized case study (Figure 6). It represents an upstream plant for the separation of crude oil from gas and water, ideally placed in Viggiano city (Italy), a high seismic prone area. The plant contains different lines for the oil treatment, which includes several types of equipment as slug catchers, oil/water and gas/water separators, oil stabilization columns, gas treatment columns, heat exchangers, oil storage tanks, piping systems, and many others.

FIGURE 6

FIGURE 6. Plan view of the case study.

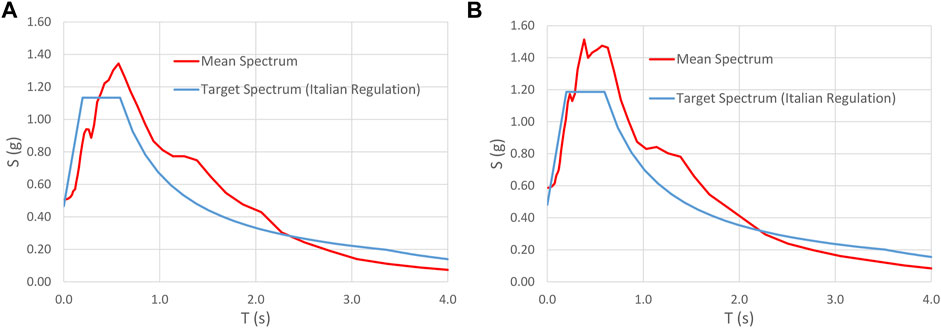
In addition, the plant is equipped with an emergency system, which includes a blown-down pipeline and a fire protection system with compressors, water storage tanks, and a buried pipeline network. A series of seven return periods (T_R = 60, 75, 101, 712, 949, 1950, and 2,475 years) have been used to generate many response spectra. Thus, for each return period, a set of seven natural accelerograms have been selected from the PEER Strong Motion Database (PEER, 2021) and used to perform the fragility analysis. A specific deaggregation analysis suggested, for the records’ identification, the use of a Magnitude and Distance M = 5.5–6.5 and D = 4–7 km. The mean spectra for T_R = 949 and T_R = 2,475 years are illustrated in Figure 7 together with the spectra of the Italian seismic regulation (NTC 2018, 2018). The former account for the soil condition, derived by a site-specific ground motion analysis, whose details are omitted here for brevity.

FIGURE 7

FIGURE 7. (A) Response spectra for T_r = 949 years. (B) Response spectra for T_r = 2,475 years.

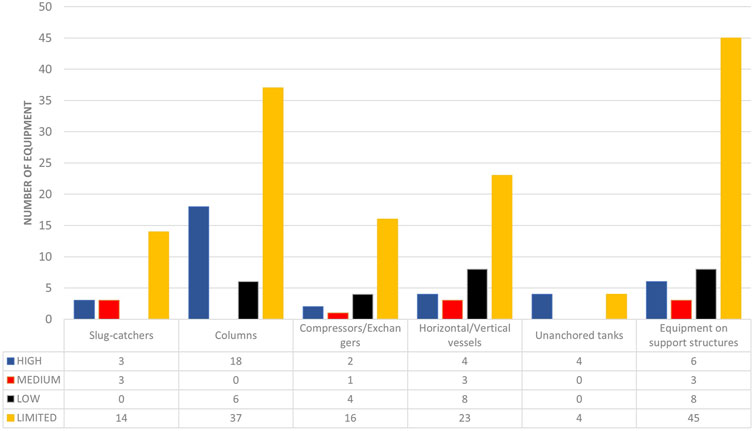
The plant has more than 400 units, but not all of them contain hazardous materials; for this reason, the safety report has been firstly analyzed, which allows us to extract a list of 139 units, potentially at risk. Subsequently, for the preliminary identification of the most critical units, the proposed screening methodology has been applied. For each unit, the Risk Index I_R has been evaluated starting from the definition of the Vulnerability Index and Exposition Index, whose results are reported in Figure 8. Subsequently, a sublist of about 21 units has been identified, which are characterized by a Risk Index I_R > 9; it includes mainly columns, oil/water separators, a broad oil storage tank, and a series of elevated equipment such as heat exchanger, air-cooler, and vertical separators.

FIGURE 8

FIGURE 8. Risk Index I_R for the several types of equipment of the plant.

For the derivation of fragility curves, a linear dynamic analysis has been performed. This choice depends essentially on the hypothesis that a short-cut methodology is generally based on low-fidelity models. For each equipment, a FE model has been built using MIDAS software (MIDAS, 2017). Some of them are illustrated in Figure 9. For example, the stabilization oil columns have been modeled using shell elements, including the column vessel and the skirt at the column base. Also, the pipes have been modeled to evaluate their influence on column deformability. The bottom flange joint has been modeled as suggested in (Cook et al., 2001), where a rotational spring is defined through two different damage mechanisms in which either the contributions of flange and anchor bolts are involved (PEC, 2017).

FIGURE 9

FIGURE 9. Examples of finite element models of the main equipment.

These models have been employed to build fragility curves by means of Cloud Analysis. In this respect, by adopting linear models, the response spectrum analysis would be deemed sufficient rather than using T-H analysis. Nevertheless, given the complexity of the equipment, even in the linear field, it is preferable to perform analysis in the time domain to better account for this dynamic complexity.

Examples of fragility curves for a stabilization oil column are shown in Figure 10A and Figure 10B. The column is clearly characterized by a high vulnerability due to the weakness of its base (50% of probability of exceeding yielding and collapse corresponds, respectively, to PGA = 0.4 and 0.75 g), which corresponds to a LOC3 event. Figure 10B shows the fragility curve for excessive rotation (failure) at the flange joint of the outlet acid gas pipe that, according to Table 4, corresponds to LOC2.

FIGURE 10

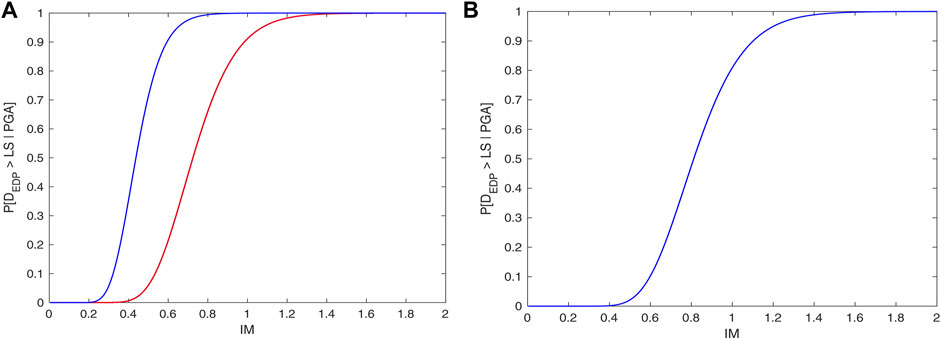
FIGURE 10. (A) Fragility curves of a stabilization oil column: excessive rotation of the columns’ base (blue line: yielding; red line: collapse). (B) Fragility curves of a stabilization oil column: excessive rotation at the flange joint of the outlet acid gas pipe.

The results show that the slug catcher is extremely vulnerable against damage conditions that imply structural collapse (LOC3). This is due to the weakness of the anchor bolts of the foundation, whereas LOC1 and LOC2 events are less frequent. In fact, the structure itself is particularly rigid, and high rotations of the bolted flange joints are unlikely. Differently, the columns are more flexible structures; this indicates a more likely excessive rotation of the bolted flange joints at the pipe-column connections. As a matter of fact, LOC1 has the highest frequency. Elevated equipment could result vulnerable to earthquakes due to the filtering effect of the support structure. For example, the heat exchanger of Figure 9 is extremely vulnerable with respect to all LOC events. This is due to the flexible support structure that amplifies the floor displacements which leads to excessive rotation of the pipe flange joints. The support structure is seismically vulnerable as well. The MAF of the occurrence of LOC events of each equipment allows us to establish the most critical units and the most probable DS and to define the order of priority of the interventions.

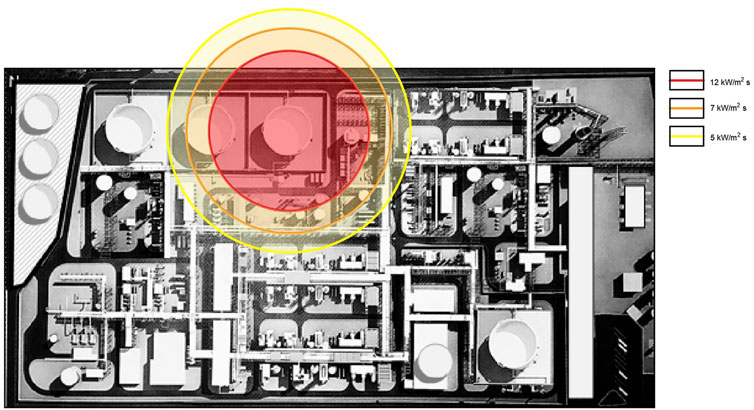
It is clear from this framework that the plant contains equipment particularly vulnerable to earthquake that could also generate severe scenarios with important consequences. As can be seen in Table 7, one of the high-risk units with a high MAF of the occurrence of LOC2 event is represented by the oil storage tank. Generally, big broad tanks have a high vulnerability class and contain a large amount of flammable material that could have serious consequences inside and/or outside the plant. As a matter of fact, on the basis of the definition of the stored substance in the most critical tank (Figure 11), a hypothetical scenario (pool fire) has been considered by adopting the environmental parameters reported in Table 8. As shown in Table 3, for equipment placed on the ground, a LOC2 is associated with a continuous release from the connected pipe section.

TABLE 7

TABLE 7. MAF of LOC events.

FIGURE 11

FIGURE 11. Contour lines of the impact: LOC2 scenario due to the oil spillage from a storage tank.

TABLE 8

TABLE 8. Parameters for the scenario simulation.

The continuous release of crude oil material from the connected pipe section of the oil tank (LOC2) has a MAF of occurrence equal to 3.34E-04. According to Table 5, PI = 3 can be associated with this damage scenario. In this example, the ALOHA (Areal Locations of Hazardous Atmospheres) software has been used to simulate the scales of impact (threat zones) in the event of Stationary Thermal Radiation (Jones et al., 2013), caused by LOC2 event. A pool fire triggered by the continuous release of crude oil material from the connected pipe section of the oil tank could cause high lethality and structural damage because a thermal radiation level of 12 kW/m²s is reached (Figure 11). According to Table 6, CI = 5 can be assigned, with a GRI equal to 15, which provides a measure of the severity of this scenario.

By analyzing all possible damage scenarios triggered by the critical unit, GRI can be evaluated to create a ranking of events with decreasing level of risk and draw up a list of priorities.

In conclusion, a dedicated decision-making analysis with the indication of the most suitable mitigation strategies would be necessary.

5 Conclusion

The paper deals with a new selection method for risk analysis of critical process plant components under seismic loading. An index-based approach is proposed to identify the most critical damage scenarios entailing hazardous material release. Using closed-form solutions for seismic hazard and fragility analysis, a simplified solution for the risk assessment is proposed.

Based on predefined DS/LOC matrices, the MAF of standardized LOC events is evaluated. Finally, a decision-making analysis with the use of a simple risk-consequence matrix allows the identification of the most critical equipment.

The methodology has been applied to a realistic case study, demonstrating its simplicity and novelty in evaluating the most frequent LOC events that could generate hazardous consequences.

Future developments will concern the application of the last stage of the method and the application of more rigorous procedures for its validation. Moreover, the domino effects will be implemented to complete the framework of risk analysis of hazardous facilities.

In the knowledge of the authors, this is the first attempt to summarize in a simplified but complete framework a complex matter as the risk assessment of existing process plants under seismic loading.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

FP developed the conceptual aspects of the methodology; DC implemented the methodology; SC dealt with the analysis of the case study.

Funding

This project has received funding from the Italian Ministry of Education, University and Research (MIUR) 482 in the frame of the Departments of Excellence (Grant L. 232/2016).

Conflict of Interest

SC was employed by the company Safeplant Srl.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.

Acknowledgments

The company Safeplant Srl is also acknowledged for the discussions and help in developing the procedure.

References

Alessandri, S., Caputo, A. C., Corritore, D., Giannini, R., Paolacci, F., and Phan, H. N. (2018). Probabilistic Risk Analysis of Process Plants under Seismic Loading Based on Monte Carlo Simulations. J. Loss Prev. Process Industries 53, 136–148. doi:10.1016/j.jlp.2017.12.013

CrossRef Full Text | Google Scholar

Alessandri, S., Caputo, A. C., Corritore, D., Renato, G., Paolacci, F., and Phan, H. N. (2017). “On the Use of Proper Fragility Models for Quantitative Seismic Risk Assessment of Process Plants in Seismic Prone Areas,” in American Society of Mechanical Engineers, Pressure Vessels and Piping Division (Publication) PVP, Waikoloa, HA, July 16–20, 2017, 8. doi:10.1115/PVP2017-65137

CrossRef Full Text | Google Scholar

Antonioni, G., Spadoni, G., and Cozzani, V. (2007). A Methodology for the Quantitative Risk Assessment of Major Accidents Triggered by Seismic Events. J. Hazard. Mater. 147, 48–59. doi:10.1016/J.JHAZMAT.2006.12.043

CrossRef Full Text | Google Scholar

Aristizábal, C., Bard, P.-Y., Beauval, C., and Gómez, J. (2018). Integration of Site Effects into Probabilistic Seismic Hazard Assessment (PSHA): A Comparison between Two Fully Probabilistic Methods on the Euroseistest Site. Geosciences 8, 285. doi:10.3390/geosciences8080285

CrossRef Full Text | Google Scholar

Bakalis, K., Vamvatsikos, D., and Fragiadakis, M. (2015). “Seismic Fragility Assessment of Steel Liquid Storage Tanks,” in ASME 2015 Pressure Vessels and Piping Conference, Boston, Massachusetts, USA, July 19–23, 2015. doi:10.1115/pvp2015-45370

CrossRef Full Text | Google Scholar

Buratti, N., and Tavano, M. (2014). Dynamic Buckling and Seismic Fragility of Anchored Steel Tanks by the Added Mass Method. Earthquake Engng Struct. Dyn. 43, 1–21. doi:10.1002/eqe.2326

CrossRef Full Text | Google Scholar

Bursi, O., Paolacci, F., Reza, M., Alessandri, S., and Tondini, N. (2016). Seismic Assessment of Petrochemical Piping Systems Using a Performance-Based Approach. J. Press. Vessel Technol. Trans. ASME 138, 031801. doi:10.1115/1.4032111

CrossRef Full Text | Google Scholar

Bursi, O., and Reza, M. (2018a). INDUSE-2-SAFETY - Component Fragility Evaluation and Seismic Safety Assessment of ‘Special Risk’ Petrochemical Plants Under Design Basis and Beyond Design Basis Accidents. Luxembourg: European Union.

Google Scholar

Bursi, O., and Reza, M. (2018b). XP-RESILIENCE - Extreme Loading Analysis of Petrochemical Plants and Design of Metamaterial-Based Shields for Enhanced Resilience. Luxembourg: European Union.

Google Scholar

Campedel, M., Cozzani, V., Garcia-Agreda, A., and Salzano, E. (2008). Extending the Quantitative Assessment of Industrial Risks to Earthquake Effects. Risk Anal. 28, 1231–1246. doi:10.1111/j.1539-6924.2008.01092.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Caputo, A. (2015). “A Seismic Probabilistic Risk Assessment Model for Process Plants,” in Proc. 33rd International System Safety Conference, San Diego, USA, August 24-272015.

Google Scholar

Caputo, A. C. (2016). “A Model for Probabilistic Seismic Risk Assessment of Process Plants,” in ASME 2016 Pressure Vessels and Piping Conference, Vancouver, British Columbia, July 17–21, 2016. doi:10.1115/pvp2016-63280

CrossRef Full Text | Google Scholar

Caputo, A. C., Paolacci, F., Bursi, O. S., and Giannini, R. (2018). Problems and Perspectives in Seismic Quantitative Risk Analysis of Chemical Process Plants. J. Press. Vessel Technol. 141, 010901. doi:10.1115/1.4040804

CrossRef Full Text | Google Scholar

CEN (1998). EUROPEAN COMMITTEE FOR STANDARDIZATION COMITÉ EUROPÉEN DE NORMALISATION EUROPÄISCHES KOMITEE FÜR NORMUNG Management Centre: rue de Stassart, 36 B-1050. Brussels.

Google Scholar

Cook, R. A., Bobo, B. J., and Ansley, M. H. (2001). Design Guidelines for Annular Base Plate, Structures Research Report N 716. Gainesville, Florida: Department of Civil and Coastal Engineering, University of Florida.

Google Scholar

Cornell, C. A. (1968). Engineering Seismic Risk Analysis. Bull. Seismological Soc. America 58, 1583–1606. doi:10.1785/BSSA0580051583

CrossRef Full Text | Google Scholar

CPS (1992). Guidelines for Hazard Evaluation Procedures. NY: Center for Chemical Process, Safety.

Google Scholar

Cruz, A. M., and Okada, N. (2008). Methodology for Preliminary Assessment of Natech Risk in Urban Areas. Nat. Hazards 46, 199–220. doi:10.1007/s11069-007-9207-1

CrossRef Full Text | Google Scholar

Directive 2012/18/EU, S. I (2012). Directive of the European Parliament and of the Council of 4 July 2012 on the Control of Major-Accident Hazards Involving Dangerous Substances, Amending and Subsequently Repealing Council Directive 96/82/EC Text with EEA Relevance. Brussels, Belgium: European Parliament and of the Council.

Google Scholar

Duijm, N. J. (2015). Recommendations on the Use and Design of Risk Matrices. Saf. Sci. 76, 21–31. doi:10.1016/j.ssci.2015.02.014

CrossRef Full Text | Google Scholar

Fabbrocino, G., Iervolino, I., Orlando, F., and Salzano, E. (2005). Quantitative Risk Analysis of Oil Storage Facilities in Seismic Areas. J. Hazard. Mater. 123, 61–69. doi:10.1016/j.jhazmat.2005.04.015

CrossRef Full Text | Google Scholar

FEMA-356 (2000). Prestandard and Commentary for the Seismic Rehabilitation of Buildings. Washington, DC 20472: Federal Emergency Management Agency.

Google Scholar

Giannelli, G., Muratore, A., Nastasi, G., and Sferruzza, V. (2020). “Earthquake Natech Risk: Index Method for Critical Plants Covered by Seveso Iii Directive,” In Proceedings of the 30th European Safety and Reliability Conference and the 15th Probabilistic Safety Assessment and Management Conference, Venice, Italia, June 2020. doi:10.3850/978-981-14-8593-0_3785-cd

CrossRef Full Text | Google Scholar

Girgin, S., and Krausmann, E. (2013). RAPID-N: Rapid Natech Risk Assessment and Mapping Framework. J. Loss Prev. Process Industries 26, 949–960. doi:10.1016/J.JLP.2013.10.004

CrossRef Full Text | Google Scholar

Gkimprixis, A., Tubaldi, E., and Douglas, J. (2019). Comparison of Methods to Develop Risk-Targeted Seismic Design Maps. Bull. Earthquake Eng. 17, 3727–3752. doi:10.1007/s10518-019-00629-w

CrossRef Full Text | Google Scholar

HAZUS (2001). Earthquake Loss Estimation Methodology. Menlo Park, CA, USA: National Institute of Building Science, Risk Management Solution.

Google Scholar

Iervolino, I., Fabbrocino, G., and Manfredi, G. (2004). Fragility of Standard Industrial Structures by a Response Surface Based Method. J. Earthquake Eng. 8, 927–945. doi:10.1080/13632460409350515

CrossRef Full Text | Google Scholar

INGV (2014). Gruppo di Lavoro per la redazione della mappa di pericolosità sismica (Ordinanza PCM 20.03.03 n.3274. Rome: Rapporto conclusivo.

Google Scholar

Jalayer, F., and Cornell, A. (2003). A Technical Framework for Probability-Based Demand and Capacity Factor Design (DCFD) Seismic Formats. Report, 08 (Berkeley: PEER)

Google Scholar

Jones, R., Lehr, W., Simecek-Beatty, D., and Reynolds, R. M. (2013). ALOHA® (Areal Locations of Hazardous Atmospheres) 5.4.4. Technical Documentation, NOAA Technical Memorandum NOS ORR 43. Seattle, WA: Emergency Response Division, NOAA, 96.

Google Scholar

Kalemi, B., Farhan, M., and Corritore, D. (2016). “Sliding Response of Unanchored Steel Storage Tanks Subjected to Seismic Loading,” in ASME 2019 Pressure Vessels and Piping Conference, San Antonio, TX, July 14–19, 2019. doi:10.1115/PVP2019-93310

CrossRef Full Text | Google Scholar

Karamanos, S., Bursi, O. S., Reza, M. S., Paolacci, F., Varelis, B., and Hoffmeister, G. (2013). INDUSE - Structural Safety of Industrial Steel Tanks, Pressure Vessels and Piping Systems Under Seismic Loading, INDUSE Project, Research Fund for Coal and Steel. Report No. RFSR-CT-2009-00022. Luxembourg: European Union.

Google Scholar

Kaynia, A. (2013). Guidelines for Deriving Seismic Fragility Functions of Elements at Risk: Buildings, Lifelines, Transportation Networks and Critical Facilities. Ispra, Italy: SYNER-G Reference Report 4, European Commission, JRC.

Google Scholar

Kikic, S., Moncraz, P., and Noakowsky, P. (1999). Cicind Report: A Preliminary Analysis of the Tupras Refinery Stack Collapse during Kocaeli Earthquake of 17 August 1999. Zurich, Switzerland: CICIND Report, 17, 1.

Google Scholar

Koller, M., and Kolz, E. (2015). “Critical Industrial Facilities: Simply Applying Current Importance Factors I Is Not Enough,” in Proc. of the Int. Conf. on Seismic Design of Industrial Facilities (SeDIF), Aachen, September 26–27, 2013, 37–52.

Google Scholar

Krausmann, E., Cruz, A. M., and Salzano, E. (2017). Natech Risk Assessment and Management Reducing the Risk of Natural-hazard Impact on Hazardous Installations. Ispra, Italy: Elsevier.

Google Scholar

Labbè, P. (2018). “Outlines of the Revision of the Eurocode 8, Part 1, Generic Clauses,” in Conference: 16th European Conference on Earthquake Engineering, Thessaloniki, June 18–21, 2018.

Google Scholar

LESSLOSS (2004). Risk Mitigation for Earthquakes and Landslides. Report No. GOCE-CT-2003-505448. Luxembourg: European Union.

Google Scholar

Mackie, K., and Stojadinovic, B. (2005). “Comparison of Incremental Dynamic, Cloud, and Stripe Methods for Computing, Probabilistic Seismic Demand Models,” in Structure Congress 2005, New York, April 20–24, 2005. doi:10.1061/40753(171)184

CrossRef Full Text | Google Scholar

MIDAS (2017). MIDAS, (v2.2). New York, NY: Midas Information Technology Co. Ltd.

Google Scholar

Musson, R., Schwarz, J., and Stucchi, M. (1998). European Macroseismic Scale 1998, 15. Luxembourg: Cahiers du Centre Européen de Geodynamique et de Seismologie.

Google Scholar

NTC2018 (2018). D\\enleadertwodots M. 17.01.2018 – Norme Tecniche Delle CostruzioniRome: Ministero delle Infrastrutture e dei Trasporti.

Google Scholar

O’Reilly, , and Calvi, G. (2021). A Seismic Risk Classification Framework for Non-structural Elements. Bull. Earthquake Eng. 19, 5471–5494. doi:10.1007/s10518-021-01177-y

CrossRef Full Text | Google Scholar

Pagani, M., Monelli, D., Weatherill, G., Danciu, L., Crowley, H., Silva, V., et al. (2014). OpenQuake Engine: An Open Hazard (And Risk) Software for the Global Earthquake Model. Seismological Res. Lett. 85, 692–702. doi:10.1785/0220130087

CrossRef Full Text | Google Scholar

Paolacci, F., Corritore, D., Caputo, A. C., Bursi, O. S., and Kalemi, B. (2018). “A Probabilistic Approach for the Assessment of LOC Events in Steel Storage Tanks Under Seismic Loading,” in ASME 2018 Pressure Vessels and Piping Conference, Prague, Czech Republic, July 15–20, 2018. doi:10.1115/PVP2018-84374

CrossRef Full Text | Google Scholar

Paolacci, F., Giannini, R., and De Angelis, M. (2013). Seismic Response Mitigation of Chemical Plant Components by Passive Control Techniques. J. Loss Prev. Process Industries 26, 924–935. doi:10.1016/J.JLP.2013.03.003

CrossRef Full Text | Google Scholar

Paolacci, F., Phan, H., Corritore, D., Alessandri, S., Bursi, O., and Reza, M. (2015). “Seismic Fragility Analysis of Steel Storage Tanks,” in Proceedings of the 5th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Crete Island, Greece, May 25–27, 2015, 2. doi:10.7712/120115.3522.1040

CrossRef Full Text | Google Scholar

Paolacci, F., Reza, S. M., and Bursi, O. S. (2011). “Seismic Analysis and Component Design of Refinery Piping Systems,” in ECCOMAS Thematic Conference - COMPDYN 2011: 3rd International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering: An IACM Special Interest Conference, Corfu, Greece, May 25–28, 2011.

Google Scholar

PEC (2017). “Deliverable D4.1 - Definition of the Structural Models and Seismic Fragility Analysis Techniques Available for the Specific Case Study, PEC Project: Post-Emergency,” in Multi-Hazard Health Risk Assessment in Chemical Disasters (Luxembourg: European Union).

Google Scholar

PEER (2021). Available at: https://peer.berkeley.edu/peer-strong-ground-motion-databases.

Phan, H. N., Paolacci, F., and Alessandri, S. (2016). “Fragility Analysis Methods for Steel Storage Tanks in Seismic Prone Areas,” in ASME 2016 Pressure Vessels and Piping Conference, Vancouver, British Columbia, July 17–21, 2016, 8. doi:10.1115/PVP2016-63102

CrossRef Full Text | Google Scholar

Phan, H. N., and Paolacci, F. (2016). “Efficient Intensity Measures for Probabilistic Seismic Response Analysis of Anchored Above-Ground Liquid Steel Storage Tanks,” in American Society of Mechanical Engineers, Pressure Vessels and Piping Division (Publication) PVP, Vancouver, British Columbia, July 17–21, 2016, 5. doi:10.1115/PVP2016-63103

CrossRef Full Text | Google Scholar

Salzano, E., Iervolino, I., and Fabbrocino, G. (2003). Seismic Risk of Atmospheric Storage Tanks in the Framework of Quantitative Risk Analysis. J. Loss Prev. Process Industries 16, 403–409. doi:10.1016/s0950-4230(03)00052-4

CrossRef Full Text | Google Scholar

TNO (1992). Methods for the Determination of Possible Damage. The Hague, Netherlands: CPR16E, Director General of Labour.

Google Scholar

Tsionis, G., Pinto, A., Giardini, D., and Mignan, A. (2016). Harmonized Approach to Stress Tests for Critical Infrastructures against Natural Hazards, STREST Reference Report: Report on Lessons Learned from Recent Catastrophic Events. Luxembourg: European Union.

Google Scholar

Uijt De Haag, A. B. (2005). Quantitative Risk Assessment, Purple Book. The Hague, Netherlands: CPR18E, Committee for the Prevention of Disasters.

Google Scholar

Young, S., Balluz, L., and Malilay, J. (2004). Natural and Technologic Hazardous Material Releases during and after Natural Disasters: A Review. Sci. Total Environ. 322, 3–20. doi:10.1016/S0048-9697(03)00446-7

PubMed Abstract | CrossRef Full Text | Google Scholar