Optimal Mixed Placement and Capacity Distribution of Buckling-Restrained Braces and Conventional Braces on a Large Metal Spatial Structure Without Rigid Diaphragm Assumption

This paper presents a design application of the proposed generalized response spectrum analysis (GRSA)-based seismic optimization method to a large metal spatial structure (constructed in Japan) where a rigid diaphragm assumption is not available and displacement responses are disproportionally distributed in a story. It also discusses the optimal mixed placement and capacity distribution of buckling-restrained braces (BRBs) and conventional braces (CBs) to minimize both the story drift response and the number of BRBs (i.e., the introduction cost of expensive energy-dissipation devices used as dampers). GRSA is a quick and efficient analysis method for estimating the reduced seismic responses of structural models with a large degree of freedom, and GRSA-based computational optimization enables a more efficient seismic design process than trial-and-error approaches with time-consuming nonlinear response history analysis. In this study, the efficiency is verified through a comparison with the Japanese standard BRB design method. According to the results, the optimal design solution by the proposed method has approximately 20% less steel tonnage of BRBs than that obtained from the standard method, whereas the seismic performance is equal to or better than the others. Moreover, although engineers should still consider the possibility of damage concentration, the brace configuration of the substructure where BRBs and CBs are arranged in adjacent stories is the most effective for reducing both the number of BRBs and the story drift response.

1 Introduction

In highly seismic regions (e.g., United States, Italy, Turkey, New Zealand, China, Taiwan, Philippines, and Japan), seismic energy-dissipation devices [i.e., dampers (Lago et al., 2019)], such as fluid viscous dampers, friction dampers, bilinear oil dampers, and buckling-restrained braces (BRBs) have been widely employed for seismic design to ensure immediate re-occupancy after a large earthquake. Particularly in Japan, where the whole country belongs to a high-seismic-hazard zone, the development and social implementation of response modification systems (Lago et al., 2019) using dampers have been vigorously pursued since the earliest days of these seismic countries. Building codes, design standards, and legal proceedings have been adjusted to be easy to employ dampers in seismic design, and then passive seismic control systems are commonly deployed in small structures, such as timber houses, to large special structures, such as spatial structures and tall buildings. Moreover, according to the common use of dampers, practical optimal damper design methods satisfying multiple design constraints composed of architectural, environmental, constructional, or economic requirements, which are not limited to structural rationality, is recently attracting attention in Japan. Among them, the development of an optimal design method that simultaneously minimizes seismic responses and the number of dampers has been strongly desired by structural engineers because of the high construction costs associated with dampers. However, while optimal damper design methods for typical multistory buildings have been proposed worldwide, there are a limited number of generic optimal design methods that are applicable even for special structures in seismic countries where the advanced use of dampers is common. A typical special structure with dampers in Japan is shown in Figure 1. The building is a metal spatial structure where a rigid diaphragm assumption is not available and displacement responses are disproportionally distributed in a story. Therefore, the empirical rules for optimal placement and capacity distribution of dampers in typical multistory buildings are unavailable. In addition, owing to the unavailability of the rigid diaphragm assumption, conventional computational optimization methods for dampers using reduced multi-degree-of-freedom systems are not feasible. Thus, in practice, structural engineers commonly rely on time-consuming trial-and-error methods using nonlinear response history analysis (NLRHA) of a three-dimensional (3D) numerical model with large degrees of freedom.

FIGURE 1

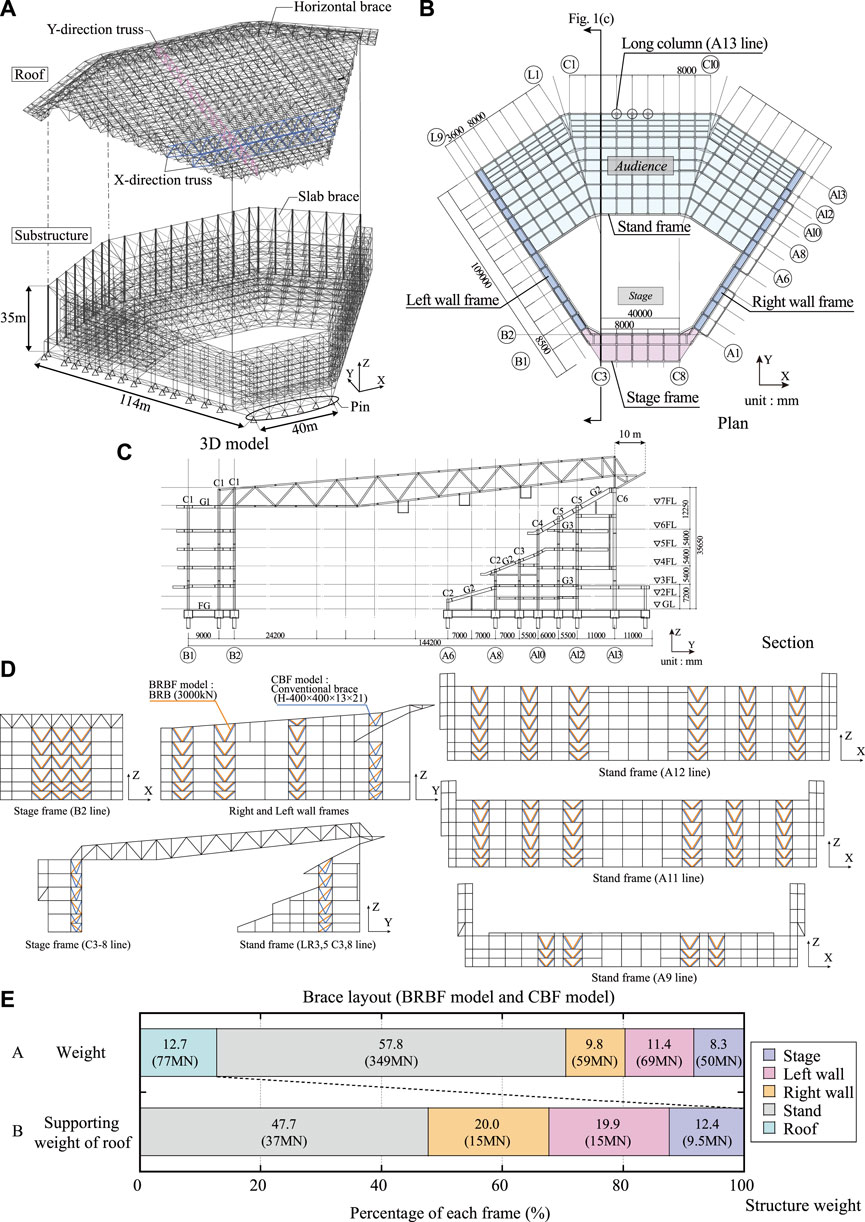
FIGURE 1. Building specifications: (A) 3D model, (B) Plan, (C) Section, (D) Brace Layout (BRBF model and CBF model), (E) Structure weight.

Hand calculation-based simple damper design methods for reducing the seismic response of a building structure to specified design criteria are well-studied all over the world. The best-known method is that proposed by Kasai et al. (1998), which is authorized by the Japan Society of Seismic Isolation (JSSI) (The Japan Society of Seismic Isolation, 2013) and Architectural Institute of Japan (AIJ) (Architectural Institute of Japan, 2014) and is commonly used in Japan. This method is hereafter referred to as the EL. In the EL method, the capacity of dampers against the demand of base shear force is designed by using the equivalent linearized elastic single degree of freedom system adjusted to the first vibration mode of the target building. The corresponding capacity of dampers in each story is then determined based on the design shear force distributions. Moreover, the seismic response reduction by dampers is visually expressed using performance curves (The Japan Society of Seismic Isolation, 2013), and the dampers are interactively designed by structural engineers and architectural designers. However, while the EL method is available on any type of dampers, it is limited to typical multistory buildings which can be reduced to a simple multi-degree-of-freedom system based on a rigid diaphragm assumption. Therefore, it is not available in the design of the spatial damper placement and combined use of different types of dampers. Special structures with complicated vibration characteristics, such as spatial structures, are naturally outside the scope of the EL method.

Numerical analysis-based damper design methods for multi-degree-of-freedom systems are also well-studied. Silvestri et al. (2010) proposed a five-step procedure to directly determine the distribution and location of additional viscous dampers in multi-degree-of-freedom systems. In this method, the target response reduction is firstly determined based on the target damping ratio, and the capacities of dampers are iteratively calibrated using the series of linear response history analyses of the multi-degree-of-freedom with equivalent linear viscous dampers, and the nonlinear response history analysis is finally conducted for the final design check. Through the fundamental studies (Palermo et al., 2013; Palermo et al., 2016), Palermo et al. (2018) simplified the method of Silvestri et al. (2010) to use equivalent linear static analysis for calibrating the capacity of dampers. In this simplified method, both viscous dampers and structural elements can be manually calibrated to obtain the target response reduction. However, this method is still limited to viscous dampers in yielding structures.

Computational optimization methods for dampers have been proposed in previous research worldwide. Takewaki (1997) proposed a gradient-based optimization method for dampers to minimize the transfer function of the story drift ratios. This is the most pioneering computational optimization method, and many similar methods have been proposed. Takewaki et al. (1999) extended the method of Takewaki (1997) to 3D shear building models. Adachi et al. (2013) extended the method of Takewaki (1997) to multistory buildings with bilinear oil dampers. Harada and Yoshitomi (2021) extended the method of Adachi et al. (2013) to multistory buildings with BRBs. Fujita et al. (2010) proposed an optimization algorithm for both dampers and supporting members to minimize a given objective under critical excitations. Akehashi and Takewaki (2019), Akehashi and Takewaki (2022) extended the method of Takewaki (1997) to elasto-plastic multistory buildings with dampers under a critical double impulse. De Domenico and Hajirasouliha (2021) proposed a practical multilevel performance-based optimization method for nonlinear viscous dampers (NVDs) for the seismic retrofitting of existing substandard steel frames.

Computational design methods for dampers with other generic optimization algorithms have also been widely studied in previous studies. García (2001) proposed a sequential search algorithm-based optimization method for viscous dampers. Singh and Moreschi (2002) proposed a genetic-algorithm-based optimization method for viscous dampers. Levy and Lavan (2006) proposed an optimization method for viscous dampers based on nonlinear programming. Apostolakis and Dargush (2009), Apostolakis (2020) proposed genetic-algorithm-based optimization methods for buckling-restrained braced frames. Lopez Garcia and Soong (2002) proposed a simplified sequential search algorithm-based optimization method for linear viscous dampers. Takagi et al. (2021) proposed a multiple-start local search algorithm-based optimization method for buckling-restrained braced frames. Cetin et al. (2019) proposed a differential evolution algorithm-based optimization method for viscous dampers in shear building structures. Aydin et al. (2019) analyzed the efficiency of the method of Cetin et al. (2019) by using response history analysis. Ozturk et al. (2022) extended the method of Cetin et al. (2019) to multiple tuned mass dampers. However, while these optimization algorithms are generic, most of the above methods require multiple NLRHAs to compute objectives and sensitivity; thus, they are not feasible for 3D models with large degrees of freedom (e.g., spatial structures without a rigid diaphragm assumption), and the optimal placement of dampers on such structures has not yet been clarified.

In contrast to these NLRHA-based seismic optimization methods, Terazawa and Takeuchi (2018a), Terazawa and Takeuchi (2019), Terazawa et al. (2020a) proposed an optimal damper design method combining generalized response spectrum analysis (GRSA) with metaheuristic optimization algorithms, focusing on the time efficiency of the computing objectives in the optimization algorithm. GRSA is a series of numerical analyses that iteratively performs complex eigenvalue analysis and response spectrum analysis. GRSA quickly evaluates the seismic response of a 3D structural analysis model with large degrees of freedom in which nonlinear viscous dampers or elastoplastic dampers are specifically arranged and, thus, is expected to be a significant improvement from the current damper design methods in terms of speed. The effectiveness of GRSA was validated using a capacity and layout optimization study (Terazawa and Takeuchi, 2018b) for the seismic retrofitting of a telecommunication tower in Japan using buckling-restrained braces and in a study investigating the seismic response characteristics of a damped outrigger system for tall buildings (Terazawa et al., 2020b; Asai et al., 2021; Terazawa et al., 2022) and a novel damped braced tube system for a supertall building planned in Japan (Ishibashi et al., 2022). GRSA-based seismic optimization (Terazawa and Takeuchi, 2018a; Terazawa and Takeuchi, 20192019; Terazawa et al., 2020a) was developed as a next-generation design method for dampers in seismic countries where the advanced use of dampers is required for creative design and is one of the few feasible optimization methods for realistic and large 3D structural analysis models. However, this method had not yet been applied in real design projects.

This paper presents a design application of the proposed GRSA-based seismic optimization method to a large metal spatial structure (constructed in Japan) where a rigid diaphragm assumption is not available, and displacement responses are disproportionally distributed in a story. The optimal mixed placement and capacity distribution of buckling-restrained braces (BRBs) and conventional braces (CBs) to minimize both the story drift response and the number of BRBs (i.e., the introduction cost of expensive energy-dissipation devices used as dampers) are discussed. In Section 2, a brief outline of the design project is presented, and the 3D structural analysis model is explained. In Section 3, the seismic response characteristics of the design solutions forcibly obtained using the EL method (the authorized damper design method) are compared with the optimization results to verify the effectiveness of the proposed method. In Section 4, a GRSA-based optimization study conducted on the design project is discussed in detail. Notably, this study was conducted at the preliminary design stage in 2019, and the design philosophy, applied structural system, and design criteria follow Japanese design practice.

2 Design Outline

2.1 Overview of the Project and Input Ground Motion

The target building is a metal spatial structure used as a music arena and constructed in the Minatomirai area of Yokohama City, Kanagawa Prefecture, Japan. The building and member specifications are presented in Figure 1 and Table 1, respectively. As shown in Figure 1A, the main structure is a steel moment-resisting-frame, and the roof consists of X-directional and Y-directional steel trusses. As shown in Figure 1B, the plan is diamond-shaped with a maximum span of approximately 150 m. The building area is approximately 30,000 m², and the maximum seating capacity is approximately 20,000. As shown in Figure 1C, the substructure has seven stories with a total height of 40 m. The roof frame protrudes approximately 10 m, and the cantilever part of the roof frame is supported by 24 long columns (C6) of 30 m length. The long columns are placed in a luxurious entrance hall. While some of these long columns are laterally supported on both the 4FL and 6FL, the others are only supported on 6FL. As shown in Figure 1D, the substructure consists of a “Stage frame,” where the stage is to be placed; a “Right wall frame” and a “Left wall frame” that cantilevers from the ground with a maximum height of 40 m; and a “Stand frame,” which consists of three floors made of precast concrete where the audience seats will bear the seats. The weight of each frame and the percentage of roof weight supported by the substructure frames are shown in Figure 1E. The weight of the stand frame is the largest and is approximately five times that of the other frames. The roof weight, including finishing materials, was approximately 77 MN, and the stand frame supported half of the weight. The structural members listed in Table 1 were designed for a load combination of the dead loads and the horizontal equivalent static seismic load using a peak ground acceleration of 0.2 g (Japanese service-level earthquake) according to the allowable strength design based on the Japanese AIJ standard (Architectural Institute of Japan, 2019). Note that this arena is designed to be extra heavy compared with typical spatial structures (an arena, hole, stadium, and dome) to improve both the sound reduction performance and sound effect.

TABLE 1

TABLE 1. Member specifications.

2.2 Numerical Model

As shown in Figure 1A, all the structural members are considered in the 3D structural analysis model without a rigid diaphragm assumption, and this large 3D model thus has approximately 24,000 degrees of freedom. The columns and beams were modeled as beam elements. Conventional braces (CBs) are modeled as truss or beam elements. The concrete slabs are modeled as two truss elements with equivalent horizontal shear stiffness values. Buckling-restrained braces (BRBs) are modeled as link elements with bilinear hysteresis characteristics. In this study, material nonlinearity was considered only for the BRBs, and the other members remained elastic. The initial equivalent axial stiffness K_d of the BRB is calculated using Eq. 1, and the post-yield stiffness ratio is 0.02, simulating the isotropic hardening effect.

$K_d=\frac{E{A}_p}{L_0}\frac{1}{\frac{L_p}{L_0}+2\frac{L_e}{L_0}\frac{A_p}{A_e}}(1)$

where E is the Young’s modulus, L₀ is the member length, L_p is the length of the plastic part, A_p is the cross-sectional area of the plastic part, and A_e is the cross-sectional area of the elastic part. In this study, L_p/L₀ and A_p/A_e are 0.7 and 0.4, respectively.

In this study, three models are defined to compare their seismic performance. The first model, denoted as the “BF (Bare moment frame) model,” has no braces. The second model, denoted as the “CBF (conventional braced frame (CBF) model,” is a moment-resisting frame with 442 conventional braces (CBs). SN490 steel and a wide flange section of H-400 × 400 × 13 × 21 were assigned to each brace. The CBs were placed at all possible locations in architectural planning. The third model, denoted as the “BRBF model,” is a moment-resisting frame with 358 BRBs in total, each having a yielding axial force of 3,000 kN located in the same locations as conventional braces in the CBF model. Figure 1D shows the brace configurations of the CBF and BRBF models. Note that the above-mentioned lateral resisting system is the Japanese equivalent of a “special moment resisting frame with another lateral resisting system (i.e., dual moment frame system)” defined in Eurocode 8 (European Committee for Standardization, 2004) and ASCE-7 (American Society of Civil Engineers, 2016). A special moment-resisting frame is common in Japan because the fabricating moment connection is widely spread throughout the country and is cheaper than in other countries. The diagonal configuration of the BRB in the BRBF model (Figure 1D) is based on architectural planning. While the CBF model was prepared only for later seismic optimization, the BRBF model was a design candidate in the initial design process.

The predominant modal characteristics of the BF model are shown in Figure 2A. The 1st mode natural period T₁ is 1.48 s. In the X-direction, the first, third^, and 12th modes were dominant. In the first and third modes, the stand frame or Stage frame swayed translationally. In the 12th mode, each truss along the Y-direction vibrated vertically. In the Y-direction, the second and third modes are dominant, in which the entire building sways in the Y-direction. The cumulative effective mass ratio using the first 200 modes in each direction is approximately 90%. This implies that numerous modes are coupled in the arena.

FIGURE 2

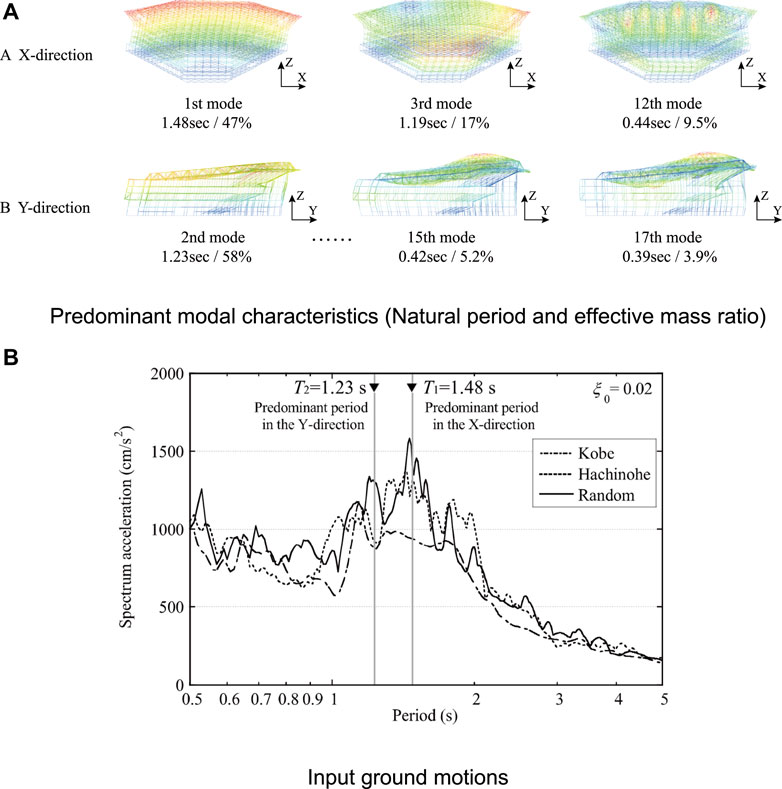
FIGURE 2. Predominant modal characteristics of the BF model and input ground motions: (A) Predominant modal characteristics (Natural period and effective mass ratio), (B) Input ground motions.

The acceleration response spectra of the input ground motions are shown in Figure 2B. These observed waves were spectrally matched following the procedure in the Japanese building code (Ministry of Construction and Japan, 2000), (Ministry of Construction and Japan, 2001) and were amplified based on the ground characteristics of the construction site. The matched waves are used in the actual design and are denoted as Kobe, Hachinohe, and Random. The 1st mode natural period corresponds to the highest peak in the response spectra owing to the intentional heaviness of the arena over the entire design period.

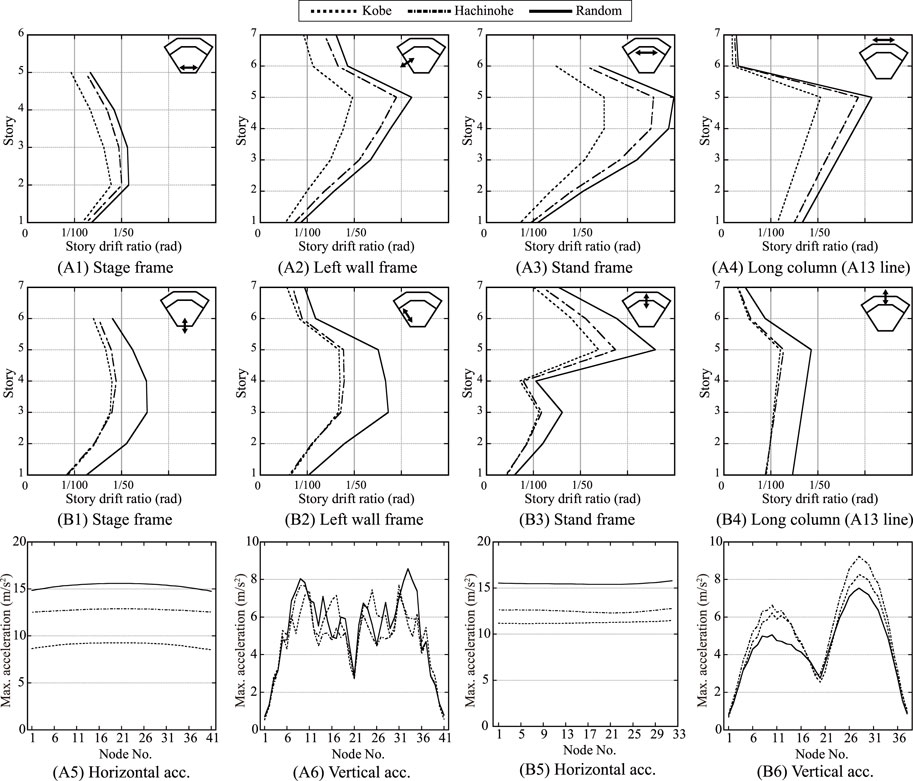
2.3 Seismic Response of Bare Frame Model and Design Requirement for Seismic Optimization

The maximum story drift ratio (SDR) and roof acceleration of the BF model are shown in Figure 3. The NLRHAs were performed using Midas iGen (iGen, 2012) against uniaxial inputs (X- or Y-directional inputs). A Rayleigh damping of 2% was assigned to the first two dominant modes. The Newmark β method (β = 0.25) is used for numerical integration. As shown in Figure 3A, owing to the heaviness and the matching between the 1st mode natural period and the peak spectral acceleration, the peak SDR by the X-directional input in the stand frame unfortunately reached approximately 4%. As shown in Figure 3B, the maximum vertical acceleration response of the roof frame is approximately 8.0 m/s², regardless of the input direction. These results show that the seismic performance of the substructure employing the special moment-resisting frame was insufficient, and a large number of seismic devices (i.e., BRBs or CBs) was required to ensure immediate re-occupancy after a large earthquake. However, the increment in construction cost following the rash introduction of a large number of BRBs (e.g., 358 BRBs in the BRBF model) was not negligible. In addition, the NLRHA-based trial-and-error method to adjust the number and capacity of BRBs was not feasible owing to the design period. Therefore, the design company requested the GRSA-based seismic optimization from the authors, and the given design requirements in the preliminary design stage were as follows: 1) to minimize the number (i.e., the introduction cost) of BRBs by employing CBs that are much cheaper than BRBs and 2) to minimize the SDRs subjected to random waves while preventing member buckling of the CBs. In addition, the given preferable design criterion of the peak SDR was approximately 1.0% (i.e., 1/100 rad) where the moment frame remains almost elastic. After the above twists and turns, this design application of the GRSA-based seismic optimization was conducted to investigate the optimal mixed placement and capacity distribution of the BRBs and CBs.

FIGURE 3

FIGURE 3. Seismic response of the BF model: (A) X-directional input, (B) Y-directional input.

2.4 Response Evaluation Using Generalized Response Spectrum Analysis

The GRSA methodology (Terazawa and Takeuchi, 2018a; Terazawa and Takeuchi, 2019; Terazawa et al., 2020a) is briefly summarized. GRSA is a series of numerical analyses that iteratively perform complex eigenvalue analysis and response spectrum analysis and is used as the analysis engine for the proposed seismic optimization. In GRSA, the nonlinearity of dampers is simulated by iterative computation of the equivalent linearization approach, and the seismic response is evaluated using the complex modal characteristics of the substitute model with the equivalent linearized damper elements and the modified complete quadratic combination method by Sinha and Igusa (Sinha and Igusa, 1995) as shown in Eq. 2.

$R_{\mathrm{CQC}}=\sqrt{{\displaystyle \sum _{s=1}^n{\displaystyle \sum _{r=1}^n{B}_s{B}_r{S}_{d_s}({\omega }_s,{\xi }_s)S_{d_r}({\omega }_r,{\xi }_r)\cos ({\theta }_s-{\theta }_r){\rho }_{sr}}}}(2)$

where s and r are the mode numbers; ξ is the modal damping ratio; ρ is the modal correlation coefficient; ω is the natural circular frequency; S_d is the spectral displacement; B is the real-valued participation vector, B = 2|Re (λ*βϕ)/sin(θ)|; and θ is the approximate phase angle, θ = tan⁻¹ [-Re (λ*βϕ)/Re (βϕ)], λ is the complex eigenvalue, β is the complex participation factor, ϕ is the complex eigenvector component, * is the conjugate property. The response spectrum values are pre-calculated for ξ₀ = 1, 2, 3, 5, 10, 15, 20, 30% stored in external files, and then adjusted to the precise damping ratio ξ using the modification factor $D_h=\sqrt{(1+75\xi 0)/(1+75\xi )}$.

In GRSA, the nonlinearity of the BRB is modeled as a complex stiffness simulating amplitude-dependent elasto-plastic damping, and the complex element stiffness matrix is obtained by multiplying the complex stiffness parameter defined in Eq. 3 by the conventional stiffness matrix of the link element.

$(a+ibsgn{\omega }_e)(3)$

where a is the equivalent stiffness parameter, b is the energy-dissipation parameter, i is the imaginary unit, and ω_e is the sign function of the virtual circular excitation frequency. In this study, following a previous study (Terazawa and Takeuchi, 2018a), the average damping method (Terazawa and Takeuchi, 2018a) was applied to evaluate these parameters.

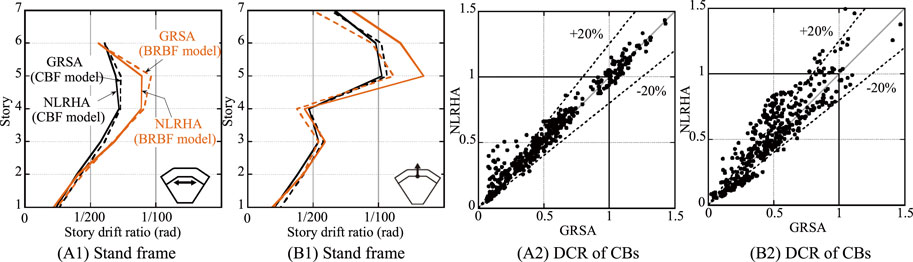
The accuracy of GRSA is verified using the CBF and BRBF models. Figure 4A compares the maximum SDRs obtained from NLRHA and GRSA. For both the models, the GRSA results agree well with the NLRHA results in the X-direction. Figure 4B compares the buckling demand to capacity ratios (the buckling DCRs) of the CBF model. The buckling DCR is calculated by dividing the maximum compressive force by the allowable capacity (Architectural Institute of Japan, 2019). Regardless of the seismic input direction, the variation in the evaluation is found to be within 20%.

FIGURE 4

FIGURE 4. Comparison of GRSAs and NLRHAs: (A) X-directional input, (B) Y-directional input.

3 Comparison of the Optimal Capacity Distribution of BRBs Between the EL Method and GRSA-Based Seismic Optimization

While the EL method assumes typical multistory buildings as described in the introduction, in the actual preliminary design stage, it was applied to the arena as a trial because it is the standard damper design method authorized in Japan. In this section, the results are discussed to compare the capacity distribution of the BRBs and the seismic performance between the EL method-based design solution and GRSA-based seismic optimization result.

In this study, the EL method is applied to the separated structural blocks of the Stage frame (B2 line), Stage frame (C3-8 line), Right and Left wall frames, Stand frame (LR3, 5 and C3, 8line), and Stand frame (A9-12 line) separately, as shown in Figures 1D and is referred to as the EL model. The equivalent single-degree-of-freedom (SDOF) systems of the EL method are individually constructed for these structural blocks. The layout of the BRBs is the same as that of the BRBF model. In the equivalent SDOF system, the ductility and damped-moment-frame-to-moment-frame stiffness ratio K_a/K_f that satisfies the target drift reduction rate R_d^’ is first determined using the performance curve (The Japan Society of Seismic Isolation, 2013). Here, K_f is the stiffness of the moment frame without dampers, and K_a is the stiffness of the moment frame with dampers. The performance curve explains the relationship among the drift reduction ratio R_d, base shear force reduction ratio R_a, ductility, and K_a/K_f, as defined in Eqs 4, 5.

$R_d=D_h{\left(\frac{T_{eq}}{T_f}\right)}^2(4)$

$R_a=R_d{\left(\frac{T_f}{T_{eq}}\right)}^2(5)$

where T_f is the target natural period of the BF model, T_eq is the equivalent period of the SDOF model, and D_h is the modification factor. In this study, the target story drift was 1.0%.

The K_a/K_f of the SDOF system is then distributed based on the design shear force distribution to the multi-degree-of-freedom system so that the story drift ratio and ductility of each story are the same. No BRBs are arranged in the story if K_a in each story is zero or less.

In contrast to the EL method, GRSA-based seismic optimization searches for an optimal solution that minimizes the root square sum of R_d and R_a which is equal to the distance from the origin in the R_d-R_a space. In a previous study (Terazawa and Takeuchi, 20192019), it was found that a multi-degree-of-freedom system has a more precise performance curve than the SDOF system, and minimizing the distance is equal to searching the design solution on the tip of the performance curve. In GRSA-based seismic optimization, particle swarm optimization (PSO) is assigned to the optimization algorithm, and the parameters used in PSO are summarized in Table 2. As with the EL method, the capacity of BRB per story is assigned to the design variables. The details of GRSA-based seismic optimization are introduced in Section 4.1.

TABLE 2

TABLE 2. Summary of optimization problems.

The maximum SDRs and capacity distribution of the BRBs between the EL model and GRSA-based seismic optimization results are compared in Figure 5. In the EL model, while the number of BRBs is reduced from 358 (the BRB model) to 274, the peak SDR of the Stand frame in the EL model exceeds approximately 40% of the design criteria (i.e., 1.0% rad.) by the Y-directional input. In contrast to the EL model, GRSA-based seismic optimization considers the exact modal shapes of the entire structure and then spatially distributes the appropriate capacity in each story to reduce the peak SDR. Therefore, as shown in Figure 5, the number of BRBs in the Size-C-2 model is further reduced to 212. Moreover, the peak SDRs are lower than those of the EL model although they are higher than 1.0%. As shown in Figure 5, the capacity distribution obtained from the GRSA-based seismic optimization is very different from that of the EL method based on the design shear force distribution, and the larger BRBs were appropriately distributed in stories with larger SDRs. In the EL method, the dynamic interaction between the frames of the substructure is not considered, and thus, larger BRBs are arranged in the Stand frame (with a large mass and stiffness). These results demonstrate that a spatial structure without a rigid diaphragm assumption is still beyond the scope of the EL method, and the design shear force distribution is not necessarily appropriate for distributing the base capacity of dampers to each story.

FIGURE 5

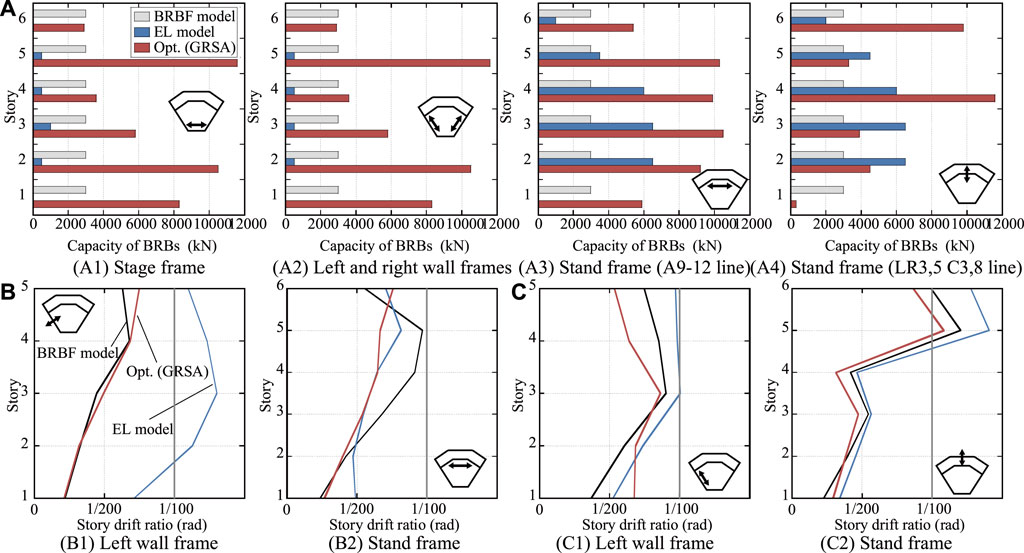
FIGURE 5. Comparisons of the EL method and the GRSA-based seismic optimization: (A) Capacity distribution of BRBs, (B) Maximum story drift ratio (X-directional input), (C) (A) Maximum story drift ratio (Y-directional input).

4 Optimal Mixed Placement and Capacity Distribution Of Buckling-Restrained Braces and Conventional Braces on a Large Metal Spatial Structure

4.1 Definition of the Optimization Problems

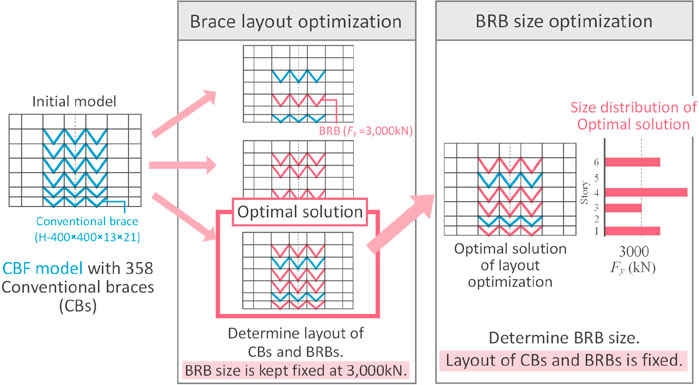
A schematic overview of the seismic optimization is shown in Figure 6, and the definitions of the optimization problems are summarized in Table 2. As shown in Figure 6, the seismic optimization procedure is divided into two stages. First, the placement of BRBs and CBs is optimized using the CBF model as an initial model. In this layout optimization stage, two types of optimization problems are considered to reduce the size of the design space. The first one (Layout-C-1 and Layout-C-2) optimizes the layout of BRBFs, and the other one (Layout-S-1 and Layout-S-2) optimizes the layout of BRBFs at each story in each of the predetermined groups. After the locations of the CBs and BRBs were fixed, the capacity (i.e., size) of the BRBs is optimized (Size-C-1, Size-C-2, Size-S-1, and Size-S-2). This two-stage procedure is selected to reduce the computation time because the possible number of solutions without any constraint is large. In addition to the above procedure, optimization problems (Layout-C-2, Layout-S-2, Size-C-2, and Size-S-2) permitting the removal of conventional braces are considered to further reduce the cost. The two stages of damper design, two types of brace configurations, and two brace operations result in eight optimization problems. As a project report, it is sufficient to discuss only the final optimization results (i.e., Size-C-1, Size-S-1, and Size-S-2). Nevertheless, the detailed results (i.e., Layout-C-1, Layout-C-2, Layout-S-1, and Layout-S-2) are carefully explained because GRSA-based seismic optimization in a real project is the first trial worldwide, and the obtained design options are helpful and interesting for engineers designing spatial structures with dampers. Sections 4.2–4.5 aim to discuss the optimal BRB layout and BRB size separately for an engineer focusing only on one of them, to compare the final optimization results produced from two types of BRB layout, and to investigate the efficiency permitting the removal of conventional braces. A summary of the study is presented in Section 4.6 and a comparison of the damper design methods is discussed in Section 4.7.

FIGURE 6

FIGURE 6. Schematic overview of the GRSA-based seismic optimizations.

The objective function Fitness defined in Eq. 6 is minimized in this study. Fitness is a weighted function of the two reduction ratios R_d and R_n. R_d is calculated as the reduction ratio of the peak SDR from the BF model, as defined in Eqs 7–9. Here, $SD{R}_j^X$ is the peak SDR of a design individual subjected to the X-directional input, $SD{R}_j^Y$ is the peak SDR of a design individual subjected to the Y-directional input, $SD{R}_{BF}^X$ is the peak SDR of the BF model subjected to the X-directional input, and $SD{R}_{BF}^Y$ is the peak SDR of the BF model subjected to the Y-directional input. R_n is the reduction ratio of the total number of BRBs to the total steel tonnage of the BRBs from that of the BRBF model. R_d and R_n are weighted by coefficients m and n. These parameters were manually adjusted for the BRB layout optimization by removing CBs and the BRB size optimization because these problems sometimes produce unrealistic solutions (i.e., local convergence) in which the number of BRB and CB is close to zero, but the story drift response is equal to that of the BF model. As a penalty to prevent member buckling, $\phi$ is defined in Eq. 10. When the buckling DCR of the CBs in a design solution exceeds 1.0, the Fitness becomes extremely high.

$Fitness=m{R}_d+n{R}_n+\phi (6)$

$R_d=\left(R_{dx}+R_{dy}\right)/2(7)$

$R_{dx}=\max \left\{SD{R}_j^X|j=\mathrm{1,2},\cdot \cdot \cdot ,5\right\}/SD{R}_{BF}^X(8)$

$R_{dy}=\max \left\{SD{R}_j^Y|j=\mathrm{1,2},\cdot \cdot \cdot ,5\right\}/SD{R}_{BF}^Y(9)$

$\phi =\{\begin{array}{l}0.0(DCR<1.0)\\ 9999(DCR\ge 1.0)\end{array}(10)$

The seismic response characteristics of these optimal solutions are analyzed using NLRHA. The details of these optimizations are as follows.

4.1.1 Elevation Layout Optimization by Replacing CBF with BRBF (Layout-C-1)

Figure 7A shows the definition of the design variables $\left\{x_i\right\}$ for Layout-C-1. The substructure is divided into 20 BRBFs (a to t), and layout optimization is performed for each of these BRBFs. The design variable x_i is the arrangement of the BRB and includes two states for each of the 20 BRBFs: replacing the CBF with the BRBF (x_i = 1) and leaving the CBF (x_i = 0). As a constraint, at least one CBF is replaced by one BRBF (Σx_i ≥ 1). R_d is the reduction ratio of the peak SDR and R_n is the reduction ratio of the number of BRBs. The yield axial force of the BRB is fixed at 3,000 kN.

FIGURE 7

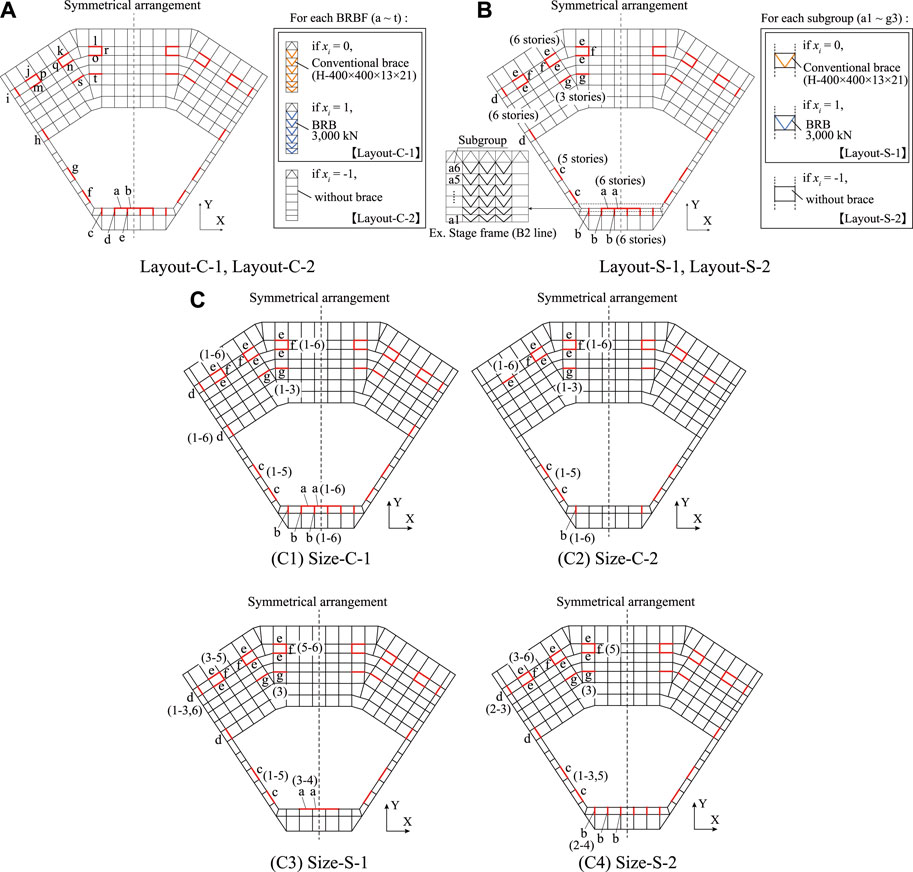
FIGURE 7. Definitions of the design variables of the GRSA-based seismic optimizations: (A) Layout optimization for each BRBF, (B) Layout optimization for each group, (C) Size optimization.

4.1.2 Elevation Layout Optimization by Replacing CBF With BRBF or Removing CBF (Layout-C-2)

An additional (to the conditions in Layout C-1) design operation is included, which corresponds to a state of removing a CBF (x_i = -1). At least one BRBF must be placed as a constraint. As in case A, R_d is the reduction ratio of the peak SDR, R_n is the reduction ratio of the number of BRBs. To prevent solutions in which R_n becomes significantly small while removing the conventional braces, m = 0.75 and n = 0.25 in Eq. 6.

4.1.3 Plan Layout Optimization for Each Group by Replacing CB With BRB (Layout-S-1)

Figure 7B shows the definition of the design variables $\left\{x_i\right\}$ for Layout-S-1. The substructure is divided into seven groups of frames (gr = {a, b, c, d, e, f, g}), which are further divided into subgroups, which are referred to as gr-story where gr is the group name and story is the story number. For example, a-2 corresponds to the second story in group (A). Layout optimization is performed for each subgroup. The constraints and objectives were the same as those in Case (A).

4.1.4 Plan Layout Optimization for Each Group by Replacing CB With BRB or Removing CB (Layout-S-2)

An additional (to the conditions in Layout S-1) design operation is included, which corresponds to a state of CB removal (x_i = −1). The constraint and objective function are the same as those in Case C.

4.1.5 BRB Size Optimization for the Solutions Obtained From the Layout Optimizations (Size-C-1, Size-C-2 and Size-S-1, Size-S-2)

Figure 7 (C1)–7(C4) shows the planar BRB layouts for BRB size optimization. The BRB size optimization is performed for each subgroup, as defined in Case C, using the solutions obtained from the layout optimization as the initial models. As a constraint, the sizes of the BRBs (based on the yield force) that can be assigned were limited to the range ran of standard sizes in Japan, where ran = (500 kN, 750 kN, 1,000 kN, 1,500 kN, 2,000 kN, 2,500 kN, 3,000 kN, 3,500 kN, 4,000 kN, 4,500 kN, 5,000 kN, and 6,000 kN). If the solution opts for a BRB of size 0 kN, a conventional brace (SN490, H-400 × 400 × 13 × 21) is assigned instead of the BRB. In this case, R_d is the reduction ratio of the peak SDR and R_n is the reduction ratio of the steel tonnage of BRBs. The coefficients m and n are assigned values of 0.87 and 0.13, respectively, while computing Fitness using Eq. 6.

The simple genetic algorithm (SGA) is used for BRB layout optimization, and PSO was used for BRB size optimization. The Python library DEAP¹ was used as the optimization tool. In the design application, two nodes (i.e., 28 × 2 processors) of a campus supercomputer (TSUBAME 3.0, Tokyo Institute of Technology) were assigned to each optimization. In each step of GA and PSO, 50 GRSAs were performed in parallel.

In the seismic optimization, the capacity of the conventional brace is explicitly considered as the constraint in which the demand-to-capacity ratio (DCR) is less than 1.0 meaning not buckling against the design earthquakes. In contrast to it, the capacities of the beam and column are implicitly considered as the objective function in which the peak story drift ratio is desired to be approximately 1.0% rad. meaning that the beam and column remain almost elastic against the design earthquakes.

4.2 Layout Optimization for Each Vertical BRBF (Layout-C-1, Layout-C-2)

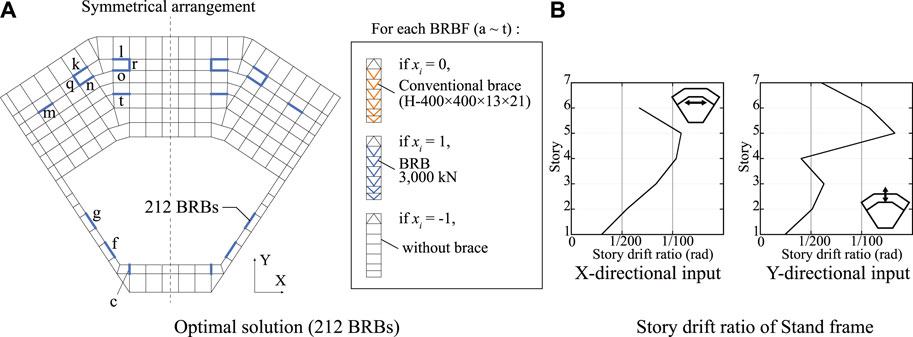
In the optimal solution of Layout-C-1, no CBF is placed, BRBFs are assigned instead, and the layout of the BRBs is the same as that in the BRBF model shown in Figure 1C. The SDRs are shown in Figure 5. Figure 8A shows the optimal layout obtained from Layout-C-2. The optimal solution has 212 BRBs, which is a 41% reduction from in the BRBF mode, and has no conventional brace. In the Stage frame, two BRBFs are placed in the Y-direction (c). In the Right and Left wall frames, only two BRBFs are placed near the Stage frame (f, g). In the Stand frame, most CBFs are replaced with BRBFs. In Layout-C-2, the BRBFs are arranged in the Right, Left, and Stand frames. The maximum SDRs of Layout-C-2 are shown in Figure 8B and are approximately 1%, except for the Stage frame and the Stand frame.

FIGURE 8

FIGURE 8. Optimal solution (Layout-C-2): (A) Optimal placement, (B) Maximum story drift ratio.

4.3 Layout Optimization for Each Story Of Each Group (Layout-S-1, Layout-S-2).

The optimal layout of Layout-S-1 is shown in Figure 9A and has 176 BRBs, which is a 51% reduction from the BRBF model and 247 CBs. In the Stage frame (B2 line) and Stand frame (A11, 12 lines), the BRBs are located exclusively in adjacent stories across the width of the frame, and the CBs are located in the upper and lower stories. In a previous study (Terazawa and Takeuchi, 2019), similar configurations were obtained as an optimal solution for layout optimization while minimizing the buckling DCR of braces in a 15-story 2D model. In the Stage frame (C3-8 lines), the CBs are placed in all stories. In the Right and Left wall frames, the BRBs are placed in all stories at the BRBFs and placed in stories, except for the upper stories of the BRBFs. In the Stand frame (LR3, 5 and C3, 8 lines), the BRBs are placed in the fifth or the upper stories where the drifts are large. Displacement concentration in a specific story is generally not preferable for seismic design. Nevertheless, this empirical rule is based on previous seismic damage of multistory buildings, where each story moves horizontally in a rigid body motion and is not always applicable for spatial structures where each part in a story moves flexibly. This optimization result indicates that the hybrid configuration, where the story-based configuration of BRBFs and CBFs, such as mid-level seismic isolation and the vertically uniform configuration of BRBFs, are mixed, is effective for reducing drift and preventing the buckling of conventional braces in large spatial structures.

FIGURE 9

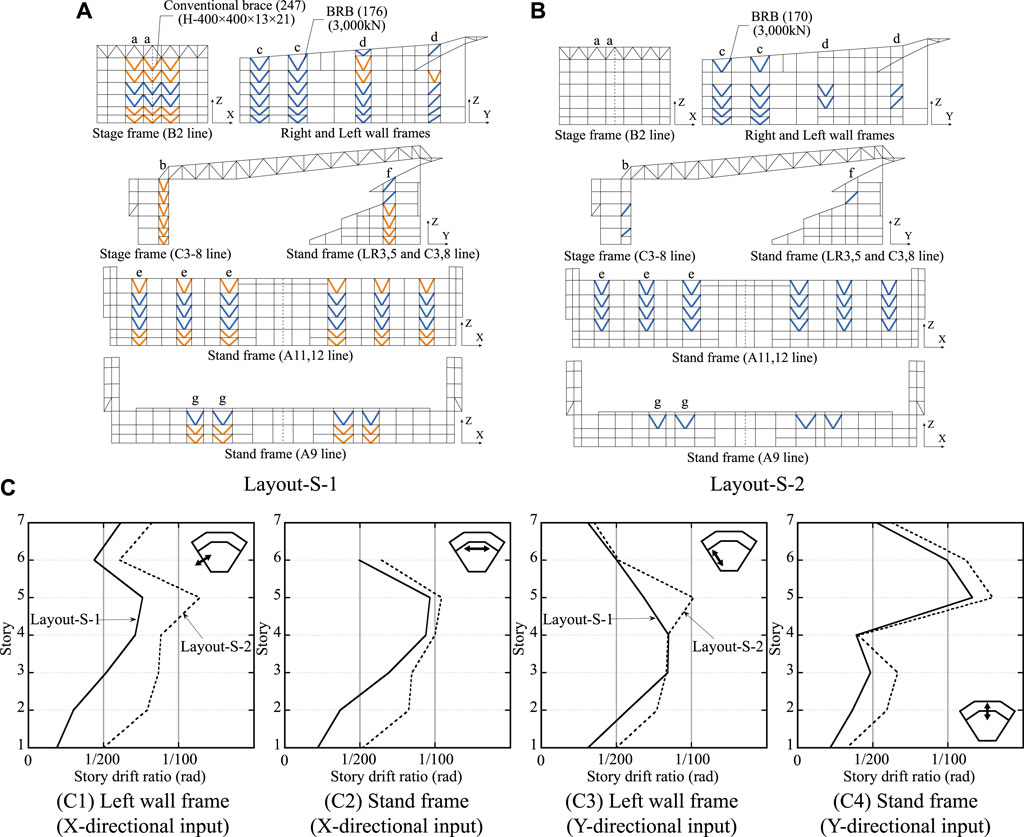
FIGURE 9. Optimal solution (Layout-S-1 and Layout-S-2): (A) and (B) Optimal placement, (C) Maximum story drift ratio.

The optimal layout of Layout-S-2 is shown in Figure 9B, and has 170 BRBs, which is a 53% reduction from the BRBF model. In the Stage frame, the BRBs are placed only in the Y-direction. In the Stand frame (A11, 12 lines), BRBs are placed in the third or upper stories. In the Stand frame (LR3, 5 and C3, 8 lines), the BRBs are placed in only the fifth story where the drift is large. On the other hand, the maximum SDRs of Layout-S-1 with CBs, shown in Figure 9C, are better than those of Layout-S-2 with no CBs.

4.4 Size Optimization for each BRBF (Size-C-1, Size-C-2)

In the Size-C-1 optimization, the BRB size is optimized using the BRBF model as an initial model because the optimal solution for Layout-C-1 was the BRBF model itself. The optimal layout of Size-C-1 is shown in Figure 10A. The layout of Size-C-2 is the same as that of Layout-C-2, as shown in Figure 8A. A comparison of the capacity distributions of the BRBs is presented in Figure 10A. Size-C-2 has 226 BRBs, which is a 37% reduction compared to the BRBF model. As shown in Figure 10A, the hybrid configuration, where the story-based configuration of BRBFs and CBFs, such as mid-level seismic isolation and the vertically uniform configuration of BRBFs, are mixed, is again produced as the optimal solution (regardless of the definitions of the design variables). This result implies that this hybrid configuration is the most effective in preventing the buckling of conventional braces and reducing the displacement of the substructure.

FIGURE 10

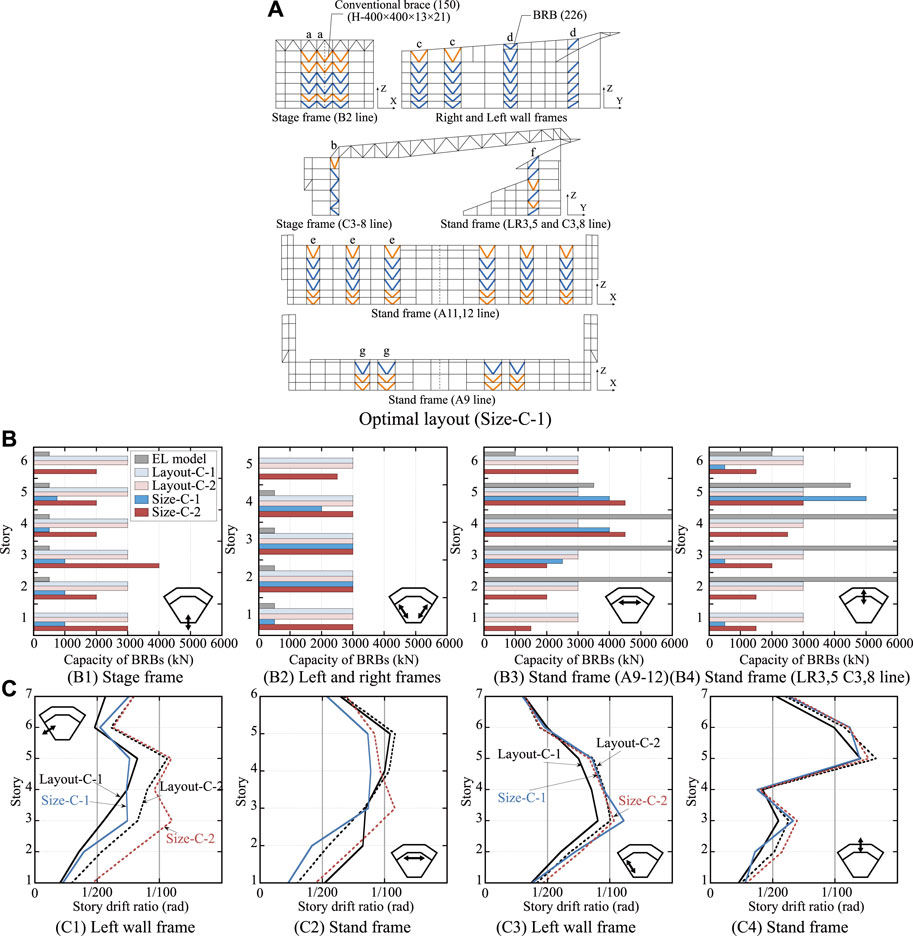
FIGURE 10. Optimal solution (Size-C-1 and Size-C-2): (A) Optimal placement (Size-C-1), (B) Capacity distribution of BRBs, (C) Maximum story drift ratio.

In Size-C-1 shown in Figure 10B, although the sizes of most BRBs are 3,000 kN or less, the sizes of the BRBs in the fourth and fifth stories of the Stand frame are more than 4,000 kN. The total steel tonnage of the BRBs of Size-C-1 is approximately 46% of that of the BRBF model. In the Size-C-2 shown in Figure 10B, while the BRBs with sizes of 3,000 kN or more are placed in the fourth and fifth stories in the Stand frame, the other frames have BRB sizes similar to that of Layout-C-2, and the total steel tonnage of the BRBs is approximately 93% of that of Layout-C-2. The maximum SDRs are shown in Figure 10C. Although the total steel tonnage of the BRBs is significantly reduced by optimizing the BRB size, the reduction in drifts was not very large.

4.5 Size Optimization for Each Story of Each Group (Size-S-1, Size-S-2).

The optimal mixed layout of BRBs and CBs in Size-S-1 is shown in Figures 11A a comparison of the capacity distribution of the BRBs is shown in Figures 11A,B comparison of the maximum SDR is shown in Figure 11C. While 176 BRBs and 247 CBs are placed in the optimal solution of Layout-S-1, the number of BRBs in the optimal solution of Size-S-1 is reduced to 156 by replacing the BRBs with conventional braces in the upper stories of the Right and Left wall frames. Because the sizes of BRBs in the other frames are larger than those in the optimal solution of Layout-S-1, the total steel tonnage of the BRBs remains 97% of that of Layout-S-1. As shown in Figure 11C, the peak SDRs of Size-S-1 in the X-direction is less than 1%, and the peak SDR of the Stand frame in the Y-direction is reduced to approximately 1% compared to that of Layout-S-1.

FIGURE 11

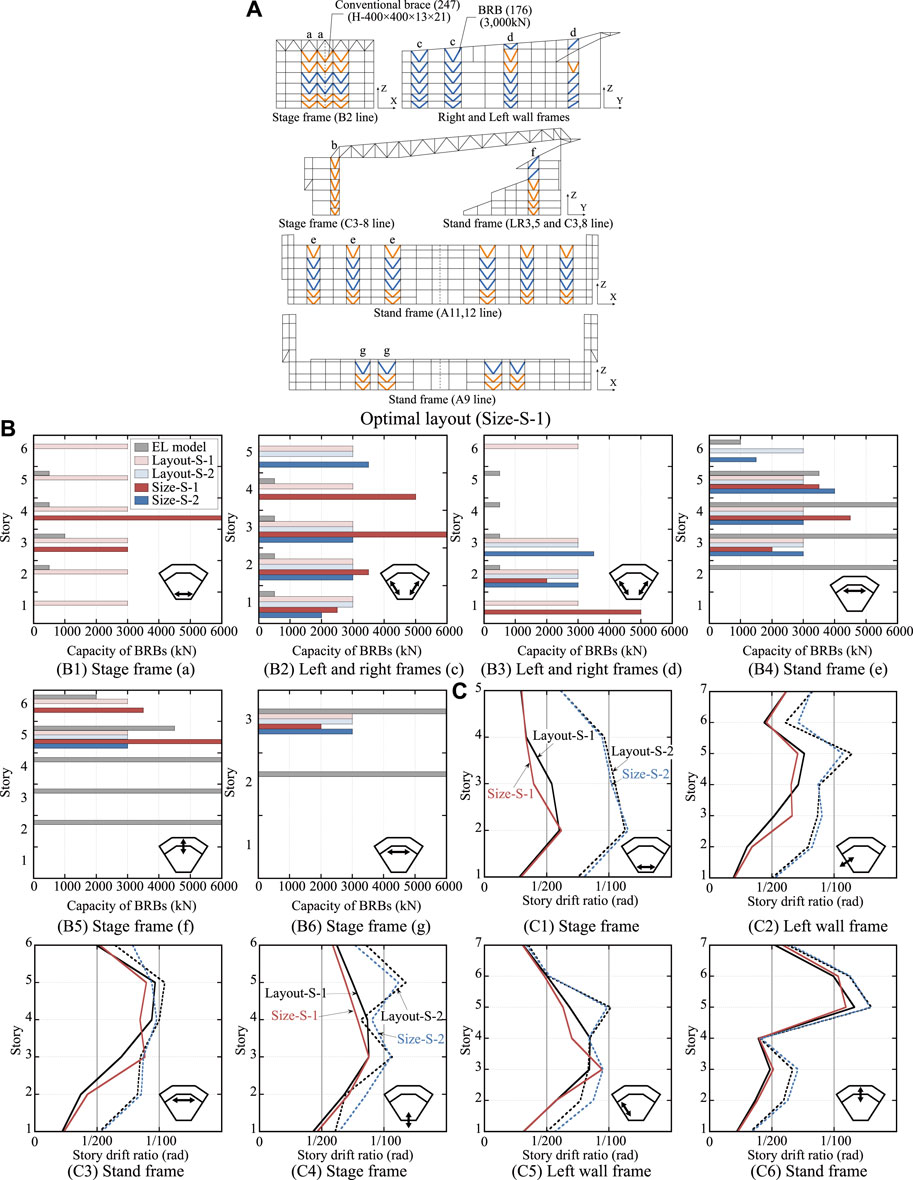
FIGURE 11. Optimal solution (Size-S-1 and Size-S-2): (A) Optimal placement (Size-S-1), (B) Capacity distribution of BRBs, (C) Maximum story drift ratio.

As shown in Figure 11B, in Size-S-2, while the sizes of the BRBs in the Stage frame are reduced, BRBs with sizes of 4000 kN or more are placed in the Stand frames, and the total steel tonnage of the BRBs is approximately 95% of that of Layout-S-2. As shown in Figure 11C, the peak SDRs in Size-S-2 are almost the same as those in Layout-S-2.

According to the results in Sections 4.4, 4.5, it can be seen that the BRB size optimization can produce solutions that have drifts equal to or less than that of the layout optimal solution despite the reduced steel tonnage of BRBs. Furthermore, the drift response of the solutions obtained from the proposed GRSA-based seismic optimization was smaller than that of the solution obtained using the EL method in Section 3.

4.6 Discussion of the Optimization Results

The results of the series of optimization study from Sections 4.2–4.5 are summarized. Both elevation layout optimization and plan layout optimization suggested a hybrid configuration (Size-C-1 and Layout-S-1). The hybrid configuration, where the story-based configuration of BRBFs and CBFs such as mid-level seismic isolation and the vertically uniform configuration of BRBFs are mixed, is very effective in preventing the buckling of conventional braces and reducing the drift of the large spatial structures where a rigid diaphragm assumption is not available. In addition, seismic optimization that only replaces conventional braces with BRB sometimes finds no solution where no conventional braces buckle. A seismic optimization permitting removing conventional braces is effective in preventing the buckling of conventional braces in such cases.

4.7 Comparison of Damper Design Methods

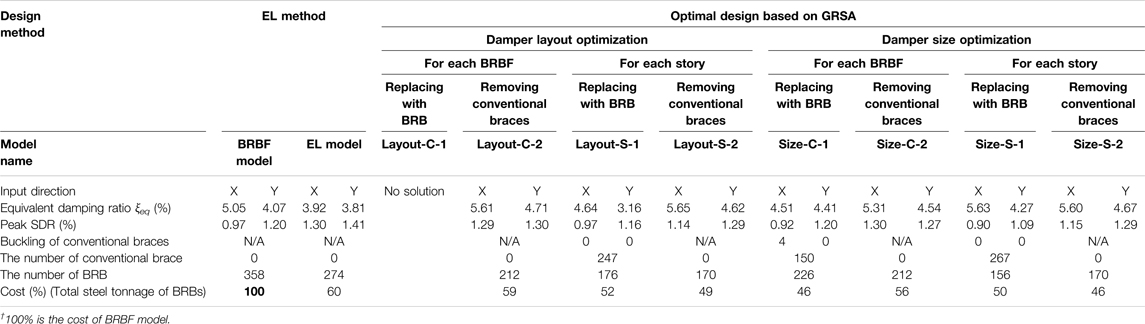
Table 3 summarizes the number and total steel tonnage of the BRBs and the seismic response characteristics of the solutions obtained by each damper design method in Sections 3, 4. The equivalent modal damping ratio ξ_eq is evaluated in the GRSA. The peak SDR of the EL model is approximately 1.4%, which is the largest among responses obtained from all solutions. The peak SDRs of the solutions obtained from the proposed GRSA-based seismic optimization method are smaller than those of the solutions obtained using other methods. The proposed GRSA-based seismic optimization method prevents the buckling of conventional braces by defining the penalty in the Fitness of braces with a DCR of more than 1.0. In the EL model, the number of BRBs is 274, which is a 23% reduction from the BRBF model, and the total steel tonnage of BRBs is approximately 60% of that of the BRBF model. In contrast with these solutions, the number of BRBs obtained from the proposed GRSA-based seismic optimization method is 156–226, which is approximately a 37%–56% reduction from that of the BRBF model, and the total steel tonnages of BRBs are reduced to 46–59%. In addition, while the equivalent modal damping ratios ξ_eq of the EL model are approximately 3.9%, those of the solutions obtained from the proposed GRSA-based seismic optimization method were 3.1%–5.7%.

TABLE 3

TABLE 3. Comparison of optimal solutions.

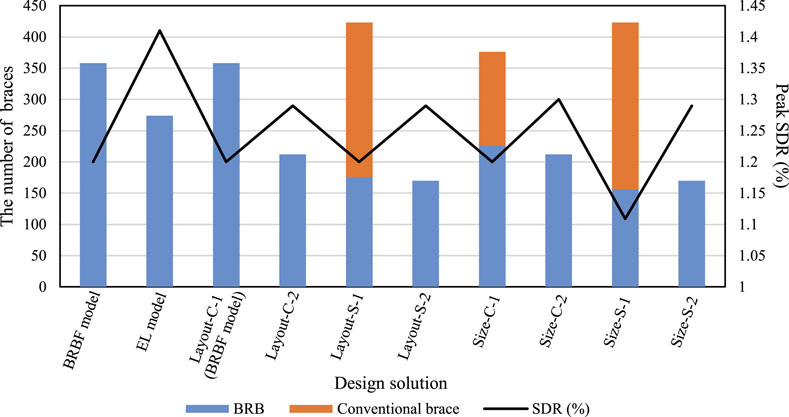
Figure 12 compares the number of braces and the peak SDR of the optimal solutions. In the layout optimization, the optimal solution of Layout-S-1 showed the best performance, despite having fewer BRBs. In size optimization, the optimal solution of Size-S-1 showed the best performance in terms of both SDR and the number of BRBs. For the target building without the rigid diaphragm assumption, designing the dampers using conventional design methods such as the EL method may not always produce the best design, and the proposed GRSA-based seismic optimization method provided solutions with much better seismic performance while reducing the number and the total steel tonnage of BRBs.

FIGURE 12

FIGURE 12. Comparison of the optimal solutions.

The proposed GRSA-based seismic optimization method required a run time of only 48 h (for each problem) to produce the optimal solution. The entire computation time was 96 h because BRB size optimization was subsequently conducted after the BRB layout was optimized. Nevertheless, in practical use, it is assumed that most engineers are only interested in BRB layout or size optimization. Note that every four problems regarding the BRB layout or BRB size optimization problems were processed in parallel (not one by one) on the supercomputer. Moreover, because all the solutions obtained during the optimization calculation process are stored, it is possible to examine the various obtained brace configurations and is useful for determining the trend of configurations with large Fitness values (bad-fit solutions). Thus, the proposed damper design method can be helpful to engineers in choosing the correct brace configuration.

5 Conclusion

This study presents a design application of the proposed GRSA-based seismic optimization to a large metal spatial structure (constructed in Japan) where a rigid diaphragm assumption is not available and displacement responses are disproportionally distributed in a story. It also discusses the optimal mixed placement and capacity distribution of BRBs and CBs to minimize both the story drift response and the number of BRBs (i.e., the introduction cost of expensive energy-dissipation devices used as dampers), and succeeds in demonstrating the GRSA-based seismic optimization method, where both the BRB layout and BRB size can be optimized within a practical time range. The following results were obtained:

1) In the design solution using the EL method (the standard damper design method authorized in Japan), the number of BRBs is 274, which is a 23% reduction from the BRBF model, and the peak SDR approximately exceeds 1.4%. The EL method cannot consider the interaction between the frames of the substructure during an earthquake because it is applied to each frame individually, and as a result, larger BRBs are arranged in the Stand frame (with large mass and stiffness). In contrast, the proposed GRSA-based seismic optimization method produces a better design solution, where the number of BRBs is 156–226, which is a 37%–56% reduction from the BRBF model, while the peak SDR is further reduced from the EL model, and the larger BRBs are appropriately distributed in the stories with the larger SDRs.

2) Thesolution obtained from the proposed GRSA-based seismic optimization method has approximately 20% less steel tonnage of BRBs than that obtained from other design methods, whereas the seismic performance is equal to or better than the others. This is because this method incorporates the effects of other major economic parameters such as the number and steel tonnage of BRBs.

3) A hybrid seismic resisting system composed of a configuration in which BRBs and CBs are arranged in adjacent stories (such as mid-level seismic isolation in multi-story structures) and a vertically uniform BRB configuration is the most effective configuration for preventing the buckling of conventional braces and reducing the drift response of the substructure of spatial structures where a rigid diaphragm assumption is not applicable.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

YT: Supervision, Conceptualization, Methodology, Investigation, Formal analysis, Writing—original draft, Writing—review, and editing. MF: Visualization. TT: Supervision.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors are grateful to Y. Mori, M. Osawa, A. Matsuura, T. Sasaki, and H. Kobayashi from Azusa Sekkei Co., Ltd. A campus supercomputer (TSUBAME 3.0 at the Tokyo Institute of Technology) was used to perform the analyses for the optimization study.

Footnotes

¹DEAP 1.1.0. https://github.com/DEAP/deap

References

Adachi, F., Yoshitomi, S., Tsuji, M., and Takewaki, I. (2013). Nonlinear Optimal Oil Damper Design in Seismically Controlled Multi-Story Building Frame. Soil Dyn. Earthq. Eng. 44, 1–13. doi:10.1016/j.soildyn.2012.08.010

CrossRef Full Text | Google Scholar

Akehashi, H., and Takewaki, I. (2022). Inverse Optimal Damper Placement via Shear Model for Elastic-Plastic Moment-Resisting Frames under Large-Amplitude Ground Motions. Eng. Struct. 250, 113457. doi:10.1016/j.engstruct.2021.113457

CrossRef Full Text | Google Scholar

Akehashi, H., and Takewaki, I. (2019). Optimal Viscous Damper Placement for Elastic-Plastic MDOF Structures under Critical Double Impulse. Front. Built Environ. 5. 07 March 2019. doi:10.3389/fbuil.2019.00020

CrossRef Full Text | Google Scholar

American Society of Civil Engineers (2016). Minimum Design Loads for Buildings and Other Structures. ASCE Standard-ASCE/SEI 7-16.

Google Scholar

Apostolakis, G. (2020). Optimal Evolutionary Seismic Design of Three-Dimensional Multistory Structures with Damping Devices. J. Struct. Eng. 146 (10), 04020205. doi:10.1061/(ASCE)ST.1943-541X.0002775

CrossRef Full Text | Google Scholar

Apostolakis, G., and Dargush, G. F. (2009). Optimal Seismic Design of Moment-Resisting Steel Frames with Hysteretic Passive Devices. Earthq. Engng Struct. Dyn. 39 (4), a–n. doi:10.1002/eqe.944

CrossRef Full Text | Google Scholar

Architectural Institute of Japan (2019). AIJ Standard for Allowable Stress Design of Steel Structures. (in Japanese).

Google Scholar

Architectural Institute of Japan (2014). Recommended Provisions for Seismic Damping Systems Applied to Steel Structures. Tokyo: Architectural Institute of Japan. (in Japanese).

Google Scholar

Asai, T., Terazawa, Y., Miyazaki, T., Lin, P.-C., and Takeuchi, T. (2021). First Mode Damping Ratio Oriented Optimal Design Procedure for Damped Outrigger Systems with Additional Linear Viscous Dampers. Eng. Struct. 247, 113229. doi:10.1016/j.engstruct.2021.113229

CrossRef Full Text | Google Scholar

Aydin, E., Öztürk, B., and Dutkiewicz, M. (2019). Analysis of Efficiency of Passive Dampers in Multistorey Buildings. J. Sound Vib. 439, 17–28. doi:10.1016/j.jsv.2018.09.031

CrossRef Full Text | Google Scholar

Cetin, H., Aydin, E., and Ozturk, B. (2019). Optimal Design and Distribution of Viscous Dampers for Shear Building Structures under Seismic Excitations. Front. Built Environ. 5. doi:10.3389/fbuil.2019.00090

CrossRef Full Text | Google Scholar

De Domenico, D., and Hajirasouliha, I. (2021). Multi-level Performance-Based Design Optimisation of Steel Frames with Nonlinear Viscous Dampers. Bull. Earthq. Eng. 19, 5015–5049. doi:10.1007/s10518-021-01152-7

CrossRef Full Text | Google Scholar

European Committee for Standardization, (2004). Eurocode 8: Design of Structures for Earthquake Resistance. EN 1998.

Google Scholar

Fujita, K., Moustafa, A., and Takewaki, I. (2010). Optimal Placement of Viscoelastic Dampers and Supporting Members under Variable Critical Excitations. Earthquakes Struct. 1 (1), 43–67. doi:10.12989/eas.2010.1.1.043

CrossRef Full Text | Google Scholar

García, D. L. (2001). A Simple Method for the Design of Optimal Damper Configurations in MDOF Structures. Earthq. spectra 17 (3), 387–398. doi:10.1193/2F1.158618010.1193/1.1586180

CrossRef Full Text | Google Scholar

Harada, D., and Yoshitomi, S. (2021). Optimal Performance and Placement Design Method of Buckling Restrained Braces for Vibration Control Building. Nihon Kenchiku Gakkai Kozokei Ronbunshu 86 (785), 1046–1055. (in Japanese). doi:10.3130/aijs.86.1046

CrossRef Full Text | Google Scholar

iGen, M. (2012). Midasuser. Available at: https://www.midasuser.com/.

Google Scholar

Ishibashi, Y., Terazawa, Y., Tanaka, H., Yokoyama, R., Mizuno, H., and Takeuchi, T. (2022). A Novel Damped Braced Tube System for Tall Buildings in High Seismic Zones, T, 31. Hoboken: Struct Design Tall Spec Build, e1926. doi:10.1002/tal.1926

CrossRef Full Text | Google Scholar

Kasai, K., Fu, Y., and Watanabe, A. (199819985). Passive Control Systems for Seismic Damage Mitigation. J. Struct. Eng. 124124 (5), 5015–5512. doi:10.1061/(ASCE)0733-944510.1061/(asce)0733-9445(1998)124:5(501)

CrossRef Full Text | Google Scholar

Lago, A., Trabucco, D., and Wood, A. (2019). Damping Technologies for Tall Buildings Theory, Design Guidance and Case Studies. Amsterdam: CTBUH, Elsiver Inc.

Google Scholar

Levy, R., and Lavan, O. (2006). Fully Stressed Design of Passive Controllers in Framed Structures for Seismic Loadings. Struct. Multidisc Optim. 32 (6), 485–498. doi:10.1007/s00158-005-0558-5

CrossRef Full Text | Google Scholar

Lopez Garcia, D., and Soong, T. T. (2002). Efficiency of a Simple Approach to Damper Allocation in MDOF Structures. J. Struct. Control 9, 19–30. doi:10.1002/stc.3

CrossRef Full Text | Google Scholar

Ministry of Construction, Japan (2001). Commentary of the Technical Background about the Regulations of the Revised Japanese Building Law, Gyousei. (in Japanese).

Google Scholar

Ministry of Construction, Japan (2000). Ministerial Notification No. 1457 of the Ministry of Construction. Japan. (in Japanese).

Google Scholar

Ozturk, B., Cetin, H., and Aydin, E. (2022). Optimum Vertical Location and Design of Multiple Tuned Mass Dampers under Seismic Excitations. Structures 41, 1141–1163. doi:10.1016/j.istruc.2022.05.014

CrossRef Full Text | Google Scholar

Palermo, M., Muscio, S., Silvestri, S., Landi, L., and Trombetti, T. (2013). On the Dimensioning of Viscous Dampers for the Mitigation of the Earthquake-Induced Effects in Moment-Resisting Frame Structures. Bull. Earthq. Eng. 11 (6), 2429–2446. doi:10.1007/s10518-013-9474-z

CrossRef Full Text | Google Scholar

Palermo, M., Silvestri, S., Landi, L., Gasparini, G., and Trombetti, T. (2018). A "direct Five-step Procedure" for the Preliminary Seismic Design of Buildings with Added Viscous Dampers. Eng. Struct. 173, 933–950. doi:10.1016/j.engstruct.2018.06.103

CrossRef Full Text | Google Scholar

Palermo, M., Silvestri, S., Landi, L., Gasparini, G., and Trombetti, T. (2016). Peak Velocities Estimation for a Direct Five-step Design Procedure of Inter-storey Viscous Dampers. Bull. Earthq. Eng. 14 (2), 599–619. doi:10.1007/s10518-015-9829-8

CrossRef Full Text | Google Scholar

Silvestri, S., Gasparini, G., and Trombetti, T. (2010). A Five-step Procedure for the Dimensioning of Viscous Dampers to Be Inserted in Building Structures. J. Earthq. Eng. 14 (3), 417–447. doi:10.1080/13632460903093891

CrossRef Full Text | Google Scholar

Singh, M. P., and Moreschi, L. M. (2002). Optimal Placement of Dampers for Passive Response Control. Earthq. Engng. Struct. Dyn. 31, 955–976. doi:10.1002/eqe.132

CrossRef Full Text | Google Scholar

Sinha, R., and Igusa, T. (1995). CQC and SRSS Methods for Non-classically Damped Structures. Earthq. Engng. Struct. Dyn. 24 (4), 615–619. doi:10.1002/eqe.4290240410

CrossRef Full Text | Google Scholar

Takagi, J., OhsakiCao, M. Y., and Cao, Y. (2021). Structural Properties of Superior Design Solutions of Steel Buildings Associated with BRBs. Structures 34, 3851–3865. doi:10.1016/j.istruc.2021.10.006

CrossRef Full Text | Google Scholar

Takewaki, I. (1997). Optimal Damper Placement for Minimum Transfer Functions. Earthq. Engng. Struct. Dyn. 26 (11), 1113–1124. doi:10.1002/(sici)1096-9845(199711)26:11<1113::aid-eqe696>3.0.co;2-x

CrossRef Full Text | Google Scholar

Takewaki, I., Yoshitomi, S., Uetani, K., and Tsuji, M. (1999). Non‐monotonic Optimal Damper Placement via Steepest Direction Search. Earthq. Engng. Struct. Dyn. 28 (6), 655–670. doi:10.1002/(sici)1096-9845(199906)28:6<655::aid-eqe833>3.0.co;2-t

CrossRef Full Text | Google Scholar

Terazawa, Y., Asai, T., Ishibashi, Y., and Takeuchi, T. (2020). Effect of Design Parameters on Dynamic Response Characteristic of Single Damped Outrigger System Incorporating Linear Viscous Dampers. Nihon Kenchiku Gakkai Kozokei Ronbunshu 85 (774), 1067–1077. (in Japanese). doi:10.3130/aijs.85.1067

CrossRef Full Text | Google Scholar

Terazawa, Y., Ishibashi, Y., Omura, H., Asai, T., and Takeuchi, T. (2022). Non-linear Dynamic Response Characteristic of Single-Damped Outrigger Systems with Oil Dampers or Elasto-Plastic Dampers Considering Design Earthquake Levels. Nihon Kenchiku Gakkai Kozokei Ronbunshu 87 (791), 149–160. (in Japanese). doi:10.3130/aijs.87.149

CrossRef Full Text | Google Scholar

Terazawa, Y., Sano, W., and Takeuchi, T. (2020). Design Method of Seismically Isolated Structures Based on Generalized Response Spectrum Analysis. Nihon Kenchiku Gakkai Kozokei Ronbunshu 85 (775), 1187–1197. (in Japanese). doi:10.3130/aijs.85.1187

CrossRef Full Text | Google Scholar

Terazawa, Y., and Takeuchi, T. (2018). Elasto-plastic Damper Optimization Routine for Lattice Towers Based on Generalized Response Spectrum Analysis. J. Int. Assoc. Shell Spatial Struct. 59 (4), 243–250. doi:10.20898/j.iass.2018.198.035

CrossRef Full Text | Google Scholar

Terazawa, Y., and Takeuchi, T. (2018). Generalized Response Spectrum Analysis for Structures with Dampers. Earthq. spectra 34 (3), 1459–1479. doi:10.1193/092217EQS188M

CrossRef Full Text | Google Scholar

Terazawa, Y., and Takeuchi, T. (20192019). Optimal Damper Design Strategy for Braced Structures Based on Generalized Response Spectrum Analysis. Jpn. Archit. Rev. 2, 477–493. doi:10.1002/2475-8876.12122

CrossRef Full Text | Google Scholar

The Japan Society of Seismic Isolation (2013). Design and Construction Manual for Passive Control System. 3rd edition. Tokyo: The Japan Society of Seismic Isolation. (in Japanese).

Google Scholar