Structural performance of steel plates

In general, plates are classified as thick plates when the minimum dimension to thickness ratio (b/h) is less than 10, thin plates when the b/h ratio ranges from 10 to about 100, provided that the plate maximum deflection to thickness ratio (w/h) is less than 0.2, and membranes when the b/h ratio approaches 100 and w/h $\ge$ 0.2. Thick plates develop internal stress resultants governed by three-dimensional elasticity similar to that of a solid body. Thin plates behave as plane stress members governed by two-dimensional elasticity. Membranes can only develop internal tensile stress within the plate’s neutral plane. Few studies have adopted b/h ratios between 90 and 110 to investigate the feasibility of the utilization of such plates in their various available forms. The current study with the b/h ratio of 100 aims to fill the gap. Steel Plates are available in different forms such as intact plates, stiffened, perforated, and stiffened perforated plates. They are used in buildings, bridges, ships, as well as aerospace structures. In this study, the investigated steel plate has a square shape and is subjected to uniaxial loading. The plate edges are simply supported. The plate is 200 mm wide and 2 mm thick. In this case, the critical buckling strength is, in general, less than the plate maximum strength. With further loading, the plate would experience an undesirable sudden mode of failure owing to buckling instability. This study aims at investigating the performance of the different forms of square steel plates, such as intact, stiffened, perforated, and perforated stiffened, when the minimum dimension to thickness ratio is 100. A pushover finite element linear elastic buckling analysis as well as a nonlinear large deflection buckling analysis have been carried out. The study indicated that the increase in the plate maximum strength in single, double, and triple stiffener plates was 75.6%, 174%, and 196%, respectively, compared to that of the intact plate. Based on the obtained results, it is concluded that the utilization of plates having the b/h ratio of 100 is feasible provided that the appropriate plate form is adopted.

Introduction

Steel plates are commonly used in buildings, bridges, hydraulic structures, containers, ships, aerospace structures, and planes, as well as instruments and machines (Giovanni et al., 2014). They may be subjected to in plane loads or lateral loads or both.

Plates are generally classified as: 1) thick plates when the plate minimum dimension to thickness ratio (b/h) is less than 10. Thick plates develop internal load resultants, governed by three-dimensional elasticity to counterbalance the applied load. 2) Thin plates when b/h ranges from 10 to 100. Thin plates behave as plane stress members provided that the plate maximum deflection to plate thickness ratio (w/h) is less than 0.2. In this case, the plate develops internal load resultants, governed by two-dimensional elasticity to counterbalance the applied loading. 3) Membranes when the b/h ratio approaches 100 and w/h > 0.2. Membranes are only capable of developing internal tensile stress resultants, namely, membrane tensile force resultants acting within the plate middle plane (Yamaguchi and Wai-Fah, 1999; Ventsel and Krauthammer, 2001; Stephen et al., 2010).

Buckling instability is a mode of failure that the thin plate may experience under compression. This happens when the critical buckling load is less than the plate maximum strength. At low b/h values, strain hardening is generally attained without plate buckling. For medium b/h values, the plate imperfections as well as the plate residual stresses both give rise to inelastic buckling depicted as a transition curve. On the other hand, for large b/h values, the maximum plate strength exceeds the critical buckling load. In this case, the plate may experience elastic buckling, followed by nonlinear buckling when the incremental load increases. Buckling nonlinearity is caused by deformed thin plate geometry, geometric imperfections, residual steel stresses, and inelastic material behavior (Yamaguchi and Wai-Fah, 1999; Stephen et al., 2010). AISC (2017) provisions require preventing local plate buckling at any stress below the steel yield strength. On performing the pushover nonlinear buckling finite element (FE) analysis, subsequent to the critical buckling load, one of the following scenarios may take place: 1) the applied load remains constant whereas the lateral displacement upsurges, 2) the applied load declines however the lateral displacement upsurges, or 3) the applied load and the lateral displacement both upsurge, resulting in an additional cycle of buckling (Malhas et al., 2020). Post buckling response encompasses large displacement owing to the combined effect of both the geometric and the material nonlinearities due to the inelastic material behavior existing in the steel stress and strain constitutive relationship.

When plate buckling is experienced in a simply supported steel plate under a uniaxial compressive loading applied, membrane tensile stresses develop in the direction normal to the applied load. The tensile stresses are triggered by the stretching of the deformed neutral plane while the unloaded side edges are constrained against in plane translation. The developed tensile stresses hamper the lateral out of plane displacement.

Researches have been performed on buckling of intact plates as well as perforated plates in plane axial edge loading (Behzad et al., 2018). They indicated that in the case of large perforations, the critical buckling strength is generally higher than the plate maximum strength.

Aydin and Mustafa Sonmez (2015) stated that the perforations modify the plate buckling modal shape. Several researcher works (Ul-Nyeon et al., 2009; Aydin and Mustafa Sonmez, 2015; AISC, 2017; Behzad et al., 2018; Malhas et al., 2020) have indicated that cutouts reduce the elastic buckling load as well as the plate maximum strength. If large cutouts exist in the plate, the elastic buckling load becomes higher than the plate maximum strength. A plate with large openings may undergo either buckling or alternative yielding that may result in fractures (Saad-Eldeen et al., 2014). The local disturbance in the stress flow and the experienced peak stresses at the edges of the openings result in plate fracture when the steel’s von Mises (σ_e) stresses at the edges of cutouts reach the steel ultimate stress (σ_u).

The plate maximum strength is influenced by its width to thickness ratio and the steel stress strain constitutive model, as well as the steel elastic properties such as the modulus of elasticity and yield strength. Several researcher works (Grondin et al., 1999; Gunay et al., 2013) have investigated the nonlinear buckling behavior of the stiffened plates, and they have concluded that the single sinusoidal half wave–shaped global buckling of an unstiffened intact plate converts to multiple local buckling in the form of half waves extending between every two nearby stiffeners. They also stated that the critical buckling stress is enhanced as the number of stiffeners is increased. Thus, in stiffened plate forms, instability might be experienced as local half waves existing between every two adjacent stiffeners, provided that the stiffeners possess relatively large flexural and torsional stiffnesses. Moreover, instability may be initiated as local buckling of the part of the plate spanning between the two adjacent stiffeners, followed by plate global buckling with further loading.

On the other hand, instability may be first experienced in stiffeners in the form of stiffener tripping, namely, stiffeners lateral torsional buckling owing to the relatively low values of torsional and flexural stiffnesses of the provided stiffeners.

A stiffened plate may be designed to experience local buckling for the parts of the plate spanning between each two adjacent stiffeners at a fraction of the failure load, followed by global buckling of the stiffened plate with further loading. Such design approach improves the critical buckling strength and is cost effective (Quin et al., 2009).

Plates are typified examples of plane stress members. In addition to the aforementioned factors, nonlinearity in the behavior of steel plates is also attributed to the low plate thickness, which is considerably low compared to the plate geometry. Such dimensions pave the way toward large deflection behavior. On the other hand, the steel behavior is linear elastic up to the steel yield stress. Subsequently, it is inelastic and involves both elastic and plastic strains. The plastic strains increase with further loading. Thus, nonlinearity is attributed to both geometry and material inelasticity.

In this study, the minimum plate dimension to thickness ratio is 100. Few studies have adopted b/h ratios between 90 and 110 to examine the performance and the feasibility of utilization of the plates in their various available forms such as intact, stiffened, perforated, and perforated stiffened under uniaxial uniform compression. The current study aims to fill the gap.

Problem statement

When the elastic buckling strength of the plate is less than the maximum plate strength, the plate in general experiences buckling failure. It is an undesirable mode of failure as it gives no warning. If the opposite is true, with further loading, nonlinear buckling may occur as the incrementally applied load approaches the plate maximum strength, which is defined as the highest load value in the load axial shortening curve. Nonlinearity is first caused by geometry as well as residual stresses and surface imperfections. When the developed internal steel’s von Mises (σ_e) stresses reach the steel yield stress, the associated total strain becomes inelastic. They comprise both elastic and plastic strains. Nonlinearity is now attributed to the aforementioned factors as well as material plasticity. The plastic strains permit stress redistribution and result in the development of larger internal load resultants that counterbalance the incremental applied loading. Ultimately, failure occurs when the plate section is not capable anymore of developing the appropriate internal load resultants that would maintain equilibrium.

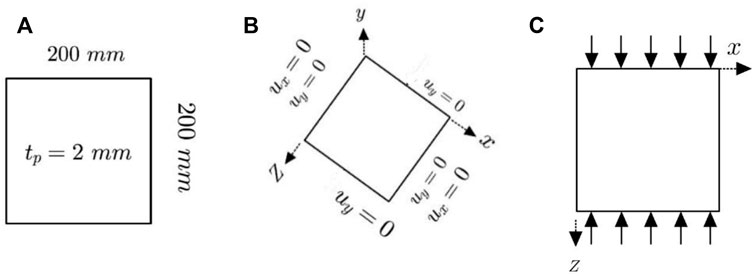
This study intends to investigate the performance, buckling behavior, and mode of failure of plates subjected to uniaxial edge loading at the two opposite edges. All plate forms have simply supported edges. The study has embraced the following cases, shown in Figure 1:

• Square intact plates of 200 mm width (b) and thickness (tp) equals 2 mm.

• Stiffened plates; depth of stiffeners equals 20 mm and thickness of stiffeners (ts) is 4 mm. Thickness of stiffeners to thickness of plate $\left(\text{ts}/\text{tp}\right)$ equals 2.

• Perforated plates; circular perforations of diameter (d) equals 30 mm.

• Perforated stiffened plates; circular perforations of diameter (d) = 30 mm, and stiffeners are identical in dimensions and shape to those in stiffened plates.

FIGURE 1

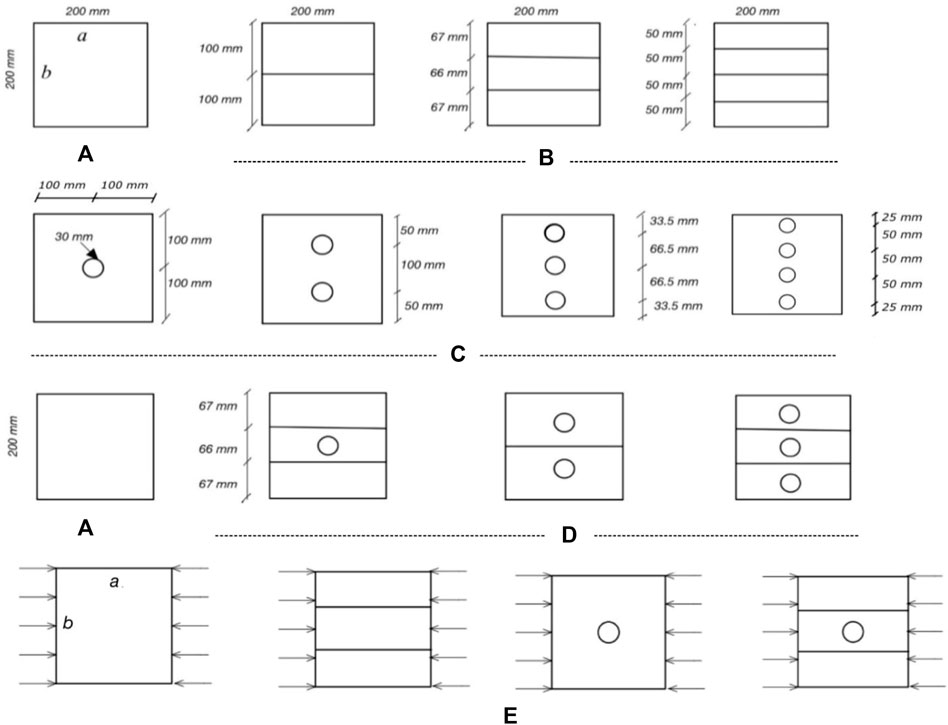
FIGURE 1. (A) Intact plates, (B) stiffened plates, (C) perforated plates, (D) stiffened perforated plates, (E) loading.

All the plate end edges are simply supported, shown in Figure 2

FIGURE 2

FIGURE 2. (A) Plate geometry, (B) plate boundary conditions, (C) plate loading.

It is assumed that the plate and the stiffeners are steel and are rigidly attached together.

Analysis and numerical modeling:

The FE numerical analysis has been performed in two stages:

The initial stage was the pushover linear elastic buckling analysis. The second stage involved nonlinear post elastic buckling analysis due to nonlinearity in geometry, residual stresses, and surface imperfections, followed by material nonlinearity that has initiated when the steel’s von Mises stresses (σ_e) exceeded the material yield stress (σ_y), as follows:

1) Initial stage: elastic buckling analysis.

2) In the second stage, the distorted shape from the initial stage was employed as the deformed geometry in the pushover nonlinear large deflection buckling analysis.

Modeling

Analysis has been performed using Ansys (2021). Shell 181 element has been used. It simulates both flexural and membrane behaviors. It is a four noded element. Each node possesses three translational as well as three rotational degrees of freedom. Modulus of elasticity of steel = 200 GPa, Poison ratio = 0.3, yield strength of steel = 250 MPa, and ultimate strength of steel = 460 Mpa. The maximum size of the shell element is b/20. In the regions close to perforations, the element max size is the least of b/20 or d/55, where d is the perforation size.

Validation

A validation analysis has been performed to confirm that the chosen element sizes are appropriate, and the adopted element type numerically simulates the behavior of the considered structural member. A sensitivity analysis for the mesh was performed to investigate the appropriateness of the size of mesh. Eventually the attained analysis results have been validated for the case of the intact plate in both elastic linear as well as nonlinear pushover buckling analyses. The recorded finite element results compared well with the results of the relevant mathematical expressions presented in literature. Subsequently, a buckling analysis has been performed for all considered plate forms subjected to uniaxial loading under simple span end conditions, shown in Figures 1, 2.

The obtained results for the elastic linear as well as the nonlinear buckling analyses for intact plates compare well with the closed form solutions as follows:

• Elastic buckling analysis

The recorded critical buckling load (P_cr) for the intact solid square plate using finite element simulation (P_cr) is 28.64 kN or N_cr = 143.2 N/mm.

It can be observed that it is relatively close to the critical buckling load N_cr of 144.61 N/mm for the solid square plate, obtained by Eq. 1 (Ventsel and Krauthammer, 2001).

$D=\frac{E{t}^3}{12\left(1-{\upsilon }^2\right)}=\frac{2.0x{10}^5{\left(2\right)}^3}{12\left(1-{0.3}^2\right)}=146520.146 \mathrm{m}{\mathrm{m}}^4,(1)$

whereD: plate flexural rigidity;E: steel modulus of elasticity;$\upsilon :$ Poisson ratio.

$N_{cr}=4\frac{{\pi }^{2}D}{b^2}=4\frac{{\pi }^2\ast 146520.146}{{200}^2}=144.61N/mm,(2)$

whereNcr: critical buckling load;b: plate width.

Finite element analysis: P_cr = 28.64 kN; N_cr = 28.64 kN*1000.0/200.0 mm = 143.2 N/mm.

• Nonlinear buckling analysis

The intact square 200 mm plate maximum strength that has been determined by FE analysis is 47.43 kN. The calculated value according to Equation 4 suggested by Soares (1992) is 48.64 kN.

The difference is (47.43–48.64)/48.64 = −2.5%.

The results are acceptably close.

$\lambda =\frac{b}{t}\sqrt{\frac{{\sigma }_y}{E}}=\frac{200}{2}\sqrt{\frac{250}{2.0E5}}=3.53,(3)$

$\frac{{\sigma }_u}{{\sigma }_y}=\frac{a_1}{\lambda }-\frac{a_2}{{\lambda }^2}, \lambda \ge 1 ,(4)$

$a_1=2;a_2=1,$

$\frac{{\sigma }_u}{250}=\frac{2}{3.53}-\frac{1}{{\left(3.53\right)}^2} =0.486,$

${\sigma }_u=\left(250\right)\left(0.486\right)=121\text{.}6\text{MPa,}$

$P_{max}=\left({\sigma }_u\right)\left(b\right)\left(t_p\right),$

$P_{max}=\left(121.6\right)\frac{\left(200\right)\left(2\right)}{1000}=48.64 kN.$

Parametric study

This study investigates the performance of the following different available forms of steel plates under uniaxial compression. The intact plate smaller dimension to thickness ratio (b/h) is 100. The intact plate has been considered as the control specimen. The performance of the stiffened plates, perforated plates, and stiffened perforated plates had been compared with that of the control plate, and the results are shown as follows.

Stiffened plates

The following cases of stiffened plates have been investigated:

• Single stiffener stiffened plates.

• Two stiffeners stiffened plates.

• Three stiffeners stiffened plates.

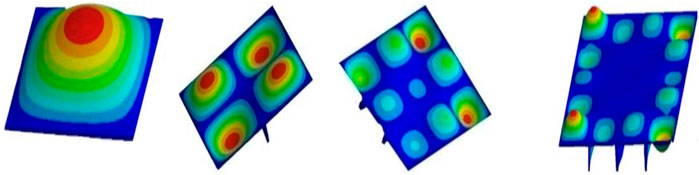
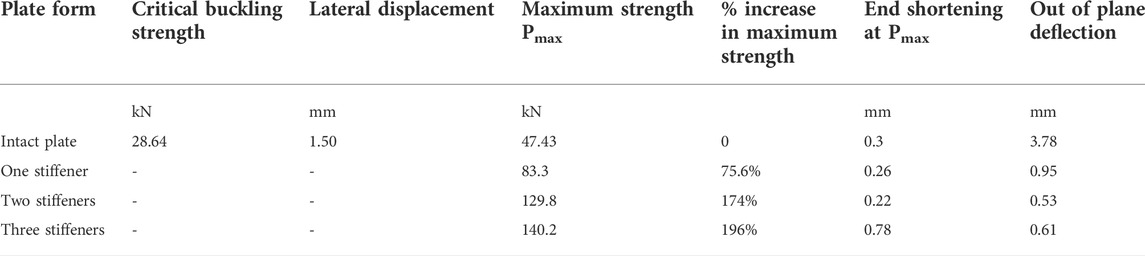
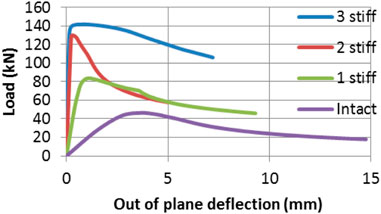
A pushover elastic linear buckling analysis has been carried out for the aforementioned forms of square steel plates. The obtained mode shapes representing the first mode of vibration are illustrated in Figure3. It is obvious that the stiffeners converted the two global orthogonal identical half waves experienced by the intact plate into orthogonal multiple identical half wave–shaped local buckling between nearby stiffeners. The space between the nearby stiffeners has controlled the length of the half waves in both directions as illustrated in Figure 3. If the plate is properly designed, the local buckling would result into global buckling for the whole stiffened plate. The analysis results indicate that the critical buckling load was 60.3% of the maximum plate strength in the intact plate. However, in all the stiffened plates, the critical buckling load was larger than the plate maximum strength as indicated in Table 1.

FIGURE 3

FIGURE 3. First modal vibration mode shapes for the intact and the stiffened square plates.

TABLE 1

TABLE 1. Summary of analysis results for intact and stiffened plates.

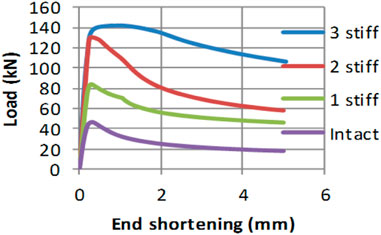
Figures 4, 5 show the end shortening as well as the lateral buckling versus load relationships, respectively, for all the aforementioned stiffened forms as well as the intact plate. Table 1 lists the recorded results. The maximum obtained load for the intact plate as well as the stiffened plates with single, double, and triple stiffeners having ratios of plate area to sum of stiffeners areas of 5.0, 2.50, and 1.67 were 47.43, 83.3, 129.8, and 140.2 kN, respectively. The increase in strength compared to that of the intact plate is 75.6%, 174%, and 196%.

FIGURE 4

FIGURE 4. Load end shortening relationship of stiffened plates compared with the intact plate.

FIGURE 5

FIGURE 5. Load buckling relationship of stiffened plates compared with the intact plate.

The mere situation for stiffener tripping has been for single stiffener plate of Ap/As = 5.0, as shown in Figure 6. Stiffener tripping has been experienced when the summation of the values of the lateral torsional stiffness for all stiffeners was lower than the plate flexural stiffness value.

FIGURE 6

FIGURE 6. Tripping in a single stiffened plate.

Perforated plates

The following cases have been considered:

1) Single opening perforated plates.

2) Two openings perforated plates.

3) Three openings perforated plates.

4) Four openings perforated plates.

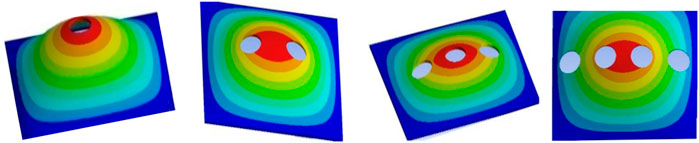
The mode shapes for the aforementioned forms of perforated plates are illustrated in Figure 7. The ratios of the sum of hole diameters to plate width for single, double, triple, and four openings are 0.150, 0.3, 0.45, and 0.60, respectively.

FIGURE 7

FIGURE 7. First modal vibration mode shapes for the perforated square plates.

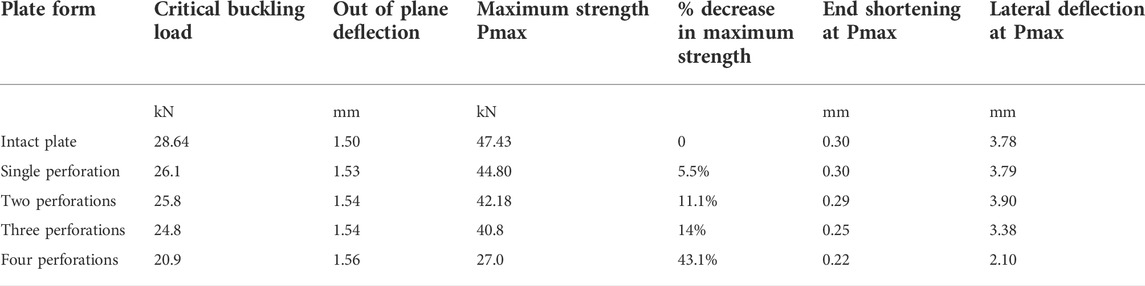
Table 2summarizes the critical buckling load for the intact solid plate as well as all other forms of perforated plates. The reduction in the critical buckling load for single, double, triple, and four perforations with respect to the intact plate is 5.50%, 11.1%, 14.%, and 43.1% respectively.

TABLE 2

TABLE 2. Summary of analysis results for intact and perforated plates.

Figures 8, 9 indicate that the shapes of the load end shortening curves as well as the load buckling curves for all cases have kept an analogous form. Critical buckling strength was recorded as 0.58 of the plate maximum strength in single perforation plate and up to 0.61 of the plate maximum strength for triple perforations plate. In plates with four perforations, the critical buckling strength became 0.78 of the plate maximum strength.

FIGURE 8

FIGURE 8. Load end shortening relationship of perforated plates compared with the intact plate.

FIGURE 9

FIGURE 9. Load buckling relationship of perforated plates compared with the intact plate.

The post elastic buckling stage has initiated, as nonlinear buckling due to nonlinearity in geometry, followed by material plasticity when steel’s von Mises stresses (σ_e) have exceeded the material yield stress (σ_y) threshold as a direct result of excessive buckling. Kinematic instability was inevitable with further loading. However, the critical buckling strength was less than the plate maximum strength for all forms of perforated plates.

Stiffened and stiffened perforated plates

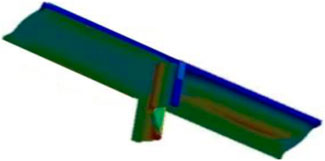
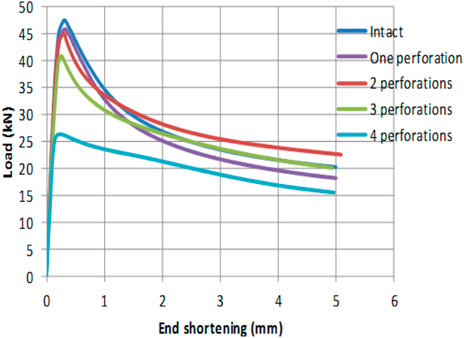
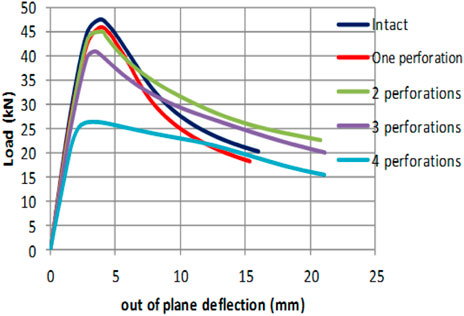
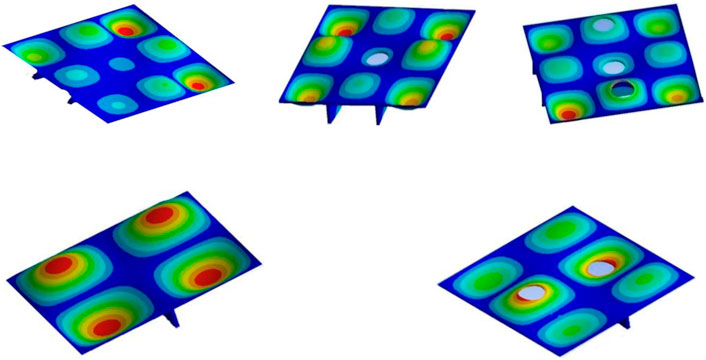
Figure 10 illustrates the modal shapes pertaining to the fundamental mode for the different forms of stiffened and stiffened perforated square plates. Figures 11, 12 illustrate the load end shortening as well as the load buckling curves for the intact plate as well as single stiffener, single stiffener double perforations, double stiffeners, and double stiffeners with single perforation plate.

FIGURE 10

FIGURE 10. First modal vibration mode shape for perforated stiffened plates.

FIGURE 11

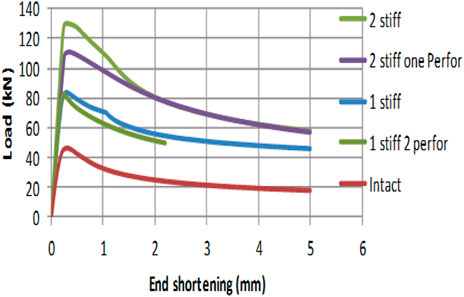
FIGURE 11. Load end shortening relationship for stiffened and stiffened perforated compared with the intact plates.

FIGURE 12

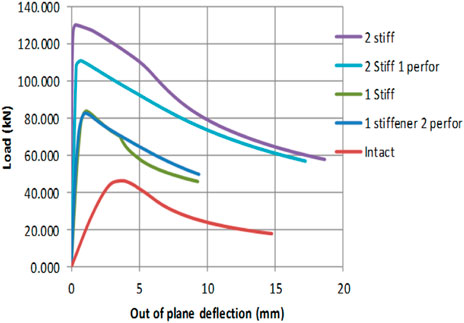
FIGURE 12. Load buckling relationship for stiffened and stiffened perforated compared with the intact plates.

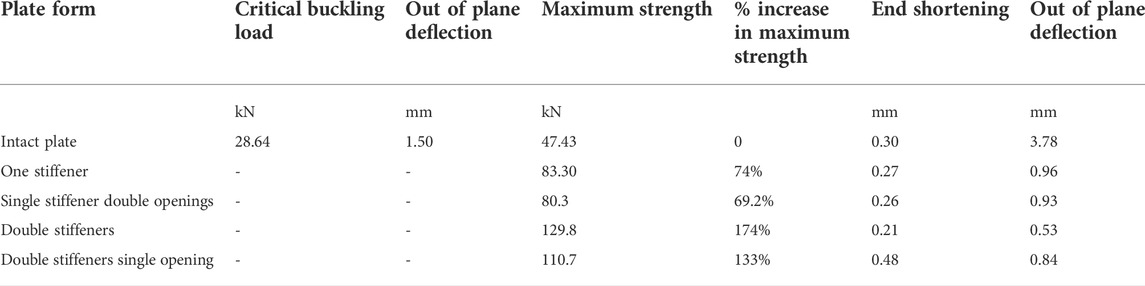
Table 3 summarizes the results for the stiffened and stiffened perforated plates. The analysis results indicate that the increase in plate maximum strength for the case of single stiffener, single stiffener with two perforations, double stiffeners, and double stiffeners with one perforation were 74.0%, 69.2%, 174%, and 133%, respectively, compared to that of the intact plate. Stiffener tripping has only been experienced in the single stiffener plate of Ap/As = 5. In all the remaining stiffened as well as stiffened perforated plate forms, the plate has not experienced any noticeable stiffener tripping. The effect of the two openings was dropping the amount of the plate flexural stiffness to values that were lower than the torsional stiffness of stiffeners. In such a case stiffener tripping can be avoided. The critical buckling loads for all the investigated forms of stiffened and perforated stiffened plates have been larger than the plate maximum strength. All forms of the stiffened and stiffened perforated plates have not experienced buckling instability during the elastic linear stage as well as the post elastic nonlinear stage and up to failure. Initially, the plate response has been linear elastic. Upon surpassing the steel yield stress (σ_y) threshold, the plate has experienced inelastic deformation that resulted in stress redistribution, enabling the plate section to develop the appropriate internal loads that would counterbalance the incrementally applied load. Eventually, the developed internal load resultants were unable to counterbalance the incrementally applied load. A gradual failure has been experienced owing to geometric nonlinearity followed by material nonlinearilty that lead to the required ample warning. It is a desirable mode of failure compared to buckling instability that was experienced by unstiffened thin plate forms.

TABLE 3

TABLE 3. Summary of analysis results for the stiffened and perforated stiffened plates.

Results and discussion

Although in columns, the development of elastic buckling is an instability failure mode. This might not be the case in plate buckling because in general the plate has four supporting edges. Plate buckling develops in the two perpendicular directions. In general, the plate might experience kinematic based buckling instability failure. This may happen if the critical buckling strength is less than the maximum plate strength. However, if the opposite is true, the plate experiences strength-based failure when the developed internal force resultants are not capable anymore of counterbalancing the incrementally applied loading.

The current study has indicated that in the case of intact square plate having width to thickness ratio of 100, the critical buckling strength was 60.3% of the maximum strength of the plate. Elastic buckling has initiated while steel von Mises stresses $\left({\sigma }_{eq}\right)$ were less than ${\sigma }_y$. With further loading, more plate buckling was experienced. Boosted by geometric nonlinearity, residual stresses and imperfections in the geometry. Followed by material nonlinearity when steel von Mises stresses $\left({\sigma }_{eq}\right)$ exceeded ${\sigma }_y$. Both geometric and material nonlinearities raised the amount of plate buckling. Eventually, the resulting excessive buckling lead to kinematic instability. It is an undesirable mode of failure because it gives no warning.

In stiffened plates, the study has shown that stiffener tripping was merely experienced in single stiffener plate at $\left(ts/tp\right)$ ratio of 2. In all the remaining cases, the large torsional stiffness values of stiffeners have obstructed stiffener tripping development.

The results also indicated that in all stiffened plates, the critical buckling strength was larger than the plate maximum strength. With further loading, the plate post buckling strength has initiated associated first with geometric nonlinearity, then with material nonlinearity when steel von Mises stresses $\left({\sigma }_{eq}\right)$ exceeded ${\sigma }_y$. Both geometric and material nonlinearities raised the amount of plate buckling. With further load, the amount of internally developed load resultant within the section was insufficient to balance the applied load. Steel plasticity lead to gradual failure with ample warning.

Perforations decreased the critical buckling strength as well as the plate maximum strength and lead to the development of larger stresses that surpassed ${\sigma }_y$ owing to the plate reduced section. The steel plasticity enhanced the plate ductility, however the plate maximum strength was reduced.

The stiffened perforated plates lead to an increase in both plate maximum strength and ductility.

The adopted numerical analysis has been FE modeling using Ansys software (Ansys, 2021).

Conclusion

This study involves investigating the performance of different forms of simply supported square plates with a minimum dimension to thickness ratio of 100. At this slenderness ratio the intact plate flexural stiffness is relatively low. Based on the results and the pertaining discussion, it is concluded that:

1) When an intact plate with a relatively high slenderness value, is under uniaxial load, the critical buckling load is generally below the plate maximum strength. When the incremental load reaches the critical buckling load, buckling occurs in the form of one-half sinusoidal wave along the two orthogonal plate directions. With further loading and owing to the excessive lateral deformation, the plate experiences kinematically based buckling instability. It is sudden and gives no warning. It is an undesirable mode of failure and does not permit to fully exploit the full plate strength capacity.

2) Using another plate form, such as the stiffened plate modifies the buckling shape and increases the plate slenderness ratio to a level where the critical buckling load exceeds the plate maximum strength capacity. In this case, and depending upon the number of provided stiffeners, the failure mode changes from the undesirable sudden buckling instability to gradual failure that involves post buckling strength and gives the appropriate pre-failure warning owing to geometric nonlinearity and steel yielding that takes place prior to failure.

3) The perforations disturb the internal stress path and raises the peak values of the developed internal stresses within the reduced section. When the steel von Mises stresses surpass ${\sigma }_y$, steel plasticity enhances the ductility prior to failure. However Fracture may occur at the edge of the openings when steel von Mises stresses reach the ultimate stress $\left({\sigma }_u\right)$.

4) The perforated stiffened plate form if properly designed in terms of the number of stiffeners. The ratio of the sum of the diameters of perforations to the plate width, would alter the mode of failure from kinematic based buckling instability sudden failure to gradual failure involving geometric nonlinearity and material plasticity that pave the way for stress redistribution. Failure occurs when the developed internal load resultants are not able anymore to counterbalance any further applied loading.

5) Stiffener tripping must be checked in stiffened and stiffened perforated plates. Both forms of square plates might experience stiffener tripping when the torsional stiffness of a stiffener becomes less than the plate flexural stiffness.

6) Using the available different forms of plates enables the effective utilization of thin stiff plates of plate minimum dimension to depth ratio of 100.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Acknowledgments

The author is pleased to acknowledge the support of The University of Jordan.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

AISC (2017). Steel construction manual. 15th edition. Illinois, United States: American Institute of Steel Construction.

Google Scholar

Ansys (2021). Ansys 2021 R1. Canonsburg, US: Inc. Academic version.

Google Scholar

Aydin, Komur M., and Mustafa Sonmez, (2015). Elastic buckling behavior of rectangular plates with holes subjected to partial edge loading. J. Constr. Steel Res. 112, 54–60. doi:10.1016/j.jcsr.2015.04.020

CrossRef Full Text | Google Scholar

Behzad, M., Eunsoo, C., and Woo, J. (2018). Compressive investigation of buckling behavior of plates considering the effect of holes. Struct. Eng. Mech. 68, 261–275. doi:10.12989/sem.2018.68.2.261

CrossRef Full Text | Google Scholar

Giovanni, G., Antonio, M., Giuseppe, Z., and Casciaro, R. (2014). A Numerical Asymptotic Formulation for the post buckling analysis of structures in case of coupled instability. Romanian J. Tech. Analysis 59 (1-2), 38–55.

Google Scholar

Grondin, G. Y., Elwi, A. E., and Cheng, J. J. R. (1999). Buckling of stiffened steel plates/a parametric study. J. Constr. Steel Res. 50 (2), 151–175. doi:10.1016/s0143-974x(98)00242-9

CrossRef Full Text | Google Scholar

Gunay, E., Aygun, C., and Yildiz, Y. (2013). Nonlinear buckling finite element analysis of stiffened steel plates. Adv. Mat. Res. 669, 450–456. doi:10.4028/www.scientific.net/amr.699.450

CrossRef Full Text | Google Scholar

Malhas, A., Johnson, E., and Salmon, G. (2020). Steel structures design and behavior. London, United Kingdom: Pearson.

Google Scholar

Quin, D., Murphy, A., McEwan, W., and Lemaitre, F. (2009). Stiffened panel stability behavior and performance gains with plate prismatic sub-stiffening. Thin-walled Struct. 47 (12), 1457–1468. doi:10.1016/j.tws.2009.07.004

CrossRef Full Text | Google Scholar

Saad-Eldeen, S., Garbatov, Y., and Soares, G. (2014). Ultimate strength assessment of steel plates with a large opening. London: Taylor and Francis Group. ISBN 978-1-138-00124-4.

Google Scholar

Soares, G. C. (1992). Design equation for ship plate elements under uniaxial compression. J. Constr. Steel Res. 22, 99–114. doi:10.1016/0143-974x(92)90010-c

CrossRef Full Text | Google Scholar

Stephen, P., Timoshenko, S., and Woinowsky, k. (2010). Theory of plates and shells. New York, United States: McGraw-Hill.

Google Scholar

Ul-Nyeon, K., Ick-Heung, C., and Jeom-Kee, P. (2009). Buckling and ultimate strength of perforated plate panels subject to axial compression. Taylor Francis 4 (14), 337–361.doi:10.1080/17445300902990606

CrossRef Full Text | Google Scholar

Ventsel, E., and Krauthammer, T. (2001). Thin plates and shells theory analysis and applications. New York, United States: Marcel Dekker.

Google Scholar

Yamaguchi, E. (1999). in Basic theory of plates and elastic stability” structural engineering handbook. Editor Chen Wai-Fah (Boca Raton: CRC Press LLC).

Google Scholar