- Department of Civil and Environmental Engineering, Indian Institute of Technology Patna, Patna, India
Introduction: Embankments are constructed in many places for transportation purposes such as railways and roads. The stability of slopes in embankments has always been a concern, especially in cohesionless soils. There are many methods to increase the safety factor of cohesionless soil slopes using geogrids, geocells, concrete piles, and so on. The conventional material used to stabilize slopes has a huge impact on the environment. Nowadays, researchers are using natural fibers such as bamboo and coir fiber for stabilization purposes.
Methods: In this paper, bamboo piles are used to stabilize slopes. The bamboo piles are inserted vertically on the slope face to increase the shear strength and stability against slope failure. A limit equilibrium method has been developed to estimate the stability of a slope improved by friction piles after modifying the Bishop method of slices. The stability of the slope is analyzed for both the reinforced conditions and the unreinforced conditions using the developed analytical formula.
Results and Discussion: The analytical equations were developed by considering three modes of slope failure: shear failure of the bamboo piles along the failure surface, movement of the upper part of the soil, leaving the bamboo pile embedded in the base soil, and pulling out of the bamboo along with the upper part of the soil mass. Further validation of the results is carried out with the limit equilibrium method-based software SLOPE/W using a modified Bishop method. The factor of safety increased after reinforcing the slope with bamboo piles for all three modes.
1 Introduction
Failure of natural and man-made soil slopes, such as highway and railway embankments and earth dams, is a complex phenomenon. Many problems are associated with the stability of the soil slopes, the failure of which causes serious disasters damaging, with damage to public and private property worth millions of dollars. Therefore, it is important to stabilize the slopes to mitigate the possibility of catastrophic slope failure. A suitable ground improvement technique should be adopted based on soil conditions, type of strata, economic feasibility, and the purpose of the improvement. Bamboo, which has been used as a reinforcement material for slope stability since ancient times, stands out in terms of cost-effectiveness, wide availability, and environmental suitability.
Researchers have used different materials as reinforcement in the past for stabilizing slopes. The use of geosynthetics in soil improvement has been extensively investigated and used by various researchers (Zhao, 1996; Michalowski, 1997; Kitch et al., 2011; Tang and Yang, 2013; Halder and Chakraborty, 2020). Dastpak et al. (2021) examined the behavior of a geosynthetically reinforced soil slope using deterministic and stochastic non-circular limit equilibrium methods of slope stability analysis. Passive piles used in slope stabilization are designed using pressure- or displacement-based methods (Poulos, 1995; Chen and Poulos, 1997) and numerical methods (Goh et al., 1997; Poulos and Chen, 1997). Jeong et al. (2003) numerically analyzed the lateral response of one-row piles above and below the critical surface using the load transfer approach. Griffiths et al. (2010) studied the influence of pile reinforcement on the stability of slopes by numerical analysis and presented the effects of pile length on slope stability and factor of safety (FOS). Yang et al. (2011) investigated the effect of embedded pile length and spacing between two piles on FOS. Kourkoulis et al. (2012) developed the hybrid method, which combines three-dimensional finite element simulation with an analytical technique for the design of slope-stabilizing piles. Benmebarek et al. (2021) used PLAXIS 2D and 3D to optimize the number of piles in a row for cohesive-friction slope stabilization. Moawwez et al. (2021) developed the empirical correlations for limit equilibrium (LE) methods of slope stability analysis.
Over the years, the use of bamboo as a reinforcing material in geotechnical engineering has increased dramatically. Among the possible applications, the use of slope reinforcement to improve slope stability and prevent failure has attracted a great deal of attention. Compared with these soil improvement methods, bamboo piles as slope reinforcement (Won et al., 2005) can be more innovative and environmentally friendly. Soil improvement with reinforcement is an ancient technique. This concept was used many years ago in England for landslide prevention and slope stabilization. Ngudiyono and Sulistyowati (2022) numerically investigated the stability of the slope by inserting an inclined bamboo pile perpendicular to the slope face. In recent years, even in India, the use of various forms of bamboo for stabilizing slopes has increased (Mekonnen and Mandal, 2018; Talukdar et al., 2018; Gidon and Sahoo, 2020). Nowadays, bamboo structures are also being used on slope faces for erosion control (Tardio et al., 2017). The aforementioned studies indicate that bamboo has enormous potential for soil stabilization and retention; here, bamboo is used as a pile to reinforce the slope. The main objective of this study is to develop a limit equilibrium-based methodology to estimate the stability of a slope improved by bamboo piles. An analytical study of bamboo-reinforced slopes has been conducted and is further compared with the results of the Bishop method (Section 3 and Section 4) using the limit equilibrium-based software Slope/W (GEOSLOPE, Calgary, Canada). It is concluded that the slope reinforced with bamboo piles provides significantly higher FOS values than the unreinforced case.
2 Analytical study
The analytical formulation is based on the limit equilibrium approach, and the slip surface is assumed to be a circular arc. Three failure modes were considered to find the minimum FOS. They are termed as follows in this study:
• Mode I: Slope failure considering the shearing of the bamboo along the failure surface
• Mode II: Sliding of soil above slip surface, leaving the bamboo piles behind embedded in the base soil.
• Mode III: The bamboo is pulled out along with the upper part of the soil mass along the failure surface.
Analytical equations were formulated for each mode to calculate the FOS of the slope, considering the effect of the bamboo piles. This formulation of FOS assessment is based on the concept of the Bishop method after relevant modification to incorporate the effect of reinforcement. A similar study has been reported in the literature (Kumar and Chakrabortty, 2020) for estimating the FOS of a reinforced slope using the method of slices. The Bishop method (Duncan and Wright, 1980; Kumar et al., 2018) is a more refined solution than the ordinary method of slices that considers the vertical equilibrium of each slice.
The assumptions in the formulation of the analytical equations are as follows:
• The slope is assumed to be a dry, homogeneous, isotropic, and finite slope.
• The failure surface is assumed to be a circular arc.
• The base of each slice is assumed to be a straight line.
• The bamboo piles are assumed to be vertical with a spacing s between two piles, and other parameters are shown in Figure 1. There are n number of piles used as reinforcement along a line in a perpendicular direction.
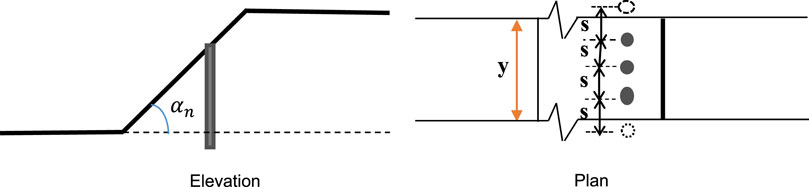
FIGURE 1. Layout of bamboo piles as reinforcement on the sloping surface. For y m, the number of bamboo piles,
2.1 Simple analytical model
Simple analytical equations were developed in this study using limit equilibrium analysis. Moment equilibrium was considered for the calculation of FOS, defined here as the ratio of the shear strength capacity and the shear strength required for equilibrium. The complexity of the calculation increases when reinforcement is considered in the limit equilibrium formulation. The additional force induced by the reinforcement has been included in the equilibrium equations (Wright and Duncan, 1991). In this study, bamboo piles are inserted along a line at a distance of 1 m to reinforce the slope and analyze its stability. Various failure modes were considered in the formulation based on the assumption of the failure and circular slip surface. The following three failure modes are considered in this study:
• Mode I: Slope failure considering the shearing of the bamboo along the failure surface.
• Mode II: Sliding off the upper part of the soil, leaving the bamboo piles embedded in the base soil.
• Mode III: Movement of the upper part of the soil mass along with pulling the bamboo out of the base soil.
Analytical equations were formulated to calculate the FOS of the slope, considering the effect of the bamboo piles for these three failure modes. A single row of bamboo piles is considered as reinforcement that provides stability to the slope. These FOS formulations were developed using two different methods (modified ordinary and Bishop method of slices). The equations developed based on the modified ordinary method of slices are reported in previous research (Kumar and Chakrabortty, 2020). The equations presented in this paper are developed based on the modified Bishop method.
2.2 Mode I: Shear failure of bamboo piles along the failure surface
In this mode, shear failure of soil mass and bamboo piles is assumed. When failure occurs due to a driving moment caused by the weight of the slice (Wm) and the weight of the bamboo (Wb), an additional resisting moment due to the shear strength of the bamboo (
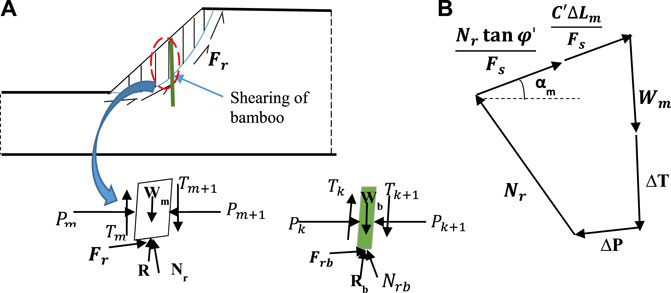
FIGURE 2. Shear failure (Mode I) of a bamboo-pile-reinforced slope. (A) Slope with the free body diagram of the bamboo pile and the mth slice of soil mass. (B) Force polygon of the mth slice showing different forces at the failure of the slope.
The normal reaction (Eq. 2) can be calculated from the equilibrium of the force polygon shown in Figure 2B. The FOS equation (Eq. 3) is obtained from the equilibrium of all wedges, considering the activating moment and the resisting moment. In the following equations,
Where,
2.3 Mode II: Sliding off the upper part of the soil, leaving the bamboo piles embedded in the base soil
In this mode of slope failure, bamboo piles were assumed to remain embedded in the base soil after failure, and the upper part of the soil mass was to be moving downward. During the failure, the friction between the soil mass and the upper part of the bamboo pile comes into effect, which is referred to here as the frictional resistance of the bamboo (τb). The free-body diagram of the bamboo pile, the mth, and the kth soil slices are shown in Figure 3. The mth slice is the general slice not in contact with the bamboo, and the kth slice is the slice adjacent to the bamboo. The expression for FOS is formulated considering the equilibrium of the soil mass using the modified Bishop method of slices, as shown in Eqs 5–9. The expression for the resisting moment can be calculated from the force polygon of the mth slice of soil mass as
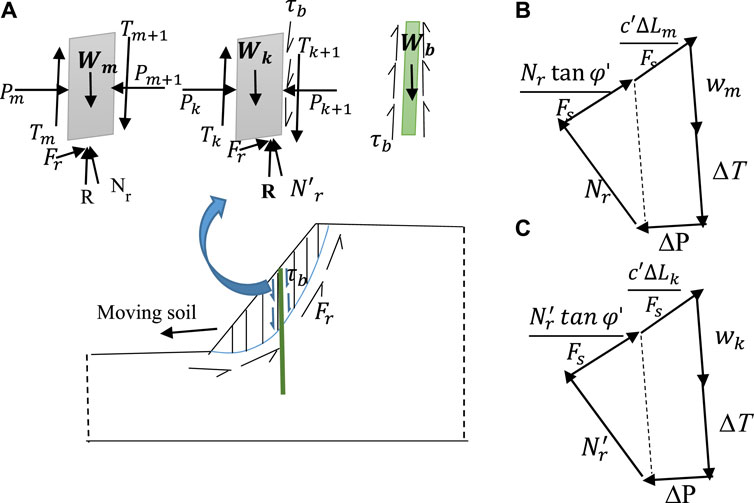
FIGURE 3. Slope failure (Mode II) due to soil mass movement. (A) Slope with free body diagram of bamboo piles and mth and kth slice of soil mass. (B) Force polygon of the mth slice. (C) Force polygon of the kth slice showing different forces at the failure of the slope.
The normal reaction of the kth slice (Eq. 7) can be calculated from the equilibrium of the force polygon, as shown in Figure 3C. Here, in Eq. 7, h is the height of the bamboo above the slip surface. The equation for FOS (Eq. 8) was obtained from the equilibrium of all slices, considering the activating moment and the resisting moment. In this mode, the weight of the bamboo does not contribute as a destabilizing force and, therefore, does not contribute to the denominator. The second term in the numerator incorporates the effect of the bamboo piles. This ultimately increases the FOS of the slope with bamboo piles as reinforcement.
Where,
2.4 Mode III: pulling the bamboo out along with the upper part of the soil mass
In this failure mode, it is assumed that the pull-out force is exerted by the soil mass that is above the critical slip surface to pull the bamboo piles out of the base soil. In this failure mode, the friction between the soil mass and the lower part of the bamboo pile comes into effect, namely, the pull-out resistance of the bamboo (τb). The free body diagram for the mth soil slices and the bamboo is shown in Figure 4. Based on the equilibrium of forces, the expression for FOS is formulated as shown in Eqs. 10–12.
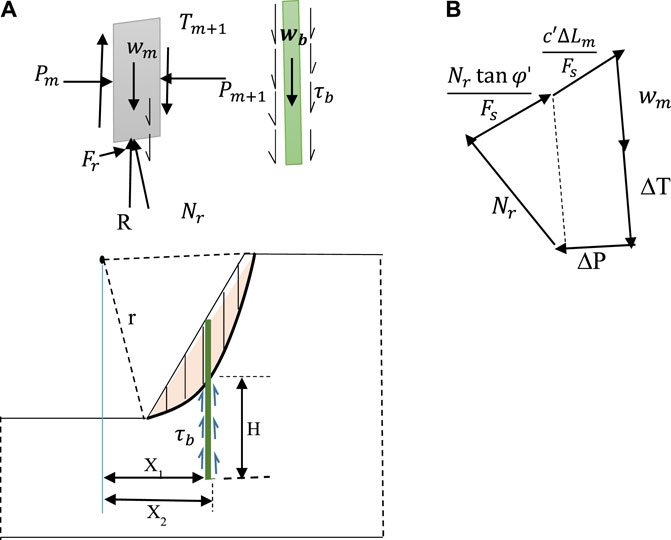
FIGURE 4. Slope failure (Mode III) of a bamboo-pile-reinforced slope. (A) Slope with free body diagram of the bamboo pile and the mth slice of soil mass. (B) Force polygon of the mth slice showing the different forces at the failure of the slope.
From the equilibrium of force polygon shown in Figure 4:
Therefore, the proposed equation is
3 Case study I: stability analysis of a sandy soil slope
Stability analyses were performed using the SLOPE/W software and analytical equations to demonstrate the efficiency of the proposed analytical equations. In this analysis, a hypothetical dry cohesionless soil slope with a 35° slope angle was considered. Bamboo with a length of 4 m and a diameter of 8 cm was considered for the reinforcement of soil slopes with different angles as shown in the Figure 5. The analytical results were compared with SLOPE/W analyses for an unreinforced slope (Table 1) and a reinforced slope (Table 2). The results of this analysis are discussed in the next subsection.
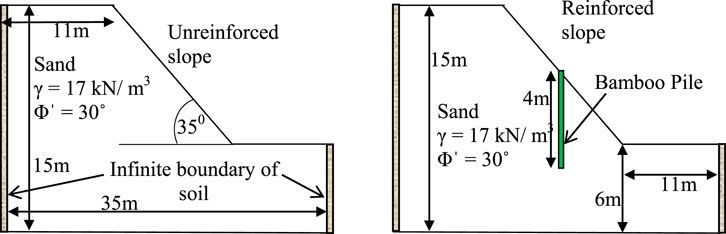
FIGURE 5. Schematic diagram of unreinforced and reinforced dry sandy slope having a slope angle of 35°.
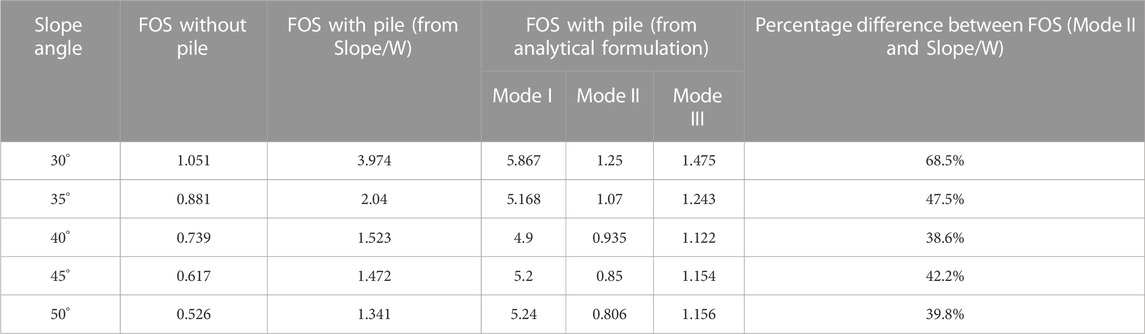
TABLE 2. FOS of a critical slip surface for a dry cohesionless soil slope with different inclination angles.
3.1 Stability analysis of reinforced slope using Slope/W
The limit equilibrium based on the modified Bishop method was chosen in SLOPE/W to analyze the aforementioned slope. The analysis was performed for two different models: unreinforced and bamboo-reinforced slope models created using the software (SLOPE/W). The Mohr–Coulomb constitutive model was used to analyze the soil slope. The critical slip surface (CSS) was searched by the grid and radius method. All the probable slip surfaces are shown in Figure 6A. The FOS for the critical slip surface was determined from the analysis to be 0.881, as shown in Figure 6B.
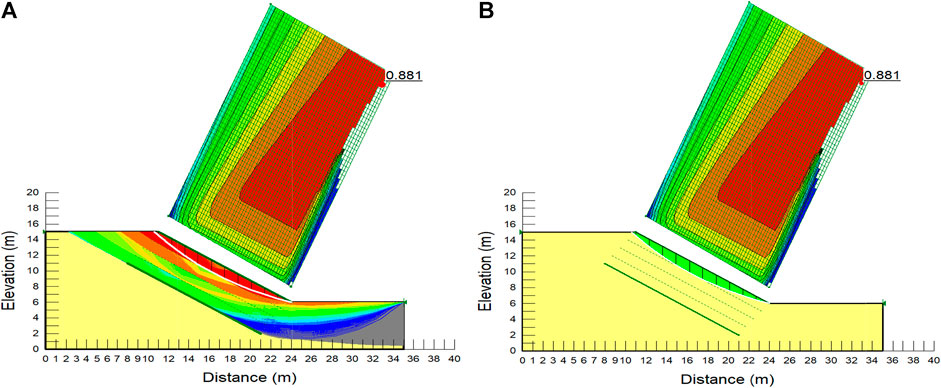
FIGURE 6. Stability analysis of unreinforced dry cohesionless soil slope using Slope/W software. (A) All circular slip surfaces, including the critical surfaces. (B) Critical slip surface.
The material parameters were taken from the literature (Bergado et al., 1987) and were also determined experimentally in the laboratory (Kumar, 2018). The shear strength and average tensile strength of bamboo obtained from the literature were 18 MPa and 128 MPa, respectively, and the pull-out resistance of bamboo, 47 kPa, was also taken from the literature. The FOS was calculated for the slip circle which was found to be critical in the case of the unreinforced soil slope. The FOS of the critical circle found for the unreinforced slope was calculated to be 1.268, as shown in Figure 7A.
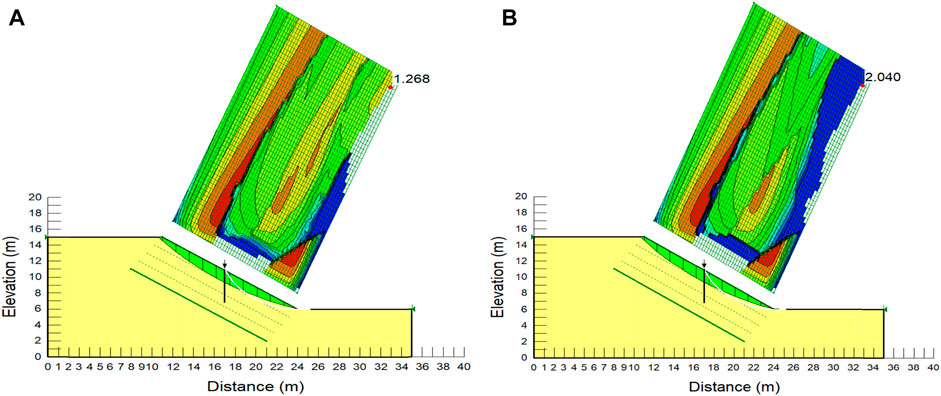
FIGURE 7. Stability analysis of reinforced dry cohesionless soil slope using Slope/W software. (A) Reinforcement material parameters taken from Bergado et al. (1987). (B) Reinforcement material parameters estimated from the experiment.
The analyses were also performed using experimentally determined bamboo material parameters as input parameters for the reinforcement. The pull-out test was conducted to find the behavior of the soil–bamboo interface. In this test, the soil was reinforced with two types of bamboo specimens, namely, bamboo with nodes and bamboo without nodes. The experimental investigation was conducted by varying the normal stress to 30 kPa, 40 kPa, and 50 kPa for a bamboo specimen with nodes and 50 kPa, 60 kPa, and 70 kPa for the specimen without nodes. The average pull-out resistance of a bamboo specimen with nodes is higher (375.4 kPa) than that without nodes (105 kPa). The experimental investigation in the laboratory estimated the tensile strength and shear strength of bamboo to be 218.75 MPa and 33.5 MPa, respectively (Kumar, 2018). A pull-out resistance of 105 KPa found in the experiment using bamboo without nodes was considered in this study (Kumar, 2018). The FOS was calculated for the same slip circle, which was found to be critical in the case of an unreinforced soil slope. The FOS increased in this case and was found to be 2.04, as shown in Figure 7B. From the comparison, it can be concluded that the reinforcement improved the slope stability against failure because the FOS increased from 0.881 to 2.04 after including the bamboo reinforcement. The model was also analyzed to estimate the critical slip circle after the improvement with a single row of piles. It was found that the CSS has a FOS of 1.01, as shown in Figure 8. Therefore, reinforcement location optimization can be considered as a scope of future study in any actual slope design.
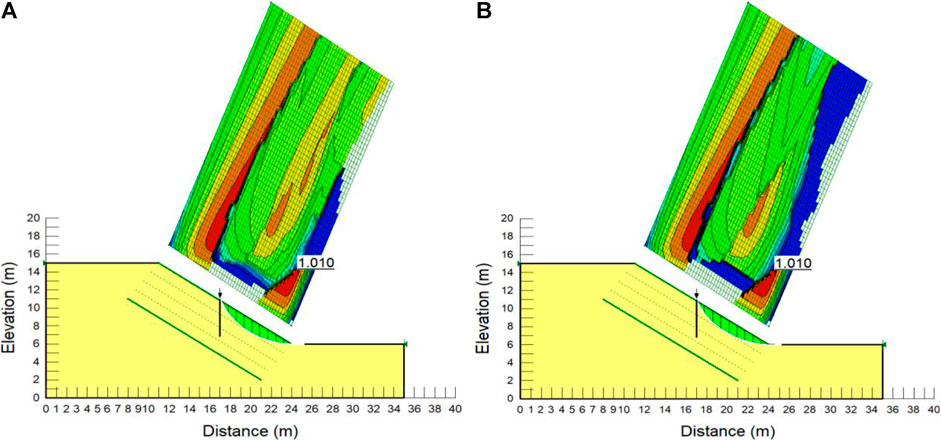
FIGURE 8. Critical slip surface of dry cohesionless slope improved with reinforcement among all slip surfaces. (A) Reinforcement material parameters taken from Bergado et al. (1987). (B) Reinforcement material parameters taken from the experiment.
3.2 Stability analysis using the proposed analytical equations
In this subsection, the proposed analytical equations were used to calculate the FOS of the critical slip surface. The FOS was calculated for a slope with an angle of 35° for both the reinforced and unreinforced conditions. The results were compared with those obtained from SLOPE/W. The FOS results are presented in Table 1. In the first part, the values of the variables (shear strength of bamboo and pull-out resistance of bamboo reinforcement in sand) in the equations were taken from the literature (Bergado et al., 1987). In the second part, the values of these variables were taken from the experimental investigation conducted in the laboratory, as discussed in Section 3.1. The FOSs were estimated considering all three failure modes. The lowest of these three will be the critical value using this analytical method.
3.3 Results and discussion
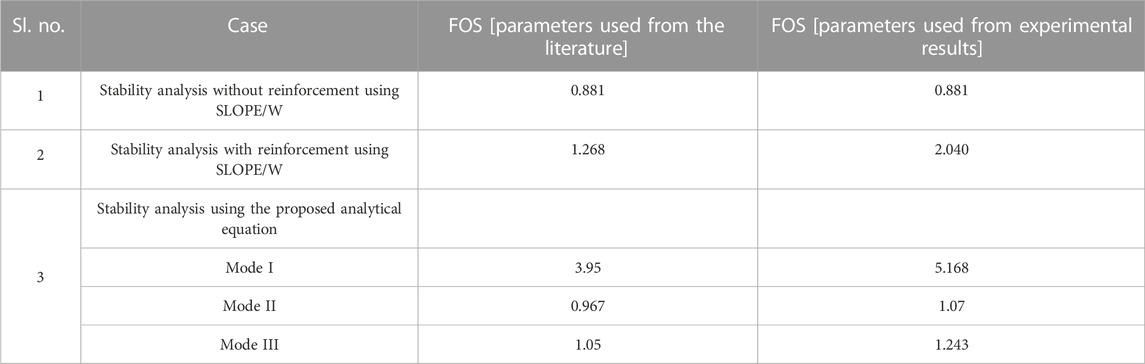
In the first part, when the values of the variables were taken from the literature, using the proposed analytical equation for the three modes, the FOS was evaluated as 3.95, 0.967, and 1.05, respectively. It can be observed from the SLOPE/W results that when reinforcement was provided, the FOS increased from 0.881 to 1.268. When the experimental results were used in the equation, the FOS for mode I, mode II, and mode III were found to be 5.168, 1.07, and 1.243, respectively, as presented in Table 1. It can be observed from Table 1 that the proposed equation gives a higher value of FOS than that obtained from SLOPE/W analyses. The frictional pullout forces were not considered in the SLOPE/W analysis; therefore, it gives a higher FOS. It is also observed that when parameter values taken from laboratory data are used, the FOS is higher than the FOS determined using reinforcement parameters taken from the literature (Bergado et al., 1987). The different bamboo species may be responsible for these differences.
4 Case study II: effect of slope angle
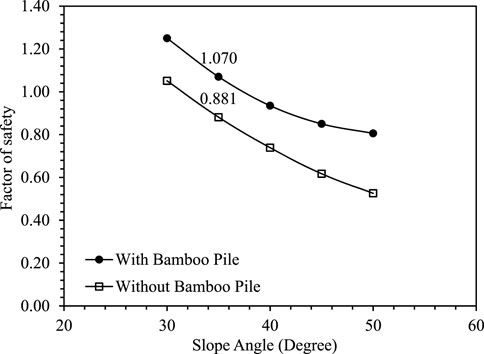
A case study is presented in this section to show the effect of slope angle on slope stability. The case study was performed using the commercial software SLOPE/W and the newly developed analytical formulation. Different dry slopes were considered with inclination angles varying between 30° and 50°. The analysis of these model slopes was performed in SLOPE/W using the Bishop method of slices. The slip surfaces in SLOPE/W were defined by the grid and radius method. In the analysis, material properties and reinforcement parameters were taken from the experiments and kept the same for all the slopes. The FOSs for each unreinforced slope and the reinforced slope corresponding to the critical slip surface of an unreinforced slope are presented in Table 2. From the table, it can be observed that FOS increases with the use of reinforcement in the slope. Moving down the column in the table, the FOS for the critical circle decreases as the slope inclination angle increases for both reinforced and unreinforced slopes. The same trend of FOS variation can be observed in Figure 9. The comparison between SLOPE/W and the developed analytical equation is presented in Figure 10. It can be inferred from these results that Mode II shows a critical slip surface with the lowest FOS value for all slope angles.
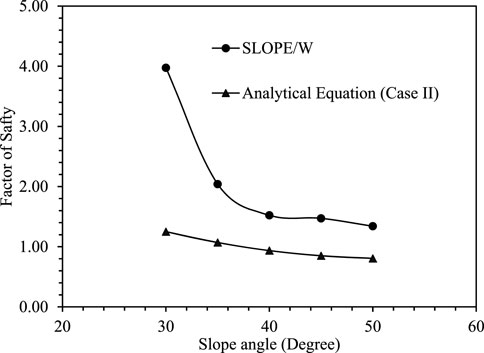
FIGURE 10. Comparison of FOS between SLOPE/W and analytical equation for the slope reinforced with bamboo piles.
5 Conclusion
In the present study, a limit equilibrium method has been developed for estimating the stability of a slope improved by friction piles after a relevant modification of the Bishop method of slices. The analytical results were compared with those obtained from the limit equilibrium method-based software SLOPE/W. The effects of bamboo reinforcement on the slope stability of sandy soils were examined as a case study. The following conclusions can be drawn:
• The proposed equations (Eqs. 3, 8, 12) can be used to calculate the FOS for bamboo pile-reinforced slopes based on the three failure modes. The critical failure mode is the one where the FOS value is the lowest.
• The proposed equations can also be used for pile reinforcements made of materials other than bamboo.
• Slope reinforcement with bamboo piles has a significant effect in increasing the FOS against slope instability. As shown in Figure 9, the FOS of the reinforced slope by the analytical equation (Mode II) is 1.07 for a 35° angle, and the FOS for an unreinforced slope is 0.881 for the same angle. Similarly, the FOSs for other slope angles in the reinforced case are calculated by analytical equations, and it is found that for all slope angles, the FOS is the smallest in Mode II.
• The possibility of slope failure by Mode II (i.e., sliding of the upper part of the soil, leaving bamboo piles behind embedded in the soil bed) is higher than the other two modes when the slope is reinforced with bamboo piles.
• Figure 8 shows that after the bamboo piles were used in the middle of the slope, the critical slip surface moved away from the bamboo reinforcements. This shows the need for optimization of the bamboo reinforcement location in the slope.
• Comparing the FOS (Figure 10) obtained from Slope/W software and the analytical equation shows that the latter (Mode II) gives a lower value of FOS than SLOPE/W software.
• The average percentage difference between the FOS obtained from Slope/W and the analytical equation (Mode II) is 47.2%.
• The second case study shows that the FOS decreases as the slope angle increases. The proposed analytical equation can be effectively used to predict the FOS in all these modes.
In the future, a parametric study can be performed to find the effect of various parameters (density, friction angle, cohesion, location of bamboo piles, and length of bamboo piles) on FOS to select the optimum reinforcement for improving slope stability.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
PC: conceptualization, formal analysis, methodology, validation, supervision, investigation, and writing—review and editing. LS: conceptualization, formal analysis, methodology, validation, investigation, and writing—original draft. PK: conceptualization, experimental investigation, formal analysis, methodology, validation, investigation, and writing—review, and editing. All authors listed have made a substantial, direct, and intellectual contribution to the work and have approved it for publication.
Acknowledgments
The author(s) would like to greatly thank IIT Patna and the Department of Higher Education (Govt. of India) for providing the funding for the present research work, for which no specific grant number has been assigned.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Abbreviations
C′, effective cohesion; CSS, critical slip surface area; FOS, factor of safety; Fr, shear force at slice base; Frb, shear force at the base of the bamboo; LE, limit equilibrium; Nr, normal reaction force at slice bottom; Nr′, normal reaction force at bottom of slices adjacent to bamboo; Nrb, normal reaction at the base of the bamboo; R, resultant reaction force at the slice base; Rb, resultant reaction force at the base of the bamboo; Wm, weight of the mth slice; Wb, weight of the bamboo; αm, angle of the mth slice base; Φ′, effective friction angle; ΔLm, width of the mth slice; Δrb, radius of the bamboo pile.
References
Benmebarek, M. A., Benmebarek, S., Rad, M. M., and Ray, R. (2021). Pile optimization in slope stabilization by 2D and 3D numerical analyses. Int. J. Geotechnical Eng. 16, 211–224. doi:10.1080/19386362.2021.1972628
Bergado, D. T., Bukkanasuta, A., and Balasubramaniam, A. S. (1987). Laboratory pull-out tests using bamboo and polymer geogrids including a case study. Geotext. Geomembranes 5, 153–189. doi:10.1016/0266-1144(87)90015-X
Chen, L. T., and Poulos, H. G. (1997). Piles subjected to lateral soil movements. J. Geotechnical Geoenvironmental Eng. 123, 802–811. doi:10.1061/(asce)1090-0241(1997)123:9(802)
Dastpak, P., Chenari, R. J., Cami, B., and Javankhoshdel, S. (2021). Noncircular deterministic and stochastic slope stability analyses and design of Simple geosynthetic-reinforced soil slopes. Int. J. Geomechanics 21, 04021155. doi:10.1061/(ASCE)GM.1943-5622.0002116
Duncan, J. M., and Wright, S. G. (1980). The accuracy of equilibrium methods of slope stability analysis. Eng. Geol. 16, 5–17. doi:10.1016/0013-7952(80)90003-4
Gidon, J. S., and Sahoo, S. (2020). Rainfall-induced slope failures and use of bamboo as a remedial measure: A review. Indian Geotechnical J. 50, 766–783. doi:10.1007/s40098-020-00409-3
Goh, A. T. C., Teh, C. I., and Wong, K. S. (1997). Analysis of piles subjected to embankment induced lateral soil movements. J. Geotechnical Geoenvironmental Eng. 123, 792–801. doi:10.1061/(asce)1090-0241(1997)123:9(792)
Griffiths, D. V., Huang, J., and Fenton, G. A. (2010). “Comparison of slope reliability methods of analysis,” in GeoFlorida 2010: Advances in Analysis, Modeling & Design, Florida, 1952–1961. doi:10.1061/41095(365)198
Halder, K., and Chakraborty, D. (2020). Influence of soil spatial variability on the response of strip footing on geocell-reinforced slope. Comput. Geotech. 122, 103533. doi:10.1016/J.COMPGEO.2020.103533
Jeong, S., Kim, B., Won, J., and Lee, J. (2003). Uncoupled analysis of stabilizing piles in weathered slopes. Comput. Geotech. 30, 671–682. doi:10.1016/J.COMPGEO.2003.07.002
Kitch, W. A., Gilbert, R. B., and Wright, S. G. (2011). “Probabilistic assessment of commercial design guides for steep reinforced slopes: Implications for design,” in Geo-Risk 2011: Risk assessment and management, Atlanta, Georgia, 1055–1062. doi:10.1061/41183(418)115
Kourkoulis, R., Gelagoti, F., Anastasopoulos, I., Gazetas, G., and Asce, M. (2012). Hybrid method for analysis and design of slope stabilizing piles. J. Geotechnical Geoenvironmental Eng. 138, 1–14. doi:10.1061/(asce)gt.1943-5606.0000546
Kumar, N., Verma, A. K., Sardana, S., Sarkar, K., and Singh, T. N. (2018). Comparative analysis of limit equilibrium and numerical methods for prediction of a landslide. Bull. Eng. Geol. Environ. 77, 595–608. doi:10.1007/s10064-017-1183-4
Kumar, P., and Chakrabortty, P. (2020). A Simple analytical model for bamboo reinforced slope using ordinary method of slices. Lect. Notes Civ. Eng. 85, 269–283. doi:10.1007/978-981-15-6086-6_22/TABLES/3
Mekonnen, A. W., and Mandal, J. N. (2018). “Feasibility of fly ash as a backfill material and bamboo geogrid as a reinforcement,” in IFCEE 2018, Orlando, Florida, 526–536. doi:10.1061/9780784481585.051
Michalowski, R. L. (1997). Stability of uniformly reinforced slopes. J. Geotechnical Geoenvironmental Eng. 123, 546–556. doi:10.1061/(asce)1090-0241(1997)123:6(546)
Moawwez, M., Wang, J. P., and Hussain, M. A. (2021). Development of empirical correlations for limit equilibrium methods of slope stability analysis. Arabian J. Geosciences 14, 2020. doi:10.1007/s12517-021-08375-7
Ngudiyono, S., and Sulistyowati, T. (2022). Numerical simulation of slope stability for soil embankment reinforced with inclined bamboo piles. Lect. Notes Civ. Eng. 225, 287–295. doi:10.1007/978-981-16-9348-9_26/COVER
Poulos, H. G., and Chen, L. T. (1997). Pile response due to excavation-induced lateral soil movement. J. Geotechnical Geoenvironmental Eng. 123, 94–99. doi:10.1061/(asce)1090-0241(1997)123:2(94)
Poulos, H. G. (1995). Design of reinforcing piles to increase slope stability. Can. Geotechnical J. 32, 808–818. doi:10.1139/T95-078
Talukdar, P., Bora, R., and Dey, A. (2018). Numerical investigation of hill slope instability due to seepage and anthropogenic activities. Indian Geotechnical J. 48, 585–594. doi:10.1007/s40098-017-0272-4
Tang, X., and Yang, M. (2013). Investigation of flexural behavior of geocell reinforcement using three-layered beam model testing. Geotechnical Geol. Eng. 31, 753–765. doi:10.1007/s10706-013-9625-7
Tardio, G., Mickovski, S. B., Stokes, A., and Devkota, S. (2017). Bamboo structures as a resilient erosion control measure. Proc. Institution Civ. Eng. Forensic Eng. 170, 72–83. doi:10.1680/jfoen.16.00033
Won, J., You, K., Jeong, S., and Kim, S. (2005). Coupled effects in stability analysis of pile–slope systems. Comput. Geotech. 32, 304–315. doi:10.1016/J.COMPGEO.2005.02.006
Wright, S. G., and Duncan, J. M. (1991). Limit equilibrium stability analyses for reinforced slopes. Transp. Res. Rec.
Yang, S., Ren, X., and Zhang, J. (2011). Study on embedded length of piles for slope reinforced with one row of piles. J. Rock Mech. Geotechnical Eng. 3, 167–178. doi:10.3724/SP.J.1235.2011.00167
Keywords: slope stability, bamboo, reinforced slope, analytical study, limit equilibrium method
Citation: Chakrabortty P, Srivastava LS and Kumar P (2023) A simple analytical model for bamboo-reinforced slopes using modified Bishop method. Front. Built Environ. 9:1080318. doi: 10.3389/fbuil.2023.1080318
Received: 26 October 2022; Accepted: 04 May 2023;
Published: 18 May 2023.
Edited by:
Avijit Burman, National Institute of Technology, Patna, IndiaReviewed by:
Shiv Shankar Kumar, National Institute of Technology, Patna, IndiaVikas Pratap Singh, National Institute of Technology, Uttarakhand, India
Copyright © 2023 Chakrabortty, Srivastava and Kumar. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Pradipta Chakrabortty, cHJhZGlwdEBpaXRwLmFjLmlu, cHJhZGlwdEBnbWFpbC5jb20=
†ORCID:Pradipta Chakrabortty, https://orcid.org/0000-0002-8852-2596; Lokesh Sharan Srivastava, https://orcid.org/0000-0001-9345-7576
 Pradipta Chakrabortty
Pradipta Chakrabortty Lokesh Sharan Srivastava
Lokesh Sharan Srivastava Pintu Kumar
Pintu Kumar