A hybrid VMD-LSTM-SVR model for landslide prediction

Landslides are one of the most prevalent natural geological disasters, causing significant economic losses, damaging public environments, and posing severe threats to human lives. Landslide displacement, influenced by various triggering factors, best reflects the landslide evolution process; when displacement reaches a certain threshold, a landslide may occur. Consequently, predicting landslide displacement has become a focal point in engineering research. This study employs the Long Short-Term Memory (LSTM) neural network and Support Vector Regression (SVR), combined with the Variational Mode Decomposition (VMD) algorithm, to construct predictive models. Initially, the VMD algorithm decomposes the landslide displacement time series into trend, periodic, and stochastic components. A novel Variational Mode Decomposition-Long Short-Term Memory (VMD-LSTM) hybrid model is then proposed for single-step landslide displacement prediction, followed by the application of a new Variational Mode Decomposition-Support Vector Regression (VMD-SVR) model for time series forecasting of landslide displacement. The results indicate that the VMD-SVR-LSTM model, with an RMSE of 0.0328 and an R² of 0.8487, demonstrates the best predictive accuracy and fitting capability. The methodology proposed in this paper offers a viable approach for landslide disaster prevention and early warning systems.

1 Introduction

Landslides, as a type of natural geological hazard, are marked by their sudden onset, immense destructive power, high frequency of occurrence, and rapid movement, often triggering secondary disasters such as floods and debris flows (Chang et al., 2020; Huang et al., 2020a; Dou et al., 2020). Between 2017 and 2021, geological disasters across the country resulted in economic losses totaling billions of yuan, causing not only extensive damage to buildings and infrastructure but also significant casualties, thereby imposing a substantial economic burden on both the nation and its people. Consequently, analyzing the influencing conditions of landslide disasters is essential (Huang et al., 2020b; Steger et al., 2021; Dai et al., 2023; Mousavi et al., 2024). Landslide displacement directly reflects the evolutionary process of landslides and is influenced by factors such as geographical location, geological conditions, and controlling elements, which collectively contribute to the occurrence of landslide disasters. When displacement reaches a certain threshold, a landslide may be imminent (Yin et al., 2021; Feng et al., 2025). Therefore, accurate and reliable displacement prediction is critical for establishing effective landslide early warning systems, which can help prevent massive casualties and alleviate economic burdens. Landslide prevention and control have long been a topic of significant concern for both the government and the public (Di Napoli et al., 2020). The development of landslide displacement prediction has roughly gone through four stages: empirical models, mathematical statistical models, nonlinear models, and integrated models (Saito, 1969; Yang et al., 2019). Currently, the conventional process for displacement prediction involves using time series analysis methods in combination with other approaches to decompose landslide displacement, predicting each component separately, and then summing them up to obtain the final result. Commonly used decomposition methods include the moving average method, exponential smoothing method, Empirical Mode Decomposition (EMD), wavelet analysis, and others (Cervantes et al., 2020). Although these methods have achieved favorable results in prediction, issues such as inadequate decomposition or unclear physical meanings of the components still persist. In contrast, Variational Mode Decomposition (VMD) offers advantages like adaptive decomposition, strong noise resistance, and more intuitive physical interpretations, providing more reliable and interpretable decomposition results for predictive models (Zhu et al., 2025; Hu et al., 2025; Zhao et al., 2024).

In modern times, numerous researchers have employed various methods to predict landslide displacement (Zhu et al., 2025; Hu et al., 2025). These predictive approaches can be broadly categorized into two main forms: the first primarily relies on statistical models, while the second is based on machine learning techniques, such as artificial neural networks, various optimization algorithms, and classification models (Zhao et al., 2024; Huang et al., 2021; Casagli et al., 2023). Statistical models for landslide displacement prediction typically focus on identifying the most relevant inducing factors to optimize mathematical model calculations, sometimes even establishing coupled relationships between mathematical and neural network models. Commonly used statistical models include the Grey System Model and the Autoregressive Integrated Moving Average (ARIMA) model, among others (Huang et al., 2021).

In recent years, deep learning models have been widely applied across various domains (Casagli et al., 2023). Both domestically and internationally, artificial neural network models have been extensively utilized for landslide displacement prediction. In real-world scenarios, time series data collected often contain noise, which can interfere with model predictions. Consequently, data preprocessing is indispensable (Scherzer et al., 2019). Many scholars have employed various methods for data processing, including signal decomposition techniques that break down the original series into multiple subsequences before applying predictive models. Approaches such as Empirical Mode Decomposition (EMD), Ensemble Empirical Mode Decomposition (EEMD), and Complete Ensemble Empirical Mode Decomposition with Adaptive Noise (CEEMDAN) have proven effective in processing raw sequences and enhancing the accuracy of predictive models. These methods underscore the critical role of data preprocessing in improving model performance (Smith et al., 2021). Therefore, preprocessing time series data can significantly enhance the precision of model predictions. In recent years, Long Short-Term Memory (LSTM) networks have been employed to address time series problems, particularly for predicting surface deformations in landslide-prone areas. For instance, Xu et al. conducted a study on surface deformation monitoring of the Fanjiaping landslide in the Three Gorges Reservoir area using SBAS-InSAR time series data and an LSTM model (Barman et al., 2023). The results demonstrated that the LSTM model achieved correlation coefficients of 0.9455 and 0.9829, significantly outperforming Back Propagation (BP) neural networks and Support Vector Regression (SVR) models (Huang et al., 2020c). Similarly, Chen et al. utilized SBAS-InSAR technology and an LSTM model to monitor surface deformations along the Yangtze River in Nanjing, revealing high consistency between the LSTM model’s deformation predictions and InSAR monitoring results, with a maximum absolute error of 2.66 mm. Liu et al. applied an AT-LSTM model to monitor land subsidence in the Pingshuo mining area of Shanxi Province, demonstrating that the model’s predicted spatial distribution closely aligned with actual conditions (Dou et al., 2023).

Landslide displacement is influenced by numerous external fluctuating factors. Therefore, enhancing the accuracy of landslide prediction not only requires improving prediction methods but also selecting appropriate influencing factors. However, during the process of a landslide, the changing trend of surface displacement continuously varies both temporally and spatially. Consequently, using a single time series algorithm based on a neural network for surface displacement prediction has certain limitations (Buia et al., 2020; Hong et al., 2020). To address these issues, in recent years, deep learning methods combined with signal decomposition techniques have gradually become a research hotspot in landslide prediction (Steger et al., 2024). Therefore, this study takes the displacement monitoring data from the Baishuihe landslide in the Three Gorges region as the research object. The VMD algorithm is employed to decompose the monitoring data into trend, periodic, and random components. A combined SVR-LSTM model is then used to predict each component separately. Finally, the cumulative prediction of landslide displacement is achieved by summing up the predicted results of each component.

The main contributions of this paper are as follows:

(1) Data Preprocessing: Given the characteristics of landslide displacement data, the preprocessing phase primarily involves data decomposition. By applying Variational Mode Decomposition (VMD), the quality of input data for the model is improved, as the decomposed subsequences capture both high-frequency and low-frequency features, optimizing model inputs and enhancing predictive performance.

(2) Model Optimization: To address the limitations of standalone LSTM models, which often exhibit large prediction errors and low accuracy, a VMD-LSTM hybrid model is proposed for landslide displacement sequence prediction. By decomposing the original sequence using VMD and integrating it with the LSTM model, prediction errors are significantly reduced, and the LSTM’s predictive capabilities are optimized. Additionally, LSTM-SVR hybrid models are developed for each decomposed component, combining the LSTM’s strength in extracting time series features with SVR’s ability to handle nonlinear problems, thereby compensating for LSTM’s shortcomings.

While traditional models like ARIMA and BP are commonly used for landslide displacement prediction, their optimization via decomposition algorithms has yielded limited improvements in predictive performance. Some studies have employed particle swarm optimization (PSO) to refine predictive models, but these methods often rely on a priori knowledge, lacking flexibility, and fall short in dynamic landslide displacement prediction. In contrast, recurrent neural networks (RNNs), which are often used for time series processing, suffer from gradient explosion or vanishing problems in long sequences. Long Short-Term Memory (LSTM) networks effectively mitigate these RNN issues, demonstrating superior accuracy in time series prediction. To address the complexity of existing hybrid models, this paper introduces a novel VMD-SVR-LSTM model for landslide displacement time series prediction. Compared to traditional LSTM models, the VMD-SVR-LSTM model captures more frequency-domain features within the raw data, offering enhanced predictive accuracy. The effectiveness and feasibility of the VMD-SVR-LSTM model are validated using the Baishuihe landslide displacement data in the Three Gorges Reservoir area.

2 Method for predicting landslide displacement

The main steps of the landslide displacement prediction process based on the VMD-SVR-LSTM model are as follows:

(1) Influencing Factor Analysis: Based on prior research, nine factors affecting periodic displacement were extracted, including: Maximum monthly rainfall, Cumulative monthly rainfall, Cumulative rainfall over the past 2 months, Monthly reservoir water level, Monthly reservoir water level change, Reservoir water level change over the past 2 months, Cumulative monthly displacement increment, Cumulative displacement increment over the past 2 months, Cumulative displacement increment over the past 3 months.

(2) Data Decomposition: Using Variational Mode Decomposition (VMD) combined with time series analysis, the total landslide displacement was decomposed into three components: Trend displacement、Periodic displacement、Random displacement.

(3) Dataset Construction: The influencing factor components served as input variables, while the corresponding displacement components acted as output variables to construct the dataset. Each dataset was further divided into training and testing subsets.

(4) Model Training and Prediction: The training set was fed into the SVR-LSTM model for iterative optimization of model parameters, establishing an optimal prediction model. Subsequently, the testing set was input into the model to generate predicted values for each displacement component, which were then compared against actual displacement data.

(5) Result Evaluation: The predicted values of individual displacement components were summed to obtain the cumulative landslide displacement prediction. Accuracy and reliability of the model’s predictions were evaluated through comparative analysis with actual displacement measurements.

2.1 VMD

Time series decomposition is a crucial preprocessing technique that enables the handling of nonlinear and nonstationary signal data in real-world applications, allowing models to effectively extract both high-frequency and low-frequency information from raw data, thereby enhancing the accuracy of predictive models (Talukdar et al., 2020; Youssef et al., 2016; Dong et al., 2023). Landslide displacement time series exhibit nonlinear and nonstationary characteristics, with general nonstationary data typically composed of components such as trend, seasonality, periodicity, or random noise (Min et al., 2019). By decomposing the original series, characteristic information at different frequencies can be extracted, facilitating the model’s analysis of each component in the raw data and uncovering underlying data patterns and developmental trends (Alabi et al., 2022). Applying predictive models to each decomposed component significantly improves the model’s predictive performance. This paper primarily employs the Variational Mode Decomposition (VMD) algorithm for this purpose.

Variational Mode Decomposition (VMD) is a novel method for decomposing complex signals, introduced by K. Dragomiretskiy and D. Zosso in 2014 as an advancement over Empirical Mode Decomposition (EMD) (Manibardo et al., 2022). Unlike EMD, VMD redefines the Intrinsic Mode Function (IMF) as an amplitude- and frequency-modulated (AM-FM) signal, denoted as $u_k\left(t\right)$, with the following mathematical representation in Equation 1:

$u_k\left(t\right)=A_k\left(t\right)\cos \left({\varphi }_k\left(t\right)\right)(1)$

In this formulation, $A_k\left(t\right)$ represents the instantaneous amplitude, and ${\varphi }_k\left(t\right)$ denotes the phase.

In Variational Mode Decomposition (VMD), the signal sifting approach used in Empirical Mode Decomposition (EMD) is abandoned for decomposing Intrinsic Mode Functions (IMFs). Instead, after configuring parameters such as the number of modes $K$, penalty parameter $a$, and update step size $\tau$, VMD decomposes the signal by solving an optimization problem within a variational framework. The mathematical formulation for this model is given in Equation 2:

$\left.\begin{array}{l}\underset{\left\{u_k\right\},\left\{{\omega }_k\right\}}{\min }\left\{{\displaystyle \sum _{k=1}^K}{‖{\mathrm{\partial }}_t\left[\left(\sigma \left(t\right)+\frac{j}{\pi t}\right)u_k\left(t\right)\right]e^{-j{\omega }_{k}t}‖}_2^2\right\}\\ s.t.{\displaystyle \sum _{k=1}^K}{u}_k=f\left(t\right)\end{array}\right\}(2)$

In the equations: $\left\{u_k\right\}$ represents the decomposed components obtained through the final decomposition process; $\left\{u_k\right\}=\left\{u_1,...,u_K\right\}$; $\left\{{\omega }_k\right\}$ corresponds to the actual center frequencies of each Intrinsic Mode Function (IMF) component; $\left\{{\omega }_k\right\}=\left\{{\omega }_1,...,{\omega }_K\right\}$; $\left[\sigma \left(t\right)+j/\left(\pi t\right)\right]u_k\left(t\right)$ denotes the analytic signals derived for each IMF component; $e^{-j{\omega }_{k}t}$ signifies the estimated center frequencies of these analytic signals; $f\left(t\right)$ represents the original input signal.

To solve for the optimal solution of this constrained variational model, Equation 4 must be reformulated into an unconstrained optimization problem:

$a{{\displaystyle \sum _k}{‖{\mathrm{\partial }}_t\left[\left(\sigma \left(t\right)+\frac{j}{\pi t}\right)u_k\left(t\right)\right]e^{-j{\omega }_{k}t}‖}_2^2+‖f\left(t\right)-{\displaystyle \sum _k}{u}_k\left(t\right)‖}_2^2+〈\lambda \left(t\right),f\left(t\right)-{\displaystyle \sum _k}{u}_k\left(t\right)〉(3)$

In the equations: $\lambda$ represents the Lagrange multiplier.

The Alternating Direction Method of Multipliers (ADMM) is utilized to compute the saddle point of the unconstrained model derived earlier, which corresponds to the optimal solution of the constrained variational model described in Equation 3. This process decomposes the original signal into $K$ Intrinsic Mode Function (IMF) components. By employing this approach, each IMF component inherits distinct scale-dependent characteristics, thereby better preserving its inherent structural information. Consequently, this study adopts Variational Mode Decomposition (VMD) to analyze landslide displacement-time curves, leveraging its capacity to isolate meaningful components that reflect the underlying dynamics of slope deformation.

2.2 LSTM

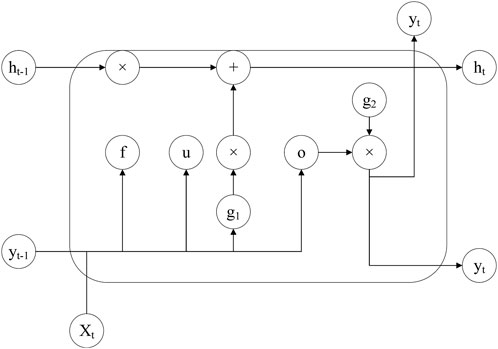
LSTM (Long Short-Term Memory) networks safeguard and regulate the information within their memory cells through three gates, with the manipulation of this information achieved via element-wise multiplication by activation functions. A set of parameters, trained through gradient descent, is employed to control the state of each gate (Zhang et al., 2024). Each gate in an LSTM serves a distinct and specific function. The forget gate, denoted as $f$, determines which pieces of information to discard from the previous state $h_{t-1}$. After the input $x_t$ and $h_{t-1}$ are processed by the update gate $u$, they, in conjunction with the adjusted forget gate $f$, decide the weightage to be given to the candidate state ${\stackrel{\sim }{h}}_t$ for updating the current state $h_t$. To generate the output $y_t$, the network first filters its current state using a nonlinear function $g_2$, and then combines it with the output of the output gate $o$ to produce $y_t$. Here, a portion of the state $y_t$ is fed back as the next input $y_{t-1}$. Each gate’s operation hinges on the current external input $x_t$ and the previous output (or more accurately, the previous hidden state $y_{t-1}$, but again, adhering to the original text’s phrasing). Figure 1 provides a detailed illustration of the LSTM’s structural principles, and the equation governing the update of the LSTM’s state is presented in Equation 4.

$\left\{\begin{array}{l}forgetgate:f_t=\sigma \left(W_f{x}_t+R_f{y}_{t-1}+b_f\right)\\ candidatestate:{\stackrel{\sim }{h}}_t=g_1\left(W_f{x}_t+R_f{y}_{t-1}+b_f\right)\\ updatestate:u_t=\sigma \left(W_u{x}_t+R_u{y}_{t-1}+b_u\right)\\ cellstate:h_t=u_t\otimes {\stackrel{\sim }{h}}_t+f_t\otimes h_{t-1}\\ outputgate:o_t=\sigma \left(W_o{x}_t+R_o{y}_{t-1}+b_o\right)\\ output:y_t=o_t\otimes g_2\left(h_t\right)\end{array}\right.(4)$

Figure 1

Figure 1. Structure of LSTM.

In the equation, $x_t$ represents the input vector at time step t; $W_f$, $W_h,W_u$ and $W_o$ are weight matrices associated with the input units and connections to the hidden layer; $R_f,R_h,R_u$ and $R_o$ are weight matrices for the connections within the hidden layer; $b_f,b_h,b_u$ and $b_o$ are bias vectors; the activation function $\sigma$ is either the sigmoid or tanh function; $g_1$ and $g_2$ are nonlinear activation functions; and $\otimes$ denotes element-wise multiplication.

2.3 Evaluation metrics

The effectiveness of predictive models is evaluated and compared using the Root Mean Square Error (RMSE) and the coefficient of determination (R²) (Praveen et al., 2025; Zhang et al., 2021; Huang et al., 2017). The primary formulas for these metrics are as follows in Equations 5, 6:

(1) RMSE

$RMSE=\sqrt{\frac{1}{N}{\displaystyle \sum _{i=1}^n}{\left({\widehat{x}}_i-x_i\right)}^2}(5)$

(2) R²

$R^2=1-\frac{{\displaystyle {\sum }_{i=1}^N}\left({\widehat{x}}_i-x_i\right)}{{\displaystyle {\sum }_{i=1}^N}\left({\overline{x}}_i-x_i\right)}(6)$

Where, $\widehat{x}$ represents the predicted values, $x$ denotes the actual values, $\overline{x}$ is the mean of the actual samples, and N indicates the total number of samples. A smaller RMSE value indicates stronger predictive capability of the model, while an R² value closer to 1 signifies better model fitting performance.

2.4 Normalization processing

Normalization is a critical preprocessing step in data analysis, particularly for time series prediction tasks like landslide displacement forecasting. The primary objective of normalization is to rescale the input data to a standardized range (typically [0, 1] or [-1, 1]), thereby eliminating the influence of varying magnitudes among different features or samples. This process ensures that all variables contribute equally to the model’s training and prevents dominant features (e.g., large-scale displacement values) from overshadowing others (e.g., subtle rate-of-change indicators) (Naemitabar and Asadi, 2021).

In the context of landslide displacement time series, raw displacement data often exhibit significant variations in scale due to factors such as sensor precision, environmental noise, or cumulative displacement effects. Without normalization, models like LSTM or hybrid VMD-SVR-LSTM architectures may struggle to converge efficiently or could produce biased predictions. For instance, if displacement values range from 0 to 1,000 m while rate-of-change values range from 0 to 1 m/day, the model might disproportionately prioritize displacement magnitude over temporal trends. The most commonly used normalization technique is Min-Max Scaling, defined as in Equation 7:

$y=\frac{\left(x_i-x_{imin}\right)}{\left(x_{imax}-x_{imin}\right)}(7)$

In the formula: $x_{imax}$ represents the maximum value of variable $i$; $x_{imin}$ represents the minimum value of variable $i$; $x_i$ denotes the original value; $y$ denotes the normalized value.

3 Landslide displacement time series prediction based on the VMD-SVR-LSTM hybrid model

3.1 Study area

The Baishuihe landslide is located on the southern bank of the Yangtze River, approximately 56 km downstream from the Three Gorges Dam site, within Baishuihe Village, Shazhenxi Township (Figure 2). Its geographical coordinates are 110°32′09″ longitude and 31°01′34″ latitude (Dou et al., 2019). The landslide mass is situated in a broad river valley section of the Yangtze, characterized by a monoclinic bedding slope that dips in the same direction as the slope face. The terrain slopes downward from south to north, exhibiting a stepped profile toward the river. The trailing edge of the landslide reaches an elevation of 410 m, bounded by the geotechnical interface, while the leading edge extends to the Yangtze River. The eastern and western boundaries are defined by bedrock ridges, with an overall slope gradient of approximately 30°. The landslide measures 600 m in north-south length and 700 m in east-west width, with an average slide mass thickness of about 30 m and a total volume of 1,260 × 10⁴ m³. Classified as a colluvial landslide, the slope exhibits a dip-slope orientation.

Figure 2

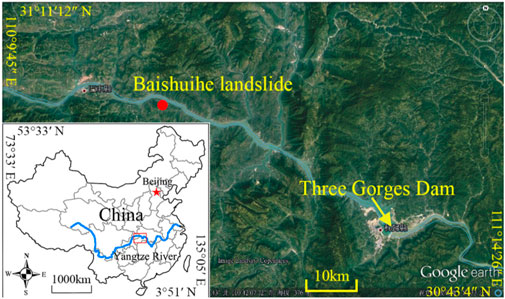
Figure 2. Location of the study area and landslide inventory map (Rodrigues et al., 2021).

Since June 2003, professional monitoring of the Baishuihe landslide has been conducted, with numerous monitoring stations deployed across the site. Among these, the ZG118 station, located in the central portion of the landslide mass, is capable of capturing the entire evolutionary process of the landslide. This station also boasts relatively comprehensive monitoring data, facilitating data-driven modeling efforts. Given these two advantages—central location and robust datasets—the monitoring data from the ZG118 station were utilized to validate the effectiveness and superiority of the proposed methodology in this study. Figure 3 illustrates the cumulative displacement, reservoir water level, and rainfall curves monitored at the ZG118 station from January 2007 to December 2012. Notably, rapid movement episodes are observed at the onset of the rainy season (May to September annually) and toward the end of reservoir water level drawdowns (June and July). Moreover, these rapid movement periods typically conclude before the rainy season’s end. It is evident that fluctuations in both reservoir water levels and rainfall significantly influence cumulative landslide displacement, suggesting that precipitation and reservoir water level variations are primary factors driving deformation and failure at the Baishuihe landslide.

Figure 3

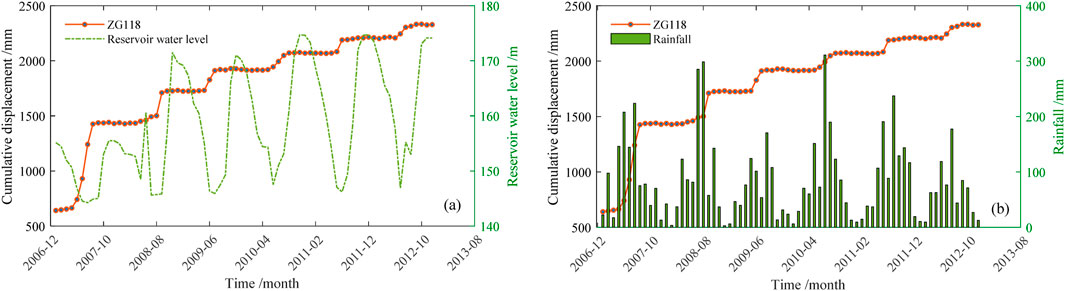
Figure 3. Monitoring curves of cumulative displacement, reservoir water level (a), and rainfall (b).

3.2 Prediction of cyclical displacement

Based on prior research, nine influential factors affecting cyclical displacement were extracted: maximum monthly rainfall, cumulative monthly rainfall, cumulative rainfall over a two-month period, monthly reservoir water level, monthly change in reservoir water level, two-month change in reservoir water level, monthly cumulative displacement increment, two-month cumulative displacement increment, and three-month cumulative displacement increment. These nine factors have demonstrated high effectiveness in predicting cyclical displacement. For the experiments, data from January 2007 to December 2011 were used as the training set, while data from January 2012 to December 2012 served as the testing set. Predictive models were developed using both Support Vector Regression (SVR) and Long Short-Term Memory (LSTM) networks.

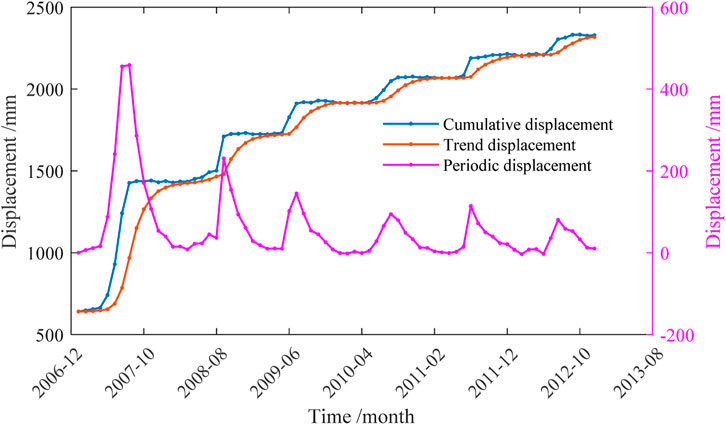
To address the challenge of insufficient data volume for direct modeling of the raw landslide displacement series, this study first employed Variational Mode Decomposition (VMD) to decompose the displacement series into several components, each with a unique central frequency. This decomposition indirectly resolved the data scarcity issue by enabling modeling of individual components rather than the raw series. The cumulative landslide displacement is decomposed into trend and periodic displacements, as shown in Figure 4. From Figure 4, it can be observed that the trend displacement obtained using VMD effectively reflects the changing trend of the cumulative landslide displacement. The periodic displacement is primarily influenced by cyclical precipitation and reservoir water level fluctuations. Therefore, before establishing a predictive model for periodic displacement, it is necessary to extract the factors affecting the periodic displacement of the landslide.

Figure 4

Figure 4. Decomposition results of cumulative displacement time series rainfall.

Subsequently, the study leveraged the LSTM network’s strength in extracting temporal sequence features and the SVR’s capability in nonlinear regression to create a hybrid modeling approach, compensating for the limitations of single-model regression performance. This combined strategy effectively tackled the data-driven landslide displacement prediction problem.

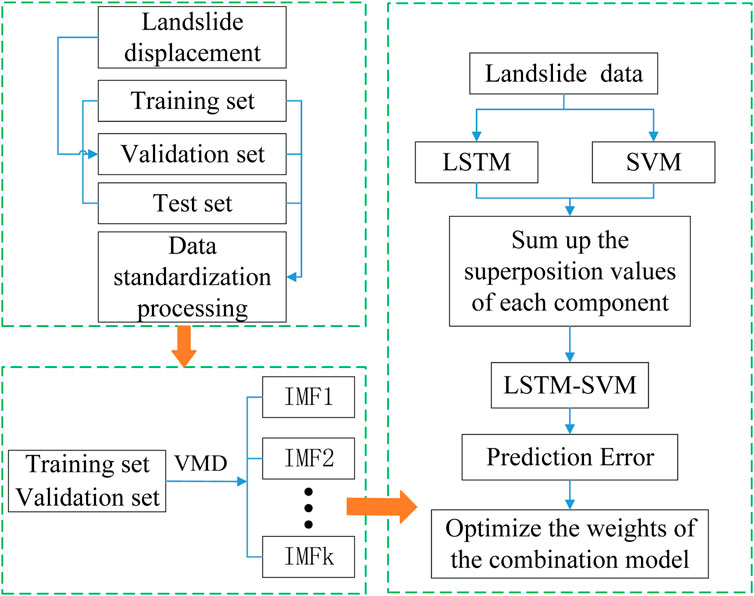
The experiments were conducted on the deep learning framework PyTorch-CPU, with the model optimized using the Adam optimizer. Based on the size of the dataset, the number of network training epochs was set to 300, and the batch size was set to 8. The LSTM network had an input layer size of 4, a time window size of 5, a step size of 1, and a hidden layer size of 50. The optimal hyperparameters for the SVR model were determined to be C = 1.015 and g = 0.01. The VMD-LSTM-SVR modeling workflow is illustrated in Figure 5, where the blue box represents the hybrid modeling process and the red box denotes the individual component modeling phase. As shown in Figure 5, the VMD-LSTM-SVR modeling approach can be broken down into the following steps.

Figure 5

Figure 5. VMD-LSTM-SVR modeling flowchart.

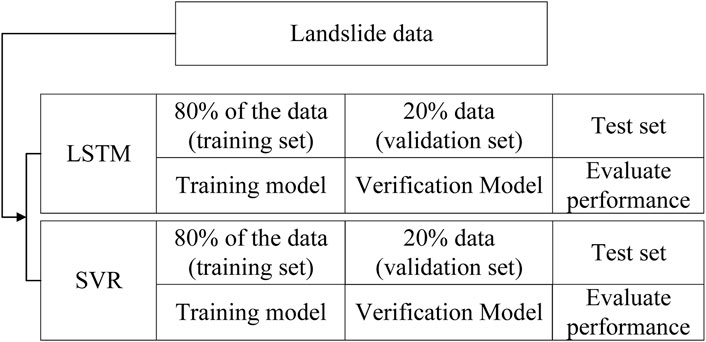
In the first step, the landslide displacement cycle data are proportionally divided into training, validation, and testing sets in sequence. The training set is used to train the landslide displacement prediction model, the validation set is employed to tune hyper parameters and validate model performance (specifically during LSTM model training), and the testing set is reserved for forecasting the landslide’s future displacement behavior. The modeling data collectively refers to the datasets utilized during both training and validation phases. The specific proportional splits are illustrated in Figure 6.

Figure 6

Figure 6. Dataset partition ratio.

In the second step, each sequential component of the training and validation sets is normalized and structured into time-series vectors to enhance convergence speed and prediction accuracy during model training.

In the third step, the degradation feature sequences, standardized using Variational Mode Decomposition (VMD), are decomposed into multiple components, each with a limited bandwidth and a unique central frequency.

In the fourth step, a hybrid LSTM-SVR predictive model is constructed for each decomposed component. Since the LSTM and SVR models operate in parallel, their respective parameters are optimized independently.

In the fifth step, the weights of the hybrid model are optimized based on the principle of minimizing the sum of squared prediction errors (SSPE), expressed mathematically as in Equation 8:

$\left\{\begin{array}{l}\mathit{min}{{\displaystyle \sum _{t=1}^N}\left(y_t-{\beta }_1{\widehat{y}}_{LSTM,t}-{\beta }_2{\widehat{y}}_{SVR,t}\right)}^2\\ s.t.{\beta }_1+{\beta }_2=1\left({\beta }_1,{\beta }_2\ge 0\right)\end{array}\right.(8)$

where ${\beta }_1$ and ${\beta }_2$ represent the predictive weights assigned to the LSTM and SVR models, respectively. The predicted output ${\widehat{y}}_t$ of the hybrid model at time t is calculated as in Equation 9:

${\widehat{y}}_t={\beta }_1{\widehat{y}}_{LSTM,t}+{\beta }_2{\widehat{y}}_{SVR,t}(9)$

In the sixth step, the LSTM-SVR predictive results for all decomposed components are aggregated, and inverse normalization is applied to obtain the final forecasted landslide displacement time series. The predictive performance is then evaluated by comparing the forecasted series with the ground truth (actual displacement data) on the testing set.

3.3 VMD decomposition

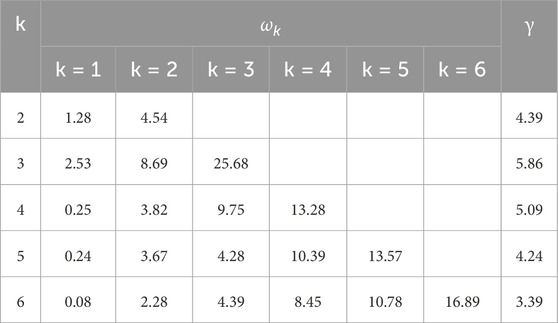
Variational Mode Decomposition (VMD) requires prior specification of the number of decomposed components (Zhu et al., 2025). An excessively high number of components risks introducing modal aliasing and noise interference, while an insufficient number may fail to fully decompose the landslide displacement sequence, thereby hindering the extraction of meaningful information. Thus, an optimal number of VMD components must be determined. This study leverages the property that VMD components possess unique central frequencies, which progressively converge as the number of components increases, to guide the selection of the component count. Table 1 presents the central frequencies of VMD components for K = 2 to 6, where γ quantifies the distinctness (or separation) of the components under different values of K.

Table 1

Table 1. Central frequencies for different numbers of VMD components.

γ can be expressed as in Equation 10:

$\gamma =\frac{1}{k-1}{\displaystyle \sum _{k=1}^{k-1}}\left|{\omega }_{k+1}-{\omega }_k\right|(10)$

A higher value of γ indicates greater distinctness among the decomposed components. As shown in Table 1, γ peaks when K = 3 and gradually stabilizes around 0.0339 as K increases to 6. For example, when K = 6, the differences between the components are minimal and significantly smaller than the disparities observed at K = 3. Consequently, K = 3 is determined as the optimal number of components for decomposition. The zero-crossing rate (ZCR), defined as the ratio of zero-crossings to the sequence length, is used to distinguish high-frequency and low-frequency components at K = 3. Empirically, a ZCR threshold of 5% is applied to classify components as either high-frequency or low-frequency. The ZCR values for Components 1–3 are 0%, 5.98%, and 16.43%, respectively, clearly identifying Component 1 as low-frequency and Components 2–3 as high-frequency. Low-frequency components capture the overall trend of the data, while high-frequency components reflect short-term fluctuations. Thus, by applying VMD to the original frequency-aliased data, the prediction task is simplified into forecasting the trend and fluctuation sequences separately, enabling the model to better capture underlying data patterns. The IMF1 component can be regarded as reflecting a long-term deformation trend influenced by internal control factors such as the landform, geological structure, etc., of the landslide itself—that is, the trend displacement. The IMF2 component can be considered to represent periodic fluctuations in landslide displacement caused by cyclical external influencing factors like rainfall and reservoir water level fluctuations—that is, the periodic displacement. The IMF3 component is typically induced by sudden, short-term influencing factors, including random factors such as human activities and microseisms. This type of displacement manifests as relatively irregular fluctuations in the time series—that is, the random displacement.

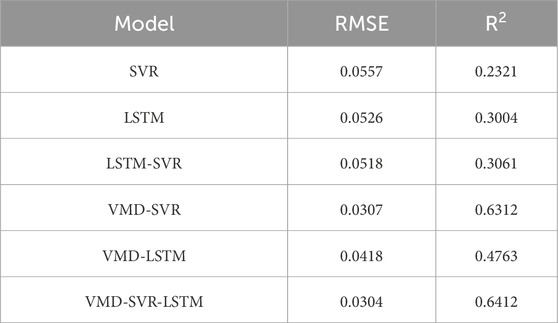
Model ablation experiments in data-driven modeling involve systematically removing certain components or factors to assess their impact on the overall model performance. To evaluate the effectiveness of the proposed model, comparative performance analyses were conducted across six models: SVR, LSTM, LSTM-SVR, VMD-SVR, VMD-LSTM, and VMD-LSTM-SVR. The experimental results are summarized in Table 2.

Table 2

Table 2. Model performance comparison.

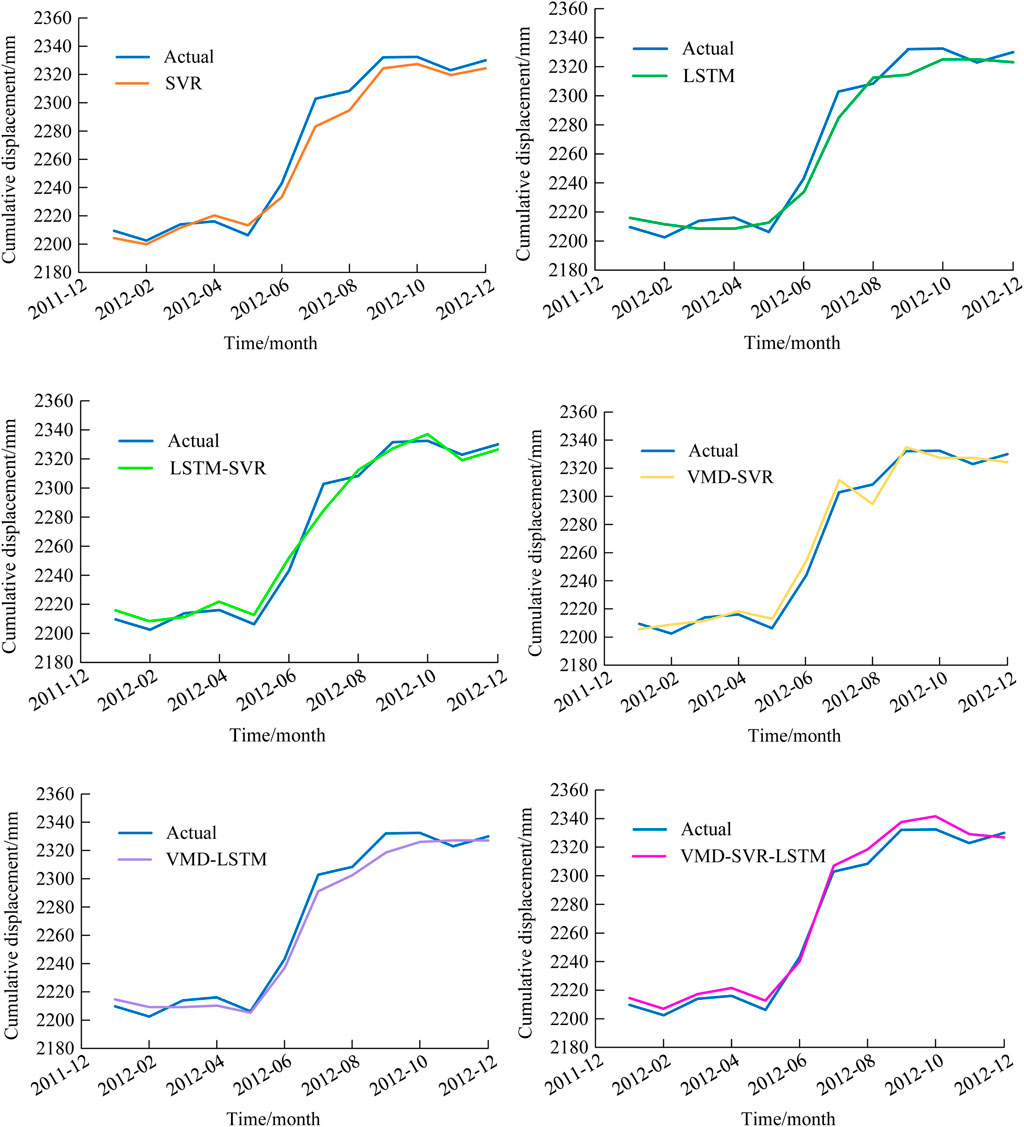
When comparing the three models (SVR, LSTM, and LSTM-SVR) without VMD integration, LSTM demonstrates superior feature extraction capabilities for time-series data compared to SVR, which does not inherently account for temporal dependencies. By combining LSTM and SVR in a weighted ensemble (LSTM-SVR), the strengths of both models are synergized, leading to improved predictive performance. After incorporating VMD, all models exhibit substantial performance enhancements, with RMSE values dropping from 0.05 to the range of 0.03–0.04. Notably, the R² score for the VMD-LSTM-SVR model surpasses 0.6, indicating strong alignment between predicted and actual trends. At this stage, the VMD-SVR and VMD-LSTM-SVR models outperform the VMD-LSTM model significantly, suggesting that VMD enables SVR to leverage its nonlinear regression strengths effectively for time-series forecasting. Figure 7 illustrates the ablation experiment results, highlighting stark differences in predictive performance between models with and without VMD. This disparity arises because VMD decomposes the original sequence into trend and fluctuation components, which are modeled separately and then aggregated. Consequently, VMD-enhanced models capture both the overarching trends (via trend component learning) and fine-grained fluctuations (via fluctuation component learning), yielding substantial performance improvements across all tested architectures.

Figure 7

Figure 7. Comparison of predictive performance in ablation experiments.

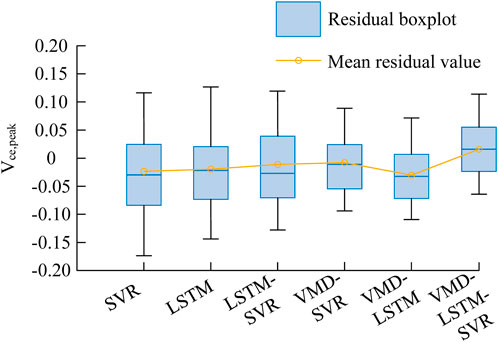
The improvement effects are illustrated in Figure 8. Compared to the single LSTM and SVR models, the LSTM-SVR model demonstrates a reduced residual range and a residual mean closer to 0, indicating improved prediction performance. After applying VMD to the original sequence, the residual range is significantly narrowed down to −0.04 to 0.1. The quartiles in the boxplot and the residual mean also notably approach 0. Therefore, the VMD-LSTM-SVR model not only captures the underlying trend effectively but also exhibits smaller prediction errors and a narrower residual range, resulting in more robust prediction outcomes.

Figure 8

Figure 8. Boxplot of prediction residuals for different models.

3.4 Algorithm experiment comparison

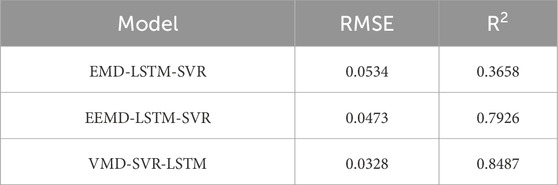
Both EMD (Empirical Mode Decomposition) and EEMD (Ensemble Empirical Mode Decomposition) are algorithms for sequence decomposition, sharing a modeling and prediction workflow similar to VMD (Variational Mode Decomposition). However, they fundamentally differ from VMD by relying on envelope and extremum-based principles, which do not inherently guarantee modal or spectral separation between decomposed components. This limitation often leads to modal/frequency aliasing, hindering improvements in model predictive performance. To effectively demonstrate the advantages of the VMD algorithm, this study establishes comparative models EMD-LSTM-SVR and EEMD-LSTM-SVR for performance evaluation. The experimental results are summarized in Table 3.

Table 3

Table 3. Comparison of model predictive performance.

A comparative analysis of Tables 2, 3 reveals that, compared to the R² value of 0.3061 achieved by the LSTM-SVR model in the ablation experiments, the LSTM-SVR models integrated with sequence decomposition algorithms (e.g., EMD, EEMD, VMD) demonstrate varying degrees of improvement in R². This enhancement stems from the inherent properties of sequence decomposition algorithms, which isolate components representing trend sequences to varying extents, thereby boosting predictive performance. However, the remaining components capturing fluctuation sequences contribute differentially to the model’s predictive capacity. For instance, the EMD-LSTM-SVR model shows no improvement or even a slight decline in RMSE compared to the standalone LSTM-SVR, suggesting that the fluctuation components extracted by EMD may not provide as much predictive value in this context.

4 Discussions

This paper has conducted a series of studies on the Baishuihe landslide disaster, achieving some progress in fields such as deformation and failure monitoring of landslide disasters and time series prediction of landslide displacements. However, due to the author’s limited expertise and the short timeframe during the paper’s preparation, in-depth and meticulous research on many landslide disaster issues remains lacking, and the depth of research on several geological hazard issues needs to be enhanced. Therefore, the author intends to conduct further exploration in the following areas in future research:

(1) Continuous monitoring of deformation characteristics of individual landslide disasters using advanced remote sensing technologies such as INSAR, LIDAR, and others. Although this paper has employed high-resolution remote sensing imagery and GPS for monitoring the Baishuihe landslide disaster and achieved some results, these monitoring techniques have already been maturely applied in multiple fields. Therefore, it is necessary to consider other more advanced technological means for landslide monitoring and improve the temporal frequency and accuracy of monitoring.

(2) Continuous monitoring of regional landslide deformation and failure characteristics. This paper has focused on monitoring the Baishuihe landslide, with a limited monitoring scope, making it difficult to apply the obtained results to a broader landslide-affected area. Therefore, in future research, real-time monitoring of regional landslides can be considered using INSAR and large-scale high-resolution imagery.

(3) Further exploration of landslide instability mechanisms and processes using numerical simulation techniques. This paper has only analyzed the deformation and failure mechanisms of landslides based on monitoring data such as surface deformation, rainfall, and reservoir water level changes, lacking simulation and tracking of the landslide deformation and failure processes. Therefore, in future research, various numerical simulation techniques such as Flac 3D can be considered to simulate and analyze the instability mechanisms and processes of landslides.

(4) Improvement of existing landslide displacement prediction models. For instance, to fully explore the changing patterns of landslide displacement time series, longer landslide sequences should be utilized for model training as much as possible. Predictions of landslide displacement time series at different scales, such as daily, weekly, and monthly displacement predictions, can be made according to actual needs. In-depth research on the mechanisms of landslide deformation should be conducted to obtain as many influencing factors of landslide deformation as possible, such as thrust forces and groundwater levels, to enrich the information content of the models. Additionally, various novel artificial intelligence models, such as deep learning techniques, VOLTERRA series adaptive models, and semi-supervised regression models, can be attempted to improve prediction accuracy by reducing the difficulty in selecting model parameters.

(5) Acquisition and screening of regional landslide environmental factors using multiple technical methods. In future research, more environmental factors, such as slope structure, human engineering activities, and surface moisture indices, can be considered, and variable screening techniques such as rough set theory can be employed for input variable selection.

(6) Furthermore, there is a lack of research on regional landslide risks. Therefore, in future research, the hazard and risk of landslides in the Three Gorges Reservoir area will be evaluated.

5 Conclusion

By combining individual predictive models, the resulting ensemble prediction model can fully leverage the strengths of each individual model, enhancing prediction accuracy while significantly improving the applicability of the predictive model. Integrating predictive models into monitoring and early warning systems is not only a crucial step in transitioning from theory to application but also an urgent need in practical engineering. With the goal of accurate landslide early warning, this paper delves into landslide displacement prediction methods starting from predictive models, providing robust support for geological hazard prevention and control. The main work and achievements of this paper are as follows:

(1) A comprehensive review and summary of the current research status of landslide prediction models were conducted, aiming to achieve landslide displacement prediction. The implementation principles and processes of the VMD (Variational Mode Decomposition) time series data decomposition method were elaborated. Additionally, the modeling principles of LSTM (Long Short-Term Memory) and SVR (Support Vector Regression) models were thoroughly analyzed.

(2) A displacement feature time series prediction method based on VMD-LSTM-SVR was proposed for landslide displacement prediction. The model decomposes feature time series using the VMD algorithm to obtain different trend and periodic displacements, thereby more accurately extracting time series patterns and reducing the difficulty of displacement prediction. Subsequently, a combined model is established by leveraging the time series feature extraction advantages of the LSTM network and the strong nonlinear problem-solving capabilities of the SVR, thereby enhancing prediction accuracy.

(3) The number of components extracted by VMD was considered, and ablation experiments were conducted to compare the model’s predictive performance. This paper validated the effectiveness on a landslide dataset, demonstrating that VMD outperforms other sequence decomposition algorithms in effectively decomposing sequences. Establishing a VMD-LSTM-SVR model for the landslide displacement dataset resulted in an increase in R² to 0.8487 and a decrease in RMSE to 0.0328 compared to other models, thereby more accurately reflecting the landslide state. However, due to the lack of relevant devices and experimental equipment, it was not possible to determine the failure threshold of landslide displacement in practical use and thus assess the landslide state. Therefore, how to effectively select failure thresholds and mine more effective features based on landslide displacement characteristics will be the primary research issues in the field of landslide displacement prediction in the future.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

NW: Writing – original draft, Methodology. MW: Project administration, Writing – review and editing. JZ: Funding acquisition, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by Excellent Science and Technology Innovation Team in Jiangsu Province’s Universities, Research and Application of Industrial Safety Environment Technology and Equipment (BY20230482); Vice President of Science and Technology of Jiangsu Province (1781). Teaching Reform Project of Yangzhou Vocational and Technical University (2025XJJG04).

Acknowledgments

The authors would like to thank the Department of Surveying and Mapping of Hubei Province for providing relevant data.

Conflict of interest

Author MW was employed by Jiangsu Province Engineering Investigation and Research Institute Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alabi, T. M., Aghimien, E. I., Agbajor, F. D., Yang, Z., Lu, L., Adeoye, A. R., et al. (2022). A review on the integrated optimization techniques and machine learning approaches for modeling, prediction, and decision making on integrated energy systems. Renew. Energy 194, 822–849. doi:10.1016/j.renene.2022.05.123

CrossRef Full Text | Google Scholar

Barman, J., Ali, S. S., Biswas, B., and Das, J. (2023). Application of index of entropy and geospatial techniques for landslide prediction in lunglei district, Mizoram, India. Nat. Hazard. Res. 3 (3), 508–521. doi:10.1016/j.nhres.2023.06.006

CrossRef Full Text | Google Scholar

Buia, D. T., Tsangaratos, P., Nguyen, V. T., Liem, N. V., and Trinh, P. T. (2020). Comparing the prediction performance of a deep learning neural network model with conventional machine learning models in landslide susceptibility assessment. Catena 188, 104426. doi:10.1016/j.catena.2019.104426

CrossRef Full Text | Google Scholar

Casagli, N., Intrieri, E., Tofani, V., Gigli, G., and Raspini, F. (2023). Landslide detection, monitoring and prediction with remote-sensing techniques. Nat. Rev. Earth and Environ. 4 (1), 51–64. doi:10.1038/s43017-022-00373-x

CrossRef Full Text | Google Scholar

Cervantes, J., Garcia-Lamont, F., Rodríguez-Mazahua, L., and Lopez, A. (2020). A comprehensive survey on support vector machine classification: applications, challenges and trends. Neurocomputing 408, 189–215. doi:10.1016/j.neucom.2019.10.118

CrossRef Full Text | Google Scholar

Chang, Z., Du, Z., Zhang, F., Huang, F., Chen, J., Li, W., et al. (2020). Landslide susceptibility prediction based on remote sensing images and GIS: comparisons of supervised and unsupervised machine learning models. Remote Sens. 12 (3), 502. doi:10.3390/rs12030502

CrossRef Full Text | Google Scholar

Dai, F., Zhu, W., Ren, M., Guan, K., Zhang, P., and Liu, F. (2023). Landslide displacement prediction based on spatio-temporal association rule mining between target case and similar cases. Stoch. Environ. Res. Risk Assess. 37 (11), 4229–4247. doi:10.1007/s00477-023-02504-2

CrossRef Full Text | Google Scholar

Di Napoli, M., Carotenuto, F., Cevasco, A., Confuorto, P., Di Martire, D., Firpo, M., et al. (2020). Machine learning ensemble modelling as a tool to improve landslide susceptibility mapping reliability. Landslides 17 (8), 1897–1914. doi:10.1007/s10346-020-01392-9

CrossRef Full Text | Google Scholar

Dong, A., Dou, J., Fu, Y., Zhang, R., and Xing, K. (2023). Unraveling the evolution of landslide susceptibility: a systematic review of 30-years of strategic themes and trends. Geocarto Int. 38 (1), 2256308. doi:10.1080/10106049.2023.2256308

CrossRef Full Text | Google Scholar

Dou, J., Xiang, Z., Xu, Q., Zheng, P., Wang, X., Su, A., et al. (2023). Application and development trend of machine learning in landslide intelligent disaster prevention and mitigation. Earth Sci. 48 (5), 1657–1674. doi:10.3799/dqkx.2022.419

CrossRef Full Text | Google Scholar

Dou, J., Yunus, A. P., Bui, D. T., Merghadi, A., and Sahana, M. (2019). Assessment of advanced random forest and decision tree algorithms for modeling rainfall-induced landslide susceptibility in the izu-oshima volcanic island. Jpn. Sci. Total Environ. 662, 332–346. doi:10.1016/j.scitotenv.2019.01.221

CrossRef Full Text | Google Scholar

Dou, J., Yunus, A. P., Merghadi, A., Shirzadi, A., Nguyen, H., Hussain, Y., et al. (2020). Different sampling strategies for predicting landslide susceptibilities are deemed less consequential with deep learning. Sci. Total Environ. 720, 137320. doi:10.1016/j.scitotenv.2020.137320

PubMed Abstract | CrossRef Full Text | Google Scholar

Feng, W. Q., Mousavi, Z., Farhadi, M., Bayat, M., Ettefagh, M. M., Varahram, S., et al. (2025). A hybrid wavelet-deep learning approach for vibration-based damage detection in monopile offshore structures considering soil interaction. J. Civ. Struct. Health Monit. 15 (2), 417–444. doi:10.1007/s13349-024-00876-9

CrossRef Full Text | Google Scholar

Hong, H., Tsangaratos, P., Ilia, I., Loupasakis, C., and Wang, Y. (2020). Introducing a novel multi-layer perceptron network based on stochastic gradient descent optimized by a meta-heuristic algorithm for landslide susceptibility mapping. Sci. Total Environ. 742, 140549. doi:10.1016/j.scitotenv.2020.140549

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, X., Li, B., Yin, J., Shi, Y., Song, B., Pang, D., et al. (2025). Utilizing GNSS data and NRBO-VMD-NRBO-transformer for accurate settlement prediction in nanshan, xining. Nat. Hazards. doi:10.1007/s11069-025-07410-0

CrossRef Full Text | Google Scholar

Huang, F., Cao, Z., Guo, J., Jiang, S., Li, S., and Guo, Z. (2020a). Comparisons of heuristic, general statistical and machine learning models for landslide susceptibility prediction and mapping. Catena 191, 104580. doi:10.1016/j.catena.2020.104580

CrossRef Full Text | Google Scholar

Huang, F., Cao, Z., Jiang, S., Zhou, C., Huang, J., and Guo, Z. (2020c). Landslide susceptibility prediction based on a semi-supervised multiple-layer perceptron model. Landslides 17 (12), 2919–2930. doi:10.1007/s10346-020-01473-9

CrossRef Full Text | Google Scholar

Huang, F., Huang, J., Jiang, S., and Zhou, C. (2017). Landslide displacement prediction based on multivariate chaotic model and extreme learning machine. Eng. Geol. 218, 173–186. doi:10.1016/j.enggeo.2017.01.016

CrossRef Full Text | Google Scholar

Huang, F., Zhang, J., Zhou, C., Wang, Y., Huang, J., and Zhu, L. (2020b). A deep learning algorithm using a fully connected sparse autoencoder neural network for landslide susceptibility prediction. Landslides 17 (1), 217–229. doi:10.1007/s10346-019-01274-9

CrossRef Full Text | Google Scholar

Huang, F., Zhou, Y., Jiang, S., Huang, J., Chang, Z., and Chen, J. (2021). Uncertainty study of landslide susceptibility prediction considering the different attribute interval numbers of environmental factors and different data-based models. Catena 202, 105250. doi:10.1016/j.catena.2021.105250

CrossRef Full Text | Google Scholar

Manibardo, E. L., Lana, I., and Ser, J. D. (2022). Deep learning for road traffic forecasting: does it make a difference? IEEE Trans. Intell. Transp. Syst. 23 (7), 6164–6188. doi:10.1109/tits.2021.3083957

CrossRef Full Text | Google Scholar

Min, M., Bai, C., Guo, J., Sun, F., Liu, C., Wang, F., et al. (2019). Estimating summertime precipitation from Himawari-8 and global forecast system based on machine learning. IEEE Trans. Geosci. Remote Sens. 57 (5), 2557–2570. doi:10.1109/tgrs.2018.2874950

CrossRef Full Text | Google Scholar

Mousavi, Z., Bayat, M., Yang, J., and Feng, W. Q. (2024). Evaluation of empirical and machine learning models for predicting shear wave velocity of granular soils based on laboratory element tests. Soil Dyn. Earthq. Eng. 183, 108805. doi:10.1016/j.soildyn.2024.108805

CrossRef Full Text | Google Scholar

Naemitabar, M., and Asadi, M. Z. (2021). Landslide zonation and assessment of farizi watershed in northeastern Iran using data mining techniques. Nat. Hazard. 108 (3), 2423–2453.

Google Scholar

Praveen, M., Dekka, S., Sai, D. M., Chennamsetty, D. P., and Chinta, D. P. (2025). Financial time series forecasting: a comprehensive review of signal processing and optimization-driven intelligent models. Comput. Econ., 1–27. doi:10.1007/s10614-025-10899-z

CrossRef Full Text | Google Scholar

Rodrigues, S. G., Silva, M. M., and Alencar, M. H. (2021). A proposal for an approach to mapping susceptibility to landslides using natural language processing and machine learning. Landslides 18 (7), 2515–2529. doi:10.1007/s10346-021-01643-3

CrossRef Full Text | Google Scholar

Saito, M. (1969). Research on forecasting the time of occurrence of slope failure. Railw. Tech. Res. Inst. Q. Rep. 17 (2), 29–38.

Google Scholar

Scherzer, S., Lujala, P., and Rød, J. K. (2019). A community resilience index for Norway: an adaptation of the baseline resilience indicators for communities (BRIC). Int. J. Disaster Risk Reduct. 36, 101107. doi:10.1016/j.ijdrr.2019.101107

CrossRef Full Text | Google Scholar

Smith, H. G., Spiekermann, R., Betts, H., and Neverman, A. J. (2021). Comparing methods of landslide data acquisition and susceptibility modelling: examples from New Zealand. Geomorphology 381, 107660. doi:10.1016/j.geomorph.2021.107660

CrossRef Full Text | Google Scholar

Steger, S., Mair, V., Kofler, C., Pittore, M., Zebisch, M., and Schneiderbauer, S. (2021). Correlation does not imply geomorphic causation in data-driven landslide susceptibility modelling—Benefits of exploring landslide data collection effects. Sci. Total Environ. 776, 145935. doi:10.1016/j.scitotenv.2021.145935

PubMed Abstract | CrossRef Full Text | Google Scholar

Steger, S., Moreno, M., Crespi, A., Luigi Gariano, S., Teresa Brunetti, M., Melillo, M., et al. (2024). Adopting the margin of stability for space–time landslide prediction–A data-driven approach for generating spatial dynamic thresholds. Geosci. Front. 15 (5), 101822. doi:10.1016/j.gsf.2024.101822

CrossRef Full Text | Google Scholar

Talukdar, S., Singha, P., Mahato, S., Pal, S., Liou, Y. A., Rahman, A., et al. (2020). Land-use land-cover classification by machine learning classifiers for satellite observations—A review. Remote Sens. 12 (7), 1135. doi:10.3390/rs12071135

CrossRef Full Text | Google Scholar

Yang, B. B., Yin, K. L., Lacasse, S., and Liu, Z. (2019). Time series analysis and long short-term memory neural network to predict landslide displacement. Landslides 16 (4), 677–694. doi:10.1007/s10346-018-01127-x

CrossRef Full Text | Google Scholar

Yin, G., Luo, J., Niu, F., Lin, Z., and Liu, M. (2021). Machine learning-based thermokarst landslide susceptibility modeling across the permafrost region on the Qinghai-Tibet Plateau. Landslides 18, 2639–2649. doi:10.1007/s10346-021-01669-7

CrossRef Full Text | Google Scholar

Youssef, A. M., Pourghasemi, H. R., Pourtaghi, Z. S., and Alkatheeri, M. (2016). Landslide susceptibility mapping using random forest, boosted regression tree, classification and regression tree, and general linear models and comparison of their performance at wadi tayyah basin, Asir region, Saudi Arabia. Landslides 13 (5), 839–856. doi:10.1007/s10346-015-0614-1

CrossRef Full Text | Google Scholar

Zhang, C., Mousavi, A. A., Masri, S. F., and Gholipour, G. (2024). The state-of-the-art on time-frequency signal processing techniques for high-resolution representation of nonlinear systems in engineering. Arch. Comput. Methods Eng. 32, 785–806. doi:10.1007/s11831-024-10153-z

CrossRef Full Text | Google Scholar

Zhang, L., Shi, B., Zhu, H., Yu, X., Han, H., and Fan, X. (2021). PSO-SVM-based deep displacement prediction of majiagou landslide considering the deformation hysteresis effect. Landslides 18 (1), 179–193. doi:10.1007/s10346-020-01426-2

CrossRef Full Text | Google Scholar

Zhao, Q., Wang, H., Zhou, H., Gan, F., Yao, L., Zhou, Q., et al. (2024). An interpretable and high-precision method for predicting landslide displacement using evolutionary attention mechanism. Nat. Hazards 120, 11943–11967. doi:10.1007/s11069-024-06668-0

CrossRef Full Text | Google Scholar

Zhu, Q., Chen, W., Zeng, Q., Li, Y., and Liu, S. (2025). Step-type landslide displacement prediction method based on VMD-mamba algorithm. Nat. Hazards 121, 9339–9362. doi:10.1007/s11069-025-07172-9

CrossRef Full Text | Google Scholar