- 1Mitrani Department of Desert Ecology, Swiss Institute for Dryland Energy and Environmental Research, Ben-Gurion University of the Negev, Midreshet Ben Gurion, Israel
- 2Department of Environmental Science, Policy, and Management, University of California, Berkeley, Berkeley, CA, United States
- 3School of Mathematical Sciences, University of KwaZulu-Natal, Durban, South Africa
Familiarity with the landscape increases foraging efficiency and safety. Thus, when animals are confronted with a novel environment, either by natural dispersal or translocation, establishing a home range becomes a priority. While the search for a home range carries a cost of functioning in an unfamiliar environment, ceasing the search carries a cost of missed opportunities. Thus, when to establish a home range is essentially a weighted sum of a two-criteria cost-minimization problem. The process is predominantly heuristic, where the animal must decide how to study the environment and, consequently, when to stop searching and establish a home range in a manner that will reduce the cost and maximize or at least satisfice its fitness. These issues fall within the framework of optimal stopping theory. In this paper we review stopping theory and three stopping rules relevant to home range establishment: the best-of-n rule, the threshold rule, and the comparative Bayes rule. We then describe how these rules can be distinguished from movement data, hypothesize when each rule should be practiced, and speculate what and how environmental factors and animal attributes affect the stopping time. We provide a set of stopping-theory-related predictions that are testable within the context of translocation projects and discuss some management implications.
Introduction
For mobile, sentient animals moving through an air-, sea-, or landscape with some level of predictability, knowledge is a major determinant of fitness. This knowledge pertains to where and when resources, threats, and refuges exist, promoting foraging efficiency and consequent fitness. Devoting time to learning comes at the cost of other fitness-related activities, thereby generating an exploration-exploitation dilemma (Berger-Tal et al., 2014). Familiarity with the landscape is therefore a key contributor to fitness because it reduces the necessity for searching and learning, allowing more time to be devoted to exploitation. Consequently, in most species, individuals will tend to establish residency in a given space, referred to as its home range (HR, Spencer, 2012).
Typically, animals venture into an unfamiliar environment during a post-natal dispersal phase, which in some species may be soon after hatching/birth while in others at time of sexual maturation. Occasionally, however, animals may find themselves in a novel environment due to external factors—e.g., translocation or forced abandonment of a former HR. Regardless of the cause, the animal becomes nomadic, searching for a new space in which to establish a HR. The establishment of a HR in unknown space is essentially a heuristic problem: as the animals explores the environment it accumulates information based on which, at some point, it should transition from a nomadic phase to a residential phase. During the nomadic phase a relatively high proportion of the individual's time needs to be devoted to exploration, while in a residential state a much greater proportion of its time can be devoted to resource exploitation.
The decision to switch phases should be based on information accumulated during exploration and previous past-experience. The timing of the transition between the two phases is important. On the one hand continued searching in an unknown landscape has considerable costs in terms of finding resources, exposure to risk, intra-specific competition (forgoing a potential HR that is then occupied by a conspecific), and even postponed reproduction. On the other, stopping the search and establishing a HR carries a cost of missed opportunities—i.e., missing out on a better HR had the search continued. Thus, the establishment of a HR is essentially a stopping problem (Hill, 2009), where an individual attempts to maximize or, at least, satisfice its fitness (i.e., additional HR improvements do not actually improve its fitness) by deciding how to search and when to stop searching and establish a HR.
Successful translocations offer a unique opportunity to study ecological processes such as range expansion, density dependence, and learning behavior (Sarrazin and Barbault, 1996). Specifically, translocated animals are released into a novel environment that in many instances is vacant (reintroductions) or nearly vacant (restocking) from conspecifics. The translocated individuals must then explore the landscape and eventually establish a HR. Studying the movement and behavior of these individuals can elucidate the stopping rules that are used to establish a HR and the conditions that impact the timing of stopping. These conditions include individual animal attributes, landscape characteristics, and population density effects resulting from the growth of the newly established population.
In this paper, we briefly review stopping theory and relevant rules and present a general model for the case of an animal searching for a place to establish a HR in an unknown environment. We then discuss various key factors that should, in theory, impact the stopping decision in a predictable manner and delineate potential scenarios where these predictions can be tested as a part of translocation projects.
Stopping Theory
Optimal stopping theory addresses the problem of when to stop a current activity and take a particular action so that expected net rewards are maximized. As such, it underpins many animal-decision-making processes. Thus, a number of behavioral transitions in animals can be studied and explained within the framework of optimal stopping theory. Examples include HR establishment, optimal foraging and patch-use theory (when to leave a patch), mate choice (particularly females deciding when to accept a particular suitor), and predation procedures (e.g., when to give up a chase). The decisions are typically based on experience and conditions (both the animal's and the environment's) from which the expected future return is estimated and the costs and benefits of executing or forgoing the action at a given time are assessed. However, while the costs and benefits of the current activity are mostly experienced at present, the costs and benefits of stopping are a projection into the future and involve levels of uncertainty that may be reduced with additional knowledge acquired through continued search. Thus, a key issue in many stopping behaviors is the search time needed to infer a reliable assessment of the long-term cost and benefits of continuing the current activity vs. stopping and establishing a HR.
Numerous formulations of stopping theory exist (e.g., Ferguson, 2006 Chapter 1), most focused on non-ecological problems. Depending on the type of data and uncertainties, several have varying relevance to ecology and can help typify the specific case of establishing a HR in a novel environment. Common examples are:
• Marriage/secretary problem (aka best choice problem). The object of this problem is to select the best (according to an a priori defined criterion) of a set of n objects (e.g., potential spouses/interviewees). The rule is that these objects must be assessed in some arbitrary sequence, with a decision on whether to accept the object and stop the process, or to move onto the next object being required to be made after each assessment (so there is no going back). Theory demonstrates that the optimal procedure is to peruse the first n/e (~0.368n) objects and then select the first object after this that is better than every object assessed thus far. This procedure selects the best object 37% of the time, though could infrequently result in the last object being a forced selection, no matter its value. A parallel ecological example would be mate choice at a lek where a given number of males (n) compose the lek and a female must evaluate the males and select one to mate with. The optimum, in terms of cost (time invested in evaluation) and benefit (quality of the male) would be to evaluate a 0.368 proportion of the males and chose the next one that is better than all those previously evaluated.
• House Selling problem (aka job search problem). An owner selling a house receives one offer per unit time for all time into the future (infinite horizon). However, keeping the house on the market has a cost (advertising, mortgage repayments, lost investment opportunities). Once an offer is received a decision must be made whether to accept or keep searching. A rejected offer cannot be reconsidered. The longer one waits, the higher the cost, but the opportunity to get a better offer than the one rejected exists. If one expects the value of an offer at time t = 0,1,2,…, denoted by Xt, is known to be randomly distributed on [0,1], and the cost per unit time is c <1/2, then the optimal solution is to choose Xt the first time it exceeds (1-(2c)1/2). In limited sense, this scenario can be applied to a sit-and-wait predator deciding whether to forgo a small prey and wait while its hunger increases for a larger prey to arrive or to consume the current prey and then set out to find a new ambush spot.
• Job Search problem. This is a generalization of the house selling problem to one that involves several factors that need to be considered each time (e.g., salary, commuting distance, work environment) where some of these parameters may not be easily quantifiable. The optimal solution to this problem varies with n (Mazalov and Konovalchikova, 2015). In an ecological context, predators may confront a similar problem when deciding whether to chase a particular quarry (e.g., size of prey, speed of prey, distance to prey, features of the terrain) or continue to search for a better quarry.
• The Parking problem. An individual wants to find the closest parking spot to a particular location (i.e., the value of the spot is its proximity to this location). There are several variants of this problem, one of ecological interest being that if an individual cannot find a parking spot close the location, a revisit to those further away may reveal, with some increasing probability over time, that these previously vacant spots have now become occupied. Solutions for particular formulations of this problem are found in Tamari (1982). In ecology, this problem has similarities to post-natal dispersal in territorial species where available vacant territories are quickly occupied by conspecifics and on a first-come-first-serve basis (i.e., scramble competition).
Although not a necessity in stopping theory, in the above examples the current activity is a search process. Thus, stopping theory is strongly linked to search theory. However, search theory is a wider concept despite this term often being interchangeably used with stopping theory (Lippman and McCall, 2001), and even being specifically applied to the Job Search problem.
In ecology, search theory is predominantly associated with movement patterns within the context of foraging theory (Bartumeus and Catalan, 2009) and typically is not associated with stopping theory. However, although not referred to by name, stopping theory is commonly used in behavioral ecology. Patch-use, in particular, is noteworthy. Here, an individual foraging in a patch slowly exhausts available resources and the effort of finding those remaining increases with time. When the costs of continued foraging in the patch equal or exceed the benefits gained from continued foraging, individuals should cease feeding in the patch and abandon it. The resource density in the patch at this stopping point is termed the giving-up-density (i.e., the amount of food left in a patch at the point when the forager leaves it; Brown and Kotler, 2004; Makin et al., 2020). In this formulation of stopping theory, the search area is restricted, the number of objects (n) is fixed (finite horizon) but unknown, and the objects sought are removed (consumed) from the available pool, so search effort increases with time.
The Home Range Establishment Problem
As with the particular problems discussed above, the current activity of individuals in the HR Establishment Problem is a search process, but it differs in presenting a more complex scenario. The HR Establishment Problem is similar to the Job Search problem in that n is not fixed (the animals may, in theory, keep searching indefinitely), several factors are involved, and evaluating the quality of objects is a complex and imperfect process. However, it also bares resemblance to the Parking Problem in that the competition may be on a first-come-first-served basis. Further, the search associated with HR establishment bears a high cost due to elevated risk of predation and inefficient foraging resulting from lack of familiarity with the landscape. In the case of translocations (as opposed to natal dispersal) there is another key difference. This is the lack of residence from which to carry out the search and no familiarity with the immediate surroundings, although habituation within a local enclosure prior to release may enable some familiarity. Hence, we view HR Establishment as a unique stopping problem with unique attributes, resulting hypotheses, and testable predictions. Empirical studies addressing these issues can provide insight into the process and may have management implications.
Stopping Rules in Home Range Establishment
Various rules for assessment and decision making in stopping problems have been proposed. Some may be applicable only to specific problems. Their efficacy may vary depending on the specific conditions and attributes of the decision maker and the environment in which the problem is set. The following three appear particularly relevant to HR establishment (Luttbeg, 2002):
• Best-of-n rule: The animal should assess n options and can select the best of these. In practice this means being able to return to any of the formerly assessed options. The optimal value of n depends on the cost of the search and the variance in the quality of options.
• Threshold rule: Based on experience (a set of n previous HR assessments), the individual sets a threshold, and chooses the next encounter that exceeds this threshold. In practice this is best applied under a no return situation that precludes a best-of-n rule. The secretary problem is a specific case of the threshold rule fixed a priori at 0.368n.
• Comparative Bayes rule: The information obtained on each option is assumed to be incomplete and the animal, after a relatively cursory study of n options, will return to gather further information on the better ones and then re-evaluate. This tactic reduces the effort involved in the initial exploration and if revisiting previously investigated options for re-evaluation is possible, is superior to the above rules (Luttbeg, 2002).
The specific stopping rule and timing for optimizing or satisficing HR establishment are expected to depend on the species characteristics, environmental conditions, and individual-animal attributes and perceptions. Two basic questions of ecological interest can be formulated regarding HR establishment: Q1. What conditions favor the use of which specific stopping rule? Q2. When to stop and establish a HR—or, more pointedly, how are varying environmental conditions, animal traits and experience expected to influence the time to HR establishment? From these questions we formulate specific predictions that are testable in the field. We note here that we consider the stopping time as the point at which an animal sets up its initial HR and does not include partial shifts and improvements of the HR that occur after settling (Maor-Cohen et al., 2021).
Q1. What Conditions Favor the Use of Which Specific Stopping Rule?
The future fitness associated with the various stopping rules depends largely on whether random re-encounters are possible (i.e., whether there is a finite set of options) and whether animals can resample previously encountered options (Luttbeg, 2002). These issues underpin potential differences between HR establishment under natural conditions and planned translocations. Seeking to establish a new HR under natural conditions is predominantly a phenomenon associated with post-natal dispersal and, to a lesser extent, catastrophic events such as fire. In both cases the availability of vacant HRs is expected to be limited, especially in vertebrates that tend to be “K-selected” and which, unless reduced by stochastic environmental conditions or heavy hunting, their population is near carrying capacity (McCullough, 1992). Thus, in contrast to the typical translocation, animals dispersing on their own initiative within relatively undisturbed populations are expected to confront a landscape nearly saturated with conspecifics and fewer opportunities for HR establishment. For example, in large territorial-predators adult survival is expected to be high, and the dynamics are dictated mostly by reproductive success and post-natal survival (Kapota and Saltz, 2018) so vacant territories are expected to be rare. Further, given that post-natal dispersal occurs within a narrow window of time, the landscape during the dispersal season will typically be flooded with individuals seeking to establish a HR (e.g., Hawlena et al., 2010). Consequently, the probability of returning to a previously evaluated area and finding that it had not yet been occupied is low. Hence, post-natal dispersers in such species are expected to rely on the threshold rule (e.g., Macdonald and Bacon, 1982). Although less restrictive, for individuals of non-territorial, semi-social species (such as many ungulates), establishing a permanent HR that likely overlaps with conspecifics, the conspecific saturation of the landscape during dispersal season is still expected to be a major factor.
By contrast, in “r-selected” species or, following a population crash, in species typified by slow growth rates, post-natal dispersers will find themselves in a relatively vacant environment where the probability is high of returning to previously explored sites and finding them still vacant. In such cases, the best-of-n rule or Comparative Bayes rule will be the better options. Further, the best of these two options will depend on whether the quality of the better sites can be reliably distinguished based on the initial exploration (thereby favoring the best-of-n rule) or further exploration is required (thereby favoring the Comparative Bayes rule).
The presence of conspecifics in sites targeted for translocation depends on the time, place, and purpose of translocations. For example, in reintroductions, individuals in the first wave of release will be confronted with a vacant environment, while later boost releases will experience an increasingly occupied landscape after successful establishment of initial releases. Thus, in reintroductions we may expect the stopping rule to shift from a best-of-n rule or comparative Bayes rule in early releases to a threshold rule in later releases.
Which rule is being practiced by specific individuals can be determined using high resolution movement tracks from GPS platforms. Specifically, the different rules can be distinguished by analyzing the movement trajectories of individual animals during the search phase and determining whether they revisited one or several sites before HR establishment and whether these revisits were associated with an area-restricted-search (Kapota et al., 2017). For example, individuals that: (i) settled in the last explored area without returning to any of the previous sites would be indicative of the Threshold rule; (ii) explored a set of potential sites and returning to the best one would be indicative of Best-of-n rule); (iii) settled after repeated returns to several sites would suggest the possible application of a Comparative Bayes rule.
Dispersal patterns will also be impacted by the starting conditions. Post-natal dispersers benefit from having a “home-base” (the maternal HR) from which to carry out pre-dispersal exploration (Debeffe et al., 2012) while benefiting from the safety offered by the maternal HR, in addition to acquiring a general understanding of the surrounding habitat characteristics from the maternal HR characteristics. This enables the animals to gain knowledge of the surrounding matrix from the safety of the maternal HR and return to it following exploratory foray in different directions—forming a start-like movement trajectory.
In translocation, animals can be released using an interim stage of adjustment by confining them to a habituation enclosure at the site of release (soft release) or released immediately on site (hard release). Soft releases enable individuals to gain some familiarity with the habitat and immediate surroundings. If soft releases provides some level of security, individuals (especially those belonging to species subject to predation) may view the release location as a safe “home-base” from which to carry out exploration forays similar to post-natal dispersal. On the other hand, hard-release individuals will not be familiar with the release site and are expected to move away immediately in search of a HR. Studies have shown that in soft-releases individuals tend to establish a HR closer to the release site (e.g., Attum and Cutshall, 2015). Regardless of the type of release, the criteria for assessing what stopping rule is being practiced still hold. Although data for determining which stopping rule is practiced clearly exist, in numerous previously reported translocation studies these ideas remain to be tested.
Q2. When to Stop Searching and Establish a Home Range?
The optimal stopping time (i.e., the point at which the animal decides to establish a HR) is the outcome of two cost functions: (i) the cost of continuing the search (not stopping); and, (ii) the missed opportunity costs (MOC, discussed more fully below) associated with stopping the search. This holds for all three rules. The costs associated with continued search are those resulting from movement through an unfamiliar environment, such as elevated risk, difficulty in finding resources, time devoted to learning the landscape, and forgoing breeding opportunities. Generally, these costs are expected to be constant over time, and the accumulated costs, therefore, are expected to increase linearly with time from the onset of the search.
MOC are those associated with foregone alternatives when stopping the search. MOC can only be assessed by the animal through exploring the novel landscape and forming some database of availability. As information is accumulated, the relative contribution of each additional bit of information declines so the MOC function is expected to be a positive, monotonically decreasing function of search time (e.g., a negative exponential function). These costs are also reduced with competition because the probability of realizing the benefits of the forgone alternatives declines as they become occupied by conspecifics. The optimal stopping time is, therefore, the point at which a weighted sum of search and missed-opportunity costs are minimized (Figure 1; the two costs have been reduced to the same units so they are given the same weightings).
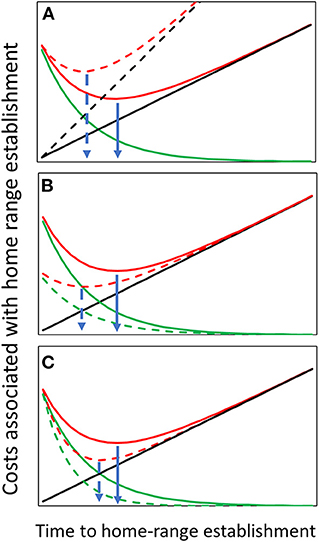
Figure 1. The two costs involved in establishing a home range: search costs in black and missed opportunity costs (MOC) in green. Search costs increase with time. MOC increase with the variability of habitat conditions over space and decrease with time as the animal's assessment of space improves. The sum of both costs is in red, and the optimal stopping time is when this sum is minimized (indicated by the blue arrows). Each of the three sub-figures (A–C) compares the stopping time between two formulations of one of the cost functions. (A) If search costs increase (black dashed line) optimal stopping time is reduced. (B) If habitat variability over space is reduced (green dashed line) stopping time is reduced. (C) If competition is high (i.e., the better areas become unavailable) the variance in potential habitats declines reducing optimal stopping time.
The exact formulation of cost-of-search and MOC functions depends on conditions, including the expected quality of the environment and its variance in terms of food and shelter, presence of conspecifics, predation risk, and individual animal attributes such as age, body conditions, gender, and behavioral type. Based on these, numerous hypotheses can be formulated. Translocations, and specifically reintroductions, offer an opportunity to test specific hypothesis derived predictions concerning the HR Establishment problem within the stopping theory framework using comparative designs:
• Quality of the environment and risk of predation. As quality of the environment decreases or risk of predation increases, the cost of continued search increases so the function becomes steeper, and the optimal stopping point is predicted to be earlier (Figure 1A). This can be tested by comparing translocations between habitat types or in the same area between seasons.
• Variance in habitat quality over space. As the variance of the quality of potential HRs over space declines, the MOC decline (Figure 1B) and expected stopping time is shorter.
• Presence of conspecifics. This depends on the social structure of the species. In territorial species (either solitary of group), as the presence of conspecifics increases, fewer opportunities become available, the better patches are expected to be unavailable causing the mean value of a potential HR and the variance around that mean to decline. Thus, as we see in Figure 1C, time to stopping shortens. Further, the probability of finding a previously visited option still unoccupied declines, so using the Threshold Rule becomes the better option. If this is combined with the decline in the variance of available HRs and lower MOC, stopping times should become particularly short. In semi-social animals that are non-territorial, the shorter stopping time may be confounded because the presence of resident conspecifics may also be used as a cue to habitat quality, potential mates, and a safer and quicker way to study the habitat by following them. Thus, in translocation projects involving multiple releases, individuals from later releases are expected to establish a HR earlier (Dolev et al., 2002). This also points to the difficulty in evaluating this response under conditions where the landscape is nearly saturated and stochastic processes in the form of the chance of finding a vacant spot overwhelm the process. As a result, few individuals may be lucky to establish a HR early on while others will have to perform a long-distance search (Lutz et al., 2015), thereby making the variance on the stopping time too large to draw any conclusions.
• Body condition. Individuals in better condition (larger/heavier) have reduced risk of starvation and depredation. They thus are expected to devote more time to search and will travel farther in an effort to find a better HR. This will result in a later stopping time (Debeffe et al., 2012). Differences will be similar to those depicted in Figure 1A but will be evident among individuals in the same translocation having different body condition (as determined prior to release by one of existing indices of body condition; see Servello et al., 2005).
• Behavioral types, sex, and age. Within a species, individuals vary in their behavior according to age, sex, and behavioral types. These behavioral tendencies—whether active, bold, exploratory, sociable, or aggressive—have been shown to be relatively consistent within individuals over a given time period and in different contexts (Réale et al., 2007). There generally appears to be a linkage between these traits—more active individuals tend to be more explorative, more aggressive, and bolder. For example, in roe deer (Capreolus capreolus) dispersers explore more than philopatric individuals (Debeffe et al., 2013), and bold, more active amphibians tend to explore more and travel farther than their counterparts (Kelleher et al., 2018). The bolder behavioral types are expected to perceive the novel environment as less threatening and evidently assume better opportunities (i.e., greater MOC). Thus, bold individuals are expected to have a later stopping times. Younger animals with greater life expectancy also have higher MOCs, as do males in polygynous species and, thus, are also expected to have delayed stopping times.
Such studies can provide insight into HR ecology and species-specific behavioral ecology which may also have management implications. Testing these predictions can be done by determining individual-based time-to-settlement analyses using, for example, the distance from the release location (or some other movement parameters) as a function of time. This could be done using a two-segment broken stick regression function that separates the search and HR residency movements (McNicol et al., 2020). The time to establishment of an individual is determined as the point the two segments meet. The time to establishment can then be used as a dependent variable in analyses assessing the impact of the various environmental and individual animal attributes on stopping time.
Management Implications
Translocation projects are typified by a high rate of failure, with the behavior of the released individuals being one of the key determinants of success (Berger-Tal et al., 2020). The process requires individuals to adapt rapidly to a novel environment and go through a behavior-adjustment process termed post-release behavioral modification (PRBM; Berger-Tal and Saltz, 2014). PRBM is dependent not only on objective environmental conditions and animal attributes, but also on how the animal perceives its own condition and surroundings.
The establishment of a HR is a vital step in this process because familiarity with the landscape is an important contributor to an animal's fitness. HR establishment is commonly considered an early indicator of translocation success (Yang et al., 2018; Briers-Louw et al., 2019) and is a parameter frequently assessed in reintroductions. Delayed HR establishment following the initial releases in a reintroduction delays recruitment and decreases survival of the released individuals, thereby slowing the growth of the population and subjecting it to stochasticity-related risk of elimination. Understanding the factors that influence the timing of HR establishment (i.e., stopping time) and validating the aforementioned predictions can help design translocation protocols and achieve better results. Not all factors affecting stopping time are manageable, but several can be manipulated to accelerate HR establishment. These include individual animal attributes such as behavioral types, age, and body condition. They also include release protocols such as timing and methods of release. Notwithstanding, it is important to realize that certain traits that favor early stopping time may also have negative aspects. For example, older animals are expected to show shorter stopping time due to lower MOC, but their life expectancy is shorter (hence the lower MOC). Similarly, release in the low-productivity season may reduce stopping-time; but it may impact the animal's condition and the resulting long-term dynamics of the population.
Individual personality and the tendency to disperse are correlated with bold individuals being more prone to disperse further (Cote et al., 2010), which translates into a later stopping time. More specifically, bold individuals perceive risk as being lower and MOC as being higher. Thus, translocating bolder animals may delay the establishment of a permanent resident population. This, in turn, may weaken propagule pressure and lower the probability of translocation success. Alternatively, translocating timid individuals may result in faster settlement in and around the release site, but continued releases of such individuals in the same location may cause “piling” near the release site. This would occur because the search and MOC costs are evaluated by the animals based on landscape conditions and how they vary over space. An individual released into an area that is locally saturated would be ignorant of the vacant landscape further from the release site. Near the release site the individual would experience few opportunities (vacant spots) with little variance between them (only the poorer spots remain unoccupied). With the perception of few opportunities, stopping-time would be shorter than needs be, resulting in “piling” that may well reduce population performance. It follows that some combination of both types may improve translocation results (Watters and Meehan, 2007). Specifically, varying the ratio of timid and bold individuals in subsequent releases may be optimal if early releases include a greater proportion of timid individuals than later releases. Empirical data, however, are needed to support this hypothesis.
Simulating future population performance can benefit the planning of translocations, specifically in the context of reintroductions (Saltz, 1998; Maor-Cohen et al., 2020). Incorporating animal and environmental attributes that affect the timing of HR establishment into population projection models may aid in deciding the composition of individual attributes and release methods that will maximize future population performance.
The ideas presented herein highlight the importance of post-release monitoring and new research opportunities regarding the impact of various parameters on stopping time because, as we have argued above, stopping times affect individual movement patterns with consequences for population viability. Findings from studies testing the predictions put forth in this paper can later be incorporated into meta-analyses supporting the formulation of hypotheses and the articulation of paradigms that can then be incorporated into translocation protocols.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.
Author Contributions
DS and WG developed the ideas and wrote the paper. All authors contributed to the article and approved the submitted version.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The reviewer DM declared a shared affiliation with one of the authors, DS, to the handling editor at the time of review.
Publisher's Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We thank O. Berger-Tal and two reviewers for constructive criticism.
References
Attum, O., and Cutshall, C. D. (2015). Movement of translocated turtles according to translocation method and habitat structure. Restor. Ecol. 23, 588–594. doi: 10.1111/rec.12233
Bartumeus, F., and Catalan, J. (2009). Optimal search behavior and classic foraging theory. J. Phys. A Math. Theor. 42:434002. doi: 10.1088/1751-8113/42/43/434002
Berger-Tal, O., Blumstein, D. T., and Swaisgood, R. R. (2020). Conservation translocations: a review of common difficulties and promising directions. Anim. Conserv. 23, 121–131. doi: 10.1111/acv.12534
Berger-Tal, O., Nathan, J., Meron, E., and Saltz, D. (2014). The exploration-exploitation dilemma: a multidisciplinary framework. PLoS ONE 9:e95693. doi: 10.1371/journal.pone.0095693
Berger-Tal, O., and Saltz, D. (2014). Using the movement patterns of reintroduced animals to improve reintroduction success. Curr. Zool. 60, 515–526. doi: 10.1093/czoolo/60.4.515
Briers-Louw, W. D., Verschueren, S., and Leslie, A.J. (2019). Big cats return to Majete Wildlife Reserve, Malawi: evaluating reintroduction success. Afr. J. of Wildlife Res. 49, 34–50. doi: 10.3957/056.049.0034
Brown, J. S., and Kotler, B. P. (2004). Hazardous duty pay and theforaging cost of predation. Ecol. Lett. 7, 999–1014. doi: 10.1111/j.1461-0248.2004.00661.x
Cote, J., Clobert, J., Brodin, T., Fogarty, S., and Sih, A. (2010). Personality-dependent dispersal: characterization, ontogeny and consequences for spatially structured populations. Philos. Trans. R. Soc. B 365, 4065–4076. doi: 10.1098/rstb.2010.0176
Debeffe, L., Morellet, N., Cargnelutti, B., Lourtet, B., Bon, R., Gaillard, J.-M., et al. (2012). Condition-dependent natal dispersal in a large herbivore: heavier animals show a greater propensity to disperse and travel further. J. Anim. Ecol. 81, 1327–1337. doi: 10.1111/j.1365-2656.2012.02014.x
Debeffe, L., Morellet, N., Cargnelutti, B., Lourtet, B., Coulon, A., Gaillard, J. M., et al. (2013). Exploration as a key component of natal dispersal: dispersers explore more than philopatric individuals in roe deer. Anim. Behav. 86, 143–151. doi: 10.1016/j.anbehav.2013.05.005
Dolev, A., Saltz, D., Bar-David, S., and Yom-Tov, Y. (2002). The impact of repeated releases on the space-use patterns of reintroduced Persian fallow deer (Dama dama mesopotamica) in Israel. J. Wildlife Manage. 66, 737–746. doi: 10.2307/3803139
Ferguson, T. (2006). “Optimal stopping and applications,” in Electronic Text (Los Angeles, CA: University of California). Available online at: https://www.math.ucla.edu/~tom/Stopping/Contents.html
Hawlena, D., Saltz, D., Abramsky, Z., and Bouskila, A. (2010). Ecological trap for desert lizards caused by anthropogenic changes in habitat structure that favor predator activity. Conserv. Biol. 24, 803–809. doi: 10.1111/j.1523-1739.2010.01477.x
Kapota, D., Dolev, A., and Saltz, D. (2017). Inferring detailed space use from movement paths: a unifying residence-time based framework. Ecol. Evol. 7, 8507–8514. doi: 10.1002/ece3.3321
Kapota, D., and Saltz, D. (2018). Unequal density-dependence between survival and recruitment impacts compensatory dynamics and harvesting effectiveness. J. Wildlife Manage. 82, 1756–1766. doi: 10.1002/jwmg.21509
Kelleher, S. R., Silla, A. J., and Byrne, P. G. (2018). Animal personality and behavioral syndromes in amphibians: a review of the evidence, experimental approaches, and implications for conservation. Behav. Ecol. Sociobiol. 72:79. doi: 10.1007/s00265-018-2493-7
Lippman, S. S., and McCall, J. J. (2001). “Information, economics” in International Encyclopedia of the Social & Behavioral Sciences, eds N. J. Smelser and P. B. Baltes (Amsterdam: Elsevier), 7480–7486.
Luttbeg, B. (2002). Assessing the robustness and optimality of alternative decision rules with varying assumptions. Animal Behavior 63, 805–814. doi: 10.1006/anbe.2001.1979
Lutz, C. L., Diefenbach, D. R., and Rosenberry, C. S. (2015). Population density influences dispersal in female white-tailed deer. J. Mammal. 96, 494–501. doi: 10.1093/jmammal/gyv054
Macdonald, D. W., and Bacon, P. J. (1982). Fox society, contact rate and rabies epizootiology. Comp. Immunol. Microbiol. Infect. Dis. 5, 247–256. doi: 10.1016/0147-9571(82)90045-5
Makin, D. F., Kotler, B. P., Brown, J. S., Garrido, M., and Menezes, J. F. S. (2020). The enemy within: how does a bacterium inhibit the foraging aptitude and risk management behavior of Allenby's Gerbils? Am. Nat. 196, 717–729. doi: 10.1086/711397
Maor-Cohen, M, Shamoon, H., Dolev, A., Reichman, A., Bar David, S., and Saltz, D. (2020). Long-term re-evaluation of spatially explicit models as a means for adaptive wildlife management. Ecol. Appl. 30:e02088. doi: 10.1002/eap.2088
Maor-Cohen, M., Bar-David, S., Dolev, A., Berger-Tal, O., Saltz, D., and Spiegel, O. (2021). Settling in: Reintroduced Persian fallow deer adjust the borders and habitats of their home-range during the first 5 years post release. Front. Conserv. Sci. 2:733703. doi: 10.3389/fcosc.2021.733703
Mazalov, V., and Konovalchikova, E. (2015). The job-search problem with incomplete information. Proc. Comput. Sci. 55, 159–164. doi: 10.1016/j.p rocs.2015.07.025
McCullough, D. R. (1992). “Concepts of large herbivorepopulation dynamics,” in: Wildlife 2001: Populations, eds D. R. McCullough and R. H. Barrett (Essex: Elsevier), 967–984.
McNicol, C. M., Bavin, D., Bearhop, S., Bridges, J., Croose, E., Gill, R., et al. (2020). Postrelease movements and habitat selection of translocated pine martens Martes martes. Ecol. Evol. 10, 5106–5118. doi: 10.1002/ece3.6265
Réale, D., Reader, S. M., Sol, D., McDougall, P. T., and Dingemanse, N. J. (2007). Integrating animal temperament within ecology and evolution. Biol. Rev. 82, 291–318. doi: 10.1111/j.1469-185X.2007.00010.x
Saltz, D. (1998). A long-term systematic approach to reintroductions:the Persian fallow deer and Arabian oryx in Israel. Anim. Conserv. 1, 245–252. doi: 10.1111/j.1469-1795.1998.tb00035.x
Sarrazin, F., and Barbault, B. (1996). Reintroduction: challenges and lessons for basic ecology. Trends Ecol. Evol. 11, 474–478. doi: 10.1016/0169-5347(96)20092-8
Servello, F. A., Hellgren, E. C., and McWilliams, S. R. (2005). “Techniques for wildlife nutritional ecology,” in Techniques for Wildlife Investigations and Management, ed C. E. Braun (Bethesda, MD: The Wildlife Society), 554–577.
Spencer, W. D. (2012). Home ranges and the value of spatial information. J. Mammal. 93, 929–947. doi: 10.1644/12-MAMM-S-061.1
Watters, J. V., and Meehan, C. L. (2007). Different strokes: can managing behavioural types increase post-release success? Appl. Anim. Behav. Sci. 102, 364–379. doi: 10.1016/j.applanim.2006.05.036
Keywords: movement ecology, stopping rule, search theory, behavioral types, translocation, dispersal
Citation: Saltz D and Getz WM (2021) Finding a Home: Stopping Theory and Its Application to Home Range Establishment in a Novel Environment. Front. Conserv. Sci. 2:714580. doi: 10.3389/fcosc.2021.714580
Received: 25 May 2021; Accepted: 10 September 2021;
Published: 18 October 2021.
Edited by:
Anthony J. Giordano, Society for the Preservation of Endangered Carnivores and Their International Ecological Study (SPECIES), United StatesReviewed by:
Douglas Ferguson Makin, Ben-Gurion University of the Negev, IsraelAlison L. Greggor, San Diego Zoo Institute for Conservation Research, United States
Shifra Z. Goldenberg, Smithsonian Institution, United States
Copyright © 2021 Saltz and Getz. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: David Saltz, ZHNhbHR6QGJndS5hYy5pbA==
 David Saltz
David Saltz Wayne M. Getz
Wayne M. Getz