- 1School of Computer and Communication Engineering, University of Science and Technology Beijing, Beijing, China
- 2Shunde Graduate School, University of Science and Technology Beijing, Foshan, China
- 3Beijing Key Laboratory of Knowledge Engineering for Materials Science, Beijing, China
- 4School of Economics and Management, Fuzhou University, Fuzhou, China
- 5School of Information Management and Engineering, Shanghai University of Finance and Economics, Shanghai, China
The dynamic behavior of memristive neural networks (MNNs), including synchronization, effectively keeps the robotic stability against numerous uncertainties from the mimic of the human brain. However, it is challenging to perform projective quasi-synchronization of coupled MNNs with low-consumer control devices. This is partly because complete synchronization is difficult to realize under various projective factors and parameter mismatch. This article aims to investigate projective quasi-synchronization from the perspective of the controller. Here, two approaches are considered to find the event-triggered scheme for lag synchronization of coupled MNNs. In the first approach, the projective quasi-synchronization issue is formulated for coupled MNNs for the first time, where the networks are combined with time-varying delays and uncertainties under the constraints imposed by the frequency of controller updates within limited system communication resources. It is shown that our methods can avoid the Zeno-behavior under the newly determined triggered functions. In the second approach, following classical methods, a novel projective quasi-synchronization criterion that combines the nonlinear property of the memristor and the framework of Lyapunov-Krasovskii functional (LKF) is proposed. Simulation results indicate that the proposed two approaches are useful for coupled MNNs, and they have less control cost for different types of quasi-synchronization.
1. Introduction
Recently, memristive neural networks (MNNs) have attracted much attention because of their widespread use in various fields, such as signal processing, image protection, and robotics (Hong et al., 2020; Yuan et al., 2020). The dynamical behaviors of the MNNs, such as chaos, synchronization, and stability, play a significant role in the above-mentioned applications (Duan et al., 2020; Liu H. et al., 2020). Synchronization is one of the most fundamental dynamic behaviors of MNNs, i.e., the approaching process of all interconnected nodes with different initial states in the systems. Therefore, based on the concept of traditional chaotic behavior, by using the synchronization of the drive-respond MNNs for multi-robot systems, the cooperative control issues of such systems can be redefined as the synchronization or consensus control issues of multi-agent systems (Wang C. et al., 2021). Accordingly, investigating the cooperative control algorithms based on the synchronization of MNNs is important, and numerous synchronization methods have been established to support robotic systems (Duong et al., 2022; Zhang Y. et al., 2022). Therefore, the synchronization of MNNs has innovative significance and prospects for multi-robot systems.
As a universal model of MNNs, coupled MNNs can imitate the human brain more truly than traditional MNNs. Considering this, the synchronization of coupled MNNs should be investigated and applied to the field of secure communication combined with the memristor that can mimic human synapses (Wang et al., 2019; Chen et al., 2021). A plethora of studies have been conducted to improve coupled MNNs for potential applications in image protection (Yuan et al., 2020), social networks (Zhu et al., 2022), pattern recognition, etc. Coupled neural networks have a coupled structure. By using the initial value sensitivity of the memristor, such networks can be applied to the field of image encryption with larger key space and higher security. However, when binary digital is extended to M-nary digital, the problem of faster communication still exists (Chee and Xu, 2006). To address this issue, projective synchronization was first introduced by Mainieri and Rehacek (1999).
In practice, different synchronizations are necessary between drive-response MNNs, especially for secure communication. Regarding the impact of the various projective factors (Chen et al., 2019; Fu et al., 2020; Ding et al., 2022) on different structures of neural networks, many research results have been obtained. Fu et al. (2020) studied the projective synchronization for fuzzy MNNs under a pinning control scheme. The fix-time projective synchronization with discrete-time delay was investigated by Chen et al. (2019). Considering the lag factor and the fractional structure of neural networks, the lag projective synchronization was studied by Ding et al. (2022). However, parameter mismatch is unavoidable in the synchronization mechanism. For time-varying delayed neural networks with parameter mismatch, projective synchronization was studied by Kumar et al. (2019). In Guo et al. (2020), the parameter-mismatch complex-valued neural networks realize quasi-projective synchronization with a linear feedback controller. Later, in Yang et al. (2021), the impulsive effect on weak projective synchronization was investigated for parameter-mismatch MNNs. However, the above studies did not consider uncertainty, and different models should be described to adapt to the complex situation for the practical requirements. Therefore, it is crucial to introduce time-varying delays and uncertainties in the modeling (Li et al., 2021; Rajchakit and Sriraman, 2021; Wu and Huang, 2022). This has inspired the authors to develop a less-conservative model to explore the synchronization of coupled MNNs.
Compared with complete synchronization, the error of synchronization should be allowed within a reasonable range for the robotic system, while keeping more operation resilience, and has been widely devoted to many practical applications, including underactuated robotic systems, underwater vehicles, and wheeled robots (Tang et al., 2016; Huang et al., 2018; Chen and Shan, 2019; Yao et al., 2020). Therefore, the investigation of quasi-synchronization is significant and necessary in theory and application. In Chen W. et al. (2022), the quasi-synchronization of a coupled neural network with fractional-order and time-varying delays was studied. Based on Halanay inequality and matrix measure techniques, quasi stability of inertial-delayed MNNs was discussed and implemented in Xin et al. (2022). In Jin et al. (2022), sufficient criteria of uncertain Lur'e networks were derived to guarantee the quasi-synchronization between dynamical systems. In Shi et al. (2022), considering the coupled heterogeneous harmonic oscillators, an event-triggered scheme was developed to ensure the quasi-bipartite synchronization under an undirected communication topology. In Zhang R. et al. (2022), under deception attacks, the time-space sampled-data control scheme was proposed to guarantee the quasi-synchronization for NNs having reaction-diffusion. However, from the perspective of engineering applications, most robotic systems are coupled systems with strong couplings among the master and slave states, therefore, the traditional control method in such a complex environment will lead to more energy consumption. Therefore, how to achieve a better quasi-synchronization effect in an energy-saving manner is still challenging.
Regarding this problem, an event-triggered scheme has been proposed to reduce computational costs under limited communication resources. For this scheme, the controller will not be updated until a certain triggered condition is satisfied. That is, the triggered function is the key to the event-triggered scheme. Apparently, a reasonable event-triggered scheme can realize synchronization and task execution with low energy consumption. In Zhu and Bao (2022), an event-triggered controller was introduced to explore the synchronization issue of coupled MNNs. In Cheng (2022), for multi-agent systems, an event-triggered method was designed to realize the output synchronization and the Zeno behavior was avoided effectively. In Li et al. (2022), two event-triggered impulsive control methods were proposed, and sufficient criteria were formulated to guarantee the globally exponential stability of impulsive systems. Till now, several effective event-triggering schemes for quasi-synchronization have been investigated by Zhou and Zeng (2019), Yan et al. (2020), and Hu et al. (2022). In Hu et al. (2022), for quasi-synchronization, an event-triggered communication mechanism under the switching topology was designed for complex NNs. Then, the hybrid event-triggered scheme was investigated to solve the quasi-synchronization problem for delayed MNNs with a novel threshold function (Zhou and Zeng, 2019; Yan et al., 2020). The above discussion indicates that the event-triggered scheme can ensure the controller to update if the variation of error exceeds the arbitrary threshold. Therefore, it is a challenging but significant issue to define event-triggered conditions including the projective factor, uncertainties, and parameter mismatch.
This article proposed an event-triggered scheme to achieve projective quasi-synchronization for coupled MNNs with time-varying delays and uncertainties. The novelties of this article include:
1. Different from general coupled MNNs, the time-varying uncertainties are considered by the proposed model, which is a type of uncertain switching system. Meanwhile, the definition of projective quasi-synchronization is first proposed based on such a system.
2. To effectively reduce energy consumption, the projective factor and time-varying uncertainties are introduced into the arbitrary triggered function of an event-triggered scheme to further extend the time span and decrease the control cost.
3. The projective quasi-synchronization criteria are formulated by designing a novel time-dependent and piecewise LKF. Meanwhile, different types of quasi-synchronization are illustrated, and an explicit error bound is provided. Besides, the Zeno behavior can be eliminated naturally.
For the rest of this article, Section 2 presents the model of coupled MNNs and the involved definitions, assumptions, as well as lemmas. Then, in Section 3, the theoretical analysis results are given, including a theorem and two corollaries. To validate the main results, two numerical examples are introduced in Section 4. Section 5 concludes the whole study.
2. Preliminaries of the neural networks model
2.1. Coupled MNNs model
Regard a class of delayed MNNs described as follows
where xl(t) shows the voltage of the capacitor cl; the memristance of memristor between the feedback function fm(xm(t)) and xl(t) is illustrated as 𝕄flm; then, ℕflm denotes the memristance between the feedback function fm(xm(t − τ(t))) and xl(t). ℜl is the resistor, and Il(t) is an external bias or input. Besides, sgnlm = 1 for l ≠ m and sgnlm = −1 for l = m.
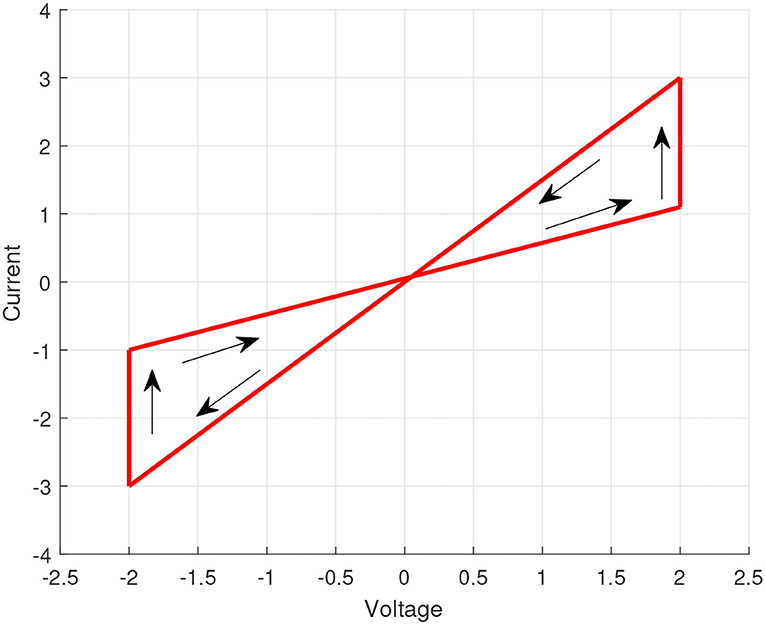
Simplifying the mathematical model of the memristor is helpful to obtain the pinched hysteresis feature, so we select a surrogate model as shown in Figure 1.
Then, the state formula of MNNs with time-varying delays and uncertainties is shown in Equation (1).
where fm(xm(t)) and fm(xm(t − τ(t))) are the neural feedback functions; Δalm(t) and Δblm(t − τ(t)) are the time-varying uncertainties that satisfy |Δalm(t)| ≤ alm and |Δblm(t − τ(t))| ≤ blm; xl(t) is the state of the l − th neuron, and τ(t) is the time-varying delay that meets 0 ≤ τ(t) ≤ τ. dl(xl(t)) is the lth neuron self-inhibition, alm(xl(t)) and blm(xl(t − τ(t))) represent the memristors synaptic connection weights memristor-based weights, and
According to the characteristics of memristor, this paper designs the corresponding connection weights dl(xl(t)), alm(xl(t)), and blm(xl(t)) as follows
where l, m = 1, 2, …, n; , , lm, lm, , and are constants. The corresponding response system connection weights dl(yl(t)), alm(yl(t)), and blm(yl(t)) are defined in a similar way.
On the basis of the solution to such a system by Filippov, let
and there exist measurable functions , , .
Combined with the differential inclusion theory and the set-valued map theory, the drive system (1) with an initial value is described as follows:
The response system in the initial conditions is
where and are time-varying uncertainties that satisfy and ; Ul(t) represents the appropriate control input to be designed.
The coupled MNNs containing N identical MNNs are represented as follows
and
where and are the states of the drive and response system. The response activation functions are , and . For the structure of the coupled system, this article defines a coupled matrix W = (wij)N×N, i, j = 1, 2, …, N, which satisfies H1: If there is a direct edge from j to i, then wij = 1; otherwise, wij = 0; H2: For i, j = 1, 2, …, N, the diffusive coupling conditions are satisfied as . σ > 0 denotes the coupling strength, and Γ refers to the inner couple matrix.
The projective synchronization error is defined as , where α represents the projective factor.
Then, the synchronization issue can be regarded as the stability of the error system:
where , f(ε(t)) = f(y(t)) − f(αx(t)).
Then, the controller U(t) is designed as follows
where represents the gain of state-feedback controller, represents the impulse strength, and δ(t) represents the Dirac function. This article defines the initial time as t0 = 0, and the subsequent events determine the sequence of impulsive instants {t1, t2, t3, … }.
Remark 1. Enlighten by Zhou and Zeng (2019), we take the time-varying uncertainties and delays of information transmission into account of designing the triggered function. As a result, it is more accurate to describe the various influences from the external environment on the networks by using the variable of the uncertainties. On the other hand, the quasi-synchronization scheme for MMNs was presented by Zhou and Zeng (2019). However, in order to meet the practical application, more types of synchronization are considered. Therefore, the event-triggered rules in Yang et al. (2018), Liu et al. (2019), Liu J. et al. (2020), and Wang W. et al. (2021) can be derived from the newly developed event-triggered scheme in (11). Consequently, the proposed scheme is more universal and can be applied to more complex communication environments than other methods.
Assume that ε(t) is right continuous at t = tk, i.e., . Therefore, the solution to the error system (10) is jumping discontinuously at t = tk, which indicates that the error system can change the state variables at t = tk with the control method (11). Thus, the system (10) under a hybrid event-triggered impulse can be represented as:
where t ≥ 0. The impulse control scheme only works at t = tk. Then, the measurement error of the error system (12) can be expressed as
where .
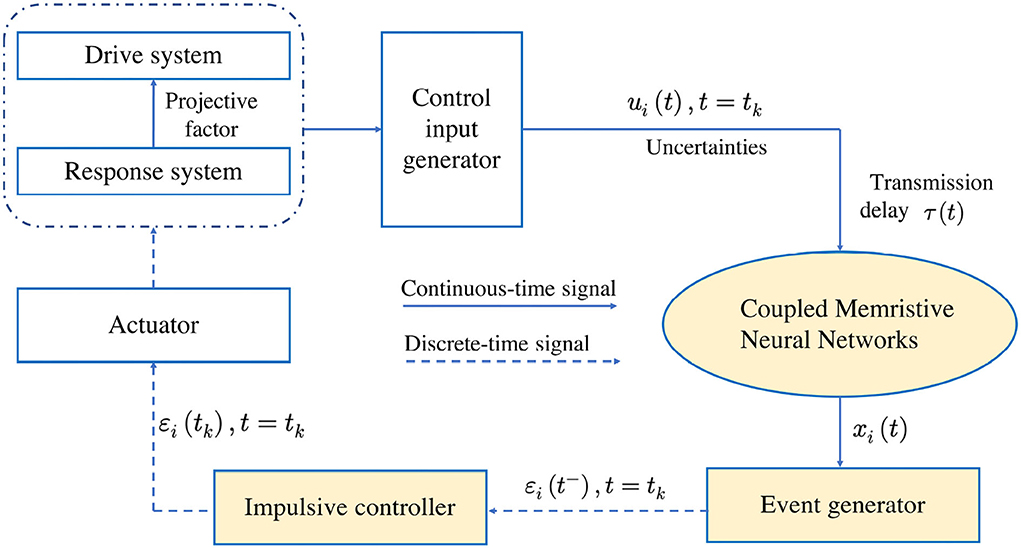
Remark 2. The event-triggered scheme for the proposed couple MNNs is illustrated in Figure 2 Comparing the currently available results, the projective factor for quasi-synchronization and uncertainties are taken into account for designing the triggered function, which determines the triggered instant tk. At each instant tk, the information εi(tk) exchange is realized from the sensors to the event generators and actuators. At the same time, the designed event-triggered scheme is activated and the sampled has occurred in the event-generators. Then the control input ui(tk) works for coupled MNNs and the system enters the new loop according to the updated events.
Then, some definitions, assumptions, as well as lemmas are presented to investigate projective quasi-synchronization for systems (8) and (9).
2.2. Some useful definitions and assumptions
Assumption 1. (Fu et al., 2020) Assume that the solution to (8) is bounded for any initial values , there is a positive constant M such that |xi(t)| ≤ M for all t ∈ [−τ, ∞).
Assumption 2. (Zhou and Zeng, 2019) The activation function fm(·) is Lipschitez continuous, and there exists a constant fm > 0 such that
for all s1, s2 ∈ ℝ, and fm(0) = 0.
Definition 1. (Tang et al., 2018) Systems (8) and (9) achieve projective quasi-synchronization with an error bound ϵ > 0 if the error ε(t) = y(t) − αx(t) exponentially converges into a compact set as t → ∞, where x(t) represents the solution to system (8) that has an initial value of ϕ(s), and y(t) represents the solution to system (9) that has an initial value of φ(s).
Definition 2. (Zhu et al., 2017) The error system (10) can eliminate Zeno behaviors if a constant ρ > 0 exists such that
Lemma 1. Assuming that the real matrices P and Q have appropriate dimensions, a positive number α exists such that
Lemma 2. (Zhang et al., 2009) Let ν1(t) and ν2(t) ∈ ℙℂ be jumping discontinuously at t = tk, t ≥ 0, for and , there is and . If there are constants β1 > 0, β2 > 0, and μ > 0 such that
and
and ν1(t) ≤ ν2(t) for −τ ≤ t ≤ 0, then ν1(t) ≤ ν2(t) for t > 0.
3. Main results
Here, this article presents the solution to the exponential projective quasi-synchronization of delayed uncertain coupled MNNs under the proposed event-triggered strategy.
For convenience, we make A = (alm)n×n, , B = (blm)n×n, , F = diag{f1, f2, …, fn}, , D = diag{d1, d2, …, dn}, = (lm)n×n, A = (alm)n×n, , B = (blm)n×n, .
Theorem 1. According to Assumptions 1 and 2, systems (8) and (9) achieve exponentially projective quasi-synchronization with the control law (11), if there are constants ρ1 > 0, αi > 0 (i = 1, 2, 3), , ω > 0 such that
where k ∈ N+, , , .
In this article, the triggered function is designed as
The triggered instant tk depends on the following event-triggered condition
Proof: For system (12), the nonnegative Lyapunov function is adopted
By differentiating V(t) and the solution to (12) for the [tk−1, tk),k ∈ N+, there is
Combining (12) and (27), there is
Consider Assumption 2, we have
Then, taking the parameters mismatched rules and uncertainties of systems (8) and (9), we have
For Ψ(t), by Assumptions 1–2 and Lemma 1, there are
As mentioned above, there is
where .
Then, considering Lemma 1, there is
Let , then there is
and
Substituting (28)–(35) into (27) yields
According to (22) and (23), there is
where .
From Lemma 2, the following observation can be obtained
When t = tk, k ∈ N+, consider (27),
When δ > 0, ν(t) is developed as a unique solution to the proposed coupled MNNs, i.e.,
According to Lemma 2,
Then,
where W(t) represents the Cauchy matrix for Equations (17) and (18), i.e.,
then we have .
Considering Theorem 1, there is {tk − tk−1} > 0, and a constant ρ1 satisfies {tk − tk−1} ≥ ρ1 > 0. Then, we have
and .
Substituting (44) into (42) yields
that is,
where .
Let . For the continuous function ℓ(ρ), according to (21), ℓ(0) < 0, ℓ(+∞) > 0, and . Besides, a unique solution ρ > 0 to exists. If −τ ≤ t ≤ 0, r > 0, , ρ > 0, and δ > 0 hold, we have
and
According to (22), taking (47) and (48) into account, for t > 0, the following inequality holds
For t > 0, Equation (49) will be testified. Thus, if Equation (49) does not hold, there is t* > 0 such that
and
Combining Equations (50) and (51), there is
When t < t*, there is
Because s ∈ (0, t*), therefore we obtain
Then, we have the following conclusion
It can be seen that Equation (55) contradicts Equation (50). Then, Equation (49) holds for t > 0. When δ > 0, based on Equation (41), there is
Setting δ → 0, according to Equation (55), there is
Combining Equation (27) and Equation (55), we have
Consider Definition 1, the projective quasi-synchronization of systems (8) and (9) is realized by the event-triggered control method. For the error system (12), its trajectory exponentially converges into the compact set 𝔻 with a convergence rate ρ of t → +∞. 𝔻 can be expressed as
The proof is complete.
Remark 3. It should be noticed that continuous communication between the drive-response systems is always required to monitor the triggered condition (25). Therefore, the self-triggered method is designed to solve this problem.
Then, this article investigates the lower bound of inter-execution time to eliminate the Zeno behavior for the error system (12). The following theorem indicates that the system avoids the Zeno behavior under the bound of tk − tk−1 > 0.
Theorem 2. The triggered instants tk(k ∈ N+) can be calculated under the error system (12) and control method (11). Meanwhile, if there is a positive constant ρ1 that satisfies {tk − tk−1} ≥ ρ1 > 0, then the error system (12) can avoid Zeno behaviors.
Proof: For [tk, tk−1), according to Assumptions 1–2, there is
where , and .
Then, according to e(tk−1) = 0, there is
and , .
According to the event-triggered condition (25), we have
and .
For Tk−1 = tk − tk−1, t ∈ [tk−1, tk), k ∈ N+, there is
Thus, it can be derived that there is a lower bound of the inter-execution time, and Tk−1 = tk − tk−1 > 0. The error system (12) can avoid Zeno behaviors.
The completion of the proof is shown above.
Although the systems between (8) and (9) can achieve projective quasi-synchronization, the triggered condition (25) is always monitored during the continuous communication process. To address this issue, this article develops a self-triggered mechanism to update the trigger sequence without monitoring the triggered condition. In this way, there is no need to use the self-triggered mechanism to obtain the state information continuously from Theorem 2 if Tk−1 satisfies Equation (63). Thus, the triggered instant should satisfy the following condition:
The sampling and control instants are calculated by Equation (64) during the self-triggered process as shown in self-triggering Algorithm 1. It is demonstrated that the instants of the controller will not update if the triggered condition is more comprehensive than the second term of Equation (64).
Theorem 3. Combining the control method (11) and error system (12) and using the self-triggered mechanism, the drive and response systems (8) and (9) can achieve projective quasi-synchronization according to the triggered sequence produced by Equation (64). Meanwhile, the error system (12) can avoid the Zeno behavior.
Proof: The self-triggered instants meet Equation (64). According to Equation (63), we have . Then, the event-triggered condition is illustrated in Equation (64). Meanwhile, we have because always holds. Therefore, the self-triggered mechanism Equation (64) guarantees the projective quai-synchronization between (8) and (9) through (11). Also, the error system (12) avoids the Zeno behavior. The proof is completed.
4. Numerical simulation
4.1. Conclusions proof
Numerical simulations are conducted to verify the correctness of the theoretical analysis results. Systems (8) and (9) including three (N = 3) nodes are considered. Each node has three (n = 3) dimensions of information. Additionally, x11 means the 1st dimension of Node 1. For the coupling framework, the coupling strength σ = 1.5; the inner connecting matrix Γ and coupled matrix W are set as
For systems (8) and (9), the time-varying delay can be represented as τ(t) = et/(et + 1). Considering Assumptions 1 and 2, this article sets Lf = 1 and Mi = 1(i = 1, 2, 3). In this example, the following initial values are taken: , , , , , .
The parameters of the systems are as follows:
The uncertainties of the proposed systems are
The nonlinear activation function F(xi(t))(i = 1, 2, 3) is given as:
As discussed above, Figure 3 represents the chaotic behavior of (8) and (9) under different initial conditions. And Figure 4 shows the states of (8) and (9) without controller. Then, this article defines the projector factor α = 1, i.e., the synchronization error ε(t) = y(t) − x(t). For Lemma 4, this article sets α1 = α2 = α3 = 0.01. Figure 5 shows the trajectory of (8) and (9) without control.
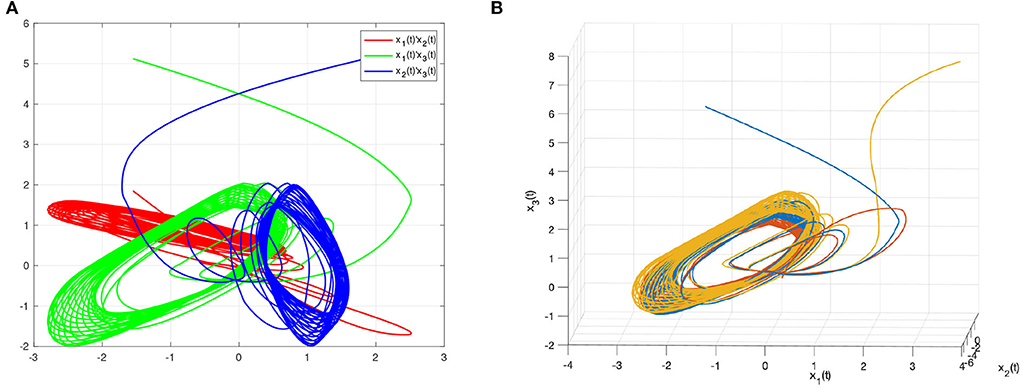
Figure 3. The chaotic dynamic behavior of systems (8) and (9). (A) Time evolutions of systems in a complex space. (B) State curves of systems in a complex plane.
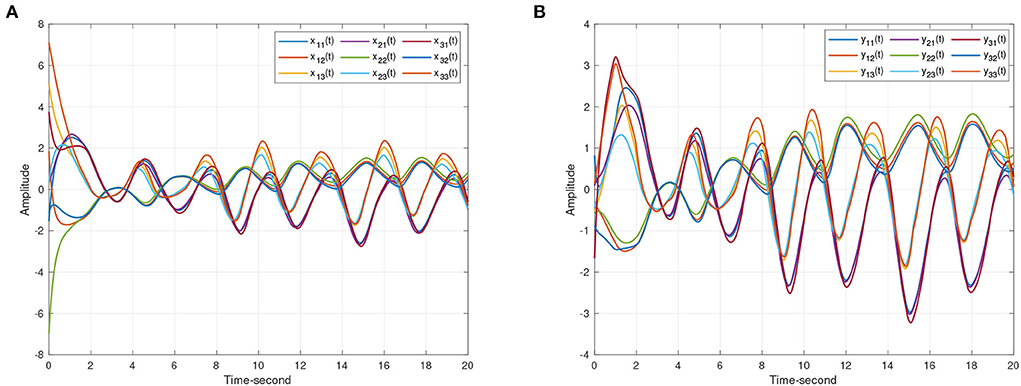
Figure 4. The state trajectories produced by systems (8) and (9) without the controller. (A) The state curves of drive system (8). (B) The state curves of response system (9).
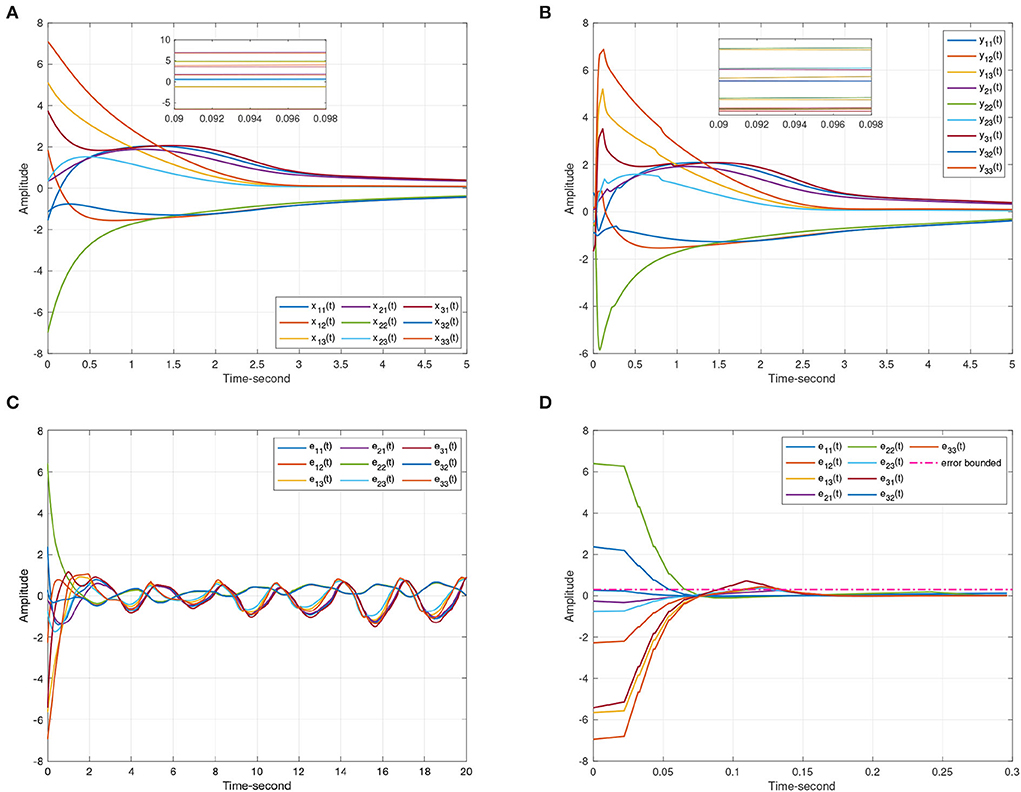
Figure 5. The synchronization state trajectories produced by systems (8) and (9). (A) The state curves of the drive system (8). (B) The state curves of the response system (9). (C) The synchronization errors ε(t) = y(t) − x(t) without control. (D) The synchronization errors ε(t) = y(t) − x(t) under the event-triggered scheme (11).
The gain matrix of the controller is
This article chooses μk = 0.9, and it can easily testify that all the rules in Theorem 1 hold, which indicates that systems (8) and (9) can achieve quasi-synchronization with the projective factor α = 1.
When the projective factor α = −1, anti quai-synchronization can be also achieved between systems (8) and (9). Considering Lemma 4, this article sets α1 = 1000, α2 = 1000, α3 = 0.01. Figure 6 shows the effectiveness of Theorem 1.
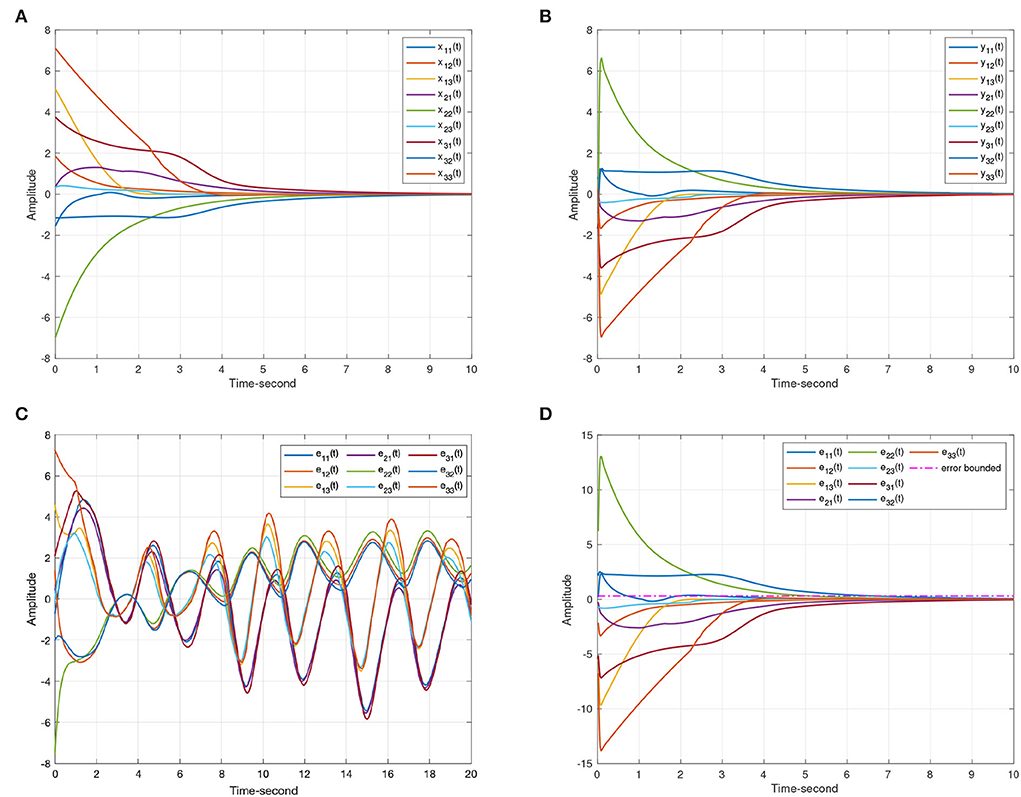
Figure 6. The anti-synchronization state trajectories produced by systems (8) and (9). (A) The state curves of the drive system (8). (B) The state curves of the response system (9). (C) The anti-synchronization errors ε(t) = y(t) + x(t). (D) The anti-synchronization errors ε(t) = y(t) + x(t) under the event-triggered scheme (11).
For systems (8) and (9), Figures 5, 6 represent the state trajectory and the synchronization error under event-triggered control for different projective factors. Also, the synchronization error norm is illustrated. Figures 7, 8 present the state-feedback controller and events under event-triggered control. Figures 9, 10 demonstrate the performance of the self-triggered scheme. The comparison between Figures 7, 10 indicates that the lower bound of the event-triggered time interval is set to the update time for the self-triggered scheme. Therefore, the self-triggered scheme has a higher update frequency than the event-triggered one. Meanwhile, the information exchange and deterioration are increased within limited network resources.
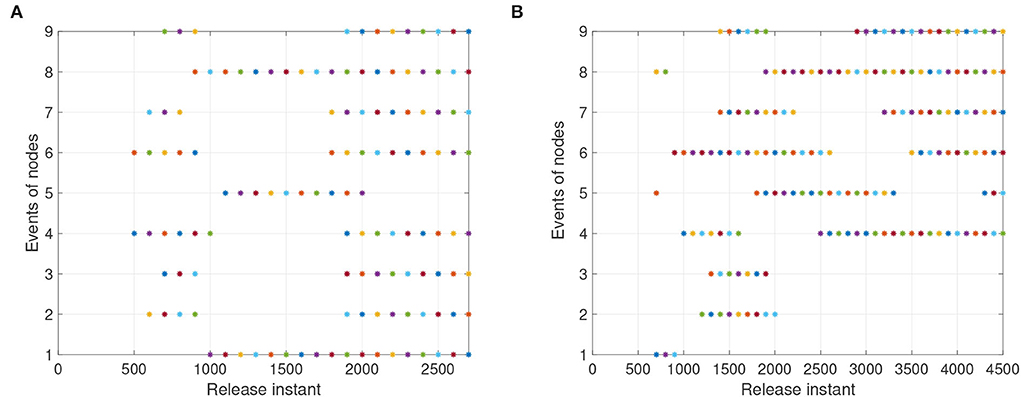
Figure 7. The events with event-triggered control. (A) Instants for synchronization ε(t) = y(t) − x(t). (B) Instants for anti-synchronization ε(t) = y(t) + x(t).
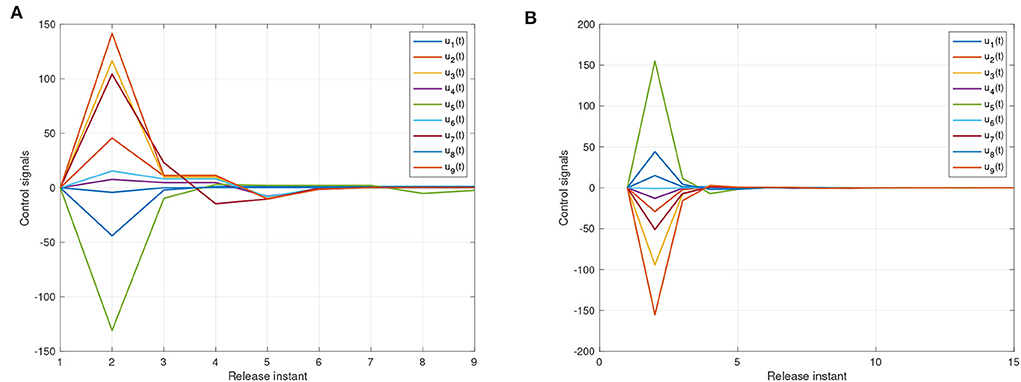
Figure 8. The states of event-triggered controller (11). (A) Instants for synchronization ε(t) = y(t) − x(t). (B) Instants for anti-synchronization ε(t) = y(t) + x(t).
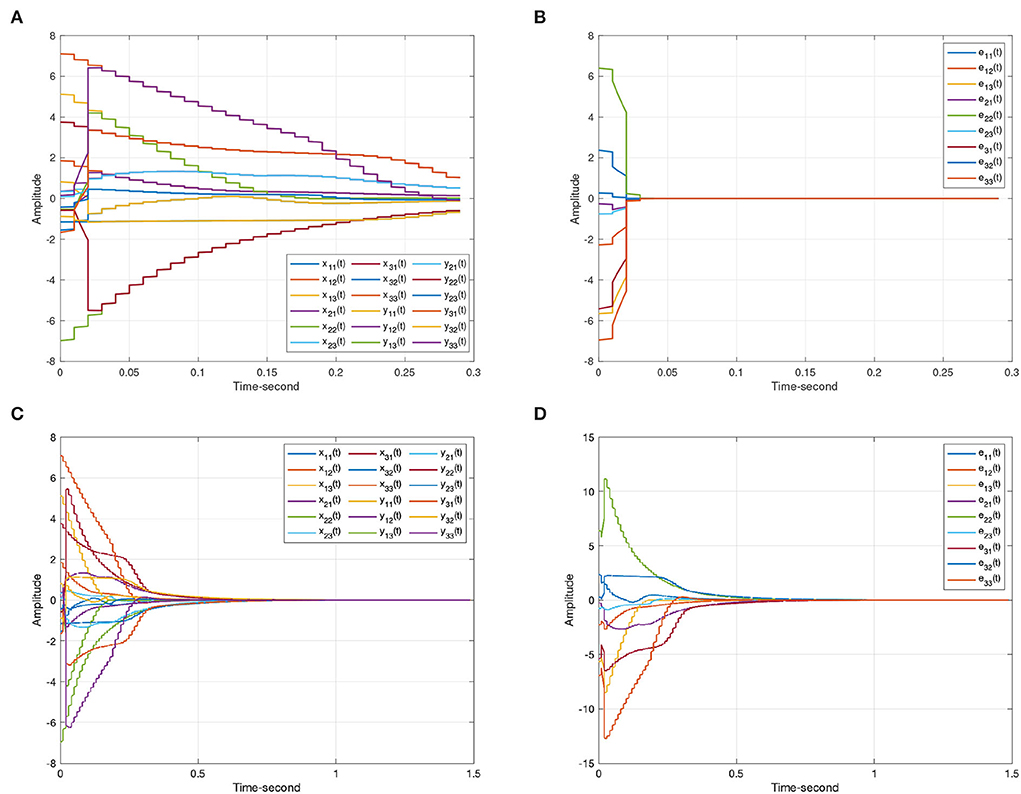
Figure 9. The state trajectories produced by systems (8) and (9) under a self-triggered scheme (11). (A) The state curves of systems (8) and (9) with α = 1. (B) The synchronization errors ε(t) = y(t) − x(t). (C) The state curves of systems (8) and (9) with α = −1. (D) The anti-synchronization errors ε(t) = y(t) + x(t).
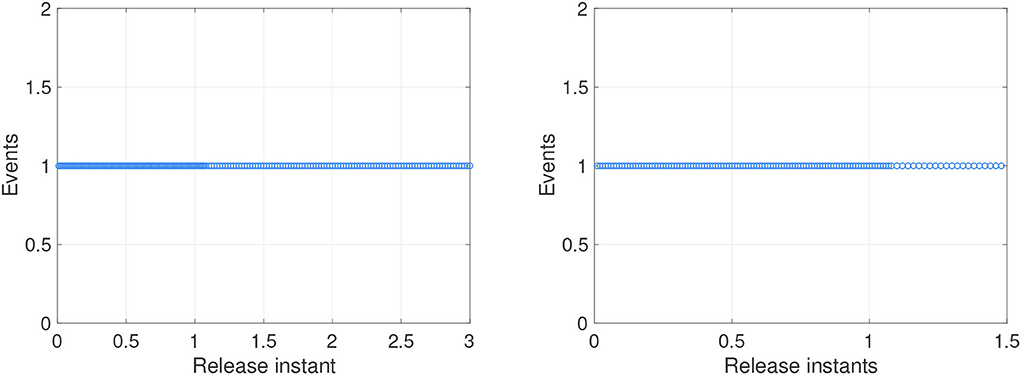
Figure 10. The events with self-triggered control. (A) Instants for synchronization ε(t) = y(t) − x(t). (B) Instants for anti-synchronization ε(t) = y(t) + x(t).
4.2. Existing achievements comparison
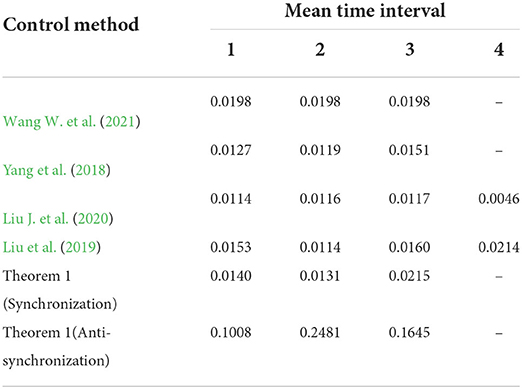
Now, we make our proposed event-triggered mechanism of coupled MNNs compared with some exciting methods to illustrate our designed method's superiority in synchronization, especially in the situation of limited bandwidth. Due to the different types of neural networks, we set the interval as [0.0, 1.0] to conduct the contrast simulations as shown in Table 1, in which the mean time interval means the average update frequency between each trigger. It is noticed that the lowest value of our method is 0.013 s, which indicates the control input can complete more than 76.92 updates/s in general.
Remark 4. Compared with some existing results (Yang et al., 2018; Liu et al., 2019; Liu J. et al., 2020; Wang W. et al., 2021), it can be seen that our event-triggered method relies on fewer triggering events from Table 1. Meanwhile, it is less likely to trigger than other methods, indicating that, in the control process, our method consumes remarkably less energy for data calculation and detection.
The proposed method in this article is the event-triggered scheme, which means the control input information exchange and update which depends on the designed triggered function. When the proposed method did not work, the proposed scheme will become the traditional time-sampled scheme, and the control updating instants just rely on the fixed interval. Therefore, the proposed method is more general and flexible than other methods, especially in the situation of limited network resources.
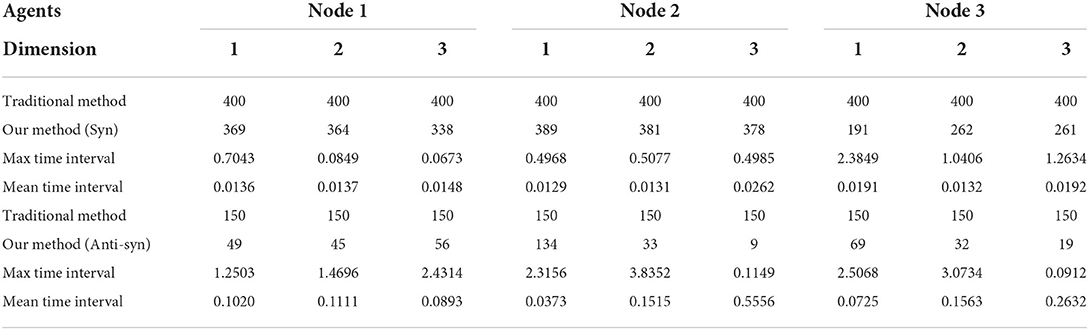
Remark 5. From Table 2, comparing the different types of synchronization, we can detect that by changing the value of the projective factor α and Lipschitz parameters α1, α2, and α3, (for synchronization, we make α = 1, α1 = α2 = α3 = 0.01, for anti-synchronization, α = −1, α1 = α2 = 1, 000, α3 = 0.01), the control updating instants can be changed. It is clearly noticed that the updating frequency of the controller for synchronization is faster than anti-synchronization. That is to say, altering the values of parameters can not only affect the updating frequency.
5. Conclusion
A fresh event-triggered impulsive control scheme for a class of time-varying uncertain coupled MNNs has been proposed in this article. Considering the parameter mismatch and coupled structure of the proposed system, the event-triggered impulsive scheme has been constructed to solve the problem of projective quasi-synchronization. Accordingly, the established triggered functions with uncertainties and projective factors make the quasi-synchronization criteria more universal than conventional neural networks. Besides, the Zeno behavior can be naturally escaped through the design of proper triggered conditions.
Furthermore, the proposed mechanism has been employed to deal with projective quasi-synchronization, which can not only expand the types of synchronization but also avoid unnecessary energy consumption. As shown in the simulation, the designed self-triggered algorithm is reasonable in terms of avoiding Zeno behavior. However, just quasi-synchronization and quasi-anti-synchronization are considered, from the projective factor point of view, the time-varying factor is more universal for application, especially in social networks (Cheng et al., 2022), object/scene reconstruction (Tang et al., 2021), and 3D object recognition (Chen Y., 2022) etc. Therefore, in future study, the obtained scheme will be developed for projective quasi-synchronization with time-varying projective factors and more practical networks will be considered.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.
Author contributions
MY designed the research and wrote the paper. MY and XL performed the research. JH contributed new reagents and analytic tools. JH and SW analyzed the data. All authors contributed to the article and approved the submitted version.
Funding
This study was supported in part by the National Natural Science Foundation of China under Grants 62106020 and U1836106, the Fundamental Research Funds for the Central Universities under Grant FRF-IDRY-20-022, the China Postdoctoral Science Foundation under Grant 2021M690355, the Beijing Natural Science Foundation under Grants 19L2029 and L211020, the Scientific and Technological Innovation Foundation of Foshan under Grants BK20BF010 and BK21BF001, andd the Postdoctoral Research Foundation of Shunde Graduate School of University of Science and Technology Beijing under Grant 2021BH008.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Chee, C., and Xu, D. (2006). Chaos-based M-ary digital communication technique using controlled projective synchronisation. IEEE Proc. Circuits Devices Syst. 153, 357–360. doi: 10.1049/ip-cds:20050139
Chen, C., Li, L., Peng, H., Yang, Y., Mi, L., and Qiu, B. (2019). Fixed-time projective synchronization of memristive neural networks with discrete delay. Phys. A 534:122248. doi: 10.1016/j.physa.2019.122248
Chen, L., Zhou, W., Li, C., and Huang, J. (2021). Forgetting memristors and memristor bridge synapses with long-and short-term memories. Neurocomputing 456, 126–135. doi: 10.1016/j.neucom.2021.05.062
Chen, T., and Shan, J. (2019). Distributed tracking of a class of underactuated lagrangian systems with uncertain parameters and actuator faults. IEEE Trans. Indus. Electron. 67, 4244–4253. doi: 10.1109/TIE.2019.2922943
Chen, W., Yu, Y., Hai, X., and Ren, G. (2022). Adaptive quasi-synchronization control of heterogeneous fractional-order coupled neural networks with reaction-diffusion. Appl. Math. Comput. 427:127145. doi: 10.1016/j.amc.2022.127145
Chen, Y., Peng, W., Tang, K., Khan, A., Wei, G., and Fang, M. (2022). Pyrapvconv: efficient 3d point cloud perception with pyramid voxel convolution and sharable attention. Comput. Intell. Neurosci. 2022:2286818. doi: 10.1155/2022/2286818
Cheng, L., Li, X., Han, Z., Luo, T., Ma, L., and Zhu, P. (2022). Path-based multi-sources localization in multiplex networks. Chaos Solitons Fract. 159:112139. doi: 10.1016/j.chaos.2022.112139
Cheng, Y. (2022). Fully distributed event-triggered output synchronization of heterogeneous multi-agent systems over directed switching networks. J. Franklin Instit. 359, 1706–1723. doi: 10.1016/j.jfranklin.2022.01.018
Ding, Z., Chen, C., Wen, S., Li, S., and Wang, L. (2022). Lag projective synchronization of nonidentical fractional delayed memristive neural networks. Neurocomputing 469, 138–150. doi: 10.1016/j.neucom.2021.10.061
Duan, Q., Jing, Z., Zou, X., Wang, Y., Yang, K., Zhang, T., et al. (2020). Spiking neurons with spatiotemporal dynamics and gain modulation for monolithically integrated memristive neural networks. Nat. Commun. 11, 1–13. doi: 10.1038/s41467-020-17215-3
Duong, T. T. C., Nguyen, C. C., and Tran, T. D. (2022). Synchronization sliding mode control of closed-kinematic chain robot manipulators with time-delay estimation. Appl. Sci. 12:5527. doi: 10.3390/app12115527
Fu, Q., Zhong, S., Jiang, W., and Xie, W. (2020). Projective synchronization of fuzzy memristive neural networks with pinning impulsive control. J. Franklin Instit. 357, 10387–10409. doi: 10.1016/j.jfranklin.2020.08.015
Guo, R., Lv, W., and Zhang, Z. (2020). Quasi-projective synchronization of stochastic complex-valued neural networks with time-varying delay and mismatched parameters. Neurocomputing 415, 184–192. doi: 10.1016/j.neucom.2020.07.033
Hong, Q., Chen, H., Sun, J., and Wang, C. (2020). Memristive circuit implementation of a self-repairing network based on biological astrocytes in robot application. IEEE Trans. Neural Netw. Learn. Syst. 33, 2106–2120. doi: 10.1109/TNNLS.2020.3041624
Hu, T., He, Z., Zhang, X., Zhong, S., Shi, K., and Zhang, Y. (2022). Adaptive fuzzy control for quasi-synchronization of uncertain complex dynamical networks with time-varying topology via event-triggered communication strategy. Inform. Sci. 582, 704–724. doi: 10.1016/j.ins.2021.10.036
Huang, J., Ri, S., Fukuda, T., and Wang, Y. (2018). A disturbance observer based sliding mode control for a class of underactuated robotic system with mismatched uncertainties. IEEE Trans. Autom. Control 64, 2480–2487. doi: 10.1109/TAC.2018.2868026
Jin, C., Wang, Z., Gong, L., Xiao, M., and Jiang, G.-P. (2022). Quasi-synchronization of heterogeneous Lur'e networks with uncertain parameters and impulsive effect. Neurocomputing 482, 252–263. doi: 10.1016/j.neucom.2021.11.057
Kumar, R., Sarkar, S., Das, S., and Cao, J. (2019). Projective synchronization of delayed neural networks with mismatched parameters and impulsive effects. IEEE Trans. Neural Netw. Learn. Syst. 31, 1211–1221. doi: 10.1109/TNNLS.2019.2919560
Li, H.-L., Hu, C., Zhang, L., Jiang, H., and Cao, J. (2021). Non-separation method-based robust finite-time synchronization of uncertain fractional-order quaternion-valued neural networks. Appl. Math. Comput. 409:126377. doi: 10.1016/j.amc.2021.126377
Li, P., Zhao, W., and Cheng, J. (2022). Event-triggered control for exponential stabilization of impulsive dynamical systems. Appl. Math. Comput. 413:126608. doi: 10.1016/j.amc.2021.126608
Liu, H., Ma, L., Wang, Z., Liu, Y., and Alsaadi, F. E. (2020). An overview of stability analysis and state estimation for memristive neural networks. Neurocomputing 391, 1–12. doi: 10.1016/j.neucom.2020.01.066
Liu, J., Wu, H., and Cao, J. (2020). Event-triggered synchronization in fixed time for complex dynamical networks with discontinuous nodes and disturbances. J. Intell. Fuzzy Syst. 38, 2503–2515. doi: 10.3233/JIFS-179538
Liu, L., Zhou, W., Li, X., and Sun, Y. (2019). Dynamic event-triggered approach for cluster synchronization of complex dynamical networks with switching via pinning control. Neurocomputing 340, 32–41. doi: 10.1016/j.neucom.2019.02.044
Mainieri, R., and Rehacek, J. (1999). Projective synchronization in three-dimensional chaotic systems. Phys. Rev. Lett. 82:3042. doi: 10.1103/PhysRevLett.82.3042
Rajchakit, G., and Sriraman, R. (2021). Robust passivity and stability analysis of uncertain complex-valued impulsive neural networks with time-varying delays. Neural Process. Lett. 53, 581–606. doi: 10.1007/s11063-020-10401-w
Shi, S., Wang, Z., Song, Q., Xiao, M., and Jiang, G.-P. (2022). Leader-following quasi-bipartite synchronization of coupled heterogeneous harmonic oscillators via event-triggered control. Appl. Math. Comput. 427:127172. doi: 10.1016/j.amc.2022.127172
Tang, K., Miao, D., Peng, W., Wu, J., Shi, Y., Gu, Z., et al. (2021). “Codes: chamfer out-of-distribution examples against overconfidence issue,” in Proceedings of the IEEE/CVF International Conference on Computer Vision, 1153–1162. doi: 10.1109/ICCV48922.2021.00119
Tang, K., Song, P., and Chen, X. (2016). “Signature of geometric centroids for 3d local shape description and partial shape matching,” in Asian Conference on Computer Vision (Taipei: Springer), 311–326. doi: 10.1007/978-3-319-54193-8_20
Tang, Z., Park, J. H., Wang, Y., and Feng, J. (2018). Distributed impulsive quasi-synchronization of Lur'e networks with proportional delay. IEEE Trans. Cybern. 49, 3105–3115. doi: 10.1109/TCYB.2018.2839178
Wang, C., Ji, J., Miao, Z., and Zhou, J. (2021). Synchronization control for networked mobile robot systems based on udwadia-kalaba approach. Nonlin. Dyn. 105, 315–330. doi: 10.1007/s11071-021-06487-z
Wang, W., Sun, Y., Yuan, M., Wang, Z., Cheng, J., Fan, D., et al. (2021). Projective synchronization of memristive multidirectional associative memory neural networks via self-triggered impulsive control and its application to image protection. Chaos Solitons Fract. 150:111110. doi: 10.1016/j.chaos.2021.111110
Wang, Z., Hong, Q., and Wang, X. (2019). Memristive circuit design of emotional generation and evolution based on skin-like sensory processor. IEEE Trans. Biomed. Circuits Syst. 13, 631–644. doi: 10.1109/TBCAS.2019.2923055
Wu, F., and Huang, Y. (2022). Finite-time synchronization and h∞ synchronization of coupled complex-valued memristive neural networks with and without parameter uncertainty. Neurocomputing 469, 163–179. doi: 10.1016/j.neucom.2021.10.067
Xin, Y., Cheng, Z., Cao, J., Rutkowski, L., and Wang, Y. (2022). Circuit implementation and quasi-stabilization of delayed inertial memristor-based neural networks. IEEE Trans. Neural Netw. Learn. Syst. doi: 10.1109/TNNLS.2022.3173620
Yan, Z., Huang, X., Fan, Y., Xia, J., and Shen, H. (2020). Threshold-function-dependent quasi-synchronization of delayed memristive neural networks via hybrid event-triggered control. IEEE Trans. Syst. Man Cybern. 51, 6712–6722. doi: 10.1109/TSMC.2020.2964605
Yang, N., Yu, Y., Zhong, S., Wang, X., Shi, K., and Cai, J. (2021). Impulsive effects on weak projective synchronization of parameter mismatched stochastic memristive neural networks. J. Franklin Instit. 358, 5909–5930. doi: 10.1016/j.jfranklin.2021.05.007
Yang, Y., Yue, D., and Dou, C. (2018). Output-based event-triggered schemes on leader-following consensus of a class of multi-agent systems with Lipschitz-type dynamics. Inf. Sci. 459, 327–340. doi: 10.1016/j.ins.2018.02.020
Yao, X.-Y., Park, J. H., Ding, H.-F., and Ge, M.-F. (2020). Event-triggered consensus control for networked underactuated robotic systems. IEEE Trans. Cybern. 52, 2896–2906. doi: 10.1109/TCYB.2020.3025604
Yuan, M., Wang, W., Wang, Z., Luo, X., and Kurths, J. (2020). Exponential synchronization of delayed memristor-based uncertain complex-valued neural networks for image protection. IEEE Trans. Neural Netw. Learn. Syst. 32, 151–165. doi: 10.1109/TNNLS.2020.2977614
Zhang, H., Ma, T., Huang, G.-B., and Wang, Z. (2009). Robust global exponential synchronization of uncertain chaotic delayed neural networks via dual-stage impulsive control. IEEE Trans. Syst. Man Cybern. Syst. 140, 831–844. doi: 10.1109/TSMCB.2009.2030506
Zhang, R., Wang, H., Park, J. H., Lam, H.-K., and He, P. (2022). Quasisynchronization of reaction-diffusion neural networks under deception attacks. IEEE Trans. Syst. Man Cybern. Syst. doi: 10.1109/TSMC.2022.3166554
Zhang, Y., Zhao, X., Tao, B., and Ding, H. (2022). Multi-objective synchronization control for dual-robot interactive cooperation using nonlinear model predictive policy. IEEE Trans. Indus. Electron. doi: 10.1109/TIE.2022.3150090
Zhou, Y., and Zeng, Z. (2019). Event-triggered impulsive control on quasi-synchronization of memristive neural networks with time-varying delays. Neural Netw. 110, 55–65. doi: 10.1016/j.neunet.2018.09.014
Zhu, P., Cheng, L., Gao, C., Wang, Z., and Li, X. (2022). Locating multi-sources in social networks with a low infection rate. IEEE Trans. Netw. Sci. Eng. 9, 1853–1865. doi: 10.1109/TNSE.2022.3153968
Zhu, S., and Bao, H. (2022). Event-triggered synchronization of coupled memristive neural networks. Appl. Math. Comput. 415:126715. doi: 10.1016/j.amc.2021.126715
Keywords: event-triggered, memristor, coupled neural networks, projective quasi-synchronization, uncertainties
Citation: Yuan M, Luo X, Hu J and Wang S (2022) Projective quasi-synchronization of coupled memristive neural networks with uncertainties and impulsive effect. Front. Neurorobot. 16:985312. doi: 10.3389/fnbot.2022.985312
Received: 03 July 2022; Accepted: 15 August 2022;
Published: 09 September 2022.
Edited by:
Keke Tang, Guangzhou University, ChinaReviewed by:
Jiang Long, Northwestern Polytechnical University, ChinaMingwen Zheng, Shandong University of Technology, China
Copyright © 2022 Yuan, Luo, Hu and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xiong Luo, xluo@ustb.edu.cn
 Manman Yuan
Manman Yuan Xiong Luo
Xiong Luo Jun Hu
Jun Hu Songxin Wang5
Songxin Wang5