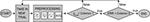1
Applied Electronics Unit, Department of Electronics, Helsinki University of Technology, Espoo, Finland
2
Graduate School of Electrical and Communications Engineering, Helsinki University of Technology, Espoo, Finland
3
Cognitive Brain Research Unit, Institute of Behavioral Sciences, Helsinki University, Helsinki, Finland
4
Finnish Centre of Excellence in Interdisciplinary Music Research, Helsinki, Finland
Reliable measurements are mandatory in clinically relevant auditory event-related potential (AERP)-based tools and applications. The comparability of the results gets worse as a result of variations in the remaining measurement error. A potential method is studied that allows optimization of the length of the recording session according to the concurrent quality of the recorded data. In this way, the sufficiency of the trials can be better guaranteed, which enables control of the remaining measurement error. The suggested method is based on monitoring the signal-to-noise ratio (SNR) and remaining measurement error which are compared to predefined threshold values. The SNR test is well defined, but the criterion for the measurement error test still requires further empirical testing in practice. According to the results, the reproducibility of average AERPs in repeated experiments is improved in comparison to a case where the number of recorded trials is constant. The test-retest reliability is not significantly changed on average but the between-subject variation in the value is reduced by 33–35%. The optimization of the number of trials also prevents excessive recordings which might be of practical interest especially in the clinical context. The efficiency of the method may be further increased by implementing online tools that improve data consistency.
The averaging of the evoked potentials is a convenient way to reduce the level of interference when highlighting event-locked electroencephalographic (EEG) responses (Picton et al., 1995
). Thus, in spite of the increasing interest in single-trial analysis, averaging is still the most commonly used method to recover event-related potentials (ERPs) from noise (Davila and Mobin, 1992
). The average ERPs, however, are distorted by, for example, latency jitter (e.g. Gibbons and Stahl, 2007
), amplitude variations, external interference, physiological artifacts, noise, and measurement errors during the experiment (Leonowicz et al., 2005
). In addition to that, the within-subject and the between-subject variations in the responses also affect the measurement outcome (e.g. Pikvik et al., 1993
; Lang et al., 1995
). Even though the average level of interference is reduced in this process (Picton et al., 1995
), the test-retest reliability of the responses on a single-subject level is too low for clinical applications (Lang et al., 1995
; Sinkkonen and Tervaniemi, 2000
; Dalebout and Fox, 2001
; Beauchemin and De Beaumont, 2005
; Kujala et al., 2007
; Duncan et al., 2009
). The mismatch negativity, for example, has been estimated to have a test-retest reliability of just over 0.5 (Sinkkonen and Tervaniemi, 2000
), 0.46–0.71 (Frodl-Bauch et al., 1997
), or 0.56–67 (Pekkonen et al., 1995
).
The replicability of the responses depends on the test subject, type and presentation of the stimulus, the response studied, and the electrode location (Pekkonen et al., 1995
; Frodl-Bauch et al., 1997
; Sinkkonen and Tervaniemi, 2000
). The test-retest reliability of the N100 response, for example, is higher than that of the mismatch negativity (MMN) because of the better latency stability (Pekkonen et al., 1995
). In addition, the variation in the remaining level of interference also affects the test-retest reliability (e.g. Sinkkonen and Tervaniemi, 2000
). This explains why the replicability of the response to the standard sound tends to be superior to the less frequent ones (Pekkonen et al., 1995
). The test-retest reliability can be influenced by careful experiment design. However, as the initial amount of noise and the level of interference will vary anyway, the quality variation should also be compensated.
The basic problem is that the number of trials recorded is typically constant, while the initial quality of the signal changes between and during experiments. Consequently, the remaining measurement error is subject to variation which affects the comparability of the responses and the test-retest reliability. Several methods have been suggested for cleaning the data (e.g. Effern et al., 2000
; Quiroga, 2000
; He et al., 2004
) and to adjust the averaging process to cope with the alternating signal quality (e.g. Woody, 1967
; Davila and Mobin, 1992
; Woldorff, 1993
; Jaskowski and Verleger, 1999
; Wang et al., 2001
; Leonowicz et al., 2005
; Gibbons and Stahl, 2007
). However, even though the average signal quality could be improved, this does not compensate the insufficiency of the data. Alternatively, it would also be possible to increase the length of the experiments. In practice, however, fatigue, for example, may affect the neuropsychological phenomena (Picton et al., 1995
; Ding and Ye, 2003
; Boksem et al., 2005
; Muller-Gass et al., 2005
; Thornton, 2008
) and the risks of equipment-related errors also increase with time (Mühler and von Specht, 1999
; Rahne et al., 2008
). As the amount of artifacts and sudden changes in the signal quality are not predictable, the sufficient number of trials cannot be reliably predefined (Möcks et al., 1988
; Sinkkonen and Tervaniemi, 2000
). Thus, the length of the experiment should rather be defined online with respect to the concurrent data quality.
In this study, the implementation of a novel autoadaptive recording procedure for auditory event-related potentials (AERP) is suggested. It aims at optimizing the length of the experiment with respect to the initial quality of the data recorded. The qualities being monitored are the contribution of noise and the remaining measurement error. The idea is to keep on recording until they meet a predefined threshold. This way, the quality of the results is guaranteed and the length of the experiment is optimized. The objectives of the study are to define appropriate estimators for the quality tests and to study the influence of the compensation on the test-retest reliability in a simulated AERP experiment. Feasibility, technical requirements and developmental aspects will be discussed on the basis of the results.
Procedure Description
The procedure involved cycling three phases (Figure 1
): preprocessing, quality estimation, and decision making. The analysis was performed trial-by-trial and the decision as to whether to continue the experiment or not was made at the end of each cycle. First, the trial being analyzed was filtered and tested to detect possible artifacts and the contaminated trials were rejected. Then, the maturity of the accumulating average was estimated on the basis of the contribution of noise and the remaining measurement error. They were compared to predefined threshold values and the experiment was concluded if both the criteria were met.
The data used in the demonstration was taken from an MMN study (Pakarinen et al., 2007
). Each trial lasted from −50 to +450 ms from the stimulus onset. The data was lowpass filtered (0–30 Hz) and the baseline was corrected on the basis of the 50 ms prestimulus interval. These are typical filter settings for this kind of data (Pekkonen et al., 1995
; Pakarinen et al., 2007
; Duncan et al., 2009
). Artifacts were detected by testing the amplitude of the response and trials exceeding ± 40 µV were rejected.
Additionally, variation in the physiological response may also affect the accumulating average. Latency variation, in particular, is harmful because it flattens the amplitude of the peaks in the average waveform (e.g. Thornton, 2008
). Several methods have been suggested to correct the error (e.g. Woody, 1967
; Woldorff, 1993
; Wang et al., 2001
). None of these, however, were considered to be feasible online and, thus, were not included into the procedure.
Figure 1. The autoadaptive recording procedure. The data recorded is analyzed one trial at a time and the experiment is continued until the quality of the accumulating average meets the predefined criteria. The qualities being tested are the contribution of noise (pnoise) and the remaining measurement error (ERR). Prior to qualitative testing, the trial being analyzed is lowpass filtered, baseline corrected, and tested for artifacts.
Estimation of the Contribution of Noise
The purpose of the noise test was to evaluate the mean level of interference in the accumulating average waveform. In particular, the test was supposed to indicate the contribution of white noise so that the significance of the responses could be assessed.
T-test is commonly used to test the statistical significance of noise over the single trials in AERP studies (e.g. Picton et al., 1995
). By definition, it estimates the probability of the null hypothesis that the value being tested is a random sample from a normal distribution with a mean of zero and unknown variance, against the alternative that the mean is different from zero. Typically, if the probability of the null hypothesis is smaller than 0.05, it is likely that the contribution of noise is negligible or small (Ewens and Grant, 2005
).
In the current context, the one-sample t-test could be applied by testing a peak in the average response, the statistical significance of which would represent the general quality of the whole waveform. The auditory N100 peak in the average waveform, for example, is relatively stable and typically easy to obtain. Thus, it could be a well-suited option for the purpose. On the other hand, the application of the t-test requires exact knowledge of the latency of the peak to be tested and the localization may prove laborious because the latency varies between trials. Thus, a simpler estimate would be preferable in terms of computational efficiency.
Alternatively, the statistical significance of noise may also be estimated from the respective signal-to-noise ratio (SNR) (Sackett, 2001
). Compared to the one-sample t-test, the computation of the SNR is simpler and it can also be applied to test the whole waveform at once. Although the accuracy of the estimation might be worse, it may still be capable of providing the number of trials required to obtain significant responses with reasonable accuracy. Derived from Möcks et al. (1988)
, the effective SNR can be estimated from the difference of the consecutive trials by eqs 1–3.
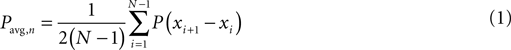


where

Here, Pavg,n represents the average power of the noise, Pavg,s represents the power of the average response, µN is the average of N trials, xi represents the ith trial, and the time frame of the trial is [t0, T]. Furthermore, the SNR values exceeding one are interpreted to indicate zero significance, because statistical significance may only have values between 0 and 1.
Estimation of the Remaining Measurement Error
The purpose of testing the remaining measurement error was to be able to estimate the stability of the accumulating results and the magnitude of the change that could still be expected. In particular, the test was supposed to indicate the magnitude of the remaining interference peaks and the uncertainty in the average waveform resulting from variations in the physiological response. In order to estimate the measurement error, two alternative estimators were considered: a convergence-based estimator and a direct estimator of the measurement error. Both alternatives derive from comparing partial averages of the data and the computation of the estimates is simple.
The convergence rate represents the magnitude of change in the average waveform as new trials are included into the sum. It can be calculated online by comparing the consecutive averages. The comparison is made with respect either to the amplitude or the form of the responses. The similarity of the form of the responses can be estimated on the basis of the correlation. The calculation of the parameter is straightforward and it provides a reasonable estimate of the similarity of the whole waveform. On the other hand, the form of the whole curve is often irrelevant and it would be more interesting to estimate the maximal error in the peak amplitudes. This could be assessed better from the differences in the consecutive averages. Thus, the convergence rate-based error estimate εc was calculated according to eqn. 5.
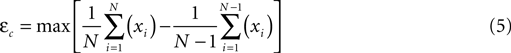
where N is the total number of averaged trials and xi represents the ith trial included into the sum.
Alternatively, the measurement error can also be estimated directly by computing the difference of two independent averages extracted from the data. Following Schimmel (1967)
, the direct estimate of the measurement error εd was calculated from the difference of the average of the odd and the even trials according to eqn. 6.
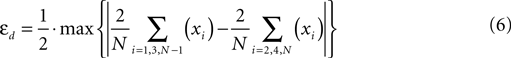
where N is the total number of averaged trials and xi represents the ith trial included into the sum. The difference of the even and the odd average represented the remaining error in the response. Thus, the maximum of the waveform could be considered to be representative of the maximal error.
Evaluation of the Procedure
Test data
The methods applied in this study were evaluated by simulating their performance with real data. With the authors’ permission, the data used were taken from Pakarinen et al. (2007)
. In that study, the multi-feature MMN paradigm was applied to obtain an auditory discrimination profile by using harmonic sinusoidal sounds. The standard tones were composed of three sinusoidal partials (523, 1046 and 1569 Hz). They were presented at an intensity of 60 dB above the subject’s hearing threshold and the length of the stimuli was 75 ms (including 5 ms rise and fall times). The deviant tones differed from the standard tones in frequency, intensity, duration, or perceived sound-source location and the magnitude of the deviation varied across six levels. The probability of the standard tone was 0.5 and the probability of each deviant tone at each level was 0.125/6. The length of each recording session was 90 min and the number of trials recorded was 5472 for the standard stimulus and 225 for each deviant stimulus (Pakarinen et al., 2007
).
For the concurrent study, data from eight test subjects was available. These data were used to simulate a series of repeated experiments with each test subject and they were each permuted 100 times to create artificial test runs. However, in order to avoid creating permutations that were too similar, datasets that were too small had to be rejected. The expected length of a single simulated experiment was about 200–600 trials. Therefore, only the standard datasets were applied. In addition, the evaluation was further limited to only the one channel having the largest SNR with respect to the physiological response (Fz referenced to the mean of the mastoids). Thus, the test data accepted for the study included eight datasets with over 5000 trials, from each of which 5% to 19% was still rejected because of artifacts.
Tests
In short, the quality estimators were tested first in order to verify the plausibility of the tests and to be able to define appropriate thresholds to be applied in the online procedure. Then, the procedure was finalized on the basis of the results and the benefits from using the active compensation were studied by comparing the application with the use of a fixed number of 200 trials. The tests prepared for the evaluation are summarized in Table 1
.
Table 1. Evaluation of the novel procedure and the quality estimators applied. The estimators are evaluated fi rst to justify their use and to define appropriate criteria for the tests. Then, the benefi ts of using the compensated procedure are studied by comparing the application with the use of a fi xed number of 200 trials.
The plausibility of the SNR estimator was evaluated by comparing the application with the use of a one-sample t-test. The t-test was made for the N1 component of the average AERP waveform. N1 was parameterized using an average time window of 40 ms placed at the peak maximum of an individual waveform at 80–140 ms. First, the SNR was computed as a function of the statistical significance of noise in order to determine a criterion that would correspond to the t-test (pnoise < 0.05). Then, both parameters were applied to estimate the required number of trials to obtain a statistically significant response in order to see how they match. In order to justify the use of the SNR test, the correlation was supposed to be high. The limit for approval was chosen to be 0.8, which indicates high correlation.
The measurement error estimators were evaluated by studying their relevance to the validity of the measurement outcome. First, the estimators were computed as a function of the validity of the respective partial averages. Then they were compared on the basis of the sensitivity, distortion and the amount of the calculus required. Validity was estimated by the correlation of the partial averages and the expected outcome. The expected outcome was estimated by computing the sorted average (Rahne et al., 2008
) of each dataset. The trials were sorted on the basis of the respective interference level and they were averaged starting from the best one, until the SNR of the average started to decrease. The remaining trials were discarded and the average with the maximum SNR was considered to be the optimal outcome. Sorted averaging maximizes the SNR of the average curve (Rahne et al., 2008
). Thus, it was considered to be a well-suited reference for the test.
The last parts of the evaluation dealt with the actual application of the procedure. First the use of the selected measurement error estimator was studied with respect to the feasibility in order to define two alternative threshold values for the test. Two such values were defined: one that would lead to recording 200 trials on average and one that represented the most stringent requirements still plausible in most cases (p = 0.6). Then, the application was simulated again with the concluded thresholds and the resulting test-retest reliability was compared with the results obtained when the total number of trials was fixed at 200. The feasibility was estimated by the probability of the requirements being reached with fewer than 300 trials on average. Test-retest reliability was computed using the one-way intra-class correlation coefficient (ICC), because it provides more accurate results than the simple Pearson’s correlation coefficient (Farahat et al., 2003
).
Evaluation of the SNR Test
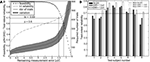
According to the results (Figure 2
A), in general, the SNR estimation indicated a smaller significance than the t-test and the correlation of the single observations was only moderate (p ≈ 0.5). A probable reason for this was that the SNR test assessed the average significance of noise in the whole waveform, while the t-test focused on a single peak in the response. On the other hand, the SNR estimator could still be applied to verify the realization of the significance criterion (pnoise < 0.05). Generally, it was met when the SNR exceeded 0.69. Using this value as a detection threshold, the required number of trials only exceeded the results from the t-test by 4 ± 17 (mean ± SD) trials (Figure 2
B). The correlation of the estimations was about 0.86, which suggests that the SNR estimator could be considered to be plausible.
Figure 2. Estimation of the contribution of noise using the one-sample t-test and SNR estimator. (A) Estimated SNR as a function of the statistical significance of noise (pnoise) that was estimated using the one sample t-test. (B) The number of trials required to realize the significance criterion on the basis of the one sample t-test (pnoise < 0.05) and the SNR test (SNR > 0.69).
Evaluation of the Measurement Error Estimators
According to the results (Figure 3
), the convergence-based estimate was a linear function of the validity, while the direct estimate had a quadratic relation. Thus, the convergence-based estimator would be simpler to apply. On the other hand, both estimators were quite distorted and the direct estimator was more sensitive (3.6 µV/unit) than the other one (0.42 µV/unit). In this respect, the direct estimate would be a better choice. In terms of computation time, the difference between the alternatives was considered to be insignificant. They both included an update operation, difference calculation and finding the maximum. The direct estimator also included an additional absolute value operation which, however, did not cause significant difference to the computation time. Thus, as a whole, the direct estimator was considered to be preferable and was chosen to be implemented into the procedure.
Figure 3. The remaining measurement error as a function of the validity of the respective partial average with respect to the expected outcome. (A) The remaining error assessed using a convergence rate-based estimator. (B) The remaining error assessed using a direct estimator.
Evaluation of the Feasibility and the Influence on the Test-Retest Reliability
Figure 4
A presents the required number of trials, the feasibility of the test, and the test-retest reliability with respect to the remaining measurement error as given by the direct error estimate. The criterion that is achieved with 200 trials on average is 1.5 µV and the criterion that has a feasibility of 0.6 is 1.2 µV. These values were applied in the last phase of the evaluation. The resulting test-retest reliabilities in the simulated repeated experiments are presented in Figure 4
B.
Figure 4. Influence of the compensation on the test-retest reliability. (A) Test-retest reliability (ttr), feasibility of the requirements (p), and the required number of trials as a function of the remaining measurement error. (B) Test-retest reliability obtained when the number of trials recorded was constant (N = 200) and when the novel procedure was applied withan error threshold of 1.5 µV and 1.2 µV. Mean test-retest reliabilities across the test subjects are indicated with horizontal lines.
On the basis of the results (Table 2
), the variation in the test-retest reliability between test subjects was reduced by 0.1 and the average test-retest reliability was improved by 0.01–0.06, depending on the measurement error threshold applied. The required number of trials in the novel procedure was 209 ± 60 (mean ± SD) when the threshold was 1.5 µV and about 310 ± 78 (mean ± SD) when the threshold was 1.2 µV. Thus, the variation between the test subjects was improved, although the average number of trials recorded was not greatly altered. The increase in the mean test-retest reliability, on the other hand, was achieved by increasing the number of trials. Thus, the feasibility dropped with the improved test-retest reliability.
Table 2. Results from the simulated series of repeated AERP experiments with eight test subjects. The tests were made by using the novel procedure (SNR > 0.69 and ERR < 1.5 μV/1.2 μV) and a comparative procedure (N = 200). Test-retest reliability (ttr) was estimated by using ICC. α represents the mean value, s represents the standard deviation and Δ represents the range of variation.
The results of this study show that the compensation for the variation in the data quality has significant relevance for the remaining measurement error and the reproducibility of the average AERPs. In the simulated series of repeated experiments, the test-retest reliability was improved by 2–9%, on average, and the variation in the value between the test subjects was reduced by 33–35%. In addition, the compensation also improved the measurement efficiency. When the number of trials recorded was a constant 200, the average resulting test-retest reliability was about 0.69. In the novel procedure, the number of recorded trials was optimized and similar results could be achieved with about 209 ± 60 (mean ± SD) trials, depending on the data quality. Thus, the length of the experiment could be decreased when the signal quality was high enough (about 40 % of simulation runs).
The findings of the study might be of practical interest particularly in the clinical context. On the one hand, the method suggested will simplify the comparison of results from repeated measurements. The level of distortion is minimized, while the number of trials is optimized. Thus, the differences between repeated measurements are more likely to occur because of the differences in the neuropsychological condition of the test subject. On the other hand, the improvement of the measurement efficiency is also an important factor. If the number of recorded trials is constant and the quality of the outcome is supposed to be high, the number of trials recorded must also be high in order to minimize the possibility of error. Some groups of patients, such as children or acutely ill patients, may not tolerate long experiments. The optimization of the number of trials prevents excessive recording, while the sufficiency of the data to obtain meaningful AERPs is still guaranteed. Thus, application of this kind of active compensation might reduce the negative impact of the investigation on them.
Regarding future developments, the efficiency of the method might be increased if the cleaning procedure and the artifact processing scheme were improved. Although most of the results were in line with each other, the results obtained using dataset 8 seem to deviate from the others. The estimation of the statistical significance was less accurate and the test-retest repeatability deviated from the others, particularly when the number of trials included was kept constant. This suggests that the variation in the quality of the data was higher than in the other datasets. Thus, the implementation of advanced means for signal processing might improve the quality of the results.
Conclusions
The findings of the study indicate that the method suggested could be applied to compensate for the changes in the quality between repeated AERP measurements. Practical investigations, however, are needed to confirm the results and to gain further information about application of the method, the possible issues and the impact in practice. From the practical perspective, the predefinition of the measurement error criterion is particularly interesting. The suitable threshold is application-specific and depends on the response studied. Thus, the recommendations have to be prepared case sensitively. In general, the successful implementation of the method requires high signal quality, a reliable method for online artifact rejection, and a device capable of both recording and analyzing the EEG data. The efficiency may be further improved by implementing an advanced tool for online data processing.
The authors declare that the research was conducted in the absence of any commercial or financial relationship that could be construed as giving rise to a potential conflict of interest.
We thank M. Linnavuo and P. Eskelinen for valuable discussions. The work was supported in part by the Graduate School of Electrical and Communications Engineering, the Society of Electronics Engineers and the Finnish Centre of Excellence in Interdisciplinary Music Research.
Duncan, C. C., Barry, R. J., Connolly, J. F., Fischer, C., Michie, P. T., Näätänen, R., Polich, J., Reinvang, I., and Van Petten, C. (2009). Event-related potentials in clinical research: guidelines for eliciting, recording, and quantifying mismatch negativity, P300, and N400. Clin. Neurophysiol. 120, 1883–1908.