Synaptic inhibition controls transient oscillatory synchronization in a model of the insect olfactory system

Introduction

The dynamics of neuronal networks have often been associated with the detection of changes in the environment or as markers of expected and ongoing behavior. In olfactory networks this association is particularly well charted. Odor detection begins when odorant molecules bind to olfactory receptors, initiating a second messenger cascade that leads to the opening of ion channels, the depolarization (usually) of the receptor neuron cell membrane (Matthews and Reisert, 2003), and the generation of action potentials. Olfactory receptor neurons (ORNs) are preferentially sensitive to some odors and less so to others (Anderson et al., 1995; Hallem et al., 2004; Hallem and Carlson, 2006). This preference appears to be static, in that, odor rank orders are retained throughout the duration of the stimulus (Friedrich and Laurent, 2001; Bhandawat et al., 2007; Olsen et al., 2007). Chemically similar odors elicit responses from overlapping groups of ORNs that project onto a significantly smaller number of excitatory projection neurons (PNs) and inhibitory local interneurons (LNs) in the antennal lobe (AL). It has been suggested that the representation of a high dimensional, complex and as a first approximation, static input by convergence onto a few, albeit dynamic, PNs and LNs must enhance the fidelity of the input while unfolding the odor representation along the temporal dimension (Laurent, 2002) [In the locust ∼50,000 ORNs converge onto ∼900 PNs and 300 LNs (Ernst et al., 1977)]. In the AL, LNs extend extensive connections to PNs and to each other (Leitch and Laurent, 1993, 1996). The interaction between AL neurons produces spatiotemporal activity that evolves over multiple time scales (Laurent et al., 1996; Wehr and Laurent, 1996; Wilson et al., 2004). This evolution produces a progressive decrease in the overlap between the representations of chemically related odors (for example, several aromatic amino acids) (Friedrich and Laurent, 2001; Wilson et al., 2004) thereby increasing the ability of the system to discriminate between odors.

Local field potentials (LFP) recordings from different insects including locust (Laurent and Davidowitz, 1994; Laurent et al., 1996; Wehr and Laurent, 1996), moth (Ito et al., 2009), honeybee (Stopfer et al., 1997) and fly (Tanaka et al., 2009) have revealed fast 20–40 Hz oscillations that persist in spite of large changes in both the identity and the concentration of an odor (Stopfer et al., 2003). Successive oscillatory cycles are constructed from a dynamically evolving constellation of PN spikes. Odor attributes determine the identity of PNs that spike during a given oscillatory cycle. A given PN may be phase locked to specific cycles following the onset of an odor and spike randomly or remain silent during other cycles. Such transient synchronization between PNs was suggested to play a key role in encoding the odor representation (Laurent, 2002). Spatiotemporal patterns generated by PNs provide input to Kenyon cells (KCs) of the mushroom body via two pathways, a direct excitatory pathway from PNs to KCs and a feed-forward inhibitory pathway leading from lateral horn interneurons (LHIs) (Perez-Orive et al., 2004). Recent studies have also identified the role of a single neuron (the giant GABAergic cell) that provides feedback inhibitory input to KCs (Papadopoulou et al., 2011) (Figure 1).

FIGURE 1

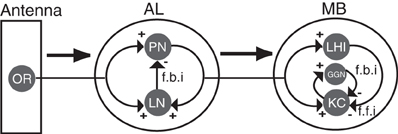
Figure 1. Schematic of the insect olfactory system. Projection neurons (PNs) and local inhibitory interneurons (LNs) receive convergent input from odorant receptor (OR) neurons. Output from PNs is sent to Kenyon cells (KCs) of the Mushroom body (MB) and that also receive feed-forward inhibition from lateral horn interneurons (LHI). Giant GABAergic neuron (GGN) provides feedback inhibition to KCs.

In this article we discuss the relationship between the structure of the AL network and the dynamics that emerges from it, within the context of our earlier theoretical studies (Bazhenov et al., 2001a,b; Assisi et al., 2011). The efficacy and the relevance of the AL in representing an odor can only be inferred from its effect on subsequent layers, namely the KCs of the mushroom body. In contrast to PNs that fire promiscuously in response to an odor input, KCs generate a sparse and highly odor specific response. Owing to the intrinsic properties of KCs and network attributes (Perez-Orive et al., 2002, 2004), these neurons act as coincidence detectors of presynaptic input; KCs respond only to PN input that arrives during short windows of time bounded by the troughs of an oscillatory LFP cycle (Perez-Orive et al., 2002, 2004). If the same subset of PNs spike synchronously throughout an odor presentation, the odor would completely specified by identity of active PNs (an identity code) and the same post-synaptic KCs would be activated in every cycle. However, in vivo recordings from the locust AL show that different subsets of PNs are recruited and become transiently synchronized during different cycles of the LFP oscillation in a manner that is predictive of attributes of the odor. Thus, not only the identity of neurons that spike, but also the timing at which the spikes occur factor in encoding the odor representation (a spatiotemporal code).

Within the framework discussed here, the odor input is considered to be static and it stimulates the same set of PNs and LNs throughout the duration of the stimulus. This provides a useful first approximation to understand odor coding by the AL. Network interactions in the AL ensure that, different odors and odor attributes result in different spatiotemporal patterns of PN activity that, in turn, trigger different KC responses (Stopfer et al., 2003). Transient synchrony of AL neurons serves an important computational idea—it vastly expands the number of states available to encode odors when compared to a purely identity code. The upper bound on the number of states of the system increases as a power of the duration (measured in oscillatory cycles of the LFP) of the stimulus presentation. This could allow small differences in input to be amplified in a manner that it can be read out by KCs. While the animal need not, necessarily, take full advantage of this increased computational power, there is evidence to suggest that transient patterning plays a role in odor discrimination, particularly during difficult discrimination tasks (MacLeod et al., 1998).

Our goal is to elucidate the intrinsic and network mechanisms that are responsible for transient synchrony seen in the AL network. In particular we elaborate the specific role played by the inhibitory sub-network of the AL in facilitating the formation of transiently synchronous ensembles of PNs. In previous papers we have conjectured that the operational principles that govern the dynamics of the AL network include competition between LNs that generates epochs of time where specific LN sub-sets are activated. These, in turn, transiently entrain PNs that provide synchronous input to KCs (Bazhenov et al., 2001b; Assisi et al., 2011). This focused review further discusses and extends our theoretical ideas regarding odor coding in insect olfaction.

Methods

Individual LNs and PNs were modeled by a single compartment with voltage and Ca²⁺ dependent currents described by Hodgkin-Huxley kinetics. The model LNs and PNs were constructed in order to closely emulate the experimentally observed dynamics of LNs and PNs using a parsimonious conductance based model [see (Bazhenov et al., 2001b) for a detailed description of the model parameters]. In vivo, PNs show overshooting sodium spikes in response to a constant depolarizing stimulus. LNs in contrast, generate low amplitude calcium spikelets that demonstrate spike frequency adaptation due to a Ca²⁺ dependent potassium current. Fast GABA (LN-PN and LN-LN connections) and nicotinic cholinergic synaptic currents (PN-LN connections) were modeled by first-order activation schemes. In addition to fast GABAergic synapses PNs in the AL are known to receive slow inhibitory input via GABA_B type conductances (Bazhenov et al., 2001a; Wilson and Laurent, 2005). These slow responses tend to last over durations of 100 s of ms and generate long epochs when the neuron is hyperpolarized. However, since we were largely interested in how transient synchrony occurs on a fast time scale (lasting the duration of a few oscillatory cycles <100 ms) we chose to minimize the contributions of this slow form of inhibition. The specific connectivity of the networks and the excitatory and inhibitory coupling strengths were varied in individual simulations. The values are specified with individual figures. The model equations and other parameter values are specified in (Assisi et al., 2011). In the insect olfactory system, odor stimulation activates odor specific subset of PNs and LNs. In this study, to focus on the network driven spatiotemporal dynamics, we considered simplified stimulus model—a suprathreshold input was simultaneously provided to all PNs and LNs. The amplitude of this input was constant across all neurons except for a low amplitude additive noise term (∼5% of the stimulus amplitude).

The Role of Inhibition in the Dynamics of Small Networks

To understand the role of inhibition in generating transiently synchronous groups of PNs we first considered the dynamics of a reciprocally coupled pair of neurons consisting of an LN that inhibits a PN and receives excitatory input from it (Figure 2A). Both these neurons received identical depolarizing input that exceeded the spiking threshold of each neuron. The reciprocally coupled pair oscillated out of phase with a frequency of ∼25 Hz. The frequency of oscillation can vary as a function of the strength of the inhibitory coupling to the PN [see Figure 2 in (Bazhenov et al., 2001b) for a detailed description]. We sought to determine the extent of PN entrainment by the inhibitory LN and the strength of inhibitory synaptic coupling required to entrain the PN. In order to quantify these features we measured the instantaneous phase of the LN by first filtering the LN membrane potential (Figure 2A, black line in the top trace) through a band pass filter (15–40 Hz) and calculating the Hilbert transform (Figure 2A, middle trace) of the resulting smoothed trace (Figure 2A, gray line in the top trace). The instantaneous phase thus determined was sampled at times when the PN generated a spike (red circles in Figure 2A, middle trace). We simulated this simple network over 20 s and calculated the distribution of these phase points corresponding to the times when the PN generated a spike (Figure 2B). The spread of the distribution provided a measure of the degree to which the LN entrained the dynamics of the PN (Figure 2D). As we varied the strength of the inhibitory synaptic coupling, the circular standard deviation of the phase of PN spikes with respect to the LN oscillation decreased until, at a specific value of g_GABA−A, it abruptly dropped from ∼1.0–∼0.05 radians followed by a gradual monotonic decrease (Figure 2D). The effect of an LN spike was to shift the onset of the following PN spike to a later phase of the oscillation as the coupling strength increased (Figure 2C). The mean phase of the distribution moved toward the peak of the LN oscillatory cycle. Thus individual PNs can be entrained by its coupling to a single LN if the strength of the inhibitory input exceeds a specific threshold.

FIGURE 2

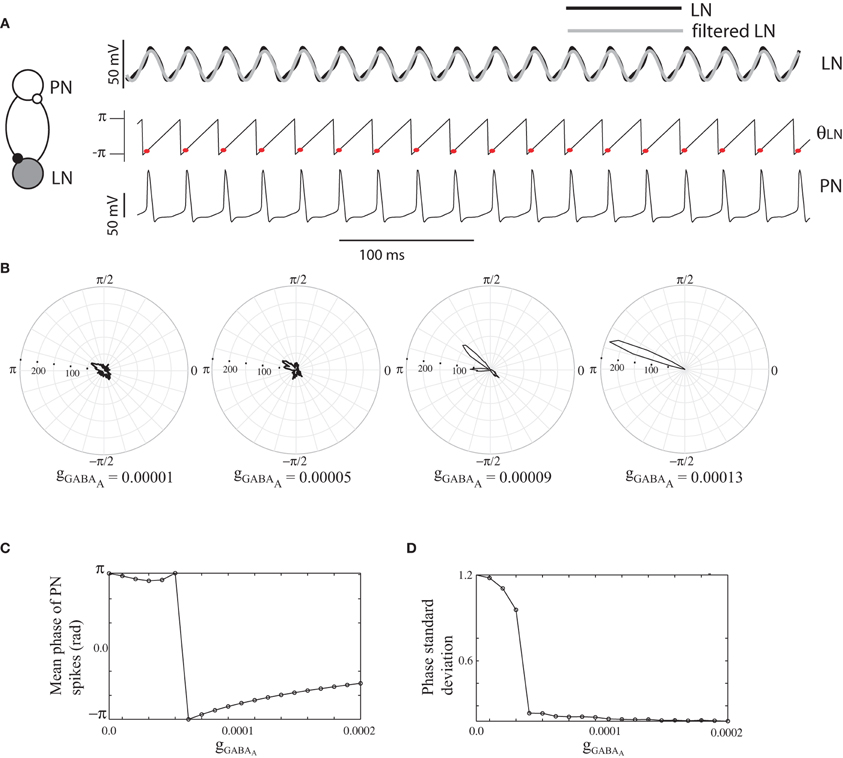
Figure 2. (A) Single PN-LN pair. The top trace shows the membrane potential of the LN (black) and a frequency filtered version (gray trace, bandpass filter 10–40 Hz). The middle trace plots the instantaneous phase of the filtered LN membrane potential. The red dots show the value of the instantaneous phase at times when the PN generates a spike. The membrane potential of the PN is shown in the bottom trace. g_ACh (PN-LN) = 0.00001. (B) Phase distribution of PN spikes. The histogram shows the distribution of the phase at which the PN spikes for different values of the strength of inhibitory coupling from LN to PN (g_GABA-A). The distribution was generated over 20 s. (C) Mean phase of PN spikes. The mean phase at which the PN spikes is shown as a function of the inhibitory coupling strength. (D) The circular standard deviation of the phase as a function of the inhibitory coupling strength.

Next we sought to determine the collective dynamics of multiple PNs, all receiving identical inhibitory input from a single LN. We simulated a network of 10 PNs that were inhibited by a single LN and provided excitatory input to it (Figure 3A). Here too we found that the collective dynamics of all PNs was strongly entrained by the LN oscillations when the strength of the inhibitory coupling exceeded a threshold value (Figures 3B,C). The standard deviation of the phase at which the PNs generated spikes abruptly decreased as the strength of inhibitory coupling increased. The dynamics of the PNs however showed complex patterns of activity relative to the LN (Figure 3D). For different values of the coupling strength, a given PN could show phase drift relative to the LN oscillations, multi-frequency phase locking and, for the strongest coupling strengths, 1:1 phase locked dynamics (Figure 3D).

FIGURE 3

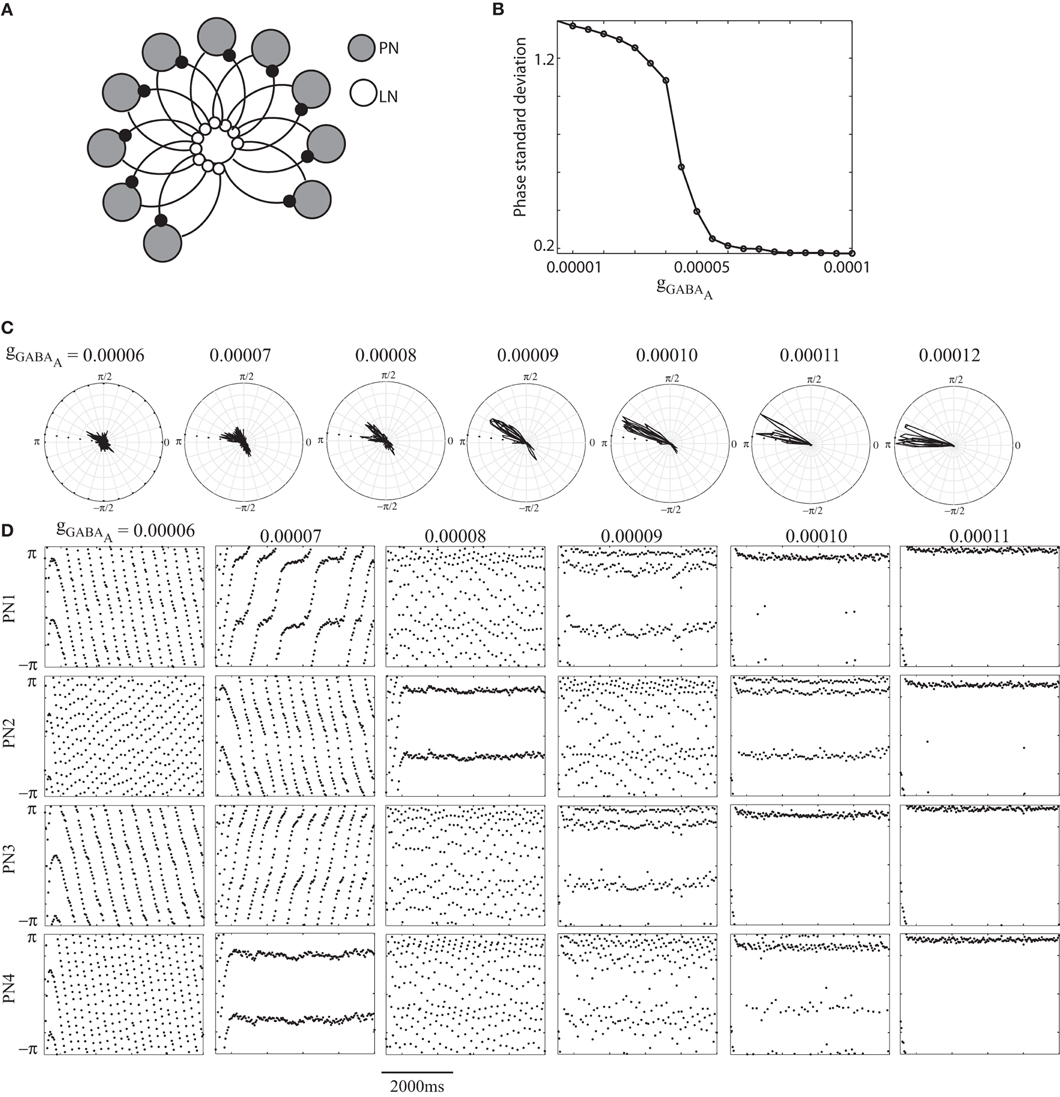
Figure 3. (A) Network consisting of a single LN inhibiting 10 PNs. The LN receives excitatory input from all PNs. g_ACh (PN-LN) = 0.00001, g_GABA-A (LN-LN) = 0.00001. (B) The standard deviation of the PN spike phases as a function increasing strength of inhibitory coupling. (C) The distribution of the phase of PN spikes for different values of g_GABA-A. (D) PN dynamics. Each dot in a panel corresponds to the instantaneous phase of a PN spike at a given time. The phase dynamics of 4 PNs of the 10 PNs simulated is shown. Each column of panels corresponds to a different value of g_{GABA-A (LN-PN)}.

These simulations show that LNs can effectively entrain the dynamics of PNs. Therefore, we hypothesize that transient synchrony between PNs, as seen in experimental recordings in the locust AL, must, to a significant extent, be driven by its interaction with the LN sub-network. Evidence for this assertion also comes from experiments where the influence of fast inhibition mediated by GABA_A was selectively abolished by the application of GABA_A antagonist picrotoxin (Stopfer et al., 1997). This had the effect of curtailing a prominent 20 Hz oscillation that is ubiquitous during odor stimulation. Since the experimentally measured oscillatory local field potential can be viewed as the synchronized activity of ensembles of PNs, we can, as subsequent modeling studies have (Bazhenov et al., 2001b), infer that inhibition indeed entrains PN activity. Our simulations (Figures 2 and 3) examine the extent of this entrainment over a broader parameter range than that simulated in earlier studies (Bazhenov et al., 2001b; Assisi et al., 2011). Furthermore, reciprocal inhibition between LNs can enforce competition between groups of inhibitory neurons. This would lead to some groups of LNs being activated in response to an odor, while other groups are quiescent or hyperpolarized by the active LNs (Assisi et al., 2011). Transient synchrony within groups of LNs, coupled with their ability to drive the activity of PNs provides a potential mechanism that explains the observed spatiotemporal patterning of PNs in the AL (see more on this below).

The role of inhibition in synchronizing the activity of excitatory PNs has also been examined models of Limax (Ermentrout et al., 1998) and honeybee (Linster and Cleland, 2001). Synchronization driven by inhibition is not limited to olfactory networks. In the hippocampus, GABAergic neurons form the hubs of a network that synchronizes the activity of pyramidal cells (Bonifazi et al., 2009). Feedback inhibition mediated by LNs can effectively synchronize distributed pyramidal cells, a mechanism termed pyramidal interneuronal network gamma (PING) (Borgers and Kopell, 2003, 2005; Borgers et al., 2005). This mechanism has also been implicated in the generation of gamma band synchrony (Llinas and Ribary, 1993; Singer and Gray, 1995; Wang and Buzsaki, 1996).

Reciprocal Inhibition can be Related to the Coloring of the Network

The two LNs in Figure 4 reciprocally inhibit each other. Over a wide range of parameters these neurons would tend to spike out of phase [see (Vreeswijk et al., 1994) for exceptions]. When one of the neurons generated a burst of spikes it suppressed activity in the other neuron. In the network simulated above, which neuron spikes is determined by the calcium concentration in the cell. Increased intracellular Ca²⁺ signals a lower propensity for firing (see (Ahn et al., 2010) for a detailed view of the effects of Ca²⁺ on the spiking pattern). We have shown that burst alternation was determined by the activation of Ca²⁺-dependent K⁺ currents (Assisi et al., 2011). Each spike led to an increase in the Ca²⁺ concentration within a cell and additional K (Ca²⁺) activation that consequently delayed the onset of the following spike, a phenomenon known as spike frequency adaptation. When the frequency of spiking reduced below certain threshold, the inhibition provided by this neuron was not sufficient to keep the other neuron from spiking; as a result, the quiescent neuron switched to an active state and suppressed activity in the post-synaptic neuron. Antagonistic interactions between reciprocally coupled inhibitory neurons allowed us to derive a relationship between the dynamics of neurons and a structural characteristic of the underlying network, namely, its coloring.

FIGURE 4

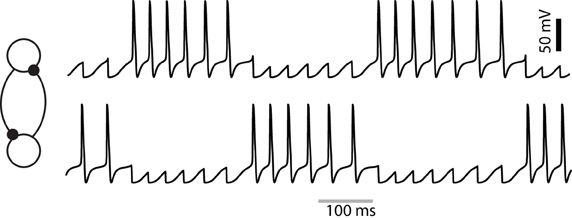
Figure 4. A pair of reciprocally coupled LNs generate alternating patterns of spikes. The two traces correspond to different LNs shown in the figure.

A coloring of the network is a prescription that assigns different colors to nodes (neurons) that are directly connected to each other (Chartrand, 1984). The minimum number of colors required to color a network is known as its chromatic number. In the example above, the two neurons are reciprocally coupled and therefore must be assigned different colors. If the coupling between neurons is inhibitory, we anticipate that neurons associated with different colors, upon stimulation by the same depolarizing input, will compete with each other and generate spikes (or bursts of spikes) at different times. In contrast, neurons that do not compete (are associated with the same color) will spike in approximate synchrony. This relationship between the coloring and the dynamics of the inhibitory network is clearly evident in the simple network constructed in Figure 4. However, does this relationship generalize to larger and more complex networks? To address this question we constructed networks that possessed the required coloring [see (Assisi et al., 2011)]. For example to construct a network with two colors, we generated two groups of neurons that were all-to-all connected across groups but possessed no connections within groups. Figure 5A1 shows an example of one such network consisting of 40 neurons with 20 being associated with one color and the remaining with another color. The adjacency matrix of this network consisted of two 20 × 20 diagonal blocks of zeros and ones in all other locations (Figure 5A2). The diagonal blocks of zeros are the shaded regions of the adjacency matrices shown in Figure 5A2. The dynamics of this network with chromatic number, two, clearly showed that neurons associated with different colors generated an alternating pattern of activity (Figure 5A3). The antagonistic interactions between inhibitory groups persisted even as the number of colors increased (Figure 5B).

FIGURE 5

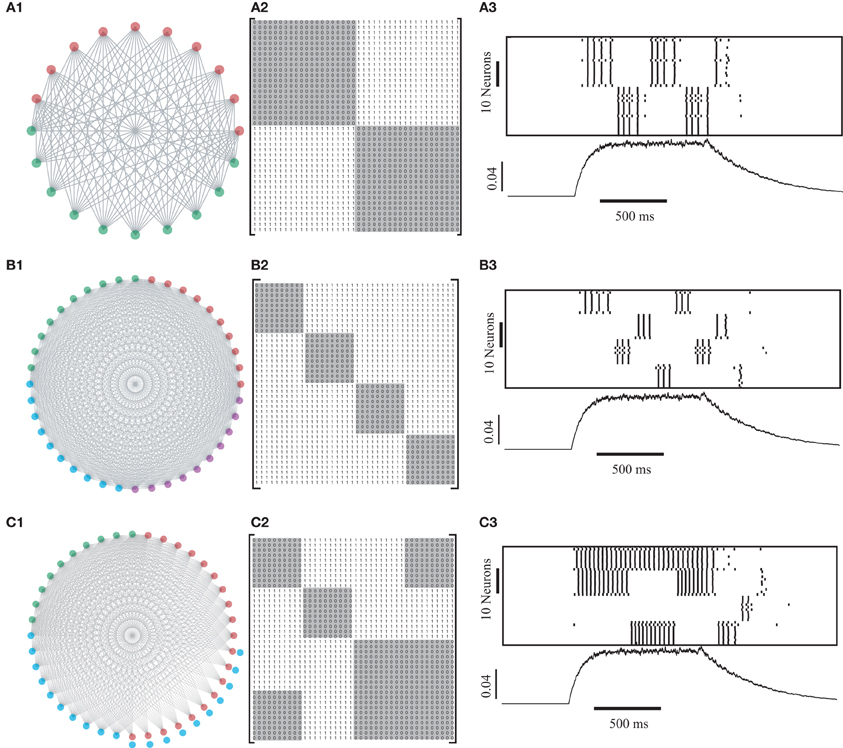
Figure 5. Dynamics of a network of reciprocally connected inhibitory LNs. (A) Bipartite graph with chromatic number 2. Each LN is reciprocally connected to all the neurons that are associated with a color different from its own (A1). The adjacency matrix of the network consists of diagonal blocks of zeros with ones elsewhere (A2). Raster plot showing the activity of 40 neurons in response to identical input to all the neurons. LNs associated with the same color spike in approximate synchrony (A3). The traces below the raster plots in Aiii, Biii, Ciii show the input that is given to all the inhibitory neurons. The parameter values used for this simulation were g_GABA-A (LN-LN) = 0.00007. (B) A graph with four colors can be constructed by picking four groups of neurons that do not extend connections within a group but possess all to all reciprocal inhibitory connections with other groups (B1). The adjacency matrix consists of four diagonal blocks of zeros with ones elsewhere (B2). As in the previous case neurons associated with the same color tend to spike in synchrony (B3) (g_GABA-A (LN-LN) = 0.00007). (C) Graph with multiple colorings. Three groups of neurons possess all-to-all reciprocal connections between groups. A fourth group of neurons extend connections only to the group marked in green and not to the others. Therefore, it may be associated with the blue or the red group (C1). Neurons associated with this group tend to spike in synchrony with either the red or the blue group but remain silent when the green groups spikes (C3) (g_GABA-A (LN-LN) = 0.00002). The corresponding adjacency matrix is shown in C2.

A number of experimental recordings show that PNs, and therefore LNs that entrain them, form transiently synchronous groups over the duration of an odor. A given PN may participate in more than one synchronous group. In Figures 5A and 5B, however, we show that a given LN associated with a particular color, can only spike in synchrony with LNs that share the same color and not with any other group. If LNs indeed drive the synchrony of PN spikes (see below), this would imply that the constitution of every synchronously spiking group of PNs would never change. One can circumvent this issue by constructing networks that possess multiple colorings. For example, the network in Figure 5C1 has chromatic number three. However, in contrast with the networks shown in Figures 5A and 5B, this network (Figure 5C1) can be colored using three colors in two different ways. A group of ten neurons in Figure 5C1 can be colored either red or blue but not green since these neurons are connected to the green group but not to the other two. The adjacency matrix of this network has three 10 × 10 diagonal blocks of zeros in addition to some off-diagonal blocks of zeros (Figure 5C2) [see Figure 3 in (Assisi et al., 2011) for a simplified rendering of this graph where all neurons associated with a color are grouped into a single node]. The dynamics of this network under constant and identical deploarizing input to all neurons evolves such that the group of neurons that can be colored using multiple colors spikes in synchrony with both the red and the blue groups while falling silent when the green group of neurons spike. Multiple colorings can therefore be associated with transient synchrony where individual neurons can participate in multiple synchronous groups as seen in experiments. This example also shows that the neurons in the inhibitory network do not have to be directly connected to each other to spike asynchronously.

While our simulations show that antagonistic interactions between LNs generates clusters of synchronously spiking neurons that respect the coloring of the network, this need not always be the case. In all-to-all connected (Golomb and Rinzel, 1993; Wang and Buzsaki, 1996) and random networks (Wang and Buzsaki, 1996), the dynamics can depend on the interaction of intrinsic (spike afterhyperpolarization, heterogeneities in spiking frequency) and synaptic (reversal potential, synaptic current decay time, sparseness of connections) factors. Clustered solutions of the type observed here form a sub-set of the full dynamical repertoire of purely inhibitory networks. Heterogeneities in network structure [Figure 6 in (Assisi et al., 2011)] and dense connectivity between neurons, resulting in a larger number of colors [Figure 2 in (Assisi et al., 2011)] can perturb the coloring based dynamics of the system. However, the inclusion of feedback excitation has been shown to reduce the extent of this perturbation [Figure 4 in(Assisi et al., 2011)].

FIGURE 6

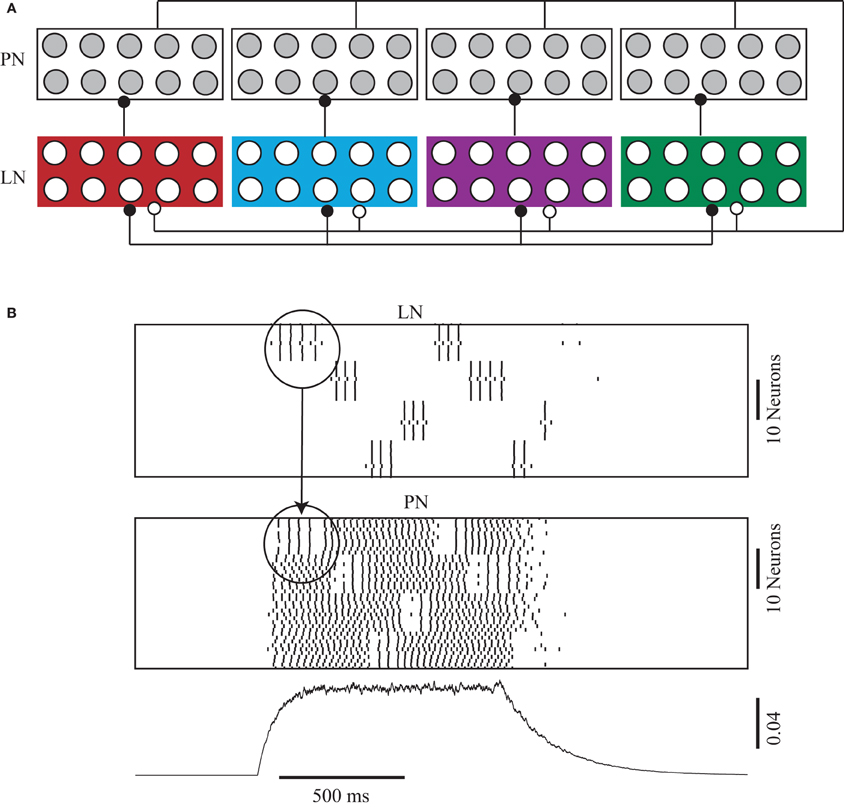
Figure 6. (A) A network of LNs with chromatic number 4 is connected to a population of PNs. The PNs were separated into four groups. Each group received inhibitory input only from LNs that were associated with one color and not others. The PNs provided excitatory input to all LNs irrespective of the coloring. (g_GABA-A (LN-LN) = 0.00004, g_GABA-A (LN-PN) = 0.00006, g_Ach (PN-LN) = 0.00004). (B) PNs (top raster) that received inhibitory input from LNs (bottom raster) of a particular color tended to spike synchronously only when those LNs were activated. The black trace at the bottom shows the input provided to all PNs and LNs.

Transient Synchrony in Projection Neurons is Driven by the Inhibitory Sub-Network

In our simulations we showed that feedback GABAergic inhibition mediated by LNs could entrain PNs to spike in synchrony (Figures 2 and 3). Further, reciprocally coupled networks of LNs could, as determined by the coloring of the network, form transiently synchronous groups that moved in and out of synchrony with each other over the duration of the odor input (Figures 4 and 5). In what follows we show that these groups of LNs can entrain PNs to generate the kind of transiently synchronous dynamics seen in recordings from PNs in the locust AL. This entrainment is seen in PNs regardless of whether the LN networks are uniquely colored or possess multiple colorings. We constructed a network consisting of forty PNs and forty LNs. The LN sub-network consisted of four groups (colors) of neurons that were all-to-all connected across groups but received no connections from within each group (Figure 5B). Each LN group provided inhibitory input to one of four groups of PNs but received excitatory input from all the PNs (Figure 6A). Non-oscillatory external input (Figure 6B, bottom panel) triggered ∼30 Hz non-synchronous spiking in all PNs of the network (Figure 6B, middle panel). As expected, the LNs generated an alternating pattern of activity consistent with the coloring of the underlying network (Figure 6B, top panel). Each burst of spikes by an active LN group synchronized the activity of post-synaptic PNs. As a result, all PNs that received input from an active LN group showed synchronized ∼20 Hz oscillations (Figure 6B, middle panel). When the group of LNs became quiescent the post-synaptic PNs drifted from synchrony during subsequent epochs of time when other LN groups generated spikes. These dynamics lead to a complex pattern of synchronization where different groups of PNs became synchronized during different epochs of odor stimulation.

Discussion

We demonstrated that competitive interactions between LNs can lead to the formation of groups of synchronously spiking LNs that can effectively entrain the dynamics of PNs. The identity of LNs that participate in each group is determined by a characteristic feature of the connectivity structure of the inhibitory network, namely, its coloring. Our simulations in Figure 6 demonstrate that spikes generated by PNs are phase locked to the dynamics of those LNs that provide direct inhibitory input to it. The degree of PN synchronization is dependent on the strength of the inhibitory coupling from LNs. In simple networks consisting of a single inhibitory neuron that was reciprocally connected to multiple PNs, we demonstrated multi-frequency coordination between PNs and the LN. Multifrequency coordination has also been reported in Lotka-Volterra models with competing interactions between the nodes (Rabinovich et al., 2006). Such dynamics clearly defines a widening of the dynamical repertoire of that these networks are capable of.

The critical feature of out model is that the strongest inhibition determines the identities of PNs that “talk” to the downstream neurons in the mushroom bodies. Indeed only PNs that receive sufficiently strong inhibition can (transiently) synchronize and drive responses in the KCs that operate as spike coincidence detectors. Therefore, we can classify our model as multiplicative—the input from olfactory receptor neurons to PNs is multiplied by feedback inhibition within AL to determine which PNs transmit information to the mushroom body. PNs receiving sensory input but no inhibitory feedback cannot reach the mushroom bodies. This is in contrast to some other theoretical models of olfactory processing (in vertebrates) where inhibition balances excitation in many principal neurons of the olfactory bulb and only the “error” signal is transmitted to the subsequent level—piriform cortex (Koulakov and Rinberg, 2011).

A long-standing conjecture in neuroscience has been that neuronal networks possess mechanisms that can string groups of synchronously spiking neurons into elaborate temporal sequences (Hebb, 1949). These spatiotemporal patterns, termed phase sequences, then form the basis of all perception (Gray and Singer, 1989), memory (Cheng and Frank, 2008) and action (Bouyer et al., 1987). Here we demonstrated that the coloring of the network determines the identity of neurons that spike together. However, the coloring does not place any specific constrains on the sequence in which successive groups of neurons are recruited. The occurrence of a specific sequence of spiking is influenced by the nature of the input, the history, and the current state of the network. In the inhibitory networks simulated here the intracellular Ca²⁺ concentration within a cell plays a prominent role in determining the order in which groups of neurons generate spikes. The lowest Ca²⁺ concentration determined the minimal activation of Ca²⁺ dependent K⁺ currents and, therefore, the most excitable group of LNs (Ahn et al., 2010; Assisi et al., 2011). In all the simulations in this paper we introduced a small amount of variability in the intrinsic properties across PNs and LNs to ensure that the network dynamics does not settle into a pathological and unstable state. This variability could potentially lead to asymmetries that define a specific ordering of the PN sequences. Explicitly imposed asymmetries in the properties of the neurons such as the excitability of different groups (either intrinsic or stimulus-dependent) could be used to enforce the stability of some sequences in lieu of myriad others that could also be present in the completely symmetric network. Finally, the LN networks simulated here possessed reciprocal connections between pairs. Directional connectivity between neurons is known to introduce a strong asymmetry in the network and restricts number of stable sequences of activity. This can be used to construct networks that possess a priori specified patterns of activity.

Our study revealed a link between the structure of the excitatory-inhibitory network and its dynamics. It presents a new approach to understand how the dynamics of the network can be predicted from the connectivity and may lead to strategies that could allow us to infer the connectivity of the network from its observed dynamics.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgment

This research is supported by grant from NIH-NIDCD.

References

Ahn, S., Smith, B. H., Borisyuk, A., and Terman, D. (2010). Analyzing neuronal networks using discrete-time dynamics. Physica D 239, 515–528.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Anderson, P., Hansson, B. S., and Lofquist, J. (1995). Plant-odour-specific receptor neurones on the antennae of female and male spodoptera littoralis. Physiol. Entomol. 20, 189–198.

Assisi, C., Stopfer, M., and Bazhenov, M. (2011). Using the structure of inhibitory networks to unravel mechanisms of spatiotemporal patterning. Neuron 69, 373–386.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bazhenov, M., Stopfer, M., Rabinovich, M., Abarbanel, H. D., Sejnowski, T. J., and Laurent, G. (2001a). Model of cellular and network mechanisms for odor-evoked temporal patterning in the locust antennal lobe. Neuron 30, 569–581.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bazhenov, M., Stopfer, M., Rabinovich, M., Huerta, R., Abarbanel, H. D., Sejnowski, T. J., and Laurent, G. (2001b). Model of transient oscillatory synchronization in the locust antennal lobe. Neuron 30, 553–567.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bhandawat, V., Olsen, S. R., Gouwens, N. W., Schlief, M. L., and Wilson, R. I. (2007). Sensory processing in the Drosophila antennal lobe increases reliability and separability of ensemble odor representations. Nat. Neurosci. 10, 1474–1482.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bonifazi, P., Goldin, M., Picardo, M. A., Jorquera, I., Cattani, A., Bianconi, G., Represa, A., Ben-Ari, Y., and Cossart, R. (2009). GABAergic hub neurons orchestrate synchrony in developing hippocampal networks. Science. 326, 1419–1424.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Borgers, C., Epstein, S., and Kopell, N. J. (2005). Background gamma rhythmicity and attention in cortical local circuits: a computational study. Proc. Natl. Acad. Sci. U.S.A. 102, 7002–7007.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Borgers, C., and Kopell, N. (2003). Synchronization in networks of excitatory and inhibitory neurons with sparse, random connectivity. Neural Comput. 15, 509–538.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Borgers, C., and Kopell, N. (2005). Effects of noisy drive on rhythms in networks of excitatory and inhibitory neurons. Neural Comput. 17, 557–608.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bouyer, J. J., Montaron, M. F., Vahnee, J. M., Albert, M. P., and Rougeul, A. (1987). Anatomical localization of cortical beta rhythms in cat. Neuroscience 22, 863–869.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Buzsáki, G. (2008). Neural inhibition. Scholarpedia 9.

Pubmed Abstract | Pubmed Full Text

Buzsáki, G., and Chrobak, J. J. (1995). Temporal structure in spatially organized neuronal ensembles: a role for interneuronal networks. Curr. Opin. Neurobiol. 5, 504–510.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Chartrand, G. (1984). Introductory Graph Theory. New York, NY: Dover Publications.

Cheng, S., and Frank, L. M. (2008). New experiences enhance coordinated neural activity in the hippocampus. Neuron 57, 303–313.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ermentrout, B., Flores, J., and Gelperin, A. (1998). Minimal model of oscillations and waves in the limax olfactory lobe with tests of the model's predictive power. J. Neurophysiol. 79, 2677–2689.

Pubmed Abstract | Pubmed Full Text

Ernst, K. D., Boeckh, J., and Boeckh, V. (1977). A neuroanatomical study on the organization of the central antennal pathways in insects. Cell Tissue Res. 176, 285–306.

Pubmed Abstract | Pubmed Full Text

Friedrich, R. W., and Laurent, G. (2001). Dynamic optimization of odor representations by slow temporal patterning of mitral cell activity. Science 291, 889–894.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Golomb, D., and Rinzel, J. (1993). Dynamics of globally coupled inhibitory neurons with heterogeneity. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics 48, 4810–4814.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gray, C. M., and Singer, W. (1989). Stimulus-specific neuronal oscillations in orientation columns of cat visual cortex. Proc. Natl. Acad. Sci. U.S.A. 86, 1698–1702.

Pubmed Abstract | Pubmed Full Text

Hallem, E. A., and Carlson, J. R. (2006). Coding of odors by a receptor repertoire. Cell 125, 143–160.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hallem, E. A., Ho, M. G., and Carlson, J. R. (2004). The molecular basis of odor coding in the Drosophila antenna. Cell 117, 965–979.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hebb, D. O. (1949). The Organization of Behavior. New York, NY: John Wiley and Sons.

Ito, I., Bazhenov, M., Ong, R. C., Raman, B., and Stopfer, M. (2009). Frequency transitions in odor-evoked neural oscillations. Neuron 64, 692–706.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Koulakov, A. A., and Rinberg, D. (2011). Sparse incomplete representations: a potential role of olfactory granule cells. Neuron 72, 124–136.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Laurent, G. (2002). Olfactory network dynamics and the coding of multidimensional signals. Nat. Rev. Neurosci. 3, 884–895.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Laurent, G., and Davidowitz, H. (1994). Encoding of olfactory information with oscillating neural assemblies. Science 265, 1872.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Laurent, G., Wehr, M., and Davidowitz, H. (1996). Temporal representations of odors in an olfactory network. J. Neurosci. 16, 3837–3847.

Pubmed Abstract | Pubmed Full Text

Leitch, B., and Laurent, G. (1993). Distribution of GABAergic synaptic terminals on the dendrites of locust spiking local interneurones. J. Comp. Neurol. 337, 461–470.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Leitch, B., and Laurent, G. (1996). GABAergic synapses in the antennal lobe and mushroom body of the locust olfactory system. J. Comp. Neurol. 372, 487–514.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Linster, C., and Cleland, T. A. (2001). How spike synchronization among olfactory neurons can contribute to sensory discrimination. J. Comput. Neurosci. 10, 187–193.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Llinas, R., and Ribary, U. (1993). Coherent 40-Hz oscillation characterizes dream state in humans. Proc. Natl. Acad. Sci. U.S.A. 90, 2078–2081.

Pubmed Abstract | Pubmed Full Text

MacLeod, K., Backer, A., and Laurent, G. (1998). Who reads temporal information contained across synchronized and oscillatory spike trains? Nature 395, 693–698.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Matthews, H. R., and Reisert, J. (2003). Calcium, the two-faced messenger of olfactory transduction and adaptation. Curr. Opin. Neurobiol. 13, 469–475.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Olsen, S. R., Bhandawat, V., and Wilson, R. I. (2007). Excitatory interactions between olfactory processing channels in the Drosophila antennal lobe. Neuron 54, 89–103.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Papadopoulou, M., Cassenaer, S., Nowotny, T., and Laurent, G. (2011). Normalization for sparse encoding of odors by a wide-field interneuron. Science 332, 721–725.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Perez-Orive, J., Bazhenov, M., and Laurent, G. (2004). Intrinsic and circuit properties favor coincidence detection for decoding oscillatory input. J. Neurosci. 24, 6037–6047.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Perez-Orive, J., Mazor, O., Turner, G. C., and Cassenaer, S. (2002). Oscillations and sparsening of odor representations in the mushroom body. Science. 297, 359–365.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rabinovich, M., Huerta, R., and Varona, P. (2006). Heteroclinic synchronization: ultrasubharmonic locking. Phys. Rev. Lett. 96, 014101.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Singer, W., and Gray, C. M. (1995). Visual feature integration and the temporal correlation hypothesis. Annu. Rev. Neurosci. 18, 555–586.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Stopfer, M., Bhagavan, S., Smith, B. H., and Laurent, G. (1997). Impaired odour discrimination on desynchronization of odour-encoding neural assemblies. Nature. 390, 70–74.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Stopfer, M., Jayaraman, V., and Laurent, G. (2003). Intensity versus identity coding in an olfactory system. Neuron 39, 991–1004.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Tanaka, N. K., Ito, K., and Stopfer, M. (2009). Odor-evoked neural oscillations in Drosophila are mediated by widely branching interneurons. J. Neurosci. 29, 8595–8603.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Vreeswijk, C., Abbott, L., and Bard Ermentrout, G. (1994). When inhibition not excitation synchronizes neural firing. J. Comput. Neurosci. 1, 313–321.

Pubmed Abstract | Pubmed Full Text

Wang, X. J., and Buzsaki, G. (1996). Gamma oscillation by synaptic inhibition in a hippocampal interneuronal network model. J. Neurosci. 16, 6402–6413.

Pubmed Abstract | Pubmed Full Text

Wehr, M., and Laurent, G. (1996). Odour encoding by temporal sequences of firing in oscillating neural assemblies. Nature 384, 162–166.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wilson, R. I., and Laurent, G. (2005). Role of GABAergic inhibition in shaping odor-evoked spatiotemporal patterns in the Drosophila antennal lobe. J. Neurosci. 25, 9069–9079.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wilson, R. I., Turner, G. C., and Laurent, G. (2004). Transformation of olfactory representations in the Drosophila antennal lobe. Science 303, 366–370.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text