- 1Data Analysis Group, InfoTech, Connected Advanced Development Division, Toyota Motor Corporation, Tokyo, Japan
- 2Graduate School of Information Science, University of Hyogo, Kobe, Japan
An information theoretic reduction of auto-regressive modeling called the Reduced Auto-Regressive (RAR) modeling is applied to several multivariate time series as a method to detect the relationships among the components in the time series. The results are compared with the results of the transfer entropy, one of the common techniques for detecting causal relationships. These common techniques are pairwise by definition and could be inappropriate in detecting the relationships in highly complicated dynamical systems. When the relationships between the dynamics of the components are linear and the time scales in the fluctuations of each component are in the same order of magnitude, the results of the RAR model and the transfer entropy are consistent. When the time series contain components that have large differences in the amplitude and the time scales of fluctuation, however, the transfer entropy fails to detect the correct relationships between the components, while the results of the RAR modeling are still correct. For a highly complicated dynamics such as human brain activity observed by electroencephalography measurements, the results of the transfer entropy are drastically different from those of the RAR modeling.
1 Introduction
To understand the dynamical properties of any complicated systems including those in physiology, we have to analyze a set of signals generated by the system under consideration, varying in time and interrelated with each other, which is referred to as multivariate time series. Though it is surely important to understand the time dependence of each component of the time series separately, it is also crucial to detect the directed relationships among the components, in which the structure and functionality of the system are partially embodied. In many cases including those in physiology, however, the system is so complicated that we have no theoretical argument to identify the relationships from the first principle and we have to detect them only from observed data.
There are several common techniques for such detection. Among them, the Granger causality is probably the most classical and well-known [Granger (1969)]. This technique tries to detect causal relationship between two components from the improvement of prediction errors of the one of the two components by including the signals of the other component. Other techniques, such as the Directed Transfer Function [Kamiński and Blinowska (1991); Kamiński et al. (2001)] or Partial Directed Coherence [Baccalá and Sameshima (2001)] are based on the Vector Auto-Regressive (VAR) model with the coefficients transformed into the frequency domain to investigate the spectral properties. Schreiber (2000) has introduced another measure to detect the relationships called transfer entropy by an extension of the concept of mutual information.
An important feature of these techniques is that they are pairwise measures. In other words, these measures are calculated by taking all pairwise combinations out of a set of the components contained in the time series. It is not obvious, however, whether the relationships among components more than three can always be broken into pairwise relationships. For instance, let us consider the case in which two pairs of components, (A, B) and (A, C), are directly related within each pair. Despite that there is no direct relationship between B and C, the pairwise measure would detect a non-zero value of indirect relationship via A and we need an appropriately chosen threshold to determine the acceptance of this relationship. Though there are several procedures such as the surrogate data method (Theiler et al. 1992) in choice of the threshold value, it would be preferable if we have a method that enables us to extract the direct relationships from an entire set of components without pairwise break-up and threshold.
When the number of components are large
In this article, we investigate multivariate time series of a moderate number of components up to 10 and show that pairwise measures such as transfer entropy might fail in detecting relationships among components even for time series of this relatively small number of components. As a technique that enables us to extract relationships from an entire set of components without pairwise break-up and threshold, we take the Reduced Auto-Regressive (RAR) modeling firstly proposed by Judd and Mees (1995) and compare the results to those of the transfer entropy proposed by Schreiber (2000), which is one of the commonest pairwise measures in the time domain.
This article is organized as follows. In Section 2, we describe the RAR modeling technique and the transfer entropy after setting the mathematical notations. In Section 3, we apply the RAR modeling technique to two artificial systems, both of which are three-component time series defined by linear equations. The results are compared to the values of transfer entropy and it is shown that the transfer entropy cannot detect correct relationships when the time series contains different time scales in fluctuation, even when the signals are generated by linear equations. In Section 4, we apply the RAR modeling technique to a set of electroencephalography (EEG) data composed of 10 channels and compare the results with those of the transfer entropy. Discussion and Summary are in Section 5.
2 Theoretical backgrounds
2.1 Multivariate time series
We consider a set of multivariate time series,
where f is a function that determines the relationship, which might be potentially non-linear. It should be emphasized that, in this article, the term “relationship” is used only in this meaning and we do not discriminate whether the relationship is “causal” or “correlational”.
2.2 Reduced auto-regressive model
The time series modeling for multivariate time series,
for each i-th component, where we denote the maximum time delay (lag) as L. When the underlying dynamics of the system generating the multivariate time series is unknown, choosing an appropriate function form, fi, for each component and an appropriate value of the maximum lag, L, in practice are no trivial tasks and necessarily become heuristic. In this article, we limit ourselves to the function form in Eq. 2 to be linear with respect to their arguments. This limitation might be considered as a drawback, since quite a few time series data generated by real-world systems are potentially non-linear. Tanizawa et al. (2018) have shown, however, that, even for the case in which the time series data are non-linearly distorted, the linear modeling technique can identify the built-in periodicities correctly. We thus believe that linear modeling has a rather wide range of applicability if the non-linearity is not so strong as to induce the dynamics to be chaotic and if the relationships and periodicities built in the time series are sufficiently retained. In linear modeling, the value of the i-th component at time t is represented as
where ai,0 is the constant term in the modeling of the i-th component, which is allowed to vanish and ɛi(t) is a dynamic noise, which is an independently and identically distributed Gaussian random variable with mean zero and finite variance at t. Apart from the constant term, the value of the i-th component at present time is represented by a linear combination of the values of other components, xj(t − li,j,k), at previous time with lag li,j,k and parameter ai,j,k. The subscripts of the lags and the parameters,
Here we take another model, which is an information theoretic reduction of linear models and referred to as the Reduced Auto-Regressive (RAR) model [Judd and Mees (1995; 1998)]. The RAR model extracts a subset of terms that are most relevant for describing the behaviors of the multivariate time series selected by a suitably chosen information criterion.
To be concrete, let us assume that we have a set of observed values of four-component multivariate time series,
Here, we represent the value of the model for the i-th component at time t as
with element 1 for the constant term. From this dictionary, we extract the optimal subset of terms and determine the values of parameters, ai0, ai,j,k corresponding to the extracted terms by minimizing a suitably chosen information criterion.
Information criteria have a general form,
The mean square prediction error is the average of the squared norm of the prediction error vector,
where N is the length of the time series to be fitted, K is the number of the parameters that take non-zero values (or the model size), and the variables δi (i = 1, 2, …, k) can be interpreted as the relative precision to which the parameters are specified. For the details of the variables δi, see Judd and Mees (1995) and Judd and Mees (1998). The number γ is a constant and typically fixed to be γ = 32 for choosing a small model size K.
To extract the optimal subset to minimize
A typical result of RAR modeling takes the form
which includes only the terms, x0(t − 1), x0(t − 3), x1(t − 4), and x3(t − 7), in the dictionary. The RAR model thus includes only terms of relevant components and lags, which is the most important difference between the RAR model and the VAR model. Due to this difference, we are able to identify the directed relationships among components in multivariate time series. For instance, Eq. 8 implies that component x0 is affected by x1 and x3 apart from x0 itself. It should also be emphasized that there are strong information theoretic arguments to support that the RAR model can detect any periodicities built into given time series [Small and Judd (1999)].
2.3 Transfer entropy
Transfer entropy is an information theoretic measure for quantifying the information flow between two univariate time series, which we denote here as
where
Noticing that
we see that the information gain in this simplest case is symmetric with respect to X and
Schreiber (2000) extended this concept to the directional information flow between two time series. As time series data have correlation in time direction, the joint probability of signals between different times, P(x(t), x(t′)) cannot be separated as the product, P(x(t)) ⋅ P(x(t′)). By taking this feature into consideration, Schreiber defined the transfer entropy from
where
Here we slightly extend the definition by Schreiber to include the time difference L that can be a positive integer larger than one to measure the effect of time delay in information flow.
The transfer entropy is non-negative and becomes zero when X and
3 Experiments on artificial linear systems
In this section, we apply the RAR modeling technique to two artificial systems, both of which are represented by linear combinations of the terms of three components with various distinctive lags to investigate the directional relationship among the components and compare the results to the ones obtained from the calculated values of transfer entropy. The difference between these two time series is the time scales of fluctuations of each component. While the time scales of fluctuations of all components in the first system (System 1) are similar, the time scales in the second system (System 2) differ from each other.
3.1 System 1: A case with fluctuations in similar time scales
The time series of System 1 are generated by the following linear equations:
where
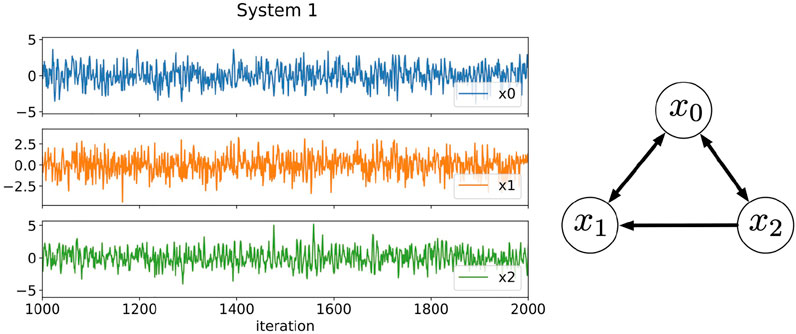
FIGURE 1. Three-component time series data generated by Eqs. 16–18 and the relationships among the components. The plotted data are a part of results from 1,000 to 2000 iterations. In System 1, the time scales of the fluctuations of each component are in the same order of magnitude.
We generate 10000 data points for each component of System 1 after sufficient number of iterations to erase initial value dependence to build the RAR model. In the modeling, we set the maximum time delay L = 25. The dictionary contains therefore 76 terms, which are 25 terms for the three components plus one constant term. Having in mind that we build RAR models from electroencephalography data with 1,025 observations in Section 4, we divide these 10,000 data points into 10 intervals each of which contains 1,000 data points and compare the results of RAR modeling corresponding to each divided interval. The results are summarized as
The notation for the values of the parameters such as 0.41(2) represents that the mean value of the parameter of x0(t − 1) over the models for 10 intervals is 0.41 with the standard deviation of 0.02. Notice that all terms included in the definitions, Eqs. 16–18, are recovered with correct values of parameters within appropriate statistical errors and contain no other unnecessary terms.
Figure 2 shows the values of transfer entropy calculated from the same data as used in the RAR modeling summarized in Eqs. 19–21, though all 10,000 data points for each component are used in this calculation. To see the effect of the values of k and l in the definition of transfer entropy, Eq. 13, we calculate the values for k = l = 1, which are most commonly used, and k = l = 2 for comparison.
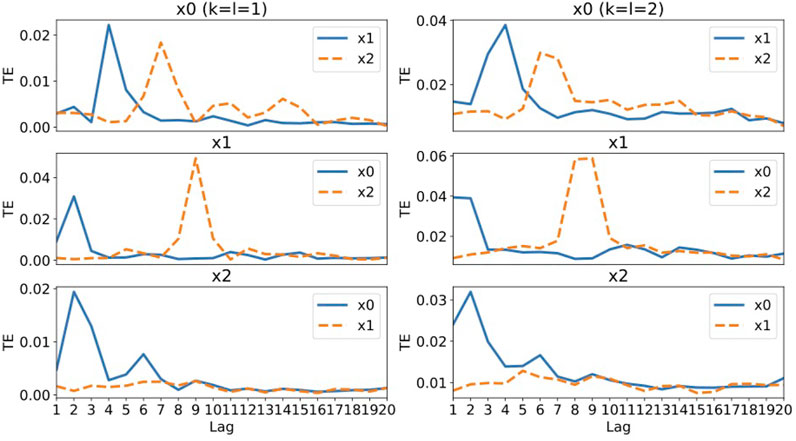
FIGURE 2. The values of transfer entropy of each component from other components for time delay (lag) up to 20. We plot the values for k = l = 1 in the left column and the values for k = l = 2 in the right column for comparison. A large value of transfer entropy indicates that a large amount of information gain exists at the lag from the corresponding components.
Let us examine the results of for k = l = 1 (the left column of Figure 2). For component x0, the large values of transfer entropy come from component x1 at lag 4 and component x3 at lag 7. Compared to the generator of x0 defined by Eq. 16, these peaks are consistent with the terms x1(t − 4) and x3(t − 7) in the generator of x0. For component x1, peaks appear at lag 2 for component x0 and at lag 9 for component x2, which are also consistent with the terms x0(t − 2) and x2(t − 9) in the generator of x1, Eq. 17. For component x2, the large value of transfer entropy at lag 2 for component x0 is consistent with the term x0(t − 2) in Eq. 18, though there is another small peak at lag 6 for component x0, which does not have any corresponding term in Eq. 18. The values for component x1 are almost zero, which is reasonable, since component x2 is independent of x1. For the results of k = l = 2 (the right column of Figure 2), the behaviors are almost the same as those of k = l = 1 except that there appear two consecutive peaks, since the correlation of x(t + L) with x(t), x(t − 1),
3.2 System 2: A case with fluctuations with different time scales
The time series of System 2 are generated by the following linear equations:
where
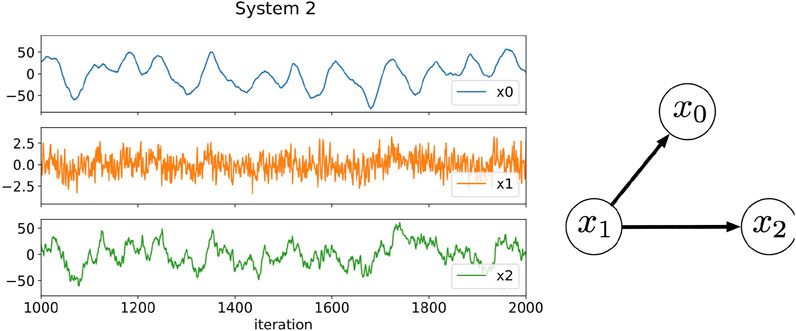
FIGURE 3. Three-component time series data generated by Eqs. 22–24 and the relationships among the components. The plotted data are a part of results from 1,000 to 2000 iterations. In this artificial system, the time scales in the fluctuations of each component are different: Component x0 fluctuates slowly, component x1 fluctuates rapidly, and component x2 fluctuates intermediately.
As in the case of System 1, we generate 10,000 data points for each component of System 2 to build the RAR model, then we divide these 10,000 data points into 10 intervals each of which contains 1,000 data points and compare the corresponding results of RAR modeling. We set the maximum lag as L = 25 and use the same dictionary containing 76 terms as used for System 1. The results are summarized as
As in the case of System 1, all terms and parameters are correctly recovered within reasonable statistical errors for System 2 in spite of the differences in the amplitude and the time scale of fluctuation for each components.
Figure 4 shows the values of transfer entropy calculated using all 10,000 data points of the same data as used in the RAR modeling summarized in Eqs. 25–27. As in the case of Systems 1, we calculate the values of transfer entropy for both k = l = 1 and k = l = 2 for comparison. First of all, the values of the transfer entropy of component x0 shows no distinctive peaks, which is remarkably different from those of components x1 and x2. Moreover, the values from component x2 are always larger than those of component x1, though the generator of x0 defined by Eq. 22 is independent of component x2. This deceptive result might be caused by the fact that the amplitudes of components x0 and x2 are in the same order. For x1, the values are very small around 0.0075 and the large values come from x2 at lags 2 and 3, though there are no such terms in the generator of x1, Eq. 23. The small values might be related to the fact that component x1 is independent of other components, though for decisive conclusion for the independence we need to estimate the effect of dynamical and/or observational noise using a method like surrogate generation based approach. For component x2, the large values of transfer entropy come from x1 at lags 3 and 4 that might corresponds to the term x1(t − 3) in Eq. 24, though the values of transfer entropy show a long tail after the peak, which might be incompatible with Eq. 24. For the results of k = l = 2 (the right column of Figure 2), the behaviors are almost the same as those of k = l = 1. Even if the dynamics is represented by linear equations and the signals contain a small amount of Gaussian noise, the transfer entropy begins to fail in capturing the correct relationships among components for System 2 containing different time scales in fluctuation of each component.
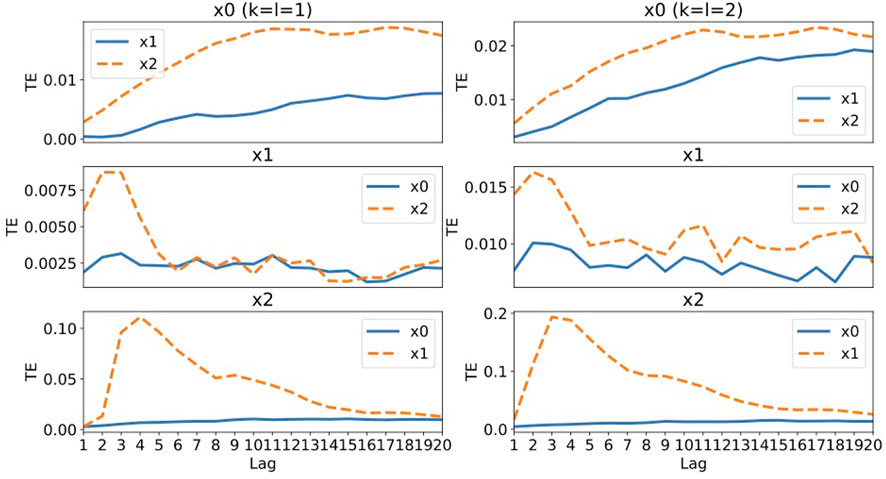
FIGURE 4. The values of transfer entropy of each component from other components for various values of time delay (lag) up to 20. We plot the values for k = l = 1 in the left column and the values for k = l = 2 in the right column for comparison. A large value of transfer entropy indicates that a large amount of information gain exists at the lag from the corresponding components.
4 Results on electroencephalography data
In this section, we apply the RAR modeling to electroencephalography (EEG) data and compare the results to the values of transfer entropy. The EEG signals used here were recorded from a healthy human adult during resting state with eyes closed in an electrically shielded room and have been analyzed by other methods in Rapp et al. (2005). The data were simultaneously obtained from 10 channels of the unipolar 10–20 Jasper registration scheme and digitized at 1,024 Hz using a twelve-bit digitizer. In Figure 5, we show the placement of 10 electrodes in International 10–20 System. Artifact corrupted records were removed from the analyses. The EEG impedances were less than 5 kΩ. The data were amplified by gain equal to 18,000, and amplifier frequency cut-off settings of 0.03 Hz and 200 Hz were used.
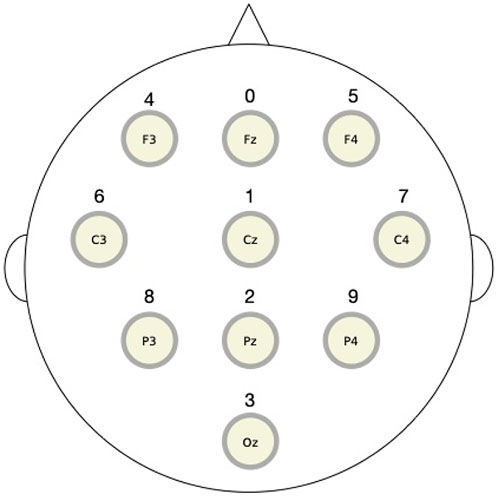
FIGURE 5. The placement of 10 electrodes in International 10–20 System for electroencephalography measurements. The top (bottom) is the front (back) direction of the head. The digits over the circles representing electrodes are the component numbers used in the RAR modeling.
The 10 channel electroencephalography signals analyzed here are plotted in Figure 6. It should be noted that the plotted data are all normalized and dimensionless. The activities of human brain are, undoubtedly, highly complicated and non-linear by nature. We should therefore be careful whether there might be suitable interval and duration of time for the dynamics to be approximated in linear forms. Tanizawa et al. (2018) have shown that the RAR modeling is able to detect correct relationships among components even for dynamical systems represented by non-linear differential equations such as the Rössler system. Since there is no explicit description of the results of RAR modeling of the EEG data in Tanizawa et al. (2018), we rebuild the RAR models for these 10 EEG time series, expecting the models contain correct information about the relationships among the components. We use 1,025 data points (1 s) for each component (channel) to build multivariate RAR models. We set the maximum lag as L = 25 and the dictionary contains therefore 251 terms, which are 25 terms for the 10 components with one constant term. We show the result for the component Fz explicitly, which is
FIGURE 6. The plots of the 10 channel electroencephalography signals analyzed in the present section. All plotted data are normalized and dimensionless.
From this model, component Fz is influenced by component Cz at lag 1 and 2 and component F3 at lag 5, 13, and 20. In Figures 11, 12 of Appendix, we show the behaviors of simulated signals generated from the RAR models and their power spectral densities.
For the transfer entropy, we use the same data points as those used in RAR model building and calculate the information gain from the correlation in the signals between all pairs of component Fz and each of other channels up to the maximum lag 30. According to the analysis described in Section 3, we set k = l = 1 in calculating transfer entropy. The results of the calculation is plotted in Figure 7. From this plot, we see that all values of transfer entropy are in the same order of magnitude and show no distinct peaks that suggest important components and lags. We also plot in Figure 8 the components and the maximum values of transfer entropy of component Fz for each lag up to 30 sorted in the descending order of the values of transfer entropy. According to the calculations of transfer entropy for component Fz, the information gain from component C3 is the largest. The component C3, however, does not appear in the RAR model of component Fz in Eq. 28. The values of transfer entropy for other components show similar behaviors.
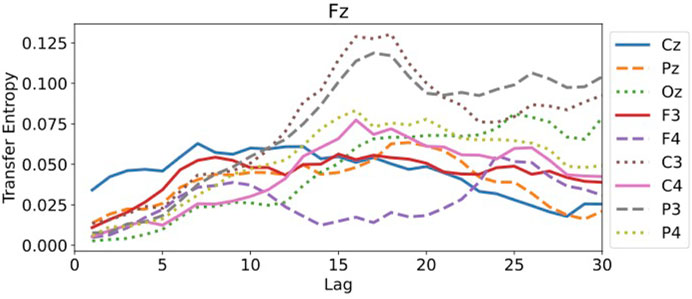
FIGURE 7. The values of transfer entropy of component Fz from other components with respect to the lags up to 30. All values are in the same order of magnitude and do not show distinct peaks.
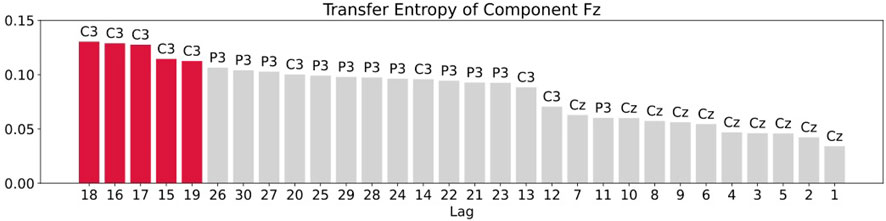
FIGURE 8. Plot of the components and the maximum values of transfer entropy of component Fz for each lag up to 30 sorted in the descending order of the values of transfer entropy. The red bars are the top five values of transfer entropy. For component Fz, all top five values come from component C3.
We summarize these results for component Fz in Figure 9. In this figure, the target component against which the RAR model and the transfer entropy are calculated (in this case, Fz), is represented by a red slightly large circle. The circles from which the arrows emanate (in this case, Cz and F3), represent the components contained in the RAR model with the width of the arrows being proportional to the number of appearance of the component in the RAR model. In this case, component Cz appears two times and component F3 appears three times. The orange circles represent the components that give the top 5 values of transfer entropy for each lag. In this case, all top 5 values only come from component C3 (See Figure 8). From this figure, we also see the spatial information of the components included in the RAR model and the components that gives large values of transfer entropy.
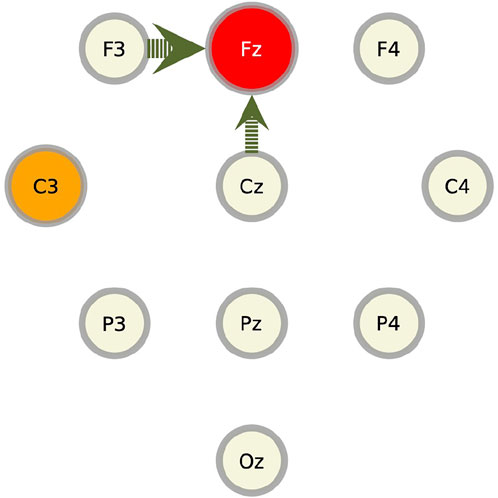
FIGURE 9. Pictorial summary of the results of the RAR model and the transfer entropy for component Fz. The target component Fz is represented by the red circle. The circles from which the arrows emanate, which are Cz and F3, represent the components contained in the RAR model with the width of the arrows being proportional to the number of appearance of the component in the RAR model. For the case of component Fz, component Cz appears two times and component F3 appears three times. The orange circles represent the components that give the top 5 values of transfer entropy for each lag, which is only C3.
As for the other nine components, we show only the summarized results in Figure 10. Generally speaking, the components that give large values of transfer entropy are not related to the components included in the RAR models. It is also to be noticed that the component Oz, which is placed at the back of the head, appears frequently as the component of large transfer entropy values, though it is not likely the outcome of direct influence of this component on the target components.
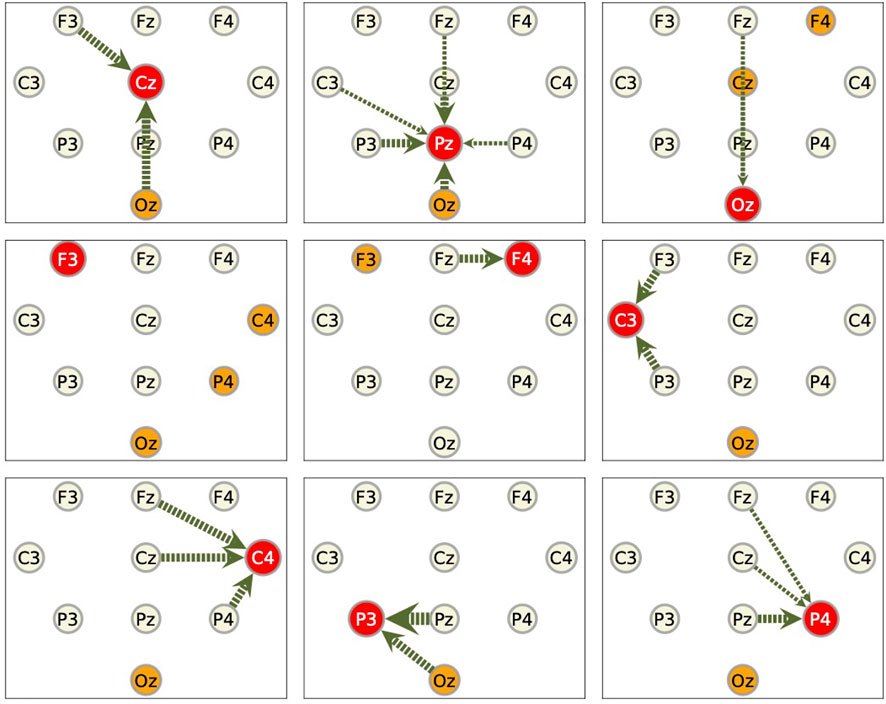
FIGURE 10. Summarized results for other components. Red circles represent the target components against which the RAR models are built. The arrows are the directed relationships indicated by the corresponding RAR models. The orange circles are the components that gives large values of transfer entropy to the target nodes. See the caption of Figure 9 for the details. Since the RAR model of component F3 contains only terms of F3 itself, there are no arrows in the picture for F3.
5 Discussion and summary
For two artificial linear systems described in Section 3, the results of the transfer entropy are consistent with those of the RAR modeling, if the values and the time scales in fluctuation of the signals are in the same order of magnitude (System 1). In this case the dynamics of the components are well separated and pairwise methods such as the transfer entropy work well. If the time series contain components whose values and time scale of fluctuation are significantly different from each other (System 2), however, the transfer entropy begins to fail in detecting correct relationships among components, while the RAR modeling is still able to give the correct relationships.
For the application to EEG data in Section 4, the relationships indicated by the results of transfer entropy are drastically different from those indicated by the RAR modeling. Though, within our knowledge, there are no decisive research work in the literature in this regard, we think it is partially because of the insufficiency of pairwise measures for detecting relationships among components that potentially contain various time scales in dynamics for those seen in brain activity. In contrast, it is known that the RAR modeling can detect correct relationships even when the underlying system is non-linear (Tanizawa et al. (2018)). We understand that it would be a controversial issue whether EEG data can be representable by linear models or not. Even in a case in which that the dynamics is represented by a linear system, however, transfer entropy might fail in detecting the correct relationships among the components in multivariate time series, if they contain several time scales in different orders of magnitude. Though we do not claim that the relationships detected by the RAR modeling technique are always correct, detecting the relationships among components in multivariate time series by RAR modeling could be a promising technique with a wide range of applicability.
In summary, we have applied the RAR modeling technique to several multivariate time series as a method to detect the relationships among the components in the time series and compared the results with those of a pairwise measure, transfer entropy in this article. When the relationships between the dynamics of the components are linear and the time scales in the fluctuation of each component are in the same order of magnitude, the results of the RAR model and the transfer entropy are consistent. When the time series contain components that have large differences in the amplitude and the time scales of fluctuation, however, the transfer entropy fails to capture the correct relationships between the components, while the results of the RAR modeling are still correct. For a highly complicated dynamics such as human brain activity observed by electroencephalography measurements, the results of the transfer entropy are drastically different from those of the RAR modeling.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
TT conceived the idea of numerical calculations presented in this article and carried out the computation. TT and TN verified and discussed the results. TT took the lead in writing the manuscript with the critical feedback from TN.
Acknowledgments
TT and TN would like to acknowledge Paul E. Rapp of Uniformed Services University for providing us with the EEG data used in Rapp et al. (2005). The authors would also like to acknowledge referees for valuable suggestions.
Conflict of interest
TT is employed by Toyota Motor Corporation.
The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Appendix
In this Appendix, we show the behaviors of simulated EEG signals generated by the RAR models and their power spectral densities in the frequency domain. Here the RAR models are constructed from the first 769 observations of each EEG channels to compare the simulated signals to the last 256 observations.
Figure 11 are the plots of simulated signals generated by the RAR models with the last 281 observed EEG signals for comparison. The RAR signals are generated with 25 observed signals prior to the last 256 signals as initial values and contain Gaussian random numbers with mean 0 and standard deviations determined from the fitting errors of each channels in RAR modeling as dynamic noise. Though the observed signals and the simulated ones are not identical because of the dynamic noise, the behaviors seem to be quite similar.
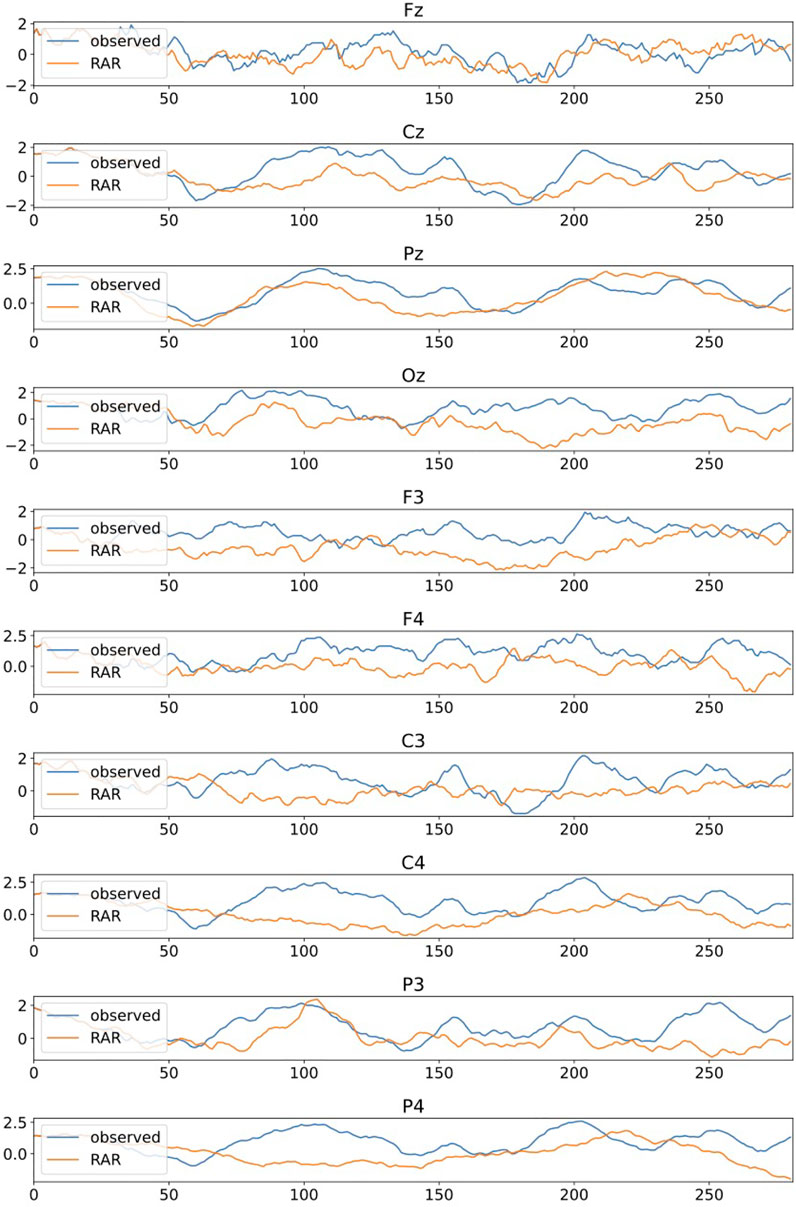
FIGURE 11. Comparative plots of the observed EEG signals and the signals generated by the RAR models, which are constructed from the first 769 observations of each channel. The observed EEG signals are the last 281 (= 25 + 256) signals of each channel and the RAR signals are generated by the corresponding RAR models with 25 observed signals prior to the last 256 signals as initial values. Simulated signals also contain Gaussian random numbers with mean 0 and standard deviations determined from the fitting errors of each channels in RAR modeling as dynamic noise.
Figure 12 are the plots of the power spectral densities of simulated signals from the RAR models. Plotted values are the averages of the power spectral densities over 100 independent runs of simulation. Significant contributions come from frequencies up to about 20 Hz that correspond to the region of α waves.
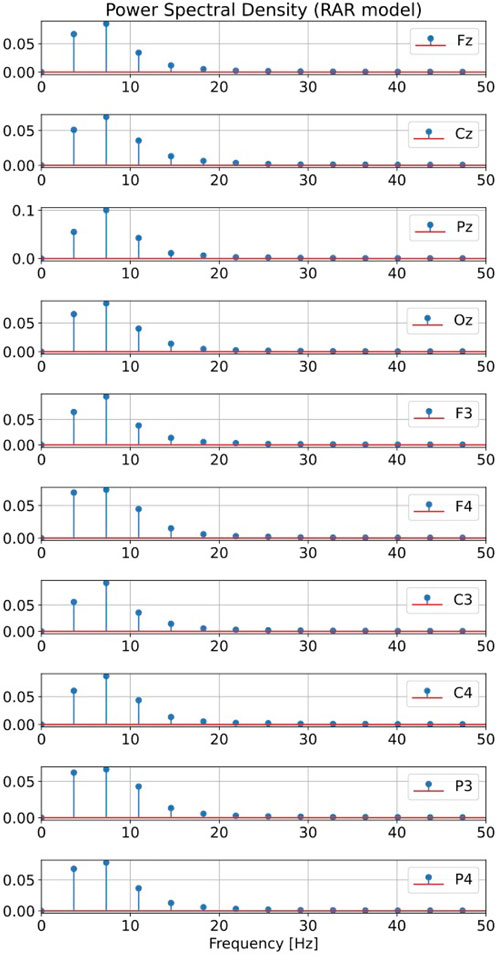
FIGURE 12. Plots of the power spectral densities of simulated signals from the RAR models. Plotted values are the averages of the power spectral densities over 100 independent runs of simulation. Significant contributions come from frequencies up to about 20 Hz.
References
Baccalá, L. A., and Sameshima, K. (2001). Partial directed coherence: A new concept in neural structure determination. Biol. Cybern. 84, 463–474. doi:10.1007/PL00007990
Breiman, L. (1995). Better subset regression using the nonnegative garrote. Technometrics 37 373–384.
Brüggemann, I. (2003). Measuring monetary policy in germany: A structural vector error correlation approach. German Economic Review 4 307–339.
Faes, L., Nollo, G., and Porta, A. (2011). Information-based detection of nonlinear granger causality in multivariate processes via a nonuniform embedding technique. Physical Review E 83 051112.
Granger, C. W. J. (1969). Investigating causal relations by econometric models and cross-spectral methods. Econometrica 37, 424–438. doi:10.2307/1912791
Judd, K., and Mees, A. (1998). Embedding as a modeling problem. Phys. D. Nonlinear Phenom. 120, 273–286. doi:10.1016/s0167-2789(98)00089-x
Judd, K., and Mees, A. (1995). On selecting models for nonlinear time series. Phys. D. Nonlinear Phenom. 82, 426–444. doi:10.1016/0167-2789(95)00050-e
Kamiński, M., Ding, M., Truccolo, W. A., and Bressler, S. L. (2001). Evaluating causal relations in neural systems: Granger causality, directed transfer function and statistical assessment of significance. Biol. Cybern. 85, 145–157. doi:10.1007/s004220000235
Kamiński, M. J., and Blinowska, K. J. (1991). A new method of the description of the information flow in the brain structures. Biol. Cybern. 65, 203–210. doi:10.1007/BF00198091
Kugiumtzis, D. (2013). Direct-coupling information measure from nonuniform embedding. Physical Review E 87 062918.
Nakamura, T., Kilminster, D., Judd, K., and Mees, A. (2004). A comperative study of model selection methods for nonlinear time series. Int. J. Bifurc. Chaos 14, 1129–1146. doi:10.1142/s0218127404009752
Papana, A., Siggiridou, E., and Kugiumtzis, D. (2021). Detecting direct causality in multivariate time series: A comparative study. Communications in Nonlinear Science and Numerical Simulation 99 105797.
Rapp, P. E., Cellucci, C. J., Watanabe, T. A. A., and Albano, A. M. (2005). Quantitative characterization of the complexity of multichannel human eegs. Int. J. Bifurc. Chaos 15, 1737–1744. doi:10.1142/s0218127405012764
Schreiber, T. (2000). Measuring information transfer. Phys. Rev. Lett. 85, 461–464. doi:10.1103/PhysRevLett.85.461
Shojaie, A., and Michailidis, G. (2010). Discovering graphical granger causality using the truncating lasso penalty. Bioinformatics 26 i517–i523.
Siggiridou, E., and Kugiumtzis, D. (2016). Granger causality in multivariate time series using a time-ordered restricted vector autoregressive model. IEEE Transactions Signal Processing 65 1759–1773.
Small, M., and Judd, K. (1999). Detecting periodicity in experimental data using linear modeling techniques. Phys. Rev. E 59, 1379–1385. doi:10.1103/physreve.59.1379
Tanizawa, T., Nakamura, T., Taya, F., and Small, M. (2018). Constructing directed networks from multivariate time series using linear modelling technique. Phys. A Stat. Mech. its Appl. 512, 437–455. doi:10.1016/j.physa.2018.08.137
Theiler, J., Eubank, S., Longtin, A., Galdrikian, B., and Farmer, J. D. (1992). Testing for nonlinearity in time series: the method of surrogate data. Physica D: Nonlinear Phenomena 58 77–94.
Yang, Y., and Wu, L. (2016). Nonnegative adaptive lasso for ultra-high dimensional regression models and a two-stage method applied in financial modeling. Journal of Statistical Planning and Inference 174 52–67.
Keywords: multivariate time series, statistical modeling, transfer entropy, model selection, auto-regressive models
Citation: Tanizawa T and Nakamura T (2022) Detecting the relationships among multivariate time series using reduced auto-regressive modeling. Front. Netw. Physiol. 2:943239. doi: 10.3389/fnetp.2022.943239
Received: 13 May 2022; Accepted: 08 September 2022;
Published: 07 October 2022.
Edited by:
Plamen Ch. Ivanov, Boston University, United StatesReviewed by:
Alessio Perinelli, University of Trento, ItalyFumikazu Miwakeichi, Institute of Statistical Mathematics (ISM), Japan
Copyright © 2022 Tanizawa and Nakamura. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Toshihiro Tanizawa, dG9zaGloaXJvX3Rhbml6YXdhQG1haWwudG95b3RhLmNvLmpw
 Toshihiro Tanizawa
Toshihiro Tanizawa Tomomichi Nakamura2
Tomomichi Nakamura2