1
Center for Complex Systems and Brain Sciences, Florida Atlantic University, Boca Raton, FL, USA
2
Intelligent Systems Research Centre, University of Ulster, Magee Campus, L’Derry, Northern Ireland
A commentary on
Early-warning signals for critical transitions
by M. Scheffer et al., Nature 461, 53 (2009)
One hazard of interdisciplinary research is that important results in one field may be unknown or totally ignored in another. To ensure that this does not happen, editors and reviewers have an even more difficult job and greater responsibility than usual. Scheffer et al.’s (2009)
recent review is a case in point. The authors identify ‘early warning signals’ such as critical slowing down in simple nonlinear models and suggest these may now be helpful in predicting upcoming transitions (‘tipping points’ in the modern idiom) in ‘real systems’ such as the climate, ecosystems and financial markets. Here I describe briefly work that used an intimate blend of theoretical concepts from the field of nonequilibrium physics (Haken, 1977/83
; Sornette, 2000
), mathematical modeling and experiments on humans to establish early warning signals and their significance for biological coordination. Though the research was published in prominent journals it may be worth considering the reasons why Scheffer et al. and their reviewers missed it.
Scheffer et al.’s strategy is to present simple catastrophe theoretic models and suggest that some of the features they contain prior to bifurcation such as critical slowing down and increased variance may also be found in very different complex systems. Their case would have been stronger had they demonstrated an explicit connection between the phenomena observed and the theoretical concepts and mathematical models used to explain them. Failing that, the authors might have referred to other ‘real systems’ where this has been done.
Take the voluntary movements of the two hands, a system that has proved a window into tipping points and self-organization in complex biological systems. Very many sensory and motor elements are involved, neurons, muscles, joints, metabolic processes, etc. Yet when human subjects are asked to rhythmically move their index fingers they do so in one of only two patterns: an alternating, out of phase pattern where the fingers move in the same direction and a symmetric in-phase pattern where homologous muscles contract simultaneously. Under instructions to start moving in the anti-phase pattern and increase rate of movement, a spontaneous transition to in-phase occurs at a critical rate. Slowing down after the switch does not return the system to the initial pattern. No transitions occur when subjects start in-phase (Kelso, 1984
).
The simplest dynamics that captures all the observed empirical facts is:
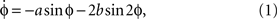
where ϕ is the relative phase between the movements of the two fingers, 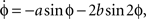 is the derivative of ϕ with respect to time, and the ratio b/a is a control parameter corresponding to the movement rate in the experiment. An equivalent formulation of Eq. (1) is
is the derivative of ϕ with respect to time, and the ratio b/a is a control parameter corresponding to the movement rate in the experiment. An equivalent formulation of Eq. (1) is
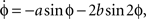 is the derivative of ϕ with respect to time, and the ratio b/a is a control parameter corresponding to the movement rate in the experiment. An equivalent formulation of Eq. (1) is
is the derivative of ϕ with respect to time, and the ratio b/a is a control parameter corresponding to the movement rate in the experiment. An equivalent formulation of Eq. (1) is
with V(ϕ) = −a cos ϕ − b cos 2ϕ
In the literature, this is called the HKB model of coordination (Haken et al., 1985
; Liese and Cohen, 2007
). The dynamics may be visualized as a particle moving in a potential function, V(ϕ). The minima of the potential are points of vanishing force, giving rise to stable solutions. As long as the speed parameter (b/a) is slow, meaning the cycle period is long, Eq. (2) has two stable fixed point attractors, coordinated states at ϕ = 0 and ϕ = ±π rad. Notice that two coordinated states coexist for the same parameter values, the essentially nonlinear feature of bistability. As the ratio b/a is decreased, meaning that the cycle period gets shorter as the fingers speed up, the formerly stable fixed point at ϕ = ±π rad becomes unstable, and turns into a repellor. Any small perturbation will now kick the system into the basin of attraction of the stable fixed point at ϕ = 0. Notice also that once there, the system’s behavior will stay in the in-phase attractor, even if the direction of the control parameter is reversed. This is called hysteresis, a basic form of memory in nonlinear dynamical systems. A significant aspect of the HKB model is that Eqs 1 and 2 can be derived from the individual components and their nonlinear interaction. Thus, though the whole is greater than the sum of the parts, the parts – as a result of nonlinear coupling – can be assembled to create the behavior of the whole.
Introducing stochastic forces into Eqs 1 and 2 turns them into a corresponding Fokker–Planck equation which describes the evolution in time of the probability distribution of the relative phase (Schöner et al., 1986
; Haken, 1988
) and allows key predictions to be tested and quantitatively evaluated. In the model, as the minima at ϕ = ±π becomes shallower and shallower, the time it takes to adjust to a small perturbation takes longer and longer. Thus, the local relaxation time is predicted to increase as the tipping point is approached because the restoring force (given as the gradient in the potential) becomes smaller and smaller. Using sensitive perturbation techniques, this prediction of critical slowing down and a test of the timescales assumptions were first confirmed in experiments by Scholz et al. (1987).
Likewise, the variability of ϕ is predicted to increase due to the flattening of the potential as the system approaches the transition point. Such critical fluctuations were observed in Kelso’s original experiments and later confirmed (Kelso et al., 1986
). Moreover, the connection between fluctuation enhancement and critical slowing was established by calculating the line width of the power spectrum of the relative phase which increased monotonically as the transition was approached (Kelso et al., 1987
). These predicted features of the HKB model, and more generally signatures of impending transitions or ‘tipping points’ have been confirmed in a wide variety of quite different experimental systems, including recordings of the human brain (see e.g. Schoner and Kelso, 1988
; Kelso et al., 1992
; Meyer-Lindenberg et al., 2002
; Swinnen, 2002
; Carson and Kelso, 2004
; Peper et al., 2004
; Jantzen et al., 2009
; Kelso, 2009
). They are important because phase transitions provide a physical mechanism for the cooperative action of neurons. Phase transitions also provide a natural switching mechanism without any switches at all (cf Abbott, 2006
). Variability, rather than a source of undesirable noise, proves to be an essential source of flexibility and adaptability. In complex systems like the financial markets and politics where difficult decisions have to be made in real time, fluctuations are always probing the stability of the system, allowing it to explore the space of possibilities – whether these be benign or not (see Kelso, 1995,
p. 60).
Though omitted in Scheffer et al., it seems that the foregoing foundational work conducted by an interdisciplinary team of physicists and neuroscientists constitutes a rather clear example of early warning signals for critical transitions in a complex biological system. Theoretically and practically, instabilities play a key role in the identification of so-called order parameters that capture the system’s collective states (Haken, 1977/83
; Kelso, 1984
). Scheffer et al. could turn this fact to their advantage since it is the low-dimensional order parameter dynamics that is revealing of early warning signals. It might be argued that it is not possible to survey all scientific fields for prior work that advanced the thesis of early warning signals anticipating abrupt change. Or that relevant research on such an arcane subject as human movement may be inaccessible because it is published in obscure and highly specialized journals. Neither argument holds water. As the present citations indicate, earlier empirical and theoretical modeling work on precursors of tipping points in complex systems was published in major journals and books. Since the authors’ stated goal was to survey work in different scientific fields in order to establish indicators of early warning signals in a wide class of systems, the sin of omission and the onus of responsibility lie with them. On a positive note, the present work amplifies the idea that phase transitions and their anticipatory signatures are common across a broad range of complex systems and disciplines, including human brains and human behavior. Although every system may be different, if they are complex, open and inherently nonlinear, what we learn about the dynamics of one may aid in understanding the dynamics of others.
Peper, C. E., Daffertshofer, A., and Beek, P. J. (2004). Dynamical models of interlimb coordination: relating pattern (in)stability to neural processes and effector properties. In Neuro-Behavioral Determinants of Interlimb Coordination: A Multidisciplinary Approach, S. P. Swinnen and J. Duysens, eds (Amsterdam, Kluwer), pp. 297–323.