- 1 Department of Cognitive and Systems Neuroscience, Swammerdam Institute for Life Sciences, University of Amsterdam, Amsterdam, Netherlands
- 2 Department of Experimental Psychology, University of Oxford, Oxford, UK
It is often assumed that decisions are made by rank-ordering and thus comparing the available choice options based on their subjective values. Rank-ordering requires that the alternatives’ subjective values are mentally represented at least on an ordinal scale. Because one alternative cannot be at the same time better and worse than another alternative, choices should satisfy transitivity (if alternative A is preferred over B, and B is preferred over C, A should be preferred over C). Yet, individuals often demonstrate striking violations of transitivity (preferring C over A). We used functional magnetic resonance imaging to study the neural correlates of intransitive choices between gambles varying in magnitude and probability of financial gains. Behavioral intransitivities were common. They occurred because participants did not evaluate the gambles independently, but in comparison with the alternative gamble presented. Neural value signals in prefrontal and parietal cortex were not ordinal-scaled and transitive, but reflected fluctuations in the gambles’ local, pairing-dependent preference-ranks. Detailed behavioral analysis of gamble preferences showed that, depending on the difference in the offered gambles’ attributes, participants gave variable priority to magnitude or probability and thus shifted between preferring richer or safer gambles. The variable, context-dependent priority given to magnitude and probability was tracked by insula (magnitude) and posterior cingulate (probability). Their activation-balance may reflect the individual decision rules leading to intransitivities. Thus, the phenomenon of intransitivity is reflected in the organization of the neural systems involved in risky decision-making.
Introduction
It is often assumed that decisions are made by rank-ordering the available choice alternatives according to their subjective desirabilities, and then selecting the most desirable alternative (Bernoulli, 1954 ; Shizgal, 1997 ; Montague and Berns, 2002 ). Because one alternative cannot be at the same time better and worse than another alternative, choices should satisfy transitivity (Samuelson, 1938 ; von Neumann and Morgenstern, 1944 ). Transitivity holds that, if choice alternative A is preferred over B, and B is preferred over C, then A should also be preferred over C. Transitivity is not just an intuitively compelling rule; it is a cornerstone of many decision theories, and a hallmark of rational action in economics (Samuelson, 1938 ; von Neumann and Morgenstern, 1944 ; Afriat, 1967 ; Varian, 1982 ), philosophy (Hume et al., 1978 ) and biology (Stephens and Krebs, 1986 ). Intriguingly, despite its intuitive appeal, humans and animals often violate transitivity (Tversky, 1969 ; Navarick and Fantino, 1972 ; Loomes et al., 1991 ; Shafir, 1994 ; Roelofsma and Read, 2000 ; Waite, 2001 ; Lee et al., 2006 , 2009 ). Intransitive choices can occur when individuals choose between outcomes that vary along several dimensions, for example, monetary gain magnitude and probability (Tversky, 1969 ), or magnitude and delay (Roelofsma and Read, 2000 ).
Violations of transitivity are important for our understanding of decision-making. If an agent systematically fails to make consistent, transitive choices, a utility function capturing the options’ subjective desirabilities cannot straightforwardly be constructed from observable choices without making further assumptions (Samuelson, 1938 ; von Neumann and Morgenstern, 1944 ; Afriat, 1967 ; Fishburn, 1982 ). This has, among others, implications for the identification of neural utility representations which often relies on the derivation of utility functions from revealed preferences (Kalenscher et al., 2005 ; Padoa-Schioppa and Assad, 2006 , 2008 ; Kable and Glimcher, 2007 ; Kalenscher and Pennartz, 2008 ; Heldmann et al., 2009 ).
Yet, despite its importance for the neurobiological investigation of decision-making, remarkably little is known about the neural mechanisms underlying intransitive choice. For example, while it has been previously shown that choice-underlying subjective values are represented in, among others, ventromedial prefrontal cortex (VMPFC), dorsolateral prefrontal cortex (DLPFC), posterior parietal cortex (PPC) and striatum (Dorris and Glimcher, 2004 ; Sugrue et al., 2004 ; Padoa-Schioppa and Assad, 2006 ; Kable and Glimcher, 2007 ; Plassmann et al., 2007 ; Tobler et al., 2007 , 2009 ; Kim et al., 2008 ; Rangel et al., 2008 ), it is unknown whether these structures are also recruited during intransitive decision-making, and whether neural value representations are intransitive. Furthermore, intransitive choices may be the consequence of particular mental rules people use to make decisions, but very little is known about the neural implementation of such decision rules (Volz et al., 2006 ; Venkatraman et al., 2009 ).
Here, we investigated neural activity related to intransitive choices during decision-making under risk. Participants frequently made intransitive decisions when choosing between pairs of gambles varying in gain magnitude and probability. Intransitive choices occurred because the desirability (subjective value) of a given option was not assessed independently, but depended on the alternative option a gamble was combined with (e.g., gamble A may be more desirable when combined with gamble B than with gamble C). We found evidence that traditional decision-areas, such as DLPFC, VMPFC, PPC and striatum, represented the local, intransitive desirability of the gambles at stake. We further found that the intransitive evaluation of the gambles was mediated by specific rules participants used for decision-making under risk. More specifically, fluctuations in the gambles’ values were the consequence of variable preferences for richer or safer gambles, which were supported by distinct neural mechanisms in areas known to be sensitive to reward magnitude and risk attitude during multi-attribute choice, such as insula (Wittmann et al., 2007 ; Smith et al., 2009 ; Xue et al., 2009 ) and posterior cingulate (McCoy and Platt, 2005 ).
Materials and Methods
Participants
A total of 31 participants (18 females, mean age 22.8 years, range 18–28 years) recruited from the University of Amsterdam participated in this experiment. All participants were right-handed and had normal or corrected-to-normal vision in the scanner. Subjects were screened to ensure they satisfied magnetic resonance imaging (MRI) safety requirements and to exclude those with a prior history of neurological or psychiatric illness. They were paid between €25 and €30 for participation, depending how much they won during the task. Participants gave their informed consent and the study was approved by the Academic Medical Center Medical Ethical Committee. Four subjects (two females) had to be excluded from the analysis because of excessive head movement inside the scanner.
Instructions
Prior to scanning, subjects were informed that they would be reimbursed with €25 for their participation, but that they could add up to €5 to this sum depending on whether they win in this game or not. They were instructed that they were playing for dummy dollars, and the final gain in Euro would be determined by dividing the won sum of dummy dollars by 100. No losses were possible, and in case of a no-win, nothing would be added to the default imbursement of €25. Subjects were further instructed that, during the task, they would not receive feedback about the success or failure of their chosen gamble, but that, at the end of the experiment, one trial would be selected at random by the computer, and only the chosen gamble in this randomly selected trial would be played and resolved.
Task
Participants made decisions between pairs of gambles that yielded probabilistic monetary rewards while we simultaneously measured blood-oxygenation level dependent (BOLD) signals using functional MRI (fMRI). To induce intransitive choices, we used a modified version of a risky decision-making task developed by Tversky (1969) . Each trial began with a white fixation cross (intertrial interval; ITI) of variable duration (mean length 1.72 s, range 1.3–2.7 s), followed by the presentation of two gambles. In every trial, subjects had 4 s to indicate which of the two gambles they would prefer to play (Figure 1 A). The difference between the actual response time and 4 s was added to the ITI, and failure to respond within 4 s resulted in a missed trial. After a response was made, the chosen gamble was enlarged for 500 ms to indicate that the response was registered by the computer. The gambles were not resolved during scanning, and participants were instructed that only one of the chosen gambles would be selected, played and paid out (in case of a win) at the end of the experiment. This enabled us to isolate neural responses related to gamble evaluation from direct outcome anticipation and experience, and examine brain activation related to the actual decision process.
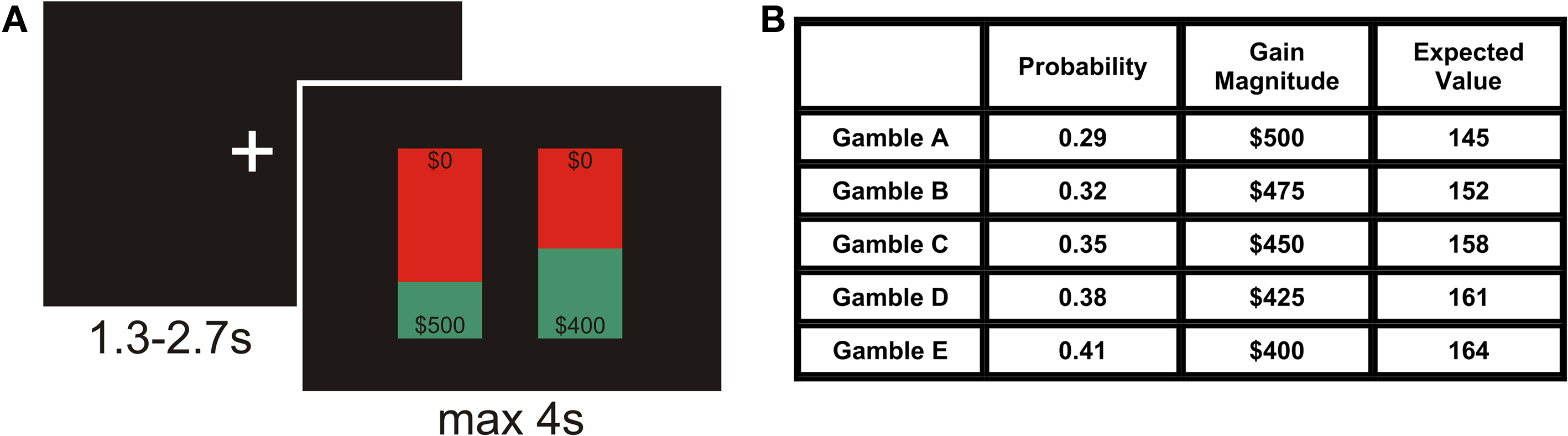
Figure 1. (A) The event-related design. Each trial began with an intertrial interval (ITI) of variable duration, followed by the presentation of a pair of gambles. Each bar represents one gamble, which contained information about the potential monetary gain magnitude to be won by playing it (numbers at the bottom of the bars) and the probability of winning this money, as specified by the expanse covered by the green area in each bar. The $0 at the top of the bars indicated that participants would receive no money in case they did not win. In every trial, one of the presented gambles had a higher gain magnitude, but a lower winning probability (Gricher), and the other gamble had a lower magnitude, but a higher probability (Gsafer). Participants had 4 s to indicate which of the two gambles they would prefer to play. After making a decision, the selected gamble was enlarged for 500 ms. (B) Gambles used in the experiment. There were five different gambles that were presented in all ten possible pairwise combinations in a randomized fashion. The winning probability increased from gamble A to E in steps of 0.03, and the gain magnitude decreased from A to E in steps of $25, so that gambles with higher magnitudes had lower probabilities and vice versa. We used the minimum step-size of changes in probability (0.03) and gain magnitude ($25) to measure the gamble-distance in every presented gamble pair (see text for details).
The experiment consisted of 440 trials, divided across six runs. These trials comprised 200 experimental trials and 240 control trials, randomly intermixed. In each experimental trial, two of five different gambles were presented. Each gamble offered a different gain magnitude (range $400 to $500) with a different probability (range p = 0.41–0.29; Figure 1 B). All gambles differed in expected value (product of probability and gain magnitude), which increased with increasing probability (cf. Figure 1 B). All 10 possible binary combinations of the five gambles were presented 20 times each. In every trial, one of the presented gambles had a higher gain magnitude, but a lower winning probability (Gricher), and the other gamble had a lower magnitude, but a higher probability (Gsafer). The degree by which gains and probabilities differed varied between gamble pairs and was characterized by gamble-distance (see below).
In control trials, gambles were presented that differed only in probability, but not in gain magnitude (probability-controls; gain magnitude was random, but identical in both gambles), or only in magnitude, but not in probability (magnitude-controls; probability was random, but identical in both gambles.). Probability- and gain-controls covered all levels of gains and probabilities of the experimental trials (Figure 1 B), but in order to reduce the overall length of the experiment, we only included control gamble pairs in which the difference in gain magnitudes was either $25 (equivalent to distance 1) or $75 (equivalent to distance 3), or the difference in probabilities was p = 0.03 and 0.09 respectively.
Probability- and magnitude-control trials had the purpose to ensure that subjects could perceptually discriminate between small differences in probability or magnitude, to identify brain areas related to tracking differences in gains and probabilities, and to exclude subjects that made random decisions. All subjects consistently and with no exception selected the more advantageous control gambles. Control trials were intermixed with experimental trials. The sequence of presentation of all trials was randomized within- and between-subjects, and the side of gamble presentation was likewise randomized across all trial repetitions.
Behavioral Analysis
Detection of intransitive preferences
Where p(x,y) indicates the probability of choices for x over y, and p(a,b) ≥ 0.5 and p(b,c) ≥ 0.5, choice satisfies stochastic transitivity if p(a,c) ≥ 0.5. We used graph theory to detect violations of stochastic transitivity in our subjects’ choices (Choi et al., 2007a ,b ). Choices between gambles were represented graphically which allows testing for acyclicity: preferred gambles were connected to non-preferred gambles by an arrow pointing in the direction of the unpreferred gamble. Indifferent gamble pairs were connected by two arrows pointing in both directions. We deemed a gamble as preferred over another gamble if the preferred gamble was chosen in more than 60% of the presentations of that pair. Indifference between two gambles in a pair was assumed when one gamble was chosen in 40% or more and in 60% or less of the presentations of that pair.
Transitivity requires that such directed graph representations are acyclical. If there are one or more loops in the graph, we can conclude that the subject had one or more occurrences of intransitive choices. For example, if a subject prefers gamble A over B, and B over C, but C over A, the arrows will point from A → B → C and back from C → A, and hence form a loop between A, B and C. Real choice data often contain at least one violation of transitivity. It is therefore important to quantify the extent of intransitivity. We used an intransitivity index that measures, for each subject, the smallest possible amount by which the subject’s choices must be adjusted in order to remove all violations of transitivity, normalized to the maximum possible number of choices to be adjusted 1 . A value of 0 means that a subject is perfectly transitive (no choice must be adjusted), a value of 1 means that a subject is perfectly intransitive (the maximum number of choices must be adjusted).
To generate a benchmark level of transitivity, we simulated choices in a random sample of 25,000 hypothetical subjects who performed the current task and implemented a rational, but error-prone choice strategy. To obtain a benchmark level of intransitivity given rational decision makers, we measured the intransitivity index in all simulated subjects (see Supplementary Material). Since a significantly small proportion (<5%) of the simulated subjects had an intransitivity index score of >0.3, we opted for a detection threshold of 0.3 and classified every actual participant as transitive who had an intransitivity index score <0.3, and every participant as intransitive who had an index score >0.3.
Context-dependent desirability of the gambles
A participant making intransitive choices may prefer gamble A when paired with B, but not when paired with C. Hence, a putative cause for intransitivity is that a gamble is not evaluated independently: the desirability of gamble A may be variable and depending on the context, i.e., which other gamble it is paired with. To determine the relative context-dependent desirability (CDD) of each gamble in each gamble pair combination, we estimated the log odds of choosing a gamble as a function of which other gamble it was paired with. This provides an expedient way to estimate the leverage that each gamble pairing has on choosing a given gamble in that pair. Log odds were determined separately for every participant and every gamble combination with the following equation:

where logiti|j indicates the log odds of choosing gamble i when paired with gamble j, pi|j indicates the probability of choosing gamble i when paired with gamble j (approximated as the fraction of choices of gamble i), and pj|i stands for the probability of choosing gamble j when paired with i, with pi|j + pj|i = 1. logiti|j can be understood as the leverage of the presence of gamble j on the choices of gamble i. Under the commonly made assumption that the relative number of choices of an option reflects its relative attractiveness (Herrnstein, 1961 , 1970 ; Navarick and Fantino, 1972 , 1975 ; Hey, 1995 ; Kalenscher et al., 2003 ; Sugrue et al., 2004 ), logiti|j measures how much more (or less) attractive a given gamble is relative to the gamble it is paired with. logiti|j can hence be interpreted as the context-dependent desirability of gamble i relative to context gamble j. For every subject and every gamble in every combination, we computed logiti|j as a measure of CDD.
Gamble-distance as operationalization of context
To investigate how the local gamble pairing (context) affects choice, we conducted a more detailed analysis of our behavioral data. To characterize context, we examined preferences as a function of distance between gambles. Gamble-distance is a quantity that measures how different two gambles in a gamble pair are: the greater the difference in probability and magnitude, the greater the gamble-distance. For example, the gambles in the adjacent pair AB are only one step apart along the probability and magnitude scale (cf. Figure 1 B), and therefore this pair is classified as gamble-distance 1. Conversely, gambles in pair AD offer relatively different probabilities and magnitudes, and the pair is consequently classified as gamble-distance 3. In total, the gamble pairs used in the present experiment could be classified into four gamble-distances. We examined the proportion of selections of Gricher or Gsafer as a function of gamble-distance.
Modeling individual decisions: the additive-difference model
Our behavioral analysis of distance-dependent choices (cf. results below and Figure 2 C) showed that participants making intransitive decisions preferred the gamble with the higher magnitude, Gricher, over the gamble with the higher probability, Gsafer, at gamble-distance 1, but the tendency to choose Gricher decreased linearly with gamble-distance until it reversed toward a preference for Gsafer. Hence, our intransitive participants behaved as if they maximized gain magnitude at gamble-distance 1, but minimized risk at higher gamble-distances. Why are preferences for risky or safe gambles variable and distance-dependent? How is it possible that a gamble is not evaluated independently, but with respect to the alternative gamble presented? It is possible that agents do not consider the choice alternatives as an integrated whole, but compare the probabilities and gain magnitudes between the two gambles separately (Tversky, 1969 ; Russo and Dosher, 1983 ; Brandstätter et al., 2006 ; but see Fishburn, 1982 ; Hey, 1995 ). According to this idea, an individual would prefer the safer gamble if she considered the difference in probabilities more important than the difference in magnitudes, and would prefer the richer gamble if she considered magnitudes more important than probabilities.
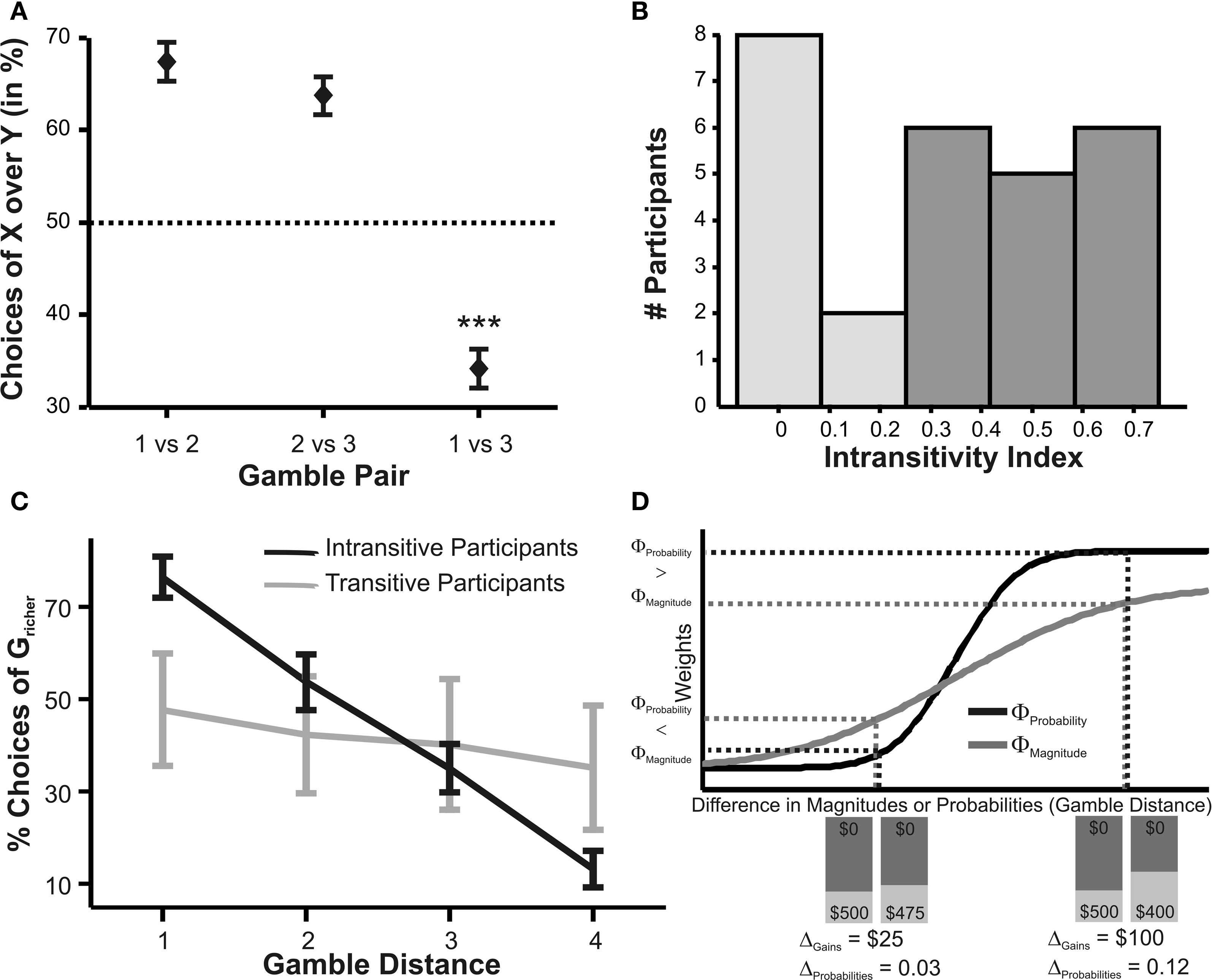
Figure 2. (A) Choices in all possible combinations of sets with three gambles in intransitive participants. Diamonds represent the mean percentage of choices of one gamble over another (±standard error of the mean) (***p < 0.0001). For reasons of simplicity, only gamble sets involving three gambles are shown here (e.g., gamble set ABC or CDE) and sets including more gambles are not displayed, although they were included in the analysis (cf. SI for a complete coverage). Gamble number 1 is a placeholder for the first gamble in any given gamble set (e.g., gamble A in gamble set ABC, or C in gamble set CDE), and gamble numbers 2 and 3 represent the second and third gambles respectively (e.g., B and C in gamble set ABC). The choices displayed were averaged across choices in all combinations of gamble triplets, they were not preselected for intransitivity. (B) Histogram of the distribution of intransitivity indices. The light-gray bars indicate the number of participants classified as transitive, the dark gray bars indicate intransitive participants. (C) Percentage of choices of the gamble yielding the relatively higher gain magnitude (Gricher) in intransitive (black line) and transitive (gray line) participants as a function of gamble-distance (mean values ± SEM). At gamble-distance 1, intransitive participants clearly preferred Gricher over Gsafer, but preference reversed with higher gamble-distances (p < 0.0001). Preference for Gricher or Gsafer was less distance-dependent in transitive subjects. (D) Sigmoidal weighting-functions can explain the context-dependent shift from preferring richer to safer gambles (cf. C). The weighting functions for probabilities (ΦProbability, black line) and magnitudes (ΦMagnitude, gray line) cross because of their presumed different shapes. As a consequence, ΦMagnitude is higher than ΦProbability when the difference in magnitudes and probabilities is minute, e.g., at a small gamble-distance (cf. left gamble pair). However, when the difference in both attributes increases (greater gamble-distance, right gamble pair), the weights reverse and ΦProbability is larger than ΦMagnitude. Accordingly, at gamble-distance 1 (illustrated by the left gamble pair in Figure 2 D), decisions should be more strongly influenced by magnitudes than by probabilities, and individuals should have a higher propensity to choose the gamble with the higher magnitude (Gricher). Conversely, at higher distances (e.g., the right gamble pair), decisions should be more strongly influenced by probabilities than by magnitudes, and individuals should be more likely to choose the gamble with the higher probability (Gsafer).
Based on this rationale, we modeled our participants’ decisions as follows (Tversky, 1969 ). X should be preferred over Y if

where n is the number of attributes (here, two: gain magnitude and probability), [ui(Xi) − ui(Yi)] is the difference in the utility of attribute i between alternatives X and Y, and Φi is the weighting function that determines the impact of the difference in attribute i on the overall decision, that is, the subjective importance of gain magnitudes or probabilities for the decision. Hence, gamble X would be preferred over Y if

Note that in the present task weighted difference in the utilities of one attribute (e.g., magnitude) is effectively subtracted from the weighted difference in the other attribute (e.g., probability) because of the inverted signs of the differences in attributes between gambles X and Y: one gamble always had a relatively higher gain magnitude, the other had a relatively higher probability.
It is a critical feature of the theory that probabilities and magnitudes affect the decision differentially depending on the difference between the gamble attributes. In its extreme, if the difference in one attribute falls below the attribute-specific threshold, the weighting factor Φ will be 0, the attribute will be ignored, and the decision will be determined by the other attribute. Note that, here, small attribute weights cannot be explained by perceptual discrimination problems as all participants, without exception, could discriminate between small differences in probability and gain magnitude in the control trials (see below). The differential weighting of gain magnitudes and probabilities can be modeled by sigmoidal gain- and probability- weighting functions that differ in shape and slope, as illustrated in Figure 2 D. We refer to this model as the additive-difference model (Tversky, 1969 ). See Section ‘Results’ and Supplementary Material for a more comprehensive discussion of this model. Also, see Supplementary Results for the discussion of alternative theories of intransitive choice.
Modeling the magnitude- and probability-weighting functions
We aimed to express the priority attached to gain magnitude over probability as the difference in the magnitude- and probability-weighting functions, and vice versa. To this end, we estimated for every subject individually the weighting functions  and
and 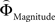 . We approximated the unweighted [u(XProbability) − u(YProbability)] and [u(XMagnitude) − u(YMagnitude)] terms in Eq. 3 as the difference between the normalized probability and magnitude values. Because the unweighted differences in normalized probabilities and gain magnitudes are equally spaced apart at all gamble-distances, any shifts in preference are attributable to the peculiar differential slopes of the fitted functions
. We approximated the unweighted [u(XProbability) − u(YProbability)] and [u(XMagnitude) − u(YMagnitude)] terms in Eq. 3 as the difference between the normalized probability and magnitude values. Because the unweighted differences in normalized probabilities and gain magnitudes are equally spaced apart at all gamble-distances, any shifts in preference are attributable to the peculiar differential slopes of the fitted functions 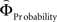 and
and 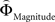 only (cf. Figure 2
C). We assumed that the more weight a participant places on differences in probability, the more often she should choose the gamble with the higher probability, Gsafer, and, vice versa, the more weight she places on differences in gains, the more often she should choose Gricher. To obtain an estimate of the individual weighting functions for each individual participant, we fitted Eq. 3 to the difference between their Gsafer- and Gricher-choices in every gamble pair with a least-square method. The individual weighting functions
only (cf. Figure 2
C). We assumed that the more weight a participant places on differences in probability, the more often she should choose the gamble with the higher probability, Gsafer, and, vice versa, the more weight she places on differences in gains, the more often she should choose Gricher. To obtain an estimate of the individual weighting functions for each individual participant, we fitted Eq. 3 to the difference between their Gsafer- and Gricher-choices in every gamble pair with a least-square method. The individual weighting functions 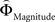 and
and 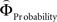 had a sigmoidal shape:
had a sigmoidal shape:
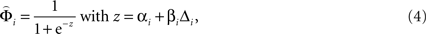
where αi and βi are the fitted parameters describing the horizontal positions and the slopes of the weighting functions of attribute i, and Δi is the normalized difference between gamble attributes in each pair. The lower bounds of βi were chosen to be 0 to ensure that the weighting functions increased with increasing attribute differences. See Figure 2 D for illustration and Tables S1–S3 in Supplementary Material for the best fitting parameters for every participant.
Image Acquisition
Functional magnetic resonance images were collected with a Phillips Intera 3.0T at the university hospital of the University of Amsterdam using a standard six-channel SENSE head coil and a T2* sensitive gradient echo (EPI) sequence (96 × 96 matrix, repetition time (TR) 2000 ms., echo time (TE) 30 ms, flip angle (FA) 80º, 34 slices, 2.3 mm × 2.3 mm voxel size, 3-mm thick transverse slices). Stimuli were projected on a screen at the front-end of the scanner and observed via a mirror mounted on the head coil. The participants’ heads were fixed by foam and they wore earplugs to reduce scanner noise. All stimuli were generated by a Pentium PC and presented using Eprime software (Psychology Tools Inc.). The behavioral responses were collected by an fMRI-compatible four-button response box (Lumitouch™).
fMRI Analysis
Preprocessing and data analysis were performed using SPM2 software (Statistical Parametric Mapping; http://www.fil.ion.ucl.ac.uk/spm ). The first four functional scans were discarded to allow for magnetic saturation. Time-series were corrected for differences in acquisition time, and realigned with reference to the first image to correct for head motion. The images were spatially normalized using the Montreal Neurological Institute (MNI) EPI template included in SPM2 and resliced to a resolution of 3 mm × 3 mm × 3 mm. Functional images were normalized and spatially smoothed using an isotropic Gaussian kernel of 8-mm at full width-half maximum.
Functional data were analyzed in an event-related design. Event-related activity was assessed by convolving a vector of the trial onset times with a canonical hemodynamic response function (HRF). Individual movement parameters and scanner drift were modeled as covariates of no interest. A high-pass filter with a cutoff period of 128 s was used to remove low-frequency noise. A general linear model (GLM) served to compute trial-type-specific betas that reflected the strength of covariance between the brain activation and the canonical response function for a given condition at each voxel for each participant (Friston et al., 1995 ).
Experimental trials
For the analysis of the experimental trials, we defined 20 event types of interest: selections of either gamble in each of the 10 gamble pairs. That is, for each pair of gambles x and y, we modeled choices of gamble x and choices of gamble y separately. Our analysis targeted BOLD signal changes during gamble evaluation, which started at stimulus onset (onset of gamble presentation). All parameter estimates reported in this paper are taken from this model.
Regions encoding the CDD of the chosen gamble were identified by first assessing the CDD values for each chosen gamble in each gamble pair and for every individual participant as described above. Then, we created individual parametric contrasts by weighting each event type (choices of each gamble in each pair) with the individual CDD estimates corresponding to the chosen gamble in each pair. All individual CDD values were centered by means of Z-scoring [Z = (X − M)/SD, X is the raw value, M is the average of the function, SD the standard deviation and Z is the Z-scored value]. We then used parametric modulation of the CDD of the chosen gamble to search for monotonic increases or decreases in activation.
Regions encoding the positive or negative difference between 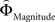 and
and 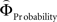 (as an approximation of the priority attached to one attribute over another) were identified by, first, estimating the weighting functions
(as an approximation of the priority attached to one attribute over another) were identified by, first, estimating the weighting functions 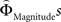 and
and 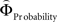 for every participant individually as described above. We thus obtained two individual weight-difference estimates ([
for every participant individually as described above. We thus obtained two individual weight-difference estimates ([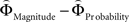 and
and 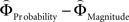 ]) for each gamble pair. Then, we created separate beta maps for all gamble pairs. This was done by combining the event types of interest from the base model (see above) according to gamble pair, thus pooling over choices of Gricher and Gsafer. Next, we created individual parametric contrasts by weighting each gamble pair event type with the corresponding difference estimates [
]) for each gamble pair. Then, we created separate beta maps for all gamble pairs. This was done by combining the event types of interest from the base model (see above) according to gamble pair, thus pooling over choices of Gricher and Gsafer. Next, we created individual parametric contrasts by weighting each gamble pair event type with the corresponding difference estimates [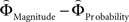 ], or [
], or [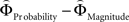 ], respectively. All difference estimates were centered by means of Z-scoring [Z = (X − M)/SD, X is the raw value, M is the average of the function, SD the standard deviation and Z is the Z-scored value).To identify brain regions modulated by the priority given to gain magnitudes over probability, parametric modulation of the difference between
], respectively. All difference estimates were centered by means of Z-scoring [Z = (X − M)/SD, X is the raw value, M is the average of the function, SD the standard deviation and Z is the Z-scored value).To identify brain regions modulated by the priority given to gain magnitudes over probability, parametric modulation of the difference between 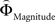 and
and  in each gamble pair was used to search for correlated activation. To identify brain regions modulated by the priority given to probability over gain magnitudes, parametric modulation of the difference between
in each gamble pair was used to search for correlated activation. To identify brain regions modulated by the priority given to probability over gain magnitudes, parametric modulation of the difference between 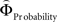 and
and 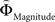 in each gamble pair was used to search for correlated activation.
in each gamble pair was used to search for correlated activation.
The effects of interest were calculated relative to an implicit baseline (the jittered ITI between 1.3 and 2.7 s; mean duration 1.72 s). Group averages were calculated for each regressor using random effects analyses. For each contrast, statistical parametric maps of the t-statistic were generated on a voxel-by-voxel basis, and these t-values were transformed into z-scores of the standard normal distribution. Because we were interested in neural correlates of intransitivity, we restricted our fMRI analysis to the data from our intransitive subjects only, except where indicated otherwise (see below). Transitive subjects were included in the behavioral analyses, however. We refrained from comparing brain activations in intransitive with transitive participants because the small number of transitive participants did not allow a reliable between-subject comparison and ambiguity about the behavioral strategies used by the transitive participants (five subjects seemed to have maximized gain magnitude, four subjects appeared to have minimized risk and one subject made arbitrary decisions) would make the interpretation of between-subject analysis dubious. Brain data from transitive subjects shown in the figures is for illustrative purposes only and should be considered anecdotal evidence.
We further asked whether the propensity to make intransitive decisions modulates desirability-related brain activations. To this end, we entered the individual intransitivity index as a covariate at the second level and performed a whole-brain analysis to identify brain regions sensitive to the CDD scores and the intransitivity index. Because we were interested in the effect of the full spectrum of intransitivity on value-related brain activation, we also included data from transitive subjects in this analysis.
For all contrasts, we performed whole-brain analyses and report activations surviving a threshold of p < 0.001 (uncorrected) with a minimum cluster size of five voxels. Reported voxels conform to MNI coordinate space, with the right side of the image corresponding to the right side of the brain.
Control trials
The analysis of the control trials was identical to the analysis of the experimental trials with the following exceptions. For the analysis of the control trials, we defined four event types of interest: Difference in gain magnitude 25, difference in gain magnitude 50, difference in probability 0.03 and difference in probability 0.09. The first two event types refer to the gain-control trials in which gambles differed only in gain magnitude (probability was chosen randomly, but kept constant across both presented gambles), the latter two event types refer to the probability control trials in which gambles differed only in probability (gain magnitude was chosen randomly, but kept constant across both presented gambles). We contrasted high- and low-gain and high- and low-probability control trials to search for differences in neural activation.
Results
Behavior: Choices were Systematically Intransitive
Participants exhibited clear, systematic and predictable intransitive choices in many instances. For example, one participant selected gamble A over gamble B in 100% of AB presentations, and chose gamble B over C in 80% of BC presentations, but chose A in only 5% of AC presentations even though A should be strongly preferred over C according to transitivity. This pattern goes on: while gamble B was revealed preferred over C (B was chosen in 80% of BC presentations) and C was revealed preferred over D (90%), B was not preferred over D (11%); likewise, although C was preferred over D (90%) and D was preferred over E (85%), C was not preferred over E (25%).
We calculated an intransitivity index for each subject as described above. Across all subjects, the index ranged from 0 to 0.7 (cf. Figure 2 B for a distribution of indices). According to our benchmark level of transitivity (see above and Supplementary Material), we classified participants as transitive if they scored lower than 0.3 on our intransitivity index (light-gray bars in Figure 2 B), and classified them as intransitive if they scored higher than 0.3 (dark gray bars in Figure 2 B). This classification coincides well with visual inspection of the distribution of intransitivity scores (Figure 2 B) which suggests that there were two groups of subjects: one transitive group with zero or near-zero intransitivity indices, and another intransitive group with non-zero indices. In total, 17 out of the 27 included participants met this intransitivity criterion.
Neuroimaging: Brain Regions Tracking the Context-Dependent Desirability of Gambles
We asked whether there is evidence for intransitive neural representations of the gambles’ local desirabilities. The participant in the example above preferred gamble A when paired with B, but not when paired with C, implying that the desirability of gamble A was variable and depended on which other gamble it was paired with. We hypothesized that such context-dependent values were encoded in brain areas that have been previously linked to decision-making and value representation. To examine this possibility, in line with previous studies (Kalenscher et al., 2005 ; Padoa-Schioppa and Assad, 2006 , 2008 ; Kable and Glimcher, 2007 ; Plassmann et al., 2007 ; Kalenscher and Pennartz, 2008 ), we defined brain areas as related to a gamble’s desirability if their activity correlated with the individual propensity to choose that gamble over another. To quantify the effect of context on desirability, we determined for every gamble the log odds of choosing that gamble given the other gamble it was paired with (Eq. 1; see Materials and Methods). We determined the individual CDDs of all gambles in all pairs, and for all intransitive participants separately. Parametric analysis revealed that BOLD responses in, among others, DLPFC, PPC and putamen were positively correlated with the CDD of the chosen gamble (Figure 3 and Table S4 in Supplementary Material). These areas are key structures in decision-making (Kim and Shadlen, 1999 ; Paulus et al., 2001 ; Dorris and Glimcher, 2004 ; Sugrue et al., 2004 ; Ernst and Paulus, 2005 ; Plassmann et al., 2007 ; Tobler et al., 2007 , 2009 ; Yang and Shadlen, 2007 ; Kim et al., 2008 ; Pesaran et al., 2008 ) and have been associated with planning, cognitive control, rational reasoning (Miller and Cohen, 2001 ; McClure et al., 2004 ; Tanaka et al., 2004 ; Hare et al., 2009 ) and representation of risk-attitude dependent subjective value (Tobler et al., 2007 , 2009 ). On the other hand, activations in several areas, incl. medial prefrontal cortex (MFPC) and VMPFC were negatively correlated with CDD (Figure 3 B and Table S4 in Supplementary Material), suggesting that activation in these regions decreased with increasing context-dependent desirability. The latter result is somewhat surprising because activity in these areas has been repeatedly shown to positively correlate with the subjective value of the expected outcome of a decision (Padoa-Schioppa and Assad, 2006 , 2008 ; Plassmann et al., 2007 ; Hare et al., 2008 , 2009 ; Rangel et al., 2008 ).
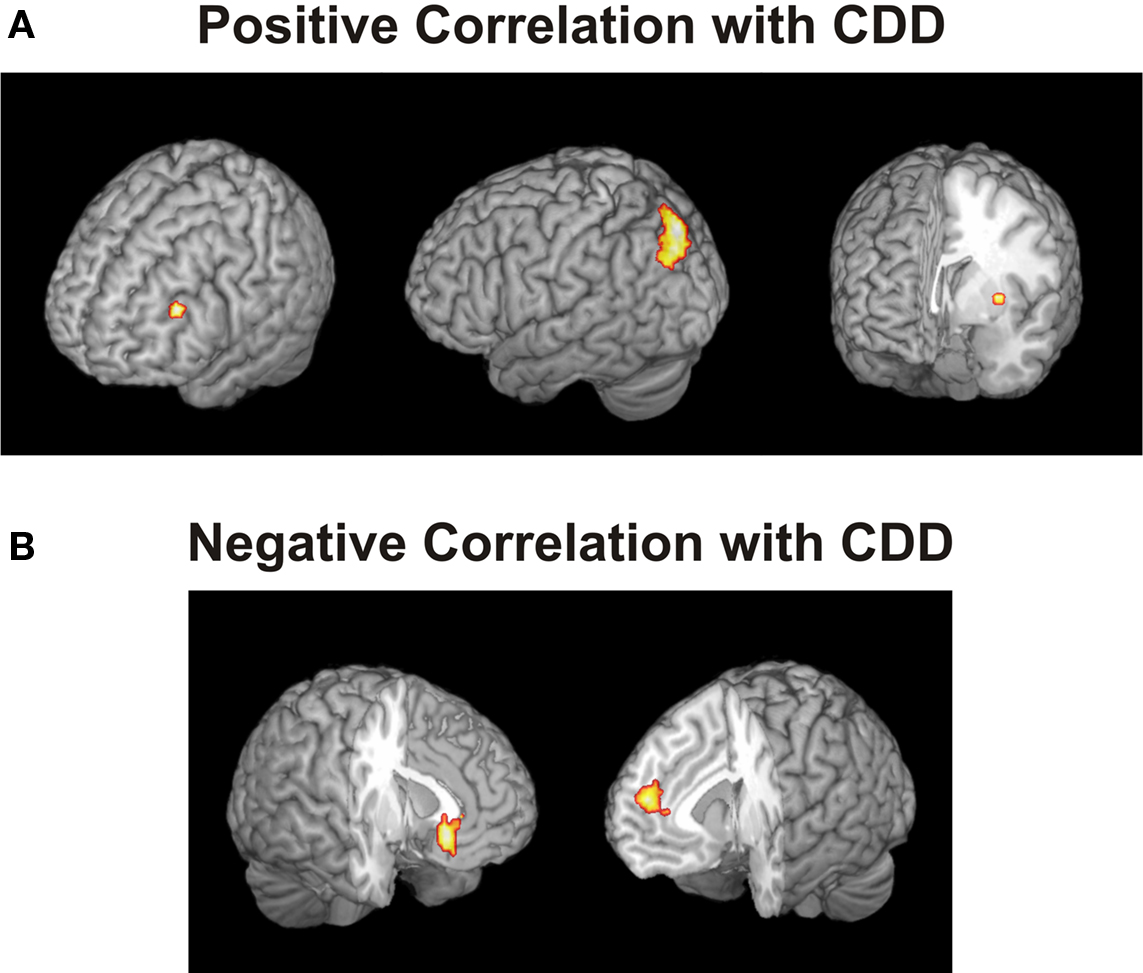
Figure 3. Areas whose activity was positively or negatively correlated with the context-dependent desirability (CDD) of the chosen gamble. The CDD quantified the subjective desirability of a gamble, given the other gamble presented, and was defined as the log odds of choosing gamble X when paired with gamble Y. (A) Activity in DLPFC (peak at MNI coordinates: −42, 36, 27), posterior parietal cortex (−21, −81, 48) and putamen (−33, −3, 0) were positively correlated with CDD, (B) activity in ventromedial (−6, 27, −12) and medial prefrontal cortex (9, 51, 15) was negatively correlated with CDD. Threshold p < 0.001, minimum five voxels.
Neural Value Signals are Intransitive
As outlined above, it is often assumed that one commodity cannot be at the same time better and worse than another commodity. Hence, subjective values should be represented at least on an ordinal scale that allows for unique ranking of options. However, the local, context-dependent desirabilities of the gambles in the present study followed an intransitive pattern. Hence, any brain regions whose activity correlates with CDD will also exhibit intransitive activation patterns, suggesting that the neural value code in these regions was not represented on an ordinal or higher scale. An analysis of activity in DLPFC, PPC, striatum, VMPFC and MPFC illustrates this implication. Figure 4 shows the difference in activation to choices of gamble x relative to choices of y in gamble pair xy in these structures, based on the mean signal in the activated voxels in the cluster identified by our parametric contrast analysis presented above: For every intransitive subject and every trial type, we extracted the activations in the identified clusters in the respective identified brain regions (remember that we had 20 trial types: choices of every gamble in each gamble pair were modeled separately). We then subtracted the activations during choices of one gamble from the activations during choices of the other gamble in each pair. Next, we averaged the resulting activation-difference values across all subjects and possible triplet combinations (remember that triplet combinations are any combinations involving three gambles, for example, choices in gamble pairs AB, BC and AC, or choices in CD, DE and DE). The bars shown in Figure 4 hence show the average difference in activation to choices of gamble x relative to choice of gamble y in gamble pair xy, i.e, how much more (or less) active a brain region was to choices of gamble x relative to choices of gamble y.
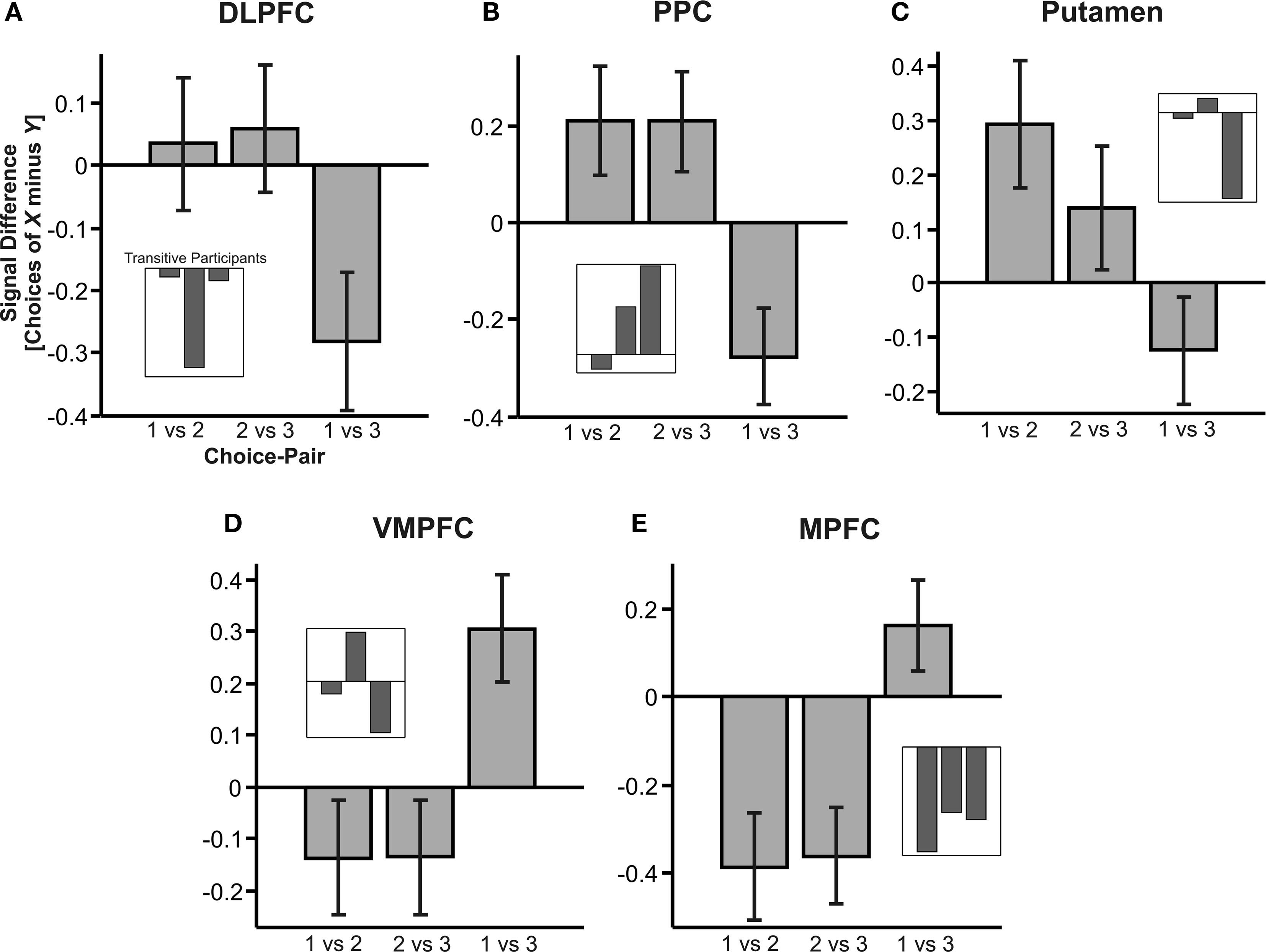
Figure 4. Activation in desirability-coding brain structures. The graph shows mean activity (±SEM) in the regions shown in Figure 3 , averaged across all triplet gamble sets. The bars represent the difference in BOLD activation to choices of gamble x relative to choice of gamble y in gamble pair xy, i.e., how much more (or less) active a brain region was in response to choices of gamble x relative to choices of gamble y. Gamble numbers 1, 2 and 3 are placeholders for the first, second and third gamble in a given gamble set (cf. legend of Figure 2 A). Insets show the activity in transitive subjects. Note that data from transitive subjects were not considered in the fMRI analysis and are merely shown here as supporting anecdotal evidence only (see text for details). (A–C) Brain regions in which activity was positively correlated with relative desirability. (D,E) Brain regions in which activity was negatively correlated with relative desirability.
A neural value signal on ordinal or higher scale should satisfy transitivity: if activation was higher in response to choices of gamble 1 compared to choices of gamble 2 in gamble pairs 1 vs 2 (1 > 2), and activation to choices of gamble 2 was likewise higher relative to choices of 3 (2 > 3), then the signal would satisfy transitivity if it was also higher to choices of gamble 1 relative to choices of gamble 3 (1 > 3). Activation in DLPFC, PPC and putamen (Figures 4 A–C) did not meet this criterion: Despite positive activation differences to choices of gamble 1 relative to 2, and 2 relative to 3 (suggesting that 1 > 2 and 2 > 3), activation was negative to choices of gamble 1 relative to 3 (1 < 3). Figures 4 D,E depict that VMPFC and MFPC inversely mirrored DLPFC and PPC activation, and hence equally failed to satisfy transitivity, although with a reversed sign. We conclude that, in the current task, the neural desirability-signals were not consistent with the assumption of an independent and ordinal-scaled neural representation of value, but instead reflected the intransitive fluctuations in preference-rank of a given gamble depending on which other gamble it was paired with.
Next, we asked if activity in value-coding regions was modulated by the individual propensity to make intransitive decisions. To this end, we used trial-by-trial CDD scores as a parametric modulator of the regressors, and the individual intransitivity indices as a subject-by-subject regressor at the second level, and then performed a whole-brain analysis. Different to the other analyses of fMRI results reported in this article, here, we also included data from transitive subjects because we were interested in the effect of the full spectrum of intransitivity on brain activation. However, the same analysis restricted to data from intransitive subjects yielded similar results. We found positive correlations between activity in CDD-coding regions and intransitivity indices in, among others, left DLPFC, bilateral striatum (caudate) and bilateral anterior cingulate cortex (Figure 5 and Table S5 in Supplementary Material). We found negative correlations in bilateral middle temporal gyrus. Figure 5 illustrates that activation in these regions increased with increasing intransitivity index.
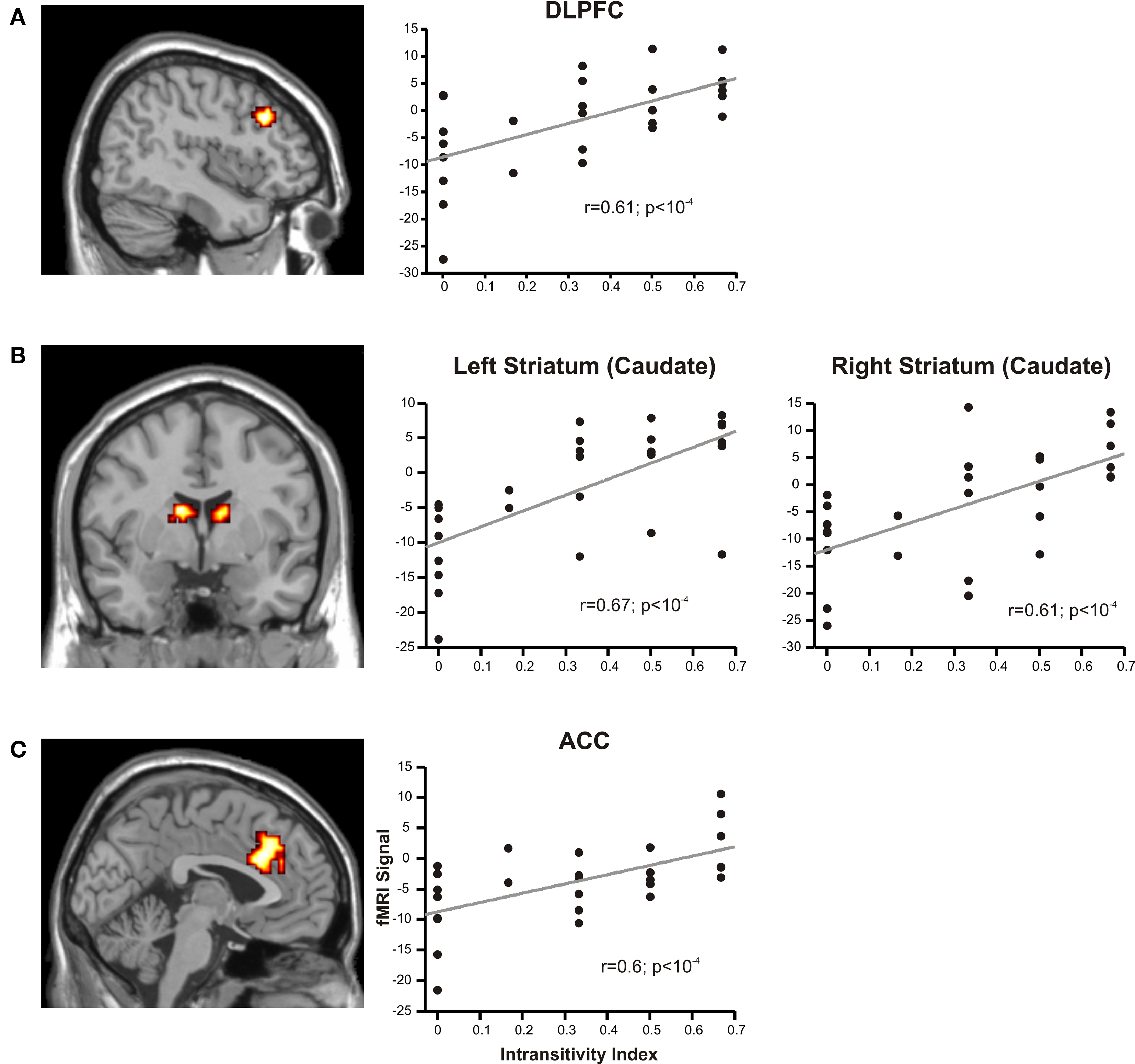
Figure 5. Relation of CDD-related activations to individual intransitivity indices. Activations in brain regions covarying with CDD values and individual intransitivity scores in (A) DLPFC (peak at −45, 24, 33), (B) bilateral striatum (caudate, −12, 0, 18 and 9, 0 15) and (C) anterior cingulate cortex (ACC; 3, 18, 27). In the scatter plots, the peak activations in the identified regions of individual participants are regressed against their intransitivity index.
Behavioral Preference for Relatively Safer or Richer Gambles Depends on the Difference between the Two Offered Gambles
Next, we performed an additional behavioral analysis in which we asked whether choices for the richer or the safer gamble depended on gamble-distance. The analysis of distance-dependent choices (Figure 2 C) showed that participants making intransitive decisions preferred the gamble with the higher magnitude, Gricher, over the gamble with the higher probability, Gsafer, at gamble-distance 1, but the tendency to choose Gricher decreased linearly with gamble-distance until it reversed toward a preference for Gsafer [F(75,3) = 30.9, p < 0.0001, analysis of variance (ANOVA) for repeated measures]. Transitive individuals showed a significantly lower degree of distance-dependency [group interaction, F(75,3) = 14.3, p < 0.0001].
Intransitive Decision Rules
Why did the intransitive subjects tend to select the richer gamble when the difference between the gambles’ attributes was minute, but selected the safer gamble when the difference between their attributes was large (Figure 2 C)? As mentioned, it is possible that intransitive agents do not consider the choice alternatives as an integrated whole, but compare the probabilities and gain magnitudes between the two gambles separately (Tversky, 1969 ; Russo and Dosher, 1983 ; Brandstätter et al., 2006 ). An individual would prefer the safer gamble if she considered the difference in probabilities more important than the difference in magnitudes, and would prefer the richer gamble if she considered magnitudes more important than probabilities. Consistent with this idea (cf. Eq. 2), our participants’ shift in tendency to prefer richer gambles at small distances to safer gambles at high distances indicates that the importance of gains relative to probabilities changed across gamble-distance. Because the objective difference in gains and probabilities incremented evenly with every step along the distance-scale (cf. Figure 1 B), the distance-dependent change in preference cannot be attributed to variation in the objective magnitude- and probability-measures. Instead, according to Eq. 3 the shift is the consequence of subjective, differential and distance-dependent weighting functions which satisfy:
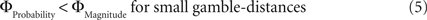
and
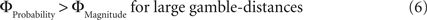
with ΦAttribute referring to the weighting functions of the difference in gain magnitude, or probability respectively. Hence, we hypothesized that the distance-dependent shift between preferring richer or safer gambles is a consequence of the balance between the individual weighting functions ΦProbability and ΦMagnitude (cf. Figure 2
D for illustration). To test this hypothesis, we modeled our participants’ decisions using Eq. 2 and estimated the individual, distance-dependent weighting functions 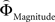 and
and  for every subject separately, as described in Eq. 4.
for every subject separately, as described in Eq. 4.
Insula and Posterior Cingulate are Sensitive to the Distance-Dependent Priority Given to Gains or Probabilities
Is there evidence for a neural underpinning of the decision rules leading to context-dependent fluctuations in gamble-desirability, and hence intransitivity? We hypothesized that brain regions sensitive to the variable priority given to gains over probabilities (and vice versa) should correlate with the difference between ΦMagnitude and ΦProbability. To isolate such regions, we performed a parametric analysis of the effect of the difference between the individually estimated 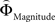 and
and 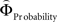 on brain activation to identify structures that are sensitive to the priority given to gain magnitudes over probabilities. Likewise, the difference between
on brain activation to identify structures that are sensitive to the priority given to gain magnitudes over probabilities. Likewise, the difference between 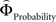 and
and 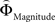 was used to reveal areas sensitive to the priority given to probabilities over gains.
was used to reveal areas sensitive to the priority given to probabilities over gains.
The parametric analysis of the context-dependent difference between 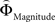 and
and 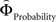 revealed activation in right posterior insula which has been previously associated with choices of larger, but riskier (Huettel et al., 2006
; Smith et al., 2009
; Xue et al., 2009
) or larger, but delayed rewards (Tanaka et al., 2004
; Wittmann et al., 2007
) (Table S6 in Supplementary Material). Figure 6
A shows that activation in insula was strongly distance-dependent: engagement was maximal at gamble-distance 1, where intransitive participants gave highest priority to gains, and decreased across gamble-distance in conjunction with the decreasing importance of gain magnitude for the decision.
revealed activation in right posterior insula which has been previously associated with choices of larger, but riskier (Huettel et al., 2006
; Smith et al., 2009
; Xue et al., 2009
) or larger, but delayed rewards (Tanaka et al., 2004
; Wittmann et al., 2007
) (Table S6 in Supplementary Material). Figure 6
A shows that activation in insula was strongly distance-dependent: engagement was maximal at gamble-distance 1, where intransitive participants gave highest priority to gains, and decreased across gamble-distance in conjunction with the decreasing importance of gain magnitude for the decision.
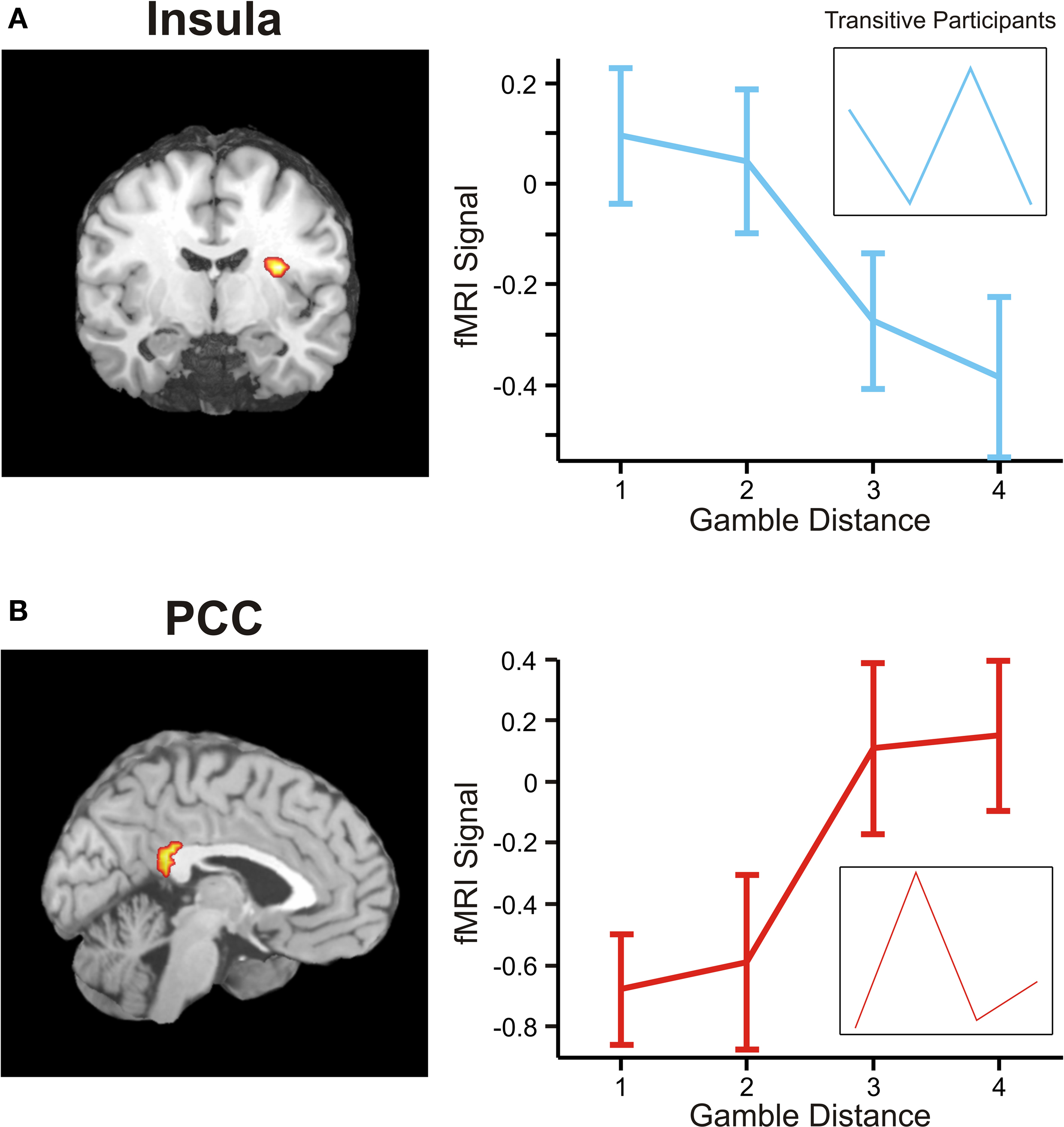
Figure 6. Areas sensitive to the difference between the individual weighting functions. Activity in these areas was positively or negatively modulated by gamble-distance. (A) Right insula (peak at 33, −9, 18) encoded the difference between magnitude- and probability-weighting functions, and thus the priority given to gain magnitude over probability. The graphs on the right of panel (A) show the mean activity of the activated voxels (±SEM). Activation was maximal at gamble-distance 1 (x-axis) and decreased with increasing gamble-distance in the intransitive participants, but not transitive participants (small insets). (B) Posterior cingulate (−3, −39, 21) was sensitive to the difference between probability- and magnitude-weighting functions and thus to the priority given to probability over gain. Activation increased as a function of gamble-distance in the intransitive, but not the transitive participants (small inset).
The inverse analysis further revealed that the difference between 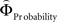 and
and 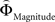 modulated activation in, among others, posterior cingulate cortex (PCC; Table S6 in Supplementary Material) which has been shown to play a role in representing subjective value (Kable and Glimcher, 2007
), and incorporating individual risk attitude into reward preference (McCoy and Platt, 2005
). Figure 6
B illustrates that activation in PCC was also highly distance- dependent: PCC was minimally recruited at gamble-distance 1, where the importance of probability for the decision was smallest, but its engagement increased with distance in proportion to the increasing priority given to probability. Taken together, these results suggest that insula encoded the context-dependent priority given to gains over probabilities, and PCC represented the priority given to probabilities over gains. A replication of the analysis with ΦMagnitude and ΦProbability modeled as linear instead of sigmoid functions revealed nearly identical brain activation patterns.
modulated activation in, among others, posterior cingulate cortex (PCC; Table S6 in Supplementary Material) which has been shown to play a role in representing subjective value (Kable and Glimcher, 2007
), and incorporating individual risk attitude into reward preference (McCoy and Platt, 2005
). Figure 6
B illustrates that activation in PCC was also highly distance- dependent: PCC was minimally recruited at gamble-distance 1, where the importance of probability for the decision was smallest, but its engagement increased with distance in proportion to the increasing priority given to probability. Taken together, these results suggest that insula encoded the context-dependent priority given to gains over probabilities, and PCC represented the priority given to probabilities over gains. A replication of the analysis with ΦMagnitude and ΦProbability modeled as linear instead of sigmoid functions revealed nearly identical brain activation patterns.
Do Insula and PCC Encode the Objective Difference in Gain Magnitude and Probability?
In the present task design, gamble-distance was not confounded with gain magnitudes or probabilities of the presented gambles, or the average gains or probabilities across gambles, or the gambles’ expected values, or even the amount of red or green on the screen. Hence, it is unlikely that the distance-dependent activation in insula and/or PCC reflected any of these parameters. However, gamble-distance by definition correlated with the objective difference in gain magnitude or probability between the gambles. This is innate in this measure as gamble-distance is a quantification of the difference in the presented gambles’ attributes. Hence, the neural activation reported here may either be a correlate of the difference in the subjective importance attached to gain magnitudes and probabilities, or alternatively, they may merely track the objective difference in these attributes. To address this possibility, we analyzed the control trials. In half of the control trials, the two gambles presented in a given trial differed only in gain magnitude, but not in probability (gain-controls). In the other half, the gambles differed only in probability, but not in gain magnitude (probability-controls). Hence, the objective difference between gain magnitude and probability was manipulated in the control-trials analogously to the experimental trials. However, in the control trials, there was no need to differentially weigh the difference in the gambles’ attributes: Because the gambles differed in only one attribute, this attribute was automatically decisive, and a trade-off and differential weighting of gain and probability was not necessary.
If insula and PCC indeed tracked the objective difference between probability and/or gain magnitude in the experimental trials, but not the subjective priorities given to the gamble attributes, these areas should also track the difference in probability in the probability-control trials, and/or they should track the difference in gains in the gain-control trials. Alternatively, if these regions indeed encoded the subjective priority given to gains and probabilities, as hypothesized, then these regions should show distance-dependent activation in the experimental trials, where weighting of attributes was necessary to reach a decision, but not in the control trials, where weighting was not necessary.
Paired t-tests revealed that activation in neither insula nor PCC significantly discriminated between difference in gain or probability in the control trials (all p > 0.22). Furthermore, a conjunction analysis revealed that neither insula nor PCC overlapped with regions sensitive to the difference in gains or probabilities in the control-trials, even at very liberal thresholds (all p > 0.8; small volume correction). Several further alternative interpretations of the insula- and PCC-activations are addressed in the Supplementary Material.
Discussion
We studied the neural correlates of intransitive decisions while participants performed a two-alternative choice task. Our results suggest that intransitive decisions occurred because participants did not assess the desirability of a given choice alternative independently, but with respect to the other alternative present. We found that activity in key regions for decision-making and value representation, incl. DLPFC,VMPFC, PPC and striatum (putamen) (Kim and Shadlen, 1999 ; Dorris and Glimcher, 2004 ; Sugrue et al., 2004 ; Yang and Shadlen, 2007 ; Hare et al., 2008 , 2009 ; Kim et al., 2008 ; Pesaran et al., 2008 ; Pessoa, 2008 ; Rangel et al., 2008 ; Hardin et al., 2009 ; Tobler et al., 2009 ) correlated with the context-dependent, intransitive desirability of the chosen gamble. We further found that neural value-codes in DLPFC, striatum (caudate) and ACC were modulated by the individual propensity to make intransitive choices. A detailed behavioral analysis of the effect of context on choice indicated that intransitivities were the consequence of participants giving variable priority to gain magnitudes or probabilities, depending on the combination of the choice alternatives. Specifically, they had a strong propensity to select the richer gamble when the difference between the gambles’ attributes was minute, but tended to select the safer gamble when the difference between their attributes was large. We found that activity in posterior insula and PCC reflected the difference between the individual and variable priority attached to gain magnitude and probability during the decision, and thus correlated with the context-dependent priority given to the different attributes during a decision.
Our finding of local desirability-coding in decision networks is not only consistent with numerous neurobiological results in humans (Knoch et al., 2006 ; Fecteau et al., 2007 ; Tobler et al., 2007 , 2009 ), but is also in line with several electrophysiological studies showing that the subjective reward value during risky or intertemporal decision-making is represented by single neurons in DLPFC (Kim et al., 2008 ) and parietal cortex (Dorris and Glimcher, 2004 ; Sugrue et al., 2004 ). Importantly, our main findings also amend recent claims about neural value coding (Platt and Glimcher, 1999 ; Padoa-Schioppa and Assad, 2006 , 2008 ; Kable and Glimcher, 2007 ; Plassmann et al., 2007 ; Tobler et al., 2007 , 2009 ; Elliott et al., 2008 ; Hare et al., 2008 ; Rangel et al., 2008 ) with the notion that representations of the desirability of a given commodity can depend also on which other commodities are available in a choice set. This latter finding is particularly noteworthy because it suggests that, at least in the present task, decision-related activation in DLPFC, VMPFC, PPC and other traditional choice regions did not encode the ordinal-scaled subjective value of a choice option, as would be expected from utility representation in the classic economic sense, but correlated with an option’s local, context-dependent and intransitive desirability. This discovery converges with recent evidence suggesting that neural value signals are not absolute, but scaled relative to a contextual reference point (Tremblay and Schultz, 1999 ; Coricelli et al., 2005 ; Elliott et al., 2008 ; De Martino et al., 2009 ; Hardin et al., 2009 ; but see Padoa-Schioppa and Assad, 2006 , 2008 ). It is therefore tempting to speculate that intransitive choices are not the consequence of a noisy implementation of independent and hierarchically organized preferences (Hey, 1995 ), but may reflect truly context-dependent, intransitive valuation. This view is corroborated by the fact that activity in several value-coding brain regions incl. DLPFC and striatum, correlated with the individual degree in the propensity to make intransitive decisions.
Our identification of brain regions encoding local desirability was based on the assumption that their activity reflected the context-dependent value of the chosen gamble. Hence, when a participant selected a generally unpreferred gamble with a consequently low local desirability, we assumed that neural activity reflected this low desirability. However, it is possible that a participant transiently preferred the selected gamble even though he generally disfavored this gamble. If that was the case, the rationale underlying our search for neural regions correlating with the local desirability of gambles would have to be called into question. However, we consider this possibility unlikely. It is a literally undisputed supposition in economics and psychology that individuals make errors when making decisions, that is, they occasionally select the actually unpreferred option. The propensity to make errors increases with increasing difference in the options’ values (Hey, 1995 ; see Supplementary Material). Because of errors when implementing subjective values during option selection, a value signal in the brain should not correlate with choice, but with the choice-underlying value of the chosen option, (Louie and Glimcher, 2010 ) which in the present case happens to be local and context-dependent. Hence, the BOLD response associated with selecting the actually unpreferred option should reflect the low value of that option.
Interestingly, activations in prefrontal regions that have been previously linked to processing goal values – the subjective values of expected choice outcomes – including medial and ventromedial prefrontal areas (Padoa-Schioppa and Assad, 2006 , 2008 ; Plassmann et al., 2007 ; Hare et al., 2008 ) were negatively correlated with context-dependent desirability in our intransitive subjects. This may point toward dissociable functions of lateral and medial prefrontal areas in context-dependent value-based decision-making. Networks consisting of DLPFC and parietal cortex are often associated with the planning and reasoning aspects of decision-making and cognitive control, whereas the affective components driving a decision are frequently attributed to medial prefrontal and orbitofrontal regions (Miller and Cohen, 2001 ; McClure et al., 2004 ; Tanaka et al., 2004 ; Hare et al., 2009 ; cf. however Pessoa, 2008 ). The prominent correlation between DLPFC/PPC activation and local desirability of the chosen gamble may hence suggest that context-dependent valuation was supported by a more cognitive control mechanism rather than an affective process. This view is supported by the fact that activation in ACC, which is often associated with supervisory cognitive control and action monitoring (Carter et al., 1998 ; Schall et al., 2002 ; Ridderinkhof et al., 2004 ) correlated positively with the participants’ tendency to make intransitive decisions. However, this interpretation does not account for the conspicuous anticorrelation between VMPFC activation and local desirability of the chosen gamble. Several studies showed that VMPFC is recruited during counterfactual thinking – the comparison of the obtained outcome with the outcome the decision maker would have obtained had she chosen the other alternative (Camille et al., 2004 ; Coricelli et al., 2005 ; Chandrasekhar et al., 2008 ; Fujiwara et al., 2009 ). Furthermore, a recent study suggested that frontopolar cortex tracks the relative advantage of the foregone alternative in a risky choice task (Boorman et al., 2009 ). In the present task, when subjects assessed the value of a gamble, the alternative gamble had leverage on the local desirability of the evaluated gamble. Hence, participants considered the alternative gamble during gamble evaluation. Given the aforementioned role of medial prefrontal regions in counterfactual comparisons, it is therefore possible that VMPFC and MPFC tracked the local desirability of the unchosen gamble. Future research needs to test this possibility, and needs to determine when and why medial prefrontal regions encode goal values or the value of the alternative course of action. In summary, we propose that context-dependent valuation in the present task is supported by a cognitive mechanism residing in lateral prefrontal and posterior parietal regions, but is modulated by a counterfactual comparison process involving medial prefrontal regions.
Decisions under risk are complex, computationally demanding and error prone. It is therefore likely that decision makers use particular decision rules to simplify the choice problem. For example, they may compare the probabilities and gain magnitudes between the two gambles separately and choose the safer gamble if they place higher priority on probability, or choose the richer gamble if they place higher priority on gain magnitude (Tversky, 1969 ; Russo and Dosher, 1983 ; Brandstätter et al., 2006 ). Consistent with this idea, our behavioral findings suggest that intransitive choices were due to a context-dependent shift in the weight attached to gains or probabilities during the computation of the context-dependent desirabilities.
Insula and PCC tracked the local, variable and context-dependent importance of gains and probabilities for the decision. The PCC’s putative function in integrating aversion against low probabilities into the decision process is consistent with its documented role in reflecting risk attitude (McCoy and Platt, 2005 ). Likewise, the finding that insula activation correlated with the subjective decision-weight attached to gain magnitude is in line with previous experiments showing that insula is recruited when choosing larger, but riskier (Huettel et al., 2006 ; Smith et al., 2009 ; Xue et al., 2009 ) or larger, but delayed rewards (Tanaka et al., 2004 ; Wittmann et al., 2007 ). However, at first glance, this interpretation might seem at variance with the insula’s documented role in arousal and pain (Ploghaus et al., 1999 ; Koyama et al., 2005 ). To reconcile the diverging opinions on the role of insula in pain processing and decision-making, it has recently been proposed that insular cortex may mediate sensitivity to homeostatic body signals (Craig, 2002 ; Weller et al., 2009 ; Xue et al., 2009 ). Because it is recruited by salient events, insula activation may signal the arousal associated with strong physiological changes, such as the anticipation of pain, but also the excitement associated with high rewards during gambling (Li et al., 2009 ; Xue et al., 2009 ). This suggests that insula may be crucial for integrating the urge to seek high rewards into the decision process, and thus modulate decisions according to the subjective priority placed on rewards.
Our results have general implications for our understanding of the neurobiological mechanisms of decision-making. We often make decisions between qualitatively different alternatives that are not straightforwardly comparable, such as whether to eat apples or oranges for dessert, or which financially risky prospect to invest in. One solution to the problem how we evaluate such diverse alternatives proposes that we assign subjective values (‘utilities’) to the available choice options. Encoding choice options as subjective values allows representing different commodities on a common scale, and therefore rank-ordering and comparing otherwise incommensurable outcomes (Bernoulli, 1954 ; Shizgal, 1997 ; Montague and Berns, 2002 ). Rank-ordering requires that values are mentally represented at least on an ordinal scale (Samuelson, 1938 ). This implies that one choice alternative cannot be at the same time better and worse than another alternative. If this was always true, then choices should at all times be transitive (but see Fishburn, 1982 ; Hey, 1995 ). Consequently, the failure to choose according to a hierarchically ordered, ordinal-scaled value system would be classified as irrational action in behavioral ecology and classic philosophic and economic theory (Samuelson, 1938 ; von Neumann and Morgenstern, 1944 ; Afriat, 1967 ; Hume et al., 1978 ; Varian, 1982 ; Stephens and Krebs, 1986 ). Recent philosophical contributions call this conception of irrationality into question and ask whether it actually is possible to act against what one thinks is best (Davidson, 2001 ; Kalis et al., 2008 ). These authors argue that values are local and it therefore proves to be adaptive to occasionally act against one’s general judgment. This view is corroborated by recent models in the optimal foraging literature according to which the consideration of alternative opportunities while evaluating a given opportunity has certain advantages for fitness maximization, even if (or because) they result in intransitive choice (Houston, 1997 ; Waite, 2001 ; Houston et al., 2007 ). Our results enrich this discussion by suggesting that local preferences are not the result of a failure of cognitive subsystems, as may be expected from the classic economic and ethological understanding of irrationality, but follow systematic rules that have identifiable neural counterparts. We argue that these neural systems have evolved because they equipped decision makers with the necessary cognitive efficiency to respond to rapidly and locally changing demands in the intricate magnitude and probability structure of the environment they evolved in. Hence, the phenomenon of intransitive decision-making may be intrinsic to the organization of the neural systems involved in risky decision-making.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Tobias Kalenscher was supported by grants from SenterNovem (BSIK-03053) and the Nederlandse Organisatie voor Wetenschappelijk Onderzoek (NWO-VENI 016.081.144). Scanning costs were in part funded by the Amsterdam Brain Imaging Platform (ABIP). We would like to thank Prof. Boek Beamer for his time and effort in helping with the fMRI analysis, and Paul Glimcher for invaluable comments on an earlier version of the manuscript.
Supplementary Material
The Supplementary Material for this article can be found online at http://www.frontiersin.org/neuroscience/human neuroscience/paper/10.3389/fnhum.2010.00049/
Footnote
- ^ Our intransitivity score was inspired by Afriat’s (1972) critical cost efficiency index. Afriat’s index measures the amount of wealth a subject is missing out by making inconsistent choices. Unlike our index, in which higher scores indicate more inconsistent choices, an Afriat’s index score of 0 indicates maximum waste of wealth and a score of 1 indicates perfectly consistent choices.
References
Afriat, S. N. (1967). The construction of utility functions from expenditure data. Int. Econ. Rev 8, 67–77.
Bernoulli, D. (1954). Exposition of a new theory on the measurement of risk. Econometrica 22, 23–36.
Boorman, E. D., Behrens, T. E., Woolrich, M. W., and Rushworth, M. F. (2009). How green is the grass on the other side? Frontopolar cortex and the evidence in favor of alternative courses of action. Neuron 62, 733–743.
Brandstätter, E., Gigerenzer, G., and Hertwig, R. (2006). The priority heuristic: making choices without trade-offs. Psychol. Rev. 113, 409–432.
Camille, N., Coricelli, G., Sallet, J., Pradat-Diehl, P., Duhamel, J. R., and Sirigu, A. (2004). The involvement of the orbitofrontal cortex in the experience of regret. Science 304,1167–1170.
Carter, C. S., Braver, T. S., Barch, D. M., Botvinick, M. M., Noll, D., and Cohen, J. D. (1998). Anterior cingulate cortex, error detection, and the online monitoring of performance. Science 280, 747–749.
Chandrasekhar, P. V., Capra, C. M., Moore, S., Noussair, C., and Berns, G. S. (2008). Neurobiological regret and rejoice functions for aversive outcomes. Neuroimage 39, 1472–1484.
Choi, S., Fisman, R., Gale, D., and Kariv, S. (2007a). Consistency and heterogeneity of individual behavior under uncertainty. Am. Econ. Rev. 97, 1921–1938.
Choi, S., Fisman, R., Gale, D., and Kariv, S. (2007b). Revealing preferences graphically: an old method gets a new tool kit. Am. Econ. Rev. 97, 153–158.
Coricelli, G., Critchley, H. D., Joffily, M., O’Doherty, J. P., Sirigu, A., and Dolan, R. J. (2005). Regret and its avoidance: a neuroimaging study of choice behavior. Nat. Neurosci. 8, 1255–1262.
Craig, A. D. (2002). How do you feel? Interoception: the sense of the physiological condition of the body. Nat. Rev. Neurosci. 3, 655–666.
Davidson, D. (2001). “How is weakness of will possible,” in Essays on Actions and Events, ed. D. Davidson (Oxford: Oxford University Press), 21–42.
De Martino, B., Kumaran, D., Holt, B., and Dolan, R. J. (2009). The neurobiology of reference-dependent value computation. J. Neurosci. 29, 3833–3842.
Dorris, M. C., and Glimcher, P. W. (2004). Activity in posterior parietal cortex is correlated with the relative subjective desirability of action. Neuron 44, 365–378.
Elliott, R., Agnew, Z., and Deakin, J. F. (2008). Medial orbitofrontal cortex codes relative rather than absolute value of financial rewards in humans. Eur. J. Neurosci. 27, 2213–2218.
Ernst, M., and Paulus, M. P. (2005). Neurobiology of decision making: a selective review from a neurocognitive and clinical perspective. Biol. Psychiatry 58, 597–604.
Fecteau, S., Knoch, D., Fregni, F., Sultani, N., Boggio, P., and Pascual-Leone, A. (2007). Diminishing risk-taking behavior by modulating activity in the prefrontal cortex: a direct current stimulation study. J. Neurosci. 27, 12500–12505.
Friston, K., Ashburner, J. D., Frith, C. D., Poline, J.-B., Heather, J. D., and Frackowiak, R. S. J. (1995). Spatial registration and normalization of images. Hum. Brain Mapp. 3, 165–189.
Fujiwara, J., Tobler, P. N., Taira, M., Iijima, T., and Tsutsui, K. (2009) A parametric relief signal in human ventrolateral prefrontal cortex. Neuroimage 44, 1163–1170.
Hardin, M. G., Pine, D. S., and Ernst, M. (2009). The influence of context valence in the neural coding of monetary outcomes. Neuroimage 48, 249–257.
Hare, T. A., Camerer, C. F., and Rangel, A. (2009). Self-control in decision-making involves modulation of the vmPFC valuation system. Science 324, 646–648.
Hare, T. A., O’Doherty, J., Camerer, C. F., Schultz, W., and Rangel, A. (2008). Dissociating the role of the orbitofrontal cortex and the striatum in the computation of goal values and prediction errors. J. Neurosci. 28, 5623–5630.
Heldmann, M., Vogt, B., Heinze, H. J., and Munte, T. F. (2009). Different methods to define utility functions yield similar results but engage different neural processes. Front. Behav. Neurosci. 3:43. doi: 10.3389/neuro.08.043.2009.
Herrnstein, R. J. (1961). Relative and absolute strength of response as a function of frequency of reinforcement. J. Exp. Anal. Behav. 4, 267–272.
Hey, J. D. (1995). Experimental investigations of errors in decision making under risk. Eur. Econ. Rev. 39, 633–640.
Houston, A. I. (1997). Natural selection and context-dependent values. Proc. R. Soc. Lond., B, Biol. Sci. 264, 1539–1541.
Houston, A. I., McNamara, J. M., and Steer, M. D. (2007). Violations of transitivity under fitness maximization. Biol. Lett. 3, 365–367.
Huettel, S. A., Stowe, C. J., Gordon, E. M., Warner, B. T., and Platt, M. L. (2006). Neural signatures of economic preferences for risk and ambiguity. Neuron 49, 765–775.
Hume, D., Selby-Bigge, L. A., and Nidditch, P. H. (1978). A Treatise of Human Nature. Oxford: Oxford University Press.
Kable, J. W., and Glimcher, P. W. (2007). The neural correlates of subjective value during intertemporal choice. Nat. Neurosci. 10, 1625–1633.
Kalenscher, T., Diekamp, B., and Güntürkün, O. (2003). Neural architecture of choice behaviour in a concurrent interval schedule. Eur. J. Neurosci. 18, 2627–2637.
Kalenscher, T., and Pennartz, C. M. (2008). Is a bird in the hand worth two in the future? The neuroeconomics of intertemporal decision-making. Prog. Neurobiol. 84, 284–315.
Kalenscher, T., Windmann, S., Diekamp, B., Rose, J., Güntürkün, O., and Colombo, M. (2005). Single units in the pigeon brain integrate reward amount and time-to-reward in an impulsive choice task. Curr. Biol. 15, 594–602.
Kalis, A., Mojzisch, A., Schweizer, T. S., and Kaiser, S. (2008). Weakness of will, akrasia, and the neuropsychiatry of decision making: an interdisciplinary perspective. Cogn. Affect. Behav. Neurosci. 8, 402–417.
Kim, J. N., and Shadlen, M. N. (1999). Neural correlates of a decision in the dorsolateral prefrontal cortex of the macaque. Nat. Neurosci. 2, 176–185.
Kim, S., Hwang, J., and Lee, D. (2008). Prefrontal coding of temporally discounted values during intertemporal choice. Neuron 59, 161–172.
Knoch, D., Gianotti, L. R., Pascual-Leone, A., Treyer, V., Regard, M., Hohmann, M., and Brugger, P. (2006). Disruption of right prefrontal cortex by low-frequency repetitive transcranial magnetic stimulation induces risk-taking behavior. J. Neurosci. 26, 6469–6472.
Koyama, T., McHaffie, J. G., Laurienti, P. J., and Coghill, R. C. (2005). The subjective experience of pain: where expectations become reality. Proc. Natl. Acad. Sci. U.S.A. 102, 12950–12955.
Lee, L., Amir, O., and Ariely, D. (2006). In Search of Homo Economicus: Preference Consistency, Emotions, and Cognition.
Lee, L., Amir, O., and Ariely, D. (2009). In search of homo economicus: cognitive noise and the role of emotion in preference consistency. J. Consum. Res. 36, 173–187.
Li, X., Lu, Z. L., D’Argembeau, A., Ng, M., and Bechara, A. (2009). The Iowa Gambling Task in fMRI images. Hum. Brain Mapp. 31, 410–423.
Loomes, G., Starmer, C., and Sugden, R. (1991). Observing violations of transitivity by experimental methods. Econometrica 59, 425–439.
Louie, K., and Glimcher, P. W. (2010). Separating value from choice: delay discounting activity in the lateral intraparietal area. J. Neurosci. 30, 5498–5507.
McClure, S. M., Laibson, D. I., Loewenstein, G., and Cohen, J. D. (2004). Separate neural systems value immediate and delayed monetary rewards. Science 306, 503–507.
McCoy, A. N., and Platt, M. L. (2005). Risk-sensitive neurons in macaque posterior cingulate cortex. Nat. Neurosci 8, 1220–1227.
Miller, E. K., and Cohen, J. D. (2001). An integrative theory of prefrontal cortex function. Annu. Rev. Neurosci. 24, 167–202.
Montague, P. R., and Berns, G. S. (2002). Neural economics and the biological substrates of valuation. Neuron 36, 265–284.
Navarick, D. J., and Fantino, E. (1972). Transitivity as a property of choice. J. Exp. Anal. Behav. 18, 389–401.
Navarick, D. J., and Fantino, E. (1975). Stochastic transitivity and the unidimensional control of choice. Learn. Motiv. 6, 179–201.
Padoa-Schioppa, C., and Assad, J. A. (2006). Neurons in the orbitofrontal cortex encode economic value. Nature 441, 223–226.
Padoa-Schioppa, C., and Assad, J. A. (2008). The representation of economic value in the orbitofrontal cortex is invariant for changes of menu. Nat. Neurosci. 11, 95–102.
Paulus, M. P., Hozack, N., Zauscher, B., McDowell, J. E., Frank, L., Brown, G. G., and Braff, D. L. (2001). Prefrontal, parietal, and temporal cortex networks underlie decision-making in the presence of uncertainty. Neuroimage 13, 91–100.
Pesaran, B., Nelson, M. J., and Andersen, R. A. (2008). Free choice activates a decision circuit between frontal and parietal cortex. Nature 453, 406–409.
Pessoa, L. (2008). On the relationship between emotion and cognition. Nat. Rev. Neurosci. 9, 148–158.
Plassmann, H., O’Doherty, J., and Rangel, A. (2007). Orbitofrontal cortex encodes willingness to pay in everyday economic transactions. J. Neurosci. 27, 9984–9988.
Platt, M. L., and Glimcher, P. W. (1999). Neural correlates of decision variables in parietal cortex. Nature 400, 233–238.
Ploghaus, A., Tracey, I., Gati, J. S., Clare, S., Menon, R. S., Matthews, P. M., and Rawlins, J. N. (1999). Dissociating pain from its anticipation in the human brain. Science 284, 1979–1981.
Rangel, A., Camerer, C., and Montague, P. R. (2008). A framework for studying the neurobiology of value-based decision making. Nat. Rev. Neurosci. 9, 545–556.
Ridderinkhof, K. R., Ullsperger, M., Crone, E. A., and Nieuwenhuis, S. (2004). The role of the medial frontal cortex in cognitive control. Science 306, 443–447.
Roelofsma, P. H. M. P., and Read, D. (2000). Intransitive intertemporal choice. J. Behav. Decis. Mak. 13, 161–177.
Russo, J. E., and Dosher, B. A. (1983). Strategies for multiattribute binary choice. J. Exp. Psychol. Learn. Mem. Cogn. 9, 676–696.
Schall, J. D., Stuphorn, V., and Brown, J. W. (2002). Monitoring and control of action by the frontal lobes. Neuron 36, 309–322.
Shafir, S. (1994). Intransitivity of preferences in honey bees: support for ‘comparative’ evaluation of foraging options. Anim. Behav. 48, 55–67.
Smith, B. W., Mitchell, D. G., Hardin, M. G., Jazbec, S., Fridberg, D., Blair, R. J., and Ernst, M. (2009). Neural substrates of reward magnitude, probability, and risk during a wheel of fortune decision-making task. Neuroimage 44, 600–609.
Stephens, D. W., and Krebs, J. R. (1986). Foraging Theory. Monographs in Behavior and Ecology. Princeton, NJ: University Press.
Sugrue, L. P., Corrado, G. S., and Newsome, W. T. (2004). Matching behavior and the representation of value in the parietal cortex. Science 304, 1782–1787.
Tanaka, S. C., Doya, K., Okada, G., Ueda, K., Okamoto, Y., and Yamawaki, S. (2004). Prediction of immediate and future rewards differentially recruits cortico-basal ganglia loops. Nat. Neurosci. 7, 887–893.
Tobler, P. N., Christopoulos, G. I., O’Doherty, J. P., Dolan, R. J., and Schultz, W. (2009). Risk-dependent reward value signal in human prefrontal cortex. Proc. Natl. Acad. Sci. U.S.A. 106, 7185–7190.
Tobler, P. N., O’Doherty, J. P., Dolan, R. J., and Schultz, W. (2007). Reward value coding distinct from risk attitude-related uncertainty coding in human reward systems. J. Neurophysiol. 97, 1621–1632.
Tremblay, L., and Schultz, W. (1999). Relative reward preference in primate orbitofrontal cortex. Nature 398, 704–708.
Venkatraman, V., Payne, J. W., Bettman, J. R., Luce, M. F., and Huettel, S. A. (2009). Separate neural mechanisms underlie choices and strategic preferences in risky decision making. Neuron 62, 593–602.
Volz, K. G., Schooler, L. J., Schubotz, R. I., Raab, M., Gigerenzer, G., and von Cramon, D. Y. (2006). Why you think milan is larger than modena: neural correlates of the recognition heuristic. J. Cogn. Neurosci. 18, 1924–1936.
von Neumann, J., and Morgenstern, O. (1944). Theory of Games and Economic Behavior. Princeton, NJ: University Press.
Waite, T. A. (2001). Intransitive preferences in hoarding gray jays (Perisoreus canadensis). Behav. Ecol. Sociobiol. 50, 116–121.
Weller, J. A., Levin, I. P., Shiv, B., and Bechara, A. (2009). The effects of insula damage on decision-making for risky gains and losses. Soc. Neurosci. 4, 347–358.
Wittmann, M., Leland, D. S., and Paulus, M. P. (2007). Time and decision making: differential contribution of the posterior insular cortex and the striatum during a delay discounting task. Exp. Brain Res. 179, 643–653.
Xue, G., Lu, Z., and Bechara, A. (2009). The insular cortex and risky decision-making: is there an urge in risk taking? In Annual Meeting of the Society for Neuroscience (Chicago: Society for Neuroscience).
Keywords: irrational, decision-making, neuroeconomics, risk, value, utility, heuristics
Citation: Kalenscher T, Tobler PN, Huijbers W, Daselaar SM and Pennartz CMA (2010) Neural signatures of intransitive preferences. Front. Hum. Neurosci. 4:49. doi: 10.3389/fnhum.2010.00049
Received: 22 December 2009;
Paper pending published: 04 February 2010;
Accepted: 16 May 2010;
Published online: 09 June 2010
Edited by:
Hauke R. Heekeren, Max Planck Institute for Human Development, Germany; Freie Universität Berlin, GermanyReviewed by:
Bernd Weber, Rheinische-Friedrich-Wilhelms Universität, GermanyHilke Plassmann, INSEAD, France
Tali Sharot, University College London, UK
Copyright: © 2010 Kalenscher, Tobler, Huijbers, Daselaar and Pennartz. This is an open-access article subject to an exclusive license agreement between the authors and the Frontiers Research Foundation, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Tobias Kalenscher, Department of Cognitive and Systems Neuroscience, Swammerdam Institute for Life Sciences, University of Amsterdam, Science Park 904, 1098 XH Amsterdam, Netherlands. e-mail:dG9iaWFzLmthbGVuc2NoZXJAZ21haWwuY29t




