- 1 Department of Organismal Biology and Anatomy, University of Chicago, Chicago, IL, USA
- 2 Committee on Computational Neuroscience, University of Chicago, Chicago, IL, USA
- 3 Section of Neurosurgery, Department of Surgery, University of Chicago, Chicago, IL, USA
Previous studies in non-human primates (NHPs) have shown that beta oscillations (15–30 Hz) of local field potentials (LFPs) in the arm/hand areas of primary motor cortex (MI) propagate as traveling waves across the cortex. These waves exhibited two stereotypical features across animals and tasks: (1) The waves propagated in two dominant modal directions roughly 180° apart, and (2) their propagation speed ranged from 10 to 35 cm/s. It is, however, unknown if such cortical waves occur in the human motor cortex. This study shows that the two properties of propagating beta waves are present in MI of a tetraplegic human patient while he was instructed to perform an instruction delay center-out task using a cursor controlled by the chin. Moreover, we show that beta waves are sustained and have similar properties whether the subject was engaged in the task or at rest. The directions of the successive sustained waves both in the human subject and a NHP subject tended to switch from one dominant mode to the other, and at least in the NHP subject the estimated distance traveled between successive waves traveling into and out of the central sulcus is consistent with the hypothesis of wave reflection between the border of motor and somatosensory cortices. Further, we show that the occurrence of the beta waves is not uniquely tied to periods of increased power in the beta frequency band. These results demonstrate that traveling beta waves in MI are a general phenomenon occurring in human as well as NHPs. Consistent with the NHP data, the dominant directions of the beta LFP waves in human aligned to the proximal to distal gradient of joint representations in MI somatotopy. This consistent finding of wave propagation may imply the existence of a hardwired organization of motor cortex that mediates this spatiotemporal pattern.
Introduction
Beta oscillations (10–35 Hz) of local field potentials (LFPs) have been observed in various parts of the brain including primary motor (MI), somatosensory (S1, areas 2 and 3a), and posterior parietal (area 5) cortices in the neocortex and subcortical areas such basal ganglia and cerebellum (Sanes and Donoghue, 1993; Murthy and Fetz, 1996a,b; Courtemanche and Lamarre, 2005; Witham and Baker, 2007; Witham et al., 2007; Kuhn et al., 2008). Beta oscillations increase their amplitude during movement planning, attenuate at the start of movement, and rebound once a movement is completed (Sanes and Donoghue, 1993; Murthy and Fetz, 1996a,b; Donoghue et al., 1998; Jurkiewicz et al., 2006; Keinrath et al., 2006; O’Leary and Hatsopoulos, 2006). Moreover, such oscillations occur sporadically throughout periods in which subjects need to maintain or increase attention (Murthy and Fetz, 1996a,b). Previous studies have shown that LFP beta oscillations in MI travel across the cortex as traveling waves, propagating at speeds between 15 and 35 cm/s along a rostral to caudal axis in the arm area of non-human primate (NHP) MI (Rubino et al., 2006; Takahashi and Hatsopoulos, 2007). Wave propagation occurs spontaneously uncoupled to sensory stimuli or motor actions but can also be evoked by visual stimuli. Interestingly, the statistical properties of wave propagation are quite similar during spontaneous and evoked periods.
In this study, we tested three specific hypotheses: (1) Do beta waves exist in MI of a tetraplegic patient having weak afferent and efferent connections between motor cortex and the periphery? (2) If so, do they exhibit similar properties to those observed in NHPs? (3) What kind of dynamics governs changes in directions of successive beta waves? We show that (1) beta waves do exist in MI of the human subject whether he was engaged in a task or at rest and are not directly tied to periods of increased beta power. (2) The range of wave speeds is comparable to the range observed in NHPs and the wave propagates in two dominant directions that are roughly 180° apart, medial to lateral within the MI hand/arm area for the human subject. (3) Successive waves tend to propagate from one dominant direction to the other for both the human subject and NHPs. Furthermore, at least in the NHP case, successive sustained waves that propagate into and out of the central sulcus travel a distance into the sulcus that is consistent with a reflection phenomenon at the boundary between MI and area 3a.
Materials and Methods
Experimental Procedures
Human subject and behavioral tasks
A tetraplegic individual (Hochberg et al., 2006; Saleh et al., 2010) was the subject of this study. Approval for this study was granted by the US Food and Drug Administration (Investigational Device Exemption) and the Rehabilitation Institute of Chicago and University of Chicago Institutional Review Boards. The patient in this study gave consent to participate in this study. In each experimental session prior to performing any behavioral task, the participant was instructed to relax for 1 min (Resting condition). During the engaged condition, the participant was instructed to perform an instructed delay, center-out task by moving a cursor with a track ball activated by his chin to one of eight peripheral targets, positioned at 45° increments starting at 0°, subtending a visual angle of 11.88° (12 cm) from the center of the screen. Each peripheral target was of a different color. The distance from the screen center to the participant’s eye was 57 cm. The human subject was instructed to fixate on the center target until movement was initiated and a shift in gaze followed movement of the chin. At the start of the trial, the participant held the cursor in the center target (hold period). One second later, the center target changed color – it turned the color of the peripheral target that was the instruction cue for that trial. At the go cue, which was signaled 2 s after the instruction, the participant was instructed to move to the peripheral target whose color matched the center target’s color. A success was recorded if the participant acquired the target in less than 5 s. The next trial started after the participant brought the cursor back to the center target. In each experimental session, 20 trials were collected for each of the eight targets yielding a total of 160 trials for each experimental session.
Surgery and data collection for the human subject
Local field potentials were collected using a 100-electrode “Utah” array (Blackrock™ Microsystems Inc.), implanted in the arm/hand area of the primary motor cortex (Hochberg et al., 2006). The arm/hand area was identified by stereotaxic coordinates and anatomical landmarks. Electrical stimulation was not used. LFP signals on each of the 96 channels were recorded continuously at 10 or 30 kHz, amplified using a gain of 5000, and band-pass filtered from 0.30 to 250 Hz. A separate wire placed near the electrode array was used as a reference. The SD of the LFP signal on each channel was calculated over the entire recording session, in order to identify outlier channels. Outlier channels, containing significant noise, were identified by visual inspection and excluded from the analysis. The task was programmed using custom software (TheGame2), which also synchronized its event timestamps with the LFPs. The following events’ timestamps were recorded: the start of a trial, the onset timing of the instruction cue, go cue, and target acquisition. We also tabulated the success rate for each experiment.
Non-human primate data
To compare the results from the human data to those of a monkey, one data set from monkey R in a previous study is used and the details of the behavioral task, surgery, and data collection can be found elsewhere (O’Leary and Hatsopoulos, 2006) and briefly described here. All of the surgical and behavioral procedures were approved by the University of Chicago’s IACUC and conform to the principles outlines in the Guide for the Care and Use of Laboratory Animals. The behavioral task associate with the NHP data is similar to that of the human task in the engaged condition except that the NHP used its arm instead of its chin. The right arm of the animal was securely placed on a two joint robot manipulandum and the animal was trained to control a cursor corresponding to the hand location of the animal. The monkey was required to hold his hand over the center target for 500 ms. A fixed instruction period of 1000 ms followed during which one of the eight targets appeared although the monkey was not allowed to move. A go cue was signaled by a blinking target, at which point the monkey was allowed to make a movement toward to the target. Thus, the direct comparison between the human and the monkey data can be made only for the engaged condition.
Analysis
All algorithms were implemented in Matlab. Across the three human data sets used for this study, a common set of channels were chosen. The power spectrum and spectrogram were computed using the multitaper method with time-bandwidth product (TW which effectively defines a bandwidth of windowing in the frequency domain) of two and three tapers from Chronux Matlab library (Mitra and Bokil, 2008).
To obtain the signal in the beta frequency range, the local field potential recorded from an electrode located at (x,y) on the array at time t, v(x,y,t) was bidirectionally filtered, to avoid phase distortion, between 10 and 45 Hz using a sixth order bandpass Butterworth filter. The Hilbert transform was applied to each bandpass-filtered LFP signal to extract its instantaneous phase, ɸ(x,y,t). The wave velocity v = [dx/dt, dy/dt] was computed by taking the derivative of a constant contour of ɸ(x,y,t) = const with respect to time:
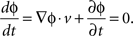
Since the direction of the velocity, −▽ɸ, is perpendicular to the constant phase contour, the speed is:
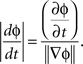
Note that velocity is well defined only when the phase gradient is non-zero and when the signal exhibits a well defined propagation direction. In order to measure how well the phase gradients align across the array, we defined a quantity, called the phase gradient directionality, PGD(t) (Rubino et al., 2006):
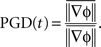
The bar here denotes the spatial average. If the phase gradients at all spatial locations align at a given time, t, then PGD(t) = 1. If the phase gradients are randomly distributed, then PGD will be close to 0. Thus, we use PGD(t) > 0.7 as a criteria to estimate mean wave direction and speed across the array which are computed as follows:
Wave direction = 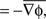
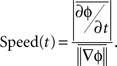
In order to take a spatial average for wave direction, averages of horizontal and vertical components are computed respectively, the angle between these averaged components defines the wave direction above.
Furthermore, if the PGD criteria is met for over an extended duration, we define a wave to be a sustained wave for that duration. For a sustained wave, the time at which the sustained wave starts is denoted by to and the time at which the same sustained wave is terminated is denoted by tt respectively. A mean speed of a sustained wave is denoted by 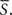
To characterize how the direction of a sustained wave changes from one instance to the next, which can be modeled as a discrete sequence of random angular variables, a homogeneous first order Markov chain was used by assuming that given the mean direction of the sustained wave, the past and the future mean directions of sustained waves are independent all the time. Here, Θn is an n-th element of a sequence of random circular variables and Θi is an i-th element of candidate binned sustained wave angles, then the conditional probability of Θn+1 taking the value of Θj given Θn taking Θi is characterized as follows:
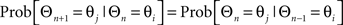
for all n. We divided the wave directions spanning from 0° to 360° into 12 equally sized bins such that
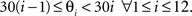
Thus, the transition matrix, P, is characterized as
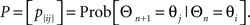
For a given data set, the corresponding transition matrices are estimated using a Matlab command, hmmestimate, which computes the maximum likelihood estimate of the transition matrix by supplying a sequence of mean wave directions which was made by concatenating subsequent trials.
Results
Beta Activity and Wave Propagation in Engaged and Resting Conditions
During the Engaged condition, the LFPs recorded across a set of electrodes showed a dominant beta frequency ranging from 15 to 18 Hz (Figure 1A, upper left panel) which was present but highly attenuated during the Resting condition (Figure 1B, upper right panel). On the other hand, propagating waves were evident in both conditions (Figures 1C,D, lower panels).
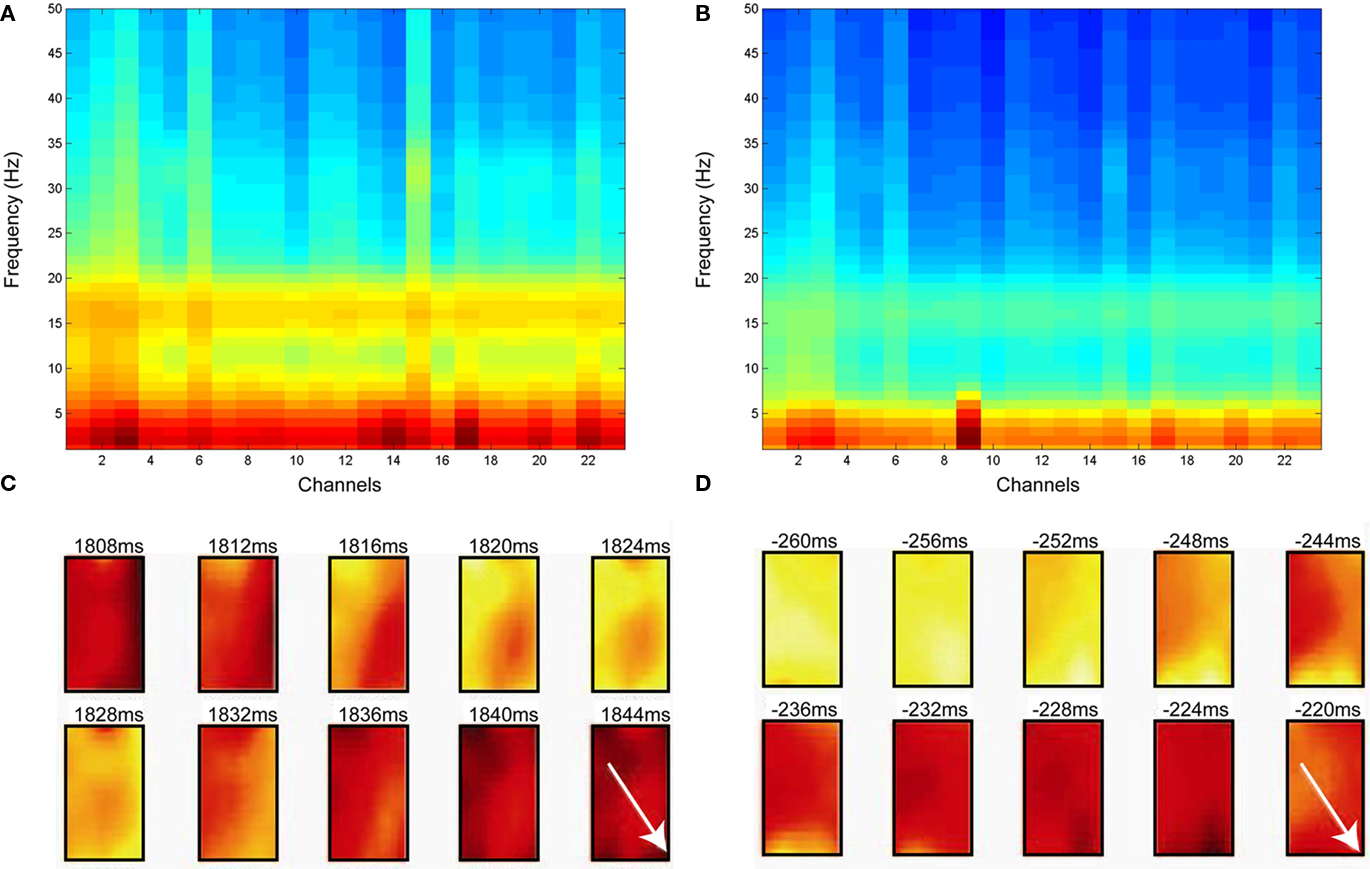
Figure 1. Frequency analysis of local field potentials for both Engaged and Resting conditions. (A) Power spectral density during Engaged condition across channels. (B) Power spectral density during the Resting condition. (A,B) share the same pseudo color scaling ranging from −40 to 25 dB/Hz. (C,D) Examples of a temporal progression of the LFP voltages during the Engaged condition (C) and the Resting condition (D). Each snap shot is 6 ms apart and time progresses from the upper left to lower right measured with respect to a cue timing and the beginning of a Resting condition for (C,D) respectively. The white arrow in both figures shows the wave propagation direction.
In the Engaged condition, the beta power was at its maximum around the onset of the instruction cue (Figure 2A). The onset of increase in beta power clustered between 400 and 200 ms prior to the onset of the instruction cue (Figure 2B). In contrast, the onsets of sustained propagating beta waves (i.e., waves with sustained PGD values of 0.7 or larger lasting for at least 20 ms) were not tightly linked to the onset of the instruction cue (Figure 2C).
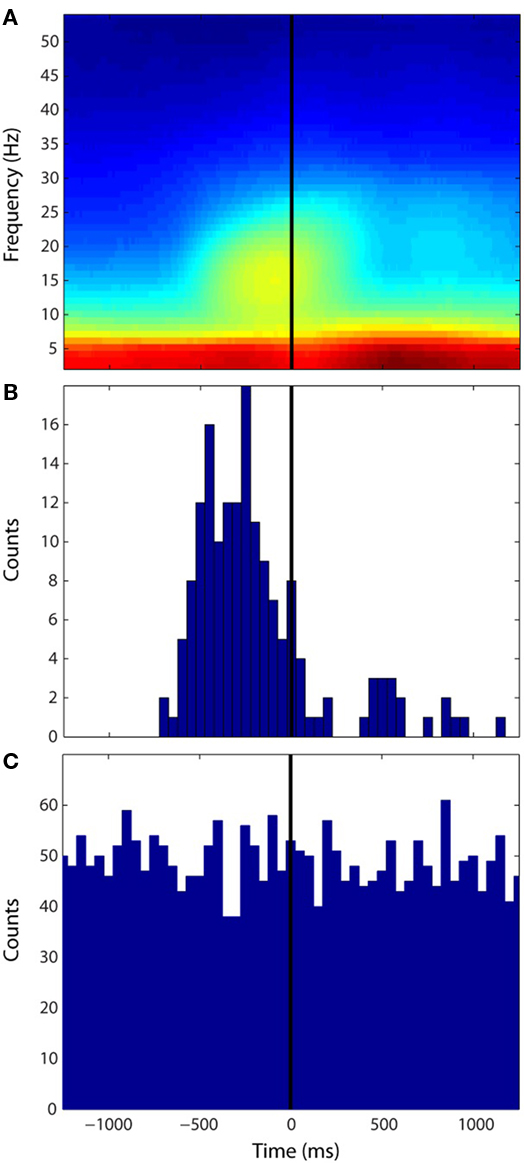
Figure 2. Distributions of onset of power increase in beta frequency and onsets of sustained wave during the Engaged condition. All three figures are aligned to the instruction cue. (A) Averaged spectrogram across all the channels and all trials. The pseudo color scaling ranges from −10 to 35 dB. (B) Distribution of onset of increase in beta power. (C) Distribution of sustained wave onsets. The bin size for the histograms (B,C) is 20 ms.
Wave Speed, Duration, and Inter Wave Intervals
To characterize the propagation speed for each sustained wave, the temporal average of instantaneous speeds over the duration of each sustained wave was computed. The empirical probability distributions of sustained wave speed under both Engaged and Resting conditions from the human data were qualitatively similar (Figure 3A) and were not significantly different from each other (Kolmogorov–Smirnov test α = 0.05, p-value = 0.04). The monkey data (Figure 3B) shows similar distribution to that of the human data, where the modes for all three distributions ranged between 15 and 35 cm/s. Figure 3C shows distributions of sustained wave durations of the human Engaged condition data and the NHP data. Both show modes around 35–40 ms and follow exponential decays in their distributions. Finally means of intervals of successive sustained waves were computed: 166.30 ms for the human Engaged condition, 165.77 ms for the human Resting condition, and 210.85 ms for the NHP subject respectively.
Figure 3. Distributions of sustained wave speeds and durations. (A,B) Normalized distributions of sustained wave mean speeds under both conditions. (A) Light Green: Engaged condition; Pink: Resting condition for the human subject (B) Light Blue: NHP subject for Engaged condition only. (C) Distributions of sustained wave durations Green: The human subject, Blue: NHP subject.
Wave Direction Distributions
Although each sustained wave could propagate in any direction across the motor cortex, waves under both Resting and Engaged conditions were more likely to propagate along a dominant axis defining two dominant directions 180° apart, as is evident from the bimodal distribution of wave directions (Rayleigh test, p < 0.01, V-test for doubled angles for both distributions with α = 0.05, Figure 4A). For the human subject, the first mode was oriented at around 100–120° (medial direction) and the second around 270–300° (lateral direction) on the array. The dominant axis was oriented along the medial to lateral directions on the knob hand area of motor cortex (Figure 4B). For the NHP subject, the directional distribution is again bimodal distribution (Rayleigh test, p < 0.01, V-test for doubled angles for both distributions with α = 0.05, Figure 4C), the first mode was oriented at around 70–90° (rostral direction) and the second around 270–290° (caudal direction) on the array. The dominant axis was oriented in the arm/hand area of motor cortex perpendicular to the central sulcus (Figure 4D).
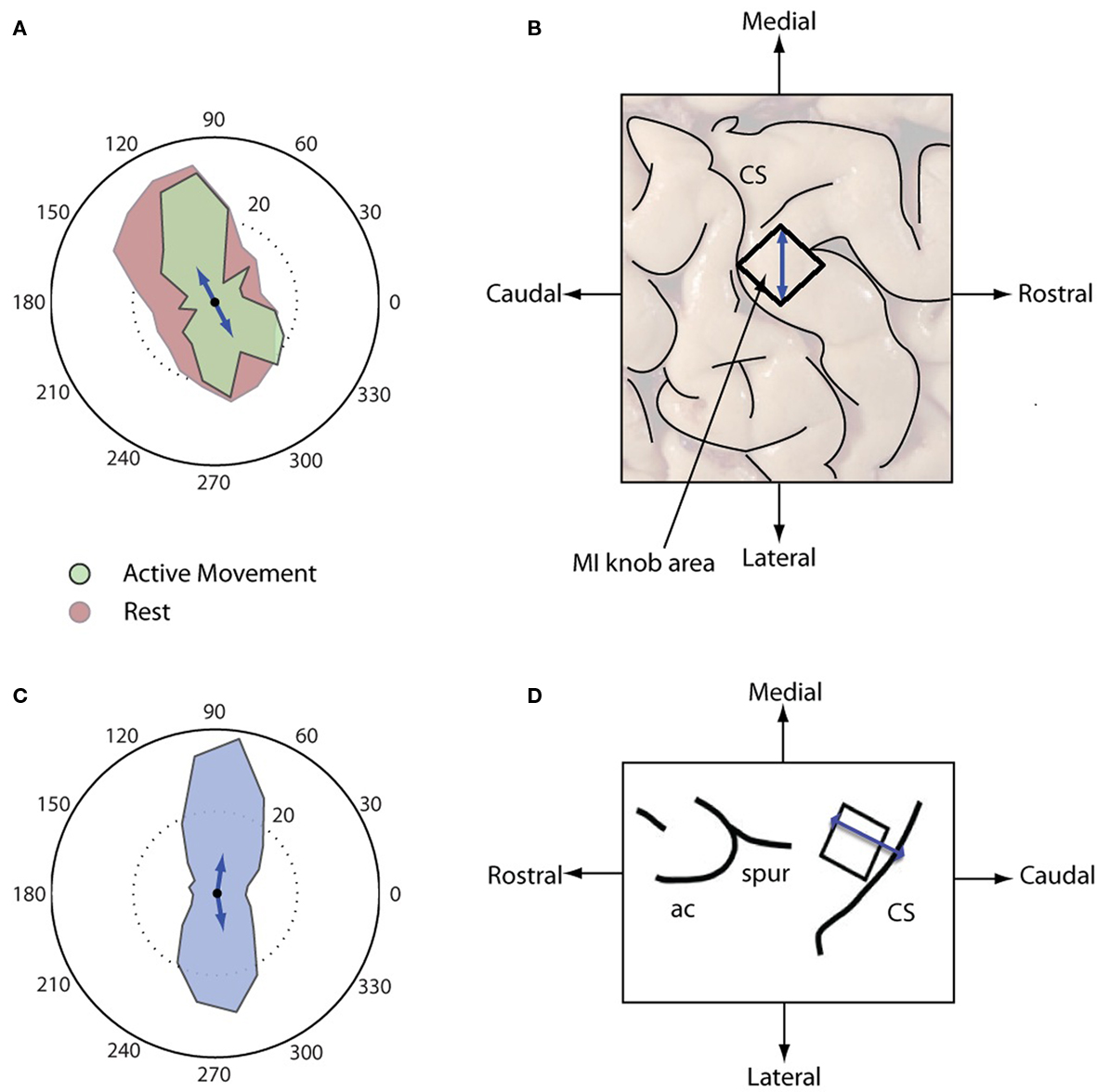
Figure 4. Distributions of directions of sustained waves. The top panels (A,B) for the human subject and the bottom panels (C,D) for the NHP subject. (A) Directions of sustained beta waves under two conditions, Red: Resting, Light green: Engaged condition. (B) Dominant propagation directions of the beta wave mapped on the cortical surface. The arrow from Lateral to Medial corresponds to the 120° arrow in (A). The black square denotes the location of the array. (C) Direction of sustained beta waves. (D) Dominant propagation directions of the beta wave mapped on the NHP subject cortical surface (modified from Figure 1 for Monkey R in O’Leary and Hatsopoulos, 2006) CS, central sulcus; ac, arcuate sulcus; and spur, spur of the arcuate sulcus. The black square denotes the location of the array.
Wave Direction Dynamics
Although instances of sustained waves tend to propagate along one of two dominant directions across the primary motor cortex, it is not evident from these distributions how waves varied in their direction across successive instances of sustained waves. To examine this issue, the sequence of sustained wave directions were considered as a stochastic process and were modeled as a homogeneous first order Markov chain. The transition matrices exhibited a consistent structure across three data sets from the human subject and one from the monkey and indicated that successive sustained waves were more likely to transition from one dominant direction to the opposite instead of maintaining the same direction: in human (chi squared test, α = 0.05, p < 0.05), 100–120° in the medial direction to 270–300° in the lateral direction and vice versa (Figure 5A), and in monkey, 60–90° in the rostromedial direction to 270–300° in the caudolateral direction and vice versa (Figure 5B).
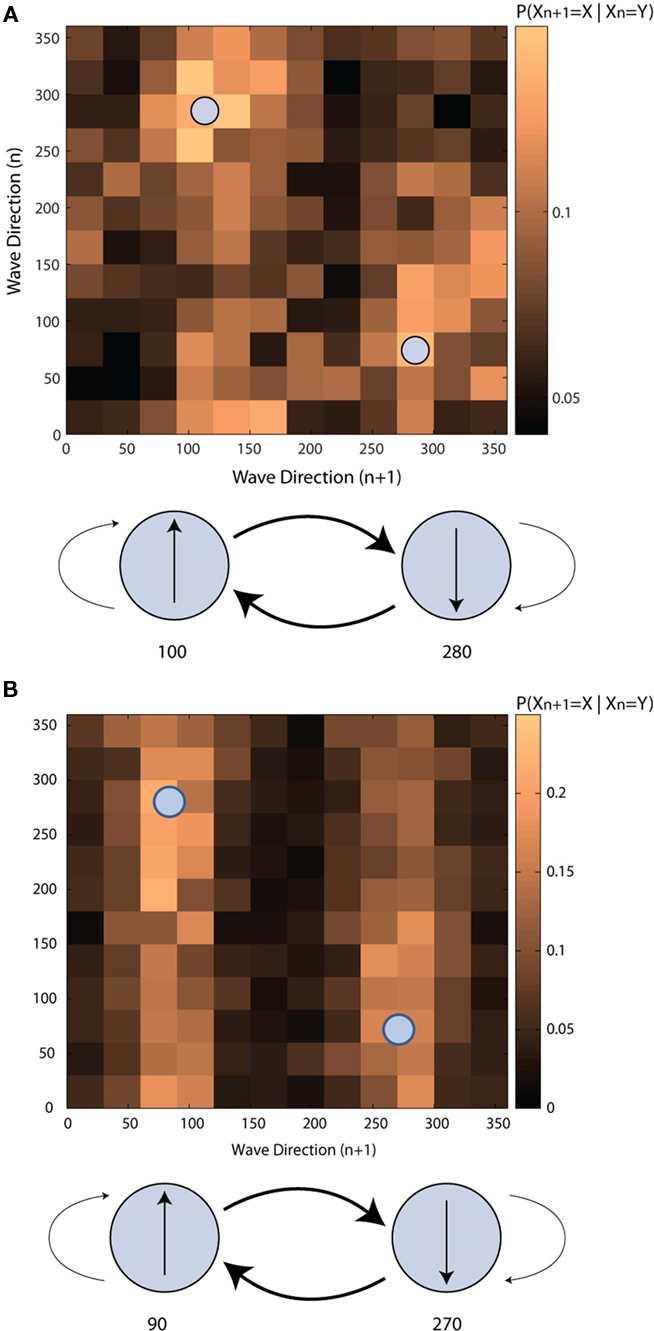
Figure 5. Transition probability matrices of directions of sustained beta waves. (A) The human subject (B) the NHP subject. Each small square in the upper figures corresponds to a conditional probability of the direction of an n + 1 th sustained wave is at a certain angle given the direction of an n-th sustained wave. The lower figure shows interactions between two dominant sustained wave directions.
Distributions of Estimated Distance that Unobservable Waves between Successive Sustained Waves
Since we cannot observe wave activity beyond our array, it is not obvious what happens to a sustained wave after it sweeps the electrode array. We can hypothesize that between two successive sustained waves, there is an unobservable sustained wave that connect the two. In order for that to happen, the two successive sustained waves need to travel in opposite directions. Specifically, if a sustained wave propagating in the caudal direction is followed by a sustained wave propagating in the rostral direction, does the caudal wave continue into the central sulcus, reflect off of the anatomical boundary between MI and area 3a of the somatosensory cortex, and then continue rostrally up the central sulcus until we observe it on the precentral gyrus as a rostral wave (Hilgetag and Barbas, 2006; Rathelot and Strick, 2009).
To test this hypothesis, we estimated the distance that an unobservable wave would travel from the time that the sustained caudal wave terminated until the moment that the sustained rostral wave was first observed. Using two possible measures for the propagation speed of the unobserved sustained wave, we observed distributions of estimated distances traveled by the unobserved wave (Figure 6). Under either measure of propagation speed, the distribution exhibited a mode at around 1 cm.
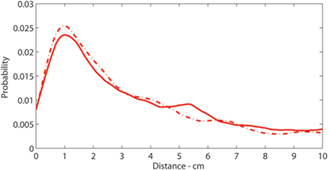
Figure 6. Distributions of intervals of successive sustained waves: Distribution of estimated distance that unobservable sustained waves travel. Solid: 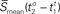 and Solid-Dashed
and Solid-Dashed 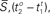 where
where 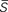 and t denote the mean speed of sustained waves and timings, superscripts o and t denote onset and termination of a sustained wave, and superscripts 1 and 2 denote the first and second of a pair of successive sustained waves that travel rostral to caudal and vice versa, and
and t denote the mean speed of sustained waves and timings, superscripts o and t denote onset and termination of a sustained wave, and superscripts 1 and 2 denote the first and second of a pair of successive sustained waves that travel rostral to caudal and vice versa, and 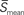 is an average mean speeds of the two successive sustained waves respectively.
is an average mean speeds of the two successive sustained waves respectively.
Discussion
The spatiotemporal dynamics of beta LFP oscillations in MI of a tetraplegic human subject were found to propagate as planar waves whose statistical properties were consistent with those observed in NHPs (Rubino et al., 2006; Takahashi and Hatsopoulos, 2007; Hatsopoulos et al., 2010). In particular, the distribution of wave directions showed two dominant directions which were roughly 180° apart, and the wave propagation speed ranged between 15 and 35 cm/s. These waves were consistently observed with or without an increase in beta power as shown previously (Rubino et al., 2006) and under both Resting and Engaged conditions. Furthermore, we show for the first time that successive beta waves tend to move from one dominant direction to the other both in the human subject and the NHP subject. Interestingly, the human subject in the current study controlled the cursor with his chin while NHPs controlled an exoskeleton robotic manipulandum with their arm suggesting that changes in beta oscillatory power may be independent on the effecter used.
Potential Functional Role of Beta Waves in Relation to Somatotopy in MI
Although it is still controversial whether there is a refined somatotopy within the arm/hand area in MI that defines distinct representations of the shoulder, elbow, wrist, and fingers (Asanuma and Rosen, 1972; Shinoda et al., 1981; Schieber and Hibbard, 1993), several studies have provided evidence for a proximal to distal gradient within the NHP motor cortex such that proximal representations of the shoulder and elbow are located within a C-shaped region much of which sits rostrally on the precentral gyrus surrounding distal representations of the wrist and fingers buried within a central core in the anterior bank of the central sulcus (Park et al., 2001, 2004). Moreover, it has been shown that shoulder- and elbow-related neurons in MI activate earlier than wrist and finger related neurons in monkeys performing a reach to push task (Murphy et al., 1985). Given that evoked beta waves in NHP motor cortex propagate along a rostral to caudal axis (Rubino et al., 2006), we have speculated that these waves may promote sequential recruitment of proximal and distal sites in motor cortex (Takahashi and Hatsopoulos, 2007; Hatsopoulos et al., 2010). Early surface electrical stimulation studies in human motor cortex by Penfield suggested a medial to lateral organization of proximal and distal representations such that shoulder and elbow sites are located more medially whereas wrist and finger sites are located more laterally (Penfield and Boldrey, 1937). Our findings that beta waves propagate along a medial to lateral axis across the human motor cortex in our tetraplegic subject are consistent with this hypothesis. It should, however, be noted that somatotopy of MI has shown to reorganize after spinal cord injury (Enzinger et al., 2008; Isa, 2009). Furthermore, the human subject in the current study used the chin cursor to control an object on a computer monitor rather than his own limb. Thus, our finding implies that the spatiotemporal dynamics of beta waves in MI are relatively stable regardless of spinal cord injury or the effectors used to perform a task.
Wave Reflections
One possible mechanism for the alternation of wave directions from one dominant direction to another is that a given sustained wave propagates in one direction until it reaches the border with another cortical area and then reflects off the border in the opposite direction. Such wave reflections have been observed in waves measured using voltage sensitive dyes in visual cortex where reflecting waves occurred at the border between V1 and V2 (Xu et al., 2007). Based on the NHP data, the distribution of estimated distance that a subset of sustained waves travel once they leave the array in the caudal direction into the central sulcus, and became observable as sustained waves again traveling in the rostral direction, shows a clear peak around 0.8–1.0 cm which is roughly the twice the distance from the edge of the array coinciding the boundary of the gyrus with central sulcus to the boundary between MI and area 3a (Kwan et al., 1978; Rathelot and Strick, 2006, 2009). Although wave propagation speeds of unobserved waves were assumed to be constant and consistent with the propagation speeds of the observed waves, the presence of a clear peak in the distribution may indicate that the sustained waves propagate into the sulcus and once they hit the boundary of MI and 3a, those waves may reflect and travel back to the surface of the cortex.
Based on the distribution of sustained wave durations and speeds, the average sustained wave both in the human subject and the NHP subject propagates for 60 ms at 25–30 cm/s so that if we assume that a wave front propagates at the mean speed over the primary motor cortex, then it travels 1.5–1.8 cm. Thus during each propagation, a sustained wave for in the NHP travels more than the entire spatial dimensions of the arm/hand representation of MI. However, this needs to be investigated in more detail using techniques that can acquire signals deep within the central sulcus.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank for the willingness of the human participant in this research and all the employees formerly at Cyberkinetics Neurotechnology Systems Inc. for manufacturing and clinical trial management. We would like to give special thanks to Drs. David Chen, John Donoghue, and Gerhard Friehs.
References
Asanuma, H., and Rosen, I. (1972). Topographical organization of cortical efferent zones projecting to distal forelimb muscles in the monkey. Exp. Brain Res. 14, 243–256.
Courtemanche, R., and Lamarre, Y. (2005). Local field potential oscillations in primate cerebellar cortex: synchronization with cerebral cortex during active and passive expectancy. J. Neurophysiol. 93, 2039–2052.
Donoghue, J. P., Sanes, J. N., Hatsopoulos, N. G., and Gaal, G. (1998). Neural discharge and local field potential oscillations in primate motor cortex during voluntary movements. J. Neurophysiol. 77, 159–173.
Enzinger, C., Ropele, S., Fazekas, F., Loitfelder, M., Gorani, F., Seifert, T., Reiter, G., Neuper, C., Pfurtscheller, G., and Müller-Putz, G. (2008). Brain motor system function in a patient with complete spinal cord injury following extensive brain computer interface training. Exp. Brain Res. 190, 215–223.
Hatsopoulos, N. G., Olmedo, L., and Takahashi, K. (2010). “Proximal-to-distal sequencing behavior and motor cortex,” in Motor Control: Theories, Experiments, and Applications eds F. Danion and M. Latash (New York: Oxford University Press), 159–176.
Hilgetag, C. C., and Barbas, H. (2006). Role of mechanical factors in the morphology of the primate cerebral cortex. PLoS Comput. Biol. 2, e22.
Hochberg, L. R., Serruya, M. D., Friehs, G. M., Mukand, J. A., Saleh, M., Caplan, A. H., Branner, A., Chen, D., Penn, R. D., and Donoghue, J. P. (2006). Neuronal ensemble control of prosthetic devices by a human with tetraplegia. Nature 442, 164–171.
Isa, T. (2009). Reconsidering somatotopy with respect to functional recovery from spinal cord injury. Brain Nerve 61, 1405–1411.
Jurkiewicz, M. T., Gaetz, W. C., Bostan, A. C., and Cheyne, D. (2006). Post-movement beta rebound is generated in motor cortex: evidence from neuromagnetic recordings. Neuroimage 32, 1281–1289.
Keinrath, C., Wriessnegger, S., Müller-Putz, G. R., and Pfurtscheller, G. (2006). Post-movement beta synchronization after kinesthetic illusion, active and passive movements. Int. J. Psychophysiol. 62, 321–327.
Kuhn, A. A., Kempf, Brucke, C., Gaynor Doyle, L., Martinez-Torres, I., Pogosyan, A., Trottenberg, T., Kupsch, A., Schneider, G., Hariz, M. I., Vandenberghe, W., Nuttin, B., and Brown, P. (2008). High-frequency stimulation of the subthalamic nucleus suppresses oscillatory beta activity in patients with parkinson’s disease in parallel with improvement in motor performance. J. Neurosci. 28, 6165–6173.
Kwan, H. C., MacKay, W. A., Murphy, J. T., and Wong, Y. C. (1978). Spatial organization of precentral cortex in awake primates. II. motor outputs. J. Neurophysiol. 41, 1120–1131.
Murphy, J. T., Wong, Y. C., and Kwan, H. C. (1985). Sequential activation of neurons in primate motor cortex during unrestrained forelimb movement. J. Neurophysiol. 717 435–445.
Murthy, V. N., and Fetz, E. E. (1996a). Synchronization of neurons during local field potential oscillations in sensorimotor cortex of awake monkeys. J. Neurophysiol. 76, 3968–3982.
Murthy, V. N., and Fetz, E. E. (1996b). Oscillatory activity in sensorimotor cortex of awake monkeys: synchronization of local field potentials and relation to behavior. J. Neurophysiol. 76, 3949–3967.
O’Leary, J. G., and Hatsopoulos, N. G. (2006). Early visuomotor representations revealed from evoked local field potentials in motor and premotor cortical areas. J. Neurophysiol. 96, 1492–1506.
Park, M. C., Belhaj-Saif, A., and Cheney, P. D. (2004). Properties of primary motor cortex output to forelimb muscles in rhesus macaques. J. Neurophysiol. 92, 2968–2984.
Park, M. C., Belhaj-Saif, A., Gordon, M., and Cheney, P. D. (2001). Consistent features in the forelimb representation of primary motor cortex in rhesus macaques. J. Neurosci. 21, 2784–2792.
Penfield, W. G., and Boldrey, E. (1937). Somatic motor and sensory representation in the cerebral cortex of man studied by electrical stimulation. Brain 60, 389–443.
Rathelot, J., and Strick, P. L. (2009). Subdivisions of primary motor cortex based on cortico-motoneuronal cells. Proc. Natl. Acad. Sci. U.S.A. 106, 918–923.
Rathelot, J. A., and Strick, P. L. (2006). Muscle representation in the macaque motor cortex: an anatomical perspective. Proc. Natl. Acad. Sci. U.S.A. 103, 8257–8262.
Rubino, D., Robbins, K. A., and Hatsopoulos, N. G. (2006). Propagating waves mediate information transfer in the motor cortex. Nat. Neurosci. 9, 1549–1557.
Saleh, M., Reimer, J., Penn, R., Ojakangas, C. L., and Hatsopoulos, N. G. (2010). Fast and slow oscillations in human primary motor cortex predict oncoming behaviorally relevant cues. Neuron 65, 461–471.
Sanes, J. N., and Donoghue, J. P. (1993). Oscillations in local field potentials of the primate motor cortex during voluntary movement. Proc. Natl. Acad. Sci. U.S.A. 90, 4470–4474.
Schieber, M. H., and Hibbard, L. S. (1993). How somatotopic is the motor cortex hand area? Science 261, 489–492.
Shinoda, Y., Yokota, J., and Futami, T. (1981). Divergent projection of individual corticospinal axons to motoneurons of multiple muscles in the monkey. Neurosci. Lett. 23, 7–12.
Takahashi, K., and Hatsopoulos, N. G. (2007). “Copropagating waves of local field potentials and single-unit spiking in motor cortex,” in Annual Meeting of Society for Neuroscience, San Diego, CA.
Witham, C. L., and Baker, S. N. (2007). Network oscillations and intrinsic spiking rhythmicity do not covary in monkey sensorimotor areas. J. Physiol. 580, 801–814.
Witham, C. L., Wang, M., and Baker, S. N. (2007). Cells in somatosensory areas show synchrony with beta oscillations in monkey motor cortex. Eur. J. Neurosci. 26, 2677–2686.
Keywords: motor cortex, local field potentials, propagating waves, human subject, non-human primate
Citation: Takahashi K, Saleh M, Penn RD and Hatsopoulos NG (2011) Propagating waves in human motor cortex. Front. Hum. Neurosci. 5:40. doi: 10.3389/fnhum.2011.00040
Received: 02 June 2010; Accepted: 30 March 2011;
Published online: 25 April 2011.
Edited by:
Kai J. Miller, University of Washington, USAReviewed by:
Kai J. Miller, University of Washington, USATimothy J. Buschman, Massachusetts Institute of Technology, USA
Copyright: © 2011 Takahashi, Saleh, Penn and Hatsopoulos. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence: Nicholas G. Hatsopoulos, Department of Organismal Biology and Anatomy, University of Chicago, 1027 E 57th Street, Room 206, Chicago, IL 60637, USA. e-mail:bmljaG9AdWNoaWNhZ28uZWR1



