- 1 McGovern Institute for Brain Research, Massachusetts Institute of Technology, Cambridge, MA, USA
- 2 Department of Brain and Cognitive Sciences, Massachusetts Institute of Technology, Cambridge, MA, USA
We propose here that the modular organization of the striatum reflects a context-sensitive modular learning architecture in which clustered striosome–matrisome domains participate in modular reinforcement learning (RL). Based on anatomical and physiological evidence, it has been suggested that the modular organization of the striatum could represent a learning architecture. There is not, however, a coherent view of how such a learning architecture could relate to the organization of striatal outputs into the direct and indirect pathways of the basal ganglia, nor a clear formulation of how such a modular architecture relates to the RL functions attributed to the striatum. Here, we hypothesize that striosome–matrisome modules not only learn to bias behavior toward specific actions, as in standard RL, but also learn to assess their own relevance to the environmental context and modulate their own learning and activity on this basis. We further hypothesize that the contextual relevance or “responsibility” of modules is determined by errors in predictions of environmental features and that such responsibility is assigned by striosomes and conveyed to matrisomes via local circuit interneurons. To examine these hypotheses and to identify the general requirements for realizing this architecture in the nervous system, we developed a simple modular RL model. We then constructed a network model of basal ganglia circuitry that includes these modules and the direct and indirect pathways. Based on simple assumptions, this model suggests that while the direct pathway may promote actions based on striatal action values, the indirect pathway may act as a gating network that facilitates or suppresses behavioral modules on the basis of striatal responsibility signals. Our modeling functionally unites the modular compartmental organization of the striatum with the direct–indirect pathway divisions of the basal ganglia, a step that we suggest will have important clinical implications.
Introduction
In a complex and uncertain world, how do we learn and select behaviors appropriately? Rather than learning behavioral patterns de novo each time our environment changes, we often select previously acquired behavioral patterns, and add new behavioral elements to the previously acquired set, depending on the situation. Learning is often context-dependent: when we are at work, we are in a different configuration than we are when at home, at the store, or on the road, and we learn to activate a different set of behaviors in each context. To accomplish multiple functions in a changing environment, reorganization of previously learned behavioral patterns tends to be more efficient than learning entirely new behaviors. The essence of this reorganization is the switching of existing behavioral modules.
In computational neuroscience, such an integration of specialized functions can be achieved by a so-called “mixture of experts” learning architecture, which consists of parallel and distributed learning modules (Jacobs et al., 1991; Jordan and Jacobs, 1994), and it has been suggested that this learning architecture closely resembles the anatomical organization of cortico-basal ganglia circuits connecting the neocortex with the striatum and other elements of the basal ganglia (Graybiel, 1998). The striatum, the primary input structure of the basal ganglia, is widely believed to function in procedural learning and in selecting among candidate movements, strategies, and interpretations of sensory information on the basis of prior success and failure (Graybiel, 1991, 2008; Schultz, 1998; Wilson, 2004). Dopamine released in the striatum by terminals of midbrain dopamine-containing neurons is thought to convey a reward prediction error signal (Schultz et al., 1997; Schultz, 1998), and dopamine-dependent long-term synaptic plasticity at corticostriatal synapses has been proposed as the basis for reinforcement learning (RL; Montague et al., 1996; Reynolds et al., 2001).
A key difficulty for a modular computational system is how to achieve the learning of a specialized function by each module. This problem has been addressed computationally, and it has been proposed that modular “responsibility signals” can properly control switching and permit modular RL (Wolpert and Kawato, 1998; Haruno et al., 2001; Doya et al., 2002). Here, we present a model of modular RL in which modules are selected on the basis of their relevance to the environment. The well-established anatomical modularity of the striatum suggests itself as a plausible substrate for a functional modularity of the kind expressed in our model. We discuss the possibility that clustered striosome–matrisome domains may form a critical part of such modules; that striosomes may assign the modular responsibility signals; and that interneurons, especially cholinergic interneurons and somatostatin-containing low-threshold spiking (LTS) interneurons, may convey these responsibility signals to matrisomes. Such signaling by striosomes and interneurons could permit both the modularization of learning and the efficient switching of behaviors in order to adapt to a changing environment. Thus, we hypothesize that computation of modular responsibility signals by the striosomes may contribute to the functional specialization of matrisomes that comprise a mixture of experts. In our proposed model, the responsibility signal for each modular striatal domain is calculated based on temporally decaying accumulated errors in the prediction of features of the environment.
Each striatal domain, thus conceived, is seen to be important for conveying responsibility signals, modulating learning, and assigning action value. In addition, the actual selection of actions from a set of candidate actions is likely to involve larger basal ganglia-thalamo-cortical modules in which the striatal modules are embedded and which the striatal modules set up by their afferent and efferent connections. We constructed a simple network model of the cortico-basal ganglia-thalamo-cortical loop, including the direct and indirect pathways through the basal ganglia, in order to examine how this neural architecture might influence module and action selection. Remarkably, this model suggested that selecting actions could be represented in the direct pathway, whereas selecting behavioral modules (i.e., the sets of actions appropriate to a given environmental context) could be represented in the indirect pathway. We propose that basal ganglia-thalamo-cortical modules may be selected on the basis of responsibility signals within their embedded striatal modules. Such basal ganglia-thalamo-cortical modules may then select an action from among the set of candidate actions corresponding to a behavioral module. We consider the plausibility of the proposed models based on anatomical and physiological evidence.
Computational Models
Modular Reinforcement Learning Model
In order to identify the functional properties of modular RL and investigate the requirements to embody it in the nervous system, we first develop a simple modular RL model.
Description of modular reinforcement learning model
We begin by introducing a simple RL module that learns actions appropriate to a given context (Figure 1). Each module contains a set of action selection policies updated by an RL architecture (Sutton and Barto, 1998; Doya et al., 2002). The model uses a Markov decision process in which state is s (e.g., the location of the agent, s = 1–14 in our simulation), action is a (e.g., moving right or left in our simulation), and immediate reward is Rt at time t. Each RL module m consists of an action-value function Qm(s, a) that represents the value of an action taken from a specific state st, and a prediction model, which generates a prediction of a certain feature of the environment based on the state st of the agent (e.g., whether there is reward or not at state st in our simulation). For each module, we also introduce a state value function Vm(s), which represents the value of each state, st. There are two “decisions” that the model must make. Firstly, it must decide which module to select, based on its knowledge of the environment. Secondly, the chosen module must decide which action to choose, based on the value of each action. This structure allows the model to specialize its modules for various environments or contexts, so that the agent can rapidly switch strategies in a changing world. For the action selection policy, we adopted the softmax rule, which assigns the probability of choosing each candidate action as: πm(s, a) = exp(βQm(s, a))/Σa′exp(βQm(s, a′)), where β > 0 is a parameter controlling the randomness of the choices.
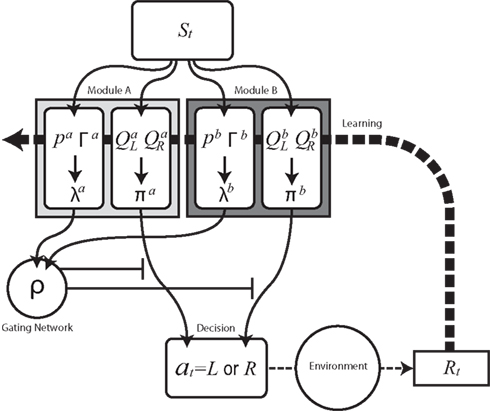
Figure 1. Schematic diagram of modular reinforcement learning (RL) model. Each module m produces a responsibility λm and a policy πm. Responsibility λm is calculated based on the accumulated squared prediction error Γm, which in turn is based on a comparison of a prediction pm of a feature of the environment with the actual feature (in this case the reward Rt). The module with greater λm is selected based on the softmax selection rule ρ, which can be seen as a description of a gating network. The modular policy πm assigns each module’s probability of choosing each candidate action based on the modular action-value function Qm. The policy πm of the selected module determines the actual action at. The learning or updating of pm and Qm is performed only within the selected module using the global reward signal Rt.
For module selection, we have adopted the responsibility signal, λm(t), which represents how well the module’s prediction model predicts the environment (Wolpert and Kawato, 1998; Haruno et al., 2001; Doya et al., 2002). The prediction model (predictor) of module m receives the current state, st, as its input and generates a prediction of a certain feature of the environment as 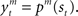 For simplicity, we adopt the reward received (Rt = 1 or Rt = 0) as the feature of the environment that the prediction model must predict. The selection of each module is based on how well the predictor in the module predicts the environment. Therefore, the criterion for the predictor of module m is proportional to the log likelihood. The log likelihood can be written as
For simplicity, we adopt the reward received (Rt = 1 or Rt = 0) as the feature of the environment that the prediction model must predict. The selection of each module is based on how well the predictor in the module predicts the environment. Therefore, the criterion for the predictor of module m is proportional to the log likelihood. The log likelihood can be written as 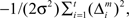 where Σ is the standard deviation (SD) of the additive Gaussian noise and
where Σ is the standard deviation (SD) of the additive Gaussian noise and 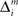 is the prediction error
is the prediction error 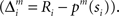 We further assume that the importance of the error decays temporally. We thus define the temporal accumulation of the log likelihood as
We further assume that the importance of the error decays temporally. We thus define the temporal accumulation of the log likelihood as 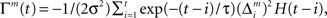 which is the sum of squared prediction errors, weighted such that prediction errors in the past become less important than more recent ones. Parameter τ is the time constant that characterizes the temporal decay of Γm(t), and H(s) is a step function (H(s) = 1 when s ≥ 0, and H(s) = 0 when s < 0). We define the likelihood value λm(t) = exp(Γm(t)) as the responsibility of module m, as it represents the goodness of prediction of module m. We further normalize the responsibility λm ← λm/Σmλm in order to describe it as a probability. Based on the softmax selection rule, the probability of choosing module m is ρm = exp(αλm(t))/Σnexp(αλn(t)), where α (α > 0) is a parameter controlling the randomness of the module selection. According to this equation, a module with a greater responsibility has a greater probability of being selected than do other modules. This architecture can be seen as a gating network that selects a module based on the set of calculated modular responsibility signals and thereby permits the selection of an action appropriate to the environment. Each module produces a policy
which is the sum of squared prediction errors, weighted such that prediction errors in the past become less important than more recent ones. Parameter τ is the time constant that characterizes the temporal decay of Γm(t), and H(s) is a step function (H(s) = 1 when s ≥ 0, and H(s) = 0 when s < 0). We define the likelihood value λm(t) = exp(Γm(t)) as the responsibility of module m, as it represents the goodness of prediction of module m. We further normalize the responsibility λm ← λm/Σmλm in order to describe it as a probability. Based on the softmax selection rule, the probability of choosing module m is ρm = exp(αλm(t))/Σnexp(αλn(t)), where α (α > 0) is a parameter controlling the randomness of the module selection. According to this equation, a module with a greater responsibility has a greater probability of being selected than do other modules. This architecture can be seen as a gating network that selects a module based on the set of calculated modular responsibility signals and thereby permits the selection of an action appropriate to the environment. Each module produces a policy 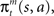 which determines a candidate action. In the original idea of a mixture of experts, the output policy was the sum of policies weighted by their respective responsibilities. However, for simplicity, in the following simulation only the candidate action in the selected module becomes an actual action.
which determines a candidate action. In the original idea of a mixture of experts, the output policy was the sum of policies weighted by their respective responsibilities. However, for simplicity, in the following simulation only the candidate action in the selected module becomes an actual action.
Learning signals for both the predictor 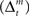 and the action and state value functions
and the action and state value functions 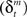 are calculated from the immediate reward signal Rt. Importantly, because the error is produced only by the selected module, the learning should occur only in the selected module. The prediction model can be updated based on the prediction error
are calculated from the immediate reward signal Rt. Importantly, because the error is produced only by the selected module, the learning should occur only in the selected module. The prediction model can be updated based on the prediction error 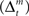 as
as 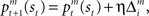 where η (0 < η < 1) is the learning rate of the predictor and m is the selected module. This formulation says that the prediction is adjusted according to the discrepancy between the prediction and the actual reward received. This is further normalized:
where η (0 < η < 1) is the learning rate of the predictor and m is the selected module. This formulation says that the prediction is adjusted according to the discrepancy between the prediction and the actual reward received. This is further normalized: 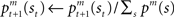 to express it as a probability. The action and state value functions are updated by temporal difference (TD) learning. The TD error can be written as
to express it as a probability. The action and state value functions are updated by temporal difference (TD) learning. The TD error can be written as 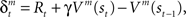 where γ is the temporal discount factor, which controls how much influence is exerted by rewards successively farther in the future. The state value is updated by the TD error as
where γ is the temporal discount factor, which controls how much influence is exerted by rewards successively farther in the future. The state value is updated by the TD error as 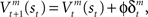 where ɸ (0 < ɸ < 1) is the learning rate of the state value. The action-value function is updated as
where ɸ (0 < ɸ < 1) is the learning rate of the state value. The action-value function is updated as 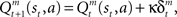 where κ (0 < κ < 1) is the learning rate of the action value. In each trial, the state and action-value functions are updated only in the selected module.
where κ (0 < κ < 1) is the learning rate of the action value. In each trial, the state and action-value functions are updated only in the selected module.
Computational simulation of modular reinforcement learning
To demonstrate how the model works, we constructed a toy example of RL (Figure 2). The agent exists in a one-dimensional grid world, in which the only action choices are “go left” or “go right.” This environment has a starting position and several positions to the left and to the right of the starting position. The agent can inhabit either of two versions of the environment. One version has a reward at the end position on one side, whereas the other version has a reward at the end position on the other side. This reward location is switched after every 2500 time steps. When the agent reaches an end position (s = 1 or s = 14) not containing a reward, it is bounced one position back (s = 2 or 13). If the agent obtains reward, it is returned back to the center position (s = 7). For simplicity, we fixed the standard RL parameters to standard values: β = 1, γ = 0.8, and φ = κ = 0.1 (cf. Sutton and Barto, 1998). We set the newly introduced modular RL parameters to α = 20, σ = 1, τ = 10, and η = 0.05.
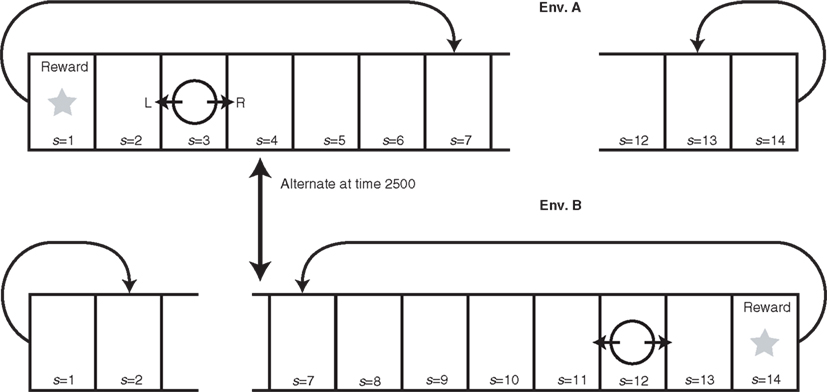
Figure 2. Dynamically changing grid world explored by modular RL model. The agent (circle) can move either left or right, and when the agent receives reward, it is returned to the center (s = 7). The reward is placed at either s = 1 or s = 14, and this location alternates every 2500 time steps. When the agent reaches the unrewarded terminal, it is moved one position back (from s = 14 to s = 13 in Env. B and from s = 1 to s = 2 in Env. A). Each of the model’s two modules becomes specialized by modular RL to maximize the agent’s accumulated reward in one of the two versions of the environment (Env. A and Env. B) defined by reward location.
The predictor in each module aims to predict the probability that a given position yields a reward. When the simulation begins, the two predictors have no prior experience on which to base their predictions; therefore, they both predict that each position has an equal probability (P = 1/14) of containing a reward. The action-value functions also give an equal action value of moving right or left from any position. Therefore, right and left directions are selected with equal probability. While tremendously simplified, this starting condition corresponds to the starting condition of a human or other animal exploring a novel environment for the first time, with no knowledge of the states required to obtain rewards in the environment or of actions required to reach those states. The agent must explore the environment in order to learn the reward structure of the environment.
When the model begins training, neither module is better suited to the environment: the selection is made randomly, with equal probability. Moreover, the selected module does not know which strategy to use, i.e., whether to move right or left from each position. By the end of training, the model selects a module that has become specialized for the environmental context, in that it makes the correct choices to receive rewards.
How does this specialization of modules occur? Again, the model initially selects the module at random. The selected module initially selects the direction of the steps randomly, with equal probability. Thus, module selection oscillates and the agent makes a random walk, stepping sometimes left, sometimes right, until by chance it reaches the reward. This reward was unpredicted by the selected module’s predictor, but now the predictor knows that reward is more likely at that location. As this process repeats in a single environment, the predictors of both modules learn to predict reward at the same location.
Suppose, however, that we now change the environment: now the reward is given in position 1 instead of 14, and the prediction error of the predictors increases. As the process of module and action selection continues, by chance, one of the modules (say B) has slightly more experiences in this new environment than the other module has. This improves its prediction signals, decreases its prediction error, increases its responsibility signal, and increases the probability that module B will be selected. Eventually, module B is selected exclusively, and it becomes specialized for this environment: not only does it make accurate reward predictions, but it has developed a set of appropriate action values for each state (position), which permit the model to make choices that reliably guide it to the reward.
If we now change the environment back to its previous version by switching the reward back to position 14, the prediction error of module B goes up and the model switches to module A. Over many trials, module A becomes increasingly specialized for this version of the environment. While module A learns this version of the environment, module B is not trained and consequently remains specialized for the previous version of the environment.
Figure 3A shows the action-value function of each module. Module A learns to choose rightward movements, and module B learns to choose leftward movements. Figure 3B illustrates the prediction of each module, which is updated over time. The learning of predictions is faster than that of action values. Because the selected module is switched if the prediction model produces an error, different prediction models tend to update their values in different environments, and hence, the prediction models tend to produce different predictions. Figure 4A shows the responsibility of each module as a function of time; as a result of learning, the responsibility of each module changes depending on the environment. As we can see in Figure 4B, the temporal dynamics of the difference of responsibilities, λB − λA, follows the location of the reward (which changes depending on the environment). Correspondingly, the model learns to select one of the modules (Figure 4C) and move in the direction of the rewarded terminal (Figure 4D) consistently in each environment.
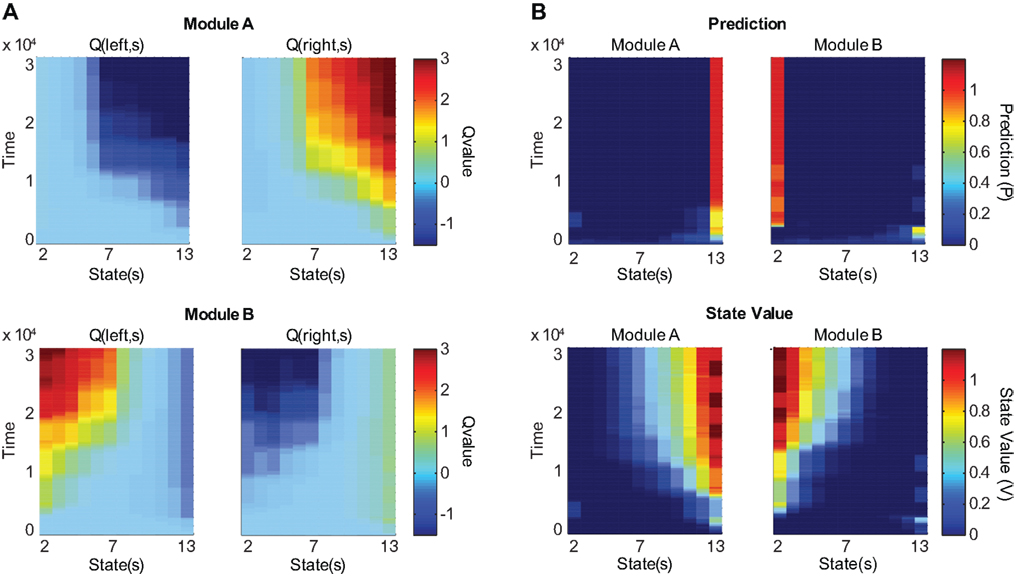
Figure 3. Action value, prediction, and state value functions of the two modules as the model learns in two versions of the environment. The reward location alternates every 2500 time steps. Columns represent different locations. States (locations) 2 through 13 are shown; terminal locations are omitted. (A) Action value (Q) as a function of state and time. Top two panels represent the action-value function of module A and bottom two panels represent that of module B. Left panels show the values for leftward movements and right panels show the values for rightward movements. After training, module A selectively prefers rightward movements and module B selectively prefers leftward movements. (B) Prediction and state value functions of each module. Top two panels represent the prediction (P) of each module. Bottom two panels represent the state value function (V) of each module. Left panels show the functions for module A and right panels show the functions for module B. After training, module A predicts that the reward is likely to be obtained in the rightmost position and assigns the rightmost position the highest state value, while module B makes these assignments for the leftmost position.
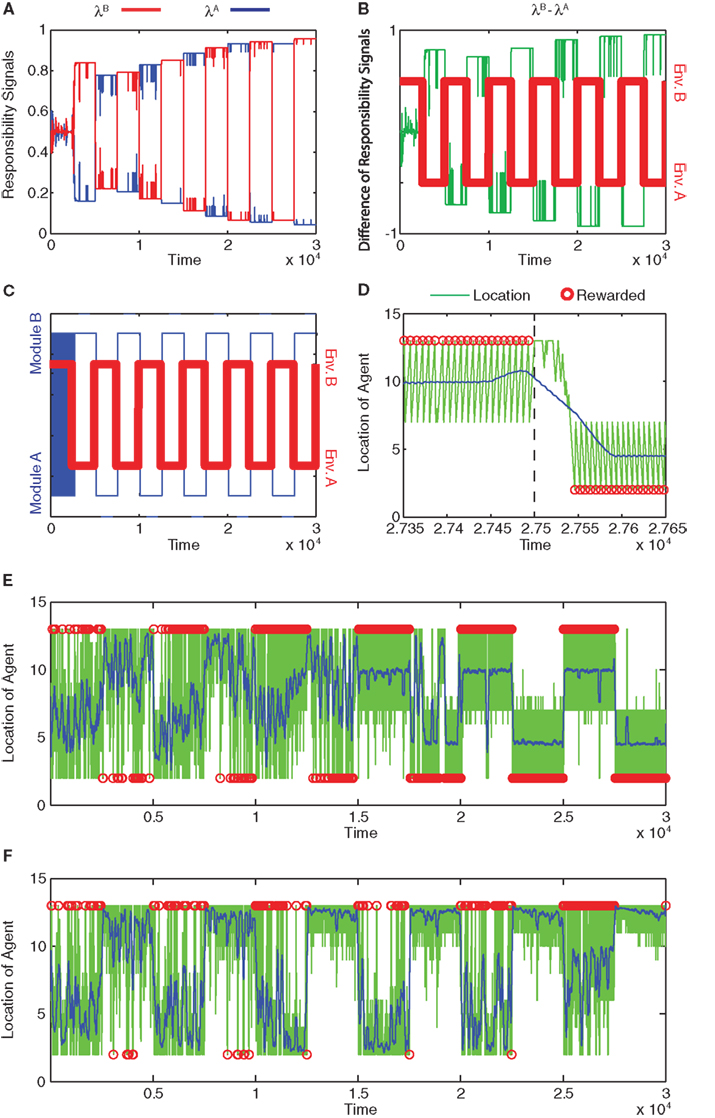
Figure 4. Module responsibility, module selection, and preferred location follow changes in environment. (A) Responsibility signals of module B (red) and module A (blue) as functions of time. (B) Difference of responsibility signals, λB − λA, (green line) plotted with the changing environment (Env. A or B; red). Positive differences imply greater module B responsibility, whereas negative differences imply greater module A responsibility. (C) Selected module (blue) and environment (red) as functions of time. In environment A (Env. A), reward is located at s = 1. In environment B (Env. B), reward is located at s = 14. Modules switch rapidly at first and then follow changes in environment. (D) Location of the agent as a function of time late in training, from time 27350 to time 27650 (green line). Blue line indicates location smoothed with a moving average with window of width 100. Red circles indicate the times and locations at which the agent obtained the reward. Environment changes from Env. B to Env. A at time 27500 (dashed line). The module switches from B to A around 27530. (E) Location of the agent as a function of time for the entire training period. Symbols are as in (D). After learning, the agent can obtain rewards in either terminal, depending on the environment. (F) Failure of learning of normal, non-modular RL. In this case, the model learns to obtain rewards only at s = 14.
The model’s learning is robust to changes of parameters. We fixed the standard RL parameters to standard values (Sutton and Barto, 1998; see above) and examined the robustness of the model’s learning by varying the newly introduced modular RL parameters. Over a wide range of values, the SD σ and decay time constant τ of the temporal accumulation of the log likelihood are not critical factors for the model’s ability to learn. However, extremely large σ or small τ cause the responsibility signal λ to decay too rapidly. We thus set them to σ = 1 and τ = 10.
The learning ability of the agent is critically dependent on the randomness of module switching α. If α ∼ β, the modular selection becomes too random and the agent fails to learn properly. The model is able to learn when α > β and to learn stably with α = 10 ∼ 1010 when we set η = 0.05. However, when α becomes very large, the model is unable to switch modules and thus has to learn with a single module. The learning rate of the predictor η also affects the learning ability. If η is too large, the responsibility value λ decays too rapidly. If η is too small, prediction errors following an environmental change cannot produce large enough changes in λ, causing the agent to fail to shift modules. The agent could learn properly between η = 0.01 and η = 0.3 when we set α = 20.
Lastly we examined the advantages of the modular architecture compared to normal RL. With α → ∞, the agent cannot shift modules and thus is equivalent to standard, non-modular RL. In this case, the model has to relearn every time the environment is changed. Figure 4E shows the time course of the location of the agent with the parameters given above (α = 20, η = 0.05, σ = 1, τ = 10, β = 1, γ = 0.8, and φ = κ = 0.1). In this grid world (Figure 2), when the agent obtains a reward at one terminal, the agent is returned back to the center. At the unrewarded terminal, the agent is simply pushed one grid position back. As a result of this asymmetry, the agent is more likely to be in the side opposite to the rewarded terminal. Our simulation confirms that, even in this difficult situation, the modular RL architecture could detect the changing of the environment and could pursue the reward appropriately, while the normal RL could not.
The modular RL architecture allows the model to shift modules following the change of environment. The number of time steps required for a shift of module was only about 30–50. Figure 4F shows the time course of the location of the agent that cannot shift modules (α → ∞). With single-module RL, the agent is trapped in the unrewarded terminal. Thus the agent can receive reward in only one environment in this case.
Network Model
In our modular RL model, a gating network (Jacobs et al., 1991) compares the responsibility signals of all the modules and selects one of them (Doya et al., 2002). The neural mechanisms underlying this gating network are still a matter of debate. As a step toward understanding how the basal ganglia circuitry might accomplish module selection, we created a simple network model of the cortico-basal ganglia-thalamo-cortical circuit. The novel hypothesis that emerged from this network modeling is that the indirect pathway could serve as the gating network, facilitating or suppressing modules on the basis of striatal responsibility signals.
Our network model is essentially a set of potential mechanisms by which striatal responsibility signals and the direct and indirect basal ganglia pathways could function in module and action selection. The network model augments our RL model by suggesting more detailed and biologically plausible mechanisms for these processes. The indirect pathway could contribute to module selection by enhancing the differences in activation of modules already present in the striatum. Unlike our modular RL model, our network model at this stage does not attempt to simulate learning and it does not include prediction models, prediction errors, TD errors, or state value functions. An important area for future research is how the corticostriosomal network could learn to make predictions for computing responsibility signals.
As a simple first step to illustrate the potential function of the indirect pathway in modular gating, we explore the idea that convergence of connections at a fine level along the indirect pathway could blur the distinctions between adjacent action-value representations within each striatal module, thus making the indirect pathway well suited to module selection rather than action selection. The required convergence is at a fine-scale level, the level of action-value representations, in contrast to the gross convergence seen, for example, at the striatonigral projection (Kaneda et al., 2002). By contrast, the direct pathway might transmit specific action-value information (as well as module information) to the thalamus, where it could influence cortical action selection. This hypothesis, which emerged from the model, is similar to the idea of selection and inhibition of competing motor programs proposed by Mink (1996), with the additional feature that in our model, selection and inhibition by the indirect pathway occur within a modular framework set up by the striosome–matrisome architecture of the striatum: modular sets of contextually inappropriate candidate actions are inhibited by the indirect pathway. One of the candidate actions in an uninhibited (i.e., selected) module is favored by the direct pathway.
Figure 5 summarizes the connectivity of our network model. The input and output regions of the neocortex could correspond, for example, to premotor and motor cortices, respectively, or to prefrontal and premotor cortices. The input cortex projects to the output cortex both directly and indirectly via the cortico-basal ganglia-thalamo-cortical pathway. Also included in Figure 5 are several components that are implicit in our network model: striosomes, which are assumed to send responsibility signals to medium spiny projections neurons (MSNs) in the matrix within the same module; evaluation cortex, which is assumed to send signals related to responsibility to striosomes; the substantia nigra pars compacta (SNc)/ventral tegmental area (VTA), which is assumed to be the source of dopamine signals; and behavioral output.
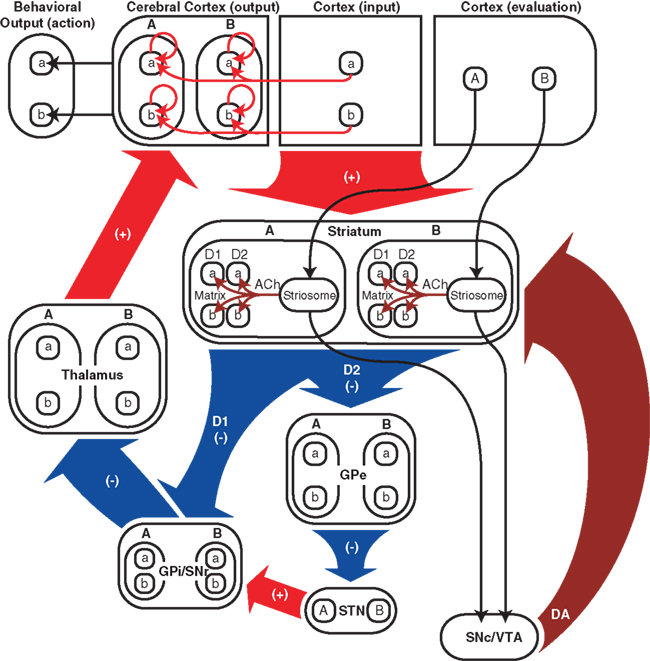
Figure 5. Schematic diagram of cortico-basal ganglia-thalamo-cortical network model. Red arrows and “(+)” indicate excitatory glutamatergic projections, blue arrows and “(−)” indicate inhibitory GABAergic projections, burgundy arrows indicate modulatory connections, i.e., responsibility signals and dopamine signals. Responsibility signals could potentially be conveyed from striosomes by cholinergic interneurons (ACh), and could modulate dopamine signals (DA) reaching D1 and D2 medium spiny neurons (MSNs) from the SNc/VTA (not explicitly included in our computational model). In addition to its input from the thalamus, the output region of the neocortex receives inputs from the input region of the neocortex and has self-feedback connections. “a” and “b” represent actions and action-related signals (e.g., action-value or action-selection signals), and “A” and “B” represent modules. “D1” and “D2” represent direct-pathway, D1-expressing matrix MSNs and their projections and indirect-pathway, D2-expressing matrix MSNs and their projections, respectively. In the model striatum, matrix MSNs can be in either module, express D1 or D2 dopamine receptors, and represent multiple action values. The evaluation cortex (also not explicitly included in our computational model) is assumed to send signals related to responsibility to striosomes. The responsibility signals then influence action-value representations of matrix MSNs. Both direct and indirect pathways in the model are topographical and convergent at a fine level corresponding to action-value representations. GPe, globus pallidus external segment; STN, subthalamic nucleus; GPi/SNr, globus pallidus internal segment/substantia nigra pars reticulata; SNc/VTA, substantia nigra pars compacta/ventral tegmental area; D1 and D2, D1 and D2 MSNs; ACh, acetylcholine; DA, dopamine.
The input cortex is assumed to contain action value-related signals, related to Qm(s, a) in the RL model, before modulation by responsibility signals in the striatum. In the present model, for simplicity, we represent the action value-related signals for actions a and b as the firing probability of two representative neurons in the input cortex. The cortical neurons send one-to-one connections to specific D1 and D2 dopamine receptor-containing matrix MSNs (D1 and D2 MSNs) in two striatal modules. The firing probabilities of direct- and indirect-pathway MSNs represent action values differentially modulated by responsibility signals; these responsibility signals have a similar function to λm in the RL model. Stated simply, the action-value signals of D1 MSNs are then sent to the globus pallidus internal segment/substantia nigra pars compacta (GPi/SNr), where these signals are integrated with modular gating signals from the indirect pathway derived from the effect of responsibility signals on the activity of D2 MSNs. These modular gating signals enhance differences in the activation of modules at the level of GPi/SNr and can be compared to ρm in our RL model. The GPi/SNr signal is then passed on to the thalamus and thence to the output cortex, where this signal is used to select an action.
The key assumption that we introduce here is that the connectivity of both the direct pathway and the indirect pathway is topographical and convergent at a fine level corresponding to modular sets of action-value representations. Although the degree of topography of the basal ganglia at this fine level is unknown, it is known that most structures of the cortico-basal ganglia-thalamo-cortical loop contain topographical maps, corresponding to parallel pathways through the whole loop system (Alexander et al., 1986). For example, the primary and supplementary motor areas, the sensorimotor striatum, the internal and external segments of the globus pallidus (GPi and GPe, respectively), the subthalamic nucleus (STN), and the thalamus in monkeys all contain somatotopic maps (Romanelli et al., 2005). It is within this more general topographic framework that the fine-scale patterns of differential convergence occur in our model (Flaherty and Graybiel, 1991, 1994; Graybiel et al., 1994). Based on this organization, we assume that the represented information is topographically preserved in each station of the cortico-basal ganglia loop. In the model, topographically mapped neurons in each structure represent different actions (action values in the striatum, motor signals in the output cortex).
The different functions of the two pathways in our model depend on a hypothetical higher degree of blurring of adjacent action-value representations within modules in the indirect pathway than in the direct pathway. The relative degree of convergence of connections in the direct and indirect pathways at this fine level is actually not fully established experimentally. However, we found that this difference emerges naturally if we simply assume that the convergent pattern of connections (Gaussian projection function) to each nucleus from its afferent nucleus is similar, but that the level of blurring of action-value information is enhanced in the indirect pathway by virtue of the two steps of projection in which a larger nucleus projects to a smaller one. Although these assumptions are clearly simplistic, they are a useful starting point for a first exploration of the hypothesis of modular gating by the indirect pathway.
The sizes of the nuclei become progressively smaller along the pathways leading from the striatum to the GPi/SNr, or from the striatum to the GPe and then to the STN (Oorschot, 1996). This fact could result in a progressive coarsening of the resolution of represented information along these pathways (Bar-Gad et al., 2003), long hypothesized as a “funneling” process (Percheron and Filion, 1991; Bolam et al., 1993; Parent and Hazrati, 1995). The degree of coarsening is likely to depend partly on the relative numbers of neurons in the pre- and postsynaptic nuclei.
The connectivity of the basal ganglia is known to be far more complex than we take into account here. For example, the pathways from the neocortex to the striatal matrix, and then to GPe and GPi, have, at least in part, a divergence–reconvergence architecture (Flaherty and Graybiel, 1994). The GPe not only projects to the STN, but also projects back to the striatum, preferentially targeting parvalbumin-containing and somatostatin- (and nitric oxide synthase-) containing interneurons that in turn influence striatal circuitry (Bevan et al., 1998). The STN not only receives input from the GPe and sends output to the GPi, but also receives input from the neocortex and has multiple outputs (Jackson and Crossman, 1981; Kita and Kitai, 1987; Bolam et al., 2000; Degos et al., 2008). We do not consider the ventral striatum and the ventral pallidum, which have extensive interconnections with key basal ganglia-related pathways (Bevan et al., 1996, 1997). In order to focus our attention on the idea of blurring or coarsening of resolution at the level of action-related representations, we have simplified the connectivity of our model to include only the classical direct- and indirect-pathway connections. The omitted connections are consistent with this core idea.
Description of network model
The membrane potential of a spiking neuron i can be modeled as 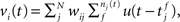 where N is the number of connections received from neuron j, nj(t) is the number of spikes generated in neuron j until time t, wij is the synaptic efficacy, and
where N is the number of connections received from neuron j, nj(t) is the number of spikes generated in neuron j until time t, wij is the synaptic efficacy, and 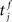 is the time at which the f-th spike arrives from neuron j. For the response function, we adopted an exponentially decaying function u(s) = (1/τ)exp(−s/τ)H(s), where H(s) is a step function (H(s) = 1 when s ≥ 0, and H(s) = 0 when s < 0). For simplicity of modeling, we assume that the spike sequence can be modeled as an inhomogeneous Poisson process (Amemori and Ishii, 2001); thus the sample mean of the membrane potential becomes
is the time at which the f-th spike arrives from neuron j. For the response function, we adopted an exponentially decaying function u(s) = (1/τ)exp(−s/τ)H(s), where H(s) is a step function (H(s) = 1 when s ≥ 0, and H(s) = 0 when s < 0). For simplicity of modeling, we assume that the spike sequence can be modeled as an inhomogeneous Poisson process (Amemori and Ishii, 2001); thus the sample mean of the membrane potential becomes 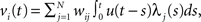 where λj(t) is the firing frequency of neuron j. We further assume that the variance of the membrane potential is constant and that the output firing frequency of a neuron can be modeled by a sigmoid activation function: λi(t) = 1/(1 + exp(α(vi(t) − θ))). We scaled the firing threshold θ by the baseline membrane potential r as θ = βr. Thus the parameters α, β, and τ determine the activity characteristics of each region, whereas the connectivity between regions is determined by wij.
where λj(t) is the firing frequency of neuron j. We further assume that the variance of the membrane potential is constant and that the output firing frequency of a neuron can be modeled by a sigmoid activation function: λi(t) = 1/(1 + exp(α(vi(t) − θ))). We scaled the firing threshold θ by the baseline membrane potential r as θ = βr. Thus the parameters α, β, and τ determine the activity characteristics of each region, whereas the connectivity between regions is determined by wij.
In the model, a neuron in the target structure receives its strongest connection from the center of the topographically corresponding region in the structure of origin and progressively weaker input from neurons farther from the center. To implement this topographical organization and convergence, we apply a Gaussian projection function, 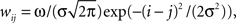 where j is the neuronal index of the neuron in the structure of origin (size M), and i is the neuronal index of the target structure (size N). To maintain topography despite differences in the sizes of the structures, the indices are resized as i = [Nj/M] when M > N, and j = [Mi/N] when M < N. The parameter σ is the SD of the projection function and the parameter ω controls the strength of influence of the presynaptic neurons on the postsynaptic neurons. When the input is inhibitory, ω is negative. We set σ = 3, in units of neurons. The Gaussian function applies to every projection in the model except for the corticostriatal and corticocortical projections. In these latter two projections, the connections are one-to-one: wij = ω for i = j, and wij = 0 otherwise.
where j is the neuronal index of the neuron in the structure of origin (size M), and i is the neuronal index of the target structure (size N). To maintain topography despite differences in the sizes of the structures, the indices are resized as i = [Nj/M] when M > N, and j = [Mi/N] when M < N. The parameter σ is the SD of the projection function and the parameter ω controls the strength of influence of the presynaptic neurons on the postsynaptic neurons. When the input is inhibitory, ω is negative. We set σ = 3, in units of neurons. The Gaussian function applies to every projection in the model except for the corticostriatal and corticocortical projections. In these latter two projections, the connections are one-to-one: wij = ω for i = j, and wij = 0 otherwise.
We used the data of Oorschot (1996) as a very rough guide to the relative sizes of our model basal ganglia, but the relative differences between nuclei are smaller in our model than in the actual basal ganglia. The size of the model striatum is set to 600: it contains 300 D1 MSNs and 300 D2 MSNs. The size of the input region of the cerebral cortex is also 300, the size of GPe is 100, the size of STN is 25, the size of GPi/SNr is 50, the size of the thalamus is 200, and the size of the output region of the cortex is set to 200. For the input region of the cortex and for the striatum, we set α = 1, θ = 2, and τ = 20. For GPe, we set α = 1, β = 1.12, and τ = 10. For STN we set α = 5, β = 1.05, and τ = 20. For GPi/SNr, we set α = 1, β = 1.11, and τ = 10. For the thalamus, we set α = 0.5, β = 1.6, and τ = 10. For the output region of the cortex, we set α = 18, β = 1.08, and τ = 20. For the projection from the striatum to GPe, we set ω = −1. For GPe to STN, we set ω = −0.3. For the striatum to GPi/SNr, we set ω = −1.2. For STN to GPi/SNr, we set ω = 0.5. For GPi/SNr to thalamus, we set ω = −3.0. For the input region to the output region of the cortex, we set ω = 2.4. For the thalamus to the output region of the cortex, we set ω = 8. In order to maintain sustained activity of the selected neuron, for the output region of the cortex we assume that each neuron has a self-feedback connection. The strength of self-feedback was set to ω = 0.55.
Results of the Network Simulation
In the model, the level of activity in matrix MSNs in each striatal module is controlled by two factors: (1) the strength of the modular responsibility signals, which determines the relative excitability of matrix MSNs in different striatal modules, and (2) the level of activity of afferent cortical neurons, which determines the relative activity levels of matrix MSNs within a module. We assume that the excitability of D1 MSNs (projecting to the GPi/SNr) is enhanced by an increased responsibility signal, whereas the excitability of D2 MSNs (projecting to the GPe) is reduced. Such responsibility signals may be conveyed from striosomes to the surrounding matrix MSNs by striatal interneurons; we will examine potential mechanisms in the Section “Discussion.” The activity of each D1 MSN can be interpreted as representing the value of an action (and thus promoting its selection), while the activity of each D2 MSN ultimately contributes to the inhibition of contextually inappropriate modular sets of actions.
The model striatum contains two modules: module A, containing the first half of the MSNs according to their index, and module B, containing the second half. Each module contains 150 pairs of D1 and D2 MSNs. We assume that the two modules are differentially modulated by different responsibility signals even while receiving the same input from the input cortex and the same phasic dopamine signal. To illustrate module selection by the model, we generate identical cortical activity patterns at two different times (Figure 6A, left). At the first time, striatal module B is influenced by a responsibility signal (Figure 6A, middle); at the second time, striatal module A is influenced instead (Figure 6A, right). Based on the possibility that these positive responsibility signals may involve an increase in phasic local striatal dopamine release resulting from a decrease in local acetylcholine release (see “Discussion.”; Rice and Cragg, 2004; Cragg, 2006), their effect is labeled “↑ DA.”
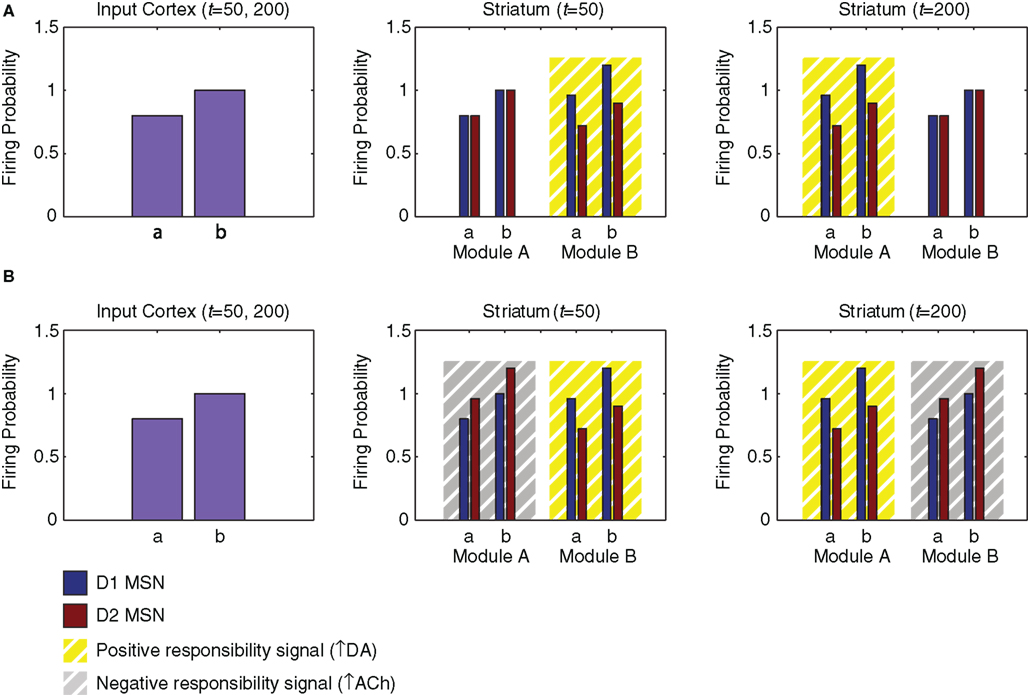
Figure 6. Influences of input cortex and responsibility signaling on striatal matrix MSN activity in the network model. We model two neurons of the input region of the cortex, each representing information related to the value of action “a” or “b.” These neurons project, respectively, to a D1 and a D2 matrix MSN in each of two modules in the striatum. (A) Cortical and striatal activity (arbitrary units) for simulation using only positive responsibility signals. The effect of positive responsibility signals is labeled “↑ DA,” based on the possibility that they may involve an increase in phasic local striatal dopamine release (triggered by a decrease in local acetylcholine release). Responsibility is assigned to module B at time 50 and module A at time 200 (yellow boxes). Such responsibility signaling transiently increases D1 MSN activity and decreases D2 MSN activity. (B) Cortical and striatal activity for simulation using both positive and negative responsibility signals. The effect of negative responsibility signals is labeled “↑ ACh,” based on the possibility that they may involve an increase in local striatal acetylcholine release. Positive responsibility is again assigned to module B at time 50 and module A at time 200 (yellow boxes). Additionally, negative responsibility is assigned to module A at time 50 and module B at time 200 (gray boxes). Negative responsibility signaling transiently increases D2 MSN activity.
Specifically, two neurons in the input region of the cortex, representing the values of two specific actions (“a” and “b”), are activated at times 50 and 200 (Figure 6A, left). The activity levels of these cortical neurons are 0.8 and 1.0. These neurons excite specific neurons in the striatum (Figure 6A, middle and right; Figures 7A,B) and the output region of the cortex (Figure 7G). Corresponding module A and module B MSNs, and corresponding D1 and D2 MSNs, all receive the same cortical input. Specifically, both the D1 and the D2 MSNs having index numbers 54 and 99 (Module A, neurons “a” and “b” in Figure 6) receive the same cortical input at the same times, as do the D1 and the D2 MSNs having index numbers 205 and 249 (Module B, neurons “a” and “b” in Figure 6). Although in our model, for simplicity, corresponding D1 and D2 MSNs receive identical cortical inputs, our modeling framework does not require that these inputs be identical or originate from the same cortical projection neuron. Thus, our model is consistent with the evidence that D1 and D2 MSNs receive their inputs from different types of layer 5 cortical pyramidal neuron (Lei et al., 2004; Reiner et al., 2010).
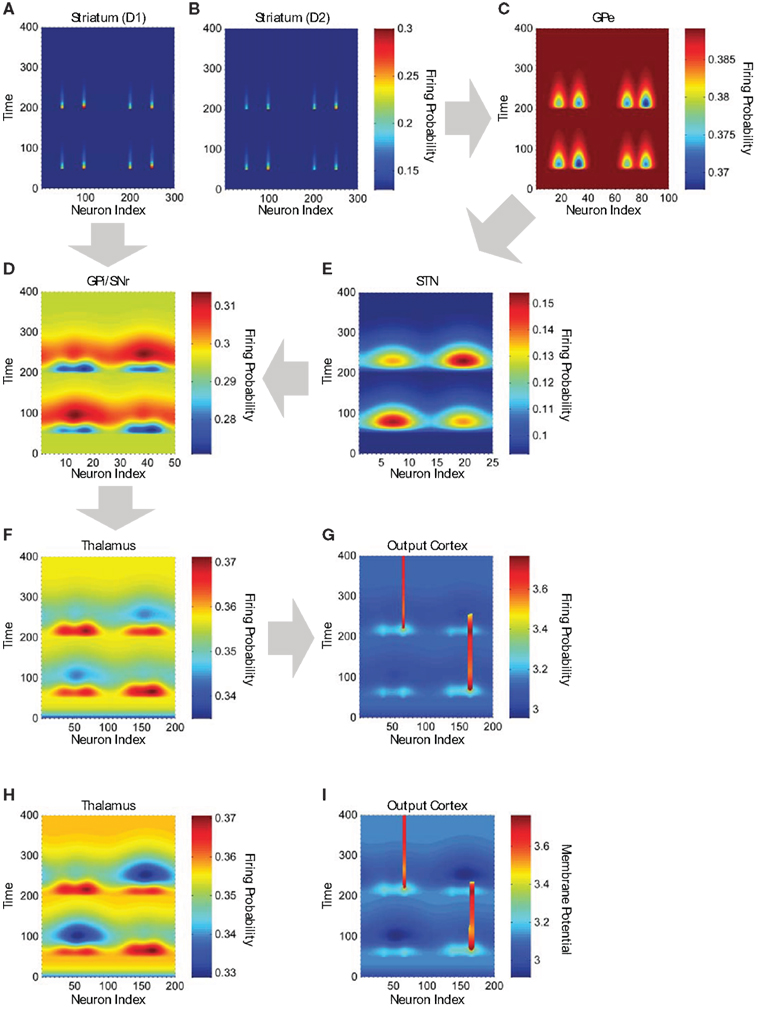
Figure 7. Neuronal activity in structures of the cortico-basal ganglia-thalamo-cortical network model. (A) Firing frequency of D1 MSNs in the striatum (n = 300). Color scale indicates firing frequency, x-axis indicates neuron index, and y-axis indicates time in arbitrary units. MSNs on the left (from x = 1 to 150) are in module A and MSNs on the right (from x = 151 to 300) are in module B. Neuron “a” in the input region of the cortex (Figure 6A, left) projects to MSNs 54 and 205, and neuron “b” projects to MSNs 99 and 249. (B) Firing frequency of D2 MSNs (n = 300), which receive exactly the same pattern of connections from the input cortex as do D1 MSNs. (C) Firing frequency of GPe neurons (n = 100). Adjacent GPe neurons receive overlapping convergent inhibitory input from adjacent striatal D2 MSNs. As a result of this overlapping convergent connectivity, the focal striatal activity causes less focal GPe inhibition (i.e., the inhibition is spread or “blurred” over adjacent GPe neurons; blue troughs). (D) Firing frequency of GPi/SNr neurons (n = 50), which receive convergent inhibitory input from striatal D1 MSNs (blue troughs) and excitatory input from STN (red peaks). (E) Firing frequency of STN neurons (n = 25), which receive convergent inhibitory input from GPe (red peaks represent lowest inhibition). (F) Firing frequency of thalamic neurons (n = 200) in the simulation using only positive responsibility signals. (G) Membrane potential of neurons in the output region of the cortex (n = 200) in the simulation using only positive responsibility signals. Vertical red bars represent persistent supra-threshold cortical depolarization maintained by self-feedback connections. (H) Firing frequency of thalamic neurons (n = 200) in the simulation using both positive and negative responsibility signals. (I) Membrane potential of neurons in the output region of the cortex (n = 200) in the simulation using both positive and negative responsibility signals. The blue troughs observed in the thalamic and cortical activity are deeper in the simulation using both positive and negative responsibility signals. Note: in (A,B), we show only about one out of every six of the inactive MSNs, to make the active MSNs more visible in the figure.
Module B has an increased responsibility at time 50 (Figure 6A, middle), and module A has an increased responsibility at time 200 (Figure 6A, right). These increases in the responsibility signals are reflected in an increase in activity by 20% for D1 MSNs and a decrease in activity by 20% for D2 MSNs. Thus the action values represented by MSN activity are determined by the joint influence of the input cortex and the responsibility signals. The downstream results of these differential changes in responsibility signaling are illustrated in Figure 7 for the D1 and D2 MSNs in the two modules, together with corresponding sites in the basal ganglia striato-pallido-thalamo-cortical loop. In Figures 7A,B, the left two activity peaks at either time 50 or time 200 correspond to module A, neurons “a” and “b”; whereas the right two peaks correspond to module B, neurons “a” and “b” (cf. Figure 6A, middle and right). As a result of responsibility signaling, the D1 MSNs of module A are slightly more active at time 50 and slightly less active at time 200, while the converse is true of the D2 MSNs. For each pair of activity peaks (which represents a modular pair of actions), the one on the right is greater, since the corresponding activity in the input cortex is greater.
Figures 7C–E contrast the activities in the direct- and indirect-pathway nuclei. Note that the indirect-pathway projection from the striatum to the GPe is convergent, so that the information represented by each neuron in the GPe is coarser than that in the striatum. Further, because the projection from the striatum to the GPe mediated by the striatal D2 MSNs is inhibitory, the effect of responsibility on modules A and B in the GPe is the inverse of that on D2 MSNs in the striatum: the deepest blue trough in activity in module A (left two troughs) is deeper than that in module B (right two troughs) at time 50, and less deep at time 200. We emphasize that this effect is entirely the result of the inhibitory connections conveying information from the striatum: no additional responsibility signals are added outside of the striatum. For each pair of activity troughs, the one on the right is deeper, since the corresponding activity in the striatum is greater.
As shown in Figure 7E, the representation of the activity stream in the STN neurons becomes even coarser, because the projection from GPe to STN is also convergent. Consequently, neurons in the model STN preserve only the information regarding which module is more active (as a result of having been assigned higher responsibility). Action-value information has been lost by virtue of the two pre-thalamic stages of convergence in the indirect pathway. Thus, in Figure 7E, the broad red peaks are higher for the modules to be selected but are too blurred to provide action-value information.
By contrast, both the module identity and the action values of the modules are preserved in the direct pathway, in which there is only one pre-thalamic stage (GPi/SNr; Figure 7D). For ease of illustrating the difference between the inputs from the two pathways to the GPi/SNr (Figure 7D), the input from the STN is delayed relative to that from the striatum by having a longer time constant, τ, of the response function in the STN. Thus the blue troughs, which are deeper for the actions to be selected, are followed by excitation. We used this time shift in our example solely to make it easier to see the different effects of the two inputs. Module and action selection occur in essentially the same way if we set the time constant of the STN to be the same as that of the other nuclei.
The net effect of the difference in degree of convergence assumed by the model thus results in the direct pathway maintaining action-value information, whereas the indirect pathway can only represent the overall inhibition of modules. We illustrate the results of these differences for thalamic firing in Figure 7F. We have omitted the input from the neocortex to the thalamus in order to make clear the results of the different responsibility signals imposed in the striatum, although we realize that this input is highly influential. Thus, the thalamic activity in the model is approximately the inverse of the GPi/SNr activity, and it can be regarded as a processed version of the striatal output to be sent to the cortex for the purpose of decision-making. The thalamic activity consists of a transient enhancement of neuronal activity containing action-value information (due to the direct pathway) followed by suppression of neuronal activity in the unselected thalamic module (due to the indirect pathway).
As illustrated in Figure 5, each neuron in the output region of the neocortex receives excitatory inputs from the thalamus, from the input region of the neocortex, and from itself. In Figures 7G,I, the light blue peaks and dark blue troughs represent sub-threshold input. The persistent supra-threshold cortical activity (red) represents the final selection of an action and is evoked by the thalamic input (light blue peaks at time 50 and 200) and sustained by the cortical self-feedback projections. Modular suppression (dark blue troughs) is produced by the indirect pathway after time 50 (left module) and 200 (right module). The action selected at time 50 is terminated by the modular suppression after time 200. At time 200, the action in the other cortical module is selected, and it is continuously activated to the end. Thus, our model suggests that action selection promoted by the direct pathway may cooperate with modular suppression by the indirect pathway.
The parameters chosen here are within appropriate ranges in terms of physiological plausibility (e.g., firing rate and stability of each nucleus). Further, most of the results are robust to changes in these parameters. However, one simulation result, the sustained cortical activity observed in Figure 7G, was sensitive to changes in the firing threshold of the output cortex, because the sustained activity was supported by self-feedback projections and for some values of the firing threshold this activity was unstable. Since the detailed cortical mechanism that stabilizes this sustained activity is beyond the scope of this study, here we simply assume that the output cortex has some neuronal mechanism that stabilizes such activity and plays a role in selection and maintenance of the representation of the selected action.
Network simulation with negative responsibility signals
It is possible that striatal modules also make use of negative responsibility signals, i.e., signals that actively label a module as irrelevant to a given environmental context. This idea may have a basis in signaling by striatal interneurons, a possibility that we will examine in the Section “Discussion.”
In order to illustrate this possibility, we performed another simulation, run as described above, but with the addition of a negative responsibility signal that enhances the activity of D2 MSNs in the unselected striatal module (Figure 6B). Based on the possibility that such negative responsibility signals may involve an increase in local striatal acetylcholine release (see “Discussion.”; Ding et al., 2010), their effect is labeled “↑ ACh.” At time 50, we apply a negative responsibility signal in striatal module A concurrently with the positive responsibility signal in module B; while at time 200, we apply a negative responsibility signal in striatal module B concurrently with the positive responsibility signal in module A. Figure 7H shows the thalamic activity induced by this simulation. Compared to the first simulation (Figure 7F), the broad troughs observed in the thalamic and cortical activity are much deeper, suggesting that the unselected module is more strongly suppressed.
These two network simulation results suggest that the direct pathway may bias actions based on action values and the indirect pathway may bias modules based on responsibility signals. These results emerge naturally from the simple combination of modular responsibility signaling in the striatum and differential blurring of action-value representations in the direct and indirect pathways. Based on these results, we hypothesize that the gating network of the RL architecture (Figure 1) corresponds to the indirect pathway of the basal ganglia circuitry.
Discussion
We have presented a pair of interrelated models: first, an abstract model of modular RL that embodies the critical idea that a modular architecture utilizing responsibility signals can facilitate learning and adapting to a changing environment; and second, a network model of cortico-basal ganglia-thalamo-cortical circuitry that embodies the novel idea that the indirect pathway could be central to behavioral module selection based on responsibility signals, while the direct pathway could be central to action selection within a modular framework.
Our model of modular RL can be seen as both a set of abstract ideas concerning RL and a set of hypotheses regarding basal ganglia function. Regarding the latter component – the neural mechanisms underlying modular RL – the basal ganglia in general and the striatum in particular have a number of key features that make them well suited to this type of modular learning based on prediction errors and responsibility signals. We emphasize, however, that experimental information is still insufficient to test definitively whether the basal ganglia implement this type of modular RL, and if so, how the parts of our models map onto the anatomical components of the basal ganglia. Despite these uncertainties, in the following sections, we discuss some of the key parallels between the models and features of the basal ganglia, in particular the modular organization of the striatum into striosomes and matrisomes, the evidence for error signals in striosomes, and the properties of striatal interneurons that could be critical for communicating responsibility signals from striosomes to the surrounding extrastriosomal matrix.
Striatal Modularity as the Basis of Modular Reinforcement Learning
The anatomical modularity of the striatum is a plausible substrate for a functional modularity of the kind expressed in our model (Figure 8). The two basic compartments of the striatum, striosomes, and matrix, are distinguished from each other on the basis of neurochemical markers, input and output connectivity with other brain structures and local connectivity (Graybiel and Ragsdale, 1978; Herkenham and Pert, 1981; Gerfen, 1984; Gerfen et al., 1987; Bolam et al., 1988; Ragsdale and Graybiel, 1988; Gimenez-Amaya and Graybiel, 1990; Eblen and Graybiel, 1995; Graybiel, 1995; Holt et al., 1997; Joel and Weiner, 2000; Saka et al., 2002; Mikula et al., 2009). The dendritic and axonal arborizations of the majority of MSNs are mostly, but not entirely, restricted to their compartment of origin (Penny et al., 1988; Kawaguchi et al., 1989; Walker et al., 1993); and striatal interneurons also tend to follow striosome–matrix divisions, notably with the cholinergic interneurons (putative tonically active neurons, TANs) and somatostatin-containing interneurons (putatively the LTS interneurons) tending to lie near the borders of striosomes, but having much of their arborizations in the matrix compartment (Graybiel et al., 1981, 1986; Gerfen, 1984; Chesselet and Graybiel, 1986; Penny et al., 1988; Kawaguchi, 1992; Aosaki et al., 1995; Kawaguchi et al., 1995; Kreitzer, 2009). Striosomes form a labyrinthine reticulum, as if to provide functional coverage throughout the volume of the striatum (Graybiel and Ragsdale, 1978; Graybiel, 1984; Groves et al., 1988; Mikula et al., 2009). Finally, the input and output connections of the matrix itself also have a modular organization in which inputs and outputs of the large matrix compartment are divided up into clustered domains called matrisomes (Gimenez-Amaya and Graybiel, 1991; Flaherty and Graybiel, 1994; Kincaid and Wilson, 1996; Parthasarathy and Graybiel, 1997). Thus, modularity appears to be a fundamental principle of the anatomical organization of the striatum.
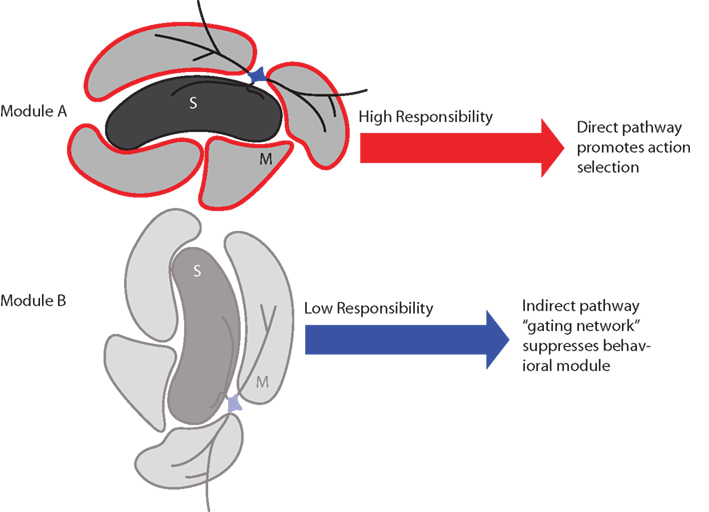
Figure 8. Schematic summary of proposed effects of striatal responsibility signals on module and action selection. Top: If the sets of actions influenced by module A are appropriate to the environmental context, its striosome (S) assigns high responsibility by sending a signal to adjacent matrisomes (M) via local circuit interneurons. This results in relatively low activity in the indirect pathway and high activity in the direct pathway, which permits the direct pathway to promote selection of an action. Bottom: If the sets of actions influenced by module B are inappropriate to the environmental context, its striosome assigns low responsibility. This results in relatively high activity in the indirect pathway, which suppresses the associated set of candidate actions (behavioral module).
We consider here that each striatal domain – module in our model – may consist of a striosome region and the adjacent matrisomes (Figure 8). It is known that matrisomes receive convergent input from corresponding somatotopic representations in different cortical areas (e.g., primary motor and somatosensory cortices; Flaherty and Graybiel, 1993) and from closely related somatotopic representations in the same cortical region (e.g., thumb and finger in the somatosensory cortex; Flaherty and Graybiel, 1991). Matrisomes also participate in a divergence–reconvergence architecture from cortex to striatum to GPe and GPi: corticostriatal projections diverge to multiple matrisomes, which then, at least in some instances, can send convergent projections to localized regions in the GPe and GPi (Flaherty and Graybiel, 1994). This architecture suggests that multiple matrisomes could participate in each striatal modular domain, a situation that could allow multiple body parts to participate in actions regulated by the same context-specific modular responsibility signal. This hypothesis is a central and key aspect of our modeling framework. It has not yet been possible to support this hypothesis with direct electrophysiological or imaging evidence, due to formidable technical hurdles, but there are at least hints of functional modularity from two sources: early response gene assays that demonstrate that cortical microstimulation produces postsynaptic gene expression in focal zones corresponding anatomically to input matrisomes (Parthasarathy and Graybiel, 1997); and documentation of focal zones of differential oscillatory activity detected in local field potentials (Courtemanche et al., 2003). We further hypothesize, again without compelling evidence but with reasonable assumptions, that corresponding basal ganglia-thalamo-cortical modules may exist, consisting of striatal modular domains together with the corresponding modules of thalamic, subthalamic, and cortical regions (Alexander et al., 1986). By the same reasoning, we thus consider that the entire circuitry related to the striatum could have a modularity reflected by the striatal modules that have been demonstrated anatomically.
Key Characteristics of Reinforcement Learning Modules
In order to function as the modules in our model, these basal ganglia circuit modules would have to contain (1) neurons that predict future outcomes or other features of the environment; (2) responsibility signals based on prediction errors that indicate the appropriateness of the corresponding set of candidate actions to the current environmental context; (3) state- and action-value signals; (4) separate TD reward prediction error signals influencing the learning of state and action values; and (5) a module selection mechanism based on the responsibility signals. Assignment of responsibility to a striatal module could consist of an enhancement of excitability of neurons representing action values within the module and an enhancement of the plasticity of synapses conveying state information to these action-value neurons. This plasticity should also be modulated by the TD reward prediction error signal as in standard RL models of the striatum. Additionally, the plasticity of synapses conveying state information to prediction neurons should also be enhanced by the responsibility signal. We propose that basal ganglia-thalamo-cortical modules, containing striatal modules consisting of striosomes and associated matrisomes, potentially meet all of these criteria.
Like others, we suggest that matrix MSNs may represent action values (Doya, 2000, 2002; Samejima et al., 2005). Action values in the model can refer to cognitive actions as well as movements: the associative striatum, which receives input from prefrontal and parietal association cortices, may more strongly influence the former, whereas the sensorimotor striatum, which receives input from sensorimotor cortices, may more strongly influence the latter (Graybiel, 1997, 2008). Also, like others, we suggest that striosomes compute or relay prediction-related signals (Houk et al., 1995; Doya, 2000, 2002).
However, unlike others, we assume that the prediction error signals of striosomes are specific to their respective modules and serve as the basis for modular responsibility and module selection signals. Further, modular RL requires modularity of learning signals (Doya et al., 2002; Samejima et al., 2003). In modular RL, only the selected modules are responsible for the learning, and the updates of the predictions and action values have to occur only in the selected modules. For such local updating, the synaptic plasticity has to occur selectively in the selected modules. These features are key to our modular RL model. As introduced here, this model contains only two modules, and only one of them at a time is assigned high responsibility, but clearly, the striatum contains many modules. The modular RL framework we introduce here can readily be extended such that any number of related striatal modules can be concurrently assigned high responsibility, selected for action, and permitted to learn in a given context.
As can be seen in Figures 4E, F, one of the advantages of modular RL compared to normal RL is that the model can rapidly adapt to changes of environment after modular learning has been established. Modular RL enables a module to learn a context-specific strategy or policy and recall this stored policy when it is required. The adaptive change of strategy by modular RL is much faster than normal RL. These fast adaptive changes of strategy are similar to attentional set-shifting and reversal learning. Parts of the prefrontal and anterior cingulate cortices and the caudate nucleus have been implicated in such shift learning (Rogers et al., 2000). These cortical and subcortical areas could therefore be candidates for producing signals used for learning to shift the modules in the striatum.
With regard to learning in a changing environment, it is of particular interest to compare modular RL with RL having an adjustable learning rate (Behrens et al., 2007; Bernacchia et al., 2011). We expect that modular RL can switch Q-functions rapidly compared to adjustable RL, which has to learn an appropriate Q-function de novo each time the environment changes. Modular RL does not have to learn a Q-function again after one has already been stored in a module. On the other hand, a disadvantage of modular RL is that it can have redundant parameters and Q-functions when the environment is less complex.
Error and Evaluation Signals Sent to Striosomes
Our first and second criteria for RL modules, above, are that they should contain neurons that predict future rewards or other features of the future state, and that they should use responsibility signals based on prediction errors. The idea that striosomes contain prediction-related signals is not new. Starting with the conceptual model of Houk et al. (1995), many models of the basal ganglia have assumed that striosomes compute a reward prediction or state value signal: just as action values may be learned via dopamine-dependent synaptic plasticity at corticostriatal synapses onto matrix MSNs, reward predictions may be learned via dopamine-dependent synaptic plasticity at corticostriatal synapses onto striosomal MSNs. Moreover, even aside from this hypothetical mechanism for learning reward prediction, striosomes in the anterior and ventromedial striatum, mainly in the caudate nucleus, receive input from cortical areas that themselves exhibit error signals.
Anterograde tracing combined with neurochemical staining in monkeys suggests that the pregenual anterior cingulate cortex (pACC) and the posterior orbitofrontal cortex are important afferents of striosomes in the caudate nucleus (Eblen and Graybiel, 1995). Recordings from the pACC implicate it in error detection (Niki and Watanabe, 1979; Matsumoto et al., 2007). Importantly, we have found that electrical microstimulation of the pACC can increase sensitivity to a prediction of an aversive outcome in monkeys making choices based on a combination of aversive and rewarding outcomes (Amemori and Graybiel, 2009, 2010). Therefore, the signal sent to striosomes in the caudate nucleus may be related to error detection and evaluation.
Our novel contribution here is the suggestion that striosomes may compute or convey prediction error signals as part of a broader role in generating responsibility signals based on the appropriateness of particular modules to the environmental context. If this suggestion proves to be correct, then the context-relevant predictions generated by striosomes could be much broader in scope than simple reward predictions. The prediction errors could include errors in the prediction of sensory cues (e.g., visual, tactile) or of other environmental features that signal context without being at the same time reliable predictors or cues for reward within that context. Determining whether striosomes contain such signals is an important goal for future experimental research.
Modularity of Dopamine Signals
In accordance with previous RL models of the basal ganglia, we assume that the TD error is represented by midbrain dopamine neurons and that action values are modified by dopamine-mediated synaptic plasticity in the striatum. However if, as our model suggests, striosomes and matrisomes are involved in the learning of fundamentally different things – the appropriate modular responsibility signals by striosomes, and the appropriate action values by matrisomes – then one might expect them to receive different dopamine signals. The fact that, at least in part, different sets of dopamine neurons appear to project to striosomes and matrix in rats (Gerfen et al., 1987), cats (Jiménez-Castellanos and Graybiel, 1989), and monkeys (Langer and Graybiel, 1989) is consistent with the hypothesis that dopamine release in striosomes conveys a separate signal from dopamine release in the matrix. Evidence from single-cell tracing in the rat suggests that there may be some separation also, but shows that collateral innervations are prominent as well, at least for the nigral axons studied (Matsuda et al., 2009). There is some evidence that striosomes send reciprocal connections to the same nigral regions that innervate them, but this does not seem to be true for matrix neurons: in rats, the ventral-tier dopamine neurons (ventral SNc and SNr) are reported to receive inputs from the striosomes preferentially as well as from the limbic striatum, and to project reciprocally to striosomes; while the dorsal-tier dopamine neurons (including dorsal SNc and VTA) are reported to receive preferential inputs from the limbic striatum and project to the matrix (Joel and Weiner, 2000). More work is needed to analyze these connections in detail. Recent evidence from single-cell tracing supports the idea that striosome, but not matrix, neurons project to the SNc (as well as other sites; Fujiyama et al., 2011).
Matsumoto and Hikosaka (2009) have observed in monkeys that, although some SNc (putatively dopamine-containing) neurons prefer reward-predicting stimuli to aversion-predicting stimuli, a large number of these neurons are excited by either of these types of stimulation. It is possible that these less-selective dopamine neurons correspond to the ventral-tier dopamine neurons in rats, and are reciprocally connected with striosomes – and that their less-selective responses reflect their function in learning to predict salient features of specific environmental contexts, as required by our model. Thus it is possible that the dorsal-tier dopamine neurons, and the corresponding neurons in monkeys, represent reward prediction error (TD error, δ), whereas ventral-tier dopamine neurons represent stimulus saliency or surprise, which may be closely related to environmental feature prediction errors (Δ).
Potential Functions of Striatal Interneurons in Responsibility Signaling
The function of responsibility signals in our models is to promote the selection of modules for learning and action selection. In our RL model, responsibility signals are based on errors in the prediction of features of the environment; after training, they reflect the appropriateness of behavioral modules to specific environmental contexts. So far, we have discussed the possibility that striosomes, together with their cortical afferents and reciprocally connected dopamine neurons, may learn to generate such environmental feature prediction errors, which could then form the basis of modular responsibility signals. We now turn to the question of how such responsibility signals could be communicated from striosomes to matrisomes.
Both cholinergic and LTS interneurons send processes into both compartments and may send axons preferentially into the matrix (Gerfen, 1984; Chesselet and Graybiel, 1986; Graybiel et al., 1986; Kawaguchi, 1992; Kawaguchi et al., 1995; Kreitzer, 2009). We have noted evidence above that these interneurons tend often to lie at the edges of striosomes, and that much of both the cholinergic neuropil and the somatostatinergic neuropil is concentrated in the matrix. The evidence is not sufficient for strong conclusions, but from these results these interneuron types are plausible candidates for conveying responsibility signals from striosomes to the surrounding matrix.
By far the better characterized of these two are the cholinergic interneurons, which are thought to correspond, largely, to the striatal neurons physiologically characterized in vivo as having tonic activity in awake behaving primates (Kimura et al., 1984) – the so-called TANs. TANs show a characteristic pause in their spontaneous activity (usually followed, and sometimes preceded, by a phasic increase in activity) in response to salient stimuli, unexpected rewards, and predictors of reward (Aosaki et al., 1994a, 1995; Apicella, 2007). This response requires striatal dopamine (Aosaki et al., 1994a), is time locked to phasic activity of midbrain dopamine neurons (Morris et al., 2004), and it can be sensitive to context (Apicella, 2007). Such a pause could serve to assign responsibility to striatal modules at precisely the time at which phasic dopamine release occurs in the striatum, which is the time at which dopamine-dependent long-term synaptic plasticity may occur. How could this work, and how would this be related to striosomes as the original calculator of responsibility signals?
There are a few mechanisms by which assignment of responsibility by TANs could potentially occur. Perhaps most intriguingly, decreased activation of nicotinic acetylcholine receptors (nAChRs) on dopaminergic terminals in the striatum modulates dopamine release in a frequency-dependent manner: dopamine release due to high-frequency local stimulation in striatal slices (corresponding, perhaps, to phasic activity of midbrain dopamine neurons) is enhanced, whereas that due to low-frequency local stimulation is reduced (Rice and Cragg, 2004; Cragg, 2006).
In our network model, we assumed that a positive responsibility signal enhances the activation of direct-pathway (D1) MSNs and reduces the activation of indirect-pathway (D2) MSNs within a striatal module. What mechanism could underlie this effect? The results of Rice and Cragg (2004) suggest one possible mechanism: the TAN pause, acting as a positive responsibility signal, could transiently reduce the release of acetylcholine, thus reducing the activation of nAChRs on dopaminergic terminals. Given that the pause is time locked to the phasic activity of dopamine neurons, it is well timed to enhance the dopamine release. This relationship between cholinergic signaling and dopamine release can be related to studies in which behavioral and neural responses to dopaminergic stimulation were altered following ablation of cholinergic interneurons, and in one study also somatostatinergic interneurons as well (Kaneko et al., 2000; Saka et al., 2002).
Consistent with our model, this enhanced dopamine release could potentially result in an enhancement of D1 MSN activity and a reduction in D2 MSN activity within a striatal module (Surmeier et al., 2010). There could be both a transient and a long-lasting component of this effect: the transient component could come about via the opposing effects of dopamine on the excitability of D1 and D2 MSNs, whereas the long-lasting component could come about as a result of the effect of dopamine on long-term synaptic plasticity. Since the TANs are widely but sparsely distributed in the striatum, this hypothetical gating function of TANs could allow the spatial regulation of dopamine-mediated synaptic plasticity, as required by TD learning within a modular RL framework.
The idea that the TAN pause could provide a window for plasticity has been proposed previously (Graybiel et al., 1994; Aosaki et al., 1995; Morris et al., 2004). Shen et al. (2008) found that activation of dopamine receptors is required for spike timing-dependent long-term potentiation (LTP) at direct-pathway MSNs and long-term depression (LTD) at indirect-pathway MSNs (Surmeier et al., 2007; Shen et al., 2008). It is possible that the TAN pause permits opposing plasticity effects in order to enhance the disinhibition of actions by direct-pathway MSNs and to reduce the inhibition of actions by indirect-pathway MSNs (Surmeier et al., 2007). If our hypothesis is correct, then this plasticity can only happen in modules assigned responsibility by the TAN pause; such spatially selective learning is a critical requirement of modular RL.
In addition to its nAChR-mediated effects, acetylcholine has also been shown to influence corticostriatal synaptic plasticity via muscarinic acetylcholine receptors. Activation of M1 muscarinic receptors is required for LTP (Calabresi et al., 1999), whereas a reduction of M1 receptor activation can lead to LTD at corticostriatal synapses onto both direct- and indirect-pathway MSNs by disinhibiting Cav1.3 Ca2+ channels (Wang et al., 2006). By contrast, activation of M2 muscarinic receptors reduces corticostriatal LTP (Calabresi et al., 1998). These plasticity effects could also play a role in long-term changes in modular responsibility assignment. A pause in acetylcholine release may also be capable of depolarizing MSNs or enhancing their excitability via effects at acetylcholine receptors on MSNs themselves (Hsu et al., 1996; Galarraga et al., 1999), on GABAergic interneurons inhibiting MSNs (Koós and Tepper, 2002), on glutamatergic terminals (Pakhotin and Bracci, 2007), on dopaminergic terminals (Zhou et al., 2001; Rice and Cragg, 2004), or on different combinations of these. Excitation of cholinergic interneurons by stimulating thalamostriatal axons in slices leads to a transient M2 receptor-mediated suppression of excitatory input to MSNs followed by a slower, M1 receptor-mediated facilitation of postsynaptic excitability in indirect-pathway MSNs (Ding et al., 2010).
Although the TAN pause is not the only signal by which interneurons could convey responsibility from striosomes to matrix, the suggestion that the TAN pause is a responsibility signal originating in striosomes implies that striosomes participate in generating this pause. However, the involvement of striosomes in generating the pause has not yet been established. We first review the well-established factors in pause generation and then examine the possibility that striosomal MSNs may also contribute to pause generation.
The acquisition and expression of the pause response is known to require input from the centromedian–parafascicular (CM–Pf) complex of the thalamus (Lapper and Bolam, 1992; Matsumoto et al., 2001) and from dopamine-containing nigrostriatal neurons (Aosaki et al., 1994a; Watanabe and Kimura, 1998). Although one proposed mechanism for TAN pause generation involves an intrinsic afterhyperpolarization following depolarization (Reynolds et al., 2004; Wilson and Goldberg, 2006), inhibitory input from MSNs could also contribute to generating the pause (Bolam et al., 1986; Watanabe and Kimura, 1998).
Given the pattern of arborization and concentration of TANs near borders of striosomes observed in primates (Aosaki et al., 1995), it seems likely that signals from striosomes contribute in some way to the pattern of TAN activity: signaling from striosomal MSNs to TANs could occur via substance P, enkephalin, and/or GABA (Bolam et al., 1986; Kaneko et al., 1993; Le Moine et al., 1994; Lee et al., 1997; Yan et al., 1997; Jabourian et al., 2005). Cholinergic interneurons express GABAA receptors, and disynaptic GABAergic IPSPs evoked in cholinergic interneurons by stimulation of corticostriatal and thalamostriatal fibers show dopamine-dependent LTP, a possible mechanism for acquisition of the pause response (Yan et al., 1997; Suzuki et al., 2001). Intriguingly, substance P is highly expressed in striosomes, and a high density of both substance P-containing fibers and substance P receptor-containing somata and dendrites overlaps at the borders of striosomes (Jakab et al., 1996). Importantly, not only cholinergic but also somatostatinergic interneurons contain substance P receptors (Kaneko et al., 1993; Aubry et al., 1994). Striosomal MSNs are themselves influenced by endogenous ligands of μ-opioid receptors (e.g., enkephalin). Miura et al. (2007, 2008) found that a μ-opioid receptor agonist decreased the amplitude of IPSPs in striosomal, but not matrix, MSNs via a presynaptic mechanism.
Additionally, it is possible that some TANs (particularly those within or near the borders of striosomes) receive input from the same dopamine neurons that appear to be reciprocally innervated by striosomal MSNs (Gerfen et al., 1987; Joel and Weiner, 2000); this is another potential pathway by which striosomes could influence the pause.
Given that the number of TANs exhibiting a pause response increases over the course of learning until they comprise the majority (50–70%) of TANs (Aosaki et al., 1994b), it is possible is that for each environment or context, many striatal modules at a time are assigned responsibility in a graded, rather than an all-or-none, manner. The environment would then dictate the pattern of modular responsibility signals across the striatum. Graded differences in the TAN response may play the role of graded responsibility assignment. Another possibility is that the sign of the selection signal is reversed and the TAN pause is a de-selection signal. For example, Wilson (2004) suggested that the phasic increase in activity preceding the pause in a relatively small set of TANs could lead to LTP at corticostriatal synapses onto associated MSNs, whereas the pause occurring by itself in a larger set of TANs could lead to LTD. Within the framework of our models, the smaller set of MSNs could correspond to modules assigned high responsibility, and the larger set could correspond to modules assigned low responsibility.
Negative Responsibility Signals
In one version of our network model, we assumed that responsibility signals could take on negative values in order to signal inappropriateness of modules to a given environmental context. Such negative responsibility signals would increase the excitability of indirect-pathway MSNs. The combination of positive responsibility signals indicating appropriateness of a given module and negative responsibility signals indicating inappropriateness of surrounding modules might not only enhance the contrasts between modules but also help to limit the spatial extent of responsibility signaling via a surround inhibition-like mechanism.
The results of Ding et al. (2010) suggest a partial physiological basis for negative responsibility signaling: they found that a brief thalamostriatal excitation of cholinergic interneurons in slices results in an enhancement of the responsiveness of indirect-pathway MSNs lasting for about a second. This effect is mediated by M1 muscarinic receptors. In the model, such an indirect-pathway enhancement within a striatal module is the result of a negative responsibility signal and enhances the suppression of the set of actions controlled by the corresponding basal ganglia-thalamo-cortical module. Thus, while decreased cholinergic activity may signal enhanced appropriateness of modules to the context, it is possible that increased cholinergic activity can signal decreased appropriateness.
Finally, we reiterate that the cellular architecture of the striatum is still incompletely analyzed, so that our assignment of particular elements of striatal circuits to the modules of our model almost certainly will be revised and changed. Nevertheless, we emphasize that applying the computational ideas of responsibility signals and modular RL to the so far known organization of the striatum seems already appropriate and, as we have outlined above, produces a novel way to move naturally from consideration of the clearly modular anatomical architecture of the striatum to the concept of basal ganglia outputs as being divided into the known direct and indirect pathways.
Comparison to Other Work
A number of authors have previously made proposals that contain elements of our models, but to our knowledge, our models are the first to provide a unified framework based on striosome–matrisome modules, in which striosomes assign responsibility on the basis of environmental context prediction errors, and in which interneurons convey these responsibility signals from striosomes to associated matrisomes. Although the view that the indirect pathway may suppress inappropriate actions is widely held, our network model is the first to suggest that such suppression may be organized according to modular sets of actions regulated by striosome–matrisome modules.
Ashby and Crossley (2011) recently proposed a model in which TANs learn to pause in rewarding environments, thereby enhancing the excitability of MSNs and permitting the learning and expression of behaviors. This idea is somewhat similar to (although more narrowly focused than) the concept of responsibility, but in their model, TAN signaling is not modularized or connected to striosomes. Houk et al. (1995) discussed the idea that multiple striosome domains may function in parallel to control dopamine neurons, but they did not address responsibility signals or the potential function of interneurons in conveying responsibility signals from striosomes to matrix. They also ascribed to striosomes a function specifically in reward prediction, in contrast to the more general function in environmental feature prediction error and responsibility signaling that we suggest, and they did not present a computational model. Wilson (2004) suggested that cholinergic signaling could potentially restrict LTP to specific parts of the striatum during learning but did not address the potential relationship between this signaling and responsibility signals, striosomes, or modular RL. The potential function of cholinergic and somatostatinergic interneurons in intercompartmental communication has been noted by a number of authors (Gerfen, 1984; Chesselet and Graybiel, 1986; Graybiel et al., 1986; Kawaguchi, 1992; Aosaki et al., 1995). Miura et al. (2008) also have discussed the potential function of cholinergic interneurons in mediating signaling from striosomes to matrix. However, none of these authors discuss this signaling in the context of modular RL and responsibility signals.
Based on the initial proposal of a modular architecture for motor learning and control (Wolpert and Kawato, 1998; Wolpert et al., 2003), Imamizu et al. (2003) examined human brain activity during a task that involved changes in the mapping between hand movements and sensory feedback. They found that activities in the cerebellum corresponding to different mappings were spatially segregated, suggesting a modular organization, and they also observed activity related to switching in the cerebellum and other structures (Imamizu et al., 2004). Haruno et al. (2001) and Doya et al. (2002) did pioneering work on the modular framework and extended it to RL. Bertin et al. (2007) used modular RL to explain the behavior of dopamine neurons in specific classical conditioning experiments, but they did not associate their RL modules with the modular architecture of the striatum or attempt to model basal ganglia-thalamo-cortical pathways. Their current model (Samejima et al., 2003) has a rich computational functionality and can decompose a complex task into subtasks, so that each module becomes specialized for a subtask. The idea of task decomposition by a modular architecture could be important for understanding the function of the basal ganglia in sequential learning.
Clinical Significance of Modular Reinforcement Learning Using Responsibility Signals
Striosomes degenerate in X-linked dystonia parkinsonism (DYT3; Goto et al., 2005), and in certain Huntington’s disease patients in whom mood disorders such as anxiety, depression, and compulsions are prominent (Tippett et al., 2007). Additionally, differential activity of striosomes is correlated with increased expression of stereotypic behaviors in animals treated with psychomotor stimulants (Canales and Graybiel, 2000; Graybiel et al., 2000; Saka et al., 2004; Canales, 2005). We suggest that these clinically and experimentally observed symptoms could be accounted for within the framework of modular RL using responsibility signals: what these conditions may have in common is a failure to regulate actions, emotions, thoughts, and urges on the basis of their appropriateness to the environmental context. In some cases, anxiety, depression, and compulsions may result from the absence of regulation of inappropriate emotions, thoughts, and urges by striosomal responsibility signals. In some stereotypies, dysfunctional striosomes may promote specific repetitive, stereotyped behaviors that are inappropriate to the environmental context – or, alternatively, striosomes may become highly active in a futile attempt to reduce such inappropriate behaviors. The nature of the disorder would depend on the affected cortico-basal ganglia network: dysfunction of responsibility signaling in the sensorimotor striatum could promote movement-related disorders, and dysfunction of such signaling in striatal districts interconnected with associative and limbic regions of the forebrain could promote cognitive disorders.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was supported by National Institutes of Health Grants NIH R01 MH060379 and NIH R01 NS025529, Office of Naval Research Grant ONR N00014-07-1-0903, and by European Union Grant 201716. We also acknowledge partial funding for L. G. Gibb from NIH Grant 5 R01 MH079076 to Terrence J. Sejnowski, whom we thank for his interest and interactions. We thank Alex McWhinnie and Emily Romano for their help with the figures.
References
Alexander, G. E., DeLong, M. R., and Strick, P. L. (1986). Parallel organization of functionally segregated circuits linking basal ganglia and cortex. Annu. Rev. Neurosci. 9, 357–381.
Amemori, K., and Graybiel, A. M. (2009). “Stimulation of the macaque rostral anterior cingulate cortex alters decision in approach-avoidance conflict,” in Program No. 194.1, 2009 Neuroscience Meeting Planner (Chicago, IL: Society for Neuroscience).
Amemori, K., and Graybiel, A. M. (2010). “Localized microstimulation of macaque pregenual anterior cingulate cortex increases rejection of cued outcomes in approach-avoidance decision-making,” in Program No. 306.4, 2010 Neuroscience Meeting Planner (San Diego, CA: Society for Neuroscience).
Amemori, K., and Ishii, S. (2001). Gaussian process approach to spiking neurons for inhomogeneous Poisson inputs. Neural Comput. 13, 2763–2797.
Aosaki, T., Graybiel, A. M., and Kimura, M. (1994a). Effect of the nigrostriatal dopamine system on acquired neural responses in the striatum of behaving monkeys. Science 265, 412–415.
Aosaki, T., Tsubokawa, H., Ishida, A., Watanabe, K., Graybiel, A. M., and Kimura, M. (1994b). Responses of tonically active neurons in the primate’s striatum undergo systematic changes during behavioral sensorimotor conditioning. J. Neurosci. 14, 3969–3984.
Aosaki, T., Kimura, M., and Graybiel, A. M. (1995). Temporal and spatial characteristics of tonically active neurons of the primate’s striatum. J. Neurophysiol. 73, 1234–1252.
Apicella, P. (2007). Leading tonically active neurons of the striatum from reward detection to context recognition. Trends Neurosci. 30, 299–306.
Ashby, F. G., and Crossley, M. J. (2011). A computational model of how cholinergic interneurons protect striatal-dependent learning. J. Cogn. Neurosci. 23, 1549–1566.
Aubry, J. M., Lundström, K., Kawashima, E., Ayala, G., Schulz, P., Bartanusz, V., and Kiss, J. Z. (1994). NK1 receptor expression by cholinergic interneurones in human striatum. Neuroreport 5, 1597–1600.
Bar-Gad, I., Morris, G., and Bergman, H. (2003). Information processing, dimensionality reduction and reinforcement learning in the basal ganglia. Prog. Neurobiol. 71, 439–473.
Behrens, T. E., Woolrich, M. W., Walton, M. E., and Rushworth, M. F. (2007). Learning the value of information in an uncertain world. Nat. Neurosci. 10, 1214–1221.
Bernacchia, A., Seo, H., Lee, D., and Wang, X. J. (2011). A reservoir of time constants for memory traces in cortical neurons. Nat. Neurosci. 14, 366–372.
Bertin, M., Schweighofer, N., and Doya, K. (2007). Multiple model-based reinforcement learning explains dopamine neuronal activity. Neural Netw. 20, 668–675.
Bevan, M. D., Booth, P. A., Eaton, S. A., and Bolam, J. P. (1998). Selective innervation of neostriatal interneurons by a subclass of neuron in the globus pallidus of the rat. J. Neurosci. 18, 9438–9452.
Bevan, M. D., Clarke, N. P., and Bolam, J. P. (1997). Synaptic integration of functionally diverse pallidal information in the entopeduncular nucleus and subthalamic nucleus in the rat. J. Neurosci. 17, 308–324.
Bevan, M. D., Smith, A. D., and Bolam, J. P. (1996). The substantia nigra as a site of synaptic integration of functionally diverse information arising from the ventral pallidum and the globus pallidus in the rat. Neuroscience 75, 5–12.
Bolam, J. P., Hanley, J. J., Booth, P. A., and Bevan, M. D. (2000). Synaptic organisation of the basal ganglia. J. Anat. 196(Pt 4), 527–542.
Bolam, J. P., Ingham, C. A., Izzo, P. N., Levey, A. I., Rye, D. B., Smith, A. D., and Wainer, B. H. (1986). Substance P-containing terminals in synaptic contact with cholinergic neurons in the neostriatum and basal forebrain: a double immunocytochemical study in the rat. Brain Res. 397, 279–289.
Bolam, J. P., Izzo, P. N., and Graybiel, A. M. (1988). Cellular substrate of the histochemically defined striosome/matrix system of the caudate nucleus: a combined golgi and immunocytochemical study in cat and ferret. Neuroscience 24, 853–875.
Bolam, J. P., Smith, Y., Ingham, C. A., von Krosigk, M., and Smith, A. D. (1993). Convergence of synaptic terminals from the striatum and the globus pallidus onto single neurones in the substantia nigra and the entopeduncular nucleus. Prog. Brain Res. 99, 73–88.
Calabresi, P., Centonze, D., Gubellini, P., and Bernardi, G. (1999). Activation of M1-like muscarinic receptors is required for the induction of corticostriatal LTP. Neuropharmacology 38, 323–326.
Calabresi, P., Centonze, D., Gubellini, P., Pisani, A., and Bernardi, G. (1998). Blockade of M2-like muscarinic receptors enhances long-term potentiation at corticostriatal synapses. Eur. J. Neurosci. 10, 3020–3023.
Canales, J. J. (2005). Stimulant-induced adaptations in neostriatal matrix and striosome systems: transiting from instrumental responding to habitual behavior in drug addiction. Neurobiol. Learn. Mem. 83, 93–103.
Canales, J. J., and Graybiel, A. M. (2000). A measure of striatal function predicts motor stereotypy. Nat. Neurosci. 3, 377–383.
Chesselet, M. F., and Graybiel, A. M. (1986). Striatal neurons expressing somatostatin-like immunoreactivity: evidence for a peptidergic interneuronal system in the cat. Neuroscience 17, 547–571.
Courtemanche, R., Fujii, N., and Graybiel, A. M. (2003). Synchronous, focally modulated beta-band oscillations characterize local field potential activity in the striatum of awake behaving monkeys. J. Neurosci. 23, 11741–11752.
Cragg, S. J. (2006). Meaningful silences: how dopamine listens to the ACh pause. Trends Neurosci. 29, 125–131.
Degos, B., Deniau, J. M., Le Cam, J., Mailly, P., and Maurice, N. (2008). Evidence for a direct subthalamo-cortical loop circuit in the rat. Eur. J. Neurosci. 27, 2599–2610.
Ding, J. B., Guzman, J. N., Peterson, J. D., Goldberg, J. A., and Surmeier, D. J. (2010). Thalamic gating of corticostriatal signaling by cholinergic interneurons. Neuron 67, 294–307.
Doya, K. (2000). Complementary roles of basal ganglia and cerebellum in learning and motor control. Curr. Opin. Neurobiol. 10, 732–739.
Doya, K., Samejima, K., Katagiri, K., and Kawato, M. (2002). Multiple model-based reinforcement learning. Neural Comput. 14, 1347–1369.
Eblen, F., and Graybiel, A. M. (1995). Highly restricted origin of prefrontal cortical inputs to striosomes in the macaque monkey. J. Neurosci. 15, 5999–6013.
Flaherty, A. W., and Graybiel, A. M. (1991). Corticostriatal transformations in the primate somatosensory system. Projections from physiologically mapped body-part representations. J. Neurophysiol. 66, 1249–1263.
Flaherty, A. W., and Graybiel, A. M. (1993). Two input systems for body representations in the primate striatal matrix: experimental evidence in the squirrel monkey. J. Neurosci. 13, 1120–1137.
Flaherty, A. W., and Graybiel, A. M. (1994). Input-output organization of the sensorimotor striatum in the squirrel monkey. J. Neurosci. 14, 599–610.
Fujiyama, F., Sohn, J., Nakano, T., Furuta, T., Nakamura, K. C., Matsuda, W., and Kaneko, T. (2011). Exclusive and common targets of neostriatofugal projections of rat striosome neurons: a single neuron-tracing study using a viral vector. Eur. J. Neurosci. 33, 668–677.
Galarraga, E., Hernández-López, S., Reyes, A., Miranda, I., Bermudez-Rattoni, F., Vilchis, C., and Bargas, J. (1999). Cholinergic modulation of neostriatal output: a functional antagonism between different types of muscarinic receptors. J. Neurosci. 19, 3629–3638.
Gerfen, C. R. (1984). The neostriatal mosaic: compartmentalization of corticostriatal input and striatonigral output systems. Nature 311, 461–464.
Gerfen, C. R., Herkenham, M., and Thibault, J. (1987). The neostriatal mosaic: II. Patch- and matrix-directed mesostriatal dopaminergic and non-dopaminergic systems. Neurosci. J. 7, 3915–3934.
Gimenez-Amaya, J. M., and Graybiel, A. M. (1990). Compartmental origins of the striatopallidal projection in the primate. Neuroscience 34, 111–126.
Gimenez-Amaya, J. M., and Graybiel, A. M. (1991). Modular organization of projection neurons in the matrix compartment of the primate striatum. J. Neurosci. 11, 779–791.
Goto, S., Lee, L. V., Munoz, E. L., Tooyama, I., Tamiya, G., Makino, S., Ando, S., Dantes, M. B., Yamada, K., Matsumoto, S., Shimazu, H., Kuratsu, J., Hirano, A., and Kaji, R. (2005). Functional anatomy of the basal ganglia in X-linked recessive dystonia-parkinsonism. Ann. Neurol. 58, 7–17.
Graybiel, A. M. (1984). Correspondence between the dopamine islands and striosomes of the mammalian striatum. Neuroscience 13, 1157–1187.
Graybiel, A. M. (1991). Basal ganglia – input, neural activity, and relation to the cortex. Curr. Opin. Neurobiol. 1, 644–651.
Graybiel, A. M. (1997). The basal ganglia and cognitive pattern generators. Schizophr. Bull. 23, 459–469.
Graybiel, A. M. (1998). The basal ganglia and chunking of action repertoires. Neurobiol. Learn. Mem. 70, 119–136.
Graybiel, A. M. (2008). Habits, rituals, and the evaluative brain. Annu. Rev. Neurosci. 31, 359–387.
Graybiel, A. M., Aosaki, T., Flaherty, A. W., and Kimura, M. (1994). The basal ganglia and adaptive motor control. Science 265, 1826–1831.
Graybiel, A. M., Baughman, R. W., and Eckenstein, F. (1986). Cholinergic neuropil of the striatum observes striosomal boundaries. Nature 323, 625–627.
Graybiel, A. M., Canales, J. J., and Capper-Loup, C. (2000). Levodopa-induced dyskinesias and dopamine-dependent stereotypies: a new hypothesis. Trends Neurosci. 23(Suppl. 10), S71–S77.
Graybiel, A. M., and Ragsdale, C. W. (1978). Histochemically distinct compartments in the striatum of human, monkeys, and cat demonstrated by acetylthiocholinesterase staining. Proc. Natl. Acad. Sci. U.S.A. 75, 5723–5726.
Graybiel, A. M., Ragsdale, C. W. Jr., Yoneoka, E. S., and Elde, R. P. (1981). An immunohistochemical study of enkephalins and other neuropeptides in the striatum of the cat with evidence that the opiate peptides are arranged to form mosaic patterns in register with the striosomal compartments visible by acetylcholinesterase staining. Neuroscience 6, 377–397.
Groves, P. M., Martone, M., Young, S. J., and Armstrong, D. M. (1988). Three-dimensional pattern of enkephalin-like immunoreactivity in the caudate nucleus of the cat. J. Neurosci. 8, 892–900.
Haruno, M., Wolpert, D. M., and Kawato, M. (2001). Mosaic model for sensorimotor learning and control. Neural Comput. 13, 2201–2220.
Herkenham, M., and Pert, C. B. (1981). Mosaic distribution of opiate receptors, parafascicular projections and acetylcholinesterase in rat striatum. Nature 291, 415–418.
Holt, D. J., Graybiel, A. M., and Saper, C. B. (1997). Neurochemical architecture of the human striatum. J. Comp. Neurol. 384, 1–25.
Houk, J. C., Adams, J. L., and Barto, A. G. (1995). “A model of how the basal ganglia generate and use neural signals that predict reinforcement,” in Models of Information Processing in the Basal Ganglia, eds J. C. Houk, J. D. Davis, and D. G. Beiser (Cambridge, MA: MIT Press), 249–270.
Hsu, K. S., Yang, C. H., Huang, C. C., and Gean, P. W. (1996). Carbachol induces inward current in neostriatal neurons through M1-like muscarinic receptors. Neuroscience 73, 751–760.
Imamizu, H., Kuroda, T., Miyauchi, S., Yoshioka, T., and Kawato, M. (2003). Modular organization of internal models of tools in the human cerebellum. Proc. Natl. Acad. Sci. U.S.A. 100, 5461–5466.
Imamizu, H., Kuroda, T., Yoshioka, T., and Kawato, M. (2004). Functional magnetic resonance imaging examination of two modular architectures for switching multiple internal models. J. Neurosci. 24, 1173–1181.
Jabourian, M., Venance, L., Bourgoin, S., Ozon, S., Pérez, S., Godeheu, G., Glowinski, J., and Kemel, M. L. (2005). Functional mu opioid receptors are expressed in cholinergic interneurons of the rat dorsal striatum: territorial specificity and diurnal variation. Eur. J. Neurosci. 21, 3301–3309.
Jackson, A., and Crossman, A. R. (1981). Subthalamic nucleus efferent projection to the cerebral cortex. Neuroscience 6, 2367–2377.
Jacobs, R. A., Jordan, M. I., Nowlan, S. J., and Hinton, G. E. (1991). Adaptive mixtures of local experts. Neural Comput. 3, 79–87.
Jakab, R. L., Hazrati, L. N., and Goldman-Rakic, P. (1996). Distribution and neurochemical character of substance P receptor (SPR)-immunoreactive striatal neurons of the macaque monkey: accumulation of SP fibers and SPR neurons and dendrites in “striocapsules” encircling striosomes. J. Comp. Neurol. 369, 137–149.
Jiménez-Castellanos, J., and Graybiel, A. M. (1989). Compartmental origins of striatal efferent projections in the cat. Neuroscience 32, 297–321.
Joel, D., and Weiner, I. (2000). The connections of the dopaminergic system with the striatum in rats and primates: an analysis with respect to the functional and compartmental organization of the striatum. Neuroscience 96, 451–474.
Jordan, M. I., and Jacobs, R. A. (1994). Hierarchical mixtures of experts and the EM algorithm. Neural Comput. 6, 181–214.
Kaneda, K., Nambu, A., Tokuno, H., and Takada, M. (2002). Differential processing patterns of motor information via striatopallidal and striatonigral projections. J. Neurophysiol. 88, 1420–1432.
Kaneko, S., Hikida, T., Watanabe, D., Ichinose, H., Nagatsu, T., Kreitman, R. J., Pastan, I., and Nakanishi, S. (2000). Synaptic integration mediated by striatal cholinergic interneurons in basal ganglia function. Science 289, 633–637.
Kaneko, T., Shigemoto, R., Nakanishi, S., and Mizuno, N. (1993). Substance P receptor-immunoreactive neurons in the rat neostriatum are segregated into somatostatinergic and cholinergic aspiny neurons. Brain Res. 631, 297–303.
Kawaguchi, Y. (1992). Large aspiny cells in the matrix of the rat neostriatum in vitro: physiological identification, relation to the compartments and excitatory postsynaptic currents. J. Neurophysiol. 67, 1669–1682.
Kawaguchi, Y., Wilson, C. J., Augood, S. J., and Emson, P. C. (1995). Striatal interneurones: chemical, physiological and morphological characterization. Trends Neurosci. 18, 527–535.
Kawaguchi, Y., Wilson, C. J., and Emson, P. C. (1989). Intracellular recording of identified neostriatal patch and matrix spiny cells in a slice preparation preserving cortical inputs. J. Neurophysiol. 62, 1052–1068.
Kimura, M., Rajkowski, J., and Evarts, E. (1984). Tonically discharging putamen neurons exhibit set-dependent responses. Proc. Natl. Acad. Sci. U.S.A. 81, 4998–5001.
Kincaid, A. E., and Wilson, C. J. (1996). Corticostriatal innervation of the patch and matrix in the rat neostriatum. J. Comp. Neurol. 374, 578–592.
Kita, H., and Kitai, S. T. (1987). Efferent projections of the subthalamic nucleus in the rat: light and electron microscopic analysis with the PHA-L method. J. Comp. Neurol. 260, 435–452.
Koós, T., and Tepper, J. M. (2002). Dual cholinergic control of fast-spiking interneurons in the neostriatum. J. Neurosci. 22, 529–535.
Kreitzer, A. C. (2009). Physiology and pharmacology of striatal neurons. Annu. Rev. Neurosci. 32, 127–147.
Langer, L. F., and Graybiel, A. M. (1989). Distinct nigrostriatal projection systems innervate striosomes and matrix in the primate striatum. Brain Res. 498, 344–350.
Lapper, S. R., and Bolam, J. P. (1992). Input from the frontal cortex and the parafascicular nucleus to cholinergic interneurons in the dorsal striatum of the rat. Neuroscience 51, 533–545.
Le Moine, C., Kieffer, B., Gaveriaux-Ruff, C., Befort, K., and Bloch, B. (1994). Delta-opioid receptor gene expression in the mouse forebrain: localization in cholinergic neurons of the striatum. Neuroscience 62, 635–640.
Lee, T., Kaneko, T., Shigemoto, R., Nomura, S., and Mizuno, N. (1997). Collateral projections from striatonigral neurons to substance P receptor-expressing intrinsic neurons in the striatum of the rat. J. Comp. Neurol. 388, 250–264.
Lei, W., Jiao, Y., Del Mar, N., and Reiner, A. (2004). Evidence for differential cortical input to direct pathway versus indirect pathway striatal projection neurons in rats. J. Neurosci. 24, 8289–8299.
Matsuda, W., Furuta, T., Nakamura, K. C., Hioki, H., Fujiyama, F., Arai, R., and Kaneko, T. (2009). Single nigrostriatal dopaminergic neurons form widely spread and highly dense axonal arborizations in the neostriatum. J. Neurosci. 29, 444–453.
Matsumoto, M., and Hikosaka, O. (2009). Two types of dopamine neuron distinctly convey positive and negative motivational signals. Nature 459, 837–841.
Matsumoto, M., Kenji, M., Hiroshi, A., and Keiji, T. (2007). Medial prefrontal cell activity signaling prediction errors of action values. Nat. Neurosci. 10, 647–656.
Matsumoto, N., Minamimoto, T., Graybiel, A. M., and Kimura, M. (2001). Neurons in the thalamic CM-Pf complex supply striatal neurons with information about behaviorally significant sensory events. J. Neurophysiol. 85, 960–976.
Mikula, S., Parrish, S. K., Trimmer, J. S., and Jones, E. G. (2009). Complete 3D visualization of primate striosomes by KChIP1 immunostaining. J. Comp. Neurol. 514, 507–517.
Mink, J. W. (1996). The basal ganglia: focused selection and inhibition of competing motor programs. Prog. Neurobiol. 50, 381–425.
Miura, M., Masuda, M., and Aosaki, T. (2008). Roles of micro-opioid receptors in GABAergic synaptic transmission in the striosome and matrix compartments of the striatum. Mol. Neurobiol. 37, 104–115.
Miura, M., Saino-Saito, S., Masuda, M., Kobayashi, K., and Aosaki, T. (2007). Compartment-specific modulation of GABAergic synaptic transmission by mu-opioid receptor in the mouse striatum with green fluorescent protein-expressing dopamine islands. J. Neurosci. 27, 9721–9728.
Montague, P. R., Dayan, P., and Sejnowski, T. J. (1996). A framework for mesencephalic dopamine systems based on predictive Hebbian learning. J. Neurosci. 16, 1936–1947.
Morris, G., Arkadir, D., Nevet, A., Vaadia, E., and Bergman, H. (2004). Coincident but distinct messages of midbrain dopamine and striatal tonically active neurons. Neuron 43, 133–143.
Niki, H., and Watanabe, M. (1979). Prefrontal and cingulate unit activity during timing behavior in the monkey. Brain Res. 171, 213–224.
Oorschot, D. E. (1996). Total number of neurons in the neostriatal, pallidal, subthalamic, and substantia nigral nuclei of the rat basal ganglia: a stereological study using the cavalieri and optical disector methods. J. Comp. Neurol. 366, 580–599.
Pakhotin, P., and Bracci, E. (2007). Cholinergic interneurons control the excitatory input to the striatum. J. Neurosci. 27, 391–400.
Parent, A., and Hazrati, L. N. (1995). Functional anatomy of the basal ganglia. I. The cortico-basal ganglia-thalamo-cortical loop. Brain Res. Brain Res. Rev. 20, 91–127.
Parthasarathy, H. B., and Graybiel, A. M. (1997). Cortically driven immediate-early gene expression reflects modular influence of sensorimotor cortex on identified striatal neurons in the squirrel monkey. J. Neurosci. 17, 2477–2491.
Penny, G. R., Wilson, C. J., and Kitai, S. T. (1988). Relationship of the axonal and dendritic geometry of spiny projection neurons to the compartmental organization of the neostriatum. J. Comp. Neurol. 269, 275–289.
Percheron, G., and Filion, M. (1991). Parallel processing in the basal ganglia: up to a point. Trends Neurosci. 14, 55–59.
Ragsdale, C. W. Jr., and Graybiel, A. M. (1988). Fibers from the basolateral nucleus of the amygdala selectively innervate striosomes in the caudate nucleus of the cat. J. Comp. Neurol. 269, 506–522.
Reiner, A., Hart, N. M., Lei, W., and Deng, Y. (2010). Corticostriatal projection neurons – dichotomous types and dichotomous functions. Front. Neuroanat. 4:142. doi: 10.3389/fnana.2010.00142
Reynolds, J. N., Hyland, B. I., and Wickens, J. R. (2004). Modulation of an afterhyperpolarization by the substantia nigra induces pauses in the tonic firing of striatal cholinergic interneurons. J. Neurosci. 24, 9870–9877.
Reynolds, N. J., Hyland, B. I., and Wickens, J. R. (2001). A cellular mechanism of reward-related learning. Nature 413, 67–70.
Rice, M. E., and Cragg, S. J. (2004). Nicotine amplifies reward-related dopamine signals in striatum. Nat. Neurosci. 7, 583–584.
Rogers, R. D., Andrews, T. C., Grasby, P. M., Brooks, D. J., and Robbins, T. W. (2000). Contrasting cortical and subcortical activations produced by attentional-set shifting and reversal learning in humans. J. Cogn. Neurosci. 12, 142–162.
Romanelli, P., Esposito, V., Schaal, D. W., and Heit, G. (2005). Somatotopy in the basal ganglia: experimental and clinical evidence for segregated sensorimotor channels. Brain Res. Brain Res. Rev. 48, 112–128.
Saka, E., Goodrich, C., Harlan, P., Madras, B. K., and Graybiel, A. M. (2004). Repetitive behaviors in monkeys are linked to specific striatal activation patterns. J. Neurosci. 24, 7557–7565.
Saka, E., Iadarola, M., Fitzgerald, D. J., and Graybiel, A. M. (2002). Local circuit neurons in the striatum regulate neural and behavioral responses to dopaminergic stimulation. Proc. Natl. Acad. Sci. U.S.A. 99, 9004–9009.
Samejima, K., Doya, K., and Kawato, M. (2003). Inter-module credit assignment in modular reinforcement learning. Neural Netw. 16, 985–994.
Samejima, K., Ueda, Y., Doya, K., and Kimura, M. (2005). Representation of action-specific reward values in the striatum. Science 310, 1337–1340.
Schultz, W., Dayan, P., and Montague, P. R. (1997). A neural substrate of prediction and reward. Science 275, 1593–1599.
Shen, W., Flajolet, M., Greengard, P., and Surmeier, D. J. (2008). Dichotomous dopaminergic control of striatal synaptic plasticity. Science 321, 848–851.
Surmeier, D. J., Ding, J., Day, M., Wang, Z., and Shen, W. (2007). D1 and D2 dopamine-receptor modulation of striatal glutamatergic signaling in striatal medium spiny neurons. Trends Neurosci. 30, 228–235.
Surmeier, D. J., Shen, W., Day, M., Gertler, T., Chan, S., Tian, X., and Plotkin, J. L. (2010). The role of dopamine in modulating the structure and function of striatal circuits. Prog. Brain Res. 183, 149–167.
Sutton, R. S., and Barto, A. G. (1998). Reinforcement Learning: An Introduction, Adaptive Computation and Machine Learning. Cambridge, MA: MIT Press.
Suzuki, T., Miura, M., Nishimura, K., and Aosaki, T. (2001). Dopamine-dependent synaptic plasticity in the striatal cholinergic interneurons. J. Neurosci. 21, 6492–6501.
Tippett, L. J., Waldvogel, H. J., Thomas, S. J., Hogg, V. M., van Roon-Mom, W., Synek, B. J., Graybiel, A. M., and Faull, R. L. (2007). Striosomes and mood dysfunction in Huntington’s disease. Brain 130(Pt 1), 206–221.
Walker, R. H., Arbuthnott, G. W., Baughman, R. W., and Graybiel, A. M. (1993). Dendritic domains of medium spiny neurons in the primate striatum: relationships to striosomal borders. J. Comp. Neurol. 337, 614–628.
Wang, Z., Kai, L., Day, M., Ronesi, J., Yin, H. H., Ding, J., Tkatch, T., Lovinger, D. M., and Surmeier, D. J. (2006). Dopaminergic control of corticostriatal long-term synaptic depression in medium spiny neurons is mediated by cholinergic interneurons. Neuron 50, 443–452.
Watanabe, K., and Kimura, M. (1998). Dopamine receptor-mediated mechanisms involved in the expression of learned activity of primate striatal neurons. J. Neurophysiol. 79, 2568–2580.
Wilson, C. J. (2004). “Basal ganglia,” in The Synaptic Organization of the Brain, ed. G. M. Shepherd (New York: Oxford University Press), 361–413.
Wilson, C. J., and Goldberg, J. A. (2006). Origin of the slow afterhyperpolarization and slow rhythmic bursting in striatal cholinergic interneurons. J. Neurophysiol. 95, 196–204.
Wolpert, D. M., Doya, K., and Kawato, M. (2003). A unifying computational framework for motor control and social interaction. Philos. Trans. R. Soc. Lond. B Biol. Sci. 358, 593–602.
Wolpert, D. M., and Kawato, M. (1998). Multiple paired forward and inverse models for motor control. Neural Netw. 11, 1317–1329.
Yan, Z., Song, W. J., and Surmeier, J. (1997). D2 dopamine receptors reduce N-type Ca2+ currents in rat neostriatal cholinergic interneurons through a membrane-delimited, protein-kinase-C-insensitive pathway. J. Neurophysiol. 77, 1003–1015.
Keywords: basal ganglia, striatum, striosome and matrix compartments, direct and indirect pathways, acetylcholine, modular reinforcement learning, responsibility signal, mixture of experts
Citation: Amemori K, Gibb LG and Graybiel AM (2011) Shifting responsibly: the importance of striatal modularity to reinforcement learning in uncertain environments. Front. Hum. Neurosci. 5:47. doi: 10.3389/fnhum.2011.00047
Received: 06 December 2010; Paper pending published: 15 February 2011;
Accepted: 06 May 2011; Published online: 27 May 2011.
Edited by:
Sven Bestmann, University College London, UKCopyright: © 2011 Amemori, Gibb and Graybiel. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence: Ann M. Graybiel, McGovern Institute for Brain Research and Department of Brain and Cognitive Sciences, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02139, USA. e-mail:Z3JheWJpZWxAbWl0LmVkdQ==


