- 1 Department of Experimental Psychology, Ghent University, Ghent, Belgium
- 2 Ghent Institute for Functional and Metabolic Imaging, Ghent University Hospital, Ghent, Belgium
The role of the anterior cingulate cortex (ACC) in cognition has been extensively investigated with several techniques, including single-unit recordings in rodents and monkeys and EEG and fMRI in humans. This has generated a rich set of data and points of view. Important theoretical functions proposed for ACC are value estimation, error detection, error-likelihood estimation, conflict monitoring, and estimation of reward volatility. A unified view is lacking at this time, however. Here we propose that online value estimation could be the key function underlying these diverse data. This is instantiated in the reward value and prediction model (RVPM). The model contains units coding for the value of cues (stimuli or actions) and units coding for the differences between such values and the actual reward (prediction errors). We exposed the model to typical experimental paradigms from single-unit, EEG, and fMRI research to compare its overall behavior with the data from these studies. The model reproduced the ACC behavior of previous single-unit, EEG, and fMRI studies on reward processing, error processing, conflict monitoring, error-likelihood estimation, and volatility estimation, unifying the interpretations of the role performed by the ACC in some aspects of cognition.
Introduction
What do I want to eat, Chinese or Italian? If Italian, how to reach a good restaurant in a fast and comfortable manner? This question, which might befall a hungry visitor in a foreign city, illustrates a more general point: that in order to act adaptively, we must estimate the values of both environmental stimuli (e.g., a picture of pizza on a sign) and our own actions (e.g., turning right or left before a bifurcation). These value estimates can then be used in later decision making.
One cortical area that has been implicated in value estimation is the medial frontal cortex (MFC), and in particular anterior cingulate cortex (ACC). Evidence for value estimation in MFC has been obtained from many different levels and methodologies (Rushworth and Behrens, 2008). Single-unit recordings conducted in the rostral ACC of macaque monkeys revealed neurons responding as a function of the expected reward magnitude of a cue (Matsumoto et al., 2003; Amiez et al., 2006). Other populations respond when the estimated or expected reward does not correspond to its actual occurrence, encoding the so-called reward prediction errors. These neurons fire either when a reward is delivered but not expected by the subject (positive prediction errors), or when a reward is not delivered but expected by the subject (negative prediction errors; Amiez et al., 2006; Matsumoto et al., 2007). Intuitively, positive prediction errors correspond to “good surprises,” and negative prediction errors to “bad surprises.” Also EEG and fMRI studies have shown a role for MFC in coding for reward prediction error (Oliveira et al., 2007; Jessup et al., 2010).
However, functions other than value estimation have also been ascribed to ACC. One influential point of view is that ACC is involved with error processing (e.g., Critchley et al., 2005). A detailed implementation was provided by Holroyd and Coles (2002), who considered ACC from the point of view of temporal difference (TD) learning, an algorithm belonging to the reinforcement learning (RL) field (Sutton and Barto, 1998). RL is a framework from machine learning, and provides a formal explanation for classical results from learning theory. Holroyd and Coles (2002) argued that the basal ganglia estimate values using TD learning, and send a prediction error signal to ACC for the latter to act as a “control filter” and choose an appropriate motor controller for the task at hand. Another view is that ACC estimates the probability that an error occurs for specific events (error-likelihood theory). Brown and Braver (2005) proposed that when stimuli or actions are associated with errors, a Hebbian learning process connects the neurons encoding the stimuli to the ACC. Hence, if a stimulus or action is often (i.e., with high likelihood) accompanied by an error, it will activate ACC. Another influential view is that ACC computes response conflict (Botvinick et al., 2001). Often, a stimulus affords two or more actions, in which case two or more responses will be activated simultaneously. This co-activation is translated into a high energy level, or response conflict, which is computed by ACC. For example, a pizza sign on the left and a dim sum sign on the right might activate both left- and right-going tendencies in the hungry traveler. Finally, a recent perspective holds that ACC computes volatility, or the extent to which the probabilities linking situations and outcomes in the environment are variable across time (Behrens et al., 2007). For example, repeatedly playing tennis against the same opponent, who has a variable tennis skill level from day to day, makes our probability of winning the match variable from day to day, leading to volatile outcomes of the match.
Hence, on the one hand single-unit data in monkeys, point toward ACC involvement in value estimation and prediction error computation. On the other hand (human) EEG and fMRI data have inspired partially related or altogether different proposals. For example, the conflict monitoring perspective is able to account for the effects arising from many experimental paradigms, but it is unable to predict error-likelihood effects (Brown and Braver, 2005). At the same time, error-likelihood theory is able to explain some aspects of conflict effects in correct trials, but it cannot explain the ACC activity following an error in the very same paradigm (Brown and Braver, 2005). Moreover both conflict monitoring and error-likelihood models seem unsuited to explain the effects of volatility on ACC (Behrens et al., 2007). Finally it is worth noticing that there is yet no single-unit neurophysiological evidence supporting error likelihood, conflict monitoring, or volatility theory (Cole et al., 2009).
The question remains, then, whether a unified view of ACC can be developed. Some steps toward reconciliation were already taken by Botvinick (2007), who proposed that response conflict can be considered as a cost for the cognitive system, which could be one aspect of the overall value of a stimulus. Unfortunately, a formal integration of the different levels and data is lacking. Before addressing this issue, however, we must first clarify two points. First, there is a rostro-caudal gradient in ACC with the caudal part (located ventrally to the supplementary motor area) exhibiting mainly motor and premotor functions (Dum and Strick, 2002), and the rostral part involved mainly with evaluative functions (Matsumoto et al., 2003, 2007; Amiez et al., 2006; Rushworth and Behrens, 2008). All models mentioned above (except (Holroyd and Coles, 2002) were concerned with the evaluative aspect of ACC, and so is this paper. Stated in the framework of RL, the rostral part can be considered as a Critic, that is, a system deputized to evaluate stimuli and possible actions in terms of expected reward. As such it can provide a map of the most convenient environmental states and of the most convenient possible actions to perform. In contrast, the more caudal part can be considered as an Actor, which is a system that selects actions based on the evaluations provided by the Critic. Second, although the ACC prefers evaluating actions rather than stimuli (Rushworth and Behrens, 2008), it has been shown in monkeys that ACC can also code stimulus values (Amiez et al., 2006). For that reason, we here consider ACC to code the value of general “cues,” being either stimuli or actions.
Here we develop a unified view of the rostral part of ACC from the perspective of value estimation, embedded in the framework of RL. The core of the model is that, to estimate values online (i.e., while interacting with the environment), agents must formulate predictions about future rewards based on incoming events (i.e., reward prediction, here called V). These predictions must then be compared with the rewards actually obtained (prediction errors, here called δ), and estimates of V must be updated using δ. Based on this key idea and on single-unit recording data, we constructed the reward value and prediction model (RVPM). In the remainder, we first describe the model in more detail. Then, we show that the model is consistent with available single-unit data (Simulation 1). After that, we report the model’s application to error processing, in particular, different experimental modulations of EEG error-related negativity (ERN) waves (Simulation 2). Next, we simulate data obtained in the framework of three influential theories of ACC, namely conflict monitoring (Simulation 3), error likelihood (Simulation 4), and volatility theory (Simulation 5). Finally, we discuss relations to earlier work and possible extensions.
General Methods
Here, we first describe in mathematical notation the general concepts of expected value and prediction error we already introduced above. Second, we show how the RVPM implements a mechanism to compute expected value online, by means of prediction errors. We describe the point of contact of RVPM with the relevant neurophysiology, and the equations determining RVPM dynamics. Third, we describe the general features of the simulations we ran to test the model behavior in several experimental paradigms.
Formal Representation of Reward Value and Prediction Error
The notation Vt(a) is used to denote the value (expected reward) for some cue (stimulus or action) a, present at time t. It can be updated online using prediction error as follows:
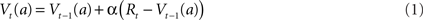
where Rt denotes reward at time t. The prediction error δt = α(Rt − Vt−1(a)) indicates the difference between the value that the system was expecting (Vt−1(a)) and the actual environmental outcome (Rt), where α is a learning rate parameter. Because firing rate is always a positive value, neurons can only encode positive values (or only negative values) via their firing rate. This causes a problem when coding this prediction error, as it can take both positive and negative values. The easiest way to solve this problem is through opponency coding (Daw et al., 2002), and consists in the current case of distinguishing two prediction errors. Positive prediction errors are denoted by:

coherently with the definition of positive prediction error, Eq. 2 corresponds to cases where the actual outcomes are better than expected. On the other hand, negative prediction errors code for situations where environmental outcomes are worse than expected. They are denoted by:

Both δ+ and δ− are non-negative, and Eq. 1 can be rewritten as:

Equation 4 describes the process of online value updating in terms of prediction errors.
Model Architecture and Dynamics
As we anticipated in the Introduction, single-unit recordings conducted in the ACC of macaque monkeys confirm the presence of the three neural populations coding for expected reward magnitude (V) (Matsumoto et al., 2003; Amiez et al., 2006), positive prediction error (δ+) (Matsumoto et al., 2007), and negative prediction error (δ−) (Amiez et al., 2005; Matsumoto et al., 2007). Figure 1A shows the architecture of the RVPM, which implements these three cell types in the ACC module. This ACC module receives afferents from units coding for external cues (C1 and C2) and from a unit (RW) generating the reward signal (RW). A plausible neural structure to generate this reward signal is the ventral tegmental area (VTA). Indeed, a subset of dopaminergic neurons in VTA code consistently for reward occurrence rather than exhibiting the well-known TD signature (Ljungberg et al., 1992; Schultz, 1998). The RW unit explicitly models this latter class of cells. The cue units code whatever event occurs external to the RVPM, be it a stimulus or a planned action.
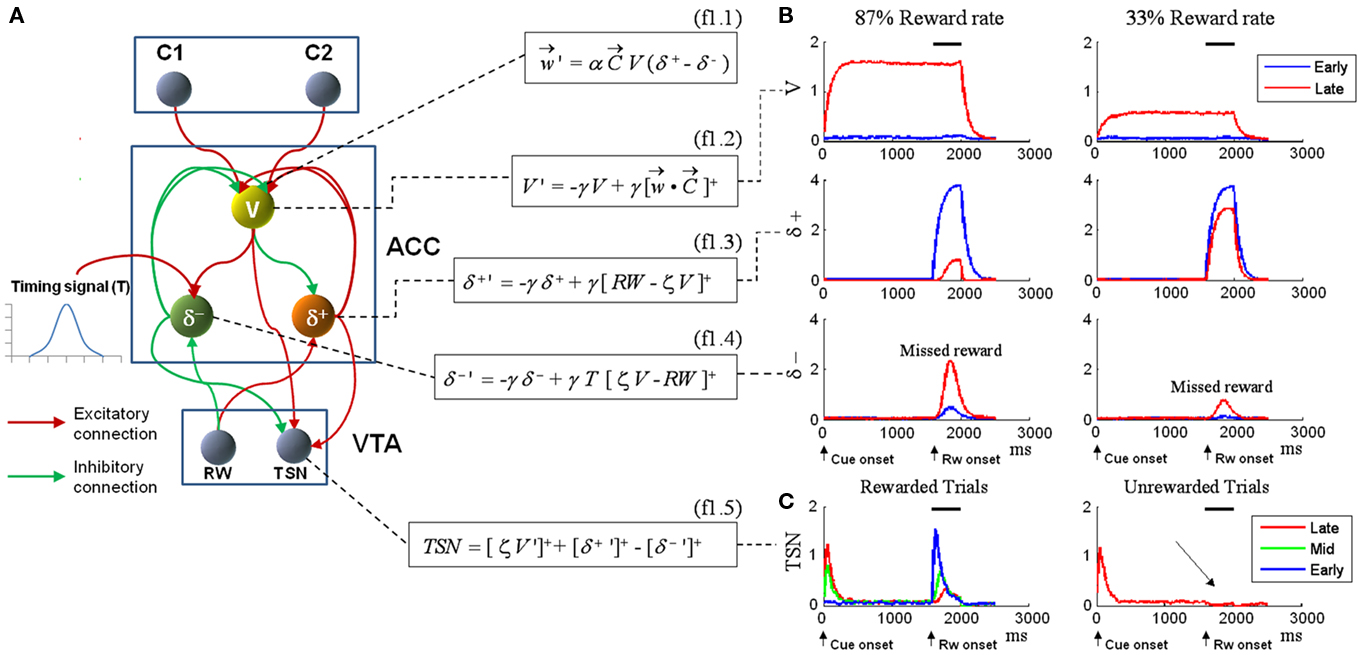
Figure 1. (A) Model structure with equations describing both model dynamics and learning process (see also Methods of Simulation 1 and Appendix). Model structure: V, reward prediction unit; δ+ and δ−, positive and negative prediction error units; C1 and C2, units coding for events; TSN, temporally shifting neuron; RW, unit generating reward signal. Model dynamics and learning: α, γ, and ζ are parameters. Equation f1.1 describes weights dynamics, 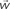 , weights vector;
, weights vector; 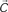 , cue units’ output vector; V, prediction unit output; δ+, δ−, output of prediction error units (positive and negative). Equations f1.2–f1.5 describe model dynamics: the symbol x ’ indicates first derivative, while [x]+ indicates the rectification max(0, x); RW, reward signal; TSN, temporally shifting neuron output. (B) Simulation 1: ACC neurophysiology. Model behavior during Pavlovian conditioning of two different stimuli, one rewarded 87% (left column) and the other 33% (right column). All plots are stimulus onset-locked, time scale in ms, signal amplitudes are in arbitrary units. Red plots: activity during the first trials of training; blue plots: activity recorded after several tens of trials (see Methods). After some tens of trials (blue plots), the response of the V unit (first row) to stimuli became proportional to the reward rate. Prediction error units (second and third row) showed, during reward periods (indicated by black bars on the top), responses proportional to the discrepancy between the expectation (V unit activity) and the actual outcome (RW signal). (C) Left: behavior of the TSN unit during three different training periods (early, middle, and late training). It exhibits temporal shifting of its response from the reward period to the cue period. Right: activity of the TSN unit during unrewarded trials, exhibiting a depression of its baseline activity (arrow) at the time when reward is expected.
, cue units’ output vector; V, prediction unit output; δ+, δ−, output of prediction error units (positive and negative). Equations f1.2–f1.5 describe model dynamics: the symbol x ’ indicates first derivative, while [x]+ indicates the rectification max(0, x); RW, reward signal; TSN, temporally shifting neuron output. (B) Simulation 1: ACC neurophysiology. Model behavior during Pavlovian conditioning of two different stimuli, one rewarded 87% (left column) and the other 33% (right column). All plots are stimulus onset-locked, time scale in ms, signal amplitudes are in arbitrary units. Red plots: activity during the first trials of training; blue plots: activity recorded after several tens of trials (see Methods). After some tens of trials (blue plots), the response of the V unit (first row) to stimuli became proportional to the reward rate. Prediction error units (second and third row) showed, during reward periods (indicated by black bars on the top), responses proportional to the discrepancy between the expectation (V unit activity) and the actual outcome (RW signal). (C) Left: behavior of the TSN unit during three different training periods (early, middle, and late training). It exhibits temporal shifting of its response from the reward period to the cue period. Right: activity of the TSN unit during unrewarded trials, exhibiting a depression of its baseline activity (arrow) at the time when reward is expected.
The aim of such a device is to act as a Critic, that is, to map the values of the cues represented by the C units. To achieve this goal, the weights vector w (which represents the map of cue values) between the C units and the V unit is updated with Hebbian learning modulated by the activity of the prediction error units (δ+, δ−). The exact learning rule for the weights vector is shown in Eq. f1.1, which is an instantiation of the general description of value updating provided in Eq. 4. The convergence of the learning algorithm is analytically proven in the Section “Appendix.” Here we just note that the learning process converges asymptotically to generate V signals that are unbiased approximations of the reward value linked to each cue. Convergence does not depend on specific values of the learning rate parameter, which basically is a discount factor: the greater it is, the stronger is the contribution of recent trials with respect to past trials.
The dynamics for δunits is described in Eq f1.3 and f1.4, which are instantiations of the general descriptions provided by Eqs 2 and 3. The differential equations describing the V and δ units’ dynamics (f1.2, f1.3, f1.4, Figure 1A) express exponential processes in which γ represents the time constant. They converge to values equal to the input of the neural unit. The ACC module also receives a bell-shaped timing signal peaking on the average delay value (Ivry, 1996; Mauk and Buonomano, 2004; O’Reilly et al., 2007; Bueti et al., 2010). See Section “Appendix” for details on the timing signal. Of course, this timing signal has to be learned as well (e.g., by spectral timing; Brown et al., 1999) but this aspect is beyond the scope of the current paper.
Finally, the output of the ACC module was combined to simulate the activity of dopaminergic neurons in VTA that exhibit a TD-like signature (here called temporally shifting neurons, TSN; Eq. f1.5, Figure 1A). Experimental findings showed that these neurons are at first phasically activated by primary rewards; then, after training, they shift their activation toward reward-predictive stimuli and show a depression of their baseline activity if the reward is not given (Schultz, 1998). Although this unit has no functional role in the current model, we addressed these data also, as a test on the broadness of our approach, and because it could provide interesting theoretical insight about the role of the ACC in higher-order learning.
The ACC contains other types of neural populations besides the ones we modeled. For example, Quilodran et al. (2008) found neural units whose activity resembled the temporal shifting of dopaminergic responses found in the VTA. Matsumoto et al. (2007) found neural units encoding for the absolute value of the prediction error. However, for theoretical parsimony we decided to include in our model only those units that are necessary for a neural implementation of RL. Future work should investigate the functionality of these other classes of neurons.
Simulations
In all simulations, the network was exposed to temporal sequences in which each cue (C unit activity) was followed by a reward (RW unit activity) with some probability and after a delay. In the EEG and fMRI simulations, this delay was a proxy for the response time (RT), as modeling the motor response is beyond the scope of the current paper. Accordingly, the RVPM lacks an explicit encoding of behavioral errors, but it can detect the presence or absence of rewards via the RW signal. We propose that ACC activity is typically influenced by errors because errors often lead to missed reward. More generally, any event preventing an expected reward would be able to evoke the ACC response. This has been experimentally proven in monkeys, where negative prediction error units responded also at the signal indicating the end of the experimental block (and thus, the end of the possibility of receiving rewards; Amiez et al., 2005). Further, both errors that are auto-detected by the subject (internal feedback) or informed by external feedback, activate the same region in ACC (Holroyd et al., 2004). Symmetrically, correct trials evoke the reward signal and thus activate the ACC.
The learning rate parameter α (Eq. f1.1) for updating the cue-value weights was set to make the activation of the V unit in response to C1 and C2 asymptotically stable within the presentation of 60 trials (30 for each cue). Its value was α = 0.005. The parameter γ (Eqs f1.2–5) is a time constant that controls how quickly the neural units (modeled as dynamical systems) respond to external inputs; its value was γ = 0.1. The parameter ζ (Eqs f1.2–5) regulates the ratio between the power (amplitude) of V relative to δ units; its value was ζ = 2. The setting for this parameter leads to a greater power of δ than V responses, simulating, at the neurophysiological level, a greater number of δ units than V units, in accordance with population statistics found in macaque ACC (Quilodran et al., 2008). The time resolution of the system was 10 ms, meaning that we arbitrarily assigned the value of 10 ms to each cycle of the program updating the network state. Although Eq f1.2–f1.4 are deterministic, at each cycle a small amount of noise (white noise with SD = 0.5) was added to their dynamics, which made the learning process smoother and less dependent on local fluctuations of reward rates. Parameters were set to simulate the neurophysiological data (Simulation 1); we did not change them for any of the later (EEG and fMRI) simulations. The model was robust in the sense that changing the parameter settings led to qualitatively similar results.
Simulation 1: ACC Neurophysiology
We first demonstrate that the model is indeed consistent with the neurophysiology of the ACC.
Methods
We presented to the model 72 trials resembling a Pavlovian conditioning setup. In each trial one of the two cue units (C1 or C2) was activated with 50% probability, generating a square wave of unit amplitude and duration equal to 2000 ms. 1600-ms after cue onset, the RW unit generated a reward signal (RW) with probability 0.87 for C1 and 0.33 for C2. RW consisted of a square wave with amplitude equal to 4 and duration equal to 400 ms (black line in Figure 1B). Initially the weights vector w was randomly set with small values (close to 0.01). We repeated the simulation 20 times (runs). The results we present are the grand average of the first five trials (i.e., early in training) and the last five trials (i.e., late in training) of all the 20 runs.
Results and Discussion
The first row of Figure 1B shows the V unit response on rewarded trials for the two cues (C1, 0.87 reward probability, left column; and C2, 0.33 reward probability, right column). Early and late unit responses are plotted separately. Late in training, the activity of the V unit (first row) codes the reward value linked to each cue. More exactly, the ratio between the asymptotic V values in response to each cue is an unbiased approximation of the ratio between their respective reward rates (see Appendix). In the current simulations, we manipulated the value of the cues by changing their reward probabilities. Cue values can alternatively be manipulated by assigning to each cue different reward magnitudes, or by manipulating both reward probabilities and reward magnitudes. Our V unit, like the biological neurons found in monkey ACC (Amiez et al., 2006), is able to encode cue values combining both reward probabilities and reward magnitudes (Appendix).
In the second and the third row of Figure 1B we plotted the responses of δ+ and δ− units, respectively. For δ+, reward trials are plotted; for δ−, missed reward trials. After training, these units showed activity levels coding the discrepancy between the expectations (V) and the outcomes (RW signal; Matsumoto et al., 2007).
Finally, in Figure 1C, we simulated the TSN population found in VTA. Like its biological counterpart (Schultz et al., 1997; Stuber et al., 2008), the TSN activation did not gradually move in time from reward to cue presentation. Instead, it presented at first a phasic response to primary reward release; during training, it started to respond to both cues and rewards, and finally it responded mainly to reward-predictive cues. At the same time, during unrewarded trials, the TSN showed a dip of its baseline activity at the time when reward would have occurred. For clarity, only Late trials are plotted in the right part of Figure 1C; a full plot is provided in Figure A3 in Appendix. We obtained such response dynamics because TSN activity was determined by the convergence of the signals from the δ units (which were reward-locked and decreased when trial number increased) and the signal from the V unit (which was cue-locked and increased with increasing trial number).
Simulation 2: Errors and Error-Related Negativity
The ERN is an EEG wave measured at midfrontal electrodes which is typically larger for error than for correct trials (Falkenstein et al., 1991; Gehring et al., 1993). For correct trials, it is referred to as CRN; CRN and ERN originate from the same neural generator (Roger et al., 2010). Because the ERN is located by dipole modeling in the ACC (Falkenstein et al., 1991; Gehring et al., 1993; Posner and Dehaene, 1994), one influential perspective on ACC holds that its function is error monitoring. Here, we evaluate the predictions of the RVPM on ACC involvement in error processing.
Methods
As noted before, an error is coded in our model as a “missed reward” feedback signal from outside ACC. Such a signal can arrive either from other parts of cortex (internal error feedback) or from an explicit error signal (external error feedback). In the latter case, it is called feedback-related negativity (FRN). It follows from the model formulation that these should be processed similarly; and indeed, FRN and ERN exhibit the same type of modulation by event frequencies (Oliveira et al., 2007; Nunez Castellar et al., 2010).
All design specifications (trial structure, duration, number of trials, etc) were as in Simulation 1. The plots represent the grand average of the whole ACC module activity (sum of the three units) during the reward periods.
Results and Discussion
When most trials are correct, the model indeed predicts a larger ACC response to error than to correct trials (Figure 2 left plot). This is because errors are less frequent, and hence, when an error occurs, there is a strong response of the δ− unit detecting a discrepancy between expectation (correct) and outcome (error). In general, this finding accounts for the fact that the size of the ERN depends on the probability of accuracy (Holroyd and Coles, 2002; Nunez Castellar et al., 2010). The ERN even reverses when errors are more expected than correct trials (Oliveira et al., 2007). Also this phenomenon is captured by the RVPM: when errors become more frequent than correct trials, the model predicts a reverse ERN (Figure 2 right plot).
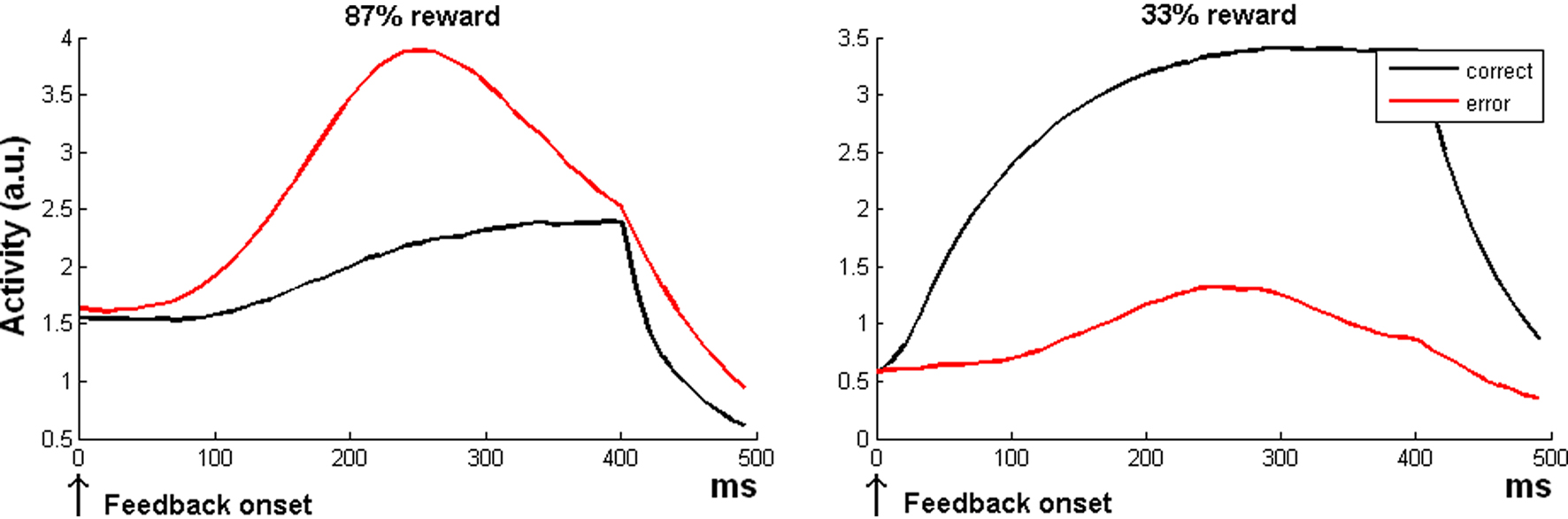
Figure 2. Simulation 2: error processing. Model global activity (sum of all the three units of the model) during the reward period. All the plots are feedback onset-locked, time scale in milliseconds. As noted in the text, feedback can be either internally generated (ERN, feedback onset close to response) or external (FRN). The two plots show the crossover of response amplitude for correct or incorrect trials as a function of the reward expectation (87 or 33%), resembling the ERN wave behavior in humans.
Simulation 3: Conflict Monitoring
Another influential perspective on ACC functioning is that it reflects the amount of response conflict (Botvinick et al., 2001; Van Veen et al., 2001). In particular, stimuli affording two or more different responses (incongruent stimuli) typically lead to higher ACC activation than stimuli that afford only one (congruent stimuli; Van Veen et al., 2001; Van Veen and Carter, 2005). For example, in a Stroop task, stimuli with color words in a different ink color than the word meaning (e.g., RED in green ink) are incongruent, while stimuli in which there is no conflict between color and word are congruent (e.g., RED in red ink). Botvinick et al. (2001) have proposed that ACC measures the simultaneous activation of different response alternatives (quantified as response conflict). As a consequence, ACC would respond more strongly to incongruent than to congruent stimuli. Instead, the current model proposes that ACC generally responds when cues (stimuli, actions) lead to an outcome that is different (e.g., worse) than expected. In this way, the estimated value of such cues can be updated using the prediction error. According to the RVPM, a reward following an incongruent stimulus is unexpected for two reasons. First, accuracy is typically lower for incongruent stimuli, so a correct response is less expected (and the effect is typically calculated on correct responses only). The second reason derives from the fact that RVPM estimates that the reward or feedback will arrive around the average RT (implemented by a timing signal, see Appendix). When this average RT is reached and a response not yet given, the δ− unit signals an unexpected event. In addition, this δ− activity decreases the value (V unit) of incongruent trials in the long run, leading to increased δ+ activity when an incongruent trial is correctly solved. Hence, because accuracies are lower and RTs slower in incongruent trials, they lead to more ACC activation. A detailed exposition of this argument is provided in Figure A1 (Appendix).
Methods
First, we mimic the RT and accuracy rates of the fMRI study of Van Veen and Carter (2005). The general sequence of events occurring within each trial was as in Simulations 1 and 2, except that two different feedback onset (i.e., RT) distributions were introduced for incongruent and congruent trials: the mean RT was 720 ms for incongruent and 600 ms for congruent trials (SD = 100 ms). The mean accuracy rate was 92% for congruent and 85% for incongruent trials. As before, we repeated the simulation 20 times (runs). The results reported in the plots (Figure 3) are the grand average of the whole ACC module (sum of the three units) during the feedback periods in the last 15 congruent and the last 15 incongruent trials. Statistics were performed as follows. We computed the mean signal power from the whole ACC during the feedback periods of the last 15 congruent and the last 15 incongruent trials, for each run separately (20 runs, mean over congruent versus incongruent trials separately). Treating the 20 runs as “subjects” in a repeated-measures design, we performed paired t-tests comparing ACC signal power in incongruent versus congruent trials for both correct and error trials.
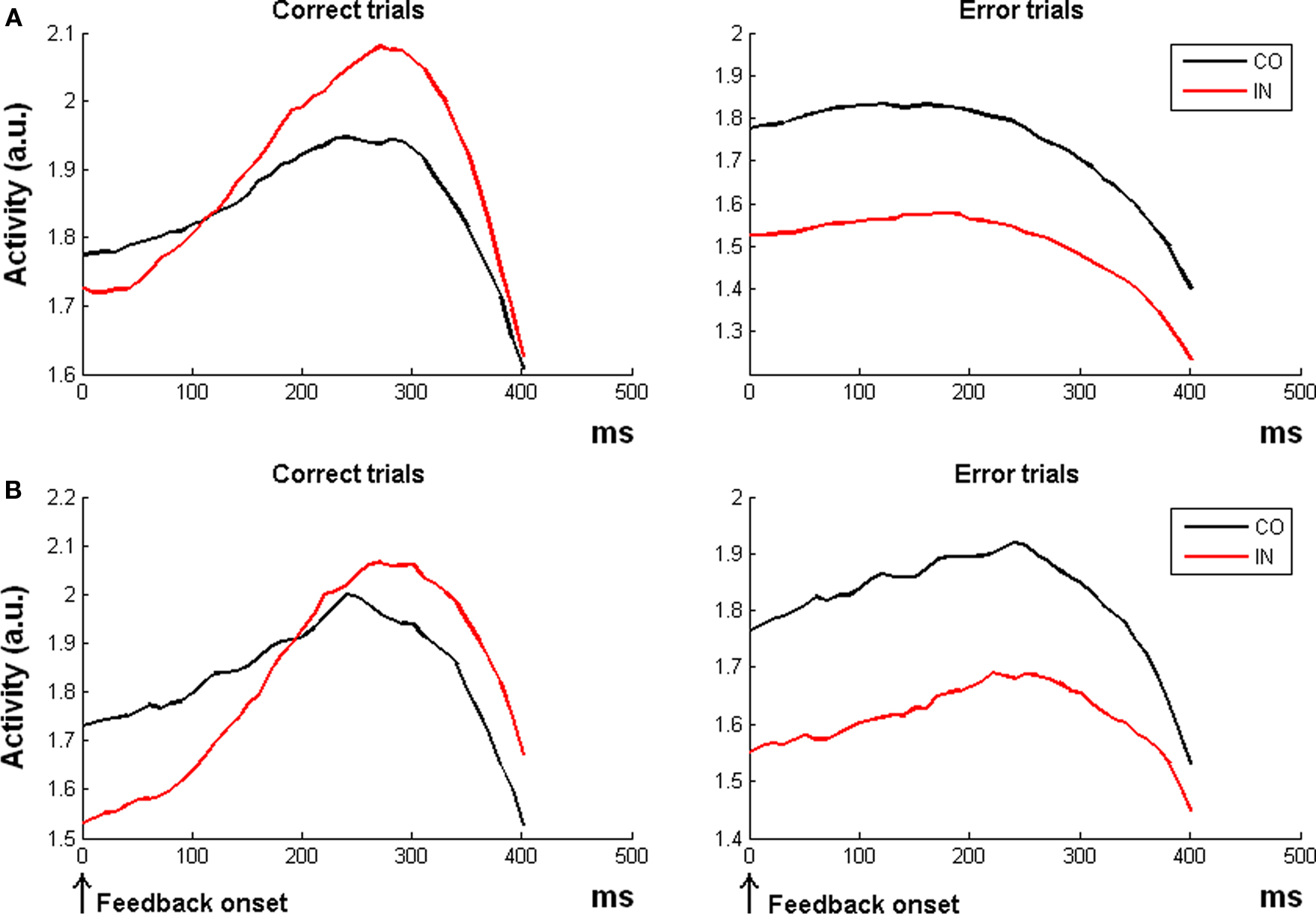
Figure 3. Simulation 3: conflict monitoring. Response amplitude for congruent (CO) and incongruent trials (IN) in two experimental paradigms. All the plots are feedback onset-locked, time scale in ms. (A) Simulation with RTs and error rates as in the fMRI study of Van Veen and Carter (2005). The ACC module of the RVPM showed a higher activation for incongruent than congruent correct trials (incongruent > congruent, left plot), but a crossover of response (congruent > incongruent) for error trials (right plot). (B) Simulation with RTs and error rates resembling the ERP study of Scheffers and Coles (2000). Coherently with the ERP findings, the model did not show a difference between the congruent and incongruent condition in correct trials (left), but it showed a higher activity for congruent than incongruent error trials.
For the second simulation, we based RT distributions and accuracy rates on those reported in the EEG study of Scheffers and Coles (2000). Congruent trials had a mean accuracy of 90% and a mean RT equal to 500 ms (SD = 100 ms). For incongruent trials, these values were 86% and 540 ms (SD = 100 ms).
Results and Discussion
For the first simulation (Van Veen and Carter, 2005), the model reproduced the fMRI results, showing a higher activation for incongruent than congruent correct trials [t(19) = 2.74, p = 0.013; Figure 3A, left plot]. Results on error trials were not reported in (Van Veen and Carter, 2005) but for completeness we here report that the model predicts a higher ACC activation for congruent error trials than incongruent error trials [t(19) = 7.14, p < 0.0001; Figure 3A, right plot].
For the second simulation, in line with empirical observations (Scheffers and Coles, 2000), the model did not predict a “conflict-like ERN effect” for correct trials [t(19) = −1.05, p = 0.30; Figure 3B, left plot]. Finally, concerning the error trials, the model was able to reproduce a reverse conflict effect with larger ERN for congruent than for incongruent trials [t(19) = 8.22, p < 0.0001; Figure 3B, right plot], again in line with empirical data (Scheffers and Coles, 2000).
According to the model, incongruent stimuli lead to more ACC activation than congruent stimuli (on correct trials) because they tend to lead to higher error rates and also to longer RTs. We already discussed (Simulation 2) that ERN is sensitive to error probability. It also follows that the model predicts ERN to be sensitive to late responding, and this is indeed empirically observed (Luu et al., 2000).
A crucial difference, according to the model, between Van Veen et al.’s and Scheffers and Coles’ experiment is that in the latter the RT difference between incongruent and congruent stimuli was too subtle. As explained above (and in more detail in Figure A1 in Appendix), if the RT distributions overlap too strongly for congruent and incongruent stimuli, the delta units exhibit less differential activity and the predicted difference also decreases. A literature search reveals that Scheffers and Coles’ (2002) RT difference is indeed smaller than in other studies (Botvinick et al., 1999; Van Veen et al., 2001; Milham et al., 2002; Kerns et al., 2004; Van Veen and Carter, 2005). The only exception we could find was Kerns (2006) who had a smaller RT difference than Scheffers and Coles but did observe ACC activation. However, this author did not report the error rates, which (in case of higher error rates for incongruent trials) could have had a crucial role in driving the ACC activation. Finally, a recent fMRI study (Carp et al., 2010) reports that the incongruency effect in MFC disappears when controlling for RTs between incongruent versus congruent trials.
Simulation 4: Error Likelihood
The ACC has also been proposed to estimate the likelihood of committing an error (Brown and Braver, 2005). In their Change Signal experiment, Brown and Braver (2005) presented arrows pointing in one of two directions, which could either switch direction (Change trial) or not (Go trial) during the trial some time after trial onset. The color of the arrow indicated the time at which the arrow could switch (color 1, late switch, high error probability; color 2, early switch, low error probability). It was found that ACC responded more strongly to correct high-error-likelihood trials than to correct low-error-likelihood trials. This was the case for both no-switch (i.e., Go) and switch (Change) trials. In addition, there was a main effect of Change versus Go trials. This was consistent with Brown and Braver’s error-likelihood model. In contrast, on error trials, there was a stronger ACC response to low-error-likelihood than to high-error-likelihood trials.
Methods
Like in Simulation 3, we simulated the different experimental conditions (change/go and high/low error probability) by manipulating both feedback onsets (mimicking RT distributions) and accuracy rates. The mean feedback onsets were the following: high error-likelihood change (HCh) = 750 ms, high error-likelihood go (HGo) = 650 ms, low error-likelihood change (LCh) = 730 ms, low error-likelihood go (LGo) = 600 ms, all of them normally distributed with SD = 100 ms. Accuracy rates were the following: HCh = 50%, HGo = 70%, LCh = 96%, LGo = 98%. Sixty-seven percentage of cues indicated Go trials (LGo + HGo). All these values were set to reproduce as closely as possible the behavioral data described by Brown and Braver (2005). The exact RTs are not critical in the current simulation, as model responses are driven mainly by the accuracy differences across conditions. Data plotting and statistical analysis were executed on the last five trials of each condition, and followed the same procedure of Simulation 3.
Results and Discussion
The left plot of Figure 4 shows that the RVPM was able to replicate the fMRI results of Brown and Braver’s (2005) study, predicting in correct trials a main effect of error likelihood [high-error-likelihood versus low-error-likelihood trials, F(1,77) = 38.37, p < 0.0001], and a main effect of Change versus Go [Change versus Go trials, F(1,77) = 15.86, p < 0.001]. Post hoc analysis showed (again in agreement with Brown and Braver’s results) an error-likelihood effect also in Go trials [HGo versus LGo, t(19) = 2.39, p < 0.05]. This response pattern was evident during the feedback period (i.e., when the system processed the outcomes), and was due to the δ+ unit activity, which responded to the discrepancy between the expectation (which was low for the high-error-likelihood conditions) and the outcome (achieved reward).
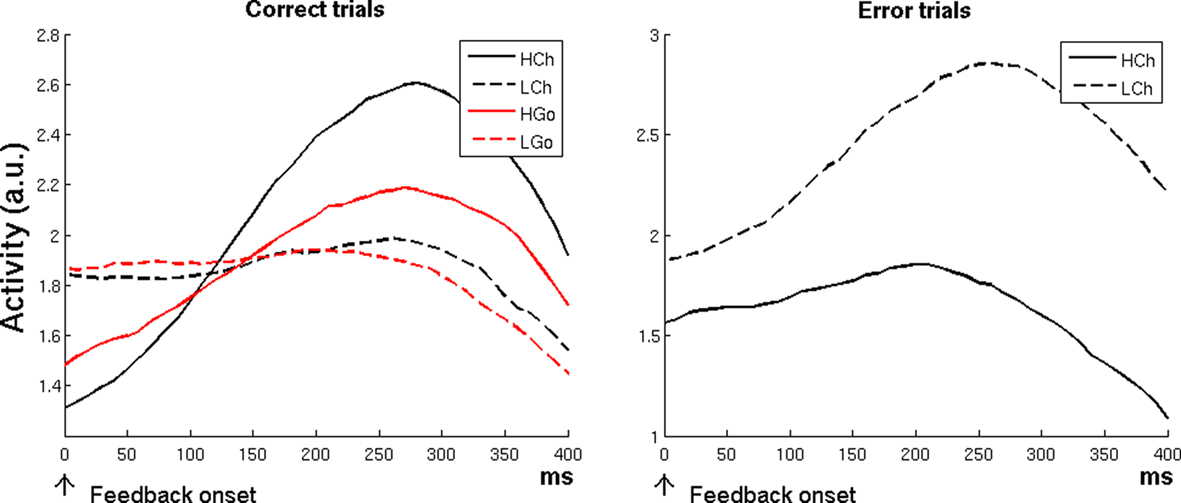
Figure 4. Simulation 4: error-likelihood estimation. Plots are feedback onset-locked, time scale in ms. HCh, high-error-likelihood incongruent trials; LCh, low-error-likelihood incongruent trials; HGo, high-error-likelihood congruent trials; LGo, low-error-likelihood congruent trials. For correct trials, the model showed a higher activity for high-error-likelihood than for low-error-likelihood trials (both Change and Go trials; left plot), but a reverse effect for error trials (right plot).
The RVPM showed, in line with the fMRI results, but differently from the Error-Likelihood model prediction, a reverse effect for error trials on high-versus-low error probability trials [Figure 4, right plot; LCh versus HCh, t(19) = 6.71, p < 0.0001]. Also in this case, the effect was evident during the feedback period, and it was due to the strong response of the δ− unit, which detected the discrepancy between the high level of expectation evoked by low-error-likelihood cues and the absence of positive feedback. In the high-error-likelihood condition, negative feedback was more expected, leading to relatively less δ− activity. In contrast, the error-likelihood model does not predict this reversal because it responds to the likelihood of errors, which does not depend on the subject’s performance on the current trial.
The RVPM predicts higher activation for low-error-likelihood conditions during the cue period (see Figure A2 in Appendix). The reason is that low-error-likelihood trials predict higher reward values (encoded by the V unit) while the δ units are not discharging yet during cue presentation. More generally, the RVPM predicts that ACC activity should vary as a function of the predicted accuracy (value) during cue periods. This has been validated both at the single-cell level (Amiez et al., 2006) and in fMRI studies on humans (Knutson et al., 2005; Kable and Glimcher, 2007; Peters and Buchel, 2010), although one fMRI study did not find any area coding for reward or error prediction (Nieuwenhuis et al., 2007). In two of the fMRI studies that evidenced the presence of reward prediction coding in ACC (Kable and Glimcher, 2007; Peters and Buchel, 2010) the local maxima corresponding to the ACC activation were more rostral than the one in Brown and Braver’s (2005)study. These activation peaks belonged to what has traditionally been defined as the affective division of ACC (Bush et al., 2000), typically involved in tasks recruiting emotional processing. Although the division between cognitive and affective zones of ACC has recently been questioned (e.g., Egner et al., 2008; Shackman et al., 2011), more generally different aspects of value are probably coded in different subregions of ACC to be used in task-specific decision making.
Simulation 5: Volatility
Recently, ACC was proposed to be involved in volatility estimation (Behrens et al., 2007). Behrens et al. (2007) argued from an optimality perspective that the learning rates of a cognitive system should vary depending on the volatility of its environment. They proposed that ACC registers this volatility and uses it to update learning rates. In an fMRI experiment, they demonstrated that volatility estimates correlate with ACC activation.
Methods
We simulated the Behrens et al. (2007) experimental task and design. We presented sequentially to the network two different environments: a stationary environment, in which two cues were rewarded with constant probabilities (75 and 25% respectively), and a volatile environment, in which the probability linking cues and rewards switched regularly between two possible values, 80 and 20%. All rewards were given 1600 ms after cue onset. In this simulation, we implemented a simplified Actor module in addition to the RVPM Critic. During each trial the model was required to choose one of the two cues according to their reward values (action selection), and then wait for the reward. We implemented a Softmax algorithm that on each trial made a choice between one of the two cues based on their value estimate (i.e., V unit activity) in the preceding trial. In particular, the probability of choosing cue i was equal to:

where p(Ci) is the probability of selecting the ith cue, Temp = 4 is the temperature parameter, and Vi is the V response to the last presentation of the ith cue. We set the temperature parameter in order to generate a small bias (55%) toward the cue evoking the higher expectation (Behrens et al., 2007). We performed 20 simulation runs. In each run, the first 72 trials were stationary (stationary epoch) and the second 72 were volatile (volatile epoch). In the volatile epoch, the reward rates were switched halfway (after 36 trials). Data plotting and statistical analysis were performed with the procedure of Simulation 3. Like in Behrens et al. (2007) we excluded from plotting and analysis the first 20 trials of each epoch (stationary and volatile), considering them as transition trials in which the system was still learning the reward contingencies. We also calculated the extent of variation (variation rate) of the connection weights between the C units and the V unit. For each weight, we computed the mean absolute value of the difference between the weight at the end versus at the beginning of a trial. The mean of these differences (over the two connections) represented the variation rate as a function of trial number. Finally, the variation rate was smoothed by a Gaussian kernel having 10 trials as full-width half-maximum.
Results and Discussion
Figure 5A shows, in agreement with fMRI data (Behrens et al., 2007) that, during the reward periods, the model exhibited a higher activation in the volatile epoch for both rewarded [left plot, t(19) = 9.15, p < 0.0001] and unrewarded [right plot, one-tailed t(19) = 1.89, p < 0.05] trials. This result was due to the higher average activation of δ units during the volatile epoch, because of the necessity of a continuous re-mapping between cues and expectations (cf. variation rate plotted in Figure 5B). Hence, what drove the model’s overall activity during the outcome period was the amount of prediction error signal.
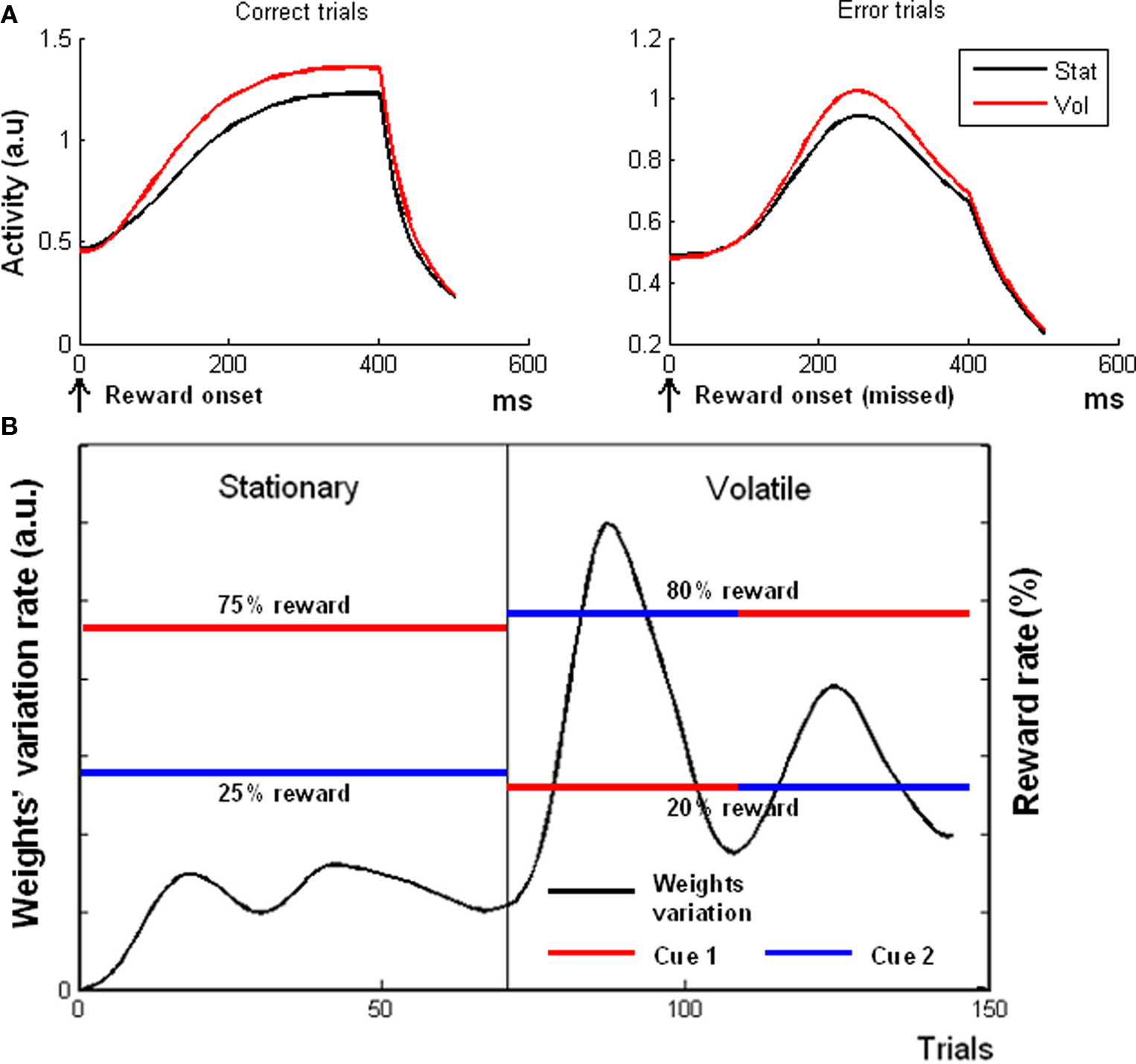
Figure 5. Simulation 5: volatility. Plots are reward onset-locked, time scale in ms (A) Model response during feedback periods in volatile and stationary environments. All the plots are feedback onset-locked, timescale in milliseconds. Stat, stationary condition; Vol, volatile condition. The model showed a higher activity in a volatile environment than in a stationary environment for both rewarded (left plot) and unrewarded (right plot) trials. (B) Variation rate of the weights (black plot) connecting the C units to the V unit, as a function of trial number. In the first epoch, the model was exposed to a Stationary environment (constant reward rates, red and blue lines indicating the reward rates of two different cues). During the second epoch, the environment became volatile (reward rate switching between red and blue), and the δ units started to re-map the associations between cues and reward rates, thus increasing the weights variation rates. The two hills in the volatile epoch correspond to the two reward rate switches.
The RVPM does not implement the dynamic adjusting of the learning parameter characterizing Behrens et al.’s model. Indeed, although the variation rate of synaptic weights was higher during the volatile condition (Figure 5B), the learning parameter α remained constant. This is because we did not provide the RVPM with the machinery to dynamically adjust learning rate as a function of the environment. We propose that such a process could emerge from the interaction between ACC and locus coeruleus (LC). The LC could receive information from ACC about environmental uncertainty (e.g., through the average activity of delta units) and set the system’s learning rate by noradrenergic signals (Yu and Dayan, 2005; Verguts and Notebaert, 2009; Tully and Bolshakov, 2010; Jepma and Nieuwenhuis, 2011). The implementation of this process is beyond the aims of this work, but it represents an interesting challenge for future developments of the RVPM.
General Discussion
Here we integrated some ACC functions from the perspective of RL theory (Sutton and Barto, 1998). We proposed that systems-level ACC data (from fMRI or EEG) are due to the activity of neural units estimating cue values, and neural units computing the errors between these predictions and the actual environmental outcomes. There is a growing interest in the literature for prediction errors in EEG and fMRI studies of ACC (Jessup et al., 2010; Nunez Castellar et al., 2010) and in behavioral cognitive control (Notebaert et al., 2009). The current paper provides a computational rationale for them and shows how they give rise to higher-level effects. For example, the RVPM shows how ACC activation ascribed to conflict and error (likelihood) can arise from prediction error computation. Error effects occur when error trials are less frequent than correct trials so that when an error occurs, a negative prediction error is detected. Similarly, incongruent trials are associated with longer RTs and/or with higher error rates than congruent trials; therefore, when positive feedback is received, the (positive) prediction error is higher for incongruent than for congruent trials. In general, the aim of the ACC is to create mappings between cues (e.g., external stimuli or actions) and values indicating their fitness for the organism (Rushworth and Behrens, 2008). Consistent with this, ACC receives input from (high-level) motor areas, which code for actions, and also from the posterior parietal cortex (Devinsky et al., 1995), which can be considered as input coding for external stimuli.
The Actor–Critic Framework
As noted before, a value computation device as described here is called a Critic in Actor–Critic models of RL (Sutton and Barto, 1998). Presumably other structures also perform part of the Critic function (e.g., orbitofrontal cortex, OFC; Schoenbaum et al., 1998; Tremblay and Schultz, 1999; O’Doherty, 2007) and insular cortex (Craig, 2010). In general, the Critic can be considered to be multidimensional with different reward and cost statistics computed by different structures. For example, whereas we have focused on value and prediction errors as estimates of mean reward (or accuracy) rates, it is conceivable that other statistics of the reward distribution besides mean reward are encoded also, such as reward variance or risk (Brown and Braver, 2007). In addition, the Critic may compute expected costs (Rudebeck et al., 2006; Kennerley et al., 2009). Further, also changes in the reward distribution across time (e.g., volatility) could be encoded in different areas of cortex. As (Behrens et al., 2007) noted, this could be useful for adapting the learning rate to the current environmental settings. These aspects represent important steps for further developments of the RVPM. As another example, Rushworth and Behrens (2008) proposed that whereas OFC computes stimulus–outcome values, ACC computes response–outcome values. Here we have ignored this distinction, arguing for simplicity that ACC represents both. Consistent with this assumption, Amiez et al. (2006) showed that monkey ACC cells can encode reward expectations linked to both stimuli and actions. Future work should investigate whether incorporating this distinction can be fruitful for capturing more subtle distinctions between ACC and OFC.
The Actor learns and takes decisions (policies) based on the evaluations computed by the Critic. In mammals, it is reasonable to identify the DLPFC, basal ganglia (dorsal striatum) and high-level motor areas as important structures of the Actor. Indeed, DLPFC, striatum, and the premotor cortex receive massive afferents from ACC (Devinsky et al., 1995), allowing a tight interaction between the two components.
Our paper is not the first to emphasize an important role for ACC in RL, and in an Actor-Critic structure in particular. For example, the influential paper of (Holroyd and Coles, 2002) proposed just this. Despite the similarities, the current work differs in many respects from that model. First, whereas Holroyd and Coles identified ACC with (part of) the Actor, we have focused on the Critic function instead. Second, consistent with available neurophysiology, we made a distinction between positive and negative prediction error cells. Further, the current model goes beyond this earlier work by explicitly showing that the RL framework is able to account not only for explicit reinforcement and error-related tasks but also for other cognitive manipulations (e.g., incongruency in conflict tasks). In line with our own model, earlier influential models such as conflict monitoring theory (Botvinick et al., 2001) and error-likelihood theory (Brown and Braver, 2005) have also ascribed an evaluative role to ACC. Like error-likelihood theory, we propose that ACC is involved with recording the statistics of the environment for the purpose of the Actor system. However, we go beyond this earlier work by explicitly addressing both the single-unit and systems-level data.
Prediction Error Beyond the ACC
Prediction error signals have been found in several brain areas not typically related to reward processing and during tasks that do not involve explicit reward administration, for example, the temporo-occipital junction (TOJ; Summerfield and Koechlin, 2008), the temporo-parietal junction (TPJ; Doricchi et al., 2009), the DLPC (Glascher et al., 2010), and intraparietal sulcus (IPS; Glascher et al., 2010). These findings suggest that prediction error could be a general mechanism for learning. Besides dopamine, other monoamines (e.g., noradrenaline), may also be involved. Reward prediction error, as found in ACC, could be just the dopamine-based variety of prediction error. It should be noted that learning by prediction error would be a neurobiologically refined version of the classic feedback-based idea of learning proposed in Cybernetics (Wiener, 1948).
In this paper we also tried to model interactions between ACC and VTA. We modeled the temporal shifting of VTA neurons from reward onset to conditional stimulus onset (TSN neurons). We proposed this shift is due to an integration of signals arriving from ACC. Recurrent connections between ACC and VTA have indeed been documented both in monkeys and in rats (Devinsky et al., 1995; Geisler et al., 2007). The TSN of our model was not functional in the current simulations. However, one reason for modeling it was to advance a computational hypothesis on a well-known experimental result (Schultz et al., 1997; Stuber et al., 2008). A second reason was to show that our model can provide a basis for TD learning, a class of algorithms from the field of RL (Montague et al., 1996). The core of this method consists of updating value estimates not only by comparing expectations and actual outcomes but also by comparing new expectations with past expectations. In other words, in order to adapt the mapping between stimuli and reward expectations, the agent does not have to wait until the actual reward. TD methods can be considered as a generalization of Rescorla-Wagner methods (Sutton and Barto, 1998), which our ACC model belongs to. As in TD learning, the TSN signal in the VTA of RVPM can be used as a proxy of the primary reward signal; in this way, stimuli which are only indirectly associated with reward, can still achieve high value estimates (i.e., higher-order conditioning) in ACC. As such, these can be used as a training signal for cortical and subcortical circuits, due to the wide efferents of the brainstem dopaminergic nuclei.
Future Work
Because of its computational nature, our theory can produce explicit experimental predictions that could be easily tested. We here discuss just a few possible future experiments. The first one is to test the prediction of a crossover of ACC activity between cue period and feedback period in correct trials. This is because the lower is the reward expectation during the cue period, the higher is the positive prediction error during the feedback period for correct trials. At the same time, for incorrect trials, we expect that cue-related and feedback-related activity (negative prediction error) covary.
A further test concerns the RVPM prediction that high ACC responsiveness in volatile environments reflects intense prediction error activity (uncertainty) rather than volatility coding. This prediction could be tested by comparing the ACC activation in a volatile environment relative to a stationary environment characterized by high levels of uncertainty (with reward rates near 50%; stationary-uncertain). Instead, Behrens et al. (2007) compared a volatile environment relative to a stationary environment with high levels of certainty (stationary-certain). Given that RVPM responds to prediction errors, it predicts higher activation in volatile than in stationary-certain conditions (as already found by Behrens et al., 2007 and replicated in Simulation 5), but it also predicts more activation for stationary-uncertain than for volatile environments. We are currently working on a test of this prediction using fMRI. Finally, future work will be also conducted on higher-order conditioning with the aim of integrating this view on ACC with higher-order learning via RL-type mechanisms. In this way, we hope to learn not only about Actor–Critic interactions, but also how this interaction is impaired in behavioral–pathological conditions in which ACC dysfunction has been reported such as ADHD (Groen et al., 2008; Herrmann et al., 2010), drug abuse (Goldstein et al., 2009), or obsessive–compulsive disorder (Breiter and Rauch, 1996).
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Massimo Silvetti and Tom Verguts were supported by Ghent University GOA grant BOF08/GOA/011. We acknowledge the support of Ghent University Multidisciplinary Research Platform “The integrative neuroscience of behavioral control.” Ruth Seurinck is a postdoctoral research fellow of the Fund for Scientific Research (Flanders Belgium). The authors thank Wim Fias and Wim Notebaert for useful comments on this work.
References
Amiez, C., Joseph, J. P., and Procyk, E. (2005). Anterior cingulate error-related activity is modulated by predicted reward. Eur. J. Neurosci. 21, 3447–3452.
Amiez, C., Joseph, J. P., and Procyk, E. (2006). Reward encoding in the monkey anterior cingulate cortex. Cereb. Cortex 16, 1040–1055.
Behrens, T. E., Woolrich, M. W., Walton, M. E., and Rushworth, M. F. (2007). Learning the value of information in an uncertain world. Nat. Neurosci. 10, 1214–1221.
Botvinick, M., Braver, T. S., Barch, D. M., Carter, C. S., and Cohen, J. D. (2001). Conflict monitoring and cognitive control. Psychol. Rev. 108, 624–652.
Botvinick, M., Nystrom, L. E., Fissell, K., Carter, C. S., and Cohen, J. D. (1999). Conflict monitoring versus selection-for-action in anterior cingulate cortex. Nature 402, 179–181.
Botvinick, M. M. (2007). Conflict monitoring and decision making: reconciling two perspectives on anterior cingulate function. Cogn. Affect. Behav. Neurosci. 7, 356–366.
Breiter, H. C., and Rauch, S. L. (1996). Functional MRI and the study of OCD: from symptom provocation to cognitive-behavioral probes of cortico-striatal systems and the amygdala. Neuroimage 4, S127–S138.
Brown, J., Bullock, D., and Grossberg, S. (1999). How the basal ganglia use parallel excitatory and inhibitory learning pathways to selectively respond to unexpected rewarding cues. J. Neurosci. 19, 10502–10511.
Brown, J. W., and Braver, T. S. (2005). Learned predictions of error likelihood in the anterior cingulate cortex. Science 307, 1118–1121.
Brown, J. W., and Braver, T. S. (2007). Risk prediction and aversion by anterior cingulate cortex. Cogn. Affect. Behav. Neurosci. 7, 266–277.
Bueti, D., Bahrami, B., Walsh, V., and Rees, G. (2010). Encoding of temporal probabilities in the human brain. J. Neurosci. 30, 4343–4352.
Bush, G., Luu, P., and Posner, M. I. (2000). Cognitive and emotional influences in anterior cingulate cortex. Trends Cogn. Sci. (Regul. Ed.) 4, 215–222.
Carp, J., Kim, K., Taylor, S. F., Fitzgerald, K. D., and Weissman, D. H. (2010). Conditional differences in mean reaction time explain effects of response congruency, but not accuracy, on posterior medial frontal cortex activity. Front. Hum. Neurosci. 4:231. doi: 10.3389/fnhum.2010.00231
Cole, M. W., Yeung, N., Freiwald, W. A., and Botvinick, M. (2009). Cingulate cortex: diverging data from humans and monkeys. Trends Neurosci. 32, 566–574.
Critchley, H. D., Tang, J., Glaser, D., Butterworth, B., and Dolan, R. J. (2005). Anterior cingulate activity during error and autonomic response. Neuroimage 27, 885–895.
Daw, N. D., Kakade, S., and Dayan, P. (2002). Opponent interactions between serotonin and dopamine. Neural Netw. 15, 603–616.
Devinsky, O., Morrell, M. J., and Vogt, B. A. (1995). Contributions of anterior cingulate cortex to behavior. Brain 118(Pt 1), 279–306.
Doricchi, F., ] Macci, E., Silvetti, M., and Macaluso, E. (2009). Neural correlates of the spatial and expectancy components of endogenous and stimulus-driven orienting of attention in the posner task. Cereb. Cortex. 20, 1574–1585.
Dum, R. P., and Strick, P. L. (2002). Motor areas in the frontal lobe of the primate. Physiol. Behav. 77, 677–682.
Falkenstein, M., Hohnsbein, J., Hoormann, J., and Blanke, L. (1991). Effects of crossmodal divided attention on late ERP components. II. Error processing in choice reaction tasks. Electroencephalogr. Clin. Neurophysiol. 78, 447–455.
Gehring, W. J., Goss, B., Coles, M. G. H., Meyer, D. E., and Donchin, E. (1993). A neural system for error detection and compensation. Psychol. Sci. 4, 385–390.
Geisler, S., Derst, C., Veh, R. W., and Zahm, D. S. (2007). Glutamatergic afferents of the ventral tegmental area in the rat. J. Neurosci. 27, 5730–5743.
Ghose, G. M., and Maunsell, J. H. (2002). Attentional modulation in visual cortex depends on task timing. Nature 419, 616–620.
Glascher, J., Daw, N., Dayan, P., and O’doherty, J. P. (2010). States versus rewards: dissociable neural prediction error signals underlying model-based and model-free reinforcement learning. Neuron 66, 585–595.
Goldstein, R. Z., Alia-Klein, N., Tomasi, D., Carrillo, J. H., Maloney, T., Woicik, P. A., Wang, R., Telang, F., and Volkow, N. D. (2009). Anterior cingulate cortex hypoactivations to an emotionally salient task in cocaine addiction. Proc. Natl. Acad. Sci. U.S.A. 106, 9453–9458.
Groen, Y., Wijers, A. A., Mulder, L. J., Waggeveld, B., Minderaa, R. B., and Althaus, M. (2008). Error and feedback processing in children with ADHD and children with Autistic Spectrum Disorder: an EEG event-related potential study. Clin. Neurophysiol. 119, 2476–2493.
Harrington, D. L., Haaland, K. Y., and Hermanowicz, N. (1998). Temporal processing in the basal ganglia. Neuropsychology 12, 3–12.
Herrmann, M. J., Mader, K., Schreppel, T., Jacob, C., Heine, M., Boreatti-Hummer, A., Ehlis, A. C., Scheuerpflug, P., Pauli, P., and Fallgatter, A. J. (2010). Neural correlates of performance monitoring in adult patients with attention deficit hyperactivity disorder (ADHD). World J. Biol. Psychiatry 11, 457–464.
Holroyd, C. B., and Coles, M. G. (2002). The neural basis of human error processing: reinforcement learning, dopamine, and the error-related negativity. Psychol. Rev. 109, 679–709.
Holroyd, C. B., Nieuwenhuis, S., Yeung, N., Nystrom, L., Mars, R. B., Coles, M. G., and Cohen, J. D. (2004). Dorsal anterior cingulate cortex shows fMRI response to internal and external error signals. Nat. Neurosci. 7, 497–498.
Ivry, R. B. (1996). The representation of temporal information in perception and motor control. Curr. Opin. Neurobiol. 6, 851–857.
Jepma, M., and Nieuwenhuis, S. (2011). Pupil diameter predicts changes in the exploration-exploitation tradeoff: evidence for the adaptive gain theory. J. Cogn. Neurosci. 23, 1587–1596.
Jessup, R. K., Busemeyer, J. R., and Brown, J. W. (2010). Error effects in anterior cingulate cortex reverse when error likelihood is high. J. Neurosci. 30, 3467–3472.
Kable, J. W., and Glimcher, P. W. (2007). The neural correlates of subjective value during intertemporal choice. Nat. Neurosci. 10, 1625–1633.
Kennerley, S. W., Dahmubed, A. F., Lara, A. H., and Wallis, J. D. (2009). Neurons in the frontal lobe encode the value of multiple decision variables. J. Cogn. Neurosci. 21, 1162–1178.
Kerns, J. G. (2006). Anterior cingulate and prefrontal cortex activity in an FMRI study of trial-to-trial adjustments on the Simon task. Neuroimage 33, 399–405.
Kerns, J. G., Cohen, J. D., Macdonald, A. W. III, Cho, R. Y., Stenger, V. A., and Carter, C. S. (2004). Anterior cingulate conflict monitoring and adjustments in control. Science 303, 1023–1026.
Knutson, B., Taylor, J., Kaufman, M., Peterson, R., and Glover, G. (2005). Distributed neural representation of expected value. J. Neurosci. 25, 4806–4812.
Leon, M. I., and Shadlen, M. N. (2003). Representation of time by neurons in the posterior parietal cortex of the macaque. Neuron 38, 317–327.
Ljungberg, T., Apicella, P., and Schultz, W. (1992). Responses of monkey dopamine neurons during learning of behavioral reactions. J. Neurophysiol. 67, 145–163.
Luu, P., Flaisch, T., and Tucker, D. M. (2000). Medial frontal cortex in action monitoring. J. Neurosci. 20, 464–469.
Matsumoto, K., Suzuki, W., and Tanaka, K. (2003). Neuronal correlates of goal-based motor selection in the prefrontal cortex. Science 301, 229–232.
Matsumoto, M., Matsumoto, K., Abe, H., and Tanaka, K. (2007). Medial prefrontal cell activity signaling prediction errors of action values. Nat. Neurosci. 10, 647–656.
Mauk, M. D., and Buonomano, D. V. (2004). The neural basis of temporal processing. Annu. Rev. Neurosci. 27, 307–340.
Milham, M. P., Erickson, K. I., Banich, M. T., Kramer, A. F., Webb, A., Wszalek, T., and Cohen, N. J. (2002). Attentional control in the aging brain: insights from an fMRI study of the stroop task. Brain Cogn. 49, 277–296.
Montague, P. R., Dayan, P., and Sejnowski, T. J. (1996). A framework for mesencephalic dopamine systems based on predictive Hebbian learning. J. Neurosci. 16, 1936–1947.
Nieuwenhuis, S., Schweizer, T. S., Mars, R. B., Botvinick, M. M., and Hajcak, G. (2007). Error-likelihood prediction in the medial frontal cortex: a critical evaluation. Cereb. Cortex 17, 1570–1581.
Notebaert, W., Houtman, F., Opstal, F. V., Gevers, W., Fias, W., and Verguts, T. (2009). Post-error slowing: an orienting account. Cognition 111, 275–279.
Nunez Castellar, E., Kuhn, S., Fias, W., and Notebaert, W. (2010). Outcome expectancy and not accuracy determines posterror slowing: ERP support. Cogn. Affect. Behav. Neurosci. 10, 270–278.
O’Doherty, J. P. (2007). Lights, camembert, action! The role of human orbitofrontal cortex in encoding stimuli, rewards, and choices. Ann. N. Y. Acad. Sci. 1121, 254–272.
Oliveira, F. T., Mcdonald, J. J., and Goodman, D. (2007). Performance monitoring in the anterior cingulate is not all error related: expectancy deviation and the representation of action-outcome associations. J. Cogn. Neurosci. 19, 1994–2004.
O’Reilly, R. C., Frank, M. J., Hazy, T. E., and Watz, B. (2007). PVLV: the primary value and learned value Pavlovian learning algorithm. Behav. Neurosci. 121, 31–49.
Peters, J., and Buchel, C. (2010). Episodic future thinking reduces reward delay discounting through an enhancement of prefrontal-mediotemporal interactions. Neuron 66, 138–148.
Quilodran, R., Rothe, M., and Procyk, E. (2008). Behavioral shifts and action valuation in the anterior cingulate cortex. Neuron 57, 314–325.
Roger, C., Benar, C. G., Vidal, F., Hasbroucq, T., and Burle, B. (2010). Rostral Cingulate Zone and correct response monitoring: ICA and source localization evidences for the unicity of correct- and error-negativities. Neuroimage 51, 391–403.
Rudebeck, P. H., Walton, M. E., Smyth, A. N., Bannerman, D. M., and Rushworth, M. F. (2006). Separate neural pathways process different decision costs. Nat. Neurosci. 9, 1161–1168.
Rushworth, M. F., and Behrens, T. E. (2008). Choice, uncertainty and value in prefrontal and cingulate cortex. Nat. Neurosci. 11, 389–397.
Scheffers, M. K., and Coles, M. G. (2000). Performance monitoring in a confusing world: error-related brain activity, judgments of response accuracy, and types of errors. J. Exp. Psychol. Hum. Percept. Perform. 26, 141–151.
Schoenbaum, G., Chiba, A. A., and Gallagher, M. (1998). Orbitofrontal cortex and basolateral amygdala encode expected outcomes during learning. Nat. Neurosci. 1, 155–159.
Schultz, W., Dayan, P., and Montague, P. R. (1997). A neural substrate of prediction and reward. Science 275, 1593–1599.
Stuber, G. D., Klanker, M., De Ridder, B., Bowers, M. S., Joosten, R. N., Feenstra, M. G., and Bonci, A. (2008). Reward-predictive cues enhance excitatory synaptic strength onto midbrain dopamine neurons. Science 321, 1690–1692.
Summerfield, C., and Koechlin, E. (2008). A neural representation of prior information during perceptual inference. Neuron 59, 336–347.
Sutton, R. S., and Barto, A. G. (1998). Reinforcement Learning: An Introduction. Cambridge, MA: MIT Press.
Tremblay, L., and Schultz, W. (1999). Relative reward preference in primate orbitofrontal cortex. Nature 398, 704–708.
Tully, K., and Bolshakov, V. Y. (2010). Emotional enhancement of memory: how norepinephrine enables synaptic plasticity. Mol. Brain 3, 15.
Van Veen, V., and Carter, C. S. (2005). Separating semantic conflict and response conflict in the Stroop task: a functional MRI study. Neuroimage 27, 497–504.
Van Veen, V., Cohen, J. D., Botvinick, M. M., Stenger, V. A., and Carter, C. S. (2001). Anterior cingulate cortex, conflict monitoring, and levels of processing. Neuroimage 14, 1302–1308.
Verguts, T., and Notebaert, W. (2009). Adaptation by binding: a learning account of cognitive control. Trends Cogn. Sci. (Regul. Ed.) 13, 252–257.
Wiener, N. (1948). Cybernetics or Control and Communication in the Animal and the Machine. Paris: Hermann & Cie Editeurs.
Keywords: ACC, dopamine, reward, reinforcement learning, conflict monitoring, volatility, error likelihood
Citation: Silvetti M Seurinck R and Verguts T (2011) Value and prediction error in medial frontal cortex: integrating the single-unit and systems levels of analysis. Front. Hum. Neurosci. 5:75. doi: 10.3389/fnhum.2011.00075
Received: 15 April 2011;
Accepted: 19 July 2011;
Published online: 03 August 2011.
Edited by:
Srikantan S. Nagarajan, University of California San Francisco, USAReviewed by:
Geoffrey Schoenbaum, University of Maryland School of Medicine, USASrikantan S. Nagarajan, University of California San Francisco, USA
Copyright: © 2011 Silvetti, Seurinck and Verguts. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence: Massimo Silvetti, Department of Experimental Psychology, Ghent University, Henri Dunantlaan 2, 9000 Ghent, Belgium; Ghent Institute for Functional and Metabolic Imaging, Ghent University Hospital, De Pintelaan 185B, 9000 Ghent, Belgium. e-mail:bWFzc2ltby5zaWx2ZXR0aUB1Z2VudC5iZQ==


