- 1 Department of Psychology, Vanderbilt Vision Research Center, Center for Cognitive and Integrative Cognitive Neuroscience, Vanderbilt University, Nashville, TN, USA
- 2 Department of Brain and Cognitive Sciences, Seoul National University, Seoul, Republic of Korea
Fluctuations in perceptual dominance during binocular rivalry exhibit several hallmark characteristics. First, dominance switches are not periodic but, instead, stochastic: perception changes unpredictably. Second, despite being stochastic, average durations of rivalry dominance vary dependent on the strength of the rival stimuli: variations in contrast, luminance, or spatial frequency produce predictable changes in average dominance durations and, hence, in alternation rate. Third, perceptual switches originate locally and spread globally over time, sometimes as traveling waves of dominance: rivalry transitions are spatiotemporal events. This essay (1) reviews recent advances in our understanding of the bases of these three hallmark characteristics of binocular rivalry dynamics and (2) provides an integrated framework to account for those dynamics using cooperative and competitive spatial interactions among local neural circuits distributed over the visual field’s retinotopic map. We close with speculations about how that framework might incorporate top-down influences on rivalry dynamics.
The brain is often portrayed as a complex, dynamical system (e.g., Friston and Price, 2001), and the phenomenon of binocular rivalry – the topic of this special Frontiers issue – certainly fits with that portrayal. Faced with conflicting monocular inputs, the visual system lapses into a state of instability in which those conflicting inputs compete for perceptual dominance. While one input dominates, the other is suppressed from awareness, a characteristic that makes rivalry attractive to those interested in the neural correlates of consciousness (e.g., Rees et al., 2002). But equally fascinating, perceptual dominance fails to settle into a single, stable state and, instead, fluctuates unpredictably over time. Because of this aspect of rivalry, the phenomenon represents a potentially revealing window onto neural events underlying brain dynamics (Kim and Blake, 2005). For the last several years we have focused intensely on the nature of the mechanisms responsible for perceptual instability during rivalry, and this paper provides a progress report on our thinking about this question. From the outset, we stress that much of our work is stimulated by recent publications out of other laboratories, and we are pleased to acknowledge their influence throughout this paper.
Our approach to understanding the dynamics of binocular rivalry is centered around its three hallmark characteristics. First, fluctuations in perception during binocular rivalry are stochastic, meaning that it is impossible to predict exactly when the next perceptual switch will occur. This characteristic shows up in the unimodal distributions of dominance durations that are skewed toward a longer tail (Levelt, 1965; Fox and Herrmann, 1967; Logothetis et al., 1996; Brascamp et al., 2005). Second, despite its stochastic nature, variations in physical characteristics of rival stimuli including contrast (Fox and Rasche, 1969; Blake et al., 1971; Hollins and Hudnell, 1980; van Ee, 2009), luminance (Kakizaki, 1960), and spatial frequency (Fahle, 1982) produce predictable changes in average dominance durations of binocular rivalry. Third, perceptual alternations during binocular rivalry are spatiotemporal in nature, meaning that perceptual dominance can arise locally within a region of rival stimulus and spread over time to culminate in dominance of the entire rival stimulus (Wheatstone, 1838; Meenes, 1930). The spatiotemporal nature of rivalry transitions is highlighted by traveling waves of binocular rivalry in which a perceptual switch within a local region propagates like a wave (Wilson et al., 2001).
Any comprehensive account of binocular rivalry dynamics needs to explain these three hallmark characteristics. In the following sections, we highlight recent advances, made by us and others, that provide a framework for such an account. We then sketch the outlines of a network model of rivalry that accounts for these three hallmark characteristics. We conclude by briefly considering how other factors influencing rivalry dynamics may be integrated into this framework.
Why Dominance Alternates during Binocular Rivalry
The most popular class of models seeking to explain perceptual alternations during binocular rivalry are built on the concepts of mutual inhibition, an idea dating back over a century (Breese, 1899). While the details vary among models, the general idea is that pools of neurons representing possible alternative stimulus representations compete for dominance via mutual inhibition, with the winner of this competition inhibiting the activity associated with the losing representation (Figure 1A). Compared to other classes of models such as those based on a clocklike neural oscillator (Pettigrew, 2001) or on cognitive inference (Walker, 1978), the mutual inhibition model parsimoniously accounts for a wide range of results showing systematic changes in rivalry dynamics dependent on sensory properties such as contrast. The model is agnostic with respect to the nature of the site at which these inhibitory interactions take place, meaning the model works in the context of eye-based rivalry (Matsuoka, 1984) or object-based rivalry (Dayan, 1998; Wilson, 2003). In addition, top-down factors such as attention (e.g., Lack, 1978; Meng and Tong, 2004), and affective connotation (e.g., Alpers and Pauli, 2006) can be incorporated into this reciprocal inhibition account, a point we return to at the end of this article.
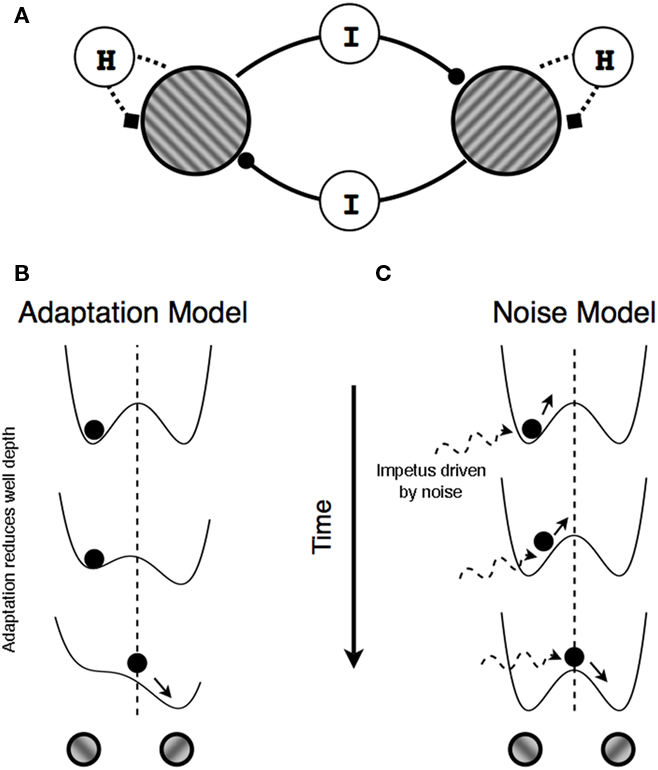
Figure 1. Mechanisms producing perceptual alternations. (A) Schematic illustration of reciprocal inhibition network in which neurons representing the left- and the right-titled tilted gratings mutually inhibit one another (components labeled I) and, at the same time, undergo self-adaptation (the components labeled H). (B,C) Double well potential landscape of the two models of rivalry alternations in which the position of the ball represents perceptual state at a given moment. (B) In adaptation models, potential landscape changes over time due to adaptation and a perceptual switch occurs when double well potentials temporarily form a single well potential owing to the reduced depth of the well in which the ball currently resides (adaptation). (C) In noise models, the two potential landscape remain unchanged but random fluctuations in the ball’s location within a given well eventually provide sufficient impetus to project that ball into the other well.
In this model, inhibition is responsible for exaggerating differences in activation levels between the competing neural representations, allowing one competitor to gain the upper hand. To account for switches in the dominant neural representation and, hence, fluctuations in perception, the mutual inhibition requires an additional mechanism, and in many instantiations of this model that mechanism is neural adaptation (Lehky, 1988; Kalarickal and Marshall, 2000; Laing and Chow, 2002; Wilson, 2003; Lankheet, 2006). According to this idea, the neural representation of the currently dominant stimulus weakens over time owing to slow adaptation, thereby reducing its inhibitory impact on the weaker, non-dominant representation. Eventually the two representations reach the point of equivalence causing an abrupt change in state. Those models typically produce variability in the durations of rivalry states by incorporating noise in the volley of neural signals representing rival stimuli, although one recent instantiation of the model successfully simulated rivalry alternations using noise just in the slow adaptation component (van Ee, 2009). There have also been attempts to model rivalry alternations primarily on the basis of noise, with adaptation playing a secondary role at best (e.g., Kim et al., 2006; Moreno-Bote et al., 2007).
Schematically, these two accounts, one based on adaptation and the other on noise, can be represented by an energy landscape (Brascamp et al., 2006; Kim et al., 2006; Moreno-Bote et al., 2007; see Seely and Chow, 2011, for a discussion of the relation between energy models and mutual inhibition models). As illustrated in Figures 1B,C, two alternative perceptual states are represented by two wells, and the current perceptual state is represented by the position of an object within one of those wells. In this scheme, the energy landscape comprises a gradient that governs the movements of the object within that landscape. In the absence of any other forces, the object settles into a location within the landscape where the energy level is locally minimal. The object remains at that location (meaning the perceptual state remains unchanged) until other forces act upon that object or upon the landscape. In the case of binocular rivalry two such forces leading to state changes have been proposed. In adaptation-based models, the gradient of the landscape itself changes such that the depth of the well in which the object is currently located decreases over time, eventually minimizing the depth of the well to the point where the object rolls into the other well; this corresponds to a switch in perceptual state (Figure 1B). In noise-based models, the depths of the two wells remain unchanged and noise provides the impetus that moves the object from its currently occupied well to the other one. A perceptual switch occurs when noise is sufficiently strong to boost the object over the energy barrier into the neighboring well (Figure 1C).
Which of these forces is primarily responsible for alternations in rivalry state, adaptation or noise? Strictly speaking, this represents an ill-posed question, for noise is almost certainly inherent in all neural events including those involved in binocular rivalry (e.g., Brascamp et al., 2006). The more tractable (i.e., empirically testable) question is to ask whether adaptation plays a significant role in the production of perceptual alternations, for once this question is answered one can then evaluate the relative contribution of noise. Until recently, however, evidence bearing on the importance of adaptation in rivalry alternations was equivocal. For one thing, adaptation predicts that a particularly long dominance duration should be associated with especially strong adaptation and, therefore, should be followed by an unusually brief duration of dominance of that stimulus; in other words, there should be evidence for sequential dependencies among successive state durations (van Ee, 2009). Whereas earlier studies failed to find robust correlations among successive dominance durations (Fox and Herrmann, 1967; Walker, 1975; Lehky, 1995; Logothetis et al., 1996), recent work using more refined methods have obtained evidence for significant, non-zero serial correlations (Gao et al., 2006; van Ee, 2009). Furthermore, computational modeling by van Ee (2009) reveals that the sequential dependencies producing those correlations can be simulated by the addition of noise to the process responsible for neural adaptation but not by noise added to mutual inhibition dynamics. Also of relevance to the question of adaptation’s involvement in rivalry are studies that sought directly to examine whether rivalry dynamics can be altered by adaptation to a rival stimulus (Blake and Overton, 1979; Hollins and Hudnell, 1980; Wade and de Weert, 1986; Blake et al., 1990; van Boxtel et al., 2008). While broadly consistent with such an influence, the conditions of adaptation employed in those studies did not mimic the actual conditions arising during continuous viewing of rival stimuli: the average dominance durations during binocular rivalry last only a few seconds at a time whereas those studies employed long periods of adaptation prior to rivalry testing. While prolonged adaptation can temporarily reduce dominance durations of a subsequently viewed rival stimulus, prolonged adaptation probably produces saturated levels of adaptation that are unlikely to be achieved during ordinary rivalry.
We set out to create a more realistic set of conditions to test whether adaptation might indeed be involved in triggering changes in perceptual state during rivalry (Kang and Blake, 2010). Unlike previous studies that assessed rivalry durations following a single, prolonged period of monocular adaptation, our technique inserted relatively short episodes of monocular adaptation into a much longer, ongoing period of rival stimulation during which observers tracked alternations in dominance. Moreover, the durations of monocular adaptation inserted into ongoing rivalry were equivalent to previously estimated durations of dominance phases of binocular rivalry. By systematically varying the durations of these periods of adaptation inserted into ongoing rivalry, we confirmed that dominance durations are inversely related to the immediately preceding duration of monocular exposure to a rival stimulus, as predicted by adaptation theory. Short-term adaptation of the sort implicated in our procedure is also very likely the source of the localized breakouts of dominance within regions of a rival target where the local strength (e.g., contrast) of the currently suppressed stimulus is higher than elsewhere in that stimulus (Paffen et al., 2008). Short-term adaptation probably also accounts for the propensity for local breaks in suppression following variable periods of monocular suppression in a flash suppression paradigm (van Ee, 2011).
The online-adaptation procedure described in the last paragraph also offers one way to ask how adaptation and noise might interact to trigger state changes in rivalry, because adaptation- and noise-based models predict very different, characteristic distributions of dominance durations. Adaptation-based models generate periodic alternations of perception and, thus, highly similar dominance durations when the stimulus energy levels of the two rival stimuli are identical. In contrast, noise-based models produce irregular alternations of perception that accrue to create an exponential distribution of dominance durations (Shpiro et al., 2009). These two distinct distributions can be indexed using the coefficient of variation (CV), an index calculated by dividing the SD of the dominance durations by the mean of those durations. For adaptation-based models, CV should approach 0 because the SD of the distribution of durations is very small; CV predicted by noise-based models should approach 1, the hallmark characteristics of an exponential distribution. With this in mind, we calculated the CV from measured dominance durations associated with different durations of adaptation. We found that CV was approximately 0.5 when there were no periods of inserted adaptation, and CV increased with increasing adaptation, approaching a value of 1 when adaptation duration was equivalent to the mean dominance durations for given observer. This result implies that noise plays a more important role in producing perceptual alternations with increasing adaptation.
Putting our findings together with other empirical and modeling results (Kim et al., 2006; Moreno-Bote et al., 2007; van Ee, 2009), the following picture emerges within the framework of the double well energy landscape. Immediately following a perceptual state change, a second change is highly unlikely because the depth of the energy well associated with the newly dominant stimulus is considerably deeper than the random, noise-produced fluctuations in the strength of that stimulus. The noise, in other words, is too weak to produce a random bounce sufficient to jump the initially high energy barrier. However, as the depth of the well decreases due to adaptation the energy barrier becomes effectively smaller and, thus, increases the probability that noise will be sufficiently strong to overcome the barrier and trigger a switch to the other well. This conceptualization, together with insight concerning the role of noise in adaptation (van Ee), helps us understand why studies tend to find only weak correlation between successive dominance durations, a finding that heretofore was a thorn in the side of the adaptation model: short and intermediate duration dominance states are predominantly determined by adaptation, with a significant contribution from noise reflected only in relatively long dominance durations that occur infrequently.
Levelt’s Second Proposition and Why It is Sometimes Violated
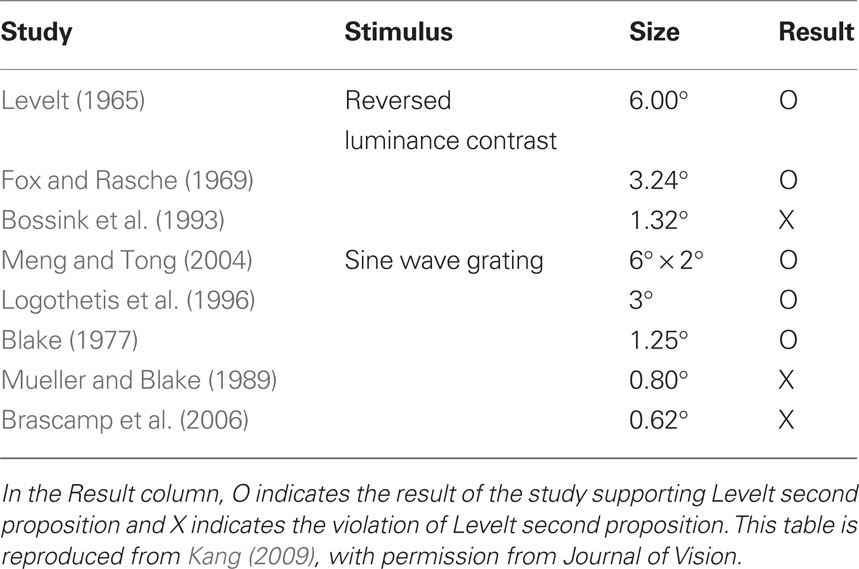
While inherently variable, dominance durations still vary systematically with changes in the strength of one or both of the rival stimuli. For example, it is well known that dominance durations vary with stimulus contrast, luminance, spatial frequency, and motion, to give examples (see review by Blake, 2001). The relation between rivalry’s time course and the strength of rival stimulation was formalized by Levelt (1965) as a set of four propositions. The first proposition states that the total percentage of time that a given stimulus is dominant in rivalry increases with the strength of that stimulus, and the third and fourth propositions state that rivalry alternation rate increase with unilateral or bilateral increases in the strength of the rival stimuli. To our knowledge there is no evidence contradicting any of those three propositions. The second proposition asserts that increases in the stimulus strength of a given rival stimulus reduce its durations of suppression but have no effect on its durations of dominance. This second proposition seems counterintuitive, for one would think that strengthening a stimulus would cause it to remain visible for longer periods of time. This proposition is also controversial, for some studies report evidence supporting it (Levelt, 1965; Fox and Rasche, 1969; Blake, 1977; Logothetis et al., 1996; Meng and Tong, 2004) but others report evidence that violate it (Mueller and Blake, 1989; Bossink et al., 1993; Brascamp et al., 2006).
Several factors have been mentioned as possible sources contributing to these mixed results, including the range of contrast values tested (Brascamp et al., 2006), the contaminating effect of mixed dominance states (Mueller and Blake, 1989) and the existence of return transitions where an exclusively dominant stimulus transitions to the mixed state but then reverts to complete dominance (Brascamp et al., 2006). A re-examination of the relevant literature by one of us (Min-Suk Kang) led to the realization that stimulus size might be a crucial factor governing whether or not Levelt’s second proposition is violated (see Table 1). That motivated a study in which rivalry alternations were measured for different sized rival stimuli whose contrast levels were varied parametrically (Kang, 2009). To assess the contribution of mixed dominance, results using two tracking strategies were compared (Figure 2A). In the whole tracking procedure, observers reported rival alternations only when one entire, spatially extended rival figure was exclusively dominant, with no hint of partial dominance of the other rival stimulus. In the partial tracking procedure, observers reported rivalry alternations within a small, central region of the larger rival stimuli. If mixed dominance contributes to the contrast-invariance of dominance durations dictated by Levelt’s second proposition, we would expect that these two tracking procedures, when implemented using different contrast values, should produce different conclusions concerning the validity of the proposition.
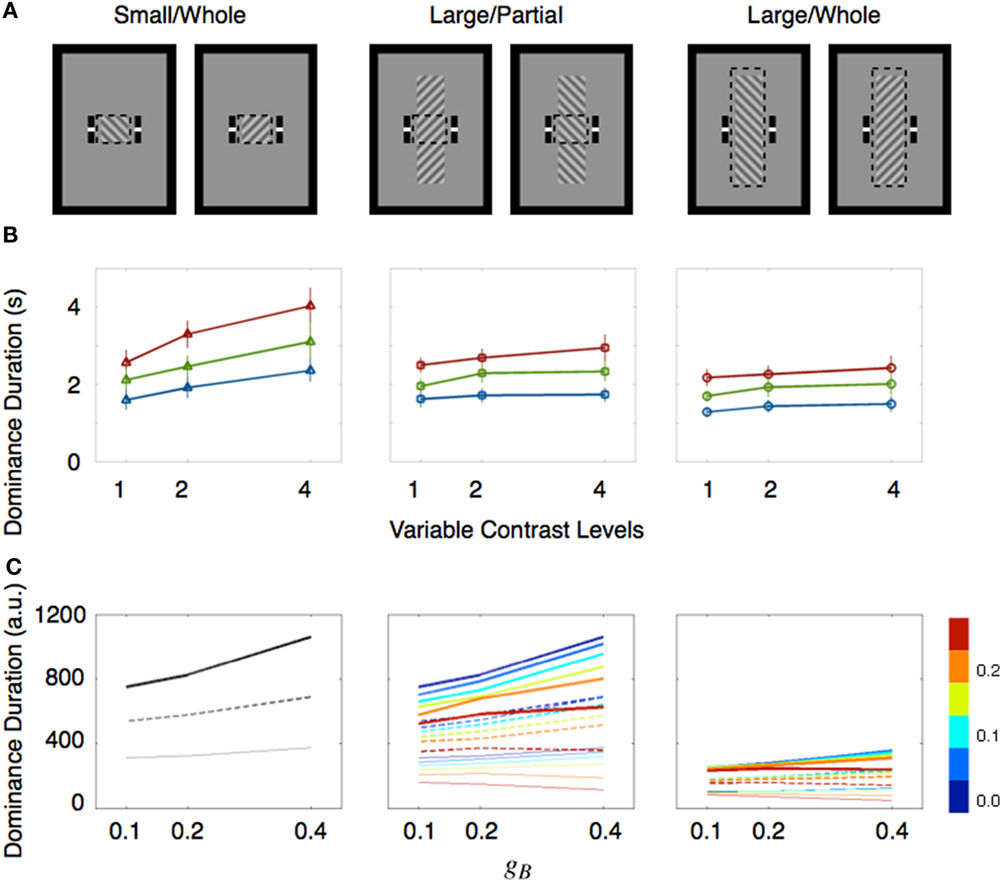
Figure 2. Size dependent rivalry dynamics. (A) Stimulus conditions are illustrated. Observers report the perceptual state within the monitoring region which is depicted with dashed boxes. These dashed boxes were not shown during the experiments. (B) Mean dominance durations of the ipsilateral stimulus are plotted as a function of the contrast of the ipsilateral stimulus. The contrasts are represented as multiples of the lowest contrast level. The contrast values of the contralateral stimulus (expressed as multiples relative to the lowest value) are drawn with three separate lines (red line for 1X; green line for 2X; blue line for 4X). Error bar equals ± 1 SE. (C) Mean dominance durations (arbitrary unit) of simulated binocular rivalry are shown as Figure 2B in which contrasts of two rival stimuli were manipulated with potential landscape parameters gA and gB. Three distinct line styles indicate the dominance durations at a given gA (thick line for gA = 0.1; dotted line for gA = 0.2; thin gray line for gA = 0.4). Strength of spatial interactions were manipulated with the coupling strength parameter represented by different colors shown in the color bar at right. These figures are reproduced from Kang et al. (2009), with permission from Journal of Vision.
Stimulus size indeed mattered: dominance durations were invariant with changing contrast when stimulus size was large but were variable when stimulus size was small (Figure 2B). Moreover, rivalry dynamics associated with return transitions could not explain the difference of the rivalry dynamics between the small and large stimulus size: dominance durations associated with perceptual switches were similar to dominance durations associated with return transitions for the same sized stimulus. In addition, when rival stimuli were large, contrast-invariant dominance durations were found for both tracking strategies, indicating that mixed dominance was not responsible for violation of that proposition. As an aside, it is interesting to note that van Ee (2009) found that mixed dominance also has no influence on the stochastic properties of rivalry alternations as indexed by serial correlations over successive dominance durations.
Having solved that riddle, however, we were left with a new one: how can we explain why stimulus size influences the time course of rivalry alternations? From earlier research, we know that binocular rivalry dynamics are spatiotemporal in nature, meaning that rivalry appears to occur within local zones of the visual field (Blake et al., 1992), with neighboring zones influencing one another (Alais et al., 2006). These properties of rivalry can be embodied in a model whose simulated dynamics provide a test of the boundary conditions under which Levelt’s second proposition would hold up. Accordingly, we constructed such a model in which rivalry transpires within local, interacting networks each representing neighboring region of the visual field. (Within the energy landscape framework, those local networks could be construed as set of neighboring energy landscapes whose dynamics spread among the set.) The combined outputs from those local networks could be any of the three interdependent perceptual states associated with spatially extended rival stimuli. By appropriate adjustment of the interaction terms, this model reproduced the contrast-invariance of dominance durations predicted by Levelt’s second proposition, even though the model’s output at each individual location violated that contrast-invariance (Figure 2C). This happens because the spatial interactions promote attraction between neighboring neural states, pulling them into synchrony. It is worth noting that these same mechanisms could also govern the dynamics of other forms of perceptual bistability including ambiguous structure from motion, which exhibits invariant dominance durations when stimulus strength is manipulated (Klink et al., 2008a).
These empirical findings and model simulations demonstrate that spatial interactions play an important role in the control of rivalry dynamics evidenced by spontaneous perceptual alternations. Those interactions are not just necessary add-on components to account for traveling waves (Wilson et al., 2001) or the spread of perceptual suppression (Maruya and Blake, 2009; Nichols and Wilson, 2009). This realization leads naturally to our next hallmark characteristic of rivalry, the spatial spread of perceptual dominance as exemplified by traveling waves.
Spatiotemporal Dynamics of Binocular Rivalry
In this section we show how it is possible to tie together binocular rivalry dynamics associated with spontaneous perceptual alternations with the dynamics associated with transitions in dominance that arise locally and spread throughout a previously suppressed rival stimulus. As pointed out earlier, these transitions often resemble traveling waves of dominance, i.e., a series of perceptual switches over space and time. Moreover, Wilson et al. (2001) have demonstrated that it is possible to create stimulus conditions where these waves can be produced and measured in a controlled manner with brief, discrete episodes of rivalry. But for our purposes, we needed to harness the control provided with this traveling wave technique while, at the same time, being able to measure spontaneous perceptual alternations during extended periods of binocular rivalry.
To achieve this, we devised a periodic perturbation technique in which we could measure these two types of rivalry dynamics using the same procedure (Kang et al., 2009). Here is how it works (see Figure 3A). We created spatially extended rivalry targets containing a small monitoring region within the middle of the rival targets, and observers reported the fluctuations in perceptual state within that monitoring region. (This is essentially the same partial tracking procedure described in the previous section.) Now, to measure traveling wave dynamics, we introduced abrupt contrast increments within small regions located at the opposite ends of the two elongated rival stimuli (Figure 3A). Thus, for example, a trigger would appear at the upper region of one eye’s stimulus and a lower region of the other eye’s stimulus, and these contrast pulses – perturbations we dubbed them – are presented periodically in antiphase to the two eyes. With the pulses are appropriately timed, observers tend to perceive upward and downward traveling waves of binocular rivalry that alternate periodically over time. Using a statistical technique based on reverse correlation, we can characterize the probability and the speed of these traveling waves based solely on the records of dominance durations measured at the monitoring region, and we can evaluate the relation between spontaneous rivalry alternations and the dynamics of the traveling waves. This allowed us to answer two questions: (1) do observers who experience relatively slow rivalry alternations (slow alternators) tend to experience slow traveling waves compared to the wave speed experienced by observers who exhibit relatively fast rivalry alternations (fast alternators), and (2) does the configuration of the stimulus patterns carrying the traveling waves jointly influence the speed of those waves and the time course of spontaneous alternations?
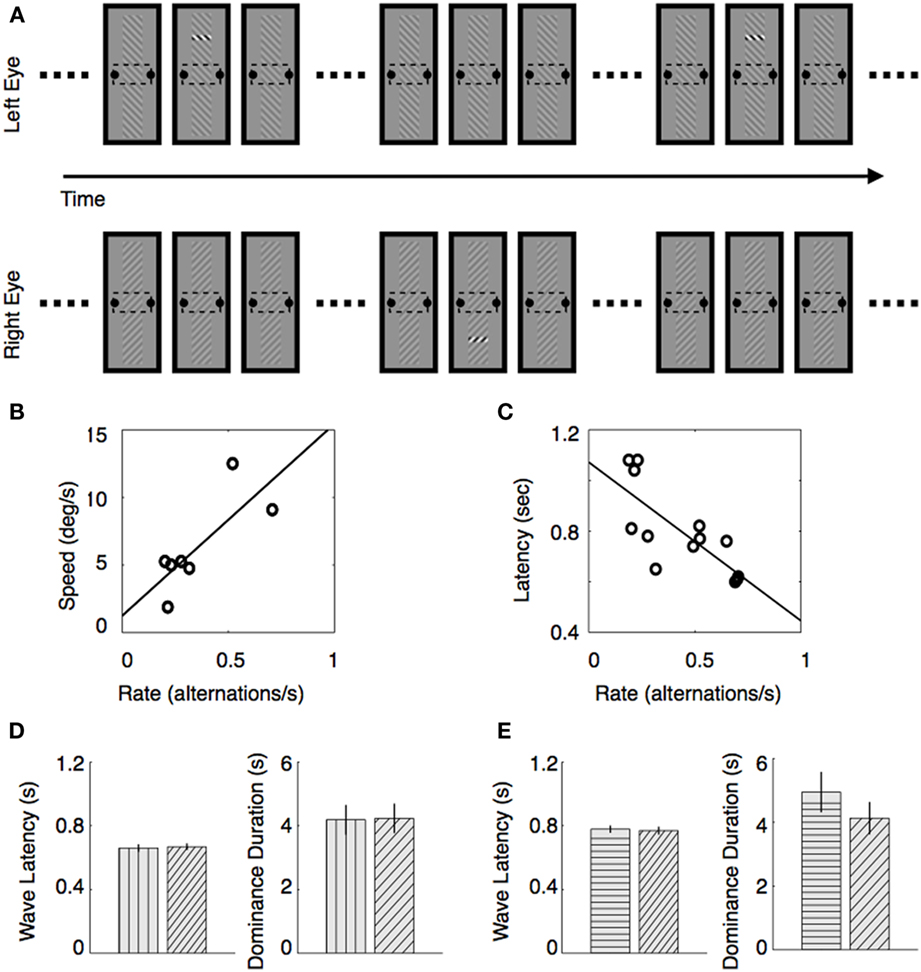
Figure 3. Relation between traveling wave dynamics and dominance durations accompanied with spontaneous perceptual alternations. (A) Stimulus conditions that implement the periodic perturbation technique. While observers are reporting perceptual alternations within the monitoring region during an extended viewing period of binocular rivalry, triggers are presented periodically in antiphase. A trigger comprises a brief contrast increment within a small region of rival figure. Trigger locations are different for the two rival stimuli: one is presented at the upper region and the other one is presented at the lower region of the two rival stimuli, respectively. (B,C) Traveling wave speed covaries with alternation rate. (B) Estimated traveling wave speed of each observer is plotted as a function of alternation rate. (C) Estimated traveling wave for each observer is plotted as a function of alternation rate. (D,E) Latency of the traveling waves and dominance durations when rival stimuli of different collinearity are presented. (D) Result when the vertical and diagonal gratings are presented: mean latency (Left) and mean dominance duration (Right). Pattern filled within the bar indicates the stimulus pattern either carrying traveling waves that emerges from suppression (Left) or being associated with perceptual dominance (Right). (E) Result when the horizontal and diagonal gratings are presented. These figures are reproduced from Kang (2009), Kang et al. (2010), with permission from Journal of Vision.
Using vertically elongated rival stimuli consisting of left- and right-tilted contours (Figure 3A), we measured the speed of traveling waves and alternation rate within the monitoring region. As shown in Figure 3B, alternation rate was strongly correlated with traveling wave speed within our sample of seven observers. With a sample of 12 observers, alternation rate was also correlated with latency, an indirect measure of speed of traveling waves (Figure 3C). This pattern of results means that fast alternators see fast traveling waves, which explains why fast alternators tend to experience difficulty seeing traveling waves: their spontaneous perceptual alternations more nearly resemble traveling waves than do the state changes experienced by slow alternators.
In another study (Kang et al., 2010), we asked whether the speed of traveling waves and the durations of dominance of a rival stimulus are both influenced by contour collinearity, a stimulus property shown by others to influence both wave speed (Wilson et al., 2001) and concurrent rivalry alternations among multiple, neighboring rival targets (Alais et al., 2006). If stimulus collinearity increases neural activity via recurrent excitation, one would predict that a rival stimulus with high collinearity will be dominant longer, on average, when it competes against a rival stimulus of low collinearity. In addition, a highly collinear rival stimulus should exhibit faster traveling waves as it emerges from suppression when that highly collinear stimulus is in rivalry with a weakly collinear rival stimulus; at the same time, the weakly collinear stimulus should emerge from suppression more slowly when in rivalry with the highly collinear stimulus.
When we measured those aspects of rivalry, however, the results did not conform to these predictions. Specifically, we prepared two pairs of vertically elongated rival stimuli like those illustrated in Figure 3A: in one pair a vertical grating seen by one eye rivaled with a diagonal grating seen by the other eye. The elongated vertical grating, it is safe to assume, possesses high collinearity relative to the diagonal grating. Contrary to our prediction, traveling waves propagated with similar speed whether they emerged from the vertical grating or from the diagonal grating, and, moreover, dominance durations of the two rival stimuli were also comparable (Figure 3D). The same was true when a horizontal grating was in rivalry with a diagonal grating (Figure 3E).
This result implies that the dynamics of traveling waves behave in a similar fashion as do the dynamics of spontaneous perceptual alternations, but we are left to explain the counterintuitive influence of stimulus collinearity. As we did to explain the emergent property of the Levelt’s second proposition of the large stimulus, we turned to computer simulations, this time modifying extant network models of traveling waves (Wilson et al., 2001; Stollenwerk and Bode, 2003; Bressloff and Webber, 2011) to develop and test a hypothesized mechanism: renormalization of overall stimulus strength by pattern dependent adaptation while retaining recurrent excitation dependent on stimulus collinearity. This refinement of the network model of rivalry outlined in the previous section (i.e., distributed, interdependent local zones of rivalry) successfully reproduced dynamics of traveling waves and dominance durations for all combinations of rival stimulus patterns (Kang et al., 2010).
An Integrated Framework: Network Models of Binocular Rivalry
This series of studies together with important work by others interested in rivalry has taught us the importance of framing seemingly incompatible psychophysical results within the context of a computational model. In the case of rivalry alternations, recent modeling efforts underscore that the question is not one of noise versus adaptation but, instead, a question of the degree of balance between these two forces. Those models inspired us to perform experiments that revealed the unfolding roles of noise and adaptation during the time course of a given rival state. And in the case of rivalry’s dependence on stimulus strength, we see that violations of Levelt’s second proposition, rather than failing to replicate results supporting the proposition, in fact reveal an important characteristic of neural mechanisms underlying rivalry: cooperative and competitive spatial interactions provide the key to understanding the conditions under which the contrast-invariance of dominance durations is observed, consistent with Levelt’s second proposition, and the conditions under which that invariance rule is violated. And finally, the model refinements that explain Levelt’s second proposition also reproduce the dynamics of both traveling waves and ongoing perceptual alternations. This outcome is particularly noteworthy in that those two forms of dynamics differ by an order of magnitude different in terms of their time scales: traveling waves occur within a few hundreds milliseconds and spontaneous perceptual alternations occur over a few seconds.
Our work is not done, however. Interest in binocular rivalry has grown considerably in recent years, the result being new findings that bring surprises and fresh challenges for extant models. We know now, for example, that the time course of rivalry alternations can be influenced by the affective connotation of the rival stimuli (e.g., Alpers and Pauli, 2006; Anderson et al., 2011), by the learned affordance of a rival stimulus (Chopin and Mamassian, 2010), by manipulations that engage visual attention (Neisser and Becklen, 1975; Ooi and He, 1999; Mitchell et al., 2004; Chong et al., 2005; Chong and Blake, 2006; Klink et al., 2008b; Paffen and Van der Stigchel, 2010), and by the activity being executed at the time rivalry is being observed (Maruya et al., 2007). Rivalry dynamics are also affected by sensory signals arising in other modalities including hearing (Kang and Blake, 2005; van Ee et al., 2009; Conrad et al., 2010), touch (Lunghi et al., 2010), and smell (Zhou et al., 2010). Moreover, there are bottom-up influences, too, that must be incorporated into models of rivalry, including eye movements, which are indeed capable of increasing the incidence of rivalry alternations (van Dam and van Ee, 2006). For that matter, eye movements could be involved in some of the putative top-down effects on rivalry, because eye movements are sensitive to top-down, cognitive influences such as memory load in a visual working memory task (Ehrlichman et al., 2007). We would not want to conclude that a given cognitive factor (e.g., memory load) influences rivalry before ruling out an involvement of eye movements. Finally, models of rivalry must be able to account for the large range of individual differences in rivalry dynamics (Carter and Pettigrew, 2003) that appear to have a significant genetic component (Miller et al., 2010; Shannon et al., 2011).
We are confident that these additional findings on rivalry dynamics can be incorporated into a refined version of existing network models of binocular rivalry. For example, individual differences in rivalry alternation rate may well stem from individual differences in gain control mechanisms that govern neural adaptation, with the additional possibility of inherent differences in noise levels. Furthermore, the cooperative and competitive spatial interactions implicated in our studies of Levelt’s second proposition probably play key roles in promoting coherent dominance of a figure defined by stimulus features distributed between the two eyes (Whittle et al., 1968; Kovacs et al., 1996; Lee and Blake, 2004). As for top-down influences related to attention, affect, expectation, and action planning, these could be embodied in feedback signals onto neural representations of the competing rival stimuli. For example, it is well known that feature-based attention is spatially extensive throughout the visual field (Saenz et al., 2002; Hayden and Gallant, 2005) and, therefore, attention to a particular feature could strengthen the excitatory drive of that feature wherever it appears within the visual field. At the same time, spatial attention, being focused on a given location in visual space, could increase the strength of neural representations of both rival stimuli since both are imaged within the attended spatial region, resulting in increases in alternation rate. Recent advances in development of connectivity maps provide tantalizing circuitry for achieving these kinds of modulatory influences (Martin, 2011).
Concluding Remarks
In this review, we summarized recent progress in understanding binocular rivalry dynamics and provided an integrated framework that can readily incorporate other empirical findings. Considering that binocular rivalry is a model system for studying perceptual multistability, implications of this advancement in rivalry dynamics may well extend to perceptual multistability arising from neural representations of competing figure/ground (face/vase), depth, and object interpretations.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank David Heeger and Sang-Hun Lee for their comments at various stages of this project. This work was supported by grants from the U.S. National Institutes of Health R01 EY013358, and Randolph Blake was also supported by the WCU program administered by the National Research Foundation of Korea and funded by the Korean Ministry of Education, Science and Technology (R32-10142).
References
Alais, D., Lorenceau, J., Arrighi, R., and Cass, J. (2006). Contour interactions between pairs of Gabors engaged in binocular rivalry reveal a map of the association field. Vision Res. 46, 1473–1487.
Alpers, G. W., and Pauli, P. (2006). Emotional pictures predominate in binocular rivalry. Cogn. Emot. 20, 596–607.
Anderson, E., Siegel, E. H., and Barrett, L. F. (2011). What you feel influences what you see: the role of affective feelings in resolving binocular rivalry. J. Exp. Soc. Psychol. 47, 856–860.
Blake, R. (1977). Threshold conditions for binocular-rivalry. J. Exp. Psychol. Hum. Percept. Perform. 3, 251–257.
Blake, R. (2001). A primer on binocular rivalry, including current controversies. Brain Mind 2, 5–38.
Blake, R., O’shea, R. P., and Mueller, T. J. (1992). Spatial zones of binocular rivalry in central and peripheral vision. Vis. Neurosci. 8, 469–478.
Blake, R., and Overton, R. (1979). The site of binocular rivalry suppression. Perception 8, 143–152.
Blake, R., Westendorf, D., and Fox, R. (1990). Temporal perturbations of binocular rivalry. Percept. Psychophys. 48, 593–602.
Blake, R. R., Fox, R., and Mcintyre, C. (1971). Stochastic properties of stabilized-image binocular rivalry alternations. J. Exp. Psychol. 88, 327–332.
Bossink, C. J., Stalmeier, P. F., and De Weert, C. M. (1993). A test of Levelt’s second proposition for binocular rivalry. Vision Res. 33, 1413–1419.
Brascamp, J. W., van Ee, R., Noest, A. J., Jacobs, R. H., and van Den Berg, A. V. (2006). The time course of binocular rivalry reveals a fundamental role of noise. J. Vis. 6, 1244–1256.
Brascamp, J. W., van Ee, R., Pestman, W. R., and van Den Berg, A. V. (2005). Distributions of alternation rates in various forms of bistable perception. J. Vis. 5, 287–298.
Bressloff, P. C., and Webber, M. A. (2011). Neural field model of binocular rivalry waves. J. Comput. Neurosci. PMID: 21748526. [Epub ahead of print].
Carter, O. L., and Pettigrew, J. D. (2003). A common oscillator for perceptual rivalries? Perception 32, 295–305.
Chong, S. C., and Blake, R. (2006). Exogenous attention and endogenous attention influence initial dominance in binocular rivalry. Vision Res. 46, 1794–1803.
Chong, S. C., Tadin, D., and Blake, R. (2005). Endogenous attention prolongs dominance durations in binocular rivalry. J. Vis. 5, 1004–1012.
Chopin, A., and Mamassian, P. (2010). Task usefulness affects perception of rivalrous images. Psychol. Sci. 21, 1886–1893.
Conrad, V., Bartels, A., Kleiner, M., and Noppeney, U. (2010). Audiovisual interactions in binocular rivalry. J. Vis. 10, 27, 1–15.
Ehrlichman, H., Micic, D., Sousa, A., and Zhu, J. (2007). Looking for answers: eye movements in non-visual cognitive tasks. Brain Cogn. 64, 7–20.
Fahle, M. (1982). Binocular rivalry: suppression depends on orientation and spatial frequency. Vision Res. 22, 787–800.
Fox, R., and Herrmann, J. (1967). Stochastic properties of binocular rivalry alternations. Percept. Psychophys. 2, 432–436.
Fox, R., and Rasche, F. (1969). Binocular rivalry and reciprocal inhibition. Percept. Psychophys. 5, 215–217.
Friston, K. J., and Price, C. J. (2001). Dynamic representations and generative models of brain function. Brain Res. Bull. 54, 275–285.
Gao, J. B., Billock, V. A., Merk, I., Tung, W. W., White, K. D., Harris, J. G., and Roychowdhury, V. P. (2006). Inertia and memory in ambiguous visual perception. Cogn. Process. 7, 105–112.
Hayden, B. Y., and Gallant, J. L. (2005). Time course of attention reveals different mechanisms for spatial and feature-based attention in area V4. Neuron 47, 637–643.
Hollins, M., and Hudnell, K. (1980). Adaptation of the binocular rivalry mechanism. Invest. Ophthalmol. Vis. Sci. 19, 1117–1120.
Kalarickal, G. J., and Marshall, J. A. (2000). Neural model of temporal and stochastic properties of binocular rivalry. Neurocomputing 32, 843–853.
Kang, M. S., and Blake, R. (2005). Perceptual synergy between seeing and hearing revealed during binocular rivalry. Psichologija 32, 7–15.
Kang, M. S., and Blake, R. (2010). What causes alternations in dominance during binocular rivalry? Atten. Percept. Psychophys. 72, 179–186.
Kang, M.-S., Heeger, D., and Blake, R. (2009). Periodic perturbations producing phase-locked fluctuations in visual perception. J. Vis. 9:8. doi: 10.1167/9.2.8
Kang, M. S., Lee, S. H., Kim, J., Heeger, D., and Blake, R. (2010). Modulation of spatiotemporal dynamics of binocular rivalry by collinear facilitation and pattern-dependent adaptation. J. Vis. 10, 3.
Kim, Y.-J., Grabowecky, M., and Suzuki, S. (2006). Stochastic resonance in binocular rivalry. Vis. Res. 46, 392–406.
Kim, C. Y., and Blake, R. (2005). Psychophysical magic: rendering the visible “invisible”. Trends Cogn. Sci. (Regul. Ed.) 9, 381–388.
Klink, P. C., Van Ee, R., and Van Wezel, R. J. A. (2008a). General validity of Levelt’s propositions reveals common computational mechanisms for visual rivalry. PLoS ONE 3, e3473. doi: 10.1371/journal.pone.0003473
Klink, P. C., Van Ee, R., Nijs, M. M., Brouwer, G. J., Noest, A. J., and Van Wezel, R. J. A. (2008b). Early interactions between neuronal adaptation and voluntary control determine perceptual choices in bistable vision. J. Vis. 8, 16.1–16.18.
Kovacs, I., Papathomas, T. V., Yang, M., and Feher, A. (1996). When the brain changes its mind: interocular grouping during binocular rivalry. Proc. Natl. Acad. Sci. U.S.A. 93, 15508–15511.
Laing, C. R., and Chow, C. C. (2002). A spiking neuron model for binocular rivalry. J. Comp. Neurosci. 12, 39–53.
Lankheet, M. J. M. (2006). Unraveling adaptation and mutual inhibition in perceptual rivalry. J. Vis. 6, 304–310.
Lee, S. H., and Blake, R. (2004). A fresh look at interocular grouping during binocular rivalry. Vision Res. 44, 983–991.
Logothetis, N. K., Leopold, D. A., and Sheinberg, D. L. (1996). What is rivalling during binocular rivalry? Nature 380, 621–624.
Lunghi, C., Binda, P., and Morrone, M. C. (2010). Touch disambiguates rivalrous perception at early stages of visual analysis. Curr. Biol. 20, R143–R144.
Martin, K. A. C. (2011). Neuroanatomy: uninhibited connectivity in neocortex. Curr. Biol. 21, R4235–R4427.
Maruya, K., and Blake, R. (2009). Spatial spread of interocular suppression is guided by stimulus configuration. Perception 38, 215–231.
Maruya, K., Yang, E., and Blake, R. (2007). Voluntary action influences visual competition. Psychol. Sci. 18, 1090–1098.
Meng, M., and Tong, F. (2004). Can attention selectively bias bistable perception? Differences between binocular rivalry and ambiguous figures. J. Vis. 4, 539–551.
Miller, S. M., Hansell, N. K., Ngo, T. T., Liu, G. B., Pettigrew, J. D., Martin, N. G., and Wright, M. J. (2010). Genetic contribution to individual variation in binocular rivalry rate. Proc. Natl. Acad. Sci. U.S.A. 107, 2664–2668.
Mitchell, J. F., Stoner, G. R., and Reynolds, J. H. (2004). Object-based attention determines dominance in binocular rivalry. Nature 429, 410–413.
Moreno-Bote, R., Rinzel, J., and Rubin, N. (2007). Noise-induced alternations in an attractor network model of perceptual bistability. J. Neurophysiol. 98, 1125–1139.
Mueller, T. J., and Blake, R. (1989). A fresh look at the temporal dynamics of binocular-rivalry. Biol. Cybern. 61, 223–232.
Neisser, U., and Becklen, R. (1975). Selective looking: attending to visually specified events. Cogn. Psychol. 7, 480–494.
Nichols, D. F., and Wilson, H. R. (2009). Stimulus specificity in spatially-extended interocular suppression. Vision Res. 49, 2110–2120.
Ooi, T. L., and He, Z. J. (1999). Binocular rivalry and visual awareness: the role of attention. Perception 28, 551–574.
Paffen, C. L., Naber, M., and Verstraten, F. A. (2008). The spatial origin of a perceptual transition in binocular rivalry. PLoS ONE 3, e2311. doi: 10.1371/journal.pone.0002311
Paffen, C. L., and Van der Stigchel, S. (2010). Shifting spatial attention makes you flip: exogenous visual attention triggers perceptual alternations during binocular rivalry. Atten. Percept. Psychophys. 72, 1237–1243.
Pettigrew, J. (2001). Searching for the switch: neural bases for perceptual rivalry alternations. Brain Mind 2, 85–118.
Rees, G., Kreiman, G., and Koch, C. (2002). Neural correlates of consciousness in humans. Nat. Rev. Neurosci. 3, 261–270.
Saenz, M., Buracas, G. T., and Boynton, G. M. (2002). Global effects of feature-based attention in human visual cortex. Nat. Neurosci. 5, 631–632.
Seely, J., and Chow, C. C. (2011). The role of mutual inhibition in binocular rivalry. J. Neurophysiol. PMID: 21775721. [Epub ahead of print].
Shannon, R. W., Patrick, C. J., Jiang, Y., Bernat, E., and He, S. (2011). Genes contribute to the switching dynamics of bistable perception. J. Vis. 11:8. doi: 10.1167/11.3.8
Shpiro, A., Moreno-Bote, R., Rubin, N., and Rinzel, J. (2009). Balance between noise and adaptation in competition models of perceptual bistability. J. Comp. Neurosci. 27, 37–54.
Stollenwerk, L., and Bode, M. (2003). Lateral neural model of binocular rivalry. Neural. Comput. 15, 2863–2882.
van Boxtel, J. J., Alais, D., and van Ee, R. (2008). Retinotopic and non-retinotopic stimulus encoding in binocular rivalry and the involvement of feedback. J. Vis. 8, 17.1–17.10.
van Dam, L. C. J., and van Ee, R. (2006). Retinal image shifts, but not eye movements per se, cause alternations in awareness during binocular rivalry. J. Vis. 6, 1172–1179.
van Ee, R. (2009). Stochastic variations in sensory awareness are driven by noisy neuronal adaptation: evidence from serial correlations in perceptual bistability. J. Opt. Soc. Am. A. Opt. Image Sci. Vis. 26, 2612–2622.
van Ee, R. (2011). Percept-switch nucleation in binocular rivalry reveals local adaptation characteristics of early visual processing. J. Vis. 11:13. doi: 10.1167/11.2.13
van Ee, R., van Boxtel, J. J. A., Parker, A. L., and Alais, D. (2009). Multisensory congruency as a mechanism for attentional control over perceptual selection. J. Neurosci. 29, 11641–11649.
Walker, P. (1975). Stochastic properties of binocular rivalry alternations. Percept. Psychophys. 18, 467–473.
Walker, P. (1978). Binocular-rivalry – central or peripheral selective processes. Psychol. Bull. 85, 376–389.
Wheatstone, C. (1838). Contributions to physiology of vision – part the first. On some remarkable, and hitherto unobserved, phenomenon of binocular vision. Philos. Trans. R. Soc. London 128, 371–394.
Whittle, P., Bloor, D. C., and Pocock, S. (1968). Some experiments on figural effects in binocular rivalry. Percept. Psychophys. 4, 183–188.
Wilson, H. R. (2003). Computational evidence for a rivalry hierarchy in vision. Proc. Natl. Acad. Sci. U.S.A. 100, 14499–14503.
Wilson, H. R., Blake, R., and Lee, S. H. (2001). Dynamics of travelling waves in visual perception. Nature 412, 907–910.
Keywords: binocular rivalry, dynamics, dynamic network models
Citation: Kang M-S and Blake R (2011) An integrated framework of spatiotemporal dynamics of binocular rivalry. Front. Hum. Neurosci. 5:88. doi: 10.3389/fnhum.2011.00088
Received: 22 June 2011; Paper pending published: 10 July 2011;
Accepted: 09 August 2011; Published online: 30 August 2011.
Edited by:
Georgios A. Keliris, Max-Planck Institute for Biological Cybernetics, GermanyReviewed by:
Shozo Tobimatsu, Kyushu University, JapanRaymond van Ee, University Utrecht, Netherlands
Copyright: © 2011 Kang and Blake. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence: Min-Suk Kang, Department of Psychology, Vanderbilt Vision Research Center, Center for Cognitive and Integrative Cognitive Neuroscience, Vanderbilt University, Wilson Hall, PMB 407817, 2301 Vanderbilt Place, Nashville, TN 37240-7817, USA. e-mail:bS5zdWsua2FuZ0BnbWFpbC5jb20=