- 1 Research on Learning and Instruction, Institute for Behavioral Sciences, Swiss Federal Institute of Technology Zurich, Switzerland
- 2 Division of MR Physics, Department of Radiology, Medical University of Graz, Graz, Austria
- 3 Division of Neuroradiology, Department of Radiology, Medical University of Graz, Graz, Austria
- 4 Section of Applied Neuropsychology, Institute of Psychology, University of Graz, Graz, Austria
The ability to extract numerical information from different representation formats (e.g., equations, tables, or diagrams) is a key component of mathematical competence but little is known about its neural correlate. Previous studies comparing mathematically less and more competent adults have focused on mental arithmetic and reported differences in left angular gyrus (AG) activity which were interpreted to reflect differential reliance on arithmetic fact retrieval during problem solving. The aim of the present functional magnetic resonance imaging study was to investigate the brain correlates of mathematical competence in a task requiring the processing of typical mathematical representations. Twenty-eight adults of lower and higher mathematical competence worked on a representation matching task in which they had to evaluate whether the numerical information of a symbolic equation matches that of a bar chart. Two task conditions without and one condition with arithmetic demands were administered. Both competence groups performed equally well in the non-arithmetic conditions and only differed in accuracy in the condition requiring calculation. Activation contrasts between the groups revealed consistently stronger left AG activation in the more competent individuals across all three task conditions. The finding of competence-related activation differences independently of arithmetic demands suggests that more and less competent individuals differ in a cognitive process other than arithmetic fact retrieval. Specifically, it is argued that the stronger left AG activity in the more competent adults may reflect their higher proficiency in processing mathematical symbols. Moreover, the study demonstrates competence-related parietal activation differences that were not accompanied by differential experimental performance.
Introduction
Mathematical competence is one of the key cognitive abilities that is acquired through formal schooling. In general, it is a central component of human intelligence and thus highly relevant for educational and occupational attainment (Neisser et al., 1996; Schmidt and Hunter, 1998). In particular, it is essential for making informed decisions in various areas of life as most of the information on which decisions are based is numerical (Parsons and Bynner, 2005). This holds particularly true in health decisions: Low mathematical competence (or low numeracy) was found to be associated with inadequate perception of risks and benefits of screening, reduced medication compliance, and, eventually, poor medical outcomes (Reyna et al., 2009). This impairment in decision-making may not only be traced back to deficits in numerical magnitude processing but also to a lack of understanding different mathematical representations such as tables, graphs, or symbolic equations (Lipkus and Peters, 2009).
In light of the considerable progress in understanding the brain mechanisms underlying number processing (for a review, cf. Ansari, 2008), there is still little research into the brain correlates of individual differences in mathematical skills. Much of this research has focused on learning disabilities in mathematics (developmental dyscalculia) and has revealed abnormal brain function and structure in the parietal cortex, specifically in the intraparietal sulcus (IPS; cf. Rubinsten and Henik, 2009; Butterworth et al., 2011). Using functional magnetic resonance imaging (fMRI), Price et al. (2007) found that distance between numbers in a simple number comparison task (requiring to decide which of two numbers is larger) less strongly modulated right IPS activation in dyscalculic compared to control children. Likewise, dyscalculic children were reported to show weaker IPS activation in approximate calculation than controls (Kucian et al., 2006). These results are complemented by voxel-based morphometry (VBM) studies revealing less gray matter density and volume in the IPS of dyscalculics compared to controls (Isaacs et al., 2001; Rotzer et al., 2008). At present, there is wide consensus that the IPS holds an amodal and format-independent representation of numerical magnitude and is therefore systematically engaged in any task drawing on magnitude manipulations – from basic number comparison to complex calculation (Dehaene et al., 2003, 2004). This suggests that one basis of learning disabilities in mathematics lies in impaired numerical magnitude processing, which is also in line with the findings from behavioral research (e.g., Butterworth and Laurillard, 2010).
Even though the IPS, as the core quantity system, can be assumed to play the most important role in many number processing demands, studies on adults’ mathematical competence within the normal achievement range suggest that more and less competent individuals do not differ in the engagement of this brain region during calculation. Rather, they seem to differentially activate the left angular gyrus (AG; Menon et al., 2000; Grabner et al., 2007, 2009a,b). Grabner et al. (2007) screened a large sample of adults with respect to their cognitive abilities and then contrasted the brain activation patterns between two groups of mathematical competence (which did not differ in verbal or figural–spatial abilities) while they were performing easy and more difficult multiplication problems. The data revealed that the more competent individuals displayed higher activation of the left AG during multiplication and that the left AG activation level was linearly related to individuals’ score in the mathematical competence test. The less competent participants did not activate any brain region more strongly (for similar evidence, see Grabner et al., 2009a).
The left AG is another brain area whose activation is frequently modulated during number processing, especially during mental calculation (Ansari, 2008; Zamarian et al., 2009), but its functional role is less well understood than that of the IPS. In their influential review paper on parietal circuits in number processing, Dehaene et al. (2003) proposed that the left AG belongs to the language system and may support the retrieval of verbally stored arithmetic facts from memory (such as the multiplication table). This notion has been corroborated by studies showing higher left AG activation while solving multiplication compared to subtraction problems (Lee, 2000), in applying fact retrieval compared to procedural (calculation) strategies (Grabner et al., 2009a), and in trained compared to untrained arithmetic problems (Delazer et al., 2003, 2005; Ischebeck et al., 2006, 2007). Against this background, Grabner et al. (2007) interpreted the finding of higher left AG activation in the more competent individuals to reflect a stronger reliance on arithmetic fact retrieval. In other words, participants with higher mathematical competence could have solved the multiplication problems more frequently by fact retrieval than their less competent peers. This interpretation was corroborated in a training study in which the individuals of both competence groups were trained on a set of multiplication problems before they were presented with trained and untrained problems in the fMRI test session (Grabner et al., 2009b). It was shown that mathematical competence had an impact on performance and left AG activation only in the untrained but no longer in the trained problems. Precisely, the more competent individuals displayed stronger left AG activation and better performance in the novel problems, but in the trained problems, when both competence groups could retrieve the multiplication facts from memory, the activation and performance difference diminished.
The retrieval of arithmetic facts from memory, however, may only be one function of the left AG in mathematical problem solving that differs between more and less competent individuals. There is growing evidence that activation of this brain region is also modulated in numerical tasks that do not draw on mental calculation or arithmetic fact retrieval. Holloway et al. (2010) administered a symbolic (Arabic digits) and non-symbolic (arrays of squares) number comparison task in which participants only had to indicate the side with the larger quantity. Consistent with several previous studies on magnitude processing (cf. Dehaene et al., 2003) both task conditions (contrasted with control tasks) activated the IPS. But most interestingly, the contrast between the task conditions revealed larger left AG activation in the symbolic (compared to the non-symbolic) representation. This result was replicated by Gullick et al. (in press) applying a similar experimental design. Moreover, Price and Ansari (2011) have reported that even passive viewing of Arabic digits compared to unfamiliar symbols and letters is associated with stronger activation of the left AG. These findings suggest that the left AG subserves a more fundamental cognitive function in mathematical thinking than just arithmetic fact retrieval. One promising candidate for this function is symbol processing. Numerous studies have implicated the AG in the processing of linguistic symbols, in particular in the mapping of graphemes to phonemes or in the mapping of words (as symbolic chunks) to their semantic referents (for reviews, cf. Price, 2000; Price, 2010). Against this background, Ansari (2008) proposed that this brain region supports similar cognitive processes in the mathematical domain. According to his symbol–referent mapping hypothesis, the AG subserves the automatic mapping between mathematical symbols and their semantic referents. In basic number processing, it is assumed that the presentation of a numerical symbol (e.g., an Arabic digit) automatically activates the internal semantic representation (e.g., the magnitude representation). This hypothesis is also compatible with neuroimaging studies on mental arithmetic as over-learned arithmetic problems (e.g., the multiplication table or extensively trained problems) could have become higher-order symbols (symbolic chunks, similar to words) whose presentation automatically activates the associated solution in memory.
It is important to note that the functional interpretation of the left AG in mathematical cognition is often hindered by the observation of deactivations compared to baseline conditions. In fact, the majority of findings in mathematical information processing reflect modulations of relative deactivation rather than activation (e.g., Zago et al., 2001; Ischebeck et al., 2006; Venkatraman et al., 2006). This partly holds true for its relation with mathematical competence. For instance, Grabner et al. (2007, 2009b) reported strong relative deactivations during mental arithmetic in the less competent adults, whereas their more competent peers exhibited a weak deactivation or some activation compared to a resting-state baseline.
Taken together, studies on mental arithmetic have revealed that adults of lower and higher mathematical competence differ in the activation of the left AG. However, it is unclear whether this activation difference indeed reflects differential reliance on arithmetic processes or whether it is related to a more general function in mathematical cognition. In the present fMRI study, we sought to answer this question by administering a task drawing on another key component of mathematical competence besides mental arithmetic, i.e., the processing of multiple mathematical representations (NCTM, 2000). Concretely, we presented adults of lower and higher mathematical competence (again matched in verbal and figural–spatial abilities) with a representation matching task, requiring them to indicate whether the mathematical information in a symbolic equation and a bar chart is identical or not. In order to evaluate the role of mental arithmetic in the link between mathematical competence and AG activity, two task conditions without and one condition with arithmetic demands were administered. If the previously observed competence-related activation differences in the left AG during mental arithmetic were indeed due to differential reliance on arithmetic processes (in particular, arithmetic fact retrieval), the individuals of lower and higher mathematical competence should only exhibit left AG activation differences in the task condition with arithmetic demands. If, however, these competence-related activation differences were due to a more general process in mathematical cognition, such as symbol processing, the groups should differ in left AG activation also in the task conditions without arithmetic demands.
Another aim of the present study was to further specify the anatomical localization of potential competence-related activation differences in the parietal cortex by additionally using probabilistic cytoarchitectonic maps (Eickhoff et al., 2005; Caspers et al., 2006). This is of particular importance for a better understanding of the AG in mathematical thinking. First, the activation clusters assigned to the AG in previous fMRI studies on number processing exhibit a high anatomical heterogeneity (see, for instance, the review paper by Dehaene et al., 2003). Second, the findings in the mathematical domain can often hardly be integrated with those in other domains as various (topographically less exact) labels for this brain region have been used (e.g., temporo-parietal junction, inferior parietal cortex). And, third, cytoarchitectonic studies of post-mortem brains have shown that the parietal cortex has a more fine-grained anatomical structure than is reflected in standard atlases used in fMRI studies (Caspers et al., 2008; Zilles and Amunts, 2010). The applied probabilistic cytoarchitectonic maps divide the AG into an anterior (PGa) and a posterior (PGp) part and the supramarginal gyrus into five areas (PFop, PFt, PF, PFm, and PFcm).
Materials and Methods
Participants
Prior to the fMRI study, a pool of 179 adults (66 males) was screened with respect to their mathematical competence (by means of a mathematics test; Ibrahimovic and Bulheller, 2005) and their intelligence structure (Berlin Intelligence Structure Test; BIS-T; Jäger et al., 1997). From this pool, we selected two groups of participants for the fMRI test session (with 18 adults each; half males) who only differed in their mathematical competence but not in verbal and figural–spatial abilities (by using a similar procedure as described in Grabner et al., 2007, 2009b). The data of six participants had to be excluded from the analysis due to technical problems (one participant) or excessive movement (larger than 3 mm in translational or 3° in rotational direction) during fMRI data acquisition (five participants). The descriptive data of the remaining sample of 28 participants (15 males) is presented in Table 1. Two-sample t-tests revealed that the group of higher mathematical competence (higher math group; n = 14) displayed significantly higher scores in the mathematics test, t(26) = −8.08, p < 0.001 than the group of lower mathematical competence (lower math group, n = 14). However, both groups did not differ significantly in verbal intelligence, t(26) = 0.64, p = 0.53, figural–spatial intelligence, t(26) = −1.03, p = 0.31, nor in age, t(26) = −0.73, p = 0.47. All participants were healthy, right-handed, and had normal or corrected-to-normal vision. They gave written informed consent and were paid for their participation. The study was approved by the local ethics committee (Medical University of Graz, Austria).
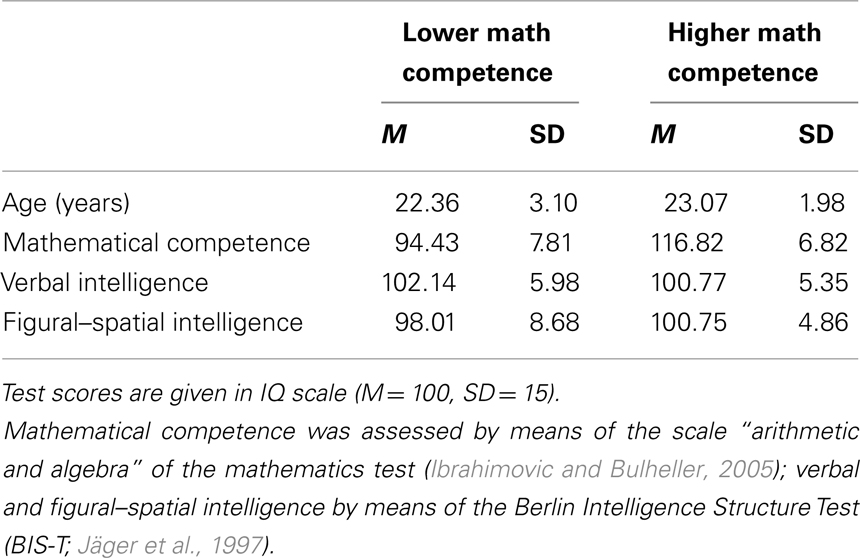
Table 1. Descriptive statistics of age and psychometric test data of the lower (n = 14) and higher (n = 14) mathematical competence group.
Experimental Tasks and Procedure
In the fMRI test session, participants worked on a mathematical representation matching (REP) task. In each problem, they were presented with a bar chart (with three variables: a, b, c) plus a symbolic equation, and had to evaluate whether the mathematical information in both representation formats is identical or not (see Figure 1). Three experimental conditions were administered. In the easiest condition (REP1), the equation described the magnitude of one variable (e.g., “a = 14”), in the second condition (REP2), the minimum or maximum magnitude of the three variables was given (e.g., “max = 13”), and in the most complex condition (REP3) an additional calculation (addition or subtraction of numbers between 1 and 6) was included (e.g., “min + 2 = 18”). Each condition comprised 42 problems. The numerical magnitude of the target variable (i.e., the variable named in REP1 or the correct value in REP2 and REP3) was between 1 and 10 (small numbers) for half of the problems and between 11 and 20 (large numbers) for the other half of the problems. Even and odd numbers were equally distributed across problems within each condition. In REP2 and REP3 minimum values were small numbers and maximum values were large numbers. In REP3 the calculation required addition or subtraction of numbers between 1 and 6. The magnitude of the distractor variables (i.e., the two other variables besides the target variable) in each problem were calculated by adding or subtracting numbers between 1 and 3 (for one distractor variable) or between 4 and 6 (for the other distractor variable). In each condition, half of the equations correctly matched the bar chart, whereas in the other half of the equations the value of one distractor bar was given.
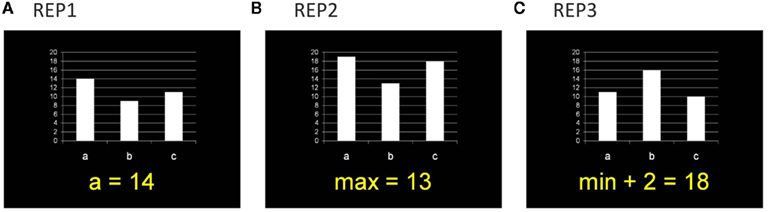
Figure 1. Example items for the three task conditions in the representation matching task (REP). Participants had to evaluate whether the mathematical information in the symbolic equation and the bar chart is identical or not. (A) In REP1, the equation described the magnitude of one variable. (B) In REP2, the minimum or maximum of the three variables was given. (C) In REP3, an additional calculation was included.
The 126 problems (42 per condition) were presented in an event-related fMRI design consisting of 3 runs with 42 problems each (14 problems per condition). The order of the problems was pseudo-randomized. Each problem was presented for 4 s, followed by an inter-trial interval of 3–5 s (jittered in 1 s steps across the problems, M = 4 s) during which a fixation point was presented on the screen. Participants responded by pressing the right-hand button if the mathematical information in the equation was identical to that of the bar chart and the left-hand button if it was not. Each run started with the number of the run (1–3) presented on the screen for 3 s, followed by a 25-s fixation period. At the end of each run, another fixation period of 20 s was included. Before imaging was performed, participants were familiarized with task and response mode and solved 12 practice problems (4 problems per REP condition). Instructions stressed speed and accuracy. The total experimental time was about 20 min.
Data Acquisition and Analysis
Imaging was performed on a 3.0 T Tim Trio system (Siemens Medical Systems, Erlangen, Germany) using an 8-channel head coil. To minimize head movement, subjects’ heads were stabilized with foam cushions. Functional images were obtained with a single shot gradient echo EPI sequence sensitive to blood oxygen level-dependent (BOLD) contrast (TR = 2000 ms, TE = 30 ms, FA = 90°, matrix size = 64 × 64, spatial resolution = 3 mm × 3 mm). In total, 586 functional volumes (first two were discarded to allow for signal stabilization) with 31 transverse slices (3 mm thickness, 0.09 mm gap) were acquired in descending order. Structural images were obtained using a T1-weighted 3D MPRAGE sequence (TR = 1900 ms, TE = 2.22 ms) which provided 1 mm isotropic resolution. Stimulus presentation was accomplished with the Eloquence system (Invivo Corporation, Orlando, FL, USA), containing an LCD display with full XGA solution, visible for the participant through a mirror mounted above the head coil. The paradigm was presented using the software package Presentation (Neurobehavioral Systems, Albany, CA, USA). For responding, two response boxes were placed in the participants’ left and right hand, respectively. Responses were given with the index finger of the right or left hand.
Functional magnetic resonance imaging data analysis was performed using SPM5 (Wellcome Department of Imaging Neuroscience, London, UK). The functional data of each participant were motion-corrected, slice-time corrected, spatially normalized into the standard Montreal Neurological Institute (MNI) space (based on the EPI template using the original voxel size of 3 mm × 3 mm × 3 mm), and smoothed using a Gaussian kernel of 8 mm FWHM. The statistical analysis was conducted on the basis of the general linear model as implemented in SPM. Model time courses for correctly solved problems in each experimental condition (REP1, REP2, REP3) and incorrectly solved problems were generated on the basis of the hemodynamic response function as given by SPM5. The time interval during the presentation of the run number (for 3 s, at the beginning of each run) and the six motion parameters were entered into the model as regressors of no interest. A high-pass filter with a cut-off frequency of 1/256 Hz was employed to remove low frequency drifts. In the analysis, the activation pattern related to each experimental condition was first computed by linear t-contrasts for each participant individually. In a second step, these images were entered into a random-effect analysis in which the two groups of mathematical competence were contrasted by means of a two-sample t-test for independent samples. Significant activation differences between the groups in each condition were identified using an initial voxel-wise threshold of p < 0.001 uncorrected. Only activation clusters significant at p < 0.05 FWE corrected for multiple comparisons at cluster level are reported. To evaluate whether the observed activation differences reflect differences in relative activation or deactivation, respectively, we extracted the individual beta weights from region-of-interests (ROIs). The anatomical location of the significant activation clusters was analyzed by means of the automated anatomical labeling (AAL) atlas (Tzourio-Mazoyer et al., 2002) and probabilistic cytoarchitectonic maps (Caspers et al., 2006, 2008) as implemented in the SPM Anatomy toolbox (Eickhoff et al., 2005).
Behavioral data (accuracy and response latencies of the correctly solved problems) were analyzed using repeated measures ANOVAs with task condition (REP1, REP2, REP3) as within-subject factor and math competence group (lower vs. higher) as between-subject factor. In all analyses, degrees of freedom were corrected for violations of the sphericity assumption by means of the Huynh–Feldt procedure; the probability of a Type I error was maintained at 0.05. If applicable, uncorrected df values together with the corrected p value and the Huynh–Feldt epsilon (ε) are reported.
Results
Behavioral Data
The ANOVA on the accuracy data revealed a main effect of task condition, F(2,52) = 50.55, p < 0.001, η2 = 0.66, ε = 0.81, as well as an interaction of task condition and math competence group, F(2,52) = 4.31, p < 0.05, η2 = 0.14. As depicted in Figure 2A, the accuracy was very high (above 95%) in the conditions REP1 and REP2, whereas it was remarkably lower in REP3. Post hoc t-tests revealed significant differences between all three conditions, all ts(27) > 2.40, ps < 0.05. Importantly, only in REP3 a significant performance difference between the mathematical competence groups emerged: The more competent individuals solved the problems more accurately than their less competent peers, t(26) = −2.29, p < 0.05.
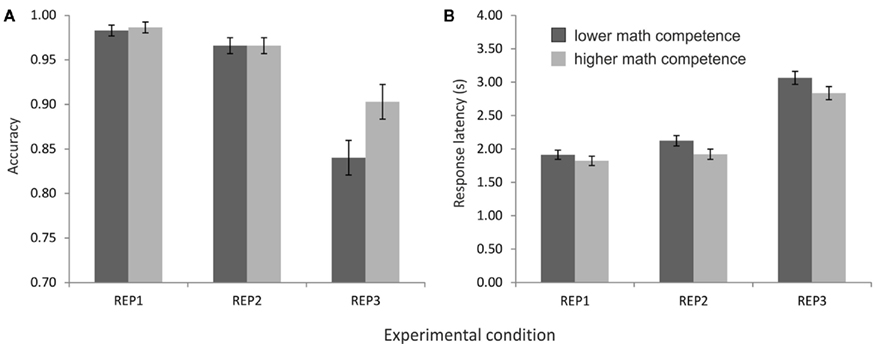
Figure 2. Performance of the mathematical competence groups in the representation matching task (REP), presented separately for the three task conditions. (A) Accuracies. (B) Response latencies of the correctly solved problems.
In the response latencies, in contrast, no effect of mathematical competence but only a significant main effect of task condition was found, F(2,52) = 579.62, p < 0.001, η2 = 0.96, ε = 0.86. As expected, the longest response latencies were observed in REP3, followed by REP2 and REP1 (see Figure 2B). All differences between task conditions reached significance in post hoc comparisons, ts(27) > 5.10, p < 0.001.
fMRI Data
Contrasting the brain activation of the two competence groups only revealed significantly higher activation in the mathematically more (compared to less) competent individuals. Most interestingly, however, the anatomical location of the activation differences was strikingly similar for all three task conditions: It mainly covered the left AG but also included parts of the supramarginal gyrus and the inferior parietal cortex (see Table 2 and Figure 3). No other brain regions displayed significant activation differences between groups. The beta weights of the three clusters showed that the observed activation difference is due to strong relative deactivation in the individuals of lower mathematical competence and weak relative activation in the more competent peers.
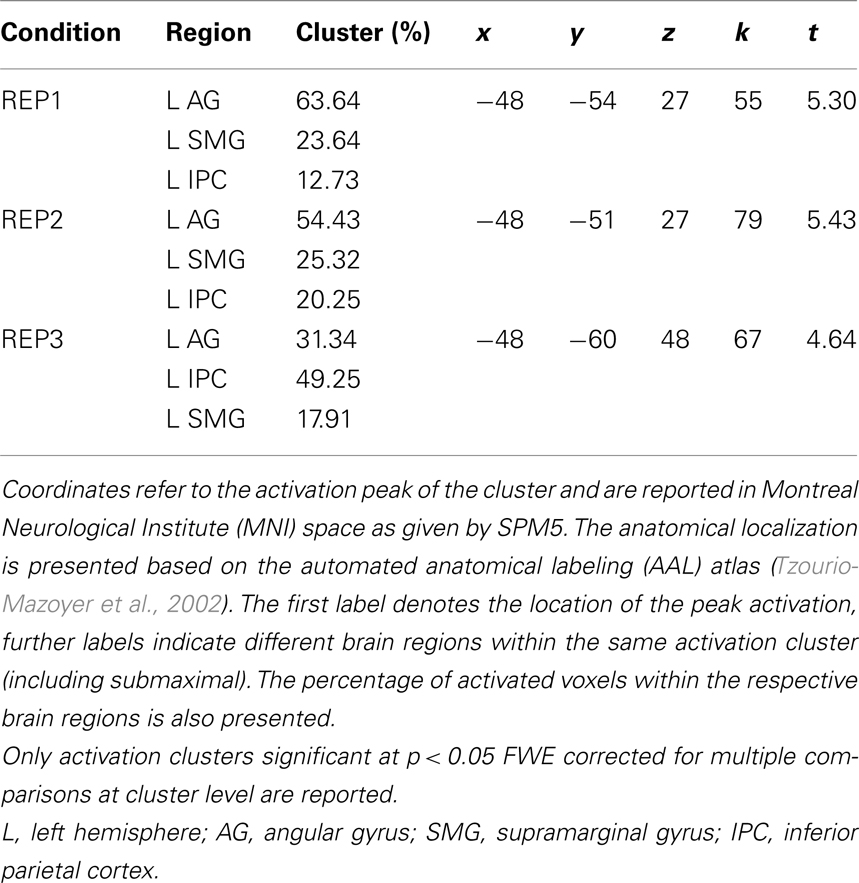
Table 2. Overview of activation clusters emerging in the contrasts of higher > lower mathematical competence in the three experimental conditions of the representation matching task (REP).
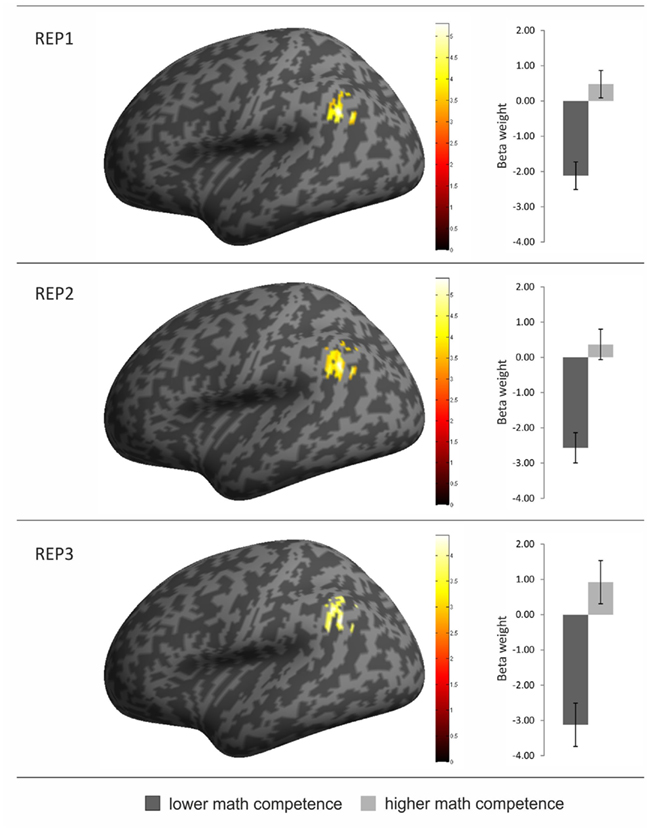
Figure 3. Overview of brain regions with greater activation in the individuals of higher (compared to lower) mathematical competence in the three conditions of the representation matching task (REP). The activation clusters are depicted on an inflated brain in left lateral view (left part of the figure). In addition, the beta weights from the three activation clusters are presented separately for the two math competence groups. Error bars depict ± 1 SE of the mean.
The probabilistic cytoarchitectonic localization of the competence-related activation difference is presented in Table 3 and depicted in Figure 4A. In all three task conditions, the largest part of the activation clusters lay within the left anterior AG (area PGa), followed by areas of the supramarginal gyrus (PFm, PF, and PFcm). To further evaluate whether the activation in the left anterior AG also differed between the task conditions and whether this may interact with the math competence group, we additionally extracted the individual beta weights from the anatomically defined PGa region in the left hemisphere. An ANOVA with task condition and math competence group only yielded a large main effect of math competence group, F(1,26) = 24.86, p < 0.001, η2 = 0.49. As depicted in Figure 4B, the activation levels of both groups in the left PGa did not differ as a function of task condition and display a stronger deactivation in the group of lower compared to higher mathematical competence.
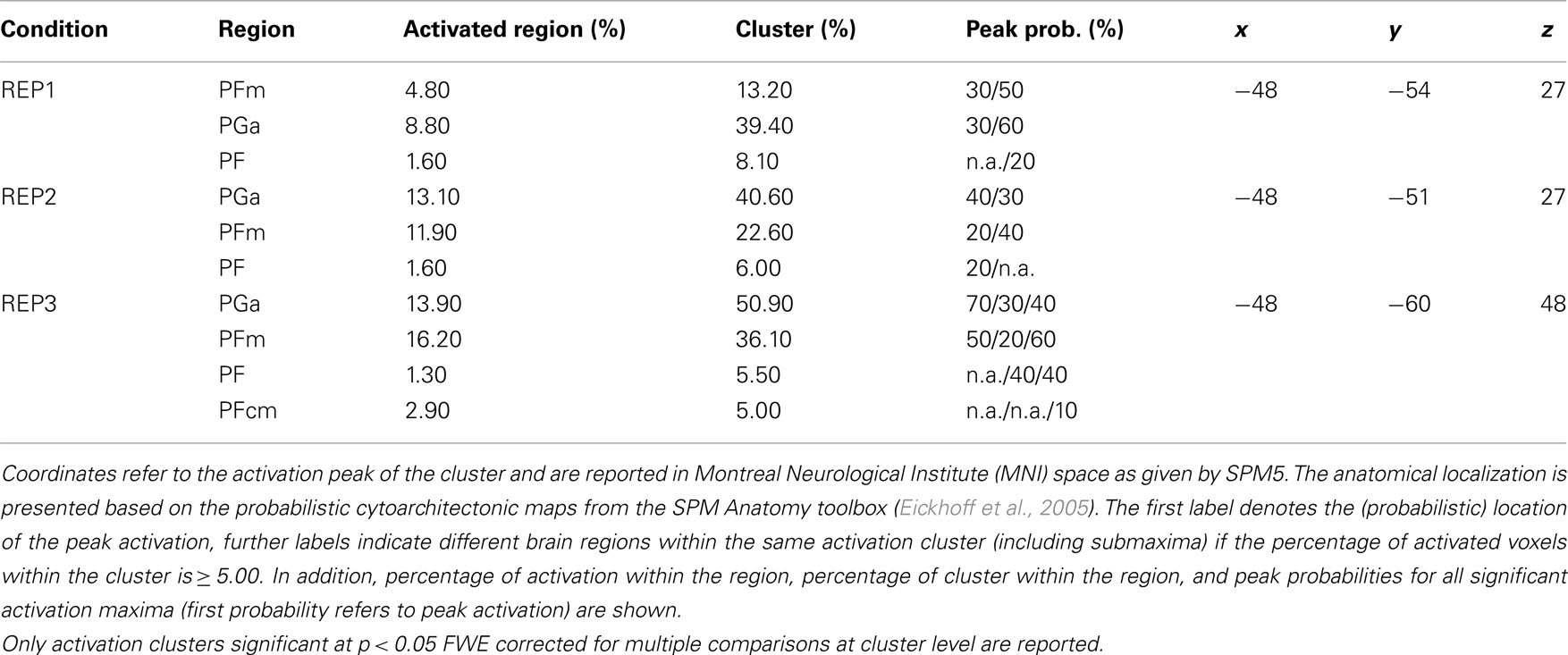
Table 3. Probabilistic cytoarchitectonic localization of left-hemispheric activation clusters emerging in the contrasts of higher > lower mathematical competence in the three experimental conditions of the representation matching task (REP).
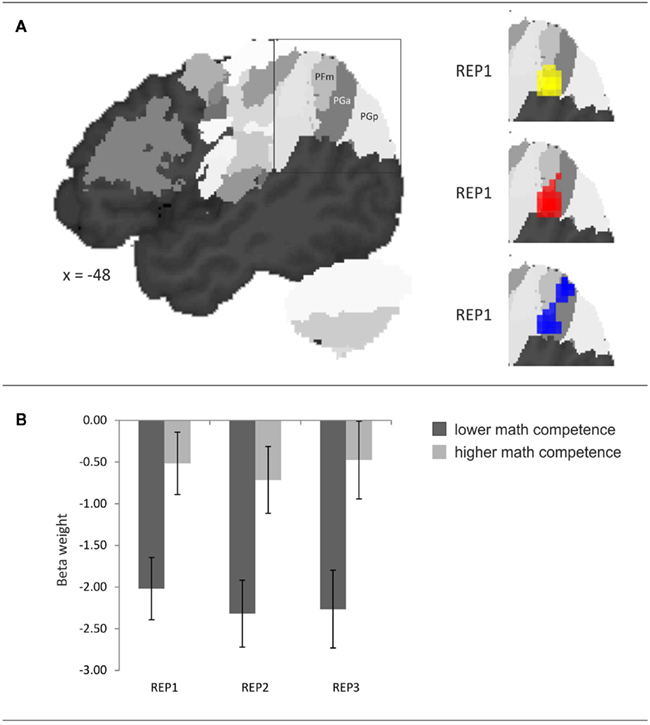
Figure 4. (A) Probabilistic cytoarchitectonic localization of the left-hemispheric activation cluster emerging in the contrast higher > lower mathematical competence in the three conditions of the representation matching task (REP). (B) Effect of mathematical competence on beta weights in area PGa. Error bars depict ± 1 SE of the mean.
Discussion
In the present fMRI study, we investigated the brain correlates of mathematical competence in a task drawing on the core ability to process mathematical representations (NCTM, 2000; Reyna et al., 2009). Specifically, we were interested in the functional significance of activation differences in the left AG observed in previous studies on mental arithmetic (Menon et al., 2000; Grabner et al., 2007, 2009b). To this end, we presented adults of lower and higher mathematical competence with a representation matching task that either only involved the processing of two representations (symbolic equation and bar chart) or additionally required mental arithmetic.
The behavioral data revealed that both groups of mathematical competence performed equally well in the two task conditions without arithmetic demands. This was true in terms of accuracy as well as response latencies. Mathematical competence only had an impact on accuracy when participants had to additionally perform a simple mental calculation (addition or subtraction). In the fMRI data, however, significant effects of mathematical competence were observed in all three task conditions: The individuals of higher mathematical competence displayed stronger activation of the left AG extending to the supramarginal gyrus than their less competent peers. The present findings extend previous research on the brain correlates of adults’ mathematical competence in two ways.
First, they demonstrate that adults of lower and higher mathematical competence show different brain activation patterns in mathematical thinking which are not accompanied by performance differences in the experimental task. In all previous studies, competence-related activation differences were confounded with differential task performance levels (Menon et al., 2000; Grabner et al., 2007, 2009b). This considerably compromised the functional interpretation of AG activation in relation to mathematical competence as it could not be ruled out that the activation differences can be attributed to differences in relative task difficulty. The AG is part of the default-mode network (DMN; Raichle et al., 2001) which typically displays lower relative activity (larger deactivation) in more difficult task conditions (McKiernan et al., 2003; Buckner et al., 2008). Since such an association between task difficulty and AG activation has been reported in practically all fMRI studies on mental arithmetic (for reviews, cf. Dehaene et al., 2003; Zamarian et al., 2009), some authors argued that the engagement of the left AG is related to difficulty-related modulations of the DMN rather than to task-specific cognitive processes (e.g., Zago et al., 2001; Wu et al., 2009). Consequently, a lower relative activity (larger deactivation) in the less (compared to the more) competent individuals may merely reflect a stronger (negative) modulation of the DMN because the task is more difficult for these individuals (in terms of accuracy and/or response latencies). The present finding of competence-related left AG activation differences in the absence of experimental performance differences stands in contrast to this explanation. Notably, a recent study on mental arithmetic has added further evidence against the difficulty explanation of AG activity in mathematical cognition. Grabner et al. (in press) investigated the neural correlates of the well-established associative confusion effect (Winkelman and Schmidt, 1974) that consists of poorer performance while verifying addition and multiplication equations whose solutions are associated with the other operation (confusion equations; e.g., “9 × 6 = 15”) compared to solutions unrelated to both operations (non-confusion equations; e.g., “9 × 6 = 52”). In comparing both task conditions, it was found that the more difficult confusion equations were associated with higher relative activation in the left AG, which is also opposite to the typical behavior of the DMN.
Second, the present study revealed that adults of higher mathematical competence more strongly activated the left AG while processing mathematical representations independently of whether the task requires cognitive processes related to mental arithmetic. The left AG activation (in the PGa region) neither differed between the task conditions nor was the competence effect moderated by them. This finding sheds new light onto the functional significance of competence-related activation differences in the left AG. In particular, it precludes the account that processes related to mental arithmetic underlie competence-related activation differences in the left AG. If this had been the case, then a different result pattern should have emerged in the condition in which an additional mental calculation had to be carried out. This also holds true for the fact retrieval account since only calculations of small problem size (results smaller or equal 20 with addends and subtrahends between 1 and 6) were presented, which are likely to be solved by retrieving the solution from memory (Campbell and Xue, 2001; Grabner and De Smedt, 2011).
Thus, the obtained findings indicate that the left AG supports a more general cognitive function in which adults of lower and higher mathematical competence differ. Besides the aforementioned fact retrieval and task difficulty accounts, it has been proposed that this brain region is implicated in the processing of mathematical symbols such as Arabic digits or even equations (Ansari, 2008; Holloway et al., 2010; Price and Ansari, 2011; Grabner et al., in press). The current results can be reconciled with this view as in all three conditions of the representation matching task participants were required to process the symbolic equation (e.g., “a = 14”) and to compare this information with the graphical representation. Following this contention, the differential left AG activation in the two competence groups may reflect subtle differences in the proficiency of mathematical symbol processing which did not appear in behavior.
At present, the most prominent account on the function of the AG in mathematical symbol processing is the symbol–referent mapping hypothesis (Ansari, 2008). According to this hypothesis, the AG supports the automatic mapping of mathematical symbols onto semantic representations, similar to the function of the AG in linguistic symbol processing. At the basic level, this mapping could occur between Arabic digits and the internal magnitude representation (similar to grapheme–phoneme mappings) but also mappings between symbolic chunks (e.g., arithmetic equations) and higher-order semantic knowledge (e.g., arithmetic solutions) have been discussed (similar to the associations between words and their meaning). While the present results are inconsistent with competence-related differences in mappings between arithmetic equations and solutions, the data do not allow to draw conclusions regarding which type of symbols are differentially processed in mathematically more and less competent individuals. It may be speculated that the groups already differ in the proficiency of processing number symbols. This assumption would be in line with recent evidence showing that the automatic access of magnitude information from symbolic representations is key in the development of mathematical competence (e.g., Rousselle and Noel, 2007; Iuculano et al., 2008; Holloway and Ansari, 2009; De Smedt and Gilmore, 2011).
Two current models on the general functional significance of the (anterior) AG are largely consistent with the symbol–referent mapping hypothesis. First, the ventral parietal cortex comprising the AG and the supramarginal gyrus have been linked to bottom-up attentional processes during direct memory retrieval. Specifically, in their attention-to-memory (AtoM) model, Cabeza et al. (2008) argued that the automatic activation of memory contents upon the presentation of an external cue (such as in automatic symbol–referent mapping) is due to bottom-up attentional processes which are mediated by the ventral parietal cortex. Top-down attentional processes engaged in retrieval after controlled memory search, in contrast, have been linked to areas of the dorsal (superior) parietal lobe (centered on the IPS). This view has been corroborated by findings of higher inferior parietal activation for items that were recognized with high compared to low confidence (Chua et al., 2006), for strong compared to weak memories (Shannon and Buckner, 2004), and for memory retrieval facilitated by semantic priming (Whitney et al., 2009). Second, there is increasing consensus that the left AG supports semantic information processing, in particular semantic integration and knowledge retrieval (Binder et al., 2009; Price, 2010). Seghier et al. (2010) additionally presented evidence that the dorsal AG (corresponding to area PGa) may specifically support the search for a semantic representation, which is a process that is likely engaged during symbol–referent mapping.
A central limitation of applying these models to the domain of mathematics, however, lies in the frequent observation of relative deactivations in the left AG even in task conditions that should elicit bottom-up attention processes or semantic information processing (Cabeza et al., 2008; Binder et al., 2009). In the present study, we observed strong relative deactivation in the less competent individuals, whereas their more competent peers displayed some activation above resting-state baseline (see Figure 3). This finding is consistent with Grabner et al. (2007) who reported an association between mathematical competence and peak activation in the left AG that ranged from deactivation to activation. The functional significance of this (de-)activation pattern is still an unresolved issue, and studies with multiple baseline conditions other than fixation are needed. Direct memory retrieval (e.g., Mazoyer et al., 2001) and semantic processes (e.g., Binder et al., 1999) have been proposed to spontaneously occur during resting state so that any task-related activation increase or decrease may reflect higher and lower engagement of these processes compared to baseline. In reference to the symbol–referent mapping hypothesis, Holloway et al. (2010) recently suggested that this deactivation may reflect a filter mechanism that is engaged whenever symbols cannot be mapped onto their semantic referents in order to allow for alternative processing. However, since no brain regions turned out to be more active in the less competent individuals, it remains elusive what alternative processing may take place if this filter is engaged.
Even though the symbol–referent mapping hypothesis provides a rational framework in which the present and many other findings have been discussed, it is important to point out that its prediction regarding the mapping of numerical symbols onto magnitude representation lacks direct empirical support from training studies so far. Lyons and Ansari (2009) required young adults to associate novel geometrical symbols with approximate numerical magnitudes during fMRI and did not find modulations of AG activity in a number comparison task involving the novel symbols. In contrast, the left IPS and prefrontal brain regions responded to magnitude processing. Similar evidence was reported by Diester and Nieder (2007) who trained two monkeys to assign visual shapes to numerical magnitudes in a delayed match-to-sample task. They recorded the neural activity from single cells in the prefrontal cortex and the IPS (but not in the AG) and observed that the responses of many prefrontal neurons were modulated by the numerical value. These findings demonstrate important roles of prefrontal and IPS regions in the early learning of associations between numerical symbols and magnitudes but do not rule out the assumption that the AG may be involved in the automatic semantic processing of numerical symbols after extended practice or in a later stage of development (Grabner, 2009). Several fMRI studies have revealed that the activation of the AG and the IPS underlie considerable developmental activation shifts (for a review, cf. Ansari, 2010). Moreover, significant activation increases in the AG have been reported after a 5-day training of the association between numerical facts and three-dimensional geometric objects (Grabner et al., 2009b). Therefore, future studies need to address the potential interplay of the prefrontal cortex, the IPS, and the AG in symbol–referent mapping.
The application of probabilistic cytoarchitectonic maps has revealed that the activation difference between the mathematical competence groups was mainly located in area PGa of the AG which corresponds to the results of all previous studies on number processing reporting probabilistic cytoarchitectonic regions (Wu et al., 2009; Rosenberg-Lee et al., 2011; Grabner et al., in press). Wu et al. (2009) found stronger PGa (and PGp) activation in mental arithmetic using Arabic compared to Roman digits. Notably, this result also nicely fits into the symbol–referent mapping hypothesis as Arabic digits are highly over-learned and can be expected to be more automatically mapped onto the semantic magnitude representation than Roman digits. Rosenberg-Lee et al. (2011) reported associations between performance in multiplication and division problems and the left PGa. Finally, also the aforementioned associative confusion effect in the Grabner et al. (in press) study was accompanied by activation increases in the area PGa. These and the present findings demonstrate a functional differentiation between the anterior and posterior AG (areas PGa and PGp) and provide first evidence that area PGa may be primarily associated with mathematical information processing, in general, and symbol processing, in particular.
In conclusion, the present study has revealed that mathematically more (compared to less) competent adults display stronger left (anterior) AG activity in a task drawing on the ability of processing multiple mathematical representations. The activation difference between competence groups was not moderated by the presence or absence of arithmetic demands, which indicates that it cannot be attributed to a differential reliance on arithmetic processes such as fact retrieval. Rather, the present results add to current evidence suggesting an important role of the left AG in the processing of symbolic mathematical representations. The stronger activity in the more competent adults may thus reflect a higher proficiency in this cognitive function. Moreover, this study provides the first demonstration of differential parietal activation patterns in mathematically more and less competent adults that were not accompanied by performance differences in the experimental task.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This research was partly supported by a grant from the Provincial Government of Styria (Landesregierung Steiermark) in Austria. We thank Daniela Gebauer for her assistance in the test sessions, Elsbeth Stern for supporting this study, and Daniel Ansari for valuable comments. Moreover, the helpful comments of the reviewers are gratefully appreciated.
References
Ansari, D. (2008). Effects of development and enculturation on number representation in the brain. Nat. Rev. Neurosci. 9, 278–291.
Ansari, D. (2010). Neurocognitive approaches to developmental disorders of numerical and mathematical cognition: the perils of neglecting the role of development. Learn. Individ. Diff. 20, 123–129.
Binder, J. R., Desai, R. H., Graves, W. W., and Conant, L. L. (2009). Where is the semantic system? A critical review and meta-analysis of 120 functional neuroimaging studies. Cereb. Cortex 19, 2767–2796.
Binder, J. R., Frost, J. A., Hammeke, T. A., Bellgowan, P. S. F., Rao, S. M., and Cox, R. W. (1999). Conceptual processing during the conscious resting state: a functional MRI study. J. Cogn. Neurosci. 11, 80–93.
Buckner, R. L., Andrews-Hanna, J. R., and Schacter, D. L. (2008). The brain’s default network – anatomy, function, and relevance to disease. Ann. N. Y. Acad. Sci. 1124, 1–38.
Butterworth, B., and Laurillard, D. (2010). Low numeracy and dyscalculia: identification and intervention. ZDM 42, 527–539.
Butterworth, B., Varma, S., and Laurillard, D. (2011). Dyscalculia: from brain to education. Science 332, 1049–1053.
Cabeza, R., Ciaramelli, E., Olson, I. R., and Moscovitch, M. (2008). The parietal cortex and episodic memory: an attentional account. Nat. Rev. Neurosci. 9, 613–625.
Campbell, J. I. D., and Xue, Q. L. (2001). Cognitive arithmetic across cultures. J. Exp. Psychol. Gen. 130, 299–315.
Caspers, S., Eickhoff, S. B., Geyer, S., Scheperjans, F., Mohlberg, H., Zilles, K., and Amunts, K. (2008). The human inferior parietal lobule in stereotaxic space. Brain Struct. Funct. 212, 481–495.
Caspers, S., Geyer, S., Schleicher, A., Mohlberg, H., Amunts, K., and Zilles, K. (2006). The human inferior parietal cortex: cytoarchitectonic parcellation and interindividual variability. Neuroimage 33, 430–448.
Chua, E. F., Schacter, D. L., Rand-Glovannetti, E., and Sperling, R. A. (2006). Understanding metamemory: neural correlates of the cognitive process and subjective level of confidence in recognition memory. Neuroimage 29, 1150–1160.
De Smedt, B., and Gilmore, C. K. (2011). Defective number module or impaired access? Numerical magnitude processing in first graders with mathematical difficulties. J. Exp. Child. Psychol. 108, 278–292.
Dehaene, S., Molko, N., Cohen, L., and Wilson, A. J. (2004). Arithmetic and the brain. Curr. Opin. Neurobiol. 14, 218–224.
Dehaene, S., Piazza, M., Pinel, P., and Cohen, L. (2003). Three parietal circuits for number processing. Cogn. Neuropsychol. 20, 487–506.
Delazer, M., Domahs, F., Bartha, L., Brenneis, C., Lochy, A., Trieb, T., and Benke, T. (2003). Learning complex arithmetic – an fMRI study. Brain Res. Cogn. Brain Res. 18, 76–88.
Delazer, M., Ischebeck, A., Domahs, F., Zamarian, L., Koppelstaetter, F., Siedentopf, C. M., Kaufmann, L., Benke, T., and Felber, S. (2005). Learning by strategies and learning by Drill – evidence from an fMRI study. Neuroimage 25, 838–849.
Diester, I., and Nieder, A. (2007). Semantic associations between signs and numerical categories in the prefrontal cortex. PLoS Biol. 5, e294. doi:10.1371/journal.pbio.0050294
Eickhoff, S. B., Stephan, K. E., Mohlberg, H., Grefkes, C., Fink, G. R., Amunts, K., and Zilles, K. (2005). A new SPM toolbox for combining probabilistic cytoarchitectonic maps and functional imaging data. Neuroimage 25, 1325–1335.
Grabner, R. H., Ansari, D., Koschutnig, K., Reishofer, G., and Ebner, F. (in press). The function of the left angular gyrus in mental arithmetic: evidence from the associative confusion effect. Hum. Brain Mapp.
Grabner, R. H., Ansari, D., Koschutnig, K., Reishofer, G., Ebner, F., and Neuper, C. (2009a). To retrieve or to calculate? Left angular gyrus mediates the retrieval of arithmetic facts during problem solving. Neuropsychologia 47, 604–608.
Grabner, R. H., Ischebeck, A., Reishofer, G., Koschutnig, K., Delazer, M., Ebner, F., and Neuper, C. (2009b). Fact learning in complex arithmetic and figural-spatial tasks: the role of the angular gyrus and its relation to mathematical competence. Hum. Brain Mapp. 30, 2936–2952.
Grabner, R. H., Ansari, D., Reishofer, G., Stern, E., Ebner, F., and Neuper, C. (2007). Individual differences in mathematical competence predict parietal brain activation during mental calculation. Neuroimage 38, 346–356.
Grabner, R. H., and De Smedt, B. (2011). Neurophysiological evidence for the validity of verbal strategy reports in mental arithmetic. Biol. Psychol. 87, 128–136.
Gullick, M. M., Sprute, L. A., and Temple, E. (in press). Individual differences in working memory, nonverbal IQ, and mathematics achievement and brain mechanisms associated with symbolic and nonsymbolic number processing. Learn. Individ. Differ.
Holloway, I. D., and Ansari, D. (2009). Mapping numerical magnitudes onto symbols: the numerical distance effect and individual differences in children’s mathematics achievement. J. Exp. Child. Psychol. 103, 17–29.
Holloway, I. D., Price, G. R., and Ansari, D. (2010). Common and segregated neural pathways for the processing of symbolic and nonsymbolic numerical magnitude: an fMRI study. Neuroimage 49, 1006–1017.
Ibrahimovic, N., and Bulheller, S. (2005). Mathematiktest [Mathematics test]. Frankfurt: Harcourt Test Services.
Isaacs, E. B., Edmonds, C. J., Lucas, A., and Gadian, D. G. (2001). Calculation difficulties in children of very low birthweight. Brain 124, 1701–1707.
Ischebeck, A., Zamarian, L., Egger, K., Schocke, M., and Delazer, M. (2007). Imaging early practice effects in arithmetic. Neuroimage 36, 993–1003.
Ischebeck, A., Zamarian, L., Siedentopf, C., Koppelstatter, F., Benke, T., Felber, S., and Delazer, M. (2006). How specifically do we learn? Imaging the learning of multiplication and subtraction. Neuroimage 30, 1365–1375.
Iuculano, T., Tang, J., Hall, C. W. B., and Butterworth, B. (2008). Core information processing deficits in developmental dyscalculia and low numeracy. Dev. Sci. 11, 669–680.
Jäger, O. A., Süß, H. M., and Beauducel, A. (1997). Berliner Intelligenzstruktur-Test [Berlin Intelligence Structure Test]. Göttingen: Hogrefe.
Kucian, K., Loenneker, T., Dietrich, T., Dosch, M., Martin, E., and Von Aster, M. (2006). Impaired neural networks for approximate calculation in dyscalculic children: a functional MRI study. Behav. Brain Funct. 2, 31.
Lee, K. M. (2000). Cortical areas differentially involved in multiplication and subtraction: a functional magnetic resonance imaging study and correlation with a case of selective acalculia. Ann. Neurol. 48, 657–661.
Lipkus, I. M., and Peters, E. (2009). Understanding the role of numeracy in health: proposed theoretical framework and practical insights. Health Educ. Behav. 36, 1065–1081.
Lyons, I. M., and Ansari, D. (2009). The cerebral basis of mapping nonsymbolic numerical quantities onto abstract symbols: an fMRI training study. J. Cogn. Neurosci. 21, 1720–1735.
Mazoyer, B., Zago, L., Mellet, E., Bricogne, S., Etard, O., Houdé, O., Crivello, F., Joliot, M., Petit, L., and Tzourio-Mazoyer, N. (2001). Cortical networks for working memory and executive functions sustain the conscious resting state in man. Brain Res. Bull. 54, 287–298.
McKiernan, K. A., Kaufman, J. N., Kucera-Thompson, J., and Binder, J. R. (2003). A parametric manipulation of factors affecting task-induced deactivation in functional neuroimaging. J. Cogn. Neurosci. 15, 394–408.
Menon, V., Rivera, S. M., White, C. D., Eliez, S., Glover, G. H., and Reiss, A. L. (2000). functional optimization of arithmetic processing in perfect performers. Brain Res. Cogn. Brain Res. 9, 343–345.
NCTM. (2000). Principles and Standards for School Mathematics. Reston, VA: The National Council of Teachers of Mathematics, Inc.
Neisser, U., Boodoo, G., Bouchard, T. J., Boykin, A. W., Brody, N., Ceci, S. J., Halpern, D. F., Loehlin, J. C., Perloff, R., Sternberg, R. J., and Urbina, S. (1996). Intelligence: knowns and unknowns. Am. Psychol. 51, 77–101.
Parsons, S., and Bynner, J. (2005). Does Numeracy Matter More? London: National Research and Development Centre for adult literacy and numeracy.
Price, C. J. (2000). The anatomy of language: contributions from functional neuroimaging. J. Anat. 197, 335–359.
Price, C. J. (2010). The anatomy of language: a review of 100 fMRI studies published in 2009. Ann. N. Y. Acad. Sci. 1191, 62–88.
Price, G. R., and Ansari, D. (2011). Symbol processing in the left angular gyrus: evidence from passive perception of digits. Neuroimage 57, 1205–1211.
Price, G. R., Holloway, I., Räsänen, P., Vesterinen, M., and Ansari, D. (2007). Impaired parietal magnitude processing in developmental dyscalculia. Curr. Biol. 17, R1042–R1043.
Raichle, M. E., Macleod, A. M., Snyder, A. Z., Powers, W. J., Gusnard, D. A., and Shulman, G. L. (2001). A default mode of brain function. Proc. Natl. Acad. Sci. U.S.A. 98, 676–682.
Reyna, V. F., Nelson, W. L., Han, P. K., and Dieckmann, N. F. (2009). How numeracy influences risk comprehension and medical decision making. Psychol. Bull. 135, 943–973.
Rosenberg-Lee, M., Chang, T. T., Young, C. B., Wu, S., and Menon, V. (2011). Functional dissociations between four basic arithmetic operations in the human posterior parietal cortex: a cytoarchitectonic mapping study. Neuropsychologia 49, 2592–2608.
Rotzer, S., Kucian, K., Martin, E., Von Aster, M., Klaver, P., and Loenneker, T. (2008). Optimized voxel-based morphometry in children with developmental dyscalculia. Neuroimage 39, 417–422.
Rousselle, L., and Noel, M. P. (2007). Basic numerical skills in children with mathematics learning disabilities: a comparison of symbolic vs non-symbolic number magnitude processing. Cognition 102, 361–395.
Rubinsten, O., and Henik, A. (2009). Developmental dyscalculia: heterogeneity might not mean different mechanisms. Trends Cogn. Sci. (Regul. Ed.) 13, 92–99.
Schmidt, F. L., and Hunter, J. E. (1998). The validity and utility of selection methods in personnel psychology: practical and theoretical implications of 85 years of research findings. Psychol. Bull. 124, 262–274.
Seghier, M. L., Fagan, E., and Price, C. J. (2010). Functional subdivisions in the left angular gyrus where the semantic system meets and diverges from the default network. J. Neurosci. 30, 16809–16817.
Shannon, B. J., and Buckner, R. L. (2004). Functional-anatomic correlates of memory retrieval that suggest nontraditional processing roles for multiple distinct regions within posterior parietal cortex. J. Neurosci. 24, 10084–10092.
Tzourio-Mazoyer, N., Landeau, B., Papathanassiou, D., Crivello, F., Etard, O., Delcroix, N., Mazoyer, B., and Joliot, M. (2002). Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. Neuroimage 15, 273–289.
Venkatraman, V., Siong, S. C., Chee, M. W. L., and Ansari, D. (2006). Effect of language switching on arithmetic: a bilingual fMRI study. J. Cogn. Neurosci. 18, 64–74.
Whitney, C., Grossman, M., and Kircher, T. T. J. (2009). The influence of multiple primes on bottom-up and top-down regulation during meaning retrieval: evidence for 2 distinct neural networks. Cereb. Cortex 19, 2548–2560.
Winkelman, J. H., and Schmidt, J. (1974). Associative confusions in mental arithmetic. J. Exp. Psychol. 102, 734–736.
Wu, S. S., Chang, T. T., Majid, A., Caspers, S., Eickhoff, S. B., and Menon, V. (2009). Functional heterogeneity of inferior parietal cortex during mathematical cognition assessed with cytoarchitectonic probability maps. Cereb. Cortex 19, 2930–2945.
Zago, L., Pesenti, M., Mellet, E., Crivello, F., Mazoyer, B., and Tzourio-Mazoyer, N. (2001). Neural correlates of simple and complex mental calculation. Neuroimage 13, 314–327.
Zamarian, L., Ischebeck, A., and Delazer, M. (2009). Neuroscience of learning arithmetic-evidence from brain imaging studies. Neurosci. Biobehav. Rev. 33, 909–925.
Keywords: angular gyrus, mathematical competence, fMRI, arithmetic, fact retrieval, symbol–referent mapping
Citation: Grabner RH, Reishofer G, Koschutnig K and Ebner F (2011) Brain correlates of mathematical competence in processing mathematical representations. Front. Hum. Neurosci. 5:130. doi: 10.3389/fnhum.2011.00130
Received: 31 August 2011;
Accepted: 19 October 2011;
Published online: 04 November 2011.
Edited by:
Filip Van Opstal, Ghent University, BelgiumReviewed by:
Guilherme Wood, Karl-Franzens-University of Graz, AustriaIan Mark Lyons, University of Chicago, USA
Copyright: © 2011 Grabner, Reishofer, Koschutnig and Ebner. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence: Roland H. Grabner, Institute for Behavioral Sciences, Swiss Federal Institute of Technology Zurich, Universitaetsstrasse 6, CH-8092 Zurich, Switzerland. e-mail:Z3JhYm5lckBpZnYuZ2Vzcy5ldGh6LmNo

 Gernot Reishofer2
Gernot Reishofer2