- 1 Department of Psychology, University of Bologna, Bologna, Italy
- 2 Department of General Psychology, University of Padova, Padova, Italy
- 3 Communication Disciplines Department, University of Bologna, Bologna, Italy
- 4 Institute of Cognitive Science and Technology, CNR, Rome, Italy
The field of numerical cognition represents an interesting case for action-based theories of cognition, since number is a special kind of abstract concept. Several studies have shown that within the parietal lobes adjacent neural regions code numerical magnitude and grasping-related information. This anatomical proximity between brain areas involved in number and sensorimotor processes may account for interactions between numerical magnitude and action. In particular, recent studies have demonstrated a causal role of action perception on numerical magnitude processing. If objects are represented in terms of actions (affordances), the causal role of action on number processing should extend to the case of objects affordances. This study investigates the relationship between numbers and objects affordances in two experiments, without (Experiment 1) or with (Experiment 2) the requirement of an action (i.e., participants were asked to hold an object in their hands during the task). The task consisted in repeating aloud the odd or even digit within a pair depending on the type of the preceding or following object. Order of presentation (object–number vs. number–object), Object type (graspable vs. ungraspable), Object size (small vs. large), and Numerical magnitude (small vs. large) were manipulated for each experiment. Experiment 1 showed a facilitation – in terms of quicker responses – for graspable over ungraspable objects preceded by numbers, and an effect of numerical magnitude after the presentation of graspable objects. Experiment 2 demonstrated that the action execution enhanced overall the sensitivity to numerical magnitude, and that at the same time it interfered with the effects of objects affordances on number processing. Overall, these findings demonstrate that numbers and graspable objects are strongly interrelated, supporting the view that abstract concepts may be grounded in the motor experience.
Introduction
According to embodied and grounded cognition theories, all human knowledge is grounded into perception–action systems, through which sensory–motor experiences build up concrete and abstract concepts during lifespan (Barsalou, 1999; Gallese and Lakoff, 2005; Pecher and Zwaan, 2005; Pulvermüller, 2005). Whereas consistent evidence of this has been provided for concrete (i.e., non-abstract) knowledge (Barsalou, 2008), only few studies have suggested the possibility of an action-based development of abstract concepts (Boroditsky and Ramscar, 2002; Glenberg et al., 2008; Borghi and Cimatti, 2009; Casasanto, 2009; Borghi and Pecher, 2011; Pecher and Boot, 2011; Pecher et al., 2011). A specific case for the latter domain is given by numerical cognition.
Indeed, the concept of natural number is an example of abstract concept which develops primary through the sensory–motor experience of finger counting (Andres et al., 2008a; Fischer and Brugger, 2011). Children learn the meaning of number as an abstract concept which can be applied to a variety of different entities through the experience of counting on their hands. Finger counting may be relevant to the development of mathematical abilities as indicated by developmental studies (Noël, 2005), and its influence on numerical cognition persists through adulthood (Di Luca et al., 2006; Di Luca and Pesenti, 2008). Classic evidence of the relevance of hand-related abilities on numerical cognition comes from neuropsychological studies. For instance, both numerical and finger gnosis impairments typically co-occur in the Gerstmann syndrome (Gerstmann, 1940). In addition, the developmental Gerstmann syndrome (Kinsbourne and Warrington, 1963) is characterized, among other symptoms, by dyscalculia and constructional dyspraxia (Rourke and Conway, 1997), which might suggest a role of hand motor planning mechanisms in the development of numerical abilities. This association between the hand and the processing of numbers extends to the fundamental activity that humans can perform with their hands, which consists in grasping and manipulating objects.
At the cortical level, the human neural circuitry devoted to grasping is close to that of number processing (Simon et al., 2002). Indeed, a number of neuroimaging studies have found that numbers are consistently represented in the parietal cortex (Dehaene et al., 2003). However, the parietal lobes are crucial for a plurality of tasks, including attention, spatial cognition, sensory–motor integration, action planning, and control (e.g., Milner and Goodale, 1995; Culham and Kanwisher, 2001; Frey et al., 2005; Culham and Valyear, 2006). Most of these functions are organized in an anterior to posterior manner along the intraparietal sulcus (IPS, Simon et al., 2002). Their anatomical organization suggests that the neural mechanisms underpinning the hand-number relationship might lie in the IPS.
Of relevance for grasping action is the human anterior portion of the IPS (aIPS; for a review, see Castiello, 2005). Several parts of the human parietal cortex have homologous areas in the monkey brain (e.g., Culham and Kanwisher, 2001; Hubbard et al., 2005). However, it has been suggested that a part of the human aIPS, evolutionarily new, is related to the planning of grasping and principally to tool manipulation (Orban et al., 2006). Importantly, the circuitry for grasping, including parietal and premotor areas (Castiello, 2005), is recruited both during action execution and action observation (Grafton, 2009), during object observation and grasping execution toward the same object (Grèzes et al., 2003), and during the observation of manipulable objects (Gerlach et al., 2002). Perceiving objects – either man-made (Chao and Martin, 2000), familiar (Grafton et al., 1997), or tools compared to graspable shapes (Creem-Regehr and Lee, 2005) – triggers the activation of both the dorsal stream, in particular in the IPS (Culham and Valyear, 2006), and the ventral one, more specifically in the ventral premotor cortex (PMv; for a review, see Johnson-Frey, 2004). Neuroimaging studies, thus, suggest that the properties of an object are coded by brain areas involved both in its observation and manipulation (for a review, see Martin, 2007). Concerning aIPS, a recent study by Cavina-Pratesi et al. (2010) has suggested that aIPS processes intrinsic (i.e., shape and size) rather than extrinsic (i.e., location) properties of the object (in accordance to Jeannerod, 1981).
With reference to numbers, many neuroimaging studies have suggested that the IPS – in particular, the horizontal segment of the IPS (hIPS) – is crucial for the semantic representation of numerical quantity (Dehaene et al., 2003; Piazza et al., 2004). For instance, its activation is specific for numbers compared to letters or colors (Eger et al., 2003), and it is modality independent (e.g., Piazza et al., 2007; for a different view, see: Cohen Kadosh and Walsh, 2009). Together with the representations of numbers, the representations of other physical dimensions, such as size, are associated to the IPS activation (Fias et al., 2003; Pinel et al., 2004; Cohen Kadosh et al., 2005), and interactions between the processing of different magnitudes have been shown, first of all, by behavioral studies (e.g., Henik and Tzelgov, 1982). These similarities have suggested that numerical and non-numerical magnitudes may be processed by a generalized magnitude system, which is domain-independent, and mediated by the parietal lobe (a theory of magnitude, ATOM: Walsh, 2003; Bueti and Walsh, 2009). Most importantly, the cognitive processes and the neural mechanisms underlying this system might subserve sensory–motor transformations for action (Walsh, 2003; Bueti and Walsh, 2009). In this sense, some aspects of the number processing might be embedded in the process of integration of the aspects of the environment that are relevant for action. As additional evidence of common circuits for number and action, some PET and fMRI data converged in indicating that, during numerical tasks, not only parietal but also precentral areas are activated, similarly to what commonly observed during hand-related activity (Pesenti et al., 2000; Zago et al., 2001).
The anatomical organization of the IPS might account for recent behavioral studies showing that numerical magnitude modulates hand movements, specifically hand grasping. This was shown by Andres et al. (2004) in a parity judgment task with grip closure/opening response modality: increasing or decreasing speed in initiating closure or opening grip movements respectively was a function of increasing digit magnitude. Similar results were observed when participants were required to respond to digit stimuli using a precision or a power grip (Lindemann et al., 2007; Moretto and Di Pellegrino, 2008): response with precision grip was faster for numerically small digits whereas response with power grip was faster for larger digits. In addition, Andres et al. (2008b) have observed that numerical magnitude modulates kinematic parameters of grasping. Specifically, they found that when participants were required to grasp an object and put it backward or forward in function of the parity of a digit presented on its surface, grip aperture during grasping was larger for numerically larger digits than for smaller ones.
Number influences on action were observed even in the absence of an explicit motor action, when action processes were mediated by objects perception (Badets et al., 2007; Chiou et al., 2009). The assumption that objects are represented in terms of actions, i.e., in terms of affordances (Gibson, 1979; Ellis and Tucker, 2000), is widely shared in the literature. Gibson (1979) defined affordances as properties in the environment that are relevant for an organism’s goals: for example, a banana offers us the possibility to be grasped and eaten. According to Gibson, affordances are registered directly by our perceptual system. Recent views of affordances differ in part from Gibson’s view, indicating affordances as brain representations of action possibilities, i.e., the result of previously stored perception–action experiences (Ellis and Tucker, 2000). Badets et al. (2007) firstly explored number effects on perceived affordances asking participants to evaluate whether they could grasp a visually presented object of variable size. Crucially, participants judgment was modulated by the magnitude of the digit they were required to name one second before. Interactions between numerical magnitude and action in absence of an explicit movement were also observed in a dual-task where a parity judgment and a consequent action judgment on an object were performed (Chiou et al., 2009). Response was faster for small digits associated to objects which could be grasped with a precision grip, and for large digits associated to objects which could be grasped with a power grip.
The studies described above mainly showed that numerical magnitude could modulate action processes, without however revealing whether action could likewise influence the processing of numbers. Importantly, recent studies have found that the interactions between numbers and action are bidirectional, describing effects of action observation on number processing (Badets and Pesenti, 2010). Badets and Pesenti (2010) asked participants to indicate the odd or the even digit in a pair depending on the opening or closing hand movement presented before or after the presentation of the digits pair. Beside an overall interaction between movements and digit magnitude, they observed a specific slowing of reaction times for large digits following closing movements performed by biological hands compared to fake hands. Authors proposed that the effect arose because a large number constitutes a non-expectable outcome for grasping, as only small numbers are associated to hand grasping (possibly as consequence of the human constraint on counting up to small quantities on the one hand). This study suggests that the way in which sensory–motor processing modulates number processing has a causal role and is not simply a cognitive epiphenomenon (see also Badets and Pesenti, 2011). It is worth noting that, in almost all these studies, the numerical tasks employed allowed only an implicit activation of the numerical magnitude (parity judgment task: Andres et al., 2004; Lindemann et al., 2007; Andres et al., 2008b; Chiou et al., 2009; Badets and Pesenti, 2010: Experiments 1 and 3; Moretto and Di Pellegrino, 2008: Experiment 1; digit color judgment task: Moretto and Di Pellegrino, 2008: Experiment 2; digit naming task: Badets et al., 2007), thus permitting to claim that number magnitude and action interactions should be considered, at least to some degree, automatic.
The present study aims at investigating the effects of action on number processing when action is mediated by objects. Badets and Pesenti (2010) have shown that observing grasping hand postures influences the processing of numbers. However, to our knowledge no previous study so far has demonstrated that observing manipulable objects, which suggest grasping actions, impacts on number processing. This is crucial also in light of the fact that different motor-related mechanisms might be implied while observing objects and while observing actions with objects. Recent behavioral evidence (Liuzza et al., 2011) obtained with a categorization task demonstrated the existence of different mechanisms underlying observation of grasping hand postures and observation of objects. Results showed that observing the image of a grasping hand priming an object activated motor information. However, this was not the case when the object alone was presented, without a prime evoking motor information. These results suggest the involvement of different motor-related underpinnings during action and during object observation. Indeed, previous studies on the monkey premotor cortex (Murata et al., 1997; Di Pellegrino et al., 1992) and further neurophysiological and brain imaging studies on humans (for a review see Rizzolatti and Craighero, 2004) have distinguished two different systems, the Mirror neuron system and the Canonical neuron ones. While mirror neurons fire both when a grasping action is perceived and performed, canonical neurons fire when a given action is performed and when the subject sees an object upon which to perform an action. In light of these results, we intend to verify whether not only observation of grasping hand postures, but also observation of objects elicits motor information interacting with number processing.
In order to explore this issue, we performed two experiments. In Experiment 1 we adopted the same paradigm of Badets and Pesenti (2010). Instead of finger movement mimicking an opening or closing movement, in our study the stimulus was an object, either graspable or ungraspable. We hypothesized that the presentation of graspable objects would modulate the number magnitude processing. Specifically, we expected that the motor information conveyed by graspable objects would prime small numbers or would interfere with large ones. In Experiment 2 we investigated how a task-irrelevant hand action modulates object–number interactions. The paradigm was the same of the previous experiment, except for the fact that participants were required to hold an object in their hands during the execution of the task. We hypothesized that this modulation would elicit an interference between the object–number interaction and the concurrent action of holding. This prediction is based on the fact that, being the grasping/motor system already engaged by the parallel task, there would be no room for the occurrence of an interaction between affordance and numerical magnitude. We mainly based our analysis on the numerical magnitude effect, consisting in quicker responses for smaller than larger numbers (Moyer and Landauer, 1967; see also Loetscher and Brugger, 2007). The numerical magnitude effect is an index of the number processing, as it is supposed to reflect the way in which numbers are encoded as magnitudes in a mental representation (metaphorically conceivable as a mental number line; Restle, 1970), and specifically it reflects the more accurate representation of small numbers compared to large ones. Observing modulations of the numerical magnitude effect induced by object affordances would confirm the hypothesis that affordances “shape” number processing.
Experiment 1
Method
Participants
Thirty-two undergraduate students from the University of Bologna (11 males and 21 females; mean age: 23.3 years; 6 left-handed) took part in the experiment for course credits. All participants had normal or corrected-to-normal vision, gave written informed consent and were naive to the purpose of the experiment.
Apparatus and stimuli
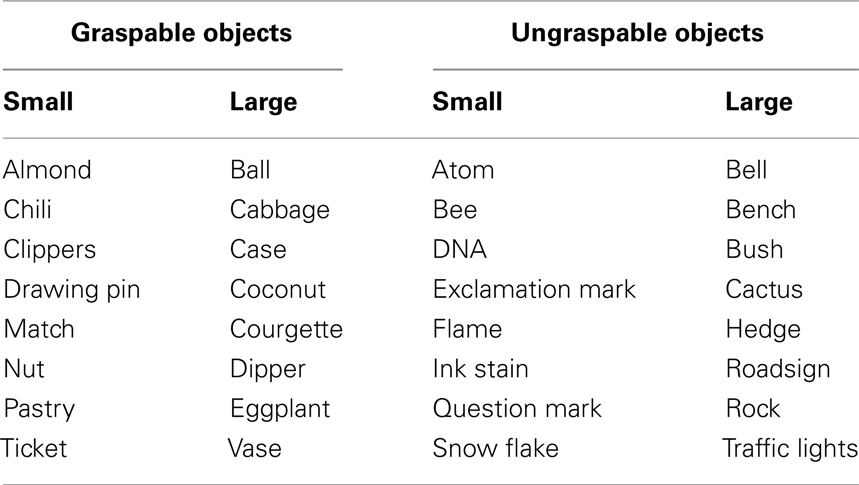
Participants sat in front of a 17″ monitor (the eye-to-screen distance was approximately 50 cm). E-Prime 1.1 software was used for presenting stimuli and collecting responses. The experimental stimuli consisted of digit pairs preceded or followed by an object. One pair of small (2 and 3) and one pair of large (8 and 9) Arabic numerals were used. The digit position within a pair (left or right) was counterbalanced. There were 32 objects either graspable or ungraspable (see Table 1), presented in small (mean pixel 82 × 138, mean cm 3 × 5) or large (mean pixel 382 × 494, mean cm 13 × 16) format. Even if the objects image size was not exactly comparable to the objects actual size, the distinction between small and large objects reflected real size disparities, as small images referred to objects that are in the reality smaller than the larger ones. Note that in the case of graspable objects, different sizes should induce different kinds of grip: power or precision grips for large or small objects, respectively. Thus, there were four categories (graspable-small objects, graspable-large objects, ungraspable-small objects, ungraspable-large objects), with eight objects for each category. Three ratings studies were preliminarily carried out to match target objects for familiarity and visual complexity, and to differentiate them for their graspability (i.e., participants evaluated an object based on whether it was possible or not to lift it with the hands and move it from one place to another). In each rating, 20 different and independent raters judged the degree of the characteristic under exam of the objects on a seven-point Likert scale (with 1 = minimum and 7 = maximum). Response means were entered into a 2 × 2 within-subject ANOVA with the factors Object type (graspable vs. ungraspable) and Object size (small vs. large). Results showed that graspable and ungraspable objects were matched for familiarity and visual complexity (p = 0.44 and p = 0.30, respectively), and that they significantly differed for manipulability, F(1,28) = 257.43, MSE = 0.43, p < 0.001 (mean graspable objects = 6.36 and mean ungraspable objects = 2.64).
Procedure
The participants were required to recall and repeat aloud the odd or the even digit within a pair, preceding or following the target object, depending on the type of object presented (i.e., graspable vs. ungraspable). For example, if the target object was graspable, half of participants were asked to recall and repeat the odd digit, whereas if the object was ungraspable, they had to recall and repeat aloud the even digit. The reverse was true for the other half of participants. At the beginning of the experiment, participants were provided with this specific definition of graspability: “the object is graspable when you can lift and move it from one place to another with the hands” (for a similar definition, see: Borghi et al., 2007a, Experiment 2). The four-factors-of-interest were: Order (object–number vs. number–object), Object type (graspable vs. ungraspable), Object size (small vs. large), and Numerical magnitude of the digits pair (small vs. large number). The numerical magnitude and the object type were randomly presented, whereas the order of presentation, the object size, and the response mapping (graspable object – odd digit or graspable object – even digit) where counterbalanced across eight different blocks. Small and large objects were presented in different blocks to minimize the perceptual effects of size. Each session consisted of one practice block of 16 trials and one experimental block of 32 trials. Each trial began with a fixation point (+) displayed for 500 ms in the center of the screen. Then, in the object–number trials, a target object was shown for 1500 ms and followed by a pair of small or large Arabic digits, one odd and one even, which remained on the screen until a vocal response was recorded or 3000 ms had elapsed. In the number–object trials, a pair of small or large Arabic digits, one odd and one even, was shown for 1500 ms and followed by a target object which remained on the screen until a vocal response was recorded or 3000 ms had elapsed. The next trial began after an interval of 2000 ms (Figure 1). The order of blocks was counterbalanced between participants. After each block, participants could take a brief break. Overall the experiment consisted of 256 experimental trials and lasted about 60 min.
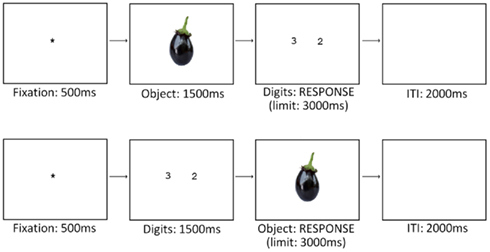
Figure 1. Sequence of events in trials of object–number (on the top) and number–object (on the bottom) conditions. At the beginning of each trial, a fixation cross appeared on the center of the screen. The fixation cross was replaced by the first target (for example, an object in the object–number condition) and then by the second target (for example, a pair of digits in the object–number condition) until the vocal response execution or until 3000 ms had elapsed. After a delay of 2000 ms, the next trial began. Note that stimuli are not drawn to scale.
Results
As instructions required participants to keep their hands on the table in a relaxed position, the data from two participants who did not follow the instructions were excluded from analyses. The resulting group consisted of 30 subjects. The incorrect responses were removed from the analysis (4.2%, range 0–10%). RTs faster/slower than the overall subject mean minus/plus 2 SDs (4.01%) and error due to imprecise microphone recording (6.28%) were excluded from the analyses. There was no evidence of speed–accuracy trade-off (r = 0.05, p > 0.8), therefore we focused on RTs analyses. Mean correct RTs were submitted to a repeated-measures ANOVA with Order (object–number vs. number–object), Object type (graspable vs. ungraspable), Object size (small vs. large), and Numerical magnitude (small vs. large) as within-subjects factors. Fisher’s LSD post hoc tests were also conducted on significant interactions.
The main effect of Order, F(1,29) = 77.35, MSE = 20206.63, p < 0.001, and of Object type, F(1,29) = 15.74, MSE = 3138.92, p < 0.001, were significant. RTs were faster for the object–number condition than for the number–object one (700 and 815 ms, respectively), and they were faster for graspable objects than for ungraspable ones (747 and 768 ms, respectively).
The interaction between Order and Object type, F(1,29) = 7.73, MSE = 4668.80, p < 0.05, was significant. Post hoc tests showed significantly faster RTs for graspable objects than for ungraspable ones only in the number–object condition (796 and 833 ms, p < 0.001, Figure 2). The interaction between Object type and Object size, F(1,29) = 11.62, MSE = 2162.17, p < 0.05, was significant. For graspable objects RTs were faster when the objects were large than small (740 and 755 ms, p < 0.05). The reverse was true for ungraspable objects: RTs were faster for small objects than large ones (760 and 775 ms, p < 0.05).
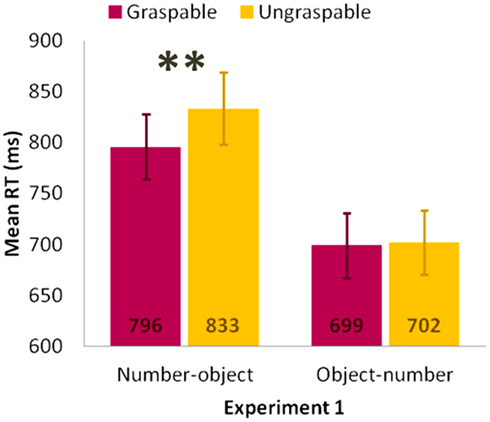
Figure 2. Significant Order × Object type interaction for RTs in Experiment 1, values are in ms and bars are SEM. Significant comparisons are indicated with *(p < 0.05) or **(p < 0.01).
Furthermore, Object size interacted also with Numerical magnitude, F(1,29) = 4.26, MSE = 3087.76, p < 0.05. Post hoc test revealed that RTs were faster for smaller digits than for larger ones only when presented with large objects (748 and 767 ms, p < 0.05). Finally, the significant interaction between Order, Object type, and Numerical magnitude factors, F(1,29) = 4.49, MSE = 2676.75, p < 0.05, revealed that affordance facilitated number processing (Figure 3). More specifically, in the number–object condition there was no significant difference between small and large numbers, neither when numbers were followed by a graspable object (801 and 791 ms, ps > 0.3), nor when they were followed by an ungraspable one (829 and 838, ps > 0.3). In the object–number condition, RTs were significantly faster for small compared to large numbers when preceded by a graspable object (685 and 713 ms, p < 0.05), but not when they were preceded by an ungraspable one (699 and 705 ms, p > 0.5). Again, there was no significant difference between the large number – graspable object association compared to the large number – ungraspable objects one (p > 0.1). The small number – graspable objects association was faster than the small number – ungraspable object one, although not significantly (p > 0.1).
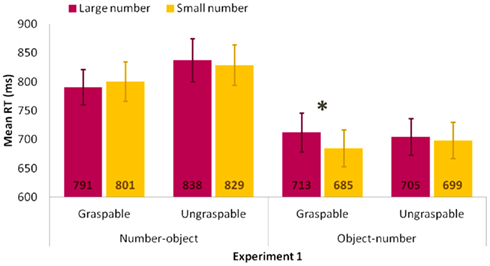
Figure 3. Significant Order × Object type × Numerical magnitude interaction for RTs in Experiment 1, values are in millisecond and bars are SEM. Significant comparisons are indicated with *(p < 0.05) or **(p < 0.01).
No other effects or interactions were significant (ps > 0.05).
Discussion
The main results of Experiment 1 showed that numerical processing is linked to object graspability. First, only graspable objects processing was speeded-up by the previous presentation of the numbers, indicating that numbers enhance graspable objects processing. Second, also graspability enhanced number processing. Indeed, the numerical magnitude effect (faster responses for smaller numbers than larger ones) emerged only after the presentation of graspable objects. It is worth noting that graspable and ungraspable objects generated different behavioral effects, suggesting that graspability was properly processed. In particular, results are in line with the view that graspable objects might be grounded in action (i.e., slower responses for graspable-small objects than large ones), as grasping a small object is a complex movement for a precise, functional grip usually requiring more time than a power grip (Bazzarin et al., 2007; Borghi et al., 2007a; Vainio et al., 2008; Ranzini et al., 2011).
Experiment 2
Experiment 1 extended previous results (Badets and Pesenti, 2010) demonstrating that not only the action perception, but also the object affordances affect number processing. In Experiment 2 we directly investigated the role of a hand action during the same task. Participants had to hold an object in their hands and keep it lifted from the table during the execution of the task of Experiment 1, so that the holding action was completely task-irrelevant. However, if similar mechanisms subtend number processing, object affordances, and action execution, we would expect the holding action to interfere with the processing of affordances and of numerical magnitude. Moreover, as previous studies have suggested that response modalities involving grasping (Anelli et al., 2010) or preliminary motor training (Borghi et al., 2007b: Experiment 2) enhanced information related to object manipulation, we expected that the holding action would enhance the sensitivity for the size of the observed graspable objects.
Method
Participants
Twenty undergraduate students (three males and 17 females; mean age: 20.2 years; all right-handed) from the University of Bologna took part in the Experiment 2 for course credits. As in Experiment 1, all participants had normal or corrected-to-normal vision, were naive as to the purpose of the experiment and gave written informed consent.
Apparatus, stimuli, and procedure
The apparatus was the same used in Experiment 1. However, in the present experiment participants were required to grasp and lift an object with both hands and continue to hold it lifted during the task. Participants could comfortably stay with their elbows on the table during the execution of the task, however they were required to keep the hand muscles in a tensed position in order to keep lifting the object from the table (at the height they were comfortable, and without interfering with the screen visibility). The object was a neutral-colored egg-shaped artifact, graspable with both hands by power grips at its central part (the body of the object was 13 cm × 6 cm), and graspable with both hands by precision grips at its extremities (extremities were 10 cm × 1 cm). Power or precision grip were counterbalanced between sessions and not considered as a factor1. The four-factors-of-interest were the same of Experiment 1: Order (object–number vs. number–object), Object type (graspable vs. ungraspable), Object size (small vs. large), and Numerical magnitude (small vs. large number). In order to reduce the number of trials, in Experiment 2 we presented six objects for each of the four categories (graspable-small objects, graspable-large objects, ungraspable-small objects, ungraspable-large objects), see Table 2. The objects could be small (mean pixel 85 × 148) or large (mean pixel 410 × 480). As in Experiment 1, there were eight different sessions, but each session consisted of one practice block of 12 trials and one experimental block of 24 trials. Overall the experiment consisted of 192 experimental trials and lasted about 45 min.
Results
The data were trimmed according to the same criteria used for Experiment 1. The incorrect responses were removed from the analysis (2.9%, range 0–9%). RTs faster/slower than the overall subject mean minus/plus 2 SDs (3.72%) and error due to the microphone recording (2.86%) were excluded from the analyses. As in Experiment 1, there was no speed–accuracy trade-off (r = 0.08, p > 0.7), therefore we focused on RTs analyses. An ANOVA with the same factors as those of Experiment 1 was conducted.
The main effects of Order, F(1,19) = 20.45, MSE = 21795.36, p < 0.001, and of Numerical magnitude, F(1,19) = 13.88, MSE = 7459.50, p < 0.001, were significant. RTs were faster for the object–number condition than for the number–object one (685 and 760 ms, respectively), and they were faster for the small number condition than for the large number one (705 and 741 ms, respectively). Furthermore, the Order × Object type × Object size × Numerical magnitude interaction was significant, F(1,19) = 5.49, MSE = 660.46, p < 0.05. No other effects nor interactions were significant (ps > 0.05). To better understand this third-order interaction, separated analyses by levels of Order were performed. The main effect of Numerical magnitude was significant both for the object–number condition, F(1,19) = 11.15, MSE = 6716.11, p < 0.05 (small and large digits, respectively: 664 and 707 ms), and for the number–object one, F(1,19) = 9.67, MSE = 3407.64, p < 0.05 (small and large digits, respectively: 746 and 774 ms), revealing in both cases quicker responses for the small digits.
Crucially, the Object type × Object size × Numerical magnitude interaction was significant only for the object–number condition, F(1,19) = 6.08, MSE = 1284.16, p < 0.05, Figure 4. Post hoc tests revealed that the size of the object and the size of the number interacted differently for the graspable and ungraspable objects. On one hand, in the ungraspable-small object combination results showed a facilitation for the small numbers (647 ms) compared to the large ones (712 ms), p < 0.001. Similarly, when the object was ungraspable and large, RTs were faster when the following number was small (674 ms) than large (713 ms), p < 0.001. On the other hand, when the object is graspable and small, no difference was found for the small (668 ms) and large numbers (688 ms), p = 0.10. Differently, in the graspable-large object combination, RTs were faster for the small numbers (665 ms) than large one (714 ms), p < 0.001. In other words, in the object–number condition, the number magnitude effect was reduced when the object was graspable and small (RTs for large minus small number difference = 20 ms, Figure 4) compared to the other conditions (RTs for large minus small number differences range between 39 and 65 ms, Figure 4).
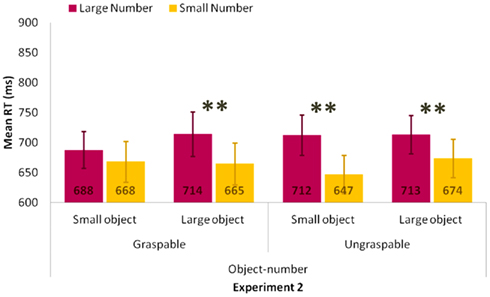
Figure 4. Significant Order × Object type × Object size × Numerical magnitude interaction for RTs in the object–number condition of Experiment 2. Values are in millisecond and bars are SEM. Significant comparisons are indicated with *(p < 0.05) or **(p < 0.01).
Comparison between Experiments 1 and 2
To statistically prove the difference between experiments in the numerical magnitude effects, a direct comparison of Experiments 1 and 2 was performed. An ANOVA with the main within-subject factors Order, Object Type, Object Size, Numerical Magnitude, and with Experiment (1, 2) as between subjects factor, was conducted. For simplicity, only the significant effects in which an interaction with the factor Experiment are reported here. Crucially, the interaction between Numerical Magnitude and Experiment was significant, F(1,48) = 5.65, MSE = 6547.69, p < 0.05, Figure 5, indicating that the numerical magnitude effect was enhanced in Experiment 2 compared to Experiment 1 (note that the main effect of Numerical Magnitude was also significant in this analysis, F(1,48) = 14.32, MSE = 6547.69, p < 0.001). Again, the interaction between Order, Object Type, Numerical Magnitude, and Experiment was significant, F(1,48) = 7.41, MSE = 2334.95, p < 0.01. Indeed, the magnitude effect was overall present in these conditions of Experiment 2, as suggested by the absence of an interaction between Order × Object Type × Numerical Magnitude in this experiment (see Results in Experiment 2). In contrast, in Experiment 1 the magnitude effect was significantly present only when a graspable object preceded the numbers presentation, as indicated by the significant triple interaction in this experiment (see Results in Experiment 1, Figure 3).
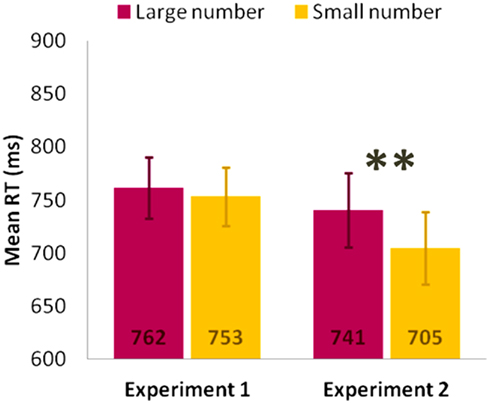
Figure 5. Significant Numerical Magnitude × Experiment interaction, values are in millisecond and bars are SEM. Significant comparisons are indicated with *(p < 0.05) or **(p < 0.01).
Discussion
Results of Experiment 2 showed that the holding action interacted with the processing of the numerical magnitude, and interfered with the object–number relationship. Firstly, we found that holding the object in the hands enhanced overall number processing, as revealed by the significant main effect of numerical magnitude not present in Experiment 1. Secondly, we found that the holding action concurrent to the task interfered with the effect of the affordances on the processing of numbers, however enhancing the sensitivity for object size. Specifically, the numerical magnitude effect was disturbed only after the presentation of graspable-small objects.
General Discussion
The present study aims at investigating the effects of objects affordances, i.e., objects possibilities for action (Gibson, 1979; Ellis and Tucker, 2000), on number processing. In two experiments, we adopted a parity judgment paradigm, where the numerical stimuli were preceded or followed by the presentation of an object, which could be graspable or ungraspable. The response to the numerical stimulus varied in function of the type of object. As previous studies suggested that numerical magnitude is grounded in action networks (e.g., Badets and Pesenti, 2010), we hypothesized that observing objects which activate grasping affordances may influence the processing of the numerical magnitude. Moreover, we were interested in investigating the link between the action network involved in object observation comparing a condition without (Experiment 1) or with (Experiment 2) the requirement of a task-irrelevant hand action (i.e., holding an object in the hands).
In Experiment 1, we observed that the numerical magnitude processing system had mechanisms in common with graspable objects. This was exploited by two major findings. Firstly, we found that responses to graspable objects compared to ungraspable ones were faster when numbers preceded the presentation of the object. A similar result was observed by Badets and Pesenti (2010), who showed that responses to biological hands were faster in the semantic-to-motor condition (i.e., when numbers preceded the presentation of the hand). While Badets and Pesenti (2010) found this effect with biological hands, which directly evoke motor information, the novelty here lies in finding this result when a graspable object was shown compared to an ungraspable one. This suggests that the simple presence of graspable objects activates motor information, probably through the mediation of the canonical neuron system. Secondly, and more crucially, we found that when graspable objects preceded the numerical stimuli there was a significant numerical magnitude effect not observed in the other conditions. It is worth noting that in this experiment, in line with a classical numerical magnitude effect, responses were overall quicker to small numbers than to large ones, even if this difference did not reach significance. This seems to suggest that activating action mechanisms, related to object grasping, enhances the sensitivity to numerical magnitude. Alternatively or in addition, in a motor account, as only small numbers should constitute an expectable outcome after the activation of grasping circuits by graspable objects (Badets and Pesenti, 2010), we predicted a facilitation for small numbers and/or an interference for large ones when preceded by graspable compared to ungraspable objects. This was exactly what we observed: responses to small numbers were overall quicker after graspable than ungraspable objects, and the opposite was true for large numbers, although both comparisons were not significant. In our opinion, the findings of Experiment 1 converge to support a sensory–motor interpretation of our results. Specifically, they suggest that number processing and object affordances involve interacting or overlapping mechanisms, and the anatomical organization of the numerical and of the grasping circuitries in the IPS supports this view. These findings add to the existing literature on number–action interactions, demonstrating that object affordances, similarly to action observation (Badets and Pesenti, 2010), modulate number processing. Importantly, the interaction we observed in Experiment 1 between the object type and the object size suggests that the graspable objects were processed at a motor level. For instance, the slower responses for graspable-small objects compared to graspable-large ones mirror the disparities between the time required to perform a precision grip when grasping small objects and the time required to perform a power grasp to large objects (Ehrsson et al., 2000; Borghi et al., 2007a).
Concerning results of Experiment 1, it remains to understand the role that objects size played in this experiment. A number of studies showed associations between numerical magnitude and other physical dimensions (e.g., Henik and Tzelgov, 1982). However, the main findings including number processing in Experiment 1 were affected in no way by the object size. On the other hand, we observed an unclear interaction between numerical magnitude and object size which was independent from other factors. To permit to motor associations to emerge irrespective of other perceptual factors, we presented small and large objects in different counterbalanced blocks, minimizing in this way possible perceptual effects of object size. Possibly, this manipulation interfered with a natural perceptual association between smallness or largeness, although we believe that this manipulation did in no case affect our main results related to the affordances.
In Experiment 2 we wanted to confirm that the effects observed in Experiment 1 were due to shared motor mechanisms belonging to both numbers and graspable objects. In fact, it is possible that, as no hand action was required during the Experiment 1, results could have alternative explanations, not necessarily involving sensory–motor systems. For this reason, in Experiment 2 we asked to another group of participants to hold an object in their hands during the execution of the same task, in order to explore the effects of the engagement of the motor system on object affordances and numerical magnitude. This manipulation was introduced in order to investigate effects of affordances on number processing, both when they were perceived through object observation and when they were experienced through object holding. We underline that – to the best of our knowledge – no previous studies have investigated the effects of a task-irrelevant holding action on the processing of numerical magnitude. Moreover, as previous studies have shown that motor action executions enhanced the sensitivity to the features of the objects related to their manipulability (Borghi et al., 2007b; Anelli et al., 2010), we expected here a contribution of object size on the effects related to numbers.
Firstly, we found that holding an object in the hands during a numerical task enhanced the sensitivity to numerical magnitude. Indeed, the classical numerical magnitude effect emerged overall, differently to what observed in Experiment 1. This confirmed that a hand action toward an object enhanced the sensitivity to target stimuli features (e.g., Anelli et al., 2010). However, interestingly, in this case this effect was found for numbers rather than for objects. In a neuro-anatomical perspective, this behavioral data go together with fMRI results showing that aIPS was more strongly activated during grasping execution than during the observation of 3D objects, although it was nonetheless activated during the latter case (Cavina-Pratesi et al., 2007). Thus, we can imagine that interactions between numbers and action-related mechanisms might be stronger in the case of greater activations of the IPS circuits.
The second result of Experiment 2 was that the effect of numerical magnitude was affected when numbers were preceded by a small graspable object. This finding leads to some main conclusions. Firstly, it provides further evidence for the view that numbers and graspable objects interact through action mechanisms. Secondly, it suggests that a crucial role in this interaction might be played by precision grip movements, as only small objects – which require precision grips – affected the sensitivity to numerical magnitude when the motor system had already been engaged. Importantly, some neuroimaging studies have suggested that the IPS can be primarily related to the precision grip (Ehrsson et al., 2001; Begliomini et al., 2007). Moreover, Valyear et al. (2007), in a study comparing tools with graspable or ungraspable objects, suggested that the activation in the left aIPS may reflect sensory–motor processes involved in the use of familiar tools, more than a general representation of grasping affordance. Taken together, these findings permit to speculate on the nature of the object–number interactions. Specifically, if the IPS is primarily responsible for the computation of small familiar objects, holding the object during the Experiment 2 might have disclosed a specific association between small objects and numbers. However, as we counterbalanced the kind of grip that participants used to hold the object, it is possible that this manipulation interfered with the effects related to the object size, leaving this hypothesis open for future studies.
In summary, this study provides evidence that number representations are grounded into perception–action systems, showing that both object affordances (Experiment 1) and task-irrelevant hand action (Experiment 2) enhanced the sensitivity to numerical magnitude. The novelty of the present study is at least twofold. First, these findings indicate that semantic numerical knowledge can emerge not only from the observation of biological grasping movements (Badets and Pesenti, 2010), but also from the observation of object affordances. Importantly, the relationship between the number processing and the grasping system was found in a task that did not directly link graspability with numerical magnitude (i.e., parity judgment task). Second, to our knowledge this is the first study in which the relationship between number processing and affordances is explored asking participants to execute a task-irrelevant hand action during the experiment. The relation between numbers and size when it is mediated by objects, in particular by graspable objects, remains however to be deeper explored. Differently to what observed by previous behavioral (Henik and Tzelgov, 1982) and neuroimaging studies (Fias et al., 2003; Pinel et al., 2004; Cohen Kadosh et al., 2005), the present study suggests that the interaction between size and numerical magnitude, when mediated by object affordances, might be more complex than a classical association of smallness or largeness. It is possible that tools-driven precision grip mechanisms might be principally related to the processing of the numerical magnitude.
In conclusion, embodied cognition theories claim that abstract and concrete concepts are grounded in perception–action systems (e.g., Glenberg, 1997; Barsalou, 1999, 2008; Gallese and Lakoff, 2005). The results of this study support this view, by showing that objects, either observed (Experiment 1) or motorily experienced (Experiment 2), evoke grasping affordances that shape the processing of numerical magnitude. The strict linkage we found between number processing and object perception and action can be accounted by ideomotor theories. In particular, it is compatible with the theory of event coding (TEC; Hommel et al., 2001), according to which perceived events, i.e., perceptions, and events to be produced, i.e., actions, are represented by the same “event codes”. Consequently, perception and action systems rely on the same representational format as they both are events in the environment. In this case, numbers and objects would rely on both perception and action, which are encoded in the same format or file.
Further studies will need to clarify to which extent the developing of the numerical knowledge on specific cultural habits (i.e., finger counting) accounts for action-based numerical magnitude processes in adulthood, and how exactly neural brain networks work to merge semantic aspects of numerical cognition to action.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was supported by the European Community, in project ROSSI: Emergence of Communication in RObots through Sensorimotor and Social Interaction (Grant agreement no: 216125).
Footnote
- ^Because it was not of our theoretical interest, analysis including Grip factor are not reported in the main text. However, since previous studies showed significant interactions between the type of grip and the numerical magnitude (e.g., Lindemann et al., 2007), we run the ANOVA with Grip (power vs. precision), Order (object–number vs. number–object), Object type (graspable vs. ungraspable), Object size (small vs. large) and Numerical magnitude (small vs. large) as within-subjects factors. The main effect of Grip was not significant, F(1,19) = 0.233, MSE = 75647.54, p = 0.635. No interactions with the Grip factor and both Numerical magnitude or Object type were significant. Interestingly, the Oder × Object type × Object size × Numerical magnitude interaction was significant, F(1,19) = 8.66, MSE = 1118.11, p < 0.05. Since the latter interaction resulted as significant, we believe that it is appropriate to not include the Grip factor in the analysis reported in the main text. Importantly, though, the mean RT values of the present analysis show a similar trend to that observed for the analysis reported in the main text. Therefore, we think that it indicates a convergence in the overall results and that the Grip factor did not interfere with our variables of interest.
References
Andres, M., Davare, M., Pesenti, M., Olivier, E., and Seron, X. (2004). Number magnitude and grip aperture interaction. Neuroreport 15, 2773–2777.
Andres, M., Di Luca, S., and Pesenti, M. (2008a). Finger counting: the missing tool? Behav. Brain Sci. 31, 642–643.
Andres, M., Ostry, D. J., Nicol, F., and Paus, T. (2008b). Time course of number magnitude interference during grasping. Cortex 44, 414–419.
Anelli, F., Nicoletti, R., and Borghi, A. M. (2010). Categorization and action: what about object consistence? Acta Psychol. (Amst.) 133, 203–211.
Badets, A., Andres, M., Di Luca, S., and Pesenti, M. (2007). Number magnitude potentiates action judgment. Exp. Brain Res. 180, 525–534.
Badets, A., and Pesenti, M. (2010). Creating number semantics through finger movement perception. Cognition 115, 46–53.
Badets, A., and Pesenti, M. (2011). Finger-number interaction. An ideomotor account. Exp. Psychol. 58, 287–292.
Bazzarin, V., Borghi, A. M., Tessari, A., and Nicoletti, R. (2007). “Is a small apple more like an apple or more like a cherry?” in Proceedings of the Meeting of the European Society of Cognitive Science, Delphi 2007, eds S. Vosniadou and D. Kayser (London: Erlbaum), 83–88.
Begliomini, C., Wall, M. B., Smith, A. T., and Castiello, U. (2007). Differential cortical activity for precision and whole-hand visually guided grasping in humans. Eur. J. Neurosci. 25, 1245–1252.
Borghi, A. M., Bonfiglioli, C., Ricciardelli, P., Rubichi, S., and Nicoletti, R. (2007a). “Do we access object manipulability while we categorize? Evidence from reaction times studies,” in Mental States: Evolution, Function, Nature, eds A. C. Schalley and D. Khlentzos (Amsterdam/Philandelphia: John Benjamins), 153–170.
Borghi, A. M., Bonfiglioli, C., Lugli, L., Ricciardelli, P., Rubichi, S., and Nicoletti, R. (2007b). Are visual stimuli sufficient to evoke motor information? Studies with hand primes. Neurosci. Lett. 411, 17–21.
Borghi, A. M., and Cimatti, F. (2009). “Words as tools and the problem of abstract words meanings,” in Proceedings of the 31st Annual Conference of the Cognitive Science Society, eds N. Taatgen and H. van Rijn (Amsterdam: Cognitive Science Society), 2304–2309.
Borghi, A. M., and Pecher, D. (2011). Introduction to the special topic emobodied and grounded cognition. Front. Psychol. 2:187. doi:10.3389/fpsyg.2011.00187
Boroditsky, L., and Ramscar, M. (2002). The roles of body and mind in abstract thought. Psychol. Sci. 13, 185–188.
Bueti, D., and Walsh, V. (2009). The parietal cortex and the representation of time, space, number and other magnitudes. Philos. Trans. R. Soc. Lond. B Biol. Sci. 364, 1831–1840.
Casasanto, D. (2009). Embodiment of abstract concepts: good and bad in right and left handers. J. Exp. Psychol. Gen. 138, 351–367.
Cavina-Pratesi, C., Goodale, M. A., and Culham, J. C. (2007). FMRI reveals a dissociation between grasping and perceiving the size of real 3D objects. PLoS ONE 2, e424. doi:10.1371/journal.pone.0000424
Cavina-Pratesi, C., Monaco, S., Fattori, P., Galletti, C., McAdam, T. D., Quinlan, D. J., Goodale, M. A., and Culham, J. C. (2010). Functional magnetic resonance imaging reveals the neural substrates of arm transport and grip formation in reach-to-grasp actions in humans. J. Neurosci. 30, 10306–10323.
Chao, L. L., and Martin, A. (2000). Representation of manipulable man-made objects in the dorsal stream. Neuroimage 12, 478–484.
Chiou, R. Y.-C., Chang, E. C., Tzeng, O. J.-L., and Wu, D. H. (2009). The common magnitude code underlying numerical and size processing for action but not for perception. Exp. Brain Res. 194, 553–562.
Cohen Kadosh, R., Henik, A., Rubinsten, O., Mohr, H., Dori, H., van de Ven, V., Zorzi, M., Hendler, T., Goebel, R., and Linden, D. E. J. (2005). Are numbers special?: the comparison systems of the human brain investigated by fMRI. Neuropsychologia 43, 1238–1248.
Cohen Kadosh, R., and Walsh, V. (2009). Numerical representation in the parietal lobes: abstract or not abstract? Behav. Brain Sci. 32, 313–328.
Creem-Regehr, S. H., and Lee, J. N. (2005). Neural representations of graspable objects: are tools special? Brain Res. Cogn. Brain Res. 22, 457–469.
Culham, J. C., and Kanwisher, N. G. (2001). Neuroimaging of cognitive functions in human parietal cortex. Curr. Opin. Neurobiol. 11, 157–163.
Culham, J. C., and Valyear, K. F. (2006). Human parietal cortex in action. Curr. Opin. Neurobiol. 16, 205–212.
Dehaene, S., Piazza, M., Pinel, P., and Cohen, L. (2003). Three parietal circuits for number processing. Cogn. Neuropsychol. 20, 487–506.
Di Luca, S., Granà, A., Semenza, C., Seron, X., and Pesenti, M. (2006). Finger-digit compatibility in Arabic numeral processing. Q. J. Exp. Psychol. 59, 1648–1663.
Di Luca, S., and Pesenti, M. (2008). Masked priming effect with canonical finger numeral configurations. Exp. Brain Res. 185, 27–39.
Di Pellegrino, G., Fadiga, L., Fogassi, L., Gallese, V., and Rizzolatti, G. (1992). Understanding motor events: a neurophysiological study. Exp. Brain Res. 91, 176–180.
Eger, E., Sterzer, P., Russ, M. O., Giraud, A.-L., and Kleinschmidt, A. (2003). A supramodal number representation in human intraparietal cortex. Neuron 37, 719–726.
Ehrsson, H. H., Fagergren, A., and Forssberg, H. (2001). Differential fronto-parietal activation depending on force used in a precision grip task: an fMRI study. J. Neurophysiol. 85, 2613–2623.
Ehrsson, H. H., Fagergren, A., Jonsson, T., Westling, G., Johansson, R. S., and Forssberg, H. (2000). Cortical activity in precision- versus power-grip tasks: an fMRI study. J. Neurophysiol. 83, 528–536.
Ellis, R., and Tucker, M. (2000). Micro-affordance: the potentiation of components of action by seen objects. Br. J. Psychol. 91, 451–471.
Fias, W., Lammertyn, J., Reynvoet, B., Dupont, P., and Orban, G. A. (2003). Parietal representation of symbolic and nonsymbolic magnitude. J. Cogn. Neurosci. 15, 47–56.
Fischer, M. H., and Brugger, P. (2011). When digits help digits: spatial-numerical associations point to finger counting as prime example of embodied cognition. Front. Psychol. 2:260. doi:10.3389/fpsyg.2011.00260
Frey, S. H., Vinton, D., Norlund, R., and Grafton, S. T. (2005). Cortical topography of human anterior intraparietal cortex active during visually guided grasping. Brain Res. Cogn. Brain Res. 23, 397–405.
Gallese, V., and Lakoff, G. (2005). The brain’s concepts: the role of the sensorimotor system in reason and language. Cogn. Neuropsychol. 22, 455–479.
Gerlach, C., Law, I., Gade, A., and Paulson, O. B. (2002). The role of action knowledge in the comprehension of artefacts: a PET study. Neuroimage 15, 143–152.
Gerstmann, J. M. D. (1940). Syndrome of finger agnosia, disorentation for right and left, agraphia and acalculia: local diagnostic value. Arch. Neurol. Psychiatry 44, 398–408.
Glenberg, A. M., Sato, M., Cattaneo, L., Riggio, L., Palumbo, D., and Buccino, G. (2008). Processing abstract language modulates motor system activity. Q. J. Exp. Psychol. 61, 905–919.
Grafton, S. T. (2009). Embodied cognition and the simulation of action to understand others. Ann. N. Y. Acad. Sci. 1156, 97–117.
Grafton, S. T., Fadiga, L., Arbib, M. A., and Rizzolatti, G. (1997). Premotor cortex activation during observation and naming of familiar tools. NeuroImage 6, 231–236.
Grèzes, J., Armony, J. L., Rowe, J., and Passingham, R. E. (2003). Activations related to “mirror” and “canonical” neurons in the human brain: an fMRI study. Neuroimage 18, 928–937.
Henik, A., and Tzelgov, J. (1982). Is three greater than five: the relation between physical and semantic size in comparison tasks. Mem. Cognit. 10, 389–395.
Hommel, B., Muesseler, J., Aschersleben, G., and Prinz, W. (2001). The theory of event coding (TEC): a framework for perception and action planning. Behav. Brain Sci. 24, 849–878.
Hubbard, E. M., Piazza, M., Pinel, P., and Dehaene, S. (2005). Interactions between number and space in the parietal cortex. Nat. Rev. Neurosci. 6, 435–448.
Johnson-Frey, S. H. (2004). The neural bases of complex tool use in humans. Trends Cogn. Sci. (Regul. Ed.) 8, 71–78.
Kinsbourne, M., and Warrington, E. K. (1963). The developmental Gerstmann syndrome. Arch. Neurol. 8, 490–501.
Lindemann, O., Abolafia, J. M., Girardi, G., and Bekkering, H. (2007). Getting a grip on numbers: numerical magnitude priming in object grasping. J. Exp. Psychol. Hum. Percept. Perform. 33, 1400–1409.
Liuzza, M. T., Setti, A., and Borghi, A. M. (2011). Kids observing other kids’ hands: visuomotor priming in children. Conscious. Cogn. (in press).
Loetscher, T., and Brugger, P. (2007). Exploring number space by random digit generation. Exp. Brain Res. 180, 655–665.
Martin, A. (2007). The representation of object concepts in the brain. Annu. Rev. Psychol. 58, 25–45.
Milner, A. D., and Goodale, M. A. (1995). The Visual Brain in Action. Oxford: Oxford University Press.
Moyer, R. S., and Landauer, T. K. (1967). Time required for judgements of numerical inequality. Nature 215, 1519–1520.
Murata, A., Fadiga, L., Fogassi, L., Gallese, V., Raos, V., and Rizzolatti, G. (1997). Object representation in the ventral premotor cortex (Area F5) of the monkey. J. Neurophysiol. 78, 2226–2230.
Noël, M.-P. (2005). Finger agnosia: a predictor of numerical abilities in children? Child Neuropsychol. 11, 413–430.
Orban, G. A., Claeys, K., Nelissen, K., Smans, R., Sunaert, S., Todd, J. T., Wardak, C., Durand, J-B., and Vanduffel, W. (2006). Mapping the parietal cortex of human and non-human primates. Neuropsychologia 44, 2647–2667.
Pecher, D., and Boot, I. (2011). Numbers in space: differences between concrete and abstract situations. Front. Psychol. 2:121. doi:10.3389/fpsyg.2011.00121
Pecher, D., Boot, I., and van Dantzig, S. (2011). “Abstract concepts: sensory-motor grounding, metaphors, andbeyond,” in The Psychology of Learning and Motivation, Vol. 54, ed. B. Ross (Burlington: Academic Press), 217–248.
Pecher, D., and Zwaan, R. A. (eds). (2005). Grounding Cognition. The role of Perception and Action in Memory, Language and Thinking. Cambridge: CUP.
Pesenti, M., Thioux, M., Seron, X., and De Volder, A. (2000). Neuroanatomical substrate of Arabic number processing, numerical comparison and simple addition: a PET study. J. Cogn. Neurosci. 12, 461–479.
Piazza, M., Izard, V., Pinel, P., LeBihan, D., and Dehaene, S. (2004). Tuning curves for approximate numerosity in the human intraparietal sulcus. Neuron 44, 547–555.
Piazza, M., Pinel, P., LeBihan, D., and Dehaene, S. (2007). A magnitude code common to numerosities and number symbols in human intraparietal cortex. Neuron 53, 293–305.
Pinel, P., Piazza, M., Le Bihan, D., and Dehaene, S. (2004). Distributed and overlapping cerebral representations of number, size, and luminance during comparative judgments. Neuron 41, 983–993.
Pulvermüller, F. (2005). Brain mechanisms linking language and action. Nat. Rev. Neurosci. 6, 576–582.
Ranzini, M., Borghi, A. M., and Nicoletti, R. (2011). With hands I don’t centre! Action- and object-related effects of hand-cueing in the line bisection. Neuropsychologia 49, 2918–2928.
Rizzolatti, G., and Craighero, L. (2004). The mirror neuron system. Annu. Rev. Neurosci. 27, 169–192.
Rourke, B. P., and Conway, J. A. (1997). Disabilities of arithmetic and mathematical reasoning: perspectives from neurology and neuropsychology. J. Learn. Disabil. 30, 34–46.
Simon, O., Mangin, J.-F., Cohen, L., Le Bihan, D., and Dehaene, S. (2002). Topographical layout of hand, eye, calculation, and language-related areas in the human parietal lobe. Neuron 33, 475–487.
Vainio, L., Symes, E., Ellis, R., Tucker, M., and Ottoboni, G. (2008). On the relations between action planning, object identification, and motor representations of observed actions and objects. Cognition 108, 444–465.
Valyear, K. F., Cavina-Pratesi, C., Stiglick, A. J., and Culham, J. C. (2007). Does tool-related fMRI activity within the intraparietal sulcus reflect the plan to grasp? Neuroimage 36, T94–T108.
Walsh, V. (2003). A theory of magnitude: common cortical metrics of time, space and quantity. Trends Cogn. Sci. (Regul. Ed.) 7, 483–488.
Keywords: number, object, affordance, action
Citation: Ranzini M, Lugli L, Anelli F, Carbone R, Nicoletti R and Borghi AM (2011) Graspable objects shape number processing. Front. Hum. Neurosci. 5:147. doi: 10.3389/fnhum.2011.00147
Received: 09 September 2011; Accepted: 08 November 2011;
Published online: 06 December 2011.
Edited by:
Filip Van Opstal, Ghent University, BelgiumCopyright: © 2011 Ranzini, Lugli, Anelli, Carbone, Nicoletti and Borghi. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Mariagrazia Ranzini, Department of General Psychology, University of Padova, via Venezia 12/2, 35131 Padova, Italy. e-mail:bWFyaS5yYW56aW5pQGdtYWlsLmNvbQ==



 Rossella Carbone3
Rossella Carbone3