- 1Department of Psychology, University of Konstanz, Konstanz, Germany
- 2Department of Biological and Medical Psychology, University of Bergen, Bergen, Norway
- 3Carl von Ossietzky University, Oldenburg, Germany
- 4Max-Planck Institute for Neurological Research, Cologne, Germany
- 5Donders Institute for Brain, Cognition and Behavior, Radboud University Nijmegen, Nijmegen, Netherlands
- 6Section for Clinical Neurophysiology, Department of Neurology, Haukeland University Hospital, Bergen, Norway
- 7Mind Research Network, Albuquerque, New Mexico, USA
- 8Department of Biomedicine, K.G. Jebsen Center for research on neuropsychiatric disorders, University of Bergen, Bergen, Norway
Errors in choice tasks are preceded by gradual changes in brain activity presumably related to fluctuations in cognitive control that promote the occurrence of errors. In the present paper, we use connectionist modeling to explore the hypothesis that these fluctuations reflect (mal-)adaptive adjustments of cognitive control. We considered ERP data from a study in which the probability of conflict in an Eriksen-flanker task was manipulated in sub-blocks of trials. Errors in these data were preceded by a gradual decline of N2 amplitude. After fitting a connectionist model of conflict adaptation to the data, we analyzed simulated N2 amplitude, simulated response times (RTs), and stimulus history preceding errors in the model, and found that the model produced the same pattern as obtained in the empirical data. Moreover, this pattern is not found in alternative models in which cognitive control varies randomly or in an oscillating manner. Our simulations suggest that the decline of N2 amplitude preceding errors reflects an increasing adaptation of cognitive control to specific task demands, which leads to an error when these task demands change. Taken together, these results provide evidence that error-preceding brain activity can reflect adaptive adjustments rather than unsystematic fluctuations of cognitive control, and therefore, that these errors are actually a consequence of the adaptiveness of human cognition.
Human performance is error-prone even when simple tasks are considered. This has typically been attributed to attentional lapses or control failures due to spontaneous fluctuations in attention and cognitive control (e.g., Weissman et al., 2006). Evidence for this notion comes from the observation of error-preceding brain activity, which refers to gradual changes in electrophysiological and hemodynamic measures that precede the occurrence of an error (Ridderinkhof et al., 2003; Allain et al., 2004; Hajcak et al., 2005; Padilla et al., 2006; Li et al., 2007; Eichele et al., 2008, 2010; Cavanagh et al., 2009; Mazaheri et al., 2009). We have previously suggested the alternative account that error-preceding brain activity reflects adaptive adjustments of cognitive control rather than unsystematic fluctuations, and that it is the adaptiveness of cognitive control which makes performance error-prone (Eichele et al., 2008, 2010). In the present paper, we employ connectionist modeling to further explore this idea.
In a recent study (Eichele et al., 2010), we examined event-related potentials (ERPs) preceding errors in the Eriksen-flanker task (Eriksen and Eriksen, 1974). In this task, participants have to categorize a target while ignoring simultaneously presented flankers that are associated with either the correct response (compatible trials) or an incorrect response (incompatible trials). We found that errors in this task were preceded by a decline of the N2 amplitude that started already several trials before an error had occurred (Eichele et al., 2010). The N2 is an endogenous component in the stimulus-locked ERP peaking at fronto-central electrodes at about 250–350 ms after stimulus onset (Nieuwenhuis et al., 2003; Folstein and van Petten, 2008). The N2 amplitude is typically larger for incompatible trials than for compatible trials—an effect presumably generated by increased activity in the anterior midcingulate cortex (aMCC) or rostral cingulate zone (RCZ), respectively, in the medial frontal cortex (Ridderinkhof et al., 2004; Huster et al., 2011).
A possible explanation for the observed decline of N2 amplitude preceding errors can be derived from conflict monitoring theory (Carter et al., 1998; Botvinick et al., 2001; Yeung et al., 2004). This framework assumes that a conflict monitor located in the medial frontal cortex registers response conflict emerging when contradicting behavioral responses are simultaneously activated, and that response conflict is reflected by the N2 amplitude, among others (Yeung et al., 2004; Yeung and Cohen, 2006; Danielmeier et al., 2009). This conflict monitor is part of a conflict adaptation mechanism which adjusts the level of cognitive control according to the previously registered response conflict. Whereas high response conflict leads to higher levels of cognitive control, low response conflict leads to lower levels of cognitive control on the subsequent trial. Evidence for this account has been provided by studies demonstrating a negative correlation between the amount of response conflict on the previous trial and the compatibility effect on the current trial in behavioral measures (e.g., Gratton et al., 1992; Ullsperger et al., 2005) and the N2 amplitude (e.g., Forster et al., 2011).
How this framework can account for the decline of N2 amplitudes preceding errors becomes clear if we consider the relation between response conflict and cognitive control in more detail. Within conflict monitoring theory, N2 amplitudes directly reflect the amount of response conflict registered in the medial frontal cortex. However, because the level of response conflict in a trial is a consequence of the state of adaptation of cognitive control in this trial, the N2 amplitude can simultaneously be interpreted as an indirect index of the state of adaptation of cognitive control. In the Eriksen-flanker task, for example, cognitive control reduces the influence of the flankers. As a consequence, low response conflict (and hence low N2 amplitudes) results when high cognitive control is exerted on an incompatible trial (on which the flankers activate the incorrect response and, therefore, increase conflict) or when low cognitive control is exerted on a compatible trial (on which the flankers activate the correct response and, therefore, decrease conflict). Following this line of reasoning, an error-preceding decline of N2 amplitude could indicate a decline of response conflict due to adaptation of cognitive control in the course of several trials, creating states of maladaptation due to conflict history. This is plausible if one takes into account that strong adaptation to a specific task demand can be detrimental when task demand is changed. For instance, a strong reduction of cognitive control following several compatible trials might lead to an error on a subsequent incompatible trial. This view implies that errors preceded by a decline of N2 amplitude are errors due to maladaptation of cognitive control and that this maladaptation is reflected by the time course of the N2 amplitude (and hence of response conflict) across trials.
In the present study, we investigated this hypothesis by examining whether an existing connectionist model of conflict adaptation (Botvinick et al., 2001), in which the N2 is simulated as the response conflict induced by the stimulus, can account for error-preceding brain activity in the Eriksen-flanker task. We started with fitting the model to data from an experiment in which the local probability of incompatible trials was manipulated. In this experiment, each block of trials consisted of five sequences of 40 trials in which conflict probability, i.e., the probability of incompatible trials was either 10%, 30%, 50%, 70%, or 90%. This manipulation allowed us to calibrate the strength of conflict adaptation in the model. Because cognitive control should be adjusted according to these local probabilities, an increasing conflict probability should imply a decreasing effect of flanker compatibility. As a consequence, the strength of this conflict probability effect should reflect the strength of conflict adaptation. By fitting the model to these data, we should obtain a realistic model of conflict adaptation. In addition to this conflict adaptation model, we also constructed alternative models in which the level of cognitive control varied in a random or a slowly oscillating manner, analogous to stochastic noise in attentional networks and resting state fluctuations, respectively.
Using the simulation data obtained from these models, we then examined whether error-preceding brain activity reflects conflict adaptation. This was achieved by comparatively analyzing empirical N2 amplitudes and simulated N2 amplitudes preceding errors. To extract the time course of these measures preceding errors, we applied a de-convolution analysis on single-trial N2 amplitudes, a method previously employed by Eichele and colleagues (Eichele et al., 2008, 2010; Eichele and Calhoun, 2009), which is preferable to within-subject averaging because it enables the inclusion of overlapping trial sequences with errors. To robustly estimate EEG activity on a trial-by-trial basis, we used independent component analysis (ICA) to extract a component that captures N2 activity, and took the amplitude of this component as an estimate of the single-trial N2 amplitude (for an overview on this method, see e.g., Eichele and Calhoun, 2009; Gentsch et al., 2009). We predicted that, if conflict adaptation is sufficient to account for error-preceding effects in the N2 amplitude, a model involving conflict adaptation should produce the same effects as found in the empirical data. Moreover, if conflict adaptation is necessary to account for error-preceding effects in the N2 amplitude, no such effects should be obtained in the alternative models. To further demonstrate that errors are caused when strong adaptation occurs together with a change of task demands, we also analyzed the empirical and simulated stimulus sequence and the time course of response times (RTs) preceding errors.
Materials and Methods
Experimental Method
Participants
Twenty-seven paid participants (15 females, 12 males)1 with mean age of 21.5 years participated in the study. All had normal or corrected to normal vision, had no history of neurological or psychiatric disease, and were not using psychotropic medication. Participants were primarily recruited from undergraduate psychology and medicine classes at the University of Bergen and had signed a written statement of informed consent. Data from three subjects were discarded due to excessive artifacts in the EEG. The experiment was approved by the regional ethical committee for western Norway.
Stimuli and task
The task was a modified Eriksen-flanker paradigm (Eriksen and Eriksen, 1974) implemented in E-prime (Psychology Software Tools, Pittsburgh, USA). Each stimulus consisted of seven arrowheads presented horizontally on a computer screen, a target arrow and three identical flanker arrows on each side. On compatible trials, all arrows pointed to the same direction (<<< < <<<, >>> > >>>). On incompatible, trials flankers and target pointed to different directions (<<< > <<<, >>> < >>>). Participants were instructed to respond to the direction of the target arrow while ignoring the flanker arrows by pressing the left or right button of a computer mouse placed under their preferred hand. Responses had to be given as quickly and as accurately as possible. Each trial started with the presentation of a fixation cross for 800 ms. Then, the flanker arrows were presented alone for 100 ms followed by the target arrow. Target and flankers remained on the screen until the registration of a response which started a new trial.
Each participant worked through five blocks of 200 trials each with short breaks in between, resulting in a total of 1000 trials. Each block consisted of five contiguous sub-blocks of 40 trials. These sub-blocks differed with respect to the probability of incompatible trials which was manipulated in five steps (0.10, 0.30, 0.50, 0.70, 0.90). The probability of a left and right response was kept constant. Trial sequences and order of probability conditions within each block was randomized separately for each participant. No explicit performance feedback was given during the experiment.
EEG data acquisition and preprocessing
Participants were seated in an electro-magnetically shielded and sound attenuated room (Rainford EMC Systems, Wigan, UK). Continuous EEG was recorded from 61 Ag/AgCl scalp electrodes (Fp1, Fpz, Fp2, AF7, AF3, AFz, AF4, AF8, F7, F5, F3, F1, Fz, F2, F4, F6, F8, FT7, FC5, FC3, FC1, FCz, FC2, FC4, FC6, FT8, T7, C5, C3, C1, Cz, C2, C4, C6, T8, TP7, CP5, CP3, CP1, CPz, CP2, CP4, CP6, TP8, P7, P5, P3, P1, Pz, P2, P4, P6, P8, PO7, PO3, POz, PO4, PO8, O1, Oz, O2, TP10) mounted in an elastic cap (Falk Minow Services, Herrsching, Germany). A recording reference was placed at TP9 and a ground electrode was placed in front of the right ear. Vertical EOG was monitored by a bipolar derivation between Fp1 and an electrode placed under the left eye. Horizontal EOG was monitored by a bipolar derivation between F7 and F8. Impedance of all electrodes was kept under 10 k. EEG recordings were done with a Brain MR plus X2 amplifier (BrainProducts, Munich, Germany) with sampling rate 1000 Hz, a time constant at 10 s and a high cut-off at 250 Hz.
The EEG data were offline re-referenced to common average reference, filtered from 0.5 to 45 Hz (12 db) and decimated to 500 Hz sampling rate. To obtain epochs comprising the previous response as well as the current response, epochs from 900 ms before target onset to 1100 after target onset were extracted from the continuous EEG. Epochs were baseline-corrected with the mean value of the entire epoch serving as baseline. Epochs containing large, non-stereotyped artifacts with amplitudes exceeding ±300 μV on any of the channels were rejected, and padded with the average of adjacent trials. Epochs from all 61 scalp channels were subjected to temporal ICA using the infomax algorithm (Bell and Sejnowski, 1995) implemented in EEGLAB (Delorme and Makeig, 2004). Thirty components were estimated after PCA compression. To obtain robust estimates of single-trial amplitudes of the N2, analyzes were conducted on independent components (ICs) representing the N2 conflict effect rather than on raw EEG data. To extract these components, automated sorting routines were applied. Spatial correlation with templates for blink and lateral eyes movements were used to identify ICs representing ocular artifacts (Viola et al., 2009). Spatial standard deviation of the topography and correlation with a spectral template were used to identify ICs with muscular and other artifacts localized at single electrodes. From the remaining components, one was extracted for each participant that (1) best matched the expected fronto-central topography of an N2, (2) produced large amplitudes on error trials (Yeung et al., 2004), and (3) was associated with a large difference between compatible and incompatible stimuli. In most participants, this procedure yielded a single matching component. In about 10% of the sample, two or three components matched the criteria, and we selected the one with the largest correlation score. Topographies of the selected components were assigned a positive maximum, and components activations were back-projected to sensor level to recover the sign and amplitude of the scalp recorded potentials.
Empirical variables
Three empirical variables were extracted from each trial. First, empirical accuracy was determined by categorizing each trial as correct trial or error. Second, empirical RT was calculated as the time difference between target onset and key press. Third, empirical N2 was calculated as the maximum amplitude in the time window between 310 ms and 350 ms after target onset.
Modeling
Model structure and simulation details. We implemented the neural network model of the Eriksen-flanker task in a customized version of the Emergent 5.1.6 simulation environment (Aisa et al., 2008)2. In the following, only general aspects and deviations from the original model are described (for a detailed description, see Yeung et al., 2004). The neural network consisted of three layers (see Figure 1). A stimulus layer contained one unit for each possible combination of stimulus (<, >) and spatial location (left flanker, target, right flanker). This allowed for representing each possible stimulus array as a unique pattern of activated stimulus units. The response layer contained one unit for each possible response (left, right). Feedforward excitatory associations connected each stimulus unit with its corresponding response unit. To ensure that the target units had the strongest influence on the response units, activation in the stimulus layer was influenced by an attention layer representing the allocation of attention to the respective stimulus locations. The attention layer contained one unit for each possible stimulus location, and each unit was bi-directionally connected to its corresponding units in the stimulus layer. Within each layer, each unit was linked with each other unit through inhibitory connections.
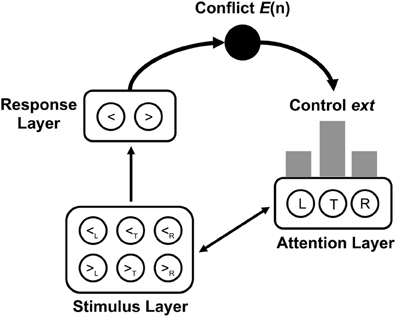
Figure 1. Architecture of the conflict adaptation model by Botvinick et al. (2001). The stimulus layer contains one unit for each combination of arrow type (<= left arrow, >= right arrow) and stimulus position (L = left flanker, T = target, R = right flanker). The response layer contains one unit for each response (<= left response, >= right response). The attention layer contains one unit for each stimulus position. Conflict E(n), resulting as a function of activity in the response layer, is used to adjust the control parameter ext, which determines activity in the attention unit. Gray bars indicate the average distribution of activity across stimulus positions in the attention layer.
The model was simulated as described by Yeung et al. (2004). A trial started by activating stimulus and attention units. Stimulus units were activated according to the stimulus presented in a trial. For simplicity, no SOA between flankers and target was implemented. Attention units were activated by setting external inputs extL, extC, and extR, respectively, to the left, central, and right unit according to the strength of selective attention in a trial (see below). A trial was simulated for 100 cycles. On each cycle, activation of a given unit was updated as a function of its activation on the previous cycle, Gaussian noise (with mean 0 and standard deviation snoise), external inputs, and the activation of units projecting to this unit weighted by connection weights. Due to within-layer inhibition, the network showed a winner-takes-all behavior. In the course of several cycles, each layer approached an attractor state with one unit converging to maximum activation and all other units converging to minimum activation. A response was selected when activation of a response unit exceeded a response criterion rcrit. On the majority of trials, the response unit representing the correct response for a given stimulus exceeded the criterion. On some trials, noise caused the incorrect response unit to become selected.
Conflict monitoring and adjustments of cognitive control. To simulate conflict monitoring in the medial frontal cortex (Botvinick et al., 2001), response conflict was calculated as the Hopfield energy of the two-unit response layer at cycle n,
with wR denoting the associative weight between the two response units with activations actLeft(n) and actRight(n), respectively. Note that E(n) is positive if both units are activated because the inhibitory weight wR is negative. If activation of one or both of the units became negative, E(n) was set to zero. Crucially, this definition of response conflict implicated that simulated response conflict was high whenever both responses were concurrently activated. Accordingly, response conflict could occur for two reasons: first, response conflict could occur before a response exceeded the criterion when target and flankers activated different response units early in the trial (pre-response conflict). Second, response conflict could occur after a response exceeded the criterion when this response was incorrect. Due to self-corrective behavior, a conflict between the still activated incorrect response and the emerging correct response can occur (post-response conflict).
According to conflict monitoring theory (Botvinick et al., 2001), response conflict on the previous trial determines cognitive control on the current trial. In the model of the Eriksen-flanker task, cognitive control is assumed to correspond to the distribution of selective attention across target and flanker stimuli. Following Botvinick et al. (2001), response conflict for a given trial was calculated by summing up response conflict across all cycles of that trial. This cumulated conflict E(t − 1) from the previous trial t − 1 is used to update the external input to the central attention unit, extC(t) for the current trial t by applying the equation:
with α and β being scaling parameters. λ is bound to the interval [0, 1] and represents the relative contribution of attention from the preceding trial to attention on the current trial. The three parameters α, β, and λ play different roles for the adjustment of cognitive control, whereas α determines the relation between conflict and attention, β establishes a lower limit of attention. Finally, λ determines the volatility by which changes in conflict lead to changes in attention. In contrast to earlier simulations of the model, an additional parameter, extCmax, was introduced representing the upper bound to extC. This allowed for simulating long sequences of high conflict trials without causing excessively high values of extC. Finally, external input to the attention units representing the flanker locations was calculated as:
which implies that total attention is constant and larger values of extC lead to smaller values of extL and extR.
Simulated variables. We used this model to generate the three simulated variables corresponding to our empirical measures. First, the simulated error rate corresponds to the relative frequency of trials on which an incorrect response unit exceeds the response criterion. Second, simulated RTs were calculated as the number of cycles until a response is selected. Then, a linear transformation was used to translate these values into milliseconds (see below). Third, the simulated N2 was obtained by calculating the average response conflict E across all cycles within a trial.
Model fitting. In a first stage, the model was fit to RTs of correct responses and error rates for each experimental condition. To this end, we applied the optimization procedure by Bogacz and Cohen (2004) that was developed for neural networks. For the optimization, five stimulus sequences with a total of 5000 trials were generated that had the same length and structure as those used in the experiment. Within each iteration, these five sequences were simulated and simulated RTs and error rates for each condition were averaged across sequences. The optimization procedure minimizes the mean squared error, MSE, calculated as the sum of squared differences between empirical and simulated data points. Differences were weighted to ensure comparability of MSE components from different variables. A difference of 1% in the error rates corresponded to a difference of 10 ms in the RTs.
Five free parameters were optimized: the response criterion rcrit, the maximum attention extCmax, two parameters of conflict adaptation, α and β, respectively, and the noise parameter snoise. These parameters were chosen because we assumed that parameters regulating the susceptibility to errors (such as the response criterion and noise) as well as the range and volatility of attentional adjustment differ between studies. All other parameters were taken from Yeung et al. (2004). In addition, the optimization procedure of Bogacz and Cohen (2004) optimizes two scaling parameters—a time constant reflecting non-decision processes, TND, and the duration of a cycle, Tcycle—that translate cycles into milliseconds by means of linear transformation.
Simulation and model variants. Using these parameters, a final simulation was conducted which served for subsequent analyses. To maximize the comparability between empirical and simulated data, we now simulated the stimulus sequences of all 24 subjects resulting in 24,000 trials. In addition to the standard model described above, which assumes that the level of cognitive control on each trial is determined by the conflict adaptation mechanism (which we call the Adaptive Control model in the following), we simulated four alternative models to investigate whether adaptive adjustments of control are necessary to explain error-preceding brain activity: In the Random Control model, the cognitive control parameter, extC(t), varied randomly across trials. In three Oscillating Control models, extC(t) oscillated across trials with either a low, an intermediate or a high frequency (see below). We wanted these models to differ only in the way cognitive control varies across trials but not in any other aspect (e.g., the quality of the fit to the averaged data). Therefore, the Random Control and the Oscillating Control models were not fit to the data, but were derived from the Adaptive Control model by applying the following four steps:
- We fitted and simulated the Adaptive Control model as described above.
- We extracted the cognitive control parameter, extC(t), for each trial t.
- For each sub-block of 40 trials, extC(t) was rearranged depending on the specific model. For the Random Control model, order was simply randomized. For the Oscillating Control model, the 40 values were sorted into q quantiles (q = 10 for the high frequency, q = 5 for the intermediate frequency, q = 2 for the high frequency). A new order was created by cycling repeatedly back and forth through these quantiles and drawing one value for each trial. Examples of extC(t) sequences for a sub-block of a single subject are provided in Figure 2.
- The models were simulated by setting these new values of extC(t) and recalculating extL(t) and extR(t) accordingly, but without adjusting extC(t) based on response conflict.
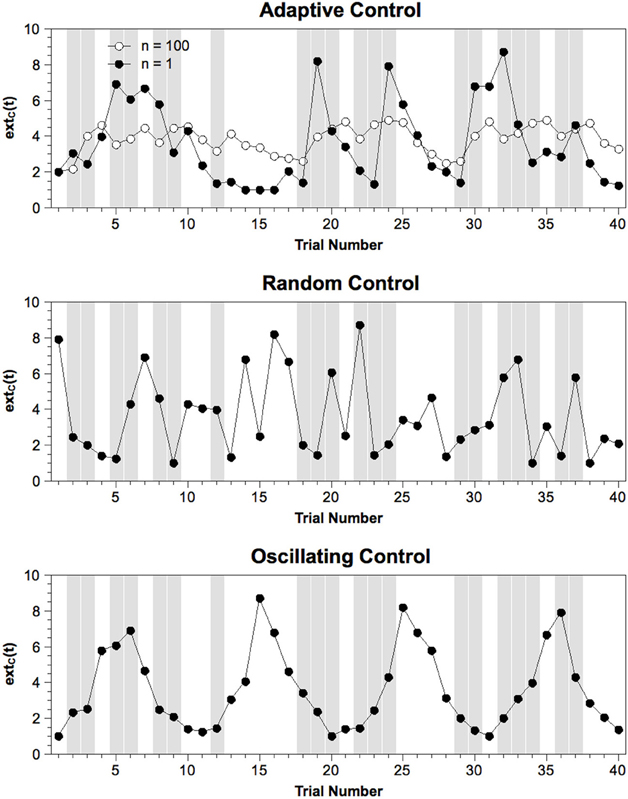
Figure 2. Exemplary sequence of extC(t) values from one sub-block of each model variant. Gray columns indicate incompatible trials. Note that the set of values is the same across models while only the order of values differs between models. For the Adaptive Control model, mean values averaged across 100 simulations are provided to illustrate how extC(t) varies as a function of stimulus sequence when noise is removed. For the Oscillating Control model, only a sequence for the intermediate frequency (10 trials per cycle) is depicted. n = number of simulations.
Note that the fact that we only rearranged extC(t) within sub-blocks, mean RTs, mean error rates, and mean simulated N2 amplitudes produced by these models are largely identical.
Analysis of model and empirical data
To quantify the effects of conflict probability and compatibility for model fitting, means of simulated and empirical RT, accuracy and N2 were computed for each condition. For the empirical RT, responses faster than 100 ms (0.03%) and slower than 1000 ms (0.48%) were not considered. Later, changes in RT and N2 before and after errors were calculated by applying the de-convolution method that has originally been introduced for hemodynamic response estimation (Eichele et al., 2008) and which has recently been applied to extract trial-by-trial effects in behavioral data and ERP amplitudes (Eichele et al., 2010). De-convolution allows for extracting systematic modulations around specific events like errors while avoiding problems with overlapping trial sequences (e.g., when two errors occur in succession) that occur with within-subject averaging (for a simulation demonstrating the validity of this method, see Eichele et al., 2010). We first eliminated variance related to stimulus types, priming, and errors from empirical and simulated single-trial RTs and N2 amplitudes following the method by Notebaert and Verguts (2007). For each variable, multiple linear regressions were computed with compatibility (compatible, incompatible), stimulus/response repetition (repetition, change), and accuracy (correct, error) as independent variables. Residuals from these regressions were taken as new estimates of empirical and simulated single-trial RTs and N2 amplitudes, and were used in further analyzes. Then, a binary vector representing response accuracy (0 = correct, 1 = error) was used to derive the modulation from five trials prior to five trials after errors using de-convolution. The de-convolved modulation of each variable preceding errors was tested by fitting a linear slope to the five error-preceding trials using linear regression, and by testing the significance of the slope as well as the trial immediately preceding the error. For the simulated data, each of the 24 simulated sequences was treated as a “subject.”
Results
Empirical Data
Conflict-related IC
Figure 4 shows spatial distribution and time course of the IC used for single-trial analysis of N2 amplitudes. Visual inspection reveals that the component has the typical fronto-central distribution of an N2 (e.g., Nieuwenhuis et al., 2003) and that component activity in the time range of the N2 (shaded area) strongly differs between compatible and incompatible stimuli (see statistical analysis in next section). Both observations are not surprising given that they reflect the main criteria for component selection. However, Figure 4 also reveals that the extracted IC captures more than the mere N2. First, there is a strong compatibility effect in the time range of the P3 (>360 ms). This phenomenon—which is also evident in ERP waveforms reported by other studies (e.g., Yeung et al., 2004)—might reflect the strong correlation between the N2 and the fronto-central P3a in a number of paradigms (for an overview, see Folstein and van Petten, 2008). Second, the component captures oscillatory activity in the theta range (4–7 Hz). This is not surprising given recent evidence provided by Nigbur et al. (2011) showing that fronto-central theta oscillations in the Eriksen-flanker task are sensitive to conflict with a peak in the N2 time range. This suggests that the conflict-related N2 and conflict-related theta oscillations may well reflect the same neurocognitive mechanisms. However, given that the compatibility effect in the present data seems to be restricted to the event-related N2/P3a complex, we conclude that, even if both phenomena represent different mechanisms, the extracted IC mainly captures the conflict-related N2 rather than conflict-related theta activity, and thus, can be used to estimate single-trial N2 amplitudes.
Condition means. Figure 3 (left column) depicts empirical RTs, error rates, and N2 amplitudes averaged for each experimental condition. RTs of correct responses and error rates were analyzed in a Two-Way ANOVA with repeated measurement on the variables Compatibility (compatible, incompatible) and Conflict Probability (10%, 30%, 50%, 70%, 90%). For the RTs, a significant effect of Compatibility, [F(1, 23) = 316.8, p < 0.001], and a significant interaction, [F(4, 92) = 41.3, p < 0.001], was obtained. With a larger Conflict Probability, RTs for incompatible stimuli became shorter and RTs for compatible stimuli became longer. For the error rates, significant effects of Compatibility, [F(1, 23) = 98.7, p < 0.001], and Conflict Probability, [F(4, 92) = 59.1, p < 0.001], as well as a significant interaction, [F(4, 92) = 68.0, p < 0.001], were obtained. Whereas error rates for incompatible stimuli decreased with an increasing Conflict Probability, error rates for compatible stimuli remained constant at a low level. Finally, for the N2, we obtained significant main effects of Compatibility, [F(1, 23) = 14.5, p < 0.001], and Conflict Probability, [F(4, 92) = 2.62, p < 0.05], as well as a significant interaction, [F(4, 92) = 9.00, p < 0.001]. Whereas for incompatible stimuli a higher Conflict Probability led to decreased N2 amplitudes, for compatible stimuli a higher Conflict Probability led to increased N2 amplitudes.
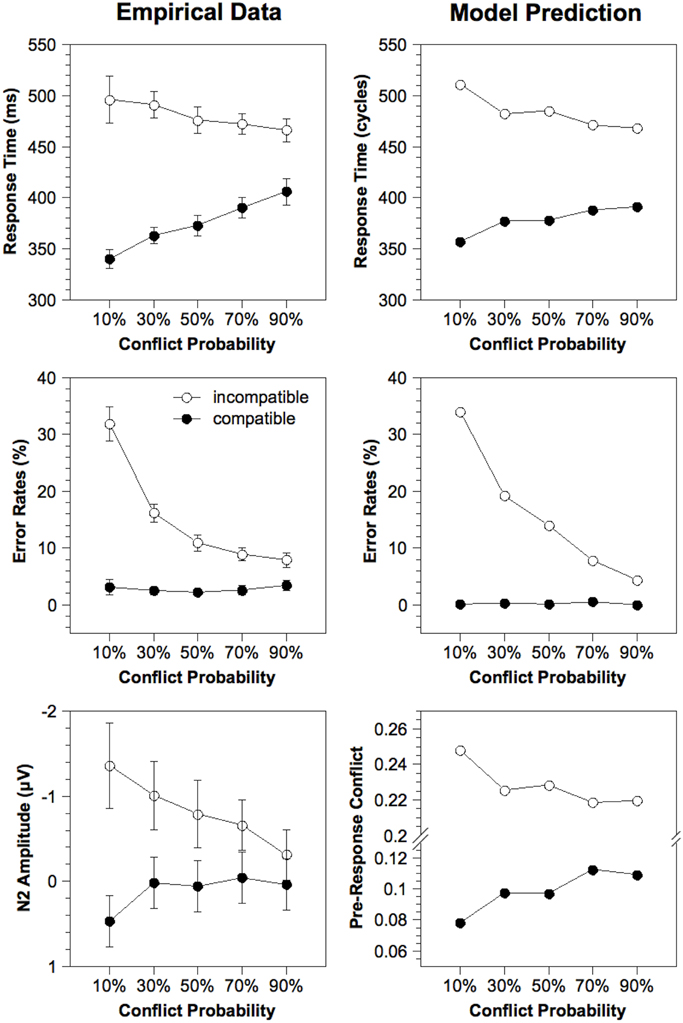
Figure 3. Response time, error rates, and estimated N2 amplitude for the empirical data and the fit of the Adaptive Control model as a function of Compatibility and Conflict Probability. Simulated N2 amplitude is estimated by the cumulated pre-response conflict in each trial. Note that the results for the alternative model variants are approximately the same because these model differ only with respect to the order of extC(t) values within each condition, which does not influence the averaged results. ms, milliseconds.
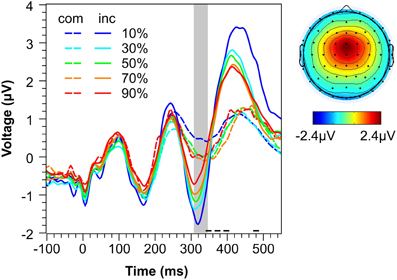
Figure 4. Conflict-related IC. Left: Mean activity of the extracted ICs representing the N2 conflict effect as a function of Compatibility and Conflict Probability. The shaded area represents the time range of the N2 used for analysis. Horizontal lines at the x-axis indicate the range of mean RTs for compatible trials (long dashed line) and incompatible trials (short continuous line). Right: Mean topography of the extracted ICs. com, compatible. inc, incompatible.
Time course preceding errors. Figure 5 (left column) depicts the result of the de-convolution analysis for the empirical data. Values extracted by the de-convolution analysis indicate the deviation from the mean. Error-preceding brain activity should be characterized by an increasing deviation from the mean reaching a maximum on the trial immediately preceding the error (e–1 trial). We concluded that such a pattern exists if there is a significant deviation from zero on the e–1 trial, and if there is a significant slope across five trials preceding the error. The latter criterion was chosen because error-preceding activity in previous studies influenced five error-preceding trials (Eichele et al., 2008, 2010).
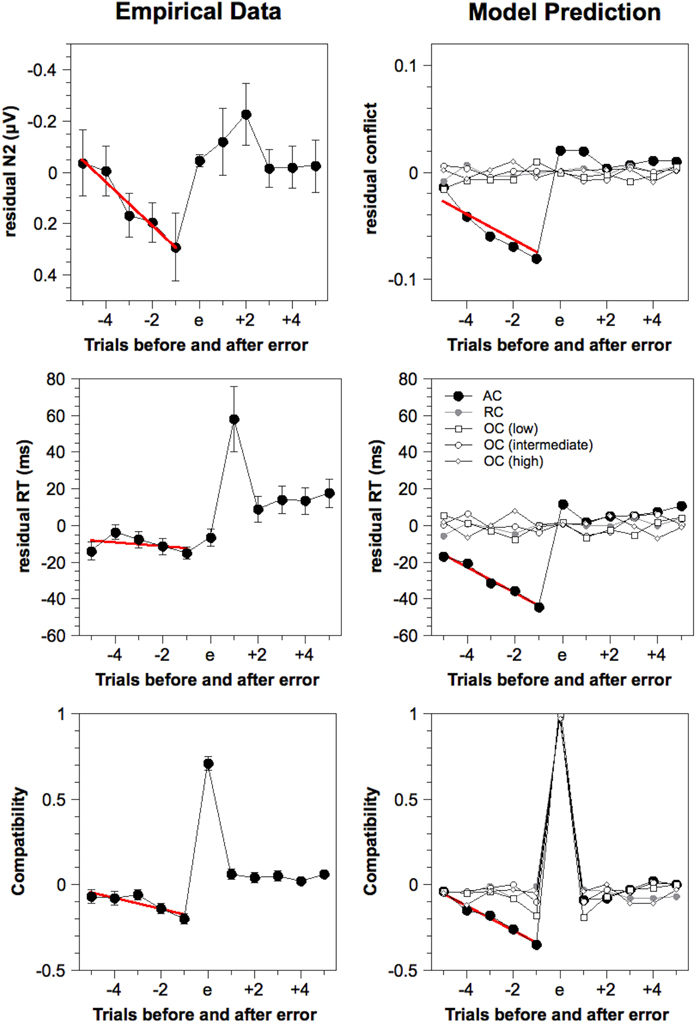
Figure 5. Residual estimated N2 amplitudes, residual response times, and compatibility around errors for the empirical and model data, as obtained by de-convolution analysis. Simulated N2 amplitude is estimated by the cumulated pre-response conflict in each trial. Red lines indicate linear regression across five trials preceding errors (only provided for the AC model). ms, milliseconds, AC, Adaptive Control, RC, Random Control, OC, Oscillating Control.
As already reported by Eichele et al. (2010) for a larger sample with additional variation of stimulus and response probabilities, errors were preceded by a linear decline of N2 amplitude, indicated by a significant slope (0.09 μV), t(23) = 2.35, p < 0.05, and a significant deviation on the e–1 trial (0.29 μV), t(23) = 2.23, p < 0.05. The same analysis applied to RTs showed only a slight decrease preceding errors with a non-significant slope (−1.03 ms), t(23) = 0.81, p = 0.43, but a significant value preceding the error (–15.0 ms). Because the non-significant slope might reflect the outlier on the e−5 trial, we additionally tested the slope for the four error-preceding trials and found this to be significant (−3.74 ms), t(23) = 2.27, p < 0.05. The data also revealed a sharp increase in RT following errors indicating a strong effect of post-error slowing (e.g., Rabbitt and Rodgers, 1977; Laming, 1979).
To examine which stimuli are typically preceding errors, de-convolution analysis was also applied to compatibility with 1 referring to an incompatible stimulus and 0 referring to a compatible stimulus. Figure 5 shows a strong positive value representing the fact that errors are more likely to occur for incompatible stimuli. Moreover, errors are preceded by a significant decline of the compatibility variable [slope: −0.03, t(23) = 3.01, p < 0.01; e−1 value: −0.21, t(23) = 7.66, p < 0.001]. This shows that errors are more likely to be preceded by compatible stimuli.
Taken together, we obtained robust error-preceding brain activity. Moreover, this effect is accompanied by a change in compatibility, which already points to maladaptation as a cause of this effect. In the next part, it is examined whether maladaptation of cognitive control is sufficient and necessary to account for systematic changes of brain activity preceding errors.
Modeling
Model fitting. To build a realistic model of our task, the model was fit to RTs and error rates in each experimental condition by optimizing five parameters related to conflict adaptation (α, β), attention (extCmax), response selection (rcrit), and noise (snoise). Inspection of Figure 3 contrasting model prediction and empirical data reveals that the model captures the main trends inherent in the empirical data, although some small deviations remain. Crucially, although the model was fit to behavioral data only, the pattern of simulated N2 amplitudes closely corresponds to that of the empirical N2 amplitudes. Note that this effect is exclusively due to the conflict adaptation mechanism which adjusts cognitive control according to the stimulus sequence.
The parameter values of the best fit are depicted in Table 1. The increase of α from 4.41 to 22.6 implies that changes in response conflict lead to a stronger adjustment of attention. These stronger adjustments were necessary to quickly adapt attention to changes in conflict probability. To avoid that strong adjustments lead to excessive levels of external input to the center attention unit, an upper bound to this external input, extCmax, was introduced which adopted a value of 8.70. Moreover, the lower limit of adjustment, β, was reduced to 0.367. Finally, the response criterion, rcrit, was increased to 0.24 and noise, snoise, was reduced to 0.23 to adapt to the generally low error rate.
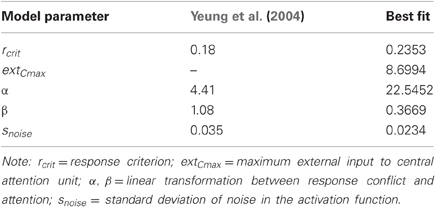
Table 1. Comparison of model parameters from the best fit of the present model and the original model by Yeung et al. (2004).
Time course preceding errors. The time course of the estimated N2 amplitude and other variables preceding errors were analyzed for different model variants in the same way as the empirical data. The results are depicted in Figure 5 (right column). The Adaptive Control model showed a significant decline of the simulated N2 amplitude preceding errors [slope: −0.01, t(23) = 8.84, p < 0.001; e−1 value: −0.07, t(23) = 18.4, p < 0.001] as well as a significant reduction of simulated RT [slope: −6.97 ms, t(23) = 8.98, p < 0.001; e−1 value: −44.4 ms, t(23) = 18.3, p < 0.001]. Note that there was no post-error slowing as in the empirical data since such a mechanism was not included in this version of the model (but see Botvinick et al., 2001). Finally, we obtained a decrease of the compatibility variable preceding errors [slope: −0.07, t(23) = 10.2, p < 0.001; e−1 value: −0.35, t(23) = 18.1, p < 0.001] that resembled that obtained in the empirical data.
The same analysis was applied to the Random Control model and three variants of the Oscillating Control model. However, as shown in Figure 5, none of these models produced substantial trends in the simulated N2 amplitude or the simulated RT preceding errors. Only for the compatibility variable, we obtained significant effects for some of the Oscillating control models. Compatibility deviated significantly on the e−1 trial for the low frequency model (−0.17), t(23) = 6.96, p < 0.001, and the intermediate model (−0.12), t(23) = 4.19, p < 0.001. This might simply reflect the fact that the highest error frequency for incompatible trials were obtained in conditions where compatible trials were frequent, an effect that should have contributed to the results also in the Adaptive Control model. However, because this effect was restricted to the e−1 trial in some Oscillating Control models, it cannot fully account for the time course of compatibility obtained in the Adaptive Control model. Taken together, these analyzes show that only the Adaptive Control model predicts error-preceding brain activity as found in the empirical data.
Discussion
In the present study, we investigated the hypothesis that the decline of N2 amplitude preceding errors reflects adaptive adjustments of cognitive control and, accordingly, that it is the adaptivity of cognitive control that promotes the occurrence of errors in this type of task. Our strategy was to fit a connectionist model of conflict adaptation (Botvinick et al., 2001) to experimental data and to test whether adaptive adjustments of cognitive control are sufficient and necessary to simulate this error-preceding brain activity. The model assumes that the N2 reflects response conflict elicited by the stimulus (Yeung et al., 2004; Yeung and Cohen, 2006), and that the strength of response conflict not only indicates the level of cognitive control but is also used by a conflict adaptation mechanism to adjust cognitive control to meet current task demands.
To calibrate this conflict adaptation mechanism, we considered an experiment in which the frequency of incompatible trials, and thus conflict probability, varied locally (e.g., Gratton et al., 1992). As expected, we found that an increased conflict probability led to a reduced effect of flanker compatibility not only in behavioral measures but also in the N2 amplitude. The model was able to reproduce these effects by means of local conflict adaptation. Although we fitted the model only to behavioral measures, the model displayed a similar pattern in the simulated N2 amplitudes as in the empirical N2 amplitudes. This supports the general assumption that the N2 reflects response conflict, and that the N2 compatibility effect can be viewed as an indirect measure of cognitive control (e.g., Forster et al., 2011).
Crucially, however, this Adaptive Control model produced similar effects preceding errors as shown in the experimental data. Most importantly, the simulated N2 amplitude showed a strong decline preceding errors. This can be interpreted as a gradual increase in adaptation of cognitive control which initially led to a reduction in response conflict, but eventually increased the probability of an error. Basically, this effect can result in two scenarios. First, it could result from an adaptive increase of control due to a series of incompatible trials, which then leads to an increased error probability on a compatible trial (Note that high control is detrimental on compatible trials because it prevents the flankers from activating the correct response). Second, it could result from an adaptive decrease of control due to a series of compatible trial, which then leads to an increased error probability on an incompatible trial. Both possibilities presumably contribute to this effect. However, the relative contribution of the latter effect should be larger because errors were more frequent on incompatible trials and were preceded by a gradually decreasing probability of incompatible stimuli—an effect that was also reflected in a decline of RT preceding errors.
Whereas the analysis of the Adaptive Control model revealed that conflict adaptation is sufficient to predict the observed time course of the N2 amplitude, we simulated additional models to show that conflict adaptation is necessary to predict these effects. Two types of models were derived by simply reordering the cognitive control parameter either in a random or an oscillating manner, representing the idea that errors are caused by intrinsic and task-unrelated fluctuations in attentional and cognitive control systems (Weissman et al., 2006). Both models were not able to reproduce the empirical data. We found no corresponding time course preceding errors in either of the variables considered. Note that this is not due to the fact that these models are less able to account for the empirical mean performance. Because the models were derived from the Adaptive Control model by reordering the control parameters within sub-blocks associated with a specific conflict probability, the alternative models produced the same averaged data as the Adaptive Control model.
Taken together, our simulations show that conflict adaptation, as implemented in the original model by Botvinick et al. (2001), is sufficient and necessary to simulate a specific type of error-preceding brain activity, namely the decline of N2 amplitudes preceding errors. Conflict adaptation is sufficient because it can fully account for the observed effects without making additional assumptions that go beyond the original model by Botvinick et al. (2001). It is necessary because simpler models without conflict adaptation (e.g., based on random or oscillatory fluctuations of attention) cannot account for the data. Given the already broad range of phenomena that have been successfully simulated using this model (like the error-related negativity, the N2, behavioral conflict adaptation effect, lateralized readiness potentials; e.g., Botvinick et al., 2001; Yeung et al., 2004; Danielmeier et al., 2009), the present results demonstrate again that conflict monitoring and conflict adaptation provide a parsimonious explanation for the interaction of conflict and control.
The question emerges whether other types of error-preceding brain activity reflect similar mechanisms. A phenomenon related to the error-preceding decline of the N2 is the finding that response-locked ERPs for correct responses preceding errors show a positive shift with a similar spatial distribution as the N2 (Ridderinkhof et al., 2003; Allain et al., 2004; Hajcak et al., 2005). Allain et al. (2004) proposed that this effect is related to the error-related negativity (Falkenstein et al., 1990; Gehring et al., 1993), another component that has been interpreted as reflecting response conflict by conflict monitoring theory (Yeung et al., 2004). As a consequence, this positive shift might reflect a decline of response conflict that only differs in timing from the N2 effects considered here. Future research might reveal whether there is a relation between both phenomena.
Finally, a further result from our simulations deserves to be mentioned. As can be seen in Figure 5, the Adaptive Control model does not account for post-error slowing, which refers to the slowing of RT following an error, and which has typically been attributed to more cautious responding to prevent further errors (e.g., Rabbitt and Rodgers, 1977; Laming, 1979; but see Notebaert et al., 2009). Our model could not account for this effect because only selective attention but not the response criterion was adjusted depending on response conflict in a trial-by-trial manner. In fact, Botvinick et al. (2001) implemented such a mechanism and could successfully account for post-error slowing. The fact that conflict adaptation and post-error slowing are modeled by different algorithms support the notion that performance monitoring can trigger a range of independent adaptation mechanisms (King et al., 2010; Danielmeier et al., 2011; Maier et al., 2011; Steinhauser and Kiesel, 2011). Moreover, the fact that our model predicted pre-error speeding but not post-error slowing implies that both phenomena are not necessarily related. Whereas pre-error speeding can reflect stimulus history preceding errors (and thus indirectly conflict adaptation), post-error slowing might reflect a criterion change.
Taken together, our results provide an answer to the question why human performance is error-prone even in simple tasks. The brain continuously monitors conflicts emerging between contradicting responses to predict upcoming task demands and to adjust the level of control accordingly (Botvinick et al., 2001, 2004). The resulting adaptation of cognitive control allows the brain to produce goal-directed performance. However, a drawback of this adaptation is that adaptive control can become maladaptive when task demands change. A level of control that is optimal in one situation can be detrimental in another situation, leading to performance decrements or even errors. Because this (mal-)adaptation is represented by error-preceding brain activity, this further implies that error-preceding brain activity can not only be used to investigate the origin of errors, it can also serve as a robust empirical marker of adaptive control.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank Aleksander H. Erga, Eva Sunde, and Katrine V. Granli for their help with data collection. This work was supported by a grant to Marco Steinhauser from the Deutsche Forschungsgemeinschaft (DFG: STE 1708/1) and a Nevronor grant to TE from the Norwegian Research council (189661).
Footnotes
- ^The data presented in this paper are part of a larger sample in which stimulus probabilities were manipulated in various ways. This larger sample was published in Eichele et al. (2010) without reporting specific analyzes of the probability manipulation in the present sub-sample.
- ^The Emergent software is available at http://grey.colorado.edu/emergent. To simulate the model by Botvinick et al. (2001), the Constraint Satisfaction class was modified in the source code of the Emergent software, and the software was re-compiled.
References
Aisa, B., Mingus, B., and O'Reilly, R. C. (2008). The emergent neural modeling system. Neural Netw. 21, 1146–1152.
Allain, S., Carbonnel, S., Falkenstein, M., Burle, B., and Vidal, F. (2004). The modulation of the Ne-like wave on correct responses foreshadows errors. Neurosci. Lett. 372, 161–166.
Bell, A. J., and Sejnowski, T. J. (1995). An information-maximization approach to blind separation and blind deconvolution. Neural Comput. 7, 1129–1159.
Bogacz, R., and Cohen, J. D. (2004). Parameterization of connectionist models. Behav. Res. Methods Instrum. Comput. 36, 732–741.
Botvinick, M. M., Braver, T. S., Barch, D. M., Carter, C. S., and Cohen, J. D. (2001). Conflict monitoring and cognitive control. Psychol. Rev. 108, 624–652.
Botvinick, M. M., Cohen, J. D., and Carter, C. S. (2004). Conflict monitoring and anterior cingulate cortex: an update. Trends Cogn. Sci. 8, 539–546.
Carter, C. S., Braver, T. S., Barch, D. M., Botvinick, M. M., Noll, D., and Cohen, J. D. (1998). Anterior cingulate cortex, error detection, and the online monitoring of performance. Science 280, 747–749.
Cavanagh, J. F., Cohen, M. X., and Allen, J. J. (2009). Prelude to and resolution of an error: EEG phase synchrony reveals cognitive control dynamics during action monitoring. J. Neurosci. 29, 98–105.
Danielmeier, C., Eichele, T., Forstmann, B. U., Tittgemeyer, M., and Ullsperger, M. (2011). Posterior medial frontal cortex activity predicts post-error adaptations in task-related visual and motor areas. J. Neurosci. 31, 1780–1789.
Danielmeier, C., Wessel, J., Steinhauser, M., and Ullsperger, M. (2009). Modulation of the error-related negativity by response conflict. Psychophysiology 46, 1288–1298.
Delorme, A., and Makeig, S. (2004). EEGLAB: an open source toolbox for analysis of single-trial EEG dynamics. J. Neurosci. Methods 134, 9–21.
Eichele, H., Juvodden, H. T., Ullsperger, M., and Eichele, T. (2010). Mal-adaptation of event-related EEG responses preceding performance errors. Front. Hum. Neurosci. 4:65. doi: 10.3389/fnhum.2010.00065
Eichele, T., and Calhoun, V. (2009). “Finding error precursors: an example of how group ICAs can be used in EEG-fMRI,” in Simultaneous EEG and fMRI: Recording, Analysis and Application, eds M. Ullsperger and S. Debener (Oxford, UK: Oxford University Press), 175–193.
Eichele, T., Debener, S., Calhoun, V., Specht, K., Engel, A. K., Hugdahl, K., von Cramon, D. Y., and Ullsperger, M. (2008). Prediction of human errors by maladaptive changes in event-related potentials and functional MRI. Proc. Natl. Acad. Sci. U.S.A. 102, 17798–17803.
Eriksen, B. A., and Eriksen, C. W. (1974). Effects of noise letters upon the identification of a target letter in a nonsearch task. Percept. Psychophys. 16, 143–149.
Falkenstein, M., Hohnsbein, J., Hoormann, J., and Blanke, L. (1990). “Effects of errors in choice reaction tasks on the ERP under focused and divided attention,” in Psychophysiological Brain Research, eds C. H. M. Brunia, A. W. K. Gaillard, and A. Kok (Tilburg, The Netherlands: Tilburg University Press), 192–195.
Folstein, J. R., and van Petten, C. (2008). Influence of cognitive control and mismatch on the N2 component of the ERP: a review. Psychophysiology 45, 152–170.
Forster, S. E., Carter, C. S., Cohen, J. D., and Cho, R. Y. (2011). Parametric manipulation of the conflict signal and control-state adaptation. J. Cogn. Neurosci. 23, 923–935.
Gehring, W. J., Goss, B., Coles, M. G., Meyer, D. E., and Donchin, E. (1993). A neural system for error detection and compensation. Psychol. Sci. 4, 385–390.
Gentsch, A., Ullsperger, P., and Ullsperger, M. (2009). Dissociable medial frontal negativities from a common monitoring system for self- and externally caused failure of goal achievement. Neuroimage 47, 2023–2030.
Gratton, G., Coles, M. G. H., and Donchin, E. (1992). Optimizing the use of information: strategic control of activation of responses. J. Exp. Psychol. Gen. 121, 480–506.
Hajcak, G., Nieuwenhuis, S., Ridderinkhof, K. R., and Simons, R. F. (2005). Error-preceding brain activity: robustness, temporal dynamics, and boundary conditions. Biol. Psychol. 70, 67–78.
Huster, R. J., Eichele, T., Enriquez-Geppert, S., Wollbrink, A., Kugel, H., Konrad, C., and Pantev, C. (2011). Multimodal imaging of functional networks and event-related potentials in performance monitoring. Neuroimage 56, 1588–1597.
King, J. A., Korb, F. M., von Cramon, D. Y., and Ullsperger, M. (2010). Post-error behavioral adjustments are facilitated by activation and suppression of task-relevant and task-irrelevant information processing. J. Neurosci. 30, 12759–12769.
Li, C. S., Yan, P., Bergquist, K. L., and Sinha, R. (2007). Greater activation of the “default” brain regions predicts stop signal errors. Neuroimage 38, 640–648.
Maier, M. E., Yeung, N., and Steinhauser, M. (2011). Error-related brain activity and adjustments of selective attention following errors. Neuroimage 56, 2339–2347.
Mazaheri, A., Nieuwenhuis, I. L., van Dijk, H., and Jensen, O. (2009). Prestimulus alpha and mu activity predicts failure to inhibit motor responses. Hum. Brain Mapp. 30, 1791–1800.
Nieuwenhuis, S., Yeung, N., van den Wildenberg, W., and Ridderinkhof, K. (2003). Electrophysiological correlates of anterior cingulate function in a go/no-go task: effects of response conflict and trial type frequency. Cogn. Affect. Behav. Neurosci. 3, 17.
Nigbur, R., Ivanova, G., and Stürmer, B. (2011). Theta power as a marker for cognitive interference. Clin. Neurophysiol. 122, 2185–2194.
Notebaert, W., Houtman, F., van Opstal, F., Gevers, W., Fias, W., and Verguts, T. (2009). Post-error slowing: an orienting account. Cognition 111, 275–279.
Notebaert, W., and Verguts, T. (2007). Dissociating conflict adaptation from feature integration: a multiple regression approach. J. Exp. Psychol. Hum. Percept. Perform. 33, 1256–1260.
Padilla, M. L., Wood, R. A., Hale, L. A., and Knight, R. T. (2006). Lapses in a prefrontal-extrastriate preparatory attention network predict mistakes. J. Cogn. Neurosci. 18, 1477–1487.
Rabbitt, P., and Rodgers, B. (1977). What does a man do after he makes an error? An analysis of response programming. Q. J. Exp. Psychol. 29, 727–743.
Ridderinkhof, K., Ullsperger, M., Crone, E., and Nieuwenhuis, S. (2004). The role of the medial frontal cortex in cognitive control. Science 306, 443.
Ridderinkhof, K. R., Nieuwenhuis, S., and Bashore, T. R. (2003). Errors are foreshadowed in brain potentials associated with action monitoring in cingulate cortex in humans. Neurosci. Lett. 348, 1–4.
Steinhauser, M., and Kiesel, A. (2011). Performance monitoring and the causal attribution of errors. Cogn. Affect. Behav. Neurosci. 11, 309–320.
Ullsperger, M., Bylsma, L., and Botvinick, M. M. (2005). The conflict adaptation effect: it's not just priming. Cogn. Affect. Behav. Neurosci. 5, 467–472.
Viola, F. C., Thorne, J., Edmonds, B., Schneider, T., Eichele, T., and Debener, S. (2009). Semi-automatic identification of independent components representing EEG artifact. Clin. Neurophysiol. 120, 868–877.
Weissman, D. H., Roberts, K. C., Visscher, K. M., and Woldorff, M. G. (2006). The neural bases of momentary lapses in attention. Nat. Neurosci. 9, 971–978.
Yeung, N., Botvinick, M. M., and Cohen, J. D. (2004). The neural basis of error detection: conflict monitoring and the error-related negativity. Psychol. Rev. 111, 939–959.
Keywords: conflict monitoring, connectionist modeling, event-related potentials, N2
Citation: Steinhauser M, Eichele H, Juvodden HT, Huster RJ, Ullsperger M and Eichele T (2012) Error-preceding brain activity reflects (mal-)adaptive adjustments of cognitive control: a modeling study. Front. Hum. Neurosci. 6:97. doi: 10.3389/fnhum.2012.00097
Received: 19 January 2012; Paper pending published: 21 February 2012;
Accepted: 03 April 2012; Published online: 24 April 2012.
Edited by:
Hans-Jochen Heinze, University of Magdeburg, GermanyReviewed by:
Douglas O. Cheyne, Hospital for Sick Children, CanadaKevin M. Spencer, VA Boston Healthcare System/Harvard Medical School, USA
Copyright: © 2012 Steinhauser, Eichele, Juvodden, Huster, Ullsperger and Eichele. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Marco Steinhauser, Department of Psychology, University of Konstanz, Fach 29, Konstanz, Germany. e-mail:bWFyY28uc3RlaW5oYXVzZXJAdW5pLWtvbnN0YW56LmRl





