Attention in a Bayesian framework

Introduction

A cornerstone of cognitive science is the idea that a process called “attention” dictates which incoming information is fully processed by a limited neural resource. However, attempts to discover exactly why the brain needs to selectively filter its input, and what the mechanisms and effects of this selection are, have floundered in a sea of heterogeneous effects. This has led to assertions that a single neural resource allocated by attention is not a useful concept (Driver, 2001; Zelinksy, 2005). By way of introduction, we briefly review the behavioral, physiological, and theoretical results that support this assertion, highlighting two different themes of attention research, and some of the debate that has gathered around them. In the main body of the paper we present a probabilistic framework under which apparently disparate resource limitations and attentional effects might be unified at the computational level. We exploit the idea of perception as Bayesian inference, and identify a general limitation in the brain’s ability to perform ideal inference over the multitude of features present in a complex scene. We then suggest that attention acts as an adaptable Bayesian hypothesis to locally improve the impoverished stimulus representations that result. (More technically, we argue that the true posterior over features is intractable due to the strong correlations induced by “explaining away,” and that this intractability forms an algorithmic bottleneck. Inference must thus be approximated, and we argue that a natural and biologically plausible approximation may be a factored one. In our view, attention introduces an additional term to this product, and thus shapes the result of the approximation.) Finally, we illustrate this framework by modeling two key groups of attentional effects in a simple, generic setting.

A Diversity of Attentional Effects

Despite James’s (1890) contention that “Everyone knows what attention is,” metaphors, and models for attention are almost as numerous as its documented effects. We focus on two apparently complementary roles that connect two substantial threads of attentional research: that of a selective filter, adjudicating on access to a sensory- or cognitive-processing bottleneck; and that of an integrative mechanism, necessary for the correct binding of features.

Attentional selection

One of the first theoretical metaphors for attention came from Broadbent’s influential (Broadbent, 1958) “filter theory,” which built on the contemporary view of the mind as a serial information processing device to suggest that an attentional filter acted at its very earliest stages, limiting the physical sources from which information would be fed to the perceptual pipeline. Although consistent with early “shadowing” experiments in which listeners were able to neglect entirely sounds presented to one ear when they were attending to a signal in the other (Cherry, 1953), this “early selection” view was challenged by the observation that semantic attributes only identifiable after substantial processing could also affect selection – for example, the listener’s own name would often “pop out” of the unattended stream (Moray, 1959; Treisman, 1960). This motivated a response in the form of “late selection” theories in which all inputs are analyzed fully, but only pertinent inputs are perceived (Deutsch and Deutsch, 1963; Norman, 1968; Duncan, 1980). Here, attention plays a very different role, selecting stimuli for access to consciousness rather than access to basic sensory processing. Both of these approaches accounted for only some of the data, faltering at the requirement to identify a single point of selection in a serial processing stream (see for example Kahneman and Treisman, 1984; Johnston and Dark, 1986; Pashler, 1998; Driver, 2001).

The single filter approach was challenged by “two-process” theories (Neisser, 1967) in which a pre-attentive, parallel processing stream can guide the allocation of an attention-demanding, deeper processing stage; and attenuation theories in which inputs have a graded likelihood of passing to later processing (Treisman, 1960, 1969). An influential proposal for reconciling early and late selection is the perceptual load theory of Lavie and Tsal (1994), in which attention only selects when limited perceptual resources are overloaded. Experiments supporting this idea suggested that the widespread challenges to early selection were in part due to the low perceptual load of the paradigms used to search for it (Lavie and Tsal, 1994; Lavie, 1995). However, it remains challenging to motivate computationally a failure to engage selective processing under low load settings even when such selection would benefit performance, raising the possibility that these experiments in fact reflect a basic consequence of distributed coding rather than variations in selection (Yu et al., 2008; Dayan and Solomon, 2010).

As Broadbent’s original model was picked apart, attention researchers moved toward a picture in which a serial “filter” was just an abstract metaphor for a variety of selection processes. Selection can occur on the basis of low-level physical attributes, or high-level semantic attributes deemed pertinent by memory or conscious control. “Bottom-up” processing can influence “top-down” processing, but there is not always a clear distinction between the two – neural processing is distributed and recurrent rather than purely serial. Information can be processed to a variety of “depths,” and attention gates access to different kinds of processing – from simple physical analysis to conscious awareness – in different situations. Throughout this research there is an enduring commitment to the concept of a limited resource, though as the field moved away from the idea of a single informational bottleneck, a sense of exactly what limitation it was that necessitated selection tended to be replaced by a catalog of conditions under which selection occurred (for reviews, see Kinchla, 1992; Wolfe, 1998; Driver, 2001).

Attentional integration

In the 1980s a focus on the “binding problem” produced theories that offered a more nuanced functional role for attention. In its most general form, the binding problem asks how the anatomically dispersed neural processing of different components of a task can be coordinated (Gray, 1999). The most prominent visual aspect of this problem is how features represented in different cortical areas are appropriately integrated or “bound” into composite objects (see Treisman, 1998; Robertson, 2005). Treisman and Gelade (1980) proposed that the effect of attention was to solve the binding problem in a local “spotlight”-like region, gluing together features into objects. Experimental support came from attentional modulation of misbinding (or “illusory conjunctions”; Prinzmetal, 1981; Treisman and Schmidt, 1982; Nissen, 1985); and from visual search experiments, in which search for a target defined by a unique conjunction of features seemed to require the sequential processing of a limited number of items at a time (Treisman, 1977, 1982, 1988; Treisman and Sato, 1990).

The origins of the binding problem lie in neurophysiological evidence for cortical specialization – different features are processed in different regions of the brain (Zeki, 1976, 1978; Maunsell and Newsome, 1987; Wade and Bruce, 2001) – and for the hierarchical broadening of receptive fields which may degrade information about feature-location. This combination of anatomical separation and spatial imprecision is thought to complicate the association of features which belong to the same objects. Thus, in Treisman’s “feature integration theory” (FIT), “feature maps” corresponding to specialized cortical areas (see Treisman and Gelade, 1980) register the presence of features but not their locations; with an attentional spotlight, presumably originating in a top-down signal from fronto-parietal areas (see Itti and Koch, 2001, for discussion of this correspondence), resolving the resultant ambiguity of binding in a manner never completely specified.

Despite successes, FIT also faced many challenges. The distinction between serial, attention-demanding search and parallel pre-attentive analysis has been repeatedly contested (Pashler, 1987; Geisler and Chou, 1995; Palmer, 1995; Eckstein, 1998), as search behavior has been found to depend on target-distractor similarity (Duncan and Humphreys, 1989; Palmer, 1994; Verghese and Nakayama, 1994), eccentricity (Carrasco et al., 1995), and lateral inhibition and masking (Wertheim et al., 2006); and to be guided by both bottom-up and top-down pre-attentive processes (Wolfe et al., 1989). Questions have also been raised about the analysis of illusory conjunction experiments, and the role of memory and report mechanisms in apparent failures of binding (Neill, 1977; Johnston and Pashler, 1990; Butler et al., 1991; Ashby et al., 1996; Saarinen, 1996b,a; Donk, 1999, 2001; Prinzmetal et al., 2001). Indeed, some have argued that there is in fact no binding problem (Ghose and Maunsell, 1999), arguing that the cortex, rather than consisting of a parallel array of simple feature maps as FIT would suggest, embodies a hierarchy of increasingly complex representations that at the top can correspond to complex objects such as a person or tool (Barlow, 1972). Researchers using this principle to build models for invariant object recognition suggest that their success implies that “high-level” representations for all objects would suffice, leaving attention with no role in binding per se (for example, Treisman, 1995; Riesenhuber and Poggio, 1999); though others have suggested that there would still be a role for a more complex form of object-based attentional selection (Tsotsos et al., 1995).

Despite these problems with the interpretation of the classic visual search and illusory conjunction paradigms, the impression remains that feature integration taxes a neural resource of limited capacity, and that attention assists with the interpretation of cluttered visual scenes (Desimone and Duncan, 1995; Pelli et al., 2007). But once again, it has been difficult to clearly identify the nature of that neural resource, and the mechanism by which attention aides its allocation.

Unification?

So what is “attention”? The metaphors above, as well as others not discussed, have been built on separate streams of experiments. Although each has been at least partly successful in its own domain, agreement on a single account of the many different phenomena has proven elusive (Driver, 2001; Zelinksy, 2005). Attention might indeed be a single term misapplied to a heterogeneous collection of phenomena; however, it is also possible that this failure to come to a unified understanding stems from the historical emphasis, which has been more on the putative effects of attention rather than on the nature of the resource limitation which necessitates it.

Some have argued that many of the effects ascribed to attention may instead be explained by the impact of uncertainty within traditional sensory models (Pelli, 1985). This is perhaps most obvious in the simple Posnerian task, where the location of an upcoming stimulus is signaled to the observer, leading to improvements in judgments of its features. It is possible that such improvements derive solely from the cued reduction in positional uncertainty; an idea investigated in existing Bayesian models described below. Although this simple interpretation of uncertainty reduction sits uncomfortably with experiments in which the display remains constant but behavior is altered by different task demands – for example when two stimuli always appear and the cue only signals which of them must be attended – one might still see an attentive mechanism as reducing noise, excluding distractors or empty locations that could otherwise be confused with the target, or reducing spatial uncertainty. Again, accounts of many observed phenomena would flow naturally from this view (Cohn and Lasley, 1974; Shiu and Pashler, 1995; Lu and Dosher, 1998, 2008; Morgan et al., 1998; Dosher and Lu, 2000a,b; Lu et al., 2002; Baldassi and Burr, 2004).

The unifying potential of this approach is clear, but it is nonetheless incomplete. If “attention” is able to reduce uncertainty or noise, why does that noise corrupt perception in the first place? The energetic cost of noise suppression may play a role, but, by itself, metabolism cannot explain why attentive processing seems to have limited concurrent scope, rather than applying more globally for limited periods of time. And by what algorithmic mechanism might uncertainty be manipulated?

Below, we develop a new framework that offers resolutions to these challenges. The framework relies on a model of Bayesian perception in potentially cluttered environments, and so we first review the Bayesian approach.

Bayesian Models of Perception

Bayesian models view perception as a process of probabilistic inference, fusing Helmholtz’s (1856) theories of unconscious inference on the one hand, with the likelihood-based “internal noise” models of signal detection theory on the other. Many are normative in structure, with accounts of perceptual phenomena emerging naturally by the consideration of optimal inference – that is, the attempt to infer the physical state of the world from the sensory neural activity it evokes – within appropriately constrained probabilistic models (see, for example, Knill and Richards, 1996). Both sensory neural responses (Tolhurst et al., 1983) and simple perceptual decisions (Green and Swets, 1989) are variable, even when derived from apparently identical physical stimuli, suggesting that noise pervades the early sensory system. In addition, the goal of perceptual inference is often ill-posed (Helmholtz, 1856; Marr, 1982), making the mapping even from hypothetical noiseless early neural activity to an optimal perception ambiguous. A simple example of this ambiguity is the confusion between the distance and size of a faraway object, or, more generally, the many possible three-dimensional configurations of objects that give rise to the same two-dimensional pattern of light on the retina. Noise and ambiguity work together to make perceptual inference uncertain. In the Bayesian view such uncertainty is properly quantified by distributions that represent degrees of belief, and is manipulated using the usual rules of probability. Perception and action are then derived from such probabilistic representations.

Here we adopt a slightly elaborated Bayesian framework developed for the treatment of cue combination in cluttered settings (Sahani and Whiteley, 2011). The state of the world is represented at two levels: first, at a “high–level,” through a description of the objects present, their properties and their relationships; and second at the “mid-level” of the spatial and temporal distribution of “features” engendered by these objects. This description is motivated by vision, but a similar approach may be taken for the other senses with space replaced by a modality-appropriate axis. This separation of levels represents a computationally useful structure in the hierarchy of sensory generation. Sensation is most proximally related to the features present, and these features are in turn derived from the objects that appear. As different possible objects may share potential features it makes sense to represent these features explicitly within the model. Indeed, similar hierarchies appear in many models used in computational graphics and vision, and represent in part a practical strategy for efficiently modeling variation in image structure in relation to particular states of the world. The sensory activity, represented by s, reflects the true pattern of features in the world imperfectly¹, with ambiguity and noise that are captured by the probability distribution or likelihood p(s|features). An observer has knowledge of both the typical patterns of objects in the world, and of how these objects generate features. This knowledge is encoded in the “prior” probability distributions p(objects) and p(features|objects). Inference, then, is a simple matter of applying Bayes rule to find the “posterior”:

$\begin{array}{c}p\left(\text{objects}|\mathbf{\text{s}}\right)={\int }_{\text{features}}p\left(\text{objects},\text{features}|\mathbf{\text{s}}\right)\\ ={\int }_{\text{features}}\frac{p\left(\mathbf{\text{s}}|\text{features}\right)}{p\left(\mathbf{\text{s}}\right)}p\left(\text{features}|\text{objects}\right)p\left(\text{objects}\right)\end{array}$(1)

Whilst this posterior over objects is often the distribution of greatest ethological significance, experimental studies of “mid-level” perception frequently emphasize the posterior over features instead, which is obtained by replacing the integral over features by one over objects. Models of hierarchical inference (Figure 1) may naturally and simultaneously yield estimates of the posteriors at these different levels.

FIGURE 1

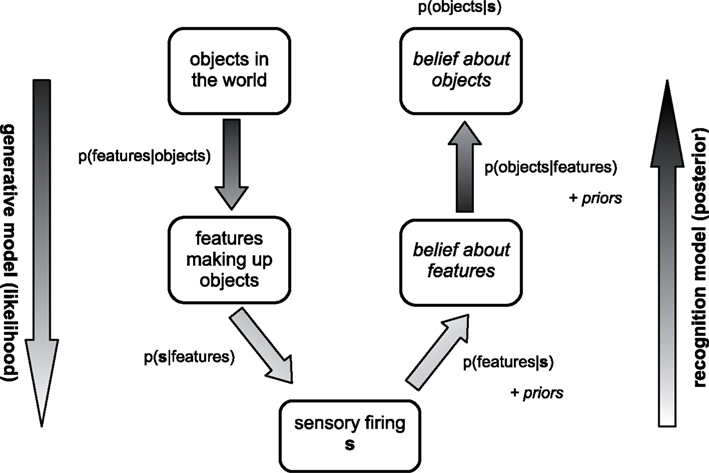
Figure 1. Simple schematic of the Bayesian view of hierarchical perception. Sensory activity s is generated by a set of unknown features belonging to an unknown set of objects. The relationship between these elements in the world and s is captured by a probability distribution. The brain learns to use a recognition model to find a posterior belief distribution about the objects and features based on s, which incorporates prior knowledge of the environment collected during learning.

The term p(s) in the denominator of equation (1), sometimes called the “Bayesian evidence,” ensures that the posterior is a properly normalized probability distribution over the possible states of the world. However, when more than one generative model of the world is to be considered, it plays a larger role, hinted at by the name (c.f. Mackay, 2004). In that case, a separate calculation is performed for each model, giving a separate posterior distribution, and a separate value of p(s). This value is the “marginal” probability of obtaining the sensory information s under the model in question (it is also called the “marginal likelihood”). We might ask what is the probability that each of our possible models is correct. This is again answered by Bayes rule, but where we now consider distributions over models of the world, rather than single states. In this application of Bayes rule, the evidence for each model plays the role that the likelihood of each state did in equation (1). If the models are all equally likely a priori, then the evidence gives the unnormalized probability that each is correct a posteriori.

A substantial body of behavioral evidence has accumulated in support of the Bayesian characterization of perception, showing that observers optimally incorporate uncertainty during cue combination (Jacobs, 1999; Deneve et al., 2001; Landy and Kojima, 2001; Ernst and Banks, 2002; Knill and Saunders, 2003; Hillis et al., 2004), motor planning (Trommershauser et al., 2003, 2005; Kording and Wolpert, 2004; Saunders and Knill, 2004, 2005; Tassinari et al., 2006; Seydell et al., 2008), and single-modality perceptual decision-making (Landy et al., 2007; Whiteley and Sahani, 2008). There is also evidence that perception is influenced by prior knowledge matched to the evolutionary environment (Geisler et al., 2001; Weiss et al., 2002; Schwartz et al., 2005; Stocker and Simoncelli, 2005, 2006). These successes have prompted some to propose that the machinery of Bayesian inference is explicit within neural circuitry (see Knill and Richards, 1996; Knill and Pouget, 2004; Friston, 2005; Doya et al., 2007), and theoretical work has focused on possible neural implementations for the encoding and manipulation of probability distributions (Pouget et al., 1998, 2003; Eliasmith and Anderson, 2003; Sahani and Dayan, 2003; Ma et al., 2006). Whilst such an explicitly probabilistic neural calculus might be most flexible, the possibility remains that Bayesian behavior might emerge in ethological settings through implicit calculations, rendering Bayes optimal decisions without explicit representation of Bayesian quantities. We will express our proposal in this paper in terms of explicit probability distributions, because this makes exposition clearer and helps to provide motivation. However the computational behavioral analysis we describe is largely agnostic to implementation. The same computational considerations apply whether probabilistic calculations are made explicitly or implicitly, and the same solutions must be considered.

Attention in the Bayesian Framework

Dayan and Zemel (1999) have argued that, to the extent that attentional cues reduce perceptual uncertainty by manipulating expectations (Pelli, 1985), their effect may best be seen in terms of the incorporation of a Bayesian prior into perception. Consider the simple experiment illustrated in Figure 3A, where a pre-stimulus cue to location improves judgments of stimulus orientation. An initial representation (“V1”) is hypothesized to carry a sensory-derived likelihood over the location, x and orientation, o, of the object: p(s|o,x). A second stage (“V4”) then integrates this information to obtain a marginal posterior over orientation alone: p(o|s), which guides the observer’s judgment. Prior information about the location of the stimulus can be used to limit the range of locations that must be considered when determining the orientation. In Dayan and Zemel’s (1999) example, this prior was set to 0 outside a “spotlight” region determined by the cue, effectively reducing the limits of the integration over space to an attention-defined region R_a:

$p_a\left(o|\mathbf{\text{s}}\right)\propto {\int }_{-\infty }^{\infty }dxp\left(\mathbf{\text{s}}|o,x\right)p_a\left(x\right)={\int }_{R_a}dxp\left(\mathbf{\text{s}}|o,x\right)$(2)

If R_a is centered on the true location of the stimulus, it acts to reject potential activity away from the stimulus that might otherwise contribute noise and uncertainty to the estimate of o. This scheme was developed further by Yu and Dayan (2004) who proposed an explicit neural representation of the mathematical quantities involved, and relaxed the limited support of the attentional focus to allow for a uniform prior probability outside the central peak region. They found that many features of their model neuronal responses matched experimental reports. Furthermore, by considering explicit temporal integration of information in combination with a likelihood threshold they were also able to model the distribution of reaction times in this task.

These models provide the Bayesian analog to the theories of attentional manipulation of noise cited above. In this simple case, the interpretation of the cue as conveying prior information about a following stimulus is normatively accurate; but the link grows more tenuous when the cue signals not the stimulus but the task (for example, when two oriented patches appear, but responses are required for only one). Rao (2005) has suggested that other attentional phenomena may indeed be captured by representing the action of cued attention as a prior within a generative model; but leaves unanswered the key question of why this should be so when a modified prior is normatively inappropriate.

Below, we describe a quite different rationale for the action of attention on inference, which extends its scope to situations in which the cue carries no true prior information, and indeed to the role of attention in natural perception where its allocation is driven by internal processing rather than external cues. The construction of this rationale begins with an hypothesis about the nature of the resource limitation which attention must overcome.

A New Approach to Attention in Bayesian Perception

Our novel approach to understanding attention rests on the basis that optimal probabilistic inference in the context of a natural perceptual task of realistic complexity is computationally intractable (Sahani and Whiteley, 2011) and, in the face of this complexity, any feasible allocation of perceptual resources is necessarily limited. Thus an efficient strategy must rely on approximation. This process of approximation forms a bottleneck: albeit an implicit computational one rather than an explicit architectural one. Our view is that the role of attention is to locally refine the nature of the approximation, focusing computational resources to suit it to the task and context at hand. As we will see, this computational view has the potential to unify the apparent heterogeneity of attentional effects.

Computational Limitations

Scenes in the real-world comprise many objects with many constituent features, and thus a true posterior belief about the state of the world is a complex joint probability distribution over a multitude of variables. The resources needed to compute and represent this posterior distribution grow exponentially in the extent of the dependencies between these variables.

Dependencies between sensory features emerge systematically in several ways from generative models that express the causal structure of the world. Some dependencies are expressed directly by the generative prior. For instance, the extent of an object (in space for visual or somatosensory input; in time and frequency for sound) determines a common extent for many of its elementary features, thus introducing a strong positive correlation in the value of such features over the typical object size. Conversely, prior beliefs that objects appear infrequently or sparsely, and take on a limited set of feature values when they do appear, may introduce anti-correlation between features – if the ball is red it won’t also be green. The identity of coincident features may also be guided by natural statistics, for example a luminance-defined texture that corresponds to grass is very likely to be green, yellow, or brown. Dependencies also emerge systematically through the likelihood as well as the prior. In particular, when multiple features of the world combine to affect the sensory observations together, a fundamental phenomenon of probabilistic reasoning known as “explaining away” (Pearl, 1988) induces structure in the posterior even if the prior is entirely independent. Intuitively, selecting one putative cause of an observation from amongst many possibilities “explains away” the observation, making the competing causes less likely. This logic leads to posterior anti-correlation between feature variables associated with the alternative causes.

The ubiquity of these dependencies means that when parsing a realistic scene the brain cannot have the resources to represent the full posterior, and therefore cannot act optimally in all respects. In the language of complexity theory (Papadimitriou, 1994; Tsotsos, 2001), representing and computing over large joint distributions is “algorithmically intractable.”

Probabilistic Models for Multiple Objects

The complexity of the inferential problem can readily be observed in the probabilistic structures necessary to express the relevant distributions. As we have before (Sahani and Dayan, 2003; Sahani and Whiteley, 2011), we consider vision as the canonical example. Visual features – orientations, colors, textural elements, direction of motion, depth, and so on – each assume a potential value at each point in visual space. Indeed, some may potentially take on more than one value simultaneously, as is the case for transparency of motion, or form (Sahani and Dayan, 2003). Thus, at the level of these features, a state of the world must be described by a series of “map” functions, m^k(x,θ^k). The superscript k labels the feature that is being mapped. The function m^k indicates the “strength” with which the feature takes on value θ^k at location x. In the case of motion, for instance, this strength might correspond to “motion energy.” For other features it may depend on color saturation or luminance contrast. Clearly such functions easily express the distribution of features over space. Furthermore, the strength m^k(x,θ^k) may be non-zero for more than one feature value θ^k at the same location, thus capturing potential transparency (or “multiplicity” in the language of Sahani and Dayan, 2003). A posterior belief distribution based on sensory data s over a scene decomposed into K feature dimensions would therefore extend over K such maps, each expressing a possible spatial distribution of a particular feature:

$p\left({\left\{m^k\left(\text{x},{\theta }^k\right)\right\}}_{k=1}^k|s\right)$(3)

Having such functions defined over the spatial location of particular feature values has important representational, computational, and biological properties. These functions roughly correspond to the “feature maps” invoked in many computational models of attention, which provide a compact and flexible representation of a complex scene. Pairing features with space is important because the two are intimately connected – all features are spatially distributed. This notation also corresponds to observed properties of cortical neurons – at the simplest level, they represent something about the spatial location of at least one feature. Populations that respond to more than one feature participate in the encoding of distributions over several maps, and various levels of uncertainty over location and feature value can be represented by changing the form of the distribution. Sahani and Dayan (2003) give a biologically plausible proposal for how populations of neurons could represent these “doubly distributional” representations, which could easily be extended to the generalized feature map case presented here.

The Structure of Approximation

To compute and represent all of the dependencies between feature map values for all the different features, and for all the possible values of those features at all locations, is a formidable task. Even in the simple discretized two-feature setting we consider below, a complete description of the spatial distribution of features is a 162-dimensional vector. Without constraints, the need for resources to represent a full joint probability distribution on these maps grows exponentially with the dimensionality of the space. Even with the constraints imposed by realistic priors and likelihood functions, the immensity of the space precludes tractability.

Thus, the internal model of the posterior is forced to be an approximation to the true value. We write

$q\left({\left\{m^k\left(\text{x},{\theta }^k\right)\right\}}_{k=1}^k\right)\sim p\left({\left\{m^k\left(\text{x},{\theta }^k\right)\right\}}_{k=1}^k|s\right),$(4)

where q(·) is the approximating distribution, and the symbol ∼ represents the operation of approximation. There are two features of this approximation to consider – first, what form q(·) takes and how it differs from p(·); and second, how q(·) is computed.

One common probabilistic modeling approach to alleviate intractability is to use a factored approximation, by which q(·) is restricted to be a product of a number of component distributions each defined over a small collection of feature values. The factored distribution thus approximates the structure of dependencies, both positive and negative, between these collections (see, e.g., Mackay, 2004). In our setting, a sensible factorization might separate the different feature maps:

$q\left({\left\{m^k\left(\text{x},{\theta }^k\right)\right\}}_{k=1}^K\right)=\prod _{k=1}^{K}q\left(m^k\left(x,{\theta }^k\right)\right),$(5)

or might extend over limited conjunctions of features, and might perhaps also limit the extent of spatial correlations modeled. For most proposed neural codes of distributions such a factorization would result naturally from the limited spatial tuning and feature separation of neural responses². Note that by “factored” we do not mean to imply that the representation is necessarily “factorial” – that is, the sets of variables appearing in each factor need not be disjoint. An example of a non-factorial representation would be one in which neuronal receptive fields spanned conjunctions of features, with single feature dimensions appearing in more than one conjunction: for instance, one population of cells might be tuned to color and orientation, and another to orientation and disparity. For simplicity, however, we will continue to use the factorial form of equation (5) in the remainder of this paper.

To compute an approximation that gives the best match to the true posterior, a sensible approach is to minimize (within constraints) a distance measure between the two distributions. Here we use the Kullback-Leibler (KL) divergence KL[p(·)||q(·)], which results in an approximation covering as much of the true distribution as possible, rather than approximating it more finely within a limited region (Minka, 2005). This seems intuitively appealing for a brain that often needs to respond to the gross structure of stimuli across the visual field. Our challenge, then, will be to describe how this generality interacts with the narrower focus of attention. The unconstrained minimum of KL[p(·)||q(·)] is achieved when q(·) = p(·). Thus, q(·) is only an approximation because of constraints that prevent complete minimization. One constraint is structural: p(·) may not fall in the class described by equation (5), in which case the factored q(·) cannot reach the true minimum. A further constraint is algorithmic. For general distributions p(·) which are intractable to compute exactly, the minimum-divergence factored approximation is also intractable. Again, appealing to the theory of probabilistic modeling, a family of algorithms including belief propagation and expectation propagation (see Minka, 2005, for a review) approaches the minimum by iteratively minimizing local versions of the KL divergence³. In our simulations below we use a particularly simple version of these algorithms. Some recent work has speculated about how such algorithms might be implemented by neurons (Rao, 2007; Deneve, 2008; Steimer et al., 2009). Alternatively, the brain might learn during development to compute an approximate recognition model (see, e.g., Hinton et al., 1995). In all of these cases, the prior and likelihood are encoded implicitly in an inferential machinery that approximates the posterior without ever explicitly representing it – a crucial point, as representation of the true posterior is exactly the intractable step that we suggest is to be avoided.

To summarize, for an approximation that factors over feature maps, q(·) approximates the product of the prior and likelihood, and is found by minimizing (within algorithmic constraints) the KL divergence between this product and the factored distribution:

$\begin{array}{l}\prod _{k=1}^{K}q\left(m^k\left(\mathbf{\text{x}},{\theta }^k\right)\right)\sim \frac{1}{Z}p\left(\mathbf{\text{s}}{\left\{m^k\left(\mathbf{\text{x}},{\theta }^k\right)\right\}}_{k=1}^K\right)\\ \times p\left({\left\{m^k\left(\mathbf{\text{x}},{\theta }^k\right)\right\}}_{k=1}^K\right)\text{(6)}\hfill \\ =\underset{q\left(\cdot \right)}{\text{argmin}}\text{KL}\left[\frac{1}{Z}p\left(\text{s}|{\left\{m^k\left(\mathbf{\text{x}},{\theta }^k\right)\right\}}_{k=1}^K\right)\right.\hfill \\ \left.p\left({\left\{m^k\left(\mathbf{\text{x}},{\theta }^k\right)\right\}}_{k=1}^K\right)∥\prod _{k=1}^{K}q\left(m^k\left(\mathbf{\text{x}},{\theta }^k\right)\right)\right],\text{(7)}\hfill \end{array}$

where the constant Z normalizes the product of likelihood and prior.

The Action of Attention

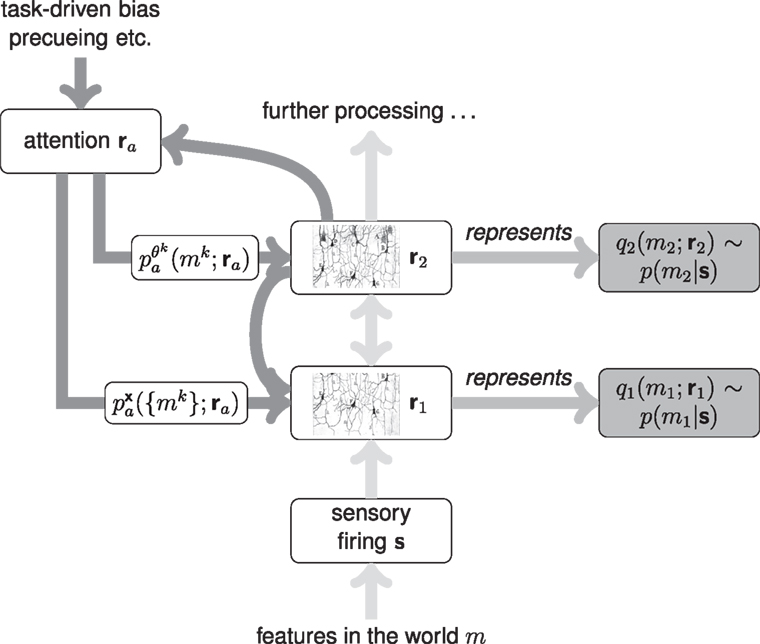
While the iterative procedure that arrives at the approximation of equation (7) may be dynamic, the approximation itself is not. It is defined by the generative model and the sensory observations; not by the task, or by volitional control. How, then, do we see the action of attention on this approximation? Our goal is to have the attentional mechanism act to locally refine the approximate posterior. One simple hypothesis would be that attention dictates the relative allocation of iterative updates; but this would slightly beg the issue – there is little fundamental difficulty with executing updates everywhere in parallel. Instead, we suggest that attention imposes parameterized local “hypotheses” about the true distribution, most likely through “top-down” neural connections within the sensory system. The approximated posterior is then adjusted to match as well as possible the product between the likelihood, the prior and this hypothesized distribution [compare equation (6) to equation (8)]:

$\begin{array}{l}\prod _{k=1}^K{q}_a\left(m^k\left(x,{\theta }^k\right)\right)\sim \frac{1}{Z_a}p\left(\text{s}|{\left\{m^k\left(\mathbf{\text{x}},{\theta }^k\right)\right\}}_{k=1}^K\right)\hfill \\ \times p\left({\left\{m^k\left(\mathbf{\text{x}},{\theta }^k\right)\right\}}_{k=1}^K\right)p_a\left({\left\{m^k\left(\mathbf{\text{x}},{\theta }^k\right)\right\}}_{k=1}^K;{\mathbf{\text{r}}}_a\right).\text{(8)}\hfill \end{array}$

The incorporation of this attentional hypothesis has two effects. First, it acts as a modified, but adjustable, “prior,” thus directly affecting the posterior. Second, and more important in our view, it modifies the region in which the approximation is matched to the true posterior. Indeed, in principle the attentional term might not carry normative information about any reasonable belief at all and it may be factored out of the approximated posterior once inference has been performed; but, even so, it would leave a modified approximation that was more accurate where the value of the attentional hypothesis was high. Thus, it does not replace the pre-attentive, normative prior – a prior which we imagine would have been embodied in the bottom-up process of pre-attentive inference and thus be difficult to remove. For now, we will assume that the approximated posterior does indeed incorporate the attention hypothesis as an additional prior, but the alternative approach will be explored further in the Discussion.

The attentional hypothesis in equation (6) P_a(·;r _a) is parameterized by a vector r _a, which reflects the internal state of the attention-directing systems of the brain, embodied in their neuronal firing rates, or perhaps some other aspect of activity. The introduction of this new term alters the normalizing constant in a way that depends on the hypothesis:

$\begin{array}{l}{Z}_a={\int }_{\left\{m^k\right\}}p\left(\text{s}|{\left\{m^k\left(\mathbf{\text{x}},{\theta }^k\right)\right\}}_{k=1}^K\right)p\left({\left\{m^k\left(\mathbf{\text{x}},{\theta }^k\right)\right\}}_{k=1}^K\right)\\ \times p_a\left({\left\{m^k\left(\mathbf{\text{x}},{\theta }^k\right)\right\}}_{k=1}^K;r_a\right),\text{(9)}\hfill \end{array}$

where the integral is taken over all possible values of the feature maps. The value of this integral may be seen as a version of the Bayesian Evidence (Mackay, 2004) in favor of an attentional hypothesis P_a(·;r _a), and reflects the compatibility between the hypothesis and the sensory observations. It will play an important role in the dynamic refinement of attention within our proposal.

The attentional hypothesis itself must be formed and encoded within the brain, and is thus subject to the same general resource limitation as the posterior. It would therefore be unreasonable to propose that it represents complex conjunctive relationships across the visual scene. Instead we suggest it comprises one (or possibly a small number) of local modes. This concurs with behavioral observations that attention tends to be spatially limited, observations that have previously contributed to the discrete “bottleneck” and “spotlight” metaphors discussed above. Behavioral observations also support distinct modes of spatial and feature-based attention (McAdams and Maunsell, 2000; Martinez-Trujillo and Treue, 2004; Maunsell and Treue, 2006), and the architecture of the visual system suggests that these signals would be processed in different ways. These observations suggest that the hypothesis may be further factored into spatial and featural components.

The value of such a locally defined attentional term lies in its ability to guide sequential exploration of alternative accounts of local regions of the sensory data. Consider the dependencies in the true posterior that are induced by explaining away. If two different combinations of features provide roughly equally good but mutually exclusive causal explanations of the sensory data, a factored approximation will assign appreciable probability to all feature values in both combinations, with independence between the feature dimensions. As such, it does not have the representational power to distinguish the valid accounts from configurations in which features from the two alternative combinations are mixed. This is the situation encountered in a later section on feature binding and misbinding. However, if an attentional hypothesis focuses on the value of one feature in one combination, the same factored approximation will concentrate probability on the corresponding features of that same combination at the expense of the other. This relieves the ambiguity at the cost of selecting only one of the two possible accounts. Yet recovery of both combinations is possible by the sequential application of attention to each in turn, in a manner reminiscent of bistable perception. In a similar way, spatially localized attention will focus the approximation on feature values that originate from the corresponding point in space at the expense of others. Here, sequential exploration may map out a positive correlation between feature values or their locations. This approach of setting one variable within a complicated joint distribution to a series of known values and recomputing the distribution over the other variables is similar to a probabilistic inference algorithm called “cutset conditioning.” This is the exactly the role that the attentional hypothesis plays here – trying out the different possible feature values or locations, allowing the simple factored approximation to operate within the probabilistically conditioned problem.

The Direction of Attention

The primary goal of this paper is to propose a theory of the computational need for attention and its effect on perception. It is not to study the processes by which attention is directed to different parts of the sensory environment. However, we would expect there to be interplay between the role of attention and its allocation, and so we briefly consider this interplay here.

The attentional hypothesis – often encapsulated by the location of the mode or “spotlight” – can reflect genuine prior information; top-down instructions or task demands; bottom-up cues, and the results of salience computations; or the dynamic fluctuations of attentional search. For example, a spatial cue that indicated the location of an upcoming stimulus would be reflected straightforwardly by a mode centered on the cue location in the spatial component of the attentional hypothesis. However, a similar spatial hypothesis might derive from other sources, and thus carry a different semantic interpretation. Thus, if driven by local salience in one feature, it might reflect the expected association of significant values in other features; alternatively, in the course of attentional search it would reflect a “trial” hypothesis whose quality was to be evaluated. In each case, the underlying mathematical form is the same, which is a particular strength of this framework – different forces act to bias the ongoing allocation of limited representational resources, with potentially different semantic significance: but are unified at the algorithmic level.

In the absence of direct biasing signals, we expect the attentional hypothesis to evolve smoothly toward a better match between itself and the true posterior. This match can be measured by the size of the normalizing constant Z_a of their product [i.e., the normalizing constant of the distribution on the right-hand side of equation (8)]. This is a simple consequence of the fact that the normalizing constant is the sum of the probabilities given to all possible values. The more similar the true posterior and attentional hypothesis are, the more likely it is they will both award high probabilities to the same values, increasing the sum of their product. The attentional hypothesis, which is parameterized by r _a, therefore evolves to find a local maximum in Z_a;

$\frac{d{\mathbf{\text{r}}}_a}{dt}\propto \frac{d{Z}_a}{d{\mathbf{\text{r}}}_a}$(10)

The normalization constant is often referred to as the “model evidence” when Bayes rule is used for model comparison. The evolution of the attentional hypothesis can thus be conceptualized as a process of continuous model comparison or hypothesis testing, moving the attentional hypothesis always in the direction of a better model of the true posterior. As described above, the brain’s approximate posterior belief distribution is found by minimizing the KL divergence between the product of the prior, likelihood, and attentional hypothesis, and the approximating distribution. Therefore, as the attentional hypothesis evolves, the KL divergence will also evolve, and as it continuously works to minimize the KL divergence the approximate posterior will reflect the attentional hypothesis and whatever influences on it are currently dominant.

Summary of the Proposal

We have argued here that the true posterior distribution over features in the world may be strongly correlated, making it computationally and representationally intractable. Thus, the perceptual system must often need to approximate it. We have suggested that one approximation, which agrees well with the featural specialization of neural responses, would be a factored one. Finally, we have proposed that attention interacts with this approximation system by imposing an additional distribution, which plays a mathematical role similar to a (possibly dynamic) “prior.” Although the mathematics is that of a prior, this distribution may or may not reflect a normative belief. Instead, it acts to shape the action of inference to better match the likelihood and pre-attentive prior within a region of interest.

Simulating Key Attentional Phenomena

Within the formidable variety of documented attentional phenomena, two paradigms stand out for their centrality to two apparently disparate domains of action of attention.

The first involves scenarios in which selective attention improves stimulus judgments; most prominent is the stimulus precueing or Posnerian experiment, in which an observer is alerted to the likely location of a stimulus by a cue of variable validity; and the inferentially different “task cueing” experiment in which two or more stimuli always appear, a cue indicating which of them is behaviorally relevant. The second pair of paradigms studies the role of attention in binding through tachistoscopic misbindings or illusory conjunctions on the one hand, and conjunctive visual search on the other.

Our goal is to demonstrate the conceptual basis of the framework we have proposed, rather than to provide a detailed account of any particular experiment. As such, we make use of the simple discretized feature map model and approximation approach of Sahani and Whiteley (2011). We begin by reviewing this model briefly.

The Discrete Feature Model

The essential elements of the image generative process – that is, sparsely populated and spatially extended feature maps, observed with uncertainty – can be captured by a simplified discrete “grid world” consisting of sparsely distributed oriented and colored objects observed through a noisy, low-resolution process (Figure 2).

FIGURE 2

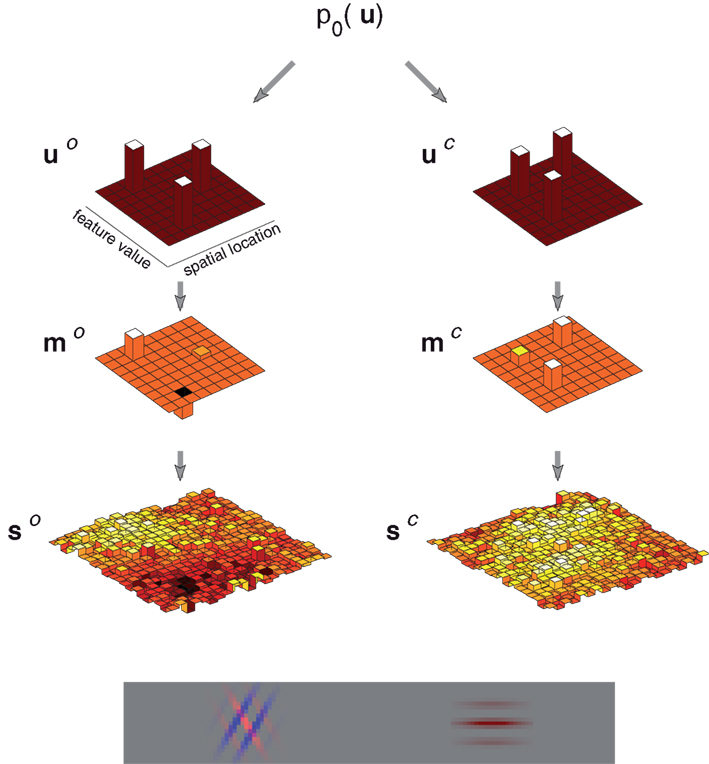
Figure 2. Example image generated by the discrete feature model. The model generates images comprising oriented, colored objects (depicted as Gabor wavelets) arrayed along a single spatial dimension. The example image at the bottom contains three such objects two of which are superimposed. The top row of figures shows the orientation (left) and color (right) object vectors (u), which determine the locations and feature values. The examples correspond to two distinct spatial locations (one with two objects), three orientations and two colors. The second row shows the associated feature maps (m), which include information about feature strength and polarity. Finally, the third row (s) shows the effective sensory cues, or observed information about the feature values. These are flattened and noisy, reflecting uncertainty in position, feature value, and strength, as might result from a brief presentation of the image and the incorporation of sensory noise.

Objects in the model are arrayed along a single, discretized spatial dimension (x), and take on features in each of the two discretized feature dimensions, orientation (o), and color (c) (despite our use of these feature names for concreteness, the prior, and observation process of the model will remain abstract without being tailored to these particular features). Each feature dimension is associated with a map function, m^o(x,o) and m^c(x,c). These specify the strength with which each feature is present at each point in space: the contrast of orientation o at location x, and the saturation of the hue c at x, respectively. The maps may each be non-zero for more than one value of the feature at a single location, corresponding to superimposed orientations or dithered color.

The locations, orientations, and colors at which the feature maps are non-zero are determined by a shared, sparse, “object” prior. This prior is expressed as a distribution on a binary vector u, with one element for each possible (x, o, c) triplet; a “1” entry in this vector at the element corresponding to (x₁,o₂,c₃), say, indicates the presence of an object at x₁, with orientation o₂ and hue c₃. Thus, u is conveniently represented as a 3-dimensional binary array, which is “unrolled” into the vector by scan-rasterization. This 3-dimensional array is “projected” onto two of its faces, to yield two reduced vectors that indicate the spatial locations of non-zero orientation values (u ^o) and color values (u ^c) is a similar scan-rasterized fashion. The projection is represented by the action of two rectangular matrices (P^o and P^c):

$\begin{array}{l}{\text{u}}^o={\text{P}}^o\text{u,}\\ {\text{u}}^c={\text{P}}^c\text{u}.\end{array}$(11)

These vectors represent the locations and feature values of the objects in the scene, but not the feature strengths. That information is encoded in the generative values of the map functions, which are non-zero only for entries corresponding to the ones in the binary vectors. At those entries, the strength is drawn independently from a zero-mean, unit variance, normal distribution. Equivalently, we may view the multiplicity functions themselves as vectors drawn from zero-mean multivariate normal distributions with diagonal covariances U^o and U^c, whose diagonal elements are given by the vectors u ^o and u ^c:

$\begin{array}{c}{\mathbf{\text{m}}}^o~\mathcal{𝒩}\left(\mathbf{\text{0}};{\text{U}}^o\right)where{\text{U}}^o=\text{diag}\left[{\mathbf{\text{u}}}^o\right],\\ {\mathbf{\text{m}}}^c~\mathcal{𝒩}\left(\mathbf{\text{0}};{\text{U}}^c\right)where{\text{U}}^c=\text{diag}\left[{\mathbf{\text{u}}}^c\right],\end{array}$(12)

where the zero variance corresponding to “0” entries in u ^c or u ^o ensures zeros in the corresponding feature map. Note that because the Gaussian is zero-mean, high feature strengths may be represented by high positive or high negative values. This concurs with neurally inspired representations of features in terms of a pair of opposing axes – for example a red-green axis for color or a positive-negative polarity axis for orientation contrast.

The feature maps are not observed directly; instead, a noisy observation process introduces uncertainty in the location, feature value, and feature strength of each object, as well as interference between nearby features. The complicated neural processes by which orientation and color are extracted are simplified in the model to a canonical cascade of smoothing and perturbation. Each feature map m^θ(x,θ); θ ∈ {o, c} is convolved with a Gaussian-shaped kernel in both space and feature value, upsampled, and then corrupted by independent normally distributed noise with diagonal covariance Ψ^θ to yield an observed vector s^θ. Expressing the linear convolution operation through the action of matrices Λ^θ we have:

$\begin{array}{c}{\mathbf{\text{s}}}^o~\mathcal{𝒩}\left({\Lambda }^o{\mathbf{\text{m}}}^o;{\Psi }^o\right),\\ {\mathbf{\text{s}}}^c~\mathcal{𝒩}\left({\Lambda }^c{\mathbf{\text{m}}}^c;{\Psi }^c\right).\end{array}$(13)

This simplification of the observation process will facilitate the development of a straightforward form of approximate inference and thus allow us to focus on the role of attention in shaping this approximation. While more detailed observation models (including, for example, signal-dependent levels of noise) would alter the particulars of the inference process and its approximation, we believe the essential hallmarks of attention within the model would remain unchanged.

The distributions of equations (12) and (13) can be written more compactly by concatenating the two feature dimensions as follows:

$\begin{array}{lll}\mathbf{\text{m}}& =\left[\begin{array}{c}\hfill {\mathbf{\text{m}}}^c\hfill \\ \hfill {\mathbf{\text{m}}}^o\hfill \\ \end{array}\right]~\mathcal{𝒩}\left(\mathbf{\text{0}};\text{U}\right)where\text{U}=\left[\begin{array}{cc}\hfill {\text{U}}^o\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\text{U}}^c\hfill \\ \end{array}\right],\hfill & \text{(14)}\\ \mathbf{\text{s}}& =\left[\begin{array}{c}\hfill {\mathbf{\text{s}}}^c\hfill \\ \hfill {\mathbf{\text{s}}}^o\hfill \\ \end{array}\right]~\mathcal{𝒩}\left(\Lambda m;\Psi \right)where\Lambda =\left[\begin{array}{cc}\hfill {\Lambda }^o\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\Lambda }^c\hfill \\ \end{array}\right]and\hfill \\ \Psi & =\left[\begin{array}{cc}\hfill {\Psi }^o\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\Psi }^c\hfill \\ \end{array}\right].\hfill & \text{(15)}\end{array}$

These equations represent a hierarchical generative model for noisy feature observations, expressed as a prior on feature maps given by ∫du p(m|u) p₀(u), where p₀ is the sparse prior; and a likelihood p(s|m). Perceptual inference involves inverting the generative model to compute a posterior belief about the state of the world (say the true feature map) given the noisy observations generated by that state; i.e., p(m|s) (see Figure 1).

In the framework laid out above, we proposed that a generic, computational resource limitation in the brain is the ability to represent large joint posteriors with complex correlational structure. A natural scene contains a sparse distribution of features bound into objects, and a reasonable prior might therefore consist of a mixture of sparse distributions for different numbers of objects. In other words, the probability of the spatial distribution of features given one object, plus the probability of the spatial distribution of features given two objects, and so on. This is exactly the kind of correlational structure that, when scaled up to a real-world scene, would hit the representational resource limit in terms of the number of neurons needed to represent it. Even in the discrete and impoverished model described here, with only two features each taking on one of nine values, and nine possible locations, the true posterior distribution on feature maps cannot be computed exactly (Sahani and Whiteley, 2011); its form is that of a mixture of Gaussians with one component for each possible configuration of the vector u. Naively, there are 2^{9 × 9 × 9} of these. Even if we restrict consideration to vectors that represent no more than 5 objects present, the count still exceeds 10¹². Thus, we are forced to use a simple approximation which treats the feature-location pairs as independent.

To derive this approximation, first note that when conditioned on u, m and s are jointly Gaussian with zero-mean:

$\begin{array}{l}p\left(\left[\begin{array}{c}\text{m}\\ \text{s}\end{array}\right]|\text{u}\right)=p(\text{s|m})p(\text{m|u)}\\ =𝒩\text{(}\Lambda \text{m;}\Psi \text{)}\times 𝒩\text{(0;U)}\\ =𝒩\left(0;\left[\begin{array}{cc}\text{U}& \text{U}{\Lambda }^{\text{Τ}}\\ \Lambda \text{U}& \Lambda \text{U}{\Lambda }^{\text{Τ}}+\Psi \end{array}\right]\right).\end{array}$(16)

Thus the joint distribution over m and s, marginalizing out u, is a mixture of zero-mean Gaussians:

$p\left(\left[\begin{array}{c}\hfill \mathbf{\text{m}}\hfill \\ \hfill \mathbf{\text{s}}\hfill \\ \end{array}\right]\right)=\sum _{\text{U}}{p}_0\left(\mathbf{\text{u}}\right)p\left(\left[\begin{array}{c}\hfill m\hfill \\ \hfill s\hfill \\ \end{array}\right]|\mathbf{\text{u}}\right).$(17)

The complex form of the prior over u makes this sum intractable, so we approximate the joint by minimizing the KL divergence between the true joint and a Gaussian approximation. This optimal approximating distribution is also zero-mean, and is obtained simply by replacing the covariance matrix U in the conditional distribution [equation (16)] with its average under the prior, ${\overline{\text{U}}}_0$ (see Appendix):

$\begin{array}{l}q\left(\left[\begin{array}{c}\text{m}\\ \text{s}\end{array}\right]\right)=\underset{q(\cdot )\in 𝒩}{\text{argmin}}\mathbf{\text{KL}}\\ \left[{\displaystyle \sum _{\text{u}}{p}_0(\text{u})𝒩}\left(0;\left[\begin{array}{cc}\text{U}& \text{U}{\Lambda }^{\text{Τ}}\\ \Lambda \text{U}& \Lambda \text{U}{\Lambda }^{\text{Τ}}+\Psi \end{array}\right]\right)||q\left(\left[\begin{array}{c}\text{m}\\ \text{s}\end{array}\right]\right)\right]\\ =𝒩\left(0;\left[\begin{array}{cc}{\overline{\text{U}}}_{\text{0}}& {\overline{\text{U}}}_{\text{0}}{\Lambda }^{\text{Τ}}\\ \Lambda {\overline{\text{U}}}_{\text{0}}& \Lambda {\overline{\text{U}}}_{\text{0}}{\Lambda }^{\text{Τ}}+\Psi \end{array}\right]\right).\end{array}$(18)

For each object vector u, the corresponding covariance matrix U is diagonal, with “1” entries on the diagonal indicating the presence of a particular feature-location combination. Thus, the prior-averaged matrix will also be diagonal, with entries between 0 and 1 corresponding to the prior probability of each feature-location combination.

From equation (18), it is straightforward to derive the two quantities we need for perceptual inference (see Appendix): the approximate posterior belief distribution [equation (19)], and the normalizing constant [equation (20)]:

$\begin{array}{l}{q}_0\left(\mathbf{\text{m}}|\mathbf{\text{s}}\right)=\mathcal{𝒩}\left({\overline{\text{U}}}_0{\Lambda }^{\text{T}}{\left(\Lambda {\overline{\text{U}}}_0{\Lambda }^{\text{T}}+\Psi \right)}^{-1}\mathbf{\text{s}};\right.\\ \left.{\overline{\text{U}}}_0-{\overline{\text{U}}}_0{\Lambda }^{\text{T}}{\left(\Lambda {\overline{\text{U}}}_0{\Lambda }^{\text{T}}+\Psi \right)}^{-1}\Lambda {\overline{\text{U}}}_0\right),\text{(19)}\\ log{Z}_0=-\frac{1}{2}\left[log\left|2\pi \left(\Lambda {\overline{\text{U}}}_0{\Lambda }^{\text{T}}+\Psi \right)\right|\right.\\ \left.+{\mathbf{\text{s}}}^{\text{T}}{\left(\Lambda {\overline{\text{U}}}_0{\Lambda }^{\text{T}}+\Psi \right)}^{-1}\mathbf{\text{s}}\right].\text{(20)}\end{array}$

This approximate posterior is, in a sense, “factorized.” The true prior carries the information that the world comprises a sparse mixture of objects; by approximating the model with a single Gaussian we lose this information – the prior is expressed only in terms of the marginal probability of each feature-location pair individually. The approximate posterior also factors over the two multiplicity functions m ^c and m ^o, neglecting information from the prior about the conjunctive co-location of features. This factorization damages the ability of the posterior to represent relationships between features in different locations.

The final component of the model is an attentional hypothesis, which acts to locally refine the impoverished representation of the true posterior. As in equation (8), the attentional hypothesis takes the form of a distribution over latent variables. In the context of a model structured as above, it turns out to be most straightforward to treat it as a distribution on the object vector p_a(u), rather than directly on the maps; although such a distribution over u clearly implies a consequent distribution over m. The introduction of such an hypothesis can thus be seen as a modification of the sparse prior p(u), which in turn modifies the average covariance that appears in the approximation. We label this new covariance ${\overline{\text{U}}}_0.$ Besides this change, the derivation of the approximation proceeds as before, and we have [compare equations (19) and (20) to equations (21) and (22)]:

$\begin{array}{l}{q}_a\left(\mathbf{\text{m}}|\mathbf{\text{s}}\right)=\mathcal{𝒩}\left({\overline{\text{U}}}_a{\Lambda }^{\text{T}}{\left(\Lambda {\overline{\text{U}}}_a{\Lambda }^{\text{T}}+\Psi \right)}^{-1}\mathbf{\text{s}};\right.\\ \left.{\overline{\text{U}}}_a-{\overline{\text{U}}}_a{\Lambda }^{\text{T}}{\left(\Lambda {\overline{\text{U}}}_a{\Lambda }^{\text{T}}+\Psi \right)}^{-1}\Lambda {\overline{\text{U}}}_a\right),\text{(21)}\\ log{Z}_a=-\frac{1}{2}\left[log\left|2\pi \left(\Lambda {\overline{\text{U}}}_a{\Lambda }^{\text{T}}+\Psi \right)\right|\right.\\ \left.+{\mathbf{\text{s}}}^{\text{T}}{\left(\Lambda {\overline{\text{U}}}_a{\Lambda }^{\text{T}}+\Psi \right)}^{-1}\mathbf{\text{s}}\right].\text{(22)}\end{array}$

With the model thus specified, we turn now to simulations of two canonical attentional phenomena.

Attentional Selection

Many studies have shown that precueing the location of a stimulus, or instructing observers about the relevance of a particular stimulus location, can improve detection, discrimination, and identification of that stimulus (e.g., Downing, 1988; Conner et al., 1997; Morgan et al., 1998; Baldassi and Burr, 2000; Cameron et al., 2002; Golla et al., 2004). A classic precueing task is illustrated in Figure 3A (adapted from Cameron et al., 2002), in which a brief spatial cue precedes the appearance of an oriented patch. If the cue is valid – that is, if it correctly indicates the location of the upcoming stimulus – then judgments about stimulus orientation are improved. Figure 4 illustrates perceptual inference in our model of this task, and the effect of attention on this inference. Stimuli in the experiment were monochromatic, so the model was limited to a single feature map m = m ^o and a single observation vector s = s ^o. The experimental stimulus corresponded to a single compact oriented Gabor patch. Thus the modeled sensory observations were based on vectors u and m that each contained a single non-zero entry. The amplitude of this entry in m, and thus the signal-to-noise ratio in s, varied with the contrast of the stimulus. The observations s introduced uncertainty by smearing out the single value in m and adding noise – with a different random sample of noise drawn on each simulated trial.

FIGURE 3

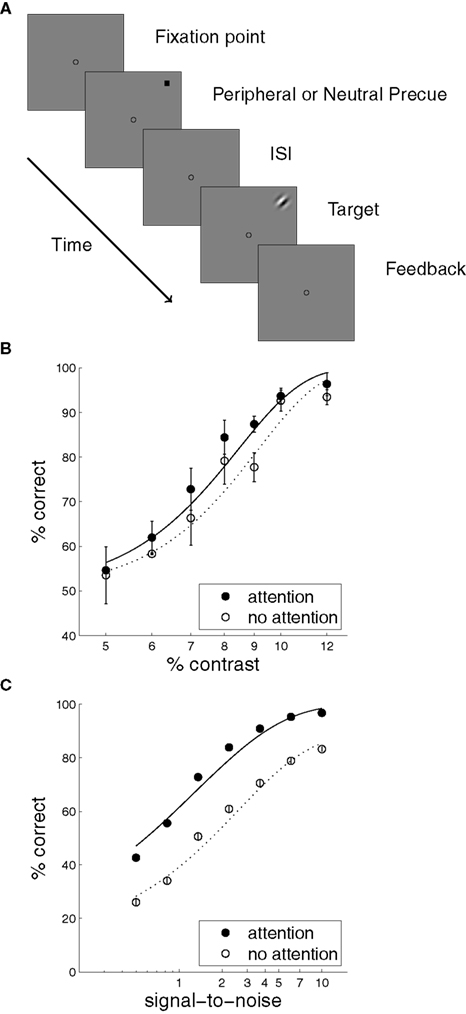
Figure 3. The precueing task, with human and model results. (A) A schematic of a typical precueing task. Observers fixate the centre of the screen, and report whether a Gabor patch (“Target”) presented briefly at one of eight locations with 4.5° eccentricity is tilted to the left or right. Shortly before the patch appears a small transient black square is shown. This “precue” may either appear at fixation (Neutral, or “no attention”), or at the location of the upcoming target patch (Peripheral, or “attention”) (Adapted from Cameron et al., 2002). (B) Human observers’ mean performance with and without precue-directed attention, as a function of stimulus contrast. (Data from Cameron et al., 2002, 8 cycle per degree condition, averaged over three subjects and replotted. Error bars reflect inter-subject variation.) (C) Model performance with and without attention. Signal-to-noise in the sensory cue signal stands in for contrast.

FIGURE 4

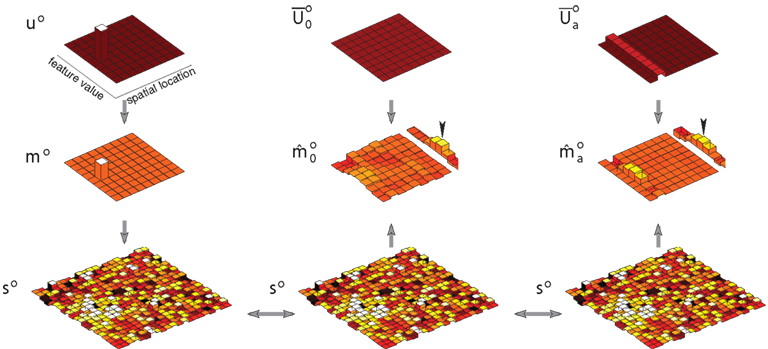
Figure 4. Generation, inference, and decision in a model of precued orientation recognition. Left column: The generative process. Only orientation maps are modeled. The object (u ^o) and feature (m ^o) maps each contain a single non-zero entry, corresponding to the location, and orientation of the object shown. Sensory observations s ^o convey this value with a signal-to-noise ratio that reflects contrast. Center column: Inference without attention. The generated sensory observations are approximately combined with a uniform distribution over object location, leading to equal values for each location-orientation pair on the diagonal of the matrix ${\bar{\text{U}}}_{\text{0}}^o$ (the diagonal entries are shown rearranged to form a matrix in space and orientation, analogous to the maps). The resulting modal feature map estimate $\left({\widehat{\mathbf{\text{m}}}}_a^o\right)$ is averaged over space to yield an expectation over orientation (shown adjacent), the peak of which gives the reported orientation (arrow head). Right column: Inference with attention. The same sensory observations combine with an attentional hypothesis focused on the cued location but uniform over orientation (reflected in ${\bar{\text{U}}}_{\text{0}}^o$). The modal feature map estimate $\left({\widehat{\mathbf{\text{m}}}}_a^o\right)$ is averaged as in the inattentive case, yielding a more accurate orientation estimate.

The approximate posterior based on this observation s represented the outcome of perceptual inference without attention. This posterior was computed according to equation (19) using a generic prior that gave a small constant probability of appearance for any object at any location. Importantly, the inference procedure did not assume that only one object was present in the scene. See Figure 4, center column.

The cue in this experiment may be seen as triggering a simple initial attentional hypothesis that an object is present at the cued location, thereby increasing the probability of the appearance in the feature map of any orientation value at that location. As a result, each diagonal element that corresponds to that location in the modified average covariance ${\overline{\text{U}}}_a$ is boosted. Inference under attention then follows equation (21) with this modified covariance matrix. See Figure 4, right column.

Inference, whether with or without attention, yields an approximate posterior distribution over the orientation feature map, which forms the basis for a simulated decision. The decision was derived from the mean of the posterior distribution, by integrating over space to yield a mean strength for each orientation, and taking the orientation with maximal strength as the model’s “judgment.” In the example shown in Figure 4 the posterior computed with attention produces a more accurate decision, with the peak of the mean orientation strength occurring in the correct location. Repeating the simulation with different instances of noise in s, we obtain a percentage of correct orientation judgments with and without attention. Figure 3C shows these results as a function of signal-to-noise ratio (simulating different stimulus contrasts). The results provide a good qualitative match to the behavioral improvements seen by Cameron et al. (2002) (Figure 3B).

It is worth noting that these results depend primarily on the action of attention as a prior, and thus they arise here through essentially the same mechanism as in earlier work on Bayesian attention (Zemel and Dayan, 1999; Yu and Dayan, 2004). However, as we see below, the same mechanism can also act in settings where no genuine prior information is available.

Attentional Integration

The second paradigmatic attentional phenomenon concerns the perception of objects defined by the conjunction of features, and presented in crowded displays. Perhaps the simplest illustration of this setting is in the illusory conjunction experiment of Treisman and Schmidt (1982) ⁴. Figure 5A illustrates the sort of display used, although we have replaced the letters of Treisman and Schmidt (1982) by bars in order to preserve our exposition in terms of a mid-level representation over orientation and color alone. The observer must report the color and form of the central objects. In some trials they are free to attend to these objects. On others, their attention is diverted by a primary task involving the peripheral black digits. Treisman and Schmidt (1982) reported that observers more frequently misbound the central color and form cues when attention was distracted than when it was not.

FIGURE 5

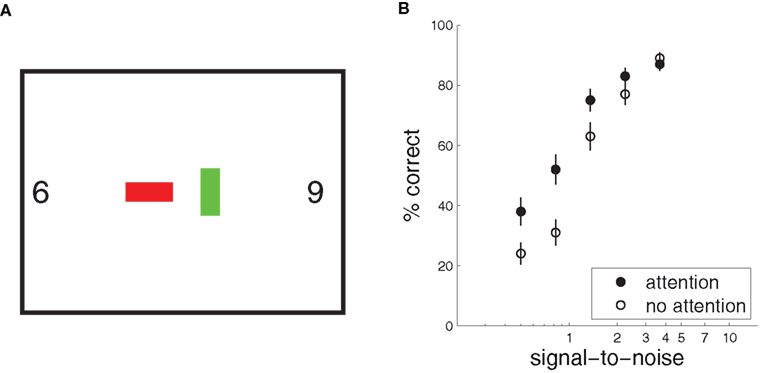
Figure 5. The illusory conjunction task. (A) A typical display. Observers were asked to report on the form and color of the central objects (we have used bars, where Treisman and Schmidt, 1982 used letters), whilst attention was sometimes distracted by a task involving the peripheral digits. (B) Model performance with and without attention. More binding errors are made when attention is unavailable.

The generative picture corresponding to the relevant central region of this display is illustrated in Figure 6. Two feature maps were required in order to represent both form and color. The two objects in the illustrated scene corresponded to two non-zero entries in u, each with a different location, color, and orientation. These led to two non-zero entries in each of u ^o and u ^c, thence in m ^o and m ^c, and finally to two noisy bumps in each of s ^o and s ^c.

FIGURE 6

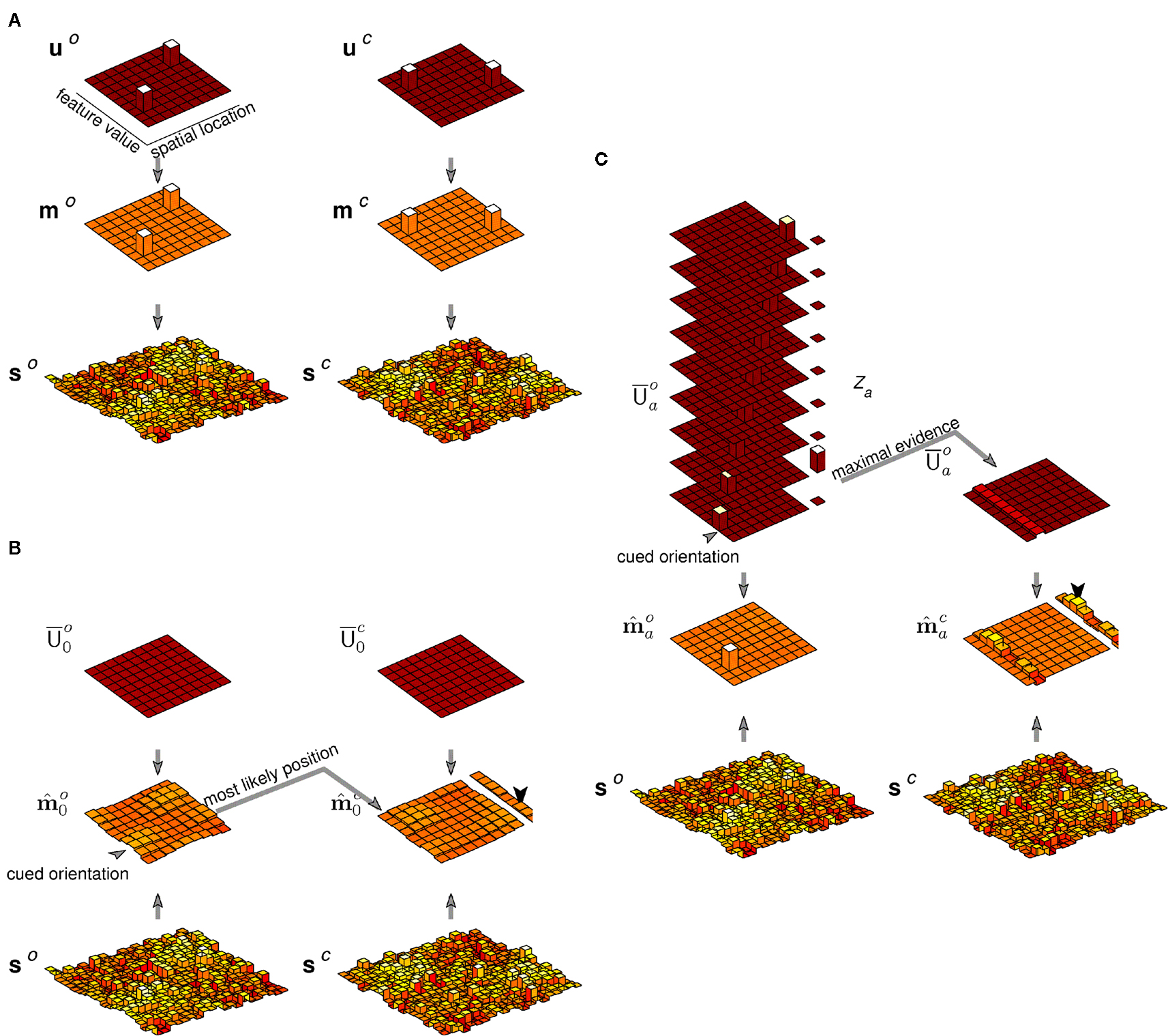
Figure 6. Generation, inference, and decision in a model of binding. (A) Generation. Two non-zero entries in each of u ^o, u ^c, m ^o, and m ^c represent the two oriented, colored bars. Each yields a smeared and noisy bump of activity in the sensory cue maps s ^o and s ^c. (B) Inference and decision without attention. The mean posterior maps ${\widehat{\mathbf{\text{m}}}}_a^o$ and ${\widehat{\mathbf{\text{m}}}}_0^o$ are obtained from the generated sensory cue maps s ^o and s ^c under non-specific priors (shown as in Figure 4 by the diagonal elements of ${\overline{\text{U}}}_0,$ rearranged into a map). The maximum strength value in ${\widehat{\mathbf{\text{m}}}}_0^o$ at the cued orientation selects a location. The maximum strength value in ${\widehat{\mathbf{\text{m}}}}_0^c$ at this location determines the reported color. Noise in the inferred feature maps leads to an error in the example shown. (C) Inference and decision with attention. The evidence Z_a is evaluated for each hypothesis corresponding to an object at different positions with the cued orientation, depicted by the stack of possible priors. The mean posterior maps ${\widehat{\mathbf{\text{m}}}}_a^o$ and ${\widehat{\mathbf{\text{m}}}}_a^c$ are obtained under the attentional hypothesis with greatest evidence. The mean color map ${\widehat{\mathbf{\text{m}}}}_a^c$ is then summed over space, and the maximum strength value determines the reported color. This process recovers the correct binding with exactly the same instantiation of sensory activity as in (B).

Inference with attention distracted acted according to equation (19) as before, yielding independent approximated posteriors over both feature maps. Once again, these posteriors formed the basis for the decision. The approach that was adopted for the precueing experiments – with the mean feature maps integrated over space before the decision is made – would here lead to loss of all spatial information about feature pairing. Whilst this approach would fit with the extreme form of FIT, it would introduce an approximation in the decision process that was more extreme than that necessitated by the inferential approximation alone. Instead, we simulated the response to a question such as, “What color was the vertical bar”? First, the location with maximum strength at the specified orientation in the posterior-mean orientation feature map ${\widehat{\mathbf{\text{m}}}}_0^o$ was identified. The corresponding location in the posterior-mean color feature map was then found, and the color with the greatest strength at this location formed the report⁵. The inference and decision process are illustrated in Figure 6.

With attention available, the search for the vertical bar was replaced by a set of attentional hypothesis tests, one for each location. The location hypothesis associated with the highest Bayesian evidence was selected, and inference repeated to find both posterior means ${\widehat{\mathbf{\text{m}}}}_a^o$ and ${\widehat{\mathbf{\text{m}}}}_a^c$ under this hypothesis. The color report could now proceed by summing the mean posterior color map as in the precueing simulation; although similar results were obtained by selecting the single location as in the unattended case. The fraction of correct binding reports is shown as a function of signal-to-noise and the availability of attention in Figure 5.

In this setting there is no straightforward, externally imposed, prior belief as there was for the precuing experiment. Instead an evaluation of all the different possible attentional hypotheses is used to find a focused posterior consistent with the sensory data and the task instructions. Thus, by invoking the various mechanisms suggested in the present framework we are able to model phenomena beyond the reach of previous Bayesian attention models.

Discussion

The framework introduced in this paper provides a new, probabilistic perspective on attentional selection. Whilst bound by a single unifying computational imperative, the scheme’s flexibility allows it to encompass a variety of attentional phenomena. This flexibility was illustrated in the context of a simple, abstract model which captured the essential elements of two quite disparate paradigms, holding out promise of a resolution to some of the apparent dichotomies and disagreements in attention research.

In this final section of the paper we attempt to relate this framework more closely to work that has gone before, discuss some of the challenges that remain in implementing more detailed models under the framework, and consider how such models would be situated in a cortical hierarchy.

Relationship to Other Theories

The field of attentional research is littered with compelling metaphors, and it is unsurprising that shades of many of these theories can be seen in the unifying framework we propose.

Any selective process may be seen as competitive, and the dominant metaphor for selection in neural processing is that of “biased competition” (Desimone and Duncan, 1995; Desimone, 1998). In this view, inputs compete for access to higher levels of processing and top-down influences bias this competition to the point that only a single object is represented. In this neural view, the competition is between inputs attempting to gain representation at a higher level. Inputs that lose this competition fall away. By contrast, the competition that we envisage is between different hypotheses, each of which seeks to explain as much of the sensory data as possible. Ideally, no input would go unaccounted for – although the limited capacity of the possible hypotheses might indeed favor solutions in which some inputs are treated as noise.

In this sense, then, our view comes closer to a computational account that is often linked to neural phenomena of biased competition, known as “selective tuning” (Tsotsos et al., 1995). Indeed, Tsotsos has written elsewhere of the role of computational complexity in constraining visual processing and opening the door to attention (Tsotsos, 2001). This scheme is rooted in a template-driven visual hierarchy, with selection occurring in later, more complex templates, and propagating down to the contributory features. The probabilistic formulation adopted in our framework confers a number of advantages over the template-based model. Competition between hypotheses rather than between high-level templates allows for greater flexibility in the level at which attention acts, and in the nature of the attentional focus – as in the experimental phenomenology, it can be localized in space, on an object or on a feature dimension. Furthermore, our view is that inference proceeds, albeit with approximation, everywhere – even outside the focus of attention. This may fit better with known pre-attentive capabilities than would the more absolute competition.

As a method based on probabilistic inference, our proposal inevitably comes closest to earlier Bayesian theories of attention (Dayan and Zemel, 1999; Yu and Dayan, 2004; Rao, 2005; Chikkerur et al., 2010). It differs from these models in three substantial ways:

• in the generality of the assumed generative model for images, and therefore of the hypothesized process of perceptual inference;

• in the consequent necessity for, and centrality of, approximate inference – which provides a role for attention during natural viewing;

• and, finally, in the precise way in which attention acts, and the nature of the resulting benefits to processing.

In all four Bayesian studies cited above, attention is introduced as a “prior” in a process of otherwise exact inference with regard to the features and location of a single object. As we argued in the Introduction, this accords with the semantics of the inferential problem in settings similar to the precueing experiment of Figure 3. In this case, the cue comes before a stimulus that does indeed contain only a single object, and the cue is designed to provide information regarding the likely location of that object. The right way to represent this in a probabilistic model is indeed as a prior over object location, and once such a prior is assumed, inference about object features becomes more accurate by the rejection of noise. Thus, this view essentially formalizes earlier work on uncertainty reduction by attention (Pelli, 1985). In this setting of a simple stimulus containing only a single object whose location is indicated by a preceding cue, all of the Bayesian models (including ours) are in agreement, and are equally valid.

However, attention seems to modify behavior and neural activity in many other settings. Behavioral effects similar to those seen in the precueing experiment are also obtained when attention is directed endogenously toward one of two or more stimuli that are simultaneously present. Indeed, the most profound physiological effects of attention are seen when both an attended and unattended object fall within a single neuron’s receptive field (Moran and Desimone, 1985). But in such cases, the cue that directs attention does not carry any legitimate prior information about the appearance of the stimulus: the probability distribution of the visual stimulus is the same whatever the value of the cue. Instead, the cue carries information about the cost function: observers must report the features of one of the objects. Attention also seems to play a role in visual search, and in the natural process of scene understanding. Again, in neither setting is the interpretation of attention as a prior a natural one. In a probabilistic model that allowed exact inference, the optimal action in these cases would be to compute the full posterior distribution over objects and features, and then to base subsequent decisions on this posterior by minimizing expected loss. There is no normative reason to believe that the inference process itself would be affected by the cost function, but this is what models such as that of Rao (2005) seem to require. Thus there is element of dissonance. Where does the attentional prior come from?

Our resolution to this problem – and the way in which our proposal differs from previous Bayesian models – is to consider a somewhat more realistically elaborated model in which more than one object is present and contributes features to the image. Exact inference is intractable in such a model, and the resulting need for approximation makes room for a task-dependent refinement, or (in natural viewing) a serial refinement of the approximation. This is the role that we suggest for attention. The fact that this refinement is guided by a multiplicative term allows attention to take on the function of a prior when this is semantically appropriate. It other settings it may be adjusted dynamically to maximize the estimated normalizing constant of the product – thus settling on domains where the unapproximated posterior is high. In all cases, it works to shape the approximation, emphasizing the KL divergence in the domains where it is large. In the specific discretized model studied here, optimal inference over u in the complete model would, in fact, be able to reject noise and improve feature estimates simply by virtue of the sparse prior. This capacity is destroyed by the Gaussian approximation, and so must be recovered by an attentional hypothesis that focuses integration on a single putative object location – thus reimposing a form of sparsity. This action plays as great a role in our model as does the addition of the prior information itself.

This effect of shaping the approximation would be more central in a variant of our approach that we mentioned only briefly above. In principle, the attentional hypothesis could multiply both the left- and right-hand sides of the approximation represented by equation (8). As such, its role as a prior would become negligible. Instead, it would act only to establish the context for the approximation (in much the same way that messages from adjacent factors shape the context of local approximation in expectation propagation message-passing algorithms), emphasizing the divergence in those regions where the attentional signal is high. However, whilst attractive in the setting of externally instructed attention, as in the precueing experiment, this alternative formulation does not provide as compelling an account of the dynamic evolution of natural attention, in the absence of external instruction. In the current version, the hypothesis can be adapted to match the sensory data by optimizing the approximated normalization constant Z_a, the value of which emerges directly from the approximation. In the alternative, this normalizer would have to be computed separately, and it is less obvious that benefit would accrue from driving it up. Nonetheless, this alternative approach may deserve further enquiry.

A more recent Bayesian attention proposal by Chikkerur et al. (2010) has also sought to extend the inferential approach to the multi-object setting; however, rather than approximating inference in the multi-object model directly, these authors suggest that inference is performed exactly within an approximated generative model in which only a single object and its features are represented. As a result, the possibility of multiple objects and their associated feature assignments are not considered during inference. Object recognition and feature binding are forced to operate entirely serially, with or without attention. Within this single object approximation, attention then acts as a prior on either location or feature in very much the same way as it did in the earlier models. Thus, attention in their model acts outside the approximation, rather than shaping it as we propose here, and there is no clear principle to guide the natural evolution of attention.

Speculations Regarding Implementation

A full specification of a hierarchical probabilistic model for perception, capable of object- and feature-recognition in cluttered environments and under conditions of uncertainty, is still beyond our reach. From the neuroscientific standpoint, current knowledge about coding properties of neurons in different cortical areas, and their interconnections, is not specific enough to inform such a model (or in the words of Roskies, 1999, we do not currently have enough anatomical knowledge to properly constrain the binding problem). However, it is still valuable to situate detailed models of specific, simplified computations in a bigger picture of how the hierarchical, recurrent structure of the brain might perform Bayesian inference. Figure 7 illustrates a schematic of this “bigger picture,” based on coarse anatomical properties.

FIGURE 7

Figure 7. A simple schematic of a neural framework for top-down attentional effects.

As described in Figure 1, a configuration of objects in the world evokes firing in the early sensory system (s), from which the posterior belief p(objects|s) is constructed. However, this is not a unitary computation. Rather, the sensory firing is passed through a loose hierarchy of cortical regions, each of which represents an approximation to the posterior distribution over a set of intermediate features (m _i) to which its neurons respond (with firing rates r _i). In Figure 1 and in our simple model, this intermediate layer was abstracted to a single set of parallel feature maps. In reality, many feature maps are more likely to be arrayed hierarchically, as sketched in Figure 7.

The natural action of priors in such a hierarchy is “top-down,” corresponding to the graphical structure of the generative model. However, attentional hypotheses may play a role directly at intermediate layers: framing an independent hypothesis about features on a particular level. Such an hypothesis would interact with natural priors, as well as with the indirect effect of attentional hypotheses that applied to higher levels. Thus, whilst a flexible attentional scheme would include feedback from parietal or other attention-directing areas to feature representations at all stages, attention effects in a feature layer would not depend exclusively on the activation of these connections.

Clearly, without a much more detailed account of how neural populations perform probabilistic computation, it is impossible to draw a tighter connection between our computational model and neurophysiology. Although many speculations have been advanced regarding neural implementations of probabilistic reasoning (Sahani and Dayan, 2003; Ma et al., 2006; Rao, 2007; Deneve, 2008), there is still considerably uncertainty about the relative merits of the different schemes. Indeed distributions might also be represented by samples (Hoyer and Hyvärinen, 2003), or be implicit in learned but ad hoc representations. The computations we propose could be implemented in any one of these schemes, but with different physiological predictions. At the same time, although we have taken some strides toward framing a more complex generative model for perception, the model is still substantially impoverished when compared to natural vision. Thus on both counts we believe that it would be premature to attempt a more detailed comparison with neural data. One consequence of this absence of neural implementation bears special mention. Many reports of the behavioral phenomena of attention involve measurements of reaction times and it is unclear how such reaction time effects would emerge within a purely computational inferential framework (although, as shown by Yu and Dayan, 2004, they may become accessible once that framework is embodied in an explicit neural model). Thus, our present work remains limited in its capacity to model not only neurophysiological findings, but also this broad class of behavioral observations.

Conclusion

Bayesian inference in cluttered, real-world settings necessarily involves the computation and manipulation of complex distributions over many features and objects. Here we have proposed that an inability to represent such complex posterior belief distributions is precisely the resource limitation that is addressed by sensory attention. We have argued that the brain is able only to represent a simplified approximation to the full joint posterior, and that attention helps to locally refine this approximation. Simulations illustrated the ability of the framework to model disparate attentional phenomena, whilst also embodying many of the intuitions that have informed cognitive metaphors. In our view, the processing bottleneck is not to be found in a particular location, with particular functional parameters, or at a particular level of processing; but is rather a fundamental and stringent constraint on computation throughout the brain. The form of the approximating distributions may vary depending on the properties of each cortical area, and this allows for the subtly different forms of attentional action implied by the behavioral literature. In sum, then, the framework provides a unifying rationale for many diverse documented attentional phenomena, bringing them together into a computationally motivated theory.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnotes

1. ^In our cue combination work we have distinguished between sensory activity and “cues” derived from that activity that carry information about single features. This distinction is not crucial to the discussion here, and so we dispense with it; using s to represent both proximal sensation and cues derived there from as appropriate.
2. ^“Distributed” codes, (e.g., Sahani and Dayan, 2003), and “energy” codes, (e.g., Hinton and Brown, 2000; Rao, 2004; Ma et al., 2006) are essentially complementary representations; the former encoding through the mean parameters and the latter through the natural parameters of similar exponential family distributions. It thus comes as no surprise that they have essential computational properties in common. Sampling codes could, in principle, encode arbitrary joint distributions using neurons with limited receptive fields. However, the issues of computational tractability would apply to the generation of suitably correlated samples, suggesting that even here the effective representation might remain factored.
3. ^These are different to the most common form of “variational” approximation, in which the opposite divergence KL[q(·)||p(·)] is minimized over a factorial q(·). Much of our analysis would go through with such a variational approach, or indeed with other schemes of approximation. Nonetheless, we see the factorized (but non-factorial) approximation and the minimization of KL[p(·)||q(·)] as appealing choices in the neural context.
4. ^We focus on this design for its directness notwithstanding a history of subsequent debate about the interpretation of the experimental data (see for example Ashby et al., 1996).
5. ^This serial process, although reasonable, is not the only choice. The posterior-mean color feature map also contains implicit information about the location of objects, though not their orientations, and could be used to refine the location judgment.

References

Ashby, F. G., Prinzmetal, W., Ivry, R., and Maddox, W. T. (1996). A formal theory of feature binding in object perception. Psychol. Rev. 103, 165–192.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Baldassi, S., and Burr, D. C. (2000). Feature-based integration of orientation signals in visual search. Vision Res. 40, 1293–1300.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Baldassi, S., and Burr, D. C. (2004). “Pop-out” of targets modulated in luminance or colour: the effect of intrinsic and extrinsic uncertainty. Vision Res. 44, 1227–1233.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Barlow, H. B. (1972). Single units and sensation: a neuron doctrine for perceptual psychology? Perception 1, 371–394.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Broadbent, D. E. (1958). Perception and Communication. Oxford: Pergamon.

Butler, B. E., Mewhort, D. J., and Browse, R. A. (1991). When do letter features migrate? A boundary condition for feature-integration theory. Percept. Psychophys. 49, 91–99.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Cameron, E. L., Tai, J. C., and Carrasco, M. (2002). Covert attention affects the psychometric function of contrast sensitivity. Vision Res. 42, 949–967.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Carrasco, M., Evert, D. L., Chang, I., and Katz, S. M. (1995). The eccentricity effect – target eccentricity affects performance on conjunction searches. Percept. Psychophys. 57, 1241–1261.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Cherry, E. C. (1953). Some experiments on the recognition of speech with one and with two ears. J. Acoust. Soc. Am. 25, 975–979.

CrossRef Full Text

Chikkerur, S., Serre, T., Tan, C., and Poggio, T. (2010). What and where: a Bayesian inference theory of attention. Vision Res. 50, 2233–2247.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Cohn, T. E., and Lasley, D. J. (1974). Detectability of a luminance increment: effect of spatial uncertainty. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 64, 1715–1719.

CrossRef Full Text

Conner, C. E., Preddie, D. C., Gallant, J. L., and VanEssen, D. C. (1997). Spatial attention effects in macaque area V4. J. Neurosci. 17, 3201–3214.

Pubmed Abstract | Pubmed Full Text

Dayan, P., and Solomon, J. A. (2010). Selective Bayes: attentional load and crowding. Vision Res. 50, 2248–2260.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Dayan, P., and Zemel, R. (1999). “Statistical models and sensory attention,” in Proceedings of the International Conference on Artificial Neural Networks, London, 1017–1022.

Deneve, S. (2008). Bayesian spiking neurons I: inference. Neural Comput. 20, 91–117.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Deneve, S., Latham, P. E., and Pouget, A. (2001). Efficient computation and cue integration with noisy population codes. Nat. Neurosci. 4, 826–831.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Desimone, R. (1998). Visual attention mediated by biased competition in extrastriate visual cortex. Philos. Trans. R. Soc. Lond. B Biol. Sci. 353, 1245–1255.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Desimone, R., and Duncan, J. (1995). Neural mechanisms of selective visual attention. Annu. Rev. Neurosci. 18, 193–222.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Deutsch, J. A., and Deutsch, D. (1963). Attention: some theoretical considerations. Psychol. Rev. 87, 272–300.

Donk, M. (1999). Illusory conjunctions are an illusion: the effects of target-nontarget similarity on conjunction and feature errors. J. Exp. Psychol. Hum. Percept. Perform. 25, 1207–1233.

CrossRef Full Text

Donk, M. (2001). Illusory conjunctions die hard: a reply to Prinzmetal, Diedrichsen, and Ivry (2001). J. Exp. Psychol. Hum. Percept. Perform. 27, 542–546.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Dosher, B. A., and Lu, Z. L. (2000a). Mechanisms of perceptual attention in precuing of location. Vision Res. 40, 1269–1292.

CrossRef Full Text

Dosher, B. A., and Lu, Z. L. (2000b). Noise exclusion in spatial attention. Psychol. Sci. 11, 139–146.

CrossRef Full Text

Downing, C. J. (1988). Expectancy and visual-spatial attention: effects on perceptual quality. J. Exp. Psychol. Hum. Percept. Perform. 14, 188–202.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Doya, K., Ishii, S., Pouget, A., and Rao, R. P. N. (eds). (2007). Bayesian Brain: Probabilistic Approaches to Neural Coding. Cambridge, MA: MIT Press.

Driver, J. (2001). A selective review of selective attention research from the past century. Br. J. Psychol. 92, 53–78.

CrossRef Full Text

Duncan, J. (1980). The locus of interference in the perception of simultaneous stimuli. Psychol. Rev. 87, 272–300.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Duncan, J., and Humphreys, G. W. (1989). Visual search and stimulus similarity. Psychol. Rev. 96, 433–458.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Eckstein, M. P. (1998). The lower efficiency for conjunctions is due to noise and not serial attentional processing. Psychol. Sci. 2, 111–118.

CrossRef Full Text

Eliasmith, C., and Anderson, C. H. (2003). Neural Engineering: Computation, Representation, and Dynamics in Neurobiological Systems. Computational Neuroscience. Cambridge, MA: MIT Press.

Ernst, M. O., and Banks, M. S. (2002). Humans integrate visual and haptic information in a statistically optimal fashion. Nature 415, 429–433.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Friston, K. (2005). A theory of cortical responses. Philos. Trans. R. Soc. Lond. B Biol. Sci. 360, 815–836.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Geisler, W. S., and Chou, K. (1995). Separation of low-level and high-level factors in complex tasks: visual search. Psychol. Rev. 102, 356–378.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Geisler, W. S., Perry, J. S., Super, B. J., and Gallogly, D. P. (2001). Edge co-occurrence in natural images predicts contour grouping performance. Vision Res. 41, 711–724.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ghose, G. M., and Maunsell, J. (1999). Specialized representations in visual cortex: a role for binding? Neuron 24, 79–85.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Golla, H., Ignashchenkova, A., Haarmeier, T., and Thier, P. (2004). Improvement of visual acuity by spatial cueing: a comparative study in human and non-human primates. Vision Res. 44, 1589–1600.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gray, C. M. (1999). The temporal correlation hypothesis of visual feature integration: still alive and well. Neuron 24, 31–47.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Green, D. M., and Swets, J. A. (1989). Signal Detection Theory and Psychophysics. Los Altos Hills: Peninsula Publishing.

Helmholtz, H. L. F. (1856). Treatise on Physiological Optics. Bristol: Thoemmes Continuum.

Hillis, J., Watt, S., Landy, M., and Banks, M. (2004). Slant from texture and disparity cues: optimal cue combination. J. Vis. 4, 967–992.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hinton, G. E., and Brown, A. D. (2000). “Spiking Boltzmann machines,” in Advances in Neural Information Processing Systems, Vol. 12, eds S. A. Solla, T. K. Leen, and K.-R. Müller (Cambridge: MIT Press), 122–128.

Hinton, G. E., Dayan, P., Frey, B. J., and Neal, R. M. (1995). The “wake-sleep” algorithm for unsupervised neural networks. Science 268, 1158–1161.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hoyer, P. O., and Hyvärinen, A. (2003). “Interpreting neural response variability as Monte Carlo sampling of the posterior,” in Advances in Neural Information Processing Systems, Vol. 15 (Cambridge: MIT Press), 277–284.

Itti, L., and Koch, C. (2001). Computational modelling of visual attention. Nat. Rev. Neurosci. 2, 194–203.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Jacobs, R. A. (1999). Optimal integration of texture and motion cues to depth. Vision Res. 39, 3621–3629.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

James, W. (1890). Principles of Psychology. New York: Holt.

Johnston, J. C., and Pashler, H. (1990). Close binding of identity and location in visual feature perception. J. Exp. Psychol. Hum. Percept. Perform. 16, 843–856.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Johnston, W. A., and Dark, V. J. (1986). Selective attention. Annu. Rev. Neurosci. 37, 43–75.

Kahneman, D., and Treisman, A. (1984). “Changing views of attention and automaticity,” in Varieties of Attention, eds R. Parasuraman, and D. R. Davies (Orlando, FL: Academic Press), 29–61.

Kinchla, R. A. (1992). Attention. Annu. Rev. Psychol. 43, 711–742.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Knill, D. C., and Pouget, A. (2004). The Bayesian brain: the role of uncertainty in neural coding and computation. Trends Neurosci. 27, 712–719.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Knill, D. C., and Saunders, J. A. (2003). Do humans optimally integrate stereo and texture information for judgments of surface slant? Vision Res. 43, 2539–2558.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Knill, E. C., and Richards, W. (eds). (1996). Perception as Bayesian Inference. Cambridge: Cambridge University Press.

Kording, K. P., and Wolpert, D. M. (2004). Bayesian integration in sensorimotor learning. Nature 427, 244–247.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Landy, M., Goutcher, R., Trommershauser, J., and Mamassian, P. (2007). Visual estimation under risk. J. Vis. 7, 1–15.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Landy, M. S., and Kojima, H. (2001). Ideal cue combination for localizing texture-defined edges. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 18, 2307–2320.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lavie, N. (1995). Perceptual load as a necessary condition for selective attention. J. Exp. Psychol. Hum. Percept. Perform. 21, 451–468.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lavie, N., and Tsal, Y. (1994). Perceptual load as a major determinant of the locus of selection in visual attention. Percept. Psychophys. 56, 183–197.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lu, Z. L., and Dosher, B. A. (1998). External noise distinguishes attention mechanisms. Vision Res. 38, 1183–1198.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lu, Z. L., and Dosher, B. A. (2008). Characterizing observers using external noise and observer models: assessing internal representations with external noise. Psychol. Rev. 115, 44–82.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lu, Z. L., Lesmes, L. A., and Dosher, B. A. (2002). Spatial attention excludes external noise at the target location. J. Vis. 2, 312–323.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ma, W. J., Beck, J. M., Latham, P. E., and Pouget, A. (2006). Bayesian inference with probabilistic population codes. Nat. Neurosci. 9, 1432–1438.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mackay, D. J. C. (2004). Information Theory, Inference, and Learning Algorithms. Cambridge: Cambridge University Press.

Marr, D. (1982). Vision. New York: Freeman.

Martinez-Trujillo, J. C., and Treue, S. (2004). Feature-based attention increases the selectivity of population responses in primate visual cortex. Curr. Biol. 14, 744–751.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Maunsell, J. H., and Newsome, W. T. (1987). Visual processing in monkey extrastriate cortex. Annu. Rev. Neurosci. 10, 363–401.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Maunsell, J. H. R., and Treue, S. (2006). Feature-based attention in visual cortex. Trends Neurosci. 29, 317–322.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

McAdams, C. J., and Maunsell, J. H. R. (2000). Attention to both space and feature modulates neuronal responses in macaque area V4. J. Neurophysiol. 83, 1751–1755.

Pubmed Abstract | Pubmed Full Text

Minka, T. (2005). Divergence Measures and Message Passing. Technical Report MSR-TR-2005-173. Cambridge: Microsoft Research.

Moran, J., and Desimone, R. (1985). Selective attention gates visual processing in the extrastriate cortex. Science 229, 782–784.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Moray, N. P. (1959). Attention in dichotic listening: affective cues and the influence of instructions. Q. J. Exp. Psychol. 11, 56–60.

CrossRef Full Text

Morgan, M. J., Ward, R. M., and Castet, E. (1998). Visual search for a tilted target: tests of spatial uncertainty models. Q. J. Exp. Psychol. A Hum. Exp. Psychol. 51, 347–370.

CrossRef Full Text

Neill, W. T. (1977). Inhibitory and facilitatory processes in attention. J. Exp. Psychol. Hum. Percept. Perform. 3, 444–450.

CrossRef Full Text

Neisser, U. (1967). Cognitive Psychology. New York: Appleton Century Crofts.

Nissen, M. J. (1985). “Accessing features and objects: is location special?” in Attention and Performance XI, eds M. I. Posner, and O. S. Marin (Hillsdale, NJ: Erlbaum), 205–219.

Norman, D. A. (1968). Toward a theory of memory and attention. Psychol. Rev. 75, 522–536.

CrossRef Full Text

Palmer, J. (1994). Set-size effects in visual-search – the effect of attention is independent of the stimulus for simple tasks. Vision Res. 34, 1703–1721.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Palmer, J. (1995). Attention in visual search: distinguishing four causes of a set-size effect. Curr. Dir. Psychol. Sci. 4, 118–123.

CrossRef Full Text

Papadimitriou, C. H. (1994). Computational Complexity. Reading: Addison Wesley.

Pashler, H. (1987). Detecting conjunctions of color and form: reassessing the serial search hypothesis. Percept. Psychophys. 41, 191–201.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Pashler, H. (1998). The Psychology of Attention. Cambridge, MA: MIT Press.

Pearl, J. (1988). Embracing causality in default reasoning. Artif. Intell. 35, 259–271.

CrossRef Full Text

Pelli, D. G. (1985). Uncertainty explains many aspects of visual contrast detection and discrimination. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2, 1508–1532.

CrossRef Full Text

Pelli, D. G., Cavanagh, P., Desimone, R., Tjan, B., and Treisman, A. (2007). Crowding: including illusory conjunctions, surround suppression, and attention. J. Vis. 7.2.1.

CrossRef Full Text

Pouget, A., Dayan, P., and Zemel, R. S. (2003). Inference and computation with population codes. Annu. Rev. Neurosci. 26, 381–410.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Pouget, A., Zhang, K. C., Deneve, S., and Latham, P. E. (1998). Statistically efficient estimation using population coding. Neural Comput. 10, 373–401.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Prinzmetal, W. (1981). Principles of feature integration in visual perception. Percept. Psychophys. 30, 330–340.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Prinzmetal, W., Diedrichsen, J., and Ivry, R. B. (2001). Illusory conjunctions are alive and well: a reply to Donk (1999). J. Exp. Psychol. Hum. Percept. Perform. 27, 538–541.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rao, R. P. N. (2004). Bayesian computation in recurrent neural circuits. Neuroreport 16, 1–38.

Rao, R. P. N. (2005). Bayesian inference and attentional modulation in the visual cortex. Neuroreport 16, 1843–1848.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rao, R. P. N. (2007). “Neural models of Bayesian belief propagation,” in Bayesian Brain: Probabilistic Approaches to Neural Coding, eds K. Doya, S. Ishii, A. Pouget, and R. P. N. Rao (Cambridge: MIT Press), 239–268.

Riesenhuber, M., and Poggio, T. (1999). Are cortical models really bound by the “binding problem”? Neuron 24, 87–93.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Robertson, L. (2005). “Attention and binding,” in The Neurobiology of Attention, eds L. Itti, G. Rees, and J. K. Tsotsos (Amsterdam: Elsevier Academic Press), 135–139.

Roskies, A. L. (1999). The binding problem. Neuron 24, 7–9, 111–125.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Saarinen, J. (1996a). Localization and discrimination of “pop-out” targets. Vision Res. 36, 313–316.

CrossRef Full Text

Saarinen, J. (1996b). Target localisation and identification in rapid visual search. Perception 25, 305–311.

CrossRef Full Text

Sahani, M., and Dayan, P. (2003). Doubly distributional population codes: simultaneous representation of uncertainty and multiplicity. Neural Comput. 15, 2255–2279.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sahani, M., and Whiteley, L. (2011). “Modeling cue integration in cluttered environments,” in Sensory Cue Integration, eds M. Landy, K. Körding, and J. Trommershäuser (Oxford: Oxford University Press), 82–100.

Saunders, J. A., and Knill, D. C. (2004). Visual feedback control of hand movements. J. Neurosci. 24, 3223–3234.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Saunders, J. A., and Knill, D. C. (2005). Humans use continuous visual feedback from the hand to control both the direction and distance of pointing movements. Exp. Brain Res. 162, 458–473.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Schwartz, O., Sejnowski, T. J., and Dayan, P. (2005). A Bayesian framework for tilt perception and confidence. Adv. Neural Inf. Process Syst. 17, 1201–1208.

Seydell, A., McCann, B. C., Trommershäuser, J., and Knill, D. C. (2008). Learning stochastic reward distributions in a speeded pointing task. J. Neurosci. 28, 4356–4367.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Shiu, L. P., and Pashler, H. (1995). Spatial attention and vernier acuity. Vision Res. 35, 337–343.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Steimer, A., Maass, W., and Douglas, R. (2009). Belief propagation in networks of spiking neurons. Neural Comput. 21, 2502–2523.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Stocker, A. A., and Simoncelli, E. P. (2005). “Constraining a Bayesian model of human visual speed perception,” in Advances in Neural Information Processing Systems, Vol. 17, eds L. K. Saul, Y. Weiss, and L. Bottou (Cambridge: MIT Press), 1361–1368.

Stocker, A. A., and Simoncelli, E. P. (2006). Noise characteristics and prior expectations in human visual speed perception. Nat. Neurosci. 9, 578–585.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Tassinari, H., Hudson, T., and Landy, M. (2006). Combining priors and noisy visual cues in a rapid pointing task. J. Neurosci. 26, 10154–10163.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Tolhurst, D. J., Movshon, J. A., and Dean, A. F. (1983). The statistical reliability of signals in single neurons in cat and monkey visual cortex. Vision Res. 23, 775–785.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Treisman, A. (1960). Contextual cues in selective listening. Q. J. Exp. Psychol. 12, 242–248.

CrossRef Full Text

Treisman, A. (1969). Strategies and models of selective attention. Psychol. Rev. 76, 282–299.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Treisman, A. (1977). Focused attention in the perception and retrieval of multidimensional stimuli. Percept. Psychophys. 22, 1–11.

CrossRef Full Text

Treisman, A. (1982). Perceptual grouping and attention in visual search for features and for objects. J. Exp. Psychol. Hum. Percept. Perform. 8, 194–214.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Treisman, A. (1988). Features and objects: the fourteenth Bartlett memorial lecture. Q. J. Exp. Psychol. 40, 201–237.

CrossRef Full Text

Treisman, A. (1995). Modularity and attention: is the binding problem real? Vis. Cogn. 2, 303–311.

CrossRef Full Text

Treisman, A. (1998). Feature binding, attention and object perception. Philos. Trans. R. Soc. Lond. B Biol. Sci. 353, 1295–1306.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Treisman, A., and Gelade, G. (1980). A feature-integration theory of attention. Cogn. Psychol. 12, 97–136.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Treisman, A., and Sato, S. (1990). Conjunction search revisited. J. Exp. Psychol. Hum. Percept. Perform. 16, 459–478.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Treisman, A., and Schmidt, H. (1982). Illusory conjunctions in the perception of objects. Cogn. Psychol. 14, 107–141.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Trommershauser, J., Gepshtein, S., Maloney, L. T., Landy, M. S., and Banks, M. S. (2005). Optimal compensation for changes in task-relevant movement variability. J. Neurosci. 25, 7169–7178.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Trommershauser, J., Maloney, L. T., and Landy, M. (2003). Statistical decision theory and trade-offs in the control of motor response. Spat. Vis. 16, 255–275.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Tsotsos, J. K. (2001). “Complexity, vision, and attention,” in Vision and Attention (New York: Springer), 105–128.

Tsotsos, J. K., Culhane, S. M., Kei Wai, W. Y., Lai, Y., Davis, N., and Nuflo, F. (1995). Modeling visual attention via selective tuning. Artif. Intell. 78, 507–545.

CrossRef Full Text

Verghese, P., and Nakayama, K. (1994). Stimulus discriminability in visual search. Vision Res. 34, 2453–2467.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wade, N. J., and Bruce, V. (2001). Surveying the seen: 100 years of British vision. Br. J. Psychol. 92, 79–112.

CrossRef Full Text

Weiss, Y., Simoncelli, E. P., and Adelson, E. H. (2002). Motion illusions as optimal percepts. Nat. Neurosci. 5, 598–604.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wertheim, A. H., Hooge, I. T., Krikke, K., and Johnson, A. (2006). How important is lateral masking in visual search? Exp. Brain Res. 170, 387–402.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Whiteley, L., and Sahani, M. (2008). Implicit knowledge of visual uncertainty guides decisions with asymmetric outcomes. J. Vis. 8, 1–15.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wolfe, J. M. (1998). “Visual search,” in Attention, ed. H. Pashler (Hove: Psychology Press Ltd.), 13–74.

Wolfe, J. M., Cave, K. R., and Franzel, S. L. (1989). Guided search: an alternative to the feature integration model for visual search. J. Exp. Psychol. Hum. Percept. Perform. 15, 419–433.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Yu, A., and Dayan, P. (2004). Inference, attention, and decision in a Bayesian neural architecture. Adv. Neural Inf. Process Syst. 16, 1577–1584.

Yu, A. J., Dayan, P., and Cohen, J. D. (2008). Dynamics of attentional selection under conflict: toward a rational Bayesian account. J. Exp. Psychol. Hum. Percept. Perform. 35, 700–717.

Zeki, S. M. (1976). The functional organization of projections from striate to prestriate visual cortex in the rhesus monkey. Cold Spring Harb. Symp. Quant. Biol. 15, 591–600.

CrossRef Full Text

Zeki, S. M. (1978). Functional specialisation in the visual cortex of the rhesus monkey. Nature 274, 423–428.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Zelinksy, G. (2005). “Specifying the components of attention in a visual search task,” in The Neurobiology of Attention, eds L. Itti, G. Rees, and J. K. Tsotsos (Amsterdam: Elsevier Academic Press), 395–400.

Zemel, R., and Dayan, P. (1999). Distributional population codes and multiple motion models. Adv. Neural Inf. Process Syst. 11, 174–180.

Appendix

Derivation of equation (18)

We wish to find

$q\left(\left[\begin{array}{c}\hfill \mathbf{\text{m}}\hfill \\ \hfill \mathbf{\text{s}}\hfill \\ \end{array}\right]\right)=\underset{q\left(\cdot \right)\in \mathcal{𝒩}}{\text{argmin}}\mathbf{\text{KL}}\left[\sum _u{p}_0\left(\mathbf{\text{u}}\right)\mathcal{𝒩}\left(\mathbf{\text{0}};\left[\begin{array}{cc}\hfill \text{U}\hfill & \hfill \text{U}{\Lambda }^{\text{T}}\hfill \\ \hfill \Lambda \text{U}\hfill & \hfill \Lambda \text{U}{\Lambda }^{\text{T}}+\Psi \hfill \\ \end{array}\right]\right)∥q\left(\left[\begin{array}{c}\hfill \mathbf{\text{m}}\hfill \\ \hfill \mathbf{\text{s}}\hfill \\ \end{array}\right]\right)\right].$

First, let us consider the solution to

$q\left(z\right)=\underset{q\left(\cdot \right)\in \mathcal{𝒩}}{\text{argmin}}\mathbf{\text{KL}}\left[p\left(z\right)\parallel q\left(z\right)\right]$

for an arbitrary vector z and distribution p(z). The Gaussian q() is defined by its mean μ_q and covariance matrix Σ_q. Writing 〈·〉_p for expectations over p and H[p] for the entropy of p, we have

$\begin{array}{l}\mathbf{\text{KL}}\left[p\left(\mathbf{\text{z}}\right)\parallel q\left(\mathbf{\text{z}}\right)\right]={⟨-logq\left(\mathbf{\text{z}}\right)⟩}_p-\mathbf{\text{H}}\left[p\right]\\ =\frac{1}{2}{⟨log\left|2\pi {\Sigma }_q\right|+{\left(\mathbf{\text{z}}-{\mu }_q\right)}^{\text{T}}{\Sigma }_q^{-1}\left(\mathbf{\text{z}}-{\mu }_q\right)⟩}_p-\mathbf{\text{H}}\left[p\right]\\ =\frac{1}{2}\left[log\left|2\pi {\Sigma }_q\right|+{⟨{\left(\mathbf{\text{z}}-{\mu }_q\right)}^{\text{T}}{\Sigma }_q^{-1}\left(\mathbf{\text{z}}-{\mu }_q\right)⟩}_p\right]-\mathbf{\text{H}}\left[p\right]\end{array}$

Setting the derivatives with respect to μ_q and ${\Sigma }_q^{-1}$ to 0 to find the stationary points we obtain:

$\begin{array}{l}\frac{\partial }{\partial {\mu }_q}\mathbf{\text{KL}}\left[p\left(\mathbf{\text{z}}\right)\parallel q\left(\mathbf{\text{z}}\right)\right]=\frac{1}{2}{⟨{\Sigma }_q^{-1}\left(\mathbf{\text{z}}-{\mu }_q\right)⟩}_p=0\\ \Rightarrow {\mu }_q={⟨\mathbf{\text{z}}⟩}_p\end{array}$

and

$\begin{array}{l}\frac{\partial }{\partial {\Sigma }_q^{-1}}\mathbf{\text{KL}}\left[p\left(z\right)\parallel q\left(\mathbf{\text{z}}\right)\right]=\frac{1}{2}\left[-{\Sigma }_q+{⟨\left(\mathbf{\text{z}}-{\mu }_q\right){\left(\mathbf{\text{z}}-{\mu }_q\right)}^{\text{T}}⟩}_p\right]=0\\ \Rightarrow {\Sigma }_q={⟨\left(\mathbf{\text{z}}-{\mu }_q\right){\left(\mathbf{\text{z}}-{\mu }_q\right)}^{\text{T}}⟩}_p.\end{array}$

So the constrained minimum of the KL divergence is achieved by setting the mean and covariance of the Gaussian q to equal the mean and covariance of the distribution p. To minimize the KL divergence of equation (18), we thus need to find the mean and covariance of a mixture of Gaussians. Let

$p\left(\mathbf{\text{z}}\right)=\sum _u{p}_0\left(\mathbf{\text{u}}\right)\mathcal{𝒩}\left(0;\Sigma \left(\mathbf{\text{u}}\right)\right)$

Then

$\begin{array}{l}{⟨\mathbf{\text{z}}⟩}_p=\int \left(\sum _u{p}_0\left(\mathbf{\text{u}}\right)\mathcal{𝒩}\left(z|0;\Sigma \left(\mathbf{\text{u}}\right)\right)\right)\mathbf{\text{z}}d\mathbf{\text{z}}\\ =\sum _u{p}_0\left(\mathbf{\text{u}}\right)\int \mathcal{𝒩}\left(\mathbf{\text{z}}|0;\Sigma \left(\mathbf{\text{u}}\right)\right)\mathbf{\text{z}}d\mathbf{\text{z}}\\ =\sum _u{p}_0\left(\mathbf{\text{u}}\right)\cdot 0=0\end{array}$

and

$\begin{array}{l}{⟨\mathbf{\text{z}}{\mathbf{\text{z}}}^{\text{T}}⟩}_p=\int \left(\sum _u{p}_0\left(\mathbf{\text{u}}\right)\mathcal{𝒩}\left(\mathbf{\text{z}}|0;\Sigma \left(\mathbf{\text{u}}\right)\right)\right)\mathbf{\text{z}}{\mathbf{\text{z}}}^{\text{T}}d\mathbf{\text{z}}\\ =\sum _{\mathbf{\text{u}}}{p}_0\left(\mathbf{\text{u}}\right)\int \mathcal{𝒩}\left(\mathbf{\text{z}}|0;\Sigma \left(\mathbf{\text{u}}\right)\right)\mathbf{\text{z}}{\mathbf{\text{z}}}^{\text{T}}d\mathbf{\text{z}}\\ =\sum _u{p}_0\left(\mathbf{\text{u}}\right)\Sigma \left(\mathbf{\text{u}}\right)\end{array}$

Equation (18) then follows by averaging the elements of the block matrix form of Σ(u).

Derivation of equations (19) and (20)

These equations depend on standard results for conditional and marginal Gaussian forms. Let

$\left[\begin{array}{c}\hfill \mathbf{\text{x}}\hfill \\ \hfill \mathbf{\text{y}}\hfill \\ \end{array}\right]~\mathcal{𝒩}\left(\mathbf{\text{0}};\left[\begin{array}{cc}\hfill A\hfill & \hfill C\hfill \\ \hfill C^{\text{T}}\hfill & \hfill B\hfill \\ \end{array}\right]\right)$

Then we have that

$\mathbf{\text{y}}~\mathcal{𝒩}\left(\mathbf{\text{0}};B\right)\text{and}\mathbf{\text{x}}|\mathbf{\text{y}}~\mathcal{𝒩}\left(C{B}^{-1}\mathbf{\text{y}};A-C{B}^{-1}{C}^{\text{T}}\right).$

Now, equation (19) follows by applying this conditional form to the Gaussian of equation (18). Equation (20) results by noting that Z₀ = q₀ (s) and simply evaluating the log density of the marginal Gaussian on s at the observed value of the sensory input.