- 1 Department of General Psychology and Center for Cognitive Science, University of Padova, Padova, Italy
- 2 DiSCoF, University of Trento, Rovereto, Italy
- 3 Conselve Rehabilitation Center, Padova Hospital, Padova, Italy
- 4 Laboratory of Neuropsychology, IRCCS San Camillo Hospital, Lido-Venice, Italy
Converging evidence suggests that visuospatial attention plays a pivotal role in numerical processing, especially when the task involves the manipulation of numerical magnitudes. Visuospatial neglect impairs contralesional attentional orienting not only in perceptual but also in numerical space. Indeed, patients with left neglect show a bias toward larger numbers when mentally bisecting a numerical interval, as if they were neglecting its leftmost part. In contrast, their performance in parity judgments is unbiased, suggesting a dissociation between explicit and implicit processing of numerical magnitude. Here we further investigate the consequences of these visuospatial attention impairments on numerical processing and their interaction with task demands. Patients with right hemisphere damage, with and without left neglect, were administered both a number comparison and a parity judgment task that had identical stimuli and response requirements. Neglect patients’ performance was normal in the parity task, when processing of numerical magnitude was implicit, whereas they showed characteristic biases in the number comparison task, when access to numerical magnitude was explicit. Compared to patients without neglect, they showed an asymmetric distance effect, with slowing of the number immediately smaller than (i.e., to the left of) the reference and a stronger SNARC effect, particularly for large numbers. The latter might index an exaggerated effect of number-space compatibility after ipsilesional (i.e., rightward) orienting in number space. Thus, the effect of neglect on the explicit processing of numerical magnitude can be understood in terms of both a failure to orient to smaller (i.e., contralesional) magnitudes and a difficulty to disengage from larger (i.e., ipsilesional) magnitudes on the number line, which resembles the disrupted pattern of attention orienting in visual space.
Introduction
Interactions between numbers and space are a major issue in numerical cognition research. The dominant view posits that numerical representations are rooted in cortical networks that also subserve spatial cognition (for reviews, see Walsh, 2003; Hubbard et al., 2005; Umiltà et al., 2009). A more specific hypothesis is that numbers are represented as local activations (points or regions) along a spatially oriented mental number line (Dehaene et al., 1993; Zorzi et al., 2002; Dehaene, 2003; also see Moyer and Landauer, 1967, and Restle, 1970, for earlier proposals of mental number line). Spatial coding of numbers would be at the core of number meaning because number magnitude is conveyed by its position on the number line (Dehaene, 2003). The spatial orientation of the number line is influenced by cultural factors (Göbel et al., 2011, for review), and in Western cultures it conforms to a left-to-right (and small-to-large) horizontal layout (Dehaene et al., 1993; Zorzi et al., 2002).
The strongest evidence supporting the number line hypothesis comes from neuropsychological studies on patients with left hemispatial neglect, who following a lesion of the right hemisphere fail to report, orient to, or verbally describe stimuli in the contralesional left hemispace (Halligan et al., 2003, for a review). When asked to mark the midpoint of a visual line, neglect patients systematically displace it to the right of the true midpoint, as if they ignore the leftmost part of the line. The rightward displacement is, in most patients, directly proportional to the length of the segment, but for very short segments a paradoxical leftward displacement of the midpoint is typically observed (i.e., the crossover effect). Note that neglect is not confined to stimuli that are actually present in the environment, but extends, in some patients, also to mental imagery (e.g., Bisiach and Luzzatti, 1978). For example, the bisection bias was also observed when neglect patients had to bisect imagined lines (e.g., Bisiach et al., 1994). Zorzi et al. (2002) reasoned that if the number line were a representation with a truly spatial nature rather than a mere metaphor (as hitherto believed), neglect patients would show a bias in mentally bisecting a numerical interval that would resemble the one they show in the line bisection task. Indeed, patients with left neglect in physical space systematically misplaced the midpoint of an orally presented numerical interval (e.g., responding that 5 is halfway between 2 and 6) and their errors closely resembled the typical pattern found in the bisection of visual lines, including the modulating effect of line length and the crossover effect with very short numerical intervals. The finding that neglect affects “number space“ was replicated and extended in a number of subsequent studies (e.g., Rossetti et al., 2004; Vuilleumier et al., 2004; Doricchi et al., 2005; Priftis et al., 2006, 2008; Zorzi et al., 2006; Cappelletti et al., 2007; Zamarian et al., 2007; Hoeckner et al., 2008; Salillas et al., 2009). Converging evidence is also provided by studies on healthy participants that investigated rTMS-induced neglect (Göbel et al., 2006) and pseudoneglect (Longo and Lourenco, 2007).
The findings on number interval bisection in neglect patients led Zorzi et al. (2002) to propose a functional isomorphism (or homeomorphism) between the mental number line and visual lines, which has been recently referred to as the “strong version” of the number line hypothesis (Fias et al., 2011; van Dijck et al., 2011). It is important to emphasize, however, that Zorzi et al. did not claim that the number line is represented as a visual line. Two spaces are homeomorphic if they have the same topology; in the present context, this notion implies that the number line and visual lines have the same spatial metrics, but it does not require any common representation or shared neural mechanism. In turn, this implies that dissociations between the number space and other (perceptual or imaginary) spaces can occur (e.g., Rossetti et al., 2004; Zorzi et al., 2004; Doricchi et al., 2005; Loetscher and Brugger, 2009; Loetscher et al., 2010; van Dijck et al., 2011; see Rossetti et al., 2011, for review). Note that these dissociations are not surprising because they mirror and extend to the number space the well known double dissociation between imaginal and perceptual space in neglect patients (Anderson, 1993; Guariglia et al., 1993). It would be odd to maintain that, as a consequence of the latter dissociation, imaginal neglect should not be considered as spatial in nature, or that the imaginal space is not isomorphic to the perceptual space (for example, the patient’s mental image of her own bedroom has indeed the same spatial metrics and coordinate system of the actual bedroom). We believe that the same logic should hold for the dissociation between neglect for physical space and neglect for the number space. All these dissociations within neglect can be explained by the fact that the brain creates a variety of spatial representations implemented within distinct neural circuits and that a unitary, supramodal spatial attention system does not exist (Rizzolatti and Berti, 1993; Casarotti et al., 2012).
The effect of hemispatial neglect should not be conceived as a literal “disruption” of the number space, but as a failure in orienting to or exploring one portion of that space due to impaired attentional mechanisms, just as it is the case for visual space and for other imaginal spaces. Indeed, Priftis et al. (2006) found that left neglect affected numerical processing when the task required an explicit processing of numerical magnitude, as in the number interval bisection task (or in number comparison; Vuilleumier et al., 2004), but not when processing was implicit, as in parity judgments. The dissociation between implicit and explicit processing of contralesional information is a solid (and intriguing) phenomenon in the neuropsychological literature of neglect (see Berti, 2002, for review). Recently, Treccani et al. (2012) observed that neglected stimuli can produce spatial correspondence effects, suggesting that the spatial representation of the contralesional side is intact, but cannot be explicitly accessed. Within the numerical domain, this dissociation clearly supports the hypothesis that neglect affects the allocation of spatial attention over an intact number line (Priftis et al., 2006).
A complementary observation regarding the effect of neglect on numerical magnitude access was made by Vuilleumier et al. (2004) using the number comparison task. They found that neglect patients were abnormally slow in responding to the number immediately smaller than (that is, to the left of) the reference number. For instance, when the reference number was “5,” responses to “4” were much slower than responses to “6,” though both have the same numerical distance from the reference. In contrast, the performance of right brain damaged patients without left neglect and healthy controls was characterized by a regular, symmetric distance effect (Moyer and Landauer, 1967). When the reference number changed to “7,” neglect patients became slower in processing “6,” which is again the number immediately to the “left” of the reference. Thus, the same number was processed faster or slower depending on its spatial position relative to the reference number. Moreover, when Vuilleumier and colleagues asked their participants to think about numbers as being clock hours, neglect patients became selectively slower in responding to larger numbers, which are represented on the left part of the clock face. This remarkable flexibility in changing reference frame for the spatial coding of numbers fits well with the seminal findings of Bisiach and Luzzatti (1978) on representational neglect, whereby the neglected side of a mental image depends on the (imagined) subjective viewpoint of the patient (see also Bachtold et al., 1998). More recently, Salillas et al. (2009) presented right brain damaged patients with and without neglect with digits in the 1–4 and 6–9 ranges. Patients were asked to respond to the digit only if its magnitude was smaller (or larger, in a different block) than the reference (“5”). A selective slowing for the digit immediately smaller than the reference emerged for neglect patients, as in Vuilleumier et al.’s (2004) study. Moreover, Salillas et al. showed that this slowing was significantly reduced when a pattern of leftward-moving dots was presented on the screen. That is, coherent dot motion, which is known to induce shifts of visuospatial attention congruent with the direction of motion, influenced performance in number comparison ameliorating neglect for number space.
The earliest reaction time (RT) evidence for interactions between numbers and space in healthy participants was provided by Dehaene et al. (1993; also see Dehaene et al., 1990), who discovered the Spatial-Numerical Association of Response Codes (SNARC) effect. It consists in faster left-sided responses to small than to large numbers and in faster right-sided responses to large than to small numbers. The SNARC effect is another demonstration of the remarkable flexibility of spatial coding, because the association of a given number with “left” or “right” is not absolute but relative to the tested number range (Dehaene et al., 1993). The classic interpretation of the SNARC effect is that it indexes spatial correspondence (i.e., corresponding vs. non-corresponding trials), between position of the number on the number line and position of the response (but see Gevers et al., 2006; Proctor and Cho, 2006; Gevers et al., 2010; also see General Discussion). The SNARC effect can be induced with various effectors, such as hands, fingers of the same hand (Priftis et al., 2006), feet (Schwarz and Müller, 2006), and saccades (Fischer et al., 2004; Schwarz and Keus, 2004). The effect can be observed both in magnitude comparison and in parity judgments of Arabic digits. Note that the presence of a SNARC effect during parity judgments indexes automatic (or implicit; Priftis et al., 2006) access to numerical magnitude (Dehaene et al., 1993), because the latter is task-irrelevant. There is only one published study that focused on the SNARC effect in neglect patients. Priftis et al. (2006) found that left neglect patients, who were impaired at number interval bisection, showed a regular SNARC effect in the parity judgment task that did not differ from that of healthy controls. Also the study of Vuilleumier et al. (2004) included a manipulation of the response-key assignment in number comparison (i.e., “larger” response on the left vs. right side) that would allow to assess the SNARC effect. The latter, however, was not the focus of their study. Vuilleumier and colleagues reported that the incompatible mapping was generally slower and more error-prone. Although the type of mapping did not interact with group in the main analyses, neglect patients did not show slower responses in the incompatible mapping, as if they failed to show a regular SNARC effect. Nevertheless, performing the incompatible mapping turned out to be too difficult for some neglect patients.
It is worth noting that several types of associations between numbers and space (often variants of the SNARC effect) have been reported by a wealth of behavioral studies on healthy participants. Their review is clearly beyond the scope of the present article, but a few studies are particularly relevant in the present context because they directly speak in favor of attention-mediated interactions between the perceptual space and the number space. For instance, the involvement of visuospatial attention in number processing is clearly supported by the finding that numerical cues can orient attention in visual space (e.g., Fischer et al., 2003; Casarotti et al., 2007; Cattaneo et al., 2009). Accordingly, the rightward bias shown by neglect patients in visual line bisection can be modulated by task-irrelevant digit flankers (“1” leftwards and “9” rightwards; Bonato et al., 2008). Even more important is the demonstration of interaction in the opposite direction, with visuospatial processing influencing number processing, thereby showing that the spatial aspects of numerical processing are not epiphenomenal. Stoianov et al. (2008; also see Kramer et al., 2011) found that an irrelevant visuospatial cue primes a target number in both magnitude comparison and parity judgments. That is, responses (which were vocal and non-spatial) were faster for small than for large numbers when the prime was a left-sided visual cue and faster for large than for small numbers when the prime was a right-sided visual cue. A similar effect was found by Nicholls and McIlroy (2010) for number interval bisection. Finally, mental calculation also seems to be related to a spatial representation of numbers. One clear example is the “Operational Momentum” (OM) effect (McCrink et al., 2007). When asked to add or subtract large sets of dots (see also Knops et al., 2009a), participants underestimated the result of subtractions (“leftward” bias on the mental number line), whereas they overestimated the results of additions (“rightward” bias) in analogy with the “representational momentum” found when the spatial position of a moving object has to be estimated (Freyd and Finke, 1984). The hypothesis that mental calculation involves shifts of spatial attention along the number line (Hubbard et al., 2005) has found direct support in a recent fMRI study: Knops et al. (2009b) observed that the pattern of brain activation in the posterior superior parietal cortex resembled the activation found for rightward saccades when additions were performed and that for leftward saccades when subtractions were performed.
The main aim of the present study was to further investigate the influence of an impairment of visuospatial attention (neglect) on number processing and its interaction with task demands, with specific reference to the distinction between implicit and explicit access to numerical magnitude. As noted before, Priftis et al. (2006) interpreted the dissociation between spared SNARC effect in parity judgment and impaired number interval bisection in terms of the implicit vs. explicit nature of the two tasks. This hypothesis leads to the prediction that the SNARC effect in number comparison should be affected by neglect, because number comparison implies the explicit processing of numerical magnitude. Therefore, we sought to establish whether the SNARC effect in number comparison is affected by neglect and whether the same patients display a normal SNARC effect in parity judgments. The performance of right brain damaged patients with neglect was assessed against that of control patients with right hemisphere damage, but without neglect. Importantly, our contrast between explicit and implicit tasks is much more stringent than in Priftis et al.’s study, because our number comparison task (unlike their number interval bisection task) was identical to the parity judgment task both in terms of stimuli (i.e., a single digit presented at fixation) and response requirements (i.e., key-press responses using the index and middle fingers of the right hand; switch of the response-key assignment). Our approach is, therefore, clear-cut: Any difference in performance between the two tasks must be attributed to the way in which stimulus information is internally processed to accomplish the task. Moreover, given that the two groups of patients differed only for the presence of neglect, any difference between groups must be ascribed to an impaired orienting of visuospatial attention. Finally, our study allowed us to reassess the asymmetry of the distance effect observed by Vuilleumier et al. (2004) in neglect patients, which has only one published replication to date (Salillas et al., 2009). We also assessed whether the selective slowing of “4” during comparison (with reference 5) disappears during parity judgment, as predicted by the explicit vs. implicit account.
Materials and Methods
Participants
Twenty patients with a brain lesion affecting the right hemisphere, confirmed by CT of MR scan, participated in the study. Patients were included in the present study for the presence of right hemisphere damage affecting frontal, temporal, parietal, or subcortical areas, independently from its etiology (e.g., vascular or neoplastic). Patients were all right-handed and were affected by mild to severe motor deficits in the left hemibody. They were admitted to a rehabilitation center to undergo motor rehabilitation for left hemiplegia/hemiparesis. All patients gave written informed consent to participate in the study. None of them had positive medical history of previous neurological disease or substance abuse. The study adhered to the principles of the Declaration of Helsinki.
Neuropsychological Testing
All patients were initially tested with the Mini-Mental State Examination (MMSE; Magni et al., 1996). This was followed by a thorough assessment with a comprehensive neuropsychological battery (ENB; Mondini et al., 2003). Finally, the conventional part of the Behavioral Inattention Test (BIT; Wilson et al., 1987) was administered to investigate the presence of peripersonal neglect. BIT is a battery that includes different subtests: barrage, letter cancellation, star cancellation, bisection, coping, and drawing from memory tests. According to the score obtained on the BIT, twelve patients were assigned to the neglect group (N+) and eight patients to the group without neglect (N−).
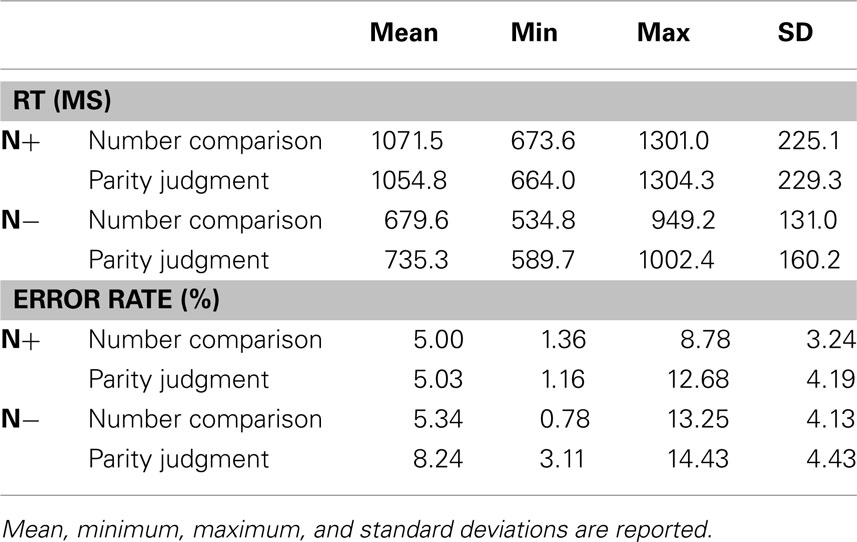
In the analysis of the computer-based task we excluded patients who had a mean error rate ≥25% in at least one of the two response-key assignments (see below), failed to accomplish with instructions, or did not complete the task. Following the application of these criteria, data from seven N− patients were analyzed for both parity and comparison tasks. For the N+ group, the data of five patients were analyzed for both parity and comparison tasks, one patient entered only in the comparison task and one patient only in the parity task. Table 1 shows demographic data and test scores for the patients who entered the analysis (7 N− and 7 N+).
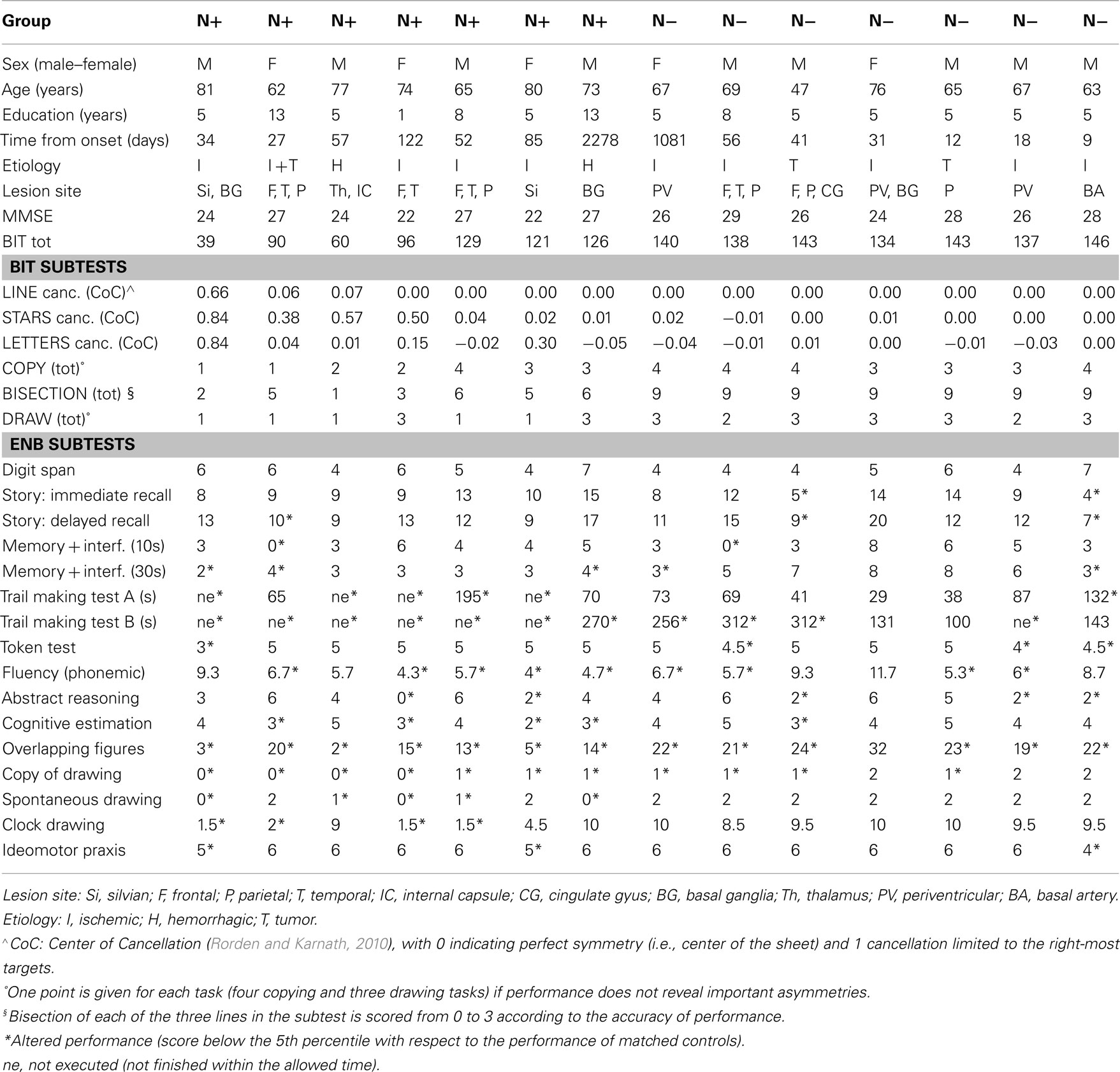
Table 1. Demographic data and test scores of right brain damaged patients with neglect (N+) and without neglect (N−).
The two groups (7 N+ and 7 N−) did not significantly differ in age, F(1, 12) = 3.66, p = 0.08 (mean N+ 73 years, SD 7.2; N− 65 years, SD 8.9), education, F(1, 12) = 0.96, p = 0.35 (mean N+ 7.1 years, SD 4.5; N− 5.4 years, SD 1.1), or time from lesion, F(1, 12) = 0.33, p = 0.58 (mean N+ 379 days, SD 838; N− 178 days, SD 398). The overall BIT score was significantly different between the two groups, F(1, 12) = 12.06, p < 0.01, with a mean score higher for N− (140, SD 4.1) than for N+ (94, SD 34.6). All BIT subtest scores, except for line cancellation, were significantly lower in N+ with respect to N− (all ps < 0.05). The scores for neuropsychological tests did not differ between N+ and N− when the task did not heavily rely on visuospatial abilities (e.g., MMSE, Digit Span, memory for a story in both immediate and delayed recall, memory with interference subtests (10 s version), verbal fluency, abstraction, cognitive estimation, ideomotor praxis). In contrast, the scores for neuropsychological tests differed between N+ and N− (all ps < 0.05) when the task demanded the use of visuospatial abilities (e.g., copy of drawing, drawing from memory – flower and clock, overlapping figures). The TMT (in both versions) was too difficult for N+ patients and most of them failed to complete the test within the time limit.
Procedure
Patients were asked to classify a single digit (1–4 and 6–9) as smaller or larger than the reference 5 (Comparison task) or as odd or even (Parity task). Following Priftis et al. (2006), patients executed their responses only with their right (non-plegic) hand, using the index and middle fingers (Unilateral SNARC Paradigm). The experimenter aligned the trunk midline of each participant with the left border of the computer screen. The viewing distance was about 60 cm. Each trial started with a blank screen, which was followed after 500 ms by a fixation cross that lasted for 1000 ms. Then an additional blank screen was presented for 500 ms, which was followed by the target digit displayed at fixation until response. Acoustic feedback (a low-frequency tone) was provided for 1000 ms following incorrect responses. At the end of each trial, the word “ready” was displayed until the experimenter pressed a button on a separate keyboard to start the next trial. The inter-trial interval was 500 ms.
The experimental manipulation for observing a SNARC effect consists in switching the response-key assignment (e.g., left response for odd numbers in the parity task) after half of the trials, such that each number is responded to with both the left and the right effector (Dehaene et al., 1993). However, as first noted by Vuilleumier et al. (2004), switching response mapping can be extremely difficult (if not impossible) for some patients. Indeed, neglect patients in Priftis et al.’s (2006) study performed the two mappings of the parity task in separate sessions (days). Accordingly, we employed the same strategy of switching response mapping (within the same task) in separate sessions: each session included both parity and comparison tasks, either with a compatible or incompatible mapping. The compatible mapping was defined in terms of magnitude for the comparison task (left response for small and right response for large numbers; i.e., SNARC compatibility; Dehaene et al., 1993) and in terms of parity status for the parity task (left response for odd and right response for even, that is MARC compatibility; Nuerk et al., 2004). For each task and mapping, two blocks with 64 trials each were presented. Task order (e.g., parity or magnitude first) and response mapping (e.g., compatible or incompatible first) were counterbalanced across participants.
Control (N−) patients performed two sessions. Neglect patients performed four sessions with the exception of patients RR, who performed only two sessions, and TM, who performed only the comparison task (in two sessions). Neglect patients’ testing occurred in two consecutive days, in two consecutive weeks (e.g., Monday–Tuesday of week 1 and Monday–Tuesday of week 2). Thus, all neglect patients (except TM and RR) performed 512 trials in the magnitude and 512 trials in the parity task. All patients without neglect performed 256 trials in the magnitude and 256 trials in the parity task. Increasing the number of trials in neglect patients was necessary because the task was difficult for most of them (which implies more variability in performance). This allowed us to obtain a more robust dataset.
Results
Trials with RTs faster than 200 ms and slower than 4500 ms in either task were classified as outliers and excluded from analyses. Table 2 shows the descriptive statistics for RTs and error rates, separately for each task (Number Comparison or Parity Judgment) and group (N− or N+). We analyzed correct RTs of both the comparison and parity tasks with linear mixed effects models (see Baayen, 2008; Baayen et al., 2008), implemented with lme4 (Bates et al., 2008) and language R packages (Baayen, 2008). These models are based on single trial data rather than on averaged data, and allowed estimating the genuine effects of the variables under investigation (i.e., fixed effects; e.g., group, SNARC compatibility, distance, etc.) and separating these effects from those of other spurious variables (i.e., random effects), such as individual variability, general response slowing, block order effects, and so on. This novel approach is particularly interesting for the analysis of patients’ RT data, which are typically more noisy than the RT data of healthy participants. We also performed a series of follow-up analyses using more conventional methods (regressions and t-tests; Fias et al., 1996).
Mixed Effects Models
Separate models were fitted to the comparison RTs and the parity RTs. For both tasks, we first defined a model with participants as a random effect. Then, we entered in the model(s) the interaction between participants and the part of the experiment to which the trial belonged (i.e., part one comprised the first two sessions, whereas part two comprised the following two sessions, when performed) – that is, the effect of the experimental part was allowed to vary between participants. A log-likelihood test was performed (here and at each successive step) to determine if the improvement in the model’s fit was significant, χ2(2) = 27.6, p < 0.0001 for comparison task and χ2(2) = 59.80, p < 0.0001 for parity task. In a third step we added the interaction between participants and the experimental block, whereas in a fourth step we included the interaction between participants and the ordinal position of the trial within the block. Both steps yielded significant improvements in the models’ fits, all χ2s ≥ 32.19, all ps < 0.0001. We then entered as fixed effects all factors (and their interactions) that could influence performance in the two tasks: SNARC compatibility (compatible or incompatible mapping between digit magnitude and response side, i.e., small-left and large-right vs. large-left and small-right), MARC compatibility (compatible or incompatible mapping between digit parity and response side, i.e. odd-left and even-right vs. even-left and odd-right), the participant’s group (i.e., N+ vs. N−), the magnitude of the target with reference to 5 (i.e., larger vs. smaller than 5), and the numerical distance between target and reference (i.e., 1–4).
Comparison task
In the analysis of the comparison data, introducing SNARC compatibility yielded a significant improvement of the model’s fit, χ2(1) = 37.52, p < 0.0001. We then added the interaction between SNARC compatibility and the participant’s group (i.e., N+ vs. N−). Importantly, this interaction improved significantly the model’s fit, χ2(2) = 16.45, p < 0.0005. Moreover, the interactive model had a better fit than the model with SNARC compatibility and group as additive factors, χ2(1) = 5.44, p < 0.05, thereby showing that the magnitude of the SNARC effect was larger in neglect patients than in control patients (mean difference between incompatible and compatible trials: 257 ms for N+ vs. 80 ms for N−). MARC compatibility, as well as its interaction with group, failed to yield any improvements in model’s fit, both χ2s ≤ 0.03, p = 0.98. We then added to the model in successive steps the magnitude of the target with reference to 5 (i.e., larger vs. smaller than 5), and the numerical distance between target and reference (i.e., 1–4). The comparisons between fits obtained at both steps showed significant improvements, both χ2s ≥ 5.05, both ps ≤ 0.05. In the next step we added the interaction between distance and magnitude. A significant improvement in the model’s fit, χ2(1) = 7.93, p < 0.005, suggested that the distance effect was asymmetric (i.e., different distance effects for numbers smaller and larger than 5). We therefore tested for the significance of the interaction between distance, magnitude and group. The (final) model including this three-way interaction (AIC = 66178, BIC = 66305, Log-Likelihood = −33069) showed a better fit, χ2(3) = 32.66, p < 0.0001, thereby showing that the asymmetry of the distance effect for small and large numbers differed between the two groups. None of the other interactions between the fixed factors, when added to the final model, resulted in a significant improvement in the model’s fit, all χ2 ≤ 2.45, all ps ≥ 0.38.
Parity task
In the analysis of parity RTs, MARC compatibility significantly improved the model’s fit, χ2(3) = 115.56, p < 0.0001. This indicates the presence of the MARC effect (Nuerk et al., 2004), that is, an advantage of the odd-left and even-right mapping over the odd-right and even-left mapping. The interaction between MARC compatibility and group did not yield a significant improvement of the model’s fit, χ2(2) = 4.03, p = 0.13. SNARC compatibility significantly improved the fit when added to the model, χ2(1) = 39.45, p < 0.0001, but its interaction with group did not (χ2(2) = 0, p = 1). The resulting (final) model (AIC = 65279, BIC = 65361, Log-Likelihood = −32626) did not significantly differ from any of the alternative models which included the additional fixed factors entered in the magnitude comparison analysis (magnitude, distance), the interaction between these two factors, or interactions between either of these factor and SNARC compatibility, all χ2 ≤ 5.20, all ps ≥ 0.07.
Regression Analyses
To further characterize the effects emerged in the mixed models analyses, we ran a series of regressions focused on the SNARC effect and on the distance effect.
SNARC effect
We first focused on the interaction between SNARC compatibility and group revealed by the mixed models analysis of the comparison RTs and by the corresponding lack of interaction in the parity RTs. For each patient, we computed an individual regression on the RT difference (dRT) between right and left effector responses using a binary predictor (0 for numbers smaller than the reference, 1 for numbers larger than the reference) for the comparison task1 and a continuous predictor (1, 2, 3,…) for the parity task (see Gevers et al., 2006). We then performed one-tailed t-tests against zero on the regression slopes (Lorch and Myers, 1990), because the SNARC effect is indexed by a significant negative slope (Fias et al., 1996). The latter reveals an advantage of the left over the right effector (i.e., positive dRTs) for small numbers that reverses (i.e., negative dRTs) for large numbers (see Figures 1 and 2).
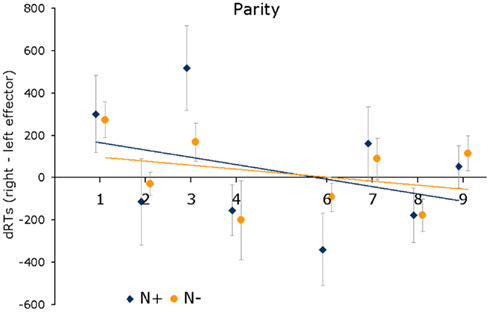
Figure 1. Parity task. The mean difference in RT between right and left effector responses (dRT) to each number is plotted as a function of numerical magnitude, separately for N+ and N− groups. The lines represent the regression fits for each group, computed using a continuous magnitude predictor. Error bars represent ± SEM.
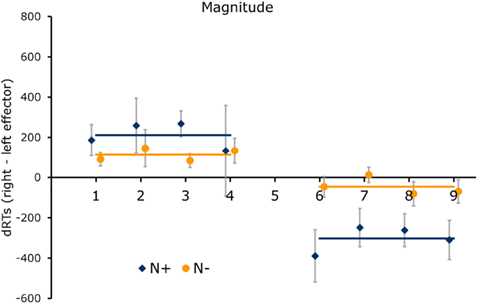
Figure 2. Comparison task. The mean difference in RT between right and left effector responses (dRT) to each number is plotted as a function of numerical magnitude, separately for N+ and N− groups. The lines represent the regression fits for each group, computed using a categorical magnitude predictor. Error bars represent ± SEM.
The regression analyses confirmed the presence of a SNARC effect in both tasks and in both groups (N+: t(5) = -3.33, p < 0.05 for comparison task and t(5) = −2.26, p < 0.05 for parity task; N−: t(6) = −1.95, p < 0.05 for comparison task and t(6) = −2.75, p < 0.05 for parity task). The direct comparison of the slopes of N+ and N− patients confirmed that the SNARC effect was significantly stronger (i.e., the slopes were more negative) for the neglect group in the comparison task (t(11) = −2.12, p < 0.05, one-tailed) but not in the parity task (t(11) = −1.0, p = 0.34, ns). Inspection of Figure 2 suggests that the difference between N+ and N− in terms of SNARC effect for number comparison is more evident for large numbers than for small numbers. We therefore analyzed the difference between groups in terms of an interaction with magnitude. The ANOVA on dRTs with group (N+ vs. N−) and magnitude (small vs. large) as factors showed an interaction that just missed significance, F(1,11) = 4.48, p = 0.058. Follow-up t-tests revealed that the mean dRT for numbers 6–9 was significantly larger in N+ than in N− (−302 ms vs. −46 ms; t(11) = −3.14, p < 0.05, two tailed), whereas the mean dRTs for numbers 1–4 did not differ (N+: 212 ms; N−: 114 ms; t(11) = 0.92, p = 0.38, ns)2. Note that there was no hint of a difference between groups in the parity task even when separating small and large numbers (1–4: t(11) = 1.1, p = 0.29; 6–9: t(11) = 1.26, p = 0.23). In summary, the SNARC effect was present in both groups and in both tasks. In the comparison task only, neglect patients showed a stronger SNARC effect than patients without neglect, particularly for numbers larger than the reference (i.e., 6–9).
MARC effect
To further investigate the effect of MARC compatibility in the parity task (also see Figure 1), we re-run the individual regression analyses on dRTs introducing a parity predictor (binary coded as 0 for odd and 1 for even) in addition to the magnitude predictor. In this way we simultaneously assessed the effect of MARC (parity predictor) and SNARC (magnitude predictor) on the dRTs within a single multiple regression. As for the SNARC, the MARC effect is indexed by negative regression weights (i.e., smaller dRTs for even than for odd numbers) and it can be statistically assessed by a one-tailed t-test against zero. As expected, in the parity task both SNARC and MARC were significant (magnitude predictor: t(12) = −3.29, p < 0.01; parity predictor: t(12) = −2.43, p < 0.05), whereas in the comparison task only the SNARC effect was significant (magnitude predictor: t(12) = −3.4, p < 0.01; parity predictor: t(12) = −0.27, p = 0.79). The MARC regression weights in the parity task did not significantly differ between neglect and control patients (t(11) = 0.54, p = 0.6, two tailed).
Distance effect
To further investigate the interaction between magnitude, distance, and group revealed by the mixed models analysis of the comparison data, we computed for each patient two regressions on the RTs using numerical distance (from 1 to 4) as predictor, separately for numbers smaller vs. larger than the reference. We reasoned that an asymmetric distance effect should be indexed by a significant difference between slopes for numbers 1–4 vs. numbers 6–9. This was indeed the case for N+ (t(5) = 2.76, p < 0.05, two tailed) but not for N− (t(6) = 1.55, p = 0.17). We then assessed whether the asymmetry could be localized to the number immediately preceding the reference (that is, 4; see Figure 3), as reported by Vuilleumier et al.’s, 2004; also Salillas et al., 2009). A t-test between the RTs to 4 (mean = 1363 ms) and 6 (mean = 1160ms) was significant in N+ (t(5) = 3.2, p < . 05, two tailed) but not in N− (t(6) = 0.92, p = 0.39, ns). As can be noted in Figure 3, this pattern was mirrored by the error rates (N+: 10.1% for 4 vs. 4.4% for 6; N−: 5.3% for 4 and 5.3% for 6). Notably, RTs to 4 and 6 in the N+ group did not differ in the parity task (t(5) = −1.28, p = 0.26, ns).
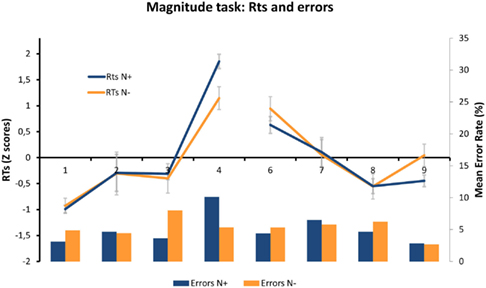
Figure 3. Distance effect in the comparison task. Mean RTs (normalized to z-scores for better visualization) and error rates (percentages) are plotted as a function of numerical distance, separately for N+ and N−. Error bars represent ± SEM.
To compare the asymmetry of the distance effect across groups, we computed regression slopes using only the two numbers immediately smaller (3 and 4) and the two numbers immediately larger (6 and 7) than the reference. We then subtracted the slopes for large numbers from the slopes for small numbers (note that distance slopes are negative) to obtain an index that quantifies the asymmetry of the distance effect, henceforth Distance Asymmetry Index (DAI). Perfect symmetry is indexed by a value of 0, stronger distance effect for small than for large numbers is indexed by a negative value, and stronger distance effect for large than for small numbers is indexed by a positive value. The DAI was negative and significantly different from zero for N+ (DAI = −243; t(5) = −5, p < 0.01, two tailed) but not for N−, (DAI = −64.7; t(6) = −1.12, p = 0.31, ns). Moreover, a direct comparison between the two groups showed that the DAI was larger for N+ than for N− (t(11) = −2.32, p < 0.05, two tailed).
Correlations with Neglect Severity
Finally, we explored whether the atypical pattern observed in N+ for both SNARC and distance effects correlated with the overall index of neglect severity, that is the BIT score. The correlations were computed across the entire sample of right brain damaged patients, that is, regardless of their classification as N+ or N−. Correlations should be treated with caution due to the small sample size and are reported only for the sake of completeness. The BIT score was positively correlated with the individual regression weights of the comparison SNARC effect (r = 0.64, p < 0.05). The correlation between BIT score and DAI just missed significance (r = 0.53, p = 0.065). We also assessed the correlations between BIT score and the two effects modulating performance in the parity task, that is SNARC and MARC, indexed by the individual regression weights. Both correlations did not reach significance (SNARC: r = 0.35, p = 0.24; MARC: r = 0.436, p = 0.136).
General Discussion
Our results supported the hypothesis that the effect of spatial neglect on number processing is modulated by task demands. When the task did not require explicit processing of numerical magnitude, as in parity judgments, the performance of neglect patients was indistinguishable from that of control patients without neglect. Indeed, group failed to interact with any of the numerical factors introduced in the mixed model, including SNARC compatibility. Moreover, direct assessment of the SNARC effect using the regression approach on dRTs showed a classic negative slope for neglect patients, thereby indexing implicit access to numerical magnitude, but the slope did not differ from that of control patients. These results replicate and extend the findings of Priftis et al. (2006), who found no difference between neglect patients and healthy controls.
In contrast, neglect patients’ performance was markedly different from that of control patients when explicit access to numerical magnitude was part of the task demands. The effect of neglect on number comparison was indexed by two distinct phenomena: (i) a stronger SNARC effect, particularly for numbers larger than (i.e., to the right of) the reference, and (ii) an asymmetric distance effect, caused by slowing of the number immediately smaller than (i.e., to the left of) the reference number (as in Vuilleumier et al., 2004). These two findings, as well as their theoretical implications, are discussed below. It is important to reiterate that the number comparison task (unlike the number bisection task used by Priftis et al., 2006) was identical to the parity judgment task both in terms of stimuli (i.e., a single digit presented at fixation) and response requirements (i.e., key-press responses using the index and middle fingers of the right hand). Both tasks also required to switch the response-key assignment between blocks of trials. Thus, any difference in performance between the two tasks must be attributed to how stimulus information is internally processed to accomplish the task. Moreover, since both groups of participants had right hemisphere lesions (and lesion site was quite heterogeneous across patients; see Table 1), any difference that emerged between tasks in neglect patients must be attributed to their failure in orienting to or exploring the contralesional portion of number space due to impaired attentional mechanisms. The manipulation of the task whilst keeping constant the stimuli allows one to establish that the differences between the two groups are due to the aspect under investigation (Bonato et al., 2012, for discussion).
Our findings on the comparison SNARC effect suggest that, after processing a large number, the difference in speed between responses in contralesional (relative left) space and ipsilesional (relative right) space is unusually large for neglect patients with respect to patients without neglect. Assuming that processing a large number entails a rightward shift of attention, the exaggerated effect of number-space compatibility after ipsilesional (i.e., rightward) orienting seems to resemble the marked difficulty of neglect patients in “disengaging” from an ispilesional (i.e., right) location where attention has been directed (Posner et al., 1984). This bias, known as the “disengage deficit,” is consistently found in neglect patients following both stimulus-driven orienting to peripheral cues (Losier and Klein, 2001) and reflexive orienting following central symbolic cues (Bonato et al., 2009). Thus, we propose that the stronger SNARC effect for large numbers observed in neglect patients in comparison to control patients might be an instance of the ipsilesional hyper-attention and/or contralesional impaired orienting that, in physical space, manifests itself as a disengage deficit. That is, neglect patients would have a difficulty to disengage from larger magnitudes (right on the mental number line) to respond in the left (physical) space. Interestingly, the index of neglect severity (BIT score) correlated with the size of the SNARC effect across the entire sample of right brain damaged patients, suggesting again a parallel with the visuospatial domain, where Bonato et al. (2009) found that the same index correlated with the size of the disengage deficit. A modulation of the SNARC effect during number comparison, but not during parity judgments, was also observed by Rusconi et al. (2011) in healthy participants when rTMS was delivered to the frontal regions that support attention orienting. Most notably, TMS over the right frontal eye fields (FEF) in healthy participants decreased the comparison SNARC effect for small numbers. The finding that FEF has a key role for orienting in number space fits well with the hypothesis that attentional orienting in parietal spatial maps is driven by eye movement programming (i.e., premotor theory of attention; Casarotti et al., 2012).
The result that the SNARC effect is modulated by neglect has important theoretical implications. Our findings fit well with the assumption that numbers are spatially coded and that the SNARC effect taps their spatial correspondence with the position of response. However, the visuospatial origin of the SNARC effect is strongly disputed (Gevers et al., 2006, 2010; Proctor and Cho, 2006; Santens and Gevers, 2008). A computational model of the SNARC effect (Gevers et al., 2006) dispenses with the spatial coding of numbers and assumes that left and right response codes are activated by a verbal-conceptual coding of numbers as small and large, respectively (Fias et al., 2011, for review). This association can also be cast within the broader theoretical framework of polarity matching (Proctor and Cho, 2006), where binary choice tasks induce polarity coding (+ vs. −) of stimuli and responses. Thus, the SNARC effect would be the result of coding large numbers as [+] and small numbers as [−], which would then produce match or mismatch with the coding of responses as [+] for right and [−] for left. However, if the SNARC effect were merely an instance of polarity correspondence, neglect should not have any effect on it, or at least it should exert identical effects on the parity and the comparison tasks. Of course the notion of implicit vs. explicit processing may be invoked by any theory of the SNARC effect to explain the fact that neglect affected only the comparison task, but what still needs to be explained is why the comparison SNARC effect is affected by neglect. In this regards, it is difficult to envisage how a deficit of visuospatial attention (i.e., neglect) would influence the SNARC effect if number–space interactions do not involve a visuospatial code, as posited by verbal–conceptual accounts. One could still argue that neglect may affect the verbal–conceptual association between numbers and space. If so, this should hold for another type of number–space association that has a firm verbal–conceptual basis, that is the association between parity status and response space (MARC effect; Nuerk et al., 2004; Iversen et al., 2006). This issue was not investigated in the study of Priftis et al. (2006); in the present study, we found that the MARC effect in the parity task was not modulated by neglect, even though number parity was the task-relevant dimension and had to be explicitly processed. This rules out the hypothesis that the effect of neglect emerges only on the task-relevant dimension irrespectively of the nature of the task. Taken together, our findings are inconsistent with a purely verbal–conceptual account of number–space interactions. More generally, any explicit account of the effect of neglect on number processing requires – as a minimum – that visuospatial representations substantially contribute in shaping the number–space interaction, as in the computational model of Chen and Verguts (2010).
Our findings are also consistent with the recent proposal that numbers might be associated with multiple spatial codes, and that, depending on the task, these codes have a verbal or visuospatial basis (van Dijck et al., 2009; Gevers et al., 2010). Van Dijck and colleagues investigated the effect of working memory load on the SNARC effect. They found that the SNARC effect in parity judgments disappeared under verbal load but not under spatial load, whereas the opposite was found for the SNARC effect in number comparison (also see Herrera et al., 2008). Further evidence for the co-existence of verbal–spatial and visuospatial coding of numbers was provided by Gevers et al. (2010), although they concluded that the former is the dominant one. A dual-coding account of our findings would suggest that the SNARC effect in number comparison is primarily driven by the visuospatial coding of numbers (Herrera et al., 2008; van Dijck et al., 2009), which in turn is affected by neglect, whereas the SNARC effect in parity judgment is primarily driven by the verbal–spatial code, which is not affected by neglect. Note that this alternative account does not necessarily require the distinction between explicit and implicit processing. Nevertheless, our results are still inconsistent with the claim that verbal–spatial coding is predominant across tasks (Gevers et al., 2010) and that the SNARC effect does not imply a visuospatial coding of numbers (Gevers et al., 2006; Proctor and Cho, 2006; Santens and Gevers, 2008; Fias et al., 2011).
While the modulation of the comparison SNARC effect shows that neglect affects the interaction between numbers and physical space (i.e., upon spatially organized responses), the asymmetric distance effect is complementary (and orthogonal) to the latter, because it shows that neglect can affect number processing per se, regardless of the spatial characterization of the responses (i.e., irrespectively of response side). Both effects, however, can be observed only when magnitudes must be explicitly manipulated on the mental number line. The asymmetry of the distance effect was largely due to the slowing of the number immediately smaller than (i.e., to the left of) the reference number; importantly, our asymmetry index (DAI) allowed us to characterize this effect in relative (rather than absolute) terms and to establish that this contralesional bias specifically affects neglect patients. Crucially, as predicted by the explicit vs. implicit processing account (Priftis et al., 2006), response speed to the same number (4) was unaffected by neglect in the parity task. Therefore, our results replicate and extend those of Vuilleumier et al. (2004) and Salillas et al. (2009). We suggest that the asymmetric distance effect indexes a difficulty of contralesional orienting in the number space. That is, we assume that numbers are flexibly coded as left or right with respect to the reference number (also see Vuilleumier et al., 2004) and that spatial attention is shifted (leftward or rightward) from this anchor point to the spatial position of the target number on the mental number line. The apparent selectivity of the bias for the number immediately to the left of the reference might be a consequence of the interaction with the distance effect, which makes that number more difficult to process than any other number on the same side of the number line. An ERP signature of the orienting bias in the number space was reported by Priftis et al. (2008) using a numerical oddball task. With respect to right hemisphere damaged controls without neglect, neglect patients had slower P3b brain waves (see Lhermitte et al., 1985, for comparable results with visuospatial stimuli) in response to a small target number (“one,” which is to the left of the non-target “five”), but faster brain waves in response to a large target number (“nine,” which is to the right of “five”). This pattern resembles that of neglect patients in allocating visuospatial attention in the physical space (Làdavas et al., 1990).
The orienting bias in the number space is theoretically important because it is inconsistent with the recent proposal that a position-specific deficit to initial items in verbal working memory (Fias et al., 2011; van Dijck et al., 2011) could explain the biases in numerical processing that were originally attributed to spatial neglect (Zorzi et al., 2002). The verbal working memory account was developed in the context of a single case study to explain the patient’s rightward bias in number interval bisection as due to a difficulty to efficiently keep in mind the initial numbers of the to-be-bisected interval, but it has also been proposed as a general and alternative account of the (putative) effect of neglect on number processing. In this regard, the verbal working memory account falls short in explaining the pattern observed in our number comparison task, where the only number that must be kept in working memory is the reference (note that the same applies to the numerical oddball task of Priftis et al., 2008), and more generally it cannot explain the dissociation between explicit and implicit processing of numerical magnitude. Moreover, its prediction that the interval bisection bias should be identical for any kind of ordered information is challenged by the dissociations observed in neglect patients by Zorzi et al., 2006; also see Zamarian et al., 2007) between numerical and non-numerical ordered sequences (i.e., intervals formed by numbers, letters, or months). Note also that the cortical overlap in the human intraparietal sulcus for the processing of numerical and non-numerical order revealed by fMRI (Fias et al., 2007) can be resolved into distinct clusters of activation using multivariate classifiers (Zorzi et al., 2011). Finally, Priftis et al. (2012) recently showed that optokinetic stimulation – a technique inducing visuospatial attention shifts by means of activation of the optokinetic nystagmus – modulated the number bisection bias in one neglect patient, thereby demonstrating that the rightward bias had an attentional origin.
While the studies on neglect patients clearly show that a deficit of visuospatial attention can affect number processing, there is also mounting evidence that experimental manipulations of the deployment of visuospatial attention in healthy participants affects performance in numerical tasks. For example, Göbel et al. (2006) induced neglect-like performance in number interval bisection by applying rTMS on the right parietal lobe of healthy participants. Notably, the stimulation site was functionally (and individually) defined such that TMS interfered with visuospatial attention (i.e., visual search task). Stoianov et al. (2008) demonstrated that task-irrelevant lateralized visuospatial cues, which are known to induce stimulus-driven orienting of attention, can modulate performance in both number comparison and parity judgment. Even though responses were verbal and non-spatial, left cues interfered with the processing of large numbers, whereas right cues interfered with small numbers (also see Kramer et al., 2011). Consistent results were found by Nicholls and McIlroy (2010) using the number interval bisection task. Finally, Loetscher et al. (2008) observed response biases in random number generation that were congruent with the direction of lateral head turns (leftward or rightward), which are known to reallocate visuospatial attention. Together, the findings on neglect patients and healthy participants across a variety of different methods converge in supporting the hypothesis that the spatial aspects of numerical processing are not epiphenomenal and that spatial attention is routinely involved in number processing tasks.
In conclusion, the hypothesis that the manipulation of numerical magnitudes entails shifts of attention on a spatially oriented mental number line remains the most viable explanation for the intriguing phenomenon of number space neglect and, more generally, for the interactions between numbers and space. The effect of neglect on the explicit processing of numerical magnitude can be understood in terms of both a failure to orient to smaller (i.e., contralesional) magnitudes and a difficulty to disengage from larger (i.e., ipsilesional) magnitudes on the number line, which resembles the disrupted pattern of attention orienting in visual space. Though many details still need to be worked out, this conclusion is consistent with the idea that cortical circuits originally subserving spatial cognition and attention are “recycled” for mathematical learning (Dehaene and Cohen, 2007). It also fits well with the idea that componential, dynamic sensorimotor simulations underlie the representation of concepts (Barsalou, 1999), as also shown by the remarkable flexibility of spatial coding for numbers as a function of context. Notwithstanding the dissociations between number space and physical space, which are rather unsurprising given the complex and multi-faceted nature of hemispatial neglect, the “strong” (i.e., homeomorphic) number line hypothesis has still a long way to go.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This study was supported by grants from Italian Ministry of University and Research (PRIN 2008) and by the European Research Council (grant # 210922) to Marco Zorzi.
Footnotes
- ^The use of a categorical rather than continuous magnitude predictor for the analysis of comparison dRTs has become a standard approach after Gevers et al.’s (2006) study. We also performed the same regressions with a continuous predictor and the results were virtually identical.
- ^Note that the three-way interaction between SNARC compatibility, magnitude and group was not significant in the mixed models analysis. This discrepancy might reflect a higher sensitivity of the dRT analysis, which is specifically designed to investigate the SNARC effect (i.e., other effects that strongly modulate RTs are canceled out by the subtraction).
References
Anderson, B. (1993). Spared awareness for the left side of internal visual images in patients with left-sided extrapersonal neglect. Neurology 1, 213–216.
Baayen, H. (2008). Analyzing Linguistic Data: A Practical Introduction to Statistics. Cambridge: Cambridge University Press.
Baayen, H., Davidson, D. J., and Bates, D. M. (2008). Mixed-effects modelling with crossed random effects for subjects and items. J. Mem. Lang. 59, 390–412.
Bachtold, D., Baumuller, M., and Brugger, P. (1998). Stimulus-response compatibility in representational space. Neuropsychologia 36, 731–735.
Bates, D., Maechler, M., and Dai, B. (2008). Lme4: Linear mixed-effects models using S4 classes. R package version 0.999375–24. Available at: http://lme4.r-forge.r-project.org/
Berti, A. (2002). “Unconscious processing in neglect,” in The Cognitive and Neural Bases of Spatial Neglect, eds H. O. Karnath, A. D. Milner, and G. Vallar (Oxford: Oxford University Press), 313–326.
Bisiach, E., and Luzzatti, C. (1978). Unilateral neglect of representational space. Cortex 14, 129–133.
Bisiach, E., Rusconi, M. L., Peretti, V., and Vallar, G. (1994). Challenging current accounts of unilateral neglect. Neuropsychologia 32, 1431–1434.
Bonato, M., Priftis, K., Marenzi, R., and Zorzi, M. (2008). Modulation of hemispatial neglect by directional and numerical cues in the line bisection task. Neuropsychologia 46, 426–433.
Bonato, M., Priftis, K., Marenzi, R., and Zorzi, M. (2009). Normal and impaired reflexive orienting of attention following central non-predictive cues. J. Cogn. Neurosci. 21, 745–759.
Bonato, M., Sella, F., Berteletti, I., and Umiltà, C. (2012). Neuropsychology is nothing without control: a potential fallacy hidden in clinical studies. Cortex 48, 353–355.
Cappelletti, M., Freeman, E. D., and Cipolotti, L. (2007). The middle house or the middle floor: bisecting horizontal and vertical mental number lines in neglect. Neuropsychologia 45, 2989–3000.
Casarotti, M., Lisi, M., Umiltà, C., and Zorzi, M. (2012). Paying attention through eye movements: a computational investigation of the premotor theory of spatial attention. J. Cogn. Neurosci.
Casarotti, M., Michielin, M., Zorzi, M., and Umiltà, C. (2007). Temporal order judgment reveals how number magnitude affects visuospatial attention. Cognition 102, 101–117.
Cattaneo, Z., Silvanto, J., Battelli, L., and Pascual-Leone, A. (2009). The mental number line modulates visual cortical excitability. Neurosci. Lett. 462, 253–256.
Chen, Q., and Verguts, T. (2010). Beyond the mental number line: a neural network model of number-space interactions. Cogn. Psychol. 60, 218–240.
Dehaene, S. (2003). The neural basis of the Weber-Fechner law: a logarithmic mental number line. Trends Cogn. Sci. (Regul. Ed.) 7, 145–147.
Dehaene, S., Bossini, S., and Giraux, P. (1993). The mental representation of parity and numerical magnitude. J. Exp. Psychol. Gen. 122, 371–396.
Dehaene, S., Dupoux, E., and Mehler, J. (1990). Is numerical comparison digital? Analogical and symbolic eVects in two-digit number comparison. J. Exp. Psychol. Hum. Percept. Perform. 16, 626–641.
Doricchi, F., Guariglia, P., Gasparini, M., and Tomaiuolo, F. (2005). Dissociation between physical and mental number line bisection in right hemisphere brain damage. Nat. Neurosci. 8, 1663–1665.
Fias, W., Brysbaert, M., Geypens, F., and d’Ydewalle, G. (1996). The importance of magnitude information in numerical processing: evidence from the SNARC effect. Math. Cogn. 2, 95–110.
Fias, W., Lammertyn, J., Caessens, B., and Orban, G. A. (2007). Processing of abstract ordinal knowledge in the horizontal segment of the intraparietal sulcus. J. Neurosci. 27, 8952–8956.
Fias, W., van Dijck, J. F., and Gevers, W. (2011). “How number is associated with space? The role of working memory,” in Space, Time and Number in the Brain: Searching for the Foundations of Mathematical Thought, eds S. Dehaene, and E. M. Brannon (Burlington, MA: Elsevier/Academic Press), 133–148.
Fischer, M. H., Castel, A. D., Dodd, M. D., and Pratt, J. (2003). Perceiving numbers causes spatial shifts of attention. Nat. Neurosci. 6, 555–556.
Fischer, M. H., Warlop, N., Hill, R. L., and Fias, W. (2004). Oculomotor bias induced by number perception. Exp. Psychol. 51, 91–97.
Freyd, J., and Finke, R. A. (1984). Representational momentum. J. Exp. Psychol. Learn. Mem. Cogn. 10, 126–132.
Gevers, W., Santens, S., Dhooge, E., Chen, Q., van den Bossche, L., Fias, W., and Verguts, T. (2010). Verbal-spatial and visuospatial coding of number-space interactions. J. Exp. Psychol. Gen. 139, 180–190.
Gevers, W., Verguts, T., Reynvoet, B., Caessens, B., and Fias, W. (2006). Numbers and space: a computational model of the SNARC effect. J. Exp. Psychol. Hum. Percept. Perform. 32, 32–44.
Göbel, S. M., Calabria, M., Farné, A., and Rossetti, Y. (2006). Parietal rTMS distorts the mental number line: simulating ‘spatial’ neglect in healthy subjects. Neuropsychologia 44, 860–868.
Göbel, S. M., Shaki, S., and Fischer, M. H. (2011). The cultural number line: a review of cultural and linguistic influences on the development of number processing. J. Cross Cult. Psychol. 42, 543–565.
Guariglia, C., Padovani, A. P., Pantano, O., and Pizzamiglio, L. (1993). Unilateral neglect restricted to visual imagery. Nature 364, 235–237.
Halligan, P. W., Fink, G. R., Marshall, J. C., and Vallar, G. (2003). Spatial cognition: evidence from visual neglect. Trends Cogn. Sci. (Regul. Ed.) 7, 125–133.
Herrera, A., Macizo, P., and Semenza, C. (2008). The role of working memory in the association between number magnitude and space. Acta Psychol. (Amst.) 128, 225–237.
Hoeckner, S. H., Zauner, H., Moeller, K., Wood, G., Haider, C., Gaßner, A., and Nuerk, H. C. (2008). Impairments of the mental number line for two digit numbers in neglect. Cortex 44, 429–438.
Hubbard, E. M., Piazza, M., Pinel, P., and Dehaene, S. (2005). Interactions between number and space in parietal cortex. Nat. Rev. Neurosci. 6, 435–448.
Iversen, W., Nuerk, H.-C., Jäger, L., and Willmes, K. (2006). The influence of an external symbol system on number parity representation, or what’s odd about 6? Psychon. Bull. Rev. 13, 730–736.
Knops, A., Viarouge, A., and Dehaene, S. (2009a). Dynamic representations underlying symbolic and nonsymbolic calculation: evidence from the operational momentum effect. Atten. Percept. Psychophys. 71, 803–821.
Knops, A., Thirion, B., Hubbard, E. M., Michel, V., and Dehaene, S. (2009b). Recruitment of an area involved in eye movements during mental arithmetic. Science 324, 1583–1585.
Kramer, P., Stoianov, I., Umiltà, C., and Zorzi, M. (2011). Interactions between perceptual and numerical space. Psychon. Bull. Rev. 18, 722–728.
Làdavas, E., Petronio, A., and Umiltà, C. (1990). The deployment of visual attention in the intact Weld of hemineglect patients. Cortex 26, 307–317.
Lhermitte, F., Turell, E., LeBrigand, D., and Chain, F. (1985). Unilateral visual neglect and wave P 300. A study of nine cases with unilateral lesions of the parietal lobes. Arch. Neurol. 42, 567–573.
Loetscher, T., and Brugger, P. (2009). Random number generation in neglect patients reveals enhanced response stereotypy, but no neglect in number space. Neuropsychologia 47, 276–279.
Loetscher, T., Nicholls, M. E. R., Towse, J. N., Bradshaw, J. L., and Brugger, P. (2010). Lucky numbers: spatial neglect affects physical, but not representational, choices in a Lotto task. Cortex 46, 685–690.
Loetscher, T., Schwarz, U., Schubiger, M., and Brugger, P. (2008). Head turns bias the brain’s internal random generator. Curr. Biol. 18, R60–R62.
Longo, M. R., and Lourenco, S. F. (2007). Spatial attention and the mental number line: evidence for characteristic biases and compression. Neuropsychologia 45, 1400–1407.
Lorch, R. F. Jr., and Myers, J. L. (1990). Regression analyses of repeated measures data in cognitive research: a comparison of three different methods. J. Exp. Psychol. Learn. Mem. Cogn. 16, 149–157.
Losier, B. J. W., and Klein, R. M. (2001). A review of the evidence for a disengage deficit following parietal lobe damage. Neurosci. Biobehav. Rev. 25, 1–13.
Magni, E., Binetti, G., Padovani, A., Cappa, S. F., Bianchetti, A., and Trabucchi, M. (1996). The Mini-Mental State Examination in Alzheimer’s disease and multi-infarct dementia. Int. Psychogeriatr. 8, 127–134.
McCrink, K., Dehaene, S., and Dehaene-Lambertz, G. (2007). Moving along the number line: operational momentum in nonsymbolic arithmetic. Percept. Psychophys. 69, 1324–1333.
Mondini, S., Mapelli, D., Vestri, A., and Bisiacchi, P. S. (2003). Esame neuropsicologico breve. Milano: Raffaello Cortina Editore.
Moyer, R. S., and Landauer, T. K. (1967). Time required for judgments of numerical inequality. Nature 215, 1519–1520.
Nicholls, M. E. R., and McIlroy, A. M. (2010). Spatial cues affect mental number line bisections. Exp. Psychol. 57, 315–319.
Nuerk, H. C., Iversen, W., and Willmes, K. (2004). Notational modulation of the SNARC and the MARC (linguistic markedness of response codes) effect. Q. J. Exp. Psychol. A 57, 835–863.
Posner, M. I., Walker, J. A., Friedrich, F. J., and Rafal, R. D. (1984). Effects of parietal injury on covert orienting of attention. J. Neurosci. 4, 1863–1874.
Priftis, K., Piccione, F., Giorgi, F., Meneghello, F., Umiltà, C., and Zorzi, M. (2008). Lost in number space after right brain damage: a neural signature of representational neglect. Cortex 44, 449–453.
Priftis, K., Pitteri, M., Meneghello, F., Umiltà, C., and Zorzi, M. (2012). Otokinetic stimulation modulates neglect for the number space: evidence from mental number interval bisection. Front. Hum. Neurosci. 6:23.
Priftis, K., Zorzi, M., Meneghello, F., Marenzi, R., and Umità, C. (2006). Explicit vs. implicit processing of representational space in neglect: dissociations in accessing the mental number line. J. Cogn. Neurosci. 18, 680–688.
Proctor, R. W., and Cho, Y. S. (2006). Polarity correspondence: a general principle for performance of speeded binary classification tasks. Psychol. Bull. 132, 416–442.
Rizzolatti, G., and Berti, A. (1993). “Neural mechanisms of spatial neglect,” in Unilateral Neglect: Clinical and Experimental Studies, eds I. H. Robertson, and J. C. Marshall (London: Taylor & Francis), 87–105.
Rorden, C., and Karnath, H. O. (2010). A simple measure of neglect severity. Neuropsychologia 48, 2558–2563.
Rossetti, Y., Jacquin-Courtois, S., Aiello, M., Ishihara, M., Brozzoli, C., and Doricchi, F. (2011). “Neglect ‘around the clock’: dissociating number and spatial neglect in right brain damage,” in Space, Time and Number in the Brain: Searching for the Foundations of Mathematical Thought, eds S. Dehaene, and E. M. Brannon (Burlington, MA: Elsevier/Academic Press), 149–173.
Rossetti, Y., Jacquin-Courtois, S., Rode, G., Ota, H., Michel, C., and Boisson, D. (2004). Does action make the link between number and space representation? Visuo-manual adaptation improves number bisection in unilateral neglect. Psychol. Sci. 15, 426–430.
Rusconi, E., Bueti, D., Walsh, V., and Butterworth, B. (2011). Contribution of frontal cortex to the spatial representation of number. Cortex 47, 2–13.
Salillas, E., Graná, A., Juncadella, M., Rico, I., and Semenza, C. (2009). Leftward motion restores number space in neglect. Cortex 45, 730–737.
Santens, S., and Gevers, W. (2008). The SNARC effect does not imply a mental number line. Cognition 108, 263–270.
Schwarz, W., and Keus, I. M. (2004). Moving along the mental number line: comparing SNARC effects with saccadic and manual response. Percept. Psychophys. 66, 651–664.
Schwarz, W., and Müller, D. (2006). Spatial associations in number related tasks: a comparison of manual and pedal responses. Exp. Psychol. 53, 4–15.
Stoianov, I., Kramer, P., Umiltà, C., and Zorzi, M. (2008). Visuospatial priming of the mental number line. Cognition 106, 770–779.
Treccani, B., Cubelli, R., Sellaro, R., Umiltà, C., and Della Sala, S. (2012). Dissociation between awareness and spatial coding: evidence from unilateral neglect. J. Cogn. Neurosci. 24, 854–867.
Umiltà, C., Priftis, K., and Zorzi, M. (2009). The spatial representation of numbers: evidence from neglect and pseudoneglect. Exp. Brain Res. 192, 561–569.
van Dijck, J. P., Gevers, W., and Fias, W. (2009). Numbers are associated with different types of spatial information depending on the task. Cognition 113, 248–253.
van Dijck, J. P., Gevers, W., Lafosse, C., Doricchi, F., and Fias, W. (2011). Non-spatial neglect for the mental number line. Neuropsychologia 49, 2570–2583.
Vuilleumier, P., Ortigue, S., and Brugger, P. (2004). The number space and neglect. Cortex 40, 399–410.
Walsh, V. (2003). A Theory of magnitude: common cortical metrics of time, space, and quantity. Trends Cogn. Sci. (Regul. Ed.) 7, 483–488.
Wilson, B., Cockburn, J., and Halligan, P. W. (1987). The Behavioural Inattention Test. Bury St. Edmunds: Thames Valley Test Company.
Zamarian, L., Egger, C., and Delazer, M. (2007). The mental representation of ordered sequences in visual neglect. Cortex 43, 542–550.
Zorzi, M., Di Bono, M. G., and Fias, W. (2011). Distinct representations of numerical and non-numerical order in the human intraparietal sulcus revealed by multivariate pattern recognition. Neuroimage 56, 674–680.
Zorzi, M., Priftis, K., Meneghello, F., Marenzi, R., and Umiltà, C. (2004). “Dissociations in the bisection of visual lines and number lines in neglect,” Poster presented at the First Congress of the European Neuropsychological Societies, Modena.
Zorzi, M., Priftis, K., Meneghello, F., Marenzi, R., and Umiltà, C. (2006). The spatial representation of numerical and non-numerical sequences: evidence from neglect. Neuropsychologia 44, 1061–1067.
Keywords: neglect, spatial attention, mental number line, SNARC effect, distance effect, mixed effects models
Citation: Zorzi M, Bonato M, Treccani B, Scalambrin G, Marenzi R and Priftis K (2012) Neglect impairs explicit processing of the mental number line. Front. Hum. Neurosci. 6:125. doi: 10.3389/fnhum.2012.00125
Received: 26 September 2011; Accepted: 18 April 2012;
Published online: 21 May 2012.
Edited by:
Filip Van Opstal, Ghent University, BelgiumReviewed by:
Wim Gevers, Université Libre de Bruxelles, BelgiumHans-Christoph Nuerk, University of Tuebingen, Germany
Copyright: © 2012 Zorzi, Bonato, Treccani, Scalambrin, Marenzi and Priftis. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Marco Zorzi and Mario Bonato, Department of General Psychology, University of Padova, via Venezia 8, 35131 Padova, Italy. e-mail:bWFyY28uem9yemlAdW5pcGQuaXQ=;bWFyaW8uYm9uYXRvQHVuaXBkLml0



 Giovanni Scalambrin1
Giovanni Scalambrin1