- Institute of Cognitive Neuroscience, University College London, London, UK
Empirical research and theoretical accounts have traditionally emphasized the function of the hippocampus in episodic memory. Here we draw attention to the importance of the hippocampus to generalization, and focus on the neural representations and computations that might underpin its role in tasks such as the paired associate inference (PAI) paradigm. We make a principal distinction between two different mechanisms by which the hippocampus may support generalization: an encoding-based mechanism that creates overlapping representations which capture higher-order relationships between different items [e.g., Temporal Context Model (TCM): Howard et al., 2005]—and a retrieval-based model [Recurrence with Episodic Memory Results in Generalization (REMERGE): Kumaran and McClelland, in press] that effectively computes these relationships at the point of retrieval, through a recurrent mechanism that allows the dynamic interaction of multiple pattern separated episodic codes. We also discuss what we refer to as transfer effects—a more abstract example of generalization that has also been linked to the function of the hippocampus. We consider how this phenomenon poses inherent challenges for models such as TCM and REMERGE, and outline the potential applicability of a separate class of models—hierarchical Bayesian models (HBMs) in this context. Our hope is that this article will provide a basic framework within which to consider the theoretical mechanisms underlying the role of the hippocampus in generalization, and at a minimum serve as a stimulus for future work addressing issues that go to the heart of the function of the hippocampus.
Introduction
Empirical work in the field of memory has tended to emphasize the importance of the hippocampus to episodic memory, the capacity to store and recall unique episodes from the past (Scoville and Milner, 1957; Brown and Aggleton, 2001; Burgess et al., 2002; Tulving, 2002; Squire et al., 2004). This research focus has in part been driven by prevailing computational perspectives of the hippocampus as a fast learning system optimized for the rapid storage and retrieval of input patterns, with interference between similar memories minimized through the process of pattern separation (Marr, 1971; McNaughton and Morris, 1987; Treves and Rolls, 1992; O'Reilly and McClelland, 1994; McClelland et al., 1995; O'Reilly and Rudy, 2001; Norman and O'Reilly, 2003; Burgess, 2006). Consequently, the role of the hippocampus in generalization—whereby the structure of a set of related experiences sharing common features is captured and exploited to perform certain tasks—has been relatively understudied from an empirical and theoretical perspective. Here we focus on these issues, which provoke challenging questions about the underlying hippocampal representations and computations that support generalization.
Types of Generalization
The term generalization refers to a broad array of phenomena whereby past experience can be applied to novel settings. A range of experimental paradigms have been developed to characterize the cognitive and neural mechanisms underlying generalization (Posner and Keele, 1968; Nosofsky, 1984; Shepard, 1987; Knowlton and Squire, 1993; Bunsey and Eichenbaum, 1996; Eichenbaum, 2004; Preston et al., 2004; Shohamy and Wagner, 2008; Zeithamova and Preston, 2010). These include tasks involving stimulus generalization (e.g., generalizing reward expectation from a 450 Hz tone to a 500 Hz tone), categorization (e.g., assigning a new stimulus to a category based on its similarity to previously seen stimuli) (Posner and Keele, 1968; Knowlton and Squire, 1993), inferential tasks [e.g., paired associate inference (PAI)] [see (Zeithamova et al., 2012) in this Research Topic], and transfer effects (Kumaran et al., 2009). It is important to note that the hippocampus is not thought to be involved in all forms of generalization—its role in categorization is controversial (Squire et al., 2004; Zaki, 2004), and stimulus generalization does not depend critically on the hippocampus, for reasons that we consider in a later section. Empirical evidence, however, does suggest that the hippocampus plays an important role in a set of “inferential” tasks: the PAI (Bunsey and Eichenbaum, 1996; Preston et al., 2004; Zeithamova and Preston, 2010), transitive inference [e.g., (Dusek and Eichenbaum, 1997; Heckers et al., 2004; Greene et al., 2006; Moses et al., 2006)] and acquired equivalence paradigms (Coutureau et al., 2002; Myers et al., 2003; Shohamy and Wagner, 2008). These experimental settings form the focus of the current article: here successful performance depends on the ability to appreciate the relationship between discrete items presented in a set of related experiences [also see (Zeithamova et al., 2012) in this Research Topic].
Paired Associate Inference (PAI) Paradigm
To frame the discussion of theoretical models of generalization, we first give a brief description of a recently used version of the PAI task [Figure 1A: see (Zeithamova and Preston, 2010) for further details]. Here participants were first instructed to learn the association between many different pairs of objects, which were presented as a single exposure during the training phase of the experiment. Critically, objects were organized into triplets, such that objects pairs were overlapping: for example object B was paired with object A on one trial, but object C on another trial (e.g., pairs AB, BC, XY, YZ). During the test phase of the experiment, subjects needed to generalize: for example, when presented with object A, they were required to select object C, (Figure 1A) over object Z—which was equally familiar (i.e., had been seen once previously) but had been associated with a different set of objects (i.e., X, Y, and Z).
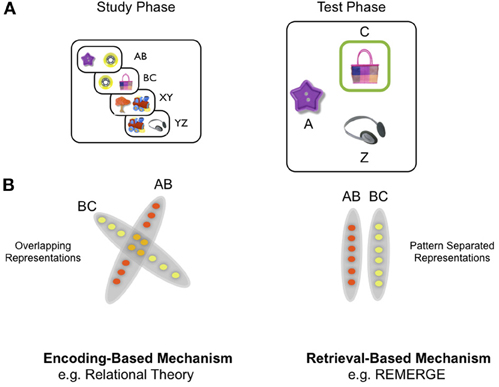
Figure 1. Paired associative inference (PAI) task and schematic of difference between encoding-based and retrieval-based models of inference. (A) Overall design of PAI task: participants see overlapping object pairs during study (e.g., AB, BC) and are required to generalize during the test phase by exploiting indirect relationships between objects (e.g., A—C): see main text for details. (B) Schematic of difference at the representational level between encoding-based and retrieval-based models, exemplified by the relational theory and REMERGE model, respectively. Left panel: encoding-based models (e.g., relational theory: Cohen and Eichenbaum): A—C relationship represented through overlapping conjunctive representations in the hippocampus which are created during the study phase. In this highly simplified illustration, each circle denotes a single neuron (or population of neurons)—red circles denote neurons which code for study episode AB and yellow circles denote those coding for episode BC. Orange circles denote neurons that participate in the representation of both AB and BC episodes (cf. nodal codings—see main text). Neuronal representations of AB and BC are overlapping, as if within a “memory space” (see Eichenbaum et al., 1999). Right panel: Retrieval-based models (e.g., REMERGE: Kumaran and McClelland) emphasize a principle of pattern separation in the hippocampus—depicted in extreme form as zero overlap between related episodes (AB, BC). Indirect relationships are not actually represented, therefore, but computed at the point of retrieval—which in REMERGE occurs through a recurrent mechanism which supports the dynamic interaction of pattern separated codes for related experiences.
Generalization in the PAI task, therefore, involves exploiting the relationship between individual items which are presented in different training experiences (e.g., A—C), and has been shown to depend on the hippocampus (Bunsey and Eichenbaum, 1996). As such, we regard the PAI task as a prototypical example of an inferential task that captures the basic essence of more complex inferential tasks such as the transitivity paradigm, the latter involving more distant relationships between individual items (e.g., the B and E items in a six-item transitivity task). We, therefore, use the PAI task to provide a simple scenario in which to illustrate the different ways in which the hippocampus may contribute to generalization. Whilst we emphasize the conceptual similarity among inferential tasks (e.g., PAI and transitivity paradigm), it is worth noting that there are substantial procedural differences between them. As such, we acknowledge that any single mechanism is unlikely to be able to account for a capacity for inference across these settings: indeed, it has often been argued that multiple mechanisms may mediate successful performance in any given cognitive task (e.g., Poldrack and Packard, 2003).
Overview of Different Mechanisms of Hippocampal Generalization
We next consider possible mechanisms by which the hippocampus may support generalization in the PAI task [also see (Zeithamova et al., 2012) in this Research Topic]. Of note, it is worth emphasizing that the phenomenon of interest, and the underlying mechanisms we consider, relate to what could be termed “rapid generalization” i.e., where generalization is based on only limited numbers of trials often within a single experimental session. In contrast, backpropagation neural networks designed to simulate learning in the neocortex, though powerful at discovering and representing the structure present in a set of training experiences, are viewed to learn too slowly to merit consideration in the context of tasks such as the PAI paradigm, being more naturally suited to accounting for the acquisition of knowledge during childhood (Rumelhart, 1990; McClelland et al., 1995; Rogers and McClelland, 2004).
Our focus in subsequent sections is on providing a conceptual overview of models of hippocampal generalization, and illustrating their key operating principles in the context of the PAI task. The empirical work which forms the basis for these models is reviewed in a companion article in this Research Topic (Zeithamova et al., 2012). In other work, the results of quantitative simulations of empirical data of the PAI and related tasks are discussed—in addition to divergent predictions between these competing accounts [Temporal Context Model (TCM): Howard et al., 2005; Recurrence with Episodic Memory Results in Generalization (REMERGE) (Kumaran and McClelland, in press)].
We make a principal distinction between two classes of models, which exemplify the fundamentally different ways by which the hippocampus might support generalization (Figure 1B): (1) “encoding-based overlap” models (Eichenbaum et al., 1999; Howard et al., 2005; Shohamy and Wagner, 2008; Zeithamova and Preston, 2010) [also see (O'Reilly and Rudy, 2001)]: these create representations during the training/study phase of the task that capture the higher-order relationships between individual items during training (e.g., A—C in the PAI task)—through the use of overlapping neuronal codes for related episodes. (2) “retrieval-based” models (Kumaran and McClelland, in press) [also see (Wu and Levy, 2001)]: in contrast to encoding-based models, these models tend to emphasize the role of the hippocampus in pattern separation, which effectively acts to minimize the overlap between neural codes for related episodes during training. A capacity for inference, therefore, emerges at the point of retrieval—in the case of the REMERGE model (see below), through a recurrent mechanism—which allows multiple pattern separated codes for related conjunctive experiences (i.e., AB, BC pairs in PAI task) to interact, and therefore support inference.
Encoding-Based Overlap Models of Inference
This class of qualitative (Eichenbaum et al., 1999; Shohamy and Wagner, 2008; Zeithamova and Preston, 2010) and quantitative (Howard et al., 2005) models, as well as other broadly related perspectives [autoencoder model of the hippocampus (Gluck and Myers, 1993; Gluck et al., 2003)], all suggest that it is the overlap of hippocampal neural codes for related experiences that is critical to generalization. For instance, according to the integrative encoding hypothesis (Shohamy and Wagner, 2008; Zeithamova and Preston, 2010) it is argued that a new experience (e.g., the pair of objects B and C in the PAI task) triggers the retrieval through pattern completion of related episodes from the past (i.e., the object pair AB). The concurrent activation of multiple episodes (i.e., AB, BC) results in the formation of an integrated representation in the hippocampus (i.e., ABC) that directly links the relevant items, and acts as a basis for generalization and inference. Further, according to the relational theory (Cohen and Eichenbaum, 1993; Eichenbaum et al., 1999), a prominent account that has long espoused the importance of the hippocampus to generalization, this process is viewed to occur as part of the networking of experience codes within a “memory space” (Eichenbaum et al., 1999) (Figure 1B). In this way, it is proposed that the structure of a set of experiences may be captured and directly represented in the hippocampus.
The TCM, originally developed to account for essential properties of behavioral data on tasks involving free recall (Kahana, 1996; Howard et al., 2005; Polyn and Kahana, 2008; Sederberg et al., 2008; Polyn et al., 2009), can be considered a formal encoding-based account of the hippocampal role in generalization (Howard et al., 2005). Whilst links between the relational theory and TCM have been previously noted (Wallenstein et al., 1998; Howard et al., 2005), we are not aware of this point having been made in relation to the more recently formulated integrative encoding hypothesis (Shohamy and Wagner, 2008). Nevertheless, it is worth noting that the integrative encoding account, like TCM, also emphasizes the point that generalization depends on the creation of new representations during training that in some way capture the structure of the task (Shohamy and Wagner, 2008).
Temporal Context Model (TCM)
Briefly, TCM consists of two main layers, an item layer (f) and a contextual layer (t) (Figure 2A). Connections from the item to context layer are specified in the matrix MFT, whilst those from the context to item layer are stored in matrix MTF. As such, the presentation of items to the feature layer can cue the recall of previous states of context, and contextual states can also cue items. In TCM, therefore, the evolution of context is driven by the activation of items, rather than through random drift as is usually the case in contextual models (e.g., see Polyn and Kahana, 2008 for review). New learning occurs by updating matrices MFT and MTF as items are linked, typically through a simple Hebbian rule, to the current contextual state. In TCM, therefore, associations between individual items (e.g., A and B in the PAI task) are mediated by their shared context, rather than through direct item–item associations. At the stage of retrieval, therefore, items are retrieved as a function of their similarity to the current state of context. Although many items may be retrieved to some extent by the contextual cue, a competitive mechanism [e.g., leaky competing accumulator model (Sederberg et al., 2008), or luce choice rule (Polyn and Kahana, 2008)], ensures that only one item is recalled at a time. The winning item in turn is used as a cue to the contextual layer.
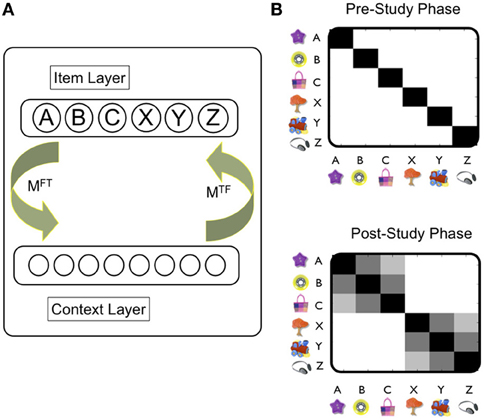
Figure 2. Temporal Context Model (TCM): overview of operation and representations. (A) The TCM: Howard et al., 2005: there are two main layers (Item, Context). Training trials are presented as input to the item layer. MFT indicates connections between item and context layer. MTF indicates connections between context and item layer. Hebbian learning typically used to update these connections. See main text for details. (B) Similarity (i.e., overlap) of representations over the context layer induced by each object captures direct (e.g., A-B) and indirect associations (e.g., A—C). White shading indicates a value of zero, and black a value of one. Prior to the experiment, the contextual states activated by each objects are assumed to be orthogonal to each other—denoted by black shading only across the diagonal (upper figure). After the study phase, the contextual representations induced by objects in a triplet (A, B, C) have now become similar to each other—but not to objects in other triplets (e.g., X, Y, Z). Critically, this is the case for contextual representations associated with A and C objects [i.e., denoted by shading in [A, C] square: even though these objects were presented in different study pairs (i.e., AB, BC)]. It is worth noting that the similarity between objects presented in the same study pair (e.g., A, B) is greater than that between different pairs (i.e., A, C). Note that the similarity between different objects reflects the dot product between vectors specifying the contextual representation associated with each object. See Howard et al., 2005 for implementational details of the TCM model.
Whilst initially intended as a model of episodic memory, TCM has more recently been applied to generalization-related phenomena such as the PAI paradigms and transitive inference paradigms (Howard et al., 2005). We illustrate the basic mechanism by which TCM works in the setting of the PAI task (Figure 2B): during the study phase, experiences involving the AB pair induce new learning in the associative connections between item and contextual layer such that the contextual representation associated with items A and B comes to shares common features due to their temporal co-occurrence. Importantly, this process means that the contextual states associated with non-adjacent items (e.g., A and C) also evolves through learning to be similar to one another: a BC pair, for example, tends to cue the reinstatement of the contextual state associated with the presentation of the AB pair. Consequently, the contextual state to which item C becomes bound shares features with that of item A. Over the course of the study phase, therefore, the similarity structure of the contextual states cued by each of the individual items comes to reflect the indirect relationships between items in overlapping pairs: e.g., the contextual state cued by object A is more similar to that cued by object C (cf. object Z). Importantly, new item-contextual learning in the model is proposed to be hippocampal-dependent, which is therefore, viewed to be critical to the development of representations that capture the higher-order structure of the task—and therefore, generalization.
TCM, therefore, forms overlapping item-contextual representations during the study phase of the PAI paradigm that code the indirect relationships between items in adjacent pairs (e.g., A—C). Notably, the generalization capacity of TCM extends beyond the PAI task—for example to the transitive inference task, where TCM is able to capture more distant relations between individual items within a linear hierarchy (e.g., B and E). Indeed, TCM is also not restricted to supporting the representation of linear structures, and can be shown to capture the higher order structure of semantic datasets (Howard et al., 2010), in a fashion that bears relation to the technique of latent semantic analysis (see Howard et al., 2005).
Encoding-Based Models vs. Pattern Separation?
Encoding-based models, therefore, propose that the hippocampus is critical to generalization because it creates representations that directly reflect the relationships between items presented in a set of experiences—through the use of overlapping neuronal codes [cf. nodal codings: (Eichenbaum et al., 1999)] that are “similarity-capturing” in nature. Notably, however, such a coding scheme contrasts markedly with highly influential computational accounts arguing that the hippocampus, and in particular the DG subregion (Leutgeb et al., 2007; Deng et al., 2010), acts to orthogonalize similar input patterns—effectively using a “similarity-reducing” coding scheme to discard the commonalities between related experiences (e.g., AB, BC)—so as to minimize interference within a system optimized for episodic memory (Marr, 1971; McNaughton and Morris, 1987; Treves and Rolls, 1992; O'Reilly and McClelland, 1994; McClelland et al., 1995). Indeed, the specific anatomical [i.e., divergent projection from the downstream entorhinal cortex (ERC)] and physiological properties (i.e., sparse activity) of the dentate gyrus have been often viewed as making this subregion of the hippocampus ideally suited to performing the process of orthogonalization/pattern separation (Treves and Rolls, 1992). Though in reality hippocampal pattern separation is not viewed to be perfect, the apparent tension between computational accounts of the hippocampus as an episodic memory system and encoding-based models of generalization raises the question of whether efficient generalization might nevertheless be possible in the context of pattern separated episodic codes viewed to exist within the hippocampus. In the next section, we provide a high-level overview of the essential operating principles of a recently developed retrieval-based model of the hippocampal contribution to inference: REMERGE (Kumaran and McClelland, in press), which suggests that this may be the case.
Retrieval-Based Models of Inference
Crucially REMERGE retains a principle of pattern separation in the hippocampus and involves a recurrent mechanism operating at the retrieval stage that supports the dynamic interaction of multiple pattern separated codes for related experiences (e.g., AB, BC). Whilst a previous retrieval-based model based on the storage of temporal sequences, has been shown to be perform generalization, this has only been demonstrated within a specific paradigm (i.e., the transitive inference task)—leaving open the question of whether a capacity for generalization would be supported in a wider setting (Wu and Levy, 2001).
The core architecture of our model, which reflects a synthesis of interactive activation competitive (IAC) networks (McClelland and Rumelhart, 1981) and exemplar models of memory (Medin and Schaffer, 1978; Nosofsky, 1984; Hintzman, 1986), can be regarded as a simplification of the multi-stage circuitry of the hippocampal system into two principal layers: a feature layer and a conjunctive layer, broadly ascribed to the ERC and the hippocampus proper, respectively. The model instantiates key principles shared by prevailing computational accounts of the hippocampus: (1) pattern separated representations in the dentate gyrus/CA3 regions of the hippocampus (Marr, 1971; McNaughton and Morris, 1987; Treves and Rolls, 1992; O'Reilly and McClelland, 1994; McClelland et al., 1995)—each individual training episode (e.g., AB, BC, XY, YZ in the PAI task) is represented in the network by a localist unit in the conjunctive layer (see Figure 3)—mirroring a principle of optimal pattern separation in the hippocampus, where conjunctive codes for related experiences are rendered orthogonal to one another. (2) Componential codes in neocortical regions such as the ERC (e.g., coding for items A, B, C, X, Y, Z in the PAI task)—which are ascribed to the feature layer of the model, and viewed to derive from the operation of a slow-learning neocortical system (McClelland et al., 1995; McClelland and Goddard, 1996).
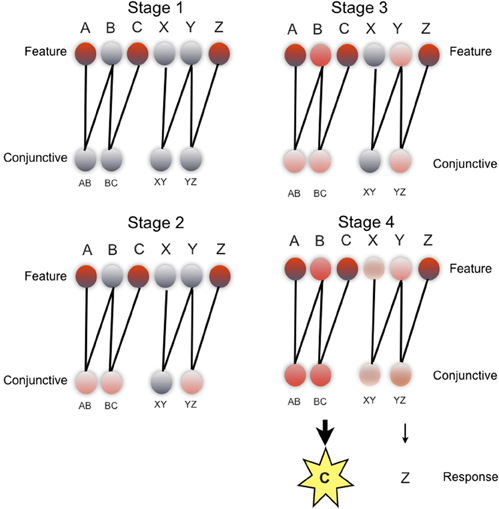
Figure 3. REMERGE model: schematic of evolution of network activity during a ACZ test trial in the paired associate inference task. Each stage illustrates pattern of network activity over feature layer (upper) and conjunctive layer (lower), during key phases of processing (see main text for details). Feature layer units (upper) denote individual objects (i.e., A, B, C, X, Y, Z). Conjunctive layer units (lower) code pairs of objects presented during the study phase of the experiment, in localist fashion (i.e., AB, BC, XY, YZ). Feature layer and conjunctive layer connected by recurrent excitatory connections. Response layer not shown. Unit activity denoted by color: from gray (low activity) to red (high activity). Details of transfer functions and parameters used in the network, and quantitative simulations of empirical data are described elsewhere (Kumaran and McClelland, in press).
The model, however, diverges from traditional perspectives of the hippocampal system as a unidirectional feedforward circuit, where information is thought to flow from associational areas of the neocortex in a single pass through the ERC (superficial layers)/DG/CA3/CA1/subiculum in sequential stages, finally, being projected via the deep layers of the ERC back to the neocortex (Treves and Rolls, 1992; Amaral and Lavenex, 2006). Critically, therefore, REMERGE incorporates a principle of “big-loop” recurrence, between the hippocampus proper (e.g., DG/CA3) and neocortical regions such as the ERC, which allows a recirculation of the output as a successive input to the system. Notably, our notion of big-loop recurrence draws on anatomical and physiological evidence—for example, the anatomical connections known to exist between the superficial and deep layers of the ERC (van Strien et al., 2009)—and differs from the internal recurrence known to exist within the CA3 region, which has been presumed to exist within a globally unidirectional (cf. recurrent) hippocampal system. Whilst internal CA3 recurrence is agreed to be critical to the reinstatement (i.e., pattern completion) of individual episodic memories (Marr, 1971; Treves and Rolls, 1992; McClelland et al., 1995; Nakazawa et al., 2003; Burgess, 2006), big-loop recurrence is needed to allow multiple pattern separated codes for related conjunctive experiences to interact in the service of generalization (see below).
To bring out more clearly the mechanism by which generalization is achieved, we consider how REMERGE performs inference in the PAI task (Figure 3), during an ACZ test trial (Figure 1A) where successful performance requires the choice of object C over object Z, based on the indirect association of objects A and C. Whilst in reality, the network operates continuously over a number of timesteps (e.g., 300), for illustrative purposes we provide a conceptual description of the activity patterns that arise in the network over successive key stages of processing.
In stage 1 (Figure 3: top left), the presentation of external input to the A, C, and Z units on the feature layer causes the activity of these units to rise. In stage 2 (Figure 3: bottom left), the activity of these feature units flows forward to the conjunctive layer and drives a rise in activation of three conjunctive units: AB, BC, YZ—all of which code for training episodes that share one feature with the test input (i.e., ACZ). Indeed, the initially equal activity of these three units can be interpreted in more formal terms as reflecting the equivalent similarity of each of the relevant training episodes to the current test input as computed by a classical exemplar models (Nosofsky, 1984). What happens in stage 3 (Figure 3: top right) is critical to the network's ability to perform inference: the recurrent excitatory connections allow the pattern of activity over the conjunctive layer to drive a new pattern of activity over the feature layer that includes activation of the B and Y units which do not receive any external inputs. Critically, the activity of the B unit in the feature layer rises above that of the Y unit because the B unit receives convergent drive from both the AB and BC conjunctive units (cf. the Y unit—only input from YZ unit). In stage 4 (Figure 3: bottom right), the greater activity of the B (cf. Y) unit combined with a form of inhibitory competition operating over the conjunctive layer causes the activity of the AB and BC conjunctive units to rise above that of the YZ and XY, units. It is this graded pattern of activity over multiple conjunctive units that leads the network to correctly choose C over Z in the response layer (not shown), with the greater activity of the BC unit, as compared to the YZ unit, resulting in the selection of C.
More formally, the operation of the network can be interpreted as involving a process of recurrent similarity computation: whereby similarity computation to be performed not only on externally presented sensory inputs, as is the case in classical exemplar models in which REMERGE is grounded (Nosofsky, 1984), but also on new feature layer activity patterns constructed by the network. In this respect, it is worth noting that a classical exemplar model (Nosofsky, 1984) would not typically support a capacity for inference in the PAI task: processing would effectively be complete in such a model at stage 2 (Figure 3), resulting an equal tendency to choose C or Z in the ACZ trial. REMERGE is only able to support inference in the PAI and related tasks through the operation of recurrence, which effectively allows it to exploit the higher-order structure present within a set of related episodes where pairwise similarities alone are uninformative (also see below).
Our aim here has been to provide an intuitive overview of how REMERGE operates, by illustrating the basic mechanism by which it performs inference using the setting of the PAI task. In other work, we consider the performance of REMERGE in relation to empirical data in the PAI, acquired equivalence and transitive inference tasks, as well as other generalization-related phenomena [e.g., categorization (Kumaran and McClelland, in press)]. There, we also consider other implications of our model. We discuss how REMERGE offers a parsimonious mechanism for how a capacity for inference may emerge through training [e.g., in the transitive inference task (Moses et al., 2006)], simply through an increase in the strength of weights coding individual memories formed during the training/study phase (e.g., AB, BC). We also suggest that the reason why some subjects generalize successfully, and others poorly, in such tasks [e.g., in the acquired equivalence and PAI tasks (Shohamy and Wagner, 2008; Zeithamova and Preston, 2010)] may be accounted for by positing a difference the strength of premise pair memories—rather than necessitating a qualitative difference in terms of the nature of neural representations (i.e., integrated representations in the good group only: Shohamy and Wagner, 2008). Our model also has implications for perspectives on the nature and function of hippocampal replay activity that occurs during offline periods (e.g., slow-wave sleep). Conventionally, hippocampal replay activity is thought to consist of the reactivation of a CA3 ensemble representing a single conjunctive experience (e.g., sequence of locations visited), which is transmitted to the neocortex (Buzsaki, 1989; Wilson and McNaughton, 1994; McClelland et al., 1995; O'Neill et al., 2010). Our perspective, which holds big-loop recurrency as central to the function of the hippocampal system, predicts that hippocampal replay activity may under certain conditions be “generalized” in nature, reflecting the replay of multiple-related episodes, a notion that receives initial support from empirical evidence (Gupta et al., 2010).
Encoding-Based vs. Retrieval-Based Mechanisms
We have sought to highlight that REMERGE achieves inference in a fundamentally different fashion from the class of encoding-based models described above. In REMERGE, inference can be considered as an emergent phenomenon—through the linkage of related pattern separated episodes occurring “on the fly,” within a dynamically created memory space that is effectively created at the point of retrieval (i.e., during a test trial) through recurrence. In contrast to encoding-based models (Eichenbaum et al., 1999; Howard et al., 2005; Shohamy and Wagner, 2008), therefore, the distant relationship between items experienced in different episodes (e.g., A—C) is not actually represented in any part of the REMERGE network—nor is the relationship between adjacent study episodes (e.g., AB, BC) captured through the actual overlap of their respective conjunctive codes.
It is important, however, to bear in mind that despite their fundamental differences, encoding- and retrieval-based models have much in common: indeed, REMERGE can be considered to marry key insights of a relational view of memory (Cohen and Eichenbaum, 1993; Eichenbaum et al., 1999; Eichenbaum, 2004) (i.e., compositionality of conjunctive memories, critical contribution of the hippocampus to generalization through linking of episodes within a memory space) with prevailing computational theories that the hippocampus is optimized to be an efficient episodic memory system (i.e., rapid learning of pattern separated conjunctive representations) (Marr, 1971; McNaughton and Morris, 1987; McClelland et al., 1995). Further, it may be the case that in reality the distinction between retrieval-based and encoding-based models is not absolute—indeed, generalized replay activity occurring within a recurrent hippocampal system (see above) may facilitate the recombination of multiple-related episode, which could potentially result in the creation of new representations that directly capture distant relationships between items (cf. encoding-based mechanisms) (see Kumaran and McClelland, in press).
At a more basic level, encoding and retrieval-based mechanisms both emphasize that the hippocampus is critical to generalization in tasks that involve exploiting the higher-order structure present within a set of tasks. This point speaks to the question of why certain forms of generalization (e.g., stimulus generalization, categorization) seem to be relatively, though perhaps not entirely (Zaki, 2004), hippocampal-independent—and other forms to rely critically upon the hippocampus (e.g., PAI). What is needed in inferential tasks, but not tasks such as categorization (Squire et al., 2004) [but see (Zaki, 2004)], is the ability to detect higher-order similarities, or relationships, which exist between items (e.g., A—C) presented within a structured set of episodes. We suggest that this capacity, which REMERGE formally provides through the process of recurrent similarity computation, and which encoding-based models more broadly capture through the use of overlapping representations, may explain the primary contribution of the hippocampus to inference.
Transfer Effects: A Different Form of Generalization
In the last section, we consider a quite different form of generalization from that examined thus far—a phenomenon which we refer to as “transfer,” which has also recently been linked to the function of the hippocampus (Kumaran et al., 2009). We do this to examine whether, and how, models of hippocampal inference such as TCM and REMERGE are capable of generalization in such a setting, and to consider alternative schemes for successfully solving this kind of problem.
We illustrate the essence of a transfer effect with a hypothetical experiment using the transitive inference task, an intuitive task in which to consider this phenomenon—indeed one might also construct an analogous scenario using the PAI task. Participants would first learn the linear ordering of a set of items in the “initial” experimental session [see (Zeithamova et al., 2012) for overview of the transitive inference task]. Then one could examine their ability to transfer their performance to a new setting where the task structure is the same (i.e., linear hierarchy), but the stimuli novel. If the performance of participants in the perceptually novel setting was significantly improved (cf. initial session), over and above any non-specific skill effect, then this would suggest that they had acquired knowledge about the structure of the task (i.e., linear hierarchy) in the initial session which could be transferred to the perceptually novel setting. Whilst no such experiments have been performed to our knowledge using the transitive, PAI, or acquired equivalence tasks—successful transfer has been demonstrated in a conceptually related experimental task which has also been shown to be hippocampal-dependent: here we term this task the “associative weather prediction (AWP) task” (Kumaran et al., 2009) (also see: Kumaran et al., 2007).
We restrict our focus to the aspects of this experiment relevant to the issue of transfer: in the intial session, participants were required to learn the outcome (i.e., sun or rain) associated with a set of individual patterns, created from combinations of four different fractals (Figure 4A). Notably, there was an underlying task structure that efficiently captured the relevant contingencies—e.g., that fractal 1 on the left predicted sun regardless of the identity of the central shape. Participants demonstrated a behavioral transfer effect that was evident as superior learning performance in a perceptually novel (“new”) session—where the fractals were novel, though critically the underlying task structure the same. Interestingly, this behavioral transfer effect could be linked to neural activity in the hippocampus in two ways (Figure 4B) (Kumaran et al., 2009): firstly, activity in the left hippocampus during the initial session showed a significant between-subject correlation with performance in the New session. Importantly, this correlation was specific to transfer, and remained significant even once effects of performance during the Initial session had been partialled out. Further, we observed that activity in the left posterior hippocampus showed a significantly stronger correlation with successful performance during the New (cf. Initial) session (for further discussion, see Kumaran and McClelland, in press).
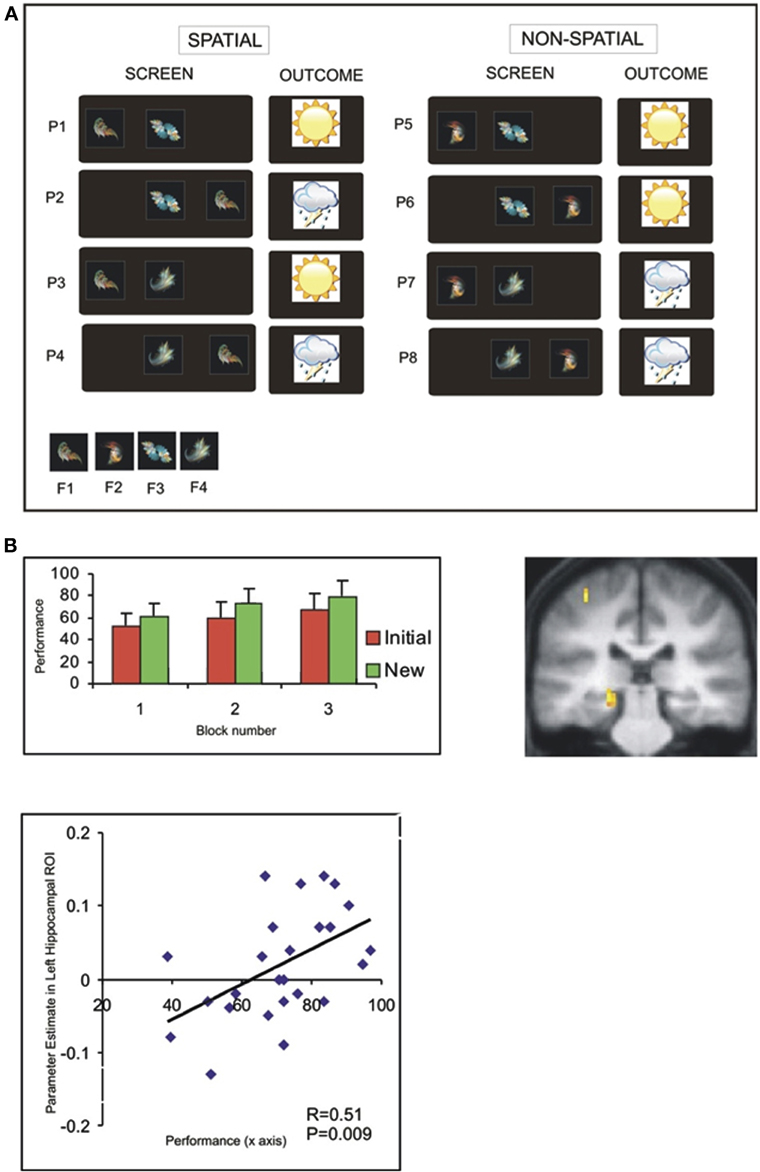
Figure 4. Associative weather prediction task: task structure and evidence that neural activity in hippocampus correlates with transfer ability (Kumaran et al., 2009). (A) Depiction of eight patterns presented during training: the terms “spatial” and “non-spatial” refer to the type of information which determines the outcome (i.e., shape-location, or shape-shape, respectively). (B) Behavioral evidence of superior performance in New session (left). Neural activity in left posterior hippocampus shows greater correlation with performance in New session cf. Initial session (right). Significant between-subjects correlation between activity in left hippocampus (averaged across anatomical ROI) during Initial session and performance in New session (see Kumaran et al., 2009 for details).
These findings provide initial evidence implicating the hippocampus in supporting generalization to a setting that is entirely novel from a perceptual point of view, but shares the same abstract underlying structure. Whilst it would be illuminating to test the role of the hippocampus in supporting transfer in other settings, perhaps including inferential tasks such as the transitivity paradigm, it is interesting to ask how this kind of generalization phenomena might be mediated, and in particular to consider this question in relation to the models already discussed (i.e., TCM, REMERGE).
A key issue in this respect is that transfer effects of this type must depend in some way on abstract representations of the task structure that are not inherently linked to specific stimuli (“stimulus-bound”). This poses a substantial challenge for the encoding-based and retrieval-based models outlined: both REMERGE and TCM are by nature stimulus-bound, a property often shared by connectionist style models of cognition [although see (Hinton et al., 1986; Flusberg et al., 2011)]. For example, TCM, through the very nature of its operation, derives representations of the task structure that are intimately linked to the actual stimuli experienced during the training phase (i.e., items A, B, C … F in a transitivity paradigm) (Howard et al., 2005). This raises the question of how such models could account for transfer effects. One speculative possibility is that interactions between the hippocampus and another region such as the prefrontal cortex might perhaps allow the stimulus-bound representations derived by TCM or REMERGE to be transformed into a more abstract coding scheme, for example one that is symbolic in form (cf. language), that would then be useful for supporting transfer effects.
Hierarchical Bayesian Model
Whilst extensions of REMERGE and TCM could potentially be developed to encompass transfer effects, it is worth noting that a class of models exists that more naturally account for this phenomena—hierarchical Bayesian models [HBMs: (Kemp and Tenenbaum, 2008)] (Figure 5). Though the HBM developed by Kemp and Tenenbaum has generally been considered in a different context—for example how conceptual knowledge (e.g., the properties of different animals) is acquired and represented (Kemp and Tenenbaum, 2008, 2009)—we suggest that they could be fruitfully applied to the kinds of rapid generalization tasks discussed in this article. Indeed, they would seem to have a number of attractive features, which make them well suited to offering insights into how transfer effects in the AWP paradigm—and other tasks such as the transitive inference paradigm—could potentially be accounted for.
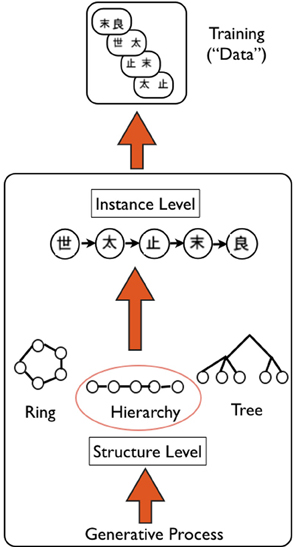
Figure 5. Schematic of Hierarchical Bayesian Model (HBM), as applied to transitive inference task. Overview of the generative HBM of Kemp and Tenenbaum (2008): the model is specified at two levels: a high “structure” level that specifies the type of structure that best explains data—in this case a hierarchy of kanji characters (e.g., used in experiment by Greene et al., 2006)—a generative process based on graph grammars is used to create a library of possible structures. A lower “instance” level specifies the exact version of the structure that is most likely given the data—in this case A>B>C>D>E. The model simultaneously finds the best structure and instance that likely accounts for the data. Upward arrows indicate the generative nature of the HBM.
We provide a high level overview of the key principles of the HBM developed by Kemp and Tenenbaum (2008). The key question addressed by the model is how structure present in a set of data can be discovered. The problem is posed at two separate levels (Figure 5): the higher level problem is to identify the type of structural form (e.g., hierarchy, tree, cluster) with the lower level problem then to define the instance of this form that best explains the available data. A simple generative model is used to “grow” structural forms, using a language of graph grammars. This process can be used to produce simple structures such as linear orders and trees, as well as more complex forms. The discovery of structure is then specified computationally as a process of probabilistic inference, involving simultaneously finding the appropriate structure and “instance” that best explain the observed data. As is typically the case in Bayesian inference, simpler models are preferred over more complex models. As an example, the authors consider data relating to the attributes of a number of species of animals, actually obtained from human judgments. The model successfully finds that the structural form that best explains the data is a tree, and defines the instance of this tree which correctly represents categories at different levels of resolution (e.g., birds vs. primates, insects vs. flying insects) (Kemp and Tenenbaum, 2008). Of note, the model can handle different types of data: from those denoting the attributes of items, to relational data, and similarity matrices.
The HBM, therefore, benefits from specification at both an abstract (i.e., type of structure) and a stimulus-bound (i.e., instance) level. In this way, they would seem to provide an intuitively appealing way of accounting for the kinds of abstract transfer effects discussed above. In the AWP task, or putatively in the transitivity paradigm, speeded learning in the New session might be simulated by increasing the prior (i.e., likelihood) over the type of structure which was found to best capture the relationship between different experiences in the Initial session. Armed with this prior knowledge, participants might more readily be able to solve the AWP task in the New session, given that the problem has now been reduced to discovering the appropriate instance (i.e., involving perceptually novel fractals) of a known form.
Whilst HBMs are powerful engines of structure discovery in high dimensional datasets, and may potentially offer insights into the mechanisms underlying behavioral transfer effects, it is also important to bear in mind possible limitations: firstly, the ability of HBMs to produce an infinite number of structural forms, and weight these hypotheses appropriately to reflect prior knowledge, can be both an advantage in terms of offering flexibility, but also raises questions. For example, one could ask how the space of possible hypotheses and the prior probability distribution over them is specified. Secondly, HBMs offer an abstract description of the basic algorithms necessary to perform inference, akin to Marr's computational level (Marr, 1971; McClelland et al., 2010). As such they are agnostic with regards to the underlying cognitive mechanisms and neural circuitry that supports such processes. In their present form, therefore, Bayesian probabilistic models do not speak to the issue of how the hippocampus might support transfer effects. In contrast REMERGE and TCM, which can both be implemented using a connectionist neural network scheme [e.g., TCM: (Sederberg et al., 2008)], have been more closely linked to the function of the hippocampus (Howard et al., 2005; Kumaran and McClelland, in press). As such, the potential advantages and disadvantages of HBMs can be related to a wider debate on the relative virtues of structured probabilistic and connectionist style models e.g., (McClelland et al., 2010)—indeed, it will be important for future work to consider whether, and how, a synthesis of ideas from both classes of models may contribute to a wider understanding of the mechanisms underlying the hippocampal contribution to generalization.
Concluding Comments
In this article, we have emphasized the importance of the hippocampus to generalization, in contrast to traditional perspectives that have long focussed on its role in episodic memory. We have considered two basic classes of mechanisms that have been proposed to underpin the hippocampal contribution to generalization, and highlighted the fundamental differences between these models in the context of a prototypical inferential task, the PAI task. The aim has been to provide a conceptual overview of two formal models, which exemplify the principal distinction made between encoding-based and retrieval-based mechanisms: the TCM and REMERGE, respectively. Our hope is that this article will provide a basic framework within which to consider the theoretical mechanisms underlying the role of the hippocampus in generalization, and stimulate future empirical and theoretical work in this relatively understudied area.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This was funded by a Wellcome Trust Fellowship. I am grateful to two anonymous reviewers for constructive comments on earlier versions of the manuscript.
References
Amaral, D. G., and Lavenex, P. (2006). “Hippocampal neuroanatomy,” in The Hippocampus Book, eds T. Bliss, P. Andersen, D. G. Amaral, R. G. Morris, and J. O'Keefe (Oxford, UK: Oxford University Press), 37–115.
Brown, M. W., and Aggleton, J. P. (2001). Recognition memory: what are the roles of the perirhinal cortex and hippocampus? Nat. Rev. Neurosci. 2, 51–61.
Bunsey, M., and Eichenbaum, H. (1996). Conservation of hippocampal memory function in rats and humans. Nature 379, 255–257.
Burgess, N. (2006). “Computational models of the spatial and mnemonic functions of the hippocampus,” in The Hippocampus Book, eds T. Bliss, P. Andersen, D. G. Amaral, R. G. Morris, and J. O'Keefe (Oxford, UK: Oxford University Press), 715–751.
Burgess, N., Maguire, E. A., and O'Keefe, J. (2002). The human hippocampus and spatial and episodic memory. Neuron 35, 625–641.
Buzsaki, G. (1989). Two-stage model of memory trace formation: a role for “noisy” brain states. Neuroscience 31, 551–570.
Cohen, N. J., and Eichenbaum, H. (1993). Memory, Amnesia and the Hippocampal System. Cambridge, MA: MIT Press.
Coutureau, E., Killcross, A. S., Good, M., Marshall, V. J., Ward-Robinson, J., and Honey, R. C. (2002). Acquired equivalence and distinctiveness of cues: II. Neural manipulations and their implications. J. Exp. Psychol. Anim. Behav. Process. 28, 388–396.
Deng, W., Aimone, J. B., and Gage, F. H. (2010). New neurons and new memories: how does adult hippocampal neurogenesis affect learning and memory? Nat. Rev. Neurosci. 11, 339–350.
Dusek, J. A., and Eichenbaum, H. (1997). The hippocampus and memory for orderly stimulus relations. Proc. Natl. Acad. Sci. U.S.A. 94, 7109–7114.
Eichenbaum, H. (2004). Hippocampus: cognitive processes and neural representations that underlie declarative memory. Neuron 44, 109–120.
Eichenbaum, H., Dudchenko, P., Wood, E., Shapiro, M., and Tanila, H. (1999). The hippocampus, memory, and place cells: is it spatial memory or a memory space? Neuron 23, 209–226.
Flusberg, S. J., Thibodeau, P. H., Sternberg, D. A., and Glick, J. J. (2011). A connectionist approach to embodied conceptual metaphor. Front. Psychol. 1:197. doi: 10.3389/fpsyg.2010.00197
Gluck, M. A., Meeter, M., and Myers, C. E. (2003). Computational models of the hippocampal region: linking incremental learning and episodic memory. Trends Cogn. Sci. 7, 269–276.
Gluck, M. A., and Myers, C. E. (1993). Hippocampal mediation of stimulus representation: a computational theory. Hippocampus 3, 491–516.
Greene, A. J., Gross, W. L., Elsinger, C. L., and Rao, S. M. (2006). An FMRI analysis of the human hippocampus: inference, context, and task awareness. J. Cogn. Neurosci. 18, 1156–1173.
Gupta, A. S., Van Der Meer, M. A., Touretzky, D. S., and Redish, A. D. (2010). Hippocampal replay is not a simple function of experience. Neuron 65, 695–705.
Heckers, S., Zalesak, M., Weiss, A. P., Ditman, T., and Titone, D. (2004). Hippocampal activation during transitive inference in humans. Hippocampus 14, 153–162.
Hinton, G. E., McClelland, J. L., and Rumelhart, D. E. (1986). “Distributed representations,” in Explorations in the Microstructure of Cognition (Cambridge, MA: MIT Press), 77–109.
Hintzman, D. L. (1986). “Schema Abstraction” in a multiple-trace memory model. Psychol. Rev. 93, 411–428.
Howard, M. W., Fotedar, M. S., Datey, A. V., and Hasselmo, M. E. (2005). The temporal context model in spatial navigation and relational learning: toward a common explanation of medial temporal lobe function across domains. Psychol. Rev. 112, 75–116.
Howard, M. W., Shankar, K. H., and Jagadisan, U. K. (2010). Constructing semantic representations from a gradually-changing representation of temporal context. Top. Cogn. Sci. 3, 48–73.
Kemp, C., and Tenenbaum, J. B. (2008). The discovery of structural form. Proc. Natl. Acad. Sci. U.S.A. 105, 10687–10692.
Kemp, C., and Tenenbaum, J. B. (2009). Structured statistical models of inductive reasoning. Psychol. Rev. 116, 20–58.
Knowlton, B. J., and Squire, L. R. (1993). The learning of categories: parallel brain systems for item memory and category knowledge. Science 262, 1747–1749.
Kumaran, D., Hassabis, D., Spiers, H. J., Vann, S. D., Vargha-Khadem, F., and Maguire, E. A. (2007). Impaired spatial and non-spatial configural learning in patients with hippocampal pathology. Neuropsychologia 45, 2699–2711.
Kumaran, D., Summerfield, J. J., Hassabis, D., and Maguire, E. A. (2009). Tracking the emergence of conceptual knowledge during human decision making. Neuron 63, 889–901.
Kumaran, D., and McClelland, J. L. (in press). Generalization through the recurrent interaction of episodic memories: a model of the hippocampal system. Psychol. Rev.
Leutgeb, J. K., Leutgeb, S., Moser, M. B., and Moser, E. I. (2007). Pattern separation in the dentate gyrus and CA3 of the hippocampus. Science 315, 961–966.
Marr, D. (1971). Simple memory: a theory for archicortex. Philos. Trans. R. Soc. Lond., B Biol. Sci. 262, 23–81.
McClelland, J. L., Botvinick, M. M., Noelle, D. C., Plaut, D. C., Rogers, T. T., Seidenberg, M. S., and Smith, L. B. (2010). Letting structure emerge: connectionist and dynamical systems approaches to cognition. Trends Cogn. Sci. 14, 348–356.
McClelland, J. L., McNaughton, B. L., and O'Reilly, R. C. (1995). Why there are complementary learning systems in the hippocampus and neocortex: insights from the successes and failures of connectionist models of learning and memory. Psychol. Rev. 102, 419–457.
McClelland, J. L., and Goddard, N. H. (1996). Considerations arising from a complementary learning systems perspective on hippocampus and neocortex. Hippocampus 6, 654–665.
McClelland, J. L., and Rumelhart, D. E. (1981). An interactive activation model of context effects in letter perception: part 1 an account of the basic findings. Psychol. Rev. 88, 375–407.
McNaughton, B. L., and Morris, R. G. (1987). Hippocampal synaptic enhancement and information storage within a distributed memory system. Trends Neurosci. 10, 408–415.
Medin, D. L., and Schaffer, M. M. (1978). Context theory of classification. Psychol. Rev. 85, 207–238.
Moses, S. N., Villate, C., and Ryan, J. D. (2006). An investigation of learning strategy supporting transitive inference performance in humans compared to other species. Neuropsychologia 44, 1370–1387.
Myers, C. E., Shohamy, D., Gluck, M. A., Grossman, S., Kluger, A., Ferris, S., Golomb, J., Schnirman, G., and Schwartz, R. (2003). Dissociating hippocampal versus basal ganglia contributions to learning and transfer. J. Cogn. Neurosci. 15, 185–193.
Nakazawa, K., Sun, L. D., Quirk, M. C., Rondi-Reig, L., Wilson, M. A., and Tonegawa, S. (2003). Hippocampal CA3 NMDA receptors are crucial for memory acquisition of one-time experience. Neuron 38, 305–315.
Norman, K. A., and O'Reilly, R. C. (2003). Modeling hippocampal and neocortical contributions to recognition memory: a complementary-learning-systems approach. Psychol. Rev. 110, 611–646.
Nosofsky, R. M. (1984). Choice, similarity, and the context theory of classification. J. Exp. Psychol. Learn. Mem. Cogn. 10, 104–114.
O'Neill, J., Pleydell-Bouverie, B., Dupret, D., and Csicsvari, J. (2010). Play it again: reactivation of waking experience and memory. Trends Neurosci. 33, 220–229.
O'Reilly, R. C., and McClelland, J. L. (1994). Hippocampal conjunctive encoding, storage, and recall: avoiding a trade-off. Hippocampus 4, 661–682.
O'Reilly, R. C., and Rudy, J. W. (2001). Conjunctive representations in learning and memory: principles of cortical and hippocampal function. Psychol. Rev. 108, 311–345.
Poldrack, R. A., and Packard, M. G. (2003). Competition among multiple memory systems: converging evidence from animal and human studies. Neuropsychologia 41, 245–251.
Polyn, S. M., Norman, K. A., and Kahana, M. J. (2009). A context maintenance and retrieval model of organizational processes in free recall. Psychol. Rev. 116, 129–156.
Polyn, S. M., and Kahana, M. J. (2008). Memory search and the neural representation of context. Trends Cogn. Sci. 12, 24–30.
Posner, M. I., and Keele, S. W. (1968). On the genesis of abstract ideas. J. Exp. Psychol. 77, 353–363.
Preston, A. R., Shrager, Y., Dudukovic, N. M., and Gabrieli, J. D. (2004). Hippocampal contribution to the novel use of relational information in declarative memory. Hippocampus 14, 148–152.
Rogers, T. T., and McClelland, J. L. (2004). Semantic Cognition: A Parallel Distributed Processing Approach. Cambrige, MA: MIT Press.
Rumelhart, D. E. (1990). “Brain style computation: learning and generalization,” in An Introduction to Electronic and Neural Networks eds S. F. Zornetzer, J. L. Davis, and C. Lau (San Diego, CA: Academic Press), 405–420.
Scoville, W. B., and Milner, B. (1957). Loss of recent memory after bilateral hippocampal lesions. J. Neurol. Neurosurg. Psychiatry 20, 11–12.
Sederberg, P. B., Howard, M. W., and Kahana, M. J. (2008). A context-based theory of recency and contiguity in free recall. Psychol. Rev. 115, 893–912.
Shepard, R. N. (1987). Toward a universal law of generalization for psychological science. Science 237, 1317–1323.
Shohamy, D., and Wagner, A. D. (2008). Integrating memories in the human brain: hippocampal-midbrain encoding of overlapping events. Neuron 60, 378–389.
Squire, L. R., Stark, C. E., and Clark, R. E. (2004). The medial temporal lobe. Annu. Rev. Neurosci. 27, 279–306.
Treves, A., and Rolls, E. T. (1992). Computational constraints suggest the need for two distinct input systems to the hippocampal CA3 network. Hippocampus 2, 189–199.
van Strien, N. M., Cappaert, N. L., and Witter, M. P. (2009). The anatomy of memory: an interactive overview of the parahippocampal-hippocampal network. Nat. Rev. Neurosci. 10, 272–282.
Wallenstein, G. V., Eichenbaum, H., and Hasselmo, M. E. (1998). The hippocampus as an associator of discontiguous events. Trends Neurosci. 21, 317–323.
Wilson, M. A., and McNaughton, B. L. (1994). Reactivation of hippocampal ensemble memories during sleep. Science 265, 676–679.
Wu, X., and Levy, W. B. (2001). Simulating symbolic distance effects in the transitive inference problem. Neurocomputing 38–40, 1603–1610.
Zaki, S. R. (2004). Is categorization performance really intact in amnesia? A meta-analysis. Psychon. Bull. Rev. 11, 1048–1054.
Zeithamova, D., Schlichting, M. L., and Preston, A. R. (2012). The hippocampus and inferential reasoning: building memories to navigate future decisions. Front. Hum. Neurosci. 6:70. doi: 10.3389/fnhum.2012.00070
Keywords: hippocampus, memory, generalization, inference, transitive, learning, computational
Citation: Kumaran D (2012) What representations and computations underpin the contribution of the hippocampus to generalization and inference? Front. Hum. Neurosci. 6:157. doi: 10.3389/fnhum.2012.00157
Received: 07 December 2011; Accepted: 17 May 2012;
Published online: 04 June 2012.
Edited by:
Joel Voss, Northwestern University Feinberg School of Medicine, USAReviewed by:
Joel Voss, Northwestern University Feinberg School of Medicine, USAAlison Preston, The University of Texas at Austin, USA
Copyright: © 2012 Kumaran. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Dharshan Kumaran, Institute of Cognitive Neuroscience, University College London, Gower Street, 17 Queen Square, London WC1N 3AR, UK. e-mail:ZC5rdW1hcmFuQGZpbC5pb24udWNsLmFjLnVr
