Commentary: “Neural signatures of intransitive preferences”

A commentary on
Neural signatures of intransitive preferences

by Kalenscher, T., Tobler, P. N., Huijbers, W., Daselaar, S. M. and Pennartz, C. (2010). Front. Hum. Neurosci. 4:49. doi: 10.3389/fnhum.2010.00049

Kalenscher et al. (2010) explored the neural signatures of intransitive preferences. This endeavor is of great interest because transitivity of preferences has long been considered a key feature of rationality. The success of this approach hinges upon appropriate methods for identifying decision makers with intransitive preferences. The authors invented a descriptive numerical “index of intransitivity” (henceforth labeled K. Index) that we argue is not grounded in a quantitative model of choice behavior. We revisit the authors' original data and reclassify the participants using two well-known and well-established quantitative criteria for transitive preferences, the random preference model of transitive linear orders (Block and Marschak, 1960; Becker et al., 1963) and weak stochastic transitivity (Block and Marschak, 1960; Tversky, 1969; Iverson and Falmagne, 1985). These two models of transitive preferences embody two different ways to capture uncertainty/variability of behavior formally. According to the random preference model, preferences are probabilistic, while responses are deterministic (error-free). According to weak stochastic transitivity, preferences are deterministic and responses are probabilistic (noisy). Suitable statistical tests for these models have only recently become broadly available.

Similar to the seminal study of Tversky (1969), Kalenscher et al.'s task consisted of two-alternative forced choices among binary lotteries, with reward size and probability of a reward trading off against each other. Using a set of five lotteries, the data of interest consist of 200 responses per person, 20 repetitions for each of the 10 pairs of lotteries. Eighteen of their 30 participants scored a K. Index > 0.3 and were classified as intransitive. The authors motivated the K. Index as a means to evaluate weak stochastic transitivity.

Economists and psychologists have studied the conceptual challenges of taking a deterministic axiom like transitivity and expanding it into a probability model to incorporate the inherent uncertainty in human behavior (Luce, 1959; Block and Marschak, 1960; Luce and Narens, 1994; Loomes and Sugden, 1995; Hey, 2005). Equally importantly, recent work has provided the statistical tools needed to evaluate such models (Myung et al., 2005; Davis-Stober, 2009; Cavagnaro and Davis-Stober, 2014; Regenwetter et al., 2014). Regenwetter et al. (2010, 2011a) gave an in-depth critique of the literature on testing transitivity of preferences. These papers contributed three main points relevant to this discussion:

1. They promoted random preference models as a compelling probabilistic specification of transitivity.

2. They offered the first proper statistical test of the random preference model using “order-constrained inference” methods, and one of the first proper direct statistical tests of weak stochastic transitivity.

3. They discussed conceptual, mathematical, and statistical problems of commonly used descriptive indices similar to K. Index (see, e.g., Regenwetter et al., 2011a, Figure 4).

According to the random preference model of transitivity (RPT), a decision maker may have any transitive preference ≻ with (unknown) probability P_≻. The binary choice probability, p(x, y) that a decision maker chooses x when offered the choice between x and y is the total probability of all those transitive preference states ≻ according to which x is preferable to y, i.e., x ≻ y. Formally,

$\begin{array}{cc}p(x,y)={\displaystyle \sum _{\begin{array}{c}\text{preference states}\succ \\ \text{ in which }x\succ y\end{array}}{P}_{\succ }}.& (1)\end{array}$

According to this model, a decision maker has probabilistic transitive preference states and responds in an error-free fashion. Understanding the mathematical and statistical properties of this model has been the subject of a sophisticated technical literature.

According to weak stochastic transitivity (WST), a decision maker has a single (unknown) deterministic transitive preference state. Regardless of that preference state, the decision maker gives probabilistic responses due to “errors” and the probability of an error is bounded above by $\frac{1}{2}$. Formally, for any triple of distinct alternatives, x, y, z,

$\text{if }p(x,y)\ge \frac{1}{2}\text{ and }p(y,z)\ge \frac{1}{2},\text{ then }p(x,z)\ge \frac{1}{2}.$

According to this model, a decision maker has one deterministic transitive preference state and responds in a noisy fashion. Despite appearances, this model is mathematically nontrivial. For five choice alternatives, it forms the disjoint union of 120 different hypercubes in a 10-dimensional parameter space (Regenwetter et al., 2010).

We also consider two models that permit, but do not require, intransitive preference states. Respondents with lexicographic semiorder preferences examine attributes (such as probability or payoff) sequentially until values on one attribute differ sufficiently (Tversky, 1969). Put very simply, a random preference model of lexicographic semiorders (RPLS) essentially uses lexicographic semiorders for ≻ in Equation 1 (Regenwetter et al., 2011b; Davis-Stober, 2012). A lexicographic semiorder error model (LSE) assumes a single (unknown) deterministic lexicographic semiorder ≻ and error-prone responses such that, essentially, x ≻ y implies $p(x,y)\ge \frac{1}{2}$. The online supplement specifies these two models fully.

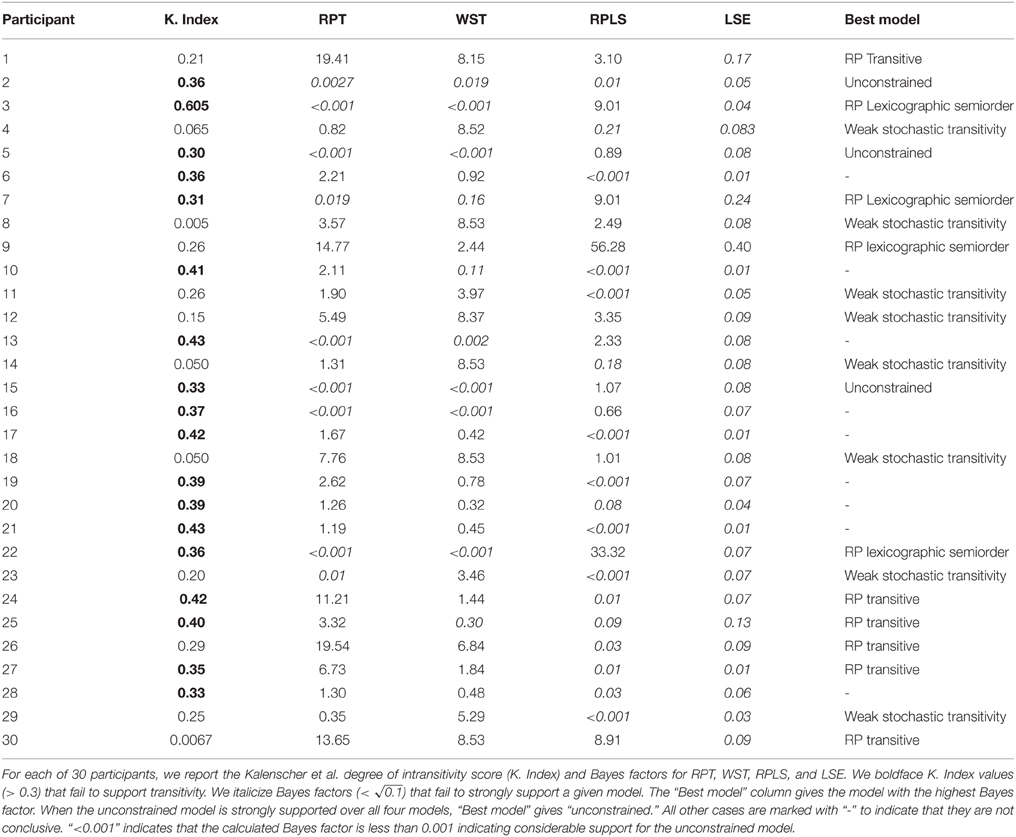
Table 1 shows our reanalysis of Kalenscher et al.'s data. Columns 3–6 give each respondent's Bayes factor for each model compared to an unconstrained model. The latter does not constrain binary choice probabilities in any way. Following standard practice (Jeffreys, 1961), a Bayes factor larger than $\sqrt{10}$ (≈ 3.16) is considered strong evidence in favor of a given model over another. The column “Best model” provides the model with the highest Bayes factor among models supported by strong evidence. Following Cavagnaro and Davis-Stober (2014), we computed these Bayes factors using the order-constrained methodology of Klugkist and Hoijtink (2007).

TABLE 1

Table 1. Reanalysis of Kalenscher et al.'s data.

Seven participants were classified according to a lexicographic model or the unconstrained model (i.e., allow intransitivity), compared to the K. Index which favored intransitivity for 18 participants. We selected RPT for six and WST for eight participants. The remaining nine cases produced insufficient evidence for classification. All participants we classified as unconstrained were also classified as intransitive by the K. Index. Notice the nonmonotonic relationship between the K. Index and the Bayes factors. Compare Participants 5 and 24. Participant 5 barely made it to be classified as intransitive by the K. Index while the Bayesian analysis found very strong evidence against both RPT and WST. Participant 24 had a much larger K. Index, while the Bayesian analysis strongly favored RPT and slightly favored WST. A frequentist test of each model, where applicable, yielded good agreement with the Bayesian approach (see Supplementary Table).

We recommend three refinements to the approach of Kalenscher et al. (2010). First, disregard the K. Index as a measure of intransitivity. Second, focus the fMRI analyses on only those participants for whom we identified a best model in Table 1. This recommendation might require additional participants to achieve sufficient statistical power. Third, look also for distinct neural signatures of random preference vs. error models as these models correspond to differences in the locus of choice variability: generated either via shifting preference states or error-prone responses.

Author Contributions

The first author communicated with Dr. Kalenscher, carried out the data analyses, and wrote the first draft of the paper as part of the requirements for a Masters in Statistics at The University of Missouri. The second and third authors assisted with conceptual, mathematical, and statistical approaches and contributed to the writing.

Funding

This work was supported by National Science Foundation grants (SES-1062045, SES-1459699, PI: Regenwetter) and (SES-1459866, PI: Davis-Stober).

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We are thankful to Dr. Tobias Kalenscher for his very helpful communications and for making the data available. We are also thankful to Aron K. Barbey for his helpful comments on a previous draft of this manuscript. We are also thankful to the action editor and our reviewer for their helpful comments on the manuscript. Any opinions, findings, and conclusions or recommendations expressed in this publication are those of the authors and do not necessarily reflect the views of their colleagues, their funding agencies, or their universities.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/article/10.3389/fnhum.2015.00509

References

Becker, G. M., DeGroot, M. H., and Marschak, J. (1963). Stochastic models of choice behavior. Behav. Sci. 8, 41–55.

Google Scholar

Block, H. D., and Marschak, J. (1960). “Random orderings and stochastic theories of responses,” in Contributions to Probability and Statistics, eds I. Olkin, S. Ghurye, H. Hoeffding, W. Madow, and H. Mann (Stanford, CA: Stanford University Press), 97–132.

Google Scholar

Cavagnaro, D. R., and Davis-Stober, C. P. (2014). Transitive in our preferences, but transitive in different ways: an analysis of choice variability. Decision 1, 102–122. doi: 10.1037/dec0000011

CrossRef Full Text | Google Scholar

Davis-Stober, C. P. (2009). Analysis of multinomial models under inequality constraints: applications to measurement theory. J. Math. Psychol. 53, 1–13. doi: 10.1016/j.jmp.2008.08.003

CrossRef Full Text | Google Scholar

Davis-Stober, C. P. (2012). A lexicographic semiorder polytope and probabilistic representations of choice. J. Math. Psychol. 56, 86–94. doi: 10.1016/j.jmp.2012.01.003

CrossRef Full Text | Google Scholar

Hey, J. D. (2005). Why we should not be silent about noise. Exp. Econ. 8, 325–345. doi: 10.1007/s10683-005-5373-8

CrossRef Full Text | Google Scholar

Iverson, G. J., and Falmagne, J.-C. (1985). Statistical issues in measurement. Math. Soc. Sci. 10, 131–153.

Google Scholar

Jeffreys, H. (1961). Theory of Probability, 3rd Edn. New York, NY: Oxford University Press.

Kalenscher, T., Tobler, P. N., Huijbers, W., Daselaar, S. M., and Pennartz, C. (2010). Neural signatures of intransitive preferences. Front. Hum. Neurosci. 4:49. doi: 10.3389/fnhum.2010.00049

PubMed Abstract | CrossRef Full Text | Google Scholar

Klugkist, I., and Hoijtink, H. (2007). The bayes factor for inequality and about equality constrained models. Comput. Stat. Data Anal. 51, 6367–6379. doi: 10.1016/j.csda.2007.01.024

CrossRef Full Text | Google Scholar

Loomes, G., and Sugden, R. (1995). Incorporating a stochastic element into decision theories. Eur. Econ. Rev. 39, 641–648.

Google Scholar

Luce, R. D., and Narens, L. (1994). “Fifteen problems in the representational theory of measurement,” in Patrick Suppes: Scientific Philosopher, Vol. 2: Philosophy of Physics, Theory Structure, Measurement Theory, Philosophy of Language, and Logic, ed P. Humphreys (Dordrecht: Kluwer), 219–245.

Google Scholar

Luce, R. D. (1959). Individual Choice Behavior: A Theoretical Analysis. New York, NY: John Wiley.

Google Scholar

Myung, J., Karabatsos, G., and Iverson, G. (2005). A Bayesian approach to testing decision making axioms. J. Math. Psychol. 49, 205–225.

Google Scholar

Regenwetter, M., Dana, J., and Davis-Stober, C. P. (2010). Testing transitivity of preferences on two-alternative forced choice data. Front. Quant. Psychol. Meas. 1:148. doi: 10.3389/fpsyg.2010.00148

PubMed Abstract | CrossRef Full Text | Google Scholar

Regenwetter, M., Dana, J., and Davis-Stober, C. P. (2011a). Transitivity of preferences. Psychol. Rev. 118, 42–56. doi: 10.1037/a0021150

PubMed Abstract | CrossRef Full Text | Google Scholar

Regenwetter, M., Dana, J., Davis-Stober, C. P., and Guo, Y. (2011b). Parsimonious testing of transitive or intransitive preferences: reply to Birnbaum (2011). Psychol. Rev. 118, 684–688. doi: 10.1037/a0025291

CrossRef Full Text | Google Scholar

Regenwetter, M., Davis-Stober, C. P., Lim, S. H., Guo, Y., Popova, A., Zwilling, C., et al. (2014). QTEST: quantitative testing of theories of binary choice. Decision 1, 2–34. doi: 10.1037/dec0000007

PubMed Abstract | CrossRef Full Text | Google Scholar

Tversky, A. (1969). Intransitivity of preferences. Psychol. Rev. 76, 31–48.

Google Scholar