- 1 Program in Neuroscience, Boston University, Boston, MA, USA
- 2 Brain Institute, University of Utah, Salt Lake City, UT, USA
- 3 Department of Biomedical Engineering, Boston University, Boston, MA, USA
- 4 Department of Biomedical Engineering, Northwestern University, Evanston, IL, USA
- 5 Department of Bioengineering, University of Utah, Salt Lake City, UT, USA
We describe General Network (GenNet), a software plugin for the real time experimental interface (RTXI) dynamic clamp system that allows for straightforward and flexible implementation of hybrid network experiments. This extension to RTXI allows for hybrid networks that contain an arbitrary number of simulated and real neurons, significantly improving upon previous solutions that were limited, particularly by the number of cells supported. The benefits of this system include the ability to rapidly and easily set up and perform scalable experiments with hybrid networks and the ability to scan through ranges of parameters. We present instructions for installing, running and using GenNet for hybrid network experiments and provide several example uses of the system.
Introduction
Hybrid networks entail the coupling, via dynamic clamp, of real neurons with simulated counterparts. This experimental paradigm represents one of the major uses of dynamic clamp (Prinz et al., 2004; White et al., 2009; Economo et al., 2010) and has been applied successfully by several groups to study the phasing and synchronization of groups of cells (Sharp et al., 1993; Ulrich and Huguenard, 1996; Debay et al., 2004; Netoff et al., 2005). Initial hybrid network studies were used to inject timed, conductance-based synaptic inputs into cells in vitro (Ulrich and Huguenard, 1996) and to analyze invertebrate circuits (Le Masson et al., 1995). Later, more sophisticated approaches have incorporated detailed biophysical representations of model cells (Hughes et al., 2008). However, the technical difficulty of implementing hybrid networks has been a barrier for widespread adoption.
In previous studies, implementations of hybrid networks often followed ad hoc approaches, in which specific networks containing the cell types and topology of interest were created in a static fashion (Sorensen et al., 2004; Netoff et al., 2005; Olypher et al., 2006; Grashow et al., 2010). While feasible for small networks containing only a few neurons, this approach becomes cumbersome when one wishes to study larger networks, permutations of a given network, or networks whose connectivity may be represented in a statistical manner. To address these limitations, we designed General Network (GenNet), a software package that allows for the construction of hybrid networks in a straightforward, reproducible, and generalized manner.
General Network is additional software that adds two important features to the real time experimental interface (RTXI) dynamic clamp system1. First, GenNet extends RTXI to enable it to perform hybrid network experiments flexibly and easily. Second, GenNet allows real-time simulation and perturbation of single model neurons. An indirect benefit of incorporating our hybrid network software into an established dynamic clamp system is the ease with which one may adopt our approach once a functional dynamic clamp system running RTXI has been established. As RTXI is currently functioning in dozens of laboratories, this mitigates the added difficulty of successfully instituting a functional dynamic clamp system, which is, in itself, a challenging task for many non-technical, experimentally-focused research groups. In addition to the application of GenNet to hybrid network experiments, we describe the utility of this system as a stand-alone simulation package, facilitating the construction of neural models and tuning of network parameters in autonomous simulations.
GenNet Software Design and Implementation Details
GenNet Implementation Emphasizes Flexible Design
General Network was designed to emphasize generality, in order to allow a large variety of hybrid networks to be implemented while maintaining simplicity and ease-of-use for end users. Simulated neurons may be represented by any computational model comprised of deterministic or stochastic systems of algebraic and differential equations. These models may be simple, as in the case of the integrate-and-fire neuron, containing only one differential equation, or complex Hodgkin Huxley-style models containing equations describing a host of voltage-dependent conductances. The particular details of each model neuron must be defined once and are only constrained to include the most basic features (a voltage, the ability to spike, etc.). Any desired pattern of connectivity may be specified in a straightforward manner. Synaptic connections are assumed to be double-exponential AMPAergic or GABAergic ionotropic conductance synapses, although synapse modules may be straightforwardly extended to include NMDA synapses, electrical synapses, or synapses with graded transmission. For a given simulation, cell types and the connectivity between cells are defined in a single configuration file using a simple syntax (see Netfile Syntax in the Appendix). The numerical integration of differential equations is achieved using fourth – order Runge Kutta or forward Euler solvers, although other (fixed time-step) numerical solvers may be added. These two numerical integration schemes were selected because of their efficiency. The real-time constraint of the dynamic clamp requires that all equations be solved in real time, making the speed of computation a high priority.
GenNet Source Code Architecture
General Network represents cells, synapses, and parameters as C++ classes or class members (Figure 1). In the schematic shown, C++ classes are represented as gray boxes with elements of the boxes representing class members such as variables or functions. Open arrows indicate a “contains” relationship. The Network class contains instances of the Cell, Synapse, and Data Logger classes. Solid arrows represent object-oriented inheritance relationships. Thus, individual cell classes all derive from a common “Cell” superclass, which consolidates elements common to all cells, including an applied current and functions for solving its own differential equations. Properties unique to individual cell models are set in the child class as appropriate. For example, each cell could contain its own model for the sodium current but all cells must have a voltage. In this manner, we were able to simplify code design and allow for the creation of any number of additional cell models. At the time of writing, approximately 12 different model cells have been created for and used with GenNet (see Table A in the Appendix). Examples of how to implement models cells are included with the GenNet source code2 and a brief code example is given in the Section “Example Model Source Code” in the Supplementary Material.
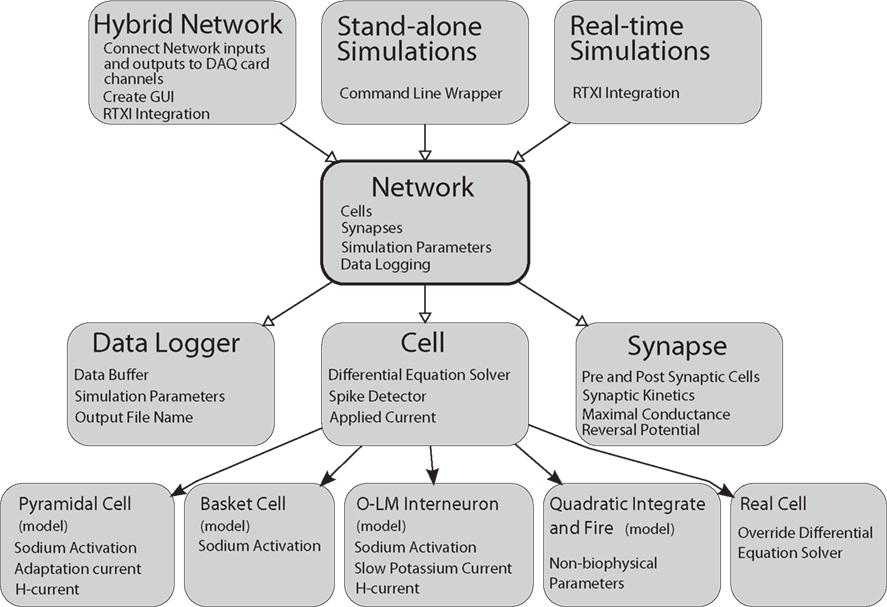
Figure 1. General Network software design diagram. Boxes represent computer code class structures and arrows represent relationships between classes. Solid arrows represent object-oriented inheritance relationships and open arrows mean that an instance of the class pointed to is contained within the class the arrows originates from. Each class lists some representative class members (functions or variables) in small text. The Network class is at the core of the simulator. It contains the list of cells and synapses that define the network as well as data logging capabilities. The Cell class is a parent class to each individual cell type. It contains functions and variables common to all cells. Individual cells can be biophysical or non-biophysical if desired. The Network class is “wrapped” by three helper classes that allow the core of GenNet to be used in three different contexts. In one, GenNet is coupled to RTXI and physical hardware channel inputs are routed between model cells and real cells in an experimental preparation. In the other context, the simulator runs “stand-alone” in a purely virtual mode. In the last, GenNet is embedded within RTXI but used for real-time, single-cell simulations rather than hybrid network applications. All cells marked (model) are computer model versions of the cells they represent. The “real cell” is a placeholder class that serves to represent a living neuron within GenNet.
The inheritance structure of GenNet enables the reduction of a large amount of redundant programming. Because all neurons inherit the attributes of the Cell class, any feature one wishes to include in multiple cell types may be specified a single time in the Cell class. While these features will be adopted by all cells, appropriate flags may be used to determine which features are exploited by each cell type. For example, the Cell class includes a description of an Ornstein–Uhlenbeck conductance process (Uhlenbeck and Ornstein, 1930), commonly used to approximate the post-synaptic effect of many irregularly firing pre-synaptic neurons (Softky and Koch, 1993; Destexhe and Pare, 1999; Destexhe et al., 2001, 2003). A substantial body of literature suggests that neurons may behave differently when subjected to the same input commonly received in an in vivo network, where cells receive large numbers of incoherent synaptic inputs not present in slice preparations (Destexhe et al., 2003). This functionality may be inherited with variable parameters by any neuron model. The ability for any defined cell type to inherit features such as the Ornstein–Uhlenbeck process greatly streamlines the cell definition process.
Another important function contained in the parent Cell class and inherited by all cell models is the capability to detect action potentials. After a cell has reported that a spike has occurred, this is detected by the Network, which queries all cells for spikes on each time step. The Network then determines which cells are post-synaptically connected to the cell that fired and alerts the appropriate Synapse objects. Connections between cells are implemented as instances of the Synapse class which has, as its main components, identifiers of the associated pre-synaptic and post-synaptic cells along with several parameters governing its kinetics and reversal potential. Internal to each Synapse object is an output variable that represents the instantaneous value of conductance at that synapse. This value continually evolves as the simulation progresses and is updated to initiate a new synaptic waveform whenever a spike occurs in its pre-synaptic partner.
The Network class is the core class of the simulator (Figure 1). It contains the list of cells and synapses that define the network topology and imports an external class that contains vital simulation parameters that describe the length of the run and the integration time step. Another core function contained in the Network class is the ability to record data produced by the simulator.
At the highest level of the diagram (Figure 1) are three classes that wrap the Network class to enable the three major execution paradigms of GenNet. These three paradigms are (1) real-time hybrid network experiments running on a dynamic clamp system and involving simulated and biological neurons, (2) real-time simulations of a single model neuron running on a dynamic clamp system, and (3) stand-alone network simulations. These classes do not themselves add any additional functionality to the simulator. However, they provide interfaces for embedding GenNet’s core within RTXI (for running in hybrid mode or performing real-time single-cell simulations) or for running stand-alone simulations at the Linux command line.
The hybrid network wrapper’s major function is to route synaptic connections between real cells and simulated cells via the appropriate channels on a data acquisition card. Additionally, this class uses existing RTXI functionality to create a high-level graphical user interface (GUI) window to control execution of the hybrid network. The window contains a field used to specify the name of the input Netfile (the user defined file that specifies all network parameters, see below), as well as other high-level parameters controlling the simulation. This functionality is duplicated when running real-time, single-neuron simulations. Real-time simulations are useful to perform virtual current-clamp experiments on model neurons. All stimulation protocols that exist in RTXI may be used to probe the model as it is simulated in real time, allowing the experimenter to gain intuition about a given model rapidly, as one would in a real experiment with a biological neuron. The stand-alone command line wrapper for GenNet contains the necessary code to parse command line options allowing for the specification of input Netfiles as well as various flags governing the simulator’s behavior. The stand-alone mode of execution allows for the running of simulations completely independent of RTXI. All wrapper classes instantiate the Network class and instruct it to begin the simulation.
As a result of its structure, GenNet is able to construct a full representation of the specified network internally, preventing the need to load individual cell models or manually set any connections. This feature reduces the possibility of errors, improves the reproducibility of simulations and experiments and decreases the time necessary to change parameters. Additionally, GenNet is capable of acting as a stand-alone network simulator, independent of RTXI.
Netfiles Uniquely and Reproducibly Describe a Simulation
Our stated goal of simulating hybrid networks easily and with general topology was facilitated by the introduction of configuration files (termed “Netfiles”) specifying cell identities, connectivity patterns, and parameters controlling the attributes of all cells and synapses. The use of separate Netfiles interpreted by the core GenNet software in order to create an internal representation of all cells, synapses, and parameters provided several advantages. First, Netfiles could be automatically generated by other scripts. This feature made it possible to describe network topologies in terms of statistical features rather than specific parameter values. Second, a Netfile uniquely and reproducibly describes a simulation or hybrid network experiment, meaning that running GenNet with the same Netfile as input would lead to analogous output both in stand-alone mode and hybrid mode in which one or more in silico neurons are replaced by biological counterparts. Finally, keeping an accurate and reproducible record of simulations was reduced to simply saving the Netfile along with corresponding data file for each experiment.
Advanced Netfile Syntax Enables Rapid Parameter Screening
At its core, the Netfile language allows for the description of a set of cells and the connections between them. The language has been extended to optionally permit the alteration of any parameter used by those cells or synapses. Because the syntax of Netfiles only necessitates the definition of basic parameters for each cell and synapse, the number of possible parameters that might need to be additionally defined is very large. To change any non-required parameter from its default value, an optional syntax extension allows any model parameter to be specified individually. This produces a Netfile syntax that remains clean and simple while allowing a powerful set of parameter changes to be available for the user. To use this feature, a cell or synapse declaration line is followed with a key–value pair that determines which parameter is to be changed and what value the parameter is to take (see Installing and Running GenNet in the Appendix). Upon initialization, the Netfile is parsed, key–value pairs are loaded, and a user-specified code block, which must be written in advance and associated with the parameter name, is executed. Thus, for every parameter that one would like to be adjustable, a small section of code specific to that parameter must be added to the Netfile interpreter. This allows for flexible, dynamically-changing definitions of any model parameter.
A common usage of the parameter changing feature is to run simulations in stand-alone mode for a range of parameters to assess the output of the network in a given parameter space. To facilitate this sort of experiment, we added another syntax extension that allows for the specification of a range of parameters. Sequential simulations, each with a different value for the parameter, are then executed. A wrapper script is used to identify and parse Netfile instructions that specify parameter ranges. A series of Netfiles are then generated dynamically and GenNet is invoked for each file creating a distinct output data file. The script operates on the source Netfile recursively, meaning that a multi-dimensional parameter space may be probed. Using this method, an arbitrarily large series of simulations iterating over any parameter space can be specified easily. This functionality is only available when the software is run in stand-alone mode. This is because in hybrid mode, GenNet loads input files via the provided GUI, a process that cannot be automated easily. Nevertheless, assessing the output of simulations over a large parameter space can be useful to determine which values are most appropriate for application in hybrid network experiments.
RTXI Integration
Integration of the core GenNet simulator with RTXI was achieved using the RTXI wrapper class designed to interface the simulator with experimental recordings (Figure 2). This class generates a GUI that controls the experimental parameters of generated hybrid networks within RTXI. These parameters control network topology (by specifying the appropriate Netfile), the integration rate of defined differential equations, experiment duration, and the manner in which data files are generated. By default, recorded data is restricted to the membrane voltage of each element of the network for efficiency purposes, although other state variables may be saved as well with minor alterations of the underlying code. To complete the integration of GenNet with RTXI, we implemented a method by which users can specify the connectivity between one or more real cells and the remaining in silico neurons in the hybrid network. By convention, the type designator of a real (biological) cell, recorded using whole-cell patch clamp, is negative one (−1, see description of Netfile Syntax in the Appendix). A custom class was written to represent biological cells which had the same inheritance pattern as each other Cell class. The differential equation solver inherited from the parent Cell class was subsequently overridden so as to perform no function. Because the voltage of a biological cell does not need to be computed, but instead only read from a data acquisition system, this change allowed GenNet to treat real cells in the same manner as simulated counterparts.
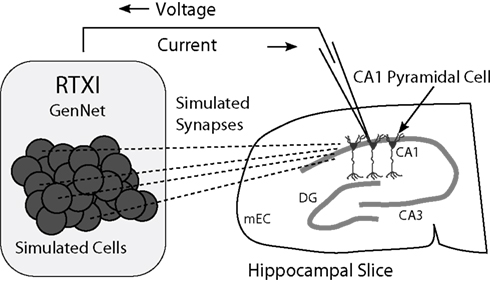
Figure 2. Schematic diagram of a hippocampal hybrid network. A set of model cells simulated with GenNet within RTXI (shaded box on left) interacts with a real pyramidal neuron being recorded with the patch-clamp technique in a hippocampal slice (right). Dark circles represent individual model cells that are connected via virtual synapses (dashed lines) to a real pyramidal neuron. A patch-clamp pipette is used to record the voltage from this neuron in real time which is then passed as input to GenNet (upper arrow). After a computational time-step has elapsed, GenNet computes the synaptic current that must be passed to the pyramidal neuron and RTXI sends this current into the cell via the pipette (lower arrow). Multiple adjacent pyramidal neurons indicate that an arbitrary number of real cells can be embedded into the hybrid network. Abbreviations refer to the regions of the hippocampal formation: mEC, medial entorhinal cortex; DG, dentate gyrus; CA3, cornu Ammonis 3; CA1: cornu Ammonis 1.
When a Netfile containing a biological cell is parsed by GenNet, the synapses impinging upon the real cell and synapses triggered by it are stored by the software. Upon initialization, the wrapper class associates hardware input and output channels with the voltage of, and current intended for, each biological neuron (schematic shown in Figure 2). At the beginning of every time step the voltage of the real cell is read from its corresponding hardware channel. This value is used during that time step in all voltage-dependent calculations. At the end of each time step, when all synaptic currents have been computed, the calculated net synaptic current onto that neuron is injected by a current-clamp amplifier through the corresponding analog output channel. In this manner, GenNet seamlessly integrates the simulated network with any biological neurons. Hybrid networks may be constructed with any number of experimentally-recorded neurons; however, that number is practically limited by the number of available hardware channels and the experimental challenge of simultaneously obtaining intracellular recordings from multiple cells.
Example GenNet Applications
Stand-Alone Model Networks
To illustrate the functionality of GenNet as a stand-alone simulator, we constructed several networks to demonstrate the ability of our software to simulate simple and complex networks and to highlight several features of GenNet. We began by implementing a two-cell model network with a single unidirectional synapse providing excitatory or inhibitory input from one cell to the other (Figure 3A). In this network, Cell 1 fires tonically (Figures 3B,C top panels), and we measured the effect of tonic spiking on the behavior of the post-synaptic cell when using either an excitatory or an inhibitory synapse. If an excitatory synapse was used, Cell 2 also spiked tonically, synchronously with Cell 1 (Figure 3B, middle panel) in response to its excitatory synaptic input (Figure 3B, bottom panel). Spiking in Cell 2 is tightly phase locked to Cell 1 as seen in the histogram of Cell 2 spike phases relative to Cell 1 firing (Figure 3D, top panel). If instead an inhibitory synapse was used (Figure 3C), Cell 2 spiked only when its intrinsic excitability could overcome the incoming hyperpolarizing synaptic input (Figure 3C, bottom panel). Spike timing in Cell 2 was biased to occur in the second half of the Cell 1 phase which allowed sufficient time for inhibition to wear off (Figure 3D, bottom panel). GenNet enabled the switch between these two simple networks by making a single parameter change in the Netfile (see Netfile Syntax in the Appendix).
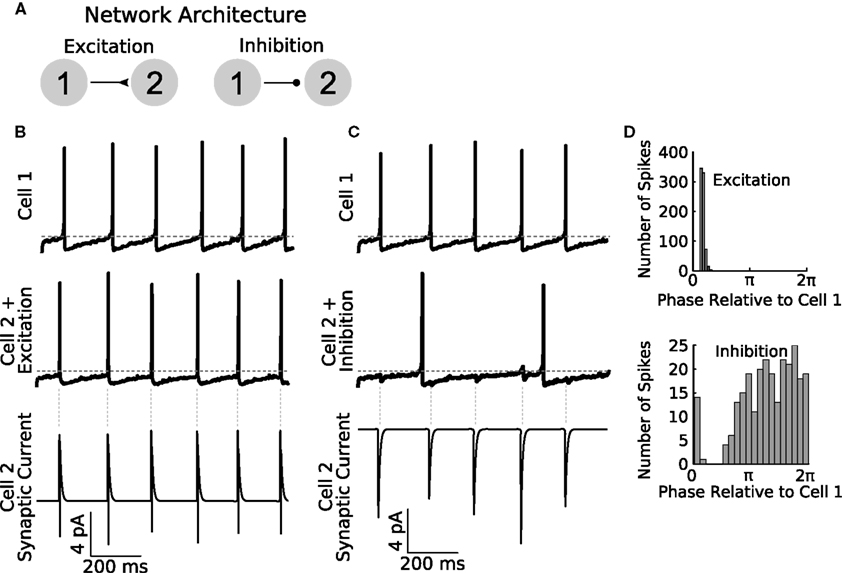
Figure 3. General Network enables rapid parameter switching for simulating diverse network types. (A) A sample feed-forward network is implemented in GenNet to illustrate the capability of the software to quickly and easily change fundamental properties. The sample network contains two cells with noisy drive coupled either by feed-forward excitation (left) or feed-forward inhibition (right). Cell 1 is made to fire tonically triggering post-synaptic currents in Cell 2. (B) When excitatory coupling is used, the spikes of Cell 2 (middle panel) closely track those of Cell 1 (top panel). The excitatory synaptic currents (bottom panel) are sufficient to elicit a spike in Cell 2 each time a Cell 1 spikes. The synaptic current also illustrates the voltage dependence of synaptic transmission. When a post-synaptic spike raises the voltage of Cell 2 past the reversal potential of the synapse, the sign of the synaptic current changes. Vertical gray dashed lines indicate the timing of spikes in Cell 1. Horizontal gray dashed line indicates −50 mV. (C) The same network can be run with the synapse switched to be inhibitory. In this case, post-synaptic spiking in Cell 2 is irregular and does not track pre-synaptic spiking (middle panel). The effect of pre-synaptic spikes (top panel) on the post-synaptic voltage can be observed as small, hyperpolarizing deflections in the voltage. Spiking in Cell 2 occurs when the natural evolution of the voltage overcomes the periodic inhibition from Cell 1. As a result, firing in Cell 2 is slower than when inputs were excitatory. (D) Spike time histograms (plotted as Cell 2 spike times relative to the phase of Cell 1) show the distribution of spikes in Cell 2 depending on the coupling type used. Excitation causes Cell 2 to become entrained to Cell 1 (top panel) and Cell 2 spike occur in a small time window only. Inhibition causes spiking in Cell 2 to be biased to occur in the second half of the Cell 1 period when inhibition has had sufficient time to wear off (bottom panel) but overall spikes are spread over a wider time window than when excitation was used.
The utility of GenNet is apparent when simple networks, like the one discussed above, are scaled up in size to probe how simple properties describing connectivity can affect complex emergent network behaviors. We increased the size of the simple two-cell network to contain 20 cells and utilized a random pattern of connectivity instead of a single synapse (Figure 4A). Switching to this alternate topology was achieved by simply listing additional cells in the configuration Netfile and using a script to randomly generate synapse definitions. We simulated this network and again asked what activity patterns would emerge when the cells were coupled with excitation versus inhibition. We first measured the instantaneous mean firing rate of neurons in the network with either connectivity type (Figure 4B). When inhibitory synapses were used, the average firing rate (computed as the number of spikes across all cells in a small time window) was nearly constant, indicating that, on average, the neurons in the network fired at approximately the same rate over time. Consistent with this observation, a raster of spiking activity in the network connected via inhibition shows unorganized and uniform spiking over time (Figure 4C). Conversely, when the network was coupled with excitatory synapses exclusively, a different pattern of spiking activity emerged. The mean rate of spiking underwent rapid rises and falls during the course of the simulation (Figure 4D) indicating a burst-like pattern of spiking. Indeed, the raster of spike times confirms this interpretation, showing that when excitatory coupling is used, all cells in the network were activated simultaneously followed by periods of quiescence.
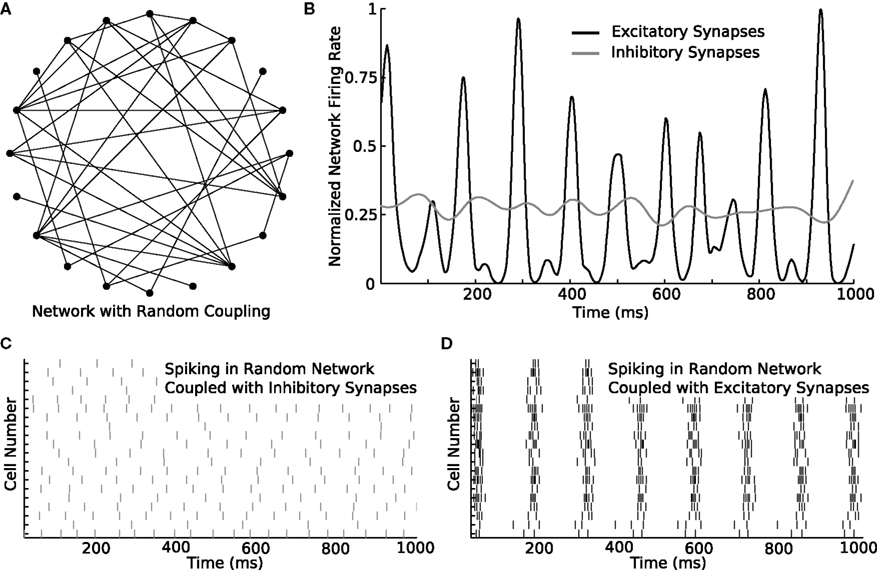
Figure 4. Switching parameters in a larger network produces diverse activity patterns. (A) An example of a larger network containing 20 neurons coupled randomly. In the diagram, filled circles represent cells and lines represent synapses. Synaptic direction is not indicated. The connection probability between each cell pair is 20%. (B) The 20-cell network is simulated with either excitatory or inhibitory synapses. While the total amount of spiking is similar in both simulations, the instantaneous rate differs considerably between the simulations. While the rate is nearly constant over time with inhibitory synapses, the rate rapidly changes in a burst-like pattern with excitatory synapses. (C) Rastergram of spiking in the network when inhibitory synapses are used. Spike rate remains approximately constant over time. (D) Rastergram of spiking when excitatory synapses are used. The network bursts periodically. As single-neurons fire, they recruit their post-synaptic partners until every member of the network is activated. After a brief period of activation, the cells become refractory together and the network becomes nearly silent until the cycle repeats.
The ability to rapidly switch between parameters is not only confined to changing the polarity of synapses. Topological changes to networks are similarly easy to achieve. We used GenNet to ask how activity would propagate through a ring network and how this propagation would change if the network included several long-distance connections in addition to nearest-neighbor connections. We again used a 20-neuron network connecting each neuron only to its nearest neighbors (Figure 5A). Thus, each neuron had two outgoing synapses and two incoming synapses. Excitatory coupling was used throughout this set of simulations. When cells in the network were tuned such that they would occasionally fire spontaneous action potentials, a clear pattern of activity propagation emerged (Figure 5B). A single spike would, after a small delay, induce spiking in the neighboring neurons, which would in turn activate their neighbors. This resulted in an activity wave propagating along the edge of the ring. The sequential pattern of activation is visible if one of the waves is magnified to show how adjacent cells are sequentially activated in time (Figure 5C, arrows). The same network can be modified by adding a small number of additional synapses to connect two previously unconnected cells (Figure 5D). This change has the effect of producing a network which is mostly connected as a ring, but contains several synapses that provide alternate paths along which an activity wave can propagate. When an activity wave initiates in this network, it propagates along the edge of the ring, but short cuts to distant neurons in the network when it reaches one of the rewired connections, some of which connect to neurons far from immediate neighbors (Figure 5E). A magnified view of one of these episodes of activity shows that the network is now activated in a more simultaneous manner as opposed to a sequential manner (Figure 5F). Overall, this example highlights how GenNet’s ability to rapidly change parameters in model networks helps build an understanding of how those parameters can lead to different qualitative network behaviors.
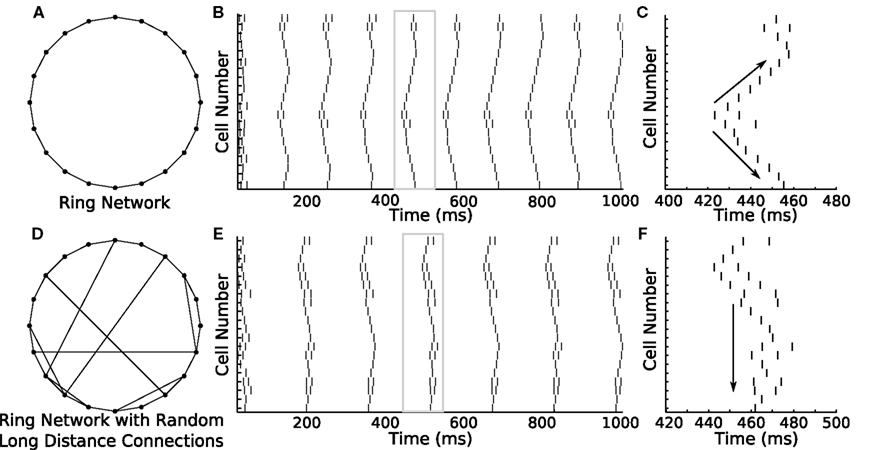
Figure 5. Ring network shows how different network connectivity can lead to different patterns of activity propagation. (A) A 20-cell ring network is constructed in GenNet with each neuron coupled via excitation to its two immediate neighbors. (B) Spontaneous activity propagates through this network along the edge of the ring. A single spike triggers a wave of spikes that travels around the ring in both directions. The window of time indicated by the gray box is magnified in the (C). (C) Magnified view of a single wave. Arrows indicate the bidirectional propagation of the activity wave from a single source. (D) A different activity pattern emerges when the connectivity is changed to include a few random connections along with connections to nearest neighbors. In this case, activity waves have the opportunity to short cut the path along the edge and can thus recruit the remaining cells in the network more quickly after the initial spiking event. (F) Magnified view [gray box in (E)] of a single activity wave shows how the propagating activity uses the long-distance connections to activate remote portions of the ring more rapidly. This causes the cells to be more simultaneously active as opposed to sequentially active.
Lastly, we constructed a network in which one of the neurons was designated as a “hub,” a neuron with a much higher degree of connectivity than its peers. We simulated a hub network comprised of 20 neurons in which one cell was randomly selected to provide diffuse inhibition to the remaining cells in the network (Figure 6A). A single spike in the hub cell causes an inhibitory response in the target cells and, as a result, a cessation of spiking activity (Figure 6B). This simulation provides another example of a biologically relevant topology (Bonifazi et al., 2009) and would have been precluded by the limitations of other hybrid network systems. The hub network topology is of particular interest because it lends itself well to integration with a biological preparation as a single biological hub neuron could impact the remaining cells in the network in a non-trivial manner, allowing one to effectively investigate how intracellular properties facilitate this function.
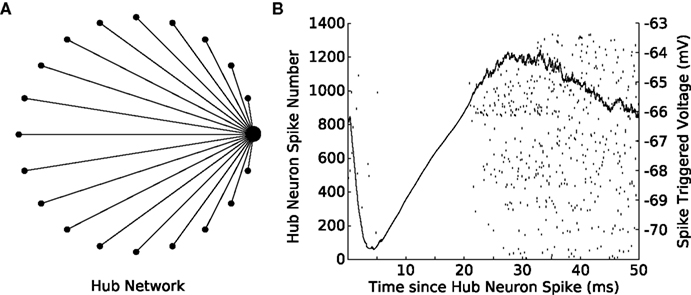
Figure 6. Spikes in a hub neuron strongly influence spike times in the remaining network. (A) A 20-cell network is constructed in GenNet with a single-neuron (the hub neuron) synapsing onto the remaining cells in the network with feed-forward inhibition. In such a network, a spike in the hub neuron has the capability to profoundly influence the activity in the remaining cells in the network. The hub neuron is drawn as the large circle with the remaining cells represented as smaller circles. Synapses are drawn as lines without indication of direction. (B) Each time the hub neuron spikes, the voltage of all post-synaptic cells is averaged (solid line) indicating that a single inhibitory pulse caused approximately a −4 mV hyperpolarization in the target cells (right axis). The rastergram indicates the spiking activity of each neuron in the network after a hub neuron spike has occurred and shows that the inhibitory input imposes a delay of approximately 20 ms before spiking can resume again in the target neurons.
Hybrid Networks
Although many neural simulators have been described in the literature that efficiently simulate the behavior of neural networks [e.g., BRIAN (Goodman, 2008)] and the voltage of spatially-extended neurons [NEURON, GENESIS (Hines and Carnevale, 1997; Bower and Beeman, 1998)], GenNet was primarily developed to facilitate integration with dynamic clamp software for the construction of hybrid networks. Similar tools exist for dynamic clamp systems that do not operate in hard real-time and are specialized to work with particular neuron types (Hughes et al., 2008). To our knowledge, GenNet is the first such system that is not constrained by predetermined network sizes, cell types, or topologies while continuing to operate in hard real time. It has the additional advantage of operating within a dynamic clamp system that is widely used in many laboratories (Iravanian and Christini, 2007; Bettencourt et al., 2008; Grashow et al., 2010; Lin et al., 2010; Lobb and Paladini, 2010). To demonstrate this functionality, we present an example hybrid network and describe how this approach may be used to explore the effect of connectivity patterns and intrinsic neuronal properties on the generation of population activity patterns in groups of neurons.
The following hybrid network experiment was motivated by previous studies (Gillies et al., 2002; Gloveli et al., 2005; Tort et al., 2007) suggesting that the theta (4–12 Hz) and gamma (30–80 Hz) rhythms may be generated by the interaction of hippocampal pyramidal neurons in region CA1 with neighboring basket and oriens–lacunosum moleculare (O–LM) interneurons. These studies hypothesized that gamma oscillations were preferentially generated during periods of strong functional coupling between, and activity of, pyramidal cells and basket interneurons while the theta rhythm arises through an interaction of the same pyramidal neurons with O–LM interneurons. This hypothesis grew from several, independent lines of research. In one study, Gloveli et al. (2005) used kainate to induce rhythmic activity in hippocampal brain slices cut either in the transverse or coronal planes. The authors reported that the transverse slice generated gamma rhythms more readily, and showed that morphologically reconstructed O–LM neurons had axonal arborizations more likely to be cut in this orientation. Conversely, they showed that the theta rhythm was preferentially generated in the coronal slice in which the axonal projections of O–LM neurons remained intact. Other studies (Pike et al., 2000; Gillies et al., 2002; Goldin et al., 2007) have postulated that O–LM neurons are well-suited for the generation of theta rhythms due to the presence of HCN channels in these cells, the relatively slow kinetics of synapses formed between these cells and neighboring principal neurons, and their ability to integrate inputs at theta frequencies preferentially. Associated theoretical (Rotstein et al., 2005; Tort et al., 2007) work has suggested a possible canonical microcircuit able to generate theta and gamma rhythms based on these studies.
We used GenNet to directly test whether the degree of connectedness of O–LM cells can influence the frequency preference of a hippocampal microcircuit. We tested this by patch clamping onto an O–LM neuron and coupling it, using GenNet, to a simulated network containing one pyramidal neuron and two basket interneurons (Figure 7A) meant to mimic the local hippocampal microcircuit (Gloveli et al., 2005; Rotstein et al., 2005; Tort et al., 2007). The model neurons and patch-clamped O–LM neuron were connected in an all-to-all fashion with appropriate synaptic kinetics at each synapse (Wang and Buzsáki, 1996; Hajos and Mody, 1997; Ali et al., 1999; Goldin et al., 2007). In the circuit (Figure 7A), excitation is represented by closed triangles and inhibition by open circles. The O–LM cell is shaded to indicate that it is a real patch-clamped neuron while other circuit members are simulated.
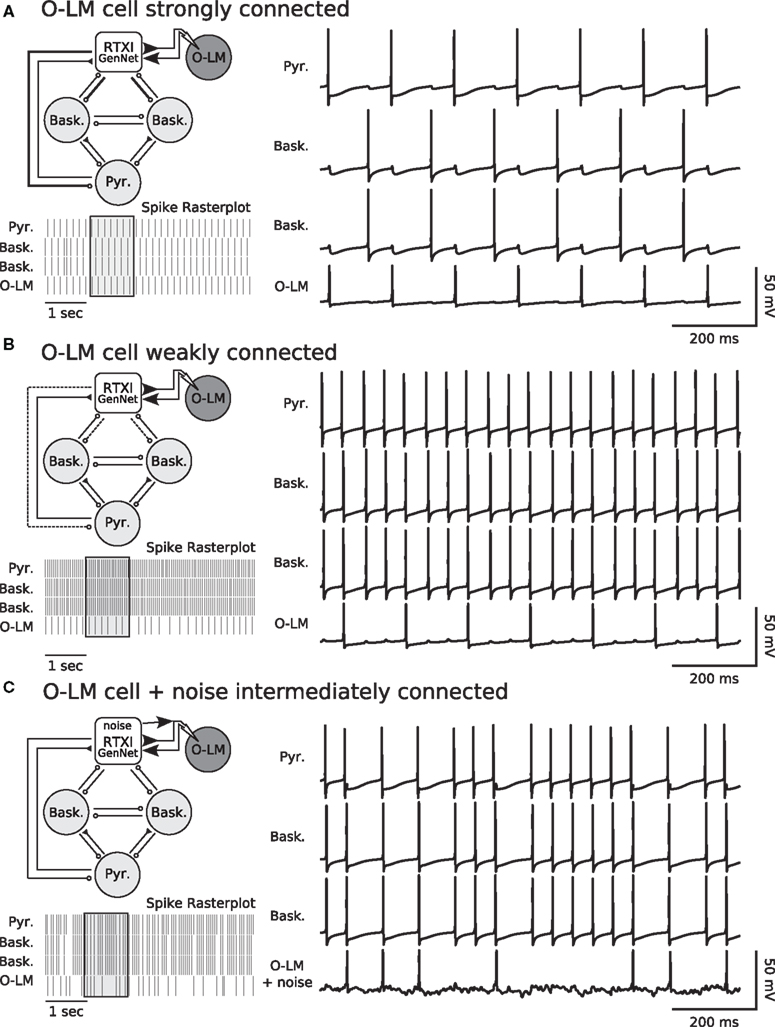
Figure 7. Degree of coupling of O–LM cells determines network frequency in hippocampal hybrid network. (A) Network diagram (top left) showing layout of the simulated network and the integration of a real cell. The single pyramidal cell and two basket cells are simulated in real-time within RTXI. This reduced hippocampal network is connected to a real, patch-clamped O–LM cell (shown with dark shading). Connectivity in the network is all-to-all with the pyramidal cell being the only source of excitation in the network. Closed triangles indicate excitation and open circles indicate inhibition. For synapses, thick, solid lines indicate strong connections, normal lines indicate intermediate connections and dotted lines indicate weak connections. In this experiment, the outgoing connections from the O–LM cell are strong. Voltage traces of the simulated network (right panel) show how the real and simulated neurons influence each other via post-synaptic currents and that the network fires in a sustained theta rhythm due to strong inhibition from the O–LM cell. A rasterplot of spiking activity (bottom left panel) shows a longer window of ongoing activity. The voltage traces correspond to the region of the rasterplot in the shaded box. (B) Weak connectivity (dotted lines, top left panel) from the real O–LM cell to the rest of the simulated network results in an ongoing gamma rhythm (spike raster and voltage traces). Excitation from the pyramidal cells and subsequent rapid feedback inhibition forms a gamma rhythm between the pyramidal cell and the basket cells. Weak, theta-frequency inputs from the real O–LM cell are insufficient to prevent gamma frequency firing. (C) Hybrid network experiments performed with GenNet can be used in combination with existing RTXI protocols. The same hybrid network is run with synapses of intermediate strength (top left panel). In addition, RTXI is used to inject conductance noise into the real O–LM cell. Noisy drive combined with intermediate synapses results in a network in which O–LM spike times are variable and the network has periods of faster spiking interspersed with periods of slower spiking (top right panel and spike raster). The noisy voltage deflections in the O–LM cell due to noise injection are visible in its voltage trace.
We tested whether the strength of the synapses originating from O–LM synapses could control the relative strengths of the theta and gamma rhythm by varying the maximal conductance of the synapses from the O–LM to both basket interneurons and the pyramidal neuron. We found that O–LM activity and connectivity can indeed mediate switching between the rhythmic states of a hippocampal microcircuit (Figure 7A,B). When the O–LM interneuron was strongly coupled (Figure 7A), the circuit (top left panel) displayed theta-frequency oscillations due to the strong inhibition provided by the O–LM cell and the slow kinetics inherent to the O–LM interneuron and the synapses originating in this cell (bottom left panel shows raster of spiking activity and right panel shows example voltage traces). Conversely, experiments in which an O–LM cell was only weakly coupled to the simulated network resulted in gamma frequency oscillations due to rapid inhibitory feedback from the basket cell interneurons (Figure 7B). Finally, to highlight the advantage of performing such experiments with GenNet, we made use of the large body of existing models for the RTXI dynamic clamp system by combining our hybrid network experiment with a stochastic conductance injection protocol in order to add noisy drive to the real O–LM neuron (Figure 7C). When synapses were of intermediate strength and O–LM cells received noisy drive, spike timing became more variable and spikes occurred at frequencies intermediate between gamma and theta (Figure 7C). The voltage fluctuations caused by the stochastic conductance injection can be seen in the voltage trace of the O–LM neuron and the effect of this variability in the O–LM output is clearly evident in the irregular spiking of other cells in the network (Figure 7C). These experiments represent a proof of concept of GenNet, as well as preliminary data confirming the specific experimental hypothesis presented in the preceding text. Further hybrid network experiments utilizing these methods would be useful to probe the role of specific channel populations in O–LM neurons in generating specific classes of rhythmic activity.
Discussion
General Network provides a flexible framework for hybrid network experiments and network simulations, offering several advantages over existing hybrid network systems. Foremost, GenNet allows for the streamlined specification and construction of hybrid networks without constraints on particular cell types or topologies. Presently, GenNet includes approximately a dozen model cell types ranging from the integrate-and-fire model to more complicated, conductance-based model cells. Construction of additional cell types is straightforward and may be achieved using existing models as templates. The topology of small networks is easy to specify directly, and more complicated, larger topologies may be specified as well using automated scripts written in higher-level languages such as MATLAB and Python. The size of the simulated components of hybrid networks is limited only by the computing power available.
The core code, compiled in C++, is capable of solving dozens to even hundreds of differential equations in real time on common desktop PCs. Under these conditions, “real time” refers to the constraint that the computations required to evolve the simulation by a given amount of model simulation time must always be completed before the corresponding amount of “wall clock” time elapses. For example, simulating model equations for 100 ms of model time must require less than 100 ms of actual computer CPU time. This requirement is independent of the update rate of the dynamic clamp system; model equations are solved at a specified time step which is decoupled from changes in the specified RTXI period. At slower dynamic clamp update rates, more iterations of model equations are computed during each dynamic clamp period. To qualitatively illustrate the performance of GenNet running on a single core Pentium 4 CPU running with a 3.6-GHz clock rate (modest hardware by modern standards), a network of 100 Izhikevich neurons (each containing two differential equations; Izhikevich, 2004) connected by 500 randomly assigned synapses could be simulated in real-time when being integrated at 10 kHz. To test the performance of a network with a more biophysically realistic neuron model we replaced the Izhikevitch model with a seven-equation model of a pyramidal neuron (Mainen and Sejnowski, 1996). With this more complex model the network could contain up to 15 neurons and 25 synapses to meet real-time simulation constraints while running on identical hardware and with identical simulation parameters.
The additional usage paradigms, stand-alone mode and single-cell real-time mode, facilitate the investigation of network and single-cell behaviors while not subject to the time constraints inherent in experimental recordings. Stand-alone mode is useful for evaluating preliminary networks as one may iterate through sets of network and single-cell parameters in an automated fashion without the requirement that equations must be solved in real-time. The advanced Netfile syntax detailed above allows for straightforward scanning through a defined range of a given parameter, or recursively through multiple parameters. Single-cell mode offers the ability to perform real-time experiments on model cells in RTXI as if they were biological cells recorded under current-clamp. This functionality enables one to take advantage of the multitude of stimulation and recording protocols included with RTXI to probe model behavior and compare it with experimental data. These modes substantially extend the functionality of GenNet, making it a useful tool for a host of computational studies.
Although similar tool kits have been described (Hughes et al., 2008), to our knowledge, no other system is capable of creating hybrid networks with arbitrary cell types, topologies, and network size. Additionally, integration with RTXI ensures that GenNet operates in hard real-time, a feature that ensures the accuracy of dynamic clamp results by preventing system processes from interrupting the solution of model equations (Bettencourt et al., 2008). With this functionality GenNet provides experimenters unprecedented access to the hybrid network technique.
Limitations of GenNet
Although the design of GenNet addresses many of the difficulties encountered when creating hybrid networks, the current implementation of GenNet has limitations. GenNet was not optimized for the efficient specification and simulation of multi-compartment neural models. If models of this type are desired, equations governing the passive flow between compartments must be specified in each model class by the end-user. As GenNet was designed for simplicity and computational efficiency, we chose not to focus on providing support for complicated morphologies, as we felt this would unnecessarily complicate the definition of network topology and further constrain the size of networks that would be possible to simulate in real time. The ability to simulate spatially extended neural models in a stand-alone fashion is already provided by simulation packages such as NEURON and GENESIS (Hines and Carnevale, 1997; Bower and Beeman, 1998) and other efforts have endeavored to make spatially extended models compatible with dynamic clamp experiments (Hughes et al., 2008; Cornelis and Coop, 2010). We are working to incorporate easier methods of adding compartmental simulations to GenNet and RTXI.
Another current limitation of GenNet is the necessity that synaptic inputs be represented by double-exponential waveforms. We believe that synapses described in this fashion maintain a good balance between computational efficiency and the desire to accurately represent the kinetics of many chemical synapses. However, electrical synapses and NMDA conductances are not currently implemented by GenNet. Because of the modular design of the GenNet system and its structural similarity to other RTXI plugins, other synapse types may be incorporated in a straightforward manner by most persons familiar with the plugin syntax of RTXI. This extensibility may be important in the future for individuals desiring to study model systems which employ graded synaptic transmission, such as the crab stomatogastric ganglion (Graubard et al., 1980; Manor et al., 1997).
Challenges in Studying Large Hybrid Networks
Although hybrid network techniques represent a valuable experimental tool, rigorous design and interpretation of such experiments requires some care. For immersing neurons in large hybrid networks, two constraints in particular should be kept in mind. First, if the goal is to study how the biophysical properties of recorded neurons affect network behavior, one should take care to verify that the recorded biological neuron or neurons can in principle have measurable effects on network activity, either because the total number of network elements is small, or because the biological elements have disproportionate influence on the rest of the network (Bonifazi et al., 2009). If feedback from the biological neurons is unimportant, an alternative approach would be study the behavior of the recorded neuron(s) in response to predefined inputs (Fernandez and White, 2008, 2009, 2010; Fernandez et al., 2011) instead of using the hybrid network technique. Second, like any kind of large-scale neural network simulation, large hybrid networks are prone to having high-dimensional parameter spaces. This problem is more of a concern for experiments than for pure simulations, because time constraints are much more prominent in recordings. For this reason, in expanding hybrid networks beyond simple cases (Netoff et al., 2005), one must impose constraints upon network organization that keep the parameter space manageable for realistic recording epochs.
Methods
Programming
All software was programmed in C++ using standard Linux-based tools. Code was compiled with version 4.x of GNU compiler collection3 all running on Ubuntu Linux4. GenNet has been successfully compiled and run on Mac OS X and Microsoft Windows based operating systems using equivalent tools. Cygwin5 was used on Windows to obtain the required software tools. Matlab (The Mathworks) was used for data analysis. Our dynamic clamp system (Dorval et al., 2001; Bettencourt et al., 2008; Lin et al., 2010) is based on a Linux kernel extension, real-time application interface, which is freely available6. Additional information regarding RTXI and free downloads of the software can be found at the project website (see text footnote 1).
Experimental
All experimental data was collected with standard patch-clamp methods described in detail elsewhere (Fernandez and White, 2008). All protocols were approved by the University of Utah Institutional Animal Use and Care Committee (IACUC). Briefly, brain slices were prepared from young (postnatal days 18–28), Long–Evans rats of both genders. Rats were anesthetized using isoflurane and decapitated. The brain was removed rapidly and placed in a beaker of ice-cold, oxygenated artificial cerebrospinal fluid (ACSF) containing (in mM): NaCl 125, KCl 2.5, NaH2PO4 1.25, CaCl2 2, MgCl 1, NaHCO3 25, D-glucose 25. Slices were cut at a thickness of 350 μm in the horizontal plane and incubated at room temperature at least 30 min prior to use. All recordings were performed in the CA1 region of the hippocampus. O–LM cells were identified under differential interference contrast (DIC) optics based on the location of the cell body in stratum oriens. Glass pipettes were filled with solution that contained (in mM): 120 K-gluconate, 20 KCl, 10 HEPES, 0.2 EGTA, 2 MgCl2, 4 Na2-ATP, 0.3 Tris-GTP, 7 diTris-phosphocreatine and 0.6% biocytin by weight. The dynamic clamp system RTXI (see text footnote 1) was used for all recordings in this study. Both excitatory and inhibitory synaptic waveforms were modeled as double-exponential functions. Kinetics for these synaptic waveforms were taken from the literature (Maccaferri et al., 2000; Netoff et al., 2005; Goldin et al., 2007).
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We would like to thank Jonathan Bettencourt for his technical assistance and Dr. Tilman Broicher for helpful comments on the manuscript. Support was provided by NIH grants R01 MH085387, R01 MH085074, and R01 RR020115 (John A. White).
Supplementary Material
The Supplementary Material for this article can be found online at http://www.frontiersin.org/neuroinformatics/10.3389/fninf.2011.00011/abstract
Footnotes
References
Acker, C. D., Kopell, N., and White, J. A. (2003). Synchronization of strongly coupled excitatory neurons: relating network behavior to biophysics. J. Comput. Neurosci. 15, 71–90.
Ali, A. B., Bannister, A. P., and Thomson, A. M. (1999). IPSPs elicited in CA1 pyramidal cells by putative basket cells in slices of adult rat hippocampus. Eur. J. Neurosci. 11, 1741–1753.
Bettencourt, J. C., Lillis, K. P., Stupin, L. R., and White, J. A. (2008). Effects of imperfect dynamic clamp: computational and experimental results. J. Neurosci. Methods 169, 282–289.
Bonifazi, P., Goldin, M., Picardo, M. A., Jorquera, I., Cattani, A., Bianconi, G., Represa, A., Ben-Ari, Y., and Cossart, R. (2009). GABAergic hub neurons orchestrate synchrony in developing hippocampal networks. Science 326, 1419–1424.
Bower, J. M., and Beeman, D. (1998). The Book of GENESIS: Exploring Realistic Neural Models with the GEneral NEural SImulation System, 2nd Edn. New York, NY: Springer Verlag.
Brette, R., and Gerstner, W. (2005). Adaptive exponential integrate-and-fire model as an effective description of neuronal activity. J. Neurophysiol. 94, 3637–3642.
Cornelis, H., and Coop, A. (2010). Realtime tuning and verification of compartmental cell models using RTXI and GENESIS. BMC Neurosci. 11, P68. doi: 10.1186/1471-2202-11-S1-P68
Dayan, P., and Abbott, L. F. (2001). Theoretical Neuroscience: Computational and Mathematical Modeling of Neural Systems, Computational Neuroscience. Cambridge, MA: Massachusetts Institute of Technology Press.
Debay, D., Wolfart, J., Le Franc, Y., Le Masson, G., and Bal, T. (2004). Exploring spike transfer through the thalamus using hybrid artificial-biological neuronal networks. J. Physiol. Paris 98, 540–558.
Destexhe, A., and Pare, D. (1999). Impact of network activity on the integrative properties of neocortical pyramidal neurons in vivo. J. Neurophysiol. 81, 1531–1547.
Destexhe, A., Rudolph, M., Fellous, J. M., and Sejnowski, T. J. (2001). Fluctuating synaptic conductances recreate in vivo-like activity in neocortical neurons. Neuroscience 107, 13–24.
Destexhe, A., Rudolph, M., and Pare, D. (2003). The high-conductance state of neocortical neurons in vivo. Nat. Rev. Neurosci. 4, 739–751.
Dorval, A. D., Christini, D. J., and White, J. A. (2001). Real-time linux dynamic clamp: a fast and flexible way to construct virtual ion channels in living cells. Ann. Biomed. Eng. 29, 897–907.
Economo, M. N., Fernandez, F. R., and White, J. A. (2010). Dynamic clamp: alteration of response properties and creation of virtual realities in neurophysiology. J. Neurosci. 30, 2407–2413.
Fernandez, F. R., Broicher, T., Truong, A., and White, J. A. (2011). Membrane voltage fluctuations reduce spike frequency adaptation and preserve output gain in CA1 pyramidal neurons in a high-conductance state. J. Neurosci. 31, 3880–3893.
Fernandez, F. R., and White, J. A. (2008). Artificial synaptic conductances reduce subthreshold oscillations and periodic firing in stellate cells of the entorhinal cortex. J. Neurosci. 28, 3790–3803.
Fernandez, F. R., and White, J. A. (2009). Reduction of spike afterdepolarization by increased leak conductance alters interspike interval variability. J. Neurosci. 29, 973–986.
Fernandez, F. R., and White, J. A. (2010). Gain control in CA1 pyramidal cells using changes in somatic conductance. J. Neurosci. 30, 230–241.
Gillies, M. J., Traub, R. D., LeBeau, F. E. N., Davies, C. H., Gloveli, T., Buhl, E. H., and Whittington, M. A. (2002). A model of atropine-resistant theta oscillations in rat hippocampal area CA1. J. Physiol. 543, 779–793.
Gloveli, T., Dugladze, T., Rotstein, H. G., Traub, R. D., Monyer, H., Heinemann, U., Whittington, M. A., and Kopell, N. J. (2005). Orthogonal arrangement of rhythm-generating microcircuits in the hippocampus. Proc. Natl. Acad. Sci. U.S.A. 102, 13295–13300.
Goldin, M., Epsztein, J., Jorquera, I., Represa, A., Ben-Ari, Y., Crépel, V., and Cossart, R. (2007). Synaptic kainate receptors tune oriens-lacunosum moleculare interneurons to operate at theta frequency. J. Neurosci. 27, 9560–9572.
Golomb, D., Donner, K., Shacham, L., Shlosberg, D., Amitai, Y., and Hansel, D. (2007). Mechanisms of firing patterns in fast-spiking cortical interneurons. PLoS Comput. Biol. 3, e156. doi: 10.1371/journal.pcbi.0030156
Goodman, D. (2008). Brian: a simulator for spiking neural networks in Python. Front. Neuroinform. 2:5. doi: 10.3389/neuro.11.005.2008
Grashow, R., Brookings, T., and Marder, E. (2010). Compensation for variable intrinsic neuronal excitability by circuit-synaptic interactions. J. Neurosci. 30, 9145–9156.
Graubard, K., Raper, J. A., and Hartline, D. K. (1980). Graded synaptic transmission between spiking neurons. Proc. Natl. Acad. Sci. U.S.A. 77, 3733–3735.
Hajos, N., and Mody, I. (1997). Synaptic communication among hippocampal interneurons: properties of spontaneous IPSCs in morphologically identified cells. J. Neurosci. 17, 8427–8442.
Hines, M. L., and Carnevale, N. T. (1997). The NEURON simulation environment. Neural. Comput. 9, 1179–1209.
Hughes, S. W., Lorincz, M., Cope, D. W., and Crunelli, V. (2008). NeuReal: an interactive simulation system for implementing artificial dendrites and large hybrid networks. J. Neurosci. Methods 169, 290–301.
Iravanian, S., and Christini, D. J. (2007). Optical mapping system with real-time control capability. Am. J. Physiol. Heart Circ. Physiol. 293, H2605–H2611.
Izhikevich, E. M. (2004). Which model to use for cortical spiking neurons? IEEE Trans. Neural Netw. 15, 1063–1070.
Le Masson, G., Le Masson, S., and Moulins, M. (1995). From conductances to neural network properties: analysis of simple circuits using the hybrid network method. Prog. Biophys. Mol. Biol. 64, 201–220.
Lin, R. J., Bettencourt, J., Wha Ite, J., Christini, D. J., and Butera, R. J. (2010). Real-time experiment interface for biological control applications. Conf. Proc. IEEE Eng. Med. Biol. Soc. 1, 4160–4163.
Lobb, C. J., and Paladini, C. A. (2010). Application of a NMDA receptor conductance in rat midbrain dopaminergic neurons using the dynamic clamp technique. J. Vis. Exp. Available at: www.jove.com/details.php?id=2275
Maccaferri, G., Roberts, J. D., Szucs, P., Cottingham, C. A., and Somogyi, P. (2000). Cell surface domain specific postsynaptic currents evoked by identified GABAergic neurones in rat hippocampus in vitro. J. Physiol. 524(Pt 1), 91–116.
Mainen, Z. F., and Sejnowski, T. J. (1996). Influence of dendritic structure on firing pattern in model neocortical neurons. Nature 382, 363–366.
Manor, Y., Nadim, F., Abbott, L. F., and Marder, E. (1997). Temporal dynamics of graded synaptic transmission in the lobster stomatogastric ganglion. J. Neurosci. 17, 5610–5621.
Netoff, T. I., Banks, M. I., Dorval, A. D., Acker, C. D., Haas, J. S., Kopell, N., and White, J. A. (2005). Synchronization in hybrid neuronal networks of the hippocampal formation. J. Neurophysiol. 93, 1197–1208.
Olypher, A., Cymbalyuk, G., and Calabrese, R. L. (2006). Hybrid systems analysis of the control of burst duration by low-voltage-activated calcium current in leech heart interneurons. J. Neurophysiol. 96, 2857–2867.
Pike, F. G., Goddard, R. S., Suckling, J. M., Ganter, P., Kasthuri, N., and Paulsen, O. (2000). Distinct frequency preferences of different types of rat hippocampal neurones in response to oscillatory input currents. J. Physiol. 529, 205–213.
Prinz, A. A., Abbott, L. F., and Marder, E. (2004). The dynamic clamp comes of age. Trends Neurosci. 27, 218–224.
Rotstein, H. G., Pervouchine, D. D., Acker, C. D., Gillies, M. J., White, J. A., Buhl, E. H., Whittington, M. A., and Kopell, N. (2005). Slow and fast inhibition and an H-current interact to create a theta rhythm in a model of CA1 interneuron network. J. Neurophysiol. 94, 1509–1518.
Saraga, F., Wu, C. P., Zhang, L., and Skinner, F. K. (2003). Active dendrites and spike propagation in multi-compartment models of oriens-lacunosum/moleculare hippocampal interneurons. J. Physiol. 552, 673–689.
Sharp, A. A., O’Neil, M. B., Abbott, L. F., and Marder, E. (1993). The dynamic clamp: artificial conductances in biological neurons. Trends Neurosci. 16, 389–394.
Softky, W., and Koch, C. (1993). The highly irregular firing of cortical cells is inconsistent with temporal integration of random EPSPs. J. Neurosci. 13, 334–350.
Sorensen, M., DeWeerth, S., Cymbalyuk, G., and Calabrese, R. L. (2004). Using a hybrid neural system to reveal regulation of neuronal network activity by an intrinsic current. J. Neurosci. 24, 5427–5438.
Tort, A. B. L., Rotstein, H. G., Dugladze, T., Gloveli, T., and Kopell, N. J. (2007). On the formation of gamma-coherent cell assemblies by oriens lacunosum-moleculare interneurons in the hippocampus. Proc. Natl. Acad. Sci. U.S.A. 104, 13490–13495.
Uhlenbeck, G. E., and Ornstein, L. S. (1930). On the theory of the Brownian motion. Phys. Rev. 36, 823.
Ulrich, D., and Huguenard, J. R. (1996). Gamma-aminobutyric acid type B receptor-dependent burst-firing in thalamic neurons: a dynamic clamp study. Proc. Natl. Acad. Sci. U.S.A. 93, 13245–13249.
Keywords: RTXI, dynamic clamp, simulation, real-time Linux, computational neuroscience
Citation: Kispersky TJ, Economo MN, Randeria P and White JA (2011) GenNet: a platform for hybrid network experiments. Front. Neuroinform. 5:11. doi: 10.3389/fninf.2011.00011
Received: 19 April 2011;
Accepted: 12 July 2011;
Published online: 26 July 2011.
Edited by:
Shiro Usui, RIKEN Brain Science Institute, JapanReviewed by:
Shiro Usui, RIKEN Brain Science Institute, JapanAstrid A. Prinz, Emory University, USA
Copyright: © 2011 Kispersky, Economo, Randeria and White. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence: John A. White, Department of Bioengineering, University of Utah, 20 South 2030 East, Room 108 BPRB, Salt Lake City, UT 84112, USA. e-mail:am9obi53aGl0ZUB1dGFoLmVkdQ==



