Voltage and spike timing interact in STDP – a unified model

Introduction

Spike-timing-dependent plasticity (STDP; Bell et al., 1997; Markram et al., 1997; Bi and Poo, 1998; Sjöström et al., 2001) is induced for most synapses by stimulating pairs of pre- and postsynaptic spikes. For synapses between cortical or hippocampal pyramidal neurons, a presynaptic spike a few milliseconds before a postsynaptic one typically leads to long-term potentiation (LTP) whereas the reverse timing leads to depression (Markram et al., 1997; Bi and Poo, 1998; Sjöström et al., 2001), but other preparations exhibit a wide range of other dependencies upon spike timing (Bell et al., 1997; Debanne et al., 1998; Abbott and Nelson, 2000). Classical models of STDP (Gerstner et al., 1996; Kempter et al., 1999; Roberts, 1999; Song et al., 2000) take the dependence upon the time difference between pre- and postsynaptic spikes explicitly into account by a learning window or STDP function with two phases, one for potentiation and another one for depression (for a review see Gerstner and van Hemmen, 1992; Morrison et al., 2008). However, the dependence upon the timing of a pair of spikes visualized in the STDP function is only one of many aspects of plasticity. First, in standard pairing experiments, pairings are repeated several times. The final outcome of experiments depends non-linearly on the number of pairings and, for a fixed number of pairings, on the repetition frequency (Markram et al., 1997; Senn et al., 2001; Sjöström et al., 2001). Second, a symmetric triplet of spikes in a post-pre-post configuration has the exact same two pairs as a symmetric pre-post-pre triplet. Hence, any pair-dependent STDP function predicts the same outcome for both protocols whereas experiments show significant differences (Wang et al., 2005). In particular, pre-post pre with the same timing difference leads to insignificant changes, whereas post-pre-post induces a strong potentiation of synapses in hippocampal cultures (Wang et al., 2005). Quite generally, triplet and quadruplet dependencies measured in various experiments (Froemke and Dan, 2002; Wang et al., 2005) cannot be explained by standard STDP models. Third, the STDP function derived from standard experiments with pairs of spikes (Markram et al., 1997; Bi and Poo, 1998; Sjöström et al., 2001) does not explain the dependence of plasticity upon the timing of bursts of several postsynaptic spikes (Kampa et al., 2006; Nevian and Sakmann, 2006). Fourth, the outcome of synaptic plasticity depends on the dendritic location of the synapse (Froemke et al., 2005; Kampa et al., 2006; Letzkus et al., 2006; Sjöström and Häusser, 2006). Finally, plasticity can also be induced in the absence of postsynaptic firing, e.g., in voltage-clamp experiments (Kelso et al., 1986; Artola et al., 1990; Ngezahayo et al., 2000). None of these aspects is taken into account in classical phenomenological STDP models (Gerstner et al., 1996; Kempter et al., 1999; Roberts, 1999; Song et al., 2000). Modifications of the classical STDP models including weight-dependence (Kistler and van Hemmen, 2000; van Rossum et al., 2000; Rubin et al., 2001) or alternative summation schemes (Izhikevich, 2003), introduction of frequency dependence (Froemke and Dan, 2002) or some voltage dependence (Brader et al., 2007) resolve at most one or two of the above issues, but not all of them.

The basic shortcoming of the family of classical phenomenological STDP models is an inappropriate focus on a single pair of pre- and postsynaptic spikes. There are a couple of promising phenomenological STDP models that go beyond the pair interaction, most notably the model of Senn and colleagues (Senn et al., 1997, 2001; Senn, 2002). This model exploits basic interactions of spike triplets, such as pre-post-post or post-pre-pre (for reviews see Gerstner and Kistler, 2002; Senn, 2002). Because of these non- linearities, it is able to account not only for the timing dependence of experimental STDP, but also for the frequency dependence of STDP and some triplet effects (Senn, 2002). Similar in spirit is the model of Pfister and Gerstner (2006). In this model depression is induced by post-pre pairs, while LTP requires at least a triplet of spikes, e.g., pre-post-post or post-pre-post. The frequency dependence of STDP (Markram et al., 1997; Sjöström et al., 2001) then follows directly from the assumptions (Pfister and Gerstner, 2006). However, neither the model of Senn et al. nor that of Pfister and Gerstner can be applied outside the realm of spike-triggered plasticity. In particular, no voltage dependence is included in these models. Effects of dendritic location are also out of the scope of these two models. Another category of models offers biophysical mechanisms of plasticity (Lisman and Zhabotinsky, 2001; Shouval et al., 2002; Miller et al., 2005; Rubin et al., 2005; Graupner and Brunel, 2007). Most of these are, however, not usually tested on more elaborate plasticity protocols.

In this paper, we aim at a unified explanation of all of the above experimental results with one single model, proposed previously (Clopath et al., 2008, 2010). The model is a minimal one in the sense that it should be complex enough to reproduce, at least qualitatively, the data mentioned above but still with a restricted number of parameters; and a phenomenological one in the sense that it is composed of abstract variables that are not directly linked to identified biophysical quantities. This approach enables the research to be generic, i.e., it presents a framework in which one can reason about synaptic plasticity experiments even when the biophysical pathways are unknown. Note that the framework could be the same, even if the biophysical implementation in terms of molecules differs from one type of synapse to the next. For example, synaptic depression in STDP experiments seems to depend crucially on calcium concentration in hippocampus (Bi and Poo, 2001), but also on retrograde messenger like endocannabinoid in visual cortex (Sjöström et al., 2003, 2004). The drawback of the phenomenological model is that the biophysical nature of synaptic plasticity cannot be addressed in this paper. In particular, we do not consider pharmacological data. Moreover the model only focuses on the induction of synaptic plasticity but not on its maintenance. It has to be combined with a model of consolidation (Clopath et al., 2008; Barrett et al., 2009) to arrive at a more complete description of synaptic plasticity across different time scales.

Even though we put some focus on a phenomenological explanation of experimental plasticity results in dendrites we did not want to implement our plasticity model in a detailed biophysical neuron model with multiple compartments and ion channels. While modeling backpropagating action potentials and dendritic spikes in biophysical models is possible (Achard and De Schutter, 2006; Druckmann et al., 2007), it is a project in its own right. Instead of explicitly modeling the dendritic effects we shortcut the argument and impose a putative time course of the voltage at the site of the synapse. The exact time course could have been the result of a more detailed model (which we did not do) or could come from experimental measurements. Whenever such experiments were available we took that data into account.

Materials and Methods

Model of Synaptic Plasticity

The plasticity model we are exploring in this paper is described in Clopath et al. (2010). It depends on the presynaptic spike time and on the (momentary or filtered) time course of the postsynaptic membrane potential. Depression and potentiation are modeled as two independent mechanisms and lead to a downregulation or upregulation of the synaptic weight w characterizing the strength of the connection from a presynaptic neuron to the postsynaptic neuron under consideration. For biophysical reasons we impose that the weight always stays between 0 and a maximal value w_max.

The synapse is depressed if a presynaptic spike occurs when the neuron is depolarized for some time. We can formalize this idea mathematically defining a presynaptic spike train as a series of delta pulses X(t) = Σ_iδ(t − t_i) where t_i are the spike times. The postsynaptic membrane potential u is low-pass filtered with a time constant τ₋

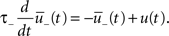
Depression is induced at the moment of presynaptic spike arrival if the postsynaptic trace 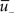is above a threshold θ₋. This typically happens if there was a postsynaptic spike some time before the presynaptic spike, leading to spike-timing dependence; if synaptic input at other synapses induced some compound EPSP and hence a depolarization at the site of the active synapse, leading to associativity of depression; if any source of depolarizing current input is given in an experiment. Mathematically, the change of the synapse is described by the differential equation

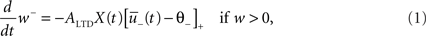
where A_LTD is an amplitude (see Figure 1A). The notation [x]₊ equals x if x is positive and is 0 otherwise. Downregulation of the synapse stops if w hits 0.

FIGURE 1

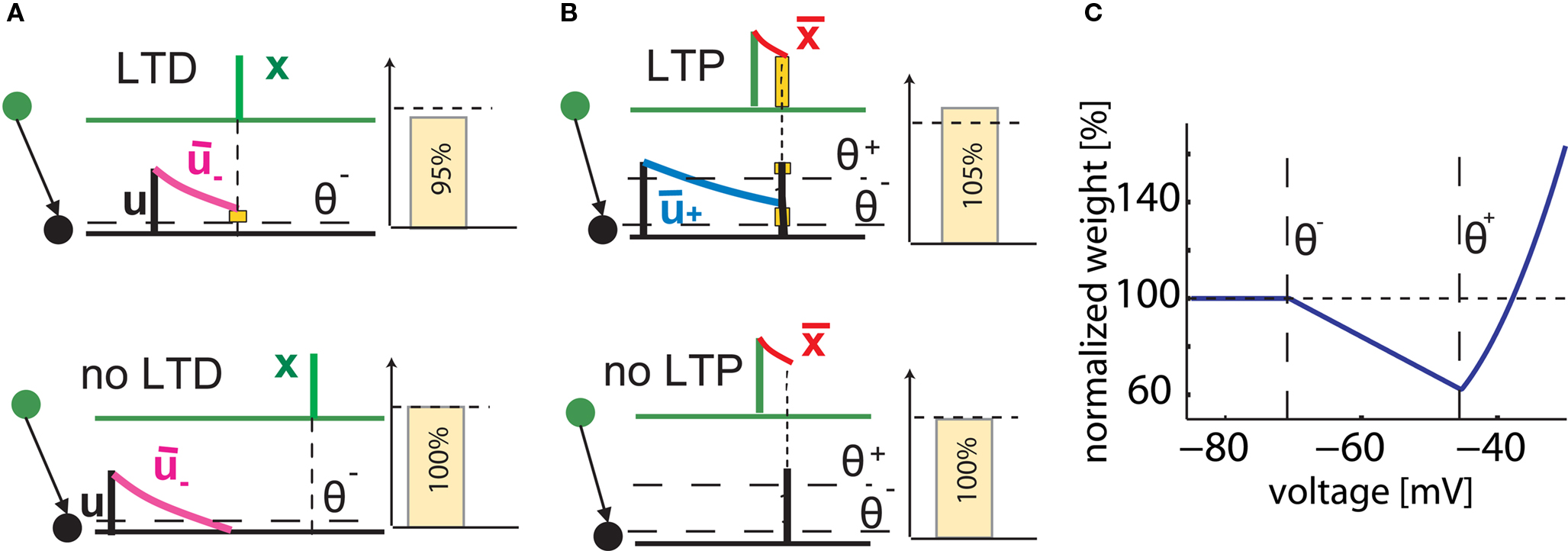
Figure 1. Schematics of the model. (A) LTD occurs at the time of a presynaptic spike (green) if the low-pass filtered voltage trace 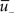(magenta) is above θ₋ (dashed line). The amount of LTD is proportional to the size of the yellow box. If the timing difference between post- and presynaptic spikes is too big, no LTD is induced (bottom). (B) LTP requires three factors: a momentary voltage u (black) above θ₊ (dashed line), the trace 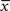(red) left from a previous presynaptic spike above 0, and the trace 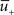(blue) of the low-pass filtered voltage above θ₋ (dashed line). The three conditions are met at the moment of the second postsynaptic spike in a post-pre-post triplet (top panel), but not after a single pre-post pair (bottom). The amount of plasticity is proportional to the multiplication of the yellow boxes. (C) Presynaptic stimulation under voltage clamp conditions shows the relevance of the threshold θ₋ for onset of LTD and θ₊ for the onset of the LTP contribution. LTP becomes dominant if the voltage is 10 mV or more above θ₊.

Potentiation of the synapse occurs if the following three conditions are met simultaneously: (i) The momentary postsynaptic voltage u is above a threshold θ₊ which is around the firing threshold of the neuron, in particular θ₊ > θ₋. (ii) The low-pass filtered voltage 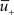is above θ₋. (iii) A presynaptic spike occurred a few milliseconds earlier and has left a “trace” 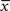at the site of the synapse. The trace could represent the amount of glutamate bound at the postsynaptic receptor; or the percentage of NMDA receptors in an upregulated state or something similar.

The weight change during potentiation can be written as

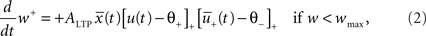
where 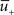is a similar to 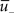but with a filter time constant τ₊ instead of τ₋ and 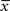is a low-pass filter of the presynaptic spike train with time constant τ_x (see Figure 1B)

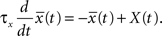
Note that the postsynaptic variable enters twice. First, we need a spike to overcome the threshold θ₊ and second, the filtered membrane must be depolarized before the spike. This depolarization could be due to earlier action potentials which have left a depolarizing spike after-potential which explains the relevance of post-pre-post or pre-post-post triplets of spikes (see Figure 1B); or to sustained input at other synapses, leading to associativity of LTP.

The total synaptic change is the contribution of depression and potentiation:

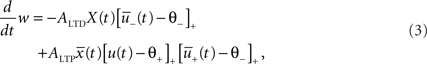
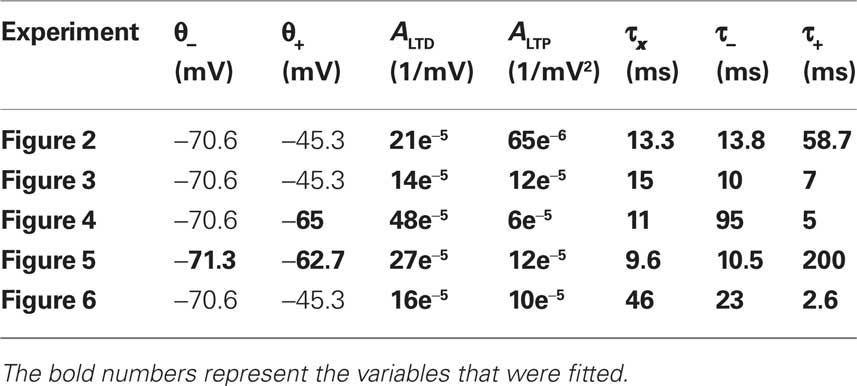
where the differential equation is applied within the hard bounds 0 < w < w_max. The initial weight is put to w = 1 (arbitrary units) and the maximal weight to w_max = 1.6 (Figure 2), corresponding to a maximal weight increase by 60%, consistent with the experiments of Markram and colleagues (Markram et al., 1997; Senn et al., 2001). The free parameters of the plasticity models that need to be fitted to experiments are the two amplitudes A_LTD and A_LTP as well as the three time constants τ_x, τ₊, and τ₋. Finally the thresholds θ₊ and θ₋ can vary but for most of the experiments they are set to the firing threshold and the resting potential respectively.

FIGURE 2

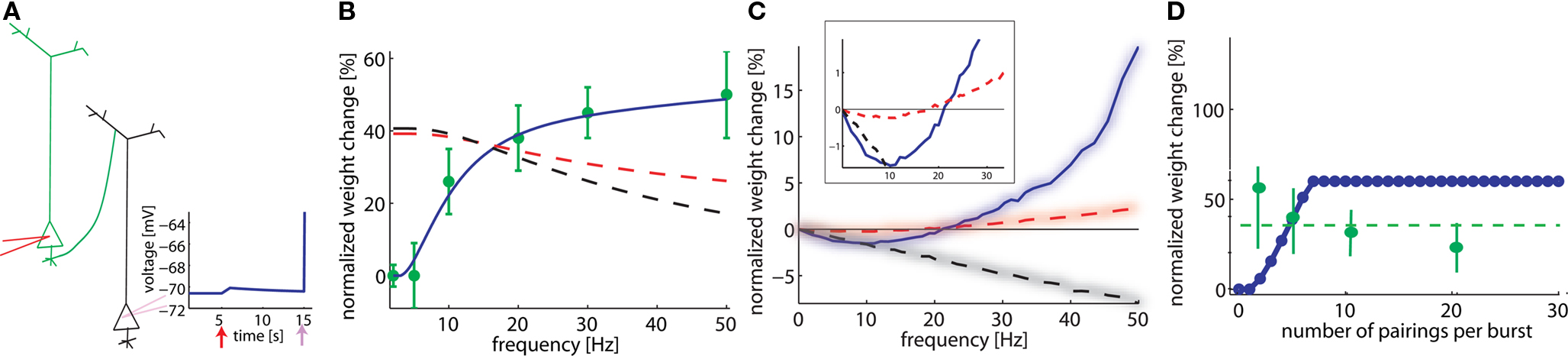
Figure 2. Model depends on spike frequency. (A). Schematics of STDP experiment. Injection of a current pulse in the presynaptic neuron at t = 5 ms leads to an EPSP which is followed t = 15 ms by an action potential triggered by a current pulse into the postsynaptic neuron. (B) If pre-post pairings at lags of 2 ms are repeated, the total amount of weight change (vertical) depends on the repetition frequency (horizontal axis). Model in blue, data redrawn from Markram et al. (1997) in green. A standard pair-based STDP model cannot account for the frequency, whatever the summation scheme (black dashed line: all pairs contribute; red dashed line: only pairs between the nearest spikes contribute to plasticity). (C) The frequency dependence is different, if both pre- and postsynaptic spikes are generated by a Poisson process (box: zoom). (D) The total amount of plasticity depends on the number of pre-post pairings at 2 ms lag. At least two pairs at 20 Hz are necessary. With our set of parameters, saturation at the maximal weight occurs for around seven pairings (model is blue, data redrawn from Senn et al. (2001) in green; in experiments, saturation is maybe already reached after two pairings, dashed green line).

Neuron Model

Since the voltage is a key quantity in our plasticity model, an appropriate neuron model is needed. Since the plasticity model is a phenomenological one, we opted also for a phenomenological neuron model. We took the Adaptive Exponential Integrate-and-Fire (AdEx) model (Brette and Gerstner, 2005) described by

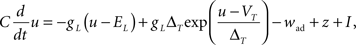
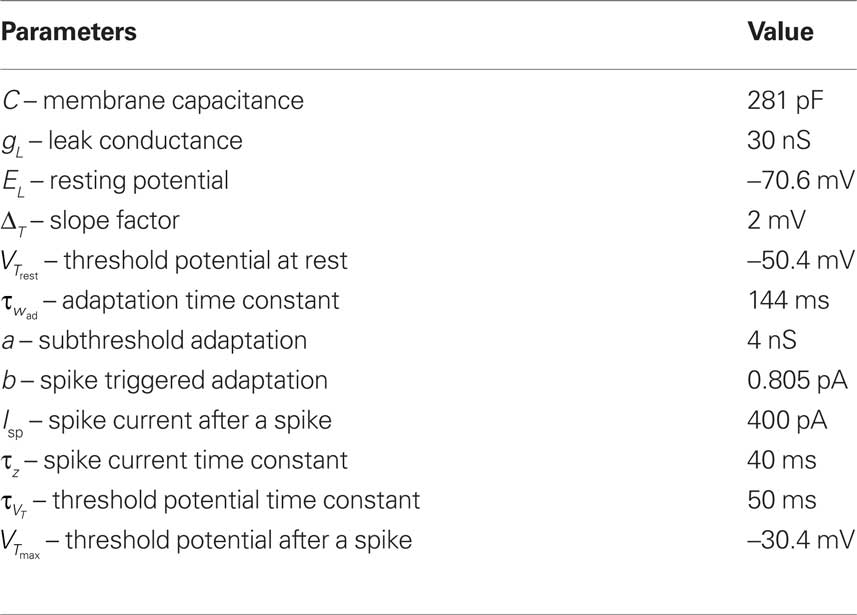
where C is the membrane capacitance, g_L the leak conductance, E_L the resting potential and I the stimulating current. The exponential term describes the rapid activation of the sodium channel, V_T is the threshold above which the dynamics is driven by this exponential and Δ_T controls the rise in the upswing of the action potential. Integration is stopped if the u reaches 100 mV above rest which corresponds to the peak of the action potential. At this time, the voltage is reset to 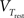. An adaptation variable w_ad (acting as a hyperpolarizing current) increases by an amount of b after each spike. Moreover adaptation is also coupled to the voltage. The adaptation dynamics is written as

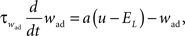
where a is responsible for a subthreshold adaptation and 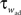is a time constant. In an extension to the AdEx model we added an additional current z responsible for a depolarizing spike afterpotential which is set to a value I_sp at each spike, decaying otherwise with a time constant τ_z

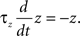
The z variable can be seen as a simplified description of a slowly inactivating sodium current such as the I_NaP (Magistretti and Alonsoa, 1999). Finally the threshold is adaptive as in Badel et al. (2008). At every spike the threshold jumps to 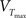and decays to 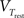otherwise with a time constant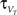

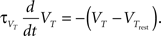
The neuron model has a number of variables listed above. For plasticity experiments considered here, it is crucial to have a spike after depolarization in order to have a trace of the spike lasting for about 50 ms, as explained in Clopath et al. (2010). It is therefore necessary to have an adaptive threshold, to prevent the neuron from spiking during this after spike phase. The exponential term and the adaption variable are not important for the results here but are part of the neuron model to make it more accurate, as shown in Clopath et al. (2007), Badel et al. (2008), and Naud et al. (2008). All the parameters are taken from Clopath et al. (2010) and are shown in Table 1.

TABLE 1

Table 1. Parameters of the neuron model.

Parameters

The free parameters of the plasticity model are fitted to the different experiments described above (Markram et al., 1997; Sjöström et al., 2001; Froemke and Dan, 2002; Wang et al., 2005; Kampa et al., 2006) (Table 2). The thresholds are fixed to the resting potential and the firing threshold for all the experiments except the ones of Froemke and Dan (2002) and Kampa et al. (2006). The error, defined as the difference between the experimental and the theoretical value squared, is minimized. For Figures 5 and 6, the STDP learning window is only characterized by two experimental data points. We thus gave those points five times more weight than the others in the computation of the error. Note that the experimental values were taken from the figures of the different experimental papers (since we did not have the raw data) and thus the data points redrawn on the figures of the present paper are not precise.

TABLE 2

Table 2. Parameters of the plasticity model fitted to different experiments.

Results

As explained in Section “Materials and Methods,” our model of voltage based plasticity (Clopath et al., 2008, 2010) requires a minimal membrane voltage at the site of the synapse in order to allow synaptic depression; and a momentary voltage larger than the firing threshold u > θ₊ to allow potentiation to occur. The combination of potentiation and depression leads, in voltage clamp experiments, to a voltage dependence shown in Figure 1C which is reminiscent of that found in earlier studies on voltage dependence of synaptic plasticity (Kelso et al., 1986; Artola et al., 1990; Ngezahayo et al., 2000). In a simulated STDP experiment, a single post-pre spike pairing leads to LTD if the time difference is short enough, but no plasticity is induced if the timing difference is too big or if the time is inversed (Figures 1A,B). However, a triplet of spikes in post-pre-post configuration can induce a small amount of LTP, since the following three conditions are met: the first postsynaptic spike induces a trace in the average voltage ; the presynaptic spike leaves a trace at the site of the synapse; and the momentary voltage during the second postsynaptic action potential is sufficiently high to surpass the second threshold u(t) > θ₊ (see Figure 1B). In our previous papers (Clopath et al., 2008, 2010), the model has already been shown to be in qualitative agreement with the voltage clamp experiment that is the basis of the Artola–Bröcher–Singer (ABS) plasticity rule (Artola et al., 1990), to yield a plausible dependence upon presynaptic frequency (Dudek and Bear, 1992), an STDP learning window (Markram et al., 1997), a burst-timing-dependent learning window (Nevian and Sakmann, 2006) as well as a tight relation between spike timing and voltage during manipulations of somatic voltage by current injection (Sjöström et al., 2001). In this paper, the model will be tested against several other classical experimental data on synaptic plasticity. Note that experimental data on STDP in different preparations and experimental conditions is now so rich, that the list of tests that can be carried out and presented in a single paper cannot be exhaustive. The result section is organized in three parts. We first turn to the data from the classical 1997 STDP paper of Markram et al. (1997) and some follow-up experiments (Senn et al., 2001). We then address a couple of more recent studies that explored plasticity in dendrites. We emphasize that dendrites are not modeled explicitly. Rather, we consider plasticity as a local event at the site of the synapse. Since the essential ingredient of our voltage based plasticity model is the time course of the voltage, it is sufficient to model the local voltage at the site of the synapse. In the final part, we focus on STDP experiments using slightly different protocols, for example extracellular stimulation, leading to a large compound EPSP in the postsynaptic neuron or hippocampal cultures which have slightly different dynamics than acute cortical slices.

STDP is Sensitive to Frequency

As early as in 1997, Markram et al. (1997) showed that the amount of plasticity resulting in pre-post pairing does not only depend on the lag between the pre- and postsynaptic spike but also on the frequency at which these pairings are repeated. By injecting short current pulses into two pyramidal cells, five pairs of pre- and postsynaptic spikes with a lag of 2 ms are elicited at different frequencies and repeated 10 times every 4 s. The data (Markram et al., 1997) show no change of synaptic weight at low frequency pairing whereas LTP is induced at high frequency. Pair-based STDP rules (Gerstner et al., 1996; Kempter et al., 1999; Song et al., 2000), where a pre-post pair leads to LTP and a post-pre pair leads to LTD, cannot account for this frequency dependency. Indeed, independent of the specific choice of parameters, pre-post pairings at low frequency will result in LTP with standard pair-based STDP models (Figure 2B, dashed lines); moreover raising the repetition frequency of the pre-post pairings induces a weak post-pre interaction which decreases the potentiation in the pair-based models, whereas LTP increases in the experiments. This picture changes completely with our model (Figure 2B). The reason is that our model needs a post-pre-post triplet to induce potentiation. At low pairing frequencies such triplets are quasi inexistent since the interval between two postsynaptic action potentials is too long whereas higher frequencies induce the triplet interaction necessary for LTP (see Figures 1 and 2B).

In the modeling literature, the frequency dependence is also studied in an alternative scenario where both the pre- and postsynaptic neuron fire stochastically with Poisson distributed interspike intervals. In our simulations, the presynaptic neuron fires at 10 Hz and the postsynaptic one fires at a fixed frequency different from one simulation experiment to the next. If plasticity is plotted as a function of the firing rate of the postsynaptic neuron (across repeated epochs of 1 s), both LTD and LTP are exhibited: low firing rates lead to LTD whereas high rates induce LTP (Figure 2C). This result is to be contrasted with the frequency dependence found in the same model with identical parameters in an experiment simulating repeated pre-post pairings as in Figure 2B. These results show that timing dependence and frequency dependence of synaptic plasticity interact. For the same firing frequency of, say 10 Hz, of pre- and postsynaptic neuron, systematic timing of action potentials in the causal order of “pre before post” leads to strong LTP, whereas random timing of the same number of action potentials leads to significant LTD. The frequency dependence in Figure 2C is similar to the one of the well known Bienenstock–Cooper–Munro (BCM) model (Bienenstock et al., 1982). A standard pair-based rule, where all the pairs are considered, is linear with respect to the frequency. For a typical case where the integral of the STDP learning window is negative, the weight change decreased linearly with frequency. However, a pair-based rule where only the nearest pair is considered results in a non-linear frequency dependence, if an appropriate set of parameters is chosen (see Izhikevich and Desai, 2003) (Figure 2C, dashed red line). The qualitative frequency dependence of the pair-based nearest-neighbor rule for the Poisson input is similar to, but much weaker than the one in our model (Figure 2, inset). For pairing experiments (Figure 2B), the models are qualitatively different.

A further question explored by Senn et al. (2001) was how many pairings were needed to induce potentiation. Pre- and postsynaptic spike trains of 20 Hz were paired with a postsynaptic spike delay of 2 ms, repeated 10 times every 4 s. The number of spikes in the paired trains was varied from 2 up to 20 in the experiment, and between 0 and 30 in our model. Isolated pre-post pairings showed no effects in the experiment (as can be seen from the LTP results at low frequency in Figure 2B), whereas pairings with two and more pre-post gave an effect (Senn et al., 2001). In our model, isolated pairings give no effect (because the triplet term is not activated), whereas two or more repetitions at 20 Hz induce LTP. In contrast to the results of Senn et al. more spikes lead in our model to a linear increase before plasticity enters into saturation (Figure 2D). This could be due to the fact that the sliding threshold for the LTD to LTP transition (Bienenstock et al., 1982; Clopath et al., 2010) is not taken into account in this simulation. Since each plasticity induction protocol lasts more than 40 s, it is possible that the first pairing leads to LTP but with time the threshold slides so that later parings result in LTD. The net effect would give less LTP. Note the large error bars in the statistics of the experiments presented in Senn et al. (2001), which make the results consistent with a horizontal fit (dashed green line) or with a decrease with the number of pairings.

Beyond the Point Neuron: What Counts is the Voltage at the Synapse

The plasticity model depends directly on the postsynaptic voltage at the synapse; depending on the location of the synapse along the dendrite, the time course of the voltage is expected to be different. A change in the time course of the modeled voltage during plasticity experiments enables us to explore the effects that the failure of a backpropagating action potential or the form of dendritic spikes could have on the outcome of plasticity experiments.

The role of backpropagating action potentials

In the protocol from Sjöström and Häusser (2006), five pre-post pairs of spikes at 50 Hz are induced 15 times every 10 s. The lag between the first pre- and the first postsynaptic spike is 10 ms. Data of Sjöström and Häusser (2006) show that such a high-frequency pairing leads to LTP in basal dendrites, but to LTD in apical dendrites. A potential explanation is that LTP does not occur in distal dendrites, if there is a failure of the backpropagating action potential to reach the synapse. In agreement with this interpretation, LTP can be rescued in the apical dendrites if, in addition to the pairing, a depolarizing current in the dendrite is injected, boosting the backpropagating action potential (Sjöström and Häusser, 2006).

In a simulation of the high-frequency pairing experiment in our model of synaptic plasticity, we consider two different situations. In both cases, a current pulse is injected in the neuron model, but two different pulse amplitudes are studied. In the first case, the current pulse is sufficient to elicit a postsynaptic spike (Figure 3A, left). We find that presence of the postsynaptic spikes resulted in LTP (Figure 3B, left). We assume that the spike in the basal dendrite has 80% of the amplitude of a somatic spike. This scenario corresponds to the situation in the basal dendrites (where the action potential is damped); but also to the apical dendrites with depolarizing current, under the assumption that the depolarizing current is sufficient to allow transmission of the backpropagating action potential.

FIGURE 3

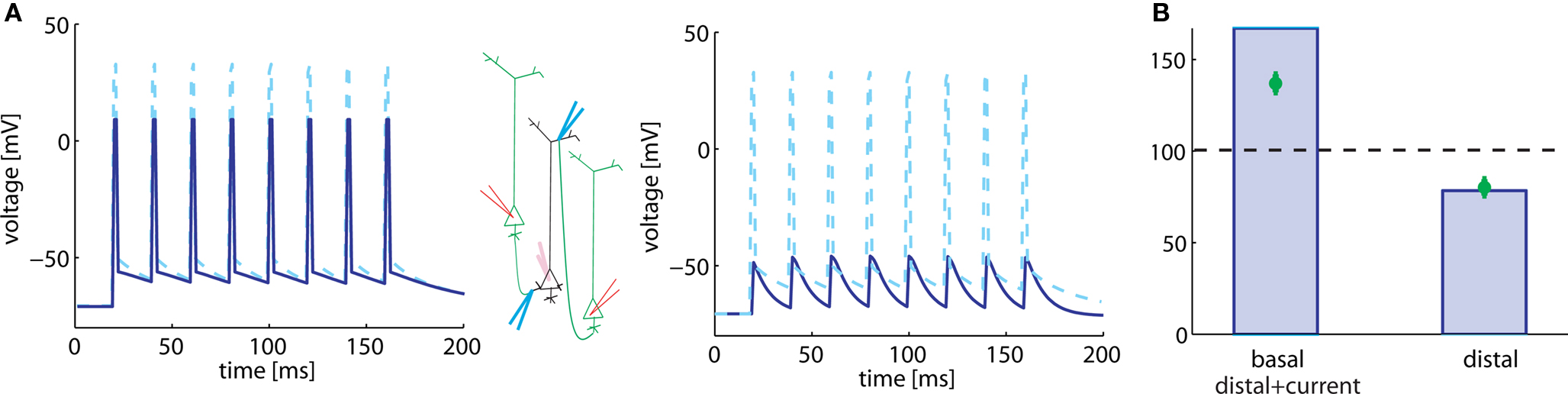
Figure 3. Plasticity results depend on voltage trajectory. (A) Eight 50 Hz pre-post pairings are induced by injection of somatic current pulses (center, schematic). We model the voltage time course at synapses located on the soma (dashed) and basal (solid) dendrite by the sequence of action potentials, shown on the left. The voltage time course at synapses located distally on apical dendrites is modeled as subthreshold response (right, solid line). (B) 50 Hz pre-post pairing leads to LTP (left column) when postsynaptic response consists of spikes as in the basal dendrite (or if the presence of backpropagating action potentials) and to LTD when the postsynaptic response stays subthreshold (right column). Green, data redrawn from Sjöström and Häusser (2006); blue, simulations.

In the second case, the pulse amplitude of the injected current is reduced so that it provokes a subthreshold response only (Figure 3A, right). We imagine that this corresponds to the situation that is seen by a synapse located distantly on the apical dendrite. Because of the large electrotonic distance, it will not feel the somatic action potential, but only voltage deflection of small amplitude. In our model, this scenario leads to LTD at the synapse, as in the apical dendrites (Figure 3B, right).

We note that the actual value of LTP in proximal synapses, predicted by the model, is slightly higher than that measured in experiments. However, the data (Sjöström and Häusser, 2006) show that the connections closest to the soma undergo a synaptic change of about 150–200%, whereas those further away show less potentiation. The experiential data in Figure 3A corresponds to an average over all “proximal” synapses.

The role of bursts in basal dendrites

Experiments of Kampa et al. (2006) studied the pairing of a presynaptic spike with a burst of three postsynaptic spikes at 200 Hz. Hence the total duration of a burst was 10 ms. The time between the presynaptic spike and the postsynaptic burst varies. Pairs of presynaptic spike and postsynaptic burst (three spikes, intra burst frequency of 200 Hz) were repeated 60 times every 10 s.

In agreement with the experimental results, a presynaptic spike followed 10 ms later by the start of the postsynaptic burst results in LTP whereas a postsynaptic burst followed 45 ms later by a presynaptic spike gives LTD (Figure 4). Hence pre-before-burst yields LTP whereas burst-before-pre yields LTD, as expected. Experiments have shown that bursts, and hence dendritic calcium spikes, are important for the induction of plasticity (Kampa et al., 2006). This aspect is modeled here by the non-linear term for potentiation. The plasticity changes for −45 and +10 ms are found to be a stable result of our model over a broad range of parameters.

FIGURE 4

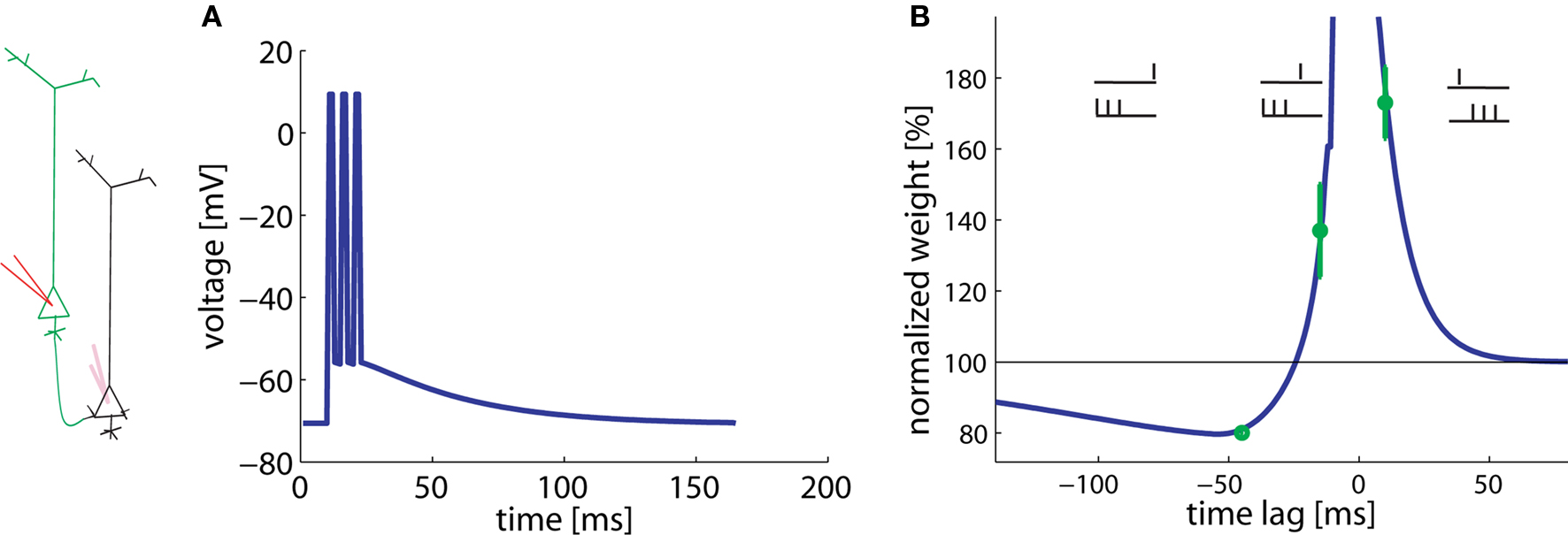
Figure 4. Burst-timing-dependent learning window. A postsynaptic burst of three spikes is paired with a presynaptic spike. (A) Assumed voltage waveform at the basal dendrite. (B) The total weight change plotted as a function of the time between the presynaptic spike and the start of the postsynaptic burst varies. Data redrawn from Kampa et al. (2006) in green, simulations in blue.

Surprisingly, however, burst-before-pre gives LTP in the experiments, if the burst starts 15 ms before the presynaptic spike. Our model shows that this effect can be explained under the assumption of a low LTP threshold (θ₊) in the basal dendrites. The optimal value is about 10 mV above rest (see Table 2). Since the spikes have a long depolarizing spike after-potential (Nevian et al., 2007) (Figure 4A), a low LTP threshold allows, for a timing difference burst-before-pre of 15 ms, an overlap between presynaptic and postsynaptic events. Thus, a low threshold corresponds to a shift in the horizontal position of the transition from LTP to LTD in the burst-timing learning window.

Plasticity in Different Preparations

In the previous sections, we focused on data obtained from experiments with multiple patch electrodes. In this last section, we explore plasticity data coming from different preparations.

Extracellular stimulation

In experiments of Froemke and Dan (2002), pairs and triplets of spikes are repeated 60 times at 0.2 Hz. The main difference to the pairing experiments of Markram et al. (1997) is that current injection into the presynaptic neuron is replaced by extracellular stimulation of axonal fibers projecting onto the postsynaptic neuron (Figure 5A). Since presynaptic stimulation in these experiments (Froemke and Dan, 2002) is extracellular and most likely triggers activity in many presynaptic fibers, we adjust the postsynaptic response to the presynaptic activity to an amplitude of 2.5 mV, corresponding to the estimated size of compound EPSP. The real compound EPSP amplitude at the site of the synapse might be even bigger (Palmer and Stuart, 2009), but this seems to be a reasonable estimate. If the time lag between the presynaptic spike arrival and postsynaptic firing is changed, the model generates a STDP function of the standard form, albeit with an amplitude slightly lower than that measured in experimental results (Figure 5B). In contrast to the results of Markram et al. (1997), LTP occurs in the pre-post configuration in our model despite the fact that the repetition frequency is only 0.2 Hz. The difference is due to the fact that extracellular stimulation leads to a significant depolarization of the postsynaptic membrane because of the large compound EPSP. This depolarization is followed in the pre-post configuration a few milliseconds later by a postsynaptic spike. Activation of the synapse, sustained depolarization before the spike, and momentary spiking are exactly the three requirements in the model to evoke LTP. The amount of potentiation in the learning window is however smaller in the model than in the experiment with this choice of EPSP amplitude; a larger amplitude yields similar results. Note that the voltage threshold θ₊ for LTP induction found by parameters optimization is about 11 mV above resting potential (see Table 2).

FIGURE 5

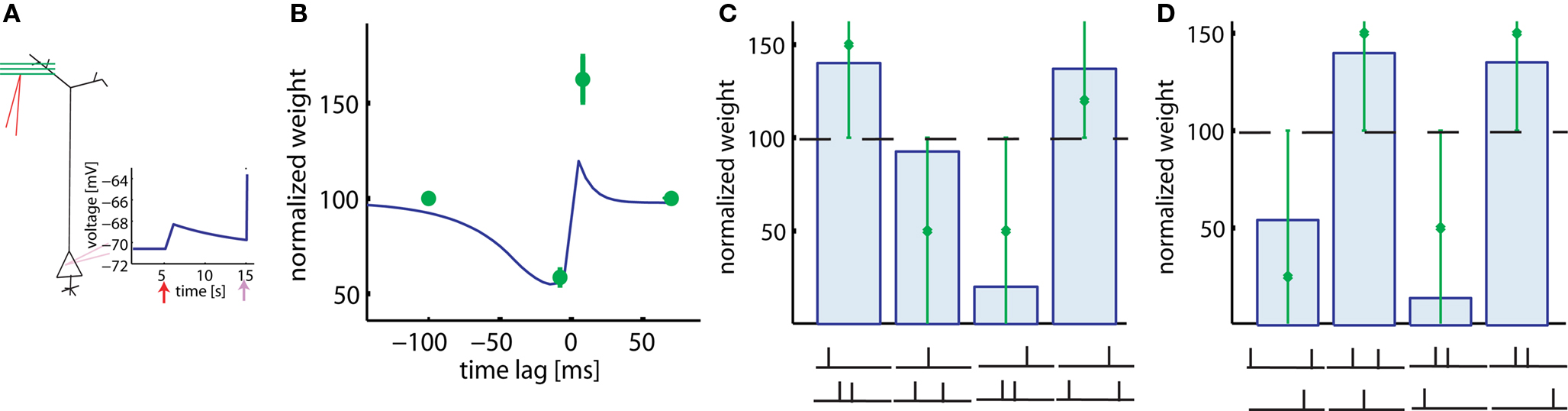
Figure 5. Results with extracellular stimulation. (A) Extracellular stimulation of presynaptic fibers followed 10 ms later by postsynaptic stimulation is described by a compound EPSP of 2.5 mV and the upswing of an action potential (schematic). (B) 60 repetitions of pre-post pairs lead to LTP despite a repetition frequency of only 0.2 Hz. The amount of LTP in our model (blue line) is smaller than in the corresponding experiment (green). The reverse firing leads to LTD. (C) Triplets consisting of two post- and one presynaptic spikes in various configurations (see drawing) are repeated at low frequencies. Presynaptic stimulation is extracellular. Line and bars: simulations, green: data redrawn from Froemke and Dan (2002). (D) Same, but triplets consisting of two pre- and one postsynaptic spike. The big error bars in (C,D) indicate that data are very noisy and thus it is only relevant whether triplets induce LTP or LTD in each configurations.

We use the same plasticity model also for the triplet experiments conducted by Froemke and Dan (2002). Triplets of one pre- and two postsynaptic spikes are induced in four different configurations: (a) pre-5ms-post-5ms-post, (b) post-5ms-pre-10ms-post, (c) post-5ms-post-5ms-pre, and (d) post-25ms-pre-5ms-post. Similarly, triplets of two pre- and one postsynaptic spikes can have one of four possible timings: (a) pre-30ms-post-10ms-pre, (b) pre-3ms-post-10ms-pre, (c) post- 5ms-pre-20ms-pre, and (d) pre-7ms-pre-3ms-post. All the eight data points can be explained qualitatively by the model (Figures 5C,D).

Pairs, triplets, and quadruplets elicited in culture hippocampal cells

In hippocampal culture, Wang et al. (2005) studied a large range of pair, triplet, and quadruplet experiments. All stimuli (pairs, triplets, or quadruplets) are repeated 60 times at 1 Hz. Since neuronal and synaptic parameters in a culture can be somewhat different, we assumed a relatively large EPSP amplitude of 7.5 mV. With such a large EPSP we find, in analogy to the results in Figure 5, a standard STDP learning window for pairing experiments at 1 Hz (Figure 6B), however with a smaller amplitude compared to that of the experiment.

FIGURE 6

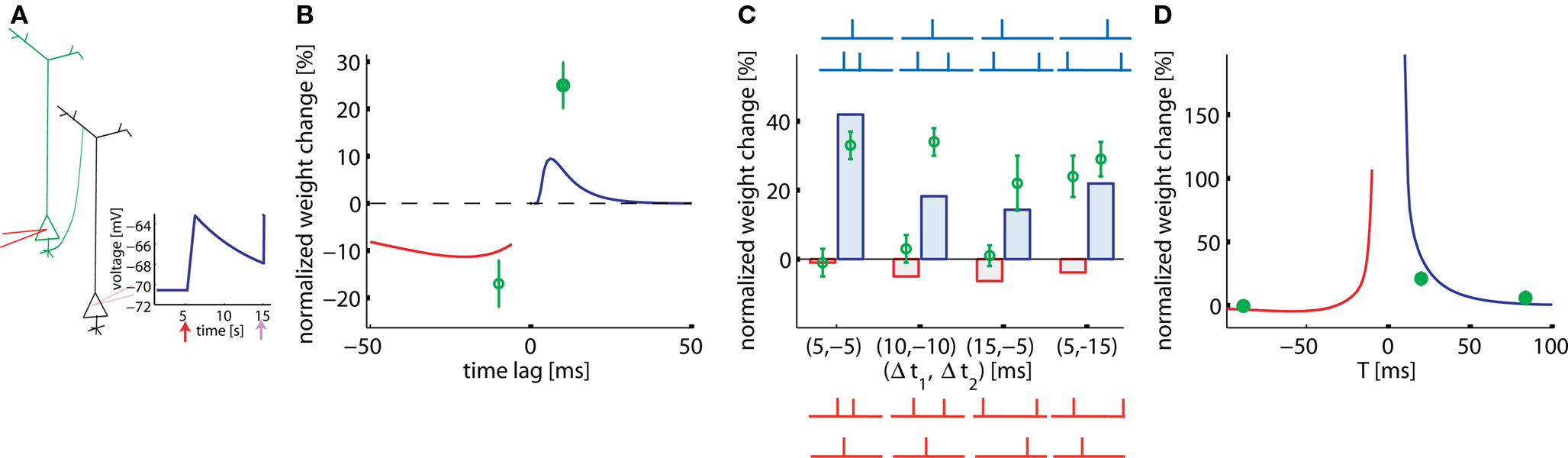
Figure 6. Pairs, triplets, and quadruplets of spikes in cultured hippocampal neurons. (A) Intracellular presynaptic stimulation results in a model EPSP of 7.5 mV (schematic). (B) STDP function in the pair-experiment. (C) Triplet experiments. Δt_1,2 in the post-pre-post configuration is the time between the single pre- and the two postsynaptic spikes (blue histogram bars and schematics) or, in the pre-post-pre experiment the time between the single post- and the two presynaptic spikes (red histogram bars and schematics). The four different post-pre-post triplets are: (a) post-5ms-pre-5ms-post, (b) post-10ms-pre-10ms-post, (c) post-5ms-pre-15ms-post, and (d) post-15ms-pre-5ms-post. The four different pre-post-pre triplets are: (a) pre-5ms-post-5ms-pre, (b) pre-10ms-post-10ms-pre, (c) pre-15ms-post-5ms-pre, and (d) pre-5ms-post-15ms-pre. Lines and bars: simulations. Green circles: data redrawn from Wang et al. (2005). (D) Quadruplet experiment (see main text).

Our model enables us to account qualitatively for seven out of eight results with triplet stimulation. Triplets in the experiments of Figure 6 are designed so that the pair interactions (pre-post or post-pre) in the pre-post-pre triplet are identical to those in the post-pre-post triplet (Figure 6C, blue and red schematic traces). Hence a pure pair-based STDP rule would predict the same result. However, in our triplet model the effective contribution of LTP is different in the two configurations (Figure 6C). Moreover, the model also enables us to explain the quadruplet experiments that used the following configurations: pre-5ms-post-T-post-5ms-pre or post-5ms-pre-T-pre-5ms-post, where T varies (Figure 6D). The only point in Figure 6C which is badly fitted is the one in the paradigm with pre-5ms-post-15ms-pre. We wondered whether the quality of the fit would increase if we included short-term plasticity into the model framework. The reason is that our plasticity model predicts too much depression, but depression would be decreased if the EPSP caused by the second presynaptic spike has a smaller amplitude than the first one. It is not clear what type of short-term plasticity is expressed hippocampal culture synapses, but, if the synapses are depressing, the scenario (5, −15) is improved without altering the qualitative behavior of the other scenarios (data not shown).

Discussion

The model presented in this paper can explain a number of synaptic plasticity experiments. It covers the presynaptic frequency dependency (Dudek and Bear, 1992), voltage-clamp experiment (ABS rule) (Artola et al., 1990), spike-timing and pairing frequency dependency (Markram et al., 1997; Sjöström et al., 2001), tight relation between voltage and spike timing (Sjöström et al., 2001), and burst-timing-dependent plasticity (Nevian and Sakmann, 2006), as shown previously (Clopath et al., 2008, 2010). In addition, the model was tested here successfully on some subtle protocols that showed an influence of the cell morphology on plasticity results (Kampa et al., 2006; Sjöström and Häusser, 2006). Our interpretation is that the morphology enters only indirectly and only as much as it leads to a change of the voltage trajectory at the site of the synapse, compared to the voltage at the soma. Accounting for presence or absence of backpropagating action potentials or dendritic location by an appropriate choice of the local voltage time course was found to be sufficient to describe the experiments considered. For example, the difference between plasticity at the basal and at the apical dendrite (failure of backpropagating action potential) can be explained only by the voltage difference. We think that this model is thus a good compromise between complexity and performance. Indeed, more detailed descriptions as provided by biophysical models (Lisman and Zhabotinsky, 2001; Shouval et al., 2002; Miller et al., 2005; Rubin et al., 2005; Graupner and Brunel, 2007) have a price to pay since they have many parameters to be tuned and cannot be treated analytically.

Some experimental results look at first sight contradictory, e.g., low frequency pairing leads to LTP in Froemke and Dan (2002) and no weight change in Sjöström et al. (2001). However, our mathematical model reconciles these two data, taking into account the different preparations. Indeed, the STDP learning window from Froemke and Dan (2002) is obtained with extracellular stimulation, which results in a large compound EPSP. This large compound EPSP allows the model to fulfill the three conditions for LTP.

The fitted parameters differ for the various experiments, up to an order of magnitude. This is however not surprising since the preparations and the synapse types are different. For example, τ_x is three times bigger in hippocampal slices (fitted from data of Wang et al., 2005) than in visual cortex (fitted from Sjöström et al., 2001). Would that mean that the dynamics of, say glutamate binding, is slower in hippocampal slices? We think a lot more experimental data are needed before such conclusions should be drawn.

What are the limitations of our model compared to the other plasticity models? First, standard STDP models (Gerstner et al., 1996; Song et al., 2000) cannot account for frequency dependency since they only consider pair interactions of spikes: pre-post for potentiation and post-pre for depression. The original model of Froemke (Froemke and Dan, 2002) did not catch the frequency dependency either, as explained in Froemke et al. (2006). This frequency dependency can be described by non-linear spiking models such as the model of Senn et al. (2001) or the one of Pfister and Gerstner as Pfister and Gerstner (2006) but, by construction, these earlier spike-based models (where action potentials are treated as momentary events) cannot deal with voltage clamp experiment and any other form of plasticity depending on the dendritic structure. Note that the model of Senn et al. (2001) can be interpreted either as a phenomenological model like ours (i.e., formal mathematical quantities that are upregulated and downregulated during spike events) or as a first step toward a biophysical model (where the formal variables are identified with the up- or downregulation of NMDA receptors and second messengers; Senn et al., 2001). Some classical biophysical models depend on (i) the voltage (Abarbanel et al., 2002; Brader et al., 2007), (ii) the calcium/calmodulin-dependent protein kinase II (CaMKII) phosphorylation and bistability (Lisman, 1985, 1989; Lisman and Zhabotinsky, 2001; Miller et al., 2005; Graupner and Brunel, 2007), (iii) the calcium concentration (Abarbanel et al., 2002; Karmarkar and Buonomano, 2002; Karmarkar et al., 2002; Shouval et al., 2002; Rubin et al., 2005), glutamate binding, AMPA receptors (Saudargiene et al., 2003), NMDA receptors (Senn et al., 2001) etc. Maybe the closest in spirit to our model is the Shouval model (Shouval et al., 2002) that also covers the frequency dependency and voltage-clamp experiments. However, this model predicts depression for pre-post pairs at medium to long lags for which only some evidence exists (Nishiyama et al., 2000; Wittenberg and Wang, 2006). Moreover, it was never compared to dendritic synaptic plasticity.

Most of the models described above show their power only qualitatively. In order to compare plasticity models quantitatively, it would be important to have common benchmarks, possibly with some raw experimental data online, and design a score measure. Such a synaptic plasticity challenge could be constructed in analogy to the competition “Quantitative Single-Neuron Modeling” (Gerstner and Naud, 2009) proposed by the International Neuroinformatics Coordinating Facility (INCF). The first step is to use as benchmarks the already published data. However, the perfect type of data would be a consistent set of experiments (same synapse type, same preparation, many repetitions) that describes each synaptic plasticity feature, i.e., frequency, spike timing, complex spike patterns, voltage control (ideally at the synapse location), and intracellular stimulation of several presynaptic neurons connecting the same postsynaptic cell with synapses at different dendritic locations. Since the neurons are highly non-linear (Larkum et al., 2009), it is important to study the precise voltage time course at the postsynaptic site as well as the dynamics of some biophysical quantities related to plasticity mechanism, e.g., calcium. What are the aspects of plasticity that need to be explored next? Apart from the functional implication of synaptic plasticity in networks that is understudied, the relation between early-long-term, late-long-term and short-term plasticity needs to be understood. Is the molecular machinery for consolidation present during standard STDP protocol (e.g., plasticity related proteins)? What is the role of neuromodulators? Are the synapse binary, do they have a few states or are they continuous? The molecular details of plasticity are not well modeled by the theoreticians except for a few promising models (Lisman and Zhabotinsky, 2001; Miller et al., 2005; Rubin et al., 2005; Graupner and Brunel, 2007). Biophysical questions have to be addressed for all major synapse types. Hopefully the structure of the model is constant across synapses, so that just the parameters vary due to different molecular roles, which would enable us theoreticians to develop consistent modeling framework but it is not clear that single model is sufficient to account for different synapse types.

An obvious extension of the work presented in this paper would be to associate the plasticity model with a detailed biophysical neuron model with multiple compartments that would automatically generate, for arbitrary stimuli, the appropriate voltage time course at the site of the synapse. This implies that active dendrites must be considered so as to allow the backpropagation of somatic action potentials as well as intrinsic dendritic spikes under appropriate stimulation. Finally, our model cannot grasp sensitivity upon synaptic strength, for example shown by Bi and Poo (1998), but in principle we can make the amplitudes for depression and potentiation dependent directly on the synaptic weight. The exact shape of this function can be inspired by previous studies (van Rossum et al., 2000; Gütig et al., 2003; Morrison et al., 2007). Additional work in that direction is planned. The list of STDP experiments is long and we did not try to fit all the available experimental data. Here we have shown that a diverse set of experiments from different labs can be explained by our model. However, we think that our model cannot provide an explanation of the following results. Letzkus et al. (2006) show that a presynaptic spike followed by a postsynaptic burst induces LTP in proximal synapses whereas reverse timing leads to depression, which is in agreement with our model. However, in distal synapses, the results are opposite: a presynaptic spike before a postsynaptic burst induces LTD and post before pre results in potentiation. These results are a priori not reproducible by our model. Maybe the neuron non-linear dynamics would allow to reconcile our model with these data, but in order to tackle this problem a more detailed neuron model is necessary. Second, the study of Wittenberg and Wang (2006) shows that a pre- and a postsynaptic spike pairing induces only LTD. Moreover, potentiation is expressed after only tens of presynaptic spike with postsynaptic burst pairing whereas depression can only be measured after hundreds of pairings. This dependency is not captured by our model; an additional long time constant would help to describe this phenomenon.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Claudia Clopath has been supported by the Swiss National Science Foundation (grant to Wulfram Gerstner) and by the Agence Nationale de la Recherche grant ANR-08-SYSC-005.

References

Abarbanel, H., Huerta, R., and Rabinovich, M. (2002). Dynamical model of long-term synaptic plasticity. Proc. Natl. Acad. Sci. U.S.A. 59, 10137–10143.

Abbott, L. F., and Nelson, S. B. (2000). Synaptic plasticity – taming the beast. Nat. Neurosci. 3, 1178–1183.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Achard, P., and De Schutter, E. (2006). Complex parameter landscape for a complex neuron model. PLoS Comput. Biol. 2, e94. doi:10.1371/journal.pcbi.0020094.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Artola, A., Bröcher, S., and Singer, W. (1990). Different voltage dependent thresholds for inducing long-term depression and long-term potentiation in slices of rat visual cortex. Nature 347, 69–72.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Badel, L., Lefort, S., Brette, R., Petersen, C., Gerstner, W., and Richardson, M. (2008). Dynamic i-v curves are reliable predictors of naturalistic pyramidal-neuron voltage traces. J. Neurophysiol. 99, 656–666.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Barrett, A., Billings, G., Morris, R., and van Rossum, M. (2009). State based model of long-term potentiation and synaptic tagging and capture. PLoS Comput. Biol. 5, e1000259. doi:10.1371/journal.pcbi.1000259.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bell, C., Han, V., Sugawara, Y., and Grant, K. (1997). Synaptic plasticity in a cerebellum-like structure depends on temporal order. Nature 387, 278–281.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bi, G., and Poo, M. (1998). Synaptic modifications in cultured hippocampal neurons: dependence on spike timing, synaptic strength, and postsynaptic cell type. J. Neurosci. 18, 10464–10472.

Pubmed Abstract | Pubmed Full Text

Bi, G., and Poo, M. (2001). Synaptic modification of correlated activity: Hebb’s postulate revisited. Annu. Rev. Neurosci. 24, 139–166.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bienenstock, E., Cooper, L., and Munro, P. (1982). Theory of the development of neuron selectivity: orientation specificity and binocular interaction in visual cortex. J. Neurosci. 2, 32–48.

Pubmed Abstract | Pubmed Full Text

Brader, J., Senn, W., and Fusi, S. (2007). Learning real-world stimuli in a neural network with spike-driven synaptic dynamics. Neural Comput. 19, 2881–2912.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Brette, R., and Gerstner, W. (2005). Adaptive exponential integrate-and-fire model as an effective description of neuronal activity. J. Neurophysiol. 94, 3637–3642.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Clopath, C., Büsing, L., Vasilaki, E., and Gerstner, W. (2010). Connectivity reflects coding: a model of voltage-based spike-timing-dependent- plasticity with homeostasis. Nat. Neurosci. 13, 344–352.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Clopath, C., Jolivet, R., Rauch, A., Luescher, H.-R., and Gerstner, W. (2007). Predicting neuronal activity with simple models of the threshold type: adaptive exponential integrate-and-fire model with two compartments. Neurocomputing 70, 1668–1673.

CrossRef Full Text

Clopath, C., Ziegler, L., Vasilaki, E., Büsing, L., and Gerstner, W. (2008). Tag-trigger-consolidation: a model of early and late long-term-potentiation and depression. PLoS Comput. Biol. 4, e1000248. doi:10.1371/journal.pcbi.1000248. http://dx.doi.org/10.1371%2Fjournal.pcbi.1000248.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Debanne, D., Gähwiler, B., and Thompson, S. (1998). Long-term synaptic plasticity between pairs of individual CA3 pyramidal cells in rat hippocampal slice cultures. J. Physiol. 507, 237–247.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Druckmann, S., Bannitt, Y., Gidon, A. A., Schuermann, F., and Segev, I. (2007). A novel multiple objective optimization framework for constraining conductance-based neuron models by experimental data. Front. Neurosci. 1, 7–18. doi:10.3389/neuro.01.1.1.001.2007.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Dudek, S. M., and Bear, M. F. (1992). Homosynaptic long-term depression in area ca1 of hippocampus and effects of N-methyl-d-aspartate receptor blockade. Proc. Natl. Acad. Sci. U.S.A. 89, 4363–4367.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Froemke, R., and Dan, Y. (2002). Spike-timing dependent plasticity induced by natural spike trains. Nature 416, 433–438.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Froemke, R. C., Poo, M.-M., and Dan, Y. (2005). Spike-timing-dependent synaptic plasticity depends on dendritic location. Nature 434, 221–225.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Froemke, R. C., Tsay, I., Raad, M., Long, J., and Dan, Y. (2006). Contribution of individual spikes in burst-induced long-term synaptic modification. J. Neurophysiol. 95, 1620–1629.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gerstner, W., Kempter, R., van Hemmen, J., and Wagner, H. (1996). A neuronal learning rule for sub-millisecond temporal coding. Nature 383, 76–78.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gerstner, W., and Kistler, W. (2002). Spiking Neuron Models. New York: Cambridge University Press.

Gerstner, W., and Naud, R. (2009). How good are neuron models? Science 326, 379–380.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gerstner, W., and van Hemmen, J. L. (1992). Universality in neural networks: the importance of the mean firing rate. Biol. Cybern. 67, 195–205.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Graupner, M., and Brunel, N. (2007). STDP in a bistable synapse model based on CaMKII and associated signaling pathways. PLOS Comput. Biol. 3, e221. doi:10.1371/journal.pcbi.0030221.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gütig, R., Aharonov, S., Rotter, S., and Sompolinsky, H. (2003). Learning input correlations through nonlinear temporally asymmetric Hebbian plasticity. J. Neurosci. 23, 3697–3714.

Pubmed Abstract | Pubmed Full Text

Izhikevich, E. (2003). Simple model of spiking neurons. IEEE Trans. Neural Netw. 14, 1569–1572.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Izhikevich, E., and Desai, N. (2003). Relating STDP to BCM. Neural Comput. 15, 1511–1523.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kampa, B., Letzkus, J., and Stuart, G. (2006). Requirement of dendritic calcium spikes for induction of spike-timing-dependent synaptic plasticity. J. Physiol. (Lond.) 574, 283–290.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Karmarkar, U., and Buonomano, D. (2002). A model of spike-timing dependent plasticity: one or two coincidence detectors. J. Neurophysiol. 88, 507–513.

Pubmed Abstract | Pubmed Full Text

Karmarkar, U., Najarian, M., and Buonomano, D. (2002). Mechanisms and significance of spike-timing dependent plasticity. Biol. Cybern. 87, 373–382.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kelso, S. R., Ganong, A. H., and Brown, T. H. (1986). Hebbian synapses in hippocampus. Proc. Natl. Acad. Sci. U.S.A. 83, 5326–5330.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kempter, R., Gerstner, W., and van Hemmen, J. L. (1999). Hebbian learning and spiking neurons. Phys. Rev. E 59, 4498–4514.

CrossRef Full Text

Kistler, W. M., and van Hemmen, J. L. (2000). Modeling synaptic plasticity in conjunction with the timing of pre- and postsynaptic potentials. Neural Comput. 12, 385–405.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Larkum, M., Nevian, T., Sandler, M., Polsky, A., and Schiller, J. (2009). Synaptic integration in tuft dendrites of layer 5 pyramidal neurons: a new unifying principle. Science 325, 756–760.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Letzkus, J., Kampa, B., and Stuart, G. (2006). Learning rules for spike timing-dependent plasticity depend on dendritic synapse location. J. Neurosci. 26, 10420–10429. http://www.jneurosci.org/cgi/content/abstract/26/41/104%20.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lisman, J. (1985). A mechanism for memory storage insensitive to molecular turnover: a bistable autophosphorylating kinase. Proc. Natl. Acad. Sci. U.S.A. 82, 3055–3057.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lisman, J. (1989). A mechanism for Hebb and anti-Hebb processes underlying learning and memory. Proc. Natl. Acad. Sci. U.S.A. 86, 9574–9578.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lisman, J., and Zhabotinsky, A. (2001). A model of synaptic memory: A CaMKII/PP1 switch that potentiates transmission by organizing an AMPA receptor anchoring assembly. Neuron 31, 191–201.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Magistretti, J., and Alonsoa, A. (1999). Biophysical properties and slow voltage-dependent inactivation of a sustained sodium current in entorhinal cortex layer-ii principal neurons. a whole-cell and single-channel study. J. Gen. Physiol. 114, 4491–509.

CrossRef Full Text

Markram, H., Lübke, J., Frotscher, M., and Sakmann, B. (1997). Regulation of synaptic efficacy by coincidence of postsynaptic APs and EPSPs. Science 275, 213–215.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Miller, P., Zhabotinsky, A., Lisman, J., and Wang, X. (2005). The stability of a stochastic CaMKII switch: dependence on the number of enzyme molecules and protein turnover. PLoS Biol. 3, e107. doi:10.1371/journal.pbio.0030107.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Morrison, A., Aertsen, A., and Diesmann, M. (2007). Spike-timing dependent plasticity in balanced random networks. Neural Comput. 19, 1437–1467.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Morrison, A., Diesmann, M., and Gerstner, W. (2008). Phenomenological models of synaptic plasticity based on spike timing. Biol. Cybern. 98, 459–478.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Naud, R., Marcille, N., Clopath, C., and Gerstner, W. (2008). Firing patterns in the adaptive exponential integrate- and fire model. Biol. Cybern. 99, 335–347.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Nevian, T., Larkum, M., Polsky, A., and Schiller, J. (2007). Properties of basal dendrites of layer 5 pyramidal neurons: a direct patch-clamp recording study. Nat. Neurosci. 10, 206–214.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Nevian, T., and Sakmann, B. (2006). Spine Ca²⁺ signaling in spike-timing- dependent plasticity. J. Neurosci. 26, 11001–11013. http://www.jneurosci.org/cgi/content/abstract/26/43/110%01.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ngezahayo, A., Schachner, M., and Artola, A. (2000). Synaptic activation modulates the induction of bidirectional synaptic changes in adult mouse hippocampus. J. Neurosci. 20, 2451–2458.

Pubmed Abstract | Pubmed Full Text

Nishiyama, M., Hong, K., Miskoshiba, K., Poo, M., and Kato, K. (2000). Calcium stores regulate the polarity and input specificity of synaptic modification. Nature 408, 584–588.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Palmer, L., and Stuart, G. (2009). Membrane potential changes in dendritic spines during action potentials and synaptic input. J. Neurosci. 29, 6897–6903.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Pfister, J.-P., and Gerstner, W. (2006). Triplets of spikes in a model of spike timing-dependent plasticity. J. Neurosci. 26, 9673–9682.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Roberts, P. (1999). Computational consequences of temporally asymmetric learning rules: I. Differential Hebbian learning. J. Comput. Neurosci. 7, 235–246.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rubin, J., Gerkin, R., Bi, G.-Q., and Chow, C. (2005). Calcium time course as a signal for spike-timing-dependent plasticity. J. Neurophysiol. 93, 2600–2613.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rubin, J., Lee, D. D., and Sompolinsky, H. (2001). Equilibrium properties of temporally asymmetric Hebbian plasticity. Phys. Rev. Lett. 86, 364–367.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Saudargiene, A., Porr, B., and Wörgötter, F. (2003). How the shape of pre- and postsynaptic signals can influence STDP: a biophysical model. Neural Comput. 16, 595–626.

CrossRef Full Text

Senn, W. (2002). Beyond spike timing: the role of non-linear plasticity and unreliable synapses. Biol. Cybern. 87, 344–355.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Senn, W., Tsodyks, M., and Markram, H. (1997). “An algorithm for synaptic modification based on exact timing of pre-and postsynaptic action potentials,” in Artificial Neural Networks – ICANN’97. Lecture Notes in Computer Science, Vol. 1327, eds W. Gerstner, A. Germond, M. Hasler, and J.-D. Nicoud (Berlin: Springer), 121–126.

Senn, W., Tsodyks, M., and Markram, H. (2001). An algorithm for modifying neurotransmitter release probability based on pre- and postsynaptic spike timing. Neural Comput. 13, 35–67.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Shouval, H. Z., Bear, M. F., and Cooper, L. N. (2002). A unified model of NMDA receptor dependent bidirectional synaptic plasticity. Proc. Natl. Acad. Sci. U.S.A. 99, 10831–10836.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sjöström, P., and Häusser, M. (2006). A cooperative switch determines the sign of synaptic plasticity in distal dendrites of neocortical pyramidal neurons. Neuron 51, 227–238.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sjöström, P., Turrigiano, G., and Nelson, S. (2001). Rate, timing, and cooperativity jointly determine cortical synaptic plasticity. Neuron 32, 1149–1164.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sjöström, P., Turrigiano, G., and Nelson, S. (2003). Neocortical LTD via coincident activation of presynaptic NMDA and cannabinoid receptors. Neuron 39, 641–654.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sjöström, P., Turrigiano, G., and Nelson, S. (2004). Endocannabinoid-dependent neocortical layer-5 LTD in the absence of postsynaptic spiking. J. Neurophysiol. 92, 3338–3343.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Song, S., Miller, K., and Abbott, L. (2000). Competitive Hebbian learning through spike-time-dependent synaptic plasticity. Nat. Neurosci. 3, 919–926.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

van Rossum, M. C. W., Bi, G. Q., and Turrigiano, G. G. (2000). Stable Hebbian learning from spike timing-dependent plasticity. J. Neurosci. 20, 8812–8821.

Pubmed Abstract | Pubmed Full Text

Wang, H.-X., Gerkin, R., Nauen, D., and Wang, G.-Q. (2005). Coactivation and timing-dependent integration of synaptic potentiation and depression. Nat. Neurosci. 8, 187–193.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wittenberg, G. M., and Wang, S. S.-H. (2006). Malleability of spike-timing dependent plasticity at the CA3–CA1 synapse. J. Neurosci. 26, 6610–6617.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text