Storage of Phase-Coded Patterns via STDP in Fully-Connected and Sparse Network: A Study of the Network Capacity

Scarpetta, Silvia; De Candia, Antonio; Giacco, ferdinando

doi:10.3389/fnsyn.2010.00032

ORIGINAL RESEARCH article

Front. Synaptic Neurosci., 23 August 2010
Volume 2 - 2010 | https://doi.org/10.3389/fnsyn.2010.00032

Storage of phase-coded patterns via STDP in fully-connected and sparse network: a study of the network capacity

Silvia Scarpetta^1,2* Antonio de Candia^2,3,4 Ferdinando Giacco^1,2

¹ Dipartimento di Fisica “E.R.Caianiello”, Università di Salerno, Fisciano, Italy
² INFN, Sezione di Napoli e Gruppo Coll. di Salerno, Naples, Italy
³ Dipartimento di Scienze Fisiche, Università di Napoli Federico II, Naples, Italy
⁴ CNR-SPIN, Unità di Napoli, Naples, Italy

We study the storage and retrieval of phase-coded patterns as stable dynamical attractors in recurrent neural networks, for both an analog and a integrate and fire spiking model. The synaptic strength is determined by a learning rule based on spike-time-dependent plasticity, with an asymmetric time window depending on the relative timing between pre and postsynaptic activity. We store multiple patterns and study the network capacity. For the analog model, we find that the network capacity scales linearly with the network size, and that both capacity and the oscillation frequency of the retrieval state depend on the asymmetry of the learning time window. In addition to fully connected networks, we study sparse networks, where each neuron is connected only to a small number z ≪ N of other neurons. Connections can be short range, between neighboring neurons placed on a regular lattice, or long range, between randomly chosen pairs of neurons. We find that a small fraction of long range connections is able to amplify the capacity of the network. This imply that a small-world-network topology is optimal, as a compromise between the cost of long range connections and the capacity increase. Also in the spiking integrate and fire model the crucial result of storing and retrieval of multiple phase-coded patterns is observed. The capacity of the fully-connected spiking network is investigated, together with the relation between oscillation frequency of retrieval state and window asymmetry.

Recent advances in brain research have generated renewed awareness and appreciation that the brain operates as a complex non-linear dynamic system, and synchronous and phase-locked oscillations may play a crucial role in information processing, such as feature grouping, saliency enhancing (Singer, 1999; Fries, 2005; Fries et al., 2007) and phase-dependent coding of objects in short-term memory (Siegel et al., 2009). Many results led to the conjecture that synchronized and phase-locked oscillatory neural activity play a fundamental role in perception, memory, and sensory computation (Buzsaki and Draguhn, 2004; Gelperin, 2006; Düzel et al., 2010).

There is increasing evidence that information encoding may depend on the temporal dynamics between neurons, namely, the specific phase alignment of spikes relative to rhythmic activity across the neuronal population (as reflected in the local field potential, or LFP) (O’Keefe and Recce, 1993; König et al., 1995; Laurent, 2002; Mehta et al., 2002; Kayser et al., 2009; Siegel et al., 2009). Indeed phase-dependent coding, that exploits the precise temporal relations between the discharges of neurons, may be an effective strategy to encode information (Singer, 1999; Scarpetta et al., 2002a; Scarpetta et al., 2002b; Yoshioka et al., 2007; Latham and Lengyel, 2008; Kayser et al., 2009; Siegel et al., 2009). Data from rodents indicate that spatial information may be encoded at specific phases of ongoing population theta oscillations in the hippocampus (O’Keefe and Recce, 1993), and that spike sequences can be replayed at a different time scale (Diba and Buzsaki, 2007), while data from monkeys (Siegel et al., 2009) show that phase coding may be a more general coding scheme.

The existence of a periodic spatio-temporal pattern of precisely timed spikes, as attractor of neural dynamics, has been investigated in different recurrent neural models (Gerstner et al., 1993; Borisyuk and Hoppensteadt, 1999; Jin, 2002; Lengyel et al., 2005b; Memmesheimer and Timme, 2006a,b). In Jin (2002) it was shown that periodic spike sequences are attractors of the dynamics, and the stronger the global inhibition of the network, the faster the rate of convergence to a periodic pattern. In Memmesheimer and Timme (2006a,b) the problem of finding the set of all networks that exhibit a predefinite periodic precisely timed pattern was studied.

Here we study how a spike timing dependent plasticity (STDP) learning rule can encode many different periodic patterns in a recurrent network, in such a way that a pattern can be retrieved initializing the network in a state similar to it, or inducing a short train of spikes extracted from the pattern.

In our model, information about an item is encoded in the specific phases of firing, and each item corresponds to a different pattern of phases among units. Multiple items can be memorized in the synaptic connections, and the intrinsic network dynamics recall the specific phases of firing when a partial cue is presented.

Each item with specific phases of firing corresponds to specific relative timings between neurons. Therefore it seems that phase coding may be well suited to facilitate long-term storage of items by means of STDP (Markram et al., 1997; Bi and Poo, 1998, 2001).

Indeed experimental findings on STDP further underlined the importance of precise temporal relationships of the dynamics, by showing that long-term changes in synaptic strengths depend on the precise relative timing of pre and postsynaptic spikes (Magee and Johnston, 1997; Markram et al., 1997; Bi and Poo, 1998, 2001; Debanne et al., 1998; Feldman, 2000).

The computational role and functional implications of STDP have been explored from many points of view (see for example Gerstner et al., 1996; Kempter et al., 1999; Song et al., 2000; Rao and Sejnowski, 2001; Abarbanel et al., 2002; Lengyel et al., 2005b; Drew and Abbott, 2006; Wittenberg and Wang, 2006; Masquelier et al., 2009 and papers of this special issue). STDP has also been supposed to play a role in the hippocampus theta phase precession phenomenon (Mehta et al., 2002; Scarpetta and Marinaro, 2005; Lengyel et al., 2005a; Florian and Muresan, 2006), even though other explanations has also been proposed for this phenomena (see Leibold et al., 2008; Thurley et al., 2008 and references therein). Here we analyze the role of a learning rule based on STDP in storing multiple phase-coded memories as attractor states of the neural dynamics, and the ability of the network to selectively retrieve a stored memory, when a partial cue is presented. The framework of storing and retrieval of memories as attractors of the dynamics is widely accepted, and recently received experimental support, such as in the work of Wills et al. (2005), which gives strong experimental evidence for the expression of rate-coded attractor states in the hippocampus.

Another characteristic of the neural network, crucial to its functioning, is its topology, that is the average number of neurons connected to a neuron, the average length of the shortest path connecting two neurons, etc. In the last decade, there has been a growing interest in the study of the topological structure of the brain network (Sporns and Zwi, 2004; Sporns et al., 2004; Bullmore and Sporns, 2009). This interest has been stimulated by the simultaneous development of the science of complex networks, that studies how the behavior of complex systems (such as societies, computer networks, brains, etc.) is shaped by the way their constituent elements are connected.

A network may have the property that the degree distribution, i.e. the probability that a randomly chosen node is connected to k other nodes, has a slow power law decay. Networks having this property are called “scale-free”. Barabási and Albert (1999) demonstrated that this property can originate from a process in which each node is added preferentially to nodes that already have high degree. Scale-free properties have been found in functional network topology using functional magnetic resonance in human brain (Eguìluz et al., 2005), and have been investigated in some models in relation with scale-free avalanche brain activity and criticality (Pellegrini et al., 2007; de Arcangelis and Herrmann, 2010).

Another important class of complex networks is the so called “small world” networks (Watts and Strogatz, 1998). They combine two important properties. The first is an high level of clustering, that is an high probability of direct connection between two nodes, given that they are both connected to a third node. This property usually occurs in networks where the nodes are connected preferentially to the nearest nodes, in a physical (for example three-dimensional) space. The second property is the shortness of paths connecting any two nodes, characteristic of random networks. Therefore, a measure of the small-worldness of a network is given by a high ratio of the clustering coefficient to the path length.

There is increasing evidence that the connections of neurons in many areas of the nervous system have a small world structure (Hellwig, 2000; Sporns and Zwi, 2004; Sporns et al., 2004; Yu et al., 2008; Bullmore and Sporns, 2009; Pajevic and Plenz, 2009). Up to now, the only nervous system to have been comprehensively mapped at a cellular level is the one of Caenorhabditis elegans (White et al., 1986; Achacoso and Yamamoto, 1991), and it has been found that is has indeed a small world structure. The same property was found for the correlation network of neurons in the visual cortex of the cat (Yu et al., 2008).

In this paper we focus on the ability of STDP to memorize multiple phase-coded items, in both fully connected and sparse networks, with varying degree of small-worldness, in a way that each phase-coded item is an attractor of the network.

Partial presentation of the pattern, i.e. short externally induced spike sequences, with phases similar to the ones of the stored phase pattern, induces the network to retrieve selectively the stored item, as far as the number of stored items is not larger then the network capacity. If the network retrieves one of the stored items, the neural population spontaneously fires with the specific phase alignments of that pattern, until external input does not change the state of the network.

We find that the proposed learning rule is really able to store multiple phase-coded patterns, and we study the network capacity, i.e. how many phase-coded items can be stored and retrieved in the network as a function of the parameters of the network and the learning rule.

In Section 1 we describe the learning rule and the analog model used. In Section 2 we study the case of an analog fully connected network, that is a network in which each neuron is connected to any other neuron. In Section 3 we study instead the case of an analog sparse network, where each neuron is connected to a finite number of other neurons, with a varying degree of small-worldness. In Section 4 we study the case of a fully connected spiking integrate and fire (IF) model, and finally the summary and discussion is in Section 5.

The Model

We consider a network of N neurons, with N(N − 1) possible (directed) connections J_ij. The synaptic connections J_ij, during the learning mode when patterns to be stored are presented, are subject to plasticity and change their efficacy according to a learning rule inspired to the STDP. In STDP (Magee and Johnston, 1997; Markram et al., 1997; Bi and Poo, 1998, 2001; Debanne et al., 1998; Feldman, 2000) synaptic strength increases or decreases whether the presynaptic spike precedes or follows the postsynaptic one by few milliseconds, with a degree of change that depends on the delay between pre and postsynaptic spikes, through a temporally asymmetric learning window. We indicate with x_i(t) the activity, or firing rate, of ith neuron at time t. It means that the firing probability of unit i in the interval (t, t + Δt) is proportional to x_i(t)Δt in the limit Δt → 0. According to the learning rule we use in this work, already introduced in (Scarpetta et al., 2001, 2002a; Yoshioka et al., 2007), the change in the connection J_ij occurring in the time interval [−T, 0] can be formulated as follows:

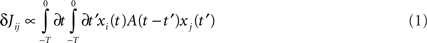
where x_j(t) is the activity of the presynaptic neuron, and x_i(t) the activity of the postsynaptic one. The learning window A(τ) is the measure of the strength of synaptic change when there is a time delay τ between pre and postsynaptic activity. To model the experimental results of STDP, the learning window A(τ) should be an asymmetric function of τ, mainly positive (LTP) for τ > 0 and mainly negative (LTD) for τ < 0. The shape of A(τ) strongly affects J_ij and the dynamics of the networks, as discussed in the following. An example of the learning window used here is shown in Figure 1.

FIGURE 1

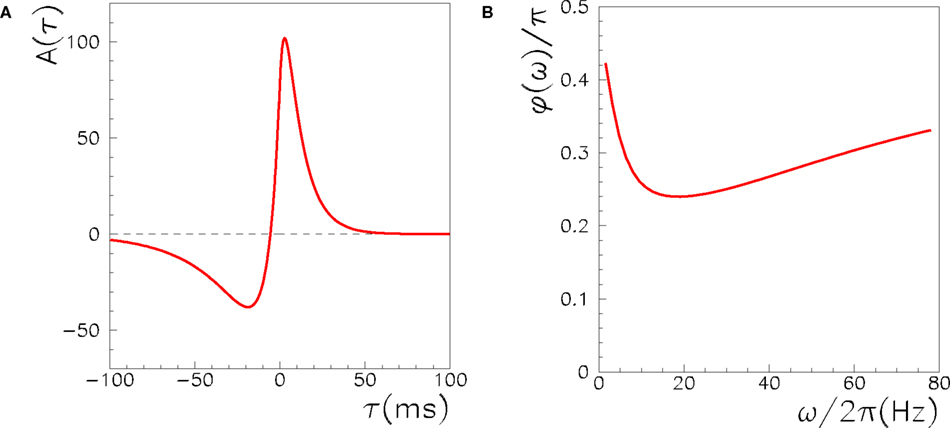
Figure 1. (A) The learning window A(τ) used in the learning rule in Eq. (1) to model STDP. The window is the one introduced and motivated by Abarbanel et al. (2002), 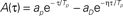yes if τ > 0, yes 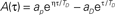if τ < 0, with the same parameters used in Abarbanel et al. (2002) to fit the experimental data of Bi and Poo (1998), a_p= γ[1/T_p+ η/T_D]⁻¹, a_D= γ[η/T_p+ 1/T_D]⁻¹, with T_p = 10.2 ms, T_D= 28.6 ms, η = 4, γ = 42. Notably, this function satisfies the condition 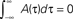yes , i.e. Ã(0) = 0. (B) The phase of the Fourier transform of A(τ) as a function of the frequency.

Writing Eq. (1), implicitly we have assumed that the effects of separate spike pairs due to STDP sum linearly. However note that non-linear effects have been observed when both pre and postsynaptic neurons fire simultaneously at more then 40 Hz (Sjostrom et al., 2001; Froemke and Dan, 2002), therefore our model holds only in the case of lower firing rates, and in cases where linear summation is a good approximation.

We consider periodic patterns of activity that are periodic patterns, in which the information is encoded in the relative phases, that is in the relative timing of the maximum firing rate of a neuron. Therefore, we define the pattern to be stored by

where phases yes are randomly chosen from a uniform distribution in [0,2π), and ω_μ/2π is the frequency of oscillation of the neurons (see Figure 2A). Each pattern μ is therefore defined by its frequency ω_μ/2π, and by the specific phases of the neurons i = 1,..,N.

FIGURE 2

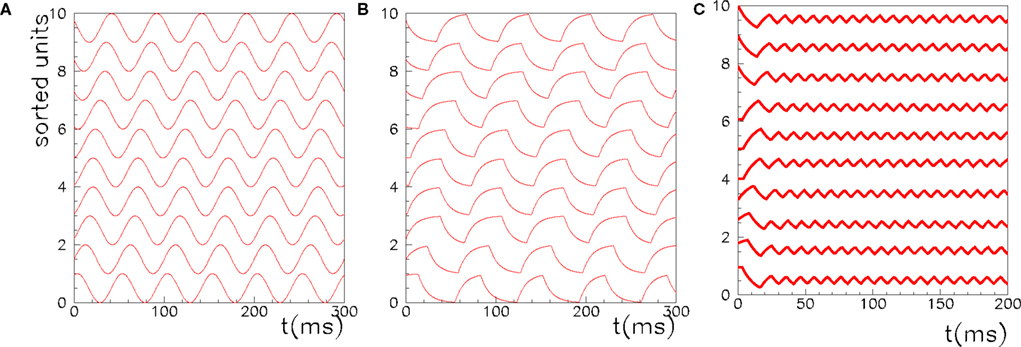
Figure 2. The activity of 10 randomly chosen neurons in a network of N = 3000 fully connected analog neurons, with P = 30 stored patterns. The learning rule is given by Eq. (4) with φ^* = 0.24π. Neurons are sorted by increasing phase yes of the first pattern, and shifted correspondingly on the vertical axis. (A) The first stored pattern, that is the activity of the network given by Eq. (2) used to encode the pattern in the learning mode, with frequency ω_μ/2π = 20 Hz. (B) The self-sustained dynamics of the network, when the initial condition is given by the first pattern yes . 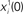The retrieved the pattern has the same phase relationships of the encoded one. In this case the overlap is 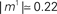yes , and the output frequency is in agreement with the analytical value tan(φ^*)/2πτ_m = 15 Hz. (C) Same as in (B), but with φ^*= 0.45π. Output frequency is in agreement with the analytical value tan(φ^*)/2πτ_m = 100 Hz.

In the limit of large T, when the network is forced in the state given by Eq. (2), using Eq. (1), the change in the synaptic strength will be given by

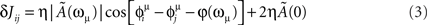
where Ã(ω) is the Fourier transform of the kernel, defined by

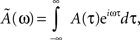
and φ(ω) = arg[Ã(ω)] is the phase of the Fourier transform. The factor η depends on the learning rate and on the total learning time T (Scarpetta et al., 2002a, 2008).

When we store multiple patterns μ = 1,2,…,P, the learned weights are the sum of the contributions from individual patterns. After learning P patterns, each with frequency ω_μ/2π and phase-shift 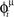yes , we get the connections

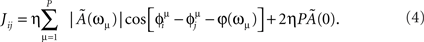
In this paper we choose 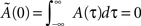yes , which gives a balance between potentiation and inhibition. Notably, the condition Ã(0) = 0 also holds when using the learning window of Figure 1. In the present study, we choose to store patterns all with the same ω_μ, and to ease the notation we define φ^* = φ(ω_μ).

In the retrieval mode, the connections are fixed to the values given in Eq. (4). In the analog model, the dynamic equations for unit x_i are given by

where the transfer function F(h) denotes the input–output relationship of neurons, h_i(t) = Σ_jJ_ijx_j(t) is the local field acting on neuron i, τ_m is the time constant of neuron i (for simplicity, τ_m has the same value for all neurons), and J_ij is the connection after the learning procedure given in Eq. (4). Spontaneous activity dynamics of the coupled non-linear system is therefore determined by the function F(h) and by the coupling matrix J_ij. We take the function F(h) to be equal to the Heaviside function Θ(h). Note that in this case the learning factor η is immaterial.

During the retrieval mode, the network selectively replays one of the stored phase-coded patterns, depending on the initial conditions. It means that if we force the network, for t < 0, with an input which resembles one of the phase-coded patterns, and then we switch off the input at times t > 0, the network spontaneously gives sustained oscillatory activity with the relative phases of the retrieved pattern, while the frequency can be different (see Figure 2). For the analog model (5), where the state of the network is represented by the rates x_i(t), the same can be achieved if we simply initialize the rates at t = 0 with values 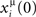yes corresponding to one of the phase-coded patterns, or also to a partially corrupted version of it. Analytical calculations (Yoshioka et al., 2007; Scarpetta et al., 2008) show that the output frequency of oscillation is given by

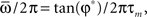
and this is confirmed by numerical simulations of Eq. (5) with connections given by Eq. (4).

As an example, the learning window in Figure 1, when the frequency of the stored pattern is ω_μ/2π = 20 Hz, gives φ^* = 0.24π, and an output frequency of oscillation 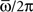yes = 15 Hz (with τ_m = 10 ms). Numerical simulations of the network with φ^* = 0.24π, N = 3000 fully connected neurons and P = 30 stored patterns, are shown in Figure 2B. In Figure 2C the case φ^* = 0.45π is shown. Here, the output frequency is much higher, while the oscillations of the firing rates with respect to the mean value 1/2 is much smaller.

In the following sections, we analyze the behavior when multiple patterns are stored and we study the network capacity as a function of learning window parameters and as a function of connectivity topology.

Capacity of the Fully Connected Network

In this section we study the network capacity, in the case of fully connected network, where all the N(N − 1) connections are subject to the learning process given by Eq. (4).

During the retrieval mode, the spontaneous dynamics of the network selectively replay one of the stored phase-coded patterns, depending on initial condition, so that, when retrieval is successful, the spontaneous activity of the network is an oscillating pattern of activity with phase of firing equal to the stored phases 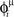yes (while the frequency of oscillation is governed by the time scale of single neuron and by the parameter φ^* of learning window). Similarity between the network activity during retrieval mode and the stored phase-coded pattern is measured by the overlap |m^μ|, introduced in (Scarpetta et al., 2002a) and studied in (Yoshioka et al., 2007),

If the activity x_i(t) is equal to the pattern 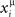yes (t) in Eq. (2), then the overlap is equal to 1/4 (perfect retrieval), while it is 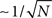yes when the phases of firing have nothing to do with the stored phases. Numerically we study the capacity of the network, α_c = P_max/N, where N is the number of neurons and P_max is the maximum number of items that can be stored and retrieved successfully.

We extract P different random patterns, choosing phases 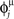yes randomly from a uniform distribution in [0, 2π). Then we define the connections J_ij with the rule Eq. (4). The values of the firing rates are initialized at time t = 0 at the value given by Eq. (2) with t = 0 and μ = 1 of the first pattern, the dynamics in Eq. (5) is simulated, and the overlap Eq. (6) with μ = 1 is evaluated. If the absolute value |m^μ(t)| tends to a constant greater than 0.1 at long times, then we consider that the pattern has been encoded and replayed well by the network. The maximum value of P at which the network is able to replay the pattern is the capacity of the network. We have verified that a small noise in the initialization do not change the results. A systematic study of the robustness of the dynamical basins of attraction from the noise in the initialization has not been carried out yet.

Here we study the dependence of the network capacity on the learning rule parameter φ^*. The parameter φ^* depends on the learning window shape, and on the frequency of oscillation ω_μ/2π of the pattern presented during the learning process. In Figure 3 we plot the capacity as a function of 0 < φ^* < π/2 for a fully connected network with N = 3000 and N = 6000, considering P_max the maximum number of patterns such that the retrieved patterns have overlaps |m^μ| > 0.1. The capacity is approximately constant with the network size, showing that the maximum number of patterns P_max scales linearly with the number of neurons.

FIGURE 3

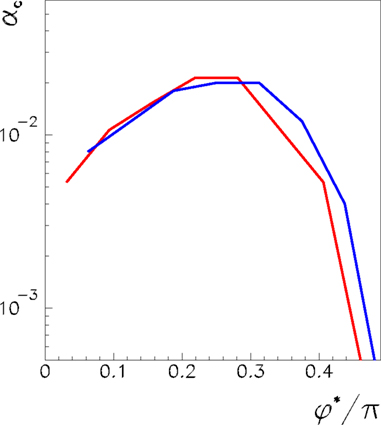
Figure 3. Maximum capacity α_c = P_max/N of a network of N = 3000 (red) and N = 6000 (blue) fully connected analog neurons, as a function of the learning window asymmetry φ^*. The limit φ^* = 0 corresponds to a symmetric learning window (J_ij−J_ji) that is to output frequency 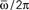yes that tends to zero. The limit φ^* = π/2 corresponds instead to a perfectly anti-symmetric learning window, and output frequency 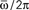yes = ∞. The intermediate value φ^* ≃ 0.25π gives the best performance of the network.

We see that capacity strongly depends on the shape of learning window through parameter φ^*. The limit of φ^* equal to zero corresponds to output frequency 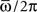yes equal to zero, and therefore to the limit of static output. We see that the capacity of the oscillating network is larger then the static limit for a large range of frequencies. When φ^* approaches π/2, then the output frequency 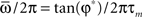yes tends to infinity, and capacity decreases. The best performance is given at intermediate values of φ^*. Therefore, since φ^* depends on the degree of time asymmetry of the learning window, we see that there is a range of time asymmetry of the learning window which provides good capacity, while both the case of perfectly symmetric learning window φ^* = 0, and the case of perfectly anti-symmetric learning window φ^* = π/2, give worse capacity performances. Interestingly, the learning window in Figure 1 gives intermediate values of φ^* for a large interval of frequencies ω_μ.

Note that the decrease in the capacity of the network when the phase φ^* approaches π/2 is essentially due to the fact that the oscillations of the firing rates with respect to the mean value 1/2 become small in this regime. When the firing rates tend to a constant, the overlap defined by Eq. (6) goes to zero.

Capacity of the Sparse Network

In this section we study the capacity of the network described through Eq. (5) in the case of sparse connectivity, where only a fraction of the connections are subject to the learning rule given by Eq. (4), while all the others are set to zero. The role of connectivity’s topology is also investigated. We start from a network in which neurons are put on the vertices of a two- or three-dimensional lattice; each neuron is connected only to neurons within a given distance (in units of lattice spacings) and we call z the number of connections of a single neuron. For each neuron, we then “rewire” a finite fraction γ of its connections, deleting the existing short-range connections and creating, in place of them, long range connections to randomly chosen neurons.

We consider a three-dimensional network with 24³ neurons, and a two-dimensional one with 118² neurons. In Figure 4A we plot the maximum capacity α_c = P_max/N as a function of the connectivity z/N for three different values of γ, for the three-dimensional case. The value γ = 0 (red curve) corresponds to the pure short-range network, in which all connections are between neurons within a given distance on the three-dimensional lattice, γ = 1 (blue curve) corresponds to the random network, where the three-dimensional topology is completely lost, and γ = 0.3 to an intermediate case, where 30% of the connections are long range, and the others are short range.

FIGURE 4

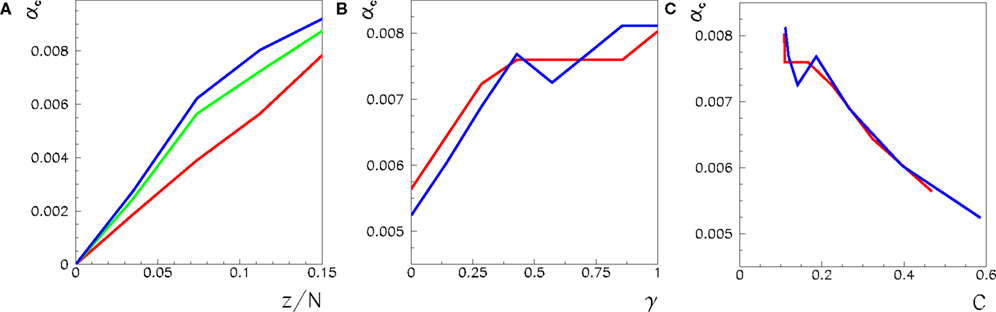
Figure 4. (A) Maximum capacity α_c = P_max/N for a network with 24³ analog neurons, with z connections per neuron, with φ^* fixed to its optimal value 0. 24π. The red curve corresponds to γ = 0, that is to a network with only short-range connections. The green one to γ = 0.3, and the blue one to γ = 1, that is to a random network where the finite dimensional topology is completely lost. (B) Maximum capacity α_c = P_max/N, for the same values of N and φ^* and for connectivity z/N = 0.11, as a function of γ, for the 24³ lattice (red) and for a two dimensional 118² lattice (blue). (C) Same data as in (B), but as a function of the clustering coefficient C.

Considering that the capacity of the fully connected network (z/N = 1) is α_c ≃ 0.02, we see that the random network with z/N ≃ 0.1 already has ∼40% of the capacity of the fully connected network. This means the capacity does not scale linearly with the density of connections, and when the density of connections grows there is a sort of saturation effect, due to the presence of partially redundant connections.

Then, we look at the dependence of the capacity from the fraction of short range and long range connections for z/N ≃ 0.11. In Figure 4B, we see that the capacity gain, with respect to the short-range network, given by 30% long range connections (γ = 0.3), is about 80% the one of the fully random network (γ = 1). Therefore, the presence of a small number of long range connections is able to amplify the capacity of the network. This is shown in Figure 4B, where the capacity as a function of γ for z/N = 0.11 is plotted (red curve). Note that the above effect is not so important in smaller networks, for example with N = 18³ neurons, where the capacity of the short-range network is nearer to that of a random network. Therefore, it seems plausible that, for very large networks, the amplifying effect of a small fraction of long range connections will be even stronger.

It is reasonable to suppose that the fraction of long range connections, in real networks, is determined by a trade-off between the increase of capacity given by long range connections, and their higher wiring cost. A large amplifying effect of long range connections on the capacity, together with a large wiring cost with respect to short range ones, will result in the optimal topology of the network being small-world like, with a small fraction of long range connections, as observed in many areas of the brain, from C. elegans (White et al., 1986; Achacoso and Yamamoto, 1991) to the visual cortex of the cat (Yu et al., 2008).

The experiments on a two-dimensional lattice with 118² neurons do not show any qualitative differences with respect to the three-dimensional case. In Figure 4B we plot the capacity of the two-dimensional network (blue curve) as a function of γ, along with the capacity of the three-dimensional one (red curve).

The Figure 4C shows the same data of Figure 4B, but as a function of the clustering coefficient C, defined as the probability that two sites, neighbors of a given site, are neighbors themselves. As reported in Figure 4C, once fixed the number of connections per neuron z, the lower the clustering coefficient, the higher the capacity of the network. This is reasonable, because a high clustering coefficient means that connections will be partially redundant, as already observed in the case of the dependence on the connectivity z/N.

Note that the mean path length λ, for the considered value of z/N = 0.11, is a decreasing function of γ from γ = 0 up to γ = 0.01, and then remains practically constant for higher values of γ. This means that the ratio between C and λ, that is the small-worldness of the network, has a maximum about γ = 0.01. The capacity therefore is not an increasing function of the small-worldness. Only when the wiring cost of the connections is taken in account, the optimal topology turns out to be one with a small fraction of long range connections. Note also that for more realistic values of z/N, much lower than z/N = 0.11, the maximum of the small-worldness shifts to higher values of γ.

Integrate and Fire Model

The previous results refer to network dynamics described in Eq. (5), that is simple enough to admit analytical predictions for dynamics when the connectivity is given by Eq. (4). The simple model defined by Eq. (5) has state variables x_i(t), representing instantaneous firing rate or probability of firing, and it has only one time scale τ_m, which is the time constant of a single unit, allowing us to focus on the effect of the learning window shape and connectivity structure. However, we expect that, while details of dynamics may depend on the model of single unit, the crucial results of storing and recall of phase-coded patterns can be seen also in a spiking model. Therefore we simulate a leaky integrate and fire (IF) spiking model. We use a simple spike response model formulation (SRM) (Gerstner and Kistler, 2002; Gerstner et al., 1993) of the leaky integrate and fire model. While integrate and fire models are usually defined in terms of differential equations, the SRM expresses the membrane potential at time t as an integral over the past (Gerstner and Kistler, 2002). This allows us to use an event-driven programming and makes the numerical simulations faster than in the differential equation formulation.

Each presynaptic spike j, with arrival time t_j, is supposed to add to the membrane potential a postsynaptic potential of the form J_ij∈(t−t_j), where

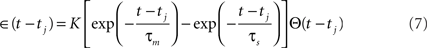
where τ_m is the membrane time constant (here 10 ms), τ_s is the synapse time constant (here 5 ms), Θ(t) is the Heaviside step function, and K is a multiplicative constant chosen so that the maximum value of the kernel is 1. The sign of the synaptic connection J_ij set the sign of the postsynaptic potential change. The synaptic signals received by neuron i, after time t_i of the last spike of neuron i, are added to find the total postsynaptic potential

When the postsynaptic potential of neuron i reaches the threshold T, a postsynaptic spike is scheduled, and postsynaptic potential is set to the resting value zero. We simulate this simple model with J_ij taken from the learning rule given by Eq. (4), with P patterns in a network of N units. The learning rule Eq. (4) comes out of the learning process given by Eq. (1), when a sequence of spikes is learned, and spikes are generated in such a way that the probability that unit i has a spike in the interval (t, t + Δt) is proportional to 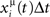yes in the limit Δt → 0, with the rate 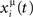yes given by Eq. (2). The J_ij are measured in units such that yes .

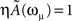After the learning process, to recall one of the encoded patterns, we give an initial signal made up of M < N spikes, taken from the stored pattern μ, and we check that after this short signal the spontaneous dynamics of the network gives sustained activity with spikes aligned to the phases 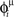yes of pattern μ (Figure 5).

FIGURE 5

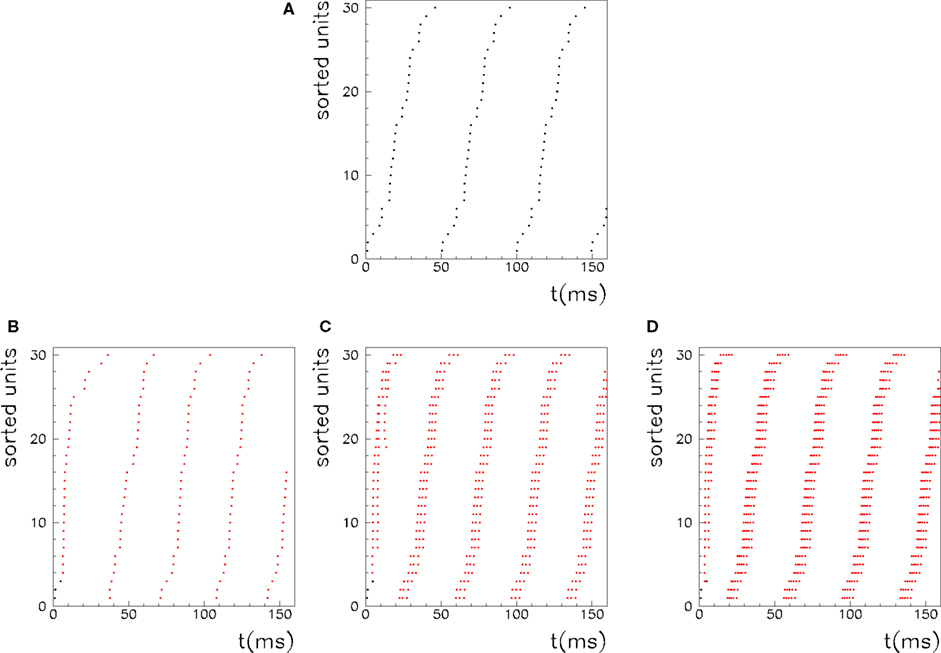
Figure 5. Recall of a pattern by the spiking IF model, with N = 1000 neurons and φ^* = 0. 24π. One pattern (P = 1) defined by the phases 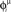yes is stored in the network with the rule given by Eq. (4). Then a short train of M = 150 spikes, at times 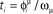yes with ω_μ/2π = 20 Hz, is induced on the neurons that have the M lowest phases yes . This short train triggers the replay of the pattern by the network. Depending on the value of T, the phase-coded pattern is replayed with a different number of spikes per cycle. Note that changing T in our model may correspond to a change in the value of physical threshold or in the value of the parameter ηÃ(ω_μ) appearing in the synaptic connections J_ij learning rule. (A) Thirty neurons of the network are randomly chosen and sorted by the value of the phase yes . Then the phases of the encoded pattern are shown, plotting on the x axis the times 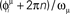yes , and on the y axis the label of the neuron. (B) The replayed pattern with threshold T = 85 is shown, plotting on the x axis the times of the spikes, and on the y axis the label of the spiking neuron. Black dots represent externally induced spikes, while red dots represent spikes generated by the intrinsic dynamics of the network. (C) The replayed pattern with threshold T = 50. (D) The replayed pattern with threshold T = 35.

We also investigate the role of the threshold T. As shown in Figure 5, when the threshold T is lower a burst of activity takes place within each cycle, with phases aligned with the pattern. Therefore the same phase-coded pattern is retrieved, but with a different number of spikes per cycle. This open the possibility to have a coding scheme in which the phases encode pattern’s informations, and rate in each cycle represents the strength and saliency of the retrieval or it may encode another variable. The recall of the same phase-coded pattern with different number of spikes per cycle, shown in Figure 5, accords well with recent observation of Huxter et al. (2003) in hippocampal place cells, showing occurrence of the same phases with different rates. They show that the phase of firing and firing rate are dissociable and can represent two independent variables, e.g. the animals location within the place field and its speed of movement through the field. Note that a change of T in our model may correspond to a change in the value of physical threshold, or to a change in the value of the parameter ηÃ(ω_μ) appearing in the synaptic connections J_ij.

The role of parameter φ^* in connections J_ijin Eq. (4) is that of changing the output frequency of collective oscillation during retrieval. Here, as well as in the analog model of Eq. (5), lower values of φ^* correspond to lower frequencies, even though in the spiking model both time constants of the single neuron (τ_m and τ_s) play a role to set output frequency. Therefore, the simple formula that holds for the output frequency of the analog model is not valid in the spiking model. Output activity during recall, for φ^* = 0.24π, is shown in Figure 5, while output activity when φ^* = 0.4π has a higher frequency, as shown in Figure 6. Selective recall of two of the stored patterns are shown in Figure 6 when P = 5 patterns are stored, and φ^* = 0.4π.

FIGURE 6

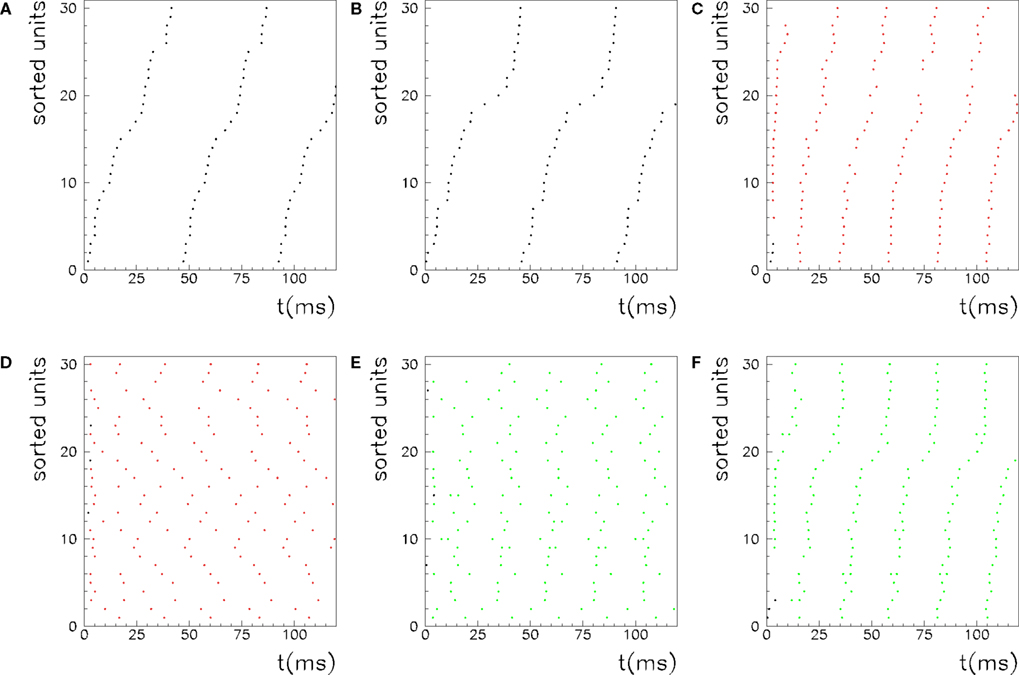
Figure 6. Example of selective retrieval of different patterns, in a network with N = 1000 IF neurons and P = 5 stored patterns. Here we choose the asymmetry parameter to be φ^* = −0.4π. Thirty neurons are chosen randomly, and then sorted by the value of 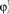yes in (A–C), and sorted by the value of 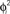yes in (D–F). In (A) and (D) we show the phases of the first two stored patterns, plotting the times 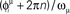yes respectively for μ = 1 and μ = 2. In (B) and (E) we show the generated dynamics when a short train of M = 100 spikes corresponding to the μ = 1 pattern is induced on the network, while in (C) and (F) the dynamics when the μ = 2 pattern is instead triggered. The network dynamics selectively replay the stored pattern, depending on the partial cue stimulation. Note that, because the parameter φ^* here is greater than in Figure 5, the frequency of the retrieved pattern here is greater.

To estimate the network capacity of the spiking model, we did numerical simulations of the IF network in Eqs. (7) and (8), with N = 3000 neurons, and connections J_ij given by Eq. (4), with different number of patterns P. We give an initial short train of M = 300 spikes chosen at times 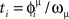yes from pattern μ = 1. To check if the initial train triggers the replay of pattern μ = 1 at large times, we measure the overlap m^μ(t) between the spontaneous dynamics of the network and the phases of pattern μ = 1. In analogy with Eq. (6), the overlap m^μ(t) is defined as

where 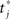yes is the spike timing of neuron j during the spontaneous dynamics, and T^* is an estimation of the period of the collective spontaneous dynamics. The overlap in Eq. (9) is equal to 1 when the phase-coded pattern is perfectly retrieved (even though on a different time scale), and is of order 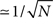yes when the phases of spikes have nothing to do with the stored phases of pattern μ. We consider a successful recall each time the overlap (averaged over 50 runs) is larger then 0.7. The capacity of the fully connected spiking network as a function of φ^* is shown in Figure 7, for threshold T = 200 and N = 3000.

FIGURE 7

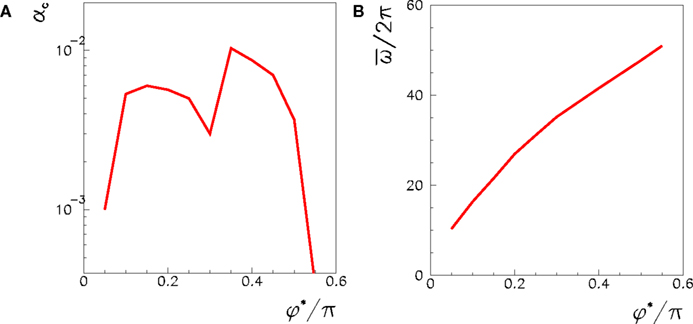
Figure 7. (A) Maximum capacity α_c = P_max/N of a network of N = 3000 fully connected spiking IF neurons, as a function of the learning window asymmetry φ^*. The spontaneous dynamics induced by a short train of M = 300 spikes with ω_μ = 20 Hz and phases given by encoded pattern μ = 1 is considered, with threshold set to T = 200. (B) The output frequency of the replay, as a function of φ^*, when P = 1, T = 200, N = 3000.

While in the analog model the output frequency tends to infinity when φ^* → π/2, in the spiking model output frequency increases but not diverge at π/2, as shown in Figure 7B. As in the analog model, the capacity decreases as soon as φ^* is near or larger then π/2. With parameters used in Figure 7, we see that, for φ^* larger then 0.55π, the stimulation spikes are not able to initiate the recall of the pattern and the network is silent, unless we choose a lower threshold. This behavior is similar to a small oscillation obtained in the analog model at φ^* → π/2.

A systematic study of the dependence of the storage capacity on the threshold T, on the number M of spikes used to trigger the recall, and on time constants τ_m and τ_s still has to be done. Future work will also consider the case in which patterns to be learned are not defined through the rate 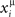yes in Eq. (2), but are defined as sequences of spikes whose timing is exactly given by yes . We expect for this case a higher storage capacity.

Summary and Discussion

In this paper we studied the storage and recall of patterns in which information is encoded in the phase-based timing of firing relative to the cycle. We analyze the ability of the learning rule given by Eq. (4) to memorize multiple phase-coded patterns, such that the spontaneous dynamics of the network, defined by Eq. (5), selectively gives sustained activity which matches one of the stored phase-coded patterns, depending on the initialization of the network. It means that if one of the stored items is presented as input to the network at time t < 0, and it is switched off at time t ≥ 0, the spontaneous activity of the network at t > 0 gives sustained activity whose phases alignments match those presented before. It is not trivial that the network performed retrieval competently, as analog associative memory is hard (Treves, 1990).

We compute the storage capacity of phase-coded patterns in the analog model, finding a linear scaling of number of patterns with network size, with maximal capacity α_c ≃ 0.02 for the fully connected network. Our model cannot be easily compared to classical models such as Hopfield’s, since the dynamical phases-coded patterns are strongly different from the classical static rate-coded patterns. Whereas the capacity of rate-coded networks has been well understood, that of spiking or phase-coded networks is not yet well understood. We are not aware of previous work who measures the storage capacity of phase-coded patterns, except of the phase-coded patterns in a spin model by Yoshioka (2009), whose capacity is in quantitative agreement with our analog model results. However, the scaling of capacity with connectivity displays properties similar to those of classical models. For strong dilution (z ≪ N), the capacity P_max, that is the maximum number of patterns encodable in the network, is proportional to z rather than to N. On the other hand, for weak dilution (z of the order of N), P_max is proportional to the number of neurons N.

Our results on the IF spiking model show that there is a qualitative agreement between the analog and the spiking model ability to store multiple phase-coded patterns and recall them selectively.

We also study the storage capacity of the analog model for different degrees of sparseness and small-worldness of the connections. We put neurons on the vertices of a two- or three-dimensional lattice, and connect each neuron to neurons that are nearer than some distance in units of lattice spacings. Then a fraction γ of these connections are rewired, deleting the short-range connection and creating a long range connection to a random neuron. The existing connections are then defined by the learning rule Eq. (4), while other connections are set to zero.

Changing the proportion γ between short-range and long-range connections, we go from a two- or three-dimensional network with only nearest-neighbors connections (γ = 0) to a random network (γ = 1). Small but finite values of γ give a “small world” topology, similar to that found in many areas of nervous system. We see that, for system size N = 24³, the capacity of a random network with only 10% connectivity already has about 40% the capacity of the fully connected network, showing that there is a saturation effect when the density of connections grows above 10%.

Looking at the dependence on the fraction of short range and long range connections, we see that at z/N = 0.11 the capacity gain with respect to the short range network, given by 30% long range connections, already is about 80% the gain given by the full random network. This last factor is likely to increase for larger system sizes, because the larger the system, the more different are long range connections with respect to short-range ones. This is interesting considering that a long-range connection clearly have a higher cost then a short-range one, and implies that a small-world network topology is optimal, as a compromise between the cost of long range connections and the capacity increase.

These results have been found for the analog model in Eq. (5). However, this is not a really spiking model, since only “firing activity” or “probability of spiking” is evaluated. Therefore we perform numerical simulation of a IF model with spike response kernels, to show that while details of dynamics may depend on the model of single unit, the crucial results of ability to store and recall of phase-coded memories can be seen also in a spiking model. Indeed numerical simulations of the spiking model in Eq. (7) shows competent storage and recall of phase-coded memories. A pattern of spikes with the stored phases, i.e. with the phase-based timing of spikes relative to the cycle, is activated by the intrinsic dynamics of the network when a partial cue of the stored pattern (few spikes at proper timings) is presented for a short time. Figure 6 shows that the network is able to store multiple phase-coded memories and selectively replay one of them depending from the partial cue that is presented. Changing the parameter φ^* of the learning rule changes the period of the cycle during recall dynamics, while changing the value of T changes the number of spikes per cycle, without changing the phase pattern. So the same phase-coded pattern can be recalled with one spike per cycle or with a short burst per cycle. This agrees well with recent observations, like occurrence of phase precession with very low as well as high firing rate (Huxter et al., 2003). The number of spikes per cycle is a sort of strength or saliency of recall. This leaves open the possibility that variations in number of spikes per cycle might convey additional information about other variables not coded in the phase pattern, as suggested in (Huxter et al., 2003; Huhn et al., 2005; Wu and Yamaguchi, 2010) for place cells, or may convey information about the saliency of retrieved pattern (Lengyel and Dayan, 2007).

In our treatment, we distinguish a learning mode, in which connections are plastic and activity is clamped to the phase-coded pattern to be stored in the synaptic connections J_ij, from a recall mode, in which connection strengths do not change. Of course, this distinction is somewhat artificial; real neural dynamics may not be separated so clearly into such distinct modes. Nevertheless, data on cholinergic neuromodulatory effects (Hasselmo, 1993, 1999) in cortical structures suggesting that high levels of acetylcholine selectively suppress intrinsic but not afferent fiber transmission and enhance long-term plasticity, seems to provide a possible neurophysiological mechanism for this distinction in two operational modes.

Another point is given by the physical constraints on the sign of synaptic connections J_ij, that for a given presynaptic unit j, are all positive when presynaptic unit j is excitatory, and all negative when presynaptic unit j is inhibitory, a condition not respected by our learning formula Eq. (4) so far. As a remedy, one may add an initial background weight J₀ to each connection, independent of i and j, such that J_ij + J₀ > 0 for all i and j, to make all the units excitatory and plastic connections positive, and then one has to add a global inhibition equal to −J₀ times the mean field y = Σ_jx_j to save equilibrium between excitation and inhibition. In such a way, we have a network of N excitatory units, with positive couplings, and a global inhibition,

that is mathematically equivalent to Eq. (5) when y = Σ_jx_j, and numerically also gives the same results when y = N/2.

Considering the IF model of section “Integrate and fire model”, also in this case we can consider a network of all excitatory neurons, with plastic positive connections given by J_ij + J₀ with J₀ constant such that J_ij + J₀ > 0, and then add a proper inhibitory term to save the equilibrium between excitation and inhibition. In this way, the postsynaptic potential of neuron i, after time t_i of its last spike, is given by

The inhibitory term yes can be realized in different ways, for example imaging that for each excitatory unit j, there is a fast inhibitory interneuron j, that emits a spike each time its excitatory unit does, and is connected with all the other excitatory neurons with constant weight connections J₀.

The task of storing and recalling phase-coded memories has been also investigated in (Lengyel et al., 2005b) in the framework of probabilistic inference. While we study the effects of couplings given by Eq. (4) in the network model Eq. (5), and in a network of IF neurons given by Eq. (7), the paper (Lengyel et al., 2005b) studies this problem from a normative theory of autoassociative memory, in which variable x_i of neuron i represents the neuron i spike timing with respect to a reference point of an ongoing field potential, and the interaction H(x_i, x_j) among units is mediated by the derivative of the synaptic plasticity rule used to store memories. In (Lengyel et al., 2005b), the case of limited connectivity is studied, showing how recall performance depends to the degree of connectivity when connections are cut randomly. Here we show that performance also depends from the topology of the connectivity, and capacity depends not only from the number of connections but also from the fraction of long range versus short-range connections.

The role of STDP in learning and detecting spatio-temporal patterns has been studied recently in (Masquelier et al., 2009). They show that a repeating spatio-temporal spike pattern, hidden in equally dense distracter spike trains, can be robustly detected by a set of “listening” neurons equipped with STDP. When a spatio-temporal pattern repeats periodically, it can be considered a periodic phase-coded pattern. While in Masquelier et al. (2009) the detection of the pattern is investigated when it is the input of the “listening” neurons, in our paper we investigate the associative memory property, which makes the pattern imprinted in the connectivity of the population an attractor of the dynamics. When a partial cue of the pattern μ is presented (or in the analog case the network is initialized with 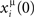yes ), then the original stored pattern is replayed. Differently from Masquelier et al. (2009), here the pattern μ is imprinted in the neural population, in such a way that exactly the same encoded phase-coded pattern is replayed during persistent spontaneous activity. This associative memory behavior, that replay the stored sequence, can be a method for recognize an item, by activating the same memorized pattern in response of a similar input, or may be also a way to transfer the memorized item to another area of the brain (such as for memory consolidation during sleep).

Our results shows that in the spiking model a critical role is played by the threshold T: changing the threshold one goes from a silent state to a spontaneously active phase-coded pattern with one spike per cycle, and then to the same phase-coded pattern with many spikes per cycle (bursting). Therefore, a possible conjecture is that when we observe the replay of a periodic spatio-temporal pattern, then if one is able to change the threshold of spiking of the neurons, one can observe the same phase pattern but with more or less spikes per cycle.

In future we will also investigate the capacity when patterns with different frequencies are encoded in the same network. In this paper we compute the capacity when encoded patterns have all the same frequency, however it would be interesting to see how the network work with different frequencies. Preliminary results on the analog model (Scarpetta et al., 2008) show that it’s possible to store two different frequencies in a manner that both are stable if a relationship holds between the two frequencies and the shape of the learning window. We plan to investigate this both in the analog and in the spiking model.

Concerning the shape of learning kernel A(τ), in our model the values of the connections J_ij depend on the kernel shape only through the time integral of the kernel, and the Fourier transform of the kernel at the frequency of the encoded pattern. As shown in our previous paper (Yoshioka et al., 2007), best results are obtained when the time integral of the kernel is equal to zero 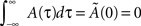yes . This choice will assure the global balance between excitation and inhibition. Hence in the present paper we choose to set this value to zero, and varied only the phase φ^* of the Fourier transform. The case of a purely symmetric kernel corresponds to φ^* = 0, while a purely anti-symmetric (causal) one corresponds to φ^* = π/2. We find that intermediate values 0 < φ^* < π/2 work better then values π/2 < φ^* < π, for which the network is not able to replay patterns competently. We study here positive values of φ^*, i.e. a causal kernel (potentiation for pre–post, and depotentiation for post–pre), however an anti-causal kernel would give a negative value of φ^*, and a negative frequency of replay, that is the pattern would be replayed in time reversed order (Scarpetta et al., 2008).

For what concerns the variety of shapes of the learning window observed in the brain, it has to be considered that they may accomplish different needs, such as maximize storage capacity, or set the time scale of replay, which in our model depends on the kernel shape. Notably, in our model we observe a good storage capacity for values of phase φ^* which correspond to a large interval of frequency of oscillation during replay, and therefore there is good storage capacity also for values of φ^* which correspond to a compressed-in-time replay of phase pattern on very short time scale. Future work will investigate the relation between this framework and the time-compressed replay of spatial experience in rat. It has been indeed observed that during pauses in exploration and during sleep, ensembles of place cells in the rat hippocampus and cortex re-express firing sequences corresponding to past spatial experience (Lee and Wilson, 2002; Foster and Wilson, 2006; David et al., 2007; Diba and Buzsaki, 2007; Hasselmo, 2008; Davidson et al., 2009). Such time-compressed hippocampal replay of behavioral sequences co-occurs with ripple events: high-frequency oscillations that are associated with increased hippocampal–cortical communication. It’s intriguing the hypothesis that sequence replay during ripple is the recall of one of the multiple stored phase-coded memories, a replay that occur on a fast time scale (high yes ), triggered by a short sequence of spike.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Abarbanel, H., Huerta, R., and Rabinovich, M. I. (2002) Dynamical model of long-term synaptic plasticity. Proc. Natl. Acad. Sci. 99, 10132–10137.