Summing across different active zones can explain the quasi-linear Ca2+-dependencies of exocytosis by receptor cells

Introduction

Fast release of neurotransmitter by neurons and by receptor cells via fusion of transmitter-containing vesicles with the cell membrane is a process which depends on calcium (Ca²⁺)-ions (Katz, 1969). If the membrane of the presynaptic cell is sufficiently depolarized, Ca²⁺ enters the cell through voltage-gated Ca²⁺-channels located near the presynaptic release sites. The binding of Ca²⁺-ions by a Ca²⁺-sensor in the membrane of a release-ready synaptic vesicle is a key step in the complex chain of events leading to its fusion with the presynaptic cell membrane and to release of neurotransmitter. For a comprehensive description of these processes, the reader is referred to authoritative reviews (e.g., Südhof, 2004). The probability or rate of fusion of available ready-release vesicles or of transmitter release events (henceforth referred to simply as exocytosis) is a function of the concentration of Ca²⁺-ions “seen” by the Ca²⁺-sensor (e.g., Beutner et al., 2001; Duncan et al., 2010). This concentration depends on a number of factors, including the amount of Ca²⁺ which enters the cell and the spatial and temporal profile of Ca²⁺-spread within the cell. The spread depends on, among other parameters, the spatial distance between Ca²⁺-source(s) and Ca²⁺-sensor and on the concentration and nature of Ca²⁺-buffers in the intracellular environment (e.g., Neher, 1998). The amount of Ca²⁺ that enters the cell at an active zone (AZ) depends on the number of Ca²⁺-channels that contribute to the local intracellular Ca²⁺-concentration, the single-channel conductance, the open time and open probability, the membrane potential, and the external Ca²⁺-concentration. Finally, exocytosis also depends on the number of release-ready vesicles, and on the properties of the Ca²⁺-sensor, including its affinity for Ca²⁺ and its intrinsic, biochemical Ca²⁺-cooperativity, reflecting, among other things, the number of Ca²⁺-ions that it must bind before exocytosis can occur. The conflicting reports about the relationship between Ca²⁺-entry and exocytosis in different experimental preparations and their potential cause are the focus of this theoretical paper.

What can we state about the intrinsic, biochemical Ca²⁺-cooperativity of the Ca²⁺-sensors involved in fast exocytosis? There now appears to be general agreement that synaptotagmins I and II function as such sensors in the central nervous system. These proteins are highly homologous and occur in a differential and complementary fashion throughout the central nervous system, with synaptotagmin I primarily expressed in the forebrain, but also in chromaffin cells (Marqueze et al., 1995), and synaptotagmin II in the brainstem and spinal chord (e.g., Südhof, 2002; Sugita et al., 2002; Koh and Bellen, 2003; Yoshihara et al., 2003). These proteins are located in the synaptic vesicle membranes and feature two cytosolic Ca²⁺-binding domains, the C2A and the C2B domain, which bind three and two Ca²⁺-ions, respectively (Ubach et al., 1998; Fernandez et al., 2001). The binding of three Ca²⁺-ions to the C2A domain occurs in a highly cooperative fashion, yielding a Hill coefficient of about 3 in phospholipid-binding assays (Davletov and Südhof, 1993; Rizo and Südhof, 1998). Furthermore, even though exocytosis can occur in the absence of a C2A domain, the binding of Ca²⁺ to the C2A domain contributes significantly to the overall triggering of neurotransmitter release and determines the Ca²⁺-cooperativity of this process (Shin et al., 2009). Hence, based on these properties of these ubiquitous Ca²⁺-sensors, exocytosis may be expected to increase with the third power of the intracellular Ca²⁺-concentration in the vicinity of the sensors.

A few studies of exocytosis, by auditory and visual receptor cells (Beutner et al., 2001; Thoreson et al. 2004; Duncan et al., 2010) and by neurosecretory adrenal chromaffin cells (Voets, 2000), have probed this dependence. In these studies, cells were loaded with photolabile Ca²⁺-chelators. Ca²⁺ was then liberated by flash photolysis, giving rise to a presumably homogeneous intracellular Ca²⁺-concentration. The observed relationships between exocytosis and intracellular Ca²⁺-concentration in these studies indeed appear consistent with a third power dependence (see also below).

Most studies, however, have measured relationships between exocytosis and some measure of Ca²⁺-entry into the cell. Such relationships yield “apparent” Ca²⁺-cooperativities which may differ from the intrinsic, biochemical Ca²⁺-cooperativity, and may differ in different experimental preparations. In fact, the differences have been used to implicate a specific form of stimulus secretion coupling (see below). Nevertheless, in most experimental preparations studied so far, the observed relationships between measures of Ca²⁺-entry into the presynaptic cell and of the rate of exocytosis are highly supralinear. Specifically, exocytosis has been reported to grow approximately with the third to fourth power of the Ca²⁺-entry at the calyx of Held in the rat auditory brainstem (Borst and Sakmann, 1996; Bollmann et al., 2000; Schneggenburger and Neher, 2000), the squid giant synapse (Augustine et al., 1985), the giant synaptic terminal of bipolar neurons in the goldfish retina (von Gersdorff and Matthews, 1994, as cited by Thoreson et al., 2004), the granule to Purkinje cell synapse in the rat cerebellum (Mintz et al., 1995), the mitral/tufted to pyramidal cell synapse in the rat piriform cortex (Murphy et al., 2004), the basket to granule cell synapse in the rat dentate gyrus (Bucurenciu et al., 2010), and the frog and fruit-fly neuromuscular junctions (Dodge and Rahamimoff, 1967; Jan and Jan, 1976; Shahrezaei et al., 2006). Similar supralinear Ca²⁺-dependencies of exocytosis have also been reported for mammalian inner and outer hair cells (IHCs and OHCs, respectively), and for vestibular hair cells (HCs), but notably only in immature or genetically modified animals, in spatially restricted locations, or under unnatural stimulus conditions. Specifically, approximately third to fourth power Ca²⁺-dependencies have been reported for IHCs from immature mice and gerbils (Johnson et al., 2005, 2009, 2010; Beurg et al., 2008), for IHCs from mature hypothyroid rats, for IHCs and OHCs from mature and immature synaptotagmin IV knockout mice (Johnson et al., 2010), for IHCs from the low-frequency apical, but not the high-frequency basal, cochlear regions of mature gerbils (Johnson et al., 2008), for IHCs from young rats when the membrane potential of these cells was clamped to positive values (Goutman and Glowatzki, 2007), and for type I vestibular HCs of otoferlin knockout mice (Dulon et al., 2009).

In contrast, some of the same studies, but also others, have reported nearly linear relationships between measures of Ca²⁺-entry and exocytosis and have concluded that exocytosis depends linearly on Ca²⁺-entry. This applies to auditory HCs of mature and genetically normal animals (Brandt et al., 2005; Johnson et al., 2005, 2008, 2009, 2010; Schnee et al., 2005; Keen and Hudspeth, 2006; Goutman and Glowatzki, 2007; Beurg et al., 2008), to OHCs of immature mice (Beurg et al., 2008; Johnson et al., 2010), to vestibular HCs (Dulon et al., 2009), to visual (Thoreson et al., 2004) and to olfactory receptor cells (Murphy et al., 2004). In the following, we will refer to these relationships as “quasi-linear”, since the powers derived in these studies in fact range from as low as 0.6 to as high as 1.5.

In some of these studies (viz., those of HCs and of visual and olfactory receptor cells) the apparent Ca²⁺-cooperativity was thought to directly reflect the intrinsic one. Consequently, to account for the apparent quasi-linear Ca²⁺-dependencies it was suggested in these studies that the biochemical Ca²⁺-cooperativity of the Ca²⁺-sensors may be altered (Murphy et al., 2004; Thoreson et al., 2004; Johnson et al., 2005, 2010; Dulon et al., 2009). At least with respect to IHCs, however, this proposal is at variance with the high biochemical cooperativity of the sensor determined by means of Ca²⁺-uncaging experiments (Beutner et al., 2001), as mentioned above and as discussed in more detail later. Furthermore, synaptotagmins I and II have recently been reported to be present also in (mouse) IHCs at different stages of development (Johnson et al., 2010), in contrast to an earlier study by Safieddine and Wenthold (1999) which did not find these molecules in the (guinea-pig) cochlea. A more plausible explanation for a quasi-linear Ca²⁺-dependency, i.e., for the difference between intrinsic and apparent Ca²⁺-cooperativity, is a nanodomain control of exocytosis (Neher, 1998). According to this model, the vesicle with its Ca²⁺-sensors is in such close proximity to a Ca²⁺-channel (within a few tens of nanometers) that it senses the gating of essentially this single channel only, and Ca²⁺-influx through this single channel is sufficient to trigger the vesicle’s fusion (e.g., Brandt et al., 2005; Goutman and Glowatzki, 2007; Bucurenciu et al., 2008; Jarsky et al., 2010). Thus, in this extreme scenario, where the Ca²⁺-channel cooperativity is zero, an n-fold increase in channel open probability would lead to the equivalent n-fold increase in the number of fused vesicles (provided the proportion of release-ready vesicles docked at the channels is unchanged). Since a nanodomain cannot yet be visualized, support for it relies on indirect evidence. Such indirect evidence includes, according to Augustine et al. (2003), the inability of the slow Ca²⁺-buffer EGTA to block Ca²⁺-triggered physiological responses or the requirement of high local intracellular Ca²⁺-concentrations (100 μM or more) to trigger exocytosis. In addition, and as argued, for example, by Augustine et al. (1991) and Brandt et al. (2005), if exocytosis is under nanodomain control, the relationship between whole-cell exocytosis and whole-cell Ca²⁺-entry depends upon how the whole-cell Ca²⁺-entry is varied experimentally. Varying it by changing the number of open channels should yield a linear relationship, whereas varying it by changing the single-channel current should reveal the intrinsic, biochemical, Ca²⁺-cooperativity of the Ca²⁺-sensor. In contrast, if exocytosis is under microdomain control, where Ca²⁺ entering through multiple clustered channels spatially summates, the two types of experiment should yield equal results. Indeed, there is strong evidence for a nanodomain control at some synapses, e.g., at the squid giant synapse (Augustine et al., 2003), the basket to granule cell synapse in the rat dentate gyrus (Bucurenciu et al., 2008, 2010), or the rod bipolar to AII amacrine cell synapse in the mouse retina (Jarsky et al., 2010). With respect to HCs, however, including IHCs, the evidence is not entirely convincing. Although two studies, of mammalian IHCs, have reported that manipulating whole-cell Ca²⁺-entry by changing the number of open channels versus changing the single-channel current have different effects on whole-cell exocytosis (Brandt et al., 2005; Goutman and Glowatzki, 2007), others have reported very similar effects of these two approaches (e.g., Johnson et al., 2005, 2010; Dulon et al., 2009). Nevertheless, the latter studies could still be compatible with a nanodomain control. These studies used rather long-duration depolarizations (100 ms or more), so that the observed exocytosis may not only comprise that of release-ready vesicles, but also of re-supplied vesicles. Hence, several processes with potentially different Ca²⁺-sensitivities, such as fusion, re-supply, priming, or site-clearance (e.g., Neher and Sakaba, 2008), may have been lumped together. And if, for example, re-supply were governed by a high Ca²⁺-cooperativity and was rate-limiting, the third to fourth power Ca²⁺-dependencies described in the same publications but in other preparations, e.g., HCs from immature or genetically modified animals, could also be reconciled with a nanodomain control.

Here, we offer a hitherto unrecognized explanation for the observations of quasi-linear relationships between Ca²⁺-entry and exocytosis in the studies cited above, viz. as the result of summing over several different supralinear, but saturating, functions. We show that published experimental data, allegedly supporting a linear Ca²⁺-dependence, can be accurately accounted for by this summation model. All that is required is that the experimental measures assess the sum of processes occurring at different AZs, which they do, and that these processes simply differ in sensitivity (or gain), for which there is strong evidence. Our assumption of differentially sensitive AZs contributing to the summed response, each operating with the established Ca²⁺-cooperativity of the ubiquitous Ca²⁺-sensors involved in exocytosis, provides a parsimonious and attractive explanation for experimental findings in different preparations.

Methods

The model to be described below was implemented in Microsoft Excel. The model was tested exclusively on data from the literature. The studies were selected based on the apparent quality of the data (reproducibility and reliability) and on the extent to which they challenged the model, the greater the challenge the better. This is not to say that data that were not used here would be considered unreliable. The figures of interest were exported from the original publications into Corel Draw and the data points were determined with the highest accuracy possible. The remaining errors are very small and negligible compared to the errors in measuring the data. Still, we cannot exclude the possibility that a single marker in a figure of an original publication might have represented more than one data point. The model was fit to the data using the Solver module of Excel and minimizing the sum of the squared residuals between model and data, unless stated otherwise.

Results

The Summation Model

Our model aims to account for both the supralinear and the quasi-linear Ca²⁺-dependencies of exocytosis reported in different preparations, with a minimum number of plausible differences underlying the different dependencies. First, it is important to realize that Ca²⁺-dependencies are commonly assessed in cells that contain several AZs; mammalian IHCs, for example, contain between about 10 and 30 (e.g., Liberman et al., 1990; Meyer et al., 2009; Johnson et al., 2010). They can be viewed as parallel processing units (Figure 1A). Second, the experimental measures of exocytosis and/or Ca²⁺-entry represent the sum of processes occurring at the different AZs (see Reports of “Quasi-Linear” Ca²⁺-Dependencies are Based on Measuring Summed Responses). We assume the intracellular Ca²⁺-concentration in the vicinity of, or “seen” by, release-ready vesicles (local [Ca²⁺]_in) to be the critical quantity determining exocytosis at each AZ. The key assumption of our model is that for a given stimulus (a given membrane potential and extracellular Ca²⁺-concentration, and hence also for a given whole-cell Ca²⁺-current), there can be differences between AZs in local [Ca²⁺]_in (Figure 1A). The factors which might contribute to such differences are discussed later (see Ca²⁺-Signals at Individual AZs of a Given Cell Differ). A second important, but also highly plausible, assumption of our model is that the rate of exocytosis is a supralinear function of the local [Ca²⁺]_in because the Ca²⁺-sensor requires the cooperative binding of several Ca²⁺-ions (biochemical cooperativity). Since exocytosis at a given AZ cannot grow infinitely, exocytosis must be a saturating function of the local [Ca²⁺]_in. In the realizations of our model, we assume this function to be a Boltzmann function:

FIGURE 1

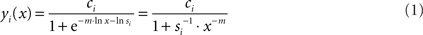
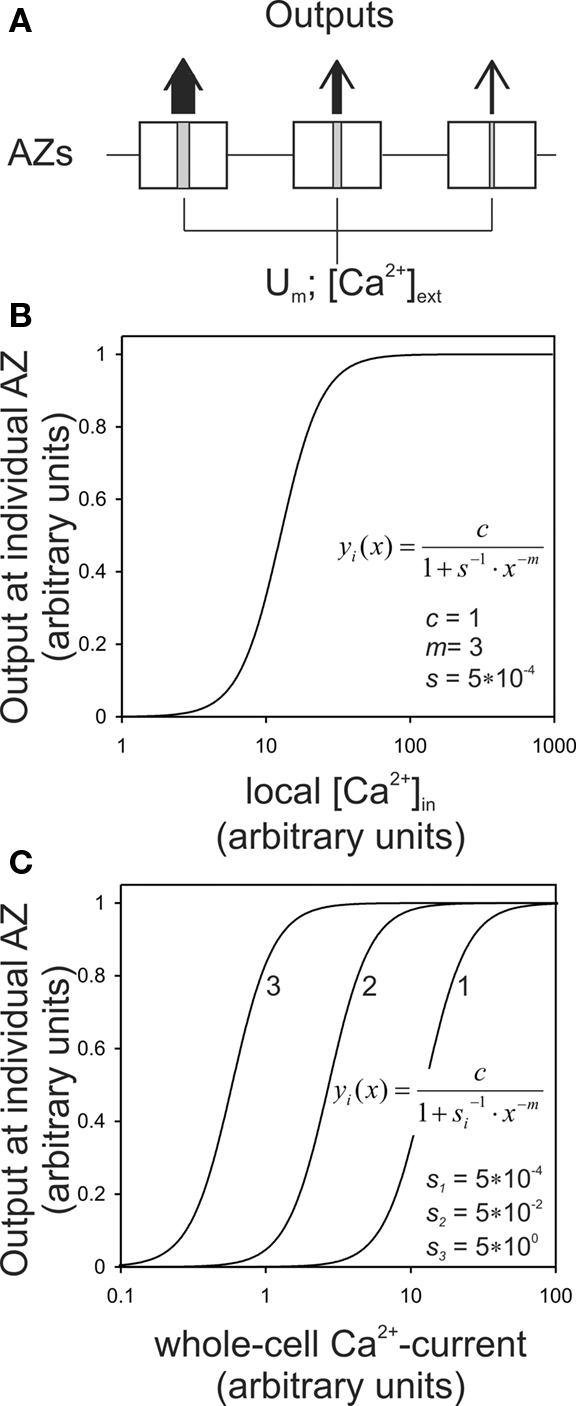
Figure 1. The summation model. (A) Schematic sketch of the model. A cell, such as a hair cell, has several different actives zones (AZs). A change in the membrane potential, U_m, will lead to changes in the open probabilities of Ca²⁺-channels, which constitute parallel conductances. The model assumes that for any given U_m and extracellular Ca²⁺-concentration, [Ca²⁺]_ext, and hence also whole-cell Ca²⁺-current, there can be differences in the intracellular Ca²⁺-concentration near the AZs (local [Ca²⁺]_in), symbolized by the width of the gray bars. These differences may result from a number of factors, e.g., differences in the number of Ca²⁺-channels at individual AZs or in their spatial arrangement relative to the location of release-ready vesicles. The output (rate of exocytosis) at each AZ, symbolized by the width of the black arrows, is a supralinear function of the local [Ca²⁺]_in. (B) The function relating the output at an individual AZ to the local [Ca²⁺]_in. The model assumes this function to be a Boltzmann function, where the power m, the sensitivity s, and the scaling parameter c are identical at individual AZs. For the function shown, m = 3, s = 5 × 10⁻⁴, and c = 1. The value of m is thought to represent the number of Ca²⁺-ions that must cooperatively bind to the Ca²⁺-sensor to trigger fusion. (C) Functions relating the output at individual AZs to the whole-cell Ca²⁺-current, under the assumption of differences in the local [Ca²⁺]_in at individual AZs for a given whole-cell Ca²⁺-current. In the model, these functions then constitute Boltzmann functions with different sensitivities, s_i.

Here, y_i(x) denotes the output (exocytosis) at a given individual AZ of index i and x the local [Ca²⁺]_in (measured in units of mol/l or M). Parameter c_i denotes the maximum output that is possible at a given AZ. Parameter s_i (measured in units of M^−m) is a measure of sensitivity; the larger s_i the larger is y_i(x) for a given x. When the local [Ca²⁺]_in equals 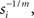the output equals half the maximum possible output, i.e., 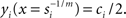Parameter m is a dimensionless power which, in the model, represents the number of Ca²⁺-ions bound by the sensor in a highly cooperative manner (biochemical cooperativity). We assume this number to be the same at all individual AZs. In our realizations of the model, we use m = 3, since this integer number appears to be best compatible with the data (see also Some Methodological Considerations in Estimating the Biochemical Ca²⁺-Cooperativity). In principle, however, the model could also work with other numbers. We further assume s_i to be identical at all AZs, so that the half-maximum output (or any other percentile) at each AZ occurs at the same local [Ca²⁺]_in. For simplicity, we also assume c_i to be identical at all AZs, although this is not necessary (see below). Equation 1 can then be written without indices. Such a function is shown in Figure 1B, for m = 3, s = 5 × 10⁻⁴, and c = 1. Consequently, the functions relating exocytosis at individual AZs to the local [Ca²⁺]_in all overlap when plotted in the same graph. The same is true when exocytosis at individual AZs is plotted as a function of the whole-cell Ca²⁺-current, but only if the local [Ca²⁺]_in at individual AZs are identical for a given whole-cell Ca²⁺-current.

When this is not the case (as in Figure 1A), the picture is different. Then, the functions relating exocytosis at individual AZs to whole-cell Ca²⁺-current lie at different positions along the abscissa. Figure 1C plots three such functions, generated with c = 1 and m = 3. In this semi-logarithmic plot, the functions are shifted parallel to each other along the abscissa. Each function is still a Boltzmann function, but the positional differences would now be captured by differences in the measure of sensitivity s_i, with the right function (1) having the lowest and the left function (3) the highest sensitivity. This measure of sensitivity differs from the previous one, since it relates exocytosis at an individual AZ to whole-cell current, rather than to local [Ca²⁺]_in, and consequently is measured in units of A^−m.

In the studies that have reported quasi-linear Ca²⁺-dependencies, as cited above, the measure of exocytosis, e.g., the change in membrane capacitance of the cell under study (see Discussion), commonly reflects the sum of outputs at several AZs. In our model, this is captured by a sum of Boltzmann functions, given by:

Here, c_i constitute individual scaling factors. They can be conceived of as representing the maximum outputs at individual AZs, which are not necessarily identical, or as the relative proportions of differentially sensitive AZs with identical maximum outputs that contribute to the summed output, Y(x), or both.

Such a sum of Boltzmann functions remains a Boltzmann function only when the values of the sensitivity parameter are identical (s_i = s). Then Eq. 2 can be written as:

It is worth noting that for low s and/or small values of x, this summed function can be well approximated by a non-saturating power function, frequently used in the literature:

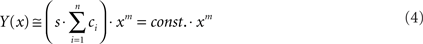
In other words, when the sensitivities at the different AZs are identical and low, the power function (Eq. 4) is likely to reveal the number m of Ca²⁺-ions that may bind to the Ca²⁺-sensor in a highly cooperative manner. When the values of the sensitivity parameter differ, however, the shape of the summed function will differ from that of a Boltzmann function. In fact, and perhaps surprisingly, the summed function can appear rather linear. Figure 2A shows three Boltzmann functions, generated according to Eq. 1, again with c = 1 and m = 3, but with different values of s_i. Figure 2B (continuous line) shows a summed function Y(x) for the simple case in which only three different functions contribute to the sum, i.e., for n = 3. The three scaling parameters and the three sensitivities were fitted such that Y(x) best approximates the particular straight line also shown in the plot (dashed line). This particular straight line, with a slope of 0.228 and an intercept of 0, was chosen since it closely matches, but also linearly extends, a set of data published by Johnson et al. (2005), relating capacitance changes to whole-cell Ca²⁺-currents from IHCs of adult mice (Figure 5 in Johnson et al., 2005; see also Figure 3 below). The three sensitivity values and the three scaling factors obtained from the fit of Eq. 2 are given in the legend of Figure 2. The scaling factors can also be expressed as the relative proportions of the three types of individual functions contributing to the summed function if their individual maximal outputs were identical. These fractions are given by the ratio of the corresponding value of s_i to the sum over all values of s_i (in this case 3 values). It is obvious from Figure 2 that adding individual saturating power functions with just three different sensitivities and proportions can result in a summed function which appears rather linear over a considerable range of input and output values. With just two different sensitivities and proportions, the range over which the summed function can appear roughly linear is of course more restricted (not shown). Conversely, with a larger number of different sensitivities and proportions the deviations of the summed function from a linear one become even smaller, and the summed function mimics a linear one over a wider range than the function shown in Figure 2B. Nevertheless, at very low input values, the summed function must increase supralinearly (inset in Figure 2B), because in this range all underlying individual functions, even the most sensitive one, are essentially unaffected by saturation. At high input values, the summed function must saturate and thus also deviate from linearity. It is obvious that a power function (Eq. 4) fitted to it would not reveal the number of Ca²⁺-ions bound to the Ca²⁺-sensor.

FIGURE 2

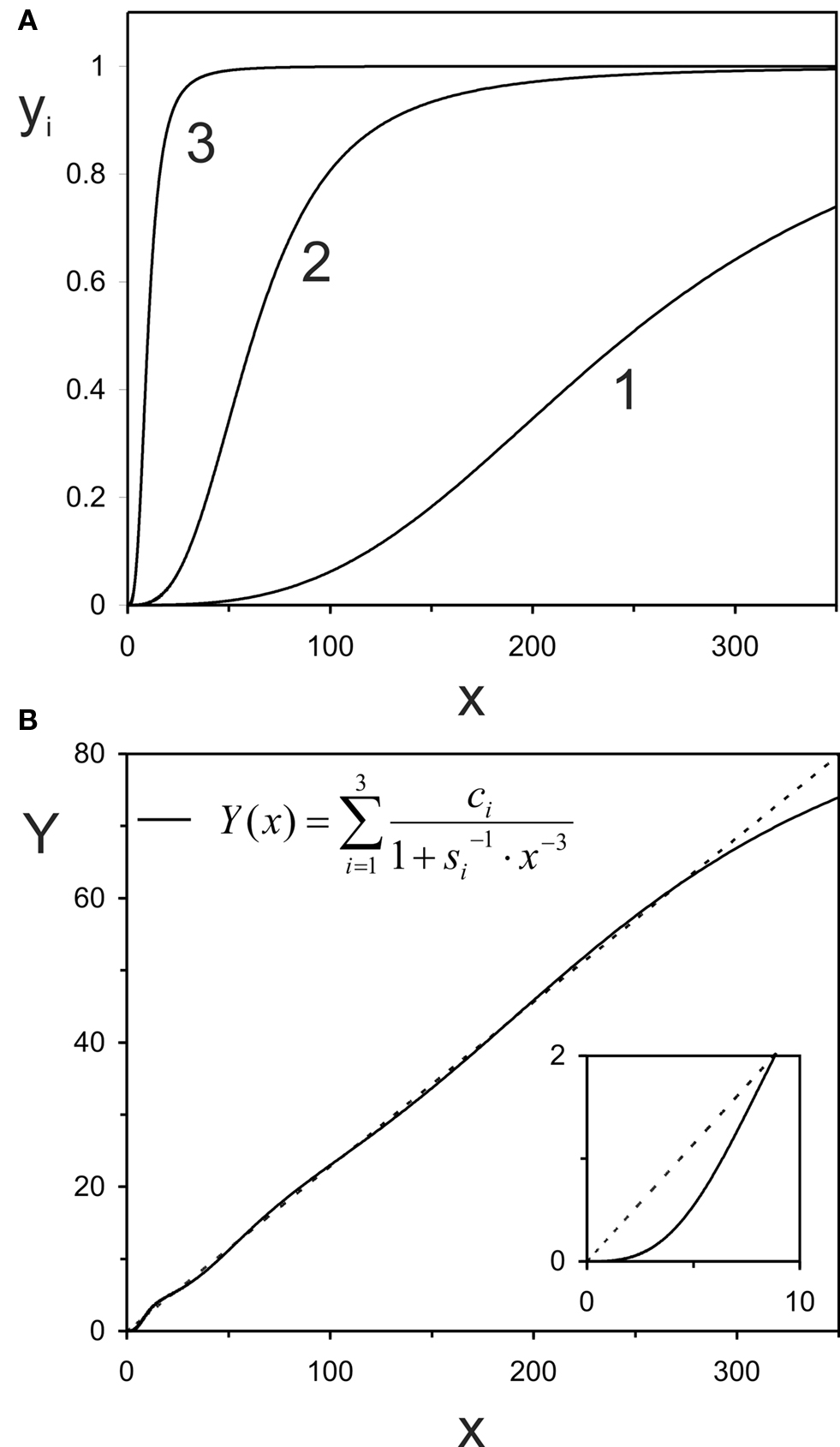
Figure 2. The sum of Boltzmann functions with different sensitivities can result in a quasi-linear function. (A) Three different Boltzmann functions, generated with a common m = 3 and c = 1, but different sensitivities (s₁ = 6.62 × 10⁻⁸; s₂ = 4.16 × 10⁻⁶; s₃ = 1.00 × 10⁻³), are shown in double-linear scales. (B) Their sum, with scaling factors of c₁ = 70.48; c₂ = 17.20; c₃ = 4.76, results in a quasi-linear function (continuous line) that approximates a straight line with a slope of 0.228 (dashed line). For small values of x, however, the summed function grows supralinearly and falls below the truly linear function (inset). At high values of x, the summed function saturates.

FIGURE 3

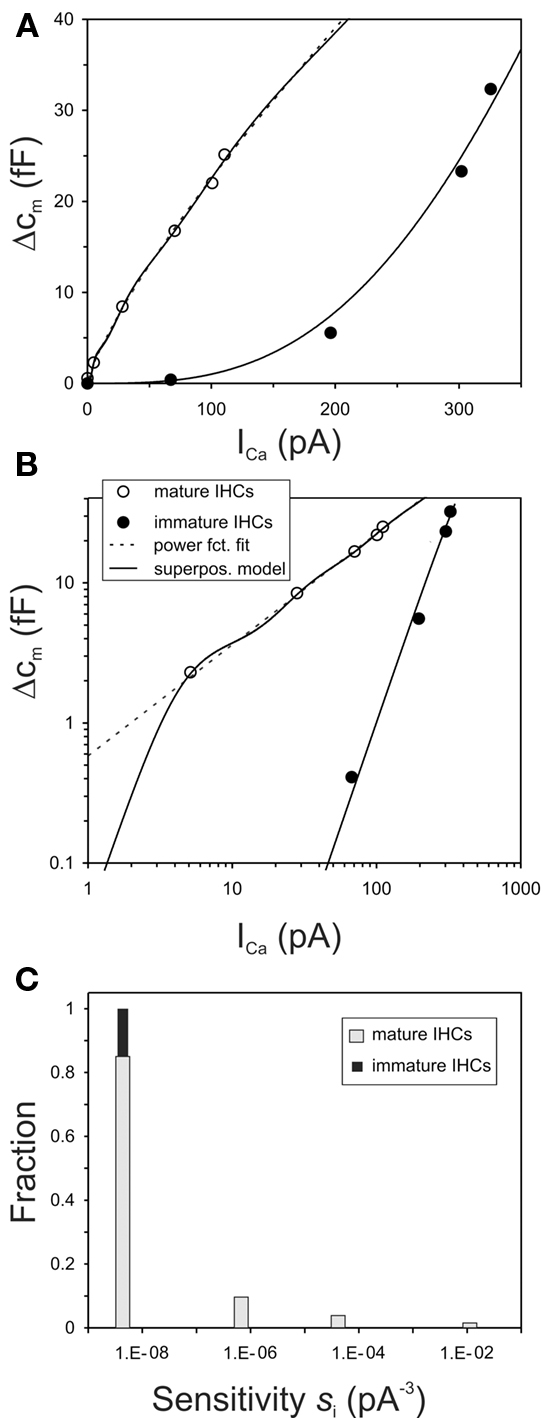
Figure 3. Application of the summation model to account for the developmental change from a supralinear to a quasi-linear Ca²⁺-dependence in mice IHCs, reported by Johnson et al. (2005). The data points from Figure 5 of their study are re-plotted here in double-linear (A) and double-logarithmic coordinates (B). The legend in (B) also applies to (A). In both panels, the dashed line represents the fit of the data from mature IHCs with a simple power function (Eq. 4), performed in double-linear coordinates as frequently done in the literature. For this data set, we obtained m = 0.79. The dashed line in (A) is barely visible, because it is largely covered by the continuous line through this data set, which represents our summation model, fitted to approximate the simple power function, not just the five data points. The continuous line through the data points from immature IHCs represents our summation model for these data. The four different sensitivities, s_i, assumed in the model for the mature IHCs, and their fractions are plotted in (C). For immature IHCs, all sensitivities are identical (left black bar, partly covered by the low-sensitivity fraction of mature IHCs). For adult IHCs, the four sensitivities are s₁ = 4.31 × 10⁻⁹; s₂ = 6.77 × 10⁻⁷; s₃ = 4.11 × 10⁻⁵; s₄ = 1.12 × 10⁻² with units of pA⁻³. The corresponding scaling factors are c₁ = 200; c₂ = 22.75; c₃ = 9.01; c₄ = 3.67 with units of fF, resulting in fractions of 0.85, 0.097, 0.038, and 0.016, respectively. For immature IHCs, all sensitivities are identical with s = 4.31 × 10⁻⁹ pA⁻³. The single scaling factor is 235.42 fF, identical to the sum of the four scaling factors for adult IHCs. In all cases m = 3.

Application of the Model to Published Data

In this section, we apply the model to selected, informative, data published in the literature.

Changes during ontogeny

As a first example, we selected measurements from IHCs of immature (postnatal day 6–7) and mature mice (postnatal day 16–20), as published by Johnson et al. (2005, their Figure 5). These authors also measured IHCs of neonatal mice (embryonic day 17 to postnatal day 3), but those data are omitted here for clarity, since they were similar to those from the immature age group. In this particular experiment, Johnson et al. measured whole-cell Ca²⁺-currents into IHCs and capacitance changes of the same cells as the read-out for exocytosis in response to 100-ms voltage steps from a holding potential of −81 mV to different potentials up to −11 in 10 mV increments. The data points in their figure are associated with small error bars, derived from measurements across eight IHCs each, and they fall closely onto power functions fitted to them (see Figure 5 in Johnson et al., 2005). The power reported by Johnson et al. (2005) for their data from immature IHCs was 3.3, close to the value of m = 3 that would be expected from the biochemical cooperativity of the Ca²⁺-sensor (see Introduction), while that for the data from the mature IHCs was 0.7. Thus, these data represent a particularly challenging case for our model.

Figures 3A,B show these data points from the study of Johnson et al. (2005), in double-linear and double-logarithmic plots, respectively, as in the original publication. The dashed line through the data from the mature IHCs (open circles) represents our fit of these data with a simple, non-saturating, power law. This fit yielded a power of 0.79, close to the value of 0.7 reported by Johnson et al. (2005). The small difference could have originated from differences in the data points included in the fit. We fitted the power function to the five mean values shown in the figure, whereas Johnson et al. may have fitted the function to all individual data points. In any event, and more importantly, the continuous line through this data set represents the outcome of our summation model, fitted to approximate the quasi-linear power law (in order to please the eye), not just the five data points. It is obvious that our summation model can capture this quasi-linear function, as well as the data points, very well. The continuous line through the data points from immature IHCs represents our summation model for these data.

It is informative to scrutinize the parameters required to provide these approximations, particularly in light of the constraints which we decided to impose on the summation model. The first constraint was that, for both ages, m = 3, i.e., we assume the biochemical Ca²⁺-cooperativity to remain unaltered during ontogeny. The second constraint was that, for both ages, ∑c_i = const., i.e., we assume that the maximum possible output (here change in membrane capacitance) remains unaltered during development. This constraint also seemed reasonable given that Johnson et al. (2005) found no difference between immature and mature IHCs in total exocytosis for depolarizations to −11 mV and durations ≤100 ms (see Figure 4C in Johnson et al., 2005). The only parameter that must change, according to our model, is the sensitivity, s_i, and its variability between AZs. Work by Moser and colleagues (e.g., Beutner and Moser, 2001) suggests that the total exocytosis is not the same for immature and mature IHCs, but instead varies systematically during ontogeny. However, such variation does not constitute a problem for our model, since the data can, of course, also be fitted without the constraint ∑c_i = const.

In immature IHCs, and according to our model, all s_i are low and identical. The continuous line in Figure 3B represents this scenario. The common sensitivity is identified in the histogram of Figure 3C (left black bar). Recall that summing across Boltzmann functions with identical sensitivity at the individual AZs and identical m, results in a Boltzmann function which has the same shape as those for each individual AZ, just a different scaling factor, given by the sum of c_i (Eq. 3). The model would also work if the AZs were low but not identical, as long as they are not too dissimilar.

During ontogeny, however, and according to our model, the sensitivity s_i at individual AZs increases. At most zones, there is only a small increase or none at all, while at others the increase is more substantial. For fitting the particular data set of Johnson et al. (2005), we allowed four different values of s_i. The values obtained, and their relative proportions, are shown in Figure 3C (open bars). The lowest and highest sensitivities differ by about seven orders of magnitude, which may seem large (see Discussion), but we point out that this is not the only way in which our model could account for these data. Rather, there are numerous possibilities. For example, the data from mature (and immature) IHCs could also be fitted with more than 4 (more than 1) different s_i, but this seemed unnecessary. Thus, the specific realization of our model presented here constitutes a parsimonious, yet reasonable, solution.

Changes in knockout animals

As a second example, we selected measurements from IHCs of mature control and synaptotagmin IV knockout mice, also published by Johnson et al. (2010, their Figure 1c). Again, the authors measured whole-cell Ca²⁺-currents and capacitance changes in response to voltage steps, the means are based on large numbers of cells (28 and 27 in knockout and control mice, respectively), and the data appear very clean and reliable. The power reported by Johnson et al. (2010) for their data from IHCs of the knockout mice was 3.1, close to the value of m = 3 expected from the biochemical cooperativity of the Ca²⁺-sensor, while that for the data from the IHCs of control mice was 1.2. The authors also studied IHCs of immature control and knockout mice (their Figure 2c). These data from both groups were similar to those reported by Johnson et al. (2005) for immature IHCs, and as illustrated in Figures 3A,B (filled circles), both in terms of the power derived (3.3 for both control and knockout mice) and in terms of the sensitivity. Therefore, these data from immature IHCs are not reproduced here.

Figure 4A shows the data points from the mature IHCs, in double-linear coordinates, as in the original publication. As before, the dashed line (barely visible) through the data from the IHCs of control mice (gray circles) represents our fit of these data with a simple, non-saturating, power function (Eq. 4). In this case, the fit yielded the same power (1.2) as that reported by Johnson et al. (2010). The continuous line through this data set represents a realization of our summation model, again fitted to approximate the quasi-linear power function and not just the six data points. The continuous line through the data points from IHCs of synaptotagmin IV knockout mice (filled squares) represents our summation model for these data. These fits were achieved with similar constraints as above for IHCs from mice of different ages. In particular, we set m = 3, i.e., we assume the biochemical Ca²⁺-cooperativity to be the same in control and knockout mice. This differs from the assumption of Johnson et al. (2010), who interpreted these data as reflecting a lowered biochemical Ca²⁺-cooperativity in control mice, mediated by synaptotagmin IV. Furthermore, we also required ∑c_i = const., i.e., we assume that the maximum possible output (change in membrane capacitance) is the same in control and knockout mice. In addition, we assumed this sum to have the same value as that for the mature and the immature IHCs of mice from the study of Johnson et al. (2005). Again, the only parameter that differs between IHCs from control and knockout mice, according to our model, is the sensitivity, s_i, and its variability between AZs. For fitting the particular data set from IHCs of mature control mice, we again allowed four different values of s_i. The values and their relative proportions obtained from the fit are shown in Figure 4B (gray bars). They are similar to those derived from the mature IHCs of the earlier study of Johnson et al. (2005) (cf. with Figure 3C; open bars). In contrast, in mature IHCs of synaptotagmin IV knockout mice, all s_i are relatively low and similar or even identical. The continuous line in Figure 4A represents a solution where the s_i values are assumed to be identical. The value is shown in the histogram in Figure 4B (black bar). It is higher (by a factor of about 4) than that of IHCs from immature controls (cf. Figure 3C; black bar), which in turn is very similar to that of IHCs from immature knockout mice (see Figure 2c in Johnson et al., 2010). Thus, according to our model, the sensitivity of IHCs from synaptotagmin IV knockout mice also increases (by a factor of 4) during ontogeny, but the sensitivities at all individual AZs remain very similar. In IHCs of mature controls, however, a range of differentially sensitive AZs develops during ontogeny. Thus, our summation model casts a very different light on the possible role of synaptotagmin IV.

FIGURE 4

Figure 4. The summation model accounts for the quasi-linear Ca²⁺-dependence of exocytosis in IHCs of control mice and the supralinear dependence in IHCs of synaptotagmin IV knockout mice, as reported by Johnson et al. (2010). (A) The data points from Figure 1C of their study are re-plotted here. The dashed line through the data from control mice represents a fit with a simple power function with a power of 1.2. Other conventions as in Figure 3A. (B) Plot of the four different sensitivities, s_i, assumed in the model for the mature IHCs from control mice, and their fractions (gray bars), and of the single sensitivity assumed for mature IHCs from knockout mice (black bar). For mature IHCs from control mice, the four sensitivities are s₁ = 1.73 × 10⁻⁸; s₂ = 1.43 × 10⁻⁶; s₃ = 3.14 × 10⁻⁵; s₄ = 3.35 × 10⁻³ with units of pA⁻³. The corresponding scaling factors are c₁ = 214.83; c₂ = 13.83; c₃ = 5.27; c₄ = 1.50 with units of fF, resulting in fractions of 0.913, 0.059, 0.022, and 0.006, respectively. For mature IHCs from knockout mice, all sensitivities are identical with s = 7.14 × 10⁻⁸ pA⁻³. The single scaling factor is 235.42 fF, identical to the sum of the four scaling factors for IHCs from control mice. In all cases m = 3.

Some Methodological Considerations in Estimating the Biochemical Ca²⁺-Cooperativity

As stated above, the supralinear Ca²⁺-dependencies reported in the literature are generally interpreted to reflect the intrinsic, biochemical, Ca²⁺-cooperativity, and the power values reported usually fall in the range of 3–4. Hence, these numbers suggest that at least four Ca²⁺-ions would have to bind to the sensor in a cooperative manner. One factor that might contribute to this variability is sub-optimal fitting of the data. Two issues are noteworthy here. First, many fits appear to have been performed in double-linear coordinates. Scrutiny of plots showing means and associated error bars consistently reveal increasing lengths of error bars with increasing means (e.g., Beurg et al., 2008 [their Figure 2c]; Dulon et al. 2009 [Figure 7]; Johnson et al., 2005 [Figure 5a]; Johnson et al., 2008 [Figures 2c, 3c,e]), reflecting increasing variability of individual data points around the model function. This effect is directly seen in (less common) plots of the individual measures. In Figure 5A, we re-plot such data points from Figure 6D of Johnson et al. (2005). The points identify capacitance changes and whole-cell Ca²⁺-currents in IHC of immature mice, manipulated by varying the external Ca²⁺-concentration. Johnson et al. (2005) fitted a simple power function (Eq. 4) to these data, in double-linear coordinates, and reported a power of 3.97. Their function is also shown in Figure 5A (gray line). When we fitted the same data with Eq. 4, we derived a very different power, viz. 1.93 (dashed line). One possibility for this discrepancy is that individual markers represent more than one data point or that some data points were not shown. Indeed, we could recover only 19 of the 20 data points reported to have been obtained with an external Ca²⁺-concentration of 1.3 mM. Another possibility is that Johnson et al. may have excluded some of the data points from the fit. For example, when we excluded the two rightmost data points, we obtained a power of 3.41. Figure 5B re-plots the data and the two fitted power functions of Figure 5A in double-logarithmic coordinates. Only the Ca²⁺-free data points were omitted, just as in the original publication of Johnson et al. (2005, their Figure 6E). It is obvious that the gray line, with the slope of 3.97, is too steep, while the dashed line, with the slope of 1.93, is too shallow. The other point to note is that in this double-logarithmic plot, and in marked contrast to the double-linear plot, the vertical scatter of data points is rather similar for different values along the abscissa, i.e., after log-transformation the variance becomes homogeneous. This means that the unsystematic scatter of the output values (here ΔC_m) at any input value (here I_Ca) likely follow a lognormal, rather than a normal, distribution (see, e.g., Limpert et al., 2001). In such cases, it is recommended to first transform the data such that the variance becomes homogeneous before fitting the model (e.g., Motulsky and Christopoulos, 2004). In other words, the data should be fitted in double-logarithmic rather than in double-linear coordinates.

FIGURE 5

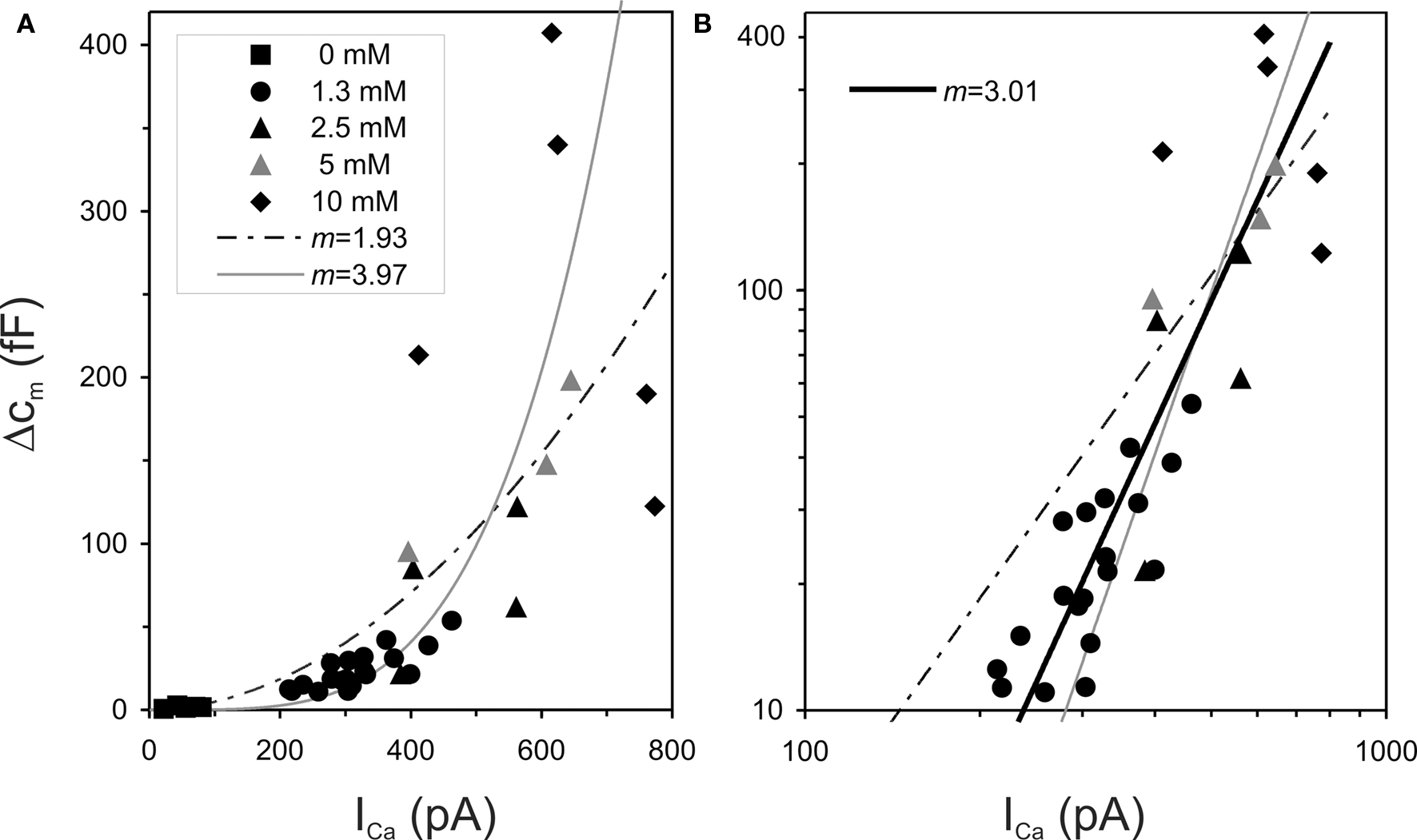
Figure 5. Sub-optimal data fitting procedures yield sub-optimal parameter estimates. (A) The data points are from Figure 6D of Johnson et al. (2005) and show measured individual capacitance changes, ΔC_m, plotted against measured whole-cell Ca²⁺-currents, I_Ca, recorded from IHCs of immature mice using different external Ca²⁺-concentrations (see legend). The gray line shows the simple power function, as obtained by Johnson et al. (2005), with a power of 3.97. The dashed line shows our best fit of the same data with such a function, which yielded a power of 1.93. (B) The same data and functions as in (A) are re-plotted in double-logarithmic coordinates. Only the data points obtained with a Ca²⁺-free solution are omitted, as in Figure 6E of Johnson et al. (2005). The dashed and gray lines are clearly too steep and too shallow, respectively. The solid line shows our best fit of a simple power function in these double-logarithmic coordinates, which accounts for the fact that both variables are subject to uncertainty (see text for details). The best power obtained this way is 3.01, very close to the integer value of m = 3.

The second issue to stress is that the standard (non-linear) regression, which minimizes the sum of squared vertical errors and which appears to have been used with fits of power functions to the Ca²⁺-dependencies, is most often inappropriate. This is so because there are substantial uncertainties in the determination of both variables, the measure of exocytosis and the magnitude of Ca²⁺-entry. In such cases, regression methods should be used that account for both errors (e.g., Motulsky and Christopoulos, 2004). We have applied two such procedures to the data of Johnson et al. (2005) in double-logarithmic coordinates. In the first procedure, we calculated two regression lines, the first by minimizing the square of the vertical deviations, i.e., as if I_Ca were known without error, and the second by minimizing the square of the horizontal deviations, as if ΔC_m were known without error. The two regressions yielded slopes of 2.62 and of 3.45, respectively, yielding a mean of 3.04. In the second procedure, we calculated the sums of the squared vertical and horizontal deviations for each data point from the model and minimized the product of these sums. This procedure yielded an estimate of m of 3.01. This function is shown in Figure 5B (solid black line). For completeness, we also used both procedures with fits of the Boltzmann function, rather than its approximation by a non-saturating power function. Both procedures yielded the same estimate of m, viz. 3.01, identical to the estimates derived with the non-saturating power function. This is not surprising, since the data reveal no sign of saturation. In summary, while the analysis of Johnson et al. (2005) would suggest that a minimum of four Ca²⁺-ions have to bind in a cooperative fashion to the sensor to trigger vesicle fusion, our more appropriate analysis of the same data yields a number of 3. We feel it is plausible that appropriate data analyses would also reveal values of m closer to 3 in other studies.

Discussion

We have shown here that seemingly quasi-linear Ca²⁺-dependencies of exocytosis can be observed, despite high biochemical Ca²⁺-cooperativity, if the experimental measures assess the sum of saturating processes at several AZs with different sensitivities. Furthermore, we have shown that our model can accurately reproduce selected exemplary sets of data from IHCs. To account for all published reports of quasi-linear Ca²⁺-dependencies, our model requires that the experimental measures in these studies are based on summed responses, that exocytosis at the individual AZs is a supralinear saturating power function of the intracellular Ca²⁺-concentration in the vicinity of the Ca²⁺-sensor, and that the individual AZs of the same cell differ in sensitivity (relating exocytosis at individual AZs to whole-cell Ca²⁺-entry). In addition, our model makes certain predictions about unavoidable deviations from linearity in the summed output. In the following we provide the evidence that justifies these assumptions and that verifies the predictions, and thus supports our model. We then, more briefly, discuss some difficulties with the published interpretations of quasi-linear Ca²⁺-dependencies.

Arguments in Favor of our Model

Reports of “quasi-linear” Ca²⁺-dependencies are based on measuring summed responses

Most of the observations of quasi-linear Ca²⁺-dependencies have been made in whole-cell recordings with capacitance changes as the read-out for vesicle release from those cells. This applies to studies of mammalian IHCs (Brandt et al., 2005; Johnson et al., 2005, 2008, 2009, 2010; Beurg et al., 2008), HCs from the turtle basilar papilla (Schnee et al., 2005), vestibular HCs (Dulon et al., 2009), and salamander rod photoreceptors (Thoreson et al., 2004). Notably, auditory and vestibular HCs as well as rod photoreceptors contain several AZs (ribbons; e.g., Thoreson et al., 2004; Schnee et al., 2005; Dulon et al., 2009; Meyer et al., 2009; Johnson et al., 2010). Hence, whole-cell recordings, apart from the problem of the cell’s loss of its native Ca²⁺-buffers by their diffusion into the recording pipette in the case of “ruptured-patch” whole-cell recordings (see, e.g., Roberts, 1993), measure the sum of Ca²⁺-currents entering the cell at all presynaptic, and extrasynaptic, sites. Similarly, the capacitance changes reflect the summed effect of exocytosis at all AZs, as well as at extrasynaptic sites. In another study reporting a quasi-linear Ca²⁺-dependence, the read-out for exocytosis, from HCs of the bullfrog basilar papilla, was the time-averaged postsynaptic current of single afferent fibers (Keen and Hudspeth, 2006). However, since each fiber makes several contacts with a given HC, the average postsynaptic current also reflects the summed drive from several AZs. Similarly, in another study reporting a quasi-linear Ca²⁺-dependence (Murphy et al., 2004), the read-out of exocytosis, from olfactory receptor neurons, was the postsynaptic current in individual mitral/tufted or periglomerular cells evoked by electrical stimulation of the olfactory nerve. These currents also reflect the summed drive from all olfactory receptor neurons converging onto the target cell under study.

To our knowledge, the only study in which the output measure is not determined by the activities of several AZs is that by Goutman and Glowatzki (2007). These authors recorded excitatory postsynaptic currents (EPSCs) from single auditory-nerve fiber terminals of pre-hearing rats, 9–11 days old (onset of hearing is day 12), that typically receive input from only a single IHC ribbon synapse (Liberman et al., 1990). However, as in the other studies cited above, whole-cell recordings from the IHCs were used to measure the Ca²⁺-entry. When the IHC membrane potential was clamped to relatively positive values (+11 to +41 mV), the authors observed a third to fourth power relationship between Ca²⁺-current and postsynaptic response, presumably revealing the biochemical Ca²⁺-cooperativity of the sensor. When the IHC membrane was clamped to more physiological values (−49 to −29 mV), however, the relationship between normalized Ca²⁺-current and normalized auditory-nerve fiber responses appeared nearly linear (powers of 1.1 and 1.4 for two different measures of fiber responses). The authors suggest that a nanodomain model can account for these findings (but see The Nanodomain Model for some concerns).

The release rate at individual active zones is a supralinear saturating power function of the intracellular Ca²⁺-concentration in the vicinity of the Ca²⁺-sensor

Our model assumes that exocytosis at individual AZs is a supralinear saturating function of the intracellular Ca²⁺-concentration in the vicinity of the Ca²⁺-sensor (local [Ca²⁺]_in; Figure 1B). Specifically, we assume the relationship to be a Boltzmann function with a power of m = 3. Although so far it has been impossible to measure the Ca²⁺-dependence of exocytosis at individual AZs of a given cell, the data of Beutner et al. (2001) strongly support our assumption. These authors loaded IHCs of mature mice (postnatal days 14–25) with a photolabile Ca²⁺-cage. Ca²⁺ was then liberated by flash photolysis, giving rise to a presumably homogeneous intracellular Ca²⁺-concentration, [Ca²⁺]_in, which was measured by means of a Ca²⁺-indicator. Simultaneous measurements of changes in the IHC membrane capacitance served as an indicator for exocytosis. Figure 6 re-plots their results (Beutner et al., 2001, their Figure 3a), which clearly reveal the supralinear dependence of exocytosis on [Ca²⁺]_in. Furthermore, although Beutner et al. (2001) favor a model in which five cooperative Ca²⁺-binding steps precede an irreversible fusion step, requiring five parameters, the assumption of the cooperative binding of three Ca²⁺-ions (Eq. 1), requiring just one fixed parameter (m = 3) and two free parameters (s = 1.12 × 10⁻⁵ μM⁻³ and c = 1404 s⁻¹), can capture the data well (continuous line in Figure 6). We fitted those data in double-logarithmic coordinates, minimizing the product of the sums of the squared vertical and horizontal deviations for each data point from the model. The fit improved by only 3.8%, when m was free, which is not significant if the larger number of free parameters is taken into account. In this case, m = 2.79. For comparison, fits with m = 2 and m = 4 are also shown in Figure 6 (dashed lines). It is obvious, even by eye, that they do not capture the data as well as the fit with m = 3. The quantitative assessment is provided in the inset of Figure 6. According to our fit with m = 3, the [Ca²⁺]_in required to achieve the half-maximum rate was about 45 μM, which falls into the range of apparent Ca²⁺-affinities quoted by Sugita et al. (2002) for the C2 domains of synaptotagmin 1 in the presence of phospholipid membranes (∼5–50 μM Ca²⁺, depending on the lipid composition). Hence, these data are fully consistent with our model assumption that exocytosis is a saturating power function of the local [Ca²⁺]_in which is the same at all AZs of a given cell. The data are even compatible with the specific power of m = 3, proposed here to best capture the biochemical Ca²⁺-cooperativity of the sensor, possibly reflecting the highly cooperative binding of three Ca²⁺-ions to the C2A-domain of synaptotagmin II. It is noteworthy that Thoreson et al. (2004) performed an experiment on rod photoreceptors, similar to that of Beutner et al. (2001) on IHCs, and also suggested a power of m = 3. The [Ca²⁺]_in required to achieve the half-maximum rate was, however, lower for the photoreceptors. In a more recent paper by this group (Duncan et al., 2010), data from similar experiments, confirming a supralinear dependence of exocytosis on [Ca²⁺]_in (power of 2.5), were modeled extensively. Several models could describe the data well, including models of the type used by Beutner et al. (2001), but with no more than three binding-sites.

FIGURE 6

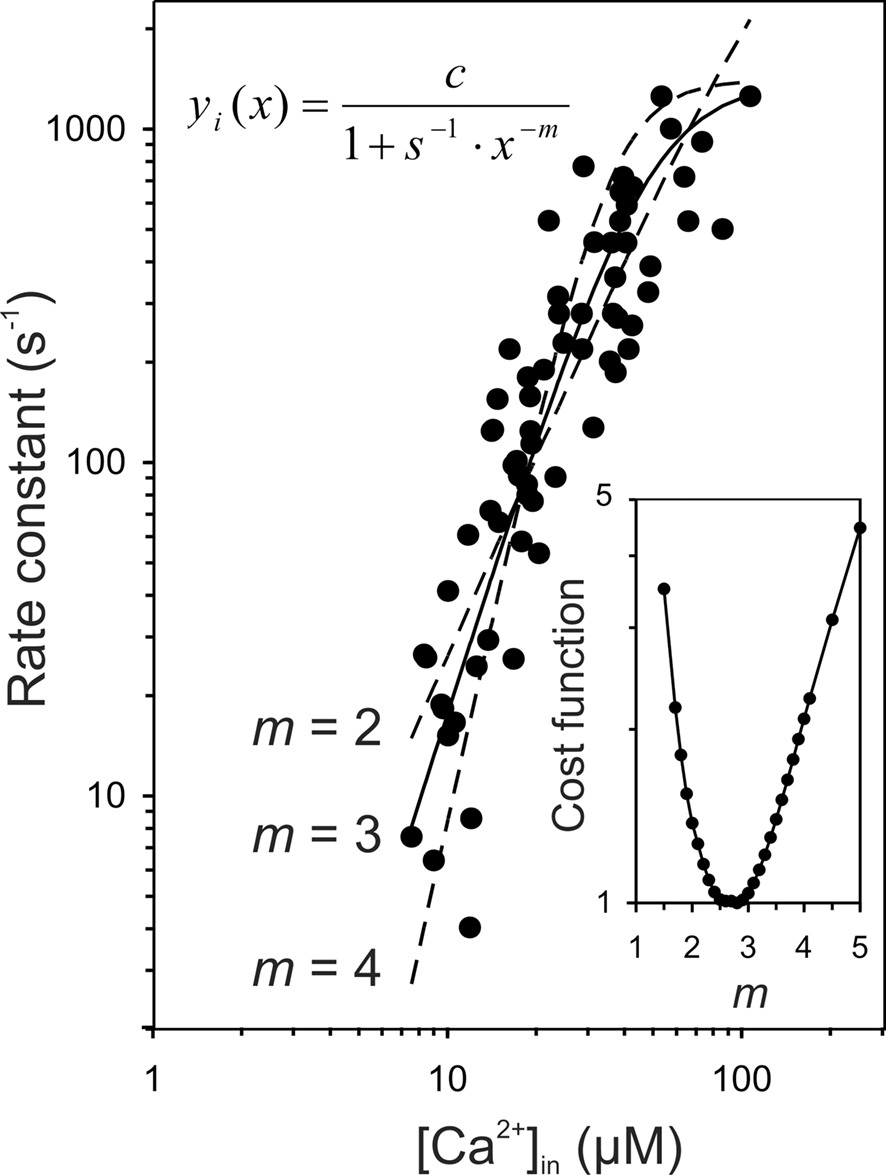
Figure 6. The release rate at individual active zones may be a saturating third power function of the intracellular Ca²⁺-concentration in the vicinity of the Ca²⁺-sensor. The data points are taken from Figure 3a of the study of Beutner et al. (2001). We recovered 67 of 68 data points. They show the rate constants of the fast component of exocytosis in IHCs of mature mice as a function of the (presumably homogeneous) intracellular Ca²⁺-concentration, [Ca²⁺_in], of the cells, which were first loaded with a photolabile Ca²⁺-cage. Ca²⁺ was then liberated by flash photolysis and the resulting [Ca²⁺]_in measured by means of a Ca²⁺-indicator. The rate constant is the reciprocal of the time constant of the fast component of exocytosis. The solid line represents our fit of these data with a Boltzmann equation (Eq. 1) and with m = 3. The values of the two free parameters are s = 1.12 × 10⁻⁵ μM⁻³ and c = 1404 s⁻¹. The dashed lines show, for comparison, the best fits with m = 2 and m = 4 which are not as good as that with m = 3. The inset plots the normalized cost function minimized in the fits, viz. the product of the sums of the squared vertical and horizontal deviations for each data point from the model, as a function of m, with its minimum at m = 2.8.

Ca²⁺-signals at individual active zones of a given cell differ

A key assumption of our model when accounting for the quasi-linear Ca²⁺-dependencies is that in response to a given stimulus (a given membrane potential and extracellular Ca²⁺-concentration, and hence also for a given whole-cell Ca²⁺-current), there are differences between AZs in the local [Ca²⁺]_in. In principle, all of the factors and parameters listed in the introduction (and others) could vary between synapses or change during ontogeny. To comply with Occam’s razor, we assume that the following factors are the same at all AZs of the presynaptic cell: the membrane potential, the extracellular Ca²⁺-concentration, the voltage-gated Ca²⁺-channels, and thus their mean open time, open probability, and conductance (though see Frank et al., 2009 for evidence of some diversity of Ca²⁺-channels in IHCs), the types, and concentrations of intrinsic Ca²⁺-buffers. We favor the assumption that AZs differ in the number of Ca²⁺-channels and/or the spatial arrangement of Ca²⁺-channels to release-ready vesicles. Recent work by Frank et al. (2009) and Meyer et al. (2009) revealed a substantial variability in the magnitude of Ca²⁺-hotspots, measured by means of fast confocal Ca²⁺-imaging, at the base of individual IHCs, building up and collapsing within a few milliseconds following membrane depolarizations. These submicrometer hotspots likely represent Ca²⁺-microdomains associated with presynaptic AZs. Frank et al. (2009) tested, and rendered unlikely, the possibilities that this variability in Ca²⁺-signals could be caused by variability in release from internal Ca²⁺-stores, mitochondrial Ca²⁺-uptake or local Ca²⁺-buffering, and suggested instead that it is due to differences in the number or density of Ca_V1.3 channels near the different ribbon synapses of an individual IHC. Hence, a given change in the IHC membrane potential would give rise to differences in Ca²⁺-entry at the different AZs. With a microdomain control of exocytosis (see Introduction), these differences could give rise also to differences in local [Ca²⁺]_in, i.e., in the concentration “seen” by individual vesicles. These differences in turn could account for, or contribute to, differences in the sensitivities of the auditory-nerve fibers contacting the cell (see Sensitivities of Auditory-Nerve Fibers Contacting IHCs Increase and Diversify During Ontogeny below), as suggested by us previously (Heil and Neubauer, 2001).

The summation model correctly predicts the observed association of quasi-linear Ca²⁺-dependence with increased sensitivity

Our model assumes that the quasi-linear Ca²⁺-dependencies result from summing over several saturating third power functions of different sensitivities (relating exocytosis at individual AZs to whole-cell Ca²⁺-entry), while the supralinear Ca²⁺-dependencies result from summing over several saturating third power functions whose sensitivities are similar to one another and generally low (Eqs. 3 and 4). If the sensitivities were similar, but high, saturation effects would become very obvious, which is generally not the case in published reports of supralinear dependencies. Consequently, our model predicts that the maturational transition from a supralinear to a quasi-linear Ca²⁺-dependence in a preparation should be associated with an increase in sensitivity (relating whole-cell exocytosis to whole-cell Ca²⁺-entry; Figure 3). Of course, some of the increase in this measure of sensitivity could simply be due to a reduction of extrasynaptic Ca²⁺-currents (see Ca²⁺-Channels Redistribute During Ontogeny), but such a reduction alone would not lead to a change in apparent Ca²⁺-cooperativity. Similarly, our model predicts that in a comparison of corresponding preparations showing different Ca²⁺-dependencies (e.g., of normal versus genetically modified animals) that exhibiting the quasi-linear dependence must be associated with a higher sensitivity than that exhibiting the supralinear dependence (Figure 4). These predictions are consistent with the reported increase in sensitivity (relating whole-cell exocytosis to whole-cell Ca²⁺-entry) which occurs concomitantly with the “linearization” during ontogeny (Johnson et al., 2005, 2009), and with the greater sensitivity in IHCs of control mice, which show a linear dependence, than in synaptotagmin IV knockout mice, which show a supralinear dependence (Johnson et al., 2010). Similarly, the quasi-linear Ca²⁺-dependence of vestibular type 1 HCs in control mice is associated with an increased sensitivity compared to that of vestibular HCs in otoferlin knockout mice which exhibit a supralinear dependence (Dulon et al., 2009). Likewise, the rod photoreceptor of salamander, for which a quasi-linear Ca²⁺-dependence has been reported, requires a much lower Ca²⁺-concentration for release than retinal bipolar cells, as stated by Thoreson et al. (2004).

Our model correctly predicts observed deviations from linearity

Our model also predicts that the Ca²⁺-dependence of exocytosis cannot be perfectly linear. Specifically, it predicts that the supralinear power relationship at individual AZs thought to underlie the quasi-linear summed response should be visible for very small Ca²⁺-currents, where even the most sensitive AZs would still be largely unaffected by saturation (Figure 2B). This rather specific prediction is consistent with the nature of the deviations from linearity reported by Keen and Hudspeth (2006) at membrane potentials more negative than the resting potential. At very high Ca²⁺-currents, our model predicts that saturation effects should become visible in the summed response. Indeed, such saturation effects are documented (e.g., Beutner et al., 2001; Murphy et al., 2004).

Ca²⁺-channels redistribute during ontogeny

Another more indirect line of evidence for our model comes from studies of Ca²⁺-channel localization in IHCs of immature and mature animals. Zampini et al. (2010) studied the localization of Ca²⁺-channels (Ca_V1.3) in IHCs of immature mice (6–7 days old). Remarkably, immunopositive Ca_V1.3 spots were not only found in presynaptic regions, but also in the neck region of IHCs. Of the 80 ± 13 immunopositive Ca_V1.3 spots measured, only 15 ± 3 co-localized with synaptic ribbons (31 ± 4 ribbons per IHC) in the base of immature IHCs. These distributions contrast with observations in IHCs from more mature mice (aged 2–4 weeks) where nearly all immunopositive Ca_V1.3 spots are located in the cells’ basal region and where they are co-localized with synaptic ribbons (Brandt et al., 2005; Meyer et al., 2009). Thus, it seems that the whole-cell Ca²⁺-current in mature IHCs is dominated by currents directly contributing to exocytosis, whereas this is not the case in immature IHCs. One would therefore expect that a given whole-cell Ca²⁺-current would result in more pronounced exocytosis in mature than in immature IHCs, just as observed (e.g., Johnson et al., 2005, 2009). In other words, the average sensitivity (relating exocytosis to whole-cell Ca²⁺-current) increases with maturation. Given the spatial re-distribution of immunopositive Ca_V1.3 spots during maturation, as just described, it seems entirely feasible that the clusters of Ca_V1.3 channels may also not be evenly distributed among the AZs (ribbons) of each mature IHC, as suggested by the work of Frank et al. (2009) and Meyer et al. (2009), described above.

Sensitivities of auditory-nerve fibers contacting IHCs increase and diversify during ontogeny

Strong evidence for increases in both average sensitivity and the differences in sensitivity between individual AZs of a given IHC with maturation comes from studies of auditory-nerve fiber responses in young and adult animals. Numerous studies have established a strong correlation between the spontaneous rates and the sensitivities of auditory-nerve fibers (for tones at each fiber’s characteristic frequency), such that insensitive fibers have low, and sensitive fibers high, spontaneous rates (e.g., Kiang et al., 1965; Kim and Molnar, 1979; Liberman, 1982; Geisler et al., 1985; Rhode and Smith, 1985; Winter et al., 1990; Yates, 1991; Versnel et al., 1992; Tsuji and Liberman, 1997; Taberner and Liberman, 2005). Most likely, this tight co-variation has a common cause (Yates, 1991; Heil et al., 2010) rather than being coincidental. Thus, a fiber’s spontaneous rate can be viewed as a surrogate measure of its sensitivity. Recordings from auditory-nerve fibers of immature cats and gerbils reveal that spontaneous activity is low and similar across fibers. During maturation, however, the distribution widens markedly, but solely due to an increase in its upper limit, so that the mean spontaneous rate also increases (Romand, 1984; Walsh and McGee, 1987; Müller, 1996). Hence, it seems likely that early in development individual AZs are all similarly insensitive while during development the sensitivity of some AZs increases, leading to an overall increase in sensitivity as well as a large diversity of individual sensitivities, just as required by our model to account for the supralinear and the quasi-linear Ca²⁺-dependencies in immature and mature HCs, respectively (Johnson et al., 2005, 2009). Although it has not yet been demonstrated directly that fibers of different sensitivity and spontaneous rate innervate the same HC, there is good indirect evidence for it. Liberman (1982) recorded from individual auditory-nerve fibers, labeled them intracellularly, and then traced the location of their terminals on the body of IHCs. He found a strong correlation of spontaneous rate and sensitivity with the location of the terminals along the circumference of the HCs. Similarly, Meyer et al. (2009) reported that the increments in Ca²⁺-signals were smaller at abneural compared to neural synapses in mouse IHCs. These data strongly suggest that fibers of different spontaneous rate and sensitivity can innervate the same HC.

The fits of our model to the data from mature IHCs of Johnson et al. (2005, 2010), and as illustrated in Figures 3 and 4, yielded a range of sensitivities covering about seven and five orders of magnitude, respectively. These ranges are somewhat larger than the range over which sensitivities of auditory-nerve fibers of similar characteristic frequency vary, covering about three to four orders of magnitude, whether based on definitions of firing-rate thresholds (which vary by 60–80 dB) or on spontaneous discharge rates (ranging from near zero to more than 100 spikes/s) (see citations above). It should be noted, however, that the vast majority (viz. 98.4 and 99.4%) of the sensitivities which emerged from our fits to the data of Johnson et al. fall within a range of three to four orders of magnitude. Furthermore, satisfactory fits of those data can be obtained when the allowed range of sensitivities is constrained to four orders of magnitude (not shown, but cf. Figure 2).

First-spike latencies and firing rates of individual auditory-nerve fibers can be modeled as saturating third power functions of sound amplitude

Another indirect line of support for our model comes from a detailed analysis of the changes in first-spike latency and firing rate of auditory-nerve fibers with changes in the temporal envelope and in the amplitude of tonal stimuli. We find, in adult animals, that such response properties can be explained by a third power relationship between a fiber’s spike rate and the (low-pass filtered) amplitude of the tone (Neubauer and Heil, 2008; Heil et al., 2008, 2010). This relationship is even reflected in perceptual tone detection thresholds (Heil and Neubauer, 2003; Neubauer and Heil, 2004). Such a third power relationship is readily compatible with a third power Ca²⁺-dependence of exocytosis, as proposed here, provided the Ca²⁺-entry at individual AZs is proportional to the (low-pass filtered) tone amplitude. Although it has not yet been possible to measure this relationship, scrutiny of a comprehensive and widely accepted model of peripheral auditory processing, developed over the years by Meddis and his colleagues (e.g., Meddis, 2006), suggests that this may well be the case.

Current Interpretations of “Quasi-Linear” Ca²⁺-Dependencies

Altered biochemical Ca²⁺-cooperativity of the Ca²⁺-sensor

A few studies have more-or-less explicitly proposed an altered (i.e., lowered) Ca²⁺-cooperativity of the Ca²⁺-sensor to account for the observed quasi-linear Ca²⁺-dependencies observed in their preparations (Murphy et al., 2004; Thoreson et al., 2004; Johnson et al., 2005, 2010; Dulon et al., 2009). Specifically, for mammalian IHCs, Johnson et al. (2010) suggested that the interaction of synaptotagmin II, which does bind Ca²⁺, with synaptotagmin IV, which does not bind Ca²⁺ (e.g., Südhof, 2002), might mediate the proposed lower Ca²⁺-cooperativity. In HCs of synaptotagmin IV knockout mice, the observed Ca²⁺-dependencies were supralinear (powers of 3.1 and 2.8 for different ways of manipulating Ca²⁺-currents), but in IHCs from normal mature (18–36 days old) mice, where they found these two proteins to be co-expressed, the Ca²⁺-dependencies were quasi-linear. In other studies, Johnson et al. (2005, 2008, 2009) had shown that the “linearization” occurs, concomitant with an increase in sensitivity, at around postnatal day 12. We believe that an altered biochemical Ca²⁺-cooperativity is an unlikely explanation for the linearization. First, the study of Beutner et al. (2001), explained above, reveals the biochemical Ca²⁺-cooperativity to be highly supralinear in IHCs from mature mice (14–25 days old). Our re-analysis of their data reveals that they are consistent with a third power relationship (Figure 6). These data appear to rule out an altered biochemical cooperativity for adult IHCs. Second, the quasi-linear Ca²⁺-dependencies are readily explained by our summation model (see Figures 3 and 4), rendering the assumption of altered biochemical cooperativity, e.g., via synaptotagmin IV, unnecessary.

The nanodomain model

According to the nanodomain model (Neher, 1998) the vesicle with its Ca²⁺-sensors is in such close proximity to a Ca²⁺-channel that the vesicle senses the gating of essentially this single channel only, and Ca²⁺-influx through this single channel is sufficient to trigger the vesicle’s fusion (e.g., Brandt et al., 2005; Goutman and Glowatzki, 2007). In this scenario, a vesicle that is directly adjacent to a channel that opens will experience a sufficient Ca²⁺-influx to trigger its fusion, whereas vesicles near closed channels will not. Their fusion probability remains near zero. Thus, and provided the proportion of release-ready vesicles docked at or near the Ca²⁺-channels does not differ between experimental conditions, the overall probability of exocytosis will change proportionally to the fraction of Ca²⁺-channels that is open, which again is directly proportional to the total Ca²⁺-current entering the cell. Hence, the Ca²⁺-dependence of exocytosis will appear linear (i.e., have a power of 1), despite a supralinear biochemical Ca²⁺-cooperativity. If more than one channel contributes to triggering exocytosis (channel cooperativity), the Ca²⁺-dependence can be expected to yield a power between 1 and the value reflecting the intrinsic Ca²⁺-cooperativity of the sensor, and the larger the number of channels contributing, the closer the power to the intrinsic Ca²⁺-cooperativity (Shahrezaei et al., 2006). The nanodomain model might also yield a power <1, viz., in the case that exocytosis saturates and a simple power law is fitted to the entire dataset. The arguments appear to hold also in the case of multivesicular release, where the neurotransmitter content of a small group of vesicles is simultaneously released in a coordinated fashion. There is accumulating evidence for such release from ribbon synapses, in HCs and rod bipolar cells, even though the mechanism is still unknown (Glowatzki and Fuchs, 2002; Edmonds et al., 2004; Singer et al., 2004; Keen and Hudspeth, 2006; Neef et al., 2007; Li et al., 2009; Grant et al., 2010; Jarsky et al., 2010).

At present, support for a nanodomain must rely on indirect evidence, such as the inability of the slow Ca²⁺-buffer EGTA to block Ca²⁺-triggered physiological responses, the requirement of high local intracellular Ca²⁺-concentrations (>100 μM) to trigger exocytosis (Augustine et al., 2003), or the differential effects on whole-cell exocytosis of manipulating whole-cell Ca²⁺-entry by changing the number of open channels or by changing the single-channel current (Augustine et al., 1991; Brandt et al., 2005). In some preparations, e.g., at the squid giant synapse (Augustine et al., 2003), the frog neuromuscular junction (Shahrezaei et al., 2006), or the basket to granule cell synapse in the rat dentate gyrus (Bucurenciu et al., 2008, 2010), there is strong evidence for a nanodomain control of exocytosis, and the number of Ca²⁺-channels that contribute to the fusion of a single vesicle appears to be very low indeed. For HCs, however, the evidence for a nanodomain control is mixed. Brandt et al. (2005), studying exocytosis from IHCs of young mice (P13–P20), reported a power of about 1.4 when the whole-cell Ca²⁺-entry was manipulated by changing the number of open channels, and powers between 2.3 and 4.2 when it was manipulated by changing the single-channel current. Goutman and Glowatzki (2007) obtained powers of 1.1 and 1.4 when the whole-cell Ca²⁺-entry was manipulated by clamping rat IHCs to different membrane voltages in a negative voltage range, thereby presumably varying the number of open channels and the single-channel current, whereas they obtained powers of 3.5 and 3.6 when the cells were clamped to different membrane voltages in the positive voltage range. Since here Ca²⁺-channel open probability is maximal (Zampini et al., 2010), changes in the whole-cell Ca²⁺-current are likely due solely to changes in the single-channel current. These data argue for a nanodomain-like control of exocytosis, or at least tight spatial coupling of the Ca²⁺-sensors to Ca²⁺-channels. Indeed, Goutman and Glowatzki (2007) obtained an estimate of the distance between Ca²⁺-sensors and Ca²⁺-channels of about 23 nm, when based on the relative effectiveness of 5 mM EGTA compared to 1 mM EGTA in reducing exocytosis. However, when the same approach was based on the relative effectiveness of 5 mM BAPTA, a fast buffer, compared to 1 mM EGTA, the estimated distance was an order of magnitude less. This order of magnitude difference raises the question as to how accurately the distances between Ca²⁺-sensors and Ca²⁺-channels can be derived by this approach. Also, exocytosis was assumed to be proportional to the fourth power of the intracellular Ca²⁺-concentration, and larger distances would be obtained if it were a third power relationship (as suggested by our analyses). Furthermore, the IHCs studied by Goutman and Glowatzki (2007) were from pre-hearing animals, in which others have suggested the spatial coupling may not be as tight as in adult IHCs (Beutner and Moser, 2001). Other data argue more directly against a nanodomain control. For example, Johnson et al. (2005, 2010), Beurg et al. (2008), and Dulon et al. (2009) reported very similar powers, independent of whether whole-cell Ca²⁺-entry was manipulated by varying the external Ca²⁺-concentration, and thus only the single-channel current, or by varying the membrane potential, thus varying the channel open probability and the single-channel current. Beutner et al. (2001) observed that intracellular Ca²⁺-concentrations of well below 100 μM are effective in triggering high rates of exocytosis (see also Figure 6). In summary, while there is good evidence for tight spatial coupling between Ca²⁺-sensors and Ca²⁺-channels at AZs of mature mammalian IHCs, as might be expected from synapses that operate with high fidelity and reliability (for recent reviews see, e.g., Fuchs, 2005; Moser et al., 2006; Nouvian et al., 2006; Glowatzki et al., 2008; but see Stanley, 1997 for a different view), the evidence for a nanodomain control is not unequivocal.

Conclusion

While we cannot exclude the possibilities that the reported quasi-linear relationships between summed Ca²⁺-currents and summed exocytosis are due to altered Ca²⁺-cooperativity of the Ca²⁺-sensor (lowered biochemical cooperativity) or due to nanodomain control (lowered channel cooperativity), they need not be. Of course, those ideas and our model are not mutually exclusive. Still, our model of differentially sensitive AZs contributing to the summed response, each operating with the established Ca²⁺-cooperativity of the ubiquitous Ca²⁺-sensors involved in exocytosis, provides a parsimonious and attractive alternative explanation. Its assumptions and even some specific predictions are well supported by data. However, to verify or falsify it directly, high-resolution measurements of Ca²⁺-entry at different individual AZs of the same cell will be needed, preferentially in combination with measurements of the resulting exocytosis. Our model predicts that in preparations where the relationship between whole-cell Ca²⁺-entry and whole-cell exocytosis is highly supralinear, the variability in Ca²⁺-entry at the individual AZs is small, whereas it is high in preparations where that relationship is quasi-linear. We hope that our study will be viewed as a constructive contribution to the field that will initiate future research that will test our model.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We are grateful to Walter Marcotti, Stefan Münkner, Jutta Engel, and Marlies Knipper for helpful comments on a much earlier version of this manuscript, and to Martin Heine, Dexter Irvine and the two now identified reviewers for helpful comments on a more recent version. This study was supported by the Deutsche Forschungsgemeinschaft (SFB-TR31, A6 to Peter Heil).

References

Augustine, G. J., Adler, E. M., and Charlton, M. P. (1991). The calcium signal for transmitter secretion from presynaptic nerve terminals. Ann. N. Y. Acad. Sci. 635, 365–381.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Augustine, G. J., Charlton, M. P., and Smith, S. J. (1985). Calcium entry and transmitter release at voltage-clamped nerve terminals of squid. J. Physiol. 369, 163–181.

Augustine, G. J., Santamaria, F., and Tanaka, K. (2003). Local calcium signaling in neurons. Neuron 40, 341–346.

CrossRef Full Text

Beurg, M., Safieddine, S., Roux, I., Bouleau, Y., Petit, C., and Dulon, D. (2008). Calcium- and otoferlin-dependent exocytosis by immature outer hair cells. J. Neurosci. 28, 1798–1803.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Beutner, D., and Moser, T. (2001). The presynaptic function of mouse cochlear inner hair cells during development of hearing. J. Neurosci. 21, 4593–4599.

Pubmed Abstract | Pubmed Full Text

Beutner, D., Voets, T., Neher, E., and Moser, T. (2001). Calcium dependence of exocytosis and endocytosis at the cochlea inner hair cell afferent synapse. Neuron 29, 681–690.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bollmann, J. H., Sakmann, B., and Borst, J. G. G. (2000). Calcium sensitivity of glutamate release in a calyx-type terminal. Science 289, 953–957.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Borst, J. G. G., and Sakmann, B. (1996). Calcium influx and transmitter release in a fast CNS synapse. Nature 383, 431–434.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Brandt, A., Khimich, D., and Moser, T. (2005). Few Cav1.3 channels regulate the exocytosis of a synaptic vesicle at the hair cell ribbon synapse. J. Neurosci. 25, 11577–11585.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bucurenciu, I., Bischofberger, J., and Jonas, P. (2010). A small number of open Ca-2+ channels trigger transmitter release at a central GABAergic synapse. Nat. Neurosci. 13, 19–21.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bucurenciu, I., Kulik, A., Schwaller, B., Frotscher, M., and Jonas, P. (2008). Nanodomain coupling between Ca-2+ channels and Ca-2+ sensors promotes fast and efficient transmitter release at a cortical GABAergic synapse. Neuron 57, 536–545.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Davletov, B. A., and Südhof, T. C. (1993). A single C2 domain from synaptotagmin I is sufficient for high affinity Ca²⁺/phospholipids binding. J. Biol. Chem. 268, 26386–26390.

Pubmed Abstract | Pubmed Full Text

Dodge, F. A., and Rahamimoff, R. (1967). Co-operative action of calcium ions in transmitter release at the neuromuscular junction. J. Physiol. 193, 419–432.

Pubmed Abstract | Pubmed Full Text

Dulon, D., Safieddine, S., Jones, S. M., and Petit, C. (2009). Otoferlin is critical for a highly sensitive and linear calcium-dependent exocytosis at vestibular hair cell ribbon synapses. J. Neurosci. 29, 10474–10487.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Duncan, G., Rabl, K., Gemp, I., Heidelberger, R., and Thoreson, W. B. (2010). Quantitative analysis of synaptic release at the photoreceptor synapse. Biophys. J. 98, 2102–2110.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Edmonds, B. W., Gregory, F. D., and Schweizer, F. E. (2004). Evidence that fast exocytosis can be predominantly mediated by vesicles not docked at active zones in frog saccular hair cells. J. Physiol. 560.2, 439–450.

CrossRef Full Text

Fernandez, I., Araç, D., Ubach, J., Gerber, S. H., Shin, O., Gao, Y., Anderson, R. G., Südhof, T. C., and Rizo, J. (2001). Three-dimensional structure of the synaptotagmin 1 C2B-domain: synaptotagmin 1 as a phospholipid binding machine. Neuron 32, 1057–1069.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Frank, T., Khimich, D., Neef, A., and Moser, T. (2009). Mechanisms contributing to synaptic Ca2+ signals and their heterogeneity in hair cells. Proc. Natl. Acad. Sci. U.S.A. 106, 4483–4488.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fuchs, P. A. (2005). Time and intensity coding at the hair cell’s ribbon synapse. J. Physiol. 566, 7–12.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Geisler, C. D., Deng, L., and Greenberg, S. R. (1985). Thresholds for primary auditory fibers using statistically defined criteria. J. Acoust. Soc. Am. 77, 1102–1109.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Glowatzki, E., and Fuchs, P. (2002). Transmitter release at the hair cell ribbon synapse. Nat. Neurosci. 5, 147–154.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Glowatzki, E., Grant, L., and Fuchs, P. (2008). Hair cell afferent synapses. Curr. Opin. Neurobiol. 18, 389–395.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Goutman, J. D., and Glowatzki, E. (2007). Time course and calcium dependence of transmitter release at a single ribbon synapse. Proc. Natl. Acad. Sci. U.S.A. 104, 16341–16346.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Grant, L., Yi, E., and Glowatzki, E. (2010). Two modes of release shape the postsynaptic response at the inner hair cell ribbon synapse. J. Neurosci. 30, 4210–4220.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Heil, P., and Neubauer, H. (2001). Temporal integration of sound pressure determines thresholds of auditory-nerve fibers. J. Neurosci. 21, 7404–7415.

Pubmed Abstract | Pubmed Full Text

Heil, P., and Neubauer, H. (2003). A unifying basis of auditory thresholds based on temporal summation. Proc. Natl. Acad. Sci. U.S.A. 100, 6151–6156.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Heil, P., Neubauer, H., and Irvine, D. R. F. (2010). “A new model for the shapes of the rate-level functions of auditory-nerve fibers,” Proceedings of the 20th International Congress on Acoustics 49.

Heil, P., Neubauer, N., Irvine, D. R. F., and Brown, M. (2008). Towards a unifying basis of auditory thresholds: distributions of the first-spike latencies of auditory-nerve fibers. Hear. Res. 238, 25–38.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Jan, L. Y., and Jan, Y. N. (1976). Properties of the larval neuromuscular junction in Drosophila melanogaster. J. Physiol. 262, 189–214.

Pubmed Abstract | Pubmed Full Text

Jarsky, T., Tian, M., and Singer, J. H. (2010). Nanodomain control of exocytosis is responsible for the signaling capability of a retinal ribbon synapse. J. Neurosci. 30, 11885–11895.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Johnson, S. L., Forge, A., Knipper, M., Münkner, S., and Marcotti, W. (2008). Tonotopic variation in the calcium dependence of neurotransmitter release and vesicle pool replenishment at mammalian auditory ribbon synapses. J. Neurosci. 28, 7670–7678.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Johnson, S. L., Franz, C., Knipper, M., and Marcotti, W. (2009). Functional maturation of the exocytotic machinery at gerbil hair cell ribbon synapses. J. Physiol. 587.8, 1715–1726.

CrossRef Full Text

Johnson, S. L., Franz, C., Kuhn, S., Furness, D. N., Rüttiger, L., Münkner, S., Rivolta, M. N., Seward, E. P., Herschman, H. R., Engel, J., Knipper, M., and Marcotti, W. (2010). Synaptotagmin IV determines the linear Ca²⁺-dependence of vesicle fusion at auditory ribbon synapses. Nat. Neurosci. 13, 45–52.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Johnson, S. L., Marcotti, W., and Kros, C. J. (2005). Increase in efficiency and reduction in Ca2+ dependence of exocytosis during development of mouse inner hair cells. J. Physiol. 563.1, 177–191.

CrossRef Full Text

Katz, B. (1969). The Release of Neural Transmitter Substances. Springfield, IL: Thomas.

Pubmed Abstract | Pubmed Full Text

Keen, E., and Hudspeth, A. J. (2006). Transfer characteristics of the hair cell’s afferent synapse. Proc. Natl. Acad. Sci. U.S.A. 103, 5537–5542.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kiang, N. Y. S., Watanabe, T., Thomas, E. C., and Clark, L. F. (1965). Discharge Patterns of Single Fibers in the Cat’s Auditory Nerve. M.I.T. Research Monograph 35. Cambridge, MA: The MIT Press.

Kim, D. O., and Molnar, C. E. (1979). A population study of cochlear nerve fibres: comparison of spatial distributions of average rate and phase-locking measures of responses to single tones. J. Neurophysiol. 42, 16–30.

Pubmed Abstract | Pubmed Full Text

Koh, T.-W., and Bellen, H. J. (2003). Synaptotagmin I, a Ca2+ sensor for neurotransmitter release. Trends Neurosci. 26, 413–422.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Li, G.-L., Keen, E., Andor-Ardó, D., Hudspeth, A. J., and von Gersdorff, H. (2009). The unitary event underlying multiquantal EPSCs at a hair cell’s ribbon synapse. J. Neurosci. 29, 7558–7568.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Liberman, M. C. (1982). Single-neuron labeling in the cat auditory nerve. Science 216, 1239–1241.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Liberman, M. C., Dodds, L. W., and Pierce, S. (1990). Afferent and efferent innervation of the cat cochlea: quantitative analysis with light and electron microscopy. J. Comp. Neurol. 301, 443–460.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Limpert, E., Stahel, W. A., and Abbt, M. (2001). Log-normal distributions across the sciences: keys and clues. Bioscience 51, 341–352.

CrossRef Full Text

Marqueze, B., Boudier, J. A., Mizuta, M., Inagaki, N., Seino, S., and Seagar, M. (1995). Cellular localization of synaptotagmin I, II, and III mRNAs in the central nervous system and pituitary and adrenal glands of the rat. J. Neurosci. 15, 4906–4917.

Pubmed Abstract | Pubmed Full Text

Meddis, R. (2006). Auditory-nerve first-spike latency and auditory absolute threshold: a computer model. J. Acoust. Soc. Am. 119, 406–417.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Meyer, A. C., Frank, T., Khimich, D., Hoch, G., Riedel, D., Chapochnikov, N. M., Yarin, Y. M., Harke, B., Hell, S. W., Egner, A., and Moser, T. (2009). Tuning of synapse number, structure and function in the cochlea. Nat. Neurosci. 12, 444–453.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mintz, I. M., Sabatini, B. L., and Regehr, W. G. (1995). Calcium control of neurotransmitter release at a cerebellar synapse. Neuron 15, 675–688.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Moser, T., Brandt, A., and Lysakowski, A. (2006). Hair cell ribbon synapses. Cell Tissue Res. 326, 347–359.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Motulsky, H., and Christopoulos, A. (2004). Fitting Models to Biological Data Using Linear and Nonlinear Regression. Oxford, NY: Oxford University Press.

Müller, M. (1996). The cochlear place-frequency map of the adult and developing Mongolian gerbil. Hear. Res. 94, 148–156.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Murphy, G. J., Glickfeld, L. L., Balsen, Z., and Issacson, J. S. (2004). Sensory neuron signalling to the brain: properties of transmitter release from olfactory nerve terminals. J. Neurosci. 24, 3023–3030.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Neef, A., Khimich, D., Pirih, P., Riedel, D., Wolf, F., and Moser, T. (2007). Probing the mechanism of exocytosis at the hair cell ribbon synapse. J. Neurosci. 27, 12933–12944.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Neher, E. (1998). Vesicle pools and Ca2+ microdomains: new tools for understanding their roles in neurotransmitter release. Neuron 20, 389–399.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Neher, E., and Sakaba, T. (2008). Multiple roles of calcium ions in the regulation of neurotransmitter release. Neuron 59, 861–872.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Neubauer, H., and Heil, P. (2004). Towards a unifying basis of auditory thresholds: the effects of hearing loss on temporal integration reconsidered. J. Assoc. Res. Otolaryngol. 5, 436–458.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Neubauer, H., and Heil, P. (2008). A physiological model for the stimulus-dependence of first-spike latency of auditory-nerve fibers. Brain Res. 1220, 208–223.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Nouvian, R., Beutner, D., Parsons, T. D., and Moser, T. (2006). Structure and function of the hair cell ribbon synapse. J. Membr. Biol. 209, 153–165.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rhode, W. S., and Smith, P. H. (1985). Characteristics of tone-pip response patterns in relationship to spontaneous rate in cat auditory nerve fibers. Hear. Res. 18, 159–168.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rizo, J., and Südhof, T. C. (1998). C2-domains, structure and function of a universal Ca²⁺-binding domain. J. Biol. Chem. 273, 15879–15882.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Roberts, W. M. (1993). Spatial calcium buffering in saccular hair cells. Nature 363, 74–76.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Romand, R. (1984). Functional properties of auditory-nerve fibers during postnatal development in the kitten. Exp. Brain Res. 56, 395–402.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Safieddine, S., and Wenthold, R. J. (1999). SNARE complexes at the ribbon synapses of cochlear hair cells: analysis of synaptic vesicle- and synaptic membrane-associated proteins. Eur. J. Neurosci. 11, 803–812.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Schnee, M. E., Lawton, D. M., Furness, D. N., Benke, T. A., and Ricci, A. J. (2005). Auditory hair cell-afferent fiber synapses are specialized to operate at their best frequencies. Neuron 47, 243–254.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Schneggenburger, R., and Neher, E. (2000). Intracellular calcium dependence of transmitter release rates at a fast central synapse. Nature 406, 889–893.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Shahrezaei, V., Cao, A., and Delaney, K. R. (2006). Ca²⁺ from one or two channels controls fusion of a single vesicle at the frog neuromuscular junction. J. Neurosci. 26, 13240–13249.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Shin, O.-K., Xu, J., Rizo, J., and Südhof, T. C. (2009). Differential but convergent functions of Ca²⁺ binding to synaptotagmin-1 C2 domains mediate neurotransmitter release. Proc. Natl. Acad. Sci. U.S.A. 106, 16469–16474.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Singer, J. H., Lassová, L., Vardi, N., and Diamond, J. S. (2004). Coordinated multivesicular release at a mammalian ribbon synapse. Nat. Neurosci. 7, 826–833.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Stanley, E. F. (1997). The calcium channel and the organization of the presynaptic transmitter release face. Trends Neurosci. 20, 404–409.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Südhof, T. C. (2002). Synaptotagmins: why so many? J. Biol. Chem. 277, 7629–7632.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Südhof, T. C. (2004). The synaptic vesicle cycle. Ann. Rev. Neurosci. 27, 509–547.

CrossRef Full Text

Sugita, S., Shin, O.-H., Han, W., Lao, Y., and Südhof, T. C. (2002). Synaptotagmins form a hierarchy of exocytotic Ca²⁺ sensors with distinct Ca²⁺ affinities. EMBO J. 3, 270–280.

CrossRef Full Text

Taberner, A. M., and Liberman, M. C. (2005). Response properties of single auditory nerve fibers in the mouse. J. Neurophysiol. 93, 557–569.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Thoreson, W. B., Rabl, K., Townes-Anderson, E., and Heidelberger, R. (2004). A highly Ca²⁺-sensitive pool of vesicles contributes to linearity at the rod photoreceptor ribbon synapse. Neuron 42, 595–605.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Tsuji, J., and Liberman, M. C. (1997). Intracellular labeling of auditory nerve fibers in guinea pig: central and peripheral projections. J. Comp. Neurol. 381, 188–202.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ubach, J., Zhang, X., Shao, X., Südhof, T. C., and Rizo, J. (1998). Ca2+ binding to synaptotagmin: how many Ca2+ ions bind to the tip of a C2-domain? EMBO J. 17, 3921–3930.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Versnel, H., Schoonhoven, R., and Prijs, V. F. (1992). Single-fibre and whole-nerve responses to clicks as a function of sound intensity in the guinea-pig. Hear. Res. 15, 249–260.

Voets, T. (2000). Dissection of three Ca²⁺-dependent steps leading to secretion in chromaffin cells from mouse adrenal slices. Neuron 28, 537–545.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

von Gersdorff, H., and Matthews, G. (1994). Dynamics of synaptic vesicle fusion and membrane retrieval in synaptic terminals. Nature 367, 735–739.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Walsh, E. J., and McGee, J. (1987). Postnatal development of auditory nerve and cochlear nucleus neuronal responses in the kittens. Hear. Res. 28, 97–116.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Winter, I. M., Roberston, D., and Yates, G. K. (1990). Diversity of characteristic frequency rate-intensity functions in guinea pig auditory nerve fibres. Hear. Res. 45, 191–202.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Yates, G. M. (1991). Auditory-nerve spontaneous rates vary predictably with threshold. Hear. Res. 57, 57–61.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Yoshihara, M., Adolfsen, B., and Littleton, J. T. (2003). Is synaptotagmin the calcium sensor? Curr. Opinion Neurobiol. 13, 315–323.

CrossRef Full Text

Zampini, V., Johnson, S. L., Franz, C., Lawrence, N. D., Münkner, S., Engel, J., Knipper, M., Magistretti, J., Masetto, S., and Marcotti, W. (2010). Elementary properties of CaV1.3 Ca²⁺ channels expressed in mouse cochlear inner hair cells. J. Physiol. 588.1, 187–199.

CrossRef Full Text