- 1Blue Brain Project, École Polytechnique Fédérale de Lausanne, Geneva, Switzerland
- 2Laboratory of Neural Microcircuitry, Brain Mind Institute, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland
Previous studies based on the ‘Quantal Model’ for synaptic transmission suggest that neurotransmitter release is mediated by a single release site at individual synaptic contacts in the neocortex. However, recent studies seem to contradict this hypothesis and indicate that multi-vesicular release (MVR) could better explain the synaptic response variability observed in vitro. In this study we present a novel method to estimate the number of release sites per synapse, also known as the size of the readily releasable pool (NRRP), from paired whole-cell recordings of connections between layer 5 thick tufted pyramidal cell (L5_TTPC) in the juvenile rat somatosensory cortex. Our approach extends the work of Loebel et al. (2009) by leveraging a recently published data-driven biophysical model of neocortical tissue. Using this approach, we estimated NRRP to be between two to three for synaptic connections between L5_TTPCs. To constrain NRRP values for other connections in the microcircuit, we developed and validated a generalization approach using published data on the coefficient of variation (CV) of the amplitudes of post-synaptic potentials (PSPs) from literature and comparing them against in silico experiments. Our study predicts that transmitter release at synaptic connections in the neocortex could be mediated by MVR and provides a data-driven approach to constrain the MVR model parameters in the microcircuit.
Introduction
Synaptic transmission is the basis for neuronal communication and information processing in the brain. Synaptic communication between neurons is mediated by neurotransmitters contained in presynaptic vesicles that are stochastically released from axonal boutons by incoming action potentials (APs) and diffuse across the synaptic cleft to bind receptors. Synaptic receptors are a class of ion channels which open as a result of transmitter binding, and the resulting transmembrane currents either depolarize or hyperpolarize the postsynaptic membrane, depending on the ion to which the channel is permeable (Mason et al., 1991; Südhof, 2000). Understanding the mechanisms behind vesicle release is crucial to unravel how information propagates between neuron types (Tsodyks and Markram, 1997). Disrupted vesicle release is implicated in pathologies such as Alzheimer’s disease or schizophrenia (Waites and Garner, 2011).
In 1954, del Castillo and Katz described the ‘Quantal model’ of synaptic transmission (Del Castillo and Katz, 1954). This model is characterized by the number of independent release sites (N), the probability of releasing a vesicle in the presynaptic cell followed by an AP (p) and the content of each vesicle, the quantal size (q), which collectively determine the efficacy of synaptic transmission (Del Castillo and Katz, 1954; Tsodyks and Markram, 1997). Previously, it was thought that no more than one vesicle could be released per synaptic contact, leading to the univesicular release hypothesis (UVR), in which N is equal to the number of physical synaptic contacts in a neuronal connection, at least for synapses in the neocortex (Korn et al., 1981, 1994; Silver et al., 2003; Biró et al., 2005). However, evidences as fluctuations of evoked postsynaptic potentials (PSPs) (Tang et al., 1994), large concentration of neurotransmitter in the synaptic cleft (Tong and Jahr, 1994) or a high range variability of receptor-mediated signals of N-methyl-D-aspartate (NMDA) and α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid (AMPA) receptors (Conti and Lisman, 2003) suggested that transmission at a single synaptic contact could be multiquantal. Consequently, a multivesicular release hypothesis (MVR) was proposed, where several release sites could underlie a synaptic contact in a neuronal connection. In fact, there are evidences showing that MVR occurs in brain regions such as the hippocampus (Tong and Jahr, 1994; Christie and Jahr, 2006), the cerebellum (Auger et al., 1998), the hypothalamus (Gordon, 2005) or the cerebral cortex (Huang et al., 2010; Rudolph et al., 2015; Molnár et al., 2016).
Recent studies in the rodent neocortex support the idea of MVR between pyramidal cells (Loebel et al., 2009; Hardingham et al., 2010; Rollenhagen et al., 2018). It has also been reported that modalities of vesicle release differ across cortical areas. For instance, connections between excitatory neurons in layer 4 exhibit UVR in the primary visual cortex, as against MVR in the primary somatosensory cortex (Huang et al., 2010). By contrast, other studies have reported that connections between layer 4 stellate cells and layer 2/3 pyramidal cells in the rat barrel cortex (Silver et al., 2003), and between pyramidal cells and interneurons in the rat cortex (Molnár et al., 2016) display UVR. A recent study has also reported that connections between pyramidal cells and fast spiking interneurons in the human neocortex exhibit MVR (Molnár et al., 2016). MVR is a complex process that is thought to regulate synaptic transmission and plasticity by increasing the dynamic range of synapses and could, therefore, influence cognitive functions such as learning and memory (Fuhrmann et al., 2004). MVR is also known to directly impact synaptic noise through spontaneous miniature postsynaptic currents (Fatt and Katz, 1950) and synaptic variability resulting in an increase of synaptic strength through larger vesicle pool sizes (Oertner et al., 2002), which could have important implications in the transmission of information between neurons (Fuhrmann et al., 2004).
Theoretical and computational models have enabled a mechanistic understanding of MVR through investigating synaptic processes such as short-term synaptic plasticity (Hennig, 2013). These models account for parameters to model presynaptic processes including the probability of neurotransmitter release and the number of vesicles available for release (Tsodyks and Markram, 1997; Loebel et al., 2009; Hennig, 2013; Zhang and Peskin, 2015). In addition, these models also assume that each synaptic contact has access to a limited amount of releasable neurotransmitter, take into account vesicle depletion and replenishment (Liley and North, 1953), and facilitation mechanisms (Betz, 1970; Varela et al., 1997; Markram et al., 1998). Some models have also demonstrated an important functional role for the number of release sites per synaptic connection in neuronal information coding (Fuhrmann et al., 2002). It has also been reported that the number and frequency of vesicles released is essential for receptor activation (Boucher et al., 2010). Some studies also outline the importance of having a readily releasable pool (NRRP) with more than one vesicle for synaptic plasticity (Nadkarni et al., 2010). Despite the importance of MVR in information transmission and processing between neurons, we lack an understanding of its role in brain regions such as the neocortex, which is the seat of higher order cognitive functions in the mammalian brain.
In this study, we leveraged a rigorously validated data-driven model of neocortical tissue at the cellular and synaptic levels of detail to estimate the average size of the NRRP for individual synaptic contacts between cell-type-specific connections (Markram et al., 2015). To compute the NRRP, we sampled synaptically connected pairs of neurons within the virtual neocortical tissue model and simulated paired whole-cell recordings in silico. The properties of in silico synaptic connections were constrained by an experimental dataset that characterized the physiology of in vitro synaptic connections between layer 5 thick-tufted pyramidal cells (L5_TTPC) in the juvenile rat somatosensory cortex, which are marked by prominent short-term depression (Ramaswamy and Markram, 2015). In particular, we used this dataset to estimate synaptic noise and the MVR free parameter NRRP, extending the work of Loebel and colleges (Loebel et al., 2009). Next, we optimized the NRRP, to reproduce response variability as observed in experiments, which is typically assessed by the coefficient of variation (CV; standard deviation/mean) of PSPs. We further developed an approach to estimate NRRP for both excitatory and inhibitory connection types using published literature that reported the CV of PSPs for synaptic connections in the neocortex. Our study combining in vitro experiments and in silico computational modeling, predicts that the vast majority of synaptic connections in the neocortex are mediated by MVR, albeit with lower NRRP values than previously reported (Loebel et al., 2009), which suggests that MVR could be a general property of local neocortical connections.
Materials and Methods
Slice Preparation and Electrophysiology
Fourteen- to eighteen-day-old Wistar rats were decapitated according to the guidelines of the Swiss Animal Welfare Act, and the Swiss National Institutional and Veterinary office guidelines in the Canton of Vaud on Animal Experimentation for the ethical use of animals. Multiple, simultaneous somatic whole cell patch-clamp recordings from clusters of 6–12 cells were carried out with Multiclamp 700B amplifiers in current clamp mode. Brain sagittal slices of 300 μM width were cut on an HR2 vibratome (Sigmann Elektronik). Temperature was maintained at 34 ± 1°C in all experiments. The extracellular solution contained 125 mM NaCl, 2.5 mM KCl, 25 mM D-glucose, 25 mM NaHCO3, 1.25 mM NaH2PO4, 2 mM CaCl2, and 1 mM MgCl2 bubbled with 95% O2 and 5% CO2. The intracellular pipette solution contained 110 mM potassium gluconate, 10 mM KCl, 4 mM ATP-Mg, 10 mM phosphocreatine, 0.3 mM GTP, 10 Hepes, and 13 mM biocytin adjusted to pH 7.3–7.4 with 5 M KOH.
Data was acquired through an ITC-1600 board (Instrutech) connected to a PC running a custom-written routine (PulseQ) under IGOR Pro (WaveMetrics, Lake Oswego, OR, United States). L5_TTPCs were selected according to their large soma size (15–25 μm) and their apparent large trunk of the apical dendrite. Cells were visualized by infrared differential interference contrast video microscopy using a VX55 camera (Till Photonics) mounted on an upright BX51WI microscope (Olympus). Sampling rates were 5–10 kHz, and the voltage signal was filtered with a 2-kHz Bessel filter. The resting membrane potential was −65.3 ± 4.3 mV, the input resistance was 59.7 ± 17.1 MΩ and the access resistance was 15.2 ± 3.7 MΩ. The stimulation protocol consisted of pre-synaptic stimulation with eight electric pulses at 20 Hz followed by a single pulse 500 ms later (recovery test), at the sufficient current intensity to generate APs in the presynaptic neuron while the postsynaptic neuron responses were recorded. The protocol was repeated between 20 to 60 times with a time between repetitions of 12 s (Figure 1A, top).
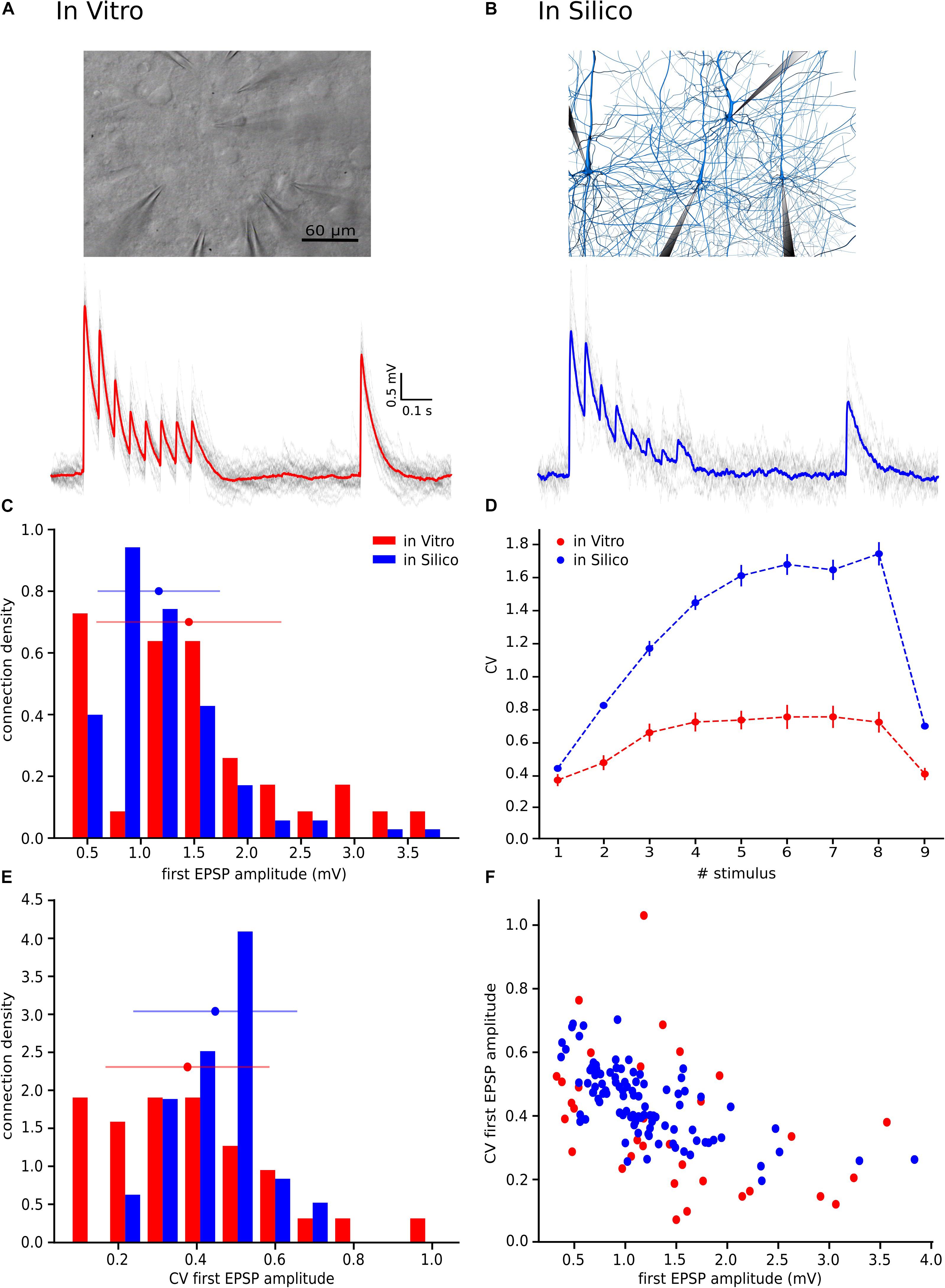
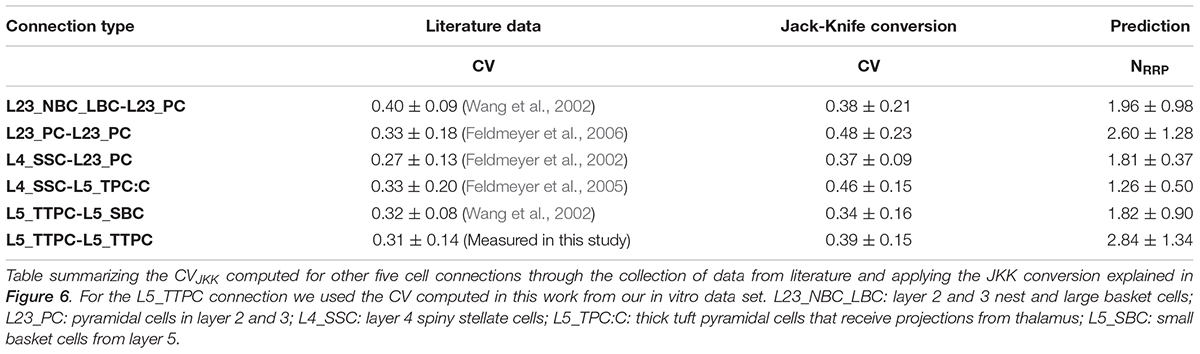
Figure 1. With the UVR hypothesis it was not possible to reproduce the variability observed in vitro. (A) Example of a multiple whole cell patch-clamp recording in L5_TTPC connections (top). In vitro mean voltage trace (bottom; red) of 20 protocol repetitions (gray). (B) Illustration of an in silico patch-clamp experiment performed on L5_TTPC connections from the data-driven model of the rat cortex microcolumn. In silico mean voltage trace (bottom; blue) of 20 protocol repetitions (gray). (C) Histogram showing the distribution of the first EPSP amplitude for in vitro (red) and for in silico (blue) experiments. (D) Mean CV profiles for the in vitro (red) and the in silico (blue) experiments. (E) CV distribution of the first EPSP amplitude for in vitro (red) and in silico (blue) data sets. (F) Raster plot of the first EPSP amplitude against the CV of the first EPSP amplitude for in vitro (red) and in silico (blue) experiments. In the distributions and the CV profile, dots represent the mean and vertical and horizontal bars represent the standard deviation of all the experiments respectively.
Stochastic Model for Short-Term Dynamics and Multi-Vesicular Release
Our model describes the short-term synaptic dynamics defined by a stochastic generalization of the Tsodyks-Markram model (TM-model) (Tsodyks and Markram, 1997; Maass and Markram, 2002) that is known to fit excitatory as well as inhibitory synapses behavior of biological experiments (Markram et al., 1998; Gupta et al., 2000). This model considers that there is a finite number of vesicles ready to be released defined by NRRP that could be in ready or recovery state. In this study we followed the synaptic dynamics described previously that is able to predict the sequence of PSP amplitudes produced by any spike train (Tsodyks and Markram, 1997). This behavior is described by four main synaptic parameters: the absolute synaptic efficacy (A), the fraction of synaptic resources used by a single spike (U), the time constant for recovery from facilitation (F) and the time constant for recovery from depression (D). The PSP amplitudes prediction obeys the following mathematical expressions:
In short, when the nth spike occurs there is certain fraction of synaptic efficacy modeled by Rn. Accordingly, the product unRn models the fraction of synaptic efficacy used by the nth spike. Combining these terms is possible to describe the fraction of synaptic efficacy available when the next spike arrives at time Δtn assuming that the synaptic efficacy has an exponential recovery with time constant D. How much fraction of synaptic efficacy (Rn+1) is used when (n + 1)th spike occurs is defined by un+1 which increases for each subsequent spike from un to U(1–un) + un and goes back to U following an exponential with time constant F (Maass and Markram, 2002).
Thus, if a vesicle is successfully released, these receptors get activated with a conductance gmax/NRRP with gmax as the maximal conductance.
Fitting Synapse Model Parameters to the Data
We constrained our synaptic model by extracting the parameters U, D and F from in vitro connections (n = 33; Figures 3C–E). To this end, we measured the peak for the excitatory postsynaptic potential (EPSP) amplitudes of each averaged voltage trace (Figure 3A). All experimental traces were normalized to their maximum value that allowed us to directly compute the peak value instead of the total amplitude. To perform an accurate computation of the peaks we used an analytical tool for deconvolving the voltage averaged trace (Richardson and Silberberg, 2008), which made it possible to exclude the smoothing effect of the low pass filtering of the cell membrane with a time scale equal to τmem, so we could extract the peaks from the EPSPs (Figure 3B).
To express this process mathematically we used the next equation:
The right-hand part of the expression is the voltage deconvolution, while the left hand contains the unfiltered synaptic current. The requirement here is to compute τmem for each in vitro connection by fitting the decay part of the recovery peak (9th EPSP) of the averaged voltage trace to an exponential.
Once the EPSP peaks were extracted from the deconvolved and normalized trace, we introduced them as an input into a genetic algorithm (GA) (Goldberg and Holland, 1988) that creates 500 generations of potential U, D and F within the following ranges U (0–1.0), D (0–1000.0) and F (0–2000.0). According to the mathematical expression of the model, the GA was able to estimate the peaks per different generation. The GA minimized the mean square distance between the original and the estimated peaks giving one solution for the minimum distance. In order to optimize the result, the GA was run 50 times. Then, we considered that the U, D, F generation related with the minimum distance out of the 50 repetitions was the best solution. We performed that process for each of the in vitro connections.
In silico Experiments: The Cortical Microcircuit
For the in silico experiments we leveraged a previously published model of juvenile rat somatosensory cortical tissue (Markram et al., 2015). In brief, the tissue model consists of 31,000 morphologically detailed neurons distributed across 6 layers within a volume of 0.29 mm3 giving rise to 8 million synaptic connections mediated by 37 million synaptic contacts. All the neuronal and synaptic models can be freely obtained through the open-access Neocortical Microcircuit Collaboration (NMC) portal (Ramaswamy et al., 2015).
Having computed the mean and the standard deviation of the synaptic parameters from fitting the in vitro data to the TM-model, we updated these parameters in the neocortical tissue model that were implemented as distributions defined by their mean and standard deviation. We also computed by scaling its values until we matched the experimentally measured amplitude of the first EPSP in a train of responses, which determined the in silico gmax value for a simulated connection. Next, we performed patch-clamp in silico experiments (Figure 1B, up), under similar conditions to actual in vitro paired recordings, with different NRRP values. These values were defined based on the mean of a Poisson distribution shifted one unit to the right, because at least one vesicle had to be released per synaptic site. The range of means of the Poisson distributions varied from 0 to 13 (1 ≤ NRRP ≥ 14) in the case of studying MVR and 0 (NRRP = 1) while studying UVR. We decided to set the maximum value to 14 vesicles on average per release site because is already the double of what Loebel and colleges predicted on their research (Loebel et al., 2009), so we considered that no more than 14 vesicles could be released per synaptic contact.
As the next step, we simulated 100 L5_TTPC connections in silico with 20 stimulus-response repetitions each. To reproduce in vitro experiments as faithfully as possible, we ensured that the U, D and F distributions in silico were identical to those extracted from in vitro recordings. We then compared the resulting EPSPs of simulated in silico connections to ascertain that they were well the range of experimentally measured values, consequently the EPSPs out of the experimental range were eliminated. Therefore, we excluded 15 connections and undertook the study with 85 connections out of 100.
Noise Calibration. Ornstein-Uhlenbeck Process
After simulating in silico connections with different NRRP values and selecting a subset where the 1st EPSP amplitude was within the experimentally observed range, we artificially applied voltage fluctuations to in silico traces to take into account the membrane noise observed experimentally. This was achieved by implementing an Ornstein-Uhlenbeck process (OU-process), which is a stochastic process that allowed us to simulate small random variability. The OU-process describes the velocity of the movement of a Brownian particle considering the friction and is a stationary Gauss-Markov process (Enrico Bibbona, 2008).
Mathematically the expression used in this work for this process was:
Where τ is the membrane time constant, σ is the standard deviation of the voltage and Wt is a random term coming from the Wiener process. In the case of σ = 0 the equation will have the solution X(t) = x0e−(t−t0)/τ so X(t) relaxes exponentially toward 0. In general, X(t) fluctuates randomly, the third term pushes it away from zero, while the second term pulls it back to zero (Bibbona et al., 2008). In Physics this process is used to describe noisy relaxation activity.
In our specific case, we defined σ and τ using the voltage values between the 8th and the 9th EPSPs, 400 ms in total, for each repetition (sweep) in a connection and then we averaged the resulting values (Figure 4A). By computing the standard deviation of these points, we obtained one σ per connection (n = 33 connections in total). By computing the autocorrelation of this part of the voltage trace and fitting it to an exponential, we obtained one τ per connection (Figure 4B), which provided constraints to implement a similar membrane noise for in silico traces (Figure 4C).
CV Profile Computation. The Jack-Knife Bootstrapping Analysis
In order to compute the CV for the EPSP amplitudes for in vitro and in silico connections in a comparable way, we implemented the Jack-Knife method (JKK) (Efron and Tibshirani, 1994).
This method consists in excluding one observation at a time from a group of observations. In our specific case, from a set of single traces we computed the average of all but one off the traces each time, obtaining a set of averaged-JKK traces in the end. From each of these averaged-JKK traces we computed the amplitudes for all nine EPSPs in a train of synaptic responses. Through this computation, we were able to compute the EPSP amplitudes more precisely considering that we removed the noise by averaging. Thereafter, we computed the CV profiles for the in vitro data set and the in silico simulations using the following equations:
Where n denotes the EPSP index (n = 1–9) and N is the number of single traces per connection.
Having two sets of simulations, to study UVR and MVR, we computed the CV profile of EPSP amplitudes using the JKK approach in both cases and compared them with the CV profile measured in the in vitro dataset. The EPSP amplitude was computed as the difference between the minimum value within 50 ms before stimulation time and the maximum value within 300 ms after stimulation time. We computed the mean square distance in order to obtain the minimum error between in vitro and in silico CV profiles (Figure 5E). We iterated this procedure 50 times and then we provided the mean and the standard deviation for the NRRP that correspond with the smallest error.
Statistical Analysis
Mean values for the EPSP amplitudes, the CVs and the synaptic parameters were expressed as their respective mean ± their standard deviation. Differences between distributions were measured using the Kruskal-Wallis test which shows a significant difference when p < 0.05. In order to compare two dimensional data sets (Figures 1F, 6F) we used the cross validated Kolmogorov-Smirnov test for two-dimensional data that shows significant differences when p < 0.2 (Press and Teukolsky, 1988). In order to test the goodness of fit for the fitting of the synaptic parameters we ran a Kolmogorov-Smirnov one sided test for three different distributions – beta, gamma and normal. Out of these three we chose the one with the highest p value and the smallest distance between the real and the expected distributions.
Results
Motivation for Implementing MVR in the Model
To reproduce the synaptic release variability observed in vitro, we began by implementing UVR at all synaptic contacts in the neocortical microcircuit model. As a result, the synaptic responses in silico were highly variable in comparison against biological data. In order to further investigate the potential causes for this difference in response variability, we undertook whole-cell recordings in vitro from 33 pairs of connected L5_TTPCs cells (Figure 1A, top) and computed the amplitude and the CV of the amplitudes for each EPSP. Figure 1 shows exemplar traces in vitro (Figure 1A, left in red) and in silico (Figure 1B, right in blue). As it was expected differences in the shape, amplitude and noise of the mean traces can be seen. The in vitro trace in red has a higher amplitude than the in silico in blue. Is also visible that the shape of the in silico mean trace is noisier than the in vitro, reflecting larger variability between protocol repetitions.
Next, we compared the distribution profiles of the first EPSP amplitude for the entire in vitro dataset (n = 33) and a subset of in silico connections (n = 100). Performing the Kruskal-Wallis test on the distributions of the first EPSP amplitude (Figure 1C) between in vitro and in silico connections revealed no significant difference in the mean values of their distributions (1.46 ± 0.86 mV for in vitro; 1.17 ± 0.57 mV for in silico; p = 0.15). However, a Kruskal-Wallis test between the distributions of the CV for the first EPSP amplitude (Figure 1E) revealed a significant difference in the mean values between in vitro and in silico connections (mean CV values: 0.38 ± 0.21 for in vitro; 0.45 ± 0.11 for in silico; p = 0.0092). Consequently, computing the CV profile for the EPSP amplitudes for every stimulus in a train showed a significant difference between in vitro and in silico data sets (Figure 1D; p < 10–9). The distributions (Figures 1C,E) were normalized to the respecting sample size such that the sum of products of width and height of each column was equal to the total count of connections (33 for in vitro, 100 for in silico). This difference was further corroborated through a Kolmogorov-Smirnov test for two-dimensional data (Press and Teukolsky, 1988), which also showed a significant difference between the first EPSP amplitude against the CV of the first EPSP amplitude for in vitro and in silico datasets (Figure 1F; p = 0.0022).
This striking difference motivated us to implement the MVR hypothesis, which is known to provide enhance the dynamic range of synapses through higher variability (Wang et al., 2006; Brémaud et al., 2007).
Validating the Method
Before applying our method to an in vitro data collection, we wanted to ensure that we were able to achieve the correct NRRP value by using our procedure. For this purpose, we built 3 in silico data sets with different averaged NRRPs with mean values around 1, 4 and 10, each of them composed of 30 L5TTPC connections, similarly to the number of connections that is possible to obtain from in vitro experiments. Next, we simulated 100 in silico L5_TTPC connections with average NRRP values ranging from 1 to 14 (see section “In silico Experiments: The Cortical Microcircuit”) and compared them against each CV profile computed through the JKK approach obtained from each of the in silico data sets (Figure 2B). Each in silico data set and the corresponding simulations consisted of different pairs of L5_TTPC connections.
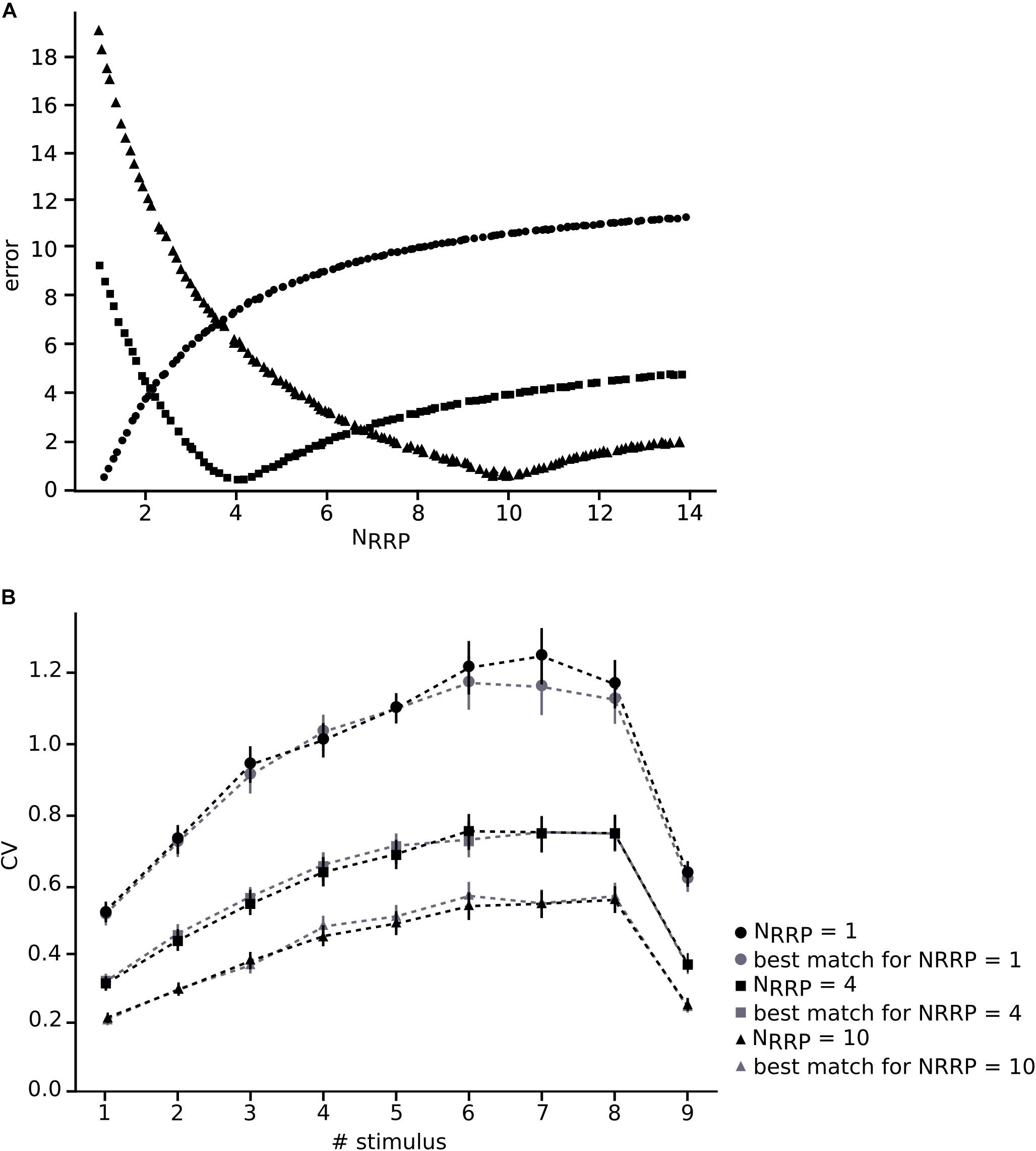
Figure 2. Validating the method. (A) Varying NRRP against error for the different in silico data sets around the appropriate corresponding NRRP (dots, NRRP = 1; squares, NRRP = 4; triangles, NRRP = 10). (B) Mean CV profiles of the three different in silico data sets (black) and the simulations (gray). Dots, squares and triangles represent the mean while the error bars show the standard deviation.
In this manner, we obtained NRRPs that characterized each of the three different in silico data sets. We computed a minimum error around the correct value of each in silico data set (1, 4 and 10) which corresponding NRRPs were 1.01 ± 0.10, 4.07 ± 0.30 and 9.85 ± 0.45, obtaining as results NRRP = 1.10 ± 0.31 (dots), NRRP = 4.11 ± 1.75 (squares) and NRRP = 10.71 ± 3.21 (triangles), respectively (Figure 2). By comparing the CV profiles between the in silico data sets (black) and the simulations (gray) (Figure 2B) we found that they were not significantly different (p > 0.4), which validated the efficacy of our method.
Extracting Values for the TM-Model and Noise Calibration
To enable comparison between the in vitro and the in silico experiments, we used the TM synapse model to extract the U, D, and F parameters from the in vitro dataset (see Materials and Methods). These parameters were obtained by the deconvolution of each in vitro averaged trace (Figure 3B) to extract the values of the peaks from the same voltage level. This resulted in three distributions, one each for U, D, and F, respectively. For U we obtained a normal distribution (goodness of fit: p = 0.92; D = 0.097) with a mean value of 0.38 ± 0.1 (Figure 3C), D fitted a gamma distribution (p = 0.81; D = 0.11) with a mean value of 365.6 ± 100.15 ms (Figure 3D) and F was also fitted to a gamma distribution (p = 0.1; D = 0.21) with mean 25.71 ± 45.87 ms (Figure 3E). These values were similar to the values found in previous studies (Tsodyks and Markram, 1997; Wang et al., 2002). As the next step we estimated the gmax for connections. We simulated in silico connections by tuning an initial gmax value until the first EPSP amplitude matched experimental measurements. The resulting gmax was 1.54 ± 1.20 nS, which is consistent with previous estimates (Markram et al., 1997, 2015; Ramaswamy and Markram, 2015; Ramaswamy et al., 2015), and enabled the in silico reproduction of synaptic physiology between L5_TTPCs connections. We also further calibrated the membrane voltage noise parameter by implementing an OU-process on the in vitro dataset (see “Materials and Methods”) to obtain σ = 0.22 ± 0.10 mV (Figure 4B, top) and τ = 28.2 ± 3.5 ms (Figure 4B, bottom). Thus, by prescribing U, D, F and gmax parameters, and adding a synthetic membrane voltage noise to each simulated in silico connection we captured the biologically observed synaptic variability in L5_TTPC connections.
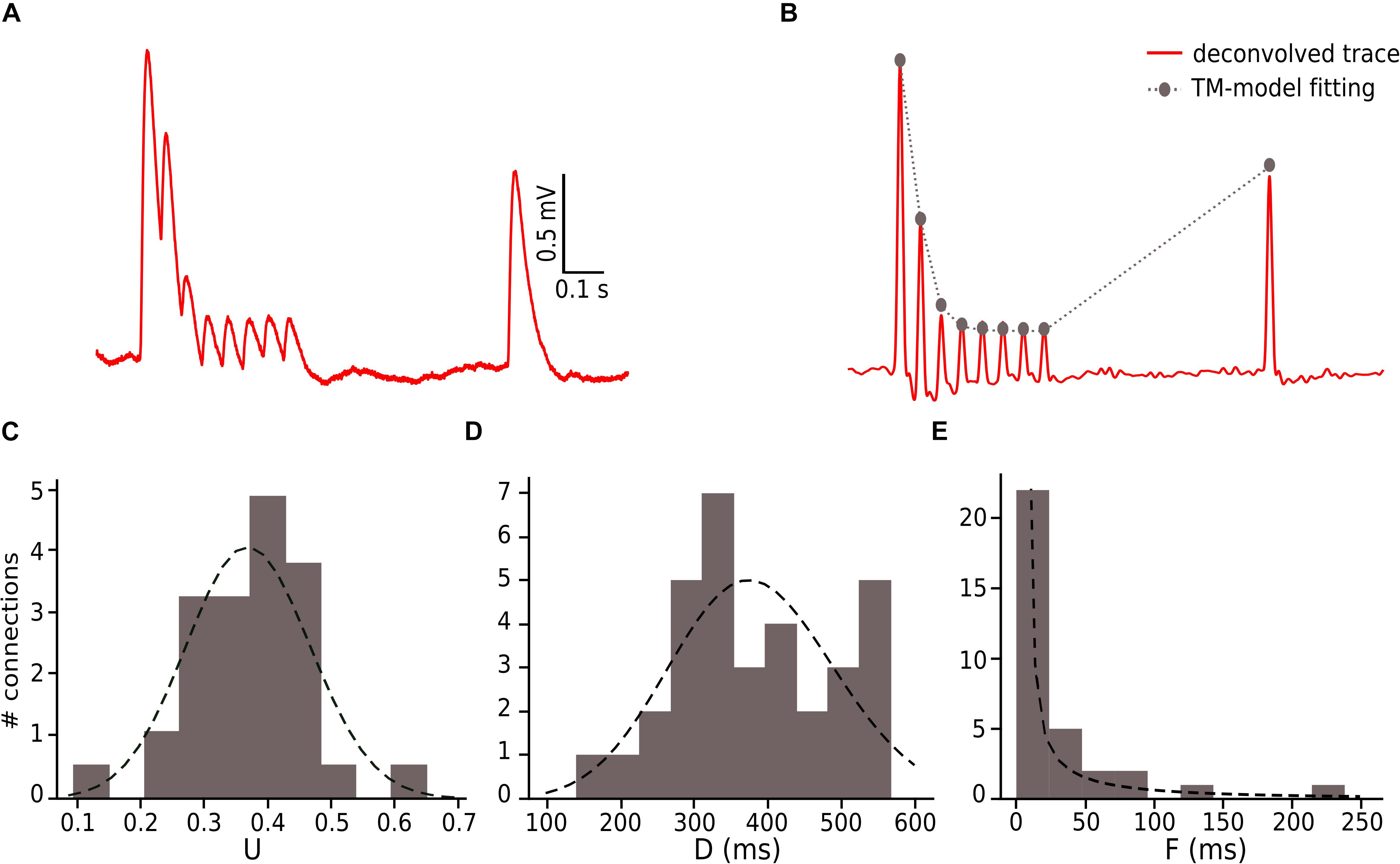
Figure 3. Fitting in vitro data to the TM-model. (A) Example of an in vitro mean voltage trace of L5_TTPC connection. (B) Corresponding deconvolved voltage trace (red) with the fit to the deterministic TM-model (gray). (C) Distribution of the probability of release parameter (U), (D) distribution of the time to recovery from depression (D) and (E) distribution of the time to recovery from facilitation (F). Values obtained from the fitting to the TM-model of 33 in vitro connections.
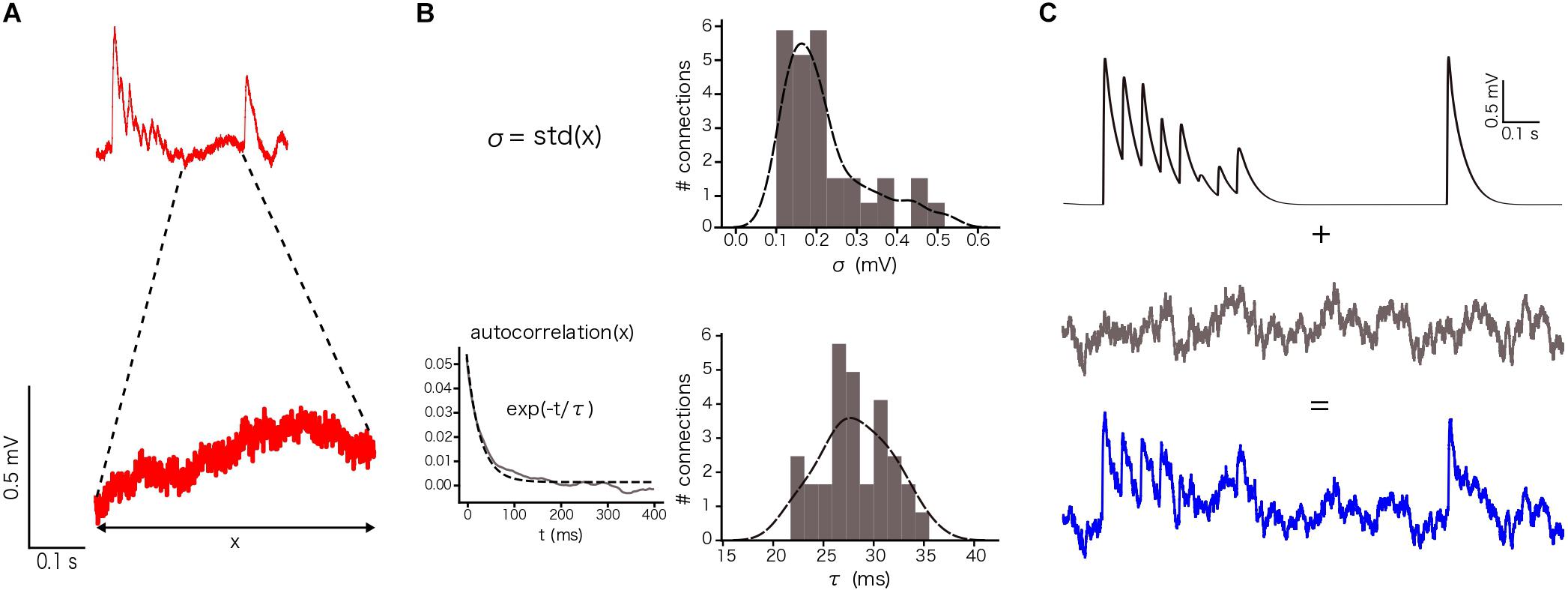
Figure 4. Noise calibration. (A) Example of an in vitro single protocol repetition (top). Zoom over 400 ms segment used to compute the parameters for noise calibration (bottom). (B) Distribution of σ (up) and τ (bottom). σ was computed as the standard deviation of the voltage segment. τ was computed by fitting the voltage segment autocorrelation to an exponential. The distributions show the mean values for the 33 in vitro connections. (C) (up) Single in silico trace without noise, (middle) OU-process generated to be added to the single in silico trace and (bottom) the noisy single protocol repetition that is the result of adding the previous two traces.
Optimizing NRRP for L5_TTPC Connections
Having defined the core synaptic parameter set, we next simulated in silico L5_TTPC connections as described before, although now we compared them against the CVJKK computed from the in vitro data set. We observed a specific relationship between NRRP and the CV for L5_TTPC connections (Figure 5C) that fits the power law with amplitude = 0.55 ± 0.015 and index = −0.39 ± 0.032. Initially, we observed that the CV for the first EPSP amplitude was higher when NRRP was smaller. Therefore, for UVR-like connections the variability between individual sweeps is larger than for MVR-like connections. This result is in agreement with previous studies (Wang et al., 2006; Brémaud et al., 2007) and is also reflected in the simulated in silico connections with NRRP = 1 (Figures 5A,B, top) and NRRP = 20 (Figures 5A,B, bottom) to illustrate how the variability and voltage profile of EPSPs changes with the number of released vesicles.
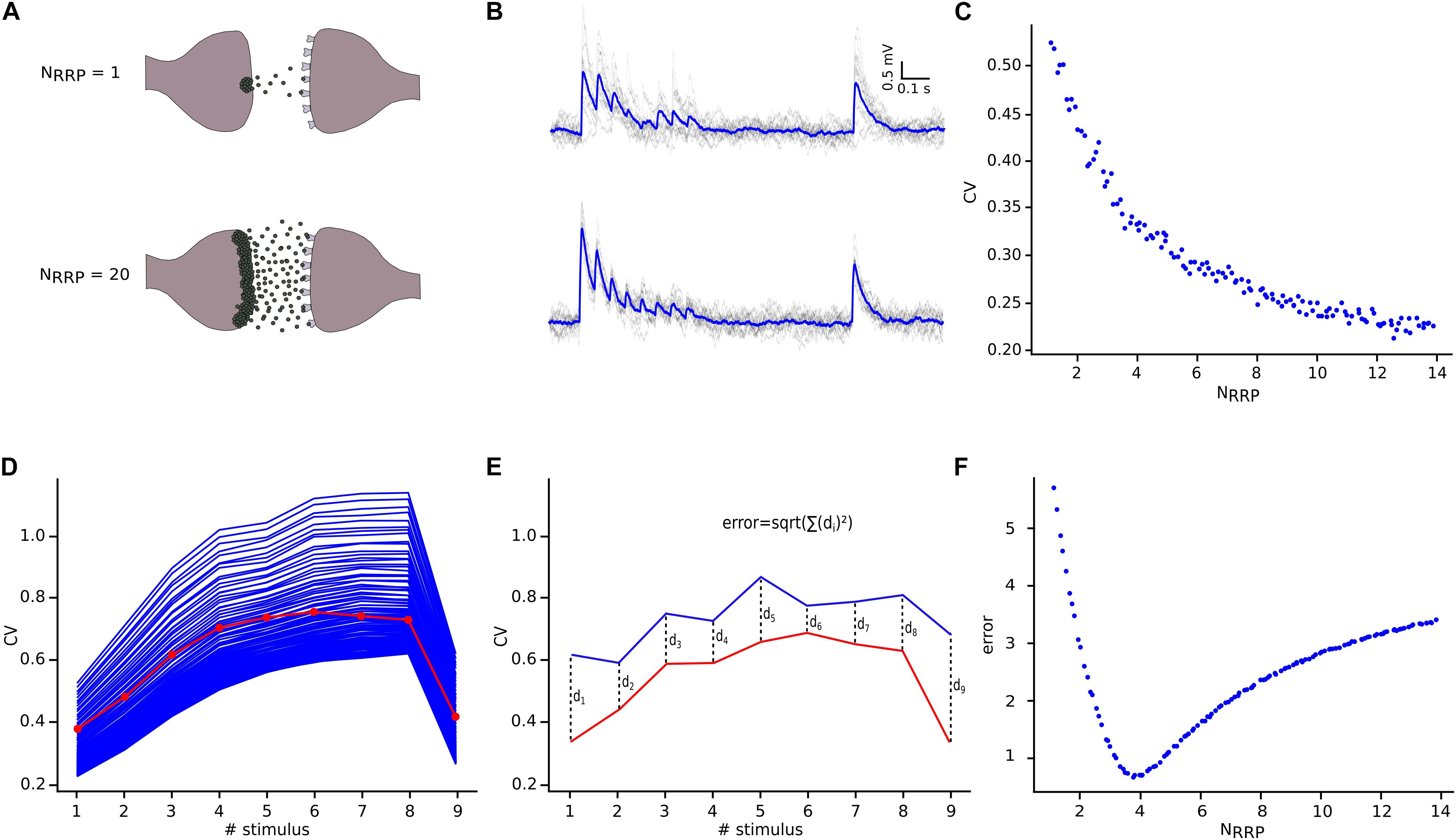
Figure 5. NRRP computation. (A) Illustration showing one synaptic connection releasing neuro transmitters from only one vesicle (top) and the same synaptic connection releasing neurotransmitters from twenty vesicles (bottom). (B) The corresponding effect of releasing neurotransmitters from one (top) or from twenty (bottom) vesicles reflected on the variability and shape of the in silico traces. The mean voltage traces are painted in blue while each protocol repetition is represented in gray. (C) Diagram showing the effect of NRRP over the CV. (D) Mean CV profile for the in vitro (red) and all the in silico connections with different NRRP values. (E) Diagram explaining the mean square distance computation. (F) NRRP against error, showed a clear minimum around the value obtained for this specific connection.
In order to determine NRRP, we next computed the CV profiles of the in silico connections simulated with different NRRPs and measured their mean square distance (Figure 5E) in comparison against the in vitro CV profile (Figure 5D). We found that for L5_TTPC connections the minimum error was obtained with NRRP = 3.78 ± 1.65 (Figure 5F), which demonstrates that our predictions of MVR for these connections is consistent with previous reports (Loebel et al., 2009; Rollenhagen et al., 2018).
Implementing MVR Improved the Variability of the Synapses in the Model
We next sought to test if our hypothesis of MVR between L5_TTPCs could better explain variability in experimental as against UVR (Figure 1). Therefore, we computed the distributions for the first EPSP amplitude, the CV of the first EPSP amplitude, and the CV profile of the EPSP amplitudes for all stimuli in a train. We found that the shape and the amplitude a randomly chosen in silico connection mediated by MVR (Figure 6B) was similar to a randomly chosen in vitro trace (Figure 6A), in contrast to an in silico connection mediated by UVR discussed before (see Motivation for implementing MVR in the model; Figure 1B, bottom). The CV profile for the EPSPs of all MVR in silico connections (Figure 6D, blue) also closely matched the in vitro dataset (red) as against UVR in silico connections (Figure 1D). Although our model has a slightly higher CV for the 6th, 7th, and 8th EPSPs, the Kruskal-Wallis test showed no significant differences between both CV profiles for any of the EPSPs (p = 0.89, p = 0.52, p = 0.42, respectively), demonstrating that the MVR hypothesis improved the synaptic variability of in silico connections.
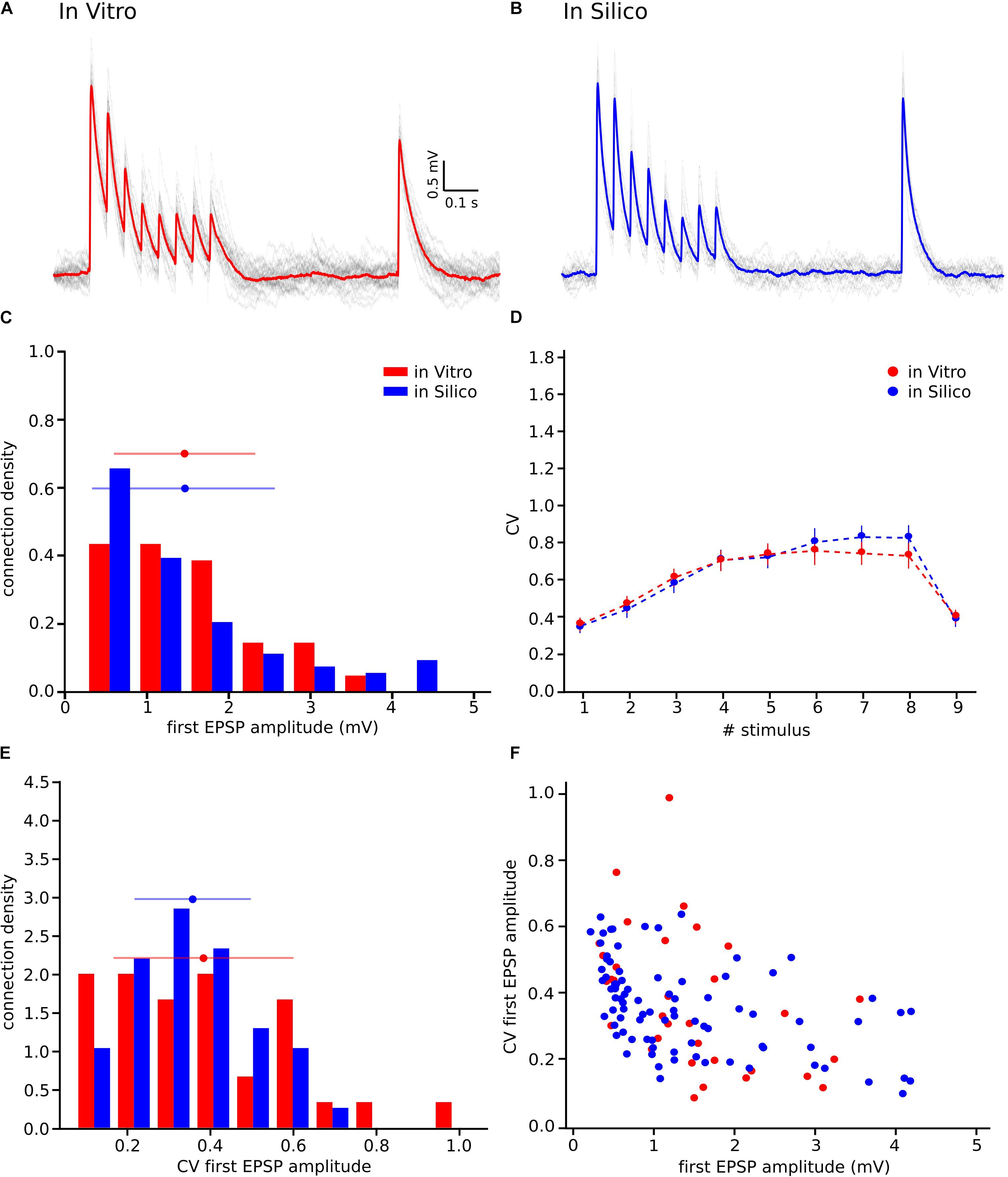
Figure 6. Releasing multiple vesicles improved the variability of the model. (A) In vitro mean voltage trace (red) of 20 protocol repetitions (gray) (same as in Figure 1A). (B) In silico mean voltage trace (blue) of 20 protocol repetitions (gray). (C) Distribution of the first EPSP amplitude for in vitro (red) and for the in silico (blue) experiments. (D) Mean CV profiles for the in vitro (red) and the in silico (blue) experiments. (E) CV Distribution of the first EPSP amplitude for in vitro (red) and the in silico (blue) data sets. (F) Raster plot of the first EPSP amplitude against the CV of the first EPSP amplitude for in vitro (red) and in silico (blue) experiments. All the in silico experiments are done with the NRRP value that produces the minimum error. In the distributions and the CV profile, dots represent the mean and vertical and horizontal bars represent the standard deviation of all the experiments.
Further results, shown in the distributions for the first EPSP amplitude (Figure 6C) and for the CV of the first EPSP amplitude (Figure 6E) corroborated the fact that MVR explained the experimentally observed variability better in contrast to UVR. The mean value of both MVR distributions was statistically insignificant compared against experimental data (mean EPSP values: 1.46 ± 0.86 mV for in vitro; 1.46 ± 0.95 mV for in silico; p = 0.69) (mean CV values: 0.38 ± 0.21 for in vitro; 0.35 ± 0.13 for in silico; p = 0.86). The distributions (Figures 6C,E) were normalized to the respective sample size such that the sum of products of width and height of each column is equal to the total count (33 for in vitro, 85 for in silico). In addition, a Kolmogorov-Smirnov test showed no significant difference between the first EPSP amplitude against the CV of the first EPSP amplitude for in vitro and in silico connections (p = 0.29) (Figure 6F), conclusively demonstrating that both data sets could, in principle, come from the same population.
NRRP Prediction for Other Cell-Type-Specific Connections
We extended this method to other cell-type-specific connections predicted in the neocortical tissue model (Markram et al., 2015; Ramaswamy et al., 2015; Reimann et al., 2015) and also independently characterized by other groups (Feldmeyer et al., 2002, 2005, 2006; Wang et al., 2002). Specifically, we computed the amplitudes and CVs of first PSP amplitudes from these published studies due to lack of access to raw experimental data. Synaptic parameter specifications for the different connections in the model are described in the NMC portal (Ramaswamy et al., 2015).
Before computing the CV for different cell-type-specific synaptic connections obtained from the literature, we had to take into account that they were not necessarily computed using the JKK bootstrapping approach. Our previous analyses demonstrate that the CV of the first EPSP computed through the JKK method has a slightly larger value than the CV computed analytically. In the case of L5_TTPC connections the CVJKK was 0.38 ± 0.21 as against the analytical CV of 0.31 ± 0.14 for the in vitro data set but the NRRPs computed after 50 iterations in both cases were mostly similar (NRRP without JKK = 2.41 ± 1.08 and NRRP with JKK = 2.73 ± 1.22; p = 0.94; Figures 7A,B, respectively). This NRRP obtained by comparing the in vitro and the in silico CVs for only the first EPSP is smaller than the previous NRRP obtained by comparing the CV for all the EPSPs, but as revealed in the previous analysis we did not match the exact CV value for the 1st pulse, although there were no significant difference.
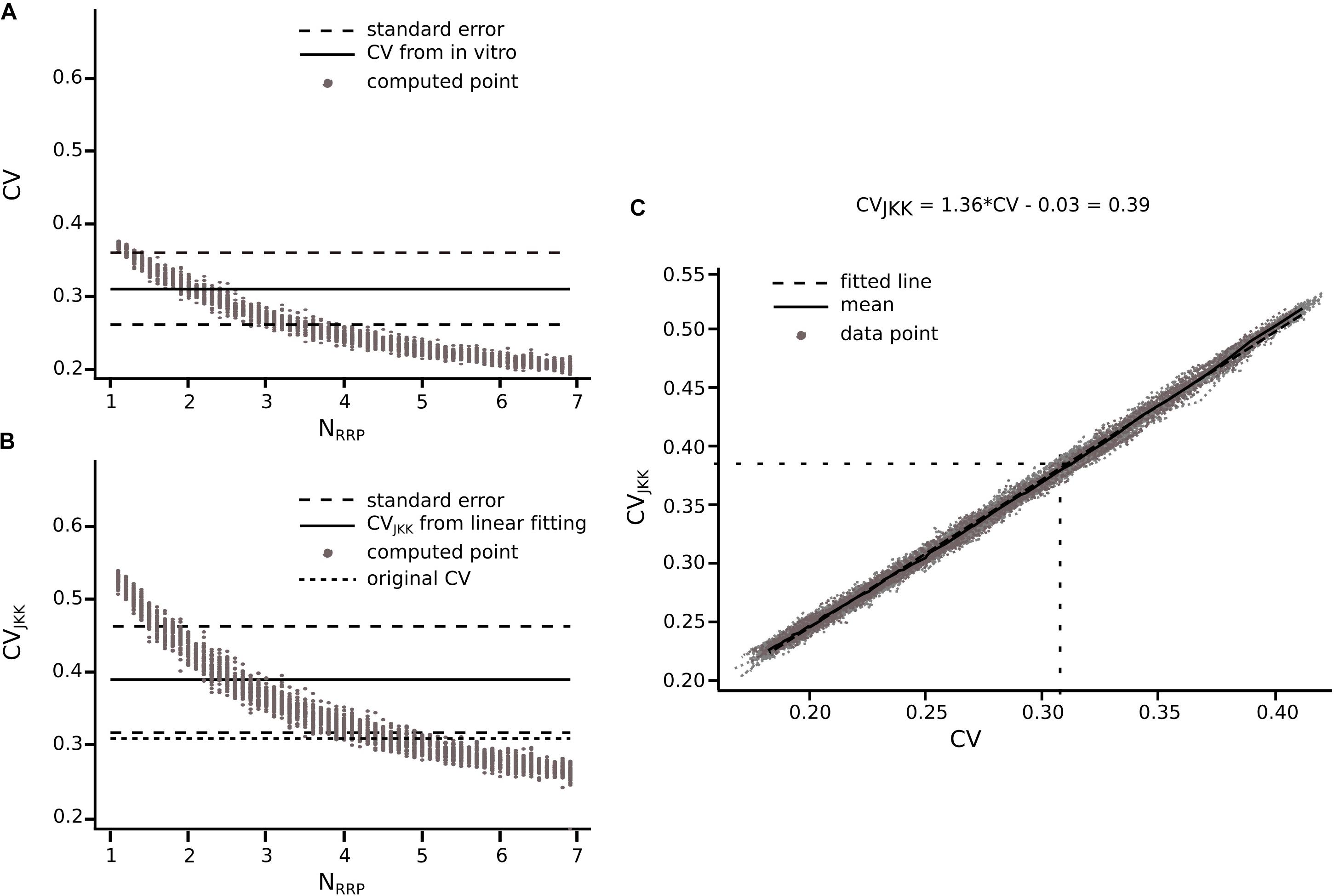
Figure 7. Extension of the method for connections reported in literature. Transformation from CV to CVJKK using L5_TTPC connection as example (A) CV computed for different NRRP. Solid black line represents the CV computed for the in vitro data. Dotted black lines represent the standard error of the CV. (B) CVJKK computed for different NRRP. Solid black line represents the CVJKK obtained from the lineal fitting on C. Dotted black lines represent the standard error for this CVJKK. Short dotted black line represents the original CV found in literature. (C) CV to CVJKK transformation. Solid black line represents the mean of the 50 iterations and dotted black line represent the linear fitting which equation is at the top of the plot. In (A,B) the gray dots show the 50 iterations from which we extract the best NRRP as the one corresponding with the closest CV.
Knowing that the JKK bootstrapping method provided a more accurate method to compute EPSP amplitudes, we applied a transformation from CV to CVJKK (Figure 7C). First, we computed the CV of the first EPSP amplitude without (Figure 7A) and with the JKK (Figure 7B) method. Second, we represented both CVs in the same plot for the different NRRP values and we performed a linear fit to the mean of 50 repetitions (Figure 7C). Next, we determined the corresponding CV value computed with the JKK approach (Figure 7B), for this connection (L5_TTPC) we obtained CVJKK = 0.39 ± 0.15 with a correspondent NRRP = 2.84 ± 1.34. We did that for every connection for which we could find data in the literature and our simulation matched the variability (Table 1).
The generalized results to five different cell-type-specific connections are summarized in Table 1. We further predict that for connections between layer 4 spiny stellate (L4_SSC) and slender-tufted layer 5 pyramidal cell connections that project across the corpus callosum (L5_TPC:C), synaptic release is mediated by UVR (see Table 1; NRRP = 1.26 ± 0.50), while for the remainder of connections the predicted NRRP is between 2 to 3 (see Table 1; NRRP = 2.60 ± 1.28 for L23_PC-L23_PC; NRRP = 1.96 ± 0.98 for L23_NBC_LBC-L23_PC; NRRP = 1.81 ± 0.37 for L4_SSC-L23_PC and NRRP = 1.82 ± 0.90 for L5_TTPC-L5_SBC).
Our results predict that synaptic release at most connections in the neocortex are more likely mediated by MVR rather than UVR, supporting the idea that the release of multiple vesicles enhances the response variability of neocortical synapses and augments information transmission.
Discussion
In this work we computed the NRRP building on the previous work of Loebel et al. (2009) but extended it to all individual synaptic contacts in a connection. Our approach is based on the comparison of the amplitudes and CV of EPSPs between cell-type-specific in vitro and in silico connections with different NRRP values within the framework of a large-scale, data driven tissue level model of juvenile rat neocortical microcircuitry (Markram et al., 2015). The CV of the amplitude distributions reliably reflects the concentration of neurotransmitter in the synaptic cleft and for the postsynaptic receptor occupancy (Faber and Korn, 1991; Auger and Marty, 2000; Neishabouri and Faisal, 2014). For example, a large quantity of presynaptic neurotransmitter release would give rise to a high amplitude EPSP. However, a large fraction of receptors would be occupied as well and consequently it would be more difficult to generate a second EPSP if more neurotransmitter is released. Thus, it is possible to measure the variability of the EPSP amplitude considering that high variability represents a small number of released vesicles.
UVR Cannot Reproduce the Variability Observed Into the Biological Data
Our analysis demonstrates that the UVR hypothesis cannot reproduce the variability observed on the in vitro traces, in fact the CV profile for the in silico experiments is significantly larger, although the first EPSP amplitude is not statistically different. This result suggests that the MVR hypothesis could be more relevant to explain the response variability in neocortical synapses. On the one hand, this idea differs from previous studies (Redman, 1990; Gulyás et al., 1993; Murphy et al., 2004), which claim that at each active zone in a synapse only one vesicle could be released, suggesting that the biological variability may come from changes in the quantal size. On the other hand, more recent studies validate our MVR hypothesis that better explains biological variability (Brémaud et al., 2007; Loebel et al., 2009; Hardingham et al., 2010; Huang et al., 2010; Rudolph et al., 2015). This discrepancy could be partly attributed to the fact that the studies validating the UVR hypothesis were undertaken in brain regions other than the neocortex, with different experimental protocols, across different species and cell-types.
Before obtaining evidence, which supports the MVR hypothesis, we extracted a core set of synaptic important parameters from an in vitro dataset obtained from L5_TTPCs. First, we computed the parameters pertaining to a deterministic model of short-term synaptic depression (Tsodyks and Markram, 1997). To this end, we had to select only those connections whose 1st EPSP amplitude was within the range of the in vitro data set and apply the deconvolution for computing the peaks. Then we introduced the peak values on a GA that calculated the synaptic parameters. The values obtained were similar to values found in previous researches (Tsodyks and Markram, 1997; Wang et al., 2006). Second, we calibrated the synaptic noise which represented the synaptic trial-to-trial variability. Many studies support the idea that background synaptic noise is not merely “noise,” but an addition of various meaningful mechanisms as channels and receptors dynamics (Azouz and Gray, 1999; Faisal et al., 2008). Synaptic noise is also thought to arise from the spontaneous fusion and release of vesicle (Fatt and Katz, 1950). This noise could not only influence the synaptic variability, but also the transmission of information (Jacobson et al., 2005). Thus, while some studies do not support our hypothesis of the contribution of the number of vesicles in synaptic noise (Mackenzie et al., 2000), several others (Korn et al., 1993; Franks et al., 2003; Faisal et al., 2008; Pulido and Marty, 2017) inspired us to include additional synaptic noise in our model. Finally, we also validated our method by building three different in silico data sets where the mean NRRP was set to 1, 4 and 10, respectively. Although the mean values obtained using the method were slightly larger, no significant differences were found, and therefore, we used the validated method with experimental data sets.
L5_TTPC Synapses Are Driven by Multiple Vesicles
Increasing the NRRP improved the variability of our model, resulting in synapses that more faithfully reproduced the experimentally observed physiology. Consequently, for synaptic connections between L5_TTPCs the predicted NRRP was 3.78 ± 1.65 within a range of 1 to 9 vesicles. Synaptic connections between L5_TTPCs are mediated by about 4 to 8 contacts on average (Markram et al., 1997). We predict that the total number of release sites for pairs synaptic contact between L5_TTPC connections ranges between 4 to 72, which is consistent with two previous studies of that have estimated vesicles in L5_TTPC synaptic contacts to range from 2 to 30 docked vesicles (Rollenhagen and Lübke, 2006), and 7 to 170 vesicles (Loebel et al., 2009). Our predictions are also consistent with a recent study, which estimated that the number of readily releasable vesicles at individual synaptic contacts of L5B PCs ranged from 1.2 to 12.8 with an average of (5.40 ± 1.24) per contact (Rollenhagen et al., 2018). The estimated mean value is slightly larger than what we predict, which could be due to a difference in the developmental age and the cortical area. While our experimental data set was obtained in the non-barrel hind limb somatosensory cortex of juvenile rats, Rollenhagen et al. (2018) investigated synapses between L5B PCs in the barrel cortex of adult rats. Compared to cortical synapses, the neuromuscular junction and the Calyx of Held, which are extensively studied synaptic assemblies, also show MVR with about two, and three vesicles per active zone, respectively (Neher and Sakaba, 2008; Ruiz et al., 2011; Sakaba, 2018). These studies support the idea that MVR occurs in different brain areas within different ranges, suggesting that MVR may be important not only for reliable information transmission, but also a key mechanism for defining synaptic functionality. Is synaptic release in other cell-type-specific connections in the rat neocortex mediated by MVR?
We extended our method to predict the NRRP for L5_TTPC synapses to other cell-type-specific connections in the neocortex reported in the literature. For five different cell-type-specific connections, we predict that the average NRRP is between 2 and 3 (see Table 1). Although our predictions are inconsistent with some observations, for connections between L4_SSC and L23_PCs (Silver et al., 2003), they are comparable with other studies that support the notion of MVR as a fundamental property of intra and inter-laminar cortical synapses (Brémaud et al., 2007; Huang et al., 2010).
Due to lack of specific data, we extrapolated synaptic parameters measured in the superficial layers (Wang et al., 2002) to deeper layers, in particular for synaptic connections between L2/3 PCs and basket cells to their counterparts L5 to predict the NRRP. Our data-driven framework is designed in to integrate specific data sets as and when they become available to enable predictions on the NRRP of cortical synapses.
Despite the occurrence of weak in silico synaptic connections between L5_TTPCs in the neocortical tissue model, the CV distribution has a lower mean because the subset of in silico connections that were sampled to reproduce experimental findings display high EPSP amplitudes. Previous work seems to suggest that weak synaptic connections are necessary to maintain synchronous activity in the cortex (Bruno and Sakmann, 2006; Ren et al., 2017). Therefore, future refinements of this approach should consider how weak connections could impact predictions of NRRP. It should be noted that other parameters relevant to predict the NRRP, such as gmax were determined indirectly in our study, which could impact our results. For instance, if gmax was underestimated, we would have had obtained a larger NRRP by increasing its value considering the same CV. It is also known that other synaptic mechanisms such as the membrane fusion, receptor saturation, and vesicle recycling directly influence vesicle release (Stevens, 2003; Watanabe et al., 2013; Rizo and Xu, 2015; Rudolph et al., 2015). We propose that future work should consider all these synaptic factors to predict NRRP for cortical connections.
In summary, we described an approach built upon previous work (Loebel et al., 2009) to predict the NRRP per active synaptic contact for neocortical connections. By systematically comparing in vitro and in silico data on the CV of the EPSP amplitude CV, we could predict the NRRP. Our preliminary results suggest that MVR could serve as a fundamental mechanism in the brain to increase the dynamic range of synapses and their variability.
Data Availability Statement
The raw data supporting the conclusions of this manuscript will be made available by the authors, without undue reservation, to any qualified researcher.
Ethics Statement
All experiments were performed according to the Swiss national and institutional guidelines.
Author Contributions
NB-Z developed and performed the data analysis and the in silico experiments, drafted the manuscript, and generated the figures. JR developed and performed the initial data analysis. GC developed and performed some data analysis and some in silico experiments. RP designed and performed the in vitro experiments. HM contributed to data interpretation and procured funding for the study. SR gathered data from the published literature, contributed to data interpretation, and drafted the manuscript. EM contributed to data interpretation and an initial draft of the manuscript. SR and EM jointly conceived and supervised the study.
Funding
This study was supported by funding to the Blue Brain Project, a research center of the École Polytechnique Fédérale de Lausanne, from the Swiss Government’s ETH Board of the Swiss Federal Institutes of Technology.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors thank Dr. Michael Reimann and the Blue Brain Project team for insightful discussions.
References
Auger, C., Kondo, S., and Marty, A. (1998). Multivesicular release at single functional synaptic sites in cerebellar stellate and basket cells. J. Neurosci. 18, 4532–4547. doi: 10.1523/jneurosci.18-12-04532.1998
Auger, C., and Marty, A. (2000). Quantal currents at single-site central synapses. J. Physiol. 526(Pt 1), 3–11. doi: 10.1111/j.1469-7793.2000.t01-3-00003.x
Azouz, R., and Gray, C. M. (1999). Cellular mechanisms contributing to response variability of cortical neurons in vivo. J. Neurosci. 19, 2209–2223. doi: 10.1523/jneurosci.19-06-02209.1999
Betz, W. J. (1970). Depression of transmitter release at the neuromuscular junction of the frog. J. Physiol. 206, 629–644. doi: 10.1113/jphysiol.1970.sp009034
Bibbona, E. (2008). The Ornstein-Uhlenbeck process as a model of a low-pass filtered white noise. Metrologia 45, S117–S126.
Bibbona, E., Panfilo, G., and Tavella, P. (2008). The Ornstein–Uhlenbeck process as a model of a low pass filtered white noise. Metrologia 45, S117–S126.
Biró, A. A., Holderith, N. B., and Nusser, Z. (2005). Quantal size is independent of the release probability at hippocampal excitatory synapses. J. Neurosci. 25, 223–232. doi: 10.1523/jneurosci.3688-04.2005
Boucher, J., Kröger, H., and Sík, A. (2010). Realistic modelling of receptor activation in hippocampal excitatory synapses: analysis of multivesicular release, release location, temperature and synaptic cross-talk. Brain Struct. Funct. 215, 49–65. doi: 10.1007/s00429-010-0273-x
Brémaud, A., West, D. C., and Thomson, A. M. (2007). Binomial parameters differ across neocortical layers and with different classes of connections in adult rat and cat neocortex. Proc. Natl. Acad. Sci. U. S. A. 104, 14134–14139. doi: 10.1073/pnas.0705661104
Bruno, R. M., and Sakmann, B. (2006). Cortex is driven by weak but synchronously active thalamocortical synapses. Science 312, 1622–1627. doi: 10.1126/science.1124593
Christie, J. M., and Jahr, C. E. (2006). Multivesicular release at schaffer collateral-CA1 hippocampal synapses. J. Neurosci. 26, 210–216. doi: 10.1523/jneurosci.4307-05.2006
Conti, R., and Lisman, J. (2003). The high variance of AMPA receptor- and NMDA receptor-mediated responses at single hippocampal synapses: evidence for multiquantal release. Proc. Natl. Acad. Sci. U.S.A. 100, 4885–4890. doi: 10.1073/pnas.0630290100
Del Castillo, J., and Katz, B. (1954). Quantal components of the end-plate potential. J. Physiol. 124, 560–573. doi: 10.1113/jphysiol.1954.sp005129
Efron, B., and Tibshirani, R. J. (1994). An Introduction to the Bootstrap. New York, NY: Chapman & Hall.
Faber, D. S., and Korn, H. (1991). Applicability of the coefficient of variation method for analyzing synaptic plasticity. Biophys. J. 60, 1288–1294. doi: 10.1016/s0006-3495(91)82162-2
Faisal, A. A., Selen, L. P. J., and Wolpert, D. M. (2008). Noise in the nervous system. Nat. Rev. Neurosci. 9, 292–303.
Fatt, P., and Katz, B. (1950). Some observations on biological noise. Nature 166, 597–598. doi: 10.1038/166597a0
Feldmeyer, D., Lübke, J., and Sakmann, B. (2006). Efficacy and connectivity of intracolumnar pairs of layer 2/3 pyramidal cells in the barrel cortex of juvenile rats. J. Physiol. 575, 583–602. doi: 10.1113/jphysiol.2006.105106
Feldmeyer, D., Lübke, J., Silver, R. A., and Sakmann, B. (2002). Synaptic connections between layer 4 spiny neurone – layer 2/3 pyramidal cell pairs in juvenile rat barrel cortex: physiology and anatomy of interlaminar signalling within a cortical column. J. Physiol. 538, 803–822. Pt 3, doi: 10.1113/jphysiol.2001.012959
Feldmeyer, D., Roth, A., and Sakmann, B. (2005). Monosynaptic connections between pairs of spiny stellate cells in layer 4 and pyramidal cells in layer 5A indicate that lemniscal and paralemniscal afferent pathways converge in the infragranular somatosensory cortex. J. Neurosci. 25, 3423–3431. doi: 10.1523/jneurosci.5227-04.2005
Franks, K. M., Stevens, C. F., and Sejnowski, T. J. (2003). Independent sources of quantal variability at single glutamatergic synapses. J. Neurosci. 23, 3186–3195. doi: 10.1523/jneurosci.23-08-03186.2003
Fuhrmann, G., Cowan, A., Segev, I., Tsodyks, M., and Stricker, C. (2004). Multiple mechanisms govern the dynamics of depression at neocortical synapses of young rats. J. Physiol. 557, 415–438. doi: 10.1113/jphysiol.2003.058107
Fuhrmann, G., Segev, I., Markram, H., and Tsodyks, M. (2002). Coding of temporal Information by activity-dependent synapses. J. Neurophysiol. 87, 140–148. doi: 10.1152/jn.00258.2001
Goldberg, D. E., and Holland, J. H. (1988). Genetic algorithms and machine learning. Mach. Learn. 3, 95–99. doi: 10.1023/A:1022602019183
Gordon, G. R. J. (2005). Noradrenaline triggers multivesicular release at glutamatergic synapses in the hypothalamus. J. Neurosci. 25, 11385–11395. doi: 10.1523/jneurosci.2378-05.2005
Gulyás, A. I., Miles, R., Sík, A., Tóth, K., Tamamaki, N., and Freund, T. F. (1993). Hippocampal pyramidal cells excite inhibitory neurons through a single release site. Nature 366, 683–687. doi: 10.1038/366683a0
Gupta, A., Wang, Y., and Markram, H. (2000). Organizing principles for a diversity of GABAergic interneurons and synapses in the neocortex. Science 287, 273–278. doi: 10.1126/science.287.5451.273
Hardingham, N. R., Read, J. C. A., Trevelyan, A. J., Nelson, J. C., Jack, J. J. B., and Bannister, N. J. (2010). Quantal analysis reveals a functional correlation between presynaptic and postsynaptic efficacy in excitatory connections from rat neocortex. J. Neurosci. 30, 1441–1451. doi: 10.1523/JNEUROSCI.3244-09.2010
Hennig, M. H. (2013). Theoretical models of synaptic short term plasticity. Front. Comput. Neurosci. 7:45. doi: 10.3389/fncom.2013.00045
Huang, C.-H., Bao, J., and Sakaba, T. (2010). Multivesicular release differentiates the reliability of synaptic transmission between the visual cortex and the somatosensory cortex. J. Neurosci. 30, 11994–12004. doi: 10.1523/JNEUROSCI.2381-10.2010
Jacobson, G. A., Diba, K., Yaron-Jakoubovitch, A., Oz, Y., Koch, C., Segev, I., et al. (2005). Subthreshold voltage noise of rat neocortical pyramidal neurones. J. Physiol. 564, 145–160. doi: 10.1113/jphysiol.2004.080903
Korn, H., Bausela, F., Charpier, S., and Faber, D. S. (1993). Synaptic noise and multiquantal release at dendritic synapses. J. Neurophysiol. 70, 1249–1254. doi: 10.1152/jn.1993.70.3.1249
Korn, H., Sur, C., Charpier, S., Legendre, P., and Faber, D. S. (1994). The one-vesicle hypothesis and multivesicular release. Adv. Second Messenger Phosphoprotein Res. 29, 301–322.
Korn, H., Triller, A., Mallet, A., and Faber, D. S. (1981). Fluctuating responses at a central synapse: n of binomial fit predicts number of stained presynaptic boutons. Science 213, 898–901. doi: 10.1126/science.6266015
Liley, A. W., and North, K. A. (1953). An electrical investigation of effects of repetitive stimulation on mammalian neuromuscular junction. J. Neurophysiol. 16, 509–527. doi: 10.1152/jn.1953.16.5.509
Loebel, A., Silberberg, G., Helbig, D., Markram, H., Tsodyks, M., and Richardson, M. J. E. (2009). Multiquantal release underlies the distribution of synaptic efficacies in the neocortex. Front. Comput. Neurosci. 3:27. doi: 10.3389/neuro.10.027.2009
Maass, W., and Markram, H. (2002). Synapses as dynamic memory buffers. Neural Netw. 15, 155–161. doi: 10.1016/s0893-6080(01)00144-7
Mackenzie, P. J., Kenner, G. S., Prange, O., and Murphy, T. H. (2000). Vesicle number does not predict postsynaptic measures of miniature synaptic activity frequency in cultured cortical neurons. Neuroscience 98, 1–7. doi: 10.1016/s0306-4522(00)00089-0
Markram, H., Lübke, J., Frotscher, M., Roth, A., and Sakmann, B. (1997). Physiology and anatomy of synaptic connections between thick tufted pyramidal neurones in the developing rat neocortex. J. Physiol. 500(Pt 2), 409–440. doi: 10.1113/jphysiol.1997.sp022031
Markram, H., Muller, E., Ramaswamy, S., Reimann, M. W., Sanchez, C., Ailamaki, A., et al. (2015). Reconstruction and simulation of neocortical microcircuitry. Cell 163, 456–492. doi: 10.1016/j.cell.2015.09.029
Markram, H., Wang, Y., and Tsodyks, M. (1998). Differential signaling via the same axon of neocortical pyramidal neurons. Proc. Natl. Acad. Sci. U.S.A. 95, 5323–5328. doi: 10.1073/pnas.95.9.5323
Mason, A., Nicoll, A., and Stratford, K. (1991). Synaptic transmission between individual pyramidal neurons of the rat visual cortex in vitro. J. Neurosci. 11, 72–84. doi: 10.1523/jneurosci.11-01-00072.1991
Molnár, G., Rózsa, M., Baka, J., Holderith, N., Barzó, P., Nusser, Z., et al. (2016). Human pyramidal to interneuron synapses are mediated by multi-vesicular release and multiple docked vesicles. eLife 5:e18167. doi: 10.7554/eLife.18167
Murphy, G. J., Glickfeld, L. L., Balsen, Z., and Isaacson, J. S. (2004). Sensory neuron signaling to the brain: properties of transmitter release from olfactory nerve terminals. J. Neurosci. 24, 3023–3030. doi: 10.1523/jneurosci.5745-03.2004
Nadkarni, S., Bartol, T. M., Sejnowski, T. J., and Levine, H. (2010). Modelling vesicular release at hippocampal synapses. PLoS Comput. Biol. 6:e1000983. doi: 10.1371/journal.pcbi.1000983
Neher, E., and Sakaba, T. (2008). Multiple roles of calcium ions in the regulation of neurotransmitter release. Neuron 59, 861–872. doi: 10.1016/j.neuron.2008.08.019
Neishabouri, A., and Faisal, A. A. (2014). Axonal noise as a source of synaptic variability. PLoS Comput. Biol. 10:e1003615. doi: 10.1371/journal.pcbi.1003615
Oertner, T. G., Sabatini, B. L., Nimchinsky, E. A., and Svoboda, K. (2002). Facilitation at single synapses probed with optical quantal analysis. Nat. Neurosci. 5, 657–664. doi: 10.1038/nn867
Press, W. H., and Teukolsky, S. A. (1988). Kolmogorov-Smirnov test for two-dimensional data. Comput. Phys. 2:74. doi: 10.1063/1.4822753
Pulido, C., and Marty, A. (2017). Quantal fluctuations in central mammalian synapses: functional role of vesicular docking sites. Physiol. Rev. 97, 1403–1430. doi: 10.1152/physrev.00032.2016
Ramaswamy, S., Courcol, J.-D., Abdellah, M., Adaszewski, S. R., Antille, N., Arsever, S., et al. (2015). The neocortical microcircuit collaboration portal: a resource for rat somatosensory cortex. Front. Neural Circuits 9:44. doi: 10.3389/fncir.2015.00044
Ramaswamy, S., and Markram, H. (2015). Anatomy and physiology of the thick-tufted layer 5 pyramidal neuron. Front. Cell. Neurosci. 9:233. doi: 10.3389/fncel.2015.00233
Redman, S. (1990). Quantal analysis of synaptic potentials in neurons of the central nervous system. Physiol. Rev. 70, 165–198. doi: 10.1152/physrev.1990.70.1.165
Reimann, M. W., King, J. G., Muller, E. B., Ramaswamy, S., and Markram, H. (2015). An algorithm to predict the connectome of neural microcircuits. Front. Comput. Neurosci. 9:120. doi: 10.3389/fncom.2015.00120
Ren, H.-P., Bai, C., Baptista, M. S., and Grebogi, C. (2017). Weak connections form an infinite number of patterns in the brain. Sci. Rep. 7:46472. doi: 10.1038/srep46472
Richardson, M. J., and Silberberg, G. (2008). Measurement and analysis of postsynaptic potentials using a novel voltage-deconvolution method. J. Neurophysiol. 99, 1020–1031. doi: 10.1152/jn.00942.2007
Rizo, J., and Xu, J. (2015). The synaptic vesicle release machinery. Annu. Rev. Biophys. 44, 339–367. doi: 10.1146/annurev-biophys-060414-034057
Rollenhagen, A., and Lübke, J. H. R. (2006). The morphology of excitatory central synapses: from structure to function. Cell Tissue Res. 326, 221–237. doi: 10.1007/s00441-006-0288-z
Rollenhagen, A., Ohana, O., Sätzler, K., Hilgetag, C. C., Kuhl, D., and Lübke, J. H. R. (2018). Structural properties of synaptic transmission and temporal dynamics at excitatory layer 5B synapses in the adult rat somatosensory cortex. Front. Synaptic Neurosci. 10:24. doi: 10.3389/fnsyn.2018.00024
Rudolph, S., Tsai, M.-C., von Gersdorff, H., and Wadiche, J. I. (2015). The ubiquitous nature of multivesicular release. Trends Neurosci. 38, 428–438. doi: 10.1016/j.tins.2015.05.008
Ruiz, R., Cano, R., Casañas, J. J., Gaffield, M. A., Betz, W. J., and Tabares, L. (2011). Active zones and the readily releasable pool of synaptic vesicles at the neuromuscular junction of the mouse. J. Neurosci. 31, 2000–2008. doi: 10.1523/jneurosci.4663-10.2011
Sakaba, T. (2018). Kinetics of transmitter release at the calyx of held synapse. Proc. Jpn. Acad. Ser. B Phys. Biol. Sci. 94, 139–152. doi: 10.2183/pjab.94.010
Silver, R. A., Lubke, J., Sakmann, B., and Feldmeyer, D. (2003). High-probability uniquantal transmission at excitatory synapses in barrel cortex. Science 302, 1981–1984. doi: 10.1126/science.1087160
Stevens, C. F. (2003). Neurotransmitter release at central synapses. Neuron 40, 381–388. doi: 10.1016/s0896-6273(03)00643-3
Tang, C. M., Margulis, M., Shi, Q. Y., and Fielding, A. (1994). Saturation of postsynaptic glutamate receptors after quantal release of transmitter. Neuron 13, 1385–1393. doi: 10.1016/0896-6273(94)90423-5
Tong, G., and Jahr, C. E. (1994). Multivesicular release from excitatory synapses of cultured hippocampal neurons. Neuron 12, 51–59. doi: 10.1016/0896-6273(94)90151-1
Tsodyks, M. V., and Markram, H. (1997). The neural code between neocortical pyramidal neurons depends on neurotransmitter release probability. Proc. Natl. Acad. Sci. U.S.A. 94, 719–723. doi: 10.1073/pnas.94.2.719
Varela, J. A., Sen, K., Gibson, J., Fost, J., Abbott, L. F., and Nelson, S. B. (1997). A quantitative description of short-term plasticity at excitatory synapses in layer 2/3 of rat primary visual cortex. J. Neurosci. 17, 7926–7940. doi: 10.1523/jneurosci.17-20-07926.1997
Waites, C. L., and Garner, C. C. (2011). Presynaptic function in health and disease. Trends Neurosci. 34, 326–337. doi: 10.1016/j.tins.2011.03.004
Wang, Y., Gupta, A., Toledo-Rodriguez, M., Wu, C. Z., and Markram, H. (2002). Anatomical, physiological, molecular and circuit properties of nest basket cells in the developing somatosensory cortex. Cereb. Cortex 12, 395–410. doi: 10.1093/cercor/12.4.395
Wang, Y., Markram, H., Goodman, P. H., Berger, T. K., Ma, J., and Goldman-Rakic, P. S. (2006). Heterogeneity in the pyramidal network of the medial prefrontal cortex. Nat. Neurosci. 9, 534–542. doi: 10.1038/nn1670
Watanabe, S., Rost, B. R., Camacho-Pérez, M., Davis, M. W., Söhl-Kielczynski, B., Rosenmund, C., et al. (2013). Ultrafast endocytosis at mouse hippocampal synapses. Nature 504, 242–247. doi: 10.1038/nature12809
Keywords: synaptic transmission, quantal analysis, multi vesicular release, neocortex, mathematical model, short-term depression
Citation: Barros-Zulaica N, Rahmon J, Chindemi G, Perin R, Markram H, Muller E and Ramaswamy S (2019) Estimating the Readily-Releasable Vesicle Pool Size at Synaptic Connections in the Neocortex. Front. Synaptic Neurosci. 11:29. doi: 10.3389/fnsyn.2019.00029
Received: 30 April 2019; Accepted: 30 September 2019;
Published: 15 October 2019.
Edited by:
Dirk Feldmeyer, Julich Research Centre, GermanyReviewed by:
Christian Stricker, Australian National University, AustraliaStefan Hallermann, Leipzig University, Germany
Copyright © 2019 Barros-Zulaica, Rahmon, Chindemi, Perin, Markram, Muller and Ramaswamy. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Natalí Barros-Zulaica, bmF0YWxpLmJhcnJvc3p1bGFpY2FAZXBmbC5jaA==; Srikanth Ramaswamy, c3Jpa2FudGgucmFtYXN3YW15QGVwZmwuY2g=
†Co-senior authors
 Natalí Barros-Zulaica
Natalí Barros-Zulaica John Rahmon1
John Rahmon1 Giuseppe Chindemi
Giuseppe Chindemi Rodrigo Perin
Rodrigo Perin Henry Markram
Henry Markram Eilif Muller
Eilif Muller Srikanth Ramaswamy
Srikanth Ramaswamy