- Information Science Directorate, U.S. Army Research Office, Research Triangle Park, NC, USA
This paper presents a restricted overview of Fractal Physiology focusing on the complexity of the human body and the characterization of that complexity through fractal measures and their dynamics, with fractal dynamics being described by the fractional calculus. Not only are anatomical structures (Grizzi and Chiriva-Internati, 2005), such as the convoluted surface of the brain, the lining of the bowel, neural networks and placenta, fractal, but the output of dynamical physiologic networks are fractal as well (Bassingthwaighte et al., 1994). The time series for the inter-beat intervals of the heart, inter-breath intervals and inter-stride intervals have all been shown to be fractal and/or multifractal statistical phenomena. Consequently, the fractal dimension turns out to be a significantly better indicator of organismic functions in health and disease than the traditional average measures, such as heart rate, breathing rate, and stride rate. The observation that human physiology is primarily fractal was first made in the 1980s, based on the analysis of a limited number of datasets. We review some of these phenomena herein by applying an allometric aggregation approach to the processing of physiologic time series. This straight forward method establishes the scaling behavior of complex physiologic networks and some dynamic models capable of generating such scaling are reviewed. These models include simple and fractional random walks, which describe how the scaling of correlation functions and probability densities are related to time series data. Subsequently, it is suggested that a proper methodology for describing the dynamics of fractal time series may well be the fractional calculus, either through the fractional Langevin equation or the fractional diffusion equation. A fractional operator (derivative or integral) acting on a fractal function, yields another fractal function, allowing us to construct a fractional Langevin equation to describe the evolution of a fractal statistical process. Control of physiologic complexity is one of the goals of medicine, in particular, understanding and controlling physiological networks in order to ensure their proper operation. We emphasize the difference between homeostatic and allometric control mechanisms. Homeostatic control has a negative feedback character, which is both local and rapid. Allometric control, on the other hand, is a relatively new concept that takes into account long-time memory, correlations that are inverse power law in time, as well as long-range interactions in complex phenomena as manifest by inverse power-law distributions in the network variable. We hypothesize that allometric control maintains the fractal character of erratic physiologic time series to enhance the robustness of physiological networks. Moreover, allometric control can often be described using the fractional calculus to capture the dynamics of complex physiologic networks.
Introduction
The theme of this paper is to indicate the necessity for a fractal view of physiology that explicitly takes into account the complexity of living matter and its dynamics. Complexity in this context incorporates the recent advances in physiology concerned with the applications of the concepts from fractal geometry, fractal statistics and nonlinear dynamics, to the formation of a new kind of understanding within the life sciences. A parallel development has been the understanding of the dynamics of fractal processes and how those dynamics are manifest in the control of physiologic networks. For a number of years the study of fractals and its application to physiology was restricted to the determination of the fractal dimension of structure, in particular, the static structure of objects and the scaling of time series. However, now we explore the dynamics of fractal processes using the fractional calculus, and apply this dynamical approach to both regular and stochastic physiologic processes. To understand the need for such an approach a historical perspective is useful.
Homeostasis
It is not a coincidence that the modern view of how the human body operates mirrors our understanding of the technological society in which we live, where a thermostat controls the temperature of a home, the sound of a voice can turn the lights on and off, and cruise control determines the speed of a car. It is not clear when this idea of how the body works began to permeate society, but in medicine the concept was introduced by the nineteenth century scientist Claude Bernard (1813–1878). He developed the notion underlying homeostasis in his study of stability of the human body. The word homeostasis was popularized half a century later by Walter Cannon (1871–1945) in his book The Wisdom of the Body (Cannon, 1932). Homeostasis is what many consider to be the guiding principle of medicine, whereby every human body has multiple automatic inhibition mechanisms that suppress disquieting influences of the environment. Homeostasis is the evolutionary strategy selected to enable the human body to maintain an internal balance, although it is not always evident how a particular suppressing response is related to a specific antagonism. Biology teaches that evolution has, over the millennia, reduced homeostatic networks to the bare minimum, so that in the spirit of parsimony, every internal mechanism of a physiological network is necessary to maintain either the structural or functional integrity of the organism.
But why should physiologic networks be homeostatic? Why has nature determined that this is the “best” way to control the various complex networks in the human body? In part, nature’s choices have to do with the fact that no physiologic network is isolated; these networks are, in fact, made up of a mind-numbing number of subnetworks, the cells. The task of a cell is simple and repetitive, but that of an organ is not. Therefore a complex network like the cardiovascular is made up of a variety of cell types, each type performing a given different function. If responses to changes in the external environment were at the cellular level, physiology would be much more complicated than it is already, and organs would no doubt be unstable. But nature has found that if the immediate environment of the cells is kept within certain narrowly defined limits, then the cells can continue to perform their specific tasks and no others, even while organs respond to sometimes extravagant external disturbances. As long as the internal environment stays within a certain operational range the cells continue to function without change. Thus, homeostasis is the presumed strategy that nature has devised to keep the internal state of the body under control.
The level of sophistication of control mechanisms was brought to light with the centrifugal fly-ball governor (1788) constructed by J. Watt for regulating the speed of the rotary steam engine. This artificial control mechanism heralded the onset of the Industrial Revolution. The first mathematical description and consequent understanding of Watt’s governor was constructed by the English physicist J. C. Maxwell in 1868, when he linearized the differential equations describing the governor’s dynamics. The solutions to the linearized differential equations (control) are stable when the eigenvalues have negative real parts (stabilizing feedback) and in this way the language for the control of dynamical networks was introduced.
The homeostatic control of physiologic networks classifies the dynamics as negative feedback, because such homeostatic networks respond in ways to dampen environmental disturbances including fluctuations. However the control of certain networks has the opposite behavior, that is, they have a positive feedback, because the networks respond in ways to amplify perturbations. Of course, such responses lead to unstable behavior in general, but such instability is sometimes useful. Consequently feedback can either amplify or suppress disturbances depending on the network’s dynamics.
The picture of reducing the variability in the size of widgets coming off an assembly line to meet specifications and the suppression of physiologic variability by homeostatic control remains compatible. However the scaling of physiologic time series and the interpretation of that scaling in terms of long-term memory and fractal dimensions (Mandelbrot, 1977, 1982) is not consistent with a simple view of the world in general or of physiology in particular. Therefore we explore some of the ways fractal dynamics has required modification of the principle of homeostasis (Goldberger, 2006) and how allometric control (West, 2009) may replace homeostatic control. Consequently we hypothesize that complex physiologic networks require allometric control.
Another important hypothesis that developed from this view of physiologic time series is that disease and aging are associated with the loss of complexity and not with the loss of regularity (Goldberger et al., 1990). This hypothesis could be a consequence of a loss of interactions among component networks, or as Pincus (1994) suggested the increased isolation of network elements can result in a decrease in the complexity of the network’s signal. The complexity hypothesis may also be related to the idea that disease marks a departure from normal physiologic behavior and because that departure may be either more or less irregular it has been called “dynamic disease” by Glass (2001) and is caused by modifications in the underlying physiologic control network.
Fractals
The fractal concept was formally introduced into the physical sciences by Beniot Mandelbrot over 20 year ago in his monograph (Mandelbrot, 1977), which brought together mathematical, experimental, and physical arguments that undermined the traditional picture of the physical world. It had been accepted that celestial mechanics and physical phenomena are, by and large, described by smooth, continuous, and unique functions, since before the time of Lagrange (1736–1813). This belief was part of the conceptual infrastructure of the physical sciences. The changes in physical processes were modeled by systems of dynamical equations and the solutions to such equations are continuous and differentiable at all but a finite number of points. Therefore the phenomena being described by these equations were thought to have these properties of continuity as well as differentiability.
From the phenomenological side, Mandelbrot called into question the fidelity of the traditional perspective by pointing to the failure of the equations of physics to explain such familiar phenomena as turbulence and phase transitions, for example, the melting of ice and the clotting of blood. In his books (Mandelbrot, 1977, 1982) Mandelbrot catalogued and described dozens of physical, social, and biological phenomena that cannot be properly described using the familiar tenants of dynamics from physics. The functions required to explain these complex phenomena have properties that for a 100 years had been thought to be mathematically pathological. Mandelbrot argued that, rather than being septic; these functions capture essential properties of reality and are therefore better descriptors of the real world than the traditional analytic functions of theoretical physics.
Schrödinger (1943), using the principles of equilibrium statistical physics, laid out his understanding of the connection between the world of the microscopic and macroscopic. In that discussion he asked why atoms are so small relative to the dimension of the human body. The high level of organization necessary for life is only possible in a macroscopic network; otherwise the order would be destroyed by microscopic (thermal) fluctuations. A living network must be sufficiently large to maintain its integrity in the presence of thermal fluctuations that randomly disrupt its constitutive elements. Thus, macroscopic phenomena are characterized by averages over ensemble distribution functions characterizing microscopic fluctuations. The dynamics of macroscopic variables therefore generally do not contain thermal fluctuations; the fluctuations typically observed in physiologic time series are macroscopic not microscopic. Consequently any strategy for modeling physiology must be based on an understanding of the statistical properties of complex macroscopic phenomena, and as we shall see, on our understanding of fluctuating phenomena that lack characteristic scales and are therefore fractal.
There are three types of fractals that appear in the life sciences: geometrical fractals, that determine the spatial properties of the tree-like structures of the mammalian lung, arterial and venous systems, and other ramified structures (West and Deering, 1994); statistical fractals (Mandelbrot, 1982), that determine the properties of the distribution of intervals in the beating of the mammalian heart (Peng et al., 1993), breathing (Altemeier et al., 2000), walking (Hausdorff et al., 1995; West and Griffin, 1998, 1999; Griffin et al., 2000) and in the firing of certain neurons (Das et al., 2003) and finally dynamical fractals (West et al., 2003a), that determine the dynamical properties of networks having a large number of characteristic time scales. In complex physiologic networks the distinctions between these three kinds of fractals often blur, and herein we focus our attention on the dynamics rather than on the geometry of fractals; although in this journal we fully expect to entertain studies involving all three types of fractals.
Summary
We have made three interrelated hypotheses in this Introduction. This first is that complex physiologic networks require allometric control; the second is that disease is the loss of complexity; and finally that the fractal dimension is a significantly better indicator of organismic functions in health and disease than are traditional averages. These hypotheses are interrelated due to the fact that complex physiologic time series have 1/f variability, manifest in an inverse power-law spectrum, an inverse power-law probability density or both. The power-law index is related to the fractal dimension, which is a measure of the complexity of the underlying process.
In support of these hypotheses we briefly review how such concepts as complexity, fractals, diverging moments, nonlinear dynamics, and other related mathematical topics along with their experimental testing are used to understand physiologic networks. Of course, a number of books have been written about any one of these ideas – books for the research expert (Meakin, 1998), books for the informed teacher (Schroeder, 1991), books for the struggling graduate student (West, 1999), and books for the intelligent lay person (Prigogine and Stengers, 1984). Different authors stress different characteristics of complex phenomena, from the erratic data collected by clinical researchers (Dewey, 1997) to the fluctuations generated by deterministic dynamical equations used to model such networks (Ott, 1993). Some authors have painted with broad brushstrokes, indicating only the panorama that these concepts reveal to us (Briggs and Peat, 1971), whereas others have sketched with painstaking detail the structure of such phenomena and have greatly enriched those that could follow the arguments (Rosen, 1991). Herein we view our efforts as being midway between the two since Fractal Physiology is itself a hypothesis that is continually being tested.
Manifestations of Variability
Healthy physiologic network give rise to time series that display erratic fluctuations not unlike those found in dynamical systems driven from the vicinity of a set point, or from an equilibrium state (Stanley et al., 1999). The statistical properties of physiological fluctuations, such as found in the time series for heartbeat dynamics, respiration, human locomotion, and posture control (Collins and DeLuca, 1994), have been the focus of interdisciplinary research on complex networks for more than two decades (West, 1999). The rationale for this persistent interest is related in part to the idea that unlike the thermal fluctuations found in physics, which perturb a system but do not contain useful information, physiologic fluctuations are often the result of internal control and therefore frequently contain useful information. The goal here is to better understand self-regulatory control systems for complex physiologic phenomena that produce such fluctuations and to describe the dynamics of such phenomena with tools capable of capturing their nonlinear and often exotic statistical character (Bassingthwaighte et al., 1994).
One outcome of the research into the properties of these fluctuations has been a profound change in our understanding of the significance of homeostasis and as suggested by Stanley et al. (1999) the possibility of their existing a “non-homeostatic physiologic variability”. The discovery of fractal and multifractal properties in physiological time series has lead to the suggestion that the intrinsic variability of many physiological phenomena reflects the adaptability of the underlying control networks (West and Goldberger, 1987). Consequently, the statistical properties, including correlations of physiological fluctuations, may be more important in the control of health and disease than are the average properties, such as those under homeostatic control.
Power Laws
Scale invariance is the property that relates the elements of time series across multiple time scales and has been found to hold empirically for a number of complex physiologic phenomena including the inter-beat intervals of the human heart (Ivanov et al., 1999; West et al., 1999a), switching times in vision (Gao et al., 2006), inter-stride intervals of human gait (Jordan et al., 2006), brain wave data from EEGs (West et al., 1995) and inter-breath intervals (Szeto et al., 1992), to name a few. One way to understand scaling in these and other experimental data is by means of a renormalization group approach. Consider an unknown function Z(t) that satisfies a relation of the form

We solve this equation in the same manner that differential equations are solved, by assuming a trial solution, inserting the trial solution into the equation of motion and solving for the appropriate constants. In the present case we assume a trail solution

Substituting Eq. 2 into both the lhs and the rhs of Eq. 1 yields the condition that the function A(t) is periodic in the logarithm of the time with period log b, that is, A(bt) = A(t), and the power-law index has the value

In the literature Z(t) is called a homogeneous function (Barenblatt, 1994). Note that the parameter a scales the amplitude of the function being measured and the parameter b scales the resolution of the time scale. The power-law index is the ratio of the logarithms of these two scaling parameters, indicating how the amplitude of the function is modified as the units of time are modified.
The homogeneous function Z(t) is now used to define the scaling observed in the moments calculated from the experimental time series with long-time memory. The second moment of a time-dependent stochastic process is assumed to be Z(t) = 〈X(t)2 〉 so that it has a long-time memory is given by (Bassingthwaighte et al., 1994)

For the same process a different scaling is given for the stationary autocorrelation function Z(τ) = 〈X(t)X(t + τ)〉 = C(τ) yielding (Bassingthwaighte et al., 1994)

Finally, the spectral density for this time series, given by the Fourier transform of the autocorrelation function and therefore in terms of the frequency f as Z(f) = S(f) is (Bassingthwaighte et al., 1994)

The solutions to each of these three scaling equations are of precisely the algebraic form implied by Eq. 2, and in the simplest case the modulation amplitude A(t) is fixed at a constant (time-independent) value.
The above renormalization scaling yields a mean-square signal level that increases nonlinearly with time according to Eq. 4 as

and the exponent H is a real constant, often called the Hurst exponent (Mandelbrot, 1977). In a complex physiologic network the response X(t) is expected to depart from the entirely random condition of a simple random walk model, because real fluctuations are expected to have memory and correlation quantified by H. In the physics literature anomalous diffusion (H ≠ 0.5) is associated with phenomena with long-time memory such that the two-time autocorrelation function is (Bassingthwaighte et al., 1994; Beran, 1994)
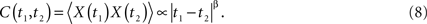
Here the power-law index is given by β = 2H − 2 in agreement with Eq. 5. Note that the two-point autocorrelation function is assumed to depend only on the time difference, thus, the underlying process is stationary. The autocorrelation function is an inverse power law in time because 0 ≤ H ≤ 1 implying that the correlation between data points decreases in time with increasing time separation. Note that inverse power law loss of memory is much slower than the exponential decay that is often assumed. This scaling behavior is also manifest in the spectrum, which according to Eq. 6 is a power law in frequency f:

and is inverse power law for H > 0.5, a superdiffusive process.
These three properties, the algebraic increase in time of the mean-square signal strength (Eq. 7), the inverse power law in time of the stationary autocorrelation function (Eq. 8) and the inverse power law in frequency of the spectrum (Eq. 9), are typical of observed physiologic time series. These properties are usually assumed to be the result of long-time memory in the underlying statistical process. Beran (1994) discusses these power-law properties of the spectrum and autocorrelation function, as well as a number of other properties for discrete and continuous time series. In particular he points out that the interpretation in terms of how to generate long-time memory in complex networks is not unique and reviews the use of fractional difference random walks. Herein we extend the discussion to fractional stochastic differential equations (West, 1999) and the dynamics of fractals. But first we note the long history associated with the 1/f spectrum (Eq. 9).
The phenomenon of 1/f noise was discovered by Schottky (1918) at the turn of the last century in his study of electrical conductivity. Between then and now this spectral form has been found in biological, economic, linguistic, medical, neurological, and social phenomena as well as in physics (West et al., 2008). The spectra of such complex phenomena are given by Eq. 9 and the spectral index falls within the interval 0.5 < α < 1.5. Complex phenomena span the dynamic range from the macroscopic behavioral level down to the microscopic level. It is evident that 1/f variability appears in body movements such as walking, postural sway, and movement in synchrony with external stimulation such as a metronome; also such variability resides in physiologic networks as manifest in heart rate variability (HRV, Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiolgy, 1996), human vision (Alvarez-Ramirez et al., 2008), the dynamics of the human brain (Gilden, 2001; Grigolini et al., 2009), and in human cognition (Van Orden et al., 2005; Kello et al., 2007); also 1/f noise is measured at the level of single-ion channels (Liebovitch and Krekora, 2002; Roy et al., 2008) and in single neuron adaptation to various stimuli (Das et al., 2003). Each of these psychophysical phenomena manifests 1/f variability (West et al., 2008). The original assertion that α = 1 was shown in these subsequent studies to extend the spectral index to the broader range indicated.
Allometric Relations
The term scaling denotes a power-law relation between two variables x and y

and as Barenblatt (1994) explained such scaling laws are not merely special cases of more general relations; they never appear by accident and they always reveal self-similarity. In biology Eq. 10 is historically referred to as an allometric relation between two observables. Such relations were introduced into biology in the nineteenth century. Typically an allometric equation relates two properties of a given organism. For example, the total mass of a deer y is proportional to the mass of the deer’s antlers x raised to a specific power α. Huxley summarized the experimental basis for this relation in his 1931 book (Huxley, 1931) and developed the mathematics to describe and explain allometric growth laws. He reasoned that in biological systems two parts of an organism grow at different rates, but the growth rates are proportional to one another. Consequently, how rapidly one part of the organism grows can be related to how rapidly the other part of the organism grows and the ratio of the two rates is constant. Another such application has y as the body’s metabolic rate with x the body’s mass and recent theory in terms of fractal transport of material within the body purports to explain the observed value of the power-law index α ≈ 0.75(West et al., 1997).
The notion of an allometric relation has been generalized to include measures of time series. In this view y is interpreted to be the variance and x the average value of the quantity being measured. The fact that these two central measures of a time series satisfy an allometric relation implies that the underlying time series is a fractal random process and therefore scales. It was first determined empirically that certain statistical data satisfy a power-law relation of the form (Eq. 10) by Taylor (1961) and this is where we begin our discussion of the allometric aggregation method of data analysis.
Taylor was interested in biological speciation. For one thing, he was curious about how many species of beetle can be found in a given area of land and he therefore sectioned off a large field into plots. In each plot he sampled the soil for the variety of beetles that were present. This enabled him to determine the distribution in the number of new species of beetle spatially distributed across the field. From the distribution he could then extract the average number of new species 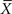 and the variance in the number of new species VarX. After this first calculation he partitioned his field into smaller plots and redid the sampling, again determining the mean and variance in the number of species at this increased resolution. This process was repeated a number of times, yielding a set of values for the mean and variance. In the ecological literature a graph of the logarithm of the variance versus the logarithm of the average value is called a power curve, which is linear in the logarithms of the two variables and b is the slope of the curve. The algebraic form of the relation between the variance and mean is
and the variance in the number of new species VarX. After this first calculation he partitioned his field into smaller plots and redid the sampling, again determining the mean and variance in the number of species at this increased resolution. This process was repeated a number of times, yielding a set of values for the mean and variance. In the ecological literature a graph of the logarithm of the variance versus the logarithm of the average value is called a power curve, which is linear in the logarithms of the two variables and b is the slope of the curve. The algebraic form of the relation between the variance and mean is

where the two parameters a and b determine how the variance and mean are related to one another.
Taylor (1961) exploited the curves obtained from data in a number of ways using the slope and intercept parameters. If the slope of the curve and the intercept are both equal to 1, a = b = 1, then the variance and mean are equal to one another. This equality is only true for a Poisson distribution, which, when it occurred, allowed him to interpret the number of new species as being randomly distributed over the field, with the number of species in any one plot being independent of the number of species in any other plot. If, however, the slope of the curve was less than unity, the number of new species appearing in the plots was interpreted to be quite regular. The spatial regularity of the number of species, in this case, was compared with the trees in an orchard and given the name evenness. Finally, if the slope of the variance versus mean curve was greater than 1, the number of new species was interpreted as being clustered in space, like disjoint herds of sheep grazing in a meadow. This clustering is a form of spatial intermittency.
Of particular interest to us here was the mechanism that Taylor and Taylor (1977) postulated to account for the experimentally observed allometric relation:
We would argue that all spatial dispositions can legitimately be regarded as resulting from the balance between two fundamental antithetical sets of behavior always present between individuals. These are, repulsion behavior, which results from the selection pressure for individuals to maximize their resources and hence to separate, and attraction behavior, which results from the selection pressure to make the maximum use of available resources and hence to congregate wherever these resources are currently most abundant.
Consequently, they postulated that it is the tension between the attraction and repulsion, migration and congregation, which produces the interdependence (scaling) of the spatial variance and the average population density. We suggest that this mechanism is generic and may underlie a number of natural phenomena including those in complex physiologic networks.
We can now reinterpret Taylor’s observations because the kind of clustering he observed in the spatial distribution of species number, when the slope of the power curve is greater than 1, is consistent with an asymptotic inverse power-law distribution of the underlying data set. Furthermore, the clustering or clumping of events is due to the fractal nature of the underlying dynamics. Willis, some 40 years before Taylor, established the inverse power-law form of the number of species belonging to a given genera (Willis, 1922). Willis used an argument associating the number of species with the size of the area they inhabit. It was not until the decade of the 1990s that it became clear to more than a handful of experts that the relationship between an underlying fractal process and its space filling character obeys a scaling law (Mandelbrot, 1977, 1982). It is this scaling law that is manifest in the allometric relation between the variance and mean.
It is possible to test the allometric relation of Taylor using computer-generated data. But before we do so, we note that Taylor and Woiwod (1980) were able to extend the discussion from the stability of the population density in space, independent of time, to the stability of the population density in time, independent of space. Consequently, just as spatial stability, as measured by the variance, is a power function of the mean population density over a given area at all times, so too the temporal stability, as measured by the variance, is a power function of the mean population density over time at all locations. With this generalization in hand we apply Taylor’s Law to time series.
Scaling Time Series
Allometric relations such as Eq. 10 have been extended to include measures of time series. In this extended view y is interpreted to be the variance and x the average value of the quantity being measured as in Taylor’s Law (Eq. 11). The fact that these two central measures of the time series satisfy an allometric relation implies that the underlying time series is a fractal random process. The scaling of time series data is here determined by grouping the data into aggregates of two, three, and more of the original data points and calculating the mean and variance at each level of aggregation. The idea is that if the data are fractal in nature then we need not increase the resolution as Taylor did. We should be able to determine the scaling behavior by coarse graining or aggregating the data. In this spirit the variance, for a monofractal random time series, is given by (Bassingthwaighte et al., 1994)

where the superscript on the variable indicates that it is determined using the aggregation of n-adjacent data points. It is well established (Mandelbrot, 1977; Bassingthwaighte et al., 1994) that the exponent in a scaling equation such as Eq. 12 is related to the fractal dimension D of the underlying time series by the relation D = 2 − H.
The allometric aggregation approach has been applied to a number of data sets implementing linear regression analysis to the logarithms of the variances and the averages as follows:
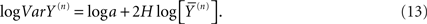
Consequently the processed data from self-similar data would appear as straight lines on log–log graph paper. For example, in Figure 1 we apply Eq. 13 to one million computer-generated data points with Gaussian statistics. The far left dot in this figure contains all the data in the calculation of the aggregated mean and variance so that n = 1 in Eq. 13. The next point to the right in the figure contains the nearest-neighbor data points added together to define a data set with a half million data points from which to calculate the mean and variance and so on moving from left to right. Consequently, this process of aggregating the data is equivalent to decreasing the resolution of the time series and as the resolution is systematically decreased, the adopted measure, the allometric relation between the mean and variance, reveals an underlying property of the time series. The increase in the variance with increasing average values for increasing aggregation number shown in the figure is not an arbitrary pattern. The curve indicates that the aggregated data points are interconnected. The original computer-generated data points are not correlated, but the adding of data points in the aggregation process induces a correlation, one that is completely predictable. The induced correlation is linear if the original data is uncorrelated, but the induced correlation is not linear if the original data is correlated.
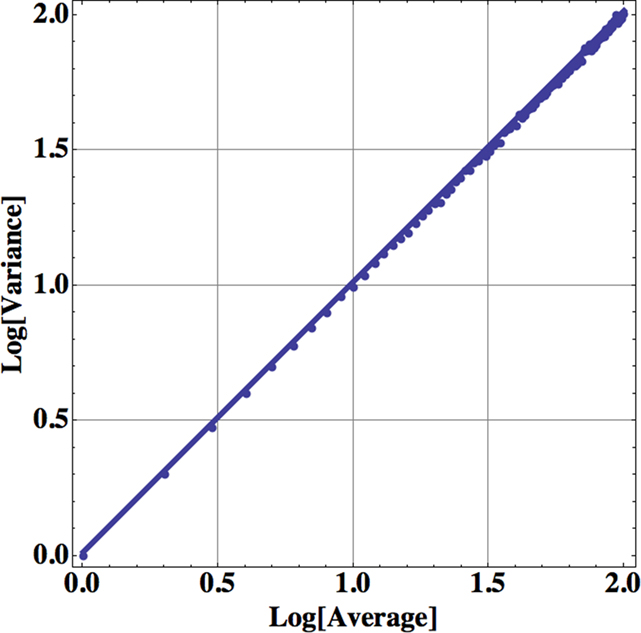
Figure 1. The logarithm of the variance is plotted versus the logarithm of the mean for the successive aggregation of 106 computer-generated random data points with Gaussian statistics. The slope of the curve is essentially one, determined by a linear regression using Eq. 13, so the fractal dimension of the time series is D = 1.5.
The aggregated variance versus the aggregated mean falls along a straight line in Figure 1 with a slope of 1 for the uncorrelated random process with computer-generated Gaussian statistics. Therefore, in the case of Gaussian statistics, we obtain from the slope of the curve b = 1, so that the fractal dimension is given by D = 2 − b/2 = 1.5 corresponding to the fractal dimension of Brownian motion (Suki et al., 2003). In the same way a completely regular time series would have b = 2, so that D = 1. The fractal dimension for most time series fall somewhere between these two extremes; the closer the fractal dimension is to 1, the more regular the process; the closer the fractal dimension is to 1.5, the more it is like an uncorrelated random process. The data analyzed in Figure 1 certainly have a single fractal dimension characterizing the entire computer-generated time series. If the power-law index, the slope of the above curve, is 1 then the data are from an uncorrelated random process. If the index is greater than 1 then the data cluster, indicating correlations in the random process as interpreted by Taylor.
We emphasize that the allometric aggregation approach is just one of many procedures designed to take advantage of the scaling properties of the central moments of time series. We refer to such methods collectively as finite variance statistical methods (FVSM). However, it should be emphasized that not all time series that scale have finite variance. Time series having Lévy α-stable statistics exemplify processes with diverging variance, but they are described by probability density functions that scale (West, 1999). We review these matters after some discussion of the scaling properties of physiological time series.
Fractal Time Series
Let us consider the time series from a number of complex physiologic networks such as the cardiovascular, the respiratory, and the motor control. In each case a time series associated with the particular physiologic network is found to be a random fractal as determined by scaling behavior. We have applied the allometric aggregation approach to these time series and others as reviewed by West (2006a) and here we begin the discussion with the observed variability of the inter-beat intervals of the heart.
The mechanisms producing the observed variability in the size of a human heart’s inter-beat intervals apparently arise from a number of sources. The sinus node (the heart’s natural pacemaker) receives signals from the autonomic (involuntary) portion of the nervous system that has two major branches: the parasympathetic, whose stimulation decreases the firing rate of the sinus node, and the sympathetic, whose stimulation increases the firing rate of the sinus node pacemaker cells. The influence of these two branches produces a continual tug-of-war on the sinus node, one decreasing and the other increasing the heart rate. It has been suggested that it is this tug-of-war that produces the fluctuations in the heart rate of healthy subjects in direct analogy with the observations of Taylor and Woiwod (1980), but alternate suggested mechanisms are pursued subsequently. Consequently, HRV provides a window through which we can observe the heart’s ability to respond to normal disturbances that can affect its rhythm. The clinician focuses on retaining the balance in regulatory impulses from the vagus nerve and sympathetic nervous system and in this effort requires a robust measure of that balance (West et al., 2008). A quantitative measure of HRV time series, such as the fractal dimension, serves this purpose.
Heart rate variability time series have been used as a quantitative indicator of autonomic activity. Physicians became interested in developing this indicator of variability because experiments indicated a relationship with lethal arrhythmias. A task force was formed and charged with the responsibility of developing the standards of measurement, physiological interpretation and clinical use of HRV. They published their findings (Task force of the European Society of Cardiology the North American Society of Pacing Electrophysiolgy, 1996) in 1996 after which time the importance of HRV to medicine became more widely apparent.
When an individual’s heart rate is not typical it is evident that quantifying the variation in heart rate is consequential. There are a number of ways to calculate measures of HRV, some sixteen at last count, each related to scaling in one way or another and most being in the FVSM category. However it would not be productive to review them all here. Instead we identify the scaling index as the most revealing of the characteristics of HRV and use the allometric aggregation approach relating the variance and mean of empirical data to determine the scaling index or equivalently the fractal dimension. We apply the allometric aggregation approach to the heart’s RR-intervals for a healthy young adult male in Figure 2.
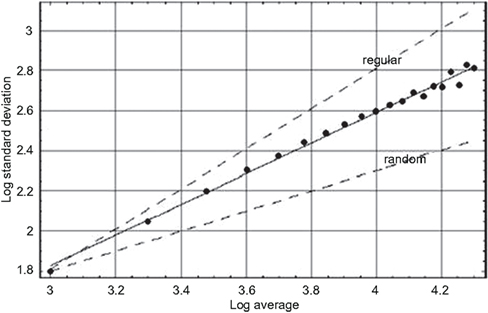
Figure 2. The logarithm of the standard deviation is plotted versus the logarithm of the average value for the heartbeat interval time series for a young adult male, using sequential values of the aggregation number (West, 2006a). The solid line segment is the best fit to the aggregated data points and yields a fractal dimension D = 1.24 midway between the curve for a regular process (D = 1) and that for an uncorrelated random process (D = 1.5) as indicated by the dashed curves.
In Figure 2 the logarithm of the standard deviation is plotted versus the logarithm of the mean value for a typical HRV time series. Note that we use the standard deviation in the figure and not the variance but there is no essential difference in the discussion. At the left-most position the data points indicates the standard deviation and mean using all the data points. Moving from left to right the next data point is constructed from the time series with two nearest-neighbor data points added together and the procedure is repeated moving right until the right-most data point has 20 nearest-neighbor data points added together. The solid line segment is the best linear representation of the scaling obtained using a mean-square minimization procedure that intercepts most of the data points with a positive slope of 0.76. We can see that the slope of the HRV data is midway between the dashed curves depicting an uncorrelated random process (slope = 1/2) and one that is deterministically regular (slope = 1).
We emphasize that the conclusions we draw here are not from this single figure or set of data presented, but are representative of a much larger body of work. The conclusions are based on a large number of similar observations (West, 1999; Glass, 2001; Suki et al., 2003) made using a variety of data processing techniques, all of which yield results consistent with the scaling of the HRV time series indicated in Figure 2. So we conclude that the heartbeat intervals do not form an uncorrelated random sequence. Instead we see that the HRV time series is a statistical fractal, indicating that the heartbeats have long-time memory. The implications of this long-time memory concerning the underlying physiological control system are taken up in the subsequent discussion of the mathematical models.
Scaling phenomena, such as shown for the HRV time series data in Figure 2, are said to be self-similar. The fact that the standard deviation and mean values change in a certain way as a function of aggregation number implies that the magnitudes of these measures depend on the size of the ruler used to measure the time interval. Recall that this is one of the defining characteristics of fractal curves; the length of the curve becomes infinite as the size of the ruler goes to 0. The dependence of the mean and standard deviation on the ruler size, for a self-similar time series, implies that the statistical process is fractal and consequently defines a fractal dimension for the HRV time series.
The average scaling exponent obtained by Peng et al. (1993) for a group of 10 healthy subjects having a mean age of 44 years, using 10000 data points for each subject, was b = 0.19 for the difference in heartbeat interval time series, not the heartbeat intervals themselves. They interpreted this value to be consistent with a theoretical value of b = 0, which they conjectured would be obtained for an infinitely long time series. The latter scaling implies that the scaling exponent for the heartbeat intervals themselves would be 1.0. However, all data sets are finite and it was determined that the asymptotic scaling coefficients for the heartbeat interval time series of healthy young adults lie in the interval 0.7 ≤ b ≤ 1.0. The value of the scaling coefficient obtained using much shorter time series and the relatively simple processing technique of allometric aggregation is consistent with these results.
We also investigate in the same way the dynamics of breathing; the apparently regular breathing as you sit quietly reading this paper. Here evolution’s design of the lung may be closely tied to the way the lung carries out its function. It is not by accident that the cascading branches of the bronchial tree become smaller and smaller, nor is it good fortune alone that ties the dynamics of our every breath to this physiologic structure. We argue that, like the heart, the lung is made up of fractal processes, some dynamic and others now static. As with the heart, the variability of the breathing rate using breath-to-breath time intervals is denoted by breathing rate variability (BRV), to maintain a consistent notation. We present a BRV plot in Figure 3 and obtain a figure similar to that in Figure 2. Both kinds of processes lack a characteristic scale and a simple argument establishes that such lack of scale has evolutionary advantages (West, 1990). Here again we observe that the data fall on a line segment midway between the regular and the random with a fractal dimension of D = 1.14, perhaps tilting more toward the regular. It is also observed that as we age the fractal dimension increases and our breathing becomes increasingly random – a loss of regularity with age (West, 2006a).
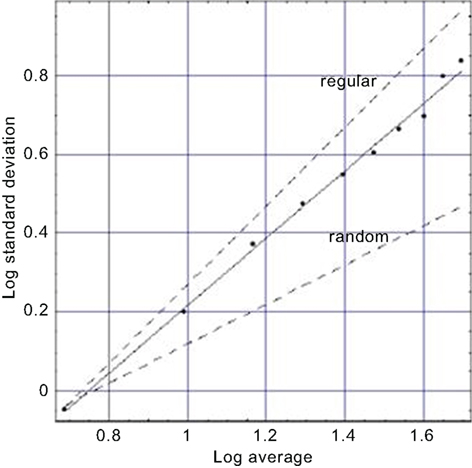
Figure 3. A fit to the aggregated standard deviation versus the aggregated mean for a typical BRV time series (West, 2006a) is depicted. The points are calculated from the data and the solid curve is the best least-square fit to the processed BRV data and yields a fractal dimension D = 1.14 midway between the curve for a regular process (D = 1) and that for an uncorrelated random process (D = 1.5) as indicated by the dashed curves.
Such observations regarding the self-similar nature of breathing time series have been used in a medical setting to produce a revolutionary way of utilizing mechanical ventilators. Historically ventilators have been used to facilitate breathing after an operation and have a built-in frequency of ventilation. The single-frequency ventilator design has recently been challenged by Mutch et al. (2000), who have used an inverse power-law spectrum of respiratory rate to drive a variable ventilator. They demonstrated that this way of supporting breathing produces an increase in arterial oxygenation over that produced by conventional control-mode ventilators. This comparison indicates that the fractal variability in breathing is not the result of happenstance, but is an important property of respiration. A reduction in variability of breathing reduces the overall efficiency of the respiratory system.
Altemeier et al. (2000) measured the fractal characteristics of ventilation and determined that not only are local ventilation and perfusion highly correlated, but they scale as well. Finally, Peng et al. (2002) analyzed the BRV time series for 40 healthy adults and found that under supine, resting, and spontaneous breathing conditions, the time series scale. This result implies that human BRV time series have: “long-range (fractal) correlations across multiple time scales.”
Another exemplar of the many fractal time series is that for walking. Applying the allometric aggregation approach to stride rate variability (SRV) time series (West and Griffin, 1998, 1999; Griffin et al., 2000) determines the scaling index as shown in Figure 4. Note the similarity of these last three figures. So, as in the cases of HRV and BRV time series, we again find an erratic physiological time series to represent a random fractal process (West, 2006b). In the SRV context, the implied clustering indicated by a slope greater than the random dashed line means that the intervals between strides change in clusters and not in a uniform manner over time. This result suggests that the walker does not smoothly adjust his/her stride from step to step. Rather, there are a number of steps over which adjustments are made followed by a number of steps over which the changes in stride are completely random. The number of steps in the adjustment process and the number of steps between adjustment periods are not independent. The results of a substantial number of stride interval experiments support the universality of this interpretation.
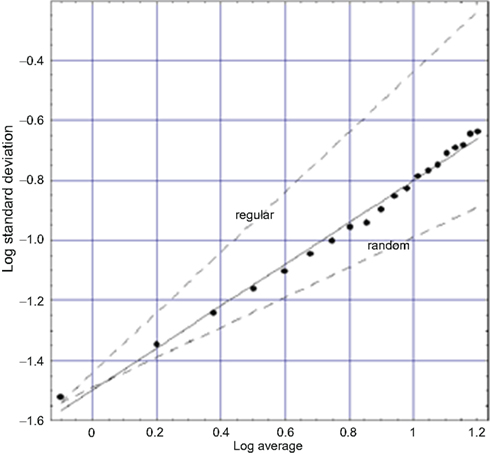
Figure 4. A fit to logarithm of the aggregated standard deviation versus the logarithm of the aggregated mean of SRV data for a typical walker (West, 2006a) is depicted. The points are calculated from the data and the solid curve is the best least-square fit to the processed SRV data and yields a fractal dimension D = 1.3 midway between the curve for a regular process (D = 1) and that for an uncorrelated random process (D = 1.5) as indicated by the dashed curves.
The SRV time series for sixteen healthy adults were downloaded from PhysioNet and the allometric aggregation approach carried out. Each of the curves looked more or less like that in Figure 4, with the experimental curve being closer to the indicated regular or the random limits (dashed curves). On average the 16 individuals have fractal dimensions for gait in the interval 1.2 ≤ D ≤ 1.3 (West and Griffin, 2003). The fractal dimension obtained from the analysis of an entirely different dataset, obtained using a completely different protocol, yields consistent results (Jordan et al., 2006). The narrowness of the interval around the fractal dimension suggests that this quantity may be a good quantitative measure of an individual’s dynamical variability. We suggest the use of the fractal dimension as a quantitative measure of how well the motor control system is doing in regulating locomotion. Furthermore, excursions outside the narrow interval of fractal dimension values for apparently healthy individuals may be indicative of hidden pathologies.
It should not go unnoticed that people use pretty much the same control system when they are standing still, maintaining balance, as they do when they are walking. This observation would lead one to suspect that the body’s slight movements around the center of mass of the body, would have the same statistical behavior as that observed during walking. These tiny movements are called postural sway in the literature and have been interpreted using random walks (Collins and DeLuca, 1994). It has been determined that postural sway may well be chaotic (Blaszczyk and Klonowski, 2001), so one might expect that there exists a relatively simple dynamical model for balance regulation that can be used in medical diagnosis. Here again fractal dynamics can be determined from the scaling properties of postural sway time series and it is determined that a decrease of postural stability is accompanied by an increase of fractal dimension. Consequently, it has been conjectured that the control of human movement and postural behaviors occurs as a scaling process (Hong et al., 2006).
Control of Variability
The physiological time series processed in the previous section clearly show that the complex phenomena supporting life, although they may appear to be random, do in fact scale in time and therefore contain information about the underlying dynamic process. This scaling indicates that the fluctuations that occur on multiple time scales are tied together and the way we understand such interdependency in the physical sciences is through underlying mechanisms that are coupled one to the other. This coupling is typically done through the equations of motion governing the dynamical description of the process. Unfortunately we generally do not have available such dynamic equations to describe physiologic phenomena. Therefore we must take a more phenomenological approach and develop mathematical models to explain the patterns in the data based on heuristic reasoning.
The individual mechanisms giving rise to the observed statistical properties in physiological networks are very different, so we do not attempt to find a common source to explain the observed scaling in walking, breathing, thinking, and the heart beating. On the other hand, the physiological time series in each of these phenomena scale in the same mathematical way; they have 1/f variability, so that at a certain level of abstraction the separate mechanisms cease to be important and only the relations matter and not those things being related. Consider that traditionally such relations have been assumed to be linear, and their control was assumed to be in direct proportion to the disturbance through negative feedback. Classical control theory has been the backbone of homeostasis, but it is not sufficient to describe the full range of variability in HRV, SRV, and BRV time series, and the variability in other physiologic networks, since it cannot explain how the statistics of these time series become fractal, or how the fractal dimension changes over time (West and Deering, 1994; Ivanov et al., 1998; West et al., 2008).
The issue we address in this section is control of variability. Such control is one of the goals of medicine, in particular, understanding and controlling physiological networks in order to insure their proper operation. We distinguish between homeostatic control and allometric control; the former is familiar and has a negative feedback character, which is both local and rapid; the latter is a relatively new concept that can take into account long-time memory (West, 2009). The long-time memory is manifest in correlations that are inverse power law in time, as well as, long-range interactions in complex phenomena as manifest by inverse power-law distributions in the network variable. Allometric control introduces the fractal character into otherwise featureless random time series to enhance the robustness of physiological networks. We introduce the fractional calculus as one way to describe the control of physiologic networks (West and Griffin, 2003).
It is not only a new kind of control that is suggested by the scaling of physiologic time series. Scaling also suggests that the historical notion of disease, which has the loss of regularity at its core, is inadequate for the treatment of dynamical diseases. Instead of loss of regularity, we identify the loss of variability with disease (Goldberger et al., 1990), so that disease not only changes average measures, such as heart rate, which it does in late stages, but is manifest in changes in HRV at very early stages. Loss of variability implies a loss of physiologic control and this loss of control is reflected in the changing of the scaling index of the corresponding time series (Mutch and Lefevre, 2003; West and Griffin, 2003), that is, in the change of fractal dimension.
The well-being of the body’s network of networks is measured by the fractal scaling properties of the various dynamic networks and such scaling determines how well the overall harmony is maintained. Once the perspective that disease is the loss of variability (complexity) has been adopted the strategies presently used for combating disease must be critically examined. For example, recent experiments (Yu et al., 2005) show a preference in the response of physiologic networks to 1/f signals over that of white noise indicating a sensitivity of physiologic networks to scaling control.
Fractional Random Walks and Scaling
Let us begin the discussion of the dynamics of fractals with a brief review of the formal generation of discrete time series. We define the variable of interest as Xj where j = 0,1,2,… indexes the time step. In the simplest random walk model a random step is taken in each increment of time and for convenience we set the time increment to 1. The shift operator B lowers the index by one unit such that

so that a simple random walk can be formally written

where ξj is +1 or −1 and the choice of values is made by flipping a coin. The solution to the discrete Eq. 15 is given by the position of the walker after N steps, the sum over the sequence of steps

The total number of steps N can be interpreted as the total time t over which the walk unfolds, since we have set the time increment to 1. Note that Eq. 16 is also equivalent to coarse graining a sequence of discrete measurements by aggregating the data. For N sufficiently large the sum in Eq. 16 can be replaced by an integral and the central limit theorem proves that the statistics of the dynamic variable X(t) are Gaussian. Consequently such sums of empirical data are often assumed to be Gaussian when closer analysis shows they are not. This is not a contradiction because the real world often does not satisfy the assumptions necessary for the proofs of mathematical theorems.
In the simple random walk the steps are statistically independent of one another. The most direct generalization of this model is to make each step dependent on the preceding steps in such a way that the second moment of the walker displacement is

The brackets in Eq. 17 denote an average over an ensemble of realizations of the walk, D is the strength of the fluctuations (diffusion coefficient) and when H ≠ 1/2 the underlying process is called anomalous diffusion in the physics literature (West and Deering, 1994). A value of H < 1/2 is interpreted as an anti-persistent process in which case a random step in one direction is preferentially followed by a reversal of direction. A value of H > 1/2 is interpreted as a persistent process in which case a random step in one direction is preferentially followed by another step in the same direction. A value of H = 1/2 is interpreted as the random walk model of classical diffusion in which case the steps are statistically independent of one another (West, 1999).
One way of introducing long-term memory into a random walk model is by means of fractional differences. Following Hosking (1982) we define a fractional difference process as

and the exponent α is not an integer. As it stands Eq. 18 is just a formal definition without physiologic content to make it interesting. To make this equation usable we must determine how to represent the operator acting on Xj as reviewed by West (1999) to obtain the formal solution

A formulation of this process in terms of fractional autoregressive integrated moving average models (FARIMA) applied to temporal physiologic signals yields similar results (Eke et al., 2002). The solution to the fractional random walk is clearly dependent on fluctuations that have occurred in the remote past; note the time lag k in the index on the fluctuations in Eq. 19 and the fact that it can be arbitrarily large. The extent of the influence of these distant fluctuations on the present time network response is determined by the relative size of the coefficients in the series. Using Stirling’s approximation on the gamma functions determines the size of the coefficients in Eq. 19 as the fluctuations recede into the past, that is, as k → ∞

since k >> α. Thus, the strength of the contributions to Eq. 20 decreases with increasing time lag as an inverse power law in the time lag as long as α < 1. The spectrum of the time series (Eq. 20) is obtained in the low-frequency limit to be (West, 1999)

where unlike the white noise spectrum that is flat, the fractal walk spectrum is inverse power law.
Thus, since the fractional-difference dynamics are linear the network response is Gaussian and from these analytic results we conclude that Xj is analogous to fractional Gaussian noise. The analogy is complete if we set α = H − 1/2 so that the spectrum (Eq. 21) can be expressed as

Taking the inverse discrete Fourier transform of the exact expression for the spectrum yields the correlation coefficient (West, 1999)
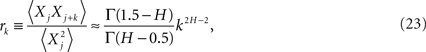
as the lag time increases without limit. It is clear that for the power-law index in the interval 1 ≥ H ≥ 1/2 then both the spectrum and the correlation coefficient are inverse power law.
The probability density function (pdf) for the fractional-difference diffusion process in the continuum limit satisfies the scaling condition

where δ = H = α − 1/2. The manifestation of complexity is indicated by two distinct quantities. The first indicator of complexity is the scaling parameter δ departing from the familiar value δ = 0.5, which it would have for a simple diffusion process. But for fractional diffusive motion considered here the value of the scaling index can be quite different. A second indicator of complexity is the function F(·) in Eq. 24 departing from the conventional Gaussian form, although in the argument presented so far it does not.
The scaling index δ is usually determined by calculating the second moment of a time series. This method of analysis is reasonable only when F(y) has the Gaussian form, or some other distribution with a finite second moment, that is, the process is a member of the FVSM class. If the scaling condition (Eq. 24) is realized it is convenient to measure the scaling parameter δ by the method of diffusion entropy analysis (DEA, Scafetta and Grigolini, 2002) that, in principle, works independently of whether the second moment is finite or not. The DEA method affords many advantages, including that of being totally independent of a constant bias.
Fractional Rates
Fractal functions often describe complex phenomena characterized by fractal time series. Such functions are known to have divergent integer-valued derivatives, and consequently traditional control theory, involving integer-valued differentials and integrals, cannot be used to determine feedback in fractal phenomena. However a fractional operator of order α acting on a fractal function of fractal dimension D yields a new fractal function with fractal dimension D + α, where α > 0 for a derivative and α < 0 for an integral. Therefore it seems reasonable that one strategy for modeling the dynamics and control of complex physiologic phenomena is through the application of the fractional calculus (West, 2009). The fractional calculus has been used to model the interdependence, organization and concinnity of complex phenomena ranging from the vestibulo-oculomotor system, to the electrical impedance of biological tissue to the biomechanical behavior of physiologic organs, see, for example Magin (2006) for an excellent review of these applications and many more. Such descriptions can also be obtained from the continuum limit of the fractional difference equations of the previous section.
We can relate the allometric aggregation approach to this recently developed branch of control theory involving the fractional calculus. The generalization of control theory to include fractional operators enables the designer to take into account memory and hereditary properties that are traditionally neglected in integer-order control theory (Podlubny, 1999), such as in traditional homeostasis. A fractional time integral is defined (West et al., 2003a; West, 2006b)
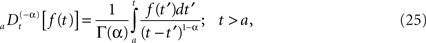
and the corresponding fractional time derivative is defined
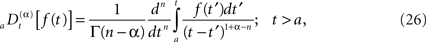
where [α] + 1 ≥ n ≥ [α] and the bracket denotes the integer value n closest to α. Consequently for α < 1 we have n = 0 and Eq. 25 is the Riemann–Liouville (RL) formula for the fractional integral operator when α > 0 and Eq. 26 is the corresponding RL-fractional-differential operator.
Fractional Langevin equation
Of course, the fractional calculus does not in itself constitute a physical/biological theory, but requires such a theory in order to interpret the fractional derivatives and integrals in terms of physical/biological phenomena (West et al., 2003a). For example how is the negative feedback, so central to homeostasis, included in the fractional calculus modeling? The generalization of a relaxation equation to fractional form is given by (Nonnenmacher and Metzler, 1995)
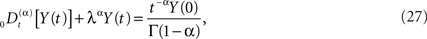
and the initial value becomes an inhomogeneous term in this fractional relaxation equation of motion. Note that the dissipation parameter is positive definite and is λα has the same units as the fractional derivative. Equations of the form (Eq. 27) are mathematically well defined, and strategies for solving such equations have been developed by a number of investigators, particularly the book by Miller and Ross (1993) that is devoted almost exclusively to solving such equations when the index is rational. Here we allow α to be irrational and consider the Laplace transform of Eq. 27 to obtain

whose inverse Laplace transform is the solution to the fractional-differential equation. Nonnenmacher and Metzler (1995) inverted the Laplace transform in Eq. 28 using Fox functions. The solution to the initial value problem for the fractional relaxation equation is given by the series for the standard Mittag-Leffler function (MLF)
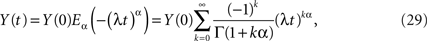
which in the limit α → 1 yields the exponential function
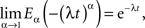
as it should, since under this condition Eq. 27 reduces to the usual relaxation rate equation. Note that in this limit the initial value term on the rhs of Eq. 27 vanishes because the gamma function of zero diverges.
The MLF has interesting properties in both the short-time and the long-time limits. In the short-time limit it yields the Kohlrausch–Williams–Watts Law from stress relaxation in rheology (West et al., 2003a) given by

also known as the stretched exponential. In the long-time limit it yields the inverse power law, known as the Nutting Law (West et al., 2003a),

clearly an inverse power law in time. Figure 5 displays the MLF as well as its two asymptotes, the dashed curve being the stretched exponential and the dotted curve the inverse power law. What is apparent from this figure is that the long-time memory associated with fractional relaxation processes is inverse power law rather than being the exponential of ordinary relaxation. The MLF smoothly joins these two empirically determined asymptotic distributions.
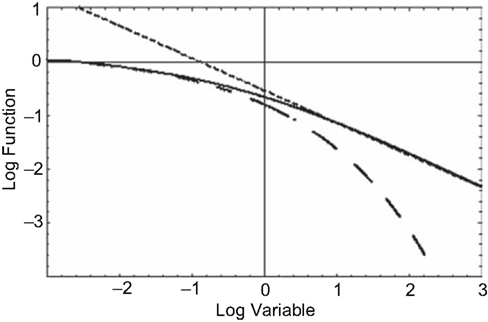
Figure 5. The solid curve is the MLF, the solution to the fractional relaxation equation (Eq. 29). The dashed curve (Eq. 30) is the stretched exponential (Kohlrausch–Williams–Watts Law) and the dotted curve (Eq. 31) is the inverse power law (Nutting Law).
We can now generalize the fractional-differential equation to include a random force ξ(t) and in this way obtain a fractional stochastic differential equation, such as we did in the last section. In physics nomenclature such a fractional stochastic differential equation is a called a fractional Langevin equation (West et al., 2003a)
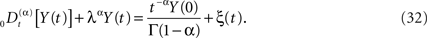
The average response of the network is given by the fractional relaxation equation for a random force that is zero-centered, which is to say, by averaging over Eq. 32 we obtain Eq. 27 for the average network response. The solution to Eq. 32 is obtained using Laplace transforms as done previously

Note the difference in the s-dependence of the two coefficients of the rhs of Eq. 33. The inverse Laplace transform of the first term yields the MLF as found for the homogeneous fractional relaxation equation, whereas the inverse Laplace transform of the second term is the convolution of the random force and a stationary kernel. The stationary kernel is given by the series (West et al., 2003a)
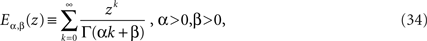
which is a generalized MLF. The function defined by Eq. 34 reduces to the usual MLF when β = 1, so that both the homogeneous and inhomogeneous terms in the solution to the fractional Langevin equation can be expressed in terms of these series.
The explicit inverse of Eq. 33 yields the solution (West et al., 2003a)
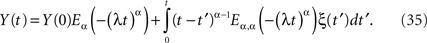
In the case α = 1, the MLF becomes the exponential, so that the solution to the fractional Langevin equation reduces to that for an Ornstein–Uhlenbeck process
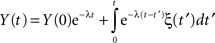
as it should. The analysis of the autocorrelation function of Eq. 35 can be quite daunting and so we do not pursue it further here, but refer the reader to the literature (Kobelev and Romanov, 2000; West et al., 2003a). However it is useful to point out that Eq. 35 is the kind of formal expression that is necessary to investigate when the physiologic phenomenon is not stationary.
Monofractal solutions
A somewhat simpler problem than Eq. 32 is the fractional Langevin equation without dissipation, that is, the solution to the fractional-dynamic stochastic equation with λ = 0. The solution to this equation expressed in terms of the fractional integral is
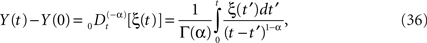
and the kernel can also be interpreted as a filter. Here we see that if the stochastic driver has fractal Gaussian statistics it scales as

which for a Wiener process would have h = 1/2, but for a more general fractal statistical process 1 ≥ h > 0. This property can be used to express the scaled-time solution to the fractional-dynamical equation as
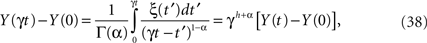
which given its linear form also has Gaussian statistics. Using the strategy of writing the scaling parameter as γ = 1/t we can express the solution (Eq. 38) in the scaling form

so that the second moment can be expressed as
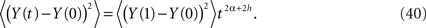
The time-dependence of the second moment (Eq. 40) agrees with that obtained for anomalous diffusion where we identify H = α + h. If the stochastic force is that of classical diffusion, that is, h = 1/2 and 1 ≥ H > 0 then the interval of values for the fractional operator in Eq. 36 is given by −1/2 ≤ α ≤ 1/2. Consequently the process described by the dissipation-free fractional Langevin equation can cover the full range of values 1 ≥ H > 0.
The interval 1/2 ≥ H > 0 has in the past been interpreted in terms of an anti-persistent random walk. An anti-persistent explanation of time series was made by Peng et al., (1993). for the differences in time intervals between heart beats. They interpreted their time series, as did a number of subsequent investigators, in terms of random walks with H < 1/2. In this model the anti-persistent behavior lead to an avoidance of the extremes, so that the time intervals did not become too large nor too small. However, we can see from Eq. 40 that the fractional Langevin equation without dissipation is an equivalent description of the underlying dynamics. The scaling behavior alone cannot distinguish between these two models, what is needed is a complete statistical distribution and not just the time-dependence (scaling behavior) of the central moments.
There are a number of ways to test the interpretation of the scaling behavior observed in Eq. 40. Podlubny (1999 showed that if reality has the dynamics of a fractional-differential equation, then attempting to control it with an integer-order feedback leads to extremely slow convergence, if not divergence, of the network output. On the other hand, a fractional-order feedback, with the indices appropriately chosen, leads to rapid convergence of output to the desired signal. Thus, we anticipate that dynamic physiologic networks with scaling properties, because they can be described by fractional dynamics, would have fractional-differential, which is to say, allometric controls (West, 2009).
Mulifractal solutions
The solution to the fractional Langevin equation (Eq. 37) is monofractal if the fluctuations are monofractal, which is to say, the time series given by the trajectory Y(t) is a fractal random process if the random force is a fractal random process. However, the model presented is not adequate as it stands for describing multifractal statistical processes. A number of investigators have recently developed multifractal random walk models to account for the multiple fractal character of various physiological phenomena and here we introduce a variant of those discussions based on the fractional calculus. The most recent generalization of the Langevin equation incorporates memory into the network’s dynamics and has the simple form of Eq. 33 with the dissipation parameter set to 0. Equation 37 could also be obtained from the construction of a fractional Langevin equation by Lutz (2001) for a free particle coupled to a fractal heat bath, when the inertial terms is negligible. The analysis of the previous section provides us with Eq. 40 as the starting point for the present discussion.
One way to make the solution to the fractional Langevin equation a multifractal is to assume that the parameter η = 1 − α in the kernel of Eq. 36 is a random variable. To construct the traditional measures of multifractal stochastic processes we calculate the qth moment of the solution (Eq. 40) by averaging over both the random force ξ(t) and the random parameter η to obtain
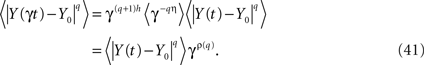
The scaling relation in Eq. 41 determines the qth order structure function exponent ρ(q). Note that if ρ(q) is linear in q the underlying process is monofractal, whereas, when it is nonlinear in q the process is multifractal. We can relate the structure function to the mass exponent (Rajagopalon and Tarboton, 1993)

Consequently we have that ρ(0) = h so that τ(0) = 2 − h, as it should because of the well known relation between the fractal dimension and the global Hurst exponent D0 = 2 − H.
A monofractal time series is characterized by a single fractal dimension. In general, time series have a local Hölder exponent h that varies over the course of the trajectory and is related to the fractal dimension by D = 2 − h (Falconer, 1990). Note that for an infinitely long time series the Hölder exponent h and the Hurst exponent H are identical, however, for a time series of finite length they need not be the same. We stress that the fractal dimension and the Hölder exponent are local quantities, whereas the Hurst exponent is a global quantity, consequently the relation D = 2 − H is only true for an infinitely long time series. The function f(h), called the multifractal or singularity spectrum, describes how the local Hölder (fractal) exponents contribute to such time series. Here h and f are independent variables, as are q and τ. The general formalism of Legendre transform pairs interrelates these two sets of variables by the relation (Feder, 1988),

The local Hölder exponent h varies with the q-dependent mass exponent through the equality

so the singularity spectrum can be written as

where the mass exponent τ(q) and its derivative are determined by data or from theory as in Eq. 42.
To determine the mass exponent in Eq. 45 we assume the statistics of the parameter μ are generated by a stable Lévy process with index β the structure function exponent can be shown to be (Feder, 1988)

Therefore the solution to the fractional Langevin equation corresponds to a monofractal process only in the case β = 1 and q > 0, otherwise the process is multifractal. We restrict the remaining discussion to positive moments.
Thus, we observe that when the exponent in the memory kernel in the fractional Langevin equation is random, the solution consists of the product of two random quantities giving rise to a multifractal process. We apply this approach to the SRV time series data previously discussed and observe, for the statistics of the multiplicative exponent given by Lévy statistics, the singularity spectrum as a function of the positive moments shown by the points in Figure 6. The solid curve in this figure is obtained from the analytic form of the singularity spectrum

which is determined by substituting Eq. 46 into the equation for the singularity spectrum (Eq. 45), through the relationship between exponents (Eq. 42). It is clear from Figure 6 that the data are well fit by the solution to the fractional Langevin equation with the parameter values β = 1.45 and b = 0.1, obtained through a mean-square fit of Eq. 47 to the SRV time series data.
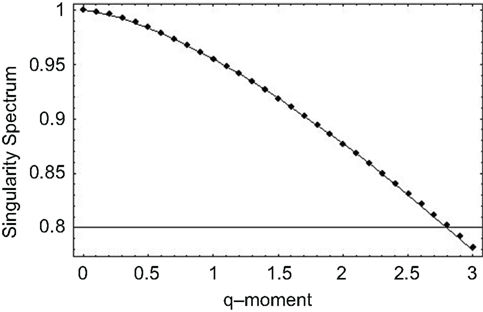
Figure 6. The singularity spectrum for q > 0 obtained through the numerical fit to the human gait data. The curve is the average over the ten data sets obtained in the experiment (Peng et al., 1993).
The nonlinear form of the mass exponent obtained from the fit in Figure 6 is evidence that the inter-stride interval time series are multifractal. This analysis is further supported by the fact that the maxima of the singularity spectra coincide with the fractal dimensions determined using the scaling properties of the time series using the allometric aggregation approach.
Of course, different physiologic processes generate different fractal time series, because the long-time memory of the underlying dynamical processes can be quite different. Physiological signals, such as cerebral blood flow (CBF), are typically generated by complex self-regulatory systems that handle inputs with a broad range of characteristics. Ivanov et al. (1999) established that healthy human heartbeat intervals, rather than being fractal, exhibit multifractal properties and uncovered the loss of multifractality for a life-threatening condition of congestive heart failure. West et al. (2003b) similarly determined that CBF in healthy humans is also multifractal and this multifractality is severely narrowed for people who suffer from migraines.
Migraine headaches have been the bane of humanity for centuries, afflicting such notables as Caesar, Pascal, Kant, Beethoven, Chopin, and Napoleon. However, its etiology and pathomechanism have to date not been satisfactorily explained. It was demonstrated (West et al., 2003b) that the characteristics of CBF time series significantly differs between normal healthy individuals and migraineurs. Transcranial Doppler ultrasonography (TCD) enables high-resolution measurement of middle cerebral artery blood flow velocity. Like the HRV, SRV, and BRV time series data, the time series of CBF velocity consists of a sequence of waveforms. These waveforms are influenced by a complex feedback system involving a number of variables, such as arterial pressure, cerebral vascular resistance, plasma viscosity, arterial oxygen, and carbon dioxide content, as well as other factors. Even though the TCD technique does not allow us to directly determine CBF values, it helps clarify the nature and role of vascular abnormalities associated with migraine.
The dynamical aspects of CBF regulation were recognized by Zhang et al. (1999). Rossitti and Stephensen (1994) used the relative dispersion, the ratio of the standard deviation to mean, of the middle cerebral artery flow velocity time series to reveal its fractal nature; a technique closely related to the allometric aggregation approach. West et al. (1999b) extended this line or research by taking into account the more general properties of fractal time series, showing that the beat-to-beat variability in the flow velocity has a long-time memory and is persistent with the average scaling exponent 0.85 ± 0.04, a value consistent with that found earlier for HRV time series. They also observed that CBF was multifractal in nature.
In Figure 7 we compare the multifractal spectrum for middle cerebral artery blood flow velocity time series for a healthy group of five subjects and a group of eight migraineurs (West et al., 2003b). A significant change in the multifractal properties of the blood flow time series is apparent. Namely, the interval for the multifractal distribution on the local scaling exponent is greatly constricted. This is reflected in the small value of the width of the multifractal spectrum for the migraineurs 0.013, which is almost three times smaller than the width for the control group 0.038 for both migraineurs with and without aura the distributions are centered at 0.81, the same as that of the control group, so the average scaling behavior would appear to be the same.
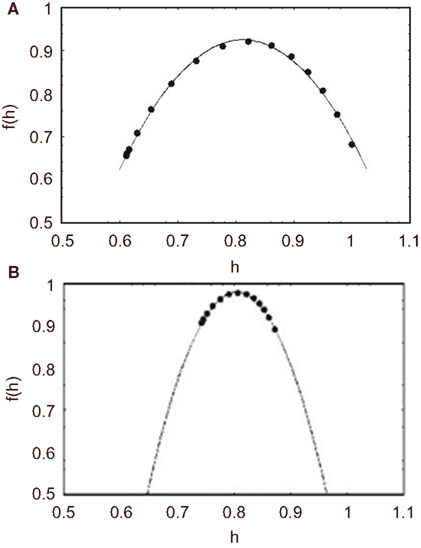
Figure 7. The average multifractal spectrum for middle CBF time series is depicted by f(h). (A) The spectrum is the average of ten time series measurements from five healthy subjects (filled circles). The solid curve is the best least-squares fit of the parameters to the predicted spectrum using Eq. 48. (B) The spectrum is the average of 14 time series measurements of eight migraineurs (filled circles). The solid curve is the best least-squares fit to the predicted spectrum using Eq. 48.
However, the contraction of the spectrum for migraineurs suggests that the underlying process has lost its flexibility. The biological advantage of multifractal processes is that they are highly adaptive, so that in this case the brain of a healthy individual adapts to the multifractality of the inter-beat interval time series. Here again we see that disease, in this case migraine, may be associated with the loss of complexity and consequently the loss of adaptability, thereby suppressing the normal multifractality of CBF time series. Thus, the reduction in the width of the multifractal spectrum is the result of excessive dampening of the CBF fluctuations and is the manifestation of the significant loss of adaptability and overall hyperexcitability of the underlying regulation system. West et al. (2003b) emphasize that hyperexcitability of the CBF control system seems to be physiologically consistent with the reduced activation level of cortical neurons observed in some transcranial magnetic simulation and evoked potential studies.
Regulation of CBF is a complex dynamical process and remains relatively constant over a wide range of perfusion pressure via a variety of feedback control mechanisms, such as metabolic, myogenic, and neurally mediated changes in cerebrovascular impedance response to changes in perfusion pressure. The contribution to the overall CBF regulation by different areas of the brain is modeled by the statistics of the fractional derivative parameter, which determines the multifractal nature of the time series. The source of the multifractality is over and above that produced by the cardiovascular system.
The multifractal nature of CBF time series is here modeled using a fractional Langevin model. We again implement the scaling properties of the random force and the memory kernel to obtain Eq. 41 as the scaling of the solution to the fractional Langevin equation. Here when we calculate the qth moment of the solution we assume Gaussian, rather than the more general Lévy statistics. Consequently we obtain the quadratic function for the singularity spectrum

which can be obtained from Eq. 47 by setting β = 2. Another way to express Eq. 48 is

where we have used the fact that the fractal dimension is given by 2 − H, which is the value of the function at h = H.
It seems that the changes in the cerebral autoregulation associated with migraine can strongly modify the multifractality of middle cerebral artery blood flow. The constriction of the multifractal to monofractal behavior of the blood flow depends on the statistics of the fractional derivative index. As the distribution of this parameter narrows down to a delta function, the nonlocal influence of the mechanoreceptor constriction disappears. On the other hand, the cerebral autoregulation does not modify the monofractal properties characterized by the single global Hurst exponent, presumably that produced by the cardiovascular system.
Conclusions and Summary
We now draw a number of conclusions. First of all, physiologic time series are often erratic and have scaling properties. The second moment is determined to scale algebraically in time, the autocorrelation function is found to be an inverse power law in time and the power spectrum is an inverse power law in frequency. The power-law nature of these second-order measures is the signature of fractal random processes. So we surmise that HRV is a fractal random point process, as are SRV and BRV, among dozens of other complex physiologic phenomena. Consequently, the dynamics of traditional stochastic processes described by differential equations for the dynamic variables, or in phase space for the probability densities, are not sufficient to describe the properties of complex physiologic networks. The fractional calculus can describe at least one class of complex phenomena for which other, more traditional, methods do not suffice. As mentioned the fractional calculus has been used to model the interlinking of elements and harmony of complex phenomena ranging from the electrical impedance of biological tissue to the biomechanical behavior of physiologic organs; see, for example, Magin (2006) for an excellent review of such applications.
The empirical evidence supports the interpretation that physiologic time series are described by fractal stochastic networks. Furthermore, the fractal nature of these time series is not constant but may change with the vagaries of the interaction of the network with its environment and internal dynamics; therefore, physiologic phenomena are often weakly multifractal. The scaling index or fractal dimension marks a physiologic network’s response and can be used as an indicator of the state of health.
We reiterate that controlling physiological networks in order to ensure their proper operation is one of the goals of medicine. We have emphasized the difference between homeostatic and allometric control. Homeostatic control is familiar and has as its basis a negative feedback character, which is both local and relatively fast. Allometric control, on the other hand, can take into account long-time memory, correlations that are inverse power law in time, as well as long-range interactions in complex phenomena as manifest by inverse power-law distributions in network variables. An allometric control network achieves its purpose through scaling, enabling a complex network such as one performing physiologic regulation to be adaptive and accomplish concinnity of its many interacting subnetworks. Allometric control is a generalization of the idea of feedback regulation implicit in homeostasis. The basic notion is to take part of the network’s output and feed it back into the input, thus making the network self-regulating by minimizing the difference between the input and the sampled output. More complex networks, such as autoregulation of the heartbeat variation, human gait variability, and cognition have more intricate feedback arrangements. In particular, because each sensor responds to its own characteristic set of frequencies, the feedback control must carry signals appropriate to each of the interacting subnetworks. The coordination of the individual responses of the separate subnetworks is manifest in the scaling of the time series in the output and the separate subnetworks select that aspect of the feedback to which they are the most sensitive. In this way an allometric control network not only regulates, but also adapts to changing environmental and biophysical conditions.
It is not merely a new kind of control that is suggested by the scaling of physiologic time series. Scaling also implies that the historical notion of disease, which has the loss of regularity at its core, is inadequate for the treatment of dynamical diseases. Instead of loss of regularity, the loss of variability is identified with disease, so that a disease not only changes an average measure, such as heart rate or breathing rate, but is manifest in changes in variability at very early stages. Loss of variability implies a loss of physiologic control, and this loss of control is reflected in the change of fractal dimension, that is, in the scaling index of the corresponding time series. The change in fractal dimension with age and with disease suggested the new definition of disease as a loss of complexity, rather than the loss of regularity (Goldberger et al., 1990; West, 1990, 2009; Van Orden et al., 2005). However this new definition has not been universally embraced (Shiau, 2008).
The well-being of the body’s network of networks is measured by the fractal scaling properties of the various dynamic networks, and such scaling determines how well the overall harmony is maintained. Once the perspective that disease is the loss of complexity has been adopted, the strategies presently used in combating disease must be critically examined. Life-support equipment is one such strategy, but the tradition of such life-support is to supply blood at the average rate of the beating heart, to ventilate the lungs at their average rate, and so on. So how does the new perspective regarding disease influence the traditional approaches to assisting the healing of the body?
Alan Mutch applied the lessons of fractal physiology to point out that blood flow and ventilation are delivered in a fractal manner in both space and time in a healthy body.
However, he argues, during critical illness, conventional life-support devices deliver respiratory gases by mechanical ventilation or blood by cardiopulmonary bypass pump in a monotonously periodic fashion. This periodic driving overrides the natural aperiodic operation of the body. Mutch speculates that these devices result in the loss of normal fractal transmission and, consequently, life support winds up doing more damage the longer it is required and becomes more problematic the sicker the patient (Mutch et al., 2000). In this perspective, the loss of complexity is the loss of the body as a cohesive whole; the body can be reduced to a disconnected set of organ systems.
One of the traditional views of disease is what Tim Buchman calls the “fix-the-number” imperative (Buchman, 2006). He argues that if the bicarbonate level is low, then give bicarbonate; if the urine output is low, then administer a diuretic; if the bleeding patient has a sinking blood pressure, then make the blood pressure normal. He goes on to say that such interventions are commonly ineffective and even harmful. For example, sepsis, which is a common predecessor of multiple organ dysfunction syndrome (MODS), is often accompanied by hypocalcemia; in controlled experimental conditions, administering calcium to normalize the laboratory value increases mortality. Consequently, one’s first choice of options, based on an assumed simple linear homeostatic relationship between input and output, is probably wrong and a more circumspective intervention based on a fractal perspective is warranted.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Altemeier, W. A., McKinney, S., and Glenny, R. W. (2000). Fractal nature of regional ventilation distribution. J. Appl. Physiol. 88, 1551–1557.
Alvarez-Ramirez, J., Ibarra-Valdez, C., Rodriguez, E., and Dagdug, E. (2008). 1/f Noise structures in Pollocks’s drip paintings star, open. Physica A 387, 281–295.
Barenblatt, G. I. (1994). Scaling Phenomena in Fluid Mechanics. Cambridge: Cambridge University Press.
Bassingthwaighte, J. B., Liebovitch, L. S., and West, B. J. (1994). Fractal Physiology. New York: Oxford University Press.
Blaszczyk, J. W., and Klonowski, W. (2001). Postural stability and fractal dynamics. Acta Neurobiol. Exp. 61, 105–112.
Buchman, T. G. (2006). “Physiologic failure: multiple organ dysfunction syndrome,” in Complex Systems Science in BioMedicine, eds T. S. Deisboeck and S. A. Kauffman (New York: Kluwer Academic/Plenum Publishers), 631–640.
Collins, J. J., and DeLuca, C. J. (1994). Random walking during quiet standing. Phys. Rev. Lett. 73, 764–767.
Das, M., Gebber, G. L., Bauman, S. M., and Lewis, C. D. (2003). Fractal Properties of sympathetic nerve discharges. J. Neurophysiol. 89, 833–840.
Eke, A., Herman, P., Kocsis, L., and Kozak, L. R. (2002). Fractal characterization of complexity in temporal physiological signals. Physiol. Meas. 23, R1–R38.
Gao, J. B., Billock, V. A., Merk, I., Tung, W. W., White, K. D., Harris, J. G., and Roychowdhury, V. P. (2006). Inertia and memory in ambiguous visual perception. Cogn. Process 7, 105–112.
Goldberger, A. L., Rigney, D. R., and West, B. J. (1990). Chaos, fractals and physiology. Sci. Am. 262, 42–49.
Griffin, L., West, D. J., and West, B. J. (2000). Random stride intervals with memory. J. Biol. Phys. 26, 185–202.
Grigolini, P., Aquino, G., Bologna, M., Lukovic, M., and West, B. J. (2009). A theory of 1/f noise in human cognition. Physica A 388, 4192–4204.
Grizzi, F., and Chiriva-Internati, M. (2005). The complexity of anatomical systems. Theor. Biol. Med. Model. 2, 26.
Hausdorff, J. M., Peng, C. K., Ladin, Z., Wei, J. Y., and Goldberger, A. L. (1995). Is walking a random walk? Evidence for long-range correlations in stride interval of human gait. J. Appl. Physiol. 78, 349–358.
Hong, S. L., Bodfish, J. W., and Newell, K. M. (2006). Power-law scaling for macroscopic entropy and microscopic complexity: evidence from human movement and posture. Chaos 16, 013135.
Ivanov, P. C., Amaral, L. A. N., Goldberger, A. L., Havlin, S., Rosenblum, M. G., Struzik, A. R., and Stanley, H. E. (1999). Multifractality in human heartbeat dynamics. Nature 399, 461–465.
Ivanov, P. C., Amaral, L. A. N, Goldberger, A. L., and Stanley, H. E. (1998). Stochastic feedback and the regulation of biological rhythms. Europhys. Lett. 43, 363–368.
Jordan, K., Challis, J., and Newell, K. (2006). Long range correlations in the stride interval of running. Gait Posture 24, 120–125.
Kello, C. T., Beltz, C., Holden, J. G., and Van Orden, G. C. (2007). The emergent coordination of cognitive function. J. Exp. Psychol. Gen. 136, 551–568.
Kobelev, V., and Romanov, E. (2000). Fractional Langevin equation to describe anomalous diffusion. Prog. Theor. Phys. Suppl. 139, 470–476.
Liebovitch, L. S., and Krekora, P. (2002). “The physical basis of ion channel kinetics: the importance of dynamics,” in Institute for Mathematics and its Applications Volumes in Mathematics and Its Applications, Membrane Transport and Renal Physiology, Vol. 129, eds H. E. Layton and A. M. Weinstein (Berlin: Springer-Verlag), 27–52.
Magin, R. L. (2006). Fractional Calculus in Bioengineering. Redding, CT: Begell House Publishers, Co.
Meakin, P. (1998). Fractals, Scaling and Growth Far From Equilibrium. Cambridge Nonlinear Science Series 5. Cambridge, UK: Cambridge University Press.
Miller, K. S., and Ross, B. (1993). An Introduction to the Fractional Calculus and Fractional Differential Equations. New York: John Wiley.
Mutch, A., and Lefevre, G. R. (2003). Health, ‘small-worlds’, fractals and complex networks: an emerging field. Med. Sci. Monit. 9, MT55–MT59.
Mutch, W. A. C., Harm, S. H., Lefevre, G. R., Graham, M. R., Girling, L. G., and Kowalski, S. E. (2000). Biologically variable ventilation increases arterial oxygenation over that seen with positive end-expiratory pressure alone in a porcine model of acute respiratory distress syndrome. Crit. Care Med. 28, 2457–64.
Nonnenmacher, T. F., and Metzler, R. (1995). On the Riemann–Liouville fractional calculus and some recent applications. Fractals 3, 557.
Peng, C. K., Metus, J., Li, Y., Lee, C., Hausdorff, J. M., Stanley, H. E., Goldberger, A. L., and Lipsitz, L. A. (2002). Quantifying fractal dynamics of human respiration: age and gender effects. Ann. Biomed. Eng. 30, 683–692.
Peng, C. K., Mistus, J., Hausdorff, J. M., Havlin, S., Stanley, H. E., and Goldberger, A. L. (1993).“Long-range anticorrelations and non-Gaussian behavior of the heartbeat. Phys. Rev. Lett. 70, 1343–1346.
Pincus, S. M. (1994). Greater signal regularity may indicate increased system isolation. Math. Biosci. 122, 161.
Rajagopalon, B., and Tarboton, D. G. (1993). Understanding complexity in the structure of rainfall. Fractals 1, 6060.
Rossitti, S., and Stephensen, H. (1994). Temporal heterogeneity of the blood flow velocity at the middle cerebral artery in the normal human characterized by fractal analysis. Acta Physiol. Scand. 151, 191.
Roy, S., Mitra, I., and Llinas, R. (2008). Non-Markovian noise mediated through anomalous diffusion with ion channels. Phys. Rev. E 78, 041920.
Scafetta, N., and Grigolini, P. (2002). Scaling detection in time series: diffusion entropy analysis. Phys. Rev. E 66, 036130.
Schottky, W. (1918). Uber spontane Stromschwaukungen in verschiedenen Elektrizitattslei-tern. Ann. Phys. 362, 541–567.
Schrödinger, E. (1943). What is Life? The Physical Aspects of the Living Cell. London: Cambridge University Press.
Shiau, Y. (2008). “Detecting well-harmonized homeostasis in heart rate fluctuations,” in Proceedings of the 2008 International Conference on BioMedical Engineering and Informatics (Washington, DC: IEEE Computer Society), 399–403.
Stanley, H. E., Amaral, L. A. N., Goldberger, A. L., Havlin, S., Ivanov, P. C., and Peng, C.-K. (1999). Statistical physics and physiology: monofractal and multifractal approaches. Physica A 270, 309–324.
Suki, B., Alencar, A. M., Frey, U., Ivanov, P. C., Buldyrev. S. V., Majumdar, A., Stanley, H. E., Dawson, C. A., Krenz, G. S., and Mishima, M. (2003). Fluctuations, noise and scaling in the cardio-pulmonary system. Fluct. Noise Lett. 3, R1–R25.
Szeto, H. H., Cheng, P. Y., Decena, J. A., Chen, Y., Wu, Y., and Dwyer, G. (1992). Fractal properties of fetal breathing dynamics. Am. J. Physiol. Regul. Integr. Comp. Physiol. 263, R141–R147.
Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiolgy. (1996). Heart rate variability: standards of measurement, physiological interpretation, and clinical use. Eur. Heart J. 17, 354–381 (and references cited therein).
Taylor, L. R., and Taylor, R. A. J. (1977). Aggregation, migration and population mechanics. Nature 265, 415–421.
Taylor, L. R., and Woiwod, I. P. (1980). Temporal stability as a density-dependent species characteristic. J. Anim. Ecol. 49, 209–224.
Van Orden, G. C., Holden, J. G., and Turvey, M. T. (2005). Human cognition and 1/f scaling. J. Exp. Psychol. Gen. 134, 117–123.
West, B. J. (1990). Physiology in fractal dimension: error tolerance. Ann. Biomed. Eng. 18, 135–149.
West, B. J. (1999). Physiology, Promiscuity and Prophecy at the Millennium: A Tale of Tails. Singapore: World Scientific.
West, B. J. (2006b). Fractal physiology, complexity and the fractional calculus,” in Fractals, Diffusion and Relaxation in Disordered Complex Systems (Advances in Chemical Physics Series), eds. W. T. Coffey and Y. P. Kalmykov (New York: Wiley & Sons), 1–92.
West, B. J. (2009). “Control from an allometric perspective,” in Progress in Motor Control: A Multidisciplinary Perspective (Advances in Experimental Medicine and Biology), Vol. 629, ed. D. Sternad (New York: Springer), 57–82.
West, B. J., Bologna, M., and Grigolini, P. (2003a). Physics of Fractal Operators. New York: Springer.
West, B. J., Latka, M., Galaubic-Latka, M., and Latka, D. (2003b). Multifractality of cerebral blood flow. Physica A 318, 453–460.
West, B. J., Geneston, E. L., and Grigolini, P. (2008). Maximizing information exchange between complex networks. Phys. Rep. 468, 1–99.
West, B. J., and Deering, W. (1994). Fractal physiology for physicists: Lévy statistics. Phys. Rep. 246, 1–100.
West, B. J., and Griffin, L. (1999). Allometric control, inverse power laws and human gait. Chaos Solitons Fractals 10, 1519–1527.
West, B. J., and Griffin, L. (2003). Biodynamics: Why the Wirewalker Doesn’t Fall. New York: Wiley & Sons.
West, B. J., Novaes, M. N., and Kavcic, V. (1995). “Fractal probability density and EEF/ERP time series (Chapter 10),” in Fractal Geometry in Biological Systems, eds. P. M. Iannoccone and M. Khokha (Boca Raton: CRC), 267–316.
West, B. J., Zhang, R., Sanders, A. W., Miniyar, S., Zuckerman, J. H., and Levine, B. D. (1999a). Fractal fluctuations in cardiac time series. Physica A 270, 552–566.
West, B. J., Zhang, R., Sanders, A. W., Miniyar, S., Zuckerman, J. H., and Levine, B. D. (1999b). Fractal fluctuations in transcranial Doppler signals. Phys. Rev. E 59, 3492–3498.
West, G. B., Brown, J. H., and Enquist, B. J. (1997). A general model for the origin of allometric scaling in biology. Science 276, 122–128.
Willis, J. C. (1922). Age and Area: A Study in Geographical Distribution and Origin of Species. Cambridge: Cambridge University Press.
Keywords: fractals, fractional calculus, physiology, allometric control, power-law statistics
Citation: West BJ (2010) Fractal physiology and the fractional calculus: a perspective. Front. Physio. 1:12. doi: 10.3389/fphys.2010.00012
Received: 05 May 2010;
Paper pending published: 28 May 2010;
Accepted: 29 May 2010;
Published online: 14 October 2010
Edited by:
Gerhard Werner, University of Texas at Austin, USAReviewed by:
Ralf Metzler, Technical University of Munich, GermanyGerhard Werner, University of Texas at Austin, USA
Copyright: © 2010 West. This is an open-access article subject to an exclusive license agreement between the authors and the Frontiers Research Foundation, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Bruce J. West, Information Science Directorate, U.S. Army Research Office, Research Triangle Park, NC 27709, USA. e-mail:Yndlc3RAbmMucnIuY29t
