- 1 Istituto di Fisiologia Clinica del Consiglio Nazionale delle Ricerche, Pisa, Italy
- 2 Centro EXTREME, Scuola Superiore Sant’Anna, Pisa, Italy
- 3 Istituto di Scienza e Tecnologie dell’Informazione “A. Faedo” del Consiglio Nazionale delle Ricerche, Pisa, Italy
- 4 Dipartmento di Scienze Fisiologiche, Università di Pisa, Pisa, Italy
Resting-state EEG signals undergo rapid transition processes (RTPs) that glue otherwise stationary epochs. We study the fractal properties of RTPs in space and time, supporting the hypothesis that the brain works at a critical state. We discuss how the global intermittent dynamics of collective excitations is linked to mentation, namely non-constrained non-task-oriented mental activity.
Introduction
Neural processing is characterized by the phenomenon of integration, each neuron collecting input from many other neurons, and sending it to many others. The process of information spreading is of paramount complication, so that has been frequently taken as a paradigm of complexity. In fact, complexity, as is becoming clearer during the last two decades, is not a mere synonym of complication, since it also implies the notion of emergence: Many elements with non-linear interactions develop collective modes dominating the system’s dynamics.
This fact has been long known by physicist and is at the basis of the thermodynamic processes known as phase transitions. The equilibrium properties and the non-equilibrium dynamics of some collective observable may become independent of the underlying microscopic equations and, as function of some macroscopic parameter (such as temperature or energy), critical points exist marking the border between macroscopic determination and macroscopic indeterminacy. In other words, while below the critical points a single solution exists, above it multiple solutions are available. Therefore, above the critical point, as the system explores only one macroscopic solution, the entire collection of possible microscopic states of the alternative solutions remains unexplored. How does this happens? Approaching the critical point from below the macroscopic fluctuations around the equilibrium become larger, with more and more extended correlations both in space and time, till the correlation scales become infinite at the critical point. Above the point the solutions separate, and the system is said to become non-ergodic. Here the mathematical notion of infinity means that, for example, the fluctuation autocorrelation in time (or, equivalently the system relaxation after a large fluctuation) is no longer an exponential decay e−γt, with a finite (though becoming larger) scale 1/γ, but, at the critical point, follows a law characterized by scale invariance
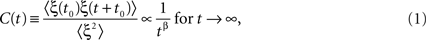
where ξ(t) is the fluctuation and averages 〈·〉 are taken on the different beginning-time values t0 This latter phenomenon is normally denoted as 1/f noise, or more specifically 1/fη noise, with η = 1 − β.
Coming back to brain activity, 1/f noise has been revealed by many authors, starting from Novikov et al. (1997). It is not yet determined if these highly correlated fluctuations are generated either by the oscillatory neural synchronization advocated by Medina (2009) or by the spontaneous phase-transition process of many interacting neurons proposed by Bianco et al. (2008), or by a yet to be uncovered complex dynamic processes. The phase-transition conjecture, dating back to the pioneering work of Turing (1957) fits the criticality condition stressed in the neurophysiological literature (see, e.g., Chialvo and Bak, 1999, or, more recently, Werner, 2009). Moreover, in the neurophysiological literature there is increasing conviction that brain dynamics are characterized by quakes (Martin, 2008) and/or avalanches (Beggs and Plenz, 2003; Plenz and Thiagarjan, 2007; Chialvo, 2008). All this literature supports the hypothesis of a critical brain, where inverse-power law correlations are present both in space and time.
Contoyiannis and Diakonos (2000) pointed out that the inverse-power law autocorrelations in critical systems (see, e.g., Stanley, 1971), correspond to an intermittent dynamics (as in Gaspard and Wang, 1988) driving the fluctuations of those macroscopic variables that integrate microscopic fluctuations. These are classically called “order parameters” since they highlight the emergence of collective behavior. Note that in the physical jargon intermittency means the dynamical activation/deactivation of metastable states, with entropy only increasing at the rapid transition from one metastable state to the next, so that the global entropy increase is kept small. This is important for living systems, and for complex systems in general, where by consensus the global entropy is smaller than it would if the system was at thermodynamic equilibrium. This is often expressed by the phrase “the whole is more than the sum of its parts”, which is the new paradigm of complexity, or, in other words the thumb-stone epigraph of last-century deterministic ideas in science.
We stress that not all inverse-power law indexes have the same properties. While they all fit the condition of emergence of collective states, with constrained dynamics, inverse-power law autocorrelation functions may be integrable or not, depending on the index β. Moreover, it is important to establish whether the system is intermittent. If this happens all properties, including the autocorrelation functions, only depend on the distribution of waiting times between events ψ(τ). In the case of Eq. 1 they also follow an inverse-power law

and the intermittency index μ is therefore an important measure of the complexity of the system. For non-ergodic systems, where 1 < μ < 3 a novel form of linear response have been recently discovered (Allegrini et al., 2007), suggesting a quenching for the response for systems with μ < 2 to regular stimuli (Sokolov and Klafter, 2007; Allegrini et al., 2009a), non-quenched information transfer for systems sharing the same or similar μ, with maximal information transfer for μ ≈ 2 (West et al., 2008). Remarkably, this is the intermittency index of human language (Allegrini et al., 2004).
In this paper we build on some recent discoveries reported in Allegrini et al. (2009b) within this context, namely that the transition processes from global metastable states is in fact intermittent, with, again, an intermittency index μ ≈ 2, the same of language. Herein we again focus on global metastable states and we corroborate the hypothesis of the brain working in a critical condition by studying a scale-invariant distribution of avalanche size, where the size is the number of EEG electrodes involved in the global intermittent process. We show however that different levels of complexity are reverberated in different regions of the brain, and that regions more prone to be recruited in global processes have an index similar to the index of the global process. In particular the electrodes most prone to be recruited in avalanches are those located in the central region, collecting electric signals from the two hemispheres. The above results lead us to link a specific EEG dynamical spatio-temporal structure to the behavioral process of mentation, namely the unstructured non-task-oriented mental activity that our set of subjects performed in our experiment, the same activity extensively studied at a metabolic level, by means of functional magnetic resonance imaging (fMRI) that has revealed a metabolic network maximally excited during resting-state mentation, and not involved in most task-oriented functions.
Materials and Methods
EEG Dataset Collection, Pre-Processing and Analysis
Thirty subjects, from 20 to 30 years old, underwent an EEG recording during a resting condition lasting 5 min. All subjects signed an informed consent according to the University of Pisa Ethical Committee guidelines. Experimental sessions were performed between 3 PM and 5 PM, while subjects were comfortably seated in an armchair in a semi-dark and sound-attenuated room. Before recordings started, it was demanded to each subject to stay still, with their eyes closed, and to avoid any structured thinking, like calculations or intentionally memories recalling.
A 32-channel acquisition systems has been used for the EEG recordings. Impedances of the recording electrodes were in the range of 2–5 kΩ, with a sampling rate of 500 Hz. All electrical potentials were reference to electrode FCz, placed slightly in front of the head vertex. EEG raw data were notch filtered at the line frequency (50 Hz) and then, in order to obtain unipolar recordings, re-referenced to the instantaneous average of the signals recorded from the earlobes. Reference electrode has been excluded from the analysis, together with two electrodes, placed at the earlobes. Movement artifacts were visually detected and discarded by an EEG-expert.
In addition to EEG signals, electrocardiogram (ECG) and electrooculogram (EOG) were recorded. While no significant ECG artifacts on EEG signals were observed, the EOG-related oscillations affecting the EEG, remarkably on the frontal channels, were removed applying the temporally constrained ICA algorithm (James and Gibson, 2003).
Rapid Transition Processes
We processed each EEG signal in order to unveil its hidden piecewise regular structure; namely, we looked for the abrupt changes in EEG amplitude that glue EEG signal segments with regular amplitude and wave shape. These points (events) were baptized rapid transition processes (RTPs) by Kaplan et al. (2005). Basically, we adopted the segmentation approach proposed by Kaplan et al. (2005). It is a non-parametric and adaptive approach since it identify RTPs on the basis of rules on local statistics of the signal around each point to be evaluated.
The segmentation algorithm can be partitioned in two main stages: (1) a preliminary identification of the RTPs; (2) a selection of the actual RTPs on the basis of the steepness of the previously detected EEG amplitude changes. The first stage, is in turn composed by two steps: the estimation of the envelope (i.e., of the local amplitude) of each EEG signal and the detection of the abrupt changes in the EEG local amplitude time series.
Step 1a is performed applying the Hilbert transform (Huang et al., 1998) to the EEG signal, and considering the modulus of the corresponding analytic signal. The obtained series constitutes the so called test sequence (TS; Brodsky et al., 1999), whose modifications are analyzed in step 1b. Step 1b, the basic procedure of segmentation, rests on comparing the ongoing instantaneous amplitude series with its average level over a surrounding window. To this aim, a smoothed TS termed level sequence (LS) has been derived from the previous one with a even-weighted moving-average filter (700 ms window length). In the case of rapid amplitude changes in the EEG, the LS will update its values with time delay with respect to the non-smoothed TS. The time locations of each intersection between TS and LS can thus be considered as preliminary RTPs (Kaplan et al., 2005).
Stage 2 aims at overcoming a first step pitfall: Some of the intersections between the two series do not correspond to a discontinuity between quasi-stationary EEG segments and thus false RTPs, related to brief anomalous peaks in the TS, may occur. According to Kaplan et al. (2005), anomalous peaks (either related to very tight pairs of intersections or without a steady separation between the two series) can be effectively selected out by noticing that the slope of the TS around a false RTP should be less steep than that around actual RTPs and should be similar to that of any other point in the TS. To filter out false RTPs we used a smoothed time derivative of the TS, calculated by means of a convolution with a anti-symmetrical step-like function (of window 50 ms wide, value −1 in the left part, +1 in the right, 0 outside the window). Looking at the modulus of the derivative signal, we remove segments (100 ms wide) centered around the time locations of the preliminary RTP and we estimate the probability density function of the remaining signal. On the basis of this distribution, a threshold aiming at discriminating actual from false RTP has been calculated as the 99th percentile of the distribution. Namely, we required that the TS at actual RTPs exhibits high slope absolute values, that are uncommon among slopes of TS generic points. Needless to say that the application of this threshold criterium for the recognition of actual RTPs implies that only a portion of the occurring RTPs are detected. A schematic representation of the segmentation procedure is shown in Figure 1.
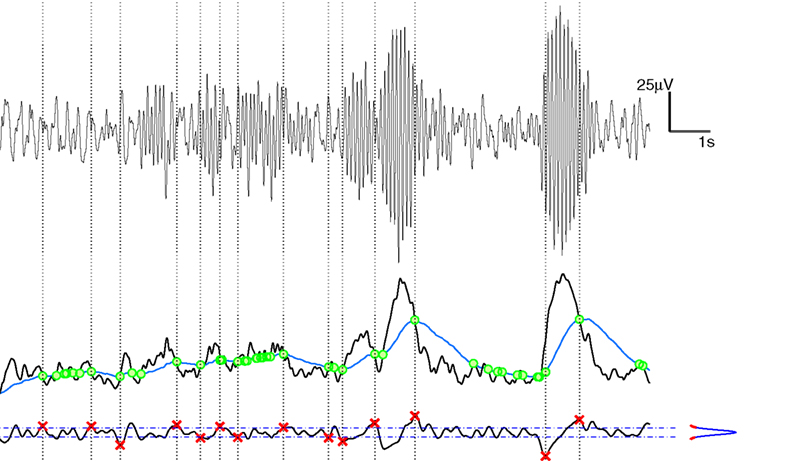
Figure 1. Schematic representation of the EEG segmentation (RTP identification). Top panel: raw EEG signal, with units labels on the right. Middle panel: Black curve represents the Test Sequence, TS, obtained from raw data via Hilbert transform; the blue curve is the Level Sequence, LS, obtained from the TS via a running-average smoothing; the green dots denote the intersections between TS and LS. Bottom panel: the black curve is the time derivative (details on text) of the TS; the blue/red curve on the right denotes the distribution density of the derivatives, with the blue part denoting the central part, between the 5th and the 95th percentile; red points (crosses) denote actual RTP, namely a selection of the green dots intersections of middle panel, with the further condition of having a large derivative value. From these points (RTP) vertical traces are drawn up to the raw data of the upper panel, for visual validation.
Multichannel RTP Detection
The identification of RTP concurrent among EEG channels (MC-RTPs) allows inferences about the dynamics of large-scale cortical interactions in recruitment/selection of neuronal populations forming metastable assemblies (Fingelkurts et al., 2003a,b, 2004). In fact, by reason of the integrated functioning of the brain, RTPs happen simultaneously in two or more EEG channels more often than expected by chance and the study of waiting times between MC-RTPs allows the estimation of the lifetime of the large-scale functional assemblies of neurones. Effectively, starting from the time-location series of the above defined single-channel RTP, transitions occurring simultaneously in N channels have been considered, with N varying from 2 to the number of recorded EEG channels, irrespective of the electrode position on the scalp. Namely, from the multivariate series of RTP locations, the time locations sequences of those RTP concurrent in N electrodes have been constructed. We consider simultaneous RTPs those events in which the time lap between two transitions is less or equal to a threshold value Δt called “lumping time”. Unless otherwise stated, we take Δt = 2 ms, i.e., the time resolution of our recordings. In case of N > 2, RTPs are simultaneous if they can be sorted so that the distance between each consecutive pair is less or equal to Δt.
Self-Organization, Cascades, and Intermittency
Following Beggs and Plenz (2003) we studied in our data the phenomenon of avalanches. This perspective is along the lines of self-organized criticality (Bak et al., 1987), evoked to explain inverse-power laws in neural dynamical patterns. In particular it is focused on the study of inverse-power laws both in the “spatial” and in the temporal dimension. They studied cortical slices of animal brain in vitro, and found results that are compatible with a simple feedforward neural network at a critical value. The theory (explained in detail in Zapperi et al., 1995; de Arcangelis et al., 2006; Pellegrini et al., 2007) predicts a probability density for the size n of avalanches (in Beggs and Plenz, 2003, the number of neurons firing) as p(n) ∝ n−1.5, while the lifetime distribution for avalanches is ψ(τ) ∝ τ−2, with excellent agreement between theory and experiment. We performed a similar study on the number of electrodes undergoing simultaneous RTP.
We defined as ψ(τ), namely the lifetime of collective modes, the waiting time distribution for consecutive avalanches. A direct evaluation of ψ(τ) cannot be used, due to distorting effects from superimposed noise. We evaluated it indirectly by studying the scaling relation for the number of MC-RTPs in time windows of different duration, as explained in the following subsection. We use the fact that the avalanches are driven by a renewal events, namely, by events that reset the memory of the system so that waiting times between two such events are all mutually independent, as proved by Allegrini et al. (2009b). This latter property is in fact a mathematical definition of the earlier mentioned phenomenon of “intermittency”, and is in fact compatible with SOC (see Discussion).
Scaling and Diffusion Entropy
Here we assume that an intermittent, i.e., renewal process, exists with ψ(τ) ∝ τ−μ for very long values of waiting times τ’s. While a direct evaluation can in principle be done, in practice it may happen that the renewal process may trigger some other dynamics (pseudoevents), or can be under threshold, or be blurred by noise. All the three mechanisms can significantly alter the value of the detected μ. Here we use a robust mechanism to unravel the index μ responsible for the renewal dynamics. This method, called diffusion entropy (DE) method has been theoretically and numerically proved to overcome the aforementioned difficulties (Grigolini et al., 2001; Allegrini et al., 2003a,b; Mega et al., 2003).
In synthesis, one defines a “marker” on a time sequences, and studies the probability p(x;t) of having a number x of markers in a window of length t. This statistical analysis is done by moving a window of length t along the sequences, counting how many times one finds x markers inside this window, and dividing this number by the total number N − t + 1 of windows of size t, where N is the total length.
Having large number values for x and t, we can adopt a continuous approximation. Moreover, in the ergodic and stationary condition, a scaling relation is expected, namely

where w is the overall marker density, δ is the scaling index and F is a function. If F is the Gauss function, δ is the known Hurst index, and if the further condition δ = 0.5 is obeyed, then the process is said to be Poissonian, and the dynamics of x is called “Brownian motion”. If this condition applies, there is no long-range memory regulating the occurrence of markers in time.
It is straightforward to show that

namely the Shannon’s entropy (information), with condition 3, leads to

where k is a constant. The evaluation of the slope according to which S increases with lnt provides a measure for the anomalous scaling δ.
Let us briefly mention what we know about applying DE to time series with known long-range correlation. We construct an artificial series by letting ξi = 1 (this means that we find the marker at the ith position), or ξi = 0 (the i-th sign is not a marker). We then assume intermittency namely that the distance between a “1” and the successive does not depend on the such previous distances. Then, if the distances t between events are distributed as

(ψ(t) ∼ t−μ asymptotically is a sufficient condition], then, using a continuous-time random-walk technique and the generalized central-limit theorem, p(x;t) is proved to follow a truncated Lévy probability distribution function (PDF; Grigolini et al., 2001). DE detects the scaling δ of the central part, namely
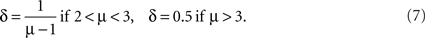
The condition 2 < μ < 3 means long-range correlation, since for truncated Lévy PDFs asymptotically 〈x2(t)〉 − 〈x(t)〉2 ∝ t4−μ and therefore the correlation function obeys Eq. 1, namely it decays as tβ. with

Note that the decay of this correlation function is non-integrable, yielding an infinite correlation time.
Results
Multichannel Avalanches and Scaling
We defined as the size of avalanche the number of EEG electrodes undergoing a simultaneous RTP at a certain time t. For each subject we constructed the histograms for the avalanche size. The results are illustrated in Figure 2. For each subject we see a smooth inverse-power law, visualized as a straight line in a log-log plot for a small number of electrodes (n ≤ 10). For larger n the probability densities P(n) are noisy. For each patient a non-linear least-square fit was performed on the first 7 points. The resulting average and standard deviation for the probability density index ζ, defined as
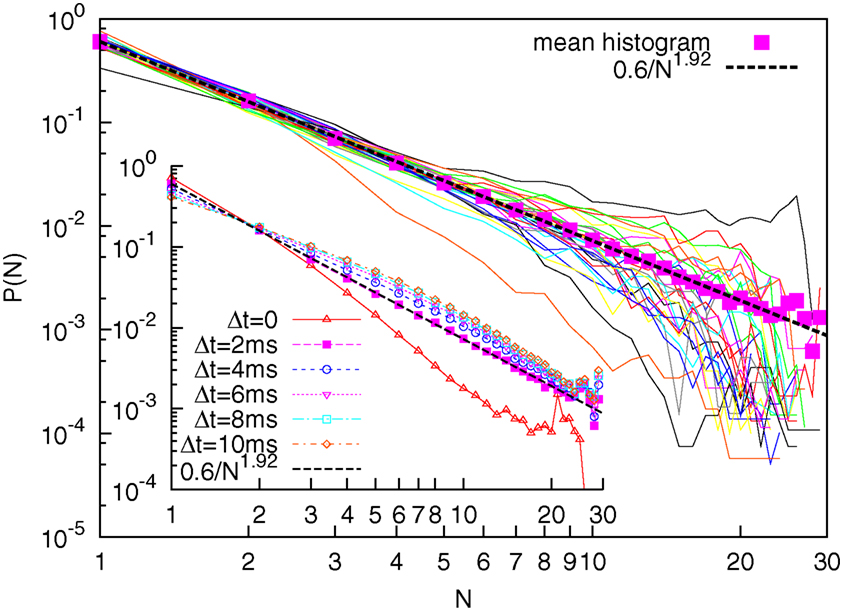
Figure 2. Main figure: Solid curves are the probability densities for avalanches sizes for 30 subjects; Solid squares denote the averaged probability density; the dashed line denotes a corresponding best fit with inverse-power law with index ζ = 1. 92. Inset: Averaged probability densities for different values of Δt (Δt = 0 corresponds on selective as consecutive events only those exactly co-occurring in the sampling-time window).

is

where we reported the average and the standard deviation. In Figure 2 (solid squares) we also plot an averaged P(n), taking into account the avalanche sizes, cumulatively for all subjects. Remarkably, the least-square fit for this cumulative histograms yields ζ = 1.92. In this latter case the fit was performed for all points, as the inverse-power law is visually more robust. The equality of the two averages suggest that the index variability for different subjects is to be interpreted more as a lack of statistics rather than as a real difference (patient effect). This is an indication of a state of criticality being present at the level of the whole cortex, although with an index that differ from that presented by Beggs and Plenz (2003) (ζ = 1.5), who looked at a smaller scale.
In line with the work of Beggs and Plenz (2003), the cumulative average has been performed for different choices of the lumping time Δt. A larger value of Δt corresponds to an higher probability of finding events with a large number of n, and a smaller probability of finding avalanches with a small value of n. Therefore we may expect a lower value of the index η with increasing Δt. The results are shown in the inset of Figure 2. We see that while the choice Δt = 2 ms corresponds to a good inverse-power law, the choices Δt > 2 ms do not result in a straight line in a log-log plot. We therefore conclude that ζ = 1.92, corresponding to Δt = 2 ms is the right avalanche-size scaling index for the process.
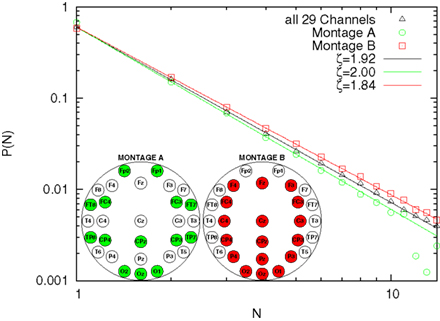
This difference between our reported 1.92 and the theoretical value 1.5 can be due to a different topology underlying connections among different brain areas or to finite-scale effects. In order to discriminate between these two possibilities, we studied the avalanche size distribution with two different sub-montages, i.e., removing some channels from the analysis. Montage A consists on a low density montage, spanning however over all scalp areas. Montage B consists on removing the external channels (while keeping the occipital ones). The analysis is shown in Figure 3, with used channels highlighted. The resulting ζ is respectively 2.00 and 1.84. Although the result for Montage A may be consistent with the finite-size effect, Montage B, yielding a result closer to the expected theoretical value, tells us that the fractal avalanching is in fact statistically modulated by electrodes in different brain areas, with a more apparent effect in the central core.
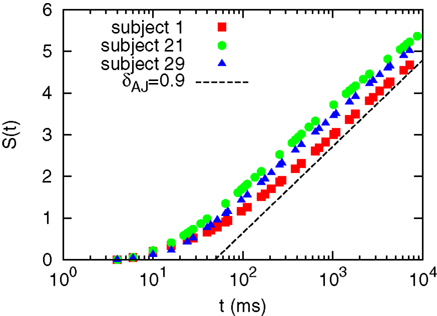
We performed the DE analysis on the events marked by MC-RTPs. The results for MC-RTPS with at least two channels are shown in Figure 4 for three subjects. The same analysis (not shown here) was repeated with different thresholds of avalanche size, with the same resulting slope. A typical slope, shown in the figure as a guide to the eye, suggest that δ ≈ 0.9, yielding μ ≈ 2.1. This is in line with the data reported in Allegrini et al. (2009b), where this result is confirmed by the use of other techniques.
A more precise evaluation of δ, hence of μ was performed with a non-linear least-square fit of the DE analysis using the form

where T, an additional fitting parameter, serves the purpose of taking into account the time necessary to approach the asymptotic regime. A lack of correlation between the detected variables ζ and δ in different subjects (Spearman’s R value: 0.033, with 0.16 z-score) again suggest a statistical spreading rather than a subject effect.
Topology of RTPs
So far we have treated each EEG channel in a “democratic” manner. It is however important to notice that not all channels have the same probability of being recruited into an avalanche event. Figure 5 shows three topological plots picturing the relative frequency Π for each channel to undergo a MC-RTP, respectively for avalanche sizes of at least 2, 4, and 10 channels. Π is defined as the ratio between the number of times that the channel is recruited in an avalanche and the total number of avalanches.
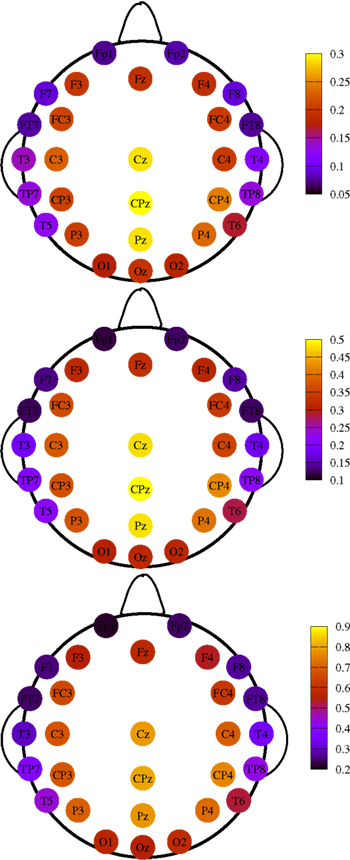
Figure 5. Topological plots for the relative frequency Π of a channel to be recruited into an avalanche. Top panel: avalanches size is of at least two channels. Middle panel: same for at least four channels. Bottom panel: same for at least 10 channels.
It is interesting to show how this topological distribution correlates with the δ values of the different channels, averaged on the subjects set. For this analysis we used all RTPs detected in a single channel for any single subject, regardless whether this RTP belongs to an avalanche or not. Then, for each channel we average the fitted values of δ over all subjects. The results are shown in Figure 6 and Table 1. A correlation is apparent by comparing Figures 5 and 6, where we plot these values for the different channels.
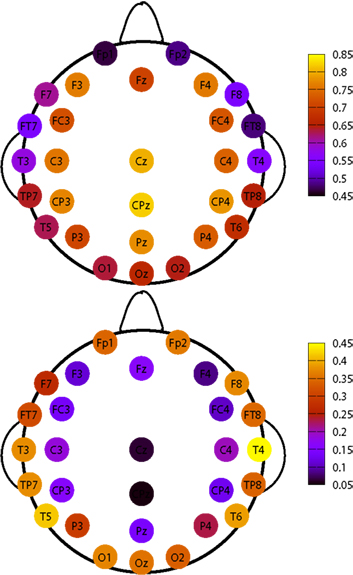
Figure 6. Top panel: topological plots for average values of δ. Bottom panel: difference between the δ values at the 75th and the 25th percentile of the distribution of the values, for each channel, in our subjects data set.
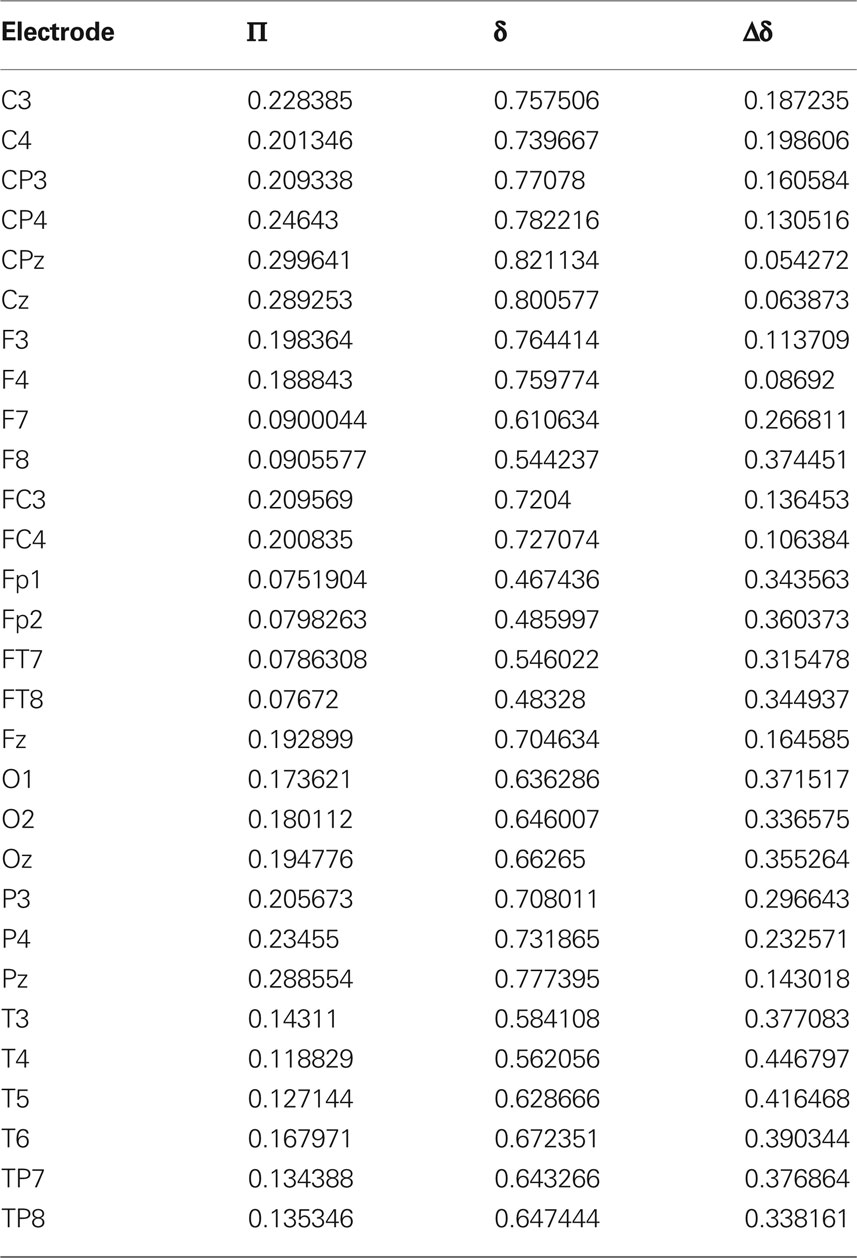
Table 1. Electrode name, global probability for the channel to be recruited in an avalanche Π (with N = 2), average values of single-electrode δ, and variability Δδ, defined as the difference between the 75th and the 25th percentile among subjects.
The upper panel of Figure 6 shows the average values of δ for each EEG channel, while the bottom one describes its variability in our data set. In particular the variability is now defined as the difference of the δ values between the 75th and the 25th percentile. Notice that channels having an higher average value of δ are those with a smaller variability, and, in turn, are the very channels with higher probability of being recruited into an avalanche.
Table 1 reports the values of the global (i.e., over all our data set) probability for the channel to be recruited in an avalanche together with the average values of δ for the different electrodes and with Δδ, namely the difference between the 75th and the 25th percentile among subjects.
The correlation between Π and δ is extremely significant, with Spearman’s correlation R = 0.94, z-score 8.4, corresponding to p < 10−30 (probability for fortuitous generation of such correlated data, under the hypothesis of null correlations). Also the (negative) correlation between δ and Δδ is significant, with Spearman’s correlation R = −0.8 and z-score −5.4.
Discussion
The experimental discovery of 1/f noise in the brain (e.g., Novikov et al., 1997; Linkenkaer-Hansen et al., 2001; Buiatti et al., 2007) has normally been interpreted as an indication of self-organization. On the other hand, the celebrated theory of self-organized criticality (Bak et al., 1987), which is frequently invoked to understand the complex emergent output of neural activity (Beggs and Plenz, 2003; Plenz and Thiagarjan, 2007; Chialvo, 2008), has been originally introduced to explain the origin of 1/f noise. In this paper we provide evidence for fractal (i.e., following an inverse-power law) distribution probability of the number of EEG electrodes involved in global metastable transitions. This is the counterpart of the fractal avalanching process in SOC. The difference between the classical SOC index ζ = 1.5 and the index we detect, ζ = 1.92, can be explained by the difference in the system we study (different scales and topologies). We have addressed the problem of whether the difference could be due to finite-size effects, or, in other words to the fact that the number of channels in our analysis is limited if compared with the original work of (Beggs and Plenz, 2003). At this scope we have further downsized our EEG montages following two different strategies. In one case we have removed three horizontal rows of electrodes, so as to keep the distribution of the relative frequency of being recruited in a coincidence similar to the original one (Montage A of Figure 3). In the other case we have removed the external electrodes, i.e., those less frequently recruited into avalanches (Montage B of Figure 3). In the former case the difference between the measured index and the theoretical 1.5 becomes larger, suggesting in fact a finite-size effect. However, in the latter case the difference between the theoretical exponent and the measured one reduces. Further studies need to be conducted with an higher density montage (128 electrodes) in order to shed light into this difference.
We also find that the dynamical activation of avalanches is driven by a process with waiting-time distribution ψ(t) ∝ t−μ, with μ slightly larger than two. Remarkably, this is compatible with μ ≈ 2 recently reported by Kitzbichler et al. (2009) for the time durations of phase synchronization in different brain regions, using fMRI and magnetoencephalography. Moreover, Allegrini et al. (2009b) have assessed the intermittent, i.e., renewal nature of the dynamical process responsible for the avalanches. Therein, the reason why long-range memory yielded by self-organization is not incompatible with the memory-resetting properties of renewal avalanches is widely discussed. The discussion in Allegrini et al. (2009b) goes along four statements.
1.Eguíluz et al. (2005) reported an fMRI voxel–voxel cross-correlation network displaying a scale-free topology. However it was later shown that this topological pattern is superimposable to the correlational structure of a paradigmatic critical system, namely the Ising model for electromagnetism (Fraiman et al., 2009).
2.It is possible to find physical systems where long-range memory and renewal processes coexist. This is true theoretically: Turalska et al. (2009) found that synchronization patterns in all-to-all coupled stochastic clocks are in fact intermittent. This is also true experimentally: Silvestri et al. (2009) proved that the 1/f-noise emerging from the self-organization of defects in liquid crystals is incompatible with the existence of stationary correlation functions, but in fact obeys a fluctuation-dissipation theorem based on renewal events.
3.The connection between phase transition and non-Poisson and renewal intermittency is a general property of phase transition process, as proved, for instance, by Contoyiannis and Diakonos (2000), who applied their theoretical approach directly to the Ising model.
4.Renewal events, rather than being incompatible with memory, do in fact yield extended memory. This can be proved mathematically using a continuous-time random-walk approach.
Notice, however, that the above discussion rests on the concept of self-organization among identically coupled identical systems. While it is true that this kind of self-organized systems display a low increase of entropy (and this is in fact a definition of complex system), it is also true that complexity increases when the system is composed by diversified elements, with diversified interactions. In the neurophysiological context, Tononi (2004) defined a complexity measure Φ that in fact describes this degree of diversity, relating it to the amount of consciousness, defined as the quantity of information that can be effectively integrated, i.e., processed by a collection of elements of the system.
In this paper we show that different cortical areas have different degrees of complexity. Herein we used the scaling-based complexity measure δ, based on fractional time. In particular, the areas located in the midline are more likely to be recruited in a global metastable transition. Moreover, a complexity index more similar to the global fractal behavior, is displayed by these very same areas, already at the level of single EEG electrode.
Midline areas are involved in the default-mode network (DMN), defined as the network of areas active during unconstrained resting state (typically lying quietly with eyes closed, as in our experiments). DMN, first identified through fMRI, involves the medial prefrontal cortex, the posterior cingulate cortex, the inferior parietal lobe, the lateral inferior temporal cortex, and the medial temporal lobes (Raichle et al., 2001; Beckmann et al., 2005). DMN was also identified through EEG in Trevis et al. (2010). In addition, some of the DMN areas have been reported to be associated to consciousness, namely the inferior parietal lobe, and the whole medial cortical core (Alkire et al., 2008).
The topological results of our investigation indicate that the probability of being recruited into avalanche is in fact higher for the posterior midline core, spreading in the lateral posterior regions, with an antero-posterior gradient. Indeed, it has been suggested that mental activity associated with DMN is characterized by both low cognitive load and executive control, which are typically sustained by lateral frontal regions (Mansouri et al., 2009). We are therefore in a position to claim that unconstrained mental activity is a fractal emergent property compatible with a critical brain, with a specific regional topological pattern, partially superimposable with the DMN. We also think that our approach, based on the study of the intermittent fractional-time transitions between metastable states, borrowing methods from the science of complexity, adds a new vista on integrated neural dynamics, adds to the understanding of the brain dynamics, beyond the temporal limitations of neuro-vascular coupling generating the fMRI signal as well as beyond the classic segregation in Fourier EEG bands, and is able to explore holistic emergent properties.
Our results opens another issue: We show that, for all electrodes, the single-electrode complexity is a function of the relative recruitment rate in global avalanches. What is the reason of what? One can assume that different areas keep their segregated complexity, and the coincidences result from the complex auto-organization of the coupling of already complex structures. It is reasonable that the global process will have a μ smaller than all of the μ’s of the component involved (West et al., 2008). It is however still to be understood why the components with smaller μ would be more involved in synchronized events. On the other hand, one may also think that a global process exists, involving maybe some region of the corticothalamic system and that the corresponding complex impulse is able to synchronize different regions through some diversified probability function, that can depend for instance on some distance from a focus or on the anatomy of neural connection, or even from the degree of freedom of their neural assembly. The results of Figure 3 (Montage B) supports this latter hypothesis.
Whatever the process, an emergent complex (fractal) process exists, dominating the unstructured, non-task-oriented mental activity, possibly in a critical state. Is it the default-mode network? Or is it the neural-integrated dynamics underlying/sustaining consciousness?
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Alkire, M. T., Hudetz, A. G., and Tononi, G. (2008). Consciousness and anesthesia. Science 322, 876–880.
Allegrini, P., Balocchi, R., Chillemi, S. Grigolini, P., Hamilton, P., Maestri, R., Palatella, L., and Raffaelli, G. (2003a). Long- and short-term analysis of heartbeat sequences: correlation with mortality risk in congestive heart failure patients. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 67, 062901.
Allegrini, P., Benci, V., Grigolini, P., Hamilton, P. Ignaccolo, M., Menconi, G., Palatella, L., Raffaelli, G., Scafetta, N., Virgilio, M., and Yang, J. (2003b). Compression and diffusion: a joint approach to detect complexity. Chaos Solitons Fractals 15, 517–535.
Allegrini, P., Bologna, M., Fronzoni, L., Grigolini, P., and Silvestri, L. (2009a). Experimental quenching of harmonic stimuli: universality of linear response theory. Phys. Rev. Lett. 103, 030602.
Allegrini, P., Menicucci, D., Bedini, R., Fronzoni, L., Gemignani, A., Grigolini, P., West, B. J., and Paradisi, P. (2009b). Spontaneous brain activity as a source of ideal 1/f noise. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 80, 061914.
Allegrini, P., Bologna, M., Grigolini, P., and West, B. J. (2007). Fluctuation-dissipation theorem for event-dominated processes. Phys. Rev. Lett. 99, 010603.
Allegrini, P., Grigolini, P., and Palatella, L. (2004). Intermittency and scale-free networks: a dynamical model for human language complexity. Chaos Solitons Fractals 20, 95–105.
Bak, P, Tang, C., and Wiesenfeld, K. (1987). Self-organized criticality: an explanation of the 1/f noise, Phys. Rev. Lett. 59, 381–384.
Beckmann, C. F., De Luca, M., Devlin, J. T., and Smith, S. N. (2005). Investigation into resting-state connectivity using independent component analysis. Philos. Trans. R. Soc. Lond., B, Biol. Sci. 360, 1001–1013.
Beggs, J. M., and Plenz, D. (2003). Neuronal avalanches in neocortical circuits. J. Neurosci. 23, 11167–11177.
Bianco, S., Geneston, E., Grigolini, P., and Ignaccolo, M. (2008). Renewal aging as emerging property of phase synchronization. Physica A 387, 1387.
Brodsky, B. E., Darkhovsky, B. S, Kaplan, A. Y., and Shishkin, S. L. (1999). A nonparametric method for the segmentation of the EEG. Comput. Methods Programs Biomed. 60, 93–106.
Buiatti, M., Papo, D., Baudonnière, P.-M., and van Vreeswijk, C. (2007). Feedback modulates the temporal scale-free dynamics of brain electrical activity in a hypothesis testing task. Neuroscience 146, 1400–1412.
Chialvo, D. R. (2008). Emergent complexity: what uphill analysis or downhill invention cannot do. New Ideas Psychol. 26, 158–173.
Contoyiannis, Y. F., and Diakonos, F. K. (2000). Criticality and intermittency in the order parameter space, Phys. Lett. A 268, 286–292.
de Arcangelis, L., Perrone-Capano, C., and Herrmann, H. J. (2006). Self-organized criticality model for brain plasticity. Phys. Rev. Lett. 96, 028107.
Eguíluz, V. M, Chialvo, D. R., Cecchi, G. A., Baliki, M., and Apkarian, A. V. (2005). Scale-free brain functional networks. Phys. Rev. Lett. 94, 018102.
Fingelkurts, A. A, Fingelkurts, A. A, Kaplan, A. Y. (2003a). The regularities of the discrete nature of multi-variability of EEG spectral patterns. Int. J. Psychophysiol. 47, 23–41.
Fingelkurts, A. A, Fingelkurts, A. A., Krause, C. M., Mottonen, R., and Sams, M. (2003b). Cortical operational syncrony during audio-visual speech integration. Brain Lang. 85, 297–312.
Fingelkurts, A. A, Fingelkurts, A. A, Kivisaari, R., Pekkonen, E., Ilmoniemi, R. J., and Kahkonen, S. (2004). Enhancement of GABA-related signalling is associated with increase of functional connectivity in human cortex. Hum. Brain Mapp. 22, 27–39.
Fraiman, D., Balenzuela, P., Foss, J., and Chialvo, D. R. (2009). Ising-like dynamics in large-scale functional brain networks. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 79, 061922.
Gaspard, P., and Wang, X.-J. (1988). Sporadicity: between periodic and chaotic dynamical behaviors. Proc. Natl. Acad. Sci. U.S.A. 85, 4591–4595.
Grigolini, P., Palatella, L., and Raffaelli, G. (2001). Asymmetric anomalous diffusion: an efficient way to detect memory in time series. Fractals 9, 439–449.
Huang, N. E., Shen, Z., Long, S. R, Wu, M. L. C., Shih, H. H, Zheng, Q. N., Yen, N. C, Tung, C. C, and Liu, H. H. (1998). The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond., B, Biol. Sci. 454, 903–995.
James, C. J., and Gibson, O. J. (2003). Temporally constrained ICA: an application to artifact rejection in electromagnetic brain signal analysis. IEEE Trans. Biomed. Eng. 50, 1108–1116.
Kaplan, A. Y., Fingelkurts, A. A., Fingelkurts, A. A., Borisov, B. S., and Darkhovsky, B. S. (2005). Nonstationary nature of the brain activity as revealed by EEG/MEG: methodological, practical and conceptual challenges. Signal Process. 85, 2190–2212.
Kitzbichler, M. G., Smith, M. L., Christensen, S. R., and Bullmore, E. (2009). Broadband criticality of human brain network synchronization. PLoS Comput. Biol. 5, e1000314. doi:10.1371/journal.pcbi.1000314.
Linkenkaer-Hansen, K., Nikouline, V. V., Palva, J. M, and Ilmoniemi, R. J. (2001). Long-range temporal correlations and scaling behavior in human brain oscillations. J. Neurosci. 21, 1370–1377.
Mansouri, F. A., Tanaka, K., and Buckley, M. J. (2009). Conflict-induced behavioural adjustment: a clue to the executive functions of the prefrontal cortex. Nat. Rev. Neurosci. 10, 141–152.
Medina, J. M. (2009). 1/fα noise in reaction times: a proposed model based on Piéron’s law and information processing. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 79, 011902.
Mega, S. M., Allegrini, P., Grigolini, P., Latora, V., Palatella, L., Rapisarda, A., and Vinciguerra, S. (2003). Power-law time distribution of large earthquakes. Phys. Rev. Lett. 90, 188501.
Novikov, E., Novikov, A., Shannahoff-Khalsa, D., Schwartz, B., and Wright, J. (1997). Scale-similar activity in the brain. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics 56, R2387–R2389.
Pellegrini, G. L., de Arcangelis, L., Herrmann, H. J., and Perrone-Capano, C. (2007). Activity-dependent neural network model on scale-free networks. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 76, 016107.
Plenz, D., and Thiagarjan, T. C. (2007). The organizing principles of neuronal avalanches: cell assemblies in the cortex? Trends Neurosci. 30, 101–110.
Raichle, M. E., Mac Leod, A. M., Snyder, A. Z, Powers, W. J., Gusnard, D. A., and Shulman, G. L. (2001). A default mode of brain function. Proc. Natl. Acad. Sci. U.S.A. 98, 676–682.
Silvestri, L., Fronzoni, L., Grigolini, P., and Allegrini, P. (2009). Event-driven power-law relaxation in weak turbulence Phys. Rev. Lett., 102, 014502.
Sokolov, I. M., and Klafter, J. (2007). Continuous-time random walks in an oscillating field: field-induced dispersion and the death of linear response. Chaos Solitons Fractals 34, 81–86.
Stanley, H. E. (1971). Introduction to Phase Transitions and Critical Phenomena. London: Oxford University Press.
Trevis, F., Hahaga, D. A. F., Hagelin, J, Tanner, M., Arenander, A., Nidick, S., Gaylord-King, C., Grosswald, S., Rainforth, M., and Schneider, R. H. (2010). A self-referential default brain state: patterns of coherence, power, and eLoreta sources during eyes-closed rest and transcendental meditation practice. Cogn. Process. 11, 21–30.
Turalska, M., Lukovic, M, West, B. J., and Grigolini, P. (2009). Complexity and synchronization. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 80, 02110.
Werner, G. (2009). Viewing brain processes as critical state transitions across levels of organization: neural events in cognition and consciousness, and general principles. Biosystems 96, 114–119.
West, B. J., Geneston, E. L., and Grigolini, P. (2008). Maximizing information exchange between complex networks. Phys. Rep. 468, 1–99.
Keywords: EEG, renewal processes, RTPs, critical phenomena, entropy
Citation: Allegrini P, Paradisi P, Menicucci D and Gemignani A (2010) Fractal complexity in spontaneous EEG metastable-state transitions: new vistas on integrated neural dynamics. Front. Physio. 1:128. doi:10.3389/fphys.2010.00128
Received: 18 June 2010;
Paper pending published: 28 June 2010;
Accepted: 06 August 2010;
Published online: 15 September 2010.
Edited by:
Dante R. Chialvo, Northwestern University, USAReviewed by:
Dante R. Chialvo, Northwestern University, USAHans Herrmann, Eidgenössische Technische Hochschule Zürich, Switzerland
Copyright: © 2010 Allegrini, Paradisi, Menicucci and Gemignani. This is an open-access article subject to an exclusive license agreement between the authors and the Frontiers Research Foundation, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Paolo Allegrini, Istituto di Fisiologia Clinica del Consiglio Nazionale delle Ricerche, Via Moruzzi 1, 56124 Pisa, Italy. e-mail:YWxsZWdyaXBAZGYudW5pcGkuaXQ=