- Division of Bioengineering, Graduate School of Engineering Science, Osaka University, Toyonaka, Osaka, Japan
An aim of systems physiology today can be stated as to establish logical and quantitative bridges between phenomenological attributes of physiological entities such as cells and organs and physical attributes of biological entities, i.e., biological molecules, allowing us to describe and better understand physiological functions in terms of underlying biological functions. This article illustrates possible schema that can be used for promoting systems physiology by integrating quantitative knowledge of biological and physiological functions at multiple levels of time and space with the use of information technology infrastructure. Emphasis will be made for systematic, modular, hierarchical, and standardized descriptions of mathematical models of the functions and advantages for the use of them.
1 Introduction
The completion of human genome sequencing was an epoch-making event in reductionism biosciences, liberating enormous amount of experimental data, and allowing us to relate specific parts of it to genes. The challenge for the biosciences and bioengineering in the twenty-first century is to integrate this information into a better understanding of biology, physiology, and human pathology. The integration is moving the world toward a new generation of bioscience and bioengineering, where biological, physiological, and pathological information from humans and other living animals can be quantitatively described in silico across multiple scales of time and size and through diverse hierarchies of organization – from molecules to cells and organs, to individuals. The systems physiology (Kitano, 2010), including physiome (Bassingthwaighte, 2000; Hunter and Borg, 2003), and systems biology (Kitano, 2002a,b) represent such emerging biosciences. Such new trends in biosciences share a common direction, namely, an “integrative” approach (Fenner et al., 2008) that allows us to understand mechanisms underlying biological and physiological functions that emerge through dynamics of each element and large aggregations of those elements.
We have a huge number of biological and physiological entities at hand – genes, molecules, cells, tissues, and organs. We are aware that each of them behaves in a more-than-simple way owing to its complex structure and non-linear dynamics underlying and controlling its behavior. Moreover, aggregations of elemental entities behave as systems. Thus, for a better understanding of mechanisms responsible for biological and physiological functions, we are required to harness that complexity in terms of both the huge number of entities and their complex dynamics. Toward this end, integrative biosciences and bioengineering in their early stages aim at establishing frameworks and information technology infrastructures for describing biological structures and physiological functions on multiple scales of time and space. Databasing and sharing of knowledge have been promoted, because it is not realistic to expect that a single research laboratory can answer comprehensively all the important questions about the life. International communities such as those for systems biology1, systems biology markup language (SBML)2, IUPS Physiome3,4, JSim5, Virtual Physiological Human Network of Excellences (VPH NoE)6, Physiome.jp7, and the Neuroinformatics platforms of the International Neuroinformatics Coordinating Facility (INCF)8,9, among others10, have been making efforts to establish those frameworks.
In this article, we illustrate possible schema that can be used for promoting systems physiology by integrating quantitative knowledge of biological and physiological functions at multiple levels with the use of the frameworks. Emphasis will be made for systematic, standardized descriptions of mathematical models of the functions. In particular, relationships between the description for biological functions at the sub-cellular level using SBML standard and that for physiological functions at the cellular, organ, and individual levels using insilicoML (ISML)11 (Asai et al., 2008) used in Physiome.jp are considered, by which we demonstrate that modular and hierarchical representation of biological and physiological functions is beneficial for the integrative approach. To this end, several use cases for simple biological and physiological functions at different levels are employed.
Considering biological modeling at molecular and sub-cellular levels and physiological modeling at cellular, organ, and individual levels, it is apparent that former two levels target biological entities, i.e., molecules including proteins, where individual or statistical behaviors of biological entities are described directly by laws of physics and chemistry. The latter two levels deal with physiological entities, i.e., hierarchical aggregations of the biological entities. Cells are located at intermediate level, where biological and physiological entities come to coexist. Attributes of a physiological entity are determined by those of biological entities comprising the physiological entity and ways of interactions among the biological entities. If we do not take care of biological entities underlying the physiological entity, most of the attributes of the physiological entity would be described merely phenomenologically. An aim of systems physiology today can be stated as to establish logical and quantitative bridges between the phenomenological attributes of the physiological entities and physical attributes of the biological entities, allowing us to describe and better understand physiological functions in terms of underlying biological functions.
2 Models in Systems Physiology and their Descriptions
Because biological and physiological functions and their pathological states are realized or emerged dynamically over time in biological and physiological systems, it is natural and inevitable that we need to describe them using mathematical and dynamic equations if we are to understand them quantitatively and integratively. Thus we are required to perform mathematical modeling and computer simulations of models of a function under consideration. Let us consider a set of ordinary differential equations (ODE) representing a biological or a physiological function as follows;
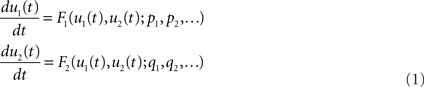
where u1(t) and u2(t) are the state variables of the system at time t. The first and second equations define the rate of change of the state variable u1 at time t as F1 and that of the state variable u2 also at time t as F2, respectively. The value of F1 may be determined as the function of u1(t) and u2(t), meaning that the state variable u1 has an interaction with u2 and the time evolution of u1 is determined under the influence of both u1 and u2. This is the same for u2 and F2. Moreover, F1 is parameterized by several or many parameters p1, p2,…, and F2 by q1, q2,…. The parameters are usually constant, but the values of some parameters are controllable and thus tuned or varied, by which the model behaves differently. There are cases where the parameter values are not constant but change over time. In those cases, however, the changes are prescribed by static functions such as like p1 = sinωt, and thus we do not consider differential equations for determining the parameter values. Because of the nature of dynamic systems theory and systems engineering theory, this type of ODE appears independently of levels and spatio-temporal scales of biological and physiological functions as exemplified below.
2.1 Biochemical Reactions
Biochemical reactions such as

representing a production of a substance P with an enzyme E and a substrate S often appear at sub-cellular level. Using the law of mass action with an algebraic constraint [E]T = [E] + [ES] = constant for the total concentration [E]T of the enzyme E, we have a set of two differential equations in the form of Eq. (1) as follows;
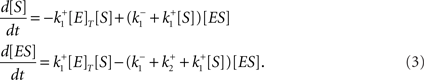
In this case, [S] and [ES] correspond to u1 and u2, respectively. 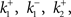 and [E]T are the parameters of the system, corresponding to p1, p2,… and q1, q2,…. The systems biology often deals with such biochemical reactions representing dynamics along signaling pathways such as cascades of phosphorylations, calcium signaling, and gene expressions, but in much more complicated manners than Eq. (3) in terms of the number of state variables and parameters, and types of reactions involved in the system. The order of time scale of such reactions, in many cases, is seconds, minutes, hours, or days. It is conventional for the researcher to describe, to share, to reuse, and to handle a large number of biochemical reactions in a system through the use of biological entities and an attribute of each entity. Each of substrates and enzymes involved can be naturally considered as such an entity of a specific “species” as called so in the SBML community, and concentration of each species in a reactor (a space where reactions take place) is also naturally associated with the attribute or the state of the corresponding entity. Relationships connecting between any of two types of species specify types of reactions, defining a sequence of biochemical reactions occurring in the system and altering the values of the attributes over time. This simple scheme is almost always applicable to modeling and model description as far as systems of biochemical reactions are concerned, regardless of the size and complexity of systems, leading to the international standardized specifications used for SBML, its tools12,13, and for EBI BioModels Database14. Related projects have been promoted to define the graphical representation of various types of entities and relationships among them15 and to establish cross-referencing capabilities with the pathway databases16 and annotating and curating efforts17 (Matsuoka et al., 2010), leading to the information technology-based quantitative understanding of biological functions.
and [E]T are the parameters of the system, corresponding to p1, p2,… and q1, q2,…. The systems biology often deals with such biochemical reactions representing dynamics along signaling pathways such as cascades of phosphorylations, calcium signaling, and gene expressions, but in much more complicated manners than Eq. (3) in terms of the number of state variables and parameters, and types of reactions involved in the system. The order of time scale of such reactions, in many cases, is seconds, minutes, hours, or days. It is conventional for the researcher to describe, to share, to reuse, and to handle a large number of biochemical reactions in a system through the use of biological entities and an attribute of each entity. Each of substrates and enzymes involved can be naturally considered as such an entity of a specific “species” as called so in the SBML community, and concentration of each species in a reactor (a space where reactions take place) is also naturally associated with the attribute or the state of the corresponding entity. Relationships connecting between any of two types of species specify types of reactions, defining a sequence of biochemical reactions occurring in the system and altering the values of the attributes over time. This simple scheme is almost always applicable to modeling and model description as far as systems of biochemical reactions are concerned, regardless of the size and complexity of systems, leading to the international standardized specifications used for SBML, its tools12,13, and for EBI BioModels Database14. Related projects have been promoted to define the graphical representation of various types of entities and relationships among them15 and to establish cross-referencing capabilities with the pathway databases16 and annotating and curating efforts17 (Matsuoka et al., 2010), leading to the information technology-based quantitative understanding of biological functions.
2.2 Electrophysiology of Cells
The following example also in the form of Eq. (1) describes a single cell level electrophysiology of a membrane (Morris and Lecar, 1981) based on the Hodgkin–Huxley formalism with the gating theory for membrane channels (Hodgkin and Huxley, 1952).
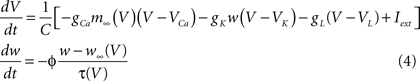
where V and w represent the membrane potential and the open fraction of the delayed rectifier K+ channels. m∞(V), w∞(V), and τ(V) are the non-linear functions of V. m∞ and w∞ are the (quasi) steady-state open fractions (gating variables) of the voltage-dependent Ca2+ channels and the delayed rectifier K+ channels, respectively. In this case, V and w correspond to u1 and u2 in Eq. (1), respectively. Equation (4) includes several parameters such as the maximum conductances of the ion channels, gCa, gK, and gL, the Nernst potential, VCa, VK, and VL, and the intensity of the externally applied current, Iext, whose values can alter model’s dynamics quantitatively and qualitatively (Rinzel and Ermentrout, 1998). The time scale of this type of model is usually milliseconds or seconds. Although construction of this model relies on electrochemical principles of physics, usual determination of voltage dependence of the channel conductances performed by curve fittings of experimentally obtained current–voltage (I–V) relationships is highly phenomenological but with high accuracy (Hille, 2001).
The membrane potential V here can be considered as an attribute of the cell as a biological entity involved in the model. It is an integrated physical quantity, and the integration is performed by the cell which is composed of several or many biological entities such as the membrane and the ion channels. The state variable V in this case is determined by the integration of ionic current flow across the cell membrane through different types of the ion channels. The open fraction w is an attribute of the potassium ion channel as another biological entity, controlling the flow of the potassium current. These two entities interact with each other to alter the values of their attributes according to the dynamic equations. The scenario used here for the systematic description of the model seems the same as the biochemical reactions at the sub-cellular level. However, unlike the case of biochemical reactions at the sub-cellular level, the model includes other important physical quantities that are not treated as the state variables, and thus correspondence between such physical quantities and their originated entities is not always simple and clear-cut. This would provide a naive separation between modeling of biological functions and that of physiological functions. For example, let us consider each of the first, the second, and the third terms of the right hand side of the first line of Eq. (4), representing the current flow of calcium ions through the Ca2+ channel, that of potassium ions through the K+ channel, and that of anions through the leak channel, respectively. Each of them can be considered as an attribute of the corresponding ion channel as the biological entity. However it is also possible to consider that these currents are the attributes of the cell. Indeed, the ion channels are part of the cell. This simple observation can trigger a development of hierarchical representation and description of physiological functions. In this simple example of Eq. (4), we might have the following relationships between the entities as well as correspondences between the entities and their attributes;
• Each ion channel is part of the cell.
• Each gate is part of the corresponding channel (though the gate is not real entity).
• The cell has the membrane potential V as its attribute.
• Each ion channel has the corresponding current as its attribute.
• Each gate has the gating variable (the open fraction m or w) as its attribute.
The relationships between the entities and the dependency between the attributes can be summarized as;
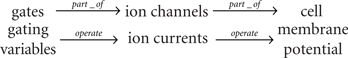
Note that the membrane potential is fed back to and operates (affects) on both gating variables and ion currents, but not shown here for simplicity. One way to represent this sort of model structure is to introduce modules, each of which is defined by an entity and its attribute, hierarchical relationships among modules, and functional linkages among modules representing how the attribute value of one module is altered by the influence (operation) from the values of attributes of other modules. Then Eq. (4) might be represented by the top-level module of cell, consisting of three modules of the ion currents, each of which is further composed of the gate module. For more sophisticated and biophysically detailed models of cellular electrophysiology such as for cardiac myocytes (Faber et al., 2007) and pancreatic beta cells (Keizer and Smolen, 1991; Fridlyand et al., 2003), we need to introduce a number of ion currents with different carriers and dynamics as well as sub-cellular organelle contributing to the cell level electrophysiology. Fortunately, mathematical equations defining a model contain most information required for representing the model using modules and relationships among modules. A set of modules representing various types of ion currents and sub-cellular dynamics described by a standardized format with well-specified relationships connecting among modules would provide a better description of physiological models. The ISML18 (Asai et al., 2008) developed at Physiome.jp is one of such specifications available for the public so far.
2.3 Population Dynamics of Tumor Growth
Ordinary differential equations in the form of Eq. (1) have been used for population dynamics such as for modeling prey–predator systems in the field of mathematical biology (Lotka, 1920). The tumor growth in prostate cancer can be described in a similar way with changes in the populations of androgen dependent (AD) and androgen independent (AI) cells (Idate et al., 2008). The proliferation and apoptosis rates of AD and AI cells are assumed to be dependent on the androgen concentration a(t). Then the tumor dynamics can be described as follows:
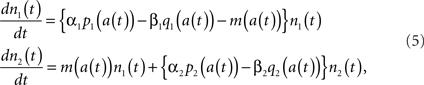
where n1(t) and n2(t) represent the populations of AD and AI cells, respectively. In this example, the coefficient of n1 in the right hand side of Eq. (5) represents the net growth rate of the AD cells, which is determined by the proliferation rate α1p1, the apoptosis rate β1q1, and the mutation rate m by which AD cells mutate into AI cells. Similar definitions are made for α2p2 and β2q2. The parameters p1, p2, q1, q2, and m are not constant in this model, and they change the values as the (static) functions of the androgen concentration a(t). Indeed, a(t) has its own dynamics that might be modeled by the following simple differential equation.

with additional parameters γ and a0, where u(t) is controlled by a medical doctor and it takes a value either 0 or 1 representing “off” or “on” state of a pharmacological treatment. That is, the amount of a(t) can be controlled by u, the administration of pharmacological agents inducing androgen deprivation. The functional forms of p, q, and m are determined phenomenologically, i.e., by curve fittings of data obtained by in vitro experiments as in the case of I–V relationships in the cellular electrophysiology. Simplicity of the model owes the phenomenological assumptions, but it does not allow us to attack underlying biological mechanisms of mutations and related aberrant cell signaling that are starting to be described quantitatively, such as in a model of epidermal growth factor receptor (EGFR) signaling (Kholodenko et al., 1999; Oda et al., 2005) in SBML format available at EBI Model repository19,20. Nevertheless, the simplicity allows us to perform detailed analyses of the model’s dynamics, leading to a quasi-optimal dynamic control of the androgen concentration by the intermittent interventions of u and enhancement of clinical efficacy of the treatment (Idate et al., 2008).
Regarding the structure of the model’s equation in Eq. (5), and its systematic description, it can be simply described by SBML format, since Eq. (5) can be viewed as the system with the following biochemical reactions;
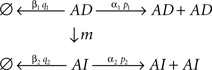
However, it is also suitable for Eq. (5) with Eq. (6) to be described using a hierarchical module representation as in Eq. (4) as discussed below in relation with the integration of biological and physiological functions.
2.4 Feedback Control Models in Physiological Systems
Block diagram representations of models are often employed in the systems and control engineering (Ogata, 2002), and physiological functions related to mechanical and electrical phenomena at organ level and individual level have been modeled using schema from the systems and control engineering. Those include lumped models (ODE models) of the circulatory system for understanding cardiovascular regulation and models for the renal regulation of urinary concentration in the kidneys, among others. A classical example from the neural control of human motor systems is a model of stochastic postural sway during human quiet standing. It can be modeled by the following stochastic delay-feedback control system.
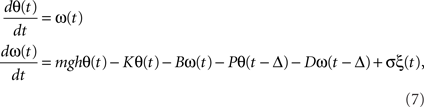
where the human body is simply modeled by an inverted pendulum of mass m and the height h. θ and ω are the tilt angle and angular velocity. The actuator controlling the posture is assumed at the ankle joint, where muscles, tendons, and other viscoelastic elements contribute to generating the ankle torque. During quiet upright standing, the torque can be simply modeled by the passive component with the passive stiffness coefficient of the ankle K and the passive viscosity B and the active component (determined by active muscle contraction generated by the neural commands) with the delayed neural feedback control whose proportional and derivative gains are P and D. Equation (7) is still with the form of Eq. (1), although it includes time-delayed variables θ(t − Δ) and ω(t − Δ) due to the neural signal transmission delay Δ, resulting in the delay-differential equations (DDE). Such delays are known to induce oscillatory dynamics and sometimes delay-induced instability, as observed many physiological systems, including the blood cell production (Bélair et al., 1995; Hauriea et al., 1999), the baroreceptor loop (Ottesen, 2000), and the pupil light reflex (Milton, 2003). Regarding the postural control, recent studies argue if the intermittency (switching between “off” with P = D = 0 and “on” with non-zero small P and D) of the active control torque exerted on the ankle joint is beneficial for avoiding the delay-induced instability and providing robust and compliant postural stability (Bottaro et al., 2008; Asai et al., 2009; Milton et al., 2009).
Interestingly, the intermittent interventions for the prostate cancer therapy exemplified above and the intermittent control of human upright posture mentioned here might share essentially the same mechanisms for stabilizing the antagonistic physiological dynamics with an unstable saddle-type phase portrait despite that they consider completely different phenomena at different levels. However, this is not surprising but even common when we study systems dynamics described by analogous sets of equations for different phenomena as exemplified in this article. At the same time, we should be aware that the systems physiology today is keen to uncover biological mechanisms underlying the dynamics. Essentially the same dynamics from the view point of mathematics but for different physiological functions might have completely different biological foundations. In other words, the systems physiology today requires biological entities enabling the system to behave for a specific function and also requires to establish quantitative bridges between those biological entities and the system’s dynamics, hopefully not only phenomenologically but based on the first principles of physics and chemistry and the molecular, cellular, and organ structure of the related entities.
2.5 Spatio-Temporal Dynamics
Importance of structure–function relationships is not only for molecular and protein biology (Shakhnovich, 2005), but it might be scale and level independent (Weibel et al., 1991). When we take biological and physiological structure into consideration (not in terms of molecular dynamics but at larger scales), dynamics of systems are formulated by partial differential equations (PDEs), whose domains are defined by structured entities such as geometrical structure of single cells and organs. Because of this, public efforts databasing and providing numerical image data allowing the researcher to reconstruct three-dimensional biological/physiological structure have been promoted21,22 (Mitsuhashi et al., 2009). It is then required to integrate models describing temporal dynamics and morphological models.
A simple example that introduces spatial diffusion of a phosphoprotein in a signaling cascade (Kholodenko, 2002) is described as follows and available in ISML format23 at Physiome.jp for simulating the model by the finite element method (FEM).
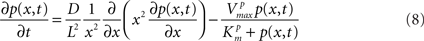
where x represent the radial position of a spherical cell, and p(x, t) the position and time dependent concentration of a phosphoprotein. L and D represent the cell radius and the diffusion coefficient of the protein. For other parameters, see the article by Kholodenko (2002). This PDE will be solved with boundary conditions at the origin of the cell x = 0 and at the plasma membrane x = L. The PDE modeling for signaling pathway simulations becomes important when the distribution of molecules within a cell is not uniform but heterogeneous, i.e., localized at specific parts of the cell possibly due to complex structure of an intracellular space. A pioneering attempt to simulate detailed dynamics of Ca2+ signaling with an image-based sub-cellular geometry has been reported recently (Cheng et al., 2010).
In the modular and hierarchical representation of biological and physiological functions employed in ISML at Physiome.jp for example, the morphological information (analytic geometry and numerical data of geometry) can be introduced simply as an additional attribute of a biological/physiological entity, leading to an easy and systematic modeling and model description toward integration.
3 Perspective for Integration
The modular and hierarchical representation of biological and physiological functions is beneficial for integrating heterogeneous systems at different levels. A possible (but not necessarily the smartest) scheme to integrate different levels of dynamics contributing to a specific function might be starting from choosing a primary level of the targeted function, for which we have enough knowledge, data, and a good model that can reproduce quantitative dynamics at that level.
3.1 Integrating Two Adjacent Levels
Let us consider a physiological function starting at the cell level. As we saw in the cellular electrophysiology, majority of cell models use phenomenological I–V relationships for ion channels and other sub-cellular signaling processes that alter the conductances of the channels. It is desirable for us if a systematic and standardized way to include detailed knowledge at the sub-cellular level into the cell level modeling, by which the phenomenological relationships can be transformed into biological processes with biological entities. For example, in a model of the pancreatic beta cell proposed by Fridlyand et al. (2003), the ion current of ATP-dependent potassium channel (KATP) is modeled as

where gmKATP is the maximum conductance. OKATP is the ATP-dependent open fraction of the channel, which is modeled by a static function of the ATP and ADP concentrations, [ATP]i and [ADP]i. Because the purpose of their modeling was to reproduce the whole cell electrophysiological behavior, the production (and consumption) of ATP was simply modeled by a first-order reaction to express the rate of ATP production from ADP. However, if we look at our knowledge at one scale finer level, models of ATP production at mitochondria have been developed for other purposes, and we can find, for example, a signaling pathway-based model of the extracellular glucose-stimulated ATP production by the TCA cycle and the respiration chain for insulin secretion network of pancreatic beta cells (Jiang et al., 2007), which is available in SBML format24 at EBI BioModels Database. The whole cell pancreatic cell model by Fridlyand et al. at the cell level is also available in ISML format25 at Model Database at Physiome.jp, where the model is represented in the modular and hierarchical form. The relationships between the entities for KATP-current related modules can be summarized as;
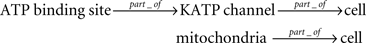
The attribute for each entity is defined as follows: the membrane potential for the cell, the KATP-current for the KATP channel, the open fraction for the ATP binding site, and the ATP concentration [ATP]i for the mitochondria. The dependency between the attributes can be summarized as;

where we omit several feedback loop operations for simplicity. Owing to the modular and hierarchical representation of the model, the mitochondria module can be easily replaced by the pathway model of the TCA cycle and the respiration chain, leading to an integrated model simulation for the cell level and the sub-cellular level. Physiome.jp effort provides a software environment to support this replacing procedure as well as the numerical integration (simulation) engine with multiple time steps.
It is worthwhile to note that this sort of multi-level modeling attempt may provide an opportunity to shed light on our ignorance, leading to new and important experimental paradigms that we need to address. For example, in the case of bridging between cellular electrophysiology of the beta cell and the ATP synthesis in the mitochondria mentioned here, the former model at the cell level assume that the cytoplasmic ATP concentration is ranged between 0 and 3 mM, while the latter at the sub-cellular level predicts the ATP concentration varying between 0 and 10 mM which is three times larger than the former. If 10 mM ATP concentration were given to the whole cell model, electrical activity of the cellular membrane would have fully saturated. Nevertheless, both models are based on careful experimental examinations, but with different experimental preparations; one with a whole cell monitoring of cytoplasmic ATP concentration, and the other with in vitro suspension of mitochondria. Thus, it is speculated that intracellular structure might have some roles for diffusing the ATP, leading to different ATP concentrations at the mitochondria and at the cell membrane. This suggests that, although systematic tools for integration are crucial, model predictions and biological/physiological experiments should interact more closely than ever for promoting the integration.
3.2 Integration via Cellular Network Modeling
Parameter values at a given level of modeling, i.e., p1, p2,… in Eq. (1), might be determined, in actual biological/physiological system, by dynamic processes whose time scale is slower than the time scale of the model. In such cases, we can assume the slow variables as constant parameters, by which the system’s dimension (degree of freedom) decreases, allowing the mode to be mathematically and intuitively tractable. Effect on the model’s dynamics against changes in some parameter values are systematically analyzed, for example, by the bifurcation theory (Morohashi et al., 2002; Lindskog et al., 2006) using software packages26,27. There might be other arguments for introducing parameters into a model of a system even if the time scale of one level is comparable to the currently targeted level of the model. Those include a case where state variables at different levels interact statistically through, for example, a mean field of a number of individual dynamics, and some other cases where the magnitude of the interaction is weaker than those involved in the model at each level.
Let us briefly consider an example of ambitious challenges as an integrative research paradigm on a motor dysfunction and its therapeutic processes in neurological disease, in particular postural instability during upright standing in patients with Parkinson disease, a typical degenerative disorder of the central nervous system. A model of postural control at the individual level has its foundation on the systems control engineering. The model uses the intermittent feedback control as mentioned above by using Eq. (7), where the feedback control gains P and D change in a phasic and state-dependent manner to establish compliant (i.e., with a low joint impedance) posture but with robust bounded stability, reproducing well natural postural sway during human quiet stance (Bottaro et al., 2008; Asai et al., 2009). Abnormality in the intensity associated with muscle tones and temporal patterns of the gain parameters might be a cause of postural impairment. Starting from this hypothesis with the individual behavior data and the model, how can we establish a bridge from this to detailed musculo-skeletal dynamics (Delp et al., 2007), the muscle rigidity, the overactive output of the GABAergic basal ganglia with the excessive GABAergic inhibition on thalamus and pedunculopontine tegmental nucleus (PPN; (Takakusaki et al., 2008), cell level electrophysiology of related neurons (Li et al., 1996), and to signaling pathways of dopaminoceptive neurons (Fernandez et al., 2006; Lindskog et al., 2006)? If these levels are quantitatively bridged, values of the gain parameters P and D and their state-dependent alteration can be represented as the function of the parameters that characterize dynamics at the sub-cellular level. Inclusion of the sub-cellular pathway models into this multi-level paradigm is crucial for predicting efficacy of drug therapy on the motor impairment. There might be a number of barriers against promotion of the research along this line. One of them is to obtain detailed anatomical structure of related neuronal networks, among others. Nevertheless, at least, integrative studies bridging between any two adjacent levels can be achieved if we fully utilize available data and computer-technologies.
4 Concluding Remarks
There are many other related technical issues that should have been described here, including automated parallel computing technologies for standardized models (Heien et al., 2009), physiological ontology (Wimalaratne et al., 2009) that can deal with modular and hierarchical relationships embedded in physiological systems, associate biological entities and functions to physiological functions, and can perform automatic creation of multi-scale models, information about a simulation experiment28 particularly for FEM and DDE simulations, as well as curating technologies for large scale models, among others. All these technologies are necessary for accelerating the systems physiology at multiple scales and levels, and should be developed by international concerted efforts for systems biology, physiome, and neuroinformatics.
The systems physiology has a huge expectation from industry, in particular from pharmaceutical companies (Miller et al., 2005), and model based drug development has been one of the areas in the drug development recommended by Food and Drug Administration (FDA) for pharmaceutical companies29. Toward this end, models should be validated with biological and physiological experiments, and cyclic processes of accumulation of knowledge in the models are highly required. It should also be mentioned here, however, that modeling is only one part of scientific investigation, and thus, all models need to resist multiple attempts of falsification with well-controlled experiments and confirmed by independent observations before we can start to rely upon them.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The author thanks Y. Asai, H. Oka, Y. Kido, K. Hagihara, Y. Kurachi, and all member of Physiome.jp for their continuous effort for developing the platform and discussion, H. Kitano, Y. Matsuoka, and S. Ghosh for joint development of SBML–ISML hybrid modeling and simulations. The author also thanks the anonymous reviewers for comments on usefulness and limitations of the model based biological and physiological studies. This work was supported in part by MEXT G-COE program “in silico medicine” at MEI center of Osaka University.
Footnotes
- ^www.systems-biology.org
- ^sbml.org
- ^www.physiome.org.nz
- ^www.cellml.org
- ^www.physiome.org
- ^www.vph-noe.eu
- ^www.physiome.jp
- ^www.incf.org
- ^www.neuroinf.jp
- ^www.nrcam.uchc.edu/about/about_vcell.html
- ^www.celldesigner.org
- ^www.copasi.org
- ^www.ebi.ac.uk/biomodels-main/
- ^www.sbgn.org
- ^www.pantherdb.org
- ^http://www.physiome.jp/wiki/
- ^www.ebi.ac.uk/biomodels-main/MODEL2463576061
- ^www.ebi.ac.uk/biomodels-main/BIOMD0000000048
- ^ccdb.ucsd.edu
- ^neuromorpho.org
- ^www.ebi.ac.uk/biomodels-main/BIOMD0000000239
- ^www.physiome.jp/modeldb/details_model.php? rmid=478
- ^www.math.pitt.edu/bard/xpp/xpp.html
- ^bunki.sat.iis.u-tokyo.ac.jp/
- ^biomodels.net/miase/
- ^www.fda.gov/ScienceResearch/SpecialTopics/CriticalPathInitiative/CriticalPathOpportunitiesReports/ucm077262.htm
References
Asai, Y., Suzuki, Y., Kido, Y., Oka, H., Heien, E., Nakanishi, M., Urai, T., Hagihara, K., Kurachi, Y., and Nomura, T. (2008). Specifications of insilicoML 1.0: a multilevel biophysical model description language. J. Physiol. Sci. 58, 447–458.
Asai, Y., Tasaka, Y., Nomura, K., Nomura, T., Casadio, M., and Morasso, P. (2009). A model of postural control in quiet standing: robust compensation of delay-induced instability using intermittent activation of feedback control. PLoS ONE 4, e6169. doi: 10.1371/journal.pone.0006169.
Bassingthwaighte, J. B. (2000). Strategies for the physiome project. Ann. Biomed. Eng. 28, 1043–1058.
Bélair, J., Mackey, M. C., and Mahaffy, J. M. (1995). Age-structured and two-delay models for erythropoiesis. Math. Biosci. 128, 317–346.
Bottaro, A., Yasutake, Y., Nomura, T., Casadio, M., and Morasso, P. (2008). Bounded stability of the quiet standing posture: an intermittent control model. Hum. Mov. Sci. 7, 473–495.
Cheng, Y., Yu, Z., Hoshijima, M., Holst, M. J., McCulloch, A. D., McCammon, J. A., and Michailova, A. P. (2010). Numerical analysis of Ca2+ signaling in rat ventricular myocytes with realistic transverse-axial tubular geometry and inhibited sarcoplasmic reticulum. PLoS Comput. Biol. 6, e1000972. doi: 10.1371/journal.pcbi.1000972
Delp, S. L., Anderson, F. C., Arnold, A. S., Loan, P., Habib, A., John, C. T., Guendelman, E., and Thelen, D. G. (2007). OpenSim: open-source software to create and analyze dynamic simulations of movement. IEEE Trans. Biomed. Eng. 54, 1940–1950.
Faber, G. M., Silva, J., Livshitz, L., and Rudy, Y. (2007). Kinetic properties of the cardiac L-type Ca2+ channel and its role in myocyte electrophysiology: a theoretical investigation. Biophys. J. 92, 1522–1543.
Fenner, J. W., Brook, B., Clapworthy, G., Coveney, P. V., Feipel, V., Gregersen, H., Hose, D. R., Kohl, P., Lawford, P., McCormack, K. M., Pinney, D., Thomas, S. R., Sint Jan, S. V., Waters, S., and Viceconti M. (2008). The EuroPhysiome, STEP and a roadmap for the virtual physiological human. Philos. Trans. R. Soc. Lond. A 366, 2979–2999.
Fernandez, é., Schiappa, R., Girault, J.-A., and Le Novére, N. (2006). DARPP-32 is a robust integrator of dopamine and glutamate signals. PLoS Comput. Biol. 2, 1619–1633. doi: 10.1371/journal.pcbi.0020176.
Fridlyand, L. E., Tamarina, N., and Philipson, L. H. (2003). Modeling of Ca2+ flux in pancreatic beta-cells: role of the plasma membrane and intracellular stores. Am. J. Physiol. Endocrinol. Metab. 285E, 138–154.
Hauriea, C., Personc, R., Dalec, D. C., and Mackey, M. C. (1999). Hematopoietic dynamics in grey collies. Exp. Hematol. 27, 1139–1148.
Heien, E. M., Asai, Y., Nomura, T., and Hagihara, K. (2009). Optimization techniques for parallel biophysical simulations generated by insilicoIDE. IPSJ Trans. Adv. Comput. Syst. 2. 131–143.
Hodgkin, A., and Huxley, A. (1952). A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 117, 500–544.
Hunter, P. J., and Borg, T. K. (2003). Integration from proteins to organs: the physiome project. Nat. Rev. Mol. Cell Biol. 4, 237–243.
Idate, M. A., Tanaka, G., Takeuchi, T., and Aihara, K. (2008). A mathematical model of intermittent androgen suppression for prostate cancer. J. Nonlinear Sci. 18, 593–614.
Jiang, N., Cox, R. D., and Hancock, J. M. (2007). A kinetic core model of the glucose-stimulated insulin secretion network of pancreatic β cells. Mamm. Genome 18, 508–520.
Keizer, J., and Smolen, P. (1991). Bursting electrical activity in pancreatic beta cells caused by Ca2+- and voltage-inactivated Ca2+ channels. Proc. Natl. Acad. Sci. U.S.A. 88, 3897–3901.
Kholodenko, B. N. (2002). MAP kinase cascade signaling and endocytic trafficking: a marriage of convenience? Trends Cell Biol. 12, 173–177.
Kholodenko, B. N., Demin, O. V., Moehren, G., and Hoek, J. B. (1999). Quantification of short term signaling by the epidermal growth factor receptor. J. Biol. Chem. 274, 30169–30181.
Kitano, H. (2010). Grand challenges in systems physiology. Front. Physiol. 1:3. doi: 10.3389/fphys.2010.00003.
Li, Y.-X., Bertram, R., and Rinzel, J. (1996). Modeling N-methyl-D-aspartate-induced bursting in dopamine neurons. Neuroscience 71, 397–410.
Lindskog, M., Kim, M., Wikstrom, M. A., Blackwell, K. T., and Kotaleski, J. H. (2006). Transient calcium and dopamine increase PKA activity and DARPP-32 phosphorylation. PLoS Comput. Biol. 2, 1045–1060. doi: 10.1371/journal.pcbi.0020119.
Lotka, A. J. (1920). Analytical note on certain rhythmic relations in organic systems. Proc. Natl. Acad. Sci. U.S.A. 6, 410–415.
Matsuoka, Y., Ghosh, S., Kikuchi, N., and Kitano, H. (2010). Payao: a community platform for SBML pathway model curation. Bioinformatics 26, 1381–1383.
Miller, R., Ewy, W., Corrigan, B. W., Ouellet, D., Hermann, D., Kowalski, K. G., Lockwood, P., Koup, J. R., Donevan, S., El-Kattan, A., Li, C. S. W., Werth, J. L., Feltner, D. E., and Lalonde, R. L. (2005). How modeling and simulation have enhanced decision making in new drug development. J. Pharmacokinet. Pharmacodyn. 32, 185–197.
Milton, J. (2003). “Pupil light reflex: delays and oscillations,” in Nonlinear Dynamics in Physiology and Medicine, eds. A. Beuter, L. Glass, M. C. Mackey, and M. S. Titcombe (New York, Berlin, Heidelberg: Springer-Verlag), 271–302.
Milton, J., Townsend, J. L., King, M. A., and Ohira, T. (2009). Balancing with positive feedback: the case for discontinuous control. Philos. Trans. R Soc. Lond. A 367, 1181–1193.
Mitsuhashi, N., Fujieda, K., Tamura, T., Kawamoto, S., Takagi, T., and Okubo, K. (2009). BodyParts3D: 3D structure database for anatomical concepts. Nucleic Acids Res. 37, D782–D785.
Morohashi, M., Winn, A. E., Borisuk, M. T., Bolouri, H., Doyle, J., and Kitano, H. (2002). Robustness as a measure of plausibility in models of biochemical networks. J. Theor. Biol. 216, 19–30.
Morris, C., and Lecar, H. (1981). Voltage oscillations in the barnacle giant muscle fiber. Biophys. J. 35, 193–213.
Oda, K., Matsuoka, Y., Funahashi, A., and Kitano, H. (2005). A comprehensive pathway map of epidermal growth factor receptor signaling. Mol. Syst. Biol. 1, 2005.0010.
Ottesen, J. T. (2000). Modelling the dynamical baroreflex-feedback control. Math. Comput. Model 31, 167–173.
Rinzel, J., and Ermentrout, B. (1998). “Analysis of neural excitability and oscillations,” in Methods of Neuronal Modeling, eds. C. Koch and I. Segev (Cambridge: MIT Press), 251–292.
Shakhnovich, B. E. (2005). Improving the precision of the structure–function relationship by considering phylogenetic context. PLoS Comput. Biol. 1, e9. doi: 10.1371/journal.pcbi.0010009.
Takakusaki, K., Tomita, N., and Yano, M. (2008). Substrates for normal gait and pathophysiology of gait disturbances with respect to the basal ganglia dysfunction. J. Neurol. 255(Suppl. 4), 19–29.
Weibel, E. R., Taylor, C. R., and Hoppeler, H. (1991). The concept of symmorphosis: a testable hypothesis of structure–function relationship. Proc. Natl. Acad. Sci. U.S.A. 88, 10357–10361.
Keywords: integrative physiology, multi-scale simulation, physiome, systems biology, model database, SBML, ISML
Citation: Nomura T (2010) Toward integration of biological and physiological functions at multiple levels. Front. Physio. 1:164. doi: 10.3389/fphys.2010.00164
Received: 01 November 2010;
Paper pending published: 27 November 2010;
Accepted: 09 December 2010;
Published online: 29 December 2010.
Edited by:
Hiroaki Kitano, The Systems Biology Institute, JapanReviewed by:
Marco Viceconti, Istituto Ortopedico Rizzoli, ItalyNorihiro Kikuchi, Mitsui Knowledge Industry Co., Ltd, Japan
Hiroyoshi Toyoshiba, Takeda Pharmaceutical Company Limited, Japan
Copyright: © 2010 Nomura. This is an open-access article subject to an exclusive license agreement between the authors and the Frontiers Research Foundation, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Taishin Nomura, Division of Bioengineering, Graduate School of Engineering Science, Osaka University, 1-3 Machikaneyama, Toyonaka, Osaka, Japan. e-mail:dGFpc2hpbkBicGUuZXMub3Nha2EtdS5hYy5qcA==
