- 1 Division of Imaging Sciences, School of Medicine, Kings College London, London, UK
- 2 Edinburgh Parallel Computing Centre, School of Physics and Astronomy, University of Edinburgh, Edinburgh, Scotland
- 3 Oxford e-Research Centre, University of Oxford, Oxford, UK
- 4 Institute of Biophysics, Medical University of Graz, Graz, Austria
In this study, the feasibility of conducting in silico experiments in near-realtime with anatomically realistic, biophysically detailed models of human cardiac electrophysiology is demonstrated using a current national high-performance computing facility. The required performance is achieved by integrating and optimizing load balancing and parallel I/O, which lead to strongly scalable simulations up to 16,384 compute cores. This degree of parallelization enables computer simulations of human cardiac electrophysiology at 240 times slower than real time and activation times can be simulated in approximately 1 min. This unprecedented speed suffices requirements for introducing in silico experimentation into a clinical workflow.
Introduction
Recent advances in computational biology and medical imaging now make the development of patient specific multiscale models an attractive and viable option. Such models offer the capacity to link cellular scale pathologies to organ scale diagnostic modalities, improve patient selection, and optimize increasingly complicated procedures (Rudy et al., 2008). Central to the introduction of patient specific computational models into a clinical workflow is the development of mathematical, numerical, and computational techniques that enable the rapid solution of the governing equations which are required to represent physiological systems.
A specific example in this context is the organ scale modeling of cardiac electrophysiology, which is one of the exemplar multiscale systems for both the international Physiome (Hunter et al., 2005) and Virtual Physiological Human modeling projects (Kohl and Noble, 2009). Current models for clinical applications have been designed and developed to facilitate patient selection and planning in the future, for interventions such as catheter ablation (Dang et al., 2005), cardiac resynchronization therapy (Niederer et al., 2010), and implantation of defibrillation devices (Jolley et al., 2010).
Such computational models have the potential to impact the clinical workflow at two distinct points. Firstly, during the 2 to 4-day period between the non-invasive imaging of a patient and an invasive procedure, simulations can be performed to assist in treatment planning and patient selection. In this period the model geometry must be extracted from the clinical images, the model parameters fitted to patient data, a diagnosis made, and treatment outcomes predicted. Both fitting and prediction require multiple model simulations to explore the large parameter space. Reducing simulations times during this phase will increase the number of simulations that can be performed, in turn improving the fidelity of the models representation of the patients data and increasing the number of treatment scenarios able to be evaluated. The second point in the clinical workflow where models could potentially play a role is the interactive use of models during an invasive procedure to guide the clinician. Such interactive scenarios require simulations to be performed on the order of real time for ease of use and to minimize the risk to the patient and the economic cost of prolonged procedures. Thus rapid model development and simulation of patient specific cardiac electrophysiology models is an essential step if the developments and insights offered by multiscale computational biology are to be routinely applied to the diagnosis and planning of cardiac patient care focused on treating electromechanical abnormalities.
Recently many of the time consuming steps in developing cardiac models have been addressed. Specifically, improved high resolution MRI, image segmentation (Zhuang et al., 2008; Plank et al., 2009) and meshing techniques (Burton et al., 2006; Prassl et al., 2009) now enable the automatization of generating patient specific, high resolution geometric models. Detailed organ scale simulations of cardiac electrophysiology have been performed in smaller animals, specifically, rabbit (Ashihara et al., 2008; Bishop et al., 2010), rat (Niederer and Smith, 2009), and canine (Xie et al., 2004) hearts as well as human hearts (Potse et al., 2006; Ten Tusscher et al., 2007; Reumann et al., 2009). However, a significant barrier to the clinical translation of these models is the computational challenge of performing organ scale cardiac simulations of human hearts in the limited time windows provided by the clinical workflow. The computational cost of these simulations is high due to the spatio-temporal characteristics of electrical impulse propagation in the heart. Transients in the heart are fast, requiring high temporal resolution, and wavefronts are steep, necessitating fine spatial resolution. Combined, these two factors result in large systems of equations that have to be solved thousands of times in order to simulate a single heart beat.
It has been suggested that significant improvements in computational power and numerical techniques and/or model simplifications will be required to effectively introduce biophysical human heart simulations into the clinic due to the large problem size and the number of simulations required. Previous human whole heart simulations have taken prolonged times to simulate clinically relevant time scales, even when using advanced numerical methods or large numbers of processors. In these simulations the ratio between the time taken to perform a simulation and the amount of time simulated (ξr) varied between 13,180 and 111,000 or 3.6 and 30.8 h per 1000 ms heart beat. In parallel simulation runs with N = 26 million degrees of freedom (dof) and Nc = 32 computational cores (Potse et al., 2006), with N = 13.5 million dof and Nc = 20 (Ten Tusscher et al., 2007), and with N = 32.5 million dof and Nc = 16,384 (Reumann et al., 2009), realtime lags of ξr = 111,000, ξr = 43,200 and ξr = 13,180, respectively, were reported. An alternate strategy to parallel programming is the use spatio-temporal adaptivity. These methods may reduce simulations times by reducing the average number of dof and number of time steps required for a simulation. Using this method simulating 800 ms of fibrillatory activity in a canine ventricular model took 6 weeks (Deuflhard et al., 2009) on a single core. Even assuming perfect parallelization up to Nc = 16,384 this method would still lag real time by ξr = 277.
These examples demonstrate the limitations of previous numerical and computational techniques to perform close to real time simulations. To address these limitations we have developed a finite element cardiac electrophysiology simulation environment using fully unstructured grids for spatial discretization, optimized cell model representations, and problem specific parallel preconditioners (Vigmond et al., 2003). As opposed to improving the efficiency of computations we have focused on improving the scalability of the code to reduce simulation times by making use of massively parallelized supercomputing facilities.
To demonstrate the potential of our approach we characterize the scalability of our simulation environment for cardiac electrophysiology simulations using a whole human ventricular model. We identify and quantify the impact of scalability bottlenecks through detailed benchmarks with massively parallel simulation runs using up to 16,384 cores. The major bottlenecks are identified as load balancing and parallel I/O. Using recent advances in mesh partitioning libraries and the development of novel problem and machine specific I/O routines the scalability of the code was extended from Nc = 1,024 to Nc = 16,384 enabling simulations to be performed with ξr = 240.
This improvement in the speed of cardiac simulations allows the simulation of a 1000-ms human heart beat in under 5 min and an activation sequence to be simulated in approximately 1 min. These results demonstrate a step change in the speed of cardiac electrophysiology simulations and open the way for new and as yet unconceived applications of cardiac modeling in a clinical setting.
Materials and Methods
The spread of electrical activation and repolarization is described by a reaction-diffusion equation referred to as the monodomain equation, given by
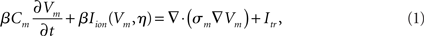
where β is the membrane surface to volume ratio, Cm is the membrane capacitance, Vm is the transmembrane voltage, Iion is the density of the total ionic current which is a function of Vm and a set of state variables η, σm is the monodomain conductivity tensor, and Itr is a transmembrane stimulus current. The eigenvalues of the conductivity tensor σm, i.e., the conductivities along the principal axes ζ of the tissue, are chosen as the harmonic mean between intracellular conductivity, σ iζ, and interstitial conductivity, σ eζ, which renders the monodomain equations axially equivalent to the more general bidomain equations. Cellular dynamics was described using the TNNP model (ten Tusscher and Panfilov, 2006). The tissue is assumed to be isolated along its boundaries, i.e., no-flux boundary conditions are imposed on Vm along all myocardial surfaces.
Numerical Solution
The reaction and diffusion part of the monodomain equations were split by employing a second-order accurate Strang scheme (Qu and Garfinkel, 1999), where the inner loop is given by
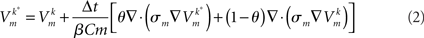


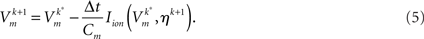
Note that the first and last time step of the splitting scheme are not explicitly shown here, only the time stepping in the inner loop. The parabolic portion (2) is solved either by choosing θ = 0.5, which results in a Crank–Nicolson scheme, or θ = 0.0, which results in an explicit forward Euler scheme. Depending on the choice of θ the overall system is solved then either with a fully explicit scheme, or an implicit–explicit (IMEX) scheme. In the latter case the linear system was solved in parallel by employing a block Jacobi preconditioner with an iterative conjugate gradient (CG) solver, using an Incomplete Cholesky [ICC(0)] factorization as a subblock preconditioner (Balay et al., 2008). The Rush–Larsen method (Rush and Larsen, 1978) was used to solve the TNNP model where an analytical solution was used to update the fast gating variables, ηf, where τ and η∞ are functions of the rate coefficients which govern channel gating, and an explicit Euler step to update all other slower state variables, ηs (Plank et al., 2008). Unlike in a recent study where a modification of the original Rush–Larsen method was proposed to achieve second-order accuracy, the method used in this study is only first order accurate, and as such second-order accuracy of the Strang splitting is not preserved in this implementation. The Cardiac Arrhythmia Research Package1 (CARP; Vigmond et al., 2003), which is built on top of the MPI-based library PETSc (Balay et al., 2008), served as a baseline simulation code for performing scalability tests.
Test Case for Benchmarking
The test case for benchmarking code scalability is derived from the heart of a cardiac resynchronization therapy candidate, the model development has been described previously (Niederer et al., 2010). Briefly, ventricular epicardium and left and right ventricular endocardium were segmented from MRI images acquired at end diastole using cmgui2. The segmented surfaces were fitted with cubic Hermite surfaces and converted into a volume mesh using CMISS3. The cubic Hermite mesh was converted to a binary image stack which was fed into the image-based mesh generation software Tarantula4 to generate a high resolution unstructured tetrahedral mesh. The resulting mesh consisted of 26 million nodes and 153 million elements with a mean edge length of 0.25 mm. To initialize the electrophysiological state of the ventricles, the isolated TNNP cell model was paced for 500 beats at 1 Hz to reach a limit cycle which was used then as the initial state in the whole ventricles. Left ventricular endocardial activation maps were used to fit monodomain conduction parameters giving values of σml = 0.035 and σmt = 0.023 Sm−1 in the fiber and transverse fiber direction, respectively. Activation at the septum was defined from left ventricular endocardial activation maps and right ventricular activation was approximated from the right ventricular activation in human hearts as described by Durrer et al. (1970). The stimulation current was applied at 50 μAmm−3 for 5 ms, first to the right ventricle activation region and then 33 ms later in the septum.
Optimization Procedures
Owing to its simplicity, only a single sparse matrix-vector product is required, strong scalability was optimized for the explicit scheme first. The optimal configuration found was applied then to the IMEX scheme without any further modifications. A global time step of 25 μs was chosen to satisfy accuracy constraints, except for solving (2) with the explicit method where the global time step was broken up into five smaller time step of 5 μs. This repetitive solution of (2) was necessitated by the fine unstructured discretization of the human heart where stability constraints were imposed on the choice of Δt as dictated by the CFL condition by the smallest elements in the grid. No stability constraints restrict time stepping when solving the TNNP ODEs with the Rush–Larsen technique, even with 1 ms stable integration with reasonable accuracy is achieved. That is, after solving the set of ODEs at the global time step of 25 μs, diffusion was solved for either by five subsequent explicit solves with dt = 5 ms or a single implicit solve with dt = 25 μs. Subsequently, the setup which was found to perform best was benchmarked then with the IMEX solver scheme. Optimization was performed stepwise. The unmodified code, as used in previous studies (Plank et al., 2009), served as a starting point. At each optimization step the same benchmark runs were executed, doubling the number of cores, Nc, starting from the minimum number required to fit the model into memory (Nc = 128), up to the critical number of cores,  at which no further performance gains could be achieved. Detailed measurements of compute and communication timings on a per-process and per-function level were performed to identify bottlenecks at each optimization step. We used the Scalasca toolset to identify and analyze high-level performance bottlenecks. To gain detailed views of specific problems, we used the Vampir trace visualization suite to analyze execution traces of the entire program. This allowed for straightforward identification of problematic areas in the code.
at which no further performance gains could be achieved. Detailed measurements of compute and communication timings on a per-process and per-function level were performed to identify bottlenecks at each optimization step. We used the Scalasca toolset to identify and analyze high-level performance bottlenecks. To gain detailed views of specific problems, we used the Vampir trace visualization suite to analyze execution traces of the entire program. This allowed for straightforward identification of problematic areas in the code.
Grid Partitioning and Load Balancing
Choosing a strategy for decomposing a computational grid into parallel partitions is a crucial step which profoundly affects parallel scaling of codes. The objective is to achieve good load balancing where both computational load as well as communication costs are distributed, as evenly as possible, among all compute cores involved. While producing a well-balanced decomposition is achieved for structured grids with relative ease (Munteanu et al., 2009), this is far more challenging in the more general case of unstructured grids, which are preferred with cardiac simulations (Vigmond et al., 2008) when general applicability is required. In this study grid partitions were created using the parallel graph partitioning library ParMeTis (Karypis and Kumar, 2009) which computes a k-way partition of the mesh’s dual graph. As opposed to the simple linear nodal-based partitioning which is the default strategy implemented in the baseline simulation code, ParMeTis computes element-based decompositions of a mesh. Grid points along the boundaries of each parallel domain are shared then between partitions and thus communication is involved when updating nodal values. Since linear algebraic functions within PETSc assemble global matrices each interface node has to be assigned to a partition. That is, the full matrix row which corresponds to a particular node resides on one partition. Therefore, after element-based grid partitioning as computed by ParMeTis, nodal indices in each domain were renumbered. Inner nodes were linearly numbered, forming the main diagonal block of the global matrix, which map onto the local rows of the linear system we solve. Interface nodes were split across adjacent partitions, aiming at evenly distributing interface nodes across the computed partitions. Interfacial nodes shared between two partitions were split equally between the first and second. Nodes shared between three or more partitions were split equally between the minimum and maximum numbered partitions. This ensured an approximately load-balanced set of interfacial nodes. Both grid partitioning and nodal renumbering were tightly integrated within the code to compute partitioning information very fast in parallel on the fly. Permutation vectors were stored to keep track of the relationship between reordered mesh and the user-provided canonical mesh. Output of results involved an additional back permutation of any result vector to write results in an ordering consistent with the canonical mesh to avoid the extra complexity of storing reordered meshes with the simulation results.
I/O Strategy
The standard approach to writing data in MPI programs uses an inline method. This method serializes the output through a single core or master processor. The master processor polls all other involved processors to send data and writes the received data serially into a file. Not only does this method effectively block all other compute cores, but the duration of each write increases with the number of cores. The introduction of this serial bottleneck into the parallel computation prevents efficient scaling.
For some file formats and machine architectures, writing in parallel is possible, however, the performance of parallel I/O is highly dependent on the system configuration. Many HPC systems optimize for multiple parallel disk accesses which allows for parallel output. Although this scheme means that the number of parallel processors that can effectively access the disk is greater than one, it is still significantly less than the maximum number of processors available. Typically, the number of parallel writes any one program can perform before performance diminishes is on the order of 100. This means that a naive implementation of this method will not continue to scale for massively parallelised simulations.
In this study an alternative asynchronous parallel output scheme is implemented which reserves a small number (<100) of cores as dedicated I/O servers. The output data are a vector distributed across all compute cores with each element describing the electrical potential at a single node. To perform output, the data are copied from the compute cores to the dedicated I/O cores. Computation of further solutions then continues immediately. Meanwhile, the I/O cores perform some post-processing on the data (mapping to a canonical ordering) and then write the data to an output file. This is a slow operation, but the latency is hidden from the overall runtime since it occurs concurrently with further computation: as long as the time to write data is shorter than the time between output calls on the compute cores, no slowdown is observed in the runtime.
Results
The speed of the code is benchmarked using a physiological monodomain simulation of human ventricles. Figure 1 shows the high resolution geometrical mesh used for the benchmark simulation and Figure 2 shows the results of the benchmark simulation. The code is benchmarked using a clinically relevant simulation of a patient suffering from left bundle branch block fitted to patient data (Niederer et al., 2010).

Figure 1. (A) Human heart mesh derived from CRT patient MRI. (B) Shows the high resolution unstructured tetrahedral mesh required to solve the monodomain equations.
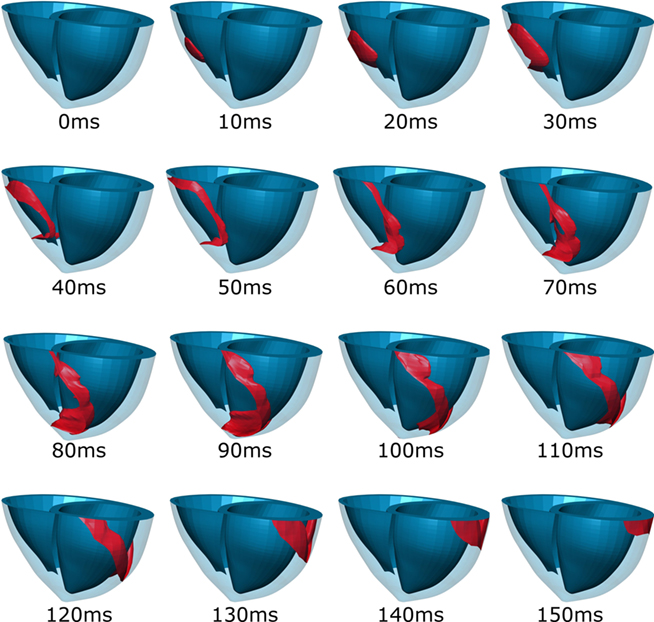
Figure 2. Activation sequence. The red isosurfaces show the points in the heart where the transmembrane potential is 0 mV. The heart is stimulated in the right ventricular freewall at 0 ms and then at the left ventricular septal endocardium at 33 ms.
Baseline Simulations
The baseline cardiac electrophysiology simulation platform (Vigmond et al., 2003) has demonstrated strong scalability with up to Nc = 128 in a smaller rabbit benchmark problem (Plank et al., 2009) before parallel efficiency degraded. Figure 3 (red traces labeled NBP-inline-EX) shows the initial scalability for a larger human heart simulation when using conventional methods implemented in the baseline code. The size of the problem means that the simulation must be performed on at least 128 processors. As Nc increased from 128 to 1024 the simulation time, continued to decrease, however, when Nc was increased from 1024 to 2048 the simulation time increased and even at Nc = 1,024 parallel efficiency was poor at only ∼40%.
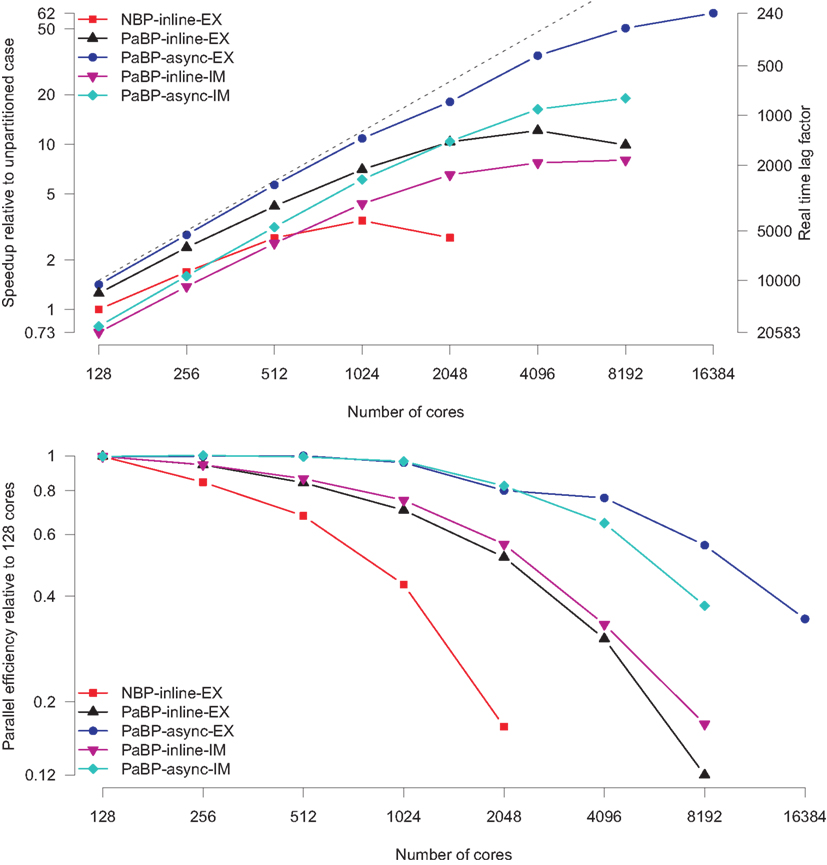
Figure 3. Benchmark results of strong scalability experiments. Shown are the effects of nodal-based (NBP) versus ParMeTis-based (PaBP) domain decomposition, implicit (IM) versus explicit (EX) solver strategy, and inline versus asynchronous (async) I/O strategy on strong scalability for a range of cores Nc between 128 and 16,384. The top panel shows parallel speedup and realtime lag factor ξr whereas the bottom panel shows parallel efficiency.
Load Balancing
The limited scalability achieved using conventional parallelization techniques can be attributed to the mesh partitioning method. The parallelization scheme used in (Vigmond et al., 2003) discretized the monodomain equations and solves them on an unstructured grid. The dof are distributed between the cores using a linear nodal-based grid partitioning. This achieves an even distribution of the computational workload, but ignores the cost of communication between mesh partitions. The information on the border of each mesh partition must be communicated to adjacent partitions. To obtain good scaling to a high Nc requires a small amount of communication relative to computation. Effective grid partitioning therefore requires a balance between both an evenly distributed computational workload and an even distribution of the communication load.
Introducing ParMeTis-based (Karypis and Kumar, 2009) partitioning, which optimizes decomposition to achieve both an even workload and communication load, improved scalability noticeably, increasing the critical number of cores, 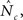 where strong scalability stalled, up to 4,096 cores. This improved performance reduced the realtime lag, ξr, from ∼5,600 to ∼1,300. Beyond 4,096 cores parallel efficiency began to degrade (Figure 3, traces PaBP-inline-EX and PaBP-inline-IM). This degradation in performance was due to the increased costs of outputting the simulation data. Measuring the time spent on this endeavor revealed an increase with Nc, reaching ∼62% of the overall execution time with Nc = 4,096. Writing data to disk was 4.3 and 4.6 times as expensive (in simulation time) as the explicit solution to the partial differential equations that model the propagation of the electrical activation and the solution of the ordinary differential equations that represent cellular dynamics, respectively.
where strong scalability stalled, up to 4,096 cores. This improved performance reduced the realtime lag, ξr, from ∼5,600 to ∼1,300. Beyond 4,096 cores parallel efficiency began to degrade (Figure 3, traces PaBP-inline-EX and PaBP-inline-IM). This degradation in performance was due to the increased costs of outputting the simulation data. Measuring the time spent on this endeavor revealed an increase with Nc, reaching ∼62% of the overall execution time with Nc = 4,096. Writing data to disk was 4.3 and 4.6 times as expensive (in simulation time) as the explicit solution to the partial differential equations that model the propagation of the electrical activation and the solution of the ordinary differential equations that represent cellular dynamics, respectively.
I/O costs
An asynchronous parallel output scheme is implemented that utilizes a limited number of specific I/O processors to improve the scalability of the code. For small Nc values (Nc < 1024) the I/O costs are of minor importance relative to the compute costs for both inline and asynchronous methods. Figure 3 shows that in this range of Nc the cost of inline and asynchronous I/O is comparable. As Nc increases beyond 1024 cores the benefits of asynchronous verses inline I/O becomes evident. Using the inline I/O scalability simulation speed peaks at Nc = 4,096 (Figure 3, top panel, trace NBP-inline-EX), however, with this number of cores a performance gain of 45% can be achieved by switching from inline to asynchronous I/O. In simulations with inline I/O and Nc > 4,096 file output begins to dominate total run times, necessitating the need to switch to asynchronous I/O to achieve further scalability. Introducing asynchronous I/O enables scaling to continue from the maximum with inline I/O of 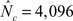 cores to
cores to 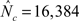 (Figure 3). This significant improvement in scalability reduces the real time lag from ξr = 1,300 to ξr = 240.
(Figure 3). This significant improvement in scalability reduces the real time lag from ξr = 1,300 to ξr = 240.
Discussion
We have demonstrated that the introduction of customized I/O and efficient mesh partitioning strategies combined with efficient code enable the simulation of a single human heart beat within 4 min and the simulation of activation time in 1 min. This step change in computational speed is essential for the introduction of multiscale cardiac tissue electrophysiology simulations into time critical clinical workflows.
The results presented in Figure 3 suggest that simulations of human cardiac electrophysiology can be performed close to but not in realtime when using current national HPC facilities such as HECToR in the United Kingdom. The benchmark shows that with the current software implementation the maximum number of cores that can be used in a simulation is approximately 16,384. Although a further speedup may be achieved by increasing Nc beyond 16,384, parallel efficiency trends (Figure 2, bottom panel, trace PaBP-async-EX) suggest that gains are expected to be insufficient to justify the increase in economic costs which incur with simulations at such a large scale. Furthermore, this setup was the largest configuration we had access to within this study. Thus even though current world leading PetaFLOPS super computers deliver up to 14 times this amount of compute power and ExaFLOPS machines will be more than 240 times more powerful, this nominal compute power will not result in faster simulation times. To reach real time simulations through hardware developments will require significant improvement in interconnect technology to reduce communication costs and the use of accelerators such as graphics processing units (GPUs) to provide faster memory access and enhanced compute power per-processing unit.
The challenge of real time simulations is formidable. A simple linear interpolation of the results in this study suggests that four million conventional CPU cores would be required to achieve realtime performance. These results indicate that new interconnect technologies are key for cardiac simulations to make effective use of the much larger number of cores available with the next generation HPC resources. Improved interconnect technology will increase simulation speed in two ways by allowing the code to effectively utilize more cores and by decreasing the actual time spent communicating. With each additional core the amount of useful compute work performed per node decreases but the total time spent on communication increases. Eventually the increase in communication cost with an additional core outweighs the reduced computational work. In the benchmark problem this occurs when the number of dof per partition drops below ∼1,500. This lower bound on the number of dof per partition is independent of the overall problem size and allows the optimal number of cores to be calculated for a given problem. Faster interconnect technology reduces the communication cost of adding an additional core and this will allow efficient scaling to much larger values of 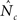 with significantly lower compute load per partition. In the benchmark problem with Nc = 16,384 approximately 50% of the overall execution time is spent on communication.
with significantly lower compute load per partition. In the benchmark problem with Nc = 16,384 approximately 50% of the overall execution time is spent on communication.
Alternatively, using accelerators such as GPUs may prove to be a viable strategy to achieve substantial performance gains. Preliminary results on GPU performance in the context of cardiac monodomain simulations have shown that solving the set of non-linear ODEs of the cellular model on the GPU could be sped up by a factor in the range 9–17 (Vigmond et al., 2009) and the solution of the linear system by a factor 12 (Haase et al., 2009) where parallel scalability over four GPUs matched scalability over four CPUs.
The results shown here demonstrate a step change in the speed of cardiac electrophysiology simulations. At the same time they expose the limitations of current HPC hardware. Simply adding in additional cores is unlikely to provide a computational framework that can be exploited by electrophysiology codes to provide realtime simulations. The simulation results motivate the need to focus design and implementation of algorithms which are suited to fully exploit the advances in GPU and interconnect technology in new HPC architectures for real time human heart electrophysiology simulations to become a reality.
Conclusions
The performance of the results shown here is a clear demonstration of the ability to simulate human heart cardiac electrophysiology compatible with the time critical needs of industrial or clinical scenarios.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work made use of the facilities of HECToR, the UK’s national high-performance computing service, which is provided by UoE HPCx Ltd at the University of Edinburgh, Cray Inc. and NAG Ltd, and funded by the Office of Science and Technology through EPSRC’s High End Computing Programme. Gernot Plank acknowledges the support of the Austrian Science Fund FWF grant F3210-N18. Lawrence Mitchell is funded under a HECToR distributed Computational Science and Engineering grant from NAG Ltd. Steven Niederer is funded by EPSRC grant EP/F043929/1. Nicolas Smith acknowledges EP/G007527/1.
Footnotes
References
Ashihara, T., Constantino, J., and Trayanova, N. A. (2008). Tunnel propagation of postshock activations as a hypothesis for fibrillation induction and isoelectric window. Circ. Res. 102, 737–745.
Balay, S., Buschelman, K., Eijkhout, V., Gropp, W. D., Kaushik, D., Knepley, M. G., McInnes, L. C., Smith, B. F., and Zhang, H. (2008). PETSc Users Manual. Technical report ANL-95/11 – Revision 3.0.0. Argonne National Laboratory, Argonne, IL.
Bishop, M. J., Plank, G., Burton, R. A. B., Schneider, J. E., Gavaghan, D. J., Grau, V., and Kohl, P. (2010). Development of an anatomically detailed MRI-derived rabbit ventricular model and assessment of its impact on simulations of electrophysiological function. Am. J. Physiol. Heart Circ. Physiol. 298, H699–H718.
Burton, R. A. B., Plank, G., Schneider, J. E., Grau, V., Ahammer, H., Keeling, S. L., Lee, J., Smith, N. P., Gavaghan, D., Trayanova, N., and Kohl, P. (2006). Three-dimensional models of individual cardiac histoanatomy: tools and challenges. Ann. N. Y. Acad. Sci. 1080, 301–319.
Dang, L., Virag, N., Ihara, Z., Jacquemet, V., Vesin, J.-M., Schlaepfer, J., Ruchat, P., and Kappenberger, L. (2005). Evaluation of ablation patterns using a biophysical model of a trial fibrillation. Ann. Biomed. Eng. 33, 465–474.
Deuflhard, P., Erdmann, B., Roitzsch, R., and Lines, G. T. (2009). Adaptive finite element simulation of ventricular fibrillation dynamics. Comput. Vis. Sci. 12, 201–205.
Durrer, D., van Dam, R. T., Freud, G. E., Janse, M. J., Meijler, F. L., and Arzbaecher, R. C. (1970). Total excitation of the isolated human heart. Circulation 41, 899–912.
Haase, G., Liebmann, M., Douglas, C., and Plank, G. (2010). “Parallel algebraic multigrid on general purpose GPUs,” in Proceedings of the 3rd Austrian Grid Symposium, Vol. 269, eds J. Volkert, T. Fahringer, D. Kranzelmueller, R. Kobler, and W. Schreiner (Linz: OCG), 28–37.
Hunter, P., Smith, N., Fernandez, J., and Tawhai, M. (2005). Integration from proteins to organs: the IUPS physiome project. Mech. Ageing Dev. 126, 187–192.
Jolley, M., Stinstra, J., Tate, J., Pieper, S., MacLeod, R., Chu, L., Wang, P., and Triedman, J. K. (2010). Finite element modeling of subcutaneous implantable defibrillator electrodes in an adult torso. Heart Rhythm 7, 692–698.
Karypis, G., and Kumar, V. (2009). MeTis: Unstructured Graph Partitioning and Sparse Matrix Ordering System. Minneapolis, MN: University of Minnesota.
Kohl, P., and Noble, D. (2009). Systems biology and the virtual physiological human. Mol. Syst. Biol. 5, 292. doi:10.1038/msb.2009.51
Munteanu, M., Pavarino, L. F., and Scacchi, S. (2009). A scalable Newton-Krylov-Schwarz method for the bidomain reaction-diffusion system. SIAM J. Sci. Comput. 31, 3861–3883.
Niederer, S. A., Plank, G., Chinchapatnam, P., Ginks, M., Lamata, P., Rhode, K. S., Rinaldi, C. A., Razavi, R., and Smith, N. P. (2010). Length-dependent tension in the failing heart and the efficacy of cardiac resynchronization therapy. Cardiovasc. Res. 89, 336–343.
Niederer, S. A., and Smith, N. P. (2009). The role of the frank-starling law in the transduction of cellular work to whole organ pump function: a computational modeling analysis. PLoS Comput. Biol. 5, e1000371.
Plank, G., Burton, R. A. B., Hales, P., Bishop, M., Mansoori, T., Bernabeu, M. O., Garny, A., Prassl, A. J., Bollensdor, C., Mason, F., Mahmood, F., Rodriguez, B., Grau, V., Schneider, J. E., Gavaghan, D., and Kohl, P. (2009). Generation of histo-anatomically representative models of the individual heart: tools and application. Philos. Transact. A Math. Phys. Eng. Sci. 367, 2257–2292.
Plank, G., Zhou, L., Greenstein, J. L., Cortassa, S., Winslow, R. L., O’Rourke, B., and Trayanova, N. A. (2008). From mitochondrial ion channels to arrhythmias in the heart: computational techniques to bridge the spatio-temporal scales. Philos. Transact. A Math. Phys. Eng. Sci. 366, 3381–3409.
Potse, M., Dube, B., Richer, J., Vinet, A., and Gulrajani, R. M. (2006). A comparison of monodomain and bidomain reaction-diffusion models for action potential propagation in the human heart. IEEE Trans. Biomed. Eng. 53, 2425–2435.
Prassl, A. J., Kickinger, F., Ahammer, H., Grau, V., Schneider, J. E., Hofer, E., Vigmond, E. J., Trayanova, N. A., and Plank, G. (2009). Automatically generated, anatomically accurate meshes for cardiac electrophysiology problems. IEEE Trans. Biomed. Eng. 56, 1318–1330.
Qu, Z., and Garfinkel, A. (1999). An advanced algorithm for solving partial differential equation in cardiac conduction. IEEE Trans. Biomed. Eng. 46, 1166–1168.
Reumann, M., Fitch, B. G., Rayshubskiy, A., Keller, D. U., Seemann, G., Doessel, O., Pitman, M. C., and Rice, J. J. (2009). Strong scaling and speedup to 16,384 processors in cardiac electro-mechanical simulations. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2795–2798.
Rudy, Y., Ackerman, M. J., Bers, D. M., Clancy, C. E., Houser, S. R., London, B., McCulloch, A. D., Przywara, D. A., Rasmusson, R. L., Solaro, R. J., Trayanova, N. A., Van Wagoner, D. R., Varro, A., Weiss, J. N., and Lathrop, D. A. (2008). Systems approach to understanding electromechanical activity in the human heart: a national heart, lung, and blood institute workshop summary. Circulation 118, 1202–1211.
Rush, S., and Larsen, H. (1978). A practical algorithm for solving dynamic membrane equations. IEEE Trans. Biomed. Eng. 25, 389–392.
Ten Tusscher, K. H., Hren, R., and Panfilov, A. V. (2007). Organization of ventricular brillation in the human heart. Circ. Res. 100, e87–e101.
ten Tusscher, K. H., and Panfilov, A. V. (2006). Alternans and spiral breakup in a human ventricular tissue model. Am. J. Physiol. Heart Circ. Physiol. 291, H1088–H1100.
Vigmond, E. J., Boyle, P. M., Leon, L., and Plank, G. (2009). Near-real-time simulations of bioelectric activity in small mammalian hearts using graphical processing units. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2009, 3290–3293.
Vigmond, E. J., Hughes, M., Plank, G., and Leon, L. J. (2003). Computational tools for modeling electrical activity in cardiac tissue. J. Electrocardiol. 36(Suppl.), 69–74.
Vigmond, E. J., Weber dos Santos, R., Prassl, A. J., Deo, M., and Plank, G. (2008). Solvers for the cardiac bidomain equations. Prog. Biophys. Mol. Biol. 96, 3–18.
Keywords: monodomain model, personalized health care, strong scalability
Citation: Niederer S, Mitchell L, Smith N and Plank G (2011) Simulating human cardiac electrophysiology on clinical time-scales. Front. Physio. 2:14. doi:10.3389/fphys.2011.00014
Received: 10 January 2011;
Paper pending published: 14 February 2011;
Accepted: 26 March 2011;
Published online: 9 April 2011.
Edited by:
Timothy W. Secomb, University of Arizona, USAReviewed by:
Ellen Kuhl, Stanford University, USAJoakim Sundnes, Simula Research Laboratory, Norway
Copyright: © 2011 Niederer, Mitchell, Smith and Plank. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence: Gernot Plank, Institute of Biophysics, Medical University of Graz, A-8010 Graz, Austria. e-mail:Z2Vybm90LnBsYW5rQG1lZHVuaWdyYXouYXQ=



