- 1 Department of Biomedical Engineering and Institute for Computational Medicine, Johns Hopkins University, Baltimore, MD, USA
- 2 Functional Genomics and Systems Biology, IBM T.J. Watson Research Center, Yorktown Heights, NY, USA
The heart is a multiphysics and multiscale system that has driven the development of the most sophisticated mathematical models at the frontiers of computational physiology and medicine. This review focuses on electromechanical (EM) models of the heart from the molecular level of myofilaments to anatomical models of the organ. Because of the coupling in terms of function and emergent behaviors at each level of biological hierarchy, separation of behaviors at a given scale is difficult. Here, a separation is drawn at the cell level so that the first half addresses subcellular/single-cell models and the second half addresses organ models. At the subcellular level, myofilament models represent actin–myosin interaction and Ca-based activation. The discussion of specific models emphasizes the roles of cooperative mechanisms and sarcomere length dependence of contraction force, considered to be the cellular basis of the Frank–Starling law. A model of electrophysiology and Ca handling can be coupled to a myofilament model to produce an EM cell model, and representative examples are summarized to provide an overview of the progression of the field. The second half of the review covers organ-level models that require solution of the electrical component as a reaction–diffusion system and the mechanical component, in which active tension generated by the myocytes produces deformation of the organ as described by the equations of continuum mechanics. As outlined in the review, different organ-level models have chosen to use different ionic and myofilament models depending on the specific application; this choice has been largely dictated by compromises between model complexity and computational tractability. The review also addresses application areas of EM models such as cardiac resynchronization therapy and the role of mechano-electric coupling in arrhythmias and defibrillation.
Introduction
The myocardium is inherently multiscale in that microscopic events at the subcellular level generate emergent properties at the macroscopic tissue level. In fact, many phenomena at the whole-heart level can be correlated with similar behaviors in myocytes or isolated muscle [e.g., interval–force relations (Wier and Yue, 1986), dynamic elastance behaviors (Campbell et al., 1993), inotropic effects of ejection (De Tombe and Little, 1994)]. In the first part of this review article, we discuss efforts to model the actin–myosin interactions and Ca-based activation events in cardiac myofilaments and single cells. The main focus is on models that are amenable to be extended to multiscale and then to organ cardiac models. However, some foundational models are discussed even if not directly applicable to organ-level cardiac models. To segregate the material, the methods to represent actin–myosin cycling are discussed first. The subsequent section describes Ca-based activation alone, although this segregation from actin–myosin cycling is simplistic given the close coupling between systems. Next, we discuss models of actin–myosin and Ca-based activation that are referred to as myofilament (MF) models. Finally, a coupling of a MF model with a cellular reconstruction of electrophysiology and Ca handling (termed EP cell models) forms an electromechanical (EM) cell model. Representative examples of existing EM cell models are described to illustrate state-of-the-art approaches.
The second half of the paper describes multiscale cardiac electromechanical modeling at the organ (ventricular) level, emphasizing the myofilament and single-cell EM models used in the organ-level models. Our choice to limit the scope of the multiscale modeling discussion to ventricular models only stems from our desire to also present the state-or-the-art in organ modeling. Multiscale EM modeling at the organ-level requires solution of coupled electrical and mechanical components. The electrical component simulates the propagation of a wave of transmembrane potential by solving a reaction–diffusion system. For the mechanical component, active tension generated by the myocytes is used to compute the deformation of the organ, as described by continuum mechanics. Solution typically involves the use of the finite element methods so that the governing equations are thus solved on a spatially discretized version of the heart volume, i.e., on the computational mesh. The properties of individual elements derive from the EM cell models discussed in the first part of this review. The multiscale nature of the system may produce properties at the organ level that may or may not translate from the cellular level in a straightforward way. Organ-level models require additional complexity in both the problem definition (i.e., representation of the complex anatomy of the ventricles) and the computational methods. For example, reentrant arrhythmias at the organ level are complex emergent behaviors that can not be simply extrapolated from the cellular level behaviors. The second half of this review covers the current use of models to understand complex problems such as mechano-electric feedback and cardiac resynchronization therapy (CRT) in heart failure.
Modeling from Myofilament to Cell
General Approach
Myofilaments have been a very difficult system to model because of controversies over the fundamental biophysical mechanisms and the appropriate mathematical representations. In brief, there is no consensus as to the correct method to mathematically represent actin–myosin interactions. In Ca-based activation, the myofilaments exhibit high sensitivity to activator Ca that is thought to arise from one or more cooperative interactions at the molecular level. An additional level of complexity arises because actin–myosin interactions and Ca-based activation are coupled in a complicated feedforward and feedback system. The feedforward is that Ca-binding produces an allosteric shift of troponin/tropomyosin on the thin filament to allow actin–myosin interactions (known as the steric hindrance model). However, feedback occurs as bound crossbridges (XBs) are also thought to produce a steric shift of troponin/tropomyosin on the thin filament that is independent of Ca activation (see discussion in Rice et al., 1999). Hence, the Ca-based activation cannot be considered as a simple switch that controls XB cycling; the system is more coupled and interdependent.
For computational efficiency, most current models are simplified and attempt to use lumped-parameter or mean-field approaches, two methods that are well known in biological mathematical modeling and simulation. In these approaches, a single scalar is used to represent properties of large populations of proteins, and the model does not track individual proteins. Hence, such approaches typically consider mean behavior as representing the population, a construct that greatly increases the computational efficiency of the model. That is, lumped-parameter or mean-field approaches can be computed with ordinary differential equations (ODE) that are similar to the governing equations for electrophysiology and Ca handling in most single-cell reconstructions of the action potential. Hence, the coupling of the latter models to an ODE-based myofilaments model produces a logical building block for tissue-based models that are discussed in the second half of the review.
Modeling crossbridge cycling
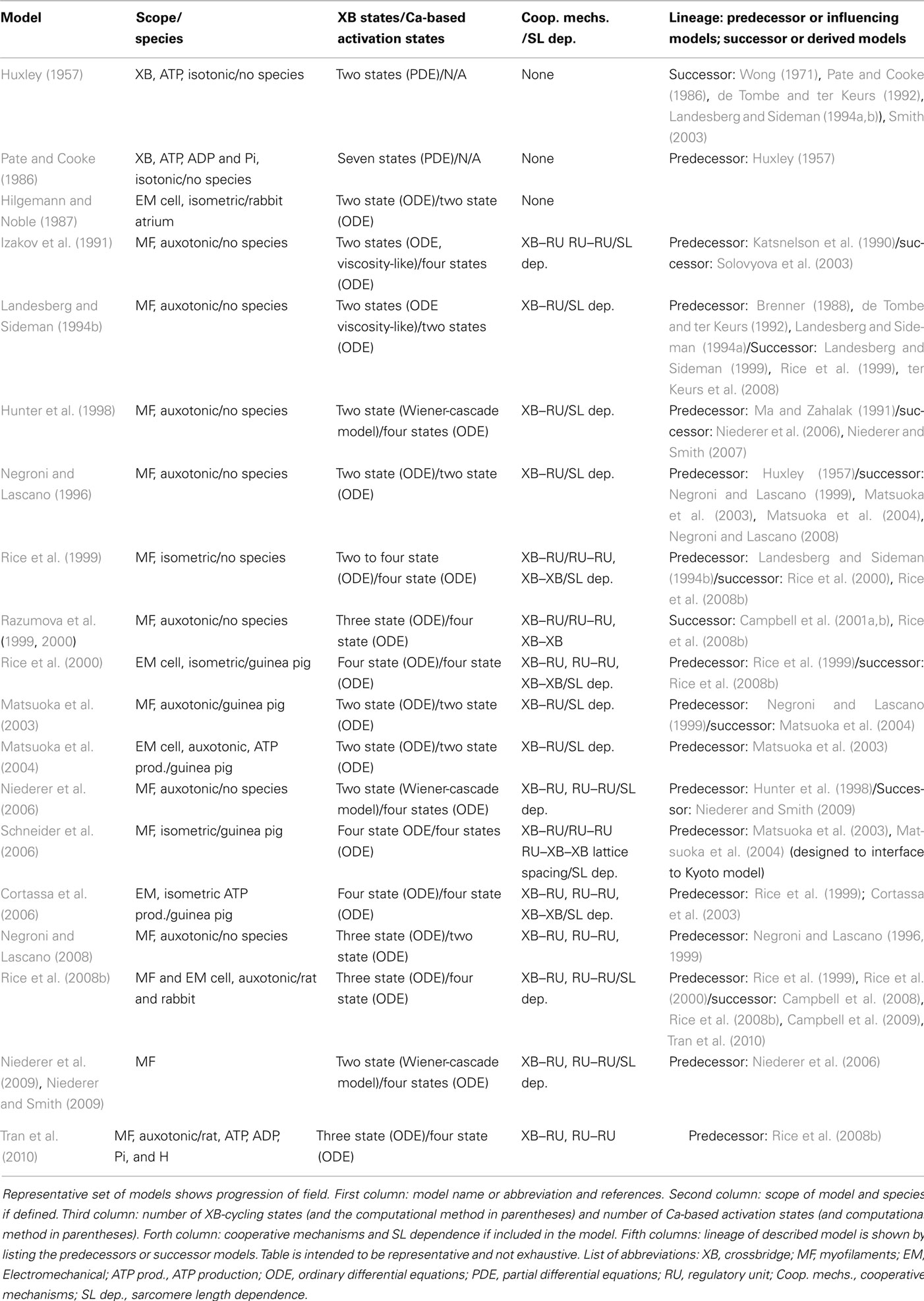
The earliest and arguably the most influential work is the model of Huxley (1957). The model, as originally described, is relatively simple and contains only two states for the XBs, attached and detached (see Figure 1A). The rate constants for attachment and detachment of the XB are assumed to be functions of the relative position of the actin-binding site to the equilibrium position of the nearest XB (see Figure 1C). The attachment rate is a linearly increasing function for positive distortions up to a limit of h. Hence, strong-bound XBs tend to attach with positive distortions that generate positive force (see X2 case in Figure 1C). The detachment rates have uniformly large values for negative distortions. The construction produces a mechanism in which the myosin tends to attach with a positive distortion that generates a positive force. If active shortening occurs, then the attached XB can become negatively strained and contribute a negative force (see X1 case in Figure 1C). The XBs tend to detach quickly, as the detachment rate is large for negative strains. The force of an attached XB is assumed to be a linear function of the distortion from the equilibrium position; hence, the attached XB acts like a simple spring. This assumption of attached XBs acting as ideal springs is carried over to essentially all later models.
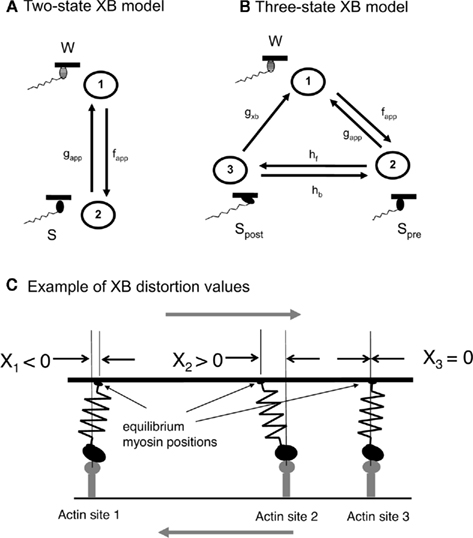
Figure 1. Models of crossbridge attachment and definition of distortion. (A) A two-state model of XB cycling in which the upper state is assumed to be either detached or weakly bound (state 1), while the lower state is attached or strongly bound (state 2). The schematic descriptions show a functional unit with troponin/tropomyosin, associated seven actin units, and one nearby XB (see text for details). (B) A three-state model of XB cycling in which state 1 corresponds to detached/weakly bound, state 2 represents strongly bound and pre-rotated, and state 3 represents strongly bound and post-rotated. The transition rates between states are bidirectional, except for the transition rate gXB between state 3 and 1 that correspond to the release of ADP and the binding of ATP, so that reverse rate is essentially zero. (C) Schematic diagram shows examples of crossbridge distortion values. The myosin heads are assumed to bind to actin sites and generate force that is directly proportional to the distortion defined as the distance from the equilibrium position to the actin site in the direction parallel to the filaments (the example shows X2 > X3 > X1). Muscle shortening causes motions of the thick and thin filaments that are shown by the gray arrows, such that distortion values decrease with time (i.e., dXn/dt < 0 for n = 1, 2, 3, etc.).
A critical feature of the Huxley model is that the population of attached XBs is computed as a function of strain (the distortion of the XB from its equilibrium position). Specifically, a probability density function (PDF) is computed that describes the fraction of attached XBs as a function of strain [the term PDF (strain = x) in Eq. 1 below]. The computation of the PDF requires the solution of a partial differential equation (PDE) in the general case. Specifically, in a spatially explicit model, the active force (Factive) is proportional to the expected value of the force of attached XBs (〈FXB〉) that is expressed as
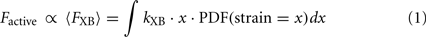
where the first two terms in the integral represent the force of an attached XB as a linear spring constant kXB multiplied by the distortion x. The third term is the PDF of an attached strongly bound XB with distortion x. The fractional occupancy of the strongly bound states for a given distortion x is computed as an interplay of two features: (1) attachment and detachment at given x, and (2) the gain and loss of strongly bound XBs at a given x as the muscle shortens or lengthens. That is, the distortion of strongly bound XBs will decrease with time if the muscle is shortening and will increase with time if the muscle is lengthening. This formalism is derived from the classic modeling work of Huxley (1957) and is used in more contemporary models with explicit spatial representations requiring the solution of PDEs (Wong, 1971; Pate and Cooke, 1986; Smith, 2003).
The main findings of the Huxley model are that increasing contraction velocities decrease force by both decreasing the fraction of attached XBs and decreasing the average distortion of the attached XBs. The combination of these effects can explain both the hyperbolic shape of the force–velocity curves and the “shortening heat,” i.e., the increase in ATP usage during active contraction. While the model provides the biophysical basis to understand certain complex muscle behaviors, other phenomena are not well reproduced. For example, the model shows increased ATPase rates for active stretching because it assumes that XBs always detach via an ATP-consuming step. In contrast, in real muscle, increased ATPase activity makes little sense given that work is being performed on the muscle, not by the muscle, in active stretching. As another example, the model fails to predict the force transients following a rapid length change observed in experiments (Ford et al., 1977). However, more realistic behaviors are found with later models incorporating additional attachment states and complex cycling schemes (Slawnych et al., 1994; Negroni and Lascano, 2008).
Despite the high level of abstraction, the two-state XB model continues to be used in models of the myofilaments, often with modifications to represent more complex phenomena. For example, the Landesberg–Sideman (LS) model (Landesberg and Sideman, 1994b) and later derivatives represent XBs by a two-states model that is essentially similar to that formulated by Brenner (1988) to represent the psoas muscle. Note that instead of detached and attached as in earlier models, the assumed states are “weakly” and “strongly bound.” In most models, weakly bound refers to a transient, electrostatic binding that is thought to precede the force-generating strongly bound state (Eisenberg and Hill, 1985). Weakly bound or completely detached are assumed to be equivalent in not generating force. In this model, the developed force is proportional to the fraction of strongly bound XBs under isometric conditions. Hence on average, each attached XB generates equivalent force.
For other than isometric conditions, the shortening or lengthening of muscle is assumed to change the average distortion of XBs. As a phenomenological approximation, the developed force is a viscosity-like function of velocity in several models, including the LS and Negroni–Lascano (NS; Negroni and Lascano, 1996). Justification for this approximation comes from the work of de Tombe and ter Keurs (1992) who showed the viscous-like behavior to be a prediction of the Huxley model under conditions of constant shortening velocity. Velocity is also assumed to affect the detachment rate of the XBs so that greater rates of shortening lead to enhanced transitions from strongly to weakly bound states, resulting in both decreased force and increased ATPase activity. These behaviors are consistent with the increased ATPase rate during active shortening, a phenomenon termed the Fenn effect (Fenn, 1924). The Fenn effect has been described for skeletal muscle but has yet to be definitively confirmed in cardiac muscle (Hisano and Cooper, 1987) and may even reverse for low Ca activation levels (Stienen et al., 1993). Some myofilaments models (e.g., Landesberg and Sideman, 1999) have included the Fenn effect as model validation; however, the lack of experimental confirmation renders these simulation results as speculative rather than positive model validations at this time.
Work by Campbell, Razumova, and co-workers (Razumova et al., 1999; Campbell et al., 2001a,b) proposed a kinetic model of the XB cycle (see Figure 1B) that has three states: weakly bound (equivalent to detached); strongly bound but pre-force (pre-rotation of the myosin head); and strongly bound and force (post-rotation of the myosin head). This simplified three-state model, referred to here as the CRC model, retains enough machinery to recapitulate many measured phenomena, including force–velocity relations, small step and harmonic responses (Razumova et al., 1999), and twitches (Campbell et al., 2001a). Unlike the two-state XB scheme of the Huxley model and its derivatives, the presence of force and pre-force states allows for separate calculations of force and stiffness. Also the system can relax back from the force-generating state to the relaxed state via reversible reactions that do not require ATP hydrolysis and hence can reduce net ATP consumption. In contrast, two-state XB models always require ATP hydrolysis to relax from the force-generating state, resulting in unrealistically large ATPase turnover at physiological rates (see discussion in Rice et al., 1999).
On the other hand, with only three states and a small number of transition rates, the CRC model lacks direct mapping of model states to biochemical states as in more complex models such as the seven-state model of Pate and Cooke (1986). Hence, the model generally lacks the versatility and the extensibility to provide insights into experimental results with manipulations such as the use of caged compounds or modified analogs of ATP. However, the work of Pate and Cooke (1986) and similar models come at the expense of requiring the solution of a system of PDEs.
Modeling calcium-based activation
In the steric hindrance model, activation is controlled by an allosteric shift of troponin/tropomyosin on the thin filament to allow actin–myosin interactions. Troponin (Tn) is a three subunit complex of troponin C (TnC), troponin I (TnI), and troponin T (TnT) (see Figure 2A). The TnC subunit can bind Ca at two high affinity sites on the C terminus and one low affinity site on the N terminus that has the regulatory function. The binding of Ca to the N terminus of TnC induces TnI to move by as much as 1.5 nm from its diastolic blocking state (tightly bound to actin) to its systolic state (tightly bound to TnC). The altered locations of TnC and TnI are thought to shift tropomyosin (Tm) to the systolic position via the intermediary TnT that is thought to contact all the other proteins (TnC, TnI, and Tm; Solaro and Rarick, 1998). Tm is a double-stranded α-helical protein that winds around the actin backbone, spanning seven subunits (see Figure 2A). Importantly, the Tm units connect end-to-end by an overlap of 5–10 residues, and TnI potentially bridges the overlap of the two adjacent Tms (Solaro and Rarick, 1998). The two separate 1-D lattices of Tms sit in the grooves of the two-stranded helical backbone of actin in the thin filaments. The most simplistic interpretation of the steric hindrance model assumes that the diastolic states of Tn/Tm completely block binding of myosin. However, considerable evidence points to weak binding of XBs with Tn/Tm in the diastolic states, a feature that could allow the thin filament to sense the number of nearby myosin heads before the strong-binding, force-generating states (Chalovich et al., 1981). This feature has implications for sensing muscle length (see Modeling Length Sensitivity).
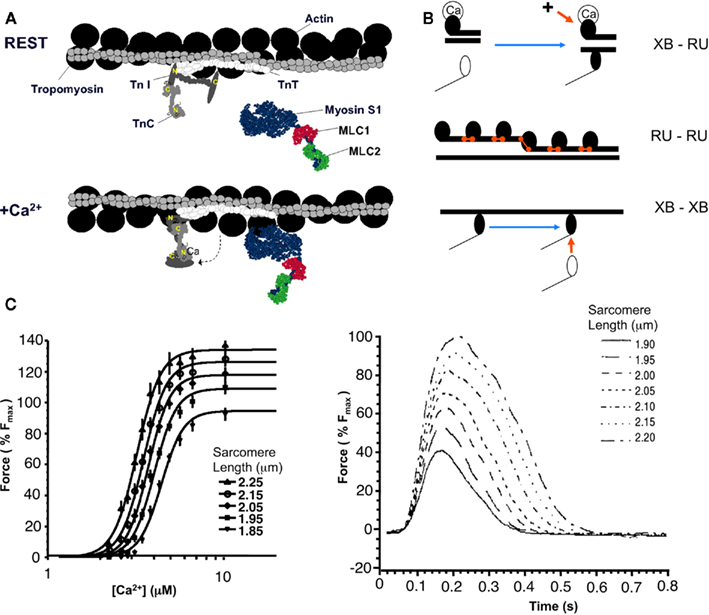
Figure 2. Proteins in Ca-based activation and cooperative mechanism. (A) The illustration shows the key proteins in muscle contraction in the rest (above) and the activated (below) positions. A myosin head (S1, blue) with light chain 1 (LC1, red) and light chain 2 (LC2) is shown in two positions, detached (above) and bound (below). Actin (black) forms a two-stranded helix that is the backbone of the thin filament. A tropomyosin unit (gray) is a two-stranded helix that spans seven actin units and connects in an end-to-end fashion with its two neighbors. Troponin is a complex of three proteins: TnC, TnI, and TnT. As shown in the lower panel below, with binding of Ca to the regulatory site on TnC, TnI rotates to change TnT and troponin to a permissive position that allows myosin to bind. (Figure modified from illustration provided by J. Solaro in Bers, 2001, with permission.) (B) The figure schematically illustrates three putative cooperative mechanisms: XB–RU shows that the binding of an XB increases the affinity of the associated RU; RU–RU shows that RU units are connected (red link) that promotes similarity with the two neighbors; and XB–XB shows that a bound XB increases the binding rate of a neighboring XB. (C) Figure shows the SL dependence of isometric responses. Left panel: average force–Ca2+ relationships (pooled data, skinned rat cardiac trabeculae, n = 10) at five SLs; data are fitted to a Hill relationship. The level of cooperativity, assessed by the Hill coefficient, is essentially not affected by SL (from Dobesh et al., 2002, with permission). Right panel: effect of SL on force during twitches. Different traces show normalized different SLs (in micrometers) as indicated in key. Force is normalized so that maximal force corresponds to a value of 1.0. As SL increases, the peak force increases, while the time to peak is mostly constant. In additions, the relaxation phase is slowed so that the total twitch duration is an increasing function of SL. (from Janssen and Hunter, 1995, with permission).
Despite the complexity of such nearest-neighbor connections, the typical myofilaments model is constructed around a formalism of discrete elements called a functional unit (FU). Each FU is composed of a Tn/Tm, spanning seven actin units, and one nearby XB (see Figure 2B). The Tn/Tm is often termed a regulatory unit (RU) as this complex can bind Ca and control the XB binding on the associated region of actin. Hence, each FU is composed of 1 RU, the associated actin, and 1 nearby XB. The 1 XB is roughly in line with experimental estimates of one to two myosin heads in the seven actin span of an FU (Gordon et al., 2000), although up to four myosin heads may be structurally possible (Lehman et al., 2001). Note that an FU is considered permissive if XBs can attach and cycle, regardless of the Ca-bound state of TnC in a loose coupling model.
While the steric hindrance model is generally accepted, the underlying biophysical mechanisms are both complex and controversial. Experimental characterizations show that cardiac muscle is highly sensitive to Ca with a Hill coefficient of approximately 7 (see Figure 2C, reprinted from Dobesh et al., 2002). In contrast, the single regulatory Ca-binding site on troponin predicts a Hill coefficient of 1 assuming that each bound Ca ion activates a single FU. The observed high cooperativity is generally attributed to the action of one or a combination of three mechanisms (Rice et al., 1999) as outlined below using the nomenclature of Razumova et al. (1999):
XB–RU interactions – cycling XBs have been shown to increase the Ca affinity of troponin (Guth and Potter, 1987; Swartz and Moss, 1992). In most models, the change in affinity (as illustrated in Figure 2B) results from an assumed change in the rate of Ca release from troponin that is a decreasing function of attached XBs. A complication is that the Ca affinity may increase to a different extent for a permissive RU without an XB attached versus a permissive with an XB attached. However, most models do not make such a distinction. Note that a strongly bound XB is assumed to hold the RU in a permissive conformation. When this assumption is coupled with the assumption that Ca is tightly bound to an activated RU, then another form of XB–RU cooperativity is possible. That is, tightly bound XBs increase effective Ca affinity by holding the RU in a permissive state (e.g., Schneider et al., 2006).
RU–RU interactions – cooperative interactions are generally thought to arise from nearest-neighbor RUs along the thin filaments. Models assume a spring-like connection between RUs (as represented by the red connections in Figure 2B) that get stretched when neighbors exist in different permissive states. The stretching of the springs requires energy, so that the preferred conformations have neighbors in similar states, e.g., the first three RUs are all permissive and the last three are all non-permissive.
XB–XB interactions – many cooperative interactions have been proposed between neighboring XBs, but the discussion here is limited to a few general classes. For example, rigor-bound S1 myosin heads show cooperative binding to regulated actin, i.e., the binding of one S1 head increases the binding rate of neighboring heads (Bremel and Weber, 1972; Trybus and Taylor, 1980). This type of cooperativity may be a secondary effect from the RUs that is, the binding of one XB holds the RU in a permissive conformation to promote binding of a nearby XB. In fact, a bound XB appears to hold the tropomyosin in a more lateral position than that produced by Ca-binding alone (Craig and Lehman, 2001), a feature that may further facilitate binding of neighboring XBs. However, an important question arises as to whether XB–XB interactions are produced by multiple XBs binding under a singe RU. Alternatively, the interactions between neighboring XBs could be mediated by activation across neighboring RUs, and hence XB–XB cooperativity could be a secondary manifestation of RU–RU cooperativity. Finally, some XB–XB interactions are thought to occur as a result of compliance in the thick and thin filaments. Specifically, binding of the first XB is postulated to increase the binding of neighboring XBs by pulling binding sites on actin into register with myosin heads that have an inherently different characteristic distance in their repeating structure.
Modeling length sensitivity
A second controversy, closely related to cooperativity, is the length sensitivity of cardiac muscle. Here, length refers to the sarcomere length (SL), which is the distance between the Z-disks. As the muscle lengthens, the Ca concentration producing half activation (known as Ca50) decreases so that more force is generated for a given intracellular Ca transient (Dobesh et al., 2002). This behavior is thought to be the cellular basis of the Frank–Starling law of the heart. Cardiac muscle shows a Hill coefficient of approximately 7 when measured with a feedback control on SL (Dobesh et al., 2002). Without SL control, the Hill coefficient would be of lower value because the onset of active force can produce a shortening of the center region of the muscle and a decrease in both SL and apparent cooperativity (see discussion in Rice et al., 2008b).
In the force–Ca relations in Figure 2C, SL modulates two main attributes, plateau force and Ca sensitivity. Plateau force refers to the maximum force at high Ca at any given SL. Because the high Ca is assumed to fully activate RUs, the change in plateau force is not attributed to Ca-based activation effects. Instead, the changes in plateau force are most likely the result of altered number of XBs that can be recruited as a result of sarcomere geometry, in that SL changes the overlap of thick and thin filaments. More specifically, cardiac muscle operates in the range of SLs from about 1.7 to 2.3 μm that corresponds mostly to the rising phase of the force–SL relationship. In this region, the active force is assumed to correspond to the “single overlap” region of thick and thin filaments where XBs can be effectively recruited to generate force. This mechanism for controlling plateau force was first used in the LS model (Landesberg and Sideman, 1994a,b). Similar constructs are used in many later models by other groups (e.g., Rice et al., 2008b), although some have used an extension ratio instead of an explicit representations of SL (e.g. Izakov et al., 1991; Hunter et al., 1998; Niederer et al., 2006). The extension ratio construct provides length-dependent mechanisms in a model without having to define exact sarcomere-based mechanisms.
Note, however, that the classic data on force–SL relationship as reported by Gordon et al. (1966) shows a rising phase up to only 2.0 μm, and in fact, by 2.3 μm, the active force should be decreasing. This discrepancy has been noted previously (Rice et al., 1999; Rice and De Tombe, 2004), and hence the LS and subsequent models assume that the lengths of thick and thin filaments in cardiac muscle are different than those commonly attributed to skeletal muscle. While there is yet to be anatomical confirmation of systematically different filament lengths in cardiac muscle, there are some reports of a greater variability in thin filament lengths in cardiac compared to skeletal muscle (Robinson and Winegrad, 1977). The greater variability may result from a lack of nebulin that acts like a template for the thin filament in skeletal muscle. While the anatomical evidence may be lacking, the observation that force (Weiwad et al., 2000) and the ATPase rate of maximally activated cardiac muscle are linear functions of the change in SL up to 2.3 μm (Wannenburg et al., 2000) is strongly suggestive of a simple linear relationship between SL and the number of recruitable XBs.
An alternative hypothesis suggests that SL changes the lattice spacing of the thick and thin filaments as a result of the isovolumetric properties of heart cells, i.e., longer SL produces a smaller cross-section that compresses the lattice to bring thick and thin filaments closer together (McDonald and Moss, 1995). This change in actin and myosin lattice spacing then modulates the XB attachment and/or detachment rates to change the developed force. However, some recent estimates of myofilament lattice spacing by synchrotron X-ray diffraction suggest that the changes in lattice spacing occurring over the physiological range cannot account for length-dependent changes in Ca sensitivity in cardiac muscle (Konhilas et al., 2002). Using similar methods, other researchers found that the fraction of weakly bound XBs is dependent on lattice spacing (Fuchs and Wang, 1996). If one assumes a constant rate of turnover from the weakly bound to the force-generating strongly bound state, then this evidence supports a mechanism for lattice spacing to modulate force. It should be noted that all the X-ray diffraction studies cited above are somewhat unphysiological as lattice spacing is measured under relaxed conditions that may not correspond to activated conditions where attached XBs may also modify the lattice spacing. The lattice spacing hypothesis could also potentially explain the changes in plateau force at high Ca, instead of the simple recruitment based on longitudinal filament overlap as proposed above. More work will be required to better quantify the effects of lattice spacing on activated, force-producing muscle.
Besides lattice spacing, a few other possible mechanisms exist that could account for the SL sensitivity. Some have suggested that titin may play a role (Cazorla et al., 1999; Fukuda et al., 2001); this protein is situated between the thick filament and the Z-disk and hence its length is modulated by SL. Another possibility, as described below, is that the SL-dependent Ca sensitivity may result from the interplay of cooperative mechanisms as discussed above, and the number of recruitable XBs, as set by length-dependent sarcomere overlap (Rice and De Tombe, 2004; Rice et al., 2008b). Early findings have indicated that the number of strongly bound XBs, as modulated by SL, affect Ca sensitivity primarily via XB–RU interactions (Akella et al., 1997). However, more recent evidence has suggested that weakly bound rather than strongly bound XBs may modulate Ca sensitivity, and hence, other cooperative mechanisms such as RU–RU interactions may play a more important role than previously thought (Farman et al., 2010).
Isotonic versus auxotonic models
Model scope can be divided into isotonic and auxotonic. When isometric, active force can be computed in a straightforward fashion as the average force per XB multiplied by the number of attached or strongly bound XBs. While isometric models appear to have limited applicability, a large body of experimental data has been collected under isometric conditions, and has shown important emergent behaviors such as SL dependence. Hence, isometric models can still provide insight into mechanism of complex behaviors (Izakov et al., 1991; Rice et al., 1999; Campbell et al., 2001a). Auxotonic models have more general applicability, but there are additional considerations. The general formalism is that active force represents the sum total force contribution of the XBs. As discussed earlier, calculation of force requires tracking both the population of attached XBs and the corresponding distortions of the attached XBs, either directly or as mean-field approximations. Direct calculation (Eq. 1) requires the solution of PDEs, while mean-field approximations can be solved with ODEs or algebraic approaches with additional a priori assumptions.
In auxotonic models, time varying length alters both the active and passive forces of cardiac muscle. The general formalism is that the contractile element (CE) generates the active force component. The CE represents the sum total contributions of all XBs and, hence, encompasses the effects of Ca-based activation and SL-dependent effects. In addition, most models include a serial elastic (SE) element and a parallel elastic (PE) elements (Fung, 1970; McMahon, 1984). In brief, the PE is parallel with the CE, and the ensemble is in series with the SE. The SE and PE contribute to passive force because a change in muscle alters the extension of the elastic elements, thus the total muscle force changes even in the absence of a contribution from the CE (i.e., passive force is measured force in the absence of XBs). The SE and PE are approximated to be simple, time-invariant elastic elements, although experimental data shows more complexity and time variation in passive force (de Tombe and ter Keurs, 1992). In most modern interpretations, the PE is attributed to the force contribution of titin (Schneider et al., 2006; Rice et al., 2008b).The SE generally represents a compliance that is an artifact of the attachment methods to artificially hold the muscle ends in experimental preparations (e.g., isolated muscle cells, papillary muscle, and ventricular trabeculae). Hence, the SE is generally not needed when modeling intact muscle such as the whole ventricle.
Myofilament Models
The discussion below examines a representative set of myofilament (MF) models that illustrate the range of approaches in the field. An exhaustive description of all existing models is not possible, but the chosen models below are formative in that the approaches are carried over to subsequent models by the same group or others. Likewise, approaches are often carried over from isometric to auxotonic and from myofilaments to singe cell EM models. Here we consider single-cell EM models as a combination of an electrophysiological cell representation with a MF model. The discussion will focus on MF models with respect to the central themes described above: XB cycling, cooperative mechanisms in Ca-based activation and SL-dependent mechanisms. For now the focus is MF models, although some references are also made to derived EM models as the developments are often linked; a more detailed description of EM models is given later in Section “Single-Cell Electromechanical Models.” A summary of all the discussed models is provided in Table 1.
The work of Izakov et al. (1991) is an early attempt to model complex phenomena such as load-dependent relaxation, an effect where SL length changes during a twitch will modify the rate of relaxation (for review, see Brutsaert et al., 1980). The model contains XB–RU and RU–RU cooperative interactions and representation of the recruitment of XBs based on muscle length, although the sarcomere geometry is not explicitly represented. The mechanism of XB–RU cooperativity can be defined in a general way as
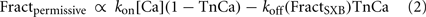
where TnCa is the fraction of troponin with Ca bound, kon is the forward binding rate and koff (FractSXB) is the reverse binding rate for Ca to troponin that is assumed to be a decreasing function of FractSXB, the fraction of strongly bound XBs. Hence, XB attachment increases the affinity of Tn for Ca. The general approach is carried over to a large fraction of later models by numerous groups. Note that RU–RU interactions are assumed to be mediated by TnC binding Ca more strongly when a neighboring RU is in the permissive state, and there is a phenomenological approach to represent this effect. In general, this feature has been less conserved as other groups represent RU–RU interaction in other ways. The general MF modeling approach of Izakov et al. (1991) has been continually refined and expanded. For example, the MF model has been combined with the Noble’98 ventricular cell description (Noble et al., 1998) to produce the Ekaterinburg–Oxford EM cell model (Markhasin et al., 2003). A similar EM model has been used recently to investigate the role of myocardial viscoelasticity in altered EM activity in Ca overloaded cardiomyocytes (Katsnelson et al., 2011).
The LS model (Landesberg and Sideman, 1994a,b) was previously discussed with respect to the representation of XBs (Modeling Crossbridge Cycling) and SL-dependent mechanisms (Modeling Length Sensitivity). Specifically the XBs are modeled with viscosity-like approach so that active force decreases in proportion to shortening velocity. The LS model also assumes that the thick and thin filament lengths are such that cardiac muscle is always operating on the ascending limb of the length–force relationship. In other words, the longer SLs are assumed to increase the number of recruitable XBs up to 2.3 μm, even though the traditional assumption is that the increases occur only to 2.0 μm. This approach is carried over to models from other groups (e.g., Rice et al., 2008b). The model also assumes that the primary cooperative mechanism is the XB–RU cooperativity, in which the fraction of XBs that is strongly bound is assumed to modulate the dissociation rate of Ca from TnC (as in Eq. 2). The model relies almost exclusively on XB–RU cooperativity to generate steep force–Ca relations. The model includes four states resulting from the coupling of two states for RUs and two states for XBs. More recently, the model was used to interpret experimental data suggesting that force feedback on Ca affinity of Tn-C is responsible for the Frank–Starling Law and that abrupt changes in SL can produce release of Ca that could potentially be pro-arrhythmic (ter Keurs et al., 2008).
The Hunter–McCulloch–ter Keurs (HMT; Hunter et al., 1998) model is likely the first that was specifically designed to couple to cell models and serve as the basis of tissue-level EM models. Unlike two or three state XB representations elsewhere, the HMT model used a fading memory XB model that involves a convolution integral approach based on previous work in modeling skeletal muscle (Ma and Zahalak, 1991; Hunter et al., 1998). The Ca-based activation mechanisms are described in more mechanistic detail, including XB–RU cooperativity that is essentially of the same form as Eq. 2. This construction contrasts with many experimental (e.g., Janssen and Hunter, 1995; Janssen et al., 2002) and modeling (e.g., Rice et al., 1999) studies that suggest XB cycling is rate limiting in relaxation. In other words, kinetic rates of Ca-based activation on the thin filament are thought to be relatively higher than those of XB cycling, and the overall rate of the ensemble system response is dictated by the slower XB dynamics. The model scope is auxotonic and includes active force with SL dependence and passive tissue properties. One distinguishing feature of the model is the extensive validation of parameters and simulated responses against a wide range of experimental measures. The rat myofilament model by Niederer et al. (2006) can be considered an updated version of the HMT model by including more recent experimental measures to refine parameters and validate model responses.
The Negroni-Lescano (NL) 1996 model has two XB states, attached and detached. The force of the attached state is determined by a spring, the distortion of which depends on the relative motions of the myosin and actin filaments. In essence, the mean distortion of the whole population of XBs is represented by the distortion of a single spring. The model includes XB–RU feedback, as Ca is assumed to bind with 40 times greater affinity when XBs are attached. The model was coupled to the Kyoto single guinea pig cell model. The model was later updated in 2008 (Negroni and Lascano, 2008) to include RU–RU cooperativity and more XB states. The model assumes that three connected RUs bind Ca and become permissive as a unit, hence raising the apparent Hill coefficient in the Ca sensitivity by a factor of 3. Another important change is the assumption of weakly and strongly bound XB states, each with assumed spring and distortion to represent the mean strains of the corresponding states. The additional XB states allow for simulation of the F1 and F2 phases of force recovery after a transient length change. The revised model is more comprehensive than the previous version because it is able to represent a wider set of steady-state and dynamic responses seen in experiments.
The Rice–Hunter–Winslow (RHW; Rice et al., 1999) series of models are incrementally constructed with increasing complexity to investigate how putative cooperative mechanisms could contribute to SL-dependent responses. The models contain phenomenological representations of XB–RU, RU–RU, and XB–XB cooperative mechanisms. Steady-state force–Ca relations were simulated and compared to experimental measurements. Salient features to reproduce are the change in plateau force and a leftward shift in Ca50 with increasing SL. Experimental characterizations initially showed the Hill coefficient (and apparent cooperativity) to increase with SL, while later characterizations showed the Hill coefficient to be mostly invariant of SL (similar to those in Figure 2C). Dynamic force responses in the form of twitches were compared with the experimental data as shown in the right panel of Figure 2C.
One approach that differed from previous models is an explicit Hill-like function to replicate the presumed effects of the RU–RU interactions. Indeed, the spatial nature of RU–RU interactions requires phenomenological representations because spatial interactions cannot be mapped into ODE-based representations (Rice and De Tombe, 2004). The formulation can be generalized as
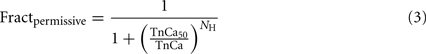
where Fractpermissive is the fraction of permissive RUs, TnCa is the fraction of troponin with Ca bound, TnCa50 is the half-activation fraction for TnCa and NH is the Hill coefficient. The fraction of troponin with Ca bound can be computed by assuming a simple binding reaction as shown below:
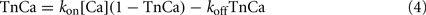
where kon is the forward binding rate and koff is the reverse binding rate of Ca to Tn.
An important feature of the construction in Eqs. 3 and 4 is that cooperativity is assumed to reside in the transition of RUs to the permissive state and not in the binding of Ca to TnC directly. The approach is phenomenological and speculative as the exact nature of RU–RU interactions remains to be defined. However, several modeling studies have pointed to the ability of RU–RU interactions to reproduce the Hill-like force–Ca relations observed in cardiac muscle (Dobrunz et al., 1995; Rice et al., 2003). In contrast, models based only on XB–RU interaction produce distorted force–Ca relations that deviate from the experimental counterparts (Rice and De Tombe, 2004; Rice et al., 2008a). Note that myofilament models often have Hill-like constructs similar to Eqs. 3 and 4 that are speculative or have little direct justification. For example, the NL 2008 model (Negroni and Lascano, 2008) assumes that three RUs act as a coupled unit, effectively increasing the Hill coefficient from 1 to 3 (mirroring the increase from 1 to 3 Ca-binding sites per unit). However, such a construct seems very speculative because experimental studies do not point to three RUs acting in concert. However, the addition of this feature allows increased apparent cooperativity over the earlier versions of the model that lacked the construct (Negroni and Lascano, 1996, 1999). In summary, phenomenological Hill-like cooperativity is often added to model the increase in Ca sensitivity and to reproduce steep force–Ca relations such as those shown in Figure 2C.
A model proposed by Schneider et al. (2006) includes features not included in previous models, specifically TnI movement and the effect of titin that is assumed to change lattice spacing as a function of SL. The attachment of strong-binding XBs is assumed to depend both on the state of TnI and lattice spacing. There is assumed cooperativity in the TnI movement that is analogous to the phenomenological representations of RU–RU interactions in other models. Titin is assumed to control passive force in the axial direction and lattice spacing in the radial direction. Decreased lattice spacing increases the binding of myosin (termed “lattice spacing-XB”). Interestingly, the model assumes a negative type of cooperativity that is a speculative feature not found in other models. Specifically, strain from strongly bound XBs is assumed to interfere with Tm-to-Tm cooperative behavior. Hence the negative cooperativity is a mixture of RU–XB and XB–XB cooperativity (referred to here as “Neg. RU–XB–XB”). The model is isometric only but seeks to understand the mechanism of SL dependence that underlies the Frank–Starling law. The model is designed to be coupled with the Kyoto ventricular cell model (Matsuoka et al., 2004).
Most of the myofilament models described above share much commonality in that approximations are made to reduce the mathematical complexity and the computational costs. As argued elsewhere, the Ca activation and XB binding are best represented as spatial models that explicitly represent nearest-neighbor interactions (Rice and De Tombe, 2004; Rice et al., 2008a), typically with Monte Carlo approaches in the general case, although simplified solutions are possible in more restricted cases (Rice et al., 2003; Smith, 2003). As a compromise between computational efficiency and spatial realism, a recently developed Markov model simulated adjacent RUs on the thin filament (Campbell et al., 2010). Simulations reproduce the observed cooperativity in both steady-state and dynamic force–Ca relationships and are further validated by comparisons with experimental results for inhibition of myosin binding and the addition of NEM-S1 (a strong-binding, non-force-producing myosin fragments). The model analysis suggests that Tm–Tm coupling potentiates the activating effects of strongly bound XBs and contributes to force–Ca dynamics in intact cardiac muscle.
Single-Cell Electromechanical Models
Extensive work has been done to model the myofilaments alone as many important issues remain to be resolved at this level. However, a central goal of much of the myofilaments modeling work is to provide force and contraction components as the end effector of the excitation–contraction coupling process in cardiac cells. Here single-cell EM models are the combination of an EP cell representation with a MF model. Virtually all the existing EM models were developed with the EP and MF components along separate tracks (or in some case, a dominant emphasis on EP with a mostly rudimentary MF representation). An EM model can, in principle, be generated by coupling any EP and MF models together with proper consideration of feedforward and feedback pathways in the Ca handling. That is, TnC represents the largest Ca buffer in the cell, and the affinity of the Ca-binding regulatory sites on TnC is generally assumed to be a function of XB binding and/or generated force. The Ca transient is altered when the developed force is changed (e.g. Rice et al., 2008b). Therefore, including myofilament binding of Ca is not only crucial for modeling force generation by the myocyte but is also important for realistic modeling of cytosolic Ca transients and Ca cycling.
As a historical note, the first coupled EM model was developed by Kaufmann et al. (1974), as detailed in a recent review (Niederer et al., 2009). Interestingly, the model was implemented with an analog computer. However, the model contained phenomenological representation of tension development that is out of scope for this review as it focuses on more mechanistic representations of the myofilaments. Other early EM models include those by Wong (1981) and Adler et al. (1985), that were based on the Wong model of the myofilaments (Wong, 1971). The latter added Ca-based activation to the XB-cycling approach of Huxley and required solution of PDEs. For the purposes here, we focus on models implemented only in ODEs that are suitable to compose into organ-level models.
The Hilgeman–Noble (HN) model (Hilgemann and Noble, 1987) of the rabbit atrium incorporated one ODE to represent Ca-based activation, and a second to represent XB binding. This formulation was incorporated as an abstract description of force generation, and some aspects of the model are known now to be inconsistent with current experimental data. For example, in the HN model, binding of Ca to both high and low affinity sites affects activation, whereas only the low affinity sites are now known to be regulatory in cardiac muscle. By assuming multiple regulatory Ca-binding sites, the HN model exhibits an increased Ca sensitivity and Hill coefficient similar to cardiac muscle. This basic formulation was carried on to models later developed by Noble and coworkers (Earm and Noble, 1990), including model extensions for describing SL sensitivity (Noble et al., 1998). Later the Noble ventricular cell reconstruction (Noble et al., 1998) was combined with a MF model from the lineage of the Izakov et al. (1991) model to produce the Ekaterinburg–Oxford EM model (Markhasin et al., 2003). The MF component has considerably more mechanistic detail than the earlier HN model, and the Ekaterinburg–Oxford EM model can be used to investigate more complex phenomena such as mechano-electric feedback on Ca transients and AP duration (Solovyova et al., 2003).
The Rice et al. (2008b) model sought to update and expand on the RHW model to have a wider scope (auxotonic versus isometric) and to be validated against a wider set of experimental protocols. Importantly, active contraction and re-lengthening can be simulated, and passive muscle properties are included to simulate muscle strips and isolated myocytes, two common experimental preparations. The model includes computationally efficient but phenomenological representations of both RU–RU cooperative interactions and a three-state model of XB attachment and distortion similar to that of the CRC model. While phenomenological approximations are employed, the overall model structure attempts to map the underlying biophysics. Thus, parameter definitions are intuitive and easily modified, as compared to highly lumped or abstracted parameters in fully phenomenological models. For example, Tran et al. (2010) have recently modified the Rice et al. (2008b) model to include binding and release of metabolites such as ATP, ADP, Pi, and H.
The rat myofilament model by Niederer et al. (2006), developed as an updated version of the HMT model, was coupled, in a subsequent modeling work (Niederer and Smith, 2007), to the myocyte EP model by Pandit et al. (2001). The combined model has been used to investigate the putative mechanisms of the slow force response (SFR), a secondary prolonged increase in force beyond the immediate force response. In brief, the immediate force response (or Frank–Starling response) is widely agreed to result from the SL-dependent increases in Ca sensitivity and force found at the level of the myofilaments themselves (see Modeling Length Sensitivity). In contrast, the SFR is assumed to involve one or more stretch-dependent mechanisms at the cellular level. The Niederer and Smith (2007) model considers the putative effects of mechanisms including stretch-dependent nitric oxide production, Na–H exchanger and stretch-activated channels (SACs). This EM model has sufficient complexity to estimate the effect of different putative mechanisms in the context of the complex and interactive EM mechanisms of the cardiac cell.
The Rice–Jaffri–Winslow (RJW) model (Rice et al., 2000) integrated the myofilament model of Rice et al. (1999) into the model of the guinea pig action potential by Jafri et al. (1998). This model reproduced experimentally measured properties of mechanical restitution and post-extrasystolic potentiation. These phenomena are examples of interval–force relations in which changing the temporal spacing between action potentials can produce dramatic changes in developed force (Bers et al., 2003). An important finding from this work was that altering the pacing protocol affected the amplitude of the Ca transient and force generation to a relatively small degree, while the cooperative properties of the myofilaments produce a much larger relative change in developed force. The model included a phenomenological representation of cooperative interactions between neighboring RU units including a SL-dependent shift in Ca50. However, the RJW model was limited since only isometric force protocols could be simulated.
The RJW model has been refined and expanded to reproduce a wider variety of experimental protocols in the Rice et al. (2008b) MF model. Importantly, active contraction and re-lengthening can be simulated, and passive muscle properties are included to simulate muscle strips and isolated myocytes. To generate an EM model, the MF component is combined with Chicago EP model of the rabbit ventricular myocyte (Shannon et al., 2004). With the combined EM model was compared to responses in single cells and to Ca transients that change for isometric versus shortening protocols. The model has been extended recently by Campbell et al. (2008, 2009) to replicate canine epicardial, endocardial, and mid-myocardial myofilament responses.
Multiscale Cardiac Electromechanical Modeling at the Organ Level
The second part of this review focuses on multiscale modeling of cardiac EM activity in the intact ventricles. In our desire to link the subcellular/cellular model developments with modeling at the organ level, we will not be able to recognize, in this limited review, the progress made at the tissue level (2D EM models developed by several groups) that has paved the way for the presented below achievements in modeling EM activity in the ventricles. Our hope is that by describing the state-or-the-art in organ modeling, we can also provide a review of the frontiers in cardiac EM modeling.
Various EM models of the ventricles have been developed, which incorporate, as part of the organ model, many of the representations of myofilament dynamics or cellular EM activity described in the first part of this review. Since the ultimate goal of any EM modeling at the organ level should be the increase in our mechanistic understanding, this section focuses, after describing the general organ-level EM modeling approach, on the applications of EM modeling of the ventricles in addressing specific basic science or clinical questions. In doing so, we underscore the particular myofilament and cellular EM models used, thus providing a link between the EM modeling efforts at the cellular and organ levels.
Finally, validating the model of cardiac EM with experimental data is a pivotal component in model development. It constrains the model parameter space and enhances the model’s physiological relevance. The scope and extent of this review do not allow us to devote space here to this important issue; instead we point our readers to a recent paper (Trayanova et al., 2011a) that reviews EM ventricular model validation.
General Approach
A schematic of the general approach to modeling the multiscale cardiac EM function is shown in Figure 3A. It consists of two coupled parts, which simulate the electrical and the mechanical functions of the heart, respectively. The electrical component of the model in Figure 3 simulates the propagation of a wave of transmembrane potential by solving the monodomain reaction–diffusion PDE (or a system of coupled PDEs if the extracellular current flow is explicitly accounted for, i.e., the bidomain problem) over the volume of the heart (Plank et al., 2008). The reaction–diffusion PDE describes current flow through myocytes that are electrically connected via low-resistance gap junctions. Cardiac tissue has orthotropic passive electrical conductivities that arise from the cellular organization of the heart into fibers and laminar sheets (LeGrice et al., 1995). Global conductivity values are obtained by combining fiber and sheet organization with myocyte-specific local conductivity values. Current flow in the tissue is driven by active processes of ionic exchanges across myocyte membranes. These processes are represented by the cellular ionic (i.e. EP) model (Figure 3A), where current flow through ion channels, pumps and exchangers as well as subcellular Ca cycling are governed by a set of ODE and algebraic equations; ionic models of different complexity are currently in use (for review, see Noble and Rudy, 2001). Simultaneous solution of the PDE(s) with the set of ionic model equations represents simulation of electrical wave propagation in the heart.
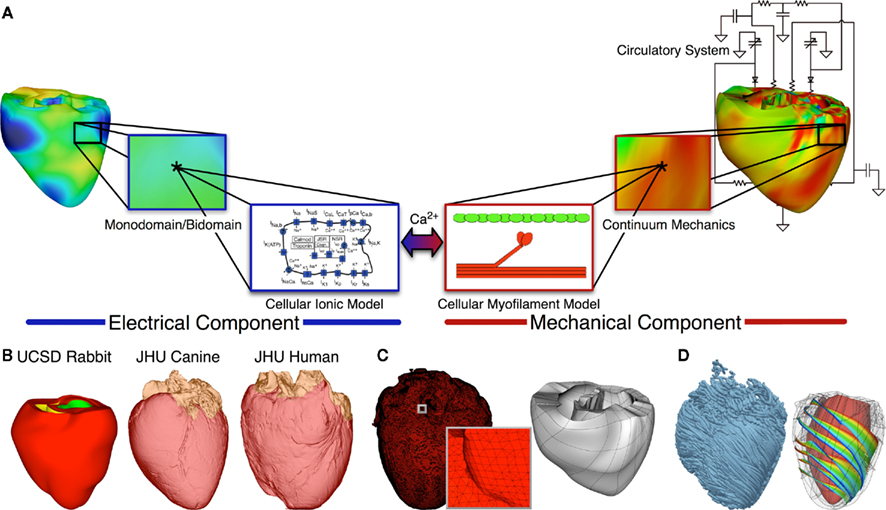
Figure 3. Whole-heart modeling. (A) Schematic of the general approach to modeling cardiac EM function. (B) Geometrical models of the heart. (C) Computational meshes of the canine heart for the electrical and mechanical problems. (D) Fiber and sheet orientations obtained from DTMR imaging of the canine heart. Modified with permission from Trayanova (2011).
The intracellular Ca released during electrical activation couples the electrical and mechanical components of the model (Figure 3A). The increase in intracellular Ca concentration serves as an input to the myofilament model, representing the generation of active tension within each myocyte, as described in the first half of this review. Contraction of the ventricles arises from the active tension generated by the myocytes. Deformation of the organ is described by the equations of continuum mechanics (Kerckhoffs et al., 2006), with the myocardium being an orthotropic, hyper-elastic, and nearly incompressible material with passive properties defined by an exponential strain energy function. Simultaneous solution of the myofilament model equations with those representing passive cardiac mechanics over the volume of the heart (Figure 3A) constitutes simulation of cardiac contraction. Finally, to simulate the cardiac cycle and the corresponding pressure-volume loop, conditions on chamber volume and pressure are imposed by a lumped-parameter models (Figure 3A) of the systemic and pulmonic circulatory systems (Kerckhoffs et al., 2007; Gurev et al., 2011). Note that currently fully coupled EM modeling is still the exception rather than the rule in the cardiac modeling community.
Solutions to organ-level EM problems entail the use of whole-heart geometries, which could be idealized (such as cylindrical and elliptical shapes; Arts et al., 1979; Bovendeerd et al., 1992) or anatomically accurate, the latter either representing averaged geometries obtained from histological sectioning (Legrice et al., 1997; Vetter and McCulloch, 1998; Stevens et al., 2003) or individual hearts’ geometry and structure (Vadakkumpadan et al., 2009; Bishop et al., 2010; Gurev et al., 2011), as obtained from MR images (Helm et al., 2005a,b). Figure 3B presents some of the whole-heart geometries used in EM modeling. The UCSD geometry (Vetter and McCulloch, 1998) is an example of averaged geometry obtained from histological sectioning, while the other two exemplify image-based individual geometries (Vadakkumpadan et al., 2009).
Solutions to electrophysiological or EM whole-heart models typically involve the use of the finite element method. The governing equations are thus solved on a spatially discretized version of the heart volume, i.e., on the computational mesh. The electrical and mechanics parts of the model have different requirements regarding the degree of discretization (i.e., element size) as well as the element type, thus the two parts of the model require two different computational meshes. The electrical mesh requirements are based on spatiotemporal characteristics of wave propagation; a spatial resolution of about 250–300 μm is appropriate for electrophysiological finite element models (Plank et al., 2008). A novel approach was recently published (Prassl et al., 2009) for electrical mesh generation directly from segmented MRI images (Figure 3C). The mechanical mesh, on the other hand, typically consists of hexahedral elements with Hermite basis. This choice of finite elements increases the degree of strain continuity and is appropriate for maintaining incompressibility constraints (Onate et al., 2004). The mechanical mesh of the heart (Figure 3C) can also be generated directly from segmented MR images (Gurev et al., 2011).
Fiber and laminar sheet organization underlie the orthotropic electrical conductivities of the tissue and its mechanical properties. In the electrical mesh, local fiber and sheet directions are typically mapped at the centroids of the finite elements, while in the mechanics mesh, fiber and sheet orientations and their derivatives are defined at mesh nodes and then interpolated over the elements. This is typically done based on histological sectioning information (Legrice et al., 1997; Vetter and McCulloch, 1998; Stevens et al., 2003) or on diffusion tensor (DT) MR data (Vadakkumpadan et al., 2009; Gurev et al., 2011). Note that the primary, secondary, and tertiary eigenvectors of the water diffusion tensors are aligned with the fiber direction, with the direction transverse to the fiber direction and in the plane of the laminar sheet, and with that normal to the laminar sheet, respectively (Helm et al., 2005a). Figure 3D presents fiber and sheet orientation, as reconstructed from DTMR images in the canine heart. In cases where neither histological nor DTMR imaging information is available, rule-based approaches have been used (Bishop et al., 2010; Niederer et al., 2011) to assign fiber and sheet orientation consistent with measurements.
Simulations of heart EM function are typically executed on parallel high performance computing hardware. The electrical problem is significantly more computationally demanding than the mechanical one. Reviews of the numerical approaches can be found in (Plank et al., 2008; Gurev et al., 2011; Trayanova, 2011); these articles also address the challenges in developing multiscale models at the organ level.
Multiscale Modeling the EM Interactions in the Normal Heart
The mechanical effect of altered cardiac activation sequence has been the subject of intense discussion since asynchronous electrical activation can cause abnormalities in perfusion and pump function. Whole-heart simulation studies have been instrumental in uncovering the relationship between the spatiotemporal pattern of electrical activation in the ventricles and the local sequence of mechanical strain. The study by Usyk and McCulloch (2003) was the first attempt to examine, by using a canine heart EM model, the delay between the onset of electrical activation and the onset of fiber shortening (EM delay, EMD) in sinus rhythm and LV pacing, assuming homogeneous excitation–contraction latency throughout the ventricles. This study (presenting the first whole-heart EM model) employed an early biophysically simplified model of membrane ionic activity and the HMT myofilament model (Hunter et al., 1998); as mentioned in the first part of this article, the HMT model was the first myofilament model designed to serve as a basis for tissue-level EM studies. The study found EMD to vary extensively throughout the ventricles, with both positive and negative values, indicating the possibility of fiber shortening before electrical depolarization. Following this first effort, EM models have been adjusted and enriched with experimental data. A recent study by Gurev et al. (2010) conducted a thorough analysis of the 3D distribution of EMD in the rabbit ventricles and its dependence on the loading conditions. To isolate the effect of the pattern of electrical activation on EMD, simulations were executed for sinus rhythm and for LV epicardial pacing; this ventricular model incorporated the single-cell EM model by Rice et al. (2008b). The results revealed that under both activation scenarios, EMD distribution is non-uniform. Consistent with experimental results (Prinzen et al., 1992; Ashikaga et al., 2007), in sinus rhythm EMD is longer at the epicardium than at the endocardium, and is greater near the base than at the apex. Following epicardial pacing, EMD distribution is markedly different; it also changes with the pacing rate. Analysis of the mechanisms revealed that for both electrical activation sequences, late-depolarized regions were characterized with significant myofiber prestretch caused by the contraction of the early depolarized regions (Figure 4). This prestretch delays myofiber-shortening onset, and results in a longer EMD. This study revealed that the loading conditions of the ventricles play an important role in the relationship between electrical and mechanical activation.
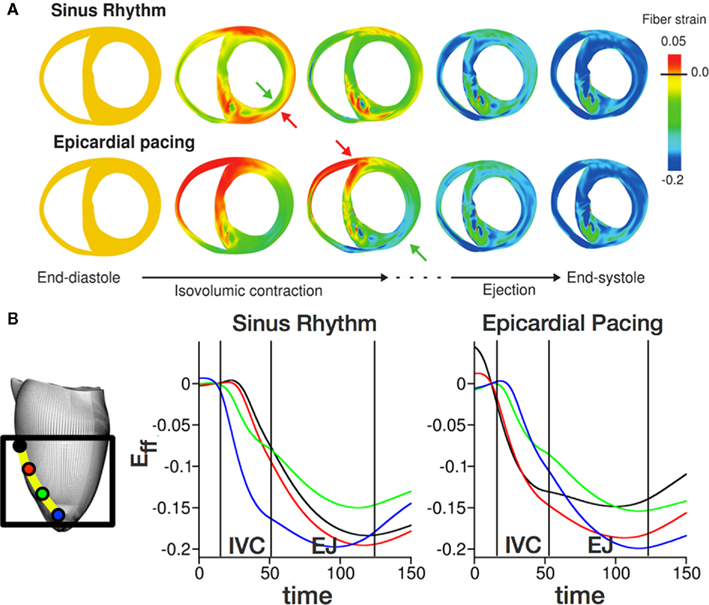
Figure 4. Mechanisms underlying the EM delay (EMD) in the rabbit heart for sinus rhythm and epicardial pacing. (A) Transmural maps of strain in the fiber direction during systole. Arrows indicate early shortening and prestretching during the isovolumic phase. (B) Epicardial fiber strain at four epicardial locations. IVC: isovolumic contraction; EJ: ejection. Modified with permission from Gurev et al. (2010).
The heart achieves an efficient coordinated contraction via a complex network of feedback mechanisms. Organ-level EM modeling by Niederer and Smith (2009) explored how cellular-level behaviors affect work transduction, stress and strain homogeneity at the whole ventricle level and the feedback loops that regulate normal contraction in an EM model of the rat LV. The myofilament model by Niederer et al. (2006) and the corresponding cellular EM model (Niederer and Smith, 2007), both reviewed in the first part of this article, were employed in the study. The simulation research demonstrated that the length-dependent changes in Ca sensitivity and the filament overlap, which are believed to constitute the Frank–Starling law, were the two dominant regulators of the efficient transduction of work. The absence of either mechanism not only altered the spatial distribution of stress and strain, but also determined the transmural variation in work. These results showed that feedback from muscle length to tension generation at the cellular level is an important control mechanism of the pumping efficiency of the heart.
Ventricular Mechano-Electric Coupling and Arrhythmias
The mechanical environment of the heart is known to affect cardiac electrophysiology in both health and disease. Abnormal deformations of cardiac tissue result in strain-dependent modulation of electrical wave propagation in the heart. The mechanisms through which this modulation can occur include the effect of stretch on intracellular Ca handling, the mechano-sensitivity of non-myocyte cell types such as fibroblasts, and most prominently, sarcolemmal channels that are activated by mechanical stimuli (Kohl et al., 2005). Of the latter, SACs have long been suspected as important contributors to the pro-arrhythmic substrate in the heart since current through SACs can lead to a pro-arrhythmic dispersion in electrophysiological properties. SACs have been shown to shorten or lengthen the action potential duration of a single myocyte or produce ectopic beats depending on the timing of the mechanical stimulus application relative to the phase of the action potential (Zabel et al., 1996; Kohl et al., 1999). Ventricular EM models have thus emerged as a valuable tool in the inquiry into the role of mechano-electric coupling in arrhythmogenesis (Li et al., 2004, 2006). Important EM modeling contributions, briefly reviewed below, include the new insights that (1) mechano-electric feedback is a mechanism responsible for the destabilization of reentrant waves and the transition from ventricular tachycardia (VT) to ventricular fibrillation (VF) and (2) in acute ischemia, mechanically induced depolarizations and their spatial distribution within the ischemic region are the mechanism by which mechanical activity contributes to the origin of spontaneous arrhythmias.
A simplified 2D electromechanical modeling study (Panfilov et al., 2007) was the first to demonstrate that SAC recruitment could induce spiral wave breakup. A follow-up study from the same group (Keldermann et al., 2010) used an EM model of the human LV to further investigate the effect of mechano-electric coupling via SAC on reentrant wave stability. In the organ-level model, cellular electromechanical activity was represented by the combination of the human ionic model developed by Panfilov’s group and the Niederer et al. (2006) myofilament model. The simulation results revealed that mechano-electric coupling results in the deterioration of stable reentrant waves into turbulent patterns characteristic of VF. While the initial scroll-wave was found to remain intact, other filaments existed for a short period only. Filament breakup was due to SAC recruitment in regions of high fiber stretch (away from the spiral core), resulting in voltage-dependent inactivation of sodium channels there, a mechanism for breakup that is different from other known mechanisms for wavebreak such as restitution (Garfinkel et al., 2000). Further simulation studies (Hu et al., 2009) dissected the role of SAC activation in the transition from VT to VF, using a rabbit heart model that incorporated the Rice et al. (2008b) myofilament/single-cell EM model. The analysis demonstrates that occurrence of heterogeneity in strain could give rise to a dispersion of electrophysiological properties, such as elevated resting potential, which may or may not lead to spiral wave breakup depending on the circumstances.
The role of SAC in the spontaneous induction of arrhythmias in the diseased heart was the subject of the study by Jie et al. (2010) which examined the role of EM dysfunction in arrhythmogenesis during acute regional ischemia, both in the induction of ventricular premature beats (VPBs), and in their subsequent degeneration into ventricular arrhythmia; the myofilament model by Rice et al. (2008b) was implemented in this organ-level model. The rabbit ventricles had a central ischemic zone (CIZ) and a border zone (BZ) and represented the electrophysiological and mechanical milieu in the heart at several stages post-occlusion. The study found that large myofiber strain developed in the ischemic region during contraction. In both BZ and CIZ, cell membranes underwent mechanically induced subthreshold depolarizations, or delayed after-depolarization (DAD)–like, whereas such depolarizations were absent in NZ. These DAD–like events resulted in mechanically induced VPBs originating from the ischemic border (particularly in the LV endocardium where fiber strain and strain rate were the largest), but not from CIZ, since in the latter ischemic injury suppressed excitability. VPBs then traveled intramurally until emerging from the ischemic border on the epicardium, initiating reentry.
Abnormal Mechanical Deformation and Its Role in Vulnerability to Electric Shocks and Defibrillation
Clinical studies have demonstrated that patients with dilated, volume or pressure overloaded hearts have elevated defibrillation thresholds (DFT). Whole-heart EM modeling was successfully used to unravel the mechanisms by which mechanical deformation may lead to increased vulnerability to electric shocks and elevated DFT. Modeling studies (Trayanova et al., 2011b) hypothesized that since ventricular geometry and fiber structure determine the large-scale distribution and magnitude of the virtual electrode polarization (VEP) induced by a strong shock (Rodríguez and Trayanova, 2003; Rodriguez et al., 2005), ventricular dilation may affect VEP through changes in ventricular geometry, leading to changes in DFT. Ventricular geometry and fiber orientation in the normal and dilated rabbit ventricles are shown in Figure 5A; the myofilament model was again the one by Rice et al. (2008b). With an implantable cardioverter-defibrillator (ICD) electrode configuration (Figure 5B), DFT in the dilated ventricles was found to be 38 ± 20% higher than that in the normal ventricles. The change in the electric field within the dilated ventricles, as compared to the normal ventricles, played a major role in decreased defibrillation efficacy. The electrical field magnitude in the normal and dilated cases is shown in Figure 5C. The regions characterized with a weak electrical field are located at the left ventricular apex and the anterolateral left ventricular wall in both the normal and the dilated ventricles; these regions have weaker field magnitudes in the dilated ventricles. These are also the locations where post-shock phase singularities formed after a near-DFT failed shock. Due to the dilation, the LV wall moved away from the electrodes, decreasing the electric field there, which in turn lowered the magnitude of VEP in the LV and allowed the fibrillatory reentrant circuits to survive there.
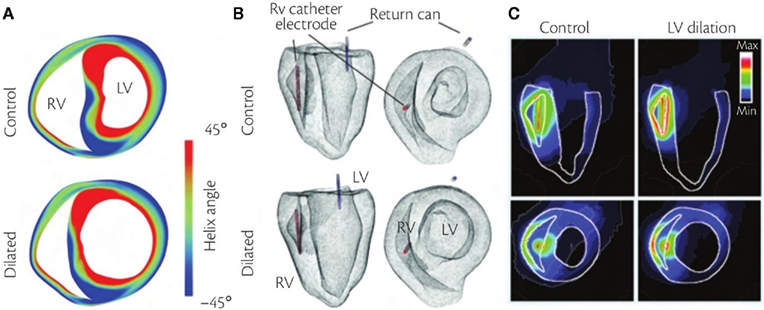
Figure 5. Defibrillation of the normal and dilated heart. (A) Short axis view of ventricular geometry and fiber helix angle. (B) The ventricles with ICD-like electrode configuration in anterior (left) and basal (right) views. RV catheter (red) is in the RV cavity and the active can (blue) is in the bath near the posterior LV wall. (C) Distribution of electrical field magnitude in the normal and dilated ventricles.
Multiscale EM Models of Cardiac Resynchronization Therapy in the Failing Heart
Heart failure patients often exhibit dyssynchrony in contraction, which diminishes the systolic function of the heart. CRT, the treatment modality that employs bi-ventricular pacing to re-coordinate the contraction of the heart, is a valuable therapeutic option for such patients. CRT has been shown to improve heart failure symptoms and reduce hospitalization, yet approximately 35% of patients fail to respond to the therapy (Abraham et al., 2002). The poor predictive capability of current approaches to identify potential responders to CRT reflects the incomplete understanding of the complex pathophysiological and EM factors that underlie mechanical dyssynchrony in failing hearts. Simulations of whole-heart EM behavior have begun to provide comprehensive analysis of the physiological responses that regulate CRT, as briefly described below. The study by Kerckhoffs et al. (2010) assessed the sensitivity, to cardiac dysfunction, of various indices of mechanical dyssynchrony typically used to quantify contractile dysfunction in patients, such as circumferential uniformity ratio estimate (CURE), internal stretch fraction (ISF), and the percentile range of time to peak shortening (WTpeak). CURE and ISF are indices that measure distribution of strain magnitudes, whereas WTpeak measures distribution of strain timing. For its myofilament component, this organ-level EM model used the Hill-based model developed by the Arts group (Lumens et al., 2009). This myofilament force model is empirical rather than mechanistic, and hence is not included in the first section of this review. While all examined indices were found sensitive to the activation sequence, only CURE and ISF were sensitive to the combination of dilation and left bundle branch block, a condition typically present in patients receiving CRT. Thus, CURE and ISF, which measure systolic strain non-uniformity, are better predictors of mechanical dyssynchrony because systolic strain non-uniformity, as this modeling study demonstrated, is the dominant determinant of variability in regional work. The results obtained in the study have also important implications for the emerging field of patient-specific modeling, and in particular, for patient-specific optimization of the LV pacing location for CRT. With geometry and electrical activation sequence, which can be established by a clinical evaluation, being the major determinants of regional cardiac function, and the hard-to-measure material properties playing a minor role, patient-specific simulations could be performed to suggest optimal CRT tailored to the individual.
A recent study (Niederer et al., 2011) used an EM model constructed from in vivo MRI data to conduct a sensitivity study of the efficacy of CRT to various cellular and organ EM parameters in the heart. A modified version of the empirical active tension model by Kerckhoffs et al. (2003) was used. The study determined that the length dependence of tension is a fundamental mechanism underpinning CRT efficacy (Figure 6H). Indeed, Figures 6B–K presents the development of active tension and its change in the septum (early activated region 1, Figure 6A) and the LV free wall (late activated regions 2 and 3, Figure 6A) with the length-dependent tension at 50, 100, and 150%, as well as the fiber stretch in these regions. The results demonstrate decreasing synchrony in strain and tension developments with decreasing length-dependent tension regulation. Further simulation results found that length-dependent tension development is key not only for the beat-to-beat regulation of stroke volume but also for the homogenization of tension development and strain. The model thus predicted that a patient with dyssynchronous electrical activation but effective length-dependent tension regulation at the cellular level is less likely to respond to CRT treatment than a patient with attenuated or no length dependence of tension.
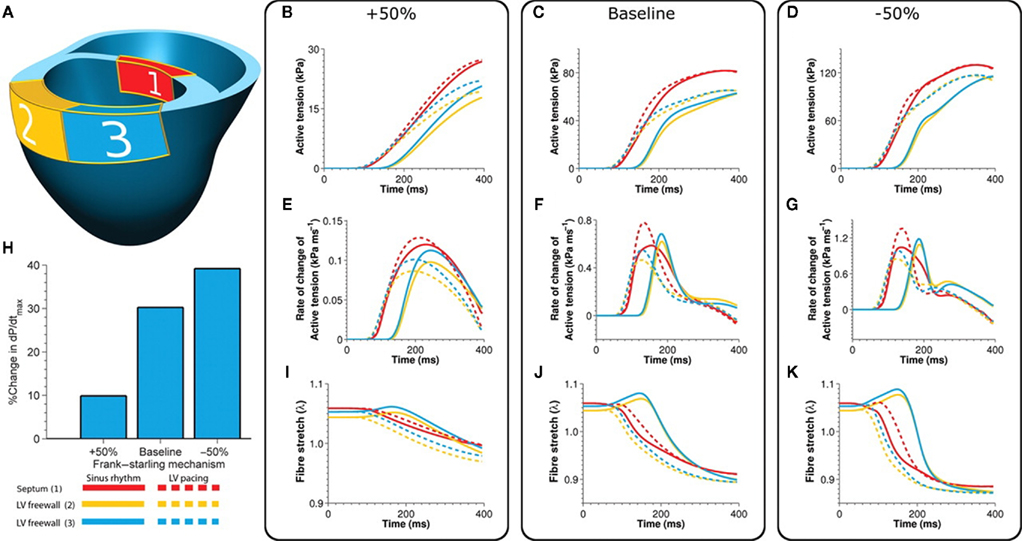
Figure 6. Active tension, rate of tension development, and regional stretch in the presence of baseline, amplified, and attenuated length-dependent tension regulation for the three regions shown in (A), (1) septum (red), (2) posterior lateral wall (yellow), and (3) anterior lateral wall (blue). Line colors correspond to these regions. Dashed and solid lines correspond to paced and sinus rhythm activations. (B–D): active tension; (E–G): rate of change of active tension; (I–K): fiber stretch. (H) Percentage change in dP/dtmax between sinus rhythm and LV pacing for the cases of −50, 100, and +50% length-dependent tension regulation. Reprinted with permission from Niederer et al. (2011).
Future Challenges in EM Modeling
Recent developments in cardiac simulation have rendered the heart the most highly integrated example of a virtual organ. These developments are firmly anchored in the long history of cardiac cell modeling and are rooted in the iterative interaction between modeling and experimentation. Since the 1990s there has been an explosion of modeling work on the heart, both at the cellular/subcellular and the organ levels. Multiple models of cellular electrophysiology and mechanics have been developed, the latter reviewed in the first part of this article, and some of them have been incorporated in organ-level EM models, as described in the second part of this review. Different organ-level models have chosen to use different ionic and myofilament models depending on the specific application; this choice has been largely dictated by the demand for compromise between model complexity and computational tractability.
These developments signal that in the near future cardiac EM modeling will increasingly become an important vehicle in the integration of knowledge of cardiac function in health and disease across the physical scales of biological complexity, from molecule to cell, tissue, the whole heart, and ultimately the patient. The goal will be to provide a quantitative understanding of the mechanisms of cardiac rhythm and pump dysfunctions, with the heart as a global dynamic system. This will involve bridging the spatial and temporal scales, from nanometer to meter, and from nanoseconds to minutes or hours. Furthermore, to address the contribution of various factors to the origin of cardiac dysfunction, simulations will increasingly become multiphysics. For instance, in examining the mechanisms for arrhythmogenesis in cardiac disease, factors stemming from soft tissue mechanics and fluid dynamics will need to be accounted for.
The role of cardiac EM modeling as a framework that unifies diverse cardiac EM insight will render such models a powerful testbed for new cardiac disease therapies and a vehicle for the development of new diagnostic modalities. Multiscale, multiphysics models that incorporate EM and structural remodeling in cardiac disease will serve as the first line of screening of new therapies and approaches, including pharmacological interventions, as well as new approaches to patient screening and diagnosis, thus expected to revolutionize twenty-first century cardiac research and the field of cardiology.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Supported by NIH grants R01-HL082729 and R01 HL103428, and NSF grant CBET-0933029 to Natalia A. Trayanova.
References
Abraham, W. T., Fisher, W. G., Smith, A. L., Delurgio, D. B., Leon, A. R., Loh, E., Kocovic, D. Z., Packer, M., Clavell, A. L., Hayes, D. L., Ellestad, M., Trupp, R. J., Underwood, J., Pickering, F., Truex, C., Mcatee, P., and Messenger, J. (2002). Cardiac resynchronization in chronic heart failure. N. Engl. J. Med. 346, 1845–1853.
Adler, D., Wong, A. Y., and Mahler, Y. (1985). Model of mechanical alternans in the mammalian myocardium. J. Theor. Biol. 117, 563–577.
Akella, A. B., Su, H., Sonnenblick, E. H., Rao, V. G., and Gulati, J. (1997). The cardiac troponin C isoform and the length dependence of Ca2+ sensitivity of tension in myocardium. J. Mol. Cell. Cardiol. 29, 381–389.
Arts, T., Reneman, R. S., and Veenstra, P. C. (1979). A model of the mechanics of the left ventricle. Ann. Biomed. Eng. 7, 299–318.
Ashikaga, H., Coppola, B., Hopenfeld, B., Leifer, E., Mcveigh, E., and Omens, J. (2007). Transmural dispersion of myofiber mechanics: implications for electrical heterogeneity in vivo. J. Am. Coll. Cardiol. 49, 909–916.
Bers, D. M. (2001). Excitation-Contraction Coupling and Cardiac Contractile Force. 2nd edn. Boston, MA: Kluwer Academic Publishers.
Bers, D. M., Eisner, D. A., and Valdivia, H. H. (2003). Sarcoplasmic reticulum Ca2+ and heart failure: roles of diastolic leak and Ca2+ transport. Circ. Res. 93, 487–490.
Bishop, M. J., Plank, G., Burton, R. A., Schneider, J. E., Gavaghan, D. J., Grau, V., and Kohl, P. (2010). Development of an anatomically detailed MRI-derived rabbit ventricular model and assessment of its impact on simulations of electrophysiological function. Am. J. Physiol. Heart Circ. Physiol. 298, H699–H718.
Bovendeerd, P. H., Arts, T., Huyghe, J. M., Van Campen, D. H., and Reneman, R. S. (1992). Dependence of local left ventricular wall mechanics on myocardial fiber orientation: a model study. J. Biomech. 25, 1129–1140.
Bremel, R. D., and Weber, A. (1972). Cooperation within actin filament in vertebrate skeletal muscle. Nature New Biol. 238, 97–101.
Brenner, B. (1988). Effect of Ca2+ on cross-bridge turnover kinetics in skinned single rabbit psoas fibers: implications for regulation of muscle contraction. Proc. Natl. Acad. Sci. U.S.A. 85, 3265–3269.
Brutsaert, D. L., Housmans, P. R., and Goethals, M. A. (1980). Dual control of relaxation. Its role in the ventricular function in the mammalian heart. Circ. Res. 47, 637–652.
Campbell, K. B., Razumova, M. V., Kirkpatrick, R. D., and Slinker, B. K. (2001a). Myofilament kinetics in isometric twitch dynamics. Ann. Biomed. Eng. 29, 384–405.
Campbell, K. B., Razumova, M. V., Kirkpatrick, R. D., and Slinker, B. K. (2001b). Nonlinear myofilament regulatory processes affect frequency-dependent muscle fiber stiffness. Biophys. J. 81, 2278–2296.
Campbell, K. B., Taheri, H., Kirkpatrick, R. D., Burton, T., and Hunter, W. C. (1993). Similarities between dynamic elastance of left ventricular chamber and papillary muscle of rabbit heart. Am. J. Physiol. 264, H1926–H1941.
Campbell, S. G., Flaim, S. N., Leem, C. H., and Mcculloch, A. D. (2008). Mechanisms of transmurally varying myocyte electromechanics in an integrated computational model. Philos. Transact. A Math. Phys. Eng. Sci. 366, 3361–3380.
Campbell, S. G., Howard, E., Aguado-Sierra, J., Coppola, B. A., Omens, J. H., Mulligan, L. J., Mcculloch, A. D., and Kerckhoffs, R. C. (2009). Effect of transmurally heterogeneous myocyte excitation-contraction coupling on canine left ventricular electromechanics. Exp. Physiol. 94, 541–552.
Campbell, S. G., Lionetti, F. V., Campbell, K. S., and Mcculloch, A. D. (2010). Coupling of adjacent tropomyosins enhances cross-bridge-mediated cooperative activation in a markov model of the cardiac thin filament. Biophys. J. 98, 2254–2264.
Cazorla, O., Vassort, G., Garnier, D., and Le Guennec, J. Y. (1999). Length modulation of active force in rat cardiac myocytes: is titin the sensor? J. Mol. Cell. Cardiol. 31, 1215–1227.
Chalovich, J. M., Chock, P. B., and Eisenberg, E. (1981). Mechanism of action of troponin. tropomyosin. Inhibition of actomyosin ATPase activity without inhibition of myosin binding to actin. J. Biol. Chem. 256, 575–578.
Cortassa, S., Aon, M. A., Marban, E., Winslow, R. L., and O’rourke, B. (2003). An integrated model of cardiac mitochondrial energy metabolism and calcium dynamics. Biophys. J. 84, 2734–2755.
Cortassa, S., Aon, M. A., O’rourke, B., Jacques, R., Tseng, H. J., Marban, E., and Winslow, R. L. (2006). A computational model integrating electrophysiology, contraction, and mitochondrial bioenergetics in the ventricular myocyte. Biophys. J. 91, 1564–1589.
Craig, R., and Lehman, W. (2001). Crossbridge and tropomyosin positions observed in native, interacting thick and thin filaments. J. Mol. Biol. 311, 1027–1036.
De Tombe, P. P., and Little, W. C. (1994). Inotropic effects of ejection are myocardial properties. Am. J. Physiol. 266, H1202–H1213.
de Tombe, P. P., and ter Keurs, H. E. (1992). An internal viscous element limits unloaded velocity of sarcomere shortening in rat myocardium. J. Physiol. (Lond.) 454, 619–642.
Dobesh, D. P., Konhilas, J. P., and De Tombe, P. P. (2002). Cooperative activation in cardiac muscle: impact of sarcomere length. Am. J. Physiol. Heart Circ. Physiol. 282, H1055–H1062.
Dobrunz, L. E., Backx, P. H., and Yue, D. T. (1995). Steady-state [Ca2+]i-force relationship in intact twitching cardiac muscle: direct evidence for modulation by isoproterenol and EMD 53998. Biophys. J. 69, 189–201.
Earm, Y. E., and Noble, D. (1990). A model of the single atrial cell: relation between calcium current and calcium release. Proc. R. Soc. Lond., B Biol. Sci. 240, 83–96.
Eisenberg, E., and Hill, T. L. (1985). Muscle contraction and free energy transduction in biological systems. Science 227, 999–1006.
Farman, G. P., Allen, E. J., Schoenfelt, K. Q., Backx, P. H., and De Tombe, P. P. (2010). The role of thin filament cooperativity in cardiac length-dependent calcium activation. Biophys. J. 99, 2978–2986.
Fenn, W. O. (1924). The relation between the work performed and the energy liberated in muscular contraction. J. Physiol. 58, 373–395.
Ford, L. E., Huxley, A. F., and Simmons, R. M. (1977). Tension responses to sudden length change in stimulated frog muscle fibres near slack length. J. Physiol. (Lond.) 269, 441–515.
Fuchs, F., and Wang, Y. P. (1996). Sarcomere length versus interfilament spacing as determinants of cardiac myofilament Ca2+ sensitivity and Ca2+ binding. J. Mol. Cell. Cardiol. 28, 1375–1383.
Fukuda, N., Sasaki, D., Ishiwata, S., and Kurihara, S. (2001). Length dependence of tension generation in rat skinned cardiac muscle: role of titin in the Frank-Starling mechanism of the heart. Circulation 104, 1639–1645.
Fung, Y. C. (1970). Mathematical representation of the mechanical properties of the heart muscle. J. Biomech. 3, 381–404.
Garfinkel, A., Kim, Y. H., Voroshilovsky, O., Qu, Z., Kil, J. R., Lee, M. H., Karagueuzian, H. S., Weiss, J. N., and Chen, P. S. (2000). Preventing ventricular fibrillation by flattening cardiac restitution. Proc. Natl. Acad. Sci. U.S.A. 97, 6061–6066.
Gordon, A. M., Homsher, E., and Regnier, M. (2000). Regulation of contraction in striated muscle. Physiol. Rev. 80, 853–924.
Gordon, A. M., Huxley, A. F., and Julian, F. J. (1966). The variation in isometric tension with sarcomere length in vertebrate muscle fibres. J. Physiol. (Lond.) 184, 170–192.
Gurev, V., Constantino, J., Rice, J. J., and Trayanova, N. A. (2010). Distribution of electromechanical delay in the heart: insights from a three-dimensional electromechanical model. Biophys. J. 99, 745–754.
Gurev, V., Lee, T., Constantino, J., Arevalo, H., and Trayanova, N. A. (2011). Models of cardiac electromechanics based on individual hearts imaging data: image-based electromechanical models of the heart. Biomech. Model. Mechanobiol. 10, 295–306.
Guth, K., and Potter, J. D. (1987). Effect of rigor and cycling cross-bridges on the structure of troponin C and on the Ca2+ affinity of the Ca2+-specific regulatory sites in skinned rabbit psoas fibers. J. Biol. Chem. 262, 13627–13635.
Helm, P., Beg, M., Miller, M., and Winslow, R. (2005a). Measuring and mapping cardiac fiber and laminar architecture using diffusion tensor MR imaging. Ann. N. Y. Acad. Sci. 1047, 296–307.
Helm, P. A., Tseng, H. J., Younes, L., Mcveigh, E. R., and Winslow, R. L. (2005b). Ex vivo 3D diffusion tensor imaging and quantification of cardiac laminar structure. Magn. Reson. Med. 54, 850–859.
Hilgemann, D. W., and Noble, D. (1987). Excitation-contraction coupling and extracellular calcium transients in rabbit atrium: reconstruction of basic cellular mechanisms. Proc. R. Soc. Lond., B Biol. Sci. 230, 163–205.
Hisano, R., and Cooper, G. T. (1987). Correlation of force-length area with oxygen consumption in ferret papillary muscle. Circ. Res. 61, 318–328.
Hu, Y., Gurev, V., Constantino, J., and Trayanova, N. (2009). Degeneration of ventricular tachycardia into ventricular fibrillation following right ventricular dilation. Circulation 120, S698.
Hunter, P. J., Mcculloch, A. D., and Ter Keurs, H. E. (1998). Modelling the mechanical properties of cardiac muscle. Prog. Biophys. Mol. Biol. 69, 289–331.
Huxley, A. F. (1957). Muscle structure and theories of contraction. Prog. Biophys. Biophys. Chem. 7, 255–318.
Izakov, V., Katsnelson, L. B., Blyakhman, F. A., Markhasin, V. S., and Shklyar, T. F. (1991). Cooperative effects due to calcium binding by troponin and their consequences for contraction and relaxation of cardiac muscle under various conditions of mechanical loading. Circ. Res. 69, 1171–1184.
Jafri, M. S., Rice, J. J., and Winslow, R. L. (1998). Cardiac Ca2+ dynamics: the roles of ryanodine receptor adaptation and sarcoplasmic reticulum load. Biophys. J. 74, 1149–1168.
Janssen, P. M., and Hunter, W. C. (1995). Force, not sarcomere length, correlates with prolongation of isosarcometric contraction. Am. J. Physiol. 269, H676–H685.
Janssen, P. M., Stull, L. B., and Marban, E. (2002). Myofilament properties comprise the rate-limiting step for cardiac relaxation at body temperature in the rat. Am. J. Physiol. Heart Circ. Physiol. 282, H499–H507.
Jie, X., Gurev, V., and Trayanova, N. (2010). Mechanisms of mechanically induced spontaneous arrhythmias in acute regional ischemia. Circ. Res. 106, 185–192.
Katsnelson, L. B., Izakov, V., and Markhasin, V. S. (1990). Heart muscle: mathematical modelling of the mechanical activity and modelling of mechanochemical uncoupling. Gen. Physiol. Biophys. 9, 219–243.
Katsnelson, L. B., Sulman, T., Solovyova, O., and Markhasin, V. S. (2011). Role of myocardial viscoelasticity in disturbances of electrical and mechanical activity in calcium overloaded cardiomyocytes: mathematical modeling. J. Theor. Biol. 272, 83–95.
Kaufmann, R., Bayer, R., Furniss, T., Krause, H., and Tritthart, H. (1974). Calcium-movement controlling cardiac contractility II. Analog computation of cardiac excitation-contraction coupling on the basis of calcium kinetics in a multi-compartment model. J. Mol. Cell. Cardiol. 6, 543–559.
Keldermann, R. H., Nash, M. P., Gelderblom, H., Wang, V. Y., and Panfilov, A. V. (2010). Electromechanical wavebreak in a model of the human left ventricle. Am. J. Physiol. Heart Circ. Physiol. 299, H134–H143.
Kerckhoffs, R. C., Neal, M. L., Gu, Q., Bassingthwaighte, J. B., Omens, J. H., and Mcculloch, A. D. (2007). Coupling of a 3D finite element model of cardiac ventricular mechanics to lumped systems models of the systemic and pulmonic circulation. Ann. Biomed. Eng. 35, 1–18.
Kerckhoffs, R. C., Omens, J. H., Mcculloch, A. D., and Mulligan, L. J. (2010). Ventricular dilation and electrical dyssynchrony synergistically increase regional mechanical nonuniformity but not mechanical dyssynchrony: a computational model. Circ. Heart Fail. 3, 528–536.
Kerckhoffs, R. C. P., Bovendeerd, P. H. M., Prinzen, F., Smits, K., and Arts, T. (2003). Intra- and interventricular asynchrony of electromechanics in the ventricularly paced heart. J. Eng. Math. 47, 201–216.
Kerckhoffs, R. C. P., Healy, S. N., Usyk, T. P., and Mcculloch, A. D. (2006). Computational methods for cardiac electromechanics. Proc. IEEE 94, 769–783.
Kohl, P., Hunter, P., and Noble, D. (1999). Stretch-induced changes in heart rate and rhythm: clinical observations, experiments and mathematical models. Prog. Biophys. Mol. Biol. 71, 91–138.
Kohl, P., Sachs, F., and Franz, M. R. (eds). (2005). Cardiac Mechano-electric Feedbackand Arrhythmias. Philadelphia: Elsevier Health Sciences.
Konhilas, J. P., Irving, T. C., and De Tombe, P. P. (2002). Frank-Starling law of the heart and the cellular mechanisms of length-dependent activation. Pflugers Arch. 445, 305–310.
Landesberg, A., and Sideman, S. (1994a). Coupling calcium binding to troponin C and cross-bridge cycling in skinned cardiac cells. Am. J. Physiol. 266, H1260–H1271.
Landesberg, A., and Sideman, S. (1994b). Mechanical regulation of cardiac muscle by coupling calcium kinetics with cross-bridge cycling: a dynamic model. Am. J. Physiol. 267, H779–H795.
Landesberg, A., and Sideman, S. (1999). Regulation of energy consumption in cardiac muscle: analysis of isometric contractions. Am. J. Physiol. 276, H998–H1011.
Legrice, I. J., Hunter, P. J., and Smaill, B. H. (1997). Laminar structure of the heart: a mathematical model. Am. J. Physiol. 272, H2466–H2476.
LeGrice, I. J., Smaill, B. H., Chai, L. Z., Edgar, S. G., Gavin, J. B., and Hunter, P. J. (1995). Laminar structure of the heart: ventricular myocyte arrangement and connective tissue architecture in the dog. Am. J. Physiol. 269, H571–H582.
Lehman, W., Rosol, M., Tobacman, L. S., and Craig, R. (2001). Troponin organization on relaxed and activated thin filaments revealed by electron microscopy and three-dimensional reconstruction. J. Mol. Biol. 307, 739–744.
Li, W., Kohl, P., and Trayanova, N. (2004). Induction of ventricular arrhythmias following mechanical impact: a simulation study in 3D. J. Mol. Histol. 35, 679–686.
Li, W., Kohl, P., and Trayanova, N. (2006). Myocardial ischemia lowers precordial thump efficacy: an inquiry into mechanisms using three-dimensional simulations. Heart Rhythm 3, 179–186.
Lumens, J., Delhaas, T., Kirn, B., and Arts, T. (2009). Three-wall segment (TriSeg) model describing mechanics and hemodynamics of ventricular interaction. Ann. Biomed. Eng. 37, 2234–2255.
Ma, S. P., and Zahalak, G. I. (1991). A distribution-moment model of energetics in skeletal muscle. J. Biomech. 24, 21–35.
Markhasin, V. S., Solovyova, O., Katsnelson, L. B., Protsenko, Y., Kohl, P., and Noble, D. (2003). Mechano-electric interactions in heterogeneous myocardium: development of fundamental experimental and theoretical models. Prog. Biophys. Mol. Biol. 82, 207–220.
Matsuoka, S., Sarai, N., Jo, H., and Noma, A. (2004). Simulation of ATP metabolism in cardiac excitation-contraction coupling. Prog. Biophys. Mol. Biol. 85, 279–299.
Matsuoka, S., Sarai, N., Kuratomi, S., Ono, K., and Noma, A. (2003). Role of individual ionic current systems in ventricular cells hypothesized by a model study. Jpn. J. Physiol. 53, 105–123.
McDonald, K. S., and Moss, R. L. (1995). Osmotic compression of single cardiac myocytes eliminates the reduction in Ca2+ sensitivity of tension at short sarcomere length. Circ. Res. 77, 199–205.
Negroni, J. A., and Lascano, E. C. (1996). A cardiac muscle model relating sarcomere dynamics to calcium kinetics. J. Mol. Cell. Cardiol. 28, 915–929.
Negroni, J. A., and Lascano, E. C. (1999). Concentration and elongation of attached cross-bridges as pressure determinants in a ventricular model. J. Mol. Cell. Cardiol. 31, 1509–1526.
Negroni, J. A., and Lascano, E. C. (2008). Simulation of steady state and transient cardiac muscle response experiments with a Huxley-based contraction model. J. Mol. Cell. Cardiol. 45, 300–312.
Niederer, S. A., Hunter, P. J., and Smith, N. P. (2006). A quantitative analysis of cardiac myocyte relaxation: a simulation study. Biophys. J. 90, 1697–1722.
Niederer, S. A., Plank, G., Chinchapatnam, P., Ginks, M., Lamata, P., Rhode, K. S., Rinaldi, C. A., Razavi, R., and Smith, N. P. (2011). Length-dependent tension in the failing heart and the efficacy of cardiac resynchronization therapy. Cardiovasc. Res. 89, 336–343.
Niederer, S. A., and Smith, N. P. (2007). A mathematical model of the slow force response to stretch in rat ventricular myocytes. Biophys. J. 92, 4030–4044.
Niederer, S. A., and Smith, N. P. (2009). The role of the Frank-Starling law in the transduction of cellular work to whole organ pump function: a computational modeling analysis. PLoS Comput. Biol. 5, e1000371. doi: 10.1371/journal.pcbi.1000371
Niederer, S. A., Ter Keurs, H. E., and Smith, N. P. (2009). Modelling and measuring electromechanical coupling in the rat heart. Exp. Physiol. 94, 529–540.
Noble, D., and Rudy, Y. (2001). Models of cardiac ventricular action potentials: iterative interaction between experiment and simulation. Philos. Trans. R. Soc. Lond. A 359, 1127–1142.
Noble, D., Varghese, A., Kohl, P., and Noble, P. (1998). Improved guinea-pig ventricular cell model incorporating a diadic space, IKr and IKs, and length- and tension-dependent processes. Can. J. Cardiol. 14, 123–134.
Onate, E., Rojek, J., Taylor, R., and Zienkiewicz, O. (2004). Finite calculus formulation for incompressible solids using linear triangles and tetrahedra. Int. J. Numer. Methods Eng. 59, 1473–1500.
Pandit, S. V., Clark, R. B., Giles, W. R., and Demir, S. S. (2001). A mathematical model of action potential heterogeneity in adult rat left ventricular myocytes. Biophys. J. 81, 3029–3051.
Panfilov, A. V., Keldermann, R. H., and Nash, M. P. (2007). Drift and breakup of spiral waves in reaction-diffusion-mechanics systems. Proc. Natl. Acad. Sci. U.S.A. 104, 7922–7926.
Pate, E., and Cooke, R. (1986). A model for the interaction of muscle cross-bridges with ligands which compete with ATP. J. Theor. Biol. 118, 215–230.
Plank, G., Zhou, L., Greenstein, J. L., Cortassa, S., Winslow, R. L., O’rourke, B., and Trayanova, N. A. (2008). From mitochondrial ion channels to arrhythmias in the heart: computational techniques to bridge the spatio-temporal scales. Philos. Transact. A Math. Phys. Eng. Sci. 366, 3381–3409.
Prassl, A. J., Kickinger, F., Ahammer, H., Grau, V., Schneider, J. E., Hofer, E., Vigmond, E. J., Trayanova, N. A., and Plank, G. (2009). Automatically generated, anatomically accurate meshes for cardiac electrophysiology problems. IEEE Trans. Biomed. Eng. 56, 1318–1330.
Prinzen, F. W., Augustijn, C. H., Allessie, M. A., Arts, T., Delhaas, T., and Reneman, R. S. (1992). The time sequence of electrical and mechanical activation during spontaneous beating and ectopic stimulation. Eur. Heart J. 13, 535–543.
Razumova, M. V., Bukatina, A. E., and Campbell, K. B. (1999). Stiffness-distortion sarcomere model for muscle simulation. J. Appl. Physiol. 87, 1861–1876.
Razumova, M. V., Bukatina, A. E., and Campbell, K. B. (2000). Different myofilament nearest-neighbor interactions have distinctive effects on contractile behavior. Biophys. J. 78, 3120–3137.
Rice, J. J., and De Tombe, P. P. (2004). Approaches to modeling crossbridges and calcium-dependent activation in cardiac muscle. Prog. Biophys. Mol. Biol. 85, 179–195.
Rice, J. J., Jafri, M. S., and Winslow, R. L. (2000). Modeling short-term interval-force relations in cardiac muscle. Am. J. Physiol. Heart Circ. Physiol. 278, H913–H931.
Rice, J. J., Stolovitzky, G., Tu, Y., and de Tombe, P. P. (2003). Ising model of cardiac thin filament activation with nearest-neighbor cooperative interactions. Biophys. J. 84, 897–909.
Rice, J. J., Tu, Y., Poggesi, C., and De Tombe, P. P. (2008a). Spatially-compressed cardiac myofilament models generate hysteresis that is not found in real muscle. Pac. Symp. Biocomput. 2008, 366–377.
Rice, J. J., Wang, F., Bers, D. M., and De Tombe, P. P. (2008b). Approximate model of cooperative activation and crossbridge cycling in cardiac muscle using ordinary differential equations. Biophys. J. 95, 2368–2390.
Rice, J. J., Winslow, R. L., and Hunter, W. C. (1999). Comparison of putative cooperative mechanisms in cardiac muscle: length dependence and dynamic responses. Am. J. Physiol. 276, H1734–H1754.
Robinson, T. F., and Winegrad, S. (1977). Variation of thin filament length in heart muscle. Nature 267, 74–75.
Rodriguez, B., Li, L., Eason, J. C., Efimov, I. R., and Trayanova, N. A. (2005). Differences between left and right ventricular chamber geometry affect cardiac vulnerability to electric shocks. Circ. Res. 97, 168–175.
Rodríguez, B., and Trayanova, N. (2003). Upper limit of vulnerability in a defibrillation model of the rabbit ventricles. J. Electrocardiol. 36(Suppl.), 51–56.
Schneider, N. S., Shimayoshi, T., Amano, A., and Matsuda, T. (2006). Mechanism of the Frank-Starling law – a simulation study with a novel cardiac muscle contraction model that includes titin and troponin I. J. Mol. Cell. Cardiol. 41, 522–536.
Shannon, T. R., Wang, F., Puglisi, J., Weber, C., and Bers, D. M. (2004). A mathematical treatment of integrated Ca dynamics within the ventricular myocyte. Biophys. J. 87, 3351–3371.
Slawnych, M. P., Seow, C. Y., Huxley, A. F., and Ford, L. E. (1994). A program for developing a comprehensive mathematical description of the crossbridge cycle of muscle. Biophys. J. 67, 1669–1677.
Smith, N. P. (2003). From sarcomere to cell: an efficient algorithm for linking mathematical models of muscle contraction. Bull. Math. Biol. 65, 1141–1162.
Solaro, R. J., and Rarick, H. M. (1998). Troponin and tropomyosin: proteins that switch on and tune in the activity of cardiac myofilaments. Circ. Res. 83, 471–480.
Solovyova, O., Markhasin, V. S., Katsnelson, L. B., Protsenko, Y., Noble, P. J., Garny, A., Kohl, P., and Noble, D. (2003). Mechanical interaction of heterogeneous cardiac muscle segments in silico: effects on Ca2+ handling and action potential. Int. J. Bifurcat. Chaos 13, 3757–3782.
Stevens, C., Remme, E., Legrice, I., and Hunter, P. (2003). Ventricular mechanics in diastole: material parameter sensitivity. J. Biomech. 36, 737–748.
Stienen, G. J., Papp, Z., and Elzinga, G. (1993). Calcium modulates the influence of length changes on the myofibrillar adenosine triphosphatase activity in rat skinned cardiac trabeculae. Pflugers Arch. 425, 199–207.
Swartz, D. R., and Moss, R. L. (1992). Influence of a strong-binding myosin analogue on calcium-sensitive mechanical properties of skinned skeletal muscle fibers. J. Biol. Chem. 267, 20497–20506.
ter Keurs, H. E., Shinozaki, T., Zhang, Y. M., Zhang, M. L., Wakayama, Y., Sugai, Y., Kagaya, Y., Miura, M., Boyden, P. A., Stuyvers, B. D., and Landesberg, A. (2008). Sarcomere mechanics in uniform and non-uniform cardiac muscle: a link between pump function and arrhythmias. Prog. Biophys. Mol. Biol. 97, 312–331.
Tran, K., Smith, N. P., Loiselle, D. S., and Crampin, E. J. (2010). A metabolite-sensitive, thermodynamically constrained model of cardiac cross-bridge cycling: implications for force development during ischemia. Biophys. J. 98, 267–276.
Trayanova, N. A. (2011). Whole-heart modeling: applications to cardiac electrophysiology and electromechanics. Circ. Res. 108, 113–128.
Trayanova, N. A., Constantino, J., and Gurev, V. (2011a). Electromechanical models of the ventricles. Am. J. Physiol. Heart Circ. Physiol. PMID: 21572017 [Epub ahead of print].
Trayanova, N. A., Gurev, V., Constantino, J., and Hu, Y. (2011b). “Mathematical models of ventricular mechano-electric coupling and arrhythmia,” in Cardiac Mechano-Electric Feedback and Arrhythmias, eds P. Kohl, F. Sachs, and M. R. Franz (Oxford, UK: Oxford University Press), 258–266.
Trybus, K. M., and Taylor, E. W. (1980). Kinetic studies of the cooperative binding of subfragment 1 to regulated actin. Proc. Natl. Acad. Sci. U.S.A. 77, 7209–7213.
Usyk, T. P., and McCulloch, A. D. (2003). Relationship between regional shortening and asynchronous electrical activation in a three-dimensional model of ventricular electromechanics. J. Cardiovasc. Electrophysiol. 14, S196–S202.
Vadakkumpadan, F., Arevalo, H., Prassl, A. J., Chen, J., Kickinger, F., Kohl, P., Plank, G., and Trayanova, N. (2009). Image-based models of cardiac structure in health and disease. Wiley Interdiscip. Rev. Syst. Biol. Med. 2, 489–506.
Vetter, F. J., and McCulloch, A. D. (1998). Three-dimensional analysis of regional cardiac function: a model of rabbit ventricular anatomy. Prog. Biophys. Mol. Biol. 69, 157–183.
Wannenburg, T., Heijne, G. H., Geerdink, J. H., Van Den Dool, H. W., Janssen, P. M., and De Tombe, P. P. (2000). Cross-bridge kinetics in rat myocardium: effect of sarcomere length and calcium activation. Am. J. Physiol. Heart Circ. Physiol. 279, H779–H790.
Weiwad, W. K., Linke, W. A., and Wussling, M. H. (2000). Sarcomere length-tension relationship of rat cardiac myocytes at lengths greater than optimum. J. Mol. Cell. Cardiol. 32, 247–259.
Wier, W. G., and Yue, D. T. (1986). Intracellular calcium transients underlying the short-term force-interval relationship in ferret ventricular myocardium. J. Physiol. (Lond.) 376, 507–530.
Wong, A. Y. (1971). Mechanics of cardiac muscle, based on Huxley’s model: mathematical stimulation of isometric contraction. J. Biomech. 4, 529–540.
Wong, A. Y. (1981). A model of excitation-contraction coupling of mammalian cardiac muscle. J. Theor. Biol. 90, 37–61.
Keywords: heart, active tension, myofilament, actin, myosin, activation, electromechanical model, stretch-induced arrhythmias
Citation: Trayanova NA and Rice JJ (2011) Cardiac electromechanical models: from cell to organ. Front. Physio. 2:43. doi: 10.3389/fphys.2011.00043
Received: 18 April 2011;
Paper pending published: 15 May 2011;
Accepted: 12 July 2011;
Published online: 11 August 2011.
Edited by:
Rajat Mittal, Johns Hopkins University, USAReviewed by:
Edward Joseph Vigmond, University of Calgary, CanadaGernot Plank, Medical University of Graz, Austria
Zhiliang Xu, University of Notre Dame, USA
Copyright: © 2011 Trayanova and Rice. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence: Natalia A. Trayanova, Department of Biomedical Engineering and Institute for Computational Medicine, Johns Hopkins University, Hackerman Hall 216, 3400 North Charles Street, Baltimore, MD 21218, USA. e-mail:bnRyYXlhbm92YUBqaHUuZWR1