Mean Field Strategies Induce Unrealistic Non-Linearities in Calcium Puffs

Mean field models are often useful approximations to biological systems, but sometimes, they can yield misleading results. In this work, we compare mean field approaches with stochastic models of intracellular calcium release. In particular, we concentrate on calcium signals generated by the concerted opening of several clustered channels (calcium puffs). To this end we simulate calcium puffs numerically and then try to reproduce features of the resulting calcium distribution using mean field models were all the channels open and close simultaneously. We show that an unrealistic non-linear relationship between the current and the number of open channels is needed to reproduce the simulated puffs. Furthermore, a single channel current which is five times smaller than the one of the stochastic simulations is also needed. Our study sheds light on the importance of the stochastic kinetics of the calcium release channel activity to estimate the release fluxes.

1 Introduction

An important problem in different areas of science is to relate phenomena that occur at different scales. In biology, an observed behavior at a certain level of organization is often the result of interactions at a lower level, with very different physical and temporal scales. Calcium (Ca²⁺) signals are an extraordinary example of a multiple scale biological system suitable for being studied with different experimental techniques, each of which focus on a particular temporal and spatial scale. Therefore, it is important to understand the interactions of processes occurring at different scales and how to infer properties at unobserved scales from experimental observations. In this respect, mathematics is invaluable (Cohen, 2004).

Ca²⁺ ions are important signaling elements that regulate a large variety of cellular functions such as fertilization, proliferation, development, learning and memory, contraction and secretion (Berridge et al., 2000). The versatility of Ca²⁺ as a intracellular cell messenger is possible because cells have mechanisms to control efficiently and precisely the distribution of Ca²⁺ in space and time. Within cells, Ca²⁺ is kept at high concentrations in stores such as the endoplasmic reticulum (ER). Release of Ca²⁺ from the ER occurs through specialized channels among which inositol triphosphate (IP₃) receptors play a most relevant role (Foskett et al., 2007). IP₃Rs are spatially organized in clusters located on the membrane of the ER and separated by a few microns (Yao et al., 1995). The open probability of IP₃Rs depends on both the IP₃ and cytosolic Ca²⁺concentration ([Ca²⁺]; Taylor, 1998; Patel et al., 1999). A key feature is the well-established biphasic action of Ca²⁺ in both facilitating and inhibiting the opening of IP₃Rs. For relatively low [Ca²⁺], the Ca²⁺ released by one channel increases the open probability of neighboring channels, whereas at high [Ca²⁺] it favors a closed state of the channel (Iino, 1990; Bezprozvanny et al., 1991; Finch et al., 1991; Mak et al., 1998; Ramos-Franco et al., 1998). This dependence of the open probability of IP₃Rs on cytosolic Ca²⁺ creates communication between channels. As a result of the spatial organization of channels and the process of Ca²⁺-induced Ca²⁺-release (CICR), cytosolic Ca²⁺ signals display a hierarchical spatiotemporal organization which in some cells (e.g., oocytes) have length scales that span over six orders of magnitude (Callamaras and Parker, 1994; Mak and Foskett, 1997; Shuai and Jung, 2003a). The hierarchy of Ca²⁺ signals go from local ones such as “blips” (Ca²⁺ release through a single IP₃R) and “puffs” (Ca²⁺ release through several IP₃Rs in a cluster; Sun et al., 1998; Bootman et al., 1997; Yao and Parker, 1991; Parker et al., 1996) to waves that propagate globally across the cell by successive cycles of CICR and Ca²⁺ diffusion between clusters (Yao and Parker, 1991; Parker et al., 1996; Callamaras et al., 1998; Sun et al., 1998). These signals have been observed using fluorescence microscopy and Ca²⁺ sensitive dyes (Bootman et al., 1997; Callamaras et al., 1998; Sun et al., 1998). However, fluorescence microscopy experiments cannot follow the kinetics of individual IP₃Rs or the detailed Ca²⁺ dynamics within a cluster of channels in most cell types. The spatial resolution of conventional light microscopy is limited by diffraction. This determines that features below the 250-nm length scales are unobservable in typical confocal images. This limit can be beaten using super-resolution techniques. Techniques of this type have been applied to Ca²⁺ signals using total internal reflection fluorescence (TIRF) and a fast CCD (Smith and Parker, 2009; Parker and Smith, 2010; Wiltgen et al., 2010). The need of using TIRF to guarantee a good axial resolution restricts the application of this approach to cells, as those of the human neuroblastoma SH-SY5Y cell line, where IP₃Rs are close enough to the plasma membrane. In particular, it does not work in oocytes. A vast body of literature on Ca²⁺ signalsin this cell type exists which is still awaiting a clarification of the underlying Ca²⁺ and IP₃R dynamics. Oocytes, on the other hand, are intact cells and can be used to explore changes in the morphology of the signals with maturation or with depth (Callamaras and Parker, 1999; Machaca, 2007). Thus, their study is of great interest. Unfortunately, fluorescence microscopy experiments in this cell type only give, so far, average (mean field) information of the underlying process. Mathematical tools have been widely used to link experimental observations at the level of puffs with the single channel activity.

As with experiments, there are different modeling approaches that differ on the spatial or time scale they try to resolve. Some models rely on the hypothesis that channels are in such close contact that the concentration of Ca²⁺ can be considered homogeneous throughout the cluster (Shuai and Jung, 2002, 2003b; Thul and Falcke, 2004; DeRemigio and Smith, 2005; Diambra and Guisoni, 2005; Ullah and Jung, 2006). This assumption allows for relatively fast simulations of cytosolic Ca²⁺ dynamics since Ca²⁺ diffusion within the cluster can be neglected. Other models inferred basic puff properties using a deterministic dynamics of spatially localized channels within a cluster combined with an analysis of fluorescence experiments (Shuai et al., 2006; Baran, 2007; Baran and Popescu, 2009; Bruno et al., 2010). These approaches have been useful as a first step for more elaborate analyses that incorporate the stochastic transitions between open and closed states of the channels. Some useful puff properties inferred with deterministic models include estimates of the current of underlying puffs, duration, and spatial width of the release sites.

We have recently analyzed experimental calcium puffs observed in Xenopus laevis oocytes using linescan experiments (Bruno et al., 2010). Using a previously developed backward algorithm (Ventura et al., 2005), we estimated the calcium flux that underlies fluorescent images. Since the algorithm is model independent, the estimates of Bruno et al. (2010) are independent of the dye or the exogenous buffer that are used in the experiments. The results we presented in Bruno et al. (2010) and those of Rose et al. (2006) could be explained by a model in which the total calcium current released through a cluster of IP₃Rs during a puff is a non-linear function of the number of open channels: linear when the number is small (between 1 and ∼20 channels) and proportional to the square root of the number of channels for larger puffs. This type of scaling could be attributed to local Ca²⁺ depletion inside the ER. In fact, in Thul and Falcke (2004), the authors presented simulations of the current and concentration profiles generated by Ca²⁺ release from the ER and compared them with signal mass measurements in X. laevis oocytes. Taking into account both the luminal and cytosolic Ca²⁺ dynamics, they found that the release current was approximately proportional to the square root of the number of open channels. In view of these results, the change of scaling could be explained as follows (Bruno et al., 2010). Puffs of small amplitude correspond to very few open channels and relatively large distances from one another in which case depletion does not affect the single channel current. Puffs of large amplitude correspond to much smaller inter-channel distances in which case local depletion affects the luminal concentration in the vicinity of any other open channel and as a result, the total Ca²⁺ current scales as the square root of the number of channels. Thul and Falcke (2004). However, these models do not describe the stochastic nature of the transitions between open and closed states of individual channels, so they can be viewed as mean field descriptions (Thul and Falcke, 2004; Bruno et al., 2010). Recently, the need of using stochastic and spatially resolved models to unveil the full repertoire of Ca²⁺ dynamics has been emphasized (Solovey et al., 2008; Thul et al., 2009; Rüdiger et al., 2010; Solovey and Ponce Dawson, 2010a,b; Diambra and Marchant, 2011; Thurley and Falcke, 2011).

In this work we compare mean field and stochastic puff models, with the latter including the description of individual channel openings and closings. In particular we show that the stochastic model reproduces the experimental observations of Bruno et al. (2010) with a fixed single channel current of ∼0.1 pA regardless of the number of open channels. This implies that the instantaneous total current is proportional to the number of open IP₃Rs at any given time. It is the average Ca²⁺ current released during the whole puff duration that scales non-linearly with the number of open or available channels, as does the (instantaneous) total current in the mean field models of Bruno et al. (2010), Thul and Falcke (2004). The studies of the present paper also show that in order to reproduce the experimental observations under the assumption that channels open and close simultaneously a smaller single IP₃R current is needed than the actual one. Therefore, using mean field models to derive the underlying channel current from an image can lead to an underestimation of its value. The present study shows the limitations of mean field models and the importance of including a detailed description of the intra-cluster dynamics in order to infer realistic single channel properties from collective signals such as puffs.

The organization of the paper is as follows. In Section 2 we describe the models and the procedure to simulate puffs. Section 3 is divided in four parts. First we compare the time course of the current and fluorescence obtained with simulations of the mean field and stochastic puffs (see Section 3.1). In Section 3.2 we show a non-linear property of the system at the level of puffs, both in experimental data and simulations. In Section 3.3 we present the main result of this work which is the artifactual non-linearities that appear in mean field puff models and in mean field based analyses of experimental puffs. A simple semi-analytical model (see Section 3.4) helps to understand the results. Discussions and conclusions are presented in Section 4.

2 Materials and Methods

2.1 Puff Models Based on a Cluster of Spatially Localized IP₃Rs

We consider two kinds of models that differ mainly on the way we deal with the channel temporal dynamics. In mean field models, all available channels open and close simultaneously at times chosen a priori while in stochastic models the transitions between the open and closed conformations of the channels is stochastic and follows a channel kinetic model. The number and spatial distribution of the channels is based on the following evidence (Bruno et al., 2010): (a) puffs result from the release of Ca²⁺ through a few tens of IP₃Rs within a cluster; (b) the size of the Ca²⁺ release region is ∼500 nm², independent of the number of channels. As we describe in Section 2.1.2, we do not include the dynamics of IP₃ binding and unbinding. Thus, by available channels we mean IP₃Rs with IP₃ bound.

Clusters consist of N_p available channels (N_p ≤ 60) randomly distributed within a circle of radius R = 230 nm (stochastic models) or a square of side ∼250 nm (mean field models) at the beginning of the simulation. We only use cluster configurations that gave nearest neighbor channel distances larger than 40 nm in the stochastic simulations or 45 nm in the deterministic case.

The stochastic transitions between open and closed states of the channels occur at time scales much faster than the time scale that the experiments can resolve. For this reason, inferred values of the puff calcium current should be taken as averaged values. In contrast, in the simulations we know exactly how many channels are open with a resolution of ∼0.1 ms, much better than the resolution with which we could infer the Ca²⁺ currents from the experimental records in Bruno et al. (2010). Therefore, in order to compare the maximum released current inferred from the experiments with the current used in the simulations we have to average the time course of the simulated current. This was done using a square moving average window.

2.1.1 Mean field models

The number of open channels, N_p, is constant during a puff and each open channel releases a constant Ca²⁺ current I_ch. However, the value of I_ch may depend on N_p. We analyze two situations: the mean field linear model where I_ch is independent of the number of open channels, in which case the total Ca²⁺ current is

with I_ch = 0.1 pA and the mean field non-linear model (Bruno et al., 2010) where I_ch depends non-linearly on the number of open channels and the total Ca²⁺ current is given by:

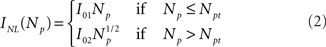
with I₀₁ = 0.017 pA, I₀₂ = 0.08 pA, and N_pt = 22. This expression corresponds to the one derived from the analysis of experimental puffs presented in Bruno et al. (2010).

2.1.2 Stochastic models

The single channel current is 0.1 pA, regardless of the number of open channels. We use this value for the current because it agrees with previous estimates of the type 1 IP₃R current in the ER membrane of X. laevis oocytes (Rose et al., 2006). It is also within the range of currents found recently for single recombinant type 3 IP₃Rs (Vais et al., 2010).

The transition between the open and closed conformations of the channels is stochastic. We use two simple IP₃R kinetic models which differ solely on the behavior of the mean open time as a function of [Ca²⁺]. We call these models CI (for which the mean open time is independent of [Ca²⁺]) and CD (for which the mean open time decreases with [Ca²⁺]). We use these models to test whether a Ca²⁺ dependent or a Ca²⁺ independent open to closed transition leaves a detectable signature on puffs or not. Both models assume that the channel can be in three states, closed (C), open (O), or inhibited (I). The stochastic transitions between states occur according to the following schemes:

These models do not consider the kinetics of IP₃ binding or unbinding to the IP₃R. According to most IP₃R kinetic models, these processes occur so fast that the fraction of IP₃Rs with IP₃ bound can be assumed to be fixed and given by an equilibrium relationship (Young and Keizer, 1992). In that sense, the kinetic scheme actually describes the transitions between states of the IP₃R with IP₃ bound. In addition, the kinetic schemes do not consider either that the channels can reopen once they enter the inhibited states. This simplification is reasonable to investigate basic puff properties. Namely, the time an IP₃R remains inhibited under the conditions for which puffs are observed has been estimated as ∼2 s (Fraiman et al., 2006), a time much larger than the duration of a puff. This long inhibition time is compatible with the IP₃R open probability obtained in reconstituted bilayer experiments (Bezprozvanny et al., 1991) but seems contradictory with the results of patch clamp experiments performed in isolated Xenopus oocyte nuclei using K⁺ as the channel carrier (Mak et al., 1998). The latter type of experiments seems less disruptive than the former one since IP₃Rs remain in a native membrane. However, the Ca²⁺ concentrations that are used on the luminal side of the channel in the patch clamp experiments are much lower than the ones encountered under physiological conditions. As discussed in Fraiman and Ponce Dawson (2004), this could explain the apparent contradiction between the long inhibition time estimated in Fraiman et al. (2006) and the observations of Mak et al. (1998). In fact, the existence of a broad variety of experimental results derived from single channel recordings calls for the definition of an optimal system where the source of the observed discrepancies can be unambiguously established (Foskett et al., 2007).

The values of the parameters of the kinetic models we consider in this paper are listed in Table 1. The open transition rate, k_CO, is taken from the De Young–Keizer IP₃R model (Young and Keizer, 1992) and the transition rate from the open to the inhibited state is defined so that the mean open time of a single IP₃R is 10 ms (a typical IP₃R open duration; Mak et al., 1998). In the case of the CD model, we choose 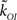so that 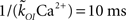with [Ca²⁺]_mouth the value of [Ca²⁺] at the mouth of an isolated open channel. We use [Ca²⁺]_mouth = 41.77 μM, an estimate obtained by numerical simulations assuming a single channel current I_ch = 0.1 pA (Solovey et al., 2008). The transitions between states of the channels are computed using a discrete time Markov Chain procedure with a time step 1 μs.

TABLE 1

Table 1. Parameters of the IP₃R models described in Section 2.1.2.

We calculate the duration of the Ca²⁺ release during a puff as:

where 1_{n(t)>0} = 1 if n(t) > 0 and 0 otherwise, with n(t) the number of open channels at time t and t_M = 0.15 s, the total time of the simulations. The Ca²⁺ release duration corresponds to the total time with at least one open channel.

We calculate the average Ca²⁺ current released as:

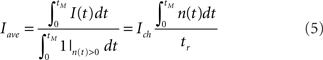
It corresponds to the current of a puff that releases the same total amount of Ca²⁺ but at a constant rate during the whole duration of the Ca²⁺ release. It is equivalent to a case where all channels of the cluster open and close simultaneously and release the same total amount of Ca²⁺ during the same time as the original puff.

2.1.3 Simulations

We solve numerically the set of coupled reaction-diffusion equations that result from the diffusion of cytosolic Ca²⁺ in the presence of localized Ca²⁺ channels. The details of the methods to simulate puffs are described in Solovey et al. (2008). Therefore, here we only present a brief description. Besides Ca²⁺, we consider the following species: an immobile endogenous buffer, a cytosolic fluorescent Ca²⁺ indicator (B) and an exogenous mobile buffer. We use the same parameters we used in Solovey et al. (2008).

In the case of the mean field models, we use a fine spatial grid where individual channels are located. We use clusters of 1, 3, 5, 10, and 15 channels for the linear mean field model and 1, 3, 5, 10, 15, 20, 25, 30, 40, and 50 channels for the simulations with the non-linear mean field model. The release duration was set to 18 ms, the mean duration of Ca²⁺ release inferred from experiments in Bruno et al. (2010). In order to do a qualitative description of the differences between stochastic and mean field models (Section 3.1), we used long release durations (∼50 ms), as illustrated in Figure 1.

FIGURE 1

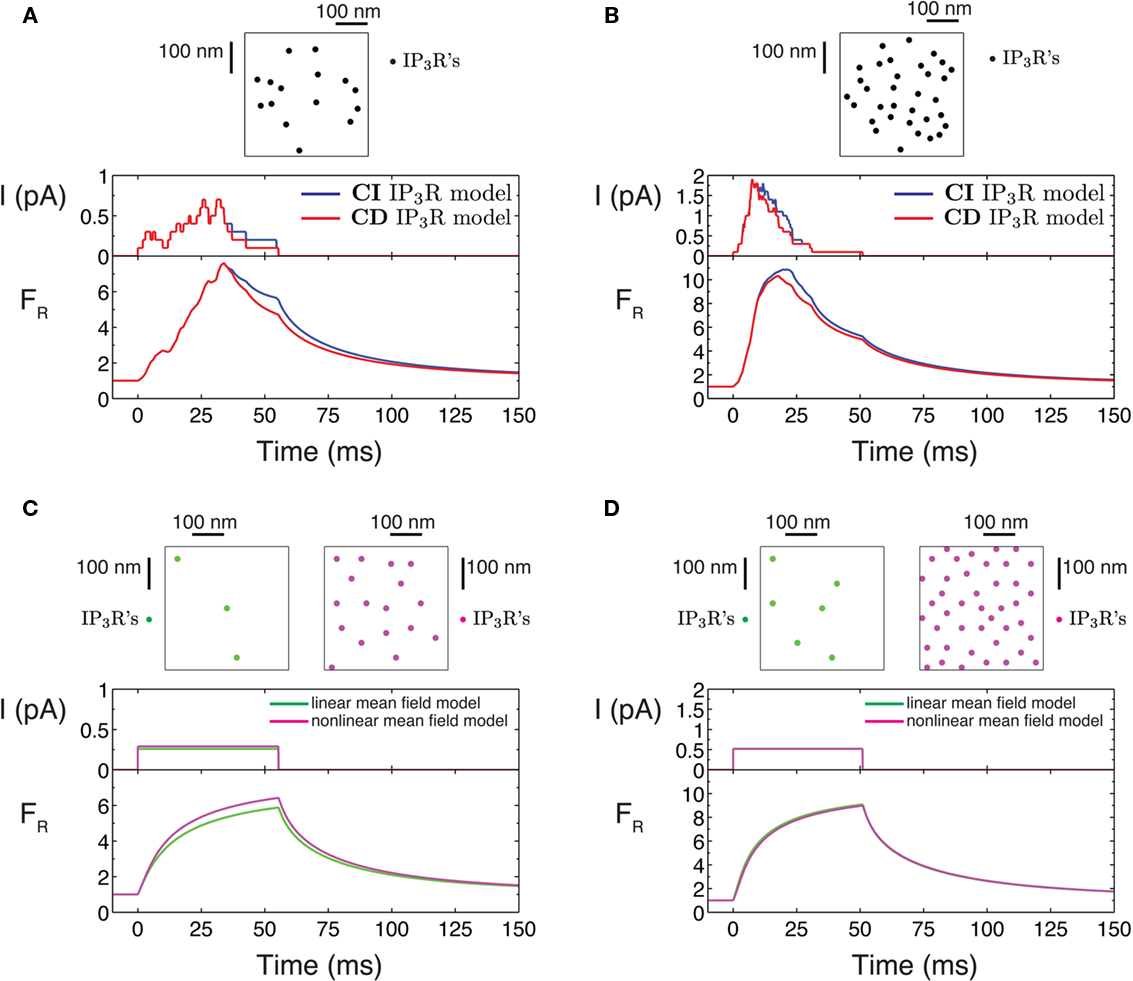
Figure 1. Puff current and fluorescence time course for the stochastic and mean field models. (A,B) Stochastic puff model: simulations of the stochastic puff model for a cluster of 15 IP₃Rs (A) and 33 IP₃Rs (B). The spatial distribution of channels is shown in the upper square plots (500 nm × 500 nm). The lower plots show the time evolution of the total current released and the resulting fluorescence signal. Red curves correspond to simulations in which the channels follow the CD model and blue lines, CI model. (C,D) Mean field puff models: simulations of the mean field puff models. In (C) the simulations of the linear (green) and the non-linear (red) mean field models are such that the Ca²⁺ current is ∼0.25 pA. The number of channels are 3 in the linear mean field and 17 in the non-linear mean field model. In (D) the release current is ∼0.5 pA and the number of channels is 6 (linear model) and 33 (non-linear model). The resulting fluorescence time course is shown in the bottom plot and the distribution of channels over a 500-nm × 500-nm region is shown in the upper plot.

To generate puffs with the stochastic model we use a simplified method also introduced in Solovey et al. (2008). The method is based on a scale separation, a similar approach as the one taken more recently by Skupin et al. (2010). Namely, we use a fine grid to determine the [Ca²⁺] distribution within the cluster but describe its dynamics with a quasi-stationary approximation. In order to determine the contribution of each open channel to the [Ca²⁺] distribution within the cluster, we first analyze this distribution when there is only one channel in the same cytosolic environment. The total [Ca²⁺] within the cluster when there are several open channels is then approximated by a linear combination of the contributions due to each individual open channel. This detailed description of [Ca²⁺] within the cluster is used to determine the openings and closings of the various channels. In this way we obtain the total Ca²⁺ current that is released from the cluster as a function of time. The spatiotemporal [Ca²⁺] distribution outside the cluster is determined using a coarser grid in which the cluster is represented by a point source whose current is proportional to the number of open channels determined before. A reaction-diffusion system is solved on this coarser grid. We simulated 10 puffs for a cluster of a given number of channels that we vary between 10 and 50.

The fluorescence F is related to the concentration of Ca²⁺ ions bound to the fluorescent dye (CaB):

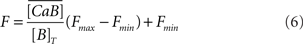
where is an averaged version of CaB due to the microscope point spread function (Bruno et al., 2010).

2.2 Semi-Analytical Puff Model

In order to gain a more intuitive understanding of the behaviors encountered with the numerical simulations, we also analyze a cartoon-like model that is amenable to analytic calculations. We consider the IP₃R kinetic models introduced in Section 2.1.2 but the Ca²⁺ dynamics is simplified in two ways. First, at time zero all N_p channels are open. All they can do is make a transition to the inhibited state. The puff ends when all channels are inhibited. This simplifies enormously the complexity of the Ca²⁺ dynamics, specially in the CI model, in which the transition from the open to the inhibited state is independent of Ca²⁺. To further simplify the dynamics of the CD model, we make a second approximation: all channels of the cluster are subject to the same [Ca²⁺] which is proportional to the number of open channels n, so that the [Ca²⁺] at time t is [Ca²⁺](t) = n(t)[Ca²⁺]_mouth, where [Ca²⁺]_mouth = 41.77 μM (Solovey et al., 2008) and n = N_p, N_p − 1, …, 1, 0.

The two versions of the semi analytic model can be considered as extreme cases regarding the channels “coupling strength” (DeRemigio and Smith, 2005; Nguyen et al., 2005; Groff and Smith, 2008). The one with the CI kinetics corresponds to a fully uncoupled case where channels close stochastically and independently after a exponentially distributed open time with mean value 1/k_OI. The one with the CD kinetics, channels are fully coupled by cytosolic Ca²⁺.

The mean puff duration can be computed analytically for both models using Equation 4 and taking t_M such that n(t_M) = 0 for the first time (see details of the derivation in the Appendix). The result is that the mean duration of puffs that start with N_p open channels is:

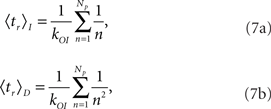
for models CI and CD, respectively.

The average released current, I_ave, is given by Equation 5. We do not have analytic expressions for the mean average current. Therefore, in order to compute it, we perform stochastic simulations of the semi analytic models (see Appendix for further details) that show that the mean average current can be approximated by the ratio of mean values:

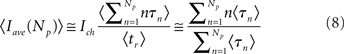
so that:

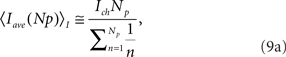
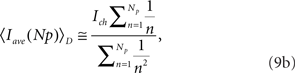
for models CI and CD, respectively.

3 Results

3.1 Time Course of Simulated Puffs

Simulations can display the time course of puffs at different scales: from the single channel activity to the fluorescence signal. Useful parameters that characterize puffs are the amplitude (A, peak fluorescence) and the rising time (t_f, time until the amplitude is reached). Qualitative differences between the stochastic and the mean field models are evident in Figure 1. In the stochastic case (Figures 1A,B), the current varies stepwise and the peak fluorescence is achieved before the end of Ca²⁺ release. However, in puffs simulated with the mean field model the current is steady and the fluorescence increases during the total duration of Ca²⁺ release (Figures 1C,D).

The examples of Figures 1A,B are representative examples of two basic features observed in stochastic puffs: (a) the time to peak current shortens if the number of available channels increases and (b) the difference between puffs simulated with the CI and CD IP₃R model is not significant. There is a rapid recruitment of IP₃Rs when Ca²⁺ release starts. This initial phase is followed by a usually larger falling phase in which channels close one by one, in agreement with Smith et al. (2009). All subsequent stochastic simulations will be done using model CI unless otherwise mentioned because the fluorescence signals of puffs simulated with the CI and CD models are statistically equivalent.

The amplitude of the puffs simulated with the non-linear mean field model is similar to the amplitudes of the puffs obtained with the stochastic model. The number of channels is also similar. However, the linear mean field model reproduces the same amplitude as the stochastic puffs but with significant fewer channels. The examples displayed in Figure 1 illustrate this difference.

Interestingly, the ratio of puff amplitudes is similar in all models when the number of channels is duplicated, as it is shown in Figure 1, comparing puffs from panels Figures 1A–D. This suggest that the ratio of amplitudes can give ambiguous results when trying to determine the “correct” puff underlying model.

As illustrated in Figures 1A,B, the rising time is shorter as more channels participate of the puff. This is a consequence of the fact that the coordination of channels due to CICR evoked by local [Ca²⁺] elevations is more effective as the distance between IP₃Rs decreases. Approximately 80% of the puffs simulated using the stochastic model are such that all available channels of the cluster participate although only approximately half of them were simultaneously open (data not shown). In the remaining ∼20% of the puffs, only ∼2 channels did not open during the 150-ms of the simulation time. This is more likely to occur in small clusters (〈N_p ∼ 13〉) where the spacing between IP₃Rs is relatively large and the coordination between channels due to CICR is less effective.

It is important to note that the average current and fluorescence time course of several stochastic simulations does not converge to the mean field counterpart. The mean field model assumes that all channels open and close simultaneously, therefore the release current is constant and the fluorescence increases during the puff.

3.2 The Amplitude and Current of Puffs are Non-Linearly Related

Observed puff amplitudes do not grow linearly with the maximum underlying current estimated from the observations (Bruno et al., 2010). Simulated puffs using the stochastic models show the same behavior, as shown in Figure 2. For large enough currents, the amplitude increases as the current increases, but at a lower rate than for small currents. One possible explanation to these observations is that the fluorescent dye is saturated at the position of the cluster due to the large amount of Ca²⁺ ions that are released during a puff. Nevertheless, this is not the case. Calibration experiments showed that dye saturation occurs at much larger amplitudes (A ∼ F_max/F₀ = 48) than those of the puffs analyzed in Bruno et al. (2010). In the stochastic simulations, the Ca²⁺-bound dye concentration is never larger than 35 μM (for N_p = 50) while the total dye concentration is 40 μM. The reason for the observed non-linearity is the combination of the various processes that modulate the Ca²⁺-bound dye concentration within the volume corresponding to the pixel of the image. This processes depend on the kinetic rates of the reaction, the Ca²⁺ current, and the rate at which the Ca²⁺ bound dye leaves the volume due to diffusion.

FIGURE 2

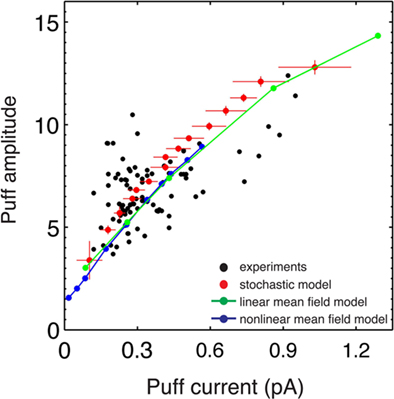
Figure 2. Non-linear relationship between the amplitude and the release current. Puff amplitude as function of the maximum released current for experimental puffs (adapted from Bruno et al., 2010) and puffs simulated with the stochastic, linear and non-linear models. In the simulations of the stochastic puff model, IP₃Rs follow the CD kinetic mode.

Although puff amplitudes depend non-linearly on the underlying maximum currents, both for the simulations and for the experiments, the mean values of the puff current can be approximated by a function of the mean puff amplitudes with a relatively small dispersion. This indicates that, even if the interaction with the dye acts as a non-linear filter, the puff amplitude could eventually be used to estimate the underlying Ca²⁺ current.

3.3 The Finite Time Resolution of the Experiments Filters the Observations Differently Depending on the Number of Open Channels

We have analyzed in the previous Section the relationship between puff amplitude and the Ca²⁺ current that underlies the signal. We have shown, in particular, that these quantities depend non-linearly on one another in mean field models (linear and non-linear), stochastic models (independently of the IP₃R kinetic scheme), and experiments. Even though the amplitude–current relationship obtained in all these cases is similar, we have observed that the number of channels involved in the linear and the non-linear mean field models are very different. In order to analyze this aspect in more detail, we now explore the dependence between number of channels and puff amplitude.

We show in Figure 3A a plot of puff amplitude as a function of the number of available channels, N_p, obtained with simulations of the stochastic puff model. We see that, as N_p grows, the mean puff amplitude saturates. This indicates that the mean puff amplitude observed at a given cluster is not a good estimator of the number of channels of the cluster that can become open. We can distinguish an approximately linear regime in which the fluorescence signals contributed by each open channel summate linearly, in agreement with the recent results of Smith et al. (2009). Interestingly, these results show that, besides the non-linear filter that the Ca²⁺-dye reaction introduces between Ca²⁺ current and fluorescence, there is an additional source of non-linearity when going from the number of channels to puff amplitude. This additional source of non-linearity is related to the temporal coarse-graining imposed by the experimental temporal resolution acting on data that is characterized by different time courses depending on the size of the puffs. As shown in Figure 1, the time it takes for the current and the fluorescence to achieve their maximum values is shorter the larger is the puff (and the number of open channels that are involved). This means that the fluorescence that is measured experimentally is integrated over a shorter time interval. The dye response time and the finite time resolution of the experiments act as filters of this rapid increment producing the observed non-linear dependence. The fact that the time course is different depending on puff size is in turn related to the spatial organization of IP₃Rs within the cluster. All models we use in the simulations assume that the spatial cluster size is constant regardless of the number of channels that they contain. Thus, the simulated puffs that involve more open channels and have larger amplitudes, occur in clusters where the mean distance between available channels is shorter. This implies that CICR occurs on a faster time scale and the peak current is achieved within a shorter time. This non-linearity is absent in the linear mean field model.

FIGURE 3

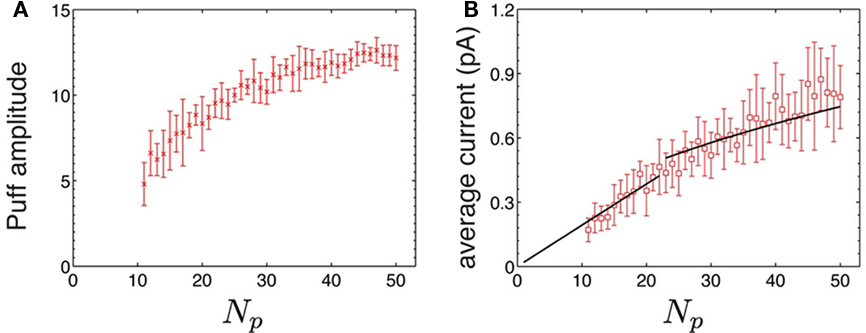
Figure 3. Non-linearities as a function of the number of available channels. (A) Puff amplitude as a function of the number of available channels, N_p for puffs simulated with the stochastic model and the CD IP₃R kinetic model. (B) Average Ca²⁺ current (Equation 5) released during a puff simulated using the stochastic model as a function of the number of available channels. The black line corresponds to the best fit to a non-linear function of the form I = I₀₁N_p for N_p ≤ 22 and 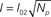for N_p > 22 which gives I₀₁ = 0.019 pA and I₀₂ = 0.105 pA. I₀₁ should not identified as the actual single IP₃R current but as an effective value that follows from the assumption that all channels open and close simultaneously.

In order to compare the new non-linearity that arises in the simulations of the stochastic puff model with the one that is intrinsic to the non-linear mean field model we compute the average current (I_ave, defined in Equation 5) released during a puff simulated using the stochastic model. This average current corresponds to a puff that releases a constant current during the whole release duration (as if all N_p channels of the cluster opened and closed simultaneously and released the same total amount of Ca²⁺ during the same time as the original puff). Therefore, it is equivalent to replacing the stochastic puff by one that could have been obtained with a mean field model. We found that the derivative of I_ave(N_p) decreases as N_p grows (Figure 3B). The deviation from linearity for large N_p occurs although the simulations were performed with the stochastic model using a constant single channel current of 0.1 pA, regardless of the number of channels. The exact scaling between the average current and N_p is not so relevant. However, it is remarkable that we can fit the data with the non-linear function I_ave = I₀₁Np for N_p ≤ 22 and 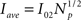for N_p ≤ 22 (black line in Figure 3B). The square root scaling for large N_p agrees with the value predicted in the simulations of Thul and Falcke (2004). From the fitting we find an effective single channel current for small N_p, I₀₁ = 0.019 pA, which is five times smaller than the actual single channel current used in the simulations. Interestingly, it agrees with the value that the non-linear mean field model needed to reproduce the experimental observations (see Equation 2).

3.4 Understanding the Results Using the Semi-Analytical Puff Model

The fact that the effective single channel current is smaller than the actual one can be understood by considering two extreme (hypothetical) puffs with N_p available channels and total release duration, t_r. In the first extreme case all N_p channels open and close simultaneously. Thus, they all remain open during a time t_r. The corresponding average current is I_ave = I_chN_pt_r/t_rI_chN_p, where I_ch is the single channel current. In this case, I_ave is a linear function of the number of channels that participate of the puff. The other extreme case is a puff in which the channels open and close sequentially so that there is one open channel at any given time. In this case, the average current is I_ave = I_ch, independent of N_p. The simulations using the stochastic puff model give results in between these two extreme behaviors so that I_eff = I_ave/N_p ≤ I_ch.

In order to get an intuitive understanding of why the slope between I_ave and N_p decreases with N_p we simulated 500 puffs using the semi-analytical model (Section 2.2). We illustrate the non-linear dependence between I_ave and N_p for this model in Figure 4. In this case, we use both kinetic models of IP₃Rs because they lead to different results. Although it is clearer for CD channels, in both cases the current grows non-linearly as N_p increases. For example, in the CI case, 〈I_ave〉 ≅ 0.4 pA for N_p = 10 and 〈I_ave〉 ≅ 1 pA for N_p = 40. This non-linear relationship is equivalent to that of the non-linear mean field model. Results from simulations of the stochastic puff model that use the CD kinetic model lie in between the semi-analytical results for the two IP₃R models for N_p > 10 (red squares and error bars in Figure 4A). The effective single channel current, I_eff = I_ave/N_p of the semi-analytical models is plotted in Figure 4B as a function of N_p. It is clear that as the number of channel increases, I_eff approaches the value ∼0.02 pA, similarly to the puffs of the stochastic model.

FIGURE 4

Figure 4. The semi-analytical puff model supports the results of the stochastic puff model. (A) Average current as a function of N_p for the semi-analytical model and for simulated puffs obtained using the stochastic puff model with the CD IP₃R kinetic model. (B) Effective single channel current as a function of N_p for puffs simulated with the stochastic model using the CD IP₃R kinetic model. In (A,B), black circles and squares correspond to the semi-analytical model using the CD and the CI kinetic model, respectively. Small red squares and error bars represent mean and SD for puffs simulated with the stochastic model.

The semi-analytical model allows us to go one step further in the analysis. We can use the approximation 8 to estimate I_ave. According to this expression, if the mean time with n simultaneously open channels, 〈τ_n〉, is independent of n, then the average current is linearly related to the number of open channels, 〈I_ave〉 ≅ I_ch(N_p + 1)/2. However, in most cases 〈τ_n〉 does depend on n. In particular, for the two IP₃R kinetic models that we considered, CI and CD, we obtain 〈τ_n〉 ∼ 1/n and 〈τ_n〉 ∼ 1/n² respectively. Approximating 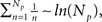which is good for large N_p, and taking into account that 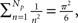we conclude that 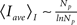and 〈I_ave(N_p)〉_D ∼ ln N_p for models CI and CD, respectively. Therefore, we conclude that I_ave is a non-linear function of N_p with a slope that decreases with N_p. Within this view, the ability to approximate I_ave by a linear function for small N_p and a relationship of the form 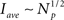instead of another non-linear function is only due to the limited interval of N_p values over which we can observe the function. These estimates also show why I_ave is smaller for the CD than for the CI model. In fact, the reason for this is that the transition from the open to the inhibited state is faster for the CD model and that the difference of time-scales increases with the number of channels that are simultaneously open. Thus, the state of the cluster with a large number of simultaneously open channels is shorter for the CD than for the CI model which results in a smaller average current.

4 Discussion

Intracellular signals that involve Ca²⁺ release from the ER through clustered IP₃R–Ca²⁺ channels are crucial in a variety of cell types. A complete understanding of the processes involved in such signals requires a combination of experiments and mathematical modeling. Given the multiple time and spatial scales involved, mean field approaches are frequently used in models and data analysis. In a sense, data from fluorescence microscopy experiments is intrinsically of mean field type since it is averaged over the finite space and time resolution of the experimental method. In this work we have compared mean field approaches to stochastic models of Ca²⁺ puffs, a type of localized signal that involves Ca²⁺ release from several IP₃Rs in a cluster and which has been observed in intact cells using optical techniques. We found that mean field models only match more accurate stochastic models under two unrealistic assumption: (a) a non-linear relationship between the current and the number of open channels and (b) a single channel current five times lower.

We have used two mean field models that we presented in a previous work (Bruno et al., 2010) where we showed that they approximate the inferred distribution of puff currents and the relationship between the puff amplitude and the underlying current. Both models assume that all available IP₃Rs of the cluster open and close simultaneously. They differ on how the current depended on the number of channels: linear (Equation 1) and non-linear (Equation 2). We compared simulations of mean field models with simulations of a stochastic puff model that includes the stochastic transitions between open and close states of the channels (Solovey et al., 2008). In order to compare both models, we defined a mean field analog of the stochastic puffs as one with a constant current given by the average current released during the whole puff duration.

The first observation is that the amplitude of puffs is non-linearly related to the released current, as it was shown in Bruno et al. (2010). This occurred although the fluorescent dye was not saturated. This result was also obtained with the simulations of the stochastic model (Figure 2). Only the non-linear mean field model was able to reproduce this non-linear relationship for the full range of the number of available channels considered here. The linear mean field model described the same behavior but using a much smaller number of channels than the number inferred from the experiments (Bruno et al., 2010; Figure 2).

Recent experimental results concluded that the total calcium current released through a cluster of IP₃Rs during a puff is a non-linear function of the number of open channels (Bruno et al., 2010): linear when the number is small and proportional to the square root of the number of channels for larger puffs. Although this type of scaling could be attributed to local Ca²⁺ depletion inside the ER (Thul and Falcke, 2004), we argue that this non-linear relationship occurs due to the assumed simultaneously action of the release sites intrinsic to mean field approaches. In fact, even though our stochastic simulations were done with a constant single channel current of 0.1 pA, we found that the average released current of stochastic puffs depended non-linearly on the number of available channels with a slope that decreased with the number of available channels (3B). Furthermore, we showed that the average current could be approximated by Equation 2 with I₀₁ approximately equal to the single channel current of the non-linear mean field model (∼0.02 pA). This results implies that the mean field assumption also underestimates the single channel current by a factor of 5 (Figure 3).

We investigated the differences between stochastic and mean field approaches analytically as well. For this purpose, we used a simplified stochastic model to describe the dynamics of clustered IP₃Rs (semi-analytical model). Results using this model confirmed that the assumption that channels open and close simultaneously leads to an underestimation of the single IP₃R channel current and that the relationship between the average current and the number of available channels is non-linear (Figure 4).

In a previous work (Bruno et al., 2010), we have shown that the non-linear mean field model reproduces the puff to trigger amplitude distribution reported in Rose et al. (2006) better than the linear model. Our results shed light on why this is could be the case. Namely, the puff to trigger amplitude distribution does not take dynamics into account. However, the non-linear mean field model captures the additional non-linear filtering that the experiments impose. Indeed, it is remarkable that the relationship between puff amplitude and current obtained with the non-linear mean field model and the stochastic model conceded using the same range of number of available channels (Figure 2).

There is some controversy on how IP₃Rs behave (Bezprozvanny et al., 1991; Mak et al., 1998). Consequently, there is a variety of IP₃R kinetic models (Young and Keizer, 1992; Fraiman and Ponce Dawson, 2004; Shuai et al., 2007) and it is not completely clear which one describes the behavior of the channel under the conditions encountered in intact cells. In particular, it is not clear if the mean open time depends on Ca²⁺ or not. Therefore, in the case of the stochastic models, we did simulations using two simple kinetic models of the IP₃R that only differed on whether the transition from the open to the closed state of the channel was Ca²⁺ dependent or not (CI and CD model respectively). The differences between both models are significant in the context of the semi-analytical model (Figure 4). This is easy to understand because the semi-analytical model maximized the differences between them. When using the CD model, the semi-analytical model is such that the [Ca²⁺] sensed by each channel is additive and proportional to the number of open channels, as if all IP₃Rs were in the same spatial location. In contrast, when using the CI model, the underlying assumption is that the Ca²⁺ released by one channel has no influence on the other open channels. The real situation is somewhere in between both, as it is shown in Figure 4. In general, we did not found any significant difference between the puffs simulated with the stochastic model using any of the two kinetic IP₃R models. We therefore conclude that this single channel property (a Ca²⁺ dependent or a Ca²⁺ independent open to closed transition) does not leave a detectable signature on puffs.

Ca²⁺ puffs are the result of a complicated underlying spatiotemporal dynamics. The relationship between puff amplitude and the underlying Ca²⁺ current can only be understood in terms of the interplay between the intensity and the dynamics of the release. The dynamics of the release, on the other hand, is strongly dependent on the spatial organization of the channels that become open. The combination of all these factors and the experimental limitations can lead to (unexpected) non-linear relationships. Modeling efforts that do not include the variability of the individual channel openings and closings provide averaged descriptions that are still valid. In particular, they can be used as building blocks of mathematical models of more global signals such as waves. However, if one is willing to understand the intra-cluster dynamics or to extract information on single channel kinetics from puff observations, a stochastic description is unavoidable.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We acknowledge useful conversations with Ian Parker and Luciana Bruno. Guillermo Solovey would also like to acknowledge Marcelo Magnasco and the staff of the Center for Studies in Physics and Biology (The Rockefeller University). Daniel Fraiman and Silvina Ponce Dawson are members of the Carrera del Investigador Científico (CONICET). This research was supported by UBA (UBACyT X145) and CONICET (PIP 11220080101612).

References

Baran, I. (2007). Characterization of local calcium signals in tubular networks of endoplasmic reticulum. Cell Calcium 42, 245–260.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Baran, I., and Popescu, A. (2009). A model-based method for estimating Ca2+ release fluxes from linescan images in Xenopus oocytes. Chaos 19, 037106.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Berridge, M. J., Lipp, P., and Bootman, M. D. (2000). The versatility and universality of calcium signalling. Nat. Rev. Mol. Cell Biol. 1, 11–21.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bezprozvanny, I., James, W., and Ehrlich, B. E. (1991). Bell-shaped calcium-response curves of lns(l,4,5)P3- and calcium-gated channels from endoplasmic reticulum of cerebellum. Nature 351, 751–754.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bootman, M., Niggli, E., Berridge, M., and Lipp, P. (1997). Imaging the hierarchical Ca2+ signalling system in HeLa cells. J. Physiol. (Lond.) 499, 307–314.

Pubmed Abstract | Pubmed Full Text

Bruno, L., Solovey, G., Ventura, A. C., Dargan, S., and Dawson, S. P. (2010). Quantifying calcium fluxes underlying calcium puffs in Xenopus laevis oocytes. Cell Calcium 47, 273–286.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Callamaras, N., Marchant, J. S., Sun, X.-P., and Parker, I. (1998). Activation and co-ordination of InsP3-mediated elementary Ca2+ events during global Ca2+ signals in Xenopus oocytes. J. Physiol. (Lond.) 509, 81–91.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Callamaras, N., and Parker, I. (1994). Inositol 1,4,5-trisphosphate receptors in Xenopus laevis oocytes, localization and modulation by Ca2+. Cell Calcium 15, 66–78.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Callamaras, N., and Parker, I. (1999). Radial localization of inositol 1,4,5-trisphosphate-sensitive ca2+ release sites in xenopus oocytes resolved by axial confocal linescan imaging. J. Gen. Physiol. 113, 199–213.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Cohen, J. E. (2004). Mathematics is biology’s next microscope, only better; biology is mathematics’ next physics, only better. PLoS Biol. 2, e439. doi: 10.1371/journal.pbio.0020439

CrossRef Full Text

Cox, D. R. (1962). Renewal Theory. London: Methuen.

DeRemigio, H., and Smith, G. D. (2005). The dynamics of stochastic attrition viewed as an absorption time on a terminating Markov chain. Cell Calcium 38, 73–86.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Diambra, L., and Guisoni, N. (2005). Modeling stochastic Ca2+ release from a cluster of IP3-sensitive receptors. Cell Calcium 37, 321332.

CrossRef Full Text

Diambra, L., and Marchant, J. S. (2011). Inositol (1,4,5)-trisphosphate receptor microarchitecture shapes ca(2+) puff kinetics. Biophys. J. 100, 822–831.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Finch, E. A., Turner, T. J., and Goldin, S. M. (1991). Calcium as a coagonist of inositol 1,4,5-trisphosphate-induced calcium release. Science 252, 443–446.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Foskett, J. K., White, C., Cheung, K. H., and Mak, D.-O. D. (2007). Inositol triphosphate receptor Ca2+ release channels. Physiol. Rev. 87, 593–658.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fraiman, D., Pando, B., Dargan, S., Parker, I., and Dawson, S. P. (2006). Analysis of puff dynamics in oocytes, interdependence of puff amplitude and interpuff interval. Biophys. J. 90, 3897–3907.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fraiman, D., and Ponce Dawson, S. (2004). A model of the IP_3 receptor with a luminal calcium binding site, stochastic simulations and analysis. Cell Calcium 35, 403–413.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Groff, J. R., and Smith, G. D. (2008). Calcium-dependent inactivation and the dynamics of calcium puffs and sparks. J. Theor. Biol. 253, 483–499.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Iino, M. (1990). Biphasic Ca2+ dependence of inositol 1,4,5-trisphosphate-induced Ca release in smooth muscle cells of the guinea pig taenia caeci. J. Gen. Physiol. 95, 1103–1122.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Machaca, K. (2007). Ca2+ signaling differentiation during oocyte maturation. J. Cell. Physiol. 213, 331–340.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mak, D.-O. D., and Foskett, J. K. (1997). Single-channel kinetics, inactivation, and spatial distribution of inositol trisphosphate (IP3) receptors in Xenopus oocyte nucleus. J. Gen. Physiol. 109, 571–587.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mak, D.-O. D., McBride, S., and Foskett, J. K. (1998). Inositol 1,4,5-tris-phosphate activation of inositol tris-phosphate receptor Ca2+ channel by ligand tuning of Ca2 + inhibition. Proc. Natl. Acad. Sci. U.S.A. 95, 15821–15825.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Nguyen, V., Mathias, R., and Smith, G. D. (2005). A stochastic automata network descriptor for Markov chain models of instantaneously coupled intracellular Ca2+ channels. Bull. Math. Biol. 67, 393–432.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Parker, I., Choi, J., and Yao, Y. (1996). Elementary events of InsP3-induced Ca2 liberation in Xenopus oocytes, hot spots, puffs and blips. Cell Calcium 20, 105–121.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Parker, I., and Smith, I. F. (2010). Recording single-channel activity of inositol trisphosphate receptors in intact cells with a microscope, not a patch clamp. J. Gen. Physiol. 136, 119–127.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Patel, S., Joseph, S. K., and Thomas, A. P. (1999). Molecular properties of inositol 1,4,5-trisphosphate receptors. Cell Calcium 25, 247–264.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ramos-Franco, J., Fill, M., and Mignery, G. A. (1998). Isoform-specific function of single inositol 1,4,5-trisphosphate receptor channels. Biophys. J. 75, 834–839.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rose, H. J., Dargan, S., Shuai, J., and Parker, I. (2006). “Trigger” events precede calcium puffs in Xenopus oocytes. Biophys. J. 91, 4024–4032.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rüdiger, S., Nagaiah, C., Warnecke, G., and Shuai, J. W. (2010). Calcium domains around single and clustered IP3 receptors and their modulation by buffers. Biophys. J. 99, 3–12.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Shuai, J., Pearson, J. E., Foskett, J. K., Mak, D. O., and Parker, I. (2007). A kinetic model of single and clustered IP_3 receptors in the absence of Ca2+ feedback. Biophys. J. 93, 1151–1162.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Shuai, J., Rose, H. J., and Parker, I. (2006). The number and spatial distribution of IP3 receptors underlying calcium puffs in Xenopus oocytes. Biophys. J. 91, 4033–4044.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Shuai, J. W., and Jung, P. (2003a). Optimal ion channel clustering for intracellular calcium signaling. Proc. Natl. Acad. Sci. U.S.A. 100, 506–510.

CrossRef Full Text

Shuai, J. W., and Jung, P. (2003b). Sub-threshold Ca2+ waves. New J. Phys. 5, 132.

CrossRef Full Text

Shuai, J.-W., and Jung, P. (2002). Stochastic properties of Ca2+ release of inositol 1,4,5-trisphosphate receptor clusters. Biophys. J. 83, 87–97.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Skupin, A., Kettenmann, H., and Falcke, M. (2010). Calcium signals driven by single channel noise. PLoS Comput. Biol. 6, e1000870. doi: 10.1371/journal.pcbi.1000870

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Smith, I. F., and Parker, I. (2009). Imaging the quantal substructure of single IP3R channel activity during Ca2+ puffs in intact mammalian cells. Proc. Natl. Acad. Sci. U.S.A. 106, 6404–6409.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Smith, I. F., Wiltgen, S. M., Shuai, J., and Parker, I. (2009). Ca(2+) puffs originate from preestablished stable clusters of inositol trisphosphate receptors. Sci. Signal. 2, ra77.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Solovey, G., Fraiman, D., Pando, B., and Ponce Dawson, S. (2008). Simplified model of cytosolic Ca[sup 2+] dynamics in the presence of one or several clusters of Ca[sup 2+]-release channels. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 78, 041915.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Solovey, G., and Ponce Dawson, S. (2010a). Intra-cluster percolation of calcium signals. PLoS ONE 5, e8997. doi: 10.1371/journal.pone.0008997

CrossRef Full Text

Solovey, G., and Ponce Dawson, S. (2010b). Observable effects of Ca2+ buffers on local Ca2+ signals. Phil. Trans. R. Soc. Lond. A 368, 5597–5603.

CrossRef Full Text

Sun, X.-P., Callamaras, N., Marchant, J. S., and Parker, I. (1998). A continuum of InsP3-mediated elementary Ca2+ signalling events in Xenopus oocytes. J. Physiol. (Lond.) 509, 67–80.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Taylor, C. W. (1998). Inositol trisphosphate receptors, Ca2+-modulated intracellular ca2+ channels. Biochim. Biophys. Acta 1436, 19–33.

Pubmed Abstract | Pubmed Full Text

Thul, R., and Falcke, M. (2004). Release currents of IP3 receptor channel clusters and concentration profiles. Biophys. J. 86, 2660–2673.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Thul, R., Thurley, K., and Falcke, M. (2009). Toward a predictive model of Ca2+ puffs. Chaos 19, 037108.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Thurley, K., and Falcke, M. (2011). Derivation of Ca2+ signals from puff properties reveals that pathway function is robust against cell variability but sensitive for control. Proc. Natl. Acad. Sci. U.S.A. 108, 427–432.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ullah, G., and Jung, P. (2006). Modeling the statistics of elementary calcium release events. Biophys. J. 90, 3485–3495.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Vais, H., Foskett, J. K., and Daniel Mak, D.-O. (2010). Unitary Ca(2+) current through recombinant type 3 InsP(3) receptor channels under physiological ionic conditions. J. Gen. Physiol. 136, 687–700.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ventura, A. C., Bruno, L., Demuro, A., Parker, I., and Dawson, S. P. (2005). A model-independent algorithm to derive Ca2+ fluxes underlying local cytosolic Ca2+ transients. Biophys. J. 88, 2403–2421.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wiltgen, S. M., Smith, I. F., and Parker, I. (2010). Superresolution localization of single functional ip3r channels utilizing ca2+ flux as a readout. Biophys. J. 99, 437–446.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Yao, Y., Choi, J., and Parker, I. (1995). Quantal puffs of intracellular Ca2+ evoked by inositol trisphosphate in Xenopus oocytes. J. Physiol. (Lond.) 482, 533–553.

Pubmed Abstract | Pubmed Full Text

Yao, Y., and Parker, I. (1991). Regenerative release of calcium from functionally discrete subcellular stores by inositol trisphosphate. Proc. Biol. Sci. 246, 269–274.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Young, G. W. D., and Keizer, J. (1992). A single-pool inositol 1,4,5-trisphosphate-receptor-based model for agonist-stimulated oscillations in Ca2+ concentration. Proc. Natl. Acad. Sci. U.S.A. 89, 9895–9899.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text