- Information Science Directorate, US Army Research Office, Durham, NC, USA
The Army Research Laboratory program on the Network Science of Human Decision Making brings together researchers from a variety of disciplines to work on a complex research problem that defies confinement within any single discipline. Consequently, new and rewarding solutions have been obtained for a problem of importance to society and the Army, that being, the human dimension of complex networks. This program investigates the basic research foundation of a science of networks supporting the linkage between the cognitive and social domains as they relate to human decision making. The research strategy extends recent methods of non-equilibrium statistical physics to non-stationary, renewal stochastic processes characteristic of the interactions among nodes in complex networks. The theoretical analyses of complex networks, although mathematically rigorous, often elude analytic solutions and require simulation and computation to analyze the underlying dynamic process. The information transfer between two complex networks is calculated using the principle of complexity management as well as direct numerical calculation of the decision making model developed within the project.
Introduction
The modern world is an interconnected mesh of networks satisfying a myriad of functions: transportation, electrical power, food distribution, finance, and health care to name a few. The interoperability of these networks developed as part of urban evolution over the past century such that these and other webs connect to national and/or global networks (National Research Council of the National Academies, 2005). This is the engineered webbing of humanity, but there are comparable natural structures in the spheres of biology, ecology, sociology, and physiology.
This modernity is manifest in the military through the development of network-centric warfare (NCW) which takes cognizance of human behavior in a networked environment of organized actions directed toward political, social, and military ends and is the basis of a new theory of war (Office of Force Transformation, 2004; Garstka and Alberts, unpublished). Thus, NCW has at its core a shift in focus from military platforms such as ships and tanks to networks having platforms as members. Army scientists need to understand the dynamics, controllability, and predictability of generic non-linear complex networks in order to realize their goal of supporting both society and the soldier through research and the development of new technologies.
It is not only our external world that is cluttered with networks, but our internal world as well. The neuronal network carrying the brain’s signal to the body’s physiological networks is even more complex than the modern city or a typical ecological network. Thus, the basic research into network science must span and encompass a multitude of disciplines; understanding each sheds light on the others.
The problem addressed within this program is to develop the basic research foundation of a science of networks that supports the linkage between the cognitive and social domains as they relate to decision making. This approach is not directed at the totality of developing a Network Science, but has the more modest goal of understanding the deeply interdependent human networks of crucial importance to society as a whole and to the Army in particular. Even such a restricted problem is a significant challenge due to the multiply interconnecting networks buttressing the common decision making objective.
On the one hand, the military is proactive in that networked forces can operate in an agile manner to promote decision making superiority. On the other hand, the Army is reactive in the need to respond to enemies who are also using the power of networks against United States interests. The research program provides insight to allow the Army to anticipate the enemy’s use of network strategy and thereby reduce the reactive mode of operation. In Grigolini and West (2011) we reviewed what is presently known about complex networks, regardless of the disciplinary context and adapted that understanding to the decision making paradigm. Moreover, the barriers to further understanding and to filling the gaps in knowledge of the linkages between social and human decision making networks were addressed.
The research strategy of the ARL program is based on theory, computation/simulation, and experiment/observation. This is a cyclic interactive process in which new theory stimulates unique simulations, yielding insight into parameter values and network configurations, which in turn suggests specific experiments, whose outcome guides the refinement and development of theory. This modern approach to scientific research is applied to the phenomenon of human decision making with a view for eventual application to NCW. The core group of Army scientists is the focal point for external researchers requiring militarily relevant challenges and internal ARL efforts.
One of the mysteries of human social interaction is how agreements are reached and cooperative alliances are made. Individuals become part of social groups or networks in a number of ways: choice, peer pressure, and subliminal seduction; but always through a sequence of decisions, either conscious or not. Network characteristics cannot be deduced from the properties of individuals; they emerge during the formation and growth of the network. Consequently we need mathematics to quantify the strength of the interactions between the network components, as well as to describe how a network develops in time and responds to perturbations (stimulation). This has been done through the construction of the decision making model (DMM) that for very weak coupling is much like the Ising model of cooperative behavior, but for strong coupling can be very different (Turalska et al., 2009); see Grigolini and West (2011) for an overview.
Ubiquitous aspects of complex networks are the appearance of non-stationary, non-ergodic, and renewal statistical processes. These properties are manifest through inverse power–law statistical distributions that not only challenge traditional understanding of complexity in physical networks, but require new strategies for understanding how information is exchanged between networks (West et al., 2008; West and Grigolini, 2011), as in the case of interest here among human networks including cognitive networks. The approach is to adapt the methods of non-equilibrium statistical physics that have been used to characterize the dynamics of complex phenomena and phase transitions. These methods were extended to the study of such social phenomena as linguistics, biofeedback techniques, and the brain’s response to music (Bianco et al., 2007) and to further develop them to model decision making with incomplete information in an uncertain environment.
The research into decision making has been addressed using a variety of strategies. The mathematics of complex networks has been examined using the newly developed DMM to understand consensus (Turalska et al., 2009); a psychophysical model of how individuals make decision and then irrationally change their minds shows agreement between theory and experiments (West and Grigolini, 2010a); renewal statistics reveal how we habituate to the familiar (West and Grigolini, 2010b) and forget the uninteresting (West and Grigolini, 2010c); 1/f variability captures how the brain processes tasks of increasing complexity during decision making (Grigolini et al., 2009); and finally we have determined how all these various pieces fit into the overall picture of exchanging information between complex networks (West et al., 2008; Grigolini and West, 2011; West and Grigolini, 2011).
The major accomplishment of the present research program has been the identification of the first universal principle in the science of networks, that being, the principle of complexity management (PCM) discussed in Grigolini and West (2011), West and Grigolini (2011). PCM states that the maximum information is exchanged between two complex networks when there is compatibility of the complexity of the two networks. A mathematical proof of this principle has been constructed over the past year (Aquino et al., 2010, 2011).
Principle of Complexity Management
The mathematician Norbert Wiener speculated that the transfer of influence from a complex network high in information to one low in information even though the latter may be higher in energy represents a new kind of interaction (Wiener, 1985), which we called Wiener’s Rule (Grigolini and West, 2011). His insight was vindicated a half century later (Aquino et al., 2010, 2011) and required the generalization of a number of concepts from statistical physics (Allegrini et al., 2007, 2011; Aquino et al., 2007; Budini and Grigolini, 2009) resulting in the PCM (West et al., 2008; West and Grigolini, 2011) as we discussed last year (Grigolini and West, 2011).
One measure of the information content of a network is provided by the probability density most often used in the determination of the negative entropy of Shannon and Wiener. An apparently ubiquitous distribution in the description of empirical complex networks is the hyperbolic, having the survival probability:

which asymptotically becomes an inverse power–law. The average time between events in complex webs such as power grid blackouts, heartbeats, time between earthquakes (West and Grigolini, 2011) of a given magnitude can be determined using the probability density ψ(t) = −dΨ(t)/dt, to be
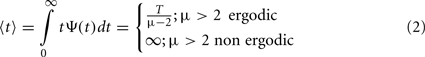
It is interesting that when the power–law index is in the interval 2 < μ < 3 the distribution has a finite first moment and the statistics are ergodic, meaning that the time average and ensemble averages yield the same result. However when the power–law index is μ < 2 there are no finite integer moments and the time and ensemble averages are not the same, that is, the process is non-ergodic. We shall have more to say about non-ergodicity subsequently.
One measure of the information transfer between two complex networks is the cross-correlation between a complex network P and a complex network S being perturbed by P with ε the strength of the perturbation. For our purposes it is sufficient to apply the generalized linear response theory (LRT; Aquino et al., 2010, 2011) we previously developed the normalized cross-correlation function:
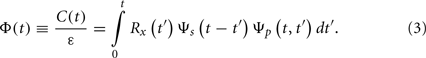
The perturbing complex network P is characterized by the non-stationary autocorrelation function Ψp (t, t′), which depends separately on the time of the last perturbation t′ and time of the measurement t. The function Rs(t′) is the rate of generating perturbing events at time t′ within the network being perturbed and is based on renewal theory (West and Grigolini, 2011). The perturbed network S is characterized by the stationary autocorrelation function Ψs (t − t′), which depends only on the difference in times from the last perturbation to the measurement.
In Figure 1 the asymptotic cross-correlation function normalized to the strength of the perturbation is graphed as a function of the power–law indices of the two networks to form a cross-correlation cube. The cube displays a number of remarkable properties: (1) when the power–law indices are both equal to two there is an abrupt jump from zero correlation in region II to perfect consensus in region III; (2) the upper plateau region III indicates that when P is non-ergodic 1 < μp < 2 and S is ergodic 2 < μs < 3 there is an information response in which the perturbed network tracks the perturbing network exactly and the information transfer is maximal; (3) when P is ergodic 2 < μp < 3 and S is non-ergodic 1 < μs < 2 there is no response asymptotically and the information transfer is minimal as shown in region II. How a complex network responds to a perturbation by another complex network is determined by the kind of mismatch that exists in the complexity of the fluctuations in the two networks.
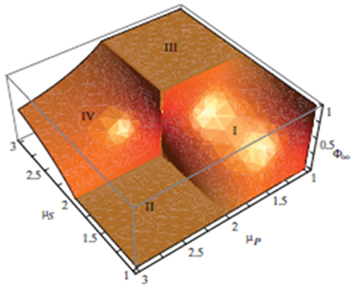
Figure 1. The cross-correlation cube. The asymptotic cross-correlation function defined by Eq. 3 is graphed as a function of the two power–law indices of the perturbed network S and the perturbing network P. (From West and Grigolini, 2011, with permission.)
Wiener’s Rule describes the influence of the perturbing network outside the lower plateau region of the cross-correlation cube. In all regions except this one the weak perturbation significantly modifies the properties of the complex network being perturbed. In the upper plateau region the perturbation by network P actually dominates the properties of the perturbed network S and reorganizes it, just as Wiener anticipated. The PCM embodied in the cross-correlation cube therefore subsumes Wiener’s Rule as we reviewed in West et al. (2008). In addition we showed the application of PCM to the phenomenon of habituation and other activities involving the human brain.
Synchronization and Information Exchange
Aquino et al. (2011) observe that the growing interest in the dynamics of complex networks is shifting research attention from the synchronization of two stochastic units (Pecora and Carroll, 1990) to the synchronization of large numbers of units (Wang, 2002), an interesting phenomenon that is closely related to the very popular model of Kuramoto (1984). The single units of the processes of chaos synchronization are chaotic and they surprisingly synchronize while maintaining the erratic dynamics that they have in isolation. Although the single units of the Kuramoto model are regular, it is becoming increasingly evident that the emergence of a global synchronization is a condition independent of whether the single units are regular or stochastic. The single units of the work of Bianco et al. (2008), Turalska et al. (2011) are Poisson processes and if one of them drives the other, they would obey the principle of aperiodic stochastic resonance (Lukovi’c et al., 2008). If the two units are bi-directionally coupled they are expected to undergo a condition of perfect synchronization if the coupling is sufficiently intense. When the number of interacting units is very large a phase transition occurs from the non-cooperative to the cooperative behavior (Bianco et al., 2008; Turalska et al., 2011).
It is important to stress that at criticality no permanent consensus is reached, and the mean value of the global field vanishes. Yet, this condition is strikingly different from the non-cooperative condition. The whole network remains in the “yes” (“no”) state for an extended time before making a transition to the “no” (“yes”) state.
It is surprising that the phase transition literature seems to have overlooked, with only a few exceptions (Contoyiannis and Diakonos, 2000; Bianco et al., 2008; Turalska et al., 2011), that the transitions from the “yes” (“no”) to the “no” (“yes”) state occurring at criticality are the “crucial” events defined in Section I of Aquino et al. (2011). In other words, the time interval between two consecutive transitions is derived from a pdf that has the asymptotic time structure of Eq. 1 with a power index μ fitting the inequality condition 1 < μ < 3. Some authors (Bianco et al., 2008; Turalska et al., 2011) argue that μ = 1.5 and others (Frantsuzov et al., 2009), releasing the condition that all the units share the same Poisson rate, generate a global condition with crucial events characterized by μ < 2, but significantly departing from the value μ = 1.5. Note that the theoretical arguments of Turalska et al. (2009), might yield the misleading impression that the crucial value of μ is a consequence of ordinary statistical physics.
An important result of Aquino et al. (2011) is the discovery of a promising road to settle the problem of information transmission from one to another complex network. In fact, if the inner synchronization corresponds to a criticality condition and criticality generates crucial events with a power–law index in the interval 1 < μ < 3, then a complex network at criticality is a generator of 1/f noise, with a power spectrum S(f ) ∝ 1/f 3 − μ. Thus, the problem of information transmission from one to another complex network becomes equivalent to the phenomenon of 1/f resonance illustrated in Aquino et al. (2011).
Aquino et al. (2011) distinguish between a phenomenological and dynamic LRT. The experiments (Onsager, 1944; Silvestri et al., 2009) support the dynamical rather than the phenomenological LRT. It is important to stress that phenomenological LRT is a natural consequence of adopting the asymptotic time perspective replacing the waiting-times pdf ψ(τ) of Eq. 1 with ψ(τ) ∝ 1/τμ. This way of proceeding, although generating the elegant mathematics of fractional derivatives, has as an ultimate effect the misleading discovery of the death of linear response. We do not adopt the asymptotic time perspective but the special form of Eq. 1. This is not a unique way of connecting the longtime to the short-time regime. However, whatever form we adopt we are convinced that there will be a parameter corresponding to the parameter T of Eq. 1. It is reasonable to assume that an external perturbation may perturb either T or μ, or both. However, the perturbation of μ is incompatible with the assumption of a weak stimulus. In fact, μ is a consequence of the cooperation among the units of the network, and a perturbation may affect μ only if its strength is large enough to influence the interaction among the units of the network. Thus, an external weak perturbation can only have an effect on T, thereby making the dynamical LRT become the proper way to study the response of a complex network to a weak external stimulus, in accordance with the experimental results (Onsager, 1944; Allegrini et al., 2009; Silvestri et al., 2009).
For these reasons, we can conclude that Figure 1 is an original, and important, result of this research program. We hope that the application of the PCM may open the door to solving the problem of information transmission from one complex network to another, a research topic that is still in its infancy.
Decision Making Model and Phase Transitions
In order to better understand the transfer of information between complex networks last year we numerically analyzing networks consisting of a large number of non-linearly interacting nodes. The properties of the DMM developed by Turalska et al. (2009) using a master equation formalism (Turalska et al., 2011) were discussed where each element of the network is a two state oscillator and is described by a master equation of the form
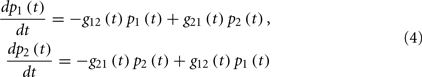
and pj(t) is the probability of being in the state j = ±1; p1 + p2 = 1. The coupling functions are time-independent for non-interacting members of the network.
Subsequently, we considered a network consisting of L discrete variables located at the nodes of a 2D square lattice. Each unit si is a stochastic oscillator and can be found in either of the above two states. For the dynamic complex lattice each element si interacts with each of its nearest neighbors and is updated in an elementary time step with transition rate g:
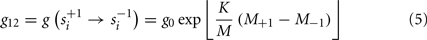
Here M is the total number of nearest neighbors; M + 1 and M − 1 are the number nearest neighbors that have made the decision “yes” and “no,” respectively. The single individual changes opinion, and as a consequence these numbers are variables fluctuating in time, while the total number of elements is constant. When K > 0 a unit who is in the state “yes” (“no”) makes a transition to the state “no” (“yes”) faster or slower according to whether the majority of the elements are in the state “no” (“yes”) or “yes” (“no”), respectively.
Turalska et al. (2011) do all calculations on a L × L lattice with periodic boundary conditions. They characterize the network in terms of the global order parameter

whose variability is not dichotomous. In Figure 2 an example of the temporal evolution for a single unit is compared with that of the global order parameter.
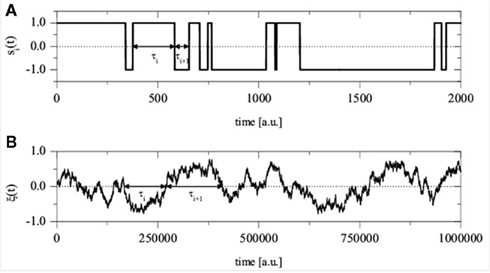
Figure 2. (A) Temporal evolution of a single unit and (B) of the global order parameter for the DMM realized on a square lattice with L = 50, g0 = 0.01, and K = 1.70. Notice the different time scales on the two plots. (From Turalska et al., 2011, with permission.)
Note that the amplitude of the global order parameter depends on the value of the coupling constant K. When K = 0, single units of the network are independent. When K > 0, single units are less and less independent, resulting in a non-zero average. The quantity Kc is the critical value of the control parameter K, at which point a phase transition to a global majority state occurs. In numerical calculations they use the time average ξeq ≡ 〈|ξ(t)|〉 as a measure of the global majority. More precisely after an initial million time steps, which is sufficient time to suppress any transients, an average is taken over the same number of consecutive time steps in the DMM.
They find that in the special case when M is the same for all the nodes and g0 ≪ 1, that DMM generates the same kind of phase transition as is observed in the 2D Ising model discussed in Onsager’s seminal paper (Onsager, 1944). The phase transition for the global variable ξeq is indicated in Figure 3 under various conditions. It is evident that the DMM phase transition on a lattice is only equivalent to the Ising model under very restricted conditions. The apparent equivalence between the Ising and DM models is merely formal, since the DMM does not have a Hamiltonian origin and its elements are not in contact with a thermal bath (Turalska et al., 2011). These differences explain why the equivalence requires the transition rate to vanish, so as to freeze the dynamics of the single units, in the absence of cooperation.
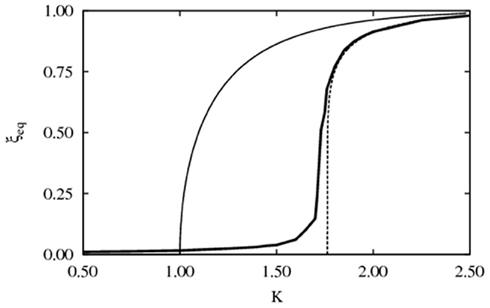
Figure 3. The phase diagram for the global variable ξeq. The thin solid line and dashed line are theoretical predictions for the fully connected and 2D regular networks, respectively. In both cases L = ∞ and the latter case is the Onsager prediction for a 2D regular lattice. The thick solid line corresponds to the global states observed for a 2D regular lattice with L = 100 and g0 = 0.01. Periodic boundary conditions were applied. (From Turalska et al., 2011, with permission.)
When the transition rate assumes a finite value the equivalence between DMM and the Ising model is lost. Turalska et al. (2011) investigate the parameter phase space to determine the domain of phase transitions and find that they can occur for values of K below that of the theoretical Kc. There is also a situation for relative high transition rates in which every unit is surrounded by nearest neighbors in the opposite state, yielding an update of its state at every time step and generating the condition in which the order parameter is exactly zero at all times.
Turalska et al. (2011) conjecture that the crossings of the origin by the global order parameter are the significant events to observe. As illustrated in Figure 2 they interpret the time interval τ between two consecutive crossings as the time duration of a given decision, even if this decision may rest on a slight and fluctuating majority. They evaluate the distribution density of decision–time duration τ, ψ(τ), and the corresponding survival probability Ψ(τ), where

Although emerging from a simple regular lattice, that is, one with no structural complexity, the survival probability presented in Figure 4 shows a scale-free property that extends over more than four orders of magnitude in time for K ≈ Kc A further increase in the coupling strength does not affect the power–law region.
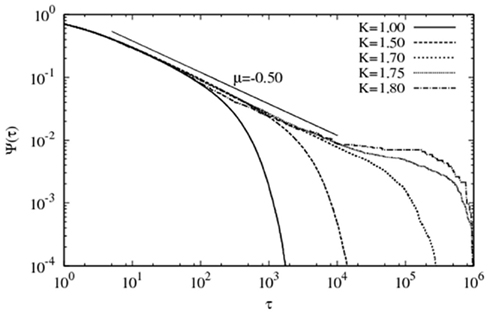
Figure 4. Survival probability function Ψ(τ) for the global order parameter evaluated on a 2D lattice with L = 50, g0 = 0.01 and increasing values of the coupling constant K. The straight line corresponds to a slope of −0.50, namely μ = 1.5 since Ψ(τ)∝1/τμ − 1. (From Turalska et al., 2011, with permission.)
Conclusion
Wiener’s Rule maintains that a network with high information can organize one with low information. For example a tightly coupled organization, with rules and policies to cover all contingencies, changes little over time and therefore is low in information. CPM quantifies Wiener’s Rule by introducing a measure of complexity allowing us to compare the level of information in interacting complex networks. This measure is determined by the power–law index of the hyperbolic distribution and a generalization of LRT enabled us to construct the cross-correlation cube to determine the degree of asymptotic influence one network has on another. In this way the 1/f variability of stimuli is found to resonate with the human brain (Grigolini et al., 2009), as when we are entranced by music or irritated by a dripping faucet (Grigolini and West, 2011; West and Grigolini, 2011).
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Allegrini, P., Bologna, M., Fronzoni, L., Grigolini, P., and Silvestri, L. (2009). Experimental quenching of harmonic stimuli: universality of linear response theory. Phys. Rev. Lett. 103, 030602.
Allegrini, P., Bologna, M., Grigolini, P., and West, B. J. (2007). Fluctuation-dissipation theorem for event-dominated processes. Phys. Rev. Lett. 99, 010603.
Allegrini, P., Paradisi, P., Menicucci, D., Bedini, R., Gemignani, A., and Fronzoni, L. (2011). Noisy cooperative intermittent processes: from blinking quantum dots to human consciousness. J. Phys. Conf. Ser. 306, 012027.
Aquino, G., Bologna, M., Grigolini, P., and West, B. J. (2010). Beyond the death of linear response theory: criticality of the 1/-noise condition. Phys. Rev. Lett. 105, 040601.
Aquino, G., Bologna, M., Grigolini, P., and West, B. J. (2011). Transmission of information between complex networks 1/f resonance. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 83, 051130.
Aquino, G., Grigolini, P., and West, B. J. (2007). Linear response and fluctuation-dissipation theorem for non-Poissonian renewal processes. Europhys. Lett. 80, 10002.
Bianco, S., Geneston, E., Grigolini, P., and Ignaccolo, M. (2008). Renewal aging as emerging property of phase synchronization. Physica A 387, 1387.
Bianco, S., Ignaccolo, M., Rider, M. S., Ross, M. J., Winsor, P., and Grigolini, P. (2007). Brain, music and non-poisson renewal processes. Phys. Rev. E. 75, 061911.
Budini, A. A., and Grigolini, P. (2009). Non-Markovian non-stationary completely positive open-quantum-system dynamics. Phys. Rev. A 80, 022103.
Contoyiannis, Y. F., and Diakonos, F. K. (2000). Criticality and intermittency in the order parameter space. Phys. Lett. A 268, 286–292.
Frantsuzov, P. A., Volkán-Kacsó, S., and Jankó, B. (2009). Model of fluorescence intermittency of single colloidal semiconductor quantum dots using multiple recombination centers. Phys. Rev. Lett. 103, 207402.
Grigolini, P., Aquino, G., Bologna, M., Lukovic, M., and West, B. J. (2009). A theory of 1/f noise in human cognition. Physica A 388, 4192.
Grigolini, P., and West, B. J. (2011). Decision Making: A Psychophysics Application of Network Science. Singapore: World Scientific.
Lukovi’c, M., Ignaccolo, M., Fronzoni, L., and Grigolini, P. (2008). The rate matching effect: a hidden property of periodic stochastic resonance. Phys. Lett. A 372, 2608.
National Research Council of the National Academies. (2005). Network Science. Washington, DC. Available at: www.nap.edu
Office of Force Transformation. (2004). The Implementation of Network-Centric Warfare. Army War College, Carlisle, PA.
Onsager, L. (1944). Crystal statistics. I. A two-dimensional model with an order-disorder transition. Phys. Rev. 65, 117.
Pecora, L. M., and Carroll, T. L. (1990). Synchronization in chaotic systems. Phys. Rev. Lett. 64, 821.
Silvestri, L., Fronzoni, L., Grigolini, P., and Allegrini, P. (2009). Event-driven power-law relaxation in weak turbulence. Phys. Rev. Lett. 102, 014502.
Turalska, M., Lukovic, M., West, B. J., and Grigolini, P. (2009). Complexity and synchronization. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 80, 021110.
Turalska, M., West, B. J., and Grigolini, P. (2011). Temporal complexity of the order parameter at the phase transition. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 83, 061142.
Wang, X. F. (2002). Complex networks: topology, dynamics and synchronization. Int. J. Bifurcat. Chaos 12, 885.
West, B. J., Geneston, E., and Grigolini, P. (2008). Maximizing information exchange between complex networks. Phys. Rep. 468, 1–99.
West, B. J., and Grigolini, P. (2010a). A psychophysical model of decision making. Physica A 389, 3580.
Keywords: complex networks, principle complexity management, decision making model
Citation: West BJ (2011) Overview 2010 of ARL program on network science for human decision making. Front. Physio. 2:76. doi: 10.3389/fphys.2011.00076
Received: 04 October 2011;
Paper pending published: 05 October 2011;
Accepted: 10 October 2011;
Published online: 17 November 2011.
Edited by:
Paolo Allegrini, Consiglio Nazionale delle Ricerche, ItalyReviewed by:
Paolo Allegrini, Consiglio Nazionale delle Ricerche, ItalyPaolo Grigolini, University of North Texas, USA
Copyright: © 2011 West. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence: Bruce J. West, Information Science Directorate, US Army Research Office, Durham, NC 27709, USA. e-mail:YnJ1Y2Uuai53ZXN0QGF0dC5uZXQ=
