- 1 Faculdade de Farmácia, Universidade de Coimbra, Coimbra, Portugal
- 2 Centro de Química de Coimbra, Universidade de Coimbra, Coimbra, Portugal
- 3 Centro de Química Física Molecular and Institute of Nanosciences and Nanotechnologies, Instituto Superior Técnico, Universidade Técnica de Lisboa, Lisboa, Portugal
Förster resonance energy transfer (FRET), in most applications used as a “spectroscopic ruler,” allows an easy determination of the donor-acceptor intermolecular distance. However, the situation becomes complex in membranes, since around each donor there is an ensemble of acceptors at non-correlated distances. In this review, state-of-the-art methodologies for this situation are presented, usually involving time-resolved data and model fitting. This powerful approach can be used to study the occurrence of phase separation (“rafts” or other type of domains), allowing their detection as well as size evaluation. Formalisms for studying lipid–protein and protein–protein interactions according to specific topologies are also addressed. The advantages and added complexity of a specific type of FRET (energy homotransfer or energy migration) are described, as well as applications of FRET under the microscope.
Introduction
Förster resonance energy transfer (FRET) is a photophysical process by which an initially electronically excited fluorophore, termed donor (D), transfers its excitation energy (and thus becomes quenched) to another chromophore, termed acceptor (A), which electronic absorption spectrum overlaps that of the emission of D. The latter, initially in the electronic ground state, becomes excited upon transfer, and may (or may not) fluoresce. FRET involves neither photon emission nor molecular contact between the two species, but is highly dependent on the distance between them. For an isolated donor–acceptor pair, the (first-order) rate coefficient for the FRET interaction is proportional to the inverse sixth power of this distance (Förster, 1949). The characteristic length for FRET is the Förster radius, R0, defined as the donor/acceptor distance for which FRET within a given D/A pair is 50% efficient (that is, as probable as the other processes of D excitation decay). In practice, the distance range for which FRET is sensitive is between 0.5 R0 and 2 R0, as FRET efficiency varies from 98.5 to 1.5% in this interval. The value of R0 is characteristic of each D/A pair in a given environment, but usually lies in the 1.5- to 6-nm range. This implies that FRET is mostly sensitive to distances in the 1- to 10-nm scale, which is out of the reach of conventional optical microscopy techniques, but is entirely adequate to the study of important questions in membrane biophysics, such as detection and characterization of nanodomains/rafts and lipid–protein or protein–protein interaction (Figure 1).
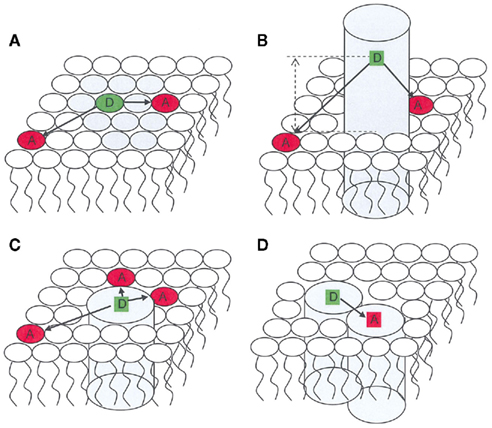
Figure 1. Schematic representation of applications of FRET in membrane biophysics. Only one bilayer leaflet is depicted. (A) membrane heterogeneity; (B) determination of transverse location of a fluorescent residue/label; (C) protein/lipid selectivity; (D) protein oligomerization.
Different approaches can be envisaged, ranging from qualitative studies of variation of FRET steady-state efficiency, without consideration of the underlying kinetics, to analysis of time-resolved fluorescence data with appropriate formalisms, allowing the quantitative recovery of topological information about the system under study. Until recently, these latter sophisticated applications were mostly restricted to simple systems (usually one- or two-component model membranes), whereas FRET studies in complex systems such as the membranes of live cells (for which acquisition of quality time-resolved fluorescence data was technically unfeasible) relied on more qualitative treatments. Nowadays, with the tremendous development of fluorescence microscopy-based techniques, spatial, and time resolution can be combined in a powerful way to the study of real biological membranes. This review describes the basic formalisms of FRET in membranes, and indicates significant illustrative applications of FRET to a variety of problems in membrane systems (Table 1).
Phenomenological Applications of FRET in Membranes
Even if FRET is used as a qualitative indicator of chromophore proximity, without accounting for its actual kinetics, there is still a wide range of applications in membrane biophysics. Additionally, the complexity of some systems is a serious deterrent to the application of complex formalisms, and a more phenomenological approach may be the only option available.
A classic use of FRET is monitoring lipid exchange or mixing and membrane fusion, such as described by Struck et al. (1981). These authors followed the fusion of phosphatidylserine (PS) vesicles induced by calcium ion. Two vesicle populations, one containing both D and A probes and the other containing solely unlabeled phospholipid, were mixed. The chosen FRET pair was composed of the labeled phospholipids N-(7-nitro-2,2,3-benzoxadiazol-4-yl)-phosphatidylethanolamine (NBD-PE, D) and N-(lissamine Rhodamine B sulfonyl)-dioleoylphosphatidyle thanolamine (Rh-PE, A), and since then has become probably the most commonly used pair in membrane FRET studies. Upon addition of calcium ion, fusion causes mixing of the labeled and unlabeled vesicles. Following lipid redistribution by lateral diffusion, the surface concentration of acceptor probes surrounding each donor is diminished. This results in a reduced extent of donor quenching by FRET, the energy transfer efficiency decreases and therefore the donor emission intensity increases. Another possibility is to monitor the increasing of FRET efficiency (decreasing of D fluorescence) upon mixing a population of vesicles labeled with D only with another solely labeled with A, as exemplified in a recent study of SNARE-mediated fusion (van den Bogaart et al., 2010).
In the study of lipid lateral distribution, FRET between probes of identical partition properties will become more efficient as a consequence of phase separation (and conversely for probes exhibiting complementary phase preference). However, probe partition is not the only phenomenon that can affect FRET efficiency. Upon altering membrane composition, variations of area/lipid, and probe photophysical parameters (and hence R0) can occur, which could potentially lead to either erroneous identification or masking of domain formation. To this effect, ingenious schemes can be designed for more precise detection of the onset of domain formation, such as that proposed by Silvius (2003), in which FRET efficiencies obtained with an acceptor with affinity for one of the lipid phases and two different donors that distribute to different membrane domains are compared. As long as the membrane is homogeneous, variations in lipid composition will affect FRET efficiencies of both D/A pairs similarly. However, if domains are formed, the two donors partition to different phases, and efficiencies of quenching for each of them will be affected in opposite ways.
As mentioned below, partition of D or A can be estimated quantitatively from the parameters of the time-resolved fluorescence of D in presence of A (analyzed globally together with that in absence of A). FRET can also be used in a simpler way as an indicator of domain preference as exemplified by the recently proposed “FRET assay of raft association” (Nelson et al., 2010). The efficiency of FRET between the protein under study (D) and one of two acceptors, pyrene–DOPE (prefers ld phase) and LcTMADPH (prefers lo phase) is measured and compared with that using other donors, LW peptide (a transmembrane helix type peptide with high affinity for ld domains) and cholera toxin-B (a protein that binds to the raft-associating lipid ganglioside GM1 and has a very high affinity for lo domains) in a ld/lo phase coexistence lipid mixture. In these authors’ examples, perfringolysin O is thus shown to have intermediate raft affinity between that of LW peptide and cholera toxin-B in vesicles containing ordered domains rich in brain sphingomyelin or 1,2-distearoyl-sn-3-glycerophosphocholine (DSPC).
In the study of lipid/protein interaction, FRET between, e.g., a membrane peptide or protein D and lipid acceptors of different classes/acyl chains may indicate preferential association or selectivity for a particular type of lipid, and FRET between D-bearing and A-bearing membrane proteins can be used to detect formation of protein hetero- or homo-oligomers. In this case, quantitative models are required for further characterization of these interactions (see Formalisms for lipid–protein or protein–protein interaction below).
Intramolecular FRET: A “Spectroscopic Ruler”
Förster resonance energy transfer between D/A pairs for which the D–A distance is the same, such as verified in a solution of a two-chromophore species, is often termed “intramolecular” FRET. A quantification of the extent of FRET is given by the FRET efficiency, E, which is calculated as

in this equation, iD(t) and iDA(t) are the D decays in absence and presence of A (respectively). The effect of FRET on the fluorescence of D is the reduction of its lifetime and quantum yield. In this simple case, the D decay law remains exponential, albeit faster than in the absence of acceptor. The relationship between the lifetime of D in absence and presence of A (τ0 and τ, respectively) is given by

where R is the D–A separation. An expression identical to Eq. 2 can be written for the fluorescence quantum yield, or the fluorescence steady-state intensity. R0 is calculated independently from spectroscopic data,
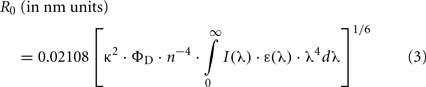
where κ2 is the orientation factor (see Van Der Meer et al., 1994 for a detailed discussion), ΦD is the D quantum yield in the absence of A, n is the refractive index, λ is the wavelength (in nm units), I(λ) is the normalized D emission spectrum, and ε(λ) is the A molar absorption spectrum In this way, R is easily computed from both steady-state and time-resolved data. This is the basis of the use of intramolecular FRET as a “spectroscopic ruler” (Stryer, 1978).
In the context of membrane biophysics, intramolecular FRET is still used to retrieve structural and dynamical information on membrane proteins. This is especially important given that high-resolution structures of many membrane proteins (traditionally obtained using X-ray crystallography, cryo-electron microscopy, or NMR spectroscopy) are still missing. Site-directed labeling allows incorporation of suitable FRET donor and acceptor groups, and, from the measurement of FRET efficiency, protein mapping, and/or kinetics of conformational changes can be studied. Recent applications are listed and briefly described in Table 1.
Uniform Distribution of Fluorophores in Membranes
In membranes, each D molecule is usually surrounded by a distribution of A molecules. Therefore, measurement of single D/A distances is neither meaningful nor feasible. The decay of D’s emission becomes complex and dependent on the topology of the system under study, as well as the concentration of A. Analytical solutions can still be derived for uniform distribution of chromophores. For planar distributions of D and A, the decay of D in presence of A is given by Fung and Stryer (1978), Wolber and Hudson (1979):
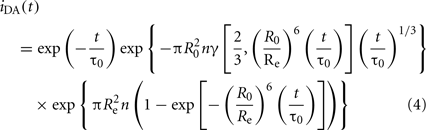
In this equation, γ is the incomplete gamma function, Re is the minimum D/A distance (exclusion distance), and n is the numerical concentration of A (molecules/unit area). Although it was originally derived for a plane of acceptors containing the donor (cis transfer), it is also valid if the D molecule is separated from the A plane by a distance Re, a situation common on membranes, as D and A are often located at different depths in the bilayer.
Upon preparation of lipid vesicles, D and A molecules are frequently inserted in either of the bilayer leaflets, with equal probability. In this case, one must consider two planes of A for a given D, one corresponding to the acceptors lying in the same bilayer leaflet as the donor, and another for those located in the opposite leaflet. The decay law in this case is obtained by simply multiplying the intrinsic D decay by the FRET terms corresponding to each plane of A.
Another common occurrence in membrane systems is a complex decay of D even in the absence of A, with a sum of two or three exponentials being required for a proper description. In this case, the above equations can be still used, provided that the exponential D intrinsic decay term is replaced by this function, and τ0 is replaced by the intensity–average (Lakowicz, 2006) decay lifetime. This is so because each lifetime component is characterized by a different R0 value, proportional to the inverse sixth power of the respective fluorescence quantum yield ΦD (Eq. 3). If all these components have identical radiative decay constants (usually a good approximation), their ΦD values are in turn proportional to those of τ0. This implies that the FRET rates to a given A located at distance R [given by (1/τ0)(R0/R)6] are the same irrespective of the D lifetime component considered, because 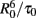 is invariant (Loura et al., 1996, 2000b). Because of this constancy, Eq. 4 can be used with the average values of R0 and τ0. The option here is to use the spectroscopic R0 (calculated with the experimental, averaged value of ΦD) and the true statistical average of τ0, which is the intensity–average.
is invariant (Loura et al., 1996, 2000b). Because of this constancy, Eq. 4 can be used with the average values of R0 and τ0. The option here is to use the spectroscopic R0 (calculated with the experimental, averaged value of ΦD) and the true statistical average of τ0, which is the intensity–average.
For steady-state applications, Eq. 4 can be integrated numerically (in a program or spreadsheet) to produce curves of FRET efficiency E (calculated using Eq. 1) as function of acceptor concentration n, with Re as a parameter. Alternatively, Re is fixed and experimental FRET decays/efficiencies are compared with theoretical expectations. Eventual failure to analyze FRET kinetics with the uniform probe distribution formalism may have relevance (e.g., addition of a new component to a given one-phase lipid bilayer system may induce compartmentalization and/or phase separation, and hence deviations to the theoretical uniform distribution expectation).
Non-Uniform Distribution of Fluorophores Contains Topological Information
Non-uniform component distribution and phase separation are common occurrences in lipid mixtures. The molecules which bear the D and A fluorophores in a FRET experiment in such a system will naturally have non-uniform distributions, following their partition between the coexisting phase domains. Let us consider that there are only two phases or types of domains present (the most common experimental situation). If these are sufficiently large to be infinite in the FRET scale (i.e., complications resulting form FRET involving molecules in different domains, or boundary effects, are negligible; this is the case if the domains are larger than ~5–10 R0), then the donor decay law is simply a linear combination of the hypothetical decay laws in each phase i DA,phase i (given by Eq. 4), weighed by the relative amount of D in each phase Ai (Loura et al., 2000a, 2001):
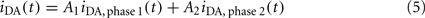
Note that the D lifetimes are usually different in the two phases, as are the A surface concentrations (and possibly also the D–A exclusion distances). This introduces a large number of fitting parameters in Eq. 5. To ensure meaningful recovery of these parameters, the decay of D in presence of A is globally analyzed together with that in the absence of A,
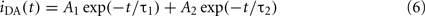
where τ1 and τ2 are the D lifetimes in each phase. The recovered parameters are usually τ1, τ2, A2/A1 (from which the D partition coefficient KpD is obtained), and the A concentrations in the two phases, C1 and C2 (from which the A partition coefficient KpA is obtained; Loura et al., 2000a). A particular case of this formalism is the so-called “isolated donors” situation, which corresponds to C2 = 0.
Being strictly valid for infinite phase separation, this model can be applied to nanoscale domain formation; in this case, the recovered A partition coefficient (“FRET” KpA) will not be equal to the true coefficient recovered from independent (fluorescence intensity, anisotropy, or lifetime of A) measurements (“non-FRET” KpA), and is affected (being closer to unity than the “non-FRET” value) by the fact that donors in one phase are sensitive to acceptors in the other. The extent of this deviation reflects the size of the nanodomains. In the very small domain size limit (<R0), the “FRET” KpA is essentially unity. Therefore, this kind of analysis can produce insights regarding the size of the domains, and in the case of infinite phase separation (which can be validated if the “FRET” and “non-FRET” KpA values are indistinguishable) it was shown that the phase diagram of a binary mixture can be obtained from the decay parameters (Loura et al., 2001). An experimental method of characterization of phase separation in lipid membranes (and determination of binary and ternary phase diagrams in the infinite phase limit) based on this formalism, but relying solely on acceptor steady-state sensitized emission, was proposed by Buboltz (2007), who termed it “Steady-State Probe-Partitioning FRET” or SP-FRET. Applications of these methodologies are listed in Table 1.
Numerical and Simplified Analytical Treatments of FRET in Non-Homogeneous Systems
No exact solution of the FRET rate or efficiency has been derived for the case of incomplete phase separation, with nanometer-sized domains of a given type dispersed in the continuous phase. This stems from the evident symmetry loss introduced by the presence of the domains. One way to tackle this complexity is to calculate the D decay using numerical simulation. Basically, the process starts by building a topology of the lipid matrix (i.e., define size of the simulated system, domain shape, average size and size distribution, and then place the domains on the matrix, ensuring that the overall fraction of each phase is as intended) and placing D and A molecules taking into account their domain preference. A given D is then selected and its interaction with all the acceptors (or those within a cutoff of several R0 lengths) is computed. This step is then repeated for all the donors in order to obtain an ensemble average value for all the system. One obtains the average D decay, and, by using Eq. 1, the FRET efficiency value.
This kind of numerical simulations was already described by Wolber and Hudson (1979) for uniform distribution in a planar geometry to test their analytical theory. The first numerical solution of FRET for non-uniform membrane probe distribution was given by Snyder and Freire (1982). In this work, heterogeneity of probe distribution was introduced by incorporating a heuristic potential function in the random placement of the probes. Therefore, no domains are actually simulated, and whereas the authors’ equations are suited to the analysis of probe aggregation in a single phase system, they are not useful regarding phase separation. Simulations in which probe distribution heterogeneity is introduced by building a biphasic system and taking into consideration probe partition have been presented by authors to provide tests for their analytical formalisms (Loura and Prieto, 2000; Loura et al., 2001; Towles and Dan, 2007; Towles et al., 2007).
Another simulation approach consists in recreating the excitation and de-excitation processes of each D or A molecule by performing stochastic simulations. These calculations take into account the probabilities of donor excitation, donor decay by non-FRET processes, FRET to a given acceptor, and acceptor de-excitation. The FRET efficiency is simply calculated by the ratio between the total number of transfers and the total number of D excitations. This type of simulation has been applied to the case of FRET in a planar geometry with disklike domains (Kiskowski and Kenworthy, 2007).
All previous works are characterized by prior fixing of the underlying lipid matrix, including domain size and shape, and the simulations concern exclusively the calculation of FRET rates and probabilities. A different approach was recently undertaken by Frazier et al. (2007), who combined statistical mechanical lattice Monte-Carlo simulations (to describe the lipid matrix and to generate chromophore positions therein) with a simplified step-function FRET distance dependence (FRET was considered to occur if and only if the D–A distance in a given pair were less than R0) to analyze experimental data of FRET in a ternary, raft-model mixture. This work demonstrates that FRET and computational techniques can be combined to create a powerful combination, suited to the study of lipid phase separation.
Globally, numerical simulations have the advantage of allowing the calculation of FRET in systems for which, due to their complexity, an exact solution is precluded. However, thus far they do not provide a way to analyze experimental data directly, as many degrees of freedom are expected in an actual experiment. For each simulation, values for R0, D lifetime, D/A exclusion distance (all being possibly different in each coexisting phase), domain shape and size, and D and A partition coefficients need to be fixed. This multiplicity of variables excludes the possibility of fitting with simple empirical functions that could describe, e.g., the variation of FRET efficiency as a function of concentration of A in a general manner, which would be convenient for most researchers. The study of a particular system requires individual setup and simulation procedures.
An alternative to numerical simulations of FRET in nanoheterogeneous bilayers is the use of simplified analytical treatments, which, unlike the former, could potentially be suited to direct analysis of experimental data enabling recovery of the parameters of interest. However, this kind of formalisms has been characterized by either severe simplifying approximations (Gutierrez-Merino, 1981; Brown et al., 2007a,b) or relying to some extent to numerical results (Towles et al., 2007; see Loura et al., 2010a for a detailed discussion), precluding their widespread use.
Formalisms for Lipid–Protein or Protein–Protein Interaction
A relatively simple application of FRET in membrane systems containing peptides/proteins bearing fluorescent residues (tryptophan and tyrosine) is the determination of the transverse location of the latter. Tryptophan and tyrosine act as energy transfer donors, since they absorb at short wavelengths, so suitable acceptors with known positions in the membrane should be used (see Table 1). Because the efficiency of transfer depends on the D–A exclusion distance, the value of Re (and hence the transverse location) can be obtained by fitting Eqs 1 and 4 to the experimental data. A series of stearic acids derivatized with the anthroyl chromophore is available, and is characterized in great detail in the literature (see e.g., Blatt et al., 1984). Because there is almost invariance of the absorption spectra of the different acceptors, the Förster radius is constant for all of them, and for tryptophan as D it is close to R0 = 25 Å. It can be shown that, when Re > approximately 1.7 R0, a Stern–Volmer type dependence is obtained (Shaklai et al., 1977; Dewey and Hammes, 1980), expressed by the very simple equation

where IDA and ID denote the steady-state emission intensity of D in the presence and absence of A, respectively. Whereas Eqs 4 and 7 assume axial distribution of A chromophores around the D residue, Yguerabide (1994) generalized the theory to include the case where D is not on the symmetry axis of the labeled protein, and extended its validity to cases where Re < R0, inevitably with some added complexity.
Proteins incorporated in model membranes containing lipids with different electrostatic properties or hydrophobic lengths may show selectivity to one lipid component at the protein–lipid interface, which traditionally has been addressed using electron spin resonance spectroscopy (Marsh and Horváth, 1998). However, essentially identical information can be obtained using FRET. Qualitative information is readily obtained by comparing the extent of FRET from a protein to fluorescently labeled lipids of different classes/acyl chains, as mentioned above. A few quantitative models have been proposed, and were critically reviewed recently (Loura et al., 2010b). Table 1 lists applications of these formalisms to experimental FRET data.
Characterization of protein–protein interaction, using FRET involving two distinct labeled derivatives of proteins or peptides, have been described since more than 30 years ago. In a now historical paper, using a simple formalism which neglected intermolecular FRET but took into account different oligomerization schemes (dimers/trimers/tetramers), Veatch and Stryer (1977) verified that the hypothesis of formation of gramicidin dimers (D: dansyl-gramicidin C; A: 4-(diethylamino)-phenylazobenzene-4-sulfonyl chloride derivative of gramicidin C) led to better model fits than both trimer and tetramer formation scenarios. Aggregation of proteins of the chromaffin granule membrane, labeled with maleimide iodoaminonaphthyl sulfonate (D) and fluorescein mercury acetate or fluorescein-5-maleimide (A), was qualitatively verified by Morris et al. (1982) upon addition of calcium ion. Following these early studies, FRET has become an important tool in the characterization of protein/peptide aggregation. One must choose carefully the formalism to be used for data analysis, as early models focus in the intra-aggregate energy transfer, neglecting “bystander” intermolecular FRET (e.g., Adair and Engelman, 1994; Li et al., 1999). This approximation is generally only valid in the limit of very dilute labeled protein, and is commonly used in recent works applying FRET or bioluminescence resonance energy transfer (BRET, see e.g., James et al., 2006) to the study of membrane protein oligomerization, listed in Table 1. Other treatments strive to compute the pure intra-aggregate term (see Raicu, 2007 for a recent example). It must be noted that the combination of the intra-aggregate and intermolecular terms should be carried out carefully. In particular, it is inaccurate to subtract the pure intermolecular efficiency from that of combined inter-aggregate and intermolecular FRET (You et al., 2005). If the donor population is subjected to quenching by two different types of acceptor (e.g., those bound and unbound to a given donor), the correct way to calculate the FRET efficiency is to multiply the FRET terms corresponding to all quenching contributions to obtain iDA(t), and integrate in the end (Eq. 1). This is exemplified in a recent study, which concluded that the N-BAR N-terminal domain forms antiparallel dimers in 1-palmitoyl-2-oleoyl-sn-glycero-3-[phospho-rac-(1-glycerol)] (POPG) vesicles (Fernandes et al., 2008).
Diffusion-Enhanced FRET
In the preceding sections, it was assumed that translational diffusion of both D and A were negligible during the lifetime of the D excited state, that is, the condition DDAτ0/s2 ≪ 1 (where DDA is the sum of D and A lateral diffusion coefficients and s is the average D–A distance) was met. Otherwise, fast chromophore diffusion leads to an enhancement in the rate of FRET, which can be intuitively understood by considering that a D/A pair, initially separated by a large distance which would prevent FRET, might become close enough for FRET to occur with high probability in the course of the D excited state lifetime as a consequence of diffusion.
The general theory of diffusion-enhanced FRET was established by Steinberg and Katchalski (1968) and verified experimentally by Thomas et al. (1978). Of particular interest is the so-called rapid-diffusion limit, characterized by DDAτ0/s2 ≪ 1, which leads to extremely simplified equations for the rate of FRET. This condition requires D lifetimes in the microsecond to millisecond range, which are typically achievable using suitable lanthanide chelates as the D species. For a uniform two-dimensional distribution of uncharged spherical chromophores, it can be shown that an exponential D decay is obtained, with lifetime

where

The latter equation (which, rather curiously, is formally identical to Eq. 7, which is an approximate solution to a very different problem) shows that the rate of FRET in this regime is highly dependent on Re. This is the reason why rapid-diffusion limit FRET found application in the measurement of the distance of closest D–A approach (where typically the A species is a protein), in the 1980s (see Table 1 for examples). Additionally, FRET-enhanced diffusion of charged D/A species is sensitive to the electrostatic potential, and therefore can be used to determine membrane potentials (Meltzer et al., 2006). Surprisingly, recent applications in membranes have been very few, which led to the spirited comment “Since the mid 1980s, the technique [diffusion-enhanced FRET] seems to have remained dormant waiting for the right opportunity to spring back to life” (Fairclough, 2006).
Homo-FRET vs. Hetero-FRET
In the preceding sections, it was assumed that the D and A chromophores were distinct (hetero-FRET). This implied the irreversibility of the transfer process, which could be monitored measuring either the extent of quenching of D or the sensitized fluorescence of A. In contrast, FRET between identical fluorophores (homo-FRET) does not lead to a reduction in donor fluorescence intensity or lifetime, because the donor excited state population is not diminished during the act of transfer. In practice, the sole observable which reflects the phenomenon is fluorescence anisotropy (Lakowicz, 2006), which is reduced as a consequence of homotransfer. Measurement of fluorescence anisotropy requires polarizers and, because these lead to a considerable reduction in the detected emission, often a larger amount of fluorophore (relative to that which would be used in an intensity measurement) is needed for a given precision. In case that instrumentation is not a problem, the decrease in anisotropy is quite clear: if the two molecules are separated by distance R = R0, the measured anisotropy will only be ~2/3 of that of the monomer, which is a significant decrease.
Despite having an obvious advantage of only requiring a single fluorophore, the use of homo-FRET is more restricted than that of hetero-FRET. The rationalization of the extent of depolarization due to homo-FRET is more complicated than that of quenching due to hetero-FRET, because: (i) there is the possibility of back-transfer to the directly excited donor, or transfer to any donor, eventually involving a large number of transfer steps, and (ii) being fluorescence anisotropy the relevant observable, in addition to RET, another source of depolarization is fluorophore rotation. If rotation and RET occur in the same timescale, the two phenomena are coupled, which constitutes the main obstacle to quantitative data analysis of homotransfer. Theoretical descriptions which do not take these features into proper account (e.g., Yeow and Clayton, 2007) should be viewed cautiously. Despite this complexity, homo-FRET is still regularly used in membrane studies, more recently in combination with fluorescence microscopy (see section below and Table 1; Bader et al., 2011) to detect and characterize chromophore (e.g., labeled protein) confinement or aggregation. In this regard, it should be noted that the use of high numerical aperture objectives results in reduction of the observed anisotropy (Axelrod, 1979). This artifact can be minimized using a lower numerical aperture (≤0.8), with loss in resolution and sensitivity, or corrected, e.g., by using a standard molecule (Tramier and Coppey-Moisan, 2008).
FRET Under the Microscope
Recent developments in multi-wavelength and polarization resolved imaging have led to a widespread use of FRET imaging in studies of functional assemblies in cell membranes. The experimental methods for visualizing membrane microdomains and quantifying FRET efficiencies in FRET microscopy with emphasis on novel strategies have been reviewed elsewhere (Rao and Mayor, 2005; Jares-Erijman and Jovin, 2006; Owen et al., 2007; Padilla-Parra et al., 2008). Several approaches were developed in order to explore, on the nanoscale range, specific protein–protein, lipid–lipid, or lipid–protein interactions in live cells, both using homo- and hetero-FRET.
Cell membranes are characterized by a large number of lipid and protein components in a non-equilibrium state. One common simplification is to assume two types of domains, e.g., raft/non-raft or ordered/disordered. The results can then be compared to, e.g., the ld/lo coexistence on a lipid phase diagram in a ternary model system. Due to intrinsic limitations such as cell stability, and because usually in cells microscopy studies are carried out (in order to control cell state, to know the fluorophore localization, and use the signal coming only from the membrane of interest) fluorescence intensity decays with a high number of photons and low background signal (necessary to the applications of most of the formalisms described above) are generally unfeasible. Usually, steady-state data is obtained and compared to an integrated FRET formalism. Even when fluorescence lifetime imaging microscopy (FLIM; see Stöckl and Herrmann, 2010 for a review of its applications to membrane heterogeneity) lifetime data is obtained (FRET–FLIM), a relatively low number of counts is often obtained, which implies that the decay is traditionally used to calculate FRET efficiency using Eq. 1, rather than directly analyzed with the underlying FRET kinetic model. However, with instrumental improvements as well as development of novel analysis approaches (Grecco et al., 2009) this trend is being reversed. Selected works combining FRET and microscopy are listed in Table 1, which succinctly describes illustrative literature reports in which FRET was used in (at least) one of the applications described above.
Conclusion
In this review, applications of FRET in membrane biophysics are described, comprising studies of membrane protein mapping, lateral heterogeneity (membrane domains), determination of the transverse location (depth) of fluorescent residues/labels inside the membrane, protein/lipid selectivity (preference of a specific lipid for the protein vicinity), and membrane protein oligomerization.
The complexity of FRET in membranes was addressed, an evaluation of hetero vs. homo-FRET is presented, and detailed topological information can be obtained from this methodology, once adequate modeling is taken into account. Examples of relevant works in this area are critically reviewed, and the recent applications of FRET under the microscope, namely from time-resolved data (FRET–FLIM), are mentioned. On the whole, the power of FRET as a tool in membrane biophysics is emphasized.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors acknowledge funding by FEDER, through the COMPETE program, and by FCT, project references FCOMP-01-0124-FEDER-010787 (FCT PTDC/QUI-QUI/098198/2008), PTDC/QUI-BIQ/099947/2008, and PTDC/QUI-BIQ/112067/2009.
References
Acasandrei, M. A., Dale, R. E., VandeVen, M., and Ameloot, M. (2006). Two-dimensional Förster resonance energy transfer (2-D FRET) and the membrane raft hypothesis. Chem. Phys. Lett. 419, 469–473.
Adair, B. D., and Engelman, D. M. (1994). Glycophorin A helical transmembrane domains dimerize in phospholipid bilayers: a resonance energy transfer study. Biochemistry 33, 5539–5544.
Albert, A. D., Young, J. E., and Yeagle, P. L. (1996). Rhodopsin-cholesterol interactions in bovine rod outer segment disk membranes. Biochim. Biophys. Acta 1285, 47–55.
Anikovsky, M., Dale, L., Ferguson, S., and Petersen, N. (2008). Resonance energy transfer in cells: a new look at fixation effect and receptor aggregation on cell membrane. Biophys. J. 95, 1349–1359.
Antollini, S. S., and Barrantes, F. J. (1998). Disclosure of discrete sites for phospholipid and sterols at the protein–lipid interface in native acetylcholine receptor-rich membrane. Biochemistry 37, 16653–16662.
Axelrod, D. (1979). Carbocyanine dye orientation in red cell membrane studied by microscopic fluorescence polarization. Biophys. J. 26, 557–574.
Bader, A. N., Hoetzl, S., Hofman, E. G., Voortman, J., van Bergen en Henegouwen, P. M. P., van Meer, G., and Gerritsen, H. C. (2011). Homo-FRET imaging as a tool to quantify protein and lipid clustering. Chemphyschem 12, 475–483.
Basu, A., Mazor, S., and Casey, J. R. (2010). Distance measurements within a concatamer of the plasma membrane Cl-/HCO3-exchanger, AE1. Biochemistry 49, 9226–9240.
Blatt, E., Chatelier, R. C., and Sawyer, W. H. (1984). The transverse location of fluorophores in lipid bilayers and micelles as dertermined by fluorescence techniques. Photochem. Photobiol. 39, 477–483.
Brown, A. C., Towles, K. B., and Wrenn, S. P. (2007a). Measuring raft size as a function of membrane composition in PC-based systems: part I – binary systems. Langmuir 23, 11180–11187.
Brown, A. C., Towles, K. B., and Wrenn, S. P. (2007b). Measuring raft size as a function of membrane composition in PC-based systems: part II – ternary systems. Langmuir 23, 11188–11196.
Buboltz, J. T. (2007). Steady-state probe-partitioning FRET: a simple and robust tool for the study of membrane phase behavior. Phys. Rev. E Stat. nonlin. Soft Matter Phys. 76, 021903.
Buboltz, J. T., Bwalya, C., Williams, K., and Schutzer, M. (2007). High-resolution mapping of phase behavior in a ternary lipid mixture: do lipid-raft phase boundaries depend on the sample preparation procedure? Langmuir 23, 11968–11971.
Capeta, R. C., Poveda, J. A., and Loura, L. M. S. (2006). Non-uniform membrane probe distribution in resonance energy transfer: application to protein-lipid selectivity. J. Fluoresc. 16, 161–172.
Cha, A., Snyder, G. E., Selvin, P. R., and Bezanilla, F. (1999). Atomic scale movement of the voltage-sensing region in a potassium channel measured via spectroscopy. Nature 402, 809–813.
Chen, Q., and Lentz, B. R. (1997). Fluorescence resonance energy transfer study of shape changes in membrane-bound bovine prothrombin and meizothrombin. Biochemistry 36, 4701–4711.
Cornea, R. L., Nitu, F., Gruber, S., Kohler, K., Satzer, M., Thomas, D. D., and Fruen, B. R. (2009). FRET-based mapping of calmodulin bound to the RyR1 Ca2+ release channel. Proc. Natl. Acad. Sci. U.S.A. 106, 6128–6133.
Cornea, R. L., Nitu, F., Samsó, M., Thomas, D. D., and Fruen, B. R. (2010). Mapping the ryanodine receptor FK506-binding protein subunit using fluorescence resonance energy transfer. J. Biol. Chem. 285, 19219–19226.
Coutinho, A., Loura, L. M. S., Fedorov, A., and Prieto, M. (2008). Pinched multilamellar structure of aggregates of lysozyme and phosphatidylserine-containing membranes revealed by FRET. Biophys. J. 95, 4726–4736.
de Almeida, R. F. M., Loura, L. M. S., Fedorov, A., and Prieto, M. (2002). Nonequilibrium phenomena in the phase separation of a two-component lipid bilayer. Biophys. J. 82, 823–834.
de Almeida, R. F. M., Loura, L. M. S., Fedorov, A., and Prieto, M. (2005). Lipid rafts have different sizes depending on membrane composition: a time-resolved fluorescence resonance energy transfer study. J. Mol. Biol. 346, 1109–1120.
Dewey, T. G., and Hammes, G. G. (1980). Calculation on fluorescence resonance energy transfer on surfaces. Biophys. J. 32, 1023–1035.
Domanov, Y. A., Molotkovsky, J. G., and Gorbenko, G. P. (2005). Coverage-dependent changes of cytochrome c transverse location in phospholipid membranes revealed by FRET. Biochim. Biophys. Acta 1716, 49–58.
Fairclough, R. H. (2006). Recalled to life: resurrection of diffusion-enhanced fluorescence energy transfer. Biophys. J. 91, 1143–1144.
Fernandes, F., Loura, L. M. S., Chichón, F. J., Carrascosa, J. L., Fedorov, A., and Prieto, M. (2008). Role of helix 0 of the N-BAR domain in membrane curvature generation. Biophys. J. 94, 3065–3073.
Fernandes, F., Loura, L. M. S., Fedorov, A., and Prieto, M. (2006). Absence of clustering of phosphatidylinositol-(4,5)-bisphosphate in fluid phosphatidylcholine. J. Lipid Res. 47, 1521–1525.
Fernandes, F., Loura, L. M. S., Koehorst, R., Spruijt, R. B., Hemminga, M. A., Fedorov, A., and Prieto, M. (2004). Quantification of protein-lipid selectivity using FRET: application to the M13 major coat protein. Biophys. J. 87, 344–352.
Fernandes, F., Loura, L. M. S., Prieto, M., Koehorst, R., Spruijt, R. B., and Hemminga, M. A. (2003). Dependence of M13 major coat protein oligomerization and lateral segregation on bilayer composition. Biophys. J. 85, 2430–2441.
Förster, T. (1949). Experimentelle und theoretische Untersuchung des Zwischenmolekularen übergangs von Elektrinenanregungsenergie. Z. Naturforsch. 4a, 321–327.
Frazier, M. L., Wright, J. R., Pokorny, A., and Almeida, P. F. F. (2007). Investigation of domain formation in sphingomyelin/cholesterol/POPC mixtures by fluorescence resonance energy transfer and Monte Carlo simulations. Biophys. J. 92, 2422–2433.
Fung, B. K., and Stryer, L. (1978). Surface density determination in membranes by fluorescence energy transfer. Biochemistry 17, 5241–5248.
Fung, J. J., Deupi, X., Pardo, L., Yao, X. J., Velez-Ruiz, G. A., Devree, B. T., Sunahara, R. K., and Kobilka, B. K. (2009). Ligand-regulated oligomerization of beta(2)-adrenoceptors in a model lipid bilayer. EMBO J. 28, 3315–3328.
Gambhir, A., Hangyás-Mihályné, G., Zaitseva, I., Cafiso, D. S., Wang, J., Murray, D., Pentyala, S. N., Smith, S. O., and McLaughlin, S. (2004). Electrostatic sequestration of PIP2 on phospholipid membranes by basic/aromatic regions of proteins. Biophys. J. 86, 2188–2207.
Goswami, D., Gowrishankar, K., Bilgrami, S., Ghosh, S., Raghupathy, R., Chadda, R., Vishwakarma, R., Rao, M., and Mayor, S. (2008). Nanoclusters of GPI-anchored proteins are formed by cortical actin-driven activity. Cell 135, 1085–1097.
Grecco, H. E., Roda-Navarro, P., and Verveer, P. J. (2009). Global analysis of time correlated single photon counting FRET-FLIM data. Opt. Express 17, 6493–6508.
Gutierrez-Merino, C. (1981). Quantitation of the Förster energy transfer for two-dimensional systems. I. Lateral phase separation in unilamellar vesicles formed by binary phospholipid mixtures. Biophys. Chem. 14, 247–257.
Gutierrez-Merino, C., Munkonge, F., Mata, A. M., East, J. M., Levinson, B. L., Napier, R. M., and Lee, A. G. (1987). The position of the ATP binding site on the (Ca2+ + Mg2+)-ATPase. Biochim. Biophys. Acta 897, 207–216.
Harding, P. J., Attrill, H., Boehringer, J., Ross, S., Wadhams, G. H., Smith, E., Armitage, J. P., and Watts, A. (2009). Constitutive dimerization of the G-protein coupled receptor, neurotensin receptor 1, reconstituted into phospholipid bilayers. Biophys. J. 96, 964–973.
Harikumar, K. G., Happs, R. M., and Miller, L. J. (2008). Dimerization in the absence of higher-order oligomerization of the G protein-coupled secretin receptor. Biochim. Biophys. Acta 1778, 2555–2563.
Heberle, F. A., Wu, J., Goh, S. L., Petruzielo, R. S., and Feigenson, G. W. (2010). Comparison of three ternary lipid bilayer mixtures: FRET and ESR reveal nanodomains. Biophys. J. 99, 3309–3318.
Herreros, J., Ng, T., and Schiavo, G. (2001). Lipid rafts act as specialized domains for tetanus toxin binding and internalization into neurons. Mol. Biol. Cell 12, 2947–2960.
Hofman, E. G., Ruonala, M. O., Bader, A. N., van den Heuvel, D., Voortman, J., Roovers, R. C., Verkleij, A. J., Gerritsen, H. C., and van Bergen en Henegouwen, P. M. P. (2008). EGF induces coalescence of different lipid rafts. J. Cell. Sci. 121, 2519–2528.
Hughes, W. E., Larijani, B., and Parker, P. J. (2002). Detecting protein-phospholipid interactions. J. Biol. Chem. 277, 22974–22979.
James, J. R., Oliveira, M. I., Carmo, A. M., Iaboni, A., and Davis, S. J. (2006). A rigorous experimental framework for detecting protein oligomerization using bioluminescence resonance energy transfer. Nat. Methods 3, 1001–1006.
Jares-Erijman, E. A., and Jovin, T. M. (2006). Imaging molecular interactions in living cells by FRET microscopy. Curr. Opin. Chem. Biol. 10, 409–416.
Johnson, D. A., and Nuss, J. M. (1994). The histrionicotoxin-sensitive ethidium binding site is located outside of the transmembrane domain of the nicotinic acetylcholine receptor: a fluorescence study. Biochemistry 33, 9070–9077.
Kenworthy, A. K., and Edidin, M. (1998). Distribution of a glycosylphosphatidylinositol-anchored protein at the apical surface of MDCK cells examined at a resolution of <100 Å using imaging fluorescence resonance energy transfer. J. Cell Biol. 142, 69–84.
Kiskowski, M. A., and Kenworthy, A. (2007). In silico characterization of resonance energy transfer for disk-shaped domains. Biophys. J. 92, 3040–3051.
Kusba, J., Li, L., Gryczynski, I., Piszczek, G., Johnson, M., and Lakowicz, J. R. (2002). Lateral diffusion coefficients in membranes measured by resonance energy transfer and a new algorithm for diffusion in two dimensions. Biophys. J. 82, 1358–1372.
Leder, R. O., Helgerson, S. L., and Thomas, D. D. (1989). The transverse location of the retinal chromophore in the purple membrane by diffusion-enhanced energy transfer. J. Mol. Biol. 209, 683–701.
Levi, V., Rossi, J. P. F. C., Castello, P. R., and Flecha, F. L. G. (2003). Quantitative analysis of membrane protein–amphiphile interactions using resonance energy transfer. Anal. Biochem. 317, 171–179.
Levi, V., Rossi, J. P. F. C., Echarte, M. M., Castello, P. R., and Flecha, F. L. G. (2000). Thermal stability of the plasma membrane calcium pump. Quantitative analysis of its dependence on lipid-protein interactions. J. Membr. Biol. 173, 215–225.
Li, M., Reddy, L. G., Bennett, R., Silva, N. D. Jr., Jones, L. R., and Thomas, D. D. (1999). A fluorescence energy transfer method for analyzing protein oligomeric structure: application to phospholamban. Biophys. J. 76, 2587–2599.
Loura, L. M. S., Coutinho, A., Silva, A., Fedorov, A., and Prieto, M. (2006). Structural effects of a basic peptide on the organization of dipalmitoylphosphatidylcholine/dipalmitoylphosphatidylserine membranes: a fluorescent resonance energy transfer study. J. Phys. Chem. B 110, 8130–8141.
Loura, L. M. S., Fedorov, A., and Prieto, M. (1996). Resonance energy transfer in a model system of membranes: application to gel and liquid crystalline phases. Biophys. J. 71, 1823–1836.
Loura, L. M. S., Fedorov, A., and Prieto, M. (2000a). Partition of membrane probes in a gel/fluid two-component lipid system: a fluorescence resonance energy transfer study. Biochim. Biophys. Acta 1467, 101–112.
Loura, L. M. S., Fedorov, A., and Prieto, M. (2000b). Membrane probe distribution heterogeneity: a resonance energy transfer study. J. Phys. Chem. B 104, 6920–6931.
Loura, L. M. S., Fedorov, A., and Prieto, M. (2001). Fluid-fluid membrane micro-heterogeneity: a fluorescence resonance energy transfer study. Biophys. J. 80, 776–788.
Loura, L. M. S., Fernandes, F., and Prieto, M. (2010a). Membrane microheterogeneity: Förster resonance energy transfer characterization of lateral membrane domains. Eur. Biophys. J. 39, 589–607.
Loura, L. M. S., Prieto, M., and Fernandes, F. (2010b). Quantification of protein-lipid selectivity using FRET. Eur. Biophys. J. 39, 565–578.
Loura, L. M. S., and Prieto, M. (2000). Resonance energy transfer in heterogeneous planar and bilayer systems: theory and simulation. J. Phys. Chem. B 104, 6911–6919.
Marsh, D., and Horváth, L. I. (1998). Structure, dynamics and composition of the lipid-protein interface. Perspectives from spin-labelling. Biochim. Biophys. Acta 1376, 267–296.
Meltzer, R. H., Lurtz, M. M., Wensel, T. G., and Pedersen, S. E. (2006). Nicotinic acetylcholine receptor channel electrostatics determined by diffusion-enhanced luminescence energy transfer. Biophys. J. 91, 1315–1324.
Mercier, J. F., Salahpour, A., Angers, S., Breit, A., and Bouvier, M. (2002). Quantitative assessment of beta 1- and beta 2-adrenergic receptor homo- and heterodimerization by bioluminescence resonance energy transfer. J. Biol. Chem. 277, 44925–44931.
Meyer, B. H., Segura, J.-M., Martinez, K. L., Hovius, R., George, N., Johnsson, K., and Vogel, H. (2006). FRET imaging reveals that functional neurokinin-1 receptors are monomeric and reside in membrane microdomains of live cells. Proc. Natl. Acad. Sci. U.S.A. 103, 2138–2143.
Morris, S. J., Sudhof, T. C., and Haynes, D. H. (1982). Calcium-promoted resonance energy transfer between fluorescently labeled proteins during aggregation of chromaffin granule membranes. Biochim. Biophys. Acta 693, 425–436.
Narayanaswami, V., and McNamee, M. G. (1993). Protein-lipid interactions and Torpedo californica nicotinic acetylcholine receptor function. 2. Membrane fluidity and ligand-mediated alteration in the accessibility of gamma subunit cysteine residues to cholesterol. Biochemistry 32, 12420–12427.
Nelson, L. D., Chaintia, S., and London, E. (2010). Perfringolysin O association with ordered lipid domains: implications for transmembrane protein raft affinity. Biophys. J. 99, 3255–3263.
Nomikos, M., Mulgrew-Nesbitt, A., Pallavi, P., Mihalyne, G., Zaitseva, I., Swann, K., Lai, F. A., Murray, D., and McLaughlin, S. (2007). Binding of phosphoinositide-specific phospholipase C-ξ (PLC-ξ) to phospholipid membranes. J. Biol. Chem. 282, 16644–16653.
Owen, D. M., Neil, M. A. A., French, P. M. W., and Magee, A. I. (2007). Optical techniques for imaging membrane lipid microdomains in living cells. Semin. Cell Dev. Biol. 18, 591–598.
Padilla-Parra, S., Auduge, N., Coppey-Moisan, M., and Tramier, M. (2008). Quantitative FRET analysis by fast acquisition time domain FLIM at high spatial resolution in living cells. Biophys. J. 95, 2976–2988.
Pap, E. H. W., Bastiaens, P. I. H., Borst, J. W., van den Berg, P. A. W., van Hoek, A., Snoek, G. T., Wirtz, K. W. A., and Visser, A. J. W. G. (1993). Quantitation of the interaction of protein kinase C with diacylglycerol and phosphoinositides by time-resolved detection of resonance energy transfer. Biochemistry 32, 13310–13317.
Picas, L., Suárez-Germà, C., Montero, M. T., Vázquez-Ibar, J. L., Hernández-Borrell, J., Prieto, M., and Loura, L. M. S. (2010). Lactose permease lipid selectivity using Förster resonance energy transfer. Biochim. Biophys. Acta 1798, 1707–1713.
Poveda, J. A., Encinar, J. A., Fernández, A. M., Mateo, C. R., Ferragut, J. A., and González-Ros, J. M. (2002). Segregation of phosphatidic acid-rich domains in reconstituted acetylcholine receptor membranes. Biochemistry 41, 12253–12262.
Raicu, V. (2007). Efficiency of resonance energy transfer in homo-oligomeric complexes of proteins. J. Biol. Phys. 33, 109–127.
Rao, M., and Mayor, S. (2005). Use of Förster’s resonance energy transfer microscopy to study lipid rafts. Biochim. Biophys. Acta 1746, 221–233.
Shaklai, N., Yguerabide, J., and Ranney, H. M. (1977). Interaction of hemoglobin with red blood cell membranes as shown by a fluorescent chromophore. Biochemistry 16, 5585–5592.
Sharma, P., Varma, R., Sarasij, R. C., Ira, Gousset, K., Krishnamoorthy, G., Rao, M., and Mayor, S. (2004). Nanoscale organization of multiple GPI-anchored proteins in living cell membranes. Cell 116, 577–589.
Silvius, J. R. (2003). Fluorescence energy transfer reveals microdomain formation at physiological temperatures in lipid mixtures modeling the outer leaflet of the plasma membrane. Biophys. J. 85, 1034–1045.
Snyder, B., and Freire, E. (1982). Fluorescence energy transfer in two dimensions. A numeric solution for random and non-random distributions. Biophys. J. 40, 137–148.
Steinberg, I. Z., and Katchalski, E. (1968). Theoretical analysis of the role of diffusion in chemical reactions, fluorescence quenching, and nonradiative energy transfer. J. Chem. Phys. 48, 2404–2410.
Stöckl, M. T., and Herrmann, A. (2010). Detection of lipid domains in model and cell membranes by fluorescence lifetime imaging microscopy. Biochim. Biophys. Acta 1798, 1444–1456.
Struck, D. K., Hoekstra, D., and Pagano, R. E. (1981). Use of resonance energy transfer to monitor membrane fusion. Biochemistry 20, 4093–4099.
Stryer, L. (1978). Fluorescence energy transfer as a spectroscopic ruler. Annu. Rev. Biochem. 47, 829–846.
Thomas, D. D., Carlsen, W. F., and Stryer, L. (1978). Fluorescence energy transfer in the rapid-diffusion limit. Proc. Natl. Acad. Sci. U.S.A. 75, 5746–5750.
Thomas, D. D., and Stryer, L. (1982). Transverse location of the retinal chromophore of rhodopsin in rod outer segment disc membranes. J. Mol. Biol. 154, 145–157.
Towles, K. B., Brown, A. C., Wrenn, S. P., and Dan, N. (2007). Effect of membrane microheterogeneity and domain size on fluorescence resonance energy transfer. Biophys. J. 93, 655–667.
Towles, K. B., and Dan, N. (2007). Determination of membrane domain size by fluorescence resonance energy transfer: effects of domain polydispersity and packing. Langmuir 23, 4737–4739.
Tramier, M., and Coppey-Moisan, M. (2008). Fluorescence anisotropy imaging microscopy for homo-FRET in living cells. Methods Cell Biol. 85, 395–414.
Valenzuela, C. F., Weign, P., Yguerabide, J., and Johnson, D. A. (1994). Transverse distance between the membrane and the agonist binding sites on the Torpedo acetylcholine receptor: a fluorescence study. Biophys. J. 66, 674–682.
van den Bogaart, G., Holt, M. G., Bunt, G., Riedel, D., Wouters, F. S., and Jahn, R. (2010). One SNARE complex is sufficient for membrane fusion. Nat. Struct. Mol. Biol. 17, 358–364.
Van Der Meer, B. W., Coker, G. III, and Chen, S.-Y. S. (1994). Resonance Energy Transfer: Theory and Data. New York: VCH.
Varma, R., and Mayor, S. (1998). GPI-anchored proteins are organized in submicron domains at the cell surface. Nature 394, 798–801.
Veatch, W., and Stryer, L. (1977). The dimeric nature of the gramicidin A transmembrane channel: conductance and fluorescence energy transfer studies of hybrid channels. J. Mol. Biol. 113, 89–102.
Von Arnim, C. A. F., Kinoshita, A., Peltan, I. D., Tangredi, M. M., Herl, L., Lee, B. M., Spoelgen, R., Hshieh, T. T., Ranganathan, S., Battey, F. D., Liu, C. X., Bacskai, B. J., Sever, S., Irizarry, M. C., Strickland, D. K., and Hyman, B. T. (2005). The low density lipoprotein receptor-related protein (LRP) is a novel beta-secretase (BACE1) substrate. J. Biol. Chem. 280, 17777–17785.
Wolber, P. K., and Hudson, B. S. (1979). An analytical solution to the Förster energy transfer problem in two dimensions. Biophys. J. 28, 197–210.
Yegneswaran, S., Wood, G. M., Esmon, C. T., and Johnson, A. E. (1997). Protein S alters the active site location of activated protein C above the membrane surface. A fluorescence resonance energy transfer study of topography. J. Biol. Chem. 272, 25013–25021.
Yeow, E. K. L., and Clayton, A. H. A. (2007). Enumeration of oligomerization states of membrane proteins in living cells by homo-FRET spectroscopy and microscopy: theory and application. Biophys. J. 92, 3098–3104.
Yguerabide, J. (1994). Theory for establishing proximity relations in biological membranes by excitation energy transfer measurements. Biophys. J. 66, 683–693.
Keywords: energy transfer, fluorescence, lipid bilayers, lipid–protein interaction, lipid rafts
Citation: Loura LMS and Prieto M (2011) FRET in membrane biophysics: an overview. Front. Physio. 2:82. doi: 10.3389/fphys.2011.00082
Received: 10 June 2011; Paper pending published: 09 July 2011;
Accepted: 26 October 2011; Published online: 15 November 2011.
Edited by:
M. M. Reddy, University of California, USAReviewed by:
Ignacio Gimenez, Aragon’s Health Sciences Institute, SpainSudipta Maiti, Tata Institute of Fundamental Research, India
Copyright: © 2011 Loura and Prieto. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence: Luís M. S. Loura, Faculdade de Farmácia, Universidade de Coimbra, Pólo das Ciências da Saúde, Azinhaga de Santa Comba, 3000-548 Coimbra, Portugal. e-mail:bGxvdXJhQGZmLnVjLnB0; Manuel Prieto, Centro de Química Física Molecular, Instituto Superior Técnico, Av. Rovisco Pais, 1049-001 Lisboa, Portugal. e-mail:bWFudWVsLnByaWV0b0Bpc3QudXRsLnB0


