A computational investigation of cardiac caveolae as a source of persistent sodium current

Recent studies of cholesterol-rich membrane microdomains, called caveolae, reveal that caveolae are reservoirs of “recruitable” sodium ion channels. Caveolar channels constitute a substantial and previously unrecognized source of sodium current in cardiac cells. In this paper we model for the first time caveolar sodium currents and their contributions to cardiac action potential morphology. We show that the β-agonist-induced opening of caveolae may have substantial impacts on peak overshoot, maximum upstroke velocity, and ultimately conduction velocity. Additionally, we show that prolonged action potentials and the formation of potentially arrhythmogenic afterdepolarizations, can arise if caveolae open intermittently throughout the action potential. Our simulations suggest that caveolar sodium current may constitute a route, which is independent of channelopathies, to delayed repolarization and the arrhythmias associated with such delays.

1. Introduction

Caveolae are small invaginations of the plasma membrane protruding into the cytosol of several cell types including cardiac myocytes. Typically, caveolae have a nearly spherical shape with a diameter of 50–100 nm or occur in clusters resembling a bunch of grapes (rosettes). Figure 1 shows an electron micrograph of a rat cardiac myocyte cross section with caveolae distributed densely around the subsarcolemma.

FIGURE 1

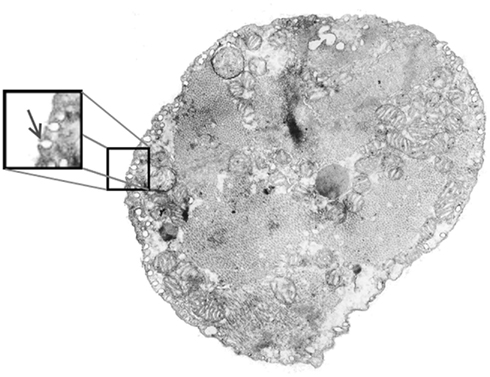
Figure 1. Electron micrograph of an adult rat ventricular myocyte showing caveolae (arrow in inset) around the perimeter. Caveolae are typically spherical in shape with a diameter of approximately 50–100 nm and can accumulate in a clustered structure around a common neck.

Recent investigations of caveolar function suggest that in addition to being a prominent structural feature on the cardiac subsarcolemma, caveolae also play a role in modulating sodium current via a direct, protein kinase-A (PKA)-independent signaling pathway. Studies reveal that the β-agonist isoproterenol, even in the presence of a PKA inhibitor, substantially increases whole-cell sodium current without changing single-channel dynamics (Lu et al., 1999; Yarbrough et al., 2002). Furthermore, it has been shown that this increase results from a direct interaction of the G_sα-subunit with caveolin-3, the primary scaffolding protein for cardiac caveolae, at a single G_sα amino acid (41histidine; Shibata et al., 2006; Palygin et al., 2008; Figure 2). Caveolae are therefore reservoirs of “recruitable” ion channels, and as such, constitute a substantial and previously unrecognized source of inward current that may significantly influence action potential morphology.

FIGURE 2

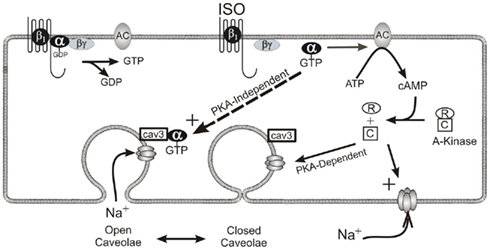
Figure 2. β-Adrenergic modulation of cardiac sodium current via two pathways. One pathway enlists PKA’s catalytic subunit to increase phosphorylation at the sodium channel thereby changing the kinetics of the channel itself. The second pathway involves a direct interaction between the α-subunit of the stimulatory G-protein and caveolin-3. This interaction results in the presentation of additional functioning sodium channels to the sarcolemma. It is important to note that this direct mechanism does not involve changes to ion channel kinetics.

While these studies provide insight into the role of G_sα and caveolin-3 in this process, the specific biophysics behind the presentation of caveolar sodium channels to the sarcolemma, remains unclear. It is well-established that caveolae are not merely static structural features of the cell membrane. One widely held view of caveolar function is that caveolae provide a clathrin-independent endocytic mechanism (Mineo and Anderson, 2001; Pelkmans and Helenius, 2002), so a kiss-and-run model of caveolar dynamics has been proposed (Pelkmans and Zerial, 2005) in which caveolae cycle between a transport vesicle state and a fused plasmalemmal invagination state. Indeed, such a mechanism is reported by Kozera et al. (2009) who show that incubation of the rat ventricular myocyte in a hypertonic solution results in significant (and reversible) increases in sarcolemmal surface density of caveolar necks, presumably from some intracellular store of caveolar vesicles.

However, there is also compelling evidence to suggest that caveolae instead constitute immobile membrane features, anchored to the subsarcolemma by the actin cytoskeleton (Thomsen et al., 2002; van Deurs et al., 2002). In this scenario, caveolar sodium channel recruitment might result from a change in conformation (from a closed to an open state) of caveolar necks already embedded in the sarcolemma. This is the mechanism hypothesized to underlie the recruitment of sodium channels via the PKA-independent β-adrenergic signaling pathway (Yarbrough et al., 2002; Shibata et al., 2006; Palygin et al., 2008). Since the specific biophysics involved in this recruitment of sodium channels are inconsequential to the formulation of our models, we have chosen, for the sake of brevity, to adopt the same terminology regarding open and closed caveolae in this study. Our goals are to model the effects that the recruitment of caveolar sodium channels may have on action potential morphology, not to model the signaling pathway through which this current is added or the specific biophysics involved.

This study investigates the effects of caveolar sodium currents on cardiac action potential in two different scenarios using computational means. We first examine the implications of simply increasing whole-cell sodium current in an existing mathematical model of cardiac action potential. This new model simulates and quantifies the effects of increasing sodium current in proportions that are reported (Lu et al., 1999; Yarbrough et al., 2002; Shibata et al., 2006; Palygin et al., 2008) to result from PKA-independent β-adrenergic modulation. Our results show little change in overall action potential morphology, except during the upstroke where upstroke velocity and peak overshoot are increased, suggesting that conduction velocity in the heart may be affected via this PKA-independent β-adrenergic pathway. Second, we examine an alternative scenario in which caveolar opening events occur throughout the course of an action potential. This scenario is simulated using a modification of the same existing model, but requiring a more sophisticated approach to channel gating to account for the intermittent isolation of caveolar sodium channels. These simulations reveal that differences in the timing of caveolar opening events can have profoundly different effects on cell repolarization and suggests a possible mechanism underpinning a late, persistent sodium current that is independent of channelopathies.

2. Materials and Methods

2.1. Model Development

In addition to evidence suggesting that caveolar sodium channels are electrically isolated from the extracellular environment in the absence of a β-agonist (Shibata et al., 2006), two other key experimental findings related to the electrophysiological role of caveolae inform the theoretical framework of our models. First, single-caveola patch clamp experiments suggest that most caveolae contain only a single sodium channel (unpublished data), so each closed caveola in our models sequesters exactly one sodium channel. Second, while it is known that caveolae contain other ion conductances (e.g., L-type calcium channels and a variety of K⁺ channels; Balijepallie et al., 2006), only sodium conductance has been definitively shown to change via the G_sα/caveolin-3 interaction. It is possible that there exist several subpopulations of caveolae containing different distributions of conductances and perhaps different caveolae subpopulations react differently to β-adrenergic stimulation, but since current research can only confirm that sodium channels are reversibly presented to the sarcolemma by caveolae, we include no other ion channels, pumps, or exchangers in these preliminary models. As more data emerge on the co-distribution of ion channels, exchangers, and pumps in the caveolar space, and on the mechanisms involved in ion current modulation by caveolae, these can be incorporated into our models.

Experimental data regarding the β-adrenergic response of caveolae come from rat cardiomyocytes, so we use the framework of an existing model of rat cardiac action potential developed by Pandit et al. (2001). The difference between our mathematical models and the Pandit et al. (2001) model is the addition of caveolar sodium currents. In the first model simulating the β-agonist-modulated increase in sodium current, this caveolar sodium current is reflected by a simple increase in maximum sodium conductance since the single-channel kinetics of caveolar Na_v1.5 channels are identical to those on the sarcolemma when the caveolae are open. All other parameter values in the Pandit et al. (2001) endocardial model are left unchanged.

In the second model simulating the opening of caveolae throughout the action potential, the caveolar sodium current behaves in a fundamentally different manner because the caveolae are presenting closed sodium channels to a depolarized sarcolemma over the duration of the action potential. The use of a more sophisticated activation mechanism than the standard Hodgkin and Huxley (1952) formalism is needed to account for this delayed presentation of sodium sources, but all parameter values in the Pandit et al. (2001) endocardial model are left unchanged. In this preliminary attempt to model such caveolar opening events, we implement the simplest opening dynamics possible – random openings throughout the action potential. Other dynamics that lead to the opening of caveolae throughout the action potential will give qualitatively similar results. The remainder of this section relates to the formulation of this more sophisticated stochastic model and the ways in which both models are implemented.

2.1.1. Behavior of a single caveola

A closed caveolae is electrically isolated from changes occurring on the sarcolemma, so the membrane of a closed caveola will remain fixed at the membrane potential experienced on the sarcolemma at the time of its closing. Thus, a caveola closing while the cell is at rest will sequester a sodium channel that remains in its closed state as long as the caveola remains closed. Likewise, the closure of a caveola while the membrane is depolarized (and its sequestered sodium channel inactive), will prevent the sequestered sodium channel from returning to its closed state. Therefore, if a caveola is open upon the arrival of a depolarizing stimulus, the sodium channel it contains will respond like any other sodium channel on the sarcolemma, but if the caveola is closed upon the arrival of the stimulus, the channels they sequester will remain closed and non-conducting.

It is only if such a caveola opens later in the action potential, when the sarcolemma is still sufficiently depolarized, that its sodium channel will open, conduct, and inactivate. Furthermore, no subsequent closing and reopening of these caveola prior to the repolarization of the myocyte will activate these channels since they will not yet have recovered from inactivation. This means that the first post-stimulus opening of any caveola which was closed at stimulus, activates a brief single-channel sodium current if the opening event occurs while the sarcolemma is still depolarized. For this reason, the collective contribution of caveolar sodium current to action potential morphology is highly dependent upon the timing of the individual caveolar openings throughout the action potential.

While the gating mechanisms of caveolar sodium channels are identical to those of the sarcolemmal sodium channels, caveolar sodium gates do not react to changes in membrane potential until they are presented to the sarcolemma via caveolar opening. Modeling such gating variable dependence upon both the time since stimulus and the time since caveolar opening requires the use of a partial differential equation (PDE) extension of the Hodgkin and Huxley (1952) formalism.

2.1.2. Caveolar first opening probability density

Random openings of caveolae throughout the action potential would imply that the first opening events of caveolae will occur according to a Poisson process, so the probability density function of first openings of caveolae is given by

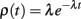
where the Poisson rate parameter, λ, represents the expected number of openings per unit time. Subsequent openings need not be considered since these openings would present the sarcolemma with inactive sodium channels. The area under the curve ρ(t) between [t, t + Δt] is the probability that a given caveola opens for the first time between t and t + Δt units of time after the stimulus. For a large number, n, of caveolae

provides a good approximation of the number of caveolae which experience a first opening in the interval [t, t + Δt] provided Δt is sufficiently small.

The Pandit et al. (2001) model assumes a whole-cell sodium conductance of 1.064 μS in myocytes with whole-cell capacitance of 100 pF and under normal physiological conditions single-channel sodium conductance is approximately 18 pS (Aidley, 1998), so the quotient (1064000/18) ≈ 59,000 provides an estimate of the number of sodium channels on the sarcolemma of a model cell. According to the literature (Lu et al., 1999; Yarbrough et al., 2002; Shibata et al., 2006; Palygin et al., 2008), sodium current increases by 25–40% via the PKA-independent β-adrenergic signaling pathway, corresponding to the addition of between 14,750 and 23,600 caveolar sodium channels, so our simulations are conducted with values of n between 14,000 and 25,000.

Other studies of cardiomyocyte ultrastructure and caveolar function have reported densities of 4 (Gabella, 1978) and 6 (Levin and Page, 1980) caveolar necks per μm². Assuming a membrane capacitance of 1 μF/cm² these estimates suggest 40,000 and 60,000 caveolae per cell, respectively, in a 100-pF cell. Since the experimentally observed increases in sodium current are inconsistent with such high numbers of sodium channel-containing caveolae, though, we adhere to our more conservative estimates which are still large enough to ensure the validity of the approximation given by (1) and validity of this continuum density approach. A larger number of caveolae would not qualitatively change the results of our modeling but would possibly make them even more substantial.

2.1.3. Channel gating in stochastic caveolae

With such large numbers of caveolae, the kinetics of caveolar sodium channels may be treated in a deterministic manner using a PDE extension of the Hodgkin and Huxley (1952) formalism. Caveolar necks act as mechanisms which, when closed, not only prevent the flow of ions, but also prevent the ion channel gates from reacting to changes in membrane potential on the sarcolemma. A model of stochastic caveolar current must not only account for how many caveolae are open at a given time, but must also account for the history of each open caveolae.

The dependence of the channel gate dynamics on the caveolar opening dynamics forces the gating variables to be functions of not only the time since the depolarizing stimulus, but also the time of caveolar first opening. So, if we let t represent time since the stimulus and τ represent time of a given caveola’s first opening, our gating variables each satisfy boundary value problems of the form

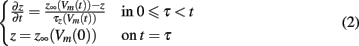
where z ∈ {m, h, j} and V_m(t) is the potential across the sarcolemma at time t.

Note that we include a second slow inactivation gate, j(t, τ), in addition to standard h-gate. This slow inactivation gate was first proposed by Haas et al. (1971) to account for incongruities that were observed between the time scales of inactivation and recovery from inactivation among sodium channels in frog cardiomyocytes. They concluded that a single inactivation variable was insufficient and that a second slower inactivation mechanism was needed to accurately model the kinetics of sodium channel recovery from inactivation. This amendment to the standard Hodgkin-Huxley kinetics (Hodgkin and Huxley, 1952) was subsequently adopted by Beeler and Reuter (1977), Luo and Rudy (1991), and Pandit et al. (2001), the developers of the model we adapt in this investigation.

To understand the meaning of m, h, and j in the context of the stochastic caveolae model, consider the set of caveolae which open at time τ. The product m³(t, τ)h(t, τ)j(t, τ) represents the proportion of sodium channels contained in this set which are permeable to sodium ions at time t. Since there are approximately nρ(τ)Δτ caveolae which open at time τ, then at time t the amount of sodium current due to caveolae which opened at time τ < t, is

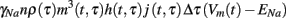
where γ_Na represents sodium single-channel conductance. The total caveolar sodium current at time t is then the sum of all the sodium currents due to all caveolae which have opened since the stimulus (at t = 0). This sum can be written succinctly in the following integral form.

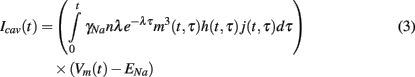
This additional caveolar current along with the three partial differential equations of the form (2) governing the gating variables are incorporated into the existing Pandit et al. (2001) model to create our stochastic caveolae model.

2.2. Computational Implementation and Simulations

We implement our models in MATLAB version 7.0.1.15 (The MathWorks Inc., Natick, MA, USA). The differential equations in the first model simulating the simple β-agonist-modulated increase in sodium current were solved numerically using the built-in MATLAB solver ode23s. The differential equations in the stochastic model were solved numerically using a fourth-order Runge-Kutta routine with a time step of 1 μs that was written by the authors. Descriptions of the simulated action potential and simulated voltage clamp protocols are as follows.

2.2.1. Action potential protocol

The simulated action potential generated by the unmodified Pandit et al. (2001) model is used as a baseline and we compare its morphology to the morphology of an action potential generated by simply increasing the maximum sodium conductance from its baseline value of 1.046–1.489 pS, an increase of whole-cell conductance corresponding to the addition of 25,000 caveolar sodium channels to the sarcolemma. To elicit action potentials, we use the same protocol as was employed by Pandit et al. (2001) in which an inward depolarizing stimulus, I_stim, has the form of a rectangular pulse with an amplitude of 0.6 nA and a duration of 5 ms. Initial conditions were chosen to be consistent with the cell’s resting state and a stimulus is applied at t = 25 ms. In the absence of any external stimuli, the membrane potential tends toward a steady-state value of approximately −81.3 mV, so the initial conditions are the steady-state values associated with this membrane potential.

To investigate the effects of random caveolar openings on action potential morphology, we simulate action potentials using the stochastic caveolae model with no change made to maximum sodium conductance of 1.046 pS. Action potentials are elicited by simulating the instantaneous depolarization of the resting cell membrane to a superthreshold level (from −81.3 to −50 mV). These action potentials are generated using a wide range of λ-value and n-value combinations. We report our results for select λn-pairs in the following section. Note that a λ-value of 0 produces the same action potential as the unmodified Pandit et al. (2001) model.

2.2.2. Voltage clamp protocol

A simulated voltage clamp protocol is used in conjunction with the stochastic caveolae model with λ = 15 to examine the effects of randomly opening caveolae on whole-cell sodium current. The cell membrane is first conditioned at a holding potential of −140 mV until equilibrium is reached. The membrane potential is then stepped up to a sustained test potential of −20 mV and the time course of the resulting whole-cell sodium current (sarcolemmal and caveolar sodium currents combined) is plotted. This protocol was run with no caveolae, 14,000 caveolae, and 24,000 caveolae, and the graphs of each sodium current time course compared.

Since the voltage is fixed during a voltage clamp experiment, every caveolar sodium channel experiences identical conditions upon their presentation to the sarcolemma, so the shape of the time courses of the m-, h-, and j-gates for every caveolar sodium channel are identical, but out of phase depending upon the time at which the caveolae opens. This substantially simplifies our caveolar sodium current formulation, I_cav. For given conditioning and test potentials, V_cond and V_test respectively, we need only calculate the solutions m(t), h(t), and j(t) to initial value problems of the form

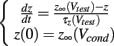
where z ∈ {m, h, j}, which can be done analytically, and substitute these solutions into our formulation of the caveolar sodium current. These solutions are simply:

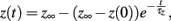
where z ∈ {m, h, j}.

Then since m, h, and j are explicitly defined functions of time, the caveolar sodium current in these voltage clamp experiments, denoted I_{vc, cav}, reduces to the convolution integral

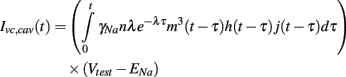
3. Results

3.1. Action Potential Simulations

3.1.1. Effects of increased sodium conductance

Comparisons of the simulated action potentials generated by the unmodified Pandit et al. (2001) model and those generated with an increase in maximum sodium conduction corresponding to the opening of 25,000 caveolae show that the inclusion of caveolar sodium currents leads to changes in action potential morphology in the upstroke phase (Figure 3).

FIGURE 3

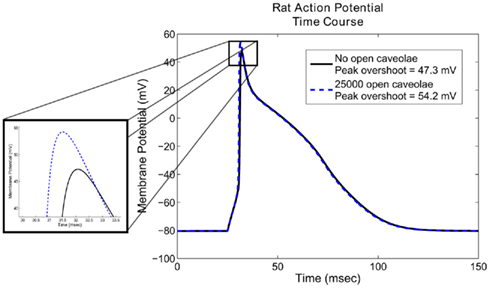
Figure 3. Action potential morphology using the Pandit et al. (2001) model with and without caveolar sodium current. Notice that the inclusion of 25,000 open caveolae results in an approximately 5.4% increase in peak overshoot of the action potential. Less evident from the graph is a 29% increase in maximum upstroke velocity, an important factor in determining the speed of the excitatory wave through the cardiac tissue. Action potential duration, is relatively unaffected by the additional sodium conductance introduced by the open caveolae.

The most noticeable effect of caveolar sodium current is an increase in peak voltage from approximately 47.3–54.2 mV, and increase of approximately 5.4% in overall height of the action potential. Less apparent from the graph are its effects on the maximum upstroke velocity. These simulations indicate that the opening of 25,000 caveolae results in an increase of 55 mV/ms in maximum upstroke velocity, an increase of approximately 29%. Aside from these differences, the overall action potential morphology is changed very little by the inclusion of a caveolar sodium current. Changes in maximum upstroke velocity, however, are known to have significant effects on conduction velocity of the excitatory wave in cardiac tissue (Walton and Fozzard, 1983), so future studies on the role of β-agonists in caveolar sodium current modulation may also reveal a conduction velocity-modulating role.

3.1.2. Effects of random caveolar openings

Comparisons of the simulated action potentials generated with the stochastic caveolae model indicate that the action potential morphology shows strong dependence on both λ and n. In each of the cases shown, the inclusion of sodium current from stochastic caveolae results in a substantial delay in myocyte repolarization, and in some cases, reactivation of the calcium current leading to an early afterdepolarization (EAD; Figure 4).

FIGURE 4

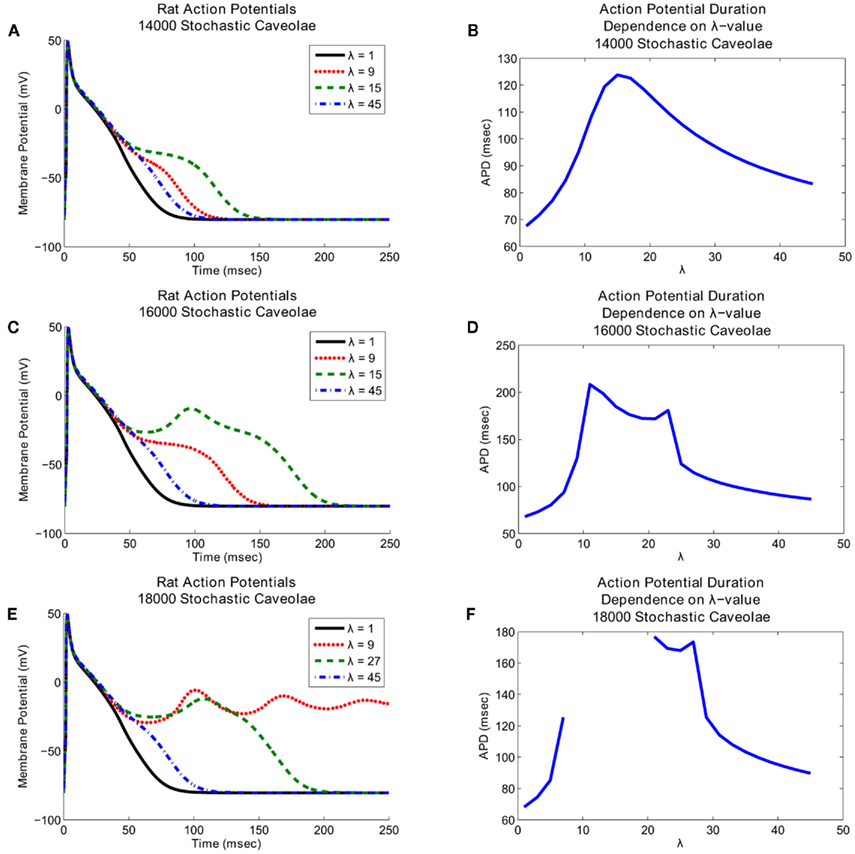
Figure 4. Effects of stochasticity in caveolar openings on action potential morphology and afterdepolarization formation. Action potential time courses are shown over a range of λ-values (left panels), where lambda represents the number of caveolar openings per second. Action potential repolarization (right panels) becomes increasingly delayed as the frequency of caveolar openings increases. Interestingly, increasing caveolar density results in fundamentally different dynamics. (A) Graphs of the action potential morphologies with 14000 caveolae for a range of λ-values and (B) the associated action potential duration dependence on λ show that substantial delays in repolarization occur for λ-values chosen near 15, but no early afterdepolarizations. (C) Early afterdepolarizations do occur for small range of λ-values when the number of caveolae is increased to 16000 and (D) even more substantial delays in repolarization result. (E) If the number of caveolae is increased still further to 18000, then early afterdepolarizations occur for certain values of λ. Furthermore, a range of λ-values exists for which the delays in repolarization last long enough for the system to settle into a new equilibrium near a membrane potential of approximately −5 mV. (F) This complete elimination of the repolarization phase shows up as a discontinuity between λ ≈ 7 and λ ≈ 21 in the graph of action potential duration dependence on λ-value.

Notice that in all three cases shown in Figure 4 relatively small and relatively large λ-values both correspond to relatively small delays in repolarization whereas intermediate λ-values correspond to much more substantial delays in repolarization. The key difference between the three cases illustrated in Figure 4 is that at these intermediate λ-values, increases in the number of caveolae result in fundamental changes in the nature of the repolarization delays. With 14000 caveolae, we see an elongation of the action potential due entirely to the inward caveolar sodium current which persists late in the action potential, but for all values of λ, the action potential time course is monotone decreasing after peak overshoot. If the number of caveolae is increased to 16000, then for a range of λ-values near λ = 15, a secondary spike (an EAD) in membrane potential interrupts the repolarization phase. In Figure 5 we see that this secondary spike is caused by a reactivation of the calcium current which is consistent with the EAD mechanisms identified experimentally (January and Riddle, 1989; Zeng and Rudy, 1995). If we increase the number of caveolae still further to 18000, then we not only see EADs for certain values of λ, but for a range of λ-values between approximately 7 and 21 a train of EADs serves to extinguish repolarization entirely and the system tends toward a new steady-state at a substantially depolarized membrane potential.

FIGURE 5

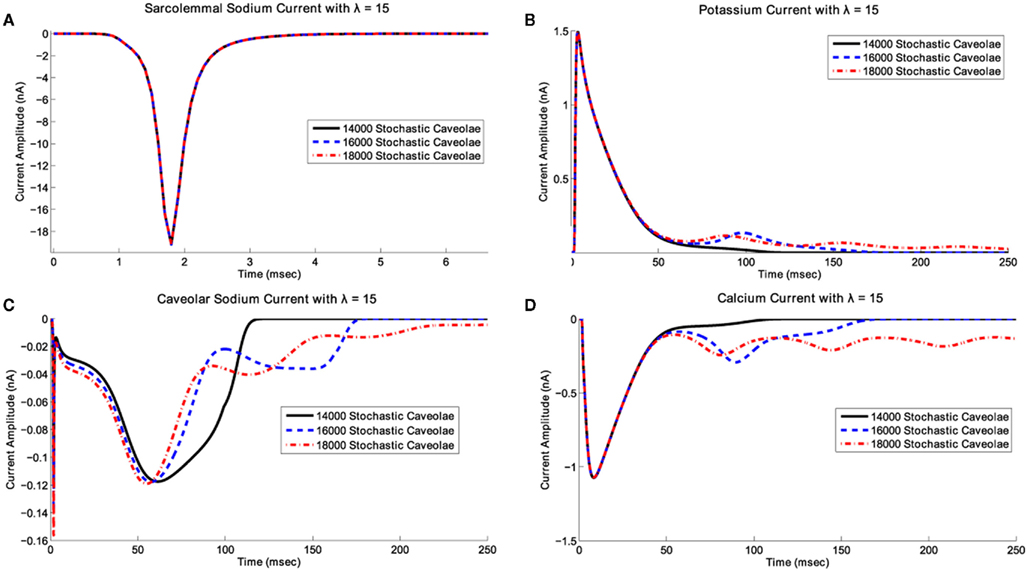
Figure 5. Effects of caveolar density variation on ionic current time courses for λ fixed. In this scenario, we have fixed λ at 15 and have superimposed plots of (A) the transient sodium current, I_Na, (B) the potassium current, I_t, (C) the caveolar sodium current, I_cav, and (D) the L-type calcium current, I_CaL, associated with 14000, 16000, and 18000 stochastic caveolae. When 16000 and 18000 caveolae are included, calcium reactivation occurs leading to a single early afterdepolarization with 16000 caveolae and a series of afterdepolarizations with 18000 caveolae. In the case of 18000 caveolae, repolarization is delayed long enough for the slower variables to enter the basin of attraction for a new fixed point and the system settles into a new equilibrium state which may not have any physiological relevance.

3.2. Voltage Clamp Simulations

Comparisons of simulated voltage clamp-induced whole-cell sodium currents produces a persistent sodium current similar to those seen experimentally in cases of incomplete sodium channel inactivation (Figure 6). The solid curve represents the transient sodium current through Na_v1.5 sodium channels on the sarcolemma while the dashed and dotted curves represent the total sodium current (the sum of this sarcolemmal and caveolar sodium currents) with n = 14000 and n = 24000, respectively, in the stochastic caveolae model. Importantly, this persistent current occurs in the absence of any simulated channelopathy and is the consequence of caveolar stochasticity alone.

FIGURE 6

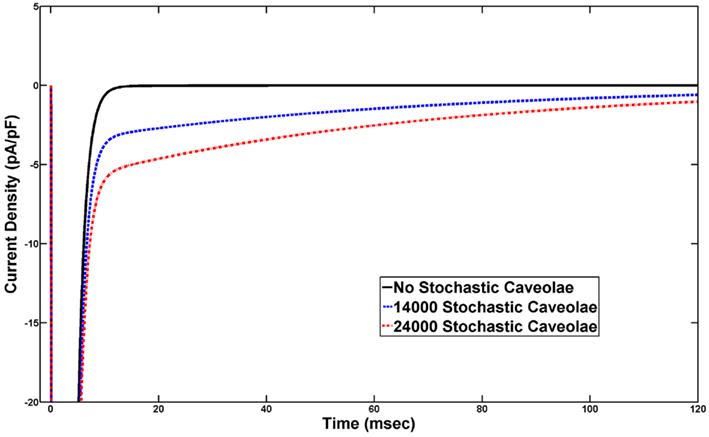
Figure 6. Voltage clamp eliciting a late, persistent sodium current. Sustained depolarization to −20 mV from a conditioning voltage of −140 mV, activates current from sodium channels on the sarcolemma and from sodium channels in any caveolae which open during this sustained depolarization. Under normal conditions in which no caveolae open we see the rapid and complete inactivation of sodium current following the step up to −20 mV. However, if caveolae stochastically open throughout the simulated voltage clamp experiment, a sodium current carried by channels in these caveolae persists at non-trivial levels long past inactivation of the sarcolemmal sodium current. These plots were generated using λ = 15 and the persistent sodium currents associated with 14000 caveolae and 24000 caveolae are shown.

4. Discussion

4.1. Caveolar Sodium Current Effects on Action Potential Morphology

The results of our simulations show that the direct, PKA-independent β-agonist-induced increases in sodium current that have been observed in the context of voltage clamp experiments may have non-trivial effects on the cardiac action potential morphology, particularly on action potential upstroke. The inclusion of caveolar sodium currents lead to increases in peak voltage overshoot and maximum upstroke velocity compared with baseline simulation data. A study conducted by Walton and Fozzard (1983) found a conduction speed dependence upon maximum upstroke velocity, so our results suggest a PKA-independent β-adrenergic role in regulating conduction in cardiac tissue. The authors reported that the normalized conduction velocity is directly related to the square root of the normalized maximum upstroke velocity. Given this relationship, our results indicate that the caveolar-associated PKA-independent β-adrenergic pathway alone can be expected to increase conduction velocity by up to approximately 13.5%.

4.2. Caveolar Stochasticity as an Arrhythmogenic Mechanism

We have shown that substantial delays in repolarization and early afterdepolarizations, can result for a variety of Poisson rate constants and caveolar densities in our stochastic caveolae model. Additionally, voltage clamp simulations demonstrate that stochastic opening of a cardiomyocyte’s caveolae can produce a late, persistent sodium current similar to those usually seen in cases of channelopathies linked to incomplete sodium inactivation. Importantly, our models do not include any changes in sodium single-channel kinetics.

Such delays in repolarization and early afterdepolarizations are the electrophysiological hallmarks of a form of congenital arrhythmia syndrome known as Long-QT Syndrome (LQTS), characterized by prolonged QT interval on the electrocardiogram and increased risk for sudden death. Interestingly, not only has caveolin-3 been shown to be critically involved in the opening of caveolae (Shibata et al., 2006; Palygin et al., 2008), but mutations in CAV3, the gene which encodes for caveolin-3, are known to be associated with a type of LQTS deemed LQT9 (Vatta et al., 2006). Vatta et al. (2006) show that human ventricular myocytes, like those of rat, also exhibit colocalization of caveolin-3 and Na_v1.5 sodium channels to caveolae. They report that expression of certain types of mutant caveolin-3 correlates with the incidence of LQT3-like symptoms in patients and the presence of a late, persistent Na_v1.5 current in cells expressing these mutant proteins.

Vatta et al. (2006) hypothesize that a mutant caveolin-3/Na_v1.5 interaction induces a gain-of-function channelopathy which results in the observed persistent sodium current and related incidence of LQT9. Our findings suggest a possible alternative hypothesis. Since a direct caveolin-3/G_sα interaction is known to result in the presentation of caveolar sodium channels to the sarcolemma, it is reasonable to believe that mutant caveolin-3 might give rise to pathological caveolar opening dynamics. If the mutations in CAV3 identified by Vatta et al. (2006) were to induce stochastic opening of caveolae, then this investigation suggests that similar persistent sodium currents could arise without any gain-of-function channelopathy. In fact, with λ = 15 and n-values in the range we tested, the simulated persistent sodium currents we generate (Figure 6) are in good agreement with the experimental results of Vatta et al. (2006) which showed that a several CAV3 mutations result in persistent sodium currents of 2–4 pA/pF under the same voltage clamp protocol. Future studies are required to determine whether specific mutations (e.g., G56S) alter caveolin-3/G_sα interactions thereby altering caveolae opening kinetics, but our results support this novel hypothesis that abnormal caveolar dynamics may provide a link between mutant caveolin-3 and persistent sodium current in LQT9.

4.3. Limitations

Since the caveolar first opening probability density function decays asymptotically to zero as a function of time, so also does the caveolar sodium current in our voltage clamp simulation. Therefore, we are unable to simulate a truly persistent sodium current, but in the short term (50–100 ms after sarcolemmal sodium channels have completely inactivated) our results are still in close agreement with the those generated by Vatta et al. (2006). One explanation for the lack of ultimate current decay in experimental results is that there may exist a mechanism by which some caveolar membranes can return to near resting potentials thereby allowing the sodium channels they contain to recover from inactivation. Subsequent opening of such caveolae would allow for the reopening of their sodium channels and an additional inward sodium current. Further computational and experimental studies are necessary to determine if a caveolar mechanism may exist that could give rise to an indefinitely persistent current.

Additionally, the inclusion of only sodium conductance in the caveolar domains is a known limitation of our models. Since only increases in sodium due to the opening of caveolae have thus far been measured experimentally, we have limited the scope of this preliminary work to the effects of caveolar sodium current alone. However, future models will include other caveolar ion conductances and will examine the differences in action potential morphology that result.

Lastly, due to its detail and reliability at simulating rat cardiac action potentials, the Pandit et al. (2001) model was a logical choice to be used in this investigation. However, this choice limited the cell types that we could simulate. Future studies may make consider multiple cell types, may make use of models of human cardiac action potential, and may model the propagation of the excitatory wave through coupled cells using a one-dimensional cable model.

Implications

This investigation suggests that a previously unrecognized biophysical mechanism may underlie certain types of Long-QT Syndrome, one that is based on pathological caveolar kinetics rather than pathological channel kinetics. Given these findings, and the results of previous experimental studies of caveolar function, we believe caveolae play a substantial, but largely unrecognized, role in cardiac electrophysiology and arrhythmogenesis. New experiments investigating this role are needed if we are to generate a more detailed understanding of both cardiac β-adrenergic response and possible caveolae-related arrhythmogenic mechanisms.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work was partially supported by NSF DMS grant 1022466 to Colleen C. Mitchell, by the NHLBI grant HL075541 to Erwin F. Shibata, and by the University of Iowa Department of Mathematics NSF VIGRE grant DAMS-0602242 which supported Ian M. Besse.

References

Aidley, D. J. (1998). The Physiology of Excitable Cells, 4th Edn. Cambridge: Cambridge University Press.

Balijepallie, R., Foell, J., Hall, D., Hell, J., and Kamp, T. (2006). Localization of cardiac l-type Ca2+ channels to a caveolar macromolecular signaling complex is required for b2-adrenergic regulation. Proc. Natl. Acad. Sci. U.S.A. 103, 7500–7505.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Beeler, G. W., and Reuter, H. (1977). Reconstruction of the action potential of ventricular myocardial fibres. J. Physiol. 268, 177–210.

Pubmed Abstract | Pubmed Full Text

Gabella, G. (1978). Inpocketings of the cell membrane (caveolae) in rat myocardium. J. Ultrastruct. Res. 65, 135–147.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Haas, H., Kern, R., Einwachter, H., and Tarr, M. (1971). Kinetics of na inactivation in frog atria. Pflugers Arch. 323, 141–157.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hodgkin, A., and Huxley, A. (1952). A quantitative description of membrane currents and its application to conduction and excitation in nerve. J. Physiol. 117, 500–544.

Pubmed Abstract | Pubmed Full Text

January, C. T., and Riddle, J. M. (1989). Early afterdepolarizations: mechanism of induction and block. a role for l-type Ca2⁺ current. Circ. Res. 64, 977–990.

Pubmed Abstract | Pubmed Full Text

Kozera, L., White, E., and Calaghan, S. (2009). Caveolae act as membrane reserves which limit mechanosensitive i_{Cl; swell} channel activation during swelling in the rat ventricular myocyte. PLoS ONE 4, e8312. doi:10.1371/journal.pone.0008312

CrossRef Full Text

Levin, K., and Page, E. (1980). Quantitative studies on plasmalemmal folds and caveolae of rabbit ventricular myocardial cells. Circ. Res. 46, 244–255.

Pubmed Abstract | Pubmed Full Text

Lu, T., Lee, H.-C., Kabat, J., and Shibata, E. (1999). Modulation of rat cardiac sodium channel by the stimulatory g protein alpha subunit. J. Physiol. 518, 371–384.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Luo, C., and Rudy, Y. (1991). A model of the ventricular cardiac action potential. Depolarization, repolarization, and their interaction. Circ. Res. 68, 1501–1526.

Pubmed Abstract | Pubmed Full Text

Mineo, C., and Anderson, R. G. (2001). Potocytosis. Histochem. Cell Biol. 116, 109–118.

Pubmed Abstract | Pubmed Full Text

Palygin, O. A., Pettus, J. M., and Shibata, E. F. (2008). Regulation of caveolar cardiac sodium current by a single gsα histidine residue. Am. J. Physiol. Heart Circ. Physiol. 294, H1693–H1699.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Pandit, S., Clark, R., Giles, W., and Demir, S. (2001). A mathematical model of action potential heterogeneity in adult rat left ventricular myocytes. Biophys. J. 81, 3029–3051.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Pelkmans, L., and Helenius, A. (2002). Endocytocis via caveolae. Traffic 3, 311–320.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Pelkmans, L., and Zerial, M. (2005). Kinase-regulated quantal assemblies and kiss-and-run recycling of caveolae. Nature 436, 128–133.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Shibata, E., Brown, T., Washburn, Z., Bai, J., Revak, T., and Butters, C. (2006). Autonomic regulation of voltage-gated cardiac ion channels. J. Cardiovasc. Electrophysiol. 17(Suppl. 1), S34–S42.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Thomsen, P., Roepstorff, K., Stahlut, M., and van Deurs, B. (2002). Caveolae are highly immobile plasma membrane microdomains, which are not involved in constitutive endocytic trafficking. Mol. Biol. Cell 13, 238–250.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

van Deurs, B., Roepstorff, K., Hommelgaard, A., and Sandvig, K. (2002). Caveolae: anchored, multifunctional platforms in the lipid ocean. Trends Cell Biol. 13, 92–100.

CrossRef Full Text

Vatta, M., Ackerman, M., Ye, B., Maliekski, J., Ughanze, E., Taylor, E., Tester, D., Balijepalli, R., Foell, J., Li, Z., Kamp, T., and Towbin, J. (2006). Mutant caveolin-3 induces persistent late sodium current and is associated with long-qt syndrome. Circulation 114, 2104–2112.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Walton, M. K., and Fozzard, H. A. (1983). The conducted action potential: models and comparison to experiments. Biophys. J. 44, 9–26.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Yarbrough, T., Lu, T., Lee, H.-C., and Shibata, E. (2002). Localization of cardiac sodium channels in caveolin-rich membrane domains: regulation of sodium current amplitude. Circ. Res. 90, 443–449.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Zeng, J., and Rudy, Y. (1995). Early afterdepolarizations in cardiac myocytes: mechanism and rate dependence. Biophys. J. 68, 949–964.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text