- Department of Physics, Northeastern University, Boston, MA, USA
Human social networks evolve on the fast timescale of face-to-face interactions and of interactions mediated by technology such as a telephone calls or video conferences. The resulting networks have a strong dynamical component that changes significantly the properties of dynamical processes. In this paper we study a general model of pairwise human social interaction intended to model both face-to-face interactions and mobile-phone communication. We study the distribution of durations of social interactions in within the model. This distribution in one limit is a power-law, for other values of the parameters of the model this distribution is given by a Weibull function. Therefore the model can be used to model both face-to-face interactions data, where the distribution of duration has been shown to be fat-tailed, and mobile-phone communication data where the distribution of duration is given by a Weibull distribution. The highly adaptable social interaction model propose in this paper has a very simple algorithmic implementation and can be used to simulate dynamical processes occurring in dynamical social interaction networks.
Introduction
In the last 10 years the network theory (Dorogovtsev and Mendes, 2003; Newman, 2003; Boccaletti et al., 2006; Caldarelli, 2007; Barrat et al., 2008) has become the fundamental theory for studying complex systems. Indeed complex networks describe a large variety of technological, biological, and social complex systems. While great attention has been addressed to static networks and the dynamical processes occurring on them, less attention has been paid to dynamical networks and in particular to dynamical social networks.
Social networks (Granovetter, 1973; Wasserman and Faust, 1994) have a very relevant community structure (Palla et al., 2007; Bianconi et al., 2009; Ahn et al., 2010) and are adaptive and extremely dynamical. In the last years several papers have proposed adaptive models of social behavior showing phase transitions in different universality classes (Davidsen et al., 2002; Marsili et al., 2004; Holme and Newman, 2006; Vazquez et al., 2008). In these models social ties are dynamically rewired in a framework of stochastic models. Social ties have in addition to that, a microscopic structure constituted by fast social interactions of the duration of a phone call or of a face-to-face interaction. Dynamical social networks characterize the social interaction at this fast timescale. Recently new network measures are started to be defined for these dynamical networks (Tang et al., 2010) and recent works focus on the implication that the network dynamics has on percolation, epidemic spreading, and opinion dynamics (Holme, 2005; Vázquez et al., 2007; Parshani et al., 2010; Isella et al., 2011; Karsai et al., 2011).
Recently, thanks to the availability of new extensive data on a wide variety of human dynamics (Barabási, 2005; Eagle and Pentland, 2006; Malmgren et al., 2008, 2009; Rybski et al., 2009), human mobility (Brockmann et al., 2006; González et al., 2008; Song et al., 2010), and dynamical social networks (Onnela et al., 2007), it has been recognized that many human activities (Vázquez et al., 2007) are not Poissonian (West et al., 2008). New data on social dynamical networks start to be collected with new technologies such as of Radio Frequency Identification Devices (Cattuto et al., 2010; Isella et al., 2011) and Bluetooth (Eagle and Pentland, 2006). These technologies are able to record the duration of social interactions and report evidence for a bursty nature of social interaction characterized by a fat tail distribution of the duration of face-to-face interactions. This bursty behavior of social networks (Hui et al., 2005; Scherrer et al., 2008; Cattuto et al., 2010; Stehlé et al., 2010; Isella et al., 2011; Zhao et al., 2011) is coexisting with modulations coming from periodic daily (circadian rhythms) or weakly patterns (Jo et al., 2011). Recently new evidence coming from the analysis of mobile-phone communication (K. Zhao, M. Karsai, and Bianconi, in preparation) shows that the duration of mobile-phone interactions is also not Poissonian but has a finite second moment and is described by a Weibull distribution.
Therefore there is a necessity to generate an efficient dynamical model that has the flexibility to account both for scale-free distribution of duration of interactions, as found in face-to-face interactions, and stretched exponential (Weibull distributed) duration of interaction as found in the data of mobile-phone communication.
The fact that the bursty behavior is observed also in social interaction of simple animals (leeches; G. Bisson, G., Bianconi, and V. Torre, in preparation), in the motion of rodents (Anteneodo and Chialvo, 2009), or in the use of words (Altmann et al., 2009), suggests that the underlying origin of this behavior is dictated by the biological and neurological processes underlying the dynamics of the social interaction.
In this paper we use a model with dynamical reinforcement to model the nature of social interaction. Disregarding for the moment the effects of circadian rhythms and weakly patterns, we assume that the decision of the agents to form or leave a group are driven by memory effects dictated by reinforcement dynamics, that can be summarized in the following statements: (i) the longer an agent is interacting in a group the smaller is the probability that he/she will leave the group; (ii) the longer an agent is isolated the smaller is the probability that he/she will form a new group. The biological origin of this principle (which has clear similarity with the Hebbian reinforcement mechanism) will be investigated in future works where it will be studied in the framework of the neuroscience of social interactions in simple animals.
In this paper we show that depending on the nature of the memory kernel used to implement this dynamics the distribution of duration of interaction changes from Weibull distributions to scale-free distributions. This indicates that human social interactions might be determined by an effective use of different memory kernel depending on the different nature of social interactions (e.g., Face-to-face interactions or mobile-phone communication).
The Proposed Model of Human Social Interactions
We consider a system consisting of N agents representing interacting agents. The agents are interacting in a social network G representing social ties such as friendships, collaborations, or acquaintances. The network G is weighted with the weights indicating the strength of the social ties between agents. To model the mechanism of human social interaction the agents can call their neighbors in the social network G forming groups of interacting agents. Since at any given time an interaction can be initiated or terminated the network is highly dynamical. For the general model defined above, we use ni(t) ∈ N to denote the number of agents in the group of agent i at time t. In this paper, we focus on a simple case with ni ≤ 2, such that only pairwise interactions are allowed in the system, or in other words, the agents can only interact with one partner at a time. Indeed, pairwise interaction is the most typical social interaction existing in reality, e.g., phone-call communication or point-to-point on-line connection. Specifically ni = 1 refers to the status of a non-interacting agent i while ni = 2 refers to the status of an interacting agent. Here we give an explicit algorithm for the model of pairwise interaction:
(1) An agent i is selected randomly at time t (initially t = 0).
(2) Agent i has two possible subsequent actions:
• If ni(t) = 1, he/she will start an interaction with probability f1(ti, t) where ti refers to the last time at which agent i has changed his/her state. Once the interaction is initiated, a partner j will be chosen from one of his/her non-interacting neighbors of G with probability proportional to Π(tj, t), and consequently ni → 2 and nj → 2.
• If ni(t) = 2, he/she will terminate his/her current interaction with probability f2(ti, t | wij) where wij is the weight of the link between i and the neighbor j that is interacting with i, and consequently ni → 1 and nj → 1.
(3) Time t is updated as t → t + 1/N and the process is iterated until t = Tmax.
One should note that, the corporation of ti in the probability functions f1, Π and f2, indeed, reflects the memory effect of agents that their current behavior is depending on the history of their previous behavior. For simplicity, we also assume f1 = Π in this paper, which means the probability of starting an interaction is identical to the probability of replying to an interaction.
Mean-Field Solution to the Model
The model of pairwise interaction can be solved analytically if we assume G is an uncorrelated and annealed network. The assumption means, at each time step, the links of G are rewired randomly while the degree distribution p(k) and the weight distribution p(w) are remained constant. We denote by 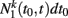 the number of non-interacting agents with degree k at time t that have not interacted with another agent since time t′ ∈ (t0, t0 + 1/N). Similarly we denote by
the number of non-interacting agents with degree k at time t that have not interacted with another agent since time t′ ∈ (t0, t0 + 1/N). Similarly we denote by 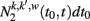 the number of interacting agent pairs (with degree respectively k and k′ and weight of the link w) at time t being in the interaction since t′ ∈ (t0, t0 + 1/N). In the continuous time limit N → ∞, the rate equation can be written as a differential form
the number of interacting agent pairs (with degree respectively k and k′ and weight of the link w) at time t being in the interaction since t′ ∈ (t0, t0 + 1/N). In the continuous time limit N → ∞, the rate equation can be written as a differential form
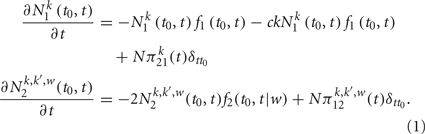
The term with normalization constant c in Eq. (1) indicates the rate of non-interacting agents with degree k being contacted by others (If G is uncorrelated, this term should be proportional to k), and c is given by
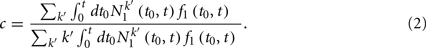
The rates πpq(t) in Eq. (1) indicate the average number of agents changing from state p = 1, 2 to state q = 1, 2 at time t. These rates can be also expressed in a self-consistent way as
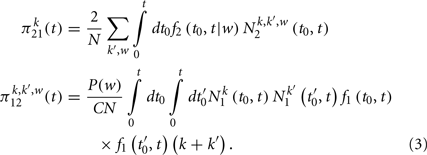
where the constant C is given by
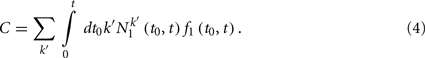
The solution to Eq. (1) is given by
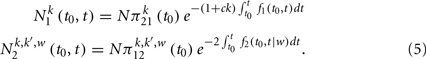
To get a complete solution to the model, we still need to utilize the conservation of the number of agents with degree k, that is
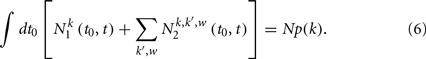
Therefore, combining Eqs (5–7), the solution to the model is completely determined.
Especially we are interested in the stationary solutions, which are expected to satisfy

where τ = t − t0 is the duration time elapsed since the last time the agent has changed his/her state. A stationary solution means that, the system reaches a dynamical equilibrium, such that the macro distribution of agents with different states are time-dependent and the transition rate is constant. In the next section, we will see a stationary solution can be achieved by specifically choice of f1 and f2 in an asymptotic time limit t → ∞.
Finally, by convenience, we denote by 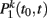 the probability distribution that an agent with degree k is non-interacting for a period from t0 to t and by
the probability distribution that an agent with degree k is non-interacting for a period from t0 to t and by 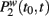 the probability that a connection of weight w at time t is active since time t0. These distributions are obviously proportional to the number of individual in a state n = 1, 2 multiplied by the probability of having a change of state, i.e.,
the probability that a connection of weight w at time t is active since time t0. These distributions are obviously proportional to the number of individual in a state n = 1, 2 multiplied by the probability of having a change of state, i.e.,
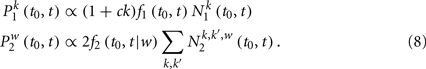
Stationary Solution of the Model
In the previous section, one should notice that the form of Eq. (5), the solution to the model of pairwise interaction, is subject to the choice of probability functions f1 and f2. A lot of evidence from recent measurements reveals that social interaction and human activities are not merely Poisson process but with bursty effect. The distribution of duration time and inter-event time from the empirical data, turn out to be non-trivial and shows scaling property. To capture these phenomena observed in reality, we define f1 and f2 as
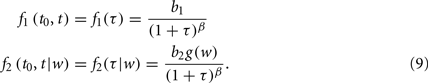
b1 > 0, b2 > 0, 0 ≤ β ≤ 1 are some characteristic parameters and g(w) is an arbitrary positive function. The definition by Eq. (9), indeed reflects a reinforcement dynamics we apply to the model, which could be summarized as “the longer an agent stays in its current state, the more possible it tends to maintain it.” The function g(w) is generally chosen as a decreasing function of w, indicating that interacting agent pairs with a stronger weight of tie interact typically for a longer time. In the asymptotic time limit, the necessary condition for the stationary solution to exist is that the summation of self-consistent constraints given by Eqs (2) and (4) together with the conservation law Eq. (6) converge under the stationary assumptions Eq. (7). The convergence depends on the value of the parameters b0, b1, β and the choice of function g(w). In particular, when 0 ≤ β < 1, the convergence is always satisfied. In the following subsections, we will characterize further the stationary state solution of this model in different limiting cases.
Case 0 < β < 1
The expression for the number of agent in a given state 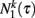 and
and 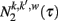 can be obtained by substituting Eq. (9) into the general solution Eq. (5), using the stationary conditions Eq. (7). In this way we get the stationary solution given by
can be obtained by substituting Eq. (9) into the general solution Eq. (5), using the stationary conditions Eq. (7). In this way we get the stationary solution given by
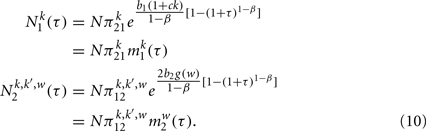
To complete the solution is necessary to determine the constants 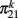 and
and 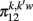 in a self-consistent type of solution. To find the expression of
in a self-consistent type of solution. To find the expression of 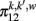 as a function of
as a function of 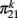 we substitute Eq. (10) in Eq. (3) and we get
we substitute Eq. (10) in Eq. (3) and we get
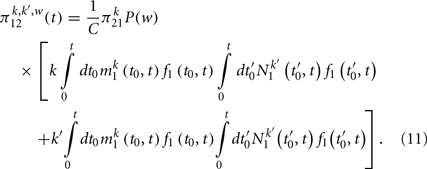
Finally we get a closed equation for 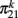 by substituting Eq. (11) in Eq. (6) and using the definition of c and C, given respectively by Eq. (2) and Eq. (4). Therefore we get
by substituting Eq. (11) in Eq. (6) and using the definition of c and C, given respectively by Eq. (2) and Eq. (4). Therefore we get
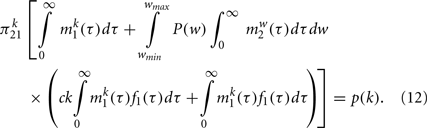
Performing explicitly the last two integrals using the dynamical solution given by Eq. (10), this equation can be simplified as
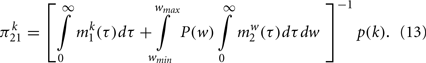
Finally the self-consistent solution of the dynamics is solved by expressing Eq. (2) by

Therefore we can use Eqs (13) and (14) to compute the numerical value of 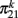 and c. Inserting in these equations the expressions for f1(τ), f2(τ | w) given by Eq. (9) and the solutions
and c. Inserting in these equations the expressions for f1(τ), f2(τ | w) given by Eq. (9) and the solutions 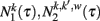 given by Eq. (10) we get
given by Eq. (10) we get
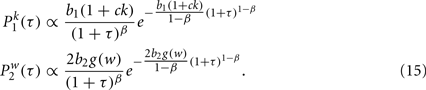
The probability distributions 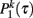 and
and 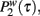 can be manipulating performing a data collapse of the distributions, i.e.,
can be manipulating performing a data collapse of the distributions, i.e.,
with  and
and  defined as
defined as

where A1 and A2 are the normalization factors. The data collapse defined by Eq. (16) of the curves  and are both described by Weibull distributions.
and are both described by Weibull distributions.
Case β = 0
For β = 0 the functions f1(τ) and f2(τ | w) given by Eq. (9) reduce to constants, therefore the process of creation of an interaction is a Poisson process and no reinforcement dynamics is taking place in the network. Assigning β = 0 to Eq. (5), we get the solution
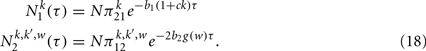
and consequently the distributions of duration of given states Eq. (8) are given by

Therefore the probability distributions 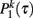 and
and 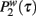 are exponentials as expected in a Poisson process.
are exponentials as expected in a Poisson process.
Case β = 1
In this section, we discuss the case for β = 1 such that 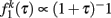 and
and 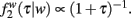 Using Eq. (1) we get the solution
Using Eq. (1) we get the solution
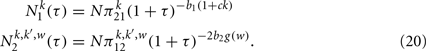
and consequently the distributions of duration of given states Eq. (8) are given by
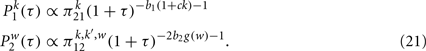
The probability distributions are power-laws. This result remains valid for every value of the parameters b1, b2, g(w) (See Zhao et al., 2011 for a full account of the detailed solution of this model) nevertheless the stationary condition is only valid for

Indeed this condition ensures that the self-consistent constraints Eqs (2) and (4) and the conservation law Eq. (6) have a stationary solution.
Comparison with Numerical Simulations
To check the validity of our annealed approximation versus quenched simulations, we performed a computer simulation according to the dynamical process on a quenched network for the cases β ∈ (0, 1), β = 0 and β = 1. In Figure 1 we compare the results of the simulation for β ∈ (0, 1) with the predictions of the analytical solution. In particular in the reported simulation we have chosen β = 0.5, b1 = 0.02, b2 = 0.05, and g(w) = w−1, the simulation is based on a number of agent N = 2000 and for a period of Tmax = 105, finally the data are averaged over 10 realizations and the network is Poisson with average 〈k〉 = 6 and weight distribution p(w) ∝ w−2. In Figure 1, we show evidence that the Weibull distribution and the data collapse of 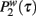 well capture the empirical Weibull behavior observed in the mobile-phone data. The simulated data are also in good agreement with the analytical predictions derived in the annealed approximation for the parameter chosen in the figure. As the network becomes more busy and many agents are in a telephone call, the quenched simulation and the annealed prediction of
well capture the empirical Weibull behavior observed in the mobile-phone data. The simulated data are also in good agreement with the analytical predictions derived in the annealed approximation for the parameter chosen in the figure. As the network becomes more busy and many agents are in a telephone call, the quenched simulation and the annealed prediction of 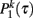 differs more significantly. In Figure 2 we plot the distribution
differs more significantly. In Figure 2 we plot the distribution 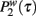 in the Poisson case β = 0 and we compare the simulation with the theoretical prediction. In particular in the reported simulation we have chosen β = 0.5, b1 = 0.02, b2 = 0.05 and g(w) = w−1, the simulation is based on a number of agent N = 2000 and for a period of Tmax = 105, finally the data are averaged over 10 realizations and the network is Poisson with average 〈k〉 = 6 and weight distribution p(w) ∝ w−2. Finally in Figure 3 we plot the distribution
in the Poisson case β = 0 and we compare the simulation with the theoretical prediction. In particular in the reported simulation we have chosen β = 0.5, b1 = 0.02, b2 = 0.05 and g(w) = w−1, the simulation is based on a number of agent N = 2000 and for a period of Tmax = 105, finally the data are averaged over 10 realizations and the network is Poisson with average 〈k〉 = 6 and weight distribution p(w) ∝ w−2. Finally in Figure 3 we plot the distribution 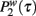 in the power-law case β = 1. In this case we have consider model in the stationary phase and therefore we have taken b1 = b2 = 0.8. All others parameter of the model are the same as in the precedent simulations. In Figure 3 we show that in this case the distribution
in the power-law case β = 1. In this case we have consider model in the stationary phase and therefore we have taken b1 = b2 = 0.8. All others parameter of the model are the same as in the precedent simulations. In Figure 3 we show that in this case the distribution 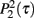 is a power-law with exponents depending on the weight of the link. The fitted exponents are in very good agreement with the exponents predicted by the mean-field solution of the model.
is a power-law with exponents depending on the weight of the link. The fitted exponents are in very good agreement with the exponents predicted by the mean-field solution of the model.
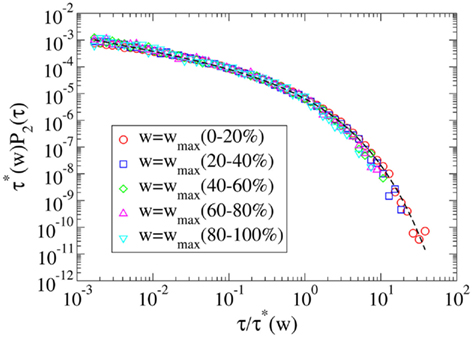
Figure 1. Data collapse of the simulation of the proposed model for cell phone communication with β = 0.5. In the figure we plot the probability 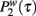 that in the model a pair of agents with strength w are interacting for a period τ. The collapses data of
that in the model a pair of agents with strength w are interacting for a period τ. The collapses data of 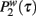 is described by Weibull distribution as expected by the theoretical prediction indicated with a solid line.
is described by Weibull distribution as expected by the theoretical prediction indicated with a solid line.
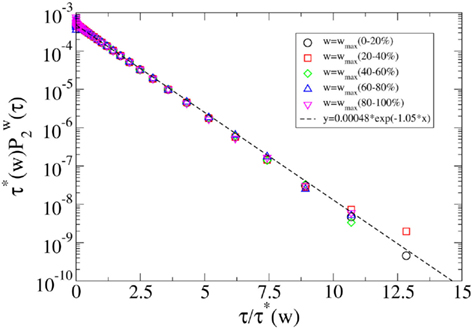
Figure 2. Data collapse of the simulation of the proposed model for cell phone communication with β = 0. In the figure we plot the probability 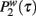 that in the model a pair of agents with strength w are interacting for a period τ. The collapses data of
that in the model a pair of agents with strength w are interacting for a period τ. The collapses data of  is described by the exponential distribution predicted theoretically and indicated by a solid line.
is described by the exponential distribution predicted theoretically and indicated by a solid line.
Figure 3. Data of the simulation of the proposed model for cell phone communication for β = 1. In the figure we plot the probability  that in the model a pair of agents with strength w are interacting for a period τ. The collapses data of
that in the model a pair of agents with strength w are interacting for a period τ. The collapses data of 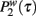 is described by power-law distribution in agreement with the theoretical predictions. In the inset we report the power-law exponent versus the theoretically predicted power-law exponent showing good agreement.
is described by power-law distribution in agreement with the theoretical predictions. In the inset we report the power-law exponent versus the theoretically predicted power-law exponent showing good agreement.
Conclusion
In the last 10 years there has been an increasing interest in the structure of complex networks. New universality class has been found characterizing small-word and scale-free networks. Recently new data on social interaction networks are changing the way we look at social networks. In fact the new data is able to record social interactions on the fast timescale of a face-to-face interaction or on the duration of a mobile-phone communication. These new data constitute evidence for the “microscopic structure” or any social tie in a social network. Moreover this data show evidence that human social interactions are dictated by a non-Poissonian dynamics. Here in this paper we discuss a model of social interactions on the fast timescale. This model is able to reproduce both scale-free distribution of duration of interactions and Weibull distribution of duration of interaction as observed respectively in the data of face-to-face and mobile-phone communication. The hypothesis of the paper is that the dynamics of social interaction is mediated by a Hebbian like type of dynamics with memory effects that is able to reproduce the data. In future works we plan to biologically validate this hypothesis in the study of social interactions in simple animals. The model well reproduce the experimental data and is very easy to implement to include the effect of circadian rhythms or the role of an information spreading on the network. This flexibility of the model makes it a perfect platform to use this model in future works for simulating dynamical processes on dynamical social networks.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Ahn, Y. Y., Bagrow, J. P., and Lehmann, S. (2010). Link communities reveal multiscale complexity in networks. Nature 466, 761–764.
Altmann, E. G., Pierrehumbert, J. B., and Motter, A. E. (2009). Beyond word frequency: bursts, lulls, and scaling in the temporal distributions of words. PLoS ONE 4, e7678. doi:10.1371/journal.pone.0007678
Anteneodo, C., and Chialvo, D. R. (2009). Unraveling the fluctuations of animal motor activity. Chaos 19, 033123.
Barabási, A. L. (2005). The origin of bursts and heavy tails in humans dynamics. Nature 435, 207–211.
Barrat, A., Barthélemy, M., and Vespignani, A. (2008). Dynamical processes on complex networks. Cambridge: Cambridge University Press.
Bianconi, G., Pin, P., and Marsili, M. (2009). Assessing the relevance of node features for network structure. Proc. Natl. Acad. Sci. U.S.A. 106, 11433–11438.
Boccaletti, S., Latora, V., Moreno, Y., Chavez, M., and Hwang, D. U. (2006). Complex networks: structure and dynamics. Phys. Rep. 424, 175–308.
Brockmann, D., Hufnagel, L., and Geisel, T. (2006). The scaling laws of human travel. Nature 439, 462–465.
Cattuto, C., Van den Broeck, W., Barrat, A., Colizza, V., Pinton, J. F., and Vespignani, A. (2010). Dynamics of person-to-person interactions from distributed RFID sensor networks. PLoS ONE 5, e11596. doi: 10.1371/journal.pone.0011596
Davidsen, J., Ebel, H., and Bornholdt, S. (2002). Emergence of a small world from local interactions: modeling acquaintance networks. Phys. Rev. Lett. 88, 128701.
Dorogovtsev, S. N., and Mendes, J. F. F. (2003). Evolution of Networks: From Biological Nets to the Internet and WWW. Oxford: Oxford Univesity Press.
Eagle, N., and Pentland, A. S. (2006). Reality mining: sensing complex social systems. Pers. Ubiquitous Comput. 10, 255–268.
González, M. C., Hidalgo, A. C., and Barabási, A. L. (2008). Understanding individual human mobility patterns. Nature 453, 779–782.
Holme, P. (2005). Network reachability of real-world contact sequences. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 71, 046119.
Holme, P., and Newman, M. E. J. (2006). Nonequilibrium phase transition in the coevolution of networks and opinions. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 74, 056108.
Hui, P., Chaintreau, A., Scott, J., Gass, R., Crowcroft, J., and Diot, C. (2005). “Pocket switched networks and human mobility in conference environments,” in Proceedings of the 2005 ACM SIGCOMM Workshop on Delay-Tolerant Networking, Philadelphia, PA, 244–251.
Isella, L., Stehlé, J., Barrat, A., Cattuto, C., Pinton, J. F., and Van den Broeck, W. (2011). What’s in a crowd? Analysis of face-to-face behavioral networks. J. Theor. Biol. 271, 166–180.
Jo, H. H., Karsai, M., Kertész, J., and Kaski, K. (2011). Circadian pattern and burstiness in human communication activity. arXiv:1101.0377.
Karsai, M., Kivelä, M., Pan, R. K., Kaski, K., Kertész, J., Barabási, A.-L., and Saramäki, J. (2011). Small but slow world: how network topology and burstiness slow down spreading. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 83, 025102.
Malmgren, R. D., Stouffer, D. B., Campanharo, A. S., and Amaral, L. A. (2009). On universality in human correspondence activity. Science 325, 1696–1700.
Malmgren, R. D., Stouffer, D. B., Motter, A. E., and Amaral, L. A. (2008). A Poissonian explanation for heavy tails in e-mail communication. Proc. Natl. Acad. Sci. U.S.A. 105, 18153–18158.
Marsili, M., Vega-Redondo, F., and Slanina, F. (2004). The rise and fall of a networked society: a formal model. Proc. Natl. Acad. Sci. U.S.A. 101, 1439–1442.
Newman, M. E. J. (2003). The structure and function of complex networks. SIAM Rev. Soc. Ind. Appl. Math. 45, 157–256.
Onnela, J. P., Saramäki, J., Hyvönen, J., Szabó, G., Lazer, D., Kaski, K., Kertész, J., and Barabàsi, A. L. (2007). Structure and tie strengths in mobile communication networks. Proc. Natl. Acad. Sci. U.S.A. 104, 7332–7336.
Palla, G., Barabási, A. L., and Vicsek, T. (2007). Quantifying social group evolution. Nature 446, 664–667.
Parshani, R., Dickison, M., Cohen, R., Stanley, H. E., and Havlin, S. (2010). Dynamic networks and directed percolation. Europhys. Lett. 90, 38004.
Rybski, D., Buldyrev, S. V., Havlin, S., Liljeros, F., and Makse, H. A. (2009). Scaling laws of human interaction activity. Proc. Natl. Acad. Sci. U.S.A. 106, 12640–12645.
Scherrer, A., Borgnat, P., Fleury, E., Guillaume, J. L., and Robardet, C. (2008). Description and simulation of dynamic mobility networks. Comput. Netw. 52, 2842–2858.
Song, C., Qu, Z., Blumm, N., and Barabási, A. L. (2010). Limits of predictability in human mobility. Science 327, 1018–1021.
Stehlé, J., Barrat, A., and Bianconi, G. (2010). Dynamical and bursty interactions in social networks. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 81, 035101.
Tang, J., Scellato, S., Musolesi, M., Mascolo, C., and Latora, V. (2010). Small-world behavior in time-varying graphs. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 81, 055101.
Vázquez, A., Rácz, B., Lukacs, A., and Barabàsi, A. L. (2007). Impact of non-Poissonian activity patterns on spreading processes. Phys. Rev. Lett. 98, 158702.
Vazquez, F., Eguíluz, V. M., and San Miguel, M. (2008). Generic absorbing transition in coevolution dynamics. Phys. Rev. Lett. 100, 108702.
Wasserman, S., and Faust, K. (1994). Social Network Analysis: Methods and Applications. Cambridge: Cambridge University Press.
West, B. J., Geneston, E. L., and Grigolini, P. (2008). Maximizing information exchange between complex networks. Phys. Rep. 68, 1.
Keywords: social networks, dynamical networks, reinforcement dynamics
Citation: Zhao K and Bianconi G (2011) Social interactions model and adaptability of human behavior. Front. Physio. 2:101. doi: 10.3389/fphys.2011.00101
Received: 20 September 2011;
Accepted: 25 November 2011;
Published online: 20 December 2011.
Edited by:
Bruce J. West, U.S. Army Research Office, USAReviewed by:
Bruce J. West, U.S. Army Research Office, USAPaolo Grigolini, University of North Texas, USA
Copyright: © 2011 Zhao and Bianconi. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Ginestra Bianconi, Department of Physics, Northeastern University, Boston, MA 02115, USA. e-mail:Zy5iaWFuY29uaUBuZXUuZWR1
 Kun Zhao
Kun Zhao