- Department of Mechanical and Industrial Engineering, Ryerson University, Toronto, ON, Canada
Purpose of Study: The aim of this study was to characterize the central-autonomic interaction underlying the multifractality in heart rate variability (HRV) of healthy humans. Materials and Methods: Eleven young healthy subjects participated in two separate ~40 min experimental sessions, one in supine (SUP) and one in, head-up-tilt (HUT), upright (UPR) body positions. Surface scalp electroencephalography (EEG) and electrocardiogram (ECG) were collected and fractal correlation of brain and heart rate data was analyzed based on the idea of relative multifractality. The fractal correlation was further examined with the EEG, HRV spectral measures using linear regression of two variables and principal component analysis (PCA) to find clues for the physiological processing underlying the central influence in fractal HRV. Results: We report evidence of a central-autonomic fractal correlation (CAFC) where the HRV multifractal complexity varies significantly with the fractal correlation between the heart rate and brain data (P = 0.003). The linear regression shows significant correlation between CAFC measure and EEG Beta band spectral component (P = 0.01 for SUP and P = 0.002 for UPR positions). There is significant correlation between CAFC measure and HRV LF component in the SUP position (P = 0.04), whereas the correlation with the HRV HF component approaches significance (P = 0.07). The correlation between CAFC measure and HRV spectral measures in the UPR position is weak. The PCA results confirm these findings and further imply multiple physiological processes underlying CAFC, highlighting the importance of the EEG Alpha, Beta band, and the HRV LF, HF spectral measures in the supine position. Discussion and Conclusion: The findings of this work can be summarized into three points: (i) Similar fractal characteristics exist in the brain and heart rate fluctuation and the change toward stronger fractal correlation implies the change toward more complex HRV multifractality. (ii) CAFC is likely contributed by multiple physiological mechanisms, with its central elements mainly derived from the EEG Alpha, Beta band dynamics. (iii) The CAFC in SUP and UPR positions is qualitatively different, with a more predominant central influence in the fractal HRV of the UPR position.
1. Introduction
Heart rate regulation in healthy humans is known to exhibit complex variability over an extensive dynamic range. Specifically in the beat-to-beat RR interval (RRi) sequence, the underlying fluctuation is intrinsic (Aoyagi et al., 2000, 2003; Amaral et al., 2001) and exhibit scale-free characteristics of the multifractal type (Ivanov et al., 1999; Sassi et al., 2009). The scale-free component of the heart rate variability (HRV) is of basic importance. Not only is this dynamic feature broadly observed in diverse natural and artificial systems (Task Force of ESC and NASPE, 1996; Gisiger, 2001), it also carry relevant information in the clinical context, where a diminishing fractal HRV was consistently reported in various heart disease processes (Task Force of ESC and NASPE, 1996; Komatsu et al., 1997; Lombardi, 2000; Mahon et al., 2002), and in old age (Makikallio et al., 2001; Kors et al., 2007). Although the HRV scale-free dynamics has been a subject of intense study, its dynamic origin and possible functional correlates remain largely unclear.
The sympathetic (SNS) and parasympathetic (PNS) branches of the autonomic nervous system (ANS) are known to have strong influence on the pace maker cells of the heart (Akselrod et al., 1981; Task Force of ESC and NASPE, 1996; Malliani et al., 1997). However, the complex interaction between SNS and PNS does not provide an immediate characterization of the fractal HRV. For example, via pharmaceutical means, SNS blockade is known to have a minor effect on the multifractal property of HRV, but PNS blockade can dramatically change the HRV scale-free dynamics into one characterized by a much narrower range of scaling exponents (Amaral et al., 2001; Gisiger, 2001). In passive head-up-tilt (HUT), where there is a SNS activation and PNS withdrawal caused by the reduced baroreflex afferent input (Tulppo et al., 2001), the change of the HRV multifractal property may not follow these pharmaceutical effects interpreted separately (Lin and Sharif, 2010). It is thus plausible, at least in passive HUT, that other factors exist to influence the HRV scale-free dynamics.
One potential source that could provide further insights of fractal HRV is the central nervous system (CNS). While fractal fluctuation can emerge from the spontaneous activity of cultured cardiac myocytes (Kucera et al., 2000), the changing fractal HRV properties reported in sleep (Bunde et al., 2000; Brandenberger et al., 2001; Van den Berg et al., 2005; Togo et al., 2006; Pereda and Gonzalez, 2008) and mental exercise (Lucini et al., 1997; Peng et al., 1999; Kubota et al., 2001; Phongsuphap et al., 2008) provide a stronger support for a central-autonomic interaction in the HRV scale-free dynamics. In general, the central influence on cardiac functions is well known (Loewy and Spyer, 1990; Dampney et al., 2002). Despite the brainstem centers that interact with the afferent inputs, “direct” central command can trigger efferent responses to influence heart rate and blood pressure in such events as anticipation of threat (Loewy and Spyer, 1990; Dampney et al., 2002), onset of exercise (Goodwin et al., 1972; Loewy and Spyer, 1990; Dampney et al., 2002). However, specific to the fractal component of HRV, the potential role of CNS, whether anatomical or functional, is mostly unclear.
The objective of the present study is to examine and characterize the central link in fractal HRV. The presence of the central component implies that the fractal properties of the heart rate and brain activity data should be correlated to each other. But fractal correlation of time series should be interpreted differently from the commonly used two-point correlation based on the second order statistics. There are at least two reasons to make such a distinction. First, fractal characterizes the property of a distribution and cannot be fully described using only the second order statistics (Falconer, 1990). For example, the two-point cross correlation of fractal signals is self-similar and qualitatively the same. Secondly, physiological data are not purely fractal signal and can exhibit rhythmic oscillation in a narrow frequency band. Such Fourier modes can lead to a false impression of the two-point cross correlation that has little to do with the fractal component. A novel solution to the fractal correlation problem in general was independently developed by Riedi and Scheuring (1997), and Lévy-Léhel and Vojak (1998). Among others, their main idea implies the scaling exponents of the time series is not sufficient to describe the fractal correlation and the need for a multivariate approach. Indeed, time series can be coupled to exhibit a wide range of fractal correlation without changing the underlying scaling exponents (Lin and Sharif, 2007; Appendix A). It is thus believed that a bi-variate multifractal approach is necessary for the current investigation.
The main goals of the paper are to report evidence of a central-autonomic fractal correlation (CAFC) in the heart rate and brain data from the passive head-up-tilt (HUT) experiment. The CAFC was further examined based on the regression with HRV and EEG frequency domain measures. Both linear regression of two variables and principal component analysis (PCA) were employed to gain insights of the physiological processes underlying CAFC.
2. Materials and Methods
2.1. Subjects and Experiments
Eleven subjects (eight males and three females; age: 25.72 ± 4.3-year-old; weight: 69.48 ± 12.2 kg; height: 173.83 ± 8.2 cm) without known cardiovascular, pulmonary, and neurological conditions participated in the study. Our experiment is a passive HUT body maneuver, which is sufficient to exert measurable effects on the ANS and the fractal HRV property (Tulppo et al., 2001). All subjects were fully explained about the goal and detail of the test reviewed and approved by the University Ethic Board, and signed an informed consent form.
The pre-test protocol requires the subject to maintain normal daily activity and routine, and have sufficient sleep. Heavy exercise and alcohol consumption were not allowed before the test. The subjects were asked to stay calm and remain steady on a tilt table with foot rest and to keep their eyes open. Moreover, only spontaneous breathing protocol was considered. For the tilt test, subjects were first in the SUP position for 10–20 min before tilted up to a 75° UPR position. The test was conducted in a temperature-controlled and shielded room of slightly dim lighting condition (≤200 lx). No syncope event occurred in the tilt test.
Standard electrocardiogram ECG (five-lead) recording and electroencephalography EEG bipolar measurement (International 10-20 system) were taken simultaneously via a 16-bit ADC ambulatory recorder at a 256 Hz sampling rate (g.MobiLab, GTEC Inc., Austria). The recorder has a hardcoded passband of 0.01–100 Hz for the ECG recording and 0.01–30 Hz for the EEG recording. The R wave in ECG was examined and any skip beat or erroneous detection (due mostly to a significant P wave in ECG) was manually corrected. These problematic beats account for a small portion of the entire record. On average, there are 3,849 uninterrupted RRi in SUP (mean ± SD: 0.965 ± 0.079 s) and 5,308 RRi in UPR (mean ± SD: 0.662 ± 0.055 s). All data analyzed below are based on the frontal site recordings (FP1-FC3, FP2-FC4). Neighboring frontal sites (AF3-F3, AF6-F4) were also recorded and showed similar results.
2.2. Relative Multifractality between Time Series
The traditional multifractal analysis of a time series is achieved in two technical steps: first, estimate the singularity exponent, α, which quantifies the fluctuation strength from one sample to the next, and, second, calculate the multifractal spectrum, f(α), of the intervals in which α is observed. The value of f(α) is also proportional to the number of intervals that exhibit the fluctuation strength α (Falconer, 1990). Hence, the larger the f(α) is, the more frequent the fluctuation strength α is observed. The width of f(α) is an important indicator for fractal complexity and one of the primary variables used in this work. When the fluctuation is characterized by one single α = α0, such as the fractional Brownian motion, f(α) reduces to a singleton: i.e., f(α0) = 1 at α = α0 and f(α) = 0 for α ≠ α0 (Falconer, 1990). In this case, the width of f(α) is 0 and the fluctuation is considered relatively simple since it is uniformly “the same.” This is to compare to the case where α spans an interval, such as the binomial cascade (Falconer, 1990; Riedi and Scheuring, 1997; Lin and Sharif, 2007 and Appendix A). In this case, f(α) has a finite width and the fluctuation is considered complex since it consists of a mixture of different fluctuation strengths. The width of f(α) can therefore properly measure the fractal complexity of a time series.
Riedi and Scheuring (1997), and Lévy-Léhel and Vojak (1998) made an important extension to the multifractal analysis. These authors introduced the idea of relative multifractality (RM) by using the fractal property of one time series to measure that of the other. While the technical details remain similar, one now focuses on the relative singularity exponent, denoted as αRM. It is in this setting that the fractal correlation is addressed. In particular, for identical fractal time series, αRM = 1, which simply reflects the same fluctuation of the time series. Having a constant αRM also implies the corresponding f(αRM) is a singleton of zero width. In general, strongly correlated fractal properties imply a small αRM range and a small f(αRM) spectrum width. As the difference of fluctuation in time series widens, in both the αRM value and the interval scale in which αRM is observed, the αRM range increases and f(αRM) attains a finite width (Lévy-Léhel and Vojak, 1998; Lin, 2008; Lin and Sharif, 2010; Lin and Sharif, 2007; Riedi and Scheuring, 1997). Hence, the width of f(αRM) of two time series measures a different property from the width of f(α) of a single time series; namely, a smaller (larger) f(αRM) width implies a stronger (weaker) fractal correlation between the time series.
To employ RM in the present work, we first constructed the aggregated EEG sequence based on the RRi. Let the EEG be e(t), and RRi, and its time stamp be r(n), t(n) = Σnr(i), respectively. The aggregated EEG sequence is defined by: y(n) = Σe(t′)/Mn for t′ in [t(n − 1), t(n)], n = 1,2, …, where Mn denotes the number of EEG samples in [t(n − 1), t(n)]. To perform RM analysis, the method of joint wavelet transform modulus maxima (JWTMM) was used to determine the relative singularity exponent, denoted as αR/E, and the corresponding f(αR/E) spectrum (Lin and Sharif, 2007, 2010; Lin, 2008). The JWTMM consists in the following four steps (Appendix B):
(i) Calculate the wavelet transforms of R(n), E(n) where R(n) = Σnr(n′), E(n) = Σny(n′), and identify the corresponding modulus maxima lines in the time scale plane. The issues of using other wavelets or higher order Gaussian derivative wavelet have been discussed in the past (Lin and Sharif, 2007). We used the first order Gaussian derivative wavelet in this work as it shows more robust scaling [see (1) below].
(ii) Estimate the scaling exponent τ(q, p) in the power law relationship
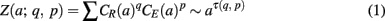
where a represents the scale, CR, CE are, respectively, the wavelet modulus maxima of R(n), E(n), of the nearest maxima lines.
(iii) Extract the (q*, p*) values from the level set L = {(q*, p*), τ(q*, p*) = 0} and, by considering p* as a function of q*, p*(q*), calculate
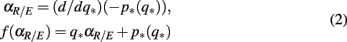
where the derivative term is approximated using finite difference.
(iv) Estimate the width of f(αR/E), 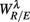 , λ = SUP, UPR, for q* in the interval (Appendix B).
, λ = SUP, UPR, for q* in the interval (Appendix B).
The background of these calculations are rooted in the mathematics of multifractal theory and has a statistical physics analog (Falconer, 1990). It should be noted that the level set extracted in step (iii) above was designed to capture the exact idea of “using the fractal of one time series to measure that of the other” in the RM analysis. We will leave these background and technical details in the references for interested readers (Falconer, 1990; Riedi and Scheuring, 1997; Lévy-Léhel and Vojak, 1998; Lin, 2008; Lin and Sharif, 2007, 2010). In order to distinguish from the traditional multifractal spectrum, f(αR/E) will henceforth be called the RM spectrum.
The RM spectrum width 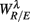 estimated in (iv) above will be used to measure the fractal correlation between the r(n) and y(n) sequences. In addition, the UPR-SUP width-ratio
estimated in (iv) above will be used to measure the fractal correlation between the r(n) and y(n) sequences. In addition, the UPR-SUP width-ratio 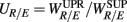 were calculated to examine the changing fractal correlation in HUT. Thus, UR/E < 1 (>1) implies the transition toward a stronger (weaker) fractal correlation in the UPR position. Note, a superscript λ = SUP, UPR is added hereafter to the variable when it is necessary to reference the body position. Separately, we also estimated the spectrum width of the RRi sequence and calculated the UPR-SUP width-ratio, URRi, to address the changing fractal complexity of HRV in HUT. Here, URRi > 1 (<1) implies the transition toward a more (less) complex RRi fluctuation in the UPR position.
were calculated to examine the changing fractal correlation in HUT. Thus, UR/E < 1 (>1) implies the transition toward a stronger (weaker) fractal correlation in the UPR position. Note, a superscript λ = SUP, UPR is added hereafter to the variable when it is necessary to reference the body position. Separately, we also estimated the spectrum width of the RRi sequence and calculated the UPR-SUP width-ratio, URRi, to address the changing fractal complexity of HRV in HUT. Here, URRi > 1 (<1) implies the transition toward a more (less) complex RRi fluctuation in the UPR position.
2.3. Surrogates
Two types of surrogates were generated from the r(n), y(n) sequences to test the fractal correlation result: shuffle and iterated amplitude adjusted Fourier transformed (IAAFT) surrogates. While the shuffle surrogates completely change the original data into uncorrelated random noise, IAAFT surrogates preserve both the 1/f-like power spectra and the amplitude distribution (Schreiber and Schmitz, 2000). We followed the algorithms documented in the literature (Schreiber and Schmitz, 2000) and verified these properties. Once the surrogates of r(n), y(n) were generated, their RM spectrum width was estimated and compared to the original data.
2.4. HRV and EEG Spectral Components
Normalized LF (0.04–0.15 Hz) and HF (0.15–0.4 Hz) spectral components (in unit nu) of HRV were calculated to characterize the SNS-PNS interaction and PNS activities in the autonomic control of the heart rate (Akselrod et al., 1981; Task Force of ESC and NASPE, 1996; Malliani et al., 1997). To track the changing ANS activities, these calculations were carried out in segments of B heart beats: Kj = {r((j − 1) B + 1), …, r(jB)}, j = 1, …, NB. For each Kj, the corresponding EEG segment over the time interval of B heart beats was obtained: Yj = {e(mjΔt), …, e(njΔt)}, where Δt denotes the sampling time, mjΔt = t((j − 1) B + 1), njΔt = t(jB). We then estimated the spectrum based on the segment Yj in Theta (4–7 Hz), Alpha (8–13 Hz), and Beta (13–30 Hz) bands and the result is normalized by the total EEG spectral power of the segment. Since RRi is unevenly spaced, the Lomb periodogram (Press et al., 2007) was used to estimate the normalized LF, HF components. The spectral measures for each EEG segment Yj was estimated using the Welch method. Results reported in this work are based on the intervals of B = 128 beats with 50% overlap (64-beat). Using B = 64,256 and/or using non-overlapping segments yield similar results (Figure A1).
2.5. Regression Analysis
To examine the underlying physiological processing in fractal correlation, regressions were performed between the RM spectrum width and the HRV, EEG spectral measures. There are a total of six variables of interest:
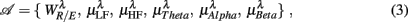
where 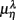 for η = LF, HF, Theta, Alpha, Beta are, respectively, the mean HRV and EEG spectral measures averaged over all segments in λ = SUP, UPR positions.
for η = LF, HF, Theta, Alpha, Beta are, respectively, the mean HRV and EEG spectral measures averaged over all segments in λ = SUP, UPR positions.
Two approaches were adopted. The first is a standard linear regression between 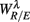 and any one of the remaining five variables in
and any one of the remaining five variables in 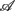 . Motivated by the possibility of multiple physiological processes influencing fractal HRV, principal component analysis, PCA, was also conducted to achieve a higher dimensional regression (Jolliffe, 2002).
. Motivated by the possibility of multiple physiological processes influencing fractal HRV, principal component analysis, PCA, was also conducted to achieve a higher dimensional regression (Jolliffe, 2002).
In PCA, we first built a 11 × 6 data array with the variables in 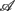 arranged from column i = 1–6. Hence, each row of this data array contains the subject’s response in RM and spectral measures. Conceptually, one could also imagine the data in a six dimensional Euclidean space spanned by the coordinate
arranged from column i = 1–6. Hence, each row of this data array contains the subject’s response in RM and spectral measures. Conceptually, one could also imagine the data in a six dimensional Euclidean space spanned by the coordinate 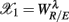 ,
, 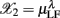 , …,
, …, 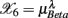 (following the order listed in
(following the order listed in  ). We then applied PCA to seek an optimal coordinate transformation of
). We then applied PCA to seek an optimal coordinate transformation of 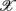 i to best capture the data scattering in the six dimensional space. The transformed axes, denoted as
i to best capture the data scattering in the six dimensional space. The transformed axes, denoted as  i, i = 1, … 6, are known as the principal axes and are given by the linear combination of the
i, i = 1, … 6, are known as the principal axes and are given by the linear combination of the 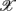 i’s:
i’s:

where dji are the coefficients that measure the contribution of the coordinate 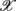 j in the ith principal axis. Each
j in the ith principal axis. Each 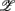 i is also associated with a principal value, PVi, that measures the data scattering along the
i is also associated with a principal value, PVi, that measures the data scattering along the 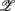 i. Arranging PVi in descending order, we used the cumulative PVi
i. Arranging PVi in descending order, we used the cumulative PVi
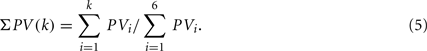
and report only the first NP principal axes that satisfy the criterion ΣPV(NP) < Th, Th ~ 1. The remaining principal axes are of little importance since they capture only a minute fraction of the data scattering. Geometrically, it means the data scatter in almost the perpendicular directions of these remaining principal axes.
2.6. Statistics
Standard methods were used to calculate the mean and SD of the EEG, RRi spectral measures. Normal distribution was verified using the Kolmogorov-Smirnov test. Differences between the spectral measures were tested for significance using the, two-tail, paired t-test. Pearson’s product moment correlation coefficient was used in the regression analysis between the spectrum width estimates and the HRV, EEG spectral measures.
3. Results
Our results will be given using two sets of variables. The first is the spectrum width. They include the width of the RM spectrum of the r(n), y(n) sequences and the width of the RRi multifractal spectrum. The width-ratios UR/E and URRi will be used to compare the response between the SUP and UPR positions. The second set of variables are the HRV and EEG spectral measures and their regression results.
3.1. RM and RRi Spectrum Width
Figure 1 shows the RRi, EEG data, the spectral measures, as well as the multifractal property of the r(n), y(n) sequences from two subjects. The power law (1) estimated in the RM analysis is given in Figure 2A. Most subjects exhibit robust scalings, ranging from one to two heart beats to about 102 heart beats (Table 1). This scaling range may be of interest as it could give a rough idea of the time scale associated with the fractal correlation.
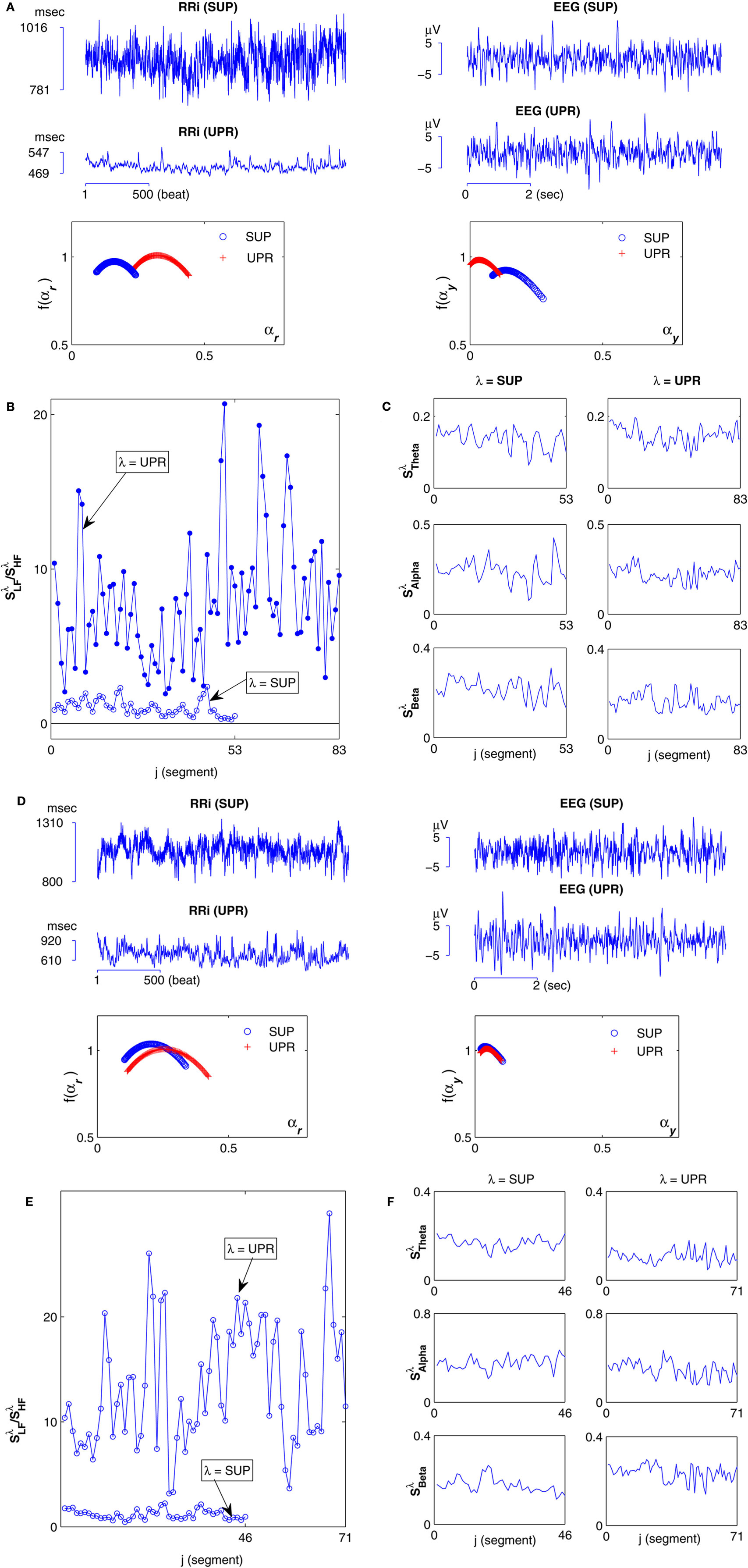
Figure 1. Data segments from a subject (S5) in the group
 : (A) Left column: RRi in SUP (top), UPR positions (middle), and their multifractal spectra f(αr) (bottom). Right column: EEG in SUP (top), UPR positions (middle), and the multifractal spectra of y(n), f(αy) (bottom). The multifractal spectra were estimated using WTMM with the third Gaussian derivative wavelet and q ∈ [−2, 2]. (B) The LF/HF spectral component ratio (sympathovagal index),
: (A) Left column: RRi in SUP (top), UPR positions (middle), and their multifractal spectra f(αr) (bottom). Right column: EEG in SUP (top), UPR positions (middle), and the multifractal spectra of y(n), f(αy) (bottom). The multifractal spectra were estimated using WTMM with the third Gaussian derivative wavelet and q ∈ [−2, 2]. (B) The LF/HF spectral component ratio (sympathovagal index), 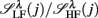 in λ = SUP (“○”) and λ = UPR positions (“•”). (C) Top to bottom rows: normalized EEG spectral components in Theta, Alpha, Beta bands,
in λ = SUP (“○”) and λ = UPR positions (“•”). (C) Top to bottom rows: normalized EEG spectral components in Theta, Alpha, Beta bands, 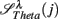 ,
, 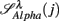 ,
, 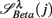 , respectively, in λ = SUP (left column) and λ = UPR (right column) positions from the same subject. (D–F) Show the same set of plots for a different subject (S11).
, respectively, in λ = SUP (left column) and λ = UPR (right column) positions from the same subject. (D–F) Show the same set of plots for a different subject (S11).
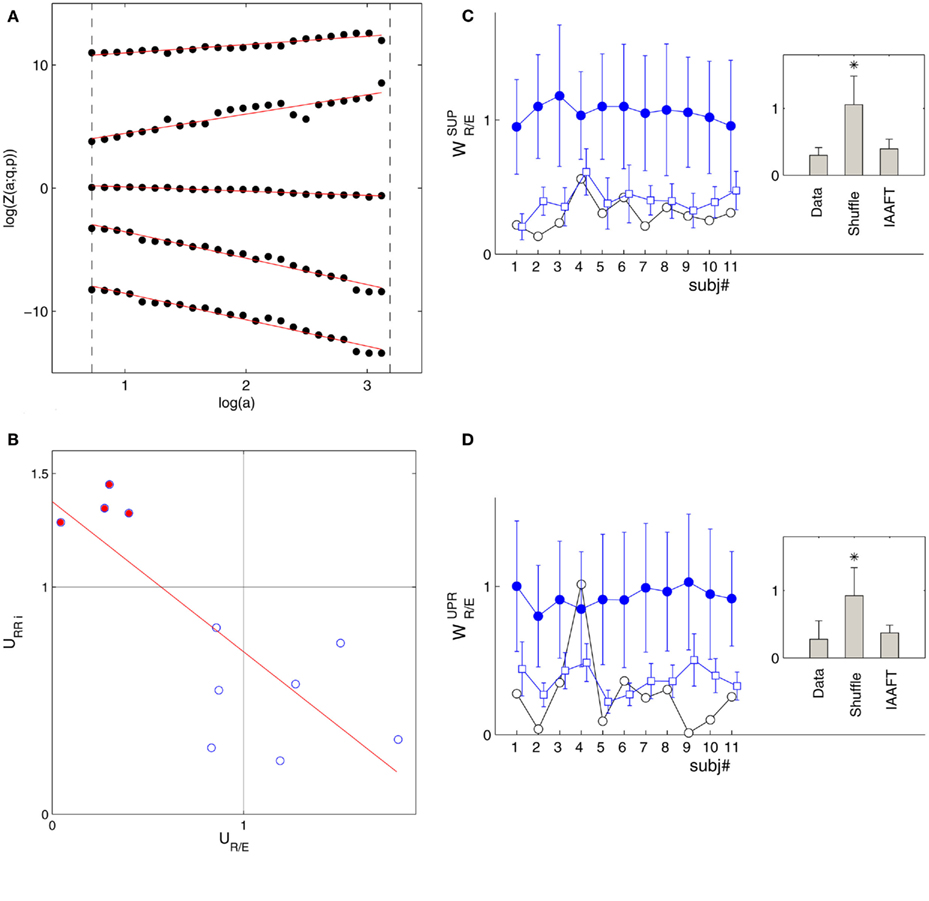
Figure 2. (A) Scaling relationship (1): log Z(a; q, p) versus log(a) in the SUP position from the same subject (S5) shown in Figure 1A; (q, p) = (−1.4, −1.4), (2.6, −1.4), (0.6, 0.6), (2.6, 2.6), (−1.4, 2.6) from bottom to top. The curves are separated for clarity purpose. The scaling range is indicated by the vertical long-dash lines. The scaling exponent τ(q, p) is estimated from the best-fit line shown as the solid line in the figure. (B) URRi versus UR/E relationship. The filled circle indicates the result from the subjects in group 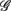 . The solid line is the regression line (ρ = −0.80, P = 0.003). The spectrum width was calculated for q in [−2, 2] (Appendix B). (C) The RM spectrum width of the shuffle surrogates (“•”) and IAAFT surrogates (“□”) in the SUP position. (D) The RM spectrum width of the shuffled surrogates (“•”) and IAAFT surrogates (“□”) in the UPR position. The width estimates of the original data are also included (“○”) for comparison. The error bars represent one SD. The results for the IAAFT surrogates are shifted slightly to the right for clarity. The insets in (C,D) show the group-mean RM spectrum width.
. The solid line is the regression line (ρ = −0.80, P = 0.003). The spectrum width was calculated for q in [−2, 2] (Appendix B). (C) The RM spectrum width of the shuffle surrogates (“•”) and IAAFT surrogates (“□”) in the SUP position. (D) The RM spectrum width of the shuffled surrogates (“•”) and IAAFT surrogates (“□”) in the UPR position. The width estimates of the original data are also included (“○”) for comparison. The error bars represent one SD. The results for the IAAFT surrogates are shifted slightly to the right for clarity. The insets in (C,D) show the group-mean RM spectrum width.

Table 1. The mean ± SD of the lower (amin) and upper (amax) scales of the scaling range in (1) (unit: heart beat).
The main result of this work is given in Figure 2B, which shows the width-ratios UR/E versus URRi. It is evident that the HUT maneuver stimulates a range of different “fractal reaction” in the subjects. In particular, we identify a subgroup of subjects 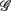 = (S2, S5, S9, S10) that are characterized by URRi > 1; i.e., these subjects exhibited more complex fractal fluctuation in the UPR position. These subjects are also characterized by a much smaller UR/E ≪ 1, indicating a stronger fractal correlation in their RRi and EEG sequences. The remaining seven subjects are characterized by URRi < 1, showing less complex RRi fluctuation in the UPR position.
= (S2, S5, S9, S10) that are characterized by URRi > 1; i.e., these subjects exhibited more complex fractal fluctuation in the UPR position. These subjects are also characterized by a much smaller UR/E ≪ 1, indicating a stronger fractal correlation in their RRi and EEG sequences. The remaining seven subjects are characterized by URRi < 1, showing less complex RRi fluctuation in the UPR position.
The overall negative trend is observed in this empirical relationship and it is significant (P = 0.003). To this end, it is important to emphasize that the fractal property of the individual sequence does not dictate the outcome of the fractal correlation. As shown in the past, fractal time series can be coupled to result in a wide range of fractal correlation without changing their scaling exponents (Lin and Sharif, 2007; Appendix A). Hence, the empirical relationship between UR/E and URRi represents a non-trivial result that suggests the change toward a more correlated EEG, RRi fractal fluctuation is associated with the change toward a more complex fractal HRV.
The above result was further examined using shuffle and IAAFT surrogates. The null hypothesis of the shuffle surrogates is to test whether there is any dynamics at all; namely, would the underlying phenomenon be simply reproduced by independent identically distributed random variates. The shuffling serves to achieve this purpose by destroying the temporal correlation of the original data. As a result, shuffle surrogates exhibit completely independent fluctuations, which, in the present context, means weaker fractal correlation, or a large RM spectrum width. The IAAFT surrogate, on the other hand, is to test the null of a linear gaussian process under (static) non-linear transformation, say, from the measurement device (Schreiber and Schmitz, 2000). The surrogate preserves both the amplitude distribution and the second order scaling property of the original sequence, e.g., the power law power spectrum. Hence, a relatively stronger fractal correlation with a smaller RM spectrum width is expected. Our result is based on the ensemble of 80 pairs of such surrogates from the original r(n), y(n) sequences.
The fractal correlation results of the surrogates are consistent to the characteristics described above; i.e., the RM spectrum width of the shuffle surrogate is consistently larger than the IAAFT’s and the original data (Figures 2C,D). Using the group-mean statistic, the averaged RM spectrum width of the shuffle surrogate is significantly larger than the original sequences’ (P < 1E−5 for both SUP, UPR positions). It implies that destroying the temporal correlation in r(n), y(n) sequences can result in a qualitatively different outcome and suggests the importance of fractal dynamics in the fractal correlation result. For the IAAFT surrogate, the RM spectrum width is seen to lie in a noticeably narrower range compared to the original data. But the group-mean statistic is not significant in the UPR position and only approaches significance in the SUP position (P = 0.07). The non-rejection of the null hypothesis means, either the width estimate fails to discriminate against the alternative in the data, or the non-linear property in r(n), y(n) may not be essential for CAFC.
3.2. HRV, EEG Spectral Measures
Typical segment-to-segment spectral components from two subjects have been shown in Figure 1. The expected SNS activation and PNS withdrawal due to the reduced baroreflex afferent input in HUT (Tulppo et al., 2001) is indicated by the consistently higher LF and HF spectral components ratio (sympathovagal index) in the UPR position (Figures 1B,E). The HRV spectral measures, 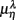 , η = LF, HF, along with their EEG counterparts:
, η = LF, HF, along with their EEG counterparts: 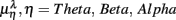 , are summarized in Figure 3, and are mostly significantly different between the λ = SUP and UPR positions (see also group averaged statistics in Table 2).
, are summarized in Figure 3, and are mostly significantly different between the λ = SUP and UPR positions (see also group averaged statistics in Table 2).
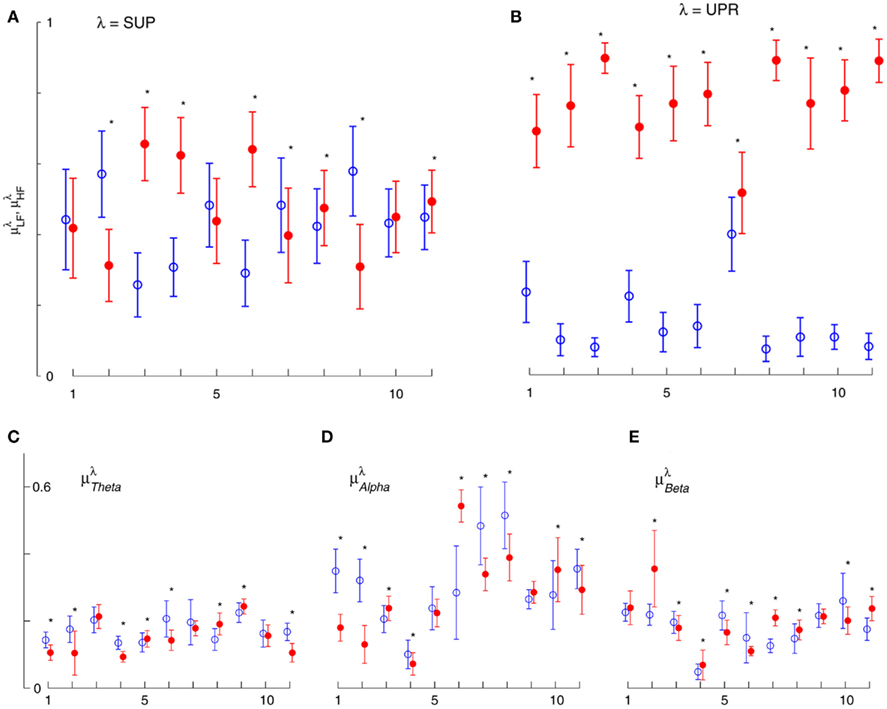
Figure 3. Averaged LF, HF spectral components 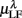 (“•”),
(“•”), 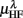 (“○”) in (A) λ = SUP, (B) λ = UPR positions, and the averaged EEG spectral components (C)
(“○”) in (A) λ = SUP, (B) λ = UPR positions, and the averaged EEG spectral components (C) 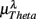 , (D)
, (D) 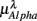 , (E)
, (E) 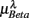 , λ = SUP (“○”), UPR (“•”). Significant difference (P < 0.05) between the SUP and UPR positions is indicated by the asterisk (*). Note that the HF components in (A,B) and the EEG spectral components in the SUP position are shifted slightly to the left for clarity. The error bar represents 1 SD of the segment-to-segment variation of the spectral components.
, λ = SUP (“○”), UPR (“•”). Significant difference (P < 0.05) between the SUP and UPR positions is indicated by the asterisk (*). Note that the HF components in (A,B) and the EEG spectral components in the SUP position are shifted slightly to the left for clarity. The error bar represents 1 SD of the segment-to-segment variation of the spectral components.
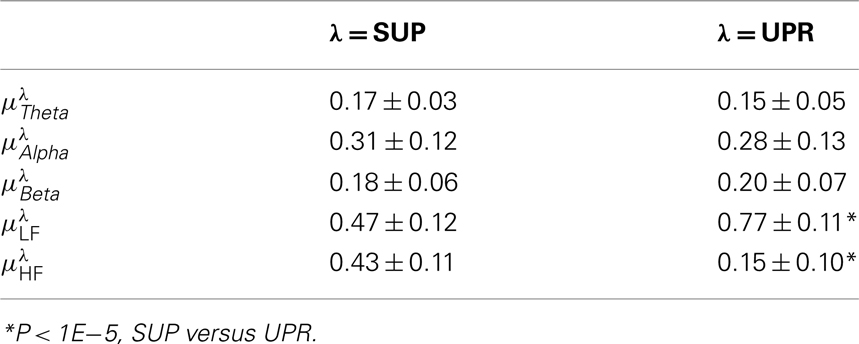
Table 2. Group averaged EEG, HRV spectral components: mean ± SD, 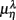 , η = Theta, Alpha, Beta, LF, HF, λ = SUP, UPR.
, η = Theta, Alpha, Beta, LF, HF, λ = SUP, UPR.
Since their physiological correlates, better understanding of the relation between these spectral measures and the RM spectrum width could shed lights into the physiological processing underlying CAFC. A standard linear regression of two variables and a multivariate PCA were conducted for this purpose. The correlation coefficient (ρλ) and the associated P value from the linear regression are reported in Table 3 and described in the next two subsections. The results from the PCA are reported last. To avoid confusion, we shall use the term correlation hereafter to refer to the two-point correlation in the linear regression result. We shall always specify fractal correlation or CAFC wherever necessary.
3.3. Linear Regression with EEG Spectral Measures
Figure 4 shows the scatter plots between the RM spectrum width 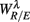 and the EEG
and the EEG 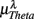 ,
, 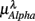 , and
, and 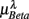 in λ = SUP, UPR positions. It is observed that
in λ = SUP, UPR positions. It is observed that 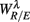 is significantly and negatively correlated with
is significantly and negatively correlated with 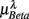 (P = 0.01 for λ = SUP, P = 0.02 for λ = UPR), followed by the weaker correlation with
(P = 0.01 for λ = SUP, P = 0.02 for λ = UPR), followed by the weaker correlation with 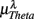 (P = 0.42 for λ = SUP, P = 0.26 for λ = UPR), and
(P = 0.42 for λ = SUP, P = 0.26 for λ = UPR), and 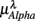 (P = 0.18 for λ = SUP, P = 0.40 for λ = UPR). Further of note is the generally larger
(P = 0.18 for λ = SUP, P = 0.40 for λ = UPR). Further of note is the generally larger 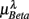 for the subjects in
for the subjects in  (inset of Figure 4C).
(inset of Figure 4C).
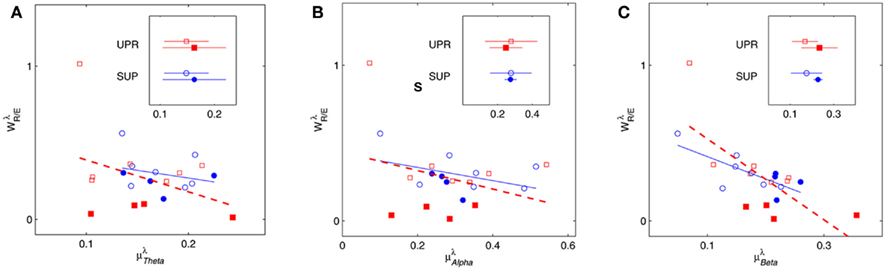
Figure 4. 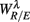 versus
versus 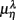 scatter plot for λ = SUP (“○”), UPR (“□”) in the (A) η = Theta band, (B) η = Alpha band, and (C) η = Beta. The regression lines for the SUP (UPR) data are shown as solid (long-dashed) lines. The subgroup of subjects
scatter plot for λ = SUP (“○”), UPR (“□”) in the (A) η = Theta band, (B) η = Alpha band, and (C) η = Beta. The regression lines for the SUP (UPR) data are shown as solid (long-dashed) lines. The subgroup of subjects 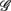 are highlighted using filled symbols (“•” for SUP and “■” for UPR data). The inserts show the comparisons of the average of
are highlighted using filled symbols (“•” for SUP and “■” for UPR data). The inserts show the comparisons of the average of 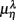 between the group
between the group 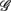 and the rest. The symbol follow the same description given in (A–C).
and the rest. The symbol follow the same description given in (A–C).
3.4. Linear Regression with HRV Spectral Measures
Figure 5 shows the scatter plots between RM spectrum width 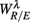 and HRV spectral components,
and HRV spectral components, 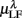 ,
, 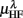 , λ = SUP, UPR. For the SUP position, strong correlations with the LF (P = 0.04), HF components (P = 0.07) are observed (Table 3). In addition, different regression trends are noted: LF component is positively correlated and HF component is negatively correlated. For the UPR position, weak correlation with the LF (P = 0.74) and HF components (P = 0.40) are observed. Observe also the larger difference of LF, HF components for subjects in
, λ = SUP, UPR. For the SUP position, strong correlations with the LF (P = 0.04), HF components (P = 0.07) are observed (Table 3). In addition, different regression trends are noted: LF component is positively correlated and HF component is negatively correlated. For the UPR position, weak correlation with the LF (P = 0.74) and HF components (P = 0.40) are observed. Observe also the larger difference of LF, HF components for subjects in 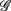 (insets of Figures 5A,B).
(insets of Figures 5A,B).
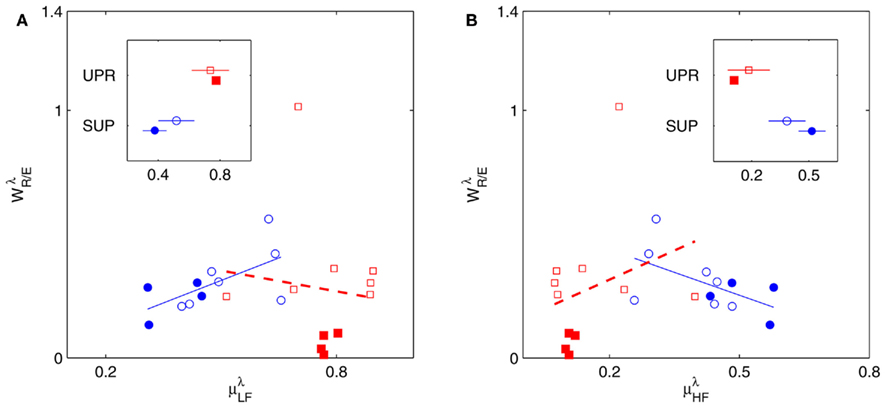
Figure 5. 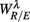 versus
versus 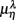 scatter plot for λ = SUP (“○”), UPR (“□”) and (A) η = LF, (B) η = HF. The regression lines for the SUP (UPR) data are shown as solid (long-dashed) lines. The subgroup of subjects
scatter plot for λ = SUP (“○”), UPR (“□”) and (A) η = LF, (B) η = HF. The regression lines for the SUP (UPR) data are shown as solid (long-dashed) lines. The subgroup of subjects 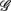 are highlighted using filled symbols (“•” for SUP and “■” for UPR data). The inserts show the comparisons of the average of
are highlighted using filled symbols (“•” for SUP and “■” for UPR data). The inserts show the comparisons of the average of 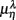 between the group
between the group 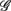 and the rest. The symbol follow the same description given in (A,B).
and the rest. The symbol follow the same description given in (A,B).
3.5. Multivariate Regression: Principal Component Analysis Results
The PCA results are summarized in Figure 6. Using Th = 0.95, most of the data scattering can be captured by the first three principal axes (Figure 6A). The actual ΣPV value sums up to a Th value of ~0.97, meaning that 97% of the data scattering is captured by the selected principal axes.
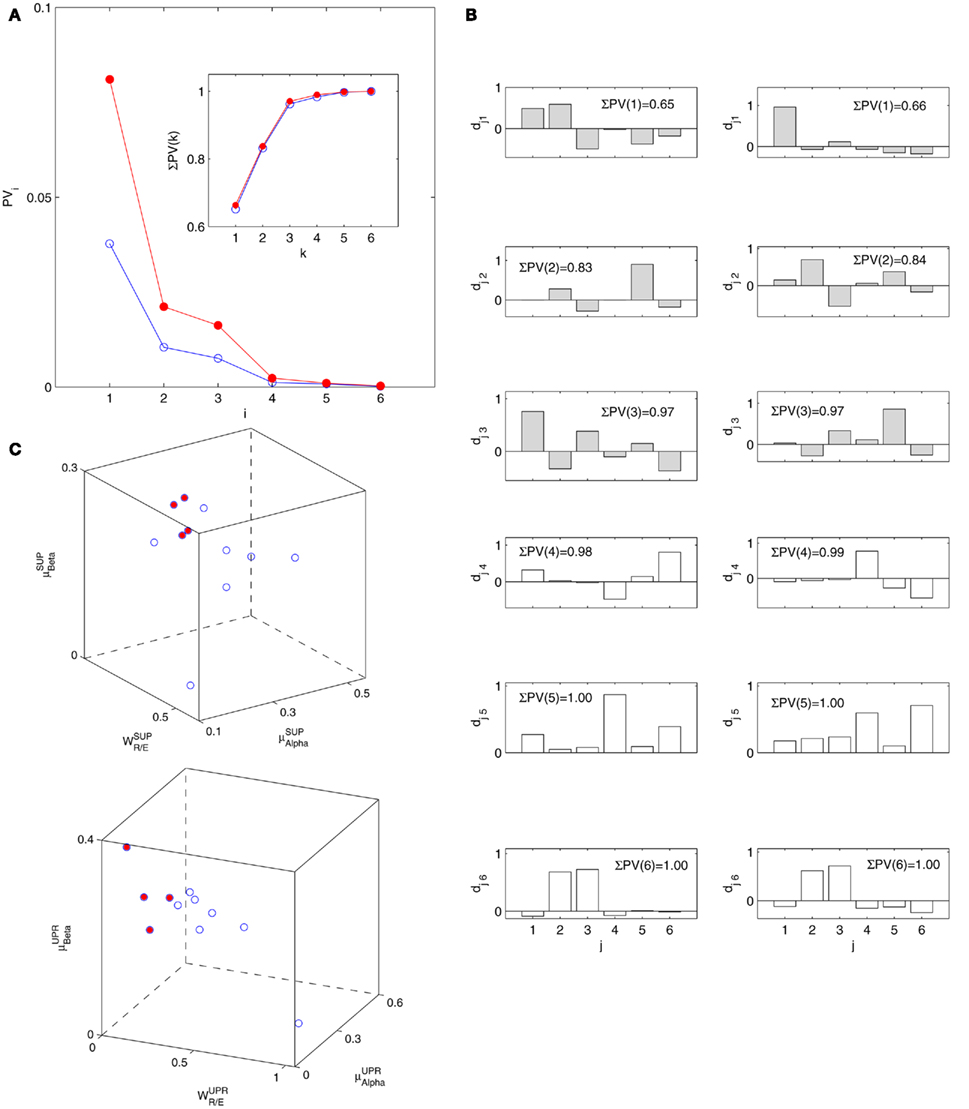
Figure 6. Principal component analysis results. (A) The principal values PVi in SUP (“○”) and UPR position (“•”). The inset shows the cumulative ΣPV(k) as given by (4). (B) The principal axis coefficients dji, i = 1, …, 6, (top to bottom) in SUP (left column) and UPR (right column) positions. The x-label, j = 1,…,6, specifies the coordinate number associated with 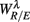 ,
, 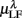 ,
, 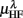 ,
, 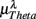 ,
, 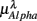 , and
, and 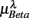 , respectively. The first three principal axes selected by the criterion ΣPV(3) < 0.97 are shown with gray bars. (C) The projection of the data 11 × 6 data array into the subspace spanned by
, respectively. The first three principal axes selected by the criterion ΣPV(3) < 0.97 are shown with gray bars. (C) The projection of the data 11 × 6 data array into the subspace spanned by 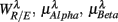 in SUP (left) and UPR (right) positions. The data correspond to the subgroup of subjects
in SUP (left) and UPR (right) positions. The data correspond to the subgroup of subjects 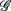 are shown as filled circles.
are shown as filled circles.
The importance of the coordinate composition of a particular principal axis is determined by the dji value in (4). We will focus mainly on the ones with a large d1i coefficient since it corresponds to the coordinate associated with 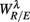 , and thus CAFC. They are
, and thus CAFC. They are 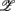 1,
1, 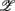 3 for the SUP position and
3 for the SUP position and 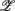 1 for the UPR position (Figure 6B). Two unique features can be found in these principal axes. The first is the relatively comparable dji values. The only exception is the much smaller d4i related to the EEG Theta band spectral measure. These principal axes also share the common characteristic of having significant d5i, d6i coefficients that are associated to the EEG Alpha, Beta band spectral measures. The second feature is the difference between the SUP, UPR positions. For
1 for the UPR position (Figure 6B). Two unique features can be found in these principal axes. The first is the relatively comparable dji values. The only exception is the much smaller d4i related to the EEG Theta band spectral measure. These principal axes also share the common characteristic of having significant d5i, d6i coefficients that are associated to the EEG Alpha, Beta band spectral measures. The second feature is the difference between the SUP, UPR positions. For 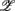 1,
1, 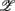 3 of the SUP position and
3 of the SUP position and 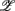 1 of the UPR position, it can be seen the different compositions associated with the HRV spectral measures: those for the SUP position are significantly larger than those for the UPR position. In this regard, the UPR position is qualitatively different in that the HRV spectral measures play a less significant role in CAFC than those in the SUP position.
1 of the UPR position, it can be seen the different compositions associated with the HRV spectral measures: those for the SUP position are significantly larger than those for the UPR position. In this regard, the UPR position is qualitatively different in that the HRV spectral measures play a less significant role in CAFC than those in the SUP position.
4. Discussions
The main finding of this work is the CAFC in fractal HRV. The surrogate testing quickly confirms that the fractal dynamics in r(n), y(n) sequences are indeed crucial for CAFC. The result from IAAFT surrogates suggests that the non-linear characteristics in r(n), y(n) sequences may not be essential for CAFC, although there is always the possibility that the RM spectrum width does not provide the discriminative statistics necessary to reflect CAFC. Further examination on other surrogate types and alternative statistic should lead to deeper insights. The potential physiological processing underlying CAFC was examined using regression on various spectral measures. These results are discussed below.
4.1. 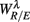 and EEG Spectral Measures
and EEG Spectral Measures
In the context of postural change, Cole reported elevated EEG Beta band activity in the SUP to UPR transition as a result of a proposed arousal factor (Cole, 1989; see also Nikulin and Brismar, 2004). Consistent to Cole, Schneider and co-workers reported decreased Beta band activity in the zero gravity phase of the parabolic flight (Schneider et al., 2008). Lipnicki pointed out a baroreflex induced cortical inhibition contributing to the phenomenon, and further suggested reduced activity in the locus coeruleus noradrenergic system of the brainstem (Lipnicki, 2009). The activation/inhibition of this area of the brain is interesting. Not only does it have widespread projections through out the brain (Berridge and Waterhouse, 2003), neural pathways to the region where preganglionic parasympathetic cardiac neurons are located were also found in the animal study (Ter Horst et al., 1991, 1996). Given the known PNS effect on fractal HRV (Aoyagi et al., 2000, 2003; Amaral et al., 2001; Makikallio et al., 2005; Heffernan et al., 2008), it is plausible that the link between the EEG Beta band activity and HRV scale-free dynamics could exist.
In the current result (Figure 3E), we did not observe a consistent Beta band elevation in the subjects. The length of the UPR test in the protocol could explain this variation. The UPR test in this work lasted mostly above 40 min and some degree of fatigue in the subject is expected to dampen the effect. But the two-point correlation between 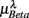 and
and 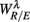 was indeed significant (P = 0.01 for λ = SUP and P = 0.02 for λ = UPR; Table 3), suggesting the possible link between EEG Beta band activity and fractal HRV. However, we were not able to further imply an arousal factor as suggested in the literature. This is because not all subjects exhibited elevated Beta band activity, notably the lower
was indeed significant (P = 0.01 for λ = SUP and P = 0.02 for λ = UPR; Table 3), suggesting the possible link between EEG Beta band activity and fractal HRV. However, we were not able to further imply an arousal factor as suggested in the literature. This is because not all subjects exhibited elevated Beta band activity, notably the lower 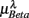 of S5, S10 in the UPR position (Figure 3E). The underlying matter is likely more complex due to the multiple processes contributing to CAFC. The PCA result provides the support of this view. In particular, the principal axes with a large
of S5, S10 in the UPR position (Figure 3E). The underlying matter is likely more complex due to the multiple processes contributing to CAFC. The PCA result provides the support of this view. In particular, the principal axes with a large 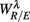 component all share the similar feature of having, not only a large d6i coefficient related to the Beta band spectral measure, but also a relatively large d5i coefficient related to the Alpha band spectral measure. If one restricts to the subspace spanned by the coordinates
component all share the similar feature of having, not only a large d6i coefficient related to the Beta band spectral measure, but also a relatively large d5i coefficient related to the Alpha band spectral measure. If one restricts to the subspace spanned by the coordinates 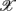 1,
1, 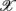 5,
5, 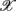 6 (associated with
6 (associated with 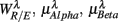 ), i.e., the group with large dji coefficients in the selected principal axes, the subgroup
), i.e., the group with large dji coefficients in the selected principal axes, the subgroup 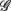 can again be singled out, as it was by using the width-ratios in Figure 2B. The same characterization achieved separately by these spectral measures suggests the importance of the EEG Alpha, Beta dynamics in CAFC.
can again be singled out, as it was by using the width-ratios in Figure 2B. The same characterization achieved separately by these spectral measures suggests the importance of the EEG Alpha, Beta dynamics in CAFC.
4.2. 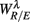 and HRV Spectral Measures
and HRV Spectral Measures
We will first discuss the results of the SUP position. The linear regression shows strong correlation between 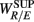 and the LF, HF HRV spectral measures. The underlying characteristics are consistent to the known SNS, PNS effects on fractal HRV. In particular, concurrent SNS activation and PNS withdrawal were found to lead to relatively simpler HRV fractal pattern (Aoyagi et al., 2000, 2003; Amaral et al., 2001; Makikallio et al., 2005; Heffernan et al., 2008). These past studies and the link between CAFC and the HRV fractal complexity (Figure 2A) are consistent to the current finding. In particular, the increase or decrease of the HRV fractal complexity can be separately predicted from the two different sets of variables, one from the known fractal effects based on the changing HRV spectral measures, and one from the empirical relationship between UR/E and URRi. For example, the HF component is negatively correlated with
and the LF, HF HRV spectral measures. The underlying characteristics are consistent to the known SNS, PNS effects on fractal HRV. In particular, concurrent SNS activation and PNS withdrawal were found to lead to relatively simpler HRV fractal pattern (Aoyagi et al., 2000, 2003; Amaral et al., 2001; Makikallio et al., 2005; Heffernan et al., 2008). These past studies and the link between CAFC and the HRV fractal complexity (Figure 2A) are consistent to the current finding. In particular, the increase or decrease of the HRV fractal complexity can be separately predicted from the two different sets of variables, one from the known fractal effects based on the changing HRV spectral measures, and one from the empirical relationship between UR/E and URRi. For example, the HF component is negatively correlated with 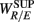 , indicating a large HF component enhances CAFC (toward more complex fractal HRV), and the LF component is positively correlated with
, indicating a large HF component enhances CAFC (toward more complex fractal HRV), and the LF component is positively correlated with 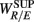 , indicating a large LF component weakens CAFC (toward less complex fractal HRV). These results imply that a strong CAFC in the SUP position can in part be attributed to the strength of the PNS activity.
, indicating a large LF component weakens CAFC (toward less complex fractal HRV). These results imply that a strong CAFC in the SUP position can in part be attributed to the strength of the PNS activity.
The linear regression result from the UPR position, however, shows quite a different picture. Here, a much weaker correlation between 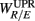 and the HRV spectral components are found. In addition, there is a dramatic increase of the P value from the SUP to the UPR positions (Table 3). The known autonomic effects on fractal HRV no longer seems to hold (Figure 2A). For example, not all subjects exhibit “simpler” fractal HRV pattern with the SNS activation and PNS withdrawal in the UPR position (Figure 2B). This is most evident from the subjects in group
and the HRV spectral components are found. In addition, there is a dramatic increase of the P value from the SUP to the UPR positions (Table 3). The known autonomic effects on fractal HRV no longer seems to hold (Figure 2A). For example, not all subjects exhibit “simpler” fractal HRV pattern with the SNS activation and PNS withdrawal in the UPR position (Figure 2B). This is most evident from the subjects in group 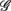 , who are characterized by the transition toward more complex HRV fractal pattern (URRi > 1), stronger CAFC (UR/E ≪ 1) in the UPR position. We do not have further insights as to why these group exhibit qualitatively different behavior from the rest, except that three of them are trained athletes that participate in the University sport teams. Reports separately on the fractal HRV and EEG spectral powers did indicate that intense exercise can have a marked effect, such as resulting in a smaller scaling exponent in HRV (Tulppo et al., 2003; Karavirta et al., 2009) and higher EEG spectral powers (Lardon and Polich, 1996). However, one of the subjects (S5) in
, who are characterized by the transition toward more complex HRV fractal pattern (URRi > 1), stronger CAFC (UR/E ≪ 1) in the UPR position. We do not have further insights as to why these group exhibit qualitatively different behavior from the rest, except that three of them are trained athletes that participate in the University sport teams. Reports separately on the fractal HRV and EEG spectral powers did indicate that intense exercise can have a marked effect, such as resulting in a smaller scaling exponent in HRV (Tulppo et al., 2003; Karavirta et al., 2009) and higher EEG spectral powers (Lardon and Polich, 1996). However, one of the subjects (S5) in 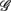 does not engage in the same level of exercise as the other three.
does not engage in the same level of exercise as the other three.
The PCA results imply similar interpretations. In particular, considering the principal axes with a large d1i coefficient (related to 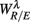 ), the coefficients d2i, d3i associated with HRV spectral measures are much more significant in the SUP position than in the UPR position (Figure 6B). This may be read in parallel to the stronger correlation between the
), the coefficients d2i, d3i associated with HRV spectral measures are much more significant in the SUP position than in the UPR position (Figure 6B). This may be read in parallel to the stronger correlation between the 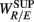 and the HRV spectral measures from above, and implies a more substantial central-autonomic interaction contributing to the fractal HRV in the SUP position.
and the HRV spectral measures from above, and implies a more substantial central-autonomic interaction contributing to the fractal HRV in the SUP position.
The main implications from the PCA are the multiple physiological processes underlying CAFC and the important roles of the EEG Alpha, Beta band dynamics. The qualitative difference of the HRV spectral measure composition reported above implies the predominant central influence in CAFC in the UPR position.
Limit of Study
The current study is limited by the number of participants and some aspects of the protocol. Particular to the ~40 min tilt test, it is expected that certain degree of stress and fatigue could develop during the test. However, these factors were not directly measured in this study. We should also remark the intrinsic limit on the methodology, which has affected the protocol used in the study. We held the view that a “free running” of the mind in wakefulness could facilitate the RM analysis, albeit the subject’s mental state was influenced by being physically constrained on the tilt table. This is because certain rhythmic patterns can emerge in the more specific brain state, such as the Alpha rhythm in meditation or Theta rhythm in cognitive processing. Such rhythmic patterns typically manifest into few dominant Fourier modes in the EEG that will inevitably “mask” the underlying fractal pattern (Lin et al., 2006) and limit one’s ability to characterize CAFC.
Conclusion
Although cardiovascular dynamics has long been a subject of intense interest, the importance and implication of its fractal dynamics are only realized in recent decades. By the general framework of RM and the autonomic perturbation induced by the postural change, we found the empirical support of a central component in fractal HRV, i.e., the CAFC. The regression analysis further implies the importance of the EEG Alpha, Beta band dynamics in CAFC, and thus fractal HRV. Evidently, such central components introduce additional factors to be included in the fractal HRV analysis. It is thus not surprising to learn the difficulty of finding a consistent “baseline” scaling property in HRV (Tan et al., 2009). The current result may offer a reasonable explanation since other psycho-physiological factors may come into play and affect the fractal HRV property.
The PCA results provide us much insight into the potential physiological processing in CAFC. Qualitatively different behaviors between the SUP, UPR position imply the importance of considering central component in fractal HRV. Additional tests on larger ensemble size and demographic differences, as well as with specifically designed protocol to provoke the Alpha, Beta band activities, are warranted to assess the robustness of these findings. In conclusion, we believe CAFC could play the key role in the manifestation and interpretation of fractal HRV. In application, CAFC may also hold the key for the state of reduced HRV, with further implications on the “simpler” HRV pattern witnessed in certain heart diseased conditions.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This research is supported by the Natural Science and Engineering Research Council of Canada. We are grateful to the valuable comments from the anonymous referees.
References
Akselrod, S., Gordon, D., Ubel, F. A., Shannon, D. C., Barger, A. C., and Cohen, R. J. (1981). A quantitative probe of beat to beat cardiovascular control. Science 213, 220–222.
Amaral, L. A. N., Ivanov, P. C. H., Aoyagi, N., Hidaka, I., Tomono, S., Goldberger, A. L., Stanley, H. E., and Yamamoto, Y. (2001). Behavioral-independent features of complex heartbeat dynamics. Phys. Rev. Lett. 86, 6027–6029.
Aoyagi, N., Ohashi, K., Tomono, S., and Yamamoto, Y. (2000). Temporal contribution of body movement to very long-term heart rate variability in humans. Am. J. Physiol. Heart Circ. Physiol. 278, H1035–H1041.
Aoyagi, N., Ohashi, K., and Yamamoto, Y. (2003). Frequency characteristics of long-term heart rate variability during constant routine protocol. Am. J. Physiol. Regul. Integr. Comp. Physiol. 285, R171–R176.
Berridge, C. W., and Waterhouse, B. D. (2003). The locus coeruleus-noradrenergic system: modulation of behavioral state and state-dependent cognitive processes. Brain Res. Brain Res. Rev. 42, 33–84.
Brandenberger, G., Ehrhart, J., Piquard, F., and Simon, C. (2001). Inverse coupling between ultradian oscillations in delta wave activity and heart rate variability during sleep. Clin. Neurophysiol. 112, 992–996.
Bunde, A., Havlin, S., Kantelhardt, J. W., Penzel, T., Peter, J. H., and Voigt, K. (2000). Correlated and uncorrelated regions in the heart-rate fluctuations during sleep. Phys. Rev. Lett. 85, 3736–3739.
Cole, R. J. (1989). Postural baroreflex stimuli may affect EEG arousal and sleep in humans. J. Appl. Physiol. 67, 2369–2375.
Dampney, R. A. L., Coleman, J. J., Fontes, M. A. P., Hirooka, Y., Horiuchi, J., Li, Y. W., Polson, J. W., Potts, P. D., and Tagawa, T. (2002). Central mechanisms underlying short- and long-term regulation of the cardiovascular system. Clin. Exp. Pharmacol. Physiol. 29, 261–268.
Falconer, K. (1990). Fractal Geometry: Mathematical Foundations and Applications. New York: John Wiley and Sons Ltd.
Gisiger, T. (2001). Scale invariance in biology: coincidence or footprint of a universal mechanism? Biol. Rev. Camb. Philos. Soc. 76, 161–207.
Goodwin, G. M., McCloskey, D. I., and Mitchell, J. H. (1972). Cardiovascular and respiratory responses to changes in central command during isometric exercise at constant muscle tension. J Physiol. 226, 173–190.
Heffernan, K. S., Sosnoff, J. J., Fahs, C. A., Shinsako, K. K., Jae, S. Y., and Fernhall, B. (2008). Fractal scaling properties of heart rate dynamics following resistance exercise training. J. Appl. Physiol. 105, 109–113.
Ivanov, P. C. H., Amaral, L. A. N., Goldberger, A. L., Havlin, S., Rosenblum, M. G., Struzik, Z. R., and Stanley, H. E. (1999). Multifractality in human heartbeat dynamics. Nature 399, 461–465.
Karavirta, L., Tulppo, M. P., Laaksonen, D. E., Nyman, K., Laukkanen, R. T., Kinnunen, H., Hakkinen, A., and Hakkinen, K. (2009). Heart rate dynamics after combined endurance and strength training in older men. Med. Sci. Sports Exerc. 41, 1436–1443.
Komatsu, T., Kimura, T., Nishiwaki, K., Fujiwara, Y., Sawada, K., and Shimada, Y. (1997). Recovery of heart rate variability profile in patients after coronary artery surgery. Anesth. Analg. 85, 713–718.
Kors, J. A., Swenne, C. A., and Greiser, K. H. (2007). Cardiovascular disease, risk factors, and heart rate variability in the general population. J. Electrocardiol. 40, S19–S21.
Kubota, Y., Sato, W., Toichi, M., Murai, T., Okada, T., Hayashi, A., and Sengoku, A. (2001). Frontal midline theta rhythm is correlated with cardiac activities during the performance of an attention demanding meditation procedure. Brain Res. Cogn. Brain Res. 11, 281–287,
Kucera, J. P., Heuschkel, M. O., Renaud, P., and Rohr, S. (2000). Power-law behavior of beat-rate variability in monolayer cultures of neonatal rat ventricular myocytes. Circ. Res. 86, 1140–1145.
Lardon, M. T., and Polich, J. (1996). EEG changes from long-term physical exercise. Biol. Psychol. 44, 19–30.
Lévy-Léhel, J., and Vojak, R. (1998). Multifractal analysis of Choquet capacities. Adv. Appl. Math. 20, 1–43.
Lin, D. C., and Sharif, A. (2007). Wavelet transform modulus maxima based fractal correlation analysis. Eur. Phys. J. B 60, 483–491.
Lin, D. C., and Sharif, A. (2010). Common multifractality in the heart rate variability and brain activity of healthy humans. Chaos 20, 023121.
Lin, D. C., Sharif, A., and Kwan, H. C. (2006). Scaling and organization of electroencephalographic background activity and alpha rhythm in healthy young adults. Biol. Cybern. 95, 401–411.
Lipnicki, D. M. (2009). Baroreceptor activity facilitates cortical inhibition in zero gravity. Neuroimage 46, 10–11.
Loewy, A., and Spyer, K. (1990). Central Regulation of Autonomic Functions. New York: Oxford University Press.
Lombardi, F. (2000). Chaos theory, heart rate variability, and arrhythmic mortality. Circulation 101, 8–10.
Lucini, D., Covacci, G., Milani, R., Mela, G. S., Malliani, A., and Pagani, M. (1997). A controlled study of effects of mental relaxation on autonomic excitatory responses in healthy subjects. Psychosom. Med. 59, 541–552.
Mahon, N. G., Hedman, A. E., Padula, M., Gang, Y., Savelieva, I., Waktare, J. E. P., Malik, M. M., Huikuri, H. V., and McKenna, W. J. (2002). Fractal correlation properties of R-R interval dynamics in asymptomatic relatives of patients with dilated cardiomyopathy. Eur. J. Heart Fail. 4, 151–158.
Makikallio, T. H., Huikuri, H. V., Makikallio, A., Sourander, L. B., Mitrani, R. D., Castellanos, A., and Myerburg, R. J. (2001). Prediction of sudden cardiac death by fractal analysis of heart rate variability in elderly subjects. J. Am. Coll. Cardiol. 37, 1395–1402.
Makikallio, T. H., Huikuri, H. V., Tulppo, M. P., Kiviniemi, A. M., Hautala, A. J., Kallio, M., and Seppanen, T. (2005). Physiological background of the loss of fractal heart rate dynamics. Circulation 112, 314–319.
Malliani, A., Montano, N., and Pagani, M. (1997). Physiological background of heart rate variability. Card. Electrophysiol. Rev. 3, 343–346.
Nikulin, V. V., and Brismar, T. (2004). Long-range temporal correlations in alpha and beta oscillations: effect of arousal level and test-retest reliability. Clin. Neurophysiol. 115, 1896–1908.
Peng, C. K., Mietus, J. E., Liu, Y., Khalsa, G., Douglas, P. S., Benson, H., and Goldberger, A. L. (1999). Exaggerated heart rate oscillations during two meditation techniques. Int. J. Cardiol. 70, 101–107.
Pereda, E., and Gonzalez, J. J. (2008). Nonlinear dynamical analysis of the interdependence between central and autonomic nervous system in neonates during sleep. J. Biol. Phys. 34, 405–412.
Phongsuphap, S., Pongsupap, Y., Chandanamattha, P., and Lursinsap, C. (2008). Changes in heart rate variability during concentration meditation. Int. J. Cardiol. 130, 481–484.
Press, W. H., Teukolsky, S. A., Vetterling, W. T., and Flannery, B. P. (2007). Numerical Recipes. New York: Cambridge University Press.
Riedi, R. H., and Scheuring, I. (1997). Conditional and relative multifractal spectra. Fractals 5, 153–168.
Sassi, R., Signorini, M. G., and Cerutti, S. (2009). Multifractality and heart rate variability. Chaos 19, 028507.
Schneider, S., Brummer, V., Carnahan, H., Dubrowski, A., Askew, C. D., and Struder, H. K. (2008). What happens to the brain in weightlessness? A first approach by EEG tomography. Neuroimage 42, 1316–1323.
Tan, C. O., Cohen, M. A., Eckberg, D. L., and Taylor, J. A. (2009). Fractal properties of human heart period variability: physiological and methodological implications. J. Physiol. 587, 3929–3941.
Task Force of ESC and NASPE. (1996). Heart rate variability, standards of measurement, physiological interpretation, and clinical use. Circulation 93, 1043–1065.
Ter Horst, G. J., Hautvast, R. W. M., De Jongste, M. J., and Korf, J. (1996). Neuroanatomy of cardiac activity-regulating circuitry: a transneuronal retrograde viral labelling study in the rat. Eur. J. Neurosci. 8, 2029–2041.
Ter Horst, G. J., Toes, G. J., and Van Willigen, J. D. (1991). Locus coeruleus projections to the dorsal motor va- gus nucleus in the rate. Neuroscience 45, 153–160.
Togo, F., Kiyono, K., Struzik, Z. R., and Yamamoto, Y. (2006). Unique very low-frequency heart rate variability during sleep in humans. IEEE Trans. Biomed. Eng. 53, 28–34.
Tulppo, M. P., Hautala, A. J., Makikallio, T. H., Laukkanen, R. T., Nissila, S., Hughson, R. L., and Huikuri, H. (2003). Effects of aerobic training on heart rate dynamics in sedentary subjects. J. Appl. Physiol. 95, 364–372.
Tulppo, M. P., Hughson, R. L., Makikallio, T. H., Airaksinen, K. E., Seppanen, T., and Huikuri, H. V. (2001). Effects of exercise and passive head-up tilt on fractal and complexity properties of heart rate dynamics. Am. J. Physiol. Heart Circ. Physiol. 280, H1081–H1087.
Van den Berg, J., Neely, G. U., Wiklund, and Landstrom, U. (2005). Heart rate variability during sedentary work and sleep in normal and sleep-deprived states. Clin. Physiol. Funct. Imaging 25, 51–57.
Appendix A
Fractal time series can be coupled together in various ways, while maintaining the same set of scaling exponents. This has been demonstrated by using binomial cascades (Falconer, 1990). Albeit being a phenomenology model, the binomial cascade is used extensively to simulate multifractal property in many natural processes. It is constructed iteratively from coarse to fine scales. Each iterative step produces a version of the time series according to the scale of resolution. As this process continues ad infinitum, the time series so generated exhibits power law power spectrum and multifractal property (Falconer, 1990), the stylized facts of fractal HRV (Ivanov et al., 1999;Sassi et al., 2009). By coupling two binomial cascades systematically can produce a wide range of fractal correlation property, while maintaining the same set of scaling exponents of the individual cascades. This was shown for the binomial cascade built by using random placement scheme and deterministic weights [equations (10, 16, 17) in Lin and Sharif, 2007]. It is an important fact since it implies the need to adopt a bi-variate approach to analyze the brain-heart fractal interaction.
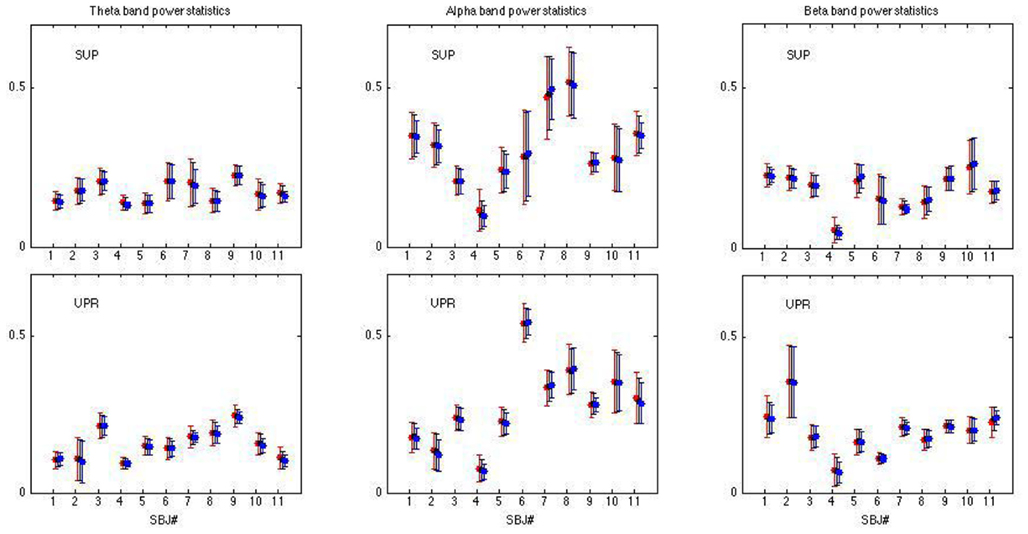
Figure A1. Spectral measures of y(n) using different aggregation: 64 beats (red), 128 beats (black), and 256 beats (blue). The error bar corresponds to 1 SD.
Appendix B
Equation (1) is generally known as the partition function in the literature; (see, e.g. Falconer, 1990). The relative scaling exponent estimated in (2) follows the multifractal formulism using the Legendre transform (Falconer, 1990). In theory, the width estimate of the multifractal spectrum is defined for q in the entire real line (−∞, ∞). But this requires accurate statistics of the very small and large αR/E exponents, which in turn demands very long time series. For this reason, only a finite interval q ∈ [−q0, q0] could be used to estimate the width since we are limited by the time a HUT test can be performed. The width estimated turns out to be robust in that the ratio UR/E does not vary sensitively with the range of q (Lin et al., 2006).
Keywords: multifractal HRV, central nervous system, autonomic nervous system, fractal correlation
Citation: Lin DC and Sharif A (2012) Integrated central-autonomic multifractal complexity in the heart rate variability of healthy humans. Front. Physio. 2:123. doi: 10.3389/fphys.2011.00123
Received: 04 September 2011;
Accepted: 28 December 2011;
Published online: 07 February 2012.
Edited by:
Riccardo Barbieri, Massachusetts Institute of Technology, USAReviewed by:
Van Toi Vo, International University of Vietnam National Universities, VietnamYoshiharu Yamamoto, University of Tokyo, Japan
Copyright: © 2012 Lin and Sharif. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: D. C. Lin, Department of Mechanical and Industrial Engineering, Ryerson University, 350 Victoria Street, Toronto, ON, Canada M5B 2K3. e-mail:ZGVybGluQHJ5ZXJzb24uY2E=


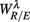 .
.