- 1 Wyss Institute for Biologically Inspired Engineering, Harvard University, Boston, MA, USA
- 2 Department of Psychology, University of Connecticut, Storrs, CT, USA
- 3 Center for the Ecological Study of Perception and Action, University of Connecticut, Storrs, CT, USA
- 4 Haskins Laboratories, New Haven, CT, USA
Self-organized criticality purports to build multi-scaled structures out of local interactions. Evidence of scaling in various domains of biology may be more generally understood to reflect multiplicative interactions weaving together many disparate scales. The self-similarity of power-law scaling entails homogeneity: fluctuations distribute themselves similarly across many spatial and temporal scales. However, this apparent homogeneity can be misleading, especially as it spans more scales. Reducing biological processes to one power-law relationship neglects rich cascade dynamics. We review recent research into multifractality in executive-function cognitive tasks and propose that scaling reflects not criticality but instead interactions across multiple scales and among fluctuations of multiple sizes.
Fractally scaled, intermittent fluctuations in biological systems (see Yates, 2010 for a review) are often interpreted as evidence of self-organized criticality (SOC; Bak, 1996; Solé et al., 1999). SOC differs from forced criticality in which similarly fractal, intermittent fluctuations arise from external tuning, as suggested for magnetospheric dynamics (Chang, 1999). Logical quandaries of distinguishing “external” from “internal” tuning forces have long plagued biological theorizing (Lewontin, 1991), making SOC more apt for explaining biological fractal scaling in terms of criticality. Specifically, in this formalism, systems composed of many components exhibit sudden avalanche-like events occurring instantaneously as a non-linear consequence of slowly driven local interactions. SOC generates fractal scaling as power-law distributed avalanche magnitudes, power-law distributed inter-avalanche time intervals, and power-law temporal correlations. “Self-organization” in SOC refers only to global structure emerging from endogenous non-global interactions under specific constraints; SOC-like phenomena occur whetheror not these constraints are themselves self-organized. In order for life to reflect SOC, it must evolve over two time scales: avalanche-like events at a short time scale, following from the slow accumulation of relatively quiescent local interactions among components over a long time scale.
It is important to distinguish model systems sometimes exhibiting SOC from the SOC formalism itself. The SOC formalism operates on strictly local interactions and predicts “finite-size scaling”: (monofractal) power-law distribution of avalanche features within constraints of system size (Brankov et al., 2000). However, models systems sometimes demonstrating the SOC formalism do not necessarily stay tethered to these criteria and, outgrowing the formalism they were originally designed to illustrate, show their deeper roots in more general cascade mechanisms permitting a wider variety in scaling. Evidence of multifractal scaling in sandpile models is not predicted by the SOC formalism (Tebaldi et al., 1999; Cernak, 2006; Bonachela and Muñoz, 2009). The SOC formalism reflects one specific cascade mechanism that explains monofractal scaling; cascades comprise a wider set of formalisms predicting a wider range of scaling, describing multiplicative processes with contingencies across potentially many scales (i.e., two or more). Sandpile or forest-fire models systems can be explained in terms of SOC when generating monofractal scaling or in more general terms of cascade mechanisms not necessarily predicting monofractal scaling. As mathematical formalisms producing structure from endogenous interactions, cascades are no less self-organized than SOC and no less compatible with an absence of extrinsic tuning (Schertzer and Lovejoy, 1994; Turcotte et al., 2002). We do not deny the need to explain monofractal scaling; we only mean to highlight the broader range of cascade formalisms beyond SOC for those cases when scaling is multifractal.
Evidence of scaling in biology once attributed to criticality has now been shown to reflect the more general case of multiplicative multifractal cascades (Ivanov et al., 2001; Plotnick and Sepkoski, 2001; Grasman et al., 2003; Newman, 2005; Ihlen and Vereijken, 2010). Similarly, we aim to align evidence of scaling with multifractal cascades rather than SOC in the domain of executive control. Executive control encompasses the goal-directed, intentional properties of behavior fundamental to living systems. Though commonly discussed in cognitive terms, executive control is treated as a prerequisite for self-regulation (Barkley, 2001), one of the major hallmarks of life (Iberall and Soodak, 1987). We review previous findings and present new results suggesting that fractal scaling in executive control reflects multiplicative, multifractal cascade dynamics rather than SOC.
Executive Control
Executive control is a crucial phenomenon in cognition and in living systems more generally. It involves the apparent coordination of a broad hierarchy of nested subsystems and nested time scales to pursue the diverse goals that are necessary for maintaining life and for operating in the environment. Consider, for example, the goal of reading a paper, an activity that unfolds at a relatively short time scale of hours (Logan, 2001). Beyond this time scale, there are goals relating to pursuing a lifelong career in this or that field. Even as a cognitive system reads a manuscript, there are goals at finer time scales, such as the goal of moving one’s eyes to the next word or comprehending a paragraph. For each of these goals, there is a similar involvement of the same neurons, muscle groups, brain structures, all coacting and reshaping one another over the course of experience (Van Orden, 2010).
In this review, we will highlight two tasks used by cognitive scientists to probe executive control. The first task probes how executive control sets the pace for the cognitive system. The cognitive system has to somehow gauge when it is appropriate to act or to postpone an action (e.g., Verbruggen and Logan, 2008). The second task probes how executive control modulates flexible use of rules. For smoothly coordinated performance, cognitive systems need to detect regularities (e.g., rules), and potentially change rules as circumstances change.
Inhibition and Pacing: Temporal Coordination of the Cognitive System
Executive control’s inhibitory effects are crucial for keeping the cognitive system in temporal coordination with events in the environment. Although these effects are often interpreted in terms of prediction from internal models (e.g., mental representations, timekeepers; Repp, 2005), it has been unclear what temporal coordination might involve when events are statistically less amenable to prediction. For instance, in previous research we asked human participants to entrain their tapping to chaotic metronomes (i.e., with onsets intervals defined by a chaotic map), that is, to tap in synchrony with – not just before or after – metronome onsets spaced chaotically through time (Stephen et al., 2008). Whereas periodic metronomes are easily predictable (i.e., exhibiting high linear redundancy), chaotically spaced onsets present difficulties for standard linear prediction (i.e., exhibiting weak linear redundancy).
Entrainment to the chaotic metronomes was variable enough to render an onset-by-onset analysis of performance intractable. However, despite failures of executive control to pace the cognitive system appropriately at an individual-onset level, participants exhibited a striking form of entrainment at relatively longer scales. Monofractal analysis of inter-onset intervals from the metronome and inter-tap intervals from the human participants revealed that both intervals exhibited a wide range of fractally scaled temporal correlations. Furthermore, fractal-scaling exponents from participants’ inter-tap intervals strongly correlated with fractal-scaling exponents from corresponding metronomes’ inter-onset intervals (Stephen et al., 2008). Against expectations from SOC, both intervals (inter-onset and inter-tap) failed to exhibit power-law relationships between magnitude and frequency. Comparison of inter-tap intervals and inter-onset intervals to phase-randomized surrogates revealed multifractality (i.e., width of the inter-tap intervals’ multifractal spectrum) driven by the multiplicativity of the inter-onset intervals rather than by additive structure in either task or behavior. Fluctuations in executive control thus appear to enlist a coordination of multiplicative multifractal cascade dynamics between organism and task environment (Stephen and Dixon, 2011).
Rule Change from Feedback and from Induction
Reanalysis of previously published data (see Anastas et al., 2011) may strengthen the relevance of multiplicative multifractal cascade dynamics to executive control. After giving informed consent (approved by the University of Connecticut Institutional Review Board), 26 adult human participants completed a dimensional card-sort task (e.g., Zelazo et al., 2003). In card-sort tasks, cards vary on multiple dimensions, and completion of the task involves sorting cards according to one dimension at a time. Research in executive control addresses selective attention to important dimensions of the task environment. Executive control also involves switching from one rule to another, and so these tasks involve changing the sorting rule, i.e., the dimension according to which cards are sorted. Effective executive control is exhibited by both stability in selective attention to one dimension and flexibility in sorting to reflect rule changes.
In our task, participants had a shuffled deck of cards depicting animals reflecting fully crossed combinations of four levels of three dimensions: (1) animal (fox, cow, lion, pig), (2) color (red, blue, green, orange), and (3) accessory (hat, glasses, bowtie, earring). They sorted individual cards into four discard piles according to one of the three dimensions and received verbal experimenter feedback for each sorted card. Once participants mastered the rule sufficiently to sort 10 consecutive cards correctly, the experimenter changed the rule. We manipulated whether participants were explicitly told the new rule. The task was complete once participants had demonstrated rule mastery five different times; each of these occasions of rule mastery was treated as a “trial.” That is, the experimenter began the task with one rule and changed the rule four times afterward. We used motion capture to measure movement trajectory of each participant’s sorting hand over the course of each trial. See Anastas et al. (2011) for further details.
We were interested in how the multiscale structure of sorting behavior would elucidate the dynamics of specifically different functions of executive control: rule application and rule induction (e.g., Crone et al., 2008). In the “explicit” condition, the experimenter instructed the participant verbally as to the proper sorting dimension at the outset of each trial; this condition thus invited rule application. In the “induction” condition, the experimenter gave no such instruction and left the participant to induce the rule strictly based on feedback. In our previous work, monofractal analysis (i.e., detrended fluctuation analysis [DFA]; Peng et al., 1994) of minimally overlapping windows (800-samples long beginning every 600 samples; e.g., Liu et al., 1997; Yuan et al., 2009) of the interpoint Euclidean displacement time series of sorting-hand movements yielded evidence of significant differences in the local Hurst exponent across trial. This monofractal DFA-based estimate of H expresses the strength of long-range correlations assuming homogeneously sized fluctuations.
Mastery of card-sort rules was predicted by different patterns of change in local H (all within the fractal range) over the course of a trial depending on the task condition. In the explicit condition, local H decreased linearly as participants repeatedly applied the known rule; in the induction condition, local H exhibited negative parabolic trajectories, with local H first increasing as participants induced the rule from feedback and later decreasing as participants’ sorting behavior settled into stable rule application. Consistent with previous findings on rule induction in problem solving (Stephen and Dixon, 2009; Stephen et al., 2009), this result suggests that selective strengthening or weakening of fractal scaling reflects the breaking or reforming of constraints on cognitive performance (Anastas et al., 2011). However, this interpretation only considered the possibility of monofractal scaling and not, more broadly, of multiplicative multifractal cascades weaving together heterogeneously sized fluctuations across multiple time scales.
Of course, an important question is: how would the local H change in this executive-control task? Is the change in scaling due to a change in strictly local interactions, as predicted from the premises of the SOC formalism, or to the coordination of heterogeneously sized fluctuations, as predicted from multifractal cascade formalism? Whereas SOC predicts that fractal scaling should result from strictly local interactions of many components, multifractal cascade dynamics allow the possibility that fractal scaling might arise from the temporally correlated fluctuations of many different sizes. Revisiting the same data with multifractal analysis would allow investigating the temporal correlations for fluctuations of different sizes within the same time series. Perhaps the dynamics of executive control reflect interactions among the temporal correlation of heterogeneously sized fluctuations.
For this reanalysis, we used multifractal DFA (MF-DFA; Kantelhardt et al., 2002) to assess temporal correlations for different-sized fluctuations. MF-DFA generalizes DFA with a parameter q that emphasizes selectively differently sized fluctuations, as
where y is the integration of the measured time series, yv is a series of linear fits to y over Ns non-overlapping windows of size s and
where H(q) reflects the temporal correlations for relatively larger fluctuations when q > 2 and for relatively smaller fluctuations when q < 2. Standard DFA tests for monofractality, only evaluating Eq. 2 for q = 2. Monofractal processes exhibit all H(q) equal to H(2). Multifractal processes exhibit non-increasing H(q) with increasing q. Legendre transformation of H(q) yields a range of Holder exponents α(q), whose range specifies the width of a multifractal spectrum.
Multifractality is evidence of heterogeneous fractal scaling. This heterogeneity could be symptomatic of non-Gaussian processes, or it could reflect interactions of heterogeneously sized fluctuations predicted from the multifractal cascade formalism (Kantelhardt et al., 2002). In the latter case, multifractal-spectrum width for the original series will be significantly different from that for phase-randomized surrogates preserving the distribution and power spectrum (e.g., Ihlen and Vereijken, 2010). Also, the multiplicative contingency of cascade dynamics suggests that different H(q) exponents should not vary independently of one another. Rather, cascade dynamics would predict that temporal structure of fluctuations of one size should have effects on temporal structure of fluctuations of other sizes.
Whereas previous work (Anastas et al., 2011) only estimated H(q) for q = 2, we now investigated whether the dynamics of executive control exhibit multifractal fluctuations and whether changes in temporal correlations at q = 2 reflect contributions of temporal correlations from other values of q. We submitted the same 800-sample windows as in Anastas et al. (2011) to MF-DFA in order to evaluate temporal correlations for different fluctuation sizes for values of q incremented from -4 to 4 by 0.5. Figure 1 shows the mean H(q) for each q and for each epoch leading up to rule mastery across all series by condition. Dynamics of executive control exhibit a monotonic decrease in H(q) with greater q, indicating multifractality, in both conditions. Consistent with cascade dynamics, multifractal spectra widths were all significantly different from those for samples of 50 iterative amplitude adjusted Fourier-transform (IAAFT; Schreiber and Schmitz, 1996) surrogates designed to preserve the original distribution and power spectrum and to randomize phase, p < 05, suggesting interactions amongst time scales.
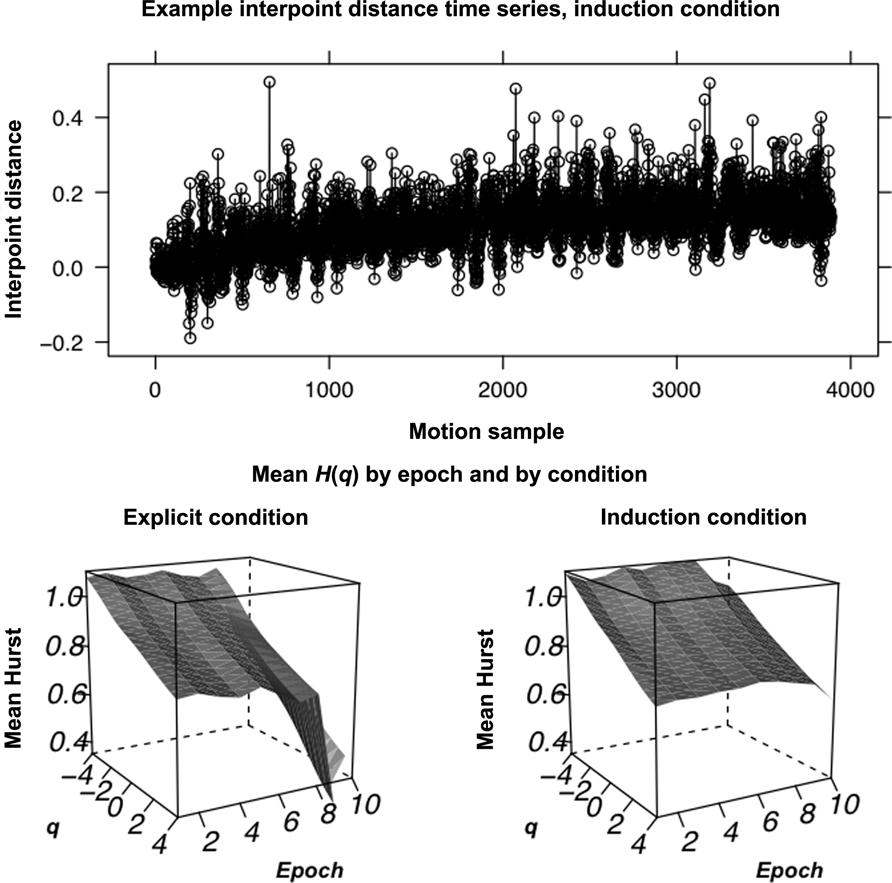
FIGURE 1. Example sorting fluctuations and mean Hurst exponents. Above: A sample interpoint distance time series, for the induction condition. The calculated Euclidean distance between each point is plotted against motion-capture sample. Below:The mean H(q) curve by condition plotted across q as well as over epochs leading up to rule mastery. As can be seen, the trajectory of H(2) is simply decreasing in the explicit condition whereas H(2) follows more of an arc in the induction condition, first increasing and then decreasing on the approach to rule mastery. We sought to use vector error-correction (VEC) modeling to test whether H(q) for other q contributed to later changes in H(2).
As noted above, we were not simply curious about interactions among time scales but also amongst fluctuations of different sizes. Could changes in local H(2) be due to interactions among relatively large or relatively small fluctuations, as might be predicted from the multiplicative multifractal cascade formalism? Because participants in the induction condition exhibited an increase in local H, compared with the general decrease in local H in the explicit condition, we predicted that changes in H for fluctuations of different sizes (i.e., for different q) would contribute significantly to increases and decreases in H(2) in the induction and explicit conditions, respectively.
To test for the cascade phenomena of interactions among fluctuations of different sizes, we modeled interactions among local H exponents for different values of q using vector error-correction (VEC) modeling. VEC modeling first tests for the long-term equilibrium relationship among a set of measured variables. This relationship may be described as “cointegrated” when the variables maintain their relationships over time. Individual variables are free to vary around this long-run equilibrium in the short term. However, the maintenance of long-run equilibrium depends on the variables correcting for each other’s error. VEC modeling tests specifically unique effects of each individual variable on each other variable in the short-term. These short-run effects allow forecasting the future responses of each individual variable to impulse (or perturbation) from each other variable (and from itself) in impulse response function (IRF). IRFs represent effects of adding one standard error to the current value of one variable on later predicted values of other variables (Sims, 1980; Lütkepohl, 2006).
If multifractality does not reflect cascade dynamics, there should be no reason to expect any short-term relationships between H(q) for different-sized fluctuations: aggregate system dynamics (e.g., drift) might make the long-term relationships agree, but there would be no reason to expect fluctuations of any single size to have unique effects on fluctuations of another size. This notion is comparable to the observation that cascade-driven time series should differ from phase-randomized, power-spectrum-preserving surrogates (Ihlen and Vereijken, 2010). However, if cascade dynamics hold, then there should be unique short-term relationships between fluctuations of different sizes above and beyond any aggregate drift in the system.
We investigated the relationship among local H(q) exponents for q = -4 through q = 4, with q incremented by 0.5 (i.e., nine endogenous variables), using VEC modeling. These local H(q) exponents for each epoch were entered into a VEC model. VEC modeling demonstrated, first, that there were eight cointegration relationships among them. Subsequent IRFs (Figure 2) indicated unique short-term effects of different H(q) on H(2).In the explicit condition (Figure 2, top panel), H(4), H(-4), and H(2) each contribute negatively to later values of H(2). In the induction condition, H(4), H(-4), and H(2) each contribute positively to later values of H(2). An increase of each of these H(q) had significant unique short-term effects on H(2) in condition-dependent directions. As predicted above, changes in local H previously found to predict rule mastery (in Anastas et al., 2011) were attributable to unique short-term interactions among fluctuations of different sizes. Thus, changes in multifractality do not simply reflect long-term aggregate drift. Changes in local H are not uniform throughout a system, and this heterogeneity may itself contribute to the change in cognitive performance.
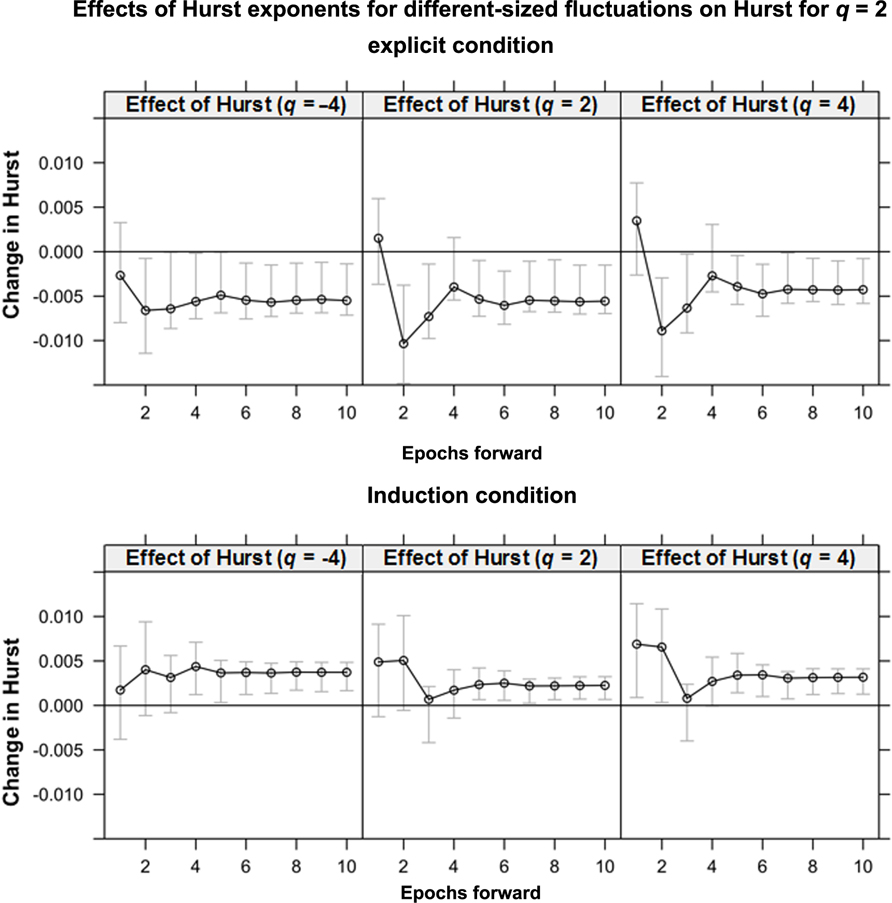
FIGURE 2. The effect of local Hurst exponent H for three different size-weightings of fluctuations (qs = -4, 2, and 4) on later H for fluctuations weighted homogeneously (i.e., q = 2). The y-axis represents the change in the Hurst exponent caused by the perturbation; the x-axis represents time steps after the perturbation. The gray bars are 95% confidence intervals. In the explicit condition, for each weighting of q, perturbation leads to a significant decrease in later H. In the induction condition, perturbation leads to a significant increase in later H.
Concluding Remarks
Executive control is a general phenomenon of biological systems whose explanation lies in generic principles of complexity, rather than specifically cognitive mechanisms (Van Orden, 2010). However, the evidence of scaling in executive control does not point simply to SOC-like dynamics. Like many other aspects of living systems (Ivanov et al.,2001; Plotnick and Sepkoski, 2001; Ihlen and Vereijken, 2010), executive control is better understood through multiplicative multifractal cascade dynamics.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgment
This work was supported by the Wyss Institute for Biologically Inspired Engineering, Harvard University.
References
Anastas, J. R., Stephen, D. G., and Dixon, J. A. (2011). The scaling behavior of hand motions reveals self-organization during an executive-function task. Physica A 390, 1539–1545.
Bak, P. (1996). How Nature Works: The Science of Self-organized Criticality. New York: Springer-Verlag.
Barkley, R. A. (2001). The executive functions and self-regulation: an evolutionary neuropsychological perspective. Neuropsychol. Rev. 11, 1–29.
Bonachela, J. A., and Muñoz, M. A. (2009). Self-organization without conservation: true or just apparent self-similarity? J. Stat. Mech. 2009, P09009.
Brankov, J. G., Danchev, D. M., and Tonchev, N. S. (2000). Theory of Critical Phenomena in Finite-size Systems: Scaling and Quantum Effects. Singapore: World Scientific.
Cernak, J. (2006). Inhomogeneous sandpile model: crossover from multifractal scaling to finite-size scaling. Phys. Rev. E 73, 066125.
Chang, T. S. (1999). Self-organized criticality, multifractal spectra, sporadic localized reconnections and intermittent turbulence in the magnetotail. Phys. Plasmas 6, 4137–4145.
Crone, E. A., Zanolie, K., Van Leijenhorst, L., Westenberg, P. M., and Rombouts, S. A. R. B. (2008). Neural mechanisms supporting flexible performance adjustment during development. Cogn. Affect. Behav. Neurosci. 2, 165–177.
Grasman, J., Brascamp, J. W., van Leeuwen, J. L., and van Putten, B. (2003). The multifractal structure of arterial trees. J. Theor. Biol. 220, 75–82.
Iberall, A., and Soodak, H. (1987). “A physics for complex systems,” in Self-organizing Systems: The Emergence of Order, ed. F. E. Yates (New York: Plenum), 499–520.
Ihlen, E. A. F., and Vereijken, B. (2010). Interaction-dominant dynamics in human cognition: beyond 1/fα fluctuation. J. Exp. Psychol. Gen. 139, 436–463.
Ivanov, P. C., Amaral, L. A. N., Havlin, S., Rosenblum, M. G., Stanley, H. E., and Struzik, Z. R. (2001). From 1/f noise to multifractal cascades in heartbeat dynamics. Chaos 11, 641–652.
Kantelhardt, J. W., Zschiegner, S. A., Koscielny-Bunde, E., Havlin, S., Bunde, A., and Stanley H. E. (2002). Multifractal detrended fluctuation analysis of nonstationary time series. Physica A 316, 87–114.
Liu, Y., Cizeau, P., Meyer, M., Peng, C.-K., and Stanley, H. E. (1997). Quantification of correlations in economic time series. Physica A 245, 437–440.
Logan, G. D. (2001). Executive control of thought and action: in search of the wild homunculus. Curr. Dir. Psychol. Sci. 12, 45–48.
Newman, M. E. J. (2005). Power laws, Pareto distributions and Zipf ’s law. Contemp. Phys. 46, 323–351.
Peng, C.-K., Buldyrev, S. V., Havlin, S., Simons M., Stanley, H. E., and Gold-berger, A. L. (1994). Mosaic organization of DNA nucleotides. Phys. Rev. E 49, 1685–1689.
Plotnick, R. E., and Sepkoski, J. J. (2001). A multiplicative multifractal model for originations and extinctions. Paleobiology 27, 126–139.
Repp, B. H. (2005). Sensorimotor synchronization: a review of the tapping literature. Psychon. Bull. Rev. 12, 969–992.
Schertzer, D., and Lovejoy, S. (1994). “Multifractal generation of self-organized criticality,” in Fractals in the Natural and Applied Sciences, ed. M. M. Novak (Amsterdam: Elsevier), 325–339.
Schreiber, T., and Schmitz, A. (1996). Improved surrogate data for non-linearity tests. Phys. Rev. Lett. 77, 635–638.
Solé, R. V., Manrubia, S. C., Benton, M., Kauffman, S., and Bak, P. (1999). Criticality and scaling in evolutionary ecology. Trends Ecol. Evol. 14, 156–160.
Stephen, D. G., Boncoddo, R. A., Magnuson, J. S., and Dixon, J. A. (2009). The dynamics of insight: mathematical discovery as a phase transition. Mem. Cogn. 37, 1132–1149.
Stephen, D. G., and Dixon, J. A. (2009). The self-organization of insight: entropy and power laws in problem solving. J. Problem Solving 2, 72–101.
Stephen, D. G., and Dixon, J. A. (2011). Strong anticipation: multifractal cascade dynamics modulate synchronization behaviors. Chaos Solitons Fractals 44, 160–168.
Stephen, D. G., Stepp, N., Dixon, J. A., and Turvey, M. T. (2008). Strong anticipation: sensitivity to long-range correlations in synchronization behavior. Physica A 387, 5271–5278.
Tebaldi, C., De Menech, M., and Stella, A. L., (1999). Multifractal scaling in the Bak–Tang–Wiesenfeld sandpile and edge events. Phys. Rev. Lett. 83, 3952–3955.
Turcotte, D. L., Malamud, B. D., Guzzetti, F., and Reichenbach, P. (2002). Self-organization, the cascade model, and natural hazards. Proc. Natl. Acad. Sci. U.S.A. 99, 2530–2537.
Verbruggen, F., and Logan,G.D.(2008). Automatic and controlled response inhibition: associative learning in the go/no-go and stop-signal paradigms. J. Exp. Psychol. Gen. 137, 649–672.
Yates, F. E. (2010). “Fractal applications in biology: scaling time in biochemical networks,” in Essential Numerical Computer Methods, ed. M. Johnson (Burlington, MA: Academic Press), 425–460.
Yuan, Y., Zhuang, X.-T., and Jin, X. (2009). Measuring multifractality of stock price fluctuation using multifractal detrended fluctuation analysis. Physica A 388, 2189–2197.
Keywords: executive control, self-organized criticality, card sort, multifractal, multiplicative
Citation: Stephen DG, Anastas JR and Dixon JA (2012) Scaling in executive control reflects multiplicative multifractal cascade dynamics. Front. Physio. 3:102. doi: 10.3389/fphys.2012.00102
Received: 20 January 2012; Accepted: 31 March 2012;
Published online: 19 April 2012.
Edited by:
Zbigniew R. Struzik, The University of Tokyo, JapanReviewed by:
Christopher Kello, University of California, USAStephane Roux, Ecole Normale Superieure de Lyon, France
Copyright: © 2012 Stephen, Anastas and Dixon. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Damian G. Stephen, Wyss Institute for Biologically Inspired Engineering, Harvard University, 3 Blackfan Circle, Floor 5, Boston, MA 02115, USA. e-mail:ZGFtaWFuLnN0ZXBoZW5Ad3lzcy5oYXJ2YXJkLmVkdQ==

 Jason R. Anastas2
Jason R. Anastas2