- Department of Internal Medicine, Institute of Clinical Medicine, University of Oulu, Oulu, Finland
This paper reviews the methods used for editing of the R–R interval time series and how this editing can influence the results of heart rate (HR) variability analyses. Measurement of HR variability from short and long-term electrocardiographic (ECG) recordings is a non-invasive method for evaluating cardiac autonomic regulation. HR variability provides information about the sympathetic-parasympathetic autonomic balance. One important clinical application is the measurement of HR variability in patients suffering from acute myocardial infarction. However, HR variability signals extracted from R–R interval time series from ambulatory ECG recordings often contain different amounts of artifact. These false beats can be either of physiological or technical origin. For instance, technical artifact may result from poorly fastened electrodes or be due to motion of the subject. Ectopic beats and atrial fibrillation are examples of physiological artifact. Since ectopic and other false beats are common in the R–R interval time series, they complicate the reliable analysis of HR variability sometimes making it impossible. In conjunction with the increased usage of HR variability analyses, several studies have confirmed the need for different approaches for handling false beats present in the R–R interval time series. The editing process for the R–R interval time series has become an integral part of these analyses. However, the published literature does not contain detailed reviews of editing methods and their impact on HR variability analyses. Several different editing and HR variability signal pre-processing methods have been introduced and tested for the artifact correction. There are several approaches available, i.e., use of methods involving deletion, interpolation or filtering systems. However, these editing methods can have different effects on HR variability measures. The effects of editing are dependent on the study setting, editing method, parameters used to assess HR variability, type of study population, and the length of R–R interval time series. The purpose of this paper is to summarize these pre-processing methods for HR variability signal, focusing especially on the editing of the R–R interval time series.
Introduction
Heart rate (HR) variability quantifies the fluctuations in the time intervals between individual heart beats. HR variability can be easily obtained, e.g., from Holter recordings, which is a non-invasive technique and has a relatively good reproducibility. The analysis of HR variability can provide insights into autonomic nervous function and provide information about the sympathetic-parasympathetic autonomic balance and cardiovascular health (Malik and Camm, 1995; Task Force of ESC and NASPE, 1996).
Numerous studies have been published during the last three decades about HR variability in many pathological conditions or during exercise or different physiological conditions. Analyses of HR variability have been considered as a way of quantifying the risk of different arrhythmic events or even death in conjunction with cardiac and non-cardiac disorders (Kleiger et al., 1987, 2005; Saul et al., 1988; Bigger et al., 1992; Nolan et al., 1998; Yoshikawa et al., 1999; Aronson and Burger, 2000; Huikuri et al., 2000; Malik et al., 2000; La Rovere et al., 2003; Aronson et al., 2004; Camm et al., 2004; Kataoka et al., 2004; Mäkikallio et al., 2005; Stein et al., 2005).
However, in most cases HR variability signals are imperfect, since they contain disturbances of technical or physiological origins. For instance, technical artifact may result from poorly fastened electrodes or be due to movement of the subject resulting missing beats or beats whose onset cannot be clearly identified. Premature beats (ectopic beats) and atrial fibrillation are examples of physiological artifact. Ectopic beats introduce a bias into HR variability results and represent a significant problem in the interpretation of these results (Task Force of ESC and NASPE, 1996; Berntson et al., 1997). For example, ectopic beats in R–R interval time series impair the reliability of the HR variability power spectrum by introducing false frequency components into the power spectrum. As HR variability analyses have become more popular, the need for and importance of artifact correction have been emphasized (Laguna et al., 1996; Task Force of ESC and NASPE, 1996; Salo et al., 2001; Mateo and Laguna, 2003; Thuraisingham, 2006; Tarkiainen et al., 2007; Sassi and Mainardi, 2008; Colak, 2009; Kumaravel and Santhi, 2010). Several pre-processing methods for HR variability signal have been introduced. For example, pre-processing can involve editing of artifact by deletion, interpolations, or filtering. However, these different editing methods may have their own distinct effects on HR variability results and one could end up with different values if the R–R interval time series have been edited by deletion or interpolation. This paper reviews the pre-processing methods for R–R interval time series as part of HR variability analysis. The main focus is to describe the common editing methods for R–R interval time series and how they influence the results of the analysis. In addition, common false beats occurring in R–R interval time series are described.
Background of HR Variability
The normal heart rhythm is defined by the rate of sinus node depolarization. Sinus rhythm oscillates around the mean HR, which is dependent on continuous regulation by the autonomic nervous system (ANS). The main components of the ANS are the vagal (parasympathetic) and sympathetic centers in the central nervous system and thus the HR represents the balance of the inputs from the sympathetic and parasympathetic (vagus) nerves. Parasympathetic activity has decelerating effects on the HR and correspondingly sympathetic activity elevates the HR. The dynamic balance between parasympathetic and sympathetic activity causes a continuous oscillation of the HR – this is called HR variability (Levy and Martin, 1979). Under resting conditions, parasympathetic activity is dominant and the fluctuations in HR are mainly controlled by changes in parasympathetic activity (Levy, 1971; Chess et al., 1975). HR variability can be used as a window into the cardiorespiratory control system and as a tool for examining the fluctuations of the sympathetic and parasympathetic arms of the ANS but interpretation of the results depends on the conditions under which the recording was obtained and the length of the recording itself. HR variability measures have been postulated to describe the complex interaction between the ANS and HR and their modulation by many physiological factors.
Heart rate variability can be analyzed by different methods, which are usually categorized as time domain methods, frequency-domain methods, and methods based on the non-linear dynamics of HR. HR variability analyses are performed using R–R interval time series obtained from continuous electrocardiographic (ECG) recording by detecting each QRS complex. Normal-to-normal (N–N) interval time series contain only R–R intervals resulting from sinus node depolarizations.
Time domain analyses consists of various statistical parameters such as SDNN, the standard deviation of N–N beats, rMSSD, the square root of the mean squared differences of the successive N–N interval and pNN50, the percentage of differences between adjacent N–N intervals that are by more than 50 ms (Task Force of ESC and NASPE, 1996). In addition, different geometrical approaches that utilize the sample density distribution of N–N interval durations or the sample density distribution of differences between adjacent N–N intervals have been used to examine HR variability in the time domain (Malik et al., 1989b; Farrell et al., 1991).
Heart rate variability analysis in frequency-domain entails the estimation of the power spectrum of the R–R interval time series. Power spectrum computation can be performed with parametric or non-parametric methods. Parametric methods involve modeling the signal with an autoregressive (AR) model. Non-parametric spectrum estimation usually contains a computation of the fast Fourier transform (FFT) or periodogram. Information about spectral estimates can be obtained by decomposing the spectrum of R–R interval time series into quantified frequency components or by integrating the signals over a defined frequency band. Decomposition of the HR variability power spectrum provides information of how the variance is distributed as a function of frequency. Four main frequency bands are distinguished in the power spectrum of the HR variability signal, i.e.: high frequency (HF, 0.15–0.4 Hz), low frequency (LF, 0.04–0.15 Hz), very low frequency (VLF, 0.0033–0.04-Hz), and ultra low frequency (ULF, <0.0033 Hz) components (Task Force of ESC and NASPE, 1996; Stein et al., 2000). Various physiological phenomena have been associated with these frequency bands (Penaz et al., 1968; Sayers, 1973; Akselrod et al., 1981; Cohen and Taylor, 2002). Power spectrum analysis of HR variability is a popular method for studying autonomic neural fluctuations and it has been investigated in many studies in different patient populations and study settings. In addition, HR variability analysis in frequency domain can include computation of higher order spectrum (Chandran and Elgar, 1993) and wavelet transform (Vetterli, 1992).
In addition to conventional time and frequency-domain HR variability analysis, there are other methods based on the non-linear system theory and beat-to-beat dynamics. Non-linear analyses include return maps, such as Poincaré plots, fractal scaling analysis (DFA analysis), different complexity measures (e.g., Lyaponov exponent, correlation dimension), and approximate entropy, for instance. The clinical utility of these non-linear HR variability analyses has been tested in various sets of R–R interval data (Skinner et al., 1991; Bigger et al., 1992, 1996; Peng et al., 1995; Lombardi et al., 1996b; Mäkikallio et al., 1996, 1999; Ho et al., 1997; Huikuri et al., 1998, 2000; Brennan et al., 2001; Berkowitsch et al., 2004; Camm et al., 2004; Carpeggiani et al., 2004). In addition, beat-to-beat dynamics can be studied with novel methods such as HR turbulence after ventricular premature beats (VPB; Schmidt et al., 1999; Bauer and Schmidt, 2003) and deceleration capacity of HR (Bauer et al., 2006).
More detailed information about the various HR variability measures and their physiological background have been reviewed previously (Cohen and Taylor, 2002; Watanabe, 2003; Reed et al., 2005; Freeman, 2006; Bansal et al., 2009; Huikuri et al., 2009; Valentini and Parati, 2009; Wheat and Larkin, 2010; Karim et al., 2011).
Assessment of the HR Variability Signal
The HR variability signal is usually obtained from an ECG recording that is captured over a certain period of time. Recording of the ECG is traditionally performed with a portable, ambulatory, electrocardiography device, a Holter monitor that enables recording of the heart rhythm continuously in outpatients although currently multiday recordings are beginning to be obtained via outpatient telemetry. Holter monitors are worn by the patients during his/her normal daily activities. Subsequently, the ECG data are uploaded to a computer for further processing and analysis. QRS complexes are detected from the ECG and the R-peak is usually used as the fiducial point due to its readily distinguishable amplitude. In fact, the true marker for HR is the P wave onset, since the P wave is a more accurate marker of onset of the atrial depolarization than the R-peak (Clifford, 2006). However, in most cases the amplitude of the P wave is too low and difficult to detect accurately. Detection of the R-peaks is an important stage in the acquisition of the HR variability signal and requires a robust algorithm, i.e., the more accurate the R-peak detection, the less error in the R–R interval time series and in the subsequent HR variability analysis. Thus, the importance of accurate R-peak detection and high-quality software cannot be over-emphasized.
QRS complexes or R-peaks can be detected with different algorithms based for example on Hilbert transform (Benitez et al., 2001) or some other digital filtering methods (Pan and Tompkins, 1985; Hamilton and Tompkins, 1986; Israel et al., 2005; Arzeno et al., 2008), pattern recognition (Mehta et al., 1996), and wavelet transform (Mehta et al., 1996; Romero et al., 2003; Abdelliche and Charef, 2009), etc. Usually these methods include a feature extraction phase and a decision phase. There can be differences in the quality between different R-peak detection methods. Problems may appear especially with ECG signals containing noise, irregular rhythm, or frequently varying morphology of the QRS complexes. The more accurate the R-peak detection method the fewer missed and false R-peaks will need to be edited in R–R interval time series (Köhler et al., 2002; Manikandan and Soman, 2012). However, currently there are no detailed or standardized recommendations in the literature about the R-peak detection methods for inclusion in HR variability analyses. High-quality R–R interval software should contain a visual view of the actual point positions in the ECG signal of the R-peak detection process and the possibility to correct any false points. The correction of false points should be performed with accurate algorithm instead of manual correction to avoid errors. More information about the QRS complex detection can be found in the review of Köhler et al. (2002).
In addition, the better the sampling frequency in the ECG recording the better the resolution of the R–R interval time series. Sampling rate is recommended to be at least 500–1000 Hz (Task Force of ESC and NASPE, 1996). A low sampling rate may cause dispersion in the R-peak estimation and furthermore it will introduce bias into HR variability results, especially into spectrum, and some non-linear measures (Merri et al., 1990).
In order to form R–R interval time series, first, the difference in time of each of two consecutive R intervals is computed. Next, durations of the consecutive R–R intervals are defined and they form the discrete R–R interval time series, called the R–R interval tachogram or the HR variability signal. The R–R interval time series is not sampled at uniform intervals due to differences in the duration of adjacent heart beats. The fact that R–R intervals are represented as a function of time has to be taken into account, especially in the frequency-domain analysis. To avoid this issue, different approaches have been used prior to spectrum analysis. One approach is to compute the power spectrum directly from R–R interval time series available in function of the beat index. However in this approach, the spectrum is not a function of frequency but instead it is a function of cycles per beat (DeBoer et al., 1984; Baselli et al., 1987). Another approach is to resample R–R interval time series with different interpolation methods, such as spline interpolation in an attempt to distribute the non-equidistantly sampled R–R intervals so that they are equally spaced (Task Force of ESC and NASPE, 1996). The third approach is to use an integral pulse frequency modulation (IPFM) model. The IPFM method utilizes delta functions representing a series of impulses occurring at those times when heart beats (DeBoer et al., 1985). The generation of the R–R interval time series is illustrated in Figure 1.
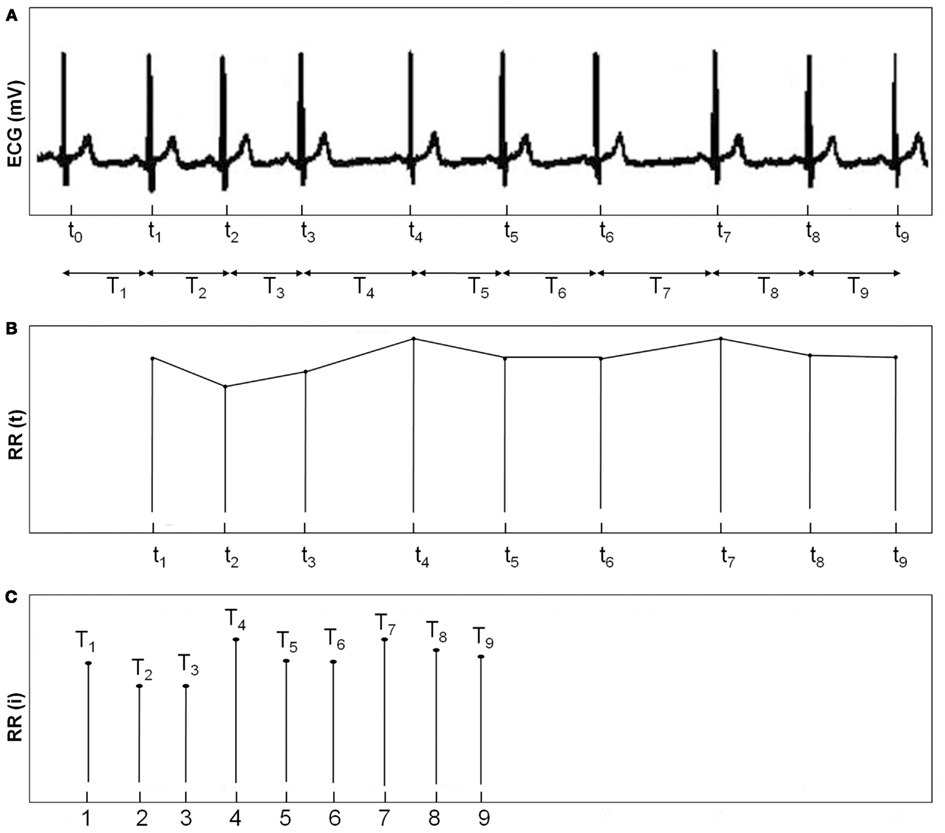
Figure 1. (A) ECG with an event series of R-peaks. (B) Interpolated R–R interval time series (C) R–R interval time series.
Artifact in the HR Variability Signal
In the ideal situation, HR variability analysis is performed with R–R interval time series including only pure sinus beats (N–N intervals). However, R–R interval time series obtained from ambulatory ECG recordings are in most cases imperfect, since they can contain a different number of abnormal beats, artifact. Abnormal R–R intervals differ from sinus rhythm in their length and they represent disturbances of both technical and physiological origins and are present in almost all Holter ECG recordings. Physiological artifacts occur especially in patients suffering from different cardiovascular diseases. For example, cardiac dysrhythmias can appear at one time or another in 90–95% of patients with acute myocardial infarction (Kamath and Fallen, 1995). If steady state conditions are maintained in a laboratory study with pre-termined duration, then it may be possible to obtain recording without artifacts, at least in healthy subjects who are not suffering from any cardiovascular disease. However, in infants or uncooperative patients or during ECG recordings lasting for several hours, it is virtually impossible to obtain steady state conditions throughout the entire recording. Therefore, artifact represent a significant problem for the measurement of HR variability since they have impact on the reliability of the results. For example, if ectopic beats are left unedited, they may bias the HR variability power spectrum by increasing the power of higher frequency bands. Ectopic beats cause also erroneously higher values of the standard deviation of the R–R intervals (Thuraisingham, 2006). In Figure 2, an example of a short-term HR variability power spectrum including false frequency components due to ventricular ectopic is shown.
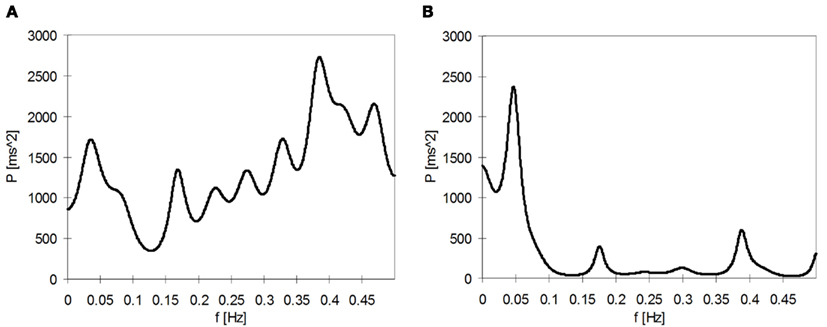
Figure 2. (A) Power spectrum of a 3-min segment of the R–R interval time series containing a VPB. (B) Corresponding power spectrum, where the VPB is edited.
Physiological artifacts appear when disturbed electrical activity in the heart produces abnormal heart rhythms. The normal rhythm originates from the sinoatrial (SA) node. Abnormal impulse formation produces disturbances such as premature (ectopic) beats and atrial or ventricular fibrillation, for instance. A premature beat of ventricular origin is known as a VPB, or a premature ventricular contraction (PVC or VPC). Correspondingly, an ectopic beat of atrial origin is known as a premature atrial contraction (PAC or SVE). These kinds of disturbances are observed in the ECG as divergent waves and QRS complexes. Disturbances in the impulse conduction can produce errors in ECG such as pauses, for example due to AV block, SA block, or variable R–R intervals due to wandering atrial pacemaker.
Almost everyone experiences ectopic beats. Ectopic beats can be common events, especially in patients with cardiovascular disease, but they can be present also in healthy subjects (Kamath and Fallen, 1995). It is possible that as many as one in every three healthy men exhibit one or more VBPs during a 1-h ECG recording (Bikkina et al., 1992). Nonetheless, the prevalence of ectopic beats will introduce a major source of error into HR variability measurement. In particular, VPBs are usually followed by a compensatory pause, before there is a return to the pre-ectopic baseline heart rhythm. In R–R interval time series, the appearance of a VPB with a compensatory pause is seen as an R–R interval of a short duration followed by a beat with a longer duration compared to normal sinus rhythm such as shown in Figure 3. Normally, both the ectopic beat and the following compensatory pause are edited.
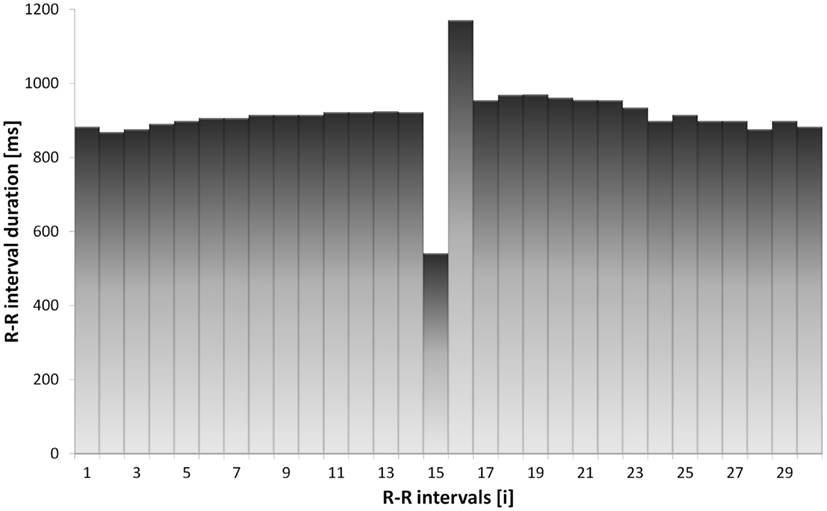
Figure 3. An example of an ectopic beat in the R–R interval time series of a MI patient. The ectopic beat appears as a short R–R interval followed by a compensatory pause.
In addition to physiological artifact, there may also be errors attributable to the technical aspects of the ECG recording. Problems may be traced to the software used to detect R–R intervals. For example, detection algorithm may fail if the threshold for R–R interval identification is set too low or too high. Technical artifact may also result from poorly fastened electrodes or from motion or sweating of the patient during the ECG recording. Technical artifact usually occur in larger epochs containing several consecutive false samples resembling random noise. Most of the Holter analysis software include some kind of automatic ECG recognition with the detection of QRS complexes and the classification of beats. Beat detection may include the possibility of labeling or annotating individual beats (Malik and Camm, 1995). However, the visual scanning of different morphologies of QRS complexes and labeling individual beats can be time consuming, especially in the case of long-term ECG recordings. For this reason, both high-quality HR data pre-processing software and the presence of an experienced Holter analysis specialist is very important if one wishes to obtain reliable HR data for analysis.
Editing of R–R Intervals
If the number of abnormal R–R intervals is relatively small and the artifact occurrence is infrequent, it is possible to reject or replace the artifacts by different correcting and editing methods before performing HR variability analysis. However, if the R–R interval time series contains many or recurrent artifacts, it is recommended that one should eliminate those entire segments with artifact prior to HR variability analysis or even to reject the entire recording (Malik and Camm, 1995). Several investigators have emphasized the importance of pre-processing of R–R interval time series to improve the quality of various HR variability analysis (Cheung, 1981; Malik et al., 1989a,b; Berntson et al., 1990, 1997; Cripps et al., 1991; Sapoznikov et al., 1992; Laguna et al., 1996; Task Force of ESC and NASPE, 1996; Salo et al., 2001; Mateo and Laguna, 2003; Thuraisingham, 2006; Tarkiainen et al., 2007; Peltola et al., 2008, 2011; Sassi and Mainardi, 2008; Colak, 2009; Kumaravel and Santhi, 2010). These studies confirm the view that the editing of R–R interval time series is an important aspect of HR variability measurement process.
Many methods and algorithms for editing or correcting the dubious R–R intervals have been developed and evaluated. Some of the common artifact correction and editing techniques involve deletion, interpolation of degree zero, interpolation of degree one (linear interpolation), and cubic spline interpolation. In addition, several other methods have been proposed for artifact correction such as comparing and merging method (Cheung, 1981), the predictive autocorrelation method (Albrecht and Cohen, 1988), non-linear predictive interpolation (Lippman et al., 1993), exclusion of R–R interval segments with divergent duration (Rottman et al., 1990; Lombardi et al., 1996a), impulse rejection (McNames et al., 2004), the integral pulse frequency model (IPFM; Mateo and Laguna, 2003; Solem et al., 2006), the sliding window average filter (Mietus, 2006), non-linear filtering combined with wavelet based trend removal (Thuraisingham, 2006), and threshold filtering also with wavelet based trend removal (Lee and Yu, 2010).
Probably the simplest way of editing is to delete the false R–R intervals. In the deletion process, the abnormal R–R intervals are removed and the preceding normal R–R intervals are then shifted to replace the deleted ones. Deletion editing decreases the length of the HR variability signal, i.e., due to the loss of deleted R–R intervals. This may have significant influence on HR variability, especially when assessing the power spectrum or analyzing R–R interval segments of short duration. However, if all the segments containing ectopic beats or other artifacts are deleted in an attempt to eliminate out any possible interference in HR variability analysis, this can lead to an unacceptable and systematic loss of information (Salo et al., 2001).
Interpolation methods replace the non-normal R–R intervals with new interpolated R–R intervals. Unlike the deletion method, interpolation methods preserve the initial number of samples. There are various interpolation algorithms such as interpolation of degree zero, linear, spline, and non-linear predictive interpolation. Most interpolation methods can be considered as serving as low-pass filters with different filtering capacities. Interpolation of degree zero substitutes the abnormal R–R intervals with an average value that is computed from the neighboring normal R–R intervals. In interpolation of degree one, called the linear interpolation, a straight line is fitted over the abnormal R–R intervals to obtain new values. One popular spline interpolation method is a cubic spline interpolation, where smooth curves are estimated through a number of data points by fitting a third degree polynomial. It has been recommended to use interpolation methods when R–R interval time series contains occasional ectopic beats and artifacts. This concerns especially the power spectrum HR variability analysis (Kamath and Fallen, 1995).
Non-linear predictive interpolation for R–R interval artifact correction was introduced by Lippman et al. (1993). This algorithm is based on the fact that beat-to-beat variations in HR appear in a deterministic way. This algorithm utilizes methods of originating from chaos theory for locating ectopy-free portions of the R–R interval sequence. The purpose of the ectopy-free R–R interval sequence is to describe trajectories in the phase space that are locally similar to those of the segments containing ectopic beats. A trajectory is chosen such that it approximates most accurately to the particular segment with ectopic beats and this is then used to determine the replacement R–R intervals for the ectopic beats (Lippman et al., 1993).
R–R interval time series of longer duration can also contain slow linear trends and non-stationarities. Trend removal is a common way to preprocess R–R interval time series and diminish the effects of non-stationarities on HR variability analysis. Trend removal is usually performed with detrending methods that can be based on the first or higher order polynomial models (Litvack et al., 1995; Mitov, 1998). The so called smoothness priors approach (Tarvainen et al., 2002) is another filtering method to detrend signal. Non-stationarities have effects especially on the computation of FFT power spectrum. One additional method to avoid the effects of artifacts is to compute FFT spectrum estimates in finite length windows, which contains data of 2 or 5 min (Stein et al., 1995; Task Force of ESC and NASPE, 1996). Next, the window is moved along the signal producing consecutive estimates of the spectrum. Most studies reject segments that contain less than 80% of normal-to-normal beats. The aim of this method is to obtain correct data for FFT power spectrum analysis of 24-h ECG recording. This method is suitable for estimating the power of higher frequencies, HF and LF components. The power of lower frequency bands, VLF and ULF, cannot be reliably estimated using 5-min measure, because it does not contain fluctuations with longer cycle lengths (Kleiger et al., 2005).
Effects of Different Editing Methods on HR Variability Analyses
There are studies which have compared how the different editing methods impact on the results of HR variability analyses (Albrecht and Cohen, 1988; Birkett et al., 1991; Lippman et al., 1994; Salo et al., 2001; Peltola et al., 2004; Tarkiainen et al., 2007; Sassi and Mainardi, 2008). However, these studies can produce different results depending on the study setting. Despite the differences in the results, the message is the same, editing methods do have effects on HR variability analysis. Differences between results can be attributable to the type of study populations used, the length of R–R interval time series, editing methods, the type of HR variability analyses and the amount of edited samples, etc.
Spectrum analyses are sensitive to the signal length and any loss of samples and discontinuity of signal can affect the results. It has been recommended that one should avoid the deletion method in artifact correction and to use some other replacement methods in HR variability spectrum analyses (Task Force of ESC and NASPE, 1996; Salo et al., 2001; Mateo and Laguna, 2003). Deletion of R–R intervals may introduce step-like shapes into R–R interval time series, resulting in an increase in abrupt changes in the beat-to-beat variability and disruptions in the natural fluctuation. Deletion shortens the waveform of R–R interval time series and produces false frequency components in the HF and also in the LF area, resulting in a broadening of the spectra in the HF and LF bands. For example, in the study of Salo et al. (2001) with AMI patients, the errors in the HF and LF components of the short-term R–R interval time series were over 5% when less than 5% of the R–R intervals were deletion edited. These effects on the waveform make the deletion method unsuitable also for the analyses of the VLF and ULF components (Salo et al., 2001). Furthermore, it has been reported to prefer interpolation methods to deletion method in the DFA analysis of short- (α1) and long-term (α2) fractal scaling exponents (Peltola et al., 2004; Tarkiainen et al., 2007; Sassi and Mainardi, 2008). Deletion editing may produce a false increase in the values of α1 in patients with acute myocardial infarction (Peltola et al., 2004) and in patients with coronary artery disease (Tarkiainen et al., 2007).
Although the deletion method may not be the most suitable method for editing, especially with respect to power spectrum HR variability analysis, it can be a feasible method of editing in the time domain for the analysis of SDNN and SDANN (Salo et al., 2001). However, in the same study of Salo et al. (2001), deletion editing was not recommended for the computation of pNN50 and RMSSD, again interpolation methods were considered superior. Nonetheless, deletion can be a suitable method for artifact removal in the case of the disturbances lasting for longer periods (Kamath and Fallen, 1995). These include artifacts such as frequent ectopic beats and AF, the duration of which can last from several minutes to several hours (AF).
Different interpolation methods, artifact and trend removal methods and spectrum estimation methods have been proposed to especially improve the quality of the power spectrum HR variability analysis (Albrecht and Cohen, 1988; Birkett et al., 1991; Lippman et al., 1994; Salo et al., 2001; Mateo and Laguna, 2003; McNames et al., 2004; Clifford and Tarassenko, 2005; Colak, 2009; Kumaravel and Santhi, 2010; Lee and Yu, 2010). However, the results of these studies are dependent on the methods being used and on the type and length of R–R interval data. For example, Albrecht and Cohen (1988) claimed that the linear interpolation produced a more accurate power spectrum compared to the predictive autocorrelation method.
Lippman et al. (1994) compared the removal of ectopic beats with linear, cubic, and non-linear predictive interpolation in HR variability analysis with short-term R–R interval time series. They reported the necessity for editing and concluded that the removal of ectopic beats and non-linear predictive interpolation lead to better performance compared to linear and cubic spline interpolation, which overestimated the LF power and underestimated the HF power.
Salo et al. (2001) compared the performance of deletion editing with the interpolation of degree zero and one in HR variability of frequency-domain parameters. They examined short- and long-term R–R interval data of healthy subjects and patients with AMI. They found that the interpolation of degree zero and one perform at least equally well and in some cases was superior compared to the deletion method. However, the interpolation of artifacts can change the power of the frequency components by introducing false shapes and trends into R–R interval time series. For example, interpolation of degree zero leads to flat shapes in R–R interval time series since it uses the same average value over a whole segment of successive non-normal R–R intervals. Similarly, interpolation of degree one produces slope-like shapes, especially in R–R interval time series of high beat-to-beat variability. The longer the R–R interval segment is to edit the larger the flat or slope-like shape is. This generation of false trends due to interpolation may explain why linear and cubic spline interpolation have been reported to increase the power of the LF and VLF components in HR variability spectrum (Birkett et al., 1991; Salo et al., 2001). In addition, large segments cannot reasonably be edited with the interpolation methods due to the increase in false trends.
Interpolation methods have been examined and tested also for DFA analysis. Peltola et al. (2004) evaluated several interpolation methods including interpolation of degree zero and one and cubic spline interpolation and considered them to be more suitable for the analysis of fractal scaling exponents α1 and α2 than the deletion method. They found that the performance of the different interpolation methods depended on the scaling exponent (α1 or α2) and on the data type (healthy vs. AMI patient). Peltola et al. stated that the interpolation of degree zero was the most suitable method for the analysis of α1. In their analysis of α2, Peltola et al. observed that the deletion method produced much larger errors than the interpolation method. This was confirmed by Sassi and Mainardi (2008) who showed that the linear interpolation (interpolation of degree one) and substitution with local mean (interpolation of degree zero) performed better and introduced smaller errors in the long-term DFA analysis than the deletion method. The effects between different editing methods may not be very significant when the number of artifacts is small. Peltola et al. (2004) reported that the effects of editing in DFA analysis were minor, i.e., interpolation methods were as good as the deletion method when there was a small number of ectopic beats (<5%). This was confirmed by Tarkiainen et al. (2007) who did not detect significant differences between the performance of deletion and linear interpolation in the short-term DFA analysis and other non-linear HR dynamics when the number of ectopic beats was less than 10%.
Short-term HR variability analyses are more sensitive to artifacts and editing (Task Force of ESC and NASPE, 1996). The more R–R interval samples in the signal the better the capability of maintaining the original beat-to-beat variability despite the presence of edited R–R intervals. A 24-h R–R interval time series contains approximately 90000 R–R intervals. Correspondingly, a 5-min segment may contain about 300 R–R intervals. Even a small number of edited R–R intervals may impact on the results of HR variability analyses, especially with the short-term R–R interval data. Long-term time domain analysis including computation of SDNN and long-term spectrum analysis including ULF, VLF, and the slope of the lower frequencies (Bigger et al., 1996) mainly suffer from the deletion of the R–R intervals. For example, Salo et al. (2001) demonstrated that in long-term R–R interval time series (24 h) one could use the interpolation methods to edit up to 50% of all R–R intervals without causing any major changes in the results (error <5%). However, with short-term R–R interval time series, even a small number of edited intervals (<5%) can affect HR variability results not only with the spectrum analysis of HF and LF components but also with statistical time domain parameters such as pNN50 and RMSSD (Salo et al., 2001).
Conclusion and Future Work
Ideally, the most reliable HR variability analysis is performed with R–R interval data with pure sinus beats. Technical developments in the ECG and R–R interval recording devices and improvement in the technology and materials of the electrodes have reduced the number of technical artifact. In addition, the importance of high-quality R-peak detection systems has also been noted. If one is able to perform an accurate R-peak detection, then it may be possible to decrease the number of artifact in the R–R interval time series. However, all the false R–R intervals, especially those of physiological origin, can never be eliminated. Since it is practically impossible to achieve data of 24-h free of artifact in ambulatory ECG recordings the focus must be directed to pre-processing and editing methods for the R–R intervals.
Accurate R–R interval artifact correction and editing methods are needed. It is possible to improve the quality of results of HR variability analyses with careful editing and by choosing appropriate editing methods. Various authors have proposed different approaches for handling ectopic beats and other artifacts. Nonetheless, currently there is no consensus about how to best edit artifact. The literature does not have any standard and detailed recommendations about suitable editing methods for different HR variability analyses. Only one agreement exists concerning the power spectrum analysis of HR variability: in most studies artifact and ectopic beats should be interpolated instead of deleted. In addition, the maximum number for edited R–R intervals for HR variability analyses has not been standardized. Most investigators edit or reject the artifact and require at least 80% normal R–R intervals, especially in frequency-domain HR variability analysis. However, in different studies the amount of editing has ranged from 1 to 30% of the R–R intervals.
Various HR variability studies may use different R–R interval pre-processing and editing methods. This can lead to problems in any comparison of results obtained with HR variability analyses. This can be due to the different numbers of edited R–R intervals, analyzed HR variability parameter, type of the study population (high or low HR variability), length of the R–R interval time series or due to editing method selected. In the future, it is recommended that HR variability papers should contain an accurate description of the methods selected for pre-processing and editing.
The selection of editing methods or the absence of manual editing can be a problem also in current HR variability software. There can be a lack of information about how to deal with ectopic beats and other artifacts. Some HR variability software may include automatic systems for artifact correction. These can be based on some type of prematurity threshold extracting those R–R intervals that exceed the threshold value. Others may handle artifact by applying some trend removal processes. These kinds of automatic R–R interval editing are convenient to use and may perform adequately, especially in the cases of R–R intervals time series with low beat-to-beat variability and distinct ectopic beats or normal healthy adult with any or only small number of false beats. Nonetheless, many experts believe that manual editing with visual verification of the R–R intervals and a careful choice of the appropriate editing method is a more reliable method and can never be fully replaced by the current automatic correction systems. High-quality R-peak detection system together with accurate artifact editing are crucial for reliable HR variability analyses. Trustworthy R–R interval pre-processing software should contain (1) a possibility to view the ECG signal and the results of the R-peak detection process and a possibility to correct the false points and (2) manual or automatic editing of artifacts with different editing methods and a visual view of the edited R–R interval time series.
Despite the differences in HR variability study settings, many studies emphasize the importance of the artifact correction and appropriate editing if one wishes to conduct reliable HR variability analyses. In the future, more comparative studies will be needed to define standard recommendations for the suitable pre-processing and editing methods of R–R interval time series and the maximum number of edited R–R intervals which can be present in any short- and long-term HR variability analyses.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Abdelliche, F., and Charef, A. (2009). “R-peak detection using a complex fractional wavelet,” in International Conference on Electrical and Electronics Engineering, Bursa, 267–270.
Akselrod, S., Gordon, D., Ubel, F. A., Shannon, D. C., Barger, A. C., and Cohen, R. J. (1981). Power spectrum analysis of heart rate fluctuation: a quantitative probe of beat to beat cardiovascular control. Science 213, 220–222.
Albrecht, P., and Cohen, R. J. (1988). Estimation of heart rate power spectrum bands from real-world data: dealing with ectopic beats and noisy data. Comput. Cardiol. 311–314.
Aronson, D., and Burger, A. J. (2000). Gender-related differences in modulation of heart rate in patients with congestive heart failure. J. Cardiovasc. Electrophysiol. 11, 1071–1077.
Aronson, D., Mittleman, M. A., and Burger, A. J. (2004). Measures of heart period variability as predictors of mortality in hospitalized patients with decompensated congestive heart failure. Am. J. Cardiol. 93, 59–63.
Arzeno, N. M., Deng, Z.-D., and Poon, C.-S. (2008). Analysis of first-derivative based QRS detection algorithms. IEEE Trans. Biomed. Eng. 55, 478–484.
Bansal, D., Khan, M., and Salhan, A. K. (2009). “A review of measurement and analysis of heart rate variability,” in International Conference on Computer and Automation Engineering, Bangkok, 243–246.
Baselli, G., Cerutti, S., Civardi, S., Lombardi, F., Malliani, A., Merri, M., Pagani, M., and Rizzo, G. (1987). Heart rate variability signal processing: a quantitative approach as an aid to diagnosis in cardiovascular pathologies. Int. J. Biomed. Comput. 20, 51–70.
Bauer, A., Kantelhardt, J. W., Barthel, P., Schneider, R., Mäkikallio, T., Ulm, K., Hnatkova, K., Schömig, A., Huikuri, H., Bunde, A., Malik, M., and Schmidt, G. (2006). Deceleration capacity of heart rate as a predictor of mortality after myocardial infarction: cohort study. Lancet 367, 1674–1681.
Benitez, D., Gaydecki, P. A., Zaidi, A., and Fitzpatrick, A. P. (2001). The use of Hilbert transform in ECG signal analysis. Comput. Biol. Med. 31, 399–406.
Berkowitsch, A., Zareba, W., Neumann, T., Erdogan, A., Nitt, S. M., Moss, A. J., and Pitschner, H. F. (2004). Risk stratification using heart rate turbulence and ventricular arrhythmia in MADIT II: usefulness and limitations of a 10-minute Holter recording. Ann. Noninvasive Electrocardiol. 9, 270–279.
Berntson, G. B., Bigger, J. T. Jr., Eckberg, D. L., Grossman, P., Kaufmann, P. G., Malik, M., Nagaraja, H. N., Porges, S. W., Saul, J. P., Stone, P. H., and Van der Molen, M. W. (1997). Heart rate variability: origins, methods and interpretive caveats. Psychophysiology 34, 623–648.
Berntson, G. G., Quigley, K. S., Jang, J. F., and Boysen, S. T. (1990). An approach to artifact identification: application to heart period data. Psychophysiology 27, 586–598.
Bigger, J. T. Jr., Fleiss, J. L., Steinman, R. C., Rolnitzky, L. M., Kleiger, R. E., and Rottman, J. N. (1992). Frequency domain measures of heart period variability and mortality after myocardial infarction. Circulation 85, 164–171.
Bigger, J. T. Jr., Steinman, R. C., Rolnitzky, L. M., Fleiss, J. L., Albrecht, P., and Cohen, R. J. (1996). Power law behavior of RR-interval variability in healthy middle-aged persons, patients with recent acute myocardial infarction, and patients with heart transplants. Circulation 93, 2142–2151.
Bikkina, M., Larson, M. G., and Levy, D. (1992). Prognostic implications of asymptomatic ventricular arrhythmias: the Farminghan Heart Study. Ann. Intern. Med. 117, 990–996.
Birkett, C. L., Kienzle, M. G., and Myers, G. A. (1991). Interpolation over ectopic beats increases low frequency power in HRV spectra. Comput. Cardiol. 257–259.
Brennan, M., Palaniswami, M., and Kamen, P. (2001). Do existing measures of Poincaré plot geometry reflect non-linear features of heart rate variability? IEEE Trans. Biomed. Eng. 48, 1342–1347.
Camm, A. J., Pratt, C. M., Schwartz, P. J., Al-Khalidi, H. R., Spyt, M. J., Holroyde, M. J., Karam, R., Sonnenblick, E. H., Brum, J. M., and AzimiLide post Infarct surVival Evaluation (ALIVE) Investigators. (2004). Mortality in patients after a recent myocardial infarction: a randomized, placebo-controlled trial of azimilide using heart rate variability for risk stratification. Circulation 109, 990–996.
Carpeggiani, C., L’Abbate, A., Landi, P., Michelassi, C., Raciti, M., Macerata, A., and Emdin, M. (2004). Early assessment of heart rate variability is predictive of in-hospital death and major complications after acute myocardial infarction. Int. J. Cardiol. 96, 361–368.
Chandran, V., and Elgar, S. (1993). Pattern recognition using invariants defined from higher order spectra – one-dimensional inputs. IEEE Trans. Signal Process. 41, 205–212.
Chess, G. F., Tam, R. M. K., and Calaresu, F. R. (1975). Influence of cardiac neural inputs on rhythmic variations of heart period in the cat. Am. J. Physiol. 228, 775–780.
Cheung, M. N. (1981). Detection of and recovery from errors in cardiac interbeat intervals. Psychophysiology 18, 341–346.
Clifford, G. D. (2006). “ECG statistics, noise, artifacts, and missing data,” in Advanced Methods and Tools for ECG Data Analysis, eds G. D. Clifford, F. Azuaje, and P. E. McSharry (Boston/London: Artech House Publishing), 55–99.
Clifford, G. D., and Tarassenko, L. (2005). Quantifying errors in spectral estimates of HRV due to beat replacement and resampling. IEEE Trans. Biomed. Eng. 52, 630–638.
Cohen, A. M., and Taylor, J. A. (2002). Short-term cardiovascular oscillations in man: measuring and modelling the physiologies. J. Physiol. 542, 669–683.
Colak, O. H. (2009). Preprocessing effects in time-frequency distributions and spectral analysis of heart rate variability. Digit. Signal Process. 19, 731–739.
Cripps, T. R., Malik, M., Farrell, T. G., and Camm, A. J. (1991). Prognostic value of reduced heart rate variability after myocardial infarction: clinical evaluation of a new analysis method. Br. Heart J. 65, 14–19.
DeBoer, R. W., Karemaker, J. M., and Strackee, J. (1984). Comparing spectra of a series of point events particularly for heart rate variability data. IEEE Trans. Biomed. Eng. 31, 384–387.
DeBoer, R. W., Karemaker, J. M., and Strackee, J. (1985). Spectrum of a series of point events, generated by the integral pulse frequency modulation model. Med. Biol. Eng. Comput. 23, 138–142.
Farrell, T. G., Bashir, Y., Cripps, T., Malik, M., Poloniecki, J., Bennett, E. D., Ward, D. E., and Camm, A. J. (1991). A simple method of risk stratification for arrhythmic events in post-infarction patients based on heart rate variability and signal averaged ECG. J. Am. Coll. Cardiol. 18, 687–697.
Freeman, R. (2006). Assessment of cardiovascular autonomic function. Clin. Neurophysiol. 117, 716–730.
Hamilton, P. S., and Tompkins, W. J. (1986). Quantitative investigation of QRS detection rules using the MIT/BIH arrhythmia database. IEEE Trans. Biomed. Eng. 33, 1157–1165.
Ho, K. K., Moody, G. B., Peng, C. K., Mietus, J. E., Larson, M. G., Levy, D., and Goldberger, A. L. (1997). Predicting survival in heart failure case and control subjects by use of fully automated methods for deriving nonlinear and conventional indices of heart rate dynamics. Circulation 96, 842–848.
Huikuri, H. V., Mäkikallio, T. H., Airaksinen, K. E., Seppänen, T., Puukka, P., Räihä, I. J., and Sourander, L. B. (1998). Power-law relationship of heart rate variability as a predictor of mortality in the elderly. Circulation 97, 2031–2036.
Huikuri, H. V., Mäkikallio, T. H., Peng, C. K., Goldberger, A. L., Hintze, U., and Møller, M. (2000). Fractal correlation properties of R–R interval dynamics and mortality in patients with depressed left ventricular function after an acute myocardial infarction. Circulation 101, 47–53.
Huikuri, H. V., Perkiömäki, J. S., Maestri, R., and Pinna, G. D. (2009). Clinical impact of evaluation of cardiovascular control by novel method for heart rate dynamics. Philos. Transact. A Math. Phys. Eng. Sci. 367, 1223–1238.
Israel, S. A., Irvine, J. M., Cheng, A., Wiederhold, M. D., and Wiederhold, B. K. (2005). ECG to identify individuals. Pattern Recognit. 38, 133–142.
Kamath, M. V., and Fallen, E. L. (1995). “Correction of heart rate variability signal for ectopics and missing beats,” in Heart Rate Variability, eds M. Malik, and A. J. Camm (Armonk, NY: Futura), 75–85.
Karim, N., Hasan, J. A., and Ali, S. S. (2011). Heart rate variability–a review. J. Basic Appl. Sci. 7, 71–77.
Kataoka, M., Ito, C., Sasaki, H., Yamane, K., and Kohno, N. (2004). Low heart rate variability is a risk factor for sudden cardiac death in type 2 diabetes. Diabetes Res. Clin. Pract. 64, 51–58.
Kleiger, R. E., Miller, J. P., Bigger, J. T. Jr., Moss, A. J., and Multicentre Post Infarction Research Group. (1987). Decreased heart rate variability and its association with increased mortality after acute myocardial infarction. Am. J. Cardiol. 59, 256–262.
Kleiger, R. E., Stein, P. K., and Bigger, J. T. Jr. (2005). Heart rate variability: measurement and clinical utility. Ann. Noninvasive Electrocardiol. 10, 88–101.
Köhler, B. E., Hennig, C., and Orglmeister, R. (2002). The principles of software QRS detection. Reviewing and comparing algorithms for detecting this important ECG waveform. IEEE Eng. Med. Biol. Mag. 21, 42–57.
Kumaravel, N., and Santhi, C. (2010). Nonlinear filters for preprocessing heart rate variability signals. Int. J. Comp. Sci. Network Secur. 10, 250–254.
La Rovere, M. T., Pinna, G. D., Maestri, R., Mortara, A., Capomolla, S., Febo, O., Ferrari, R., Franchini, M., Gnemmi, M., Opasich, C., Riccardi, P. G., Traversi, E., and Cobelli, F. (2003). Short-term heart rate variability strongly predicts sudden cardiac death in chronic heart failure patients. Circulation 107, 565–570.
Laguna, P., Jané, R., Olmos, S., Thakor, N. V., Rix, H., and Caminal, P. (1996). Adaptive estimation of QRS complex by the Hermite model for classification and ectopic beat detection. Med. Biol. Eng. Comput. 34, 58–68.
Lee, M. Y., and Yu, S. N. (2010). Improving discriminality in heart rate variability analysis using simple artifact and trend removal preprocessors. Conf. Proc. IEEE Eng. Med. Biol. Soc. 4574–4577.
Levy, M. N., and Martin, P. J. (1979). “Neural control of the heart,” in Handbook of Physiology, Section 2, The Cardiovascular System, Vol. I, The Heart, ed. R. M. Berne (Bethesda, MD: American Physiological Society), 581–620.
Lippman, N., Stein, K. M., and Lerman, B. B. (1993). Nonlinear predictive interpolation. A new method for the correction of ectopic beats for heart rate variability analysis. J. Electrocardiol. 26(Suppl.), 14–19.
Lippman, N., Stein, K. M., and Lerman, B. B. (1994). Comparison of methods for removal of ectopy in measurement of heart rate variability. Am. J. Physiol. 267(Pt 2), H411–H418.
Litvack, D. A., Oberlander, T. F., Carney, L. H., and Saul, J. P. (1995). Time and frequency domain methods for heart rate variability analysis: a methodological comparison. Psychophysiology 32, 492–504.
Lombardi, F., Sandrone, G., Spinnler, M. T., Torzillo, D., Lavezzaro, G. C., Brusca, A., and Malliani, A. (1996a). Heart rate variability in the early hours of an acute myocardial infarction. Am. J. Cardiol. 77, 1037–1044.
Lombardi, F., Sandrone, G., Mortara, A., Torzillo, D., La Rovere, M. T., Signorini, M. G., Cerutti, S., and Malliani, A. (1996b). Linear and nonlinear dynamics of heart rate variability after acute myocardial infarction with normal and reduced left ventricular ejection fraction. Am. J. Cardiol. 77, 1283–1288.
Mäkikallio, T. H., Barthel, P., Schneider, R., Bauer, A., Tapanainen, J. M., Tulppo, M. P., Schmidt, G., and Huikuri, H. V. (2005). Prediction of sudden cardiac death after acute myocardial infarction: role of Holter monitoring in the modern treatment era. Eur. Heart J. 26, 762–769.
Mäkikallio, T. H., Høiber, S., Køber, L., Torp-Pedersen, C., Peng, C. K., Goldberger, A. L., and Huikuri, H. V. (1999). Fractal analysis of heart rate dynamics as a predictor of mortality in patients with depressed left ventricular function after acute myocardial infarction. Am. J. Cardiol. 83, 836–839.
Mäkikallio, T. H., Seppänen, T., Niemelä, M., Airaksinen, K. E., Tulppo, M., and Huikuri, H. V. (1996). Abnormalities in beat to beat complexity of heart rate dynamics in patients with previous myocardial infarction. J. Am. Coll. Cardiol. 28, 1005–1011.
Malik, M., Camm, A. J., Janse, M. J., Julian, D. G., Frangin, G. A., and Schwartz, P. J. (2000). Depressed heart rate variability identifies postinfarction patients who might benefit from prophylactic treatment with amiodarone: a substudy of EMIAT (The European Myocardial Infarct Amiodarone Trial). J. Am. Coll. Cardiol. 35, 1263–1275.
Malik, M., Cripps, T., Farrell, T., and Camm, A. J. (1989a). Prognostic value of heart rate variability after myocardial infarction – a comparison of different data processing methods. Med. Biol. Eng. Comput. 27, 603–611.
Malik, M., Farrell, T., Cripps, T., and Camm, A. J. (1989b). Heart rate variability in relation to prognosis after myocardial infarction: selection of optimal processing techniques. Eur. Heart J. 10, 1060–1074.
Manikandan, M. S., and Soman, K. P. (2012). A novel method for detecting R-peaks in electrocardiogram (ECG) signal. Biomed. Signal Process. Control 7, 118–128.
Mateo, J., and Laguna, P. (2003). Analysis of heart rate variability in the presence of ectopic beats using the heart time signal. IEEE Trans. Biomed. Eng. 50, 334–343.
McNames, J., Thong, T., and Aboy, M. (2004). “Impulse rejection filter for artifact removal in spectral analysis of biomedical signals,” in Proceeding of the 26th Annual International Conference of the IEEE EMBS, San Francisco, CA, 145–148.
Mehta, S. S., Saxena, S. C., and Verma, H. K. (1996). Computer-aided interpretation of ECG for diagnostics. Int. J. Syst. Sci. 27, 43–58.
Merri, M., Farden, D. C., Mottley, J. G., and Titlebaum, E. L. (1990). Sampling frequency of the electrocardiogram for spectral analysis of the heart rate variability. IEEE Trans. Biomed. Eng. 37, 99–106.
Mietus, J. E. (2006). Time-Domain Measures: From Variance to pNNx. Boston: Beth Israel Deaconess Medical Center, Harvard Medical School.
Mitov, I. P. (1998). A method for assessment and processing of biomedical signals containing trend and periodic components. Med. Eng. Phys. 20, 660–668.
Nolan, J., Batin, P. D., Andrews, R., Lindsay, S. J., Brooksby, P., Mullen, M., Baig, W., Flapan, A. D., Cowley, A., Prescott, R. J., Neilson, J. M., and Fox, K. A. (1998). Prospective study of heart rate variability and mortality in chronic heart failure: results of the United Kingdom heart failure evaluation and assessment of risk trial (UK-Heart). Circulation 98, 1510–1516.
Pan, J., and Tompkins, W. J. (1985). A real time QRS detection algorithm. IEEE Trans. Biomed. Eng. 32, 230–236.
Peltola, M., Tulppo, M. P., Kiviniemi, A., Hautala, A. J., Seppänen, T., Barthel, P., Bauer, A., Schmidt, G., Huikuri, H. V., and Mäkikallio, T. H. (2008). Respiratory sinus arrhythmia as a predictor of sudden cardiac death after myocardial infarction. Ann. Med. 40, 376–382.
Peltola, M. A., Bloch Thomsen, P. E., Moerch Joergensen, R., Huikuri, H., and Cardiac Arrhythmias, and Risk Stratification after Acute Myocardial Infarction (CARISMA) Investigators. (2011). Effects of post-ectopic heart rate turbulence on measures of heart rate variability in patients after an acute myocardial infarction. Ann. Noninvasive Electrocardiol. 16, 123–130.
Peltola, M. A., Seppänen, T., Mäkikallio, T., and Huikuri, H. (2004). Effects and significance of premature beats on fractal correlation properties of R-R interval dynamics. Ann. Noninvasive Electrocardiol. 9, 124–135.
Penaz, J., Roukenz, J., and vander Waal, H. J. (1968). “Spectral analysis of some spontaneous rhythms in the circulation,” in Byokibernetik, eds H. Drischel and N. Tiedt (Leipzig: Karl Marx University), 233.
Peng, C. K., Havlin, S., Stanley, H. E., and Goldberger, A. L. (1995). Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time series. Chaos 5, 82–87.
Reed, M. J., Robertson, C. E., and Addison, P. S. (2005). Heart rate variability measurements and the prediction of ventricular arrhythmias. Q. J. Med. 98, 87–95.
Romero, L., Addison, P. S., and Grubb, N. (2003). R-wave detection using continuous wavelet modulus maxima. IEEE Proc. Comput. Cardiol. 30, 565–568.
Rottman, J. N., Steinman, R. C., Albrecht, P., Bigger, J. T. Jr., Rolnitzky, L. M., and Fleiss, J. L. (1990). Effcient estimation of the heart period power spectrum suitable for physiologic or pharmacologic studies. Am. J. Cardiol. 66, 1522–1524.
Salo, M., Huikuri, H., and Seppänen, T. (2001). Ectopic beats in heart rate variability analysis: effects of editing on time and frequency domain measures. Ann. Noninvasive Electrocardiol. 6, 5–17.
Sapoznikov, D., Luria, M. H., Mahler, Y., and Gotsman, M. S. (1992). Computer processing of artifact and arrhythmias in heart rate variability analysis. Comput. Methods Programs Biomed. 39, 75–84.
Sassi, R., and Mainardi, L. T. (2008). Editing RR series and computation of long-term scaling parameters. Comput. Cardiol. 35, 565–568.
Saul, J. P., Arai, Y., Berger, R. D., Lilly, L. S., Colucci, W. S., and Cohen, R. J. (1988). Assessment of autonomic regulation in chronic congestive heart failure by heart rate spectral analysis. Am. J. Cardiol. 61, 1292–1299.
Schmidt, G., Malik, M., Barthel, P., Schneider, R., Ulm, K., Rolnitzky, L., Camm, A. J., Bigger, J. T. Jr., and Schömig, A. (1999). Heart-rate turbulence after ventricular premature beats as a predictor of mortality after acute myocardial infarction. Lancet 353, 1390–1396.
Skinner, J. E., Carpeggiani, C., Landisman, C. E., and Fulton, K. W. (1991). The correlation dimension of heartbeat intervals is reduced in conscious pigs by myocardial ischemia. Circ. Res. 68, 966–976.
Solem, K., Laguna, P., and Sörnmo, L. (2006). An efficient method for handling ectopic beats using the heart timing signal. IEEE Trans. Biomed. Eng. 53, 13–20.
Stein, P. K., Domitrovich, P. P., Huikuri, H. V., and Kleiger, R. E. (2005). Traditional and nonlinear heart rate variability are each independently associated with mortality after myocardial infarction. J. Cardiovasc. Electrophysiol. 16, 13–20.
Stein, P. K., Domitrovich, P. P., Kleiger, R. E., Schechtman, K. B., and Rottman, J. N. (2000). Clinical and demographic determinants of heart rate variability in patients post myocardial infarction: insights from the cardiac arrhythmia suppression trial (CAST). Clin. Cardiol. 23, 187–194.
Stein, P. K., Rich, M. W. R., Rottman, J. N., and Kleiger, R. E. (1995). Stability of index of heart rate variability in patients with congestive heart failure. Am. Heart J. 129, 975–981.
Tarkiainen, T. H., Kuusela, T. A., Tahvanainen, K. U., Hartikainen, J. E., Tiittanen, P., Timonen, K. L., and Vanninen, E. J. (2007). Comparison of methods for editing of ectopic beats in measurements of short-term non-linear heart rate dynamics. Clin. Physiol. Funct. Imaging 27, 126–133.
Tarvainen, M. P., Ranta-Aho, P. O., and Karjalainen, P. A. (2002). An advanced detrending method with application to HRV analysis. IEEE Trans. Biomed. Eng. 49, 172–175.
Task Force of ESC and NASPE. (1996). Heart rate variability. Standards of measurement, physiological interpretation, and clinical use. Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology. Circulation 93, 1043–1065.
Thuraisingham, R. A. (2006). Preprocessing RR interval time series for heart rate variability analysis and estimates of standard deviation of RR intervals. Comput. Methods Programs Biomed. 83, 78–82.
Valentini, M., and Parati, G. (2009). Variables influencing heart rate. Prog. Cardiovasc. Dis. 52, 11–19.
Vetterli, M. (1992). Wavelet and filter banks: theory and design. IEEE Trans. Signal Process. 40, 2207–2232.
Wheat, A. L., and Larkin, K. T. (2010). Biofeedback of heart rate variability and related physiology: a critical review. Appl. Psychophysiol. Biofeedback 35, 229–242.
Keywords: heart rate variability, artifact, editing, R–R intervals
Citation: Peltola MA (2012) Role of editing of R–R intervals in the analysis of heart rate variability. Front. Physio. 3:148. doi: 10.3389/fphys.2012.00148
Received: 01 September 2011; Paper pending published: 03 October 2011;
Accepted: 02 May 2012; Published online: 23 May 2012.
Edited by:
Heikki Veli Huikuri, University of Oulu, FinlandReviewed by:
Heikki Veli Huikuri, University of Oulu, FinlandAndreas Bergdahl, Concordia University, Canada
Copyright: © 2012 Peltola. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Mirja A. Peltola, Department of Internal Medicine, Institute of Clinical Medicine, University of Oulu, PO Box 5000 (Kajaanintie 50), Oulu 90014, Finland. e-mail:bWlyamEucGVsdG9sYUBvdWx1LmZp
