- Department of Physiology, Biophysics and Systems Biology, Weill Cornell Medical College, New York, NY, USA
Cardiac repolarization alternans is a rhythm disturbance of the heart in which rapid stimulation elicits a beat-to-beat alternation in the duration of action potentials and magnitude of intracellular calcium transients in individual cardiac myocytes. Although this phenomenon has been identified as a potential precursor to dangerous reentrant arrhythmias and sudden cardiac death, significant uncertainty remains regarding its mechanism and no clinically practical means of halting its occurrence or progression currently exists. Cardiac alternans has well-characterized tissue, cellular, and subcellular manifestations, the mechanisms and interplay of which are an active area of research.
1. Introduction
Sudden cardiac death (SCD) is the most catastrophic manifestation of heart disease, responsible for the deaths of an estimated 325,000 Americans annually (Verrier et al., 2009). SCD most commonly occurs as a result of reentrant tachyarrhythmias (ventricular tachycardia (VT) and ventricular fibrillation (VF); Zipes and Jalife, 2004), but reliable identification of those patients at highest risk for these events has proven a difficult clinical challenge. Recently, an electrocardiogram (ECG) abnormality, “T-wave alternans” (TWA), has been identified as a sensitive indicator of risk for SCD, thereby becoming the focus of considerable clinical and basic science research (Walker and Rosenbaum, 2003; Narayan, 2008).
T-wave alternans is defined as a beat-to-beat alternation in the shape, amplitude, or timing of the T-wave on the ECG, indicative of an underlying alternation in ventricular repolarization (Figure 1; Narayan, 2008). TWA has been associated clinically (Rosenbaum et al., 1994; Narayan, 2008; Narayan et al., 2011) and experimentally (Chinushi et al., 1998, 2003; Pastore et al., 1999; Shimizu and Antzelevitch, 1999) with the onset of potentially fatal arrhythmias (VT/VF) in a broad range of clinical contexts, and is now established as a sensitive marker of risk for SCD. TWA testing may be useful in risk stratification for prophylactic implantable cardioverter-defibrillator (ICD) use (Narayan, 2008). The clinical utility of TWA is the subject of ongoing clinical research, however, and may be limited in part by methodological difficulties (see Nieminen and Verrier, 2010; Verrier et al., 2011, for example).

Figure 1. T-wave alternans on the ECG. Large amplitude alternations in the T-wave (arrows) are seen in this example. This TWA is indicative of an underlying alternation in the action potential durations of cardiac myocytes. Adapted from Narayan (2006).
TWA on the ECG was recently shown to be a manifestation of an alternation in the duration of consecutive action potentials (APs) of ventricular myocytes (cellular alternans; Pastore et al., 1999). Theoretical and experimental studies have established a putative mechanistic link between this tissue-level alternans and arrhythmogenesis (described below; Chinushi et al., 1998, 2003; Pastore et al., 1999; Shimizu and Antzelevitch, 1999). The underlying mechanism of cellular alternans itself remains unclear, however, and no clinically practical means of halting its formation or progression to SCD currently exists.
As imaging techniques have rapidly progressed, the complex subcellular dynamics of cardiac myocytes and their importance in physiology and disease has been increasingly recognized. Cellular alternans is now thought to result from the interplay of ion channels at the cell surface and the complex dynamics of intracellular calcium cycling that are responsible for the variation in calcium concentration seen with each beat. Most recently, so-called “subcellular alternans” has been frequently reported, in which alternations in the magnitude of intracellular calcium transients are seen to vary spatially within an individual myocyte, such that the calcium transients of adjacent regions of the cell alternate with opposite phase. Although significant uncertainty remains regarding its mechanism, the arrhythmogenic potential of subcellular alternans has already been recognized and has motivated a quickly growing field of its research.
1.1. Restitution
The duration of each cardiac action potential is an important determinant of electrical stability and arrhythmogenicity in the heart. Under normal conditions, as stimulus frequency is increased (and the diastolic interval is therefore decreased) the resulting action potentials shorten (Bass, 1975). This “action potential duration (APD) restitution” ensures that the diastolic interval (DI) is preserved even during rapid pacing, thereby allowing adequate filling of the ventricles and perfusion of the coronary system. APD restitution is frequently quantified through the “APD restitution curve,” in which the APD of each beat is plotted against the duration of the preceding diastolic interval as the cycle length is decreased (Figure 2A). APD normally decreases monotonically with decreasing diastolic interval (as in Figure 2A), but non-monotonic relationships have also been reported (Koller et al., 1998; Franz, 2003). As described below, the slope of this curve may be an important determinant of the stability of membrane voltage (Vm) dynamics.
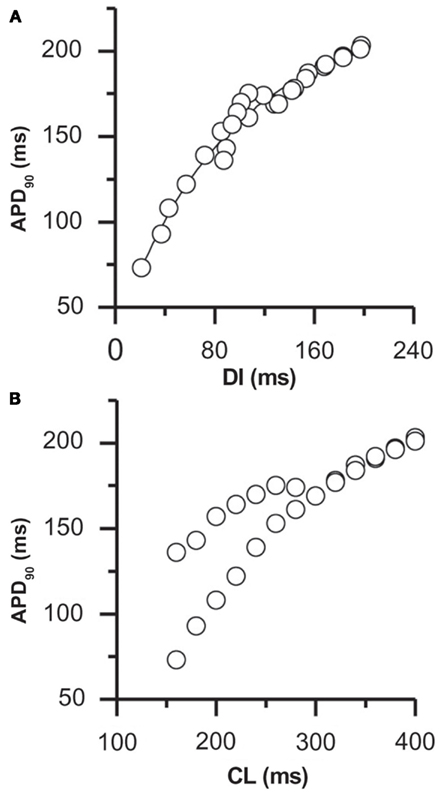
Figure 2. APD restitution in rabbit ventricular myocytes. The rate-dependence of APD is shown by plotting the APD against (A) the duration of the preceding DI and (B) the cycle length (CL; from the same data set). In this myocyte, alternans occurred at a pacing cycle length of 280 ms, corresponding to a DI of 120 ms. The slope of the restitution curve at this DI was 0.56 (from (A)), significantly less than the slope predicted to be necessary if alternans results from APD restitution alone. Adapted from Goldhaber et al. (2005). Note that similar data has been reported in human myocardium (see, for example, Koller et al., 2005).
APD restitution is primarily achieved through tight control of the duration of the AP plateau, which is maintained by a delicate balance of several inward and outward currents. The time-dependent recovery characteristics of the channels responsible for these currents make the time required for repolarization (and thus the APD) sensitive to changes in the preceding diastolic interval. Specifically, at most cycle lengths restitution is attributed to incomplete recovery from inactivation of L-type Ca2+ channels, with the decreased L-type Ca2+ channel current (ICaL) available following short DIs leading to early repolarization (and a shorter APD). In addition to ICaL, the slope of the APD restitution curve has been shown theoretically and experimentally to be dependent on the kinetics of several other sarcolemmal currents, including recovery from inactivation of depolarizing sodium channels (INa) and deactivation of hyperpolarizing potassium channels (IKr and IKs; Fox et al., 2002a; Shiferaw et al., 2006; O’Hara et al., 2011). The contribution of each of these currents to APD restitution varies with the length of the preceding DI, according to their specific time constants of recovery (Franz, 2003).
The conduction velocity (CV) of action potential propagation in tissue is similarly dependent on the duration of the preceding diastolic interval, due primarily to incomplete recovery from inactivation of the inward sodium channels responsible for the rapid upstroke of the AP (Weiss et al., 2006). Analogous to APD restitution, this “CV-restitution” dictates that APs following short DIs propagate more slowly than those following long DIs.
2. Cardiac Myocyte Calcium Cycling Dynamics
Each AP in a cardiac myocyte is accompanied by a large, transient rise in cytosolic free calcium concentration ([Ca2+]i) that, in addition to other roles, is responsible for the initiation of contraction. This Ca2+ transient is the product of the coordinated activity of a large number of cellular processes that control the release and reuptake (“cycling”) of Ca2+ during each beat, the dynamics of which are known to play important roles in health and disease.
Depending on the species, as much as 90–95% of the increase in Ca2+ during each Ca2+ transient is released from the sarcoplasmic reticulum (SR), a diffuse intracellular tubular network surrounding the contractile elements of the myocyte (myofibrils) that stores Ca2+ in high concentration (Figure 3; Stern, 1992; Stern et al., 1999). With each AP, the small influx of Ca2+ into the cell through L-type Ca2+ channels (primarily during the AP plateau) activates Ryanodine receptors (RyRs) in the SR membrane to open, thereby releasing a much larger amount of Ca2+ from the SR. This process, known as “Ca2+-induced Ca2+ release” (CICR), couples the depolarization of the membrane to the large rise in [Ca2+]i necessary to initiate myofilament contraction.
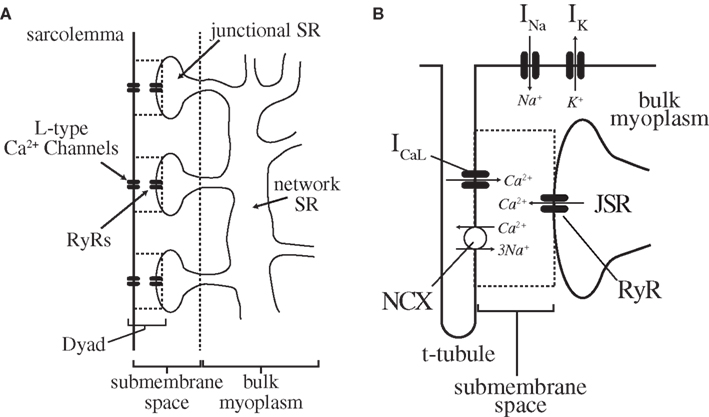
Figure 3. Cardiac myocyte intracellular Ca2+-cycling components. (A) The sarcolemma of a cardiac myocyte forms a series of regularly distributed invaginations (T-tubules) into the interior of the cell (perpendicular to the long axis). The area between each adjacent pair of T-tubules is a sarcomere, of which there are 75–100 in each myocyte. Along the T-tubules (and to a lesser degree the cell surface) lie dyadic junctions, the functional units of cardiac excitation-contraction coupling. Note that within a cardiac myocyte, these dyads are arranged in a 3-dimensional lattice throughout the cell (see Brette and Orchard, 2003) for more detail). (B) Each dyadic junction itself consists of the close apposition of a junctional branch of the SR with the sarcolemma, and contains the L-type Ca2+ channels and RyRs (in the sarcolemma and SR, respectively) necessary for CICR. A single myocyte contains on the order of 104 of these dyads arranged in a regular array, and the global Ca2+ transient is the summation of several thousand individual release events (Ca2+-sparks) occurring at these sites. For a more complete description of specific ionic currents, see Shiferaw and Karma (2006), from which this figure was adapted.
The amplitude of the SR Ca2+ release is a graded function of the magnitude and duration of the triggering L-type Ca2+-channel current. This “graded release” creates a paradox, however – given that approximately 10× the amount of Ca2+ needed to trigger CICR is released from the SR, one would expect SR Ca2+ release to trigger further release, thereby creating a regenerative, all-or-none process (Stern, 1992; Stern et al., 1999). The resolution to this paradox was ultimately found in the spatially distributed nature of subcellular Ca2+-cycling dynamics.
CICR has been shown to occur at discrete subcellular sites within cardiac myocytes at which there is close apposition of the sarcolemmal membrane and a terminal cistern of the SR (“junctional SR” (JSR)), separated by a small (∼12 nm wide) submembrane space (Cheng and Lederer, 2008). An individual cardiac myocyte contains on the order of 104 of these so-called “dyads” (alternatively, “dyadic junctions,” or “couplons”) arranged in a regular lattice (Figure 3; Brette and Orchard, 2003). These dyadic junctions are now understood to be the functional units of cardiac excitation-contraction coupling, with each containing approximately 10–25 L-type Ca2+ channels and 100 RyRs in the sarcolemmal and SR membrane, respectively (Bers, 2002; Keurs and Boyden, 2007).
During a normal Ca2+ transient, small Ca2+ releases (“Ca2+ sparks”) occur independently at several thousand dyadic junctions, spatially and temporally synchronized by the AP such that the global Ca2+ transient appears uniform throughout the cell (Bers, 2002). Graded release occurs by statistical recruitment of these independent (all-or-none) release events, with larger ICaL leading to the recruitment of more dyadic junctions and thereby a larger global Ca2+ transient (Stern et al., 1999; Greenstein and Winslow, 2002). This spatial distribution of Ca2+ release is manifest in several subcellular phenomena including Ca2+-waves and subcellular alternans (described below), and illustrates the importance of subcellular Ca2+-dynamics in myocyte physiology (Díaz et al., 2002; Kockskämper and Blatter, 2002; Blatter, 2003; Xie and Weiss, 2009; Bayer et al., 2010).
Termination of contraction is accomplished by transport of Ca2+ out of the cytosol, primarily through SR reuptake (via SR Ca2+ ATPase (SERCA) pumps) and extrusion through the sarcolemmal Na+/Ca2+ exchanger (NCX). The 3Na+:1Ca2+ stoichiometry of the NCX makes this exchange electrogenic, and the depolarizing current resulting from Ca2+ extrusion plays an important role in maintaining the late plateau phase of the AP (Katz, 2005).
In addition to the NCX, the Ca2+ transient influences AP morphology through several other Ca2+-sensitive membrane currents, including the L-type Ca2+ channel (Salama, 2006; Bers, 2008; Orchard et al., 2009). The rise in free Ca2+ concentration during the Ca2+ transient increases the rate of inactivation of L-type Ca2+ channels (“Ca2+-induced inactivation”) through a calmodulin dependent process (Peterson et al., 1999; Mahajan et al., 2008), thereby promoting repolarization of the membrane. The balance of these depolarizing and hyperpolarizing effects of the Ca2+ transient has important consequences for myocyte dynamics, as described below.
3. Tissue-Level Alternans
Optical mapping techniques using membrane voltage sensitive dyes have shown that TWA seen on the ECG is a manifestation of an underlying alternation in consecutive APDs of cardiac myocytes in large regions of myocardium (Pastore et al., 1999). Using Ca2+-sensitive dyes, this APD-alternans is seen to be accompanied by concurrent alternations in the amplitude of intracellular Ca2+ transients (Pruvot et al., 2004; Diego et al., 2008). The relationship between APD-alternans and Ca2+ transient alternans in tissue have been studied by experimental and model-based approaches (Narayan et al., 2008; Bayer et al., 2010). Tissue-level alternans normally arises as spatially concordant alternations in the APDs (and Ca2+ transients) of myocytes in large regions of tissue (Figure 4A). Although this “spatially concordant alternans” (SCA) itself is not believed to be a pro-arrhythmic state, it is usually requisite for progression to so-called “spatially discordant alternans” (SDA), which has been mechanistically linked to conduction block and the initiation of reentrant arrhythmias (Wilson and Rosenbaum, 2007).
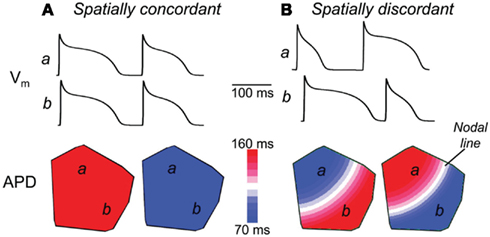
Figure 4. Spatially concordant and discordant alternans in simulated cardiac tissue. Shown are the results of rapidly pacing a 2-dimensional homogeneous sheet of simulated cardiac tissue (from the top left corner), including the spatial distribution of action potential durations (bottom) and the action potentials occurring at two sites in the tissue (top traces). (A) During pacing at a cycle length of 220 ms, spatially concordant alternans is seen, in which the APD of all myocytes alternate in-phase. (B) Pacing at a cycle length of 180 ms, however, induces spatially discordant alternans, in which the action potentials of adjacent regions of tissue alternate out-of-phase. This is seen in the top traces, where the action potentials of site a alternate short-long at the same time as those of site b alternate long-short. As seen in the bottom panel, this spatially discordant alternans causes a large gradient in APD across the tissue, with large regions of tissue with counter-phase APD-alternans, separated by a “nodal line” where alternans is not seen (and where the APD gradient is steepest). Adapted from Weiss et al. (2006).
SDA normally arises at faster pacing cycle lengths than SCA, when the alternations in APD (and Ca2+ transients) switch phase in a subset of myocytes, leading to out-of-phase alternations in adjacent regions of tissue (Figure 4B). Although the APD gradient seen in SDA was initially attributed to preexisting spatial heterogeneity in the expression of ion channels important for repolarization (Pastore et al., 1999), several mechanisms have since been proposed in which SDA can arise in homogeneous tissue (Watanabe et al., 2001).
Experimental and theoretical studies have shown that rate-dependent transition from SCA to SDA can occur by a purely dynamical phenomenon, dependent on only the interaction of conduction velocity and action potential duration restitution (Watanabe et al., 2001; Sato et al., 2007; Diego et al., 2008). Specifically, during APD-alternans conduction velocity restitution (described above) leads to an alternation in the propagation speed of waves of excitation (i.e., fast-slow-fast). Given sufficiently sized tissue, the resulting alternation in arrival times (and thereby in the local diastolic interval) of these depolarizing stimuli at more distant sites can cause alternations in the APD (due to APD restitution, as above) that are out-of-phase with those more proximal. See Watanabe et al. (2001) and Echebarria and Karma (2007) for a qualitative and quantitative description, respectively, of this phenomenon. Notably, SDA can also be induced if a propagated ectopic stimulus initiated distant from the pacing site causes a sufficient gradient in the subsequent diastolic interval (Watanabe et al., 2001).
SDA is putatively linked to the initiation of reentry by the formation of steep gradients of refractoriness across the myocardium. Such steep gradients of refractoriness have been shown computationally and experimentally to precipitate unidirectional conduction block and functional reentry, even in homogeneous tissue (as diagrammed in Figure 5; Chinushi et al., 1998; Pastore et al., 1999; Qu et al., 2000; Fox et al., 2002b). Notably, the dynamic transition to SDA described above has been shown to arise more readily in structurally heterogenous tissue, potentially contributing to the predisposition to reentrant tachyarrhythmias in humans with structural heart disease (Krogh-Madsen and Christini, 2007).
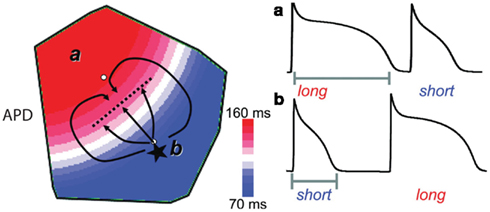
Figure 5. Spatially discordant alternans predisposes premature excitations to induce conduction block and reentry. One mechanism by which SDA predisposes otherwise benign premature beats to conduction block and reentry is diagrammed. An ectopic beat (asterisk) initiated during SDA in the region with a short APD encounters more refractory tissue as it propagates toward the region with long APD. Given a sufficiently steep gradient of refractoriness, conduction block can occur (dashed line). Meanwhile, this beat can successfully propagate laterally, allowing time for recovery of the long APD region and subsequent reentry. Adapted from Weiss et al. (2006).
4. Cellular Alternans
TWA on the ECG is understood to be a manifestation of underlying APD-alternans in individual myocytes, but the mechanism by which this cellular alternans arises remains unclear. As in tissue-level alternans, studies in enzymatically isolated cardiac myocytes have shown rapid pacing (faster than a critical threshold) to induce alternations in the APD and the Ca2+ transient amplitude (as in Figures 2B and 6A), with altered susceptibility in myocytes from the diseased heart (Chudin et al., 1999; Willms et al., 1999).
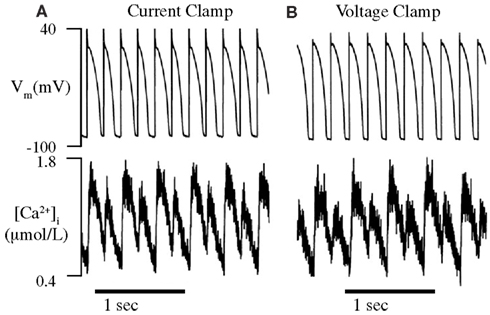
Figure 6. Alternans can be caused by intrinsic Ca2+-cycling dynamics alone. The intracellular Ca2+ transients of paced (A) and AP clamped (B) isolated rabbit ventricular myocytes are observed using a fluorescent Ca2+-sensitive dye (fura-2). (A) As expected, the APDs and Ca2+ transients of paced myocytes are seen to alternate from beat-to-beat when the cycle length is reduced to below a critical threshold (180 ms). (B) The Ca2+ transients of AP clamped myocytes were still seen to alternate below approximately the same cycle length threshold as paced myocytes, in spite of fixed membrane voltage. This indicates that Ca2+-cycling dynamics can alternate due to their own, intrinsic instability and has led many to conclude that Ca2+-dynamics are solely responsible for cellular alternans. Adapted from Chudin et al. (1999).
Determining the mechanism of cellular alternans is complicated by the multiple possible sources of instability. Theoretical and experimental work has identified mechanisms by which APD-alternans and Ca2+-alternans (beat-to-beat alternations in the peak Ca2+ transient magnitude) can result independently from one another, due only to instability in sarcolemmal ion channel and intracellular Ca2+-cycling dynamics, respectively. As described below, in each case the mechanism is thought to be a manifestation of a so-called “period-doubling bifurcation,” a phenomenon of non-linear dynamical systems in which a periodic rhythm is replaced by another with twice the period. In this case, a stable “period-1” rhythm, in which each beat’s APD and Ca2+ transient are identical, are replaced by a new “period-2” (alternans) rhythm, in which these values alternate from beat-to-beat.
The APD and Ca2+ transient are bidirectionally coupled, however, and alternations in either one is predicted to cause secondary alternans in the other, making determination of the primary source of instability a difficult experimental challenge (Qu and Weiss, 2007). This coupling naturally leads to two hypotheses: (1) instability in membrane voltage dynamics causes APD-alternans, producing secondary alternations in the intracellular Ca2+ transient (Guevara et al., 1984; Koller et al., 1998; Riccio et al., 1999; Watanabe et al., 2001; Fox et al., 2002b) and (2) instability in Ca2+-cycling dynamics causes alternans in the intracellular Ca2+ transient, producing secondary APD-alternans (Chudin et al., 1999; Hüser et al., 2000; Díaz et al., 2002, 2004; Pruvot and Rosenbaum, 2003; Goldhaber et al., 2005; Wan et al., 2005). Although mechanism (1) was favored for many years, recent experimental evidence has shifted the majority of focus to mechanism (2), with many in the field treating alternans as resulting from Ca2+-cycling dynamics alone. As described below, however, such a dichotomy is unlikely to exist in real cells.
4.1. Voltage (restitution) driven alternans
The first widely accepted theory of cellular alternans considered only the time-dependent recovery of sarcolemmal ion channels. This “Vm-driven alternans” theory centers on the APD restitution relationship, employing a simple model of myocyte dynamics in which the APD is a function solely of the preceding DI.
The role of APD restitution in alternans is diagrammed in Figure 7. During constant cycle length (“static”) pacing, a prolonged APD (An) shortens the subsequent DI (dn). APD restitution dictates that this short DI will lead to a shortened subsequent AP (An+1), which will be followed by a long subsequent DI (dn+1). This long DI will lead to another long APD (An+2), and the pattern is thus repeated (Shiferaw et al., 2006). The alternating DIs during this rhythm will also cause a secondary Ca2+-alternans, due to alternating time for recovery of ICaL (and graded release of SR Ca2+).
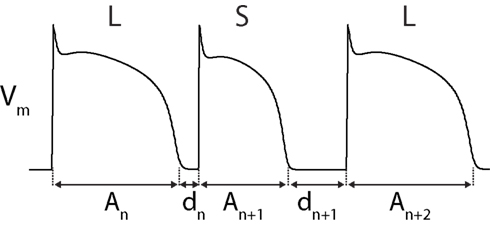
Figure 7. Diagram of APD-alternans. APD-alternans can theoretically occur due to APD restitution alone (Vm-driven alternans). See text for description.
This mechanism was first proposed in a seminal 1968 article by Nolasco and Dahlen (1968), in which an analogy to a simple electronic feedback circuit (in which the APD feeds back on itself through changes in the DI) was drawn and the principles of electrical engineering were used to account for the occurrence of alternans. Their model is equivalent to the iterated map
where An and dn are the APD and diastolic interval, respectively, of beat n and An + dn is a constant (the cycle length). Here, f is the restitution function describing the dependence of APD on the preceding diastolic interval (Karma and Gilmour, 2007). In this map, alternans occurs when its period-1 fixed point (where APD and DI are constant) loses stability and is replaced by a period-2 rhythm (alternating APDs). This period-doubling bifurcation occurs when
where f ′ represents the slope of the restitution curve, evaluated at the steady-state DI (d*; Guevara et al., 1984). Assuming a monotonic restitution curve, this condition predicts that given sufficiently steep APD restitution (f ′ > 1), small changes in DI will be amplified into stable alternations of APD (alternans; Nolasco and Dahlen, 1968; Guevara et al., 1984; Karma and Gilmour, 2007).
This hypothesis has been supported by theoretical and experimental studies showing the occurrence of arrhythmia to correlate with the slope of the APD restitution curve, including several experimental studies in which existing arrhythmias are abolished using (clinically impractical) drugs that flatten restitution (Riccio et al., 1999; Garfinkel et al., 2000; Wu et al., 2002). This model fails, however, to explain many other experimental findings (Franz, 2003). For example, alternans is often seen at pacing rates where the slope of the experimentally determined restitution curve is significantly less than 1 (as in Figure 2), and is often absent where the slope is greater than 1 (Gilmour et al., 1997; Otani and Gilmour, 1997; Hall et al., 1999; Banville and Gray, 2002; Banville et al., 2004; Pruvot et al., 2004; Wu and Patwardhan, 2004, 2006). Moreover, the restitution slope measured experimentally varies depending on the pacing history of the cell (so-called “cardiac memory”), which would not be the case if the APD is truly dependent only on the previous DI (Tolkacheva et al., 2004, 2006). Alternans must result from more than this simple relationship, and mounting experimental evidence is implicating intracellular Ca2+-cycling dynamics as a major overlooked component in this scheme.
4.2. Calcium-driven Alternans
As with the APD, beat-to-beat alternations in the magnitude of intracellular Ca2+ transients can occur due to intrinsic Ca2+-cycling dynamics alone. This “Ca2+-driven alternans” will lead to secondary APD-alternans due to Ca2+-sensitive membrane components (e.g., L-type Ca2+ channels and the NCX). This hypothesis has received the majority of recent focus, due in large part to two in vitro studies that showed Ca2+-alternans to occur even while the membrane voltage was clamped to follow a repeating (non-alternating) AP waveform (Figure 6; Chudin et al., 1999; Wan et al., 2005). During such “AP Clamp” experiments, the clamped period-1 AP cannot produce secondary alternations in Ca2+ transients, making any Ca2+-alternans seen in that context the result of Ca2+-cycling dynamics alone.
There are several proposed mechanisms by which intrinsic Ca2+-cycling dynamics can lead to rate-dependent alternans, but once again no one mechanism is likely to be the source of the instability seen. For stable control of SR Ca2+ content (and therefore Ca2+ transient amplitude), the amount of Ca2+ released from the SR during each beat must equal the amount reclaimed. Ca2+-alternans will occur as a result of intrinsic Ca2+-cycling dynamics whenever this capability of the myocyte to cycle Ca2+ is overwhelmed (Cutler and Rosenbaum, 2009). The most studied mechanism by which this can occur is by a steep load dependence of SR Ca2+ release, as follows.
The amount of Ca2+ released from the SR is known to be dependent on the load of Ca2+ it contains, with increased SR Ca2+-content resulting in a larger Ca2+ release and vice versa (Bassani et al., 1995; Díaz et al., 2004). Likewise, the amount of Ca2+ reclaimed into the SR is dependent on the amount of Ca2+ available in the cytosol. Alternations in SR Ca2+-content (and release) will result given either a steep load dependence of SR Ca2+ release or inefficient Ca2+-sequestration into the SR (Shiferaw et al., 2006).
As an example, consider the effect on Ca2+-cycling of an increase in SR Ca2+ content above its baseline. Due to the load dependence of SR Ca2+ release, this will increase the amount of Ca2+ released from the SR with the next stimulus. If this release depresses SR Ca2+ content to the extent that reuptake is unable to return it to its baseline level before the next stimulus, a smaller subsequent Ca2+ release will result (due to the decreased SR load). This smaller release will cause less depletion of SR Ca2+. If this depletion is sufficiently small, reuptake will refill the SR to above its baseline Ca2+ content once again before the next stimulus. Whether these alternations in SR Ca2+ content (and release) shrink toward a stable rhythm (at the baseline SR Ca2+ content) or grow into a marked Ca2+-alternans depends on both the steepness of the load dependence of SR Ca2+ release and the efficiency of Ca2+-reuptake (Weiss et al., 2006; Xie et al., 2008). Although Ca2+-alternans will theoretically result given either a steep load dependence or inefficient reuptake, the latter has yet to be explored in detail.
Figure 8 shows the relationship between SR Ca2+ content and release, determined experimentally in rat ventricular myocytes (Díaz et al., 2004). The load dependence of SR Ca2+ release is quantified as the slope of this curve. These results (as well as those of other studies; Bassani et al., 1995) show the dependence to be highly non-linear, with a steep slope at those SR Ca2+ contents at which alternans is seen (filled circles). Rate-dependent, Ca2+-driven alternans can occur by this mechanism due to increasing SR Ca2+-content with faster pacing (Shiferaw et al., 2003; Díaz et al., 2004). This non-linearity at high SR Ca2+ loads is primarily attributed to the triggering of propagating waves of Ca2+ release when SR release is sufficiently large to recruit neighboring dyadic junctions (discussed below; Shiferaw et al., 2003). This steep non-linearity in load dependence has been incorporated in a computational model of a cardiac myocyte and shown to cause to Ca2+-driven alternans (Shiferaw et al., 2003).
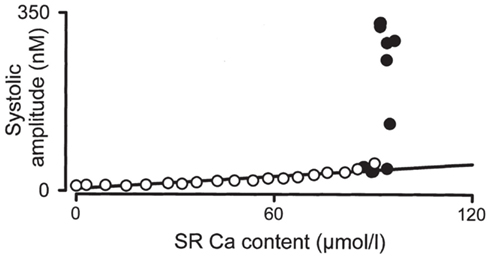
Figure 8. Load dependence of SR Ca2+ release. The relationship between the SR Ca2+ content and the amplitude of the systolic Ca2+ transient are shown for rat ventricular myocytes. Adapted from Díaz et al. (2004).
A less studied, alternative mechanism (among several) predicts that Ca2+-alternans can be induced without alternations in the SR Ca2+ concentration (the existence of which is contentious), due to slow recovery from inactivation of Ryanodine receptors. Similar to the dynamics of sarcolemmal ion channels during rapid pacing, if recovery from inactivation is sufficiently slow as to only allow full recovery after every other release, alternations in the Ca2+ transient magnitude (Ca2+-alternans) will result (Picht et al., 2006; Restrepo et al., 2008).
4.3. Bidirectional Coupling of Voltage and Calcium
As described above, the APD and the intracellular Ca2+ transient are coupled to one another through mutual effects on intracellular Ca2+ concentration, leading APD-alternans to generate secondary Ca2+-alternans and vice versa. Several modes of coupling are possible, however, and the specific type present has recently been shown to dictate important characteristics of the resulting alternans.
The duration of each AP influences the intracellular Ca2+ transient through the phenomenon of graded release, in which the magnitude of the SR calcium release of each beat is proportional to the size of its triggering L-type calcium channel current (“graded release”). Because ICaL is itself very dependent on the length of the preceding diastolic interval (due to slow recovery from inactivation), a shortened diastolic interval leads to a smaller subsequent Ca2+ release and vice versa (Figure 9A). As such, during static pacing (when APD + DI is constant), prolongation of the APD causes a shortening of the subsequent diastolic interval and a smaller Ca2+ release on the following beat. This is defined as “positive Vm → Ca2+ coupling.” Note that although this effect is, directly, a manifestation of Vm (specifically the ICaL-mediated plateau) on the Ca2+ transient of the same beat (through CICR), the strong dependence of ICaL itself on the preceding DI allows Vm → Ca2+ coupling to be modeled as an effect of APD on the amplitude of the subsequent Ca2+ transient (Figure 9A, red arrow).
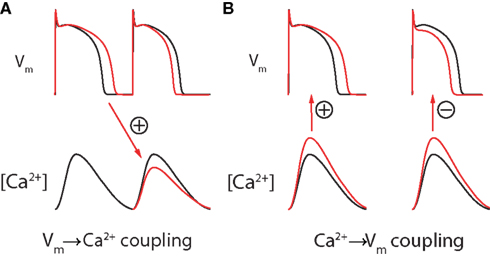
Figure 9. Bidirectional coupling of Vm and Ca2+. (A) During static pacing, Vm → Ca2+ coupling is assumed to be positive due to graded release (as shown). An increase in the preceding APD leads to a decrease in the subsequent Ca2+ transient (due to a shortening of the diastolic interval), and vice versa. Note that this change in DI will also have an APD restitution mediated effect on the subsequent APD (in this case, shortening it). (B) Ca2+ → Vm coupling can be either positive (left) or (right), dependent on species, cell type, and temperature. Adapted from Gaeta et al. (2010).
Due to positive Vm → Ca2+ coupling, the DI alternations seen during Vm-driven alternans will produce secondary Ca2+-alternans that are in-phase with the primary APD-alternans (Shiferaw et al., 2006). This is called electromechanically (EM) concordant alternans, and is a common experimental observation. Although negative Vm → Ca2+ coupling (and resulting EM discordant alternans) is theoretically possible at slower pacing rates, it has not been reported experimentally and positive Vm → Ca2+ coupling is normally assumed (Shiferaw et al., 2005; Weiss et al., 2006).
Similarly, changes in intracellular Ca2+ concentration can be positively or negatively coupled to the APD through the opposing effects of the sodium-calcium exchanger and Ca2+-induced inactivation of L-type Ca2+ channels. So-called “positive Ca2+ → Vm coupling” occurs when the depolarizing effect of NCX calcium extrusion is stronger than the hyperpolarizing effect of Ca2+-induced inactivation of L-type Ca2+ channels. In this case, an increase in the amplitude of the Ca2+ transient will prolong the concurrent AP. Alternatively, if the effect of Ca2+-induced inactivation of L-type Ca2+ channels outweighs that of the NCX, changes in intracellular Ca2+ concentration will be negatively coupled to Vm and larger Ca2+ transients will shorten the AP (Figure 9B; Shiferaw et al., 2005).
During Ca2+-driven alternans, the sign of Ca2+ → Vm coupling dictates whether the secondary APD-alternans produced will be in-phase or out-of-phase with the primary Ca2+-alternans. Given positive Ca2+ → Vm coupling, large Ca2+ transients will prolong the APD, thereby predicting EM concordant alternans. If, however, Ca2+ → Vm coupling is negative, large Ca2+ transients will shorten concurrent APs and EM discordant alternans (in which APD-alternans and Ca2+-alternans occur out-of-phase) will result (Shiferaw et al., 2006).
Although this property remains poorly characterized, the relative phase of APD and Ca2+-alternans appears to be a species and/or temperature-specific property of myocytes. Both EM concordant and EM discordant alternans have been reported in the literature (Rubenstein and Lipsius, 1995; Euler, 1999).
4.4. Alternans is the Result of Total Cellular Instability
The dichotomy between membrane voltage and Ca2+-cycling dynamics as the cause of alternans ignores the interplay between these two systems in a normal myocyte. In an unclamped cell, neither of these two mechanisms is likely to be the sole cause of alternans. Ca2+-cycling dynamics are always directly modulated by the dynamics of membrane voltage, and thus both likely contribute to the onset of alternans (Jordan and Christini, 2007; Qu and Weiss, 2007). Just as alternans is seen at cycle lengths with restitution slope <1 (indicative of a non-Vm mediated contribution), alternating Ca2+ transients often stabilize in the presence of an AP clamp (indicative of non-Ca2+ mediated influence; personal observation of experimental results). This was supported by a recent computational modeling study, in which a cycle length and cell type dependent contribution of both Vm and Ca2+-cycling instability to cellular alternans was found in mathematical models (Jordan and Christini, 2007).
5. Subcellular Alternans
Recently, so-called “subcellular alternans” (also known as “subcellular spatially discordant alternans”) has been observed, in which the Ca2+-alternans in adjacent subcellular regions within an individual myocyte alternate out-of-phase (as in Figures 10 and 11). This striking phenomenon has been frequently (though often anecdotally) reported in isolated myocytes (Díaz et al., 2002, 2004; Kockskämper and Blatter, 2002; Cordeiro et al., 2007; Karma and Gilmour, 2007; Gaeta et al., 2009) and within individual cells of the intact heart during rapid pacing (Aistrup et al., 2006, 2009; Kapur et al., 2009).
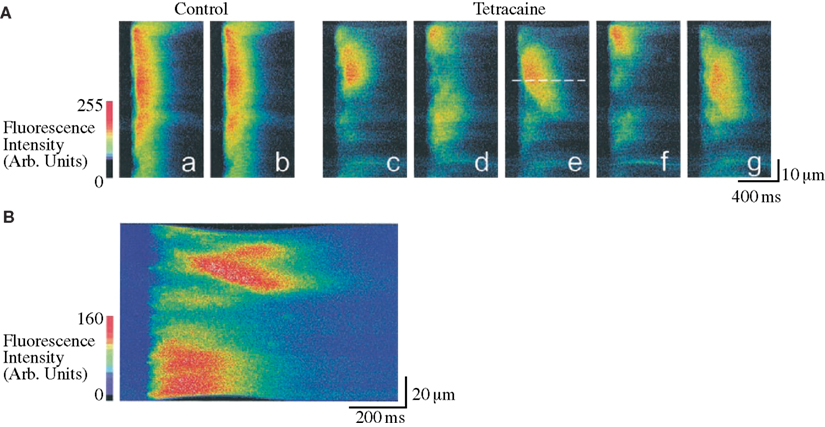
Figure 10. Tetracaine induced subcellular alternans in rat ventricular myocytes. Confocal microscopy is used to study the spatial organization of the Ca2+ transient during control conditions and during treatment with Tetracaine (causing decreased RyR open probability and an increased subcellular heterogeneity in Ca2+ release). The line-scan images shown correspond to the relative Ca2+ concentrations along a single line parallel to the long axis of the cell, plotted with time on the horizontal axis and distance on the vertical axis. (A) Although during control conditions (line-scan images a–b) the Ca2+ transient is nearly homogeneous, application of tetracaine causes a marked subcellular alternans pattern (shown in line-scan images c–g). Note the mini Ca2+-wave seen to propagate away from the dashed line in e. (B) A propagating Ca2+-wave is seen to initiate from an area of steep gradient in Ca2+ concentration (obtained in tetracaine). Adapted from Díaz et al. (2002).
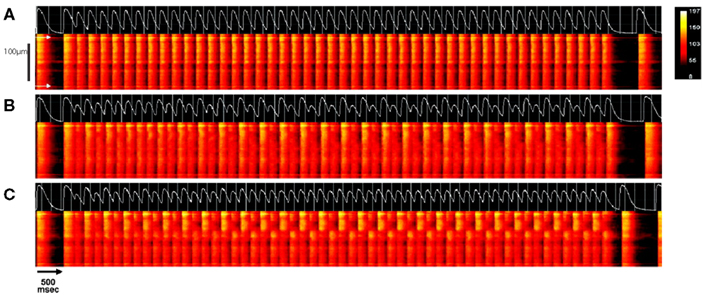
Figure 11. Pacing-induced subcellular alternans in intact rat heart. The intracellular Ca2+ concentration of individual myocytes were recorded in situ within an intact rat heart using confocal line-scan imaging. a transients recorded along the long axis of a single myocyte (with cell boundaries indicated by white arrows in (A)), are shown. Following a train of stimuli at a cycle length of 500 ms, the cycle length was decreased to 220 ms (A), 190 ms (B), or 180 ms (C) for approximately 50 stimuli, after which pacing was resumed at the original rate. In each panel, the line-scan results of the last stimulus at the basal rate, the test train at the faster cycle length, and the first beat after return to slower pacing are shown with time on the horizontal axis and position on the vertical axis. Above each of these plots is the whole-cell average Ca2+ transient of each trial (white trace). At a pacing cycle length of 220 ms (A), the whole-cell average calcium transient is seen to be at a period-1 rhythm and the Ca2+ transient is approximately uniform along the length of the cell. With faster pacing (B), the Ca2+ transient remains approximately spatially uniform, but begins to alternate in amplitude from beat-to-beat (whole-cell concordant alternans). At the fastest cycle length (C), subcellular alternans develops, in which adjacent regions of the cell (the top and bottom half, roughly) alternate out-of-phase, but the whole-cell average Ca2+ transient is at a nearly period-1 rhythm. Adapted from Aistrup et al. (2006).
Subcellular alternans is known to cause intracellular Ca2+-waves, which are potentially arrhythmogenic. Ca2+-waves are self-propagating waves of Ca2+release (and subsequent reuptake) within individual myocytes, that are most often seen when Ca2+ content is abnormally increased (“Ca2+-overload”; e.g., during ischemia-reperfusion and tachycardia; Sipido, 2006; Bers, 2008). These events are known to cause arrhythmogenic early and delayed afterdepolarizations through activation of Ca2+-sensitive membrane currents (especially the NCX; Minamikawa et al., 1997; Knot et al., 2005; Keurs and Boyden, 2007; Venetucci et al., 2008; Xie and Weiss, 2009), which if sufficiently large can lead to the generation of unstimulated APs (triggered activity). As depicted in Figure 5, such ectopic, unstimulated activations are known to play a role in the initiation of reentrant arrhythmias (Miura et al., 1993; Ferrari et al., 1995; Fujiwara et al., 2008). Nearly every study of subcellular alternans in isolated cells, including those in which Ca2+ content was presumably normal, has shown Ca2+-waves to initiate from near the boundary between adjacent subcellular regions in which Ca2+-transients are alternating out-of-phase (where the [Ca2+]i gradient is steepest; as in Figure 10B; Díaz et al., 2002, 2004; Kockskämper and Blatter, 2002; Xie and Weiss, 2009). Conversely, subcellular alternans can also be induced secondary to Ca2+-waves (described below; Xie and Weiss, 2009). A better understanding of the mechanism of subcellular alternans may help in understanding each of these phenomena and the relationship between them.
5.1. Dynamical mechanisms of subcellular alternans
Subcellular alternans can be understood as the formation of a pattern in subcellular Ca2+ transients from an initially (approximately) spatially homogeneous state. A fundamental question when studying any such pattern formation is whether the patterns seen reflect the presence of preexisting heterogeneities of the substrate in question, dynamically induced heterogeneity, or both (Gaeta et al., 2010). Examples of each of these mechanisms has been proposed to account for pacing-induced subcellular alternans in isolated cells and intact tissue.
Although subcellular alternans has been most often reported in isolated myocytes following the application of drugs that increase subcellular heterogeneity (as in Figure 10; Díaz et al., 2002, 2004; Kockskämper and Blatter, 2002), it has also been reported in otherwise healthy cells during rapid pacing (Kockskämper and Blatter, 2002; Cordeiro et al., 2007). Whereas the former studies are likely to be most relevant to the particular disease states that they model, the latter, pacing-induced subcellular alternans represents physiologic myocyte dynamics that are likely to play a role in any context. Several mechanisms have been proposed to account for the formation of subcellular alternans during rapid pacing of otherwise healthy cells, invoking either preexisting anatomical (Aistrup et al., 2009) or dynamically induced (Shiferaw and Karma, 2006; Gaeta et al., 2009, 2010; Xie and Weiss, 2009) heterogeneity in subcellular Ca2+-cycling characteristics.
Computational modeling has suggested that the heterogeneity in Ca2+ transients seen during subcellular alternans can result as a manifestation of fixed subcellular differences in the machinery of Ca2+-cycling. If different subcellular regions of a single myocyte have different Ca2+-release characteristics (e.g., degree of Ca2+-driven instability), changes in pacing protocol that reverse the phase of Ca2+ transient alternans can expose this heterogeneity by reversing the phase in some regions earlier than others (Aistrup et al., 2009). A similar effect is seen if such subcellular differences in Ca2+-release properties are instead induced dynamically by the propagation of intracellular Ca2+-waves (Xie and Weiss, 2009). An experimental study showed that if pacing is initiated during the propagation of a Ca2+-wave (induced by Ca2+-overload), the local gradients in refractoriness of SR Ca2+ release caused by the partially propagated Ca2+-wave led to a significant heterogeneity in the subsequent, pacing-induced Ca2+ transients. When rapid pacing was initiated as an intracellular Ca2+-wave propagated, a marked subcellular alternans pattern resulted (Figure 12; Xie and Weiss, 2009). This mechanism is analogous to a propagated ectopic activation inducing the transition from spatially concordant to spatially discordant alternans (described above).
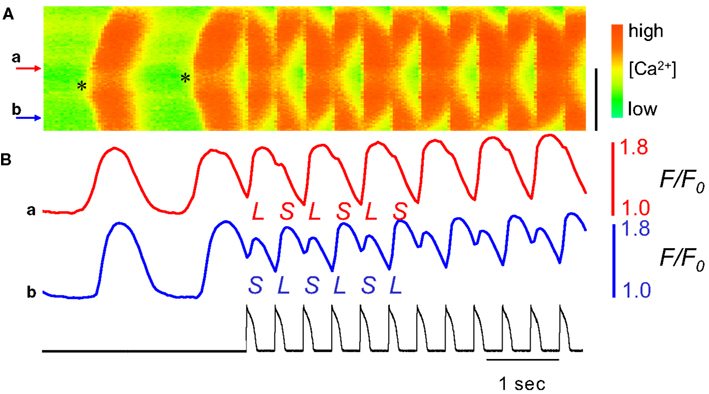
Figure 12. Ca2+-waves predispose to subcellular alternans in an isolated rabbit ventricular myocyte. Line-scan data of Ca2+ fluorescence along the length of an isolated rabbit ventricular myocyte is plotted with time on the horizontal axis and distance on the vertical axis (distance scale bar is 50 μm). Ca2+-waves were induced by application of BayK8644 + Isoproterenol (thereby inducing Ca2+-overload). (A) Two spontaneous Ca2+-waves are seen to arise near the middle of the cell (near site a) and propagate outward. Beginning during the second Ca2+-wave, a repeating AP clamp was used to rapidly pace the cell (with waveform and timing as shown in (B), black trace), causing a marked subcellular alternans pattern. (B) The time series of Ca2+-fluorescence at sites a and b show Ca2+-alternans during the AP clamp pacing to be out-of-phase at these two points. Adapted from Xie and Weiss (2009).
Finally, a theoretical study suggested that a purely dynamical mechanism– a Turing-type, symmetry breaking instability– can induce subcellular alternans in rapidly paced, structurally homogeneous cells (Shiferaw and Karma, 2006). A canonical Turing (“diffusion-driven”) instability is a mechanism by which a concentration gradient can be established from a nearly homogenous substrate due to the interaction of only two distinct, diffusing substances (“morphogens”; Turing, 1952). This occurs when an autocatalytic substance (“activating morphogen”) gives rise to its own, more quickly diffusing inhibitor (“inhibitory morphogen”). A concentration gradient arises because local increases in activator concentration will grow (autocatalysis) but will also simultaneously inhibit increases in activator concentration away from this site (due to the production of the more quickly diffusing inhibitor; Gierer and Meinhardt, 1972).
An analogy was drawn between the amplitudes of Ca2+-alternans and APD-alternans and the concentrations of the activating and inhibitory morphogen in a canonical Turing instability (Shiferaw and Karma, 2006). By defining the “Ca2+-alternans amplitude” (Δc) as the difference in peak calcium concentration of consecutive beats at each point along the length of a cell, subcellular alternans was able to be treated as the formation of a stable gradient in Δc along the length of the cell (as seen in Figure 13). For example, if on two consecutive beats the left half of a myocyte experiences a small Ca2+-transient followed by a large transient concurrent with the right half having a large followed by a small transient, Δc will be positive on the left and negative on the right.
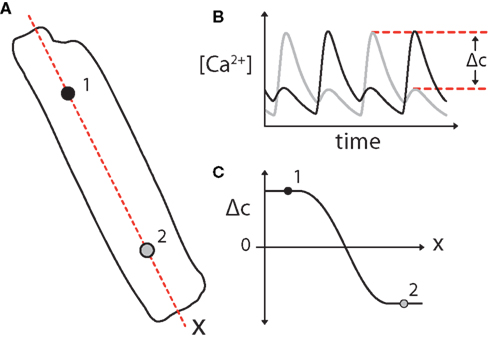
Figure 13. (A) Subcellular alternans can me modeled as the formation of a gradient in Ca2+-alternans amplitude (Δc) along the length of a cell. Subcellular alternans occurs when distinct subcellular regions of an individual myocyte exhibit Ca2+-alternans of opposite phase [as diagrammed for regions 1 and 2; (B)]. (C) This can be simplified as the formation of a gradient in Ca2+-alternans magnitude (Δc), where Δc is defined as the difference in peak Ca2+ concentration between subsequent Ca2+ transients (B). A 2-region subcellular alternans is diagrammed in this example, in which Ca2+ transients in the two halves of the cell alternate out-of-phase, separated by a “node” with period-1 (no alternans) Ca2+ transients where Δc = 0. Adapted from Gaeta et al. (2010).
Using a simplified coupled-map model, it was shown that such a gradient (subcellular alternans) will arise by a Turing instability given proper coupling between the AP and the Ca2+-transient. In particular, subcellular alternans was predicted to form by this mechanism during constant cycle length pacing of only those myocytes with negative Ca2+ → Vm coupling (Shiferaw and Karma, 2006). The same mechanism was later shown theoretically to lead to subcellular alternans in cells with positive Ca2+ → Vm coupling during pacing with a simple feedback control algorithm, “alternans control” (Gaeta et al., 2010). The latter prediction was confirmed by computational modeling and experiments using guinea pig ventricular myocytes (Figure 14; Gaeta et al., 2009, 2010). Notably, the cycle length perturbations of alternans control pacing are directly analogous to the changes in activation times seen distant from the pacing site during tissue-level spatially discordant alternans (due to alternating conduction velocity), even during pacing with a constant cycle length. In computational modeling experiments, subcellular alternans was indeed induced near the node of tissue-level spatially discordant alternans in a 1-dimensional fiber of simulated myocytes (Gaeta et al., 2009).
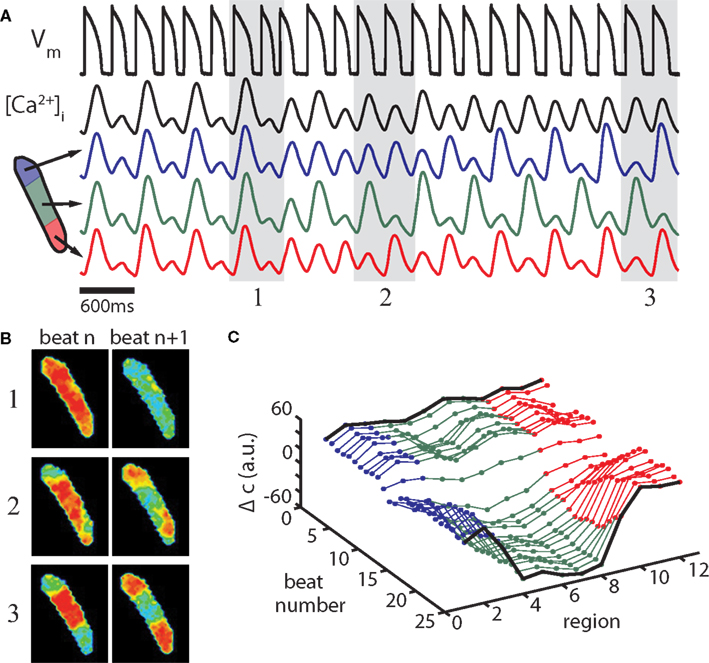
Figure 14. Alternans control induces subcellular alternans in an isolated ventricular myocyte. (A) Alternans control causes a steady-state, period-2 APD (first black trace), and whole-cell Ca2+-alternans (second black trace) to transition to a period-1 rhythm. Concurrently, the spatially homogenous Ca2+-alternans transitions to a 2-node subcellular alternans. Blue, green, and red traces are the average fluorescence from the three regions diagrammed. (B) Recorded fluorescence frames at the time of maximum calcium concentration in two successive beats during initial control (1), during the transition (2), and at nearly period-1 control (3); beat pairs are marked by gray shaded regions in (A). (C) Ca2+-alternans magnitude along the length of the cell is plotted for the experiment shown in (A). For this panel, fluorescence data are binned into 12 adjacent regions perpendicular to the length of the cell and the average Ca2+-alternans magnitude (Δc) is plotted for each region for the 25 beats shown (arbitrary fluorescence units), with colors corresponding to the regions diagrammed in (A). Fluorescence data from the extreme ends of the cell are excluded due to motion artifact. Experiments shown are from a cell paced at a cycle length of 300 ms (with alternans control). Adapted from Gaeta et al. (2009).
Regardless of pacing protocol, subcellular alternans is only predicted to occur if alternans is Ca2+-driven (Shiferaw and Karma, 2006; Gaeta et al., 2009, 2010), suggesting that in these experiments Ca2+ cycling instability was the primary mechanism of alternans. This also creates a possible utility for alternans control pacing as a test to indirectly identify the primary source of instability in different cell types and at different pacing cycle lengths (in which the presence or absence of resulting subcellular alternans indicates Ca2+-driven or Vm-driven instability, respectively; Gaeta et al., 2010).
6. Conclusion and future directions
Cardiac alternans is a clinically important electrophysiological disturbance that leads to potentially fatal reentrant arrhythmias. Multiple mechanisms have been proposed to account for its occurrence at the tissue, cellular, and subcellular level. Alternans likely results from a rich interplay of structural and dynamical mechanisms, and an interdisciplinary approach is essential to its study. Several elegant interventions have been proposed to prevent or treat cardiac alternans, including pharmacologic (Verrier and Nieminen, 2010) or molecular (Livshitz and Rudy, 2007; Mahajan et al., 2008; Cutler et al., 2009) therapies aimed at quieting its underlying instability and electrical interventions that exploit its dynamics to halt its progression to potentially fatal arrhythmia (Christini et al., 2006; Krogh-Madsen et al., 2010; Kanu et al., 2011). More work is needed, however to establish the clinical utility of experimentally available options. An improved understanding of the mechanisms of cardiac alternans will hopefully facilitate the identification of clinical interventions for the prevention of sudden cardiac death.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Aistrup, G. L., Kelly, J. E., Kapur, S., Kowalczyk, M., Sysman-Wolpin, I., Kadish, A. H., and Wasserstrom, J. A. (2006). Pacing-induced heterogeneities in intracellular Ca2+ signaling, cardiac alternans, and ventricular arrhythmias in intact rat heart. Circ. Res. 99, e65–e73.
Aistrup, G. L., Shiferaw, Y., Kapur, S., Kadish, A. H., and Wasserstrom, J. A. (2009). Mechanisms underlying the formation and dynamics of subcellular calcium alternans in the intact rat heart. Circ. Res. 104, 639–649.
Banville, I., Chattipakorn, N., and Gray, R. A. (2004). Restitution dynamics during pacing and arrhythmias in isolated pig hearts. J. Cardiovasc. Electrophysiol. 15, 455–463.
Banville, I., and Gray, R. A. (2002). Effect of action potential duration and conduction velocity restitution and their spatial dispersion on alternans and the stability of arrhythmias. J. Cardiovasc. Electrophysiol. 13, 1141–1149.
Bass, B. G. (1975). Restitution of the action potential in cat papillary muscle. Am. J. Physiol. 228, 1717–1724.
Bassani, J. W., Yuan, W., and Bers, D. M. (1995). Fractional sr ca release is regulated by trigger ca and sr ca content in cardiac myocytes. Am. J. Physiol. 268(Pt 1), C1313–C1319.
Bayer, J. D., Narayan, S. M., Lalani, G. G., and Trayanova, N. A. (2010). Rate-dependent action potential alternans in human heart failure implicates abnormal intracellular calcium handling. Heart Rhythm 7, 1093–1101.
Bers, D. M. (2008). Calcium cycling and signaling in cardiac myocytes. Annu. Rev. Physiol. 70, 23–49.
Blatter, L. A. (2003). Local calcium gradients during excitation-contraction coupling and alternans in atrial myocytes. J. Physiol. (Lond.) 546, 19–31.
Brette, F., and Orchard, C. (2003). T-tubule function in mammalian cardiac myocytes. Circ. Res. 92, 1182–1192.
Chinushi, M., Kozhevnikov, D., Caref, E. B., Restivo, M., and El-Sherif, N. (2003). Mechanism of discordant t wave alternans in the in vivo heart. J. Cardiovasc. Electrophysiol. 14, 632–638.
Chinushi, M., Restivo, M., Caref, E. B., and El-Sherif, N. (1998). Electrophysiological basis of arrhythmogenicity of qt/t alternans in the long-qt syndrome: tridimensional analysis of the kinetics of cardiac repolarization. Circ. Res. 83, 614–628.
Christini, D. J., Riccio, M. L., Culianu, C. A., Fox, J. J., Karma, A., and Gilmour, R. F. (2006). Control of electrical alternans in canine cardiac Purkinje fibers. Phys. Rev. Lett. 96, 104101.
Chudin, E., Goldhaber, J., Garfinkel, A., Weiss, J., and Kogan, B. (1999). Intracellular Ca(2+) dynamics and the stability of ventricular tachycardia. Biophys. J. 77, 2930–2941.
Cordeiro, J. M., Malone, J. E., Diego, J. M. D., Scornik, F. S., Aistrup, G. L., Antzelevitch, C., and Wasserstrom, J. A. (2007). Cellular and subcellular alternans in the canine left ventricle. Am. J. Physiol. Heart Circ. Physiol. 293, H3506–H3516.
Cutler, M. J., and Rosenbaum, D. S. (2009). Explaining the clinical manifestations of t wave alternans in patients at risk for sudden cardiac death. Heart Rhythm 6(Suppl.), S22–S28.
Cutler, M. J., Wan, X., Laurita, K. R., Hajjar, R. J., and Rosenbaum, D. S. (2009). Targeted serca2a gene expression identifies molecular mechanism and therapeutic target for arrhythmogenic cardiac alternans. Circ. Arrhythm. Electrophysiol. 2, 686–694.
Díaz, M. E., Eisner, D. A., and O’Neill, S. C. (2002). Depressed ryanodine receptor activity increases variability and duration of the systolic Ca2+ transient in rat ventricular myocytes. Circ. Res. 91, 585–593.
Díaz, M. E., O’Neill, S. C., and Eisner, D. A. (2004). Sarcoplasmic reticulum calcium content fluctuation is the key to cardiac alternans. Circ. Res. 94, 650–656.
Diego, C. D., Pai, R. K., Dave, A. S., Lynch, A., Thu, M., Chen, F., Xie, L-H., Weiss, J. N., and Valderrábano, M. (2008). Spatially discordant alternans in cardiomyocyte monolayers. Am. J. Physiol. Heart Circ. Physiol. 294, 1417–1425.
Echebarria, B., and Karma, A. (2007). Amplitude equation approach to spatiotemporal dynamics of cardiac alternans. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 76(Pt 1), :051911.
Euler, D. E. (1999). Cardiac alternans: mechanisms and pathophysiological significance. Cardiovasc. Res. 42, 583–590.
Ferrari, G. M. D., Viola, M. C., D’Amato, E., Antolini, R., and Forti, S. (1995). Distinct patterns of calcium transients during early and delayed afterdepolarizations induced by isoproterenol in ventricular myocytes. Circulation 91, 2510–2515.
Fox, J. J., McHarg, J. L., and Gilmour, R. F. (2002a). Ionic mechanism of electrical alternans. Am. J. Physiol. Heart Circ. Physiol. 282, H516–H530.
Fox, J. J., Riccio, M. L., Hua, F., Bodenschatz, E., and Gilmour, R. F. (2002b). Spatiotemporal transition to conduction block in canine ventricle. Circ. Res. 90, 289–296.
Franz, M. R. (2003). The electrical restitution curve revisited: steep or flat slope-which is better? J. Cardiovasc. Electrophysiol. 14, S140–S147.
Fujiwara, K., Tanaka, H., Mani, H., Nakagami, T., and Takamatsu, T. (2008). Burst emergence of intracellular Ca2+waves evokes arrhythmogenic oscillatory depolarization via the Na+-Ca2+ exchanger: simultaneous confocal recording of membrane potential and intracellular Ca2+ in the heart. Circ. Res. 103, 509–518.
Gaeta, S. A., Bub, G., Abbott, G. W., and Christini, D. J. (2009). Dynamical mechanism for subcellular alternans in cardiac myocytes. Circ. Res. 105, 335–342.
Gaeta, S. A., Krogh-Madsen, T., and Christini, D. J. (2010). Feedback-control induced pattern formation in cardiac myocytes: a mathematical modeling study. J. Theor. Biol. 266, 408–418.
Garfinkel, A., Kim, Y. H., Voroshilovsky, O., Qu, Z., Kil, J. R., Lee, M. H., Karagueuzian, H. S., Weiss, J. N., and Chen, P. S. (2000). Preventing ventricular fibrillation by flattening cardiac restitution. Proc. Natl. Acad. Sci. U.S.A. 97, 6061–6066.
Gierer, A., and Meinhardt, H. (1972). A theory of biological pattern formation. Kybernetik 12, 30–39.
Gilmour, R. F., Otani, N. F., and Watanabe, M. A. (1997). Memory and complex dynamics in cardiac Purkinje fibers. Am. J. Physiol. 272(Pt 2), H1826–H1832.
Goldhaber, J. I., Xie, L.-H., Duong, T., Motter, C., Khuu, K., and Weiss, J. N. (2005). Action potential duration restitution and alternans in rabbit ventricular myocytes: the key role of intracellular calcium cycling. Circ. Res. 96, 459–466.
Greenstein, J. L., and Winslow, R. L. (2002). An integrative model of the cardiac ventricular myocyte incorporating local control of Ca2+ release. Biophys. J. 83, 2918–2945.
Guevara, M., Ward, G., Shrier, A., and Glass, L. (1984). Electrical alternans and period doubling bifurcations. Comput. Cardiol. 167–170.
Hall, G., Bahar, S., and Gauthier, D. (1999). Prevalence of rate-dependent behaviors in cardiac muscle. Phys. Rev. Lett. 82, 2995–2998.
Hüser, J., Wang, Y. G., Sheehan, K. A., Cifuentes, F., Lipsius, S. L., and Blatter, L. A. (2000). Functional coupling between glycolysis and excitation-contraction coupling underlies alternans in cat heart cells. J. Physiol. (Lond.) 524(Pt 3), 795–806.
Jordan, P. N., and Christini, D. J. (2007). Characterizing the contribution of voltage- and calcium-dependent coupling to action potential stability: implications for repolarization alternans. Am. J. Physiol. Heart Circ. Physiol. 293, H2109–H2118.
Kanu, U. B., Iravanian, S., Gilmour, R. F., and Christini, D. J. (2011). Control of action potential duration alternans in canine cardiac ventricular tissue. IEEE Trans. Biomed. Eng. 58, 894–904.
Kapur, S., Wasserstrom, J. A., Kelly, J. E., Kadish, A. H., and Aistrup, G. L. (2009). Acidosis and ischemia increase cellular Ca2+ transient alternans and repolarization alternans susceptibility in the intact rat heart. Am. J. Physiol. Heart Circ. Physiol. 296, H1491–H1512.
Karma, A., and Gilmour, R. (2007). Nonlinear dynamics of heart rhythm disorders. Phys. Today 60, 51.
Keurs, H. E. D. J. T., and Boyden, P. A. (2007). Calcium and arrhythmogenesis. Physiol. Rev. 87, 457–506.
Knot, H. J., Laher, I., Sobie, E. A., Guatimosim, S., Gomez-Viquez, L., Hartmann, H., Song, L.-S., Lederer, W. J., Graier, W. F., Malli, R., Frieden, M., and Petersen, O. H. (2005). Twenty years of calcium imaging: cell physiology to dye for. Mol. Interv. 5, 112–127.
Kockskämper, J., and Blatter, L. A. (2002). Subcellular Ca2+alternans represents a novel mechanism for the generation of arrhythmogenic Ca2+waves in cat atrial myocytes. J. Physiol. (Lond.) 545(Pt 1), 65–79.
Koller, M. L., Maier, S. K. G., Gelzer, A. R., Bauer, W. R., Meesmann, M., and Gilmour, R. F. (2005). Altered dynamics of action potential restitution and alternans in humans with structural heart disease. Circulation 112, 1542–1548.
Koller, M. L., Riccio, M. L., and Gilmour, R. F. (1998). Dynamic restitution of action potential duration during electrical alternans and ventricular fibrillation. Am. J. Physiol. 275(Pt 2), H1635–H1642.
Krogh-Madsen, T., and Christini, D. J. (2007). Action potential duration dispersion and alternans in simulated heterogeneous cardiac tissue with a structural barrier. Biophys. J. 92, 1138–1149.
Krogh-Madsen, T., Karma, A., Riccio, M. L., Jordan, P. N., Christini, D. J., and Gilmour, R. F. (2010). Off-site control of repolarization alternans in cardiac fibers. Phys. Rev. E 81(Pt 1), :011915.
Livshitz, L. M., and Rudy, Y. (2007). Regulation of Ca2+ and electrical alternans in cardiac myocytes: role of camkii and repolarizing currents. Am. J. Physiol. Heart Circ. Physiol. 292, H2854–H2866.
Mahajan, A., Sato, D., Shiferaw, Y., Baher, A., Xie, L.-H., Peralta, R., Olcese, R., Garfinkel, A., Qu, Z., and Weiss, J. N. (2008). Modifying l-type calcium current kinetics: consequences for cardiac excitation and arrhythmia dynamics. Biophys. J. 94, 411–423.
Minamikawa, T., Cody, S. H., and Williams, D. A. (1997). In situ visualization of spontaneous calcium waves within perfused whole rat heart by confocal imaging. Am. J. Physiol. 272(Pt 2), H236–H243.
Miura, M., Ishide, N., Oda, H., Sakurai, M., Shinozaki, T., and Takishima, T. (1993). Spatial features of calcium transients during early and delayed afterdepolarizations. Am. J. Physiol. 265(Pt 2), H439–H444.
Narayan, S. (2006). T-wave alternans and the susceptibility to ventricular arrhythmias. J. Am. Coll. Cardiol. 47, 269–281.
Narayan, S. M. (2008). T-wave alternans testing for ventricular arrhythmias. Prog. Cardiovasc. Dis. 51, 118–127.
Narayan, S. M., Bayer, J. D., Lalani, G., and Trayanova, N. A. (2008). Action potential dynamics explain arrhythmic vulnerability in human heart failure: a clinical and modeling study implicating abnormal calcium handling. J. Am. Coll. Cardiol. 52, 1782–1792.
Narayan, S. M., Franz, M. R., Clopton, P., Pruvot, E. J., and Krummen, D. E. (2011). Repolarization alternans reveals vulnerability to human atrial fibrillation. Circulation 123, 2922–2930.
Nieminen, T., and Verrier, R. L. (2010). Usefulness of T-wave alternans in sudden death risk stratification and guiding medical therapy. Ann. Noninvasive Electrocardiol. 15, 276–288.
Nolasco, J. B., and Dahlen, R. W. (1968). A graphic method for the study of alternation in cardiac action potentials. J. Appl. Physiol. 25, 191–196.
O’Hara, T., Virág, L., Varró, A., and Rudy, Y. (2011). Simulation of the undiseased human cardiac ventricular action potential: model formulation and experimental validation. PLoS Comput. Biol. 7, e1002061.
Orchard, C. H., Pásek, M., and Brette, F. (2009). The role of mammalian cardiac t-tubules in excitation-contraction coupling: experimental and computational approaches. Exp. Physiol. 94, 509–519.
Otani, N. F., and Gilmour, R. F. (1997). Memory models for the electrical properties of local cardiac systems. J. Theor. Biol. 187, 409–436.
Pastore, J. M., Girouard, S. D., Laurita, K. R., Akar, F. G., and Rosenbaum, D. S. (1999). Mechanism linking t-wave alternans to the genesis of cardiac fibrillation. Circulation 99, 1385–1394.
Peterson, B. Z., DeMaria, C. D., Adelman, J. P., and Yue, D. T. (1999). Calmodulin is the Ca2+ sensor for Ca2+-dependent inactivation of L-type calcium channels. Neuron 22, 549–558.
Picht, E., DeSantiago, J., Blatter, L. A., and Bers, D. M. (2006). Cardiac alternans do not rely on diastolic sarcoplasmic reticulum calcium content fluctuations. Circ. Res. 99, 740–748.
Pruvot, E. J., Katra, R. P., Rosenbaum, D. S., and Laurita, K. R. (2004). Role of calcium cycling versus restitution in the mechanism of repolarization alternans. Circ. Res. 94, 1083–1090.
Pruvot, E., and Rosenbaum, D. (2003). T-wave alternans for risk stratification and prevention of sudden cardiac death. Curr. Cardiol. Rep. 5, 350–357.
Qu, Z., Garfinkel, A., Chen, P. S., and Weiss, J. N. (2000). Mechanisms of discordant alternans and induction of reentry in simulated cardiac tissue. Circulation. 102, 1664–1670.
Qu, Z., and Weiss, J. N. (2007). The chicken or the egg? Voltage and calcium dynamics in the heart. Am. J. Physiol. Heart Circ. Physiol. 293, H2054–H2055.
Restrepo, J. G., Weiss, J. N., and Karma, A. (2008). Calsequestrin-mediated mechanism for cellular calcium transient alternans. Biophys. J. 95, 3767–3789.
Riccio, M. L., Koller, M. L., and Gilmour, R. F. (1999). Electrical restitution and spatiotemporal organization during ventricular fibrillation. Circ. Res. 84, 955–963.
Rosenbaum, D. S., Jackson, L. E., Smith, J. M., Garan, H., Ruskin, J. N., and Cohen, R. J. (1994). Electrical alternans and vulnerability to ventricular arrhythmias. N. Engl. J. Med. 330, 235–241.
Rubenstein, D. S., and Lipsius, S. L. (1995). Premature beats elicit a phase reversal of mechanoelectrical alternans in cat ventricular myocytes. A possible mechanism for reentrant arrhythmias. Circulation 91, 201–214.
Salama, G. (2006). Arrhythmia genesis: aberrations of voltage or Ca2+ cycling? Heart Rhythm 3, 67–70.
Sato, D., Shiferaw, Y., Qu, Z., Garfinkel, A., Weiss, J. N., and Karma, A. (2007). Inferring the cellular origin of voltage and calcium alternans from the spatial scales of phase reversal during discordant alternans. Biophys. J. 92, L33–L35.
Shiferaw, Y., and Karma, A. (2006). Turing instability mediated by voltage and calcium diffusion in paced cardiac cells. Proc. Natl. Acad. Sci. U.S.A. 103, 5670–5675.
Shiferaw, Y., Qu, Z., Garfinkel, A., Karma, A., and Weiss, J. (2006). Nonlinear dynamics of paced cardiac cells. Ann. N. Y. Acad. Sci. 1080, 376–394.
Shiferaw, Y., Sato, D., and Karma, A. (2005). Coupled dynamics of voltage and calcium in paced cardiac cells. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 71(Pt 1), :021903.
Shiferaw, Y., Watanabe, M. A., Garfinkel, A., Weiss, J. N., and Karma, A. (2003). Model of intracellular calcium cycling in ventricular myocytes. Biophys. J. 85, 3666–3686.
Shimizu, W., and Antzelevitch, C. (1999). Cellular and ionic basis for t-wave alternans under long-qt conditions. Circulation 99, 1499–1507.
Sipido, K. R. (2006). Calcium overload, spontaneous calcium release, and ventricular arrhythmias. Heart Rhythm 3, 977–979.
Stern, M. D. (1992). Theory of excitation-contraction coupling in cardiac muscle. Biophys. J. 63, 497–517.
Stern, M. D., Song, L. S., Cheng, H., Sham, J. S., Yang, H. T., Boheler, K. R., and Ríos, E. (1999). Local control models of cardiac excitation-contraction coupling. A possible role for allosteric interactions between ryanodine receptors. J. Gen. Physiol. 113, 469–489.
Tolkacheva, E. G., Anumonwo, J. M. B., and Jalife, J. (2006). Action potential duration restitution portraits of mammalian ventricular myocytes: role of calcium current. Biophys. J. 91, 2735–2745.
Tolkacheva, E. G., Romeo, M. M., Guerraty, M., and Gauthier, D. J. (2004). Condition for alternans and its control in a two-dimensional mapping model of paced cardiac dynamics. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 69(Pt 1), :031904.
Turing, A. M. (1952). The chemical basis of morphogenesis. Philos. Trans. R. Soc. Lond. B Biol. Sci. 237, 37–72.
Venetucci, L. A., Trafford, A. W., O’Neill, S. C., and Eisner, D. A. (2008). The sarcoplasmic reticulum and arrhythmogenic calcium release. Cardiovasc. Res. 77, 285–292.
Verrier, R. L., Klingenheben, T., Malik, M., El-Sherif, N., Exner, D. V., Hohnloser, S. H., Ikeda, T., Martínez, J. P., Narayan, S. M., Nieminen, T., and Rosenbaum, D. S. (2011). Microvolt T-wave alternans physiological basis, methods of measurement, and clinical utility–consensus guideline by International Society for Holter and Noninvasive Electrocardiology. J. Am. Coll. Cardiol. 58, 1309–1324.
Verrier, R. L., Kumar, K., and Nearing, B. D. (2009). Basis for sudden cardiac death prediction by t-wave alternans from an integrative physiology perspective. Heart Rhythm 6, 416–422.
Verrier, R. L., and Nieminen, T. (2010). T-wave alternans as a therapeutic marker for antiarrhythmic agents. J. Cardiovasc. Pharmacol. 55, 544–554.
Walker, M. L., and Rosenbaum, D. S. (2003). Repolarization alternans: implications for the mechanism and prevention of sudden cardiac death. Cardiovasc. Res. 57, 599–614.
Wan, X., Laurita, K. R., Pruvot, E. J., and Rosenbaum, D. S. (2005). Molecular correlates of repolarization alternans in cardiac myocytes. J. Mol. Cell. Cardiol. 39, 419–428.
Watanabe, M. A., Fenton, F. H., Evans, S. J., Hastings, H. M., and Karma, A. (2001). Mechanisms for discordant alternans. J. Cardiovasc. Electrophysiol. 12, 196–206.
Weiss, J. N., Karma, A., Shiferaw, Y., Chen, P.-S., Garfinkel, A., and Qu, Z. (2006). From pulsus to pulseless: the saga of cardiac alternans. Circ. Res. 98, 1244–1253.
Willms, A. R., Baro, D. J., Harris-Warrick, R. M., and Guckenheimer, J. (1999). An improved parameter estimation method for hodgkin-huxley models. J. Comput. Neurosci. 6, 145–168.
Wilson, L., and Rosenbaum, D. (2007). Mechanisms of arrythmogenic cardiac alternans. Europace vi77–vi82.
Wu, R., and Patwardhan, A. (2004). Restitution of action potential duration during sequential changes in diastolic intervals shows multimodal behavior. Circ. Res. 94, 634–641.
Wu, R., and Patwardhan, A. (2006). Mechanism of repolarization alternans has restitution of action potential duration dependent and independent components. J. Cardiovasc. Electrophysiol. 17, 87–93.
Wu, T.-J., Lin, S.-F., Weiss, J. N., Ting, C.-T., and Chen, P.-S. (2002). Two types of ventricular fibrillation in isolated rabbit hearts: importance of excitability and action potential duration restitution. Circulation 106, 1859–1866.
Xie, L.-H., Sato, D., Garfinkel, A., Qu, Z., and Weiss, J. N. (2008). Intracellular ca alternans: coordinated regulation by sarcoplasmic reticulum release, uptake, and leak. Biophys. J. 95, 3100–3110.
Keywords: cardiac alternans, calcium handling, subcellular alternans, repolarization alternans, T-wave alternans, pattern formation
Citation: Gaeta SA and Christini DJ (2012) Non-linear dynamics of cardiac alternans: subcellular to tissue-level mechanisms of arrhythmia. Front. Physio. 3:157. doi: 10.3389/fphys.2012.00157
Received: 22 February 2012; Paper pending published: 23 March 2012;
Accepted: 05 May 2012; Published online: 31 May 2012.
Edited by:
Eric A. Sobie, Mount Sinai School of Medicine, USAReviewed by:
Richard Gray, Food and Drug Administration, USAThomas O’Hara, Johns Hopkins University, USA
Copyright: © 2012 Gaeta and Christini. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: David J. Christini, Greenberg Division of Cardiology, Weill Cornell Medical College, 1300 York Avenue, New York, NY 10065, USA. e-mail:ZGNocmlzdGlAbWVkLmNvcm5lbGwuZWR1
