A commentary on
Measuring fractality
by Stadnitski, T. (2012) Front. Physiol. 3:127. doi: 10.3389/fphys.2012.00127
In a recent publication Stadnitski (2012) presented an overview of methods to estimate fractal scaling in time series, outlined as an accessible tutorial1. The publication was set-up as a comparison between monofractal and ARFIMA methods, and promotes ARFIMA to distinguish between spurious and genuine 1/f noise, shedding light on “the problem that the log–log power spectrum of short-memory ARMA (p, q) processes can resemble the spectrum of 1/f noise.”
Stadnitski proposes an analytic strategy that consists of fitting 18 models to any time series. Nine of the models are ARMA (p, q) models, with p and q varying from 0 to 2, that do not contain long-range correlations. The remaining ARFIMA (p, d, q) models add to the ARMA models a fractional integration parameter d. As laid-out by the author, given a genuine fractal series, ARFIMA models should present a better fit than ARMA counterparts. Based on this logic, Stadnitski (2012) evaluates one simple reaction time (SRT) series, and concludes it is not a genuine fractal signal. This conclusion is intriguing, because it was previously argued that SRT series typically present genuine 1/f scaling (Van Orden et al., 2003; Wagenmakers et al., 2004).
In this commentary, iteratively refined spectral surrogates (Schreiber and Schmitz, 1996) were generated from the Van Orden et al. (2003) SRT series. This procedure is known to follow the original spectrum more closely than alternative procedures. Next, the performance of a monofractal method (DFA) was compared with the performance of ARFIMA modeling. Using the R-code made available in the Stadnitski tutorial, it is evaluated whether monofractal methods are indeed “distinctly inferior” to the ARFIMA method.
AIC and BIC for nine possible ARMA models and nine ARFIMA models were calculated (see Table 1). For the ten surrogate series, AIC showed best fits for the ARMA (2,0,0), ARMA (0,0,2), ARFIMA (1, d, 0) and (2, d, 2) model once, and six times for the ARFIMA (0, d, 0) model. BIC favored the ARMA (1,0,0) and (2,0,0) model and the ARFIMA (1,d,0) model once, and the ARFIMA (0, d, 0) model seven times. Given that “the smallest AIC or BIC indicates the best model,” the d parameter was estimated for the best fitting models (for the favored ARMA models, d = 0). Next, the 10 surrogate series were analyzed using DFA (converted to d), to allow for a comparison between the ARFIMA and monofractal methodologies2.
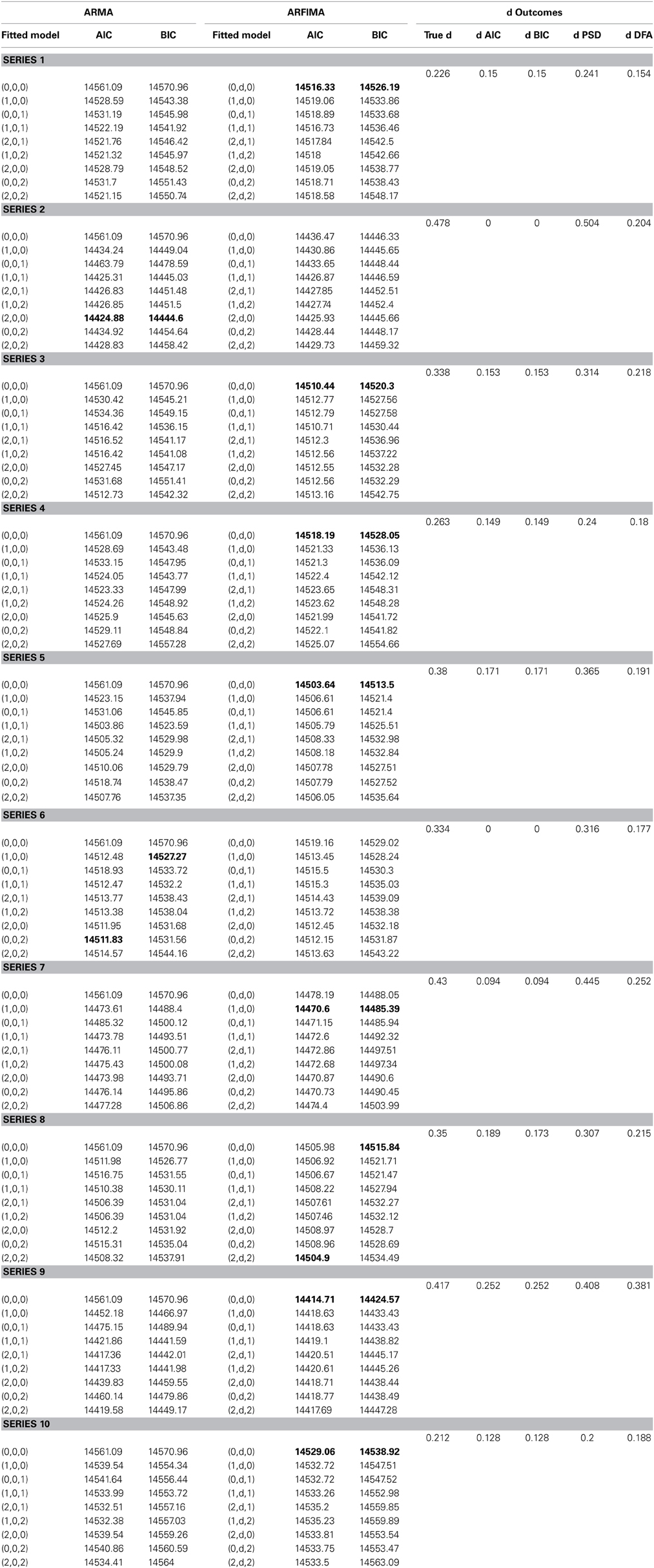
Table 1. Values of the information criteria AIC and BIC for the surrogate time series are shown at the left-hand side. The targeted scaling exponent and the estimated scaling exponents from the various methods are shown on the right-hand side.
As pointed out by Stadnitski, “good estimators are unbiased, i.e., their means equal the true parameter value.” The summed absolute difference between the estimated d-values from the surrogates and the original data was 3.86 for AIC, 3.87 for BIC, and 1.27 for DFA. Hence, DFA equaled the target parameters much more closely. DFA approached the target d-values more closely than ARFIMA in ten out of ten cases. Hence, the claim that monofractal methods are inferior to ARFIMA methods is not supported. Contrary, this analysis shows that monofractal methods in fact provide much better estimates.
This conclusion is discrepant to Stadnitski's conclusion. Stadnitski simulated a short-memory ARIMA (1,0,1) model and a long-memory ARFIMA (1, d, 1) model, and concluded that ARFIMA methods were less biased and more precise than, and therefore superior to, monofractal estimators. Here, spectral surrogates were constructed, and ARFIMA and DFA estimates were compared to the original target parameters. Here, the ARFIMA methodology was more biased than monofractal estimators. So how should one go about this discrepancy?
Accuracy concerns aside, it may be concluded that the issue raised by Stadnitski is in fact a theoretical, rather than a statistical one. By realizing that “goodness-of-fit alone cannot serve up counterexamples that falsify theories” (Gilden, 2009, p. 1463), it is argued that fitting ARFIMA algorithms to the data is not sufficient in itself to distinguish between genuine and spurious scaling properties. The true challenge should be “to compare the empirical accuracy of theoretical predictions in a program of strong inference” (Hasselman, 2012, p. 4).
That is, although often implicit, there must exist specific ontological intuitions that motivate researchers to fit ARFIMA models. As it stands, however, this inherent theoretical motivation is still to take up the challenge against theoretical predictions corroborated by fractal perspectives (see Diniz et al., 2011), like the ubiquity of 1/f scaling, consistent changes away from 1/f scaling with pathological conditions and aging (Goldberger et al., 2002; Hausdorff, 2007), consistent changes toward 1/f scaling in more skilled performances (Wijnants et al., 2009, 2012a,b), no bending at the low-frequencies in a power spectrum when longer time series are collected (Van Orden et al., 2005), and so forth. In short, spurious 1/f scaling “becomes an extraordinary hypothesis that would itself require extraordinary evidence” (Van Orden et al., 2003, p. 19), evidence that cannot come from goodness-of-fit alone, to convince that the preferred models are also theoretically viable, and consequently to be preferred methodologically.
Supplementary Material
The Supplementary Material for this article can be found online at: http://www.frontiersin.org/journal/10.3389/fphys.2014.00028/full
Footnotes
1. ^In this short commentary, the terminology of the Stadnitski paper (including acronyms and short notations) has been used.
2. ^For a full description of the methods, please consult Stadnitski (2012).
References
Diniz, A., Wijnants, M. L., Torre, K., Barreiros, J., Crato, N., Bosman, A. M. T., et al. (2011). Contemporary theories of 1/f noise in motor control. Hum. Mov. Sci. 30, 889–905. doi: 10.1016/j.humov.2010.07.006
Gilden, D. L. (2009). Global model analysis of cognitive variability. Cogn. Sci. 33, 1441–1467. doi: 10.1111/j.1551-6709.2009.01060.x
Goldberger, A. L., Peng, C.-K., and Lipsitz, L. A. (2002). What is physiologic complexity and how does it change with aging and disease? Neurobiol. Aging 23, 23–26. doi: 10.1016/S0197-4580(01)00266-4
Hasselman, F. (2012). When the blind curve is finite: dimension estimation and model inference based on empirical waveforms. Front. Physiol. 4:75. doi: 10.3389/fphys.2013.00075
Hausdorff, J. M. (2007). Gait dynamics, fractals and falls: finding meaning in the stride-to-stride fluctuations of human walking. Hum. Mov. Sci. 26, 555–589. doi: 10.1016/j.humov.2007.05.003
Schreiber, T., and Schmitz, A. (1996). Improved surrogate data for nonlinearity tests. Phys. Rev. Lett. 77, 635. doi: 10.1103/PhysRevLett.77.635
Van Orden, G., Holden, J. G., and Turvey, M. T. (2003). Self-organization of cognitive performance. J. Exp. Psychol. Gen. 132, 331–350. doi: 10.1037/0096-3445.132.3.331
Van Orden, G., Holden, J. G., and Turvey, M. T. (2005). Human cognition and 1/f scaling. J. Exp. Psychol. Gen. 134, 117–123. doi: 10.1037/0096-3445.134.1.117
Wagenmakers, E.-J., Farrell, S., and Ratcliff, R. (2004). Estimation and interpretation of 1/f α noise in human cognition. Psychon. Bull. Rev. 11, 579–615. doi: 10.3758/BF03196615
Wijnants, M. L., Bosman, A. M. T., Hasselman, F., Cox, R. F. A., and Van Orden, G. (2009). 1/f scaling in movement time changes with practice in precision aiming. Nonlinear Dynamics Psychol. Life Sci. 13, 75–94.
Wijnants, M. L., Cox, R. F. A., Hasselman, F., Bosman, A. M. T., and Van Orden, G. (2012a). A trade-off study revealing nested timescales of constraint. Front. Physiol. 3:116. doi: 10.3389/fphys.2012.00116
Keywords: 1/f noise, fractal, ARFIMA, response time, long memory, cognitive science
Citation: Wijnants ML (2014) A comment on “Measuring fractality” by Stadnitski (2012). Front. Physiol. 5:28. doi: 10.3389/fphys.2014.00028
Received: 02 September 2013; Accepted: 13 January 2014;
Published online: 05 February 2014.
Edited by:
Radhakrishnan Nagarajan, University of Kentucky, USAReviewed by:
Rathinaswamy B. Govindan, Children's National Medical Center, USACopyright © 2014 Wijnants. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence:bS53aWpuYW50c0Bwd28ucnUubmw=
 Maarten L. Wijnants
Maarten L. Wijnants