- 1Dipartimento di Fisica e Astronomia “G. Galilei”, Università degli Studi di Padova, Padova, Italy
- 2Istituto Veneto di Medicina Molecolare, Fondazione per la Ricerca Biomedica Avanzata, Padova, Italy
- 3Istituto di Neuroscienze, Consiglio Nazionale delle Ricerche, Padova, Italy
Mutations of the GJB2 gene encoding the connexin 26 (Cx26) gap junction protein, which is widely expressed in the inner ear, are the primary cause of hereditary non-syndromic hearing loss in several populations. The deafness–associated single amino acid substitution of methionine 34 (M34) in the first transmembrane helix (TM1) with a threonine (T) ensues in the production of mutant Cx26M34T channels that are correctly synthesized and assembled in the plasma membrane. However, mutant channels overexpressed in HeLa cells retain only 11% of the wild type unitary conductance. Here we extend and rationalize those findings by comparing wild type Cx26 (Cx26WT) and Cx26M34T mutant channels in silico, using molecular dynamics simulations. Our results indicate that the quaternary structure of the Cx26M34T hemichannel is altered at the level of the pore funnel due to the disruption of the hydrophobic interaction between M34 and tryptophan 3 (W3) in the N–terminal helix (NTH). Our simulations also show that external force stimuli applied to the NTHs can detach them from the inner wall of the pore more readily in the mutant than in the wild type hemichannel. These structural alterations significantly increase the free energy barrier encountered by permeating ions, correspondingly decreasing the unitary conductance of the Cx26M34T hemichannel. Our results accord with the proposal that the mutant resides most of the time in a low conductance state. However, the small displacement of the NTHs in our Cx26M34T hemichannel model is not compatible with the formation of a pore plug as in the related Cx26M34A mutant.
Introduction
Connexins are integral transmembrane proteins that form intercellular channels in vertebrates. Six connexins form a hexamerical assembly, known as connexon or hemichannel, which delineates an aqueous pore with a minimum diameter of ~1.2 nm. When two hemichannels from adjacent cells dock and join, leaving a gap of ~2–3 nm, they may form an intercellular gap junction channel which spans the two plasma membranes and allows the exchange of cytoplasmic molecules with size up to ~1 kDa (Goodenough and Paul, 2009). The importance of electrical and molecular signaling through gap junction channels is widely recognized (Evans et al., 2006; Harris, 2007). It is also well established that connexin hemichannels open in response to various types of stimuli and conditions, including mechanical, shear, ionic and ischemic stress and provide a pathway for the release of intracellular ATP, glutamate, NAD+ and prostaglandin E2, which act as paracrine messengers (Evans et al., 2006).
Virtually all cells in solid tissues are coupled by gap junctions (Goodenough and Paul, 2009), thus it is not surprising that mutations in connexin genes have been linked to a variety of human diseases, including cardiovascular anomalies, peripheral neuropathy, skin disorders, cataracts, and deafness (Wei et al., 2004; Laird, 2006; Dobrowolski and Willecke, 2009). Of notice, about half of all cases of human deafness in countries surrounding the Mediterranean have been linked to mutations in the GJB2 gene, which encodes Cx26 (Zelante et al., 1997; Petit et al., 2001). In this paper, we focus on hemichannels formed by the deafness–associated Cx26M34T mutant. According to the published X–ray model of the human Cx26WT gap junction channel (Maeda et al., 2009), M34 interacts with W3 of the NTH belonging to an adjacent connexin. The six NTHs fold inside the pore and the M34–W3 hydrophobic interactions stabilize their position at the cytoplasmic mouth (see Figure 5 of Maeda et al., 2009).
The Cx26M34T mutant, which encodes full–length products, was originally described by Kelsell et al. (1997) who associated it with a dominant form of non-syndromic deafness (DFNA3) and also noted that M34 is conserved across several species both in Cx26 and in the closely related connexin 32 (Cx32) protein. Cx26M34T was also linked to a recessive form of hearing loss by Houseman et al. (2001). However, subsequent studies on the family first described by Kelsell et al. (1997) uncovered the association of dermatological signs in deaf patients and identified another dominant mutation in GJB2 segregating with the disease, casting doubts on the significance of the Cx26M34T variant. Other authors reported normal hearing in heterozygous carriers of Cx26M34T associated with either Cx26G35del or other Cx26 recessive mutations (Denoyelle et al., 1997; Kelley et al., 1998; Scott et al., 1998; Feldmann et al., 2004) and classified it as a benign polymorphism. An attempt to rationalize these results noted that, even though Cx26M34T is significantly overrepresented among patients, its relative penetrance is about 1/10 of that of undisputedly pathogenic mutations (Pollak et al., 2007).
The functional expression of the Cx26M34T connexin in Xenopus oocytes showed that the mutant exerts a dominant negative effect on Cx26WT (White et al., 1998). Later on Thonnissen et al. (2002) observed low levels of dye transfer between HeLa cells overexpressing Cx26M34T, providing the first evidence that this mutant could traffic to the cell membrane and form intercellular channels in a mammalian expression system, albeit with reduced efficiency. In contrast, Oshima et al. (2003) reported that assembly of Cx26M34T in HeLa and Sf9 cells resembles that of Cx26WT and that dye transfer in these cells is close to normal. Other electrophysiological studies performed in paired Xenopus oocytes concluded that Cx26M34T was capable of forming functional heterotypic channels with Cx32, albeit with abnormal gating properties (Skerrett et al., 2004). Based on these results, it was suggested that Cx26M34T/Cx32 heterotypic channels are not fully open at rest but are activated when positive transjunctional voltages are applied to the Cx26M34T side (Skerrett et al., 2004).
The pathogenetic role of M34T was confirmed in a study by Bicego et al. (2006) showing that, at a cellular level, Cx26M34T is correctly synthesized and targeted to the plasma membrane in HeLa cells, but inefficiently forms intercellular channels that display an abnormal electrical behavior and retain only 11% of the unitary conductance of Cx26WT. Moreover, Cx26M34T channels failed to support the intercellular diffusion of fluorescent tracers and the spreading of mechanically induced intercellular Ca2+ waves.
In the strictly homologous Cx32 protein, several mutations of Met34 have been associated with X linked Charcot–Marie–Tooth disease (M34T, M34I Tan et al., 1996, M34V Latour et al., 1997, M34K Yum et al., 2002). Single–channel recordings performed in transfected N2A cells showed that Cx32M34T mutants reside in a low–conductance (15 pS) substate 98% of the time at −80 mV (Oh et al., 1997).
Here, starting from previously described molecular models (Zonta et al., 2012, 2013) based on the 3.5 Å X–ray data (Maeda et al., 2009), we constructed a model of the Cx26M34T hemichannel and analyzed it by use of molecular dynamics simulations. The results we present provide an interpretative framework, at atomic scale, of the reduced opening probability and conductance observed in the residual open state of the mutant hemichannel. This work advances our understanding of the molecular mechanisms that underline ion permeation and gating of connexin hemichannels and provides a mechanistic link between connexin mutations and hereditary deafness.
Methods
Equilibrium Molecular Dynamics of Cx26WT and Cx26M34T Connexons
We generated the Cx26M34T hemichannel model starting from an equilibrium configuration of the Cx26WT model published in Refs. (Zonta et al., 2012, 2013) and mutating the 34th amino acid of each connexin protomers with the mutate tool of the Swiss PDB–Viewer (Guex and Peitsch, 1997). As done previously for Cx26WT, we embedded the Cx26M34T hemichannel in a plasma membrane represented by 494 Palmytoyl Oleoyl Posphatidly Choline molecules (POPC), following the same methodology described in Pantano et al. (2008). In order to achieve a faster convergence of molecular dynamics trajectories, coordinates for the original phospholipid bilayer were obtained from an equilibrium configuration of the membrane model described in Pantano and Carafoli (2007). The system then was solvated with full atom TIP3P water containing Cl− and K+ ions at a concentration of ~0.15 M to neutralize the positive net charge of the connexon and to mimic a physiological ionic strength. The whole system comprised 204664 and 205825 atoms respectively for Cx26M34T and Cx26WT simulations.
We initially performed a short energy minimization run, followed by equilibrium molecular dynamics under periodic boundary condition using unitary cells of 12 × 12 × 11 nm for both systems, consistent with the channel density measured in a Cx26 gap–junction plaque by atomic force microscopy (Muller et al., 2002). Equilibrium molecular dynamics simulations, performed with GROMACS 4.6 software (Hess et al., 2008) using the Amber03 force field (Duan et al., 2003) under constant nPT conditions, lasted 40 ns, the last 18 ns of which were retained for data analysis. Temperature T and pressure P were kept constant, at 300 K and 1 atm respectively, using the Berendsen thermostat and barostat (Berendsen et al., 1984). Fast smooth Particle–Mesh Ewald summation (Darden et al., 1993) was used for long–range electrostatic interactions, with a cut off of 1.0 nm for the direct interactions.
Root mean squared deviation (RMSD) of the transmembrane domain stabilized after 15 ns, whereas short range interaction between membrane and protein (short range Lennard Jones plus short range Coulomb potential) stabilized after 20 ns. Moreover, root mean squared fluctuations (RMSF) were well equilibrated in the last 20 ns time window of the simulation (data not shown).
Estimate of the Potential of Mean Force (PMF) from Steered Molecular Dynamics
Simulations were performed under constant volume conditions on the previously equilibrated systems. To force the passage of a K+ ion through the channel pore (Figure 1), we connected it to one end of a linear spring with elastic constant k of 2000 kJ mol−1nm−2 and zero resting length. The other end of the spring shifted along pore axis (z direction) from the cytoplasmic to the extracellular side of the hemichannel at a constant velocity of 0.5 nm ns−1. The shifting spring was stiff enough to keep the K+ in the proximity of the z axis, with a standard deviation of 0.034 nm. The simulations spanned a total of 8.6 nm in 17.2 ns for each system. The mean force F(x, y, z) exerted on the ion by the hemichannel amino acids was gauged by the instantaneous spring extension averaged over 40 ps time intervals.
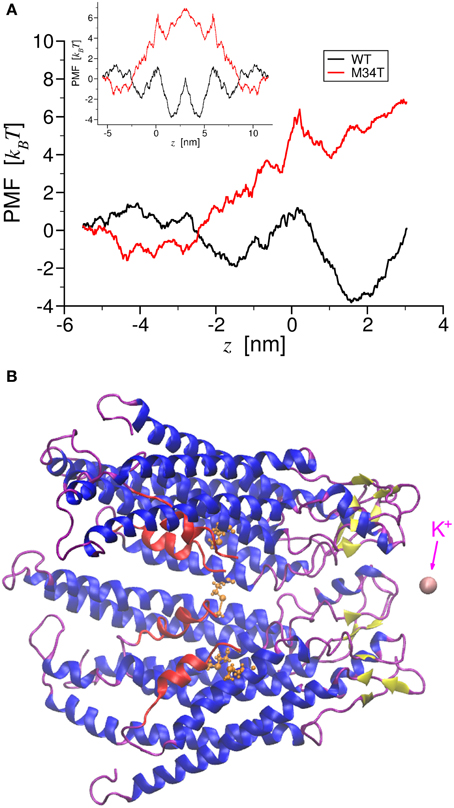
Figure 1. Potential of Mean Force of potassium ion permeation through Cx26WT and Cx26M34T. Panel (A) shows the total PMF for a single K+ ion permeating through the two different hemichannels as a function of the pore axial coordinate. The black trace corresponds to the wild type, while the red trace to the mutant. The inset shows the corresponding PMFs for the entire gap junction channel. In panel (B), a cartoon representation of a section made of four connexins protomers of the Cx26M34T hemichannel is drawn in register with the axis coordinate in A. The NTHs are colored in red, while in orange we show a ball and stick representation of Thr34. This also frame shows the K+ ion (in pink) at the final position, just outside the extracellular mouth of the hemichannel. Note that the two PMFs diverge largely in the region around the NTHs.
F(x, y, z) balanced effectively all other forces acting on the ion at each point along the K+ trajectory, therefore the work profile
which is known as the PMF, has the meaning of a free energy profile for the permeation of a single K+ ion (Kirkwood, 1935; Roux and Karplus, 1991a,b; Park and Schulten, 2004) through the hemichannel (HC) pore (Figure 1A). We derived the PMF for the full gap junction channel WGJ(z) (Figure 1A, inset) by reflecting WHC(z) about a vertical axis passing through the z coordinate corresponding to extracellular end of the hemichannel (Zonta et al., 2013).
Computation of Ionic Conductance
To link quantitatively PMF and ionic conductance, let us consider the first time an unforced K+ ion reaches one end the full gap junction channel (labeled r) given that it started at point (0, 0, z0). Such first passage time of the permeation process has mean value τ given by:
which can be computed provided the PMF WGJ(z) and the bulk diffusion coefficient D are known (Szabo et al., 1980; Zwanzig, 1988). In Equation 2 the factor β = (kB T)−1, where T is absolute temperature and kB is the Boltzmann constant. The numerical value we used for D = 1.957 · 10−9 m2/ s was experimentally determined in Samson et al. (2003) and accords with an independent estimate we obtained from molecular dynamics simulations of K+ in the bulk.
If a single ion were to occupy the pore at any time, the transition rate would be
and net unitary current could be estimated as the difference between forward (κ l → r) and reverse (κ r → l) transition rates multiplied by the charge q of the ion:
In equilibrium conditions the current is obviously null. Therefore, to compute the unitary conductance
an electrical potential difference ΔV must be applied between the two ends of the channel. Assuming that the electrical potential is a linear function of the pore axial coordinate z (Tao et al., 2012), we can take its presence into account by adding a suitable term to the PMF, yielding a new function
After replacing WGJ(z) with U(z) in Equation 2, we numerically computed the forward and reverse transition rates as:
for ten different values of the imposed ΔV. For each value, we estimated the net current I using Equation 4. We finally plotted I vs. ΔV and derived γ0 as the slope of the interpolating line.
Statistical Analysis
Means are quoted ± standard error of the mean (s.e.m.) and p-values are indicated by letter p. Statistical comparisons were made using the Mann–Whitney U-test (Mann and Whitney, 1947); p < 0.05 was selected as the criterion for statistical significance.
Results
Molecular Dynamics Predicts Conductance Values that Accord with Experimental Results for Both Cx26WT and Cx26M34T
To gain insight into the role played by the M34T mutation, we used steered molecular dynamics to derive the PMFs for K+ ion permeation (Figure 1; see Methods). The PMF profiles for Cx26WT and Cx26M34T differ primarily in the narrowing region of the pore (Figure 1A), where the six NTHs fold inside the cytoplasmic mouth of the hemichannel (Figures 1B, Supplementary Movie S1). We used these PMFs to compute the full channel unitary conductance γ0 as detailed in the Methods and obtained the values reported in Table 1, first column. Although those figures are one order of magnitude smaller than their respective measured counterparts (Table 1, third column), their ratio RMD = γ0, M34T/γ0, WT = 9.5% is in good agreement with the experimental result (REXP = 11.4%) (Bicego et al., 2006).
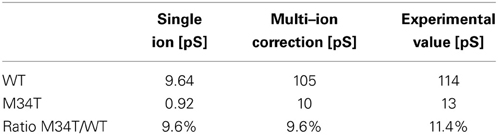
Table 1. Comparison between conductance predicted by molecular dynamics simulations and experimental values.
As detailed in the Methods section, the conductance values we computed were derived from transition rates of ion permeation through the channel assuming that a single ion can occupy the channel at a given time. This assumption is probably unrealistic. Therefore, to obtain a better estimate for the ionic conductance, we contemplated the possibility that NI K+ ions occupy the channel simultaneously. The maximum conductance is achieved when the ions permeate the channel with minimal reciprocal interaction. Indeed, ionic conductance saturates with increasing salt concentration, and, when many ions are allowed to occupy the channel simultaneously, deviation from independent ion transition is observed (Hille and Schwarz, 1978).
To estimate NI, we assumed that electrostatic repulsion is negligible if the ions are found at the relative distance 2λD, where
is the Debye length (a Debye sphere is a volume whose radius is the Debye length, outside of which charges are electrically screened; in the formula above, e is the proton's charge, NA is Avogadro's number and c the concentration). We then computed
where L is the length of the full gap junction channel. We then re-estimated the unitary conductance as γ = NIγ0 for both Cx26WT and Cx26M34T. The corrected results (Table 1, second column) agree far better with the experimental data (Table 1, third column).
The reduced conductance of Cx26M34T correlates with the observation that the first residues (M1, D2) of the NTHs in the Cx26M34T hemichannel protrude more toward the center of the pore than their WT counterparts and thus interact more efficiently with the drifting K+ ions (Figure 2, Supplementary Movie S2).
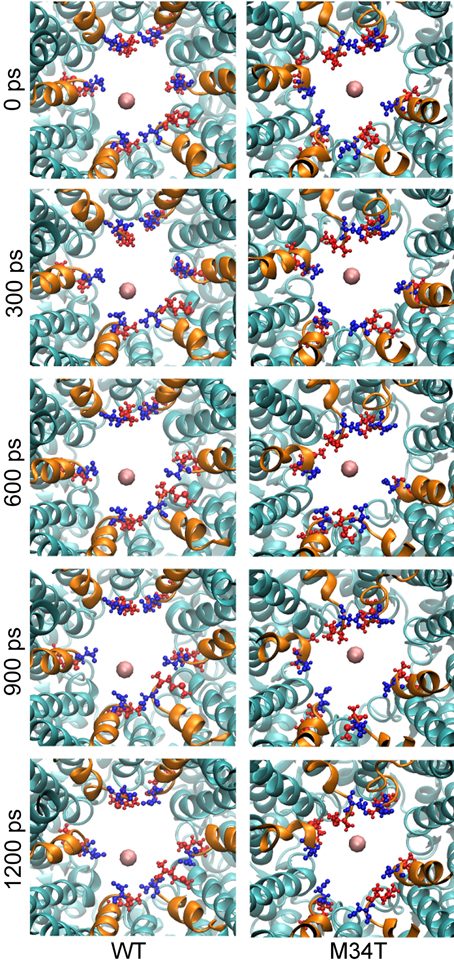
Figure 2. Snapshots of potassium steered molecular dynamics. The pictures show, from a cytoplasmic point of view, five different snapshots in a region proximal to the NTHs. The K+ ion is shown as a pink sphere and the NTHs are highlighted in orange. M1 (blue) and D2 (red) residues are drawn in ball and stick representation. In the mutant, these residues protrude more toward the center of the pore and consequently the energy of interaction with K+ is higher and results in an increased total PMF.
Analysis of Equilibrium Molecular Dynamics Trajectories Reveals an Asymmetric Configuration of NTHs in Cx26M34T Hemichannels
As shown in Figure 3, replacing a hydrophobic M with a polar T in position 34 disrupts the hydrophobic interaction between M34 and W3 in the NTH of the adjacent connexin. Consequently, the six NTHs of the Cx26M34T hemichannel rearranged in a more asymmetric configuration in the course of the 40 ns equilibration process. To measure these changes and to compare Cx26M34T to Cx26WT quantitatively, let us introduce an eccentricity coefficient E that gauges departure from a perfect hexagonal symmetry. Specifically, we define E as the ratio between the maximum (D) and the minimum (d) diameter of a hexagon built on the alpha carbons of corresponding amino acids in the six protomers (Figure 4). We computed E for amino acids number 2 to 14 of the NTHs, averaged the results over 100 configurations spanning the last 18 ns of equilibrium molecular dynamics, yielding EWT = 1.10 ± 0.05 (mean ± s.e.m.) for the Cx26WT hemichannel and EM34T = 1.16 ± 0.11 (mean ± s.e.m.) for the Cx26M34T hemichannel. Since the distributions of E-values are not normal, we analyzed the significance level of the observed difference using the Mann Whitney U-test (Mann and Whitney, 1947). The p-value of 0.03 returned by the test indicates that, compared to Cx26WT, the distribution of Cx26M34T data is significantly shifted toward larger E values (i.e., it has a higher degree of asymmetry).
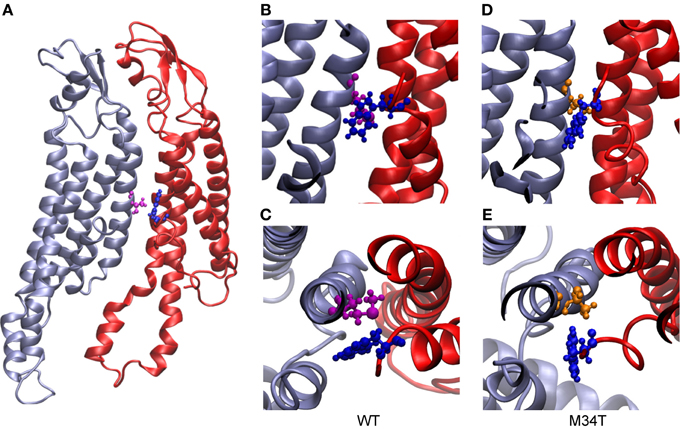
Figure 3. Structural comparison between Cx26WT and Cx26M34T. In panel (A), two adjacent wild type connexins are shown in ribbon representation. The two residues highlighted in ball and stick representation are M34 (purple) and W3 (blue). Panels (B) (top view) and (C) (side view) show details of the hydrophobic interaction between these two residues. (D) and (E), same as (B) and (C) for Cx26M34T; W3 is again represented in blue, while T34 in orange. Note that the interaction present in the wild type is disrupted in the mutant.
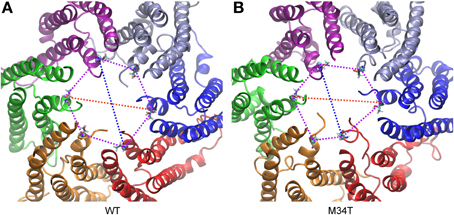
Figure 4. Analysis of symmetry index. (A) Cx26WT connexon model. (B) Cx26M34T connexon model. Shown are the major (red) and minor (blue) diameter and the angles (purple) of the hexagon built on T5 alpha carbons for a snapshot of the equilibrium dynamics. The six connexins are rendered with different colors and represented in ribbons. Each T5 alpha carbon is represented with its Van der Waals radius, while the rest of the amino acid is represented in licorice.
We further analyzed the dynamical behavior of the NTHs by tracking the angles of the hexagon built on the alpha carbon of the six T5 residues, which are located roughly half way along the NTHs. In Figure 5 we plot angular values during the last 18 ns of equilibrium dynamics for both Cx26WT (Figure 5A) and Cx26M34T (Figure 5B) vs. time. Note that angles in the Cx26M34T hemichannel display a higher degree of instability compared to Cx26WT and, correspondingly, the distribution of their values differ significantly (Figure 5C, p = 0.01, Mann–Whitney U-test).
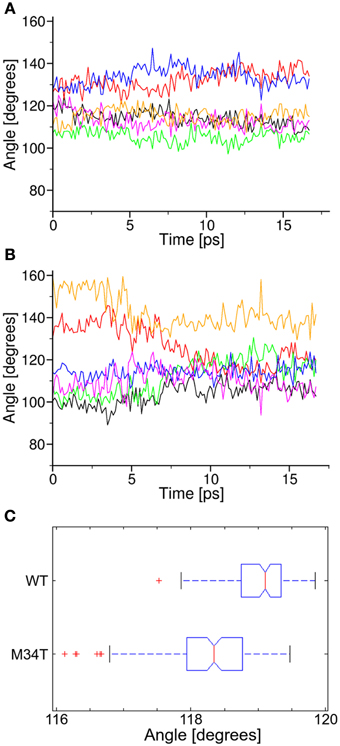
Figure 5. Analysis of angular parameters. Panels (A,B) show the time course of angular values during equilibrium dynamics for Cx26WT and Cx26M34T, respectively (see also Figure 3). (C) Box plots of the two data distribution, in which we interpreted each angle as a representation of the corresponding observable. The difference between the two distribution is significant (see text).
The M34T Mutation Reduces the Interaction Between the NTHs and the Inner Wall of the Hemichannel
It has been proposed that, for a gap junction channel to reside in the fully open state, the six NTHs must be attached to the inner wall of its cytoplasmic mouth via hydrophobic interactions between W3 and M34 (Maeda and Tsukihara, 2011; Fasciani et al., 2013). To test this hypothesis, we performed a series of steered molecular dynamics simulations by connecting the center of mass of one NTH (residues 1 to 12) to one end of a linear spring with zero resting length and elastic constant of 100 kJ mol−1nm−2 (Figure 6). Figure 6B shows six different pull force traces (one per NTH) for Cx26WT (black) and Cx26M34T (red). At the beginning of each run, the two spring ends coincided and the pull force was null. Setting the free end of the spring into motion with constant velocity of 1 nm ns−1 toward the center of the pore generated a centripetal force on the NTH. In the typical scenario, the pulled NTH did not follow immediately because the pull force was insufficient to overcome the interaction that kept the NTH attached to the inner wall of the hemichannel. Consequently the spring extended and the pull force increased linearly, until it reached a value sufficient to break the NTH–wall interaction. At this point the NTH started to move, the spring relaxed and the pull force dropped abruptly. In the Cx26M34T hemichannel the pulled NTH started to move after about 1 ns, whereas in the Cx26WT hemichannel the movement occurred at the end of the simulation period (after ~3 ns). To highlight the differences between the two data sets, we averaged the six different traces and computed a running average over these mean traces to reduce the effect of thermal noise (Figure 6C). Note the clear departure of the average traces around 105 (kJ/mol)/nm (Figure 6D). We interpret this value as the detaching force for the Cx26M34T mutant. The corresponding value for Cx26M34T was in excess of 250 (kJ/mol)/nm, almost three–fold larger.
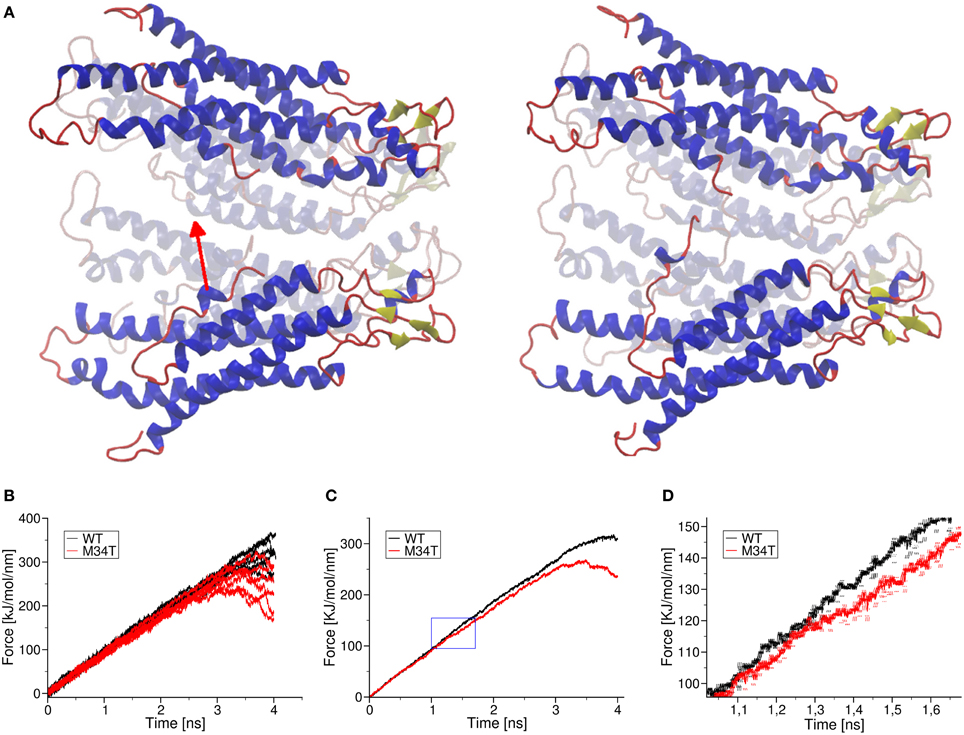
Figure 6. Effect of a pull force applied to the NTHs. Panel (A) shows schematically the effect of pulling one NTH: shown are the initial and final frames of a pulling simulation. In panel (B), we plot raw pull force data for each trajectory corresponding to the six different helices of Cx26WT (black traces) and Cx26M34T (red traces). Panel (C) shows the mean traces obtained from the corresponding raw traces, after application of a further running average over 200 fs in order to reduce thermal noise. The blue box is magnified in panel (D) to show more clearly the point where the two mean traces separate. Error bars are standard deviation obtained from the running average. Visual inspection of the molecular dynamics trajectories revealed that, in the mutant, the detached helix interacts with a neighboring NTH, due to the more asymmetric shape of the pore mouth. This interaction obstacles the motion of the helix toward the center, until the pull force is large enough to break it. This effect was not observed in wild the type Cx26WT (Supplementary Movie S3).
Discussion
At the cellular level, the deafness–associated Cx26M34T mutant is correctly synthesized and targeted to the plasma membrane in HeLa cells, but inefficiently forms intercellular channels that display an abnormal electrical behavior and retain only 11% of the unitary conductance of Cx26WT (Bicego et al., 2006). Moreover, Cx26M34T channels fail to support the intercellular diffusion of fluorescent tracers and the spreading of mechanically induced intercellular Ca2+ waves (Bicego et al., 2006). It has also been suggested that Cx26M34T/Cx32 heterotypic channels are not fully open at rest but are activated when positive transjunctional voltages are applied to the Cx26M34T side (Skerrett et al., 2004).
Our molecular dynamics simulations of Cx26WT and Cx26M34T hemichannels indicate that the quaternary structure of the mutant is altered at the level of the NTHs due to the disruption of the hydrophobic interaction between M34 (in the first transmembrane helix) and W3 (in the NTH) (Figure 3). The mutation destabilizes the NTH binding to the cytoplasmic mouth of the channel altering its shape, which is significantly more asymmetric in the mutant hemichannel model compared to the wild type model (Figures 4, 5).
The NTHs are thought to participate in voltage gating, which is rather complex in channels formed by human Cx26 that exhibit a bipolar behavior (Gonzalez et al., 2006). Single channel recordings indicate that the opening of Cx26 hemichannels upon depolarization at negative potentials involves a transition from the fully closed state to a main open state. As depolarization progresses, hemichannels remain stable in this high conductance state until polarization reaches larger positive potentials, whereupon they inactivate by closing partially to a subconductance or residual open state (Gonzalez et al., 2006).
To explain these observations, it has been proposed that connexin hemichannels possess two gating mechanisms. One mechanism has the same polarity for all the hemichannels independently of their connexin isoform composition and depends critically on the extracellular Ca2+ concentration (Ebihara and Steiner, 1993; Pfahnl and Dahl, 1999; Muller et al., 2002). A study performed on Cx32 hemichannels concluded that (i) Ca2+ can block both voltage gated opening to the higher conductance open state and ion conduction through the partially open hemichannels and (ii) the effect depends on Ca2+ binding with millimolar affinity within the extracellular vestibule of the pore (Gomez-Hernandez et al., 2003). In our prior work using molecular dynamics simulations, we provided an interpretative model showing that Ca2+ ions linger within the negatively charged extracellular mouth at a membrane potential of −80 mV. Upon depolarization to 0 mV the interactions weaken and the position of the Ca2+ ions shifts significantly toward the extracellular space (Zonta et al., 2012). This scheme is supported by the presence of negatively charged amino acids facing the pore in the extracellular mouth, in particular D46 and E47, that are highly conserved across connexin isoforms. E47 is also believed to undergo post-translational gamma carboxylation (Locke et al., 2009), which increases it affinity for Ca2+ ions. This crucial point is analyzed in Zonta et al. (2014).
The second gating mechanism shows different polarity among different connexin isoforms, and depends on the total charge of the NTHs (Verselis et al., 1994). It has been proposed that the NTHs move in response to changes in electrical potential and close the channel (Maeda and Tsukihara, 2011; Fasciani et al., 2013). Our simulations indicate that the NTHs in the Cx26M34T mutant are less bound to the channel wall (Figure 6) and we speculate that, for this reason, the gating mechanism is compromised, as proposed in Skerrett et al. (2004). The slight but significant modifications highlighted by our relatively brief (40 ns) equilibrium molecular dynamics simulations, reflect in a sizeable (90%) reduction of the unitary conductance (Table 1), in quantitative accord with the experimental results (Bicego et al., 2006). Our simulation work also agree with the proposal that the M34T mutant channels resides most of the time in a low conductance state (13 pS for Cx26M34T, 15–20 pS for Cx32M34T). However, the displacement of the NTHs in our equilibrium dynamics, is not marked enough to be compatible with the formation of the pore plug as described in Oshima et al. (2007) for the closely related Cx26M34A mutant. Further simulation work is required to test whether such a plug can be formed by Cx26M34T mutant connexins.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Supported by Telethon Italy grant GGP13114 and MIUR PRIN grant n. 2009CCZSES to Fabio Mammano. Computer simulations were performed at the CINECA supercomputer centers.
Supplementary Materials
The Supplementary Material for this article can be found on line at: http://www.frontiersin.org/journal/10.3389/fphys.2014.00085/abstract
Supplementary Movie S1. Steered molecular dynamics of K+ permeation. In this simulation, we force a K+ ion to permeate through the pore of Cx26WT and Cx26M34T hemichannels. The total PMFs for the two cases (black trace for wild type and red trace for the mutant) is shown in register with the permeating ion position (represented with its Van der Waals radius, in pink). The NTHs are highlighted in red, and two key residues are represented in ball and stick; T34 is color in green and K41 (corresponding to the maximum of the total PMF) in orange.
Supplementary Movie S2. Steered molecular dynamics of K+ permeation seen from the cytoplasmic point of view. The movie compares wild type (on the left) and mutant hemichannel (on the right). See also the caption of Figure 2.
Supplementary Movie S3. Effect of pulling one NTH toward the center of the pore. The pulled helix is colored in red, while the other NTHs in blue. The initial position is shown as a reference in white. The pulling of a helix in the wild type (on the left) and in the mutant (on the right) reveals different qualitative behaviors, in addition to the quantitative differences described in Figure 6. While in the wild type hemichannel the pulled helix moves abruptly at the end of the simulation, for the mutant this motion occurs earlier, but is then hampered by the interaction of the pulled helix with a neighboring NTH which are more mobile and do not keep the symmetric configuration of the wild type.
References
Berendsen, H. J. C., Postma, J. P. M., van Gunsteren, W. F., Dinola, A., and Haak, J. R. (1984). Molecular dynamics with coupling to an external bath. J. Chem. Phys. 81, 3684–3690. doi: 10.1063/1.448118
Bicego, M., Beltramello, M., Melchionda, S., Carella, M., Piazza, V., Zelante, L., et al. (2006). Pathogenetic role of the deafness-related M34T mutation of Cx26. Hum. Mol. Genet. 15, 2569–2587. doi: 10.1093/hmg/ddl184
Darden, T., York, D., and Pedersen, L. (1993). Particle mesh Ewald: an N·log(N) method for Ewald sums in large systems. J. Chem. Phys. 98, 10089–10093. doi: 10.1063/1.464397
Denoyelle, F., Weil, D., Maw, M. A., Wilcox, S. A., Lench, N. J., Allen-Powell, D. R., et al. (1997). Prelingual deafness: high prevalence of a 30delG mutation in the connexin 26 gene. Hum. Mol. Genet. 6, 2173–2177. doi: 10.1093/hmg/6.12.2173
Dobrowolski, R., and Willecke, K. (2009). Connexin-caused genetic diseases and corresponding mouse models. Antioxid. Redox Signal. 11, 283–295. doi: 10.1089/ars.2008.2128
Duan, Y., Wu, C., Chowdhury, S., Lee, M. C., Xiong, G., Zhang, W., et al. (2003). A point-charge force field for molecular mechanics simulations of proteins based on condensed-phase quantum mechanical calculations. J. Comput. Chem. 24, 1999–2012. doi: 10.1002/jcc.10349
Ebihara, L., and Steiner, E. (1993). Properties of a nonjunctional current expressed from a rat connexin46 cDNA in Xenopus oocytes. J. Gen. Physiol. 102, 59–74. doi: 10.1085/jgp.102.1.59
Evans, W. H., De Vuyst, E., and Leybaert, L. (2006). The gap junction cellular internet: connexin hemichannels enter the signalling limelight. Biochem. J. 397, 1–14. doi: 10.1042/BJ20060175
Fasciani, I., Temperan, A., Perez-Atencio, L. F., Escudero, A., Martinez-Montero, P., Molano, J., et al. (2013). Regulation of connexin hemichannel activity by membrane potential and the extracellular calcium in health and disease. Neuropharmacology 75, 479–490. doi: 10.1016/j.neuropharm.2013.03.040
Feldmann, D., Denoyelle, F., Loundon, N., Weil, D., Garabedian, E. N., Couderc, R., et al. (2004). Clinical evidence of the nonpathogenic nature of the M34T variant in the connexin 26 gene. Eur. J. Hum. Genet. 12, 279–284. doi: 10.1038/sj.ejhg.5201147
Gomez-Hernandez, J. M., de Miguel, M., Larrosa, B., Gonzalez, D., and Barrio, L. C. (2003). Molecular basis of calcium regulation in connexin-32 hemichannels. Proc. Natl. Acad. Sci. U.S.A. 100, 16030–16035. doi: 10.1073/pnas.2530348100
Gonzalez, D., Gomez-Hernandez, J. M., and Barrio, L. C. (2006). Species specificity of mammalian connexin-26 to form open voltage-gated hemichannels. FASEB J. 20, 2329–2338. doi: 10.1096/fj.06-5828com
Goodenough, D. A., and Paul, D. L. (2009). Gap junctions. Cold Spring Harb. Perspect. Biol. 1:a002576. doi: 10.1101/cshperspect.a002576
Guex, N., and Peitsch, M. C. (1997). SWISS-MODEL and the Swiss-PdbViewer: an environment for comparative protein modeling. Electrophoresis 18, 2714–2723. doi: 10.1002/elps.1150181505
Harris, A. L. (2007). Connexin channel permeability to cytoplasmic molecules. Prog. Biophys. Mol. Biol. 94, 120–143. doi: 10.1016/j.pbiomolbio.2007.03.011
Hess, B., Kutzner, C., van der Spoel, D., and Lindahl, E. (2008). GROMACS 4: algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theor. Comput. 4, 435–447. doi: 10.1021/Ct700301q
Hille, B., and Schwarz, W. (1978). Potassium channels as multi-ion single-file pores. J. Gen. Physiol. 72, 409–442. doi: 10.1085/Jgp.72.4.409
Houseman, M. J., Ellis, L. A., Pagnamenta, A., Di, W. L., Rickard, S., Osborn, A. H., et al. (2001). Genetic analysis of the connexin-26 M34T variant: identification of genotype M34T/M34T segregating with mild-moderate non-syndromic sensorineural hearing loss. J. Med. Genet. 38, 20–25. doi: 10.1136/jmg.38.1.20
Kelley, P. M., Harris, D. J., Comer, B. C., Askew, J. W., Fowler, T., Smith, S. D., et al. (1998). Novel mutations in the connexin 26 gene (GJB2) that cause autosomal recessive (DFNB1) hearing loss. Am. J. hum. Genet. 62, 792–799. doi: 10.1086/301807
Kelsell, D. P., Dunlop, J., Stevens, H. P., Lench, N. J., Liang, J. N., Parry, G., et al. (1997). Connexin 26 mutations in hereditary non-syndromic sensorineural deafness. Nature 387, 80–83. doi: 10.1038/387080a0
Kirkwood, J. G. (1935). Statistical mechanics of fluid mixtures. J. Chem. Phys. 3, 300–314. doi: 10.1063/1.1749657
Laird, D. W. (2006). Life cycle of connexins in health and disease. Biochem. J. 394(Pt 3), 527–543. doi: 10.1042/BJ20051922
Latour, P., Fabreguette, A., Ressot, C., Blanquet-Grossard, F., Antoine, J. C., Calvas, P., et al. (1997). New mutations in the X-linked form of Charcot-Marie-Tooth disease. Eur. Neurol. 37, 38–42. doi: 10.1159/000117403
Locke, D., Bian, S., Li, H., and Harris, A. L. (2009). Post-translational modifications of connexin26 revealed by mass spectrometry. Biochem. J. 424, 385–398. doi: 10.1042/BJ20091140
Maeda, S., Nakagawa, S., Suga, M., Yamashita, E., Oshima, A., Fujiyoshi, Y., et al. (2009). Structure of the connexin 26 gap junction channel at 3.5 A resolution. Nature 458, 597–602. doi: 10.1038/nature07869
Maeda, S., and Tsukihara, T. (2011). Structure of the gap junction channel and its implications for its biological functions. Cell. Mol. life Sci. 68, 1115–1129. doi: 10.1007/s00018-010-0551-z
Mann, H. B., and Whitney, D. R. (1947). On a test of whether one of two random variables is stochastically larger than the other. Ann. Math. Statist. 18, 50–60. doi: 10.1214/aoms/1177730491
Muller, D. J., Hand, G. M., Engel, A., and Sosinsky, G. E. (2002). Conformational changes in surface structures of isolated connexin 26 gap junctions. EMBO J. 21, 3598–3607. doi: 10.1093/emboj/cdf365
Oh, S., Ri, Y., Bennett, M. V., Trexler, E. B., Verselis, V. K., and Bargiello, T. A. (1997). Changes in permeability caused by connexin 32 mutations underlie X-linked Charcot-Marie-Tooth disease. Neuron 19, 927–938. doi: 10.1016/S0896-6273(00)80973-3
Oshima, A., Doi, T., Mitsuoka, K., Maeda, S., and Fujiyoshi, Y. (2003). Roles of Met-34, Cys-64, and Arg-75 in the assembly of human connexin 26. Implication for key amino acid residues for channel formation and function. J. Biol. Chem. 278, 1807–1816. doi: 10.1074/jbc.M207713200
Oshima, A., Tani, K., Hiroaki, Y., Fujiyoshi, Y., and Sosinsky, G. E. (2007). Three-dimensional structure of a human connexin26 gap junction channel reveals a plug in the vestibule. Proc. Natl. Acad. Sci. U.S.A. 104, 10034–10039. doi: 10.1073/pnas.0703704104
Pantano, S., and Carafoli, E. (2007). The role of phosphorylation on the structure and dynamics of phospholamban: a model from molecular simulations. Proteins 66, 930–940. doi: 10.1002/prot.21239
Pantano, S., Zonta, F., and Mammano, F. (2008). A fully atomistic model of the Cx32 connexon. PloS ONE 3:e2614. doi: 10.1371/journal.pone.0002614
Park, S., and Schulten, K. (2004). Calculating potentials of mean force from steered molecular dynamics simulations. J. Chem. Phys. 120, 5946–5961. doi: 10.1063/1.1651473
Petit, C., Levilliers, J., and Hardelin, J. P. (2001). Molecular genetics of hearing loss. Annu. Rev. Genet. 35, 589–646. doi: 10.1146/annurev.genet.35.102401.091224
Pfahnl, A., and Dahl, G. (1999). Gating of cx46 gap junction hemichannels by calcium and voltage. Pflugers Arch. 437, 345–353. doi: 10.1007/s004240050788
Pollak, A., Skorka, A., Mueller-Malesinska, M., Kostrzewa, G., Kisiel, B., Waligora, J., et al. (2007). M34T and V37I mutations in GJB2 associated hearing impairment: evidence for pathogenicity and reduced penetrance. Am. J. Med. Genet. Part A 143A, 2534–2543. doi: 10.1002/ajmg.a.31982
Roux, B., and Karplus, M. (1991a). Ion-transport in a gramicidin-like channel dynamics and mobility. J. Phys. Chem. 95, 4856–4868. doi: 10.1021/j100165a049
Roux, B., and Karplus, M. (1991b). Ion-transport in a model gramicidin channel structure and thermodynamics. Biophys. J. 59, 961–981. doi: 10.1016/S0006-3495(91)82311-6
Samson, E., Marchand, J., and Snyder, K. A. (2003). Calculation of ionic diffusion coefficients on the basis of migration test results. Mater. Struct. 36, 156–165. doi: 10.1617/14002
Scott, D. A., Kraft, M. L., Carmi, R., Ramesh, A., Elbedour, K., Yairi, Y., et al. (1998). Identification of mutations in the connexin 26 gene that cause autosomal recessive nonsyndromic hearing loss. Hum. Mutat. 11, 387–394. doi: 10.1002/(SICI)1098-1004(1998)11:5<387::AID-HUMU6>3.0.CO;2-8
Skerrett, I. M., Di, W. L., Kasperek, E. M., Kelsell, D. P., and Nicholson, B. J. (2004). Aberrant gating, but a normal expression pattern, underlies the recessive phenotype of the deafness mutant Connexin26M34T. FASEB J. 18, 860–862. doi: 10.1096/fj.03-0763fje
Szabo, A., Schulten, K., and Schulten, Z. (1980). 1st Passage time approach to diffusion controlled reactions. J. Chem. Phys. 72, 4350–4357. doi: 10.1063/1.439715
Tan, C. C., Ainsworth, P. J., Hahn, A. F., and MacLeod, P. M. (1996). Novel mutations in the connexin 32 gene associated with X-linked Charcot-Marie tooth disease. Hum. Mutat. 7, 167–171. doi: 10.1002/(SICI)1098-1004(1996)7:2<167::AID-HUMU14>3.0.CO;2-0
Tao, J., Ji, F., Liu, B., Wang, F., Dong, F., and Zhu, Y. (2012). Improvement of deficits by transplantation of lentiviral vector-modified human amniotic mesenchymal cells after cerebral ischemia in rats. Brain Res. 1448, 1–10. doi: 10.1016/j.brainres.2012.01.069
Thonnissen, E., Rabionet, R., Arbones, M. L., Estivill, X., Willecke, K., and Ott, T. (2002). Human connexin26 (GJB2) deafness mutations affect the function of gap junction channels at different levels of protein expression. Hum. Genet. 111, 190–197. doi: 10.1007/s00439-002-0750-2
Verselis, V. K., Ginter, C. S., and Bargiello, T. A. (1994). Opposite voltage gating polarities of two closely related connexins. Nature 368, 348–351. doi: 10.1038/368348a0
Wei, C. J., Xu, X., and Lo, C. W. (2004). Connexins and cell signaling in development and disease. Annu. Rev. Cell Dev. Biol. 20, 811–838. doi: 10.1146/annurev.cellbio.19.111301.144309
White, T. W., Deans, M. R., Kelsell, D. P., and Paul, D. L. (1998). Connexin mutations in deafness. Nature 394, 630–631. doi: 10.1038/29202
Yum, S. W., Kleopa, K. A., Shumas, S., and Scherer, S. S. (2002). Diverse trafficking abnormalities of connexin32 mutants causing CMTX. Neurobiol. Dis. 11, 43–52. doi: 10.1006/nbdi.2002.0545
Zelante, L., Gasparini, P., Estivill, X., Melchionda, S., D'Agruma, L., Govea, N., et al. (1997). Connexin26 mutations associated with the most common form of non-syndromic neurosensory autosomal recessive deafness (DFNB1) in Mediterraneans. Hum. Mol. Genet. 6, 1605–1609. doi: 10.1093/hmg/6.9.1605
Zonta, F., Mammano, F., Torsello, M., Fortunati, N., Orian, L., and Polimeno, A. (2014). Role of gamma carboxylated Glu47 in connexin 26 hemichannel regulation by extracellular Ca2+: insight from a local quantum chemistry study. Biochem. Biophys. Res. Comm. 445, 10–15. doi: 10.1016/j.bbrc.2014.01.063
Zonta, F., Polles, G., Sanasi, M. F., Bortolozzi, M., and Mammano, F. (2013). The 3.5 angstrom X-ray structure of the human connexin26 gap junction channel is unlikely that of a fully open channel. Cell Commun. Signal. 11:15. doi: 10.1186/1478-811X-11-15
Zonta, F., Polles, G., Zanotti, G., and Mammano, F. (2012). Permeation pathway of homomeric connexin 26 and connexin 30 channels investigated by molecular dynamics. J. Biomol. Struct. Dyn. 29, 985–998. doi: 10.1080/073911012010525027
Keywords: genetic deafness, conductance, gating, gap junction channels, potential of mean force, mean first passage time
Citation: Zonta F, Buratto D, Cassini C, Bortolozzi M and Mammano F (2014) Molecular dynamics simulations highlight structural and functional alterations in deafness–related M34T mutation of connexin 26. Front. Physiol. 5:85. doi: 10.3389/fphys.2014.00085
Received: 05 December 2013; Paper pending published: 10 January 2014;
Accepted: 12 February 2014; Published online: 04 March 2014.
Edited by:
Juan Carlos Sáez, Pontificia Universidad Católica de Chile, ChileReviewed by:
Carmen Valenzuela, Instituto de Investigaciones Biomédicas CSIC-UAM, SpainStefano Piotto, University of Salerno, Italy
Copyright © 2014 Zonta, Buratto, Cassini, Bortolozzi and Mammano. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Fabio Mammano, Istituto Veneto di Medicina Molecolare, Fondazione per la Ricerca Biomedica Avanzata, Via G. Orus 2, 35129 Padova, Italy e-mail:ZmFiaW8ubWFtbWFub0B1bmlwZC5pdA==
 Francesco Zonta
Francesco Zonta Damiano Buratto
Damiano Buratto Chiara Cassini
Chiara Cassini Mario Bortolozzi
Mario Bortolozzi Fabio Mammano
Fabio Mammano