- 1Centre for Condensed Matter Theory, Department of Physics, Indian Institute of Science, Bangalore, India
- 2Robert Bosch Centre for Cyber Physical Systems, Indian Institute of Science, Bangalore, India
- 3Jawaharlal Nehru Centre for Advanced Scientific Research, Bangalore, India
We carry out an extensive numerical study of the dynamics of spiral waves of electrical activation, in the presence of periodic deformation (PD) in two-dimensional simulation domains, in the biophysically realistic mathematical models of human ventricular tissue due to (a) ten-Tusscher and Panfilov (the TP06 model) and (b) ten-Tusscher, Noble, Noble, and Panfilov (the TNNP04 model). We first consider simulations in cable-type domains, in which we calculate the conduction velocity θ and the wavelength λ of a plane wave; we show that PD leads to a periodic, spatial modulation of θ and a temporally periodic modulation of λ; both these modulations depend on the amplitude and frequency of the PD. We then examine three types of initial conditions for both TP06 and TNNP04 models and show that the imposition of PD leads to a rich variety of spatiotemporal patterns in the transmembrane potential including states with a single rotating spiral (RS) wave, a spiral-turbulence (ST) state with a single meandering spiral, an ST state with multiple broken spirals, and a state SA in which all spirals are absorbed at the boundaries of our simulation domain. We find, for both TP06 and TNNP04 models, that spiral-wave dynamics depends sensitively on the amplitude and frequency of PD and the initial condition. We examine how these different types of spiral-wave states can be eliminated in the presence of PD by the application of low-amplitude pulses by square- and rectangular-mesh suppression techniques. We suggest specific experiments that can test the results of our simulations.
1. Introduction
Sudden cardiac arrest is caused, in many cases, by cardiac arrhythmias, such as ventricular tachyacardia (VT) and ventricular fibrillation (VF) (Roger et al., 2011, 2012). Estimates suggest that VF is the main reason for death in 30% of the cases in which heart failure occurs (Zipes and Wellens, 1998; Fogoros, 2011). Thus, the importance of studying such arrhythmias cannot be overemphasized. Such studies must use interdisciplinary approaches because they require inputs from biology, bio-medical engineering, and cardiology, on the one hand, and physics, non-linear dynamics, and numerical methods, on the other; methods from these areas must be used to study the complicated, non-linear, partial-differential-equation models that have been developed for cardiac tissue. Such equations can show, inter alia, spiral-wave turbulence and spatiotemporal chaos, which is believed to be one of the mathematical analogs of VF. The study we present here combines theoretical ideas from spatiotemporal chaos in extended dynamical systems with extensive direct numerical simulations, to elucidate the effects of periodic deformation (PD) on spiral-wave dynamics in detailed mathematical models for cardiac tissue and to investigate the elimination of such spiral waves, in the presence of PD, by the application of low-amplitude current pulses.
The mechanisms underlying VT and VF are not understood with complete certainty; however, various clinical studies (Fenton et al., 2008; Fogoros, 2011) have suggested that such arrhythmias comprise the abnormal propagation of a wave of electrical activation across the ventricles. Such irregular waves appear in various ways. For example, they can arise because of an infarction scar (De Bakker et al., 1993), which can create an anatomical path that anchors electrical waves; they are also seen around obstacles in vitro (Valderrábano et al., 2000) and in cell-culture experiments (Lim et al., 2006) (anatomically reentry). However, reentry can occur in the absence of an anatomical pathway. For instance, in vitro experiments (Davidenko et al., 1990; Ikeda et al., 1996) have shown that fibrillation can be maintained by functional reentry. However, ectopic activations (Chen et al., 1999; Zimmermann and Kalusche, 2001), because of pulmonary veins or abnormal cells, can also initiate fibrillation. In particular, both experimental (Davidenko et al., 1992; Pertsov et al., 1993; Gray et al., 1998; Jalife et al., 1998) and computational (Jalife et al., 1998; Fenton et al., 2002; Cherry and Fenton, 2008) studies have suggested that VT and VF are, respectively, manifestations of (a) a rotating spiral (RS) or scroll wave or (b) broken spiral or scroll waves that lead to spiral- or scroll-wave turbulence (ST).
Several studies have investigated the transition from RS to ST, both in experiments on cardiac tissue and in computational studies of mathematical models for cardiac tissue; they find that this transition can occur because of (a) a steep, increasing initial segment in the restitution curve, a plot of the action potential duration (APD) versus the diastolic interval (DI) (Koller et al., 1998; Garfinkel et al., 2000; Fenton et al., 2002), (b) a similar steep part in an analogous plot of the conduction velocity θ versus DI (Qu et al., 2000b; Fenton et al., 2002), (c) alternans (Karma, 1994; Koller et al., 1998; Qu et al., 1999; Cherry and Fenton, 2008), and (d) heterogeneities, such as, conduction and ionic inhomogeneities (Xie et al., 1998; Shajahan et al., 2007, 2009; Majumder et al., 2011a,b). Recently, some groups (Zhang et al., 2004, 2006; Panfilov et al., 2007; Chen et al., 2008; Weise et al., 2011) have begun to study the effects of the deformation of cardiac tissue on the RS-ST transition; such a transition arises either because of periodic deformation or the stretch-activated current associated with such deformation. These studies have used simple, two-variable mathematical models for electrical activation in such tissue. One of the goals of our study is to investigate spiral-wave dynamics in general, and RS-ST transitions in particular, in a simple mathematical model for periodic deformation (PD) of cardiac tissue (Zhang et al., 2004, 2006; Chen et al., 2008) that we couple with ionically realistic human-ventricular-tissue mathematical models, namely, (a) the TP06 model, due to ten Tusscher and Panfilov (Ten Tusscher and Panfilov, 2006), or (b) the TNNP04 model, of ten Tusscher, Noble, Noble, and Panfilov (Ten Tusscher et al., 2004). A deformation of cardiac tissue leads to modifications of ion-channel parameters, because of stretch-activated currents, and also a modification of intracellular couplings. Our model for deformation, based on Zhang et al. (2004, 2006) and Chen et al. (2008), is a very simplified one in which the effects of deformation are accounted for only by a temporal modulation of diffusion constants (see section 2), which are related to intracellular couplings; we do not include stretch-activated currents as considered in Panfilov et al. (2005, 2007) and Weise et al. (2011). However, in spite of this simplified representation of deformation, our study yields important results that have been observed in two-variable models for cardiac tissue both with periodic deformation (PD) (Zhang et al., 2004, 2006; Chen et al., 2008) or mechanical deformation (Panfilov et al., 2005, 2007; Weise et al., 2011); the latter studies include stretch-activated currents. Such stretch-activated currents with mechano-electrical feedback have also been shown to affect electrical activation in anatomically realistic human models (Keldermann et al., 2010; Kuijpers et al., 2011); mechano-electrical feedback can enhance electrical activation as discussed in Thompson et al. (2011) in the context of myofibroblast-myocyte interactions (of course, pharmacological and electrochemical interventions can also enhance electrical activation). On the positive side, our study uses ionically realistic models that have not been employed in such deformation studies so far (but see the recent Weise and Panfilov, 2013). We discuss the principal results of the studies carried out in Zhang et al. (2004, 2006), Panfilov et al. (2005, 2007), Chen et al. (2008), and Weise et al. (2011), in section 4, where we compare their findings with ours.
We also investigate the efficacy of a low-amplitude suppression scheme, developed for the suppression of spiral-wave turbulence in 2D models for cardiac tissue (Sinha et al., 2001; Pandit et al., 2002; Shajahan et al., 2009; Majumder et al., 2011a) in the absence of PD. Our study yields several interesting results that we summarize below before we discuss them in detail. We find first that PD leads to a periodic, spatial modulation of the conduction velocity θ and a temporally periodic modulation of the wavelength λ of a plane wave. We then use three different parameter sets, for both TP06 and TNNP04 models, to obtain three different prototypical spiral configurations, which we use as the initial conditions IC1, IC2, and IC3 (see section 2). We find, for the TP06 model, that spiral-wave dynamics depends sensitively on PD and the initial condition. (For similar studies of the sensitive dependence of spiral-wave dynamics on inhomogeneities, see Shajahan et al., 2007, 2009.) The initial condition IC1 can lead to (a) an RS state with n-cycle temporal evolution (here n is a positive integer), (b) rotating-spiral states with quasi-periodic (QP) temporal evolution, (c) a state with a single meandering spiral MS, which displays spatiotemporal chaos, (d) an ST state, with multiple broken spirals, and (e) a quiescent state SA, in which all spirals are absorbed; the initial condition IC2, with PD, can lead either to (a) an ST state, with multiple spirals, or (b) an SA state, with no spirals; and for IC3, it can be driven into (a) an ST state, with a single meandering spiral, (b) an ST state, with multiple spirals, and (c) the state SA. For all these initial conditions, precisely which one of these states is obtained depends on the amplitudes Ax and Ay and the frequencies fx and fy of the PD in the x and y directions. Spiral-wave dynamics in the TNNP04 model, with PD, also shows sensitive dependence on PD and the initial condition. This sensitive dependence on parameters is a hallmark of extended dynamical systems that show spatiotemporal chaos (Shajahan et al., 2007, 2009). We also study, in the presence of PD, the efficacy of a low-amplitude suppression scheme (Sinha et al., 2001; Shajahan et al., 2009) that has been suggested, hitherto only without PD, for the suppression of spiral-wave turbulence, via low-amplitude current pulses applied on a square mesh, in mathematical models for cardiac tissue. Furthermore, we develop line-mesh and rectangular-mesh variants of this suppression scheme. The latter suppresses spiral turbulence in all cases we consider.
2. Methods
The electrical activation of the transmembrane potential Vm of cardiac tissue is often modeled by a reaction-diffusion-type equation,
where Cm is the membrane capacitance density, Iion is the sum of all the ionic currents that cross the cell membrane, and Dx and Dy are, respectively, the diffusion coefficients along x and y directions; such diffusion terms are related to gap junctions (Ten Tusscher et al., 2004; Ten Tusscher and Panfilov, 2006), which are networks of protein channels that allow the passage of ions from cell to cell. We use two biophysically realistic ionic models for human cardiac myocytes: (a) the ten Tusscher and Panfilov model (the TP06 model) (Ten Tusscher and Panfilov, 2006) and (b) the ten Tusscher, Noble, Noble, and Panfilov model (the TNNP04 model) (Ten Tusscher et al., 2004). It is important to check the compatibility of the models that we consider in our study with the standard version of the original models (Ten Tusscher et al., 2004; Ten Tusscher and Panfilov, 2006). One way to check for such compatibility is by comparing the AP and its morphological properties (Figure S1 and Table S1, Supplementary Material S1) with those in our studies; we have checked this explicitly, as we discuss in detail in the Supplementary Material S1.
We follow the method suggested in Zhang et al. (2004, 2006) and Chen et al. (2008) for the introduction of PD into a mathematical model for cardiac tissue. In particular, we note that any point x = (x, y) in the medium changes to x′(t) = (x′(t), y′(t)) with
if we impose a PD with Ax(t) = Ax cos (2πfxt) and Ay(t) = Ay cos (2πfyt). By substituting Equation (2) into Equation (1), we obtain
a comparison of Equations (1, 3) shows that Equation (3) can be rewritten as
with Dx(t) = Dx (1 + Ax(t))−2 and Dy(t) = Dy (1 + Ay(t))−2.
In our numerical simulations, we use 2D square domains with 1024 × 1024 grid points and lattice spacings δx = δy = 0.25 mm for both TP06 and TNNP04 models, so the sides of our square simulation domains are L = 256 mm in the absence of PD. We use a forward-Euler method for time evolution, with a time step δt = 0.02 ms, a five-point stencil for the Laplacian, and no-flux (Neumann) boundary conditions. We set the diffusion coefficients Dx = Dy = D = 0.00154 cm2/ms (Ten Tusscher et al., 2004; Ten Tusscher and Panfilov, 2006) for both the TP06 and the TNNP04 models for our numerical investigations. Other parameters for our calculations are given in Tables 1, 2 and an examination of the numerical stability of our numerical scheme is given in the Supplementary Material S1.

Table 1. Parameters for the periodic deformation (PD) that we use to study the wave dynamics in our cable-type and square simulation domains in both TP06 and TNNP04 ventricular models.
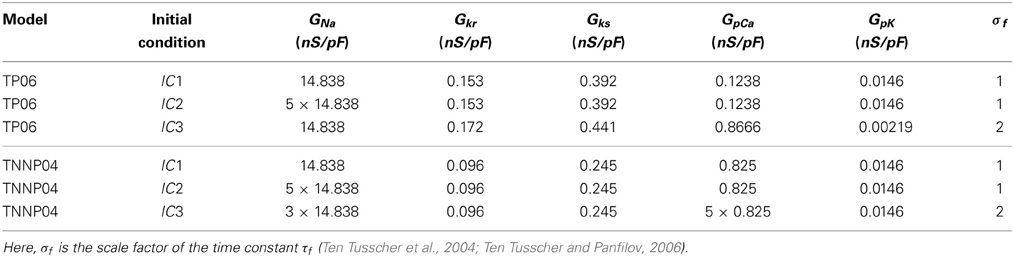
Table 2. Parameters for the initial spiral-wave configurations for TP06 and TNNP04 models; we refer to these as IC1, IC2, and IC3 initial conditions.
To examine the spatiotemporal evolution of the electrical signal of the transmembrane potential, we obtain the local time series of Vm(x, y, t), from a representative point (x = 125 mm, y = 125 mm) (shown by an asterisk in all pseudocolor plots of Vm). To obtain the plots of the inter-beat interval (IBI), we use this local time series with 4 × 105 data points; the IBI is the time interval between two successive beats in the time series of the signal Vm. For the power spectra E(ω) we use the local time series with 2 × 105 data points after the initial 105 data points have been removed to eliminate transients. We present the spatiotemporal evolution of Vm by a series of (Videos S1–S9) of its pseudocolor plots; all these videos use 10 frames per second and each frame is separated from the succeeding frame by 8 ms.
We often have to track the trajectory of the tip of a spiral wave in a 2D simulation domain. The tip of such a spiral wave is normally defined as the point where the excitation wave front and repolarization wave back meet; this point can be found by a variety of methods (Barkley et al., 1990; Fenton and Karma, 1998; Fenton et al., 2002; Otani, 2002; Gray et al., 2009; Nayak et al., 2013). We use the tip-tracking algorithm of Nayak et al. (2013) that locates the tip position by monitoring INa, the sodium current. Pseudocolor plots of INa show a fine line along the arm of a spiral wave (Figure 2A in Shajahan et al., 2009); this line terminates in the spiral tip and can, therefore, be used to obtain the spatiotemporal evolution of this tip.
In Figures S2A–F in the Supplementary Material S1, we show schematic diagrams for illustrative periodic deformations of a small part of our simulation domain, with 5 × 5 grid points (indicated by gpts on the axes of figures); in these diagrams, blue, open circles and blue, dashed lines show, at a particular instant of time, the deformed simulation domain superimposed on the undeformed one, which is represented by black, solid circles and black, full lines. We give representative diagrams for the case of expansion, with deformations along only x, only y, or both x and y directions, in Figures S2A–C, in the Supplementary Material S1, at time t = 20 ms; the corresponding plots for contraction, at time t = 180 ms, are shown in Figures S2D–F, in the Supplementary Material S1.
3. Results
We begin by exploring the effects of PD both on plane-wave propagation and on spiral-wave dynamics; here we vary the oscillation amplitude and the frequency in the ranges 0 ≲ Ax, Ay ≲ 0.5 and 0 Hz ≲ f ≲ 7.0 Hz; the deformation amplitudes we use are comparable to those in other computational (Zhang et al., 2004, 2006; Weise et al., 2011) and experimental (McCULLOCH et al., 1987; Noble, 2002) studies; to set the scale of frequencies, we note that the frequency of rotation of a single spiral wave is 4.75 Hz for the TP06 model and 3.75 Hz for the TNNP04 model (see section 3.2). We then study the effects of PD on the suppression scheme of Pandit et al. (2002) and Shajahan et al. (2009).
3.1. Plane-Wave Dynamics in a Cable
We study plane-wave propagation in a thin, cable-type simulation domain, with 16 × 4096 grid points, i.e., Lx = 4 mm and Ly = 1024 mm. We inject a stimulus of strength Istimulus = 150 pA/pF at the left end of the cable for 3 ms and then study the effects of PD on the plane wave that propagates through this cable; in particular, we measure the conduction velocity θ and wavelength λ of the propagating wave in the cable. We find that θ ≃ 70.6 cm/s and λ ≃ 21.6 cm for the TP06 model, and θ ≃ 67.8 cm/s and λ ≃ 18.9 cm for the TNNP04 model, in the absence of PD. As suggested in Clayton and Panfilov (2008), Shajahan et al. (2009), and Ten Tusscher et al. (2004), it is useful to test the accuracy of the numerical scheme by varying both the time and space steps that we use for integration. We illustrate this for the TP06 model by measuring θ for a plane wave, which is injected into the medium by stimulating the left boundary of our simulation domain. We find that, with δx = 0.025 cm, θ increases by 1.6% as we decrease δt from 0.02 to 0.01 ms; if we use δt = 0.02 ms and decrease δx from 0.025 to 0.015 cm then θ increases by 4.7%; such changes are comparable to those found in earlier studies (Ten Tusscher et al., 2004; Shajahan et al., 2009).
In Figure 1(a00–a20) we show, at time t = 600 ms, when PD is applied along the axial direction of the cable, pseudocolor plots of the transmembrane potential Vm for the TP06 model with PD along the axial direction of the cable, and the parameter sets given in Table 1. The Video S1 comprises 21 animations that show the spatiotemporal evolution of the plane waves in Figure 1(a00–a20); these animations and Figure 1(a00–a20) show that the conduction velocity θ is modulated in space and the wavelength λ is modulated in time because of the PD. Figure 2 illustrates these modulations via plots of θF and θB versus x for the conduction velocities of the wave front (Figure 2A) and the wave back (Figure 2B), respectively; here the subscripts F and B stand for wave front and wave back, respectively; and Figure 2C shows the corresponding plot for λ versus time t; in these plots we use the representative PD parameter values Ax = 0.3 and fx = 5.0 Hz for the TP06 model. We calculate the conduction velocities θF(x) and θB(x), in the cable-type domain with PD, by recording the positions of the wave front and the wave back at times t and t + Δt, with Δt = 2 ms; the wave-front and wave-back conduction velocities, at the point x at time t, are θF(x) = ΔFx/Δt and θB(x) = ΔBx/Δt, where ΔFx and ΔBx are, respectively, the distances traveled by the wave front and wave back in the time interval Δt. We locate the position of the wave front by finding the value of x at which Vm ≃ 0 mV; we define the position of the wave back as the point, behind the wave front, at which a secondary action potential can just be initiated by an additional stimulus (this turns out to occur at a value of Vm that is ≃ 75% of the repolarization phase of the action potential). We obtain the wavelength λ(t) by measuring the distance between the wave front and the wave back at time t.
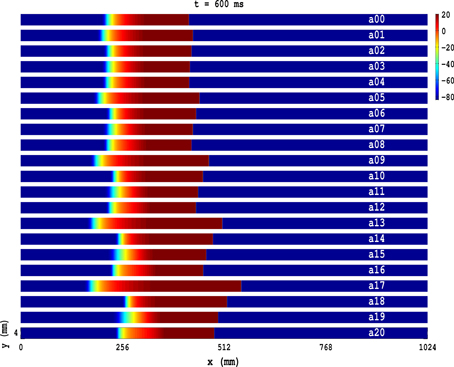
Figure 1. Pseudocolor plots of the transmembrane potential Vm for the TP06 model illustrating plane-wave propagation in a cable-type domain, with PD along the axial-direction of the cable, and the parameter sets given in Table 1. The Video S1 comprises 21 animations that show the spatiotemporal evolution of these plane waves.
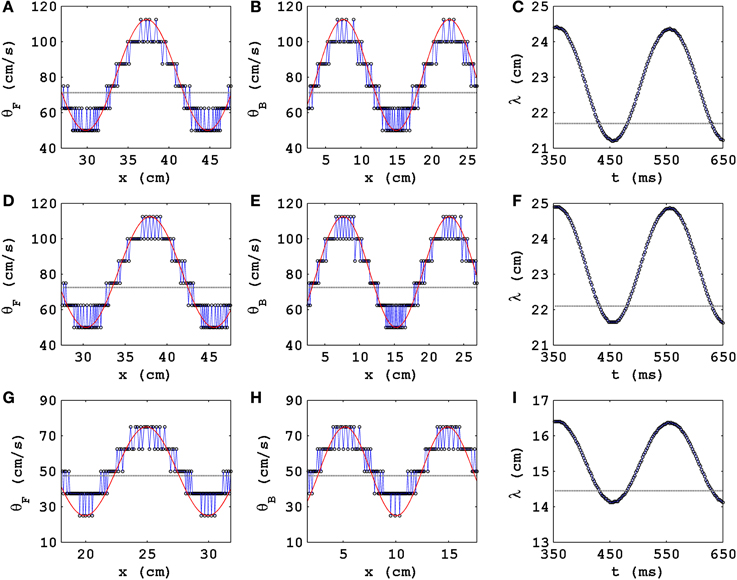
Figure 2. The spatial modulation of θ and the temporal modulation of λ of a plane wave propagating in a cable-type domain with PD. Plots versus distance x along the cable of the conduction velocities with D = 0.00154 cm2/ms, δt = 0.02 ms, and δx = 0.25 mm (A) θF, of the wave front, and (B) θB, of the wave back; (C) plot versus time t of the wavelength λ. The exact analogs of (A–C) are shown in (D–F), for D = 0.00154 cm2/ms, δt = 0.01 ms, and δx = 0.25 mm, and in (G–I), for D = 0.00077 cm2/ms, δt = 0.02 ms, and δx = 0.25 mm. We use the representative PD parameter values Ax = 0.3 and fx = 5.0 Hz for the TP06 model. Open circles show the values from our calculation; the red lines show smooth sinusoidal envelopes; in the absence of PD, θ ≃ 70.6 cm/s, ≃ 71.7 cm/s, and ≃ 47 cm/s, respectively, for above three parameter sets [gray, dashed lines in (A,B)]; in (C) the gray, dashed line shows the value of λ that we obtain in the absence of PD.
In Figures 2A,B, the open circles show the values of θF(x) and θB(x), respectively, that we obtain by the method described above; the red lines show smooth sinusoidal envelopes, with amplitude ≃ 31.2 cm/s and spatial period ≃ 14.5 cm, that give the average modulations of these conduction velocities with x. Note that, in the absence of PD, θ ≃ 70.6 cm/s (this is shown via a gray, dashed line in Figures 2A,B); therefore, the electrical wave can travel ≃ 70.6/f cm in 1/f s; hence, for a given PD frequency f, the spatial period of oscillation of θF(x) and θB(x) is ≃ 70.6/f cm; the representative plots of Figures 2A,B, in which f = 5 Hz and the period is ≃ 70.6/5 = 14.12 cm, are consistent with this estimate.
Figure 2C shows that λ is a periodic function of t with a period τ; we expect that τ = 1/f, where f is the PD frequency; the illustrative plot in Figure 2C, with f = 5 Hz, is consistent with this expectation because τ ≃ 202 ms; the gray, dashed line shows the value of λ that we obtain in the absence of PD.
It is useful to study how θ and λ of a plane wave behave, in the presence of PD, when we change the values of the time step and the diffusion coefficients. We find that, in the presence of PD, θ and λ continue to oscillate, as in Figures 2D–I, as functions of x and t, respectively; the mean values of θ and λ, about which these oscillations occur, are close to their values without PD, which depend on the diffusion coefficients and marginally on the time step: In Figures 2D,E we show, for D = 0.00154 cm2/ms, δt = 0.01 ms, and δx = 0.25 mm, the analogs of Figures 2A–C; and in Figures 2G–I we give their counterparts for D = 0.00077 cm2/ms, δt = 0.01 ms, and δx = 0.25 mm.
The TNNP04-model analogs of the TP06-model Figure 1(a00–a20) are given in Figure S4(a00–a11) in the Supplementary Material S1. Our results for the TNNP04 model are similar to those for the TP06 model.
3.2. Spiral-Wave Dynamics in a Homogeneous Domain
We move now to systematic studies of spiral-wave dynamics in a 2D, square simulation domain with side L = 256 mm, in the presence of PD, for both TP06 and TNNP04 models.
In the absence of PD, two methods are used to initiate spiral waves in simulations (Pertsov et al., 1993; Bernus et al., 2002; Ten Tusscher et al., 2004; Shajahan et al., 2009) and experiments (Davidenko et al., 1992; Pertsov et al., 1993), namely, (1) the S1, S2 cross-field protocol and (2) the S1, S2 parallel-field protocol. We describe in the Supplementary Material S1 the precise S1, S2 cross-field protocol that we use to obtain spiral waves in our simulation domain. We use three types of spiral-wave initial configurations for our subsequent studies; we refer to these as IC1, IC2, and IC3 initial conditions (see Table 2 for parameter values). In Figures S5A–C, in the Supplementary Material S1, we show the time evolution of pseudocolor plots of Vm for the TP06 model with the IC1 initial configuration; similar plots are shown in Figures S5D–E and (F,I), respectively, for the IC2 and IC3 initial configurations. The TNNP04-model analogs of Figures S5A–I are given in Figures S6A–I, in the Supplementary Material S1.
In Figures 3A–C, we show pseudocolor plots of Vm at times t = 0 s, t = 2 s, and t = 4 s, respectively, for the initial condition IC1 in the TP06 model, in the absence of PD; this initial configuration evolves to a state with a rotating spiral (RS) in the medium; the animation (a) in Video S2 shows the spatiotemporal evolution of Vm for this case. The local time series of Vm(x, y, t), from the representative point (x = 125 mm, y = 125 mm) (the asterisk in Figure 3C), is shown in Figure 3D for 2 s ≤ t ≤ 6 s; a plot of the IBI is given in Figure 3E, which shows that, after initial transients (roughly the first 10 beats), the spiral wave rotates periodically with an average rotation period T ≃ 210 ms. In Figure 3F, we plot the power spectrum E(ω), which we have obtained from the local time series of Vm mentioned above; discrete peaks in E(ω) appear at the fundamental frequency ωf ≃ 4.75 Hz and its harmonics. The periodic nature of the local time series of Vm, the flattening of the IBI, and the discrete peaks in E(ω) show that the temporal evolution of the spiral wave is periodic; therefore, the spiral-tip trajectory traces a roughly circular path with radius lc ≃ 20 mm; this circular path is shown, for 3.6 s ≤ t ≤ 4 s, by the white line that has been superimposed on the pseudocolor plot of Vm in Figure 3C; an expanded version of this path is shown in Figure 3G. The Figures S7, S8 in the Supplementary Material S1 show the analogs of Figure 3 for initial conditions IC2 and IC3, respectively; and the animations (b) and (c) in Video S2 show the spatiotemporal evolution of Vm for these cases. These animations, the pseudocolor plots of Vm, the representative local time series of Vm, the plots of the IBI, and the power spectra show that the initial conditions IC2 and IC3 lead, respectively, to spatiotemporal chaos and spiral turbulence (ST), with a single spiral meandering chaotically, and broken spirals, respectively, in the simulation domain.
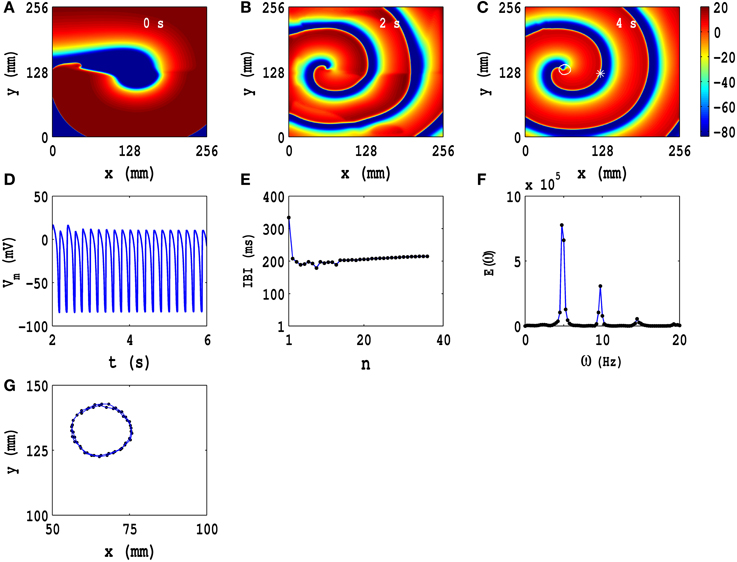
Figure 3. Spatiotemporal evolution of Vm for the initial condition IC1 for the TP06 model in the absence of PD. (A–C) Pseudocolor plots of Vm at times t = 0 s, t = 2 s, and t = 4 s, respectively, showing the evolution toward a state with a rotating spiral (RS); the animation (A) in Video S2 shows the spatiotemporal evolution of Vm for this case. (D) The local time series of Vm(x, y, t), from the representative point (x = 125 mm, y = 125 mm) (the asterisk in (C)) for 2 s ≤ t ≤ 6 s; (E) a plot of the IBI, which we obtain from this time series, of length 4 × 105 iterations; (F) the power spectrum E(ω), obtained from the local time series of (D), with discrete peaks at the fundamental frequency ωf ≃ 4.75 Hz and its harmonics. The spiral-tip trajectory traces a roughly circular path, with radius lc ≃ 20 mm, which is shown, for 3.6 s ≤ t ≤ 4 s, by the white line that has been superimposed on the pseudocolor plot of Vm in (C); a magnified view of this path is shown in (G).
Figures S9A–G, S10A–G, and S11A–F (Supplementary Material S1) show, respectively, the TNNP04 analogs of the TP06 Figures 3A–G (for IC1), Figures S7A–G in the Supplementary Material S1 (for IC2), and Figures S8A–F in the Supplementary Material S1 (for IC3); the spatiotemporal evolution of Vm for these three initial conditions for the TNNP04 model are given in animations (d), (e), and (f) in Video S2. From these animations and the Figures S9A–G, S10A–G, S11A–F (Supplementary Material S1) we conclude that the spatiotemporal evolution of Vm in the TNNP04 model, without PD, is similar to, but not identically the same as, that in the TP06 model for the initial conditions IC1, IC2, and IC3. One difference is that, in the TNNP04 model, we have a Z-type, spiral-tip trajectory in Figures S10C,G (Supplementary Material S1), whereas, for the same initial condition, we have an open spiral-tip trajectory (Figures S7C,G in the Supplementary Material S1) in the TP06 model. This shows that spiral-wave dynamics in these two models, without PD, depends sensitively on the ionic details of these models and on the initial conditions.
3.3. Spiral Waves with PD
We present systematic studies of spiral-wave dynamics here by using IC1, IC2, and IC3 initial configurations in the presence of PD. In the TP06 model, these initial configurations lead, respectively, to (a) an RS state with a roughly circular spiral-tip trajectory, (b) a single meandering spiral with turbulence (we refer to this as SMST henceforth), and (c) multiple-spiral turbulence (MST) with broken spiral waves in the absence of PD, as we have described above. For the TNNP04 model the analogs of these states are (a) RSC, a state with a rotating spiral whose tip trajectory is roughly circular, (b) RSZ, a state with a rotating spiral whose tip trajectory is roughly Z-type, and (c) an MST state.
We first consider the time evolution of IC1 for the TP06 model in the presence of PD, for which we deform the medium periodically along both x and y directions, with amplitudes and frequencies in the ranges 0.1 ≤ Ax = Ay ≤ 0.5 and 1.0 Hz ≤ fx = fy ≤ 7.0 Hz, respectively.
In Figures 4A–D we show pseudocolor plots of Vm at time t = 4 s for (a) Ax = Ay = 0.1, fx = fy = 1.0 Hz, (b) Ax = Ay = 0.1, fx = fy = 3.0 Hz, (c) Ax = Ay = 0.1, fx = fy = 5.0 Hz, and (d) Ax = Ay = 0.1, fx = fy = 7.0 Hz, respectively. The RS state, which we obtain in the absence of PD, does not evolve into an MST state in cases (a), (b) and (c); however, in case (d) the spiral arm splits into multiple spirals to yield an MST state with mild spatiotemporal chaos, in so far as the dominant spiral does not break down but continues to evolve somewhat like a mother rotor (Samie and Jalife, 2001; Chen et al., 2003; Wu et al., 2004; Ideker and Rogers, 2006); the animations (a1), (b1), (c1), and (d1) in Video S3 show the spatiotemporal evolution of Vm for these cases in the time interval 0 s ≤ t ≤ 4 s; this video uses 10 frames per second (fps) and each pseudocolor plot of Vm is separated from its predecessor by 8 ms. The spiral-tip trajectories, which follow from this spatiotemporal evolution, are shown in Figures 3E–H for 3.6 s ≤ t ≤4 s (in Figure 4H we give the tip trajectory for the main, central spiral in Figures 4A–D); these tip trajectories are nearly circular with radii lc ≃ 18 mm, but, as we show below, the temporal evolution of Vm is different in these cases. To examine this evolution, we obtain the local time series of Vm(x, y, t), from the representative point (x = 125 mm, y = 125 mm) (the asterisks in Figures 4A–D), and therefrom the plots of the IBI shown in Figures 4I–L and the power spectra of Figures 4M–P. Discrete peaks in E(ω) appear at the fundamental frequency ωf ≃ 4.75 Hz and a few other frequencies (see the caption of Figure 4). From Figures 4I–L we see that the IBI displays a slight upward trend; this implies that, although the temporal evolution is nearly periodic, there is a gentle drift, toward lower frequencies, in the rotation rate of the dominant spiral. Furthermore, there are small oscillations in the IBI in Figure 4I (a 5-cycle), (j)(a 3-cycle), and (l)(a 2-cycle), but not in Figure 4K (a 1-cycle); the natures of these oscillations and their cycle lengths are confirmed by the Poincaré-type return maps, shown in Figures 4Q–T and corresponding to the IBI plots in Figures 4I–L, respectively; in these return maps, successive points are connected by lines.
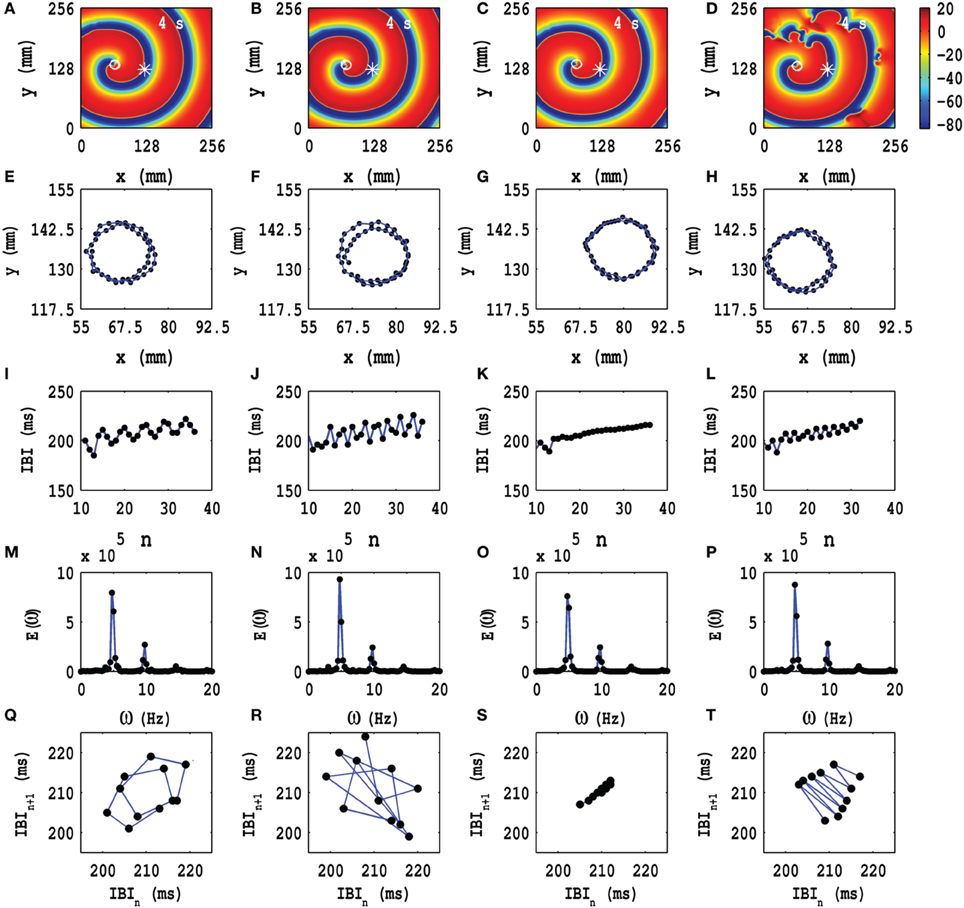
Figure 4. Time evolution of the RS state in the TP06 model in the presence of PD with a fixed amplitude. Pseudocolor plots of Vm at time t = 4 s for (A) Ax = Ay = 0.1, fx = fy = 1.0 Hz, (B) Ax = Ay = 0.1, fx = fy = 3.0 Hz, (C) Ax = Ay = 0.1, fx = fy = 5.0 Hz, and (D) Ax = Ay = 0.1, fx = fy = 7.0 Hz, respectively; the animations (a1), (b1), (c1), and (d1) in Video S3 show the spatiotemporal evolution of Vm for these cases in the time interval 0 s ≤ t ≤ 4 s. (E–H) Spiral-tip trajectories, which follow from these spatiotemporal evolutions, for 3.6 s ≤ t ≤4 s [in (H) we give the tip trajectory for the main, central spiral (D)]. We obtain the local time series of Vm(x, y, t), from the representative point (x = 125 mm, y = 125 mm) [the asterisks in (A–D)], and therefrom the plots of the IBI (I–L) and the power spectra (M–P). The discrete peaks in E(ω) appear at the following frequencies: (M) ω1 = 4.75 Hz, ω2 = 9.5 Hz, ω2 = 14.25 Hz, (N) ω1 = 4.75 Hz, ω2 = 9.5 Hz, ω2 = 14.25 Hz, and small peaks at ω1 = 3 Hz, ω2 = 7.75 Hz, ω3 = 11 Hz, ω4 = 12.5 Hz, ω5 = 15.75 Hz, (O) ω1 = 4.75 Hz, ω2 = 9.5 Hz, ω2 = 14.25 Hz, and (P) ω1 = 4.75 Hz, ω2 = 9.5 Hz, ω2 = 14.25 Hz. In (I–L) we see that the IBI shows a slight upward trend; this implies that, although the temporal evolution is nearly periodic, there is a slight drift, toward lower frequencies, in the rotation rate of the dominant spiral; note also the mild oscillations in the IBI in (I) a 5-cycle, (J) a 3-cycle, and (L) a 2-cycle, but not in (K) a 1-cycle; the natures of these oscillations and their cycle lengths are confirmed by the Poincaré-type return maps, shown in (Q–T), respectively; in these return maps, successive points are connected by lines.
Similarly, we study the dependence of spiral-wave dynamics on the amplitudes Ax and Ay of the PD, with the frequencies fx = fy held at a fixed value. In Figure 5 we show the pseudocolor plots of Vm at time t = 4 s for (a) Ax = Ay = 0.1, fx = fy = 1.0 Hz, (b) Ax = Ay = 0.2, fx = fy = 1.0 Hz, (c) Ax = Ay = 0.3, fx = fy = 1.0 Hz, and (d) Ax = Ay = 0.4, fx = fy = 1.0 Hz. The spiral wave does not split into multiple spirals for these representative values of the amplitudes and frequencies. The animations (a1), (a2), (a3), and (a4) in Video S3 show the spatiotemporal evolution of these spiral waves for the interval 0 s ≤ t ≤ 4 s. To examine this evolution, we obtain the local time series of Vm(x, y, t), from the representative point (x = 125 mm, y = 125 mm) (the asterisks in Figures 5A–D) and the corresponding tip trajectories of spiral waves, in the time interval 3.6 s ≤ t ≤ 4 s (blue lines with black points in Figures 5E,H, respectively); these tip trajectories trace nearly circular paths, with radii lc ≃ 18 mm in Figures 5E,F; they are of the meandering type in Figures 5G,H, with linear extents lc ≃ 24 mm and lc ≃ 75 mm, respectively. From the local time series of Vm mentioned above, we obtain the plots of the IBI shown in Figures 4I–L and the power spectra of Figures 4M–P; discrete peaks in E(ω) appear at the fundamental frequency ωf ≃ 4.75 Hz and at the frequencies listed in the caption of Figure 5; these peaks indicate that, in Figures 5M,N, we also have some high-order cycles; the broad-band power spectra in Figures 5O,P provide evidence for spiral turbulence with a meandering spiral (SMST). In Figures 5Q–T, we show Poincaré-type return maps which we obtain from the IBI plots in Figures 5I–L; in these maps successive points are connected by lines. These plots give additional evidence for five cycles in Figures 5I,J,M,N and of chaotic behavior in Figures 5K,L,O,P. The lines in Figures 5Q,R move from the bottom-left corner to the top-right corner; this suggests a low-frequency modulation of the spiral-wave dynamics because of the PD; this is associated with the upward trend in the IBI plots of Figures 5I,J.
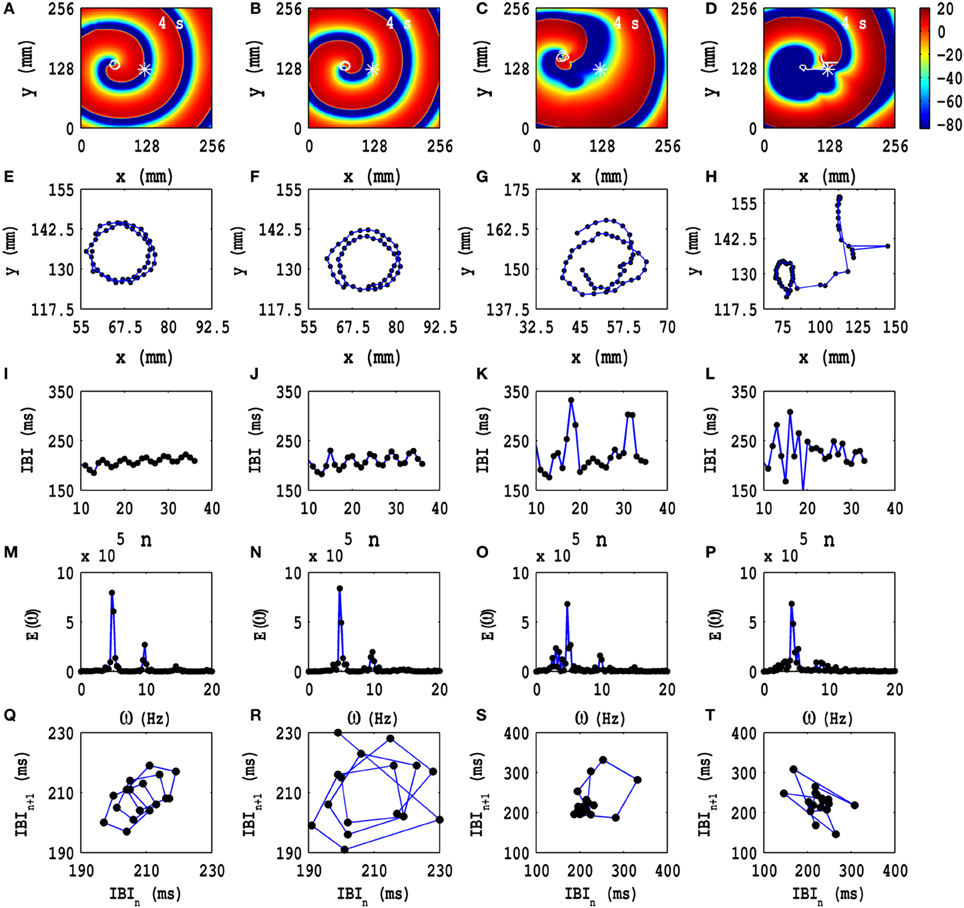
Figure 5. Time evolution of the RS state in the TP06 model in the presence of PD with a fixed frequency. Pseudocolor plots of Vm at time t = 4 s for (A) Ax = Ay = 0.1, fx = fy = 1.0 Hz, (B) Ax = Ay = 0.2, fx = fy = 1.0 Hz, (C) Ax = Ay = 0.3, fx = fy = 1.0 Hz, and (D) Ax = Ay = 0.4, fx = fy = 1.0 Hz. The animations (a1–a4) in Video S3 show the spatiotemporal evolution of these spiral waves for the interval 0 s ≤ t ≤ 4 s. (E–H) Spiral-tip trajectories, which follow from these spatiotemporal evolutions, for 3.6 s ≤ t ≤4 s. We obtain the local time series of Vm(x, y, t), from the representative point (x = 125 mm, y = 125 mm) (the asterisks in Figures 4A–D) and therefrom the plots of the IBI shown in (I–L), the power spectra E(ω) in (M–P), and the Poincaré-type return maps, which we obtain from the IBI plots and which show (Q) a 5-cycle, (R) a 5-cycle, (S) chaotic behavior, and (T) chaotic evolution; discrete peaks in E(ω) appear at the following frequencies: (M) ω1 = 4.75 Hz, ω2 = 9.5 Hz, ω2 = 14.25 Hz, (N) ω1 = 4.75 Hz, ω2 = 9.5 Hz, ω2 = 14.25 Hz and small peaks at ω1 = 3.75 Hz, ω2 = 8.5 Hz, ω3 = 13.25 Hz, ω4 = 15 Hz, ω5 = 17.75 Hz, (O) ω1 = 4.75 Hz, ω2 = 9.5 Hz, and (P) ω1 = 4.5 Hz, ω2 = 9.5 Hz.
We focus next on the types of ST states that we obtain, with PD applied along both x and y axes, when we start with the IC1 initial condition. In Figure 6 we show three representative ST states; Figures 6A–C show, respectively, pseudocolor plots of the transmembrane potential Vm for PD with (a) Ax = Ay = 0.3, fx = fy = 3.0 Hz, (b) Ax = Ay = 0.3, fx = fy = 5.0 Hz, and (c) Ax = Ay = 0.4, fx = fy = 7.0 Hz; and the animations (b3), (c3), and (d4) in Video S3 show, respectively, the spatiotemporal evolution of Vm for these cases in the time interval 0 s ≤ t ≤ 4 s. To examine this evolution, we obtain the local time series of Vm(x, y, t), from the representative points (x = 125 mm, y = 125 mm) and (x = 50 mm, y = 50 mm), both of which are indicated by asterisks in Figures 6A–C; from these local time series, we obtain the plots of the IBI shown in Figures 6D–F and the power spectra of Figures 6G–I, with open-blue and black-filled circles for the time series from (x = 125 mm, y = 125 mm) and (x = 50 mm, y = 50 mm), respectively. These pseudocolor plots and animations of Vm and the plots of the IBI and power spectra show that we have, roughly speaking, three types of ST states with (a) multiple spirals (Figure 6A), (b) a stable spiral core with broken spiral arms (Figure 6B), and (c) a single, dominant, meandering spiral (Figure 6C); the second case (b) displays a coexistence of a quasiperiodic and an ST state because of the dominant spiral at the center and the broken spirals generated from its arm. Such coexistence behaviors have been observed in both computational (Xie et al., 2001; Fenton et al., 2002; Cherry and Fenton, 2008) and experimental studies (Nash et al., 2006; Massé et al., 2007), which include in vivo experiments.
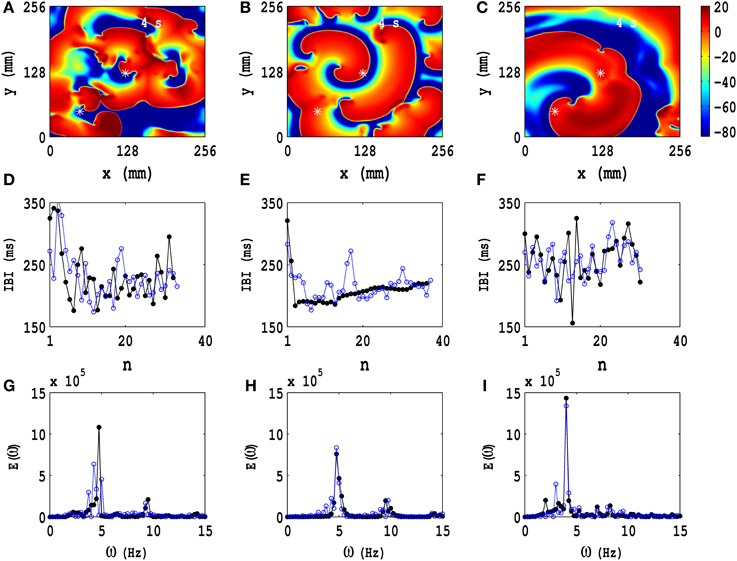
Figure 6. Temporal evolution of representative ST states in the TP06 model with PD along both spatial directions. Three ST states, which we obtain with the initial condition IC1 and PD, are shown via pseudocolor plots of the transmembrane potential Vm with (A) Ax = Ay = 0.3, fx = fy = 3.0 Hz, (B) Ax = Ay = 0.3, fx = fy = 5.0 Hz, and (C) Ax = Ay = 0.4, fx = fy = 7.0 Hz; the animations (b3), (c3), and (d4) in Video S3 show, respectively, the spatiotemporal evolution of Vm for these cases in the time interval 0 s ≤ t ≤ 4 s. We obtain the local time series of Vm(x, y, t), from the representative points (x = 125 mm, y = 125 mm) and (x = 50 mm, y = 50 mm), shown by asterisks in (A–C); from these local time series, we obtain the plots of the IBI (D–F) and the power spectra (G–I), with open-blue and black-filled circles for the time series from (x = 125 mm, y = 125 mm) and (x = 50 mm, y = 50 mm), respectively. These pseudocolor plots and animations of Vm and the plots of the IBI and power spectra show that we have, roughly speaking, three types of ST states with (A) multiple spirals, (B) a stable spiral core with broken spiral arms, and (C) a single dominant meandering spiral; the second case (B) displays a coexistence of a quasiperiodic and an ST state because of the dominant spiral at the center and the broken spirals generated from its arm.
We also obtain quiescent (Q) states with no spirals because of the absorption of spiral waves at the boundaries as shown in the pseudocolor plots of Vm in Figure S12 in the Supplementary Material S1 and in Video S3.
To illustrate the rich variety of spatiotemporal patterns, we summarize our results for the TP06 model, with the initial condition IC1, by presenting a selection of pseudocolor plots of Vm in Figure S13(a1–d5) in the Supplementary Material S1 (for parameter sets see Table 1). The animations in Video S3 show the spatiotemporal evolution of Vm for these cases in the time interval 0 s ≤ t ≤ 4 s. To examine this evolution, we obtain the local time series of Vm(x, y, t), from the representative points (x = 125 mm, y = 125 mm); these are shown in Figure S14 (Supplementary Material S1); from these local time series, we obtain the plots of the IBI (Figure S15 in the Supplementary Material S1) and the power spectra (Figure S16 in the Supplementary Material S1).
The counterparts of Figures S13–S16 in the Supplementary Material S1, for initial conditions IC2 for IC3, are given, respectively, in Figures S17–S24 in the Supplementary Material S1.
For the initial conditions IC2 and IC3 the analogs of the animations in Video S3 are given, respectively, in Videos S4, S5. For IC2, with PD along both axes and different values of the amplitude and the frequency, we examine the time series of Vm(x, y, t), from a representative point in the simulation domain (Figure S18 in the Supplementary Material S1), the plots of the IBI (Figure S19 in the Supplementary Material S1) and the power spectrum E(ω) (Figure S20 in the Supplementary Material S1), and the spatiotemporal evolution of Vm (given by the animations in Video S4) and conclude therefrom that, in this case, we obtain either (a) a Q state with no spirals [see animations (a4), (a5), (b4), (b5), (d4) and (d5) in Video S4] or (b) an MST state with broken spiral waves (see the remaining animations in Video S4). A similar analysis, for IC3 and PD along both x and y axes, based on time series of Vm (Figure S22 in the Supplementary Material S1), plots of the IBI (Figure S23 in the Supplementary Material S1), the power spectrum (Figure S24 in the Supplementary Material S1), and the spatiotemporal evolution of Vm (the animations in Video S5) suggests that here we can have (a) a Q state with no spirals [see animations (b3) (b4), (b5), (c4), (d4), and (d5) in Video S5], (b) an SMST state [see animations (a1) and (a5) in Video S5], or (c) an MST state with broken spiral waves (see the rest of the animations in Video S5).
The TNNP04 model with PD also exhibits a rich variety of spatiotemporal patterns with spiral waves like the TP06 model as we discuss in the Supplementary Material S1 (see Figures S25–S36). These figures and the associated Videos S6–S8 show that spiral-wave dynamics with PD in the TNNP04 model is quantitatively different from, but qualitatively similar to, that in the TP06 model. These differences arise because of the differences in the calcium-ion dynamics in these models; such dynamics can play an important role in the spatiotemporal evolution of spiral waves (Weiss et al., 2005; Ter Keurs and Boyden, 2007).
We have discussed spiral-wave dynamics in TP06 and TNNP04 models in the presence of PD along both x and y directions, with initial conditions of types IC1, IC2, and IC3. We have also carried out systematic simulations of spiral-wave dynamics in both these models, with PD along only one (say x) direction. Here too our results are, in the main, qualitatively similar to those we have presented above. Of course, there is anisotropic diffusion if the PD is only along one direction. However, Q, RS, and ST states appear; an overview of their spatiotemporal evolution is given in Figures S37–S42 in the Supplementary Material S1.
3.4. Suppression of Spiral Waves
One of the principal goals of our extensive numerical studies of spiral-wave dynamics in the TP06 and TNNP04 models with PD is to understand its role in enhancing or suppressing spiral-wave turbulence; this is an important step in developing an effective, low-amplitude suppression technique for the elimination of turbulence with single or multiple spirals. So far, various low-amplitude suppression algorithms have been developed to eliminate spiral waves in monodomain mathematical models of cardiac tissue; in these algorithms the control pulses are applied in several ways. These include the following: (a) periodic stimulation at a point (Zhang et al., 2003; Yuan et al., 2005); (b) a line stimulus that must be applied to one of the boundaries (Tang et al., 2008; Miguel et al., 2009); (c) an array of low-voltage control pulses, which must be swept over the simulation domain (Sinha and Sridhar, 2007; Sridhar and Sinha, 2008); or (d) the mesh-based, low-amplitude suppression scheme we describe (Sinha et al., 2001; Pandit et al., 2002). We have provided an overview of such low-amplitude suppression schemes, in the absence of PD, in earlier studies (Shajahan et al., 2009; Nayak, 2013); the most successful of these is based on a mesh-based suppression algorithm; this suppression scheme (Shajahan et al., 2009; Majumder et al., 2011a; Nayak et al., 2013) can suppress spiral waves of electrical activation even in the presence of conduction, ionic, and fibroblast heterogeneities (Shajahan et al., 2009; Majumder et al., 2011a; Nayak et al., 2013). We now investigate the efficacy of this mesh-based suppression scheme for both TP06 and TNNP04 models in the presence of PD.
In this mesh-based suppression scheme, we apply a current pulse of amplitude 75 pA/pF for 0.2 s over a mesh that divides our square simulation domain with L = 256 mm into 64 square cells of side l = 32 mm each; this pulse makes the links of the mesh refractory and, thereby, effectively imposes Neumann boundary conditions for any block inside the mesh; therefore, spiral waves inside a block are absorbed on the links of the mesh that bound the block. We have also extended this mesh-based scheme to one that uses control pulses on a set of parallel lines; in this line-based scheme, we apply a current pulse of amplitude 125 pA/pF for 0.6 s over a set of parallel lines separated from each other by l = 32 mm. As we show in the Supplementary Material S1 (see Figures S43, S44), both these schemes succeed in suppressing spiral-wave turbulence in the TP06 and TNNP04 models without PD; the line-based scheme uses a higher amplitude for the control pulse and a longer duration of application than the mesh-based one because the former has fewer control-pulse segments than the latter. Furthermore, we show (see Figures S45–S48, in the Supplementary Material S1) that the line-based scheme works with PD only if the PD is applied along one spatial direction.
A minor modification of our line-based suppression scheme suppresses spiral-wave turbulence: we use a rectangular-mesh-based control scheme, in which we add a few control lines perpendicular to the parallel lines of the line-based suppression scheme. We present a comparison of spiral-wave suppression by low-amplitude pulses on square, line, and rectangular suppression meshes in the TP06 model, with PD along both x and y directions: We impose PD along both x and y directions with the illustrative amplitudes Ax = Ay = 0.3 and frequencies fx = fy = 5 Hz for the initial configurations IC1, IC2, and IC3 (pseudocolor plots of Vm in Figures 7A,E,I, respectively). We apply the following control pulses: (1) pulses with amplitude 75 pA/pF for t = 0.2 s over a square mesh (Figures 7B,F,J), with each square block of side l = 32 mm; (2) pulses with amplitude 125 pA/pF for t = 0.6 s over a line mesh (Figures 7C,G,K), with inter-line spacing l = 32 mm; (3) pulses with amplitude 125 pA/pF for t = 0.6 s over a rectangular mesh (Figures 7D,H,L), with block sides lx = 32 mm and ly = 64 mm. These pseudocolor plots of Vm and the associated animations in Video S9 show that such spiral-wave states, with IC1, IC2, and IC3 initial conditions, are suppressed by both square- and rectangular-mesh suppression but not by line-mesh suppression. Our rectangular-mesh suppression scheme is a significant improvement over the square-mesh one because it uses fewer control lines than the latter. The results of similar studies for the TNNP04 model are given in Figure S49 (Supplementary Material S1).
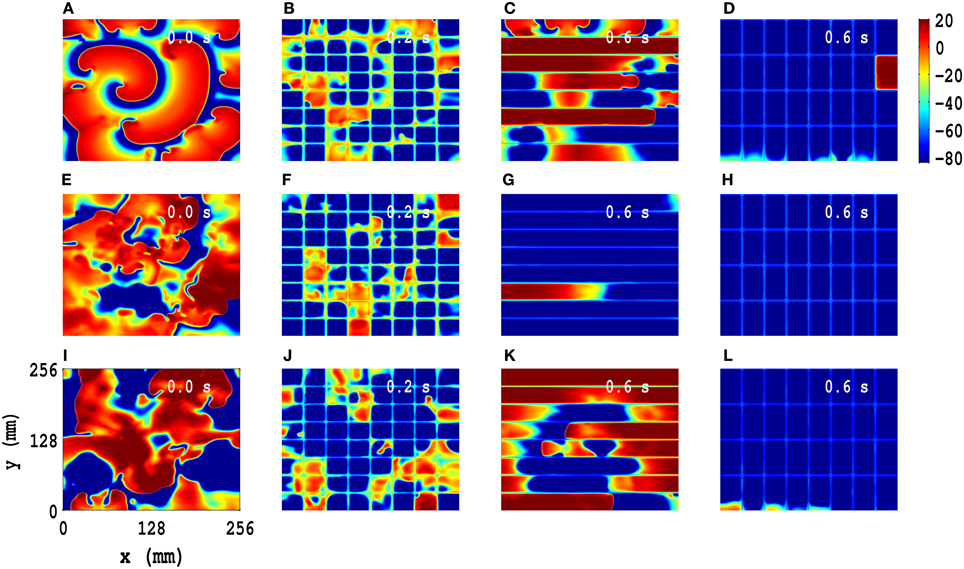
Figure 7. Comparison of spiral-wave suppression by low-amplitude pulses on square, line, and rectangular control meshes in the TP06 model, with PD along both x and y directions. We impose PD along both x and y directions with the illustrative amplitudes Ax = Ay = 0.3 and frequencies fx = fy = 5 Hz for the initial configurations IC1, IC2, and IC3 (pseudocolor plots of Vm in (A,E,I), respectively). We apply the following control pulses: amplitude 75 pA/pF for t = 0.2 s over a square mesh (B,F,J), with each square block of side l = 32 mm; amplitude 125 pA/pF for t = 0.6 s over a line mesh (C,G,K), with inter-line spacing l = 32 mm; amplitude 125 pA/pF for t = 0.6 s over a rectangular mesh (D,H,L), with block sides lx = 32 mm and ly = 64 mm. These pseudocolor plots of Vm and the associated animations in Video S9 show that these spiral states, with IC1, IC2, and IC3 initial conditions, are suppressed by both square- and rectangular-mesh control but not line-mesh control.
4. Discussion and Conclusion
We have carried out detailed and systematic numerical studies of the effects of periodic deformation (PD) on spiral-wave dynamics in ionically realistic mathematical models for cardiac tissue by introducing PD in the recently developed TP06 and TNNP04 mathematical models for human ventricular tissue (Ten Tusscher et al., 2004; Ten Tusscher and Panfilov, 2006), in which we include deformation as in Zhang et al. (2004, 2006) and Chen et al. (2008). We also investigate, in 2D simulations with PD, the efficacies of square-, rectangular-, and line-mesh-based, low-amplitude suppression techniques to eliminate spiral-wave turbulence in these models for cardiac tissue (Sinha et al., 2001; Pandit et al., 2002; Shajahan et al., 2009; Majumder et al., 2011a).
We have first considered simulations in cable-type domains, which are ideally suited for the calculation of θ and λ. We find that PD leads to a periodic, spatial modulation of θ and a temporally periodic modulation of λ; the degrees of these modulations depend on the amplitude Ax and frequency fx of the PD. To the best of our knowledge, such modulations have not been quantified in any earlier study, although a few studies (Zhang et al., 2006; Chen et al., 2008) have suggested, in the context of spiral waves, that such modulations can arise because of a Doppler-type effect (Fenton et al., 2002).
We have considered three types of initial spiral-wave configurations, IC1, IC2, and IC3, for both the TP06 and TNNP04 models. In the TP06 model, these configurations evolve, respectively, to (a) an RSC state, (b) an SMST state, and (c) an MST state, in the absence of PD; in the TNNP04 model they evolve, respectively, to (a) an RSC state, (b) an RSZ state, and (c) an MST state, in the absence of PD. We have used such initial conditions because various experimental and computational studies (Damle et al., 1992; Davidenko et al., 1992; Pertsov et al., 1993; Gray et al., 1995; Gray and Jalife, 1996; Beaumont et al., 1998; Gray et al., 1998; Witkowski et al., 1998; Qu et al., 2000a; Fenton et al., 2002; Ten Tusscher and Panfilov, 2006; Shajahan et al., 2009) have suggested that spiral-wave dynamics in cardiac tissue can lead to (a) a stable rotor (Davidenko et al., 1992; Pertsov et al., 1993; Beaumont et al., 1998), as in our RSC state, (b) a single, meandering rotor whose time series is chaotic (Gray et al., 1995; Gray and Jalife, 1996; Qu et al., 2000a), as in our SMST state, and (c) multiple rotors, which yield a state with spatiotemporal chaos (Damle et al., 1992; Gray et al., 1998; Witkowski et al., 1998; Qu et al., 2000a), as in our MST state. Thus, our initial conditions, IC1, IC2, and IC3, lead to the three major types of spiral-wave evolutions, and slight variants thereof (e.g., RSZ), which have been seen in earlier studies and whose evolution we study now with PD. This shows that spiral-wave dynamics in these two models, without PD, depends sensitively on the ionic details of these models and on the initial conditions. A rich variety of spiral-wave behaviors result when we add PD to the TP06 and TNNP04 models, which are quantitatively different from, but qualitatively similar to, that in the TP06 model. These differences arise because of the differences in the calcium-ion dynamics in these models; such dynamics can play an important role in the spatiotemporal evolution of spiral waves (Weiss et al., 2005; Ter Keurs and Boyden, 2007). Our principal findings here can be summarized as follows: In the presence of PD, an RS state may show (a) periodic behavior with high-order cycles in time, (b) temporally quasiperiodic (QP) evolution, (c) a state with spiral-wave turbulence, or (d) a quiescent state Q. For an ST state, which can be of SMST or MST types, PD can either leave the system in an ST state or make it evolve to a Q state, in which all spirals either annihilate each other or are absorbed at the boundaries of the simulation domain. Precisely which one of these states is obtained depends sensitively on our initial conditions and on the PD parameters Ax, Ay, fx, and fy. This sensitive dependence on parameters is a hallmark of extended dynamical systems that show spatiotemporal chaos (Shajahan et al., 2007, 2009). Thus, our study systematizes the effects of PD on spiral-wave dynamics and turbulence in two, biophysically realistic mathematical models for cardiac tissue; and it complements earlier studies of spiral-wave dynamics, in such models, that have concentrated on the dependence of such dynamics on ion-channel and electrophysiological properties (Karma, 1994; Qu et al., 1999, 2000a,b) and on conduction (Xie et al., 1998; Ten Tusscher and Panfilov, 2003; Shajahan et al., 2007, 2009) and ionic inhomogeneities (Shajahan et al., 2009; Majumder et al., 2011a,b). By using the biophysically realistic TP06 and TNNP04 models for cardiac tissue, our study generalizes the work of Zhang et al. (2004, 2006) and Chen et al. (2008) on spiral-wave instabilities in a simple, two-variable model for cardiac tissue, which is subject to PD.
Moreover, our studies have used three types of spiral-wave initial configurations to examine, via extensive and systematic numerical calculations, the transitions between different states of our system as the amplitude and frequency of the PD are varied. Our work extends significantly earlier studies of PD (Zhang et al., 2004, 2006; Chen et al., 2008) and mechanical deformation (Panfilov et al., 2005, 2007; Weise et al., 2011). Zhang et al. (2004) have studied the instability of a spiral wave of electrical activation by introducing, in a simple, two-variable, FitzHugh-Nagumo-type model (Aliev and Panfilov, 1996) for cardiac tissue, the possibility of periodic, temporal oscillations in the diffusion constant. Their study shows that the resulting deformation can lead to a transition from a stable, RS state to an ST state with multiple spirals. In another study Zhang et al. (2006) have shown that such an ST state can be driven into a quiescent state with no spirals, if the oscillation frequency of the PD is chosen to be close to the characteristic frequency of the spiral wave in the RS state of the system. Chen et al. (2008) have studied the effects of PD in the two-variable, Bär model (Bär and Eiswirth, 1993) on spiral-wave dynamics by varying the parameter ϵ, which sets the time scale of the slow variable in this model, and the amplitude A and frequency f of the PD; their study shows that the RS-ST transition can be effected by changing ϵ, A, and f suitably. Panfilov et al. (2007) have shown that mechanical deformation can either (a) induce a spiral wave to drift or (b) break up spiral waves and thus lead to complex spatiotemporal patterns in the three-variable Fenton–Karma model (Fenton and Karma, 1998) for cardiac tissue; the model that (Panfilov et al., 2007) use for deformation is different from, and more realistic than, the one used in Zhang et al. (2004, 2006) and Chen et al. (2008) in so far as it includes a stretch-activated current, which accounts for the mechano-electrical feedback in cardiac tissue, whose stress tensor controls the deformation; their study shows that rotating spirals become unstable both because of the stretch-activated current and the deformation of the tissue. In a related study, which also includes stretch-activated currents, Weise et al. (2011) have shown that such deformation can lead to pacemaker activity in a discrete version of the two-variable, Aliev-Panfilov, reaction-diffusion model (Aliev and Panfilov, 1996). Note that the studies in Zhang et al. (2004, 2006), Panfilov et al. (2007), Chen et al. (2008), and Weise et al. (2011) have used only a particular type of spiral-wave configuration in their two-variable models, with either PD or mechanical deformation. Moreover, Zhang et al. (2004, 2006), Panfilov et al. (2005, 2007), Chen et al. (2008), and Weise et al. (2011) have focused on simple, two-variable, mathematical models for cardiac tissue. Thus, these studies cannot address spiral-wave dynamics in such tissue at the detailed ionic level we consider in our work by using state-of-the-art, ionically realistic mathematical models for ventricular tissue. Furthermore, the authors of Zhang et al. (2004, 2006) and Chen et al. (2008) study the effects of PD on spiral-wave dynamics for a limited set of initial conditions. For example, in Zhang et al. (2004), the authors have studied the behavior of a single rotating spiral (RS) in the presence of PD; the authors of Zhang et al. (2006) have used a broken-spiral state as an initial configuration to study the elimination of spirals from the system in the presence of PD; in Chen et al. (2008), the authors have studied an RS initial configuration and its spatiotemporal evolution with PD. The authors of Panfilov et al. (2005, 2007) and Weise et al. (2011) have used an RS initial configuration to examine the effect of mechanical deformation on this RS state; they have not investigated the transitions between different spiral-wave states. None of these studies have carried out the detailed numerical investigations of spiral-wave dynamics that we present in our work, which considers a variety of initial conditions.
Furthermore, we have shown that square- and line-mesh-based, low-amplitude suppression schemes eliminate spiral-wave turbulence in both the TP06 and TNNP04 models in the absence of PD; this line-based suppression scheme is a significant improvement over the square-mesh suppression scheme of Sinha et al. (2001), Pandit et al. (2002), Shajahan et al. (2009), and Majumder et al. (2011a) because it has fewer control lines. However, we have found that the line-based scheme works with PD only if the PD is applied along one spatial direction. We have then shown that a minor modification of our line-based suppression scheme can suppress spiral-wave turbulence: in particular, we introduce a rectangular-mesh-based suppression scheme, in which we add a few control lines perpendicular to the parallel lines of the line-based suppression scheme; this rectangular-mesh scheme is also a significant improvement because it uses fewer control lines than the one based on a square mesh. We would like to emphasize here that no spiral-wave suppression scheme has been tried in the presence of PD hitherto; our study is the first to address this issue.
The formation of patterns in reaction-diffusion type system with various types of flows have been investigated in Biktashev et al. (1998), Leconte et al. (2003), Kuptsov et al. (2005), and Ermakova et al. (2009); in particular, break up of spiral excitation waves has been observed in a moving excitable medium as suggested in Biktashev et al. (1998); these studies have shown that linear shear flow can cause spiral-wave breakup in an excitable medium. Recent studies in Yoshida (2010) and Yashin et al. (2012a,b) have investigated pattern formation in a gel medium that can be oscillated mechanically; the effect of these mechanical oscillations on the underlying spatiotemporal chemical oscillations, because of a Belousov–Zhabotinsky (BZ) reaction, can be studied in such systems. Our work here presents the cardiac-tissue analogs of such chemical-oscillation studies.
Our study has used methods of non-linear-dynamics to evaluate the effects of periodic deformation on waves of excitation, both plane waves and spiral waves, and has obtained therefrom important physiological implications. In particular, we have shown, for the first time, how spiral-wave turbulence can be suppressed even in the presence of such deformation. This has potential applications in defibrillation because spiral-wave turbulence in our mathematical models is the analog of ventricular fibrillation (Davidenko et al., 1992; Pertsov et al., 1993; Gray et al., 1998; Jalife et al., 1998). Furthermore, our study has immediate implications for experiments on cell cultures with cardiac cells.
Various stretching devices have been developed to control the contraction and expansion of a cell (Barbee et al., 1994; Huang et al., 2010; Wang et al., 2010) and a layer of cells in culture (Lee et al., 1996; Sotoudeh et al., 1998; Waters et al., 2001; Winter et al., 2002; Rana et al., 2008). In these devices, both uniaxial and biaxial (Pang, 2009) stretching methods can be used to deform substrates; moreover, in some of these devices, the stretching can be applied in a cyclic manner at different frequencies. This stretching-induced deformation of the substrate leads, in turn, to the deformation of a layer of culture cells that are attached to the substrate. Examples of such studies include the following: The study in Barbee et al. (1994) has measured the strain that develops in cultured vascular smooth muscle cells when they are deformed by the stretching of a substrate to which they adhere. The authors of Lee et al. (1996) have used a device, which applies homogeneous, equibiaxial strains of 0–10% to a cell-culture substrate, to verify quantitatively the transmission of substrate deformation to a 2D sheet of cultured cardiac cells. The studies in Sotoudeh et al. (1998) have used endothelial cells in tissue culture, on a silicon elastic membrane, and have designed an apparatus that allows for the control of the magnitude and frequency of the dynamical stretching that is applied uniformly to these cells to produce equibiaxial dynamical stretches, with area changes ranging from 0% to 55% and frequencies ranging from 0 to 2 Hz. The authors of Waters et al. (2001) have developed a system for the imposition of cyclic biaxial strain to stretch cultured pulmonary epithelial cells; similar techniques have been used in Winter et al. (2002) to study the effects of strain in cell cultures and in vitro experiments. The authors of Rana et al. (2008) have studied the response to such stretching in cultured neonatal rat atrial cardiomyocytes by using a device that can impose homogeneous equibiaxial deformation. Other recent studies include those of Huang et al. (2010) and Wang et al. (2010), which have studied the mechanical activities of living cell, fiber, and tissue by applying both equiaxial and uniaxial deformation, and recording the dynamics of the response of these systems by using high-resolution imaging techniques; the former experiment has used fibroblasts and the latter endothelial cells in culture. We suggest that such experimental studies of the responses of cell cultures to an applied stress can be easily generalized to study the types of problems we have concentrated on here. In particular, by imposing a periodic deformation on cardiac tissue or cell cultures, experiments should be able to verify the predictions we have made, on the basis of our in silico studies, about the modulations of θ and λ in the presence of PD and the effects of PD on spiral-wave dynamics, which we have discussed in detail in the previous Section.
We end with some limitations of our model. The first limitation is that our model does not include stretch-activated currents (Panfilov et al., 2005, 2007; Weise et al., 2011) explicitly; but Vm depends on PD and all ionic currents depend on Vm, so PD affects all such currents implicitly. Next, the PD in our model affects the electrical activation of our medium but it is not, in turn, affected by this activation; by contrast, the model for mechanical deformation used in Panfilov et al. (2005, 2007) and Weise et al. (2011) allows for electrical feedback to affect such deformation; our model does not include soft-tissue mechanics, which can be incorporated in mathematical models for cardiac tissue by including stress and strain tensors, from elasticity theory (Nash and Hunter, 2000; Nash and Panfilov, 2004; Keldermann et al., 2009), as in the studies of Panfilov et al. (2005, 2007) and Weise et al. (2011); however, these studies use only a two-variable model for cardiac tissue and not the ionically realistic TP06 or TNNP04 models that we employ. Moreover, because of the absence of detailed ion-channel dynamics, the simple, two-variable models for cardiac tissue, which have been used in the studies of Panfilov et al. (2005, 2007) and Weise et al. (2011), do not account for the effects of deformation on ion-channel activity and the intracellular calcium concentration as suggested in Cherubini et al. (2008), Pathmanathan and Whiteley (2009), and Ambrosi et al. (2011). In spite of the simplicity of our model for PD, our study captures various features of spiral-wave dynamics that have been observed in models that include stretch-activated currents (Panfilov et al., 2007); in particular, our model displays spiral-wave breakup because of PD. Thus, this result of ours is robust. The only qualitative effect that our study misses is deformation-induced pacemaker activity, for which it has been argued (Kohl et al., 1999; Panfilov et al., 2005; Weise et al., 2011) that stretch-activated currents are essential. To the best of our knowledge, our elucidation of the effects of PD on spiral-wave dynamics in mathematical models for cardiac tissue, although simple in its modeling of PD, is the first study that explores the effects of PD on spiral-wave dynamics in ionically realistic mathematical models for ventricular tissue. A complete study of a realistic model for deformation, with stretch-activated currents, and such ionically realistic mathematical models lies beyond the scope of the present paper. While this paper was being prepared for publication, a new study appeared on a human-ventricular mathematical model with mechanical deformation (Weise and Panfilov, 2013). The authors of this study have used the same type of deformation that they have employed in their previous investigations of mechanical deformation (Weise et al., 2011); they have studied spiral-wave dynamics in the context of the drifting of a spiral wave as a function of Gs (here, Gs is the maximum conductance of the stretch-activated current). In their numerical studies they have found that, in a constantly stretched medium, there is an increase of the core size and period of a spiral wave, but no change in its rotational dynamics; in contrast, in the dynamically stretched medium, they observe spiral drift. We have found such behaviors, to some extent, in our periodically deformed medium; e.g., the initial condition IC1, which leads to a stable rotating spiral with a circular tip trajectory, in the absence of PD, can lead to a variety of behaviors, which can include slow spiral drift in the presence of PD. Our model does not include mechano-electrical feedback in a realistic way, as we have described above. Therefore, we have not attempted to study how different mechanical stimuli, other than the PD we consider, initiate or affect spiral-waves in our model; studies of other mechanical stimuli lie beyond the scope of our paper. In Weise et al. (2011) it has been noted that both electrical and mechanical stimuli can cause the formation of a pacemaker in cardiac tissue; and mechanical stimuli can translate the mechanical energy into an electrical stimulus, as argued in Janse et al. (2003) and Cooper et al. (2006). We use a monodomain description for cardiac tissue; and we do not use an anatomically realistic simulation domain (Panfilov and Keener, 1995; Trayanova and Tice, 2009), muscle-fiber orientation, and transmural heterogeneity (Majumder et al., 2011b, 2012); the inclusion of these features lies beyond the scope of this study. We note, however, that recent studies (Potse et al., 2006) have compared potentials resulting from normal depolarization and repolarization in a bidomain model with those of a monodomain model; these studies have shown that the differences between results obtained from a monodomain model and those obtained from a bidomain model are extremely small.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank the Department of Science and Technology (DST), India, the University Grants Commission (UGC), India, Council for Scientific and Industrial Research (CSIR), India, Jawaharlal Nehru Centre for Advanced Scientific Research (JNCASR), India, and the Robert Bosch Centre for Cyber Physical Systems (IISc) for support, and the Supercomputer Education and Research Centre (SERC, IISc) for computational resources.
Supplementary Material
The Supplementary Material for this article can be found online at: http://www.frontiersin.org/journal/10.3389/fphys.2014.00207/abstract
Video S1 | Spatiotemporal evolution of plane waves in cable-type domains, with PD along the axial-direction of the cables, for the TP06 model, shown via pseudocolor plots of the transmembrane potential Vm; the time evolution is shown for 0 s ≤ t ≤ 2 s; we use 10 frames per second (fps); in real time each frame is separated from the succeeding frame by 8 ms.
Video S2 | Spiral-wave dynamics in the TP06 and TNNP04 models in the absence of PD; the time evolution of pseudocolor plots of the transmembrane potential Vm is shown for 0 s ≤ t ≤ 4 s; we use 10 frames per second (fps); in real time each frame is separated from the succeeding frame by 8 ms.
Video S3 | Spiral-wave dynamics for the TP06 model in the presence of PD along both x and y directions with an initial condition of type IC1; the time evolution of pseudocolor plots of the transmembrane potential Vm is shown for 0 s ≤ t ≤ 4 s; we use 10 frames per second (fps); in real time each frame is separated from the succeeding frame by 8 ms.
Video S4 | Spiral-wave dynamics for the TP06 model in the presence of PD along both x and y directions with an initial condition of type IC2; the time evolution of pseudocolor plots of the transmembrane potential Vm is shown for 0 s ≤ t ≤ 4 s; we use 10 frames per second (fps); in real time each frame is separated from the succeeding frame by 8 ms.
Video S5 | Spiral-wave dynamics for the TP06 model in the presence of PD along both x and y directions with an initial condition of type IC3; the time evolution of pseudocolor plots of the transmembrane potential Vm is shown for 0 s ≤ t ≤ 4 s; we use 10 frames per second (fps); in real time each frame is separated from the succeeding frame by 8 ms.
Video S6 | Spiral-wave dynamics for the TNNP04 model in the presence of PD along both x and y directions with an initial condition of type IC1; the time evolution of pseudocolor plots of the transmembrane potential Vm is shown for 0 s ≤ t ≤ 4,s; we use 10 frames per second (fps); in real time each frame is separated from the succeeding frame by 8 ms.
Video S7 | Spiral-wave dynamics for the TNNP04 model in the presence of PD along both x and y directions with an initial condition of type IC2; the time evolution of pseudocolor plots of the transmembrane potential Vm is shown for 0 s ≤ t ≤ 4 s; we use 10 frames per second (fps); in real time each frame is separated from the succeeding frame by 8 ms.
Video S8 | Spiral-wave dynamics for the TNNP04 model in the presence of PD along both x and y directions with an initial condition of type IC3; the time evolution of pseudocolor plots of the transmembrane potential Vm is shown for 0 s ≤ t ≤ 4 s; we use 10 frames per second (fps); in real time each frame is separated from the succeeding frame by 8 ms.
Video S9 | Comparison of spiral-wave suppression by low-amplitude pulses on square, line, and rectangular control meshes in the TP06 model, with PD along both x and y directions, for the time interval 0 s ≤ t ≤ 1 s; we depict pseudocolor plots of Vm and use 10 frames per second (fps); in real time each frame is separated from the succeeding frame by 8 ms.
References
Aliev, R. R., and Panfilov, A. V. (1996). A simple two-variable model of cardiac excitation. Chaos Solitons Fractals 7, 293–301. doi: 10.1016/0960-0779(95)00089-5
Ambrosi, D., Arioli, G., Nobile, F., and Quarteroni, A. (2011). Electromechanical coupling in cardiac dynamics: the active strain approach. SIAM J. Appl. Math. 71, 605–621. doi: 10.1137/100788379
Bär, M., and Eiswirth, M. (1993). Turbulence due to spiral breakup in a continuous excitable medium. Phys. Rev. E 48, R1635. doi: 10.1103/PhysRevE.48.R1635
Barbee, K. A., Macarak, E. J., and Thibault, L. E. (1994). Strain measurements in cultured vascular smooth muscle cells subjected to mechanical deformation. Annal. Biomed. Eng. 22, 14–22. doi: 10.1007/BF02368218
Barkley, D., Kness, M., and Tuckerman, L. S. (1990). Spiral-wave dynamics in a simple model of excitable media: the transition from simple to compound rotation. Phys. Rev. A 42, 2489–2492. doi: 10.1103/PhysRevA.42.2489
Beaumont, J., Davidenko, N., Davidenko, J. M., and Jalife, J. (1998). Spiral waves in two-dimensional models of ventricular muscle: formation of a stationary core. Biophys. J. 75, 1–14. doi: 10.1016/S0006-3495(98)77490-9
Bernus, O., Wilders, R., Zemlin, C. W., Verschelde, H., and Panfilov, A. V. (2002). A computationally efficient electrophysiological model of human ventricular cells. Am. J. Physiol. Heart Circ. Physiol. 51, H2296–H2308. doi: 10.1152/ajpheart.00731.2001
Biktashev, V., Holden, A., Tsyganov, M., Brindley, J., and Hill, N. (1998). Excitation wave breaking in excitable media with linear shear flow. Phys. Rev. Lett. 81, 2815. doi: 10.1103/PhysRevLett.81.2815
Chen, J.-X., Xu, J.-R., Yuan, X.-P., and Ying, H.-P. (2008). Influences of periodic mechanical deformation on spiral breakup in excitable media. J. Phys. Chem. B 113, 849–853. doi: 10.1021/jp806811j
Chen, P.-S., Wu, T.-J., Ting, C.-T., Karagueuzian, H. S., Garfinkel, A., Lin, S.-F., et al. (2003). A tale of two fibrillations. Circulation 108, 2298–2303. doi: 10.1161/01.CIR.0000094404.26004.07
Chen, S.-A., Hsieh, M.-H., Tai, C.-T., Tsai, C.-F., Prakash, V., Yu, W.-C., et al. (1999). Initiation of atrial fibrillation by ectopic beats originating from the pulmonary veins electrophysiological characteristics, pharmacological responses, and effects of radiofrequency ablation. Circulation 100, 1879–1886. doi: 10.1161/01.CIR.100.18.1879
Cherry, E., and Fenton, F. (2008). Visualization of spiral and scroll waves in simulated and experimental cardiac tissue. New J. Phys. 10, 125016. doi: 10.1088/1367-2630/10/12/125016
Cherubini, C., Filippi, S., Nardinocchi, P., and Teresi, L. (2008). An electromechanical model of cardiac tissue: constitutive issues and electrophysiological effects. Prog. Biophys. Mol. Biol. 97, 562–573. doi: 10.1016/j.pbiomolbio.2008.02.001
Clayton, R., and Panfilov, A. (2008). A guide to modelling cardiac electrical activity in anatomically detailed ventricles. Prog. Biophys. Mol. Biol. 96, 19–43. doi: 10.1016/j.pbiomolbio.2007.07.004
Cooper, P. J., Epstein, A., MacLeod, I. A., Schaaf, S., Sheldon, J., Boulin, C., et al. (2006). Soft tissue impact characterisation kit (stick) for ex situ investigation of heart rhythm responses to acute mechanical stimulation. Prog. Biophys. Mol. Biol. 90, 444–468. doi: 10.1016/j.pbiomolbio.2005.07.004
Damle, R. S., Kanaan, N. M., Robinson, N. S., Ge, Y.-Z., Goldberger, J. J., and Kadish, A. H. (1992). Spatial and temporal linking of epicardial activation directions during ventricular fibrillation in dogs. Evidence for underlying organization. Circulation 86, 1547–1558. doi: 10.1161/01.CIR.86.5.1547
Davidenko, J. M., Kent, P. F., Chialvo, D. R., Michaels, D. C., and Jalife, J. (1990). Sustained vortex-like waves in normal isolated ventricular muscle. Proc. Natl. Acad. Sci. U.S.A. 87, 8785–8789. doi: 10.1073/pnas.87.22.8785
Davidenko, J. M., Pertsov, A. V., Salomonsz, R., Baxter, W., and Jalife, J. (1992). Stationary and drifting spiral waves of excitation in isolated cardiac muscle. Nature 355, 349–351. doi: 10.1038/355349a0
De Bakker, J., Van Capelle, F., Janse, M. J., Tasseron, S., Vermeulen, J. T., De Jonge, N., et al. (1993). Slow conduction in the infarcted human heart.‘zigzag’course of activation. Circulation 88, 915–926. doi: 10.1161/01.CIR.88.3.915
Ermakova, E. A., Shnol, E. E., Panteleev, M. A., Butylin, A. A., Volpert, V., and Ataullakhanov, F. I. (2009). On propagation of excitation waves in moving media: the fitzhugh-nagumo model. PLoS ONE 4:e4454. doi: 10.1371/journal.pone.0004454
Fenton, F., and Karma, A. (1998). Vortex dynamics in three-dimensional continuous myocardium with fiber rotation: filament instability and fibrillation. Chaos 8, 20–47. doi: 10.1063/1.166311
Fenton, F. H., Cherry, E. M., and Glass, L. (2008). Cardiac arrhythmia. Scholarpedia 3, 1665. doi: 10.4249/scholarpedia.1665
Fenton, F. H., Cherry, E. M., Hastings, H. M., and Evans, S. J. (2002). Multiple mechanisms of spiral wave breakup in a model of cardiac electrical activity. Chaos 12, 852–892. doi: 10.1063/1.1504242
Fogoros, R. N. (2011). Ventricular fibrillation. Heart Dis. Available online at: http://heartdisease.about.com/od/palpitationsarrhythmias/a/Ventricular-Fibrillation.htm
Garfinkel, A., Kim, Y.-H., Voroshilovsky, O., Qu, Z., Kil, J. R., Lee, M.-H., et al. (2000). Preventing ventricular fibrillation by flattening cardiac restitution. Proc. Natl. Acad. Sci. U.S.A. 97, 6061–6066. doi: 10.1073/pnas.090492697
Gray, R., and Jalife, J. (1996). Self-organized drifting spiral waves as a mechanism for ventricular fibrillation. Circulation 94, I–48.
Gray, R. A., Jalife, J., Panfilov, A. V., Baxter, W. T., Cabo, C., Davidenko, J. M., et al. (1995). Mechanisms of cardiac fibrillation. Science 270, 1222–1225. doi: 10.1126/science.270.5239.1222
Gray, R. A., Pertsov, A. M., and Jalife, J. (1998). Spatial and temporal organization during cardiac fibrillation. Nature 392, 75–78. doi: 10.1038/33537
Gray, R. A., Wikswo, J. P., and Otani, N. F. (2009). Origin choice and petal loss in the flower garden of spiral wave tip trajectories. Chaos 19, 033118. doi: 10.1063/1.3204256
Huang, L., Mathieu, P. S., and Helmke, B. P. (2010). A stretching device for high-resolution live-cell imaging. Annal. Biomed. Eng. 38, 1728–1740. doi: 10.1007/s10439-010-9968-7
Ideker, R. E., and Rogers, J. M. (2006). Human ventricular fibrillation wandering wavelets, mother rotors, or both? Circulation 114, 530–532. doi: 10.1161/CIRCULATIONAHA.106.644765
Ikeda, T., Uchida, T., Hough, D., Lee, J. J., Fishbein, M. C., Mandel, W. J., et al. (1996). Mechanism of spontaneous termination of functional reentry in isolated canine right atrium evidence for the presence of an excitable but nonexcited core. Circulation 94, 1962–1973. doi: 10.1161/01.CIR.94.8.1962
Jalife, J., Gray, R. A., Morley, G. E., and Davidenko, J. M. (1998). Self-organization and the dynamical nature of ventricular fibrillation. Chaos 8, 79–93. doi: 10.1063/1.166289
Janse, M. J., Coronel, R., Wilms-Schopman, F. J., and de Groot, J. R. (2003). Mechanical effects on arrhythmogenesis: from pipette to patient. Prog. Biophys. Mol. Biol. 82, 187–195. doi: 10.1016/S0079-6107(03)00015-4
Karma, A. (1994). Electrical alternans and spiral wave breakup in cardiac tissue. Chaos 4, 461–472. doi: 10.1063/1.166024
Keldermann, R., Nash, M., and Panfilov, A. (2009). Modeling cardiac mechano-electrical feedback using reaction-diffusion-mechanics systems. Physica D 238, 1000–1007. doi: 10.1016/j.physd.2008.08.017
Keldermann, R. H., Nash, M. P., Gelderblom, H., Wang, V. Y., and Panfilov, A. V. (2010). Electromechanical wavebreak in a model of the human left ventricle. Am. J. Physiol. Cell Physiol. 299, H134. doi: 10.1152/ajpheart.00862.2009
Kohl, P., Hunter, P., and Noble, D. (1999). Stretch-induced changes in heart rate and rhythm: clinical observations, experiments and mathematical models. Prog. Biophys. Mol. Biol. 71, 91–138. doi: 10.1016/S0079-6107(98)00038-8
Koller, M. L., Riccio, M. L., and Gilmour, R. F Jr. (1998). Dynamic restitution of action potential duration during electrical alternans and ventricular fibrillation. Am. J. Physiol. Heart Circ. Physiol. 275, H1635–H1642.
Kuijpers, N. H., Potse, M., van Dam, P. M., ten Eikelder, H. M., Verheule, S., Prinzen, F. W., et al. (2011). Mechanoelectrical coupling enhances initiation and affects perpetuation of atrial fibrillation during acute atrial dilation. Heart Rhythm 8, 429–436. doi: 10.1016/j.hrthm.2010.11.020
Kuptsov, P. V., Satnoianu, R. A., and Daniels, P. G. (2005). Pattern formation in a two-dimensional reaction-diffusion channel with poiseuille flow. Phys. Rev. Ser. E 72, 036216. doi: 10.1103/PhysRevE.72.036216
Leconte, M., Martin, J., Rakotomalala, N., and Salin, D. (2003). Pattern of reaction diffusion fronts in laminar flows. Phys. Rev. Lett. 90, 128302. doi: 10.1103/PhysRevLett.90.128302
Lee, A., Delhaas, T., Waldman, L. K., Mackenna, D. A., Villarreal, F. J., and McCulloch, A. D. (1996). An equibiaxial strain system for cultured cells. Am. J. Physiol. Cell Physiol. 271, C1400–C1408.
Lim, Z. Y., Maskara, B., Aguel, F., Emokpae, R., and Tung, L. (2006). Spiral wave attachment to millimeter-sized obstacles. Circulation 114, 2113–2121. doi: 10.1161/CIRCULATIONAHA.105.598631
Majumder, R., Nayak, A. R., and Pandit, R. (2012). Nonequilibrium arrhythmic states and transitions in a mathematical model for diffuse fibrosis in human cardiac tissue. PLoS ONE 7:e45040. doi: 10.1371/journal.pone.0045040
Majumder, R., Nayak, A. R., and Pandit, R. (2011a). “An overview of spiral-and scroll-wave dynamics in mathematical models for cardiac tissue,” in Heart Rate and Rhythm, eds O. N. Tripathi, U. Ravens, and M. C. Sanguinetti (Berlin; Heidelberg: Springer), 269–282.
Majumder, R., Nayak, A. R., Pandit, R., Majumder, R., Nayak, A., Pandit, R., et al. (2011b). Scroll-wave dynamics in human cardiac tissue: lessons from a mathematical model with inhomogeneities and fiber architecture. PLoS ONE 6:e18052. doi: 10.1371/journal.pone.0018052
Massé, S., Downar, E., Chauhan, V., Sevaptsidis, E., and Nanthakumar, K. (2007). Ventricular fibrillation in myopathic human hearts: mechanistic insights from in vivo global endocardial and epicardial mapping. Am. J. Physiol. Heart Circ. Physiol. 292, H2589–H2597. doi: 10.1152/ajpheart.01336.2006
McCulloch, A. D., Smaill, B. H., and Hunter, P. J. (1987). Left ventricular epicardial deformation in isolated arrested dog heart. Am. J. Physiol. Heart Circ. Physiol. 252, H233–H241.
Miguel, A., de la Rubia, F. J., and Ivanov, P. C. (2009). Spiral wave annihilation by low-frequency planar fronts in a model of excitable media. EPL (Europhys. Lett.) 86, 18005. doi: 10.1209/0295-5075/86/18005
Nash, M. P., and Hunter, P. J. (2000). Computational mechanics of the heart. J. Elast. Phys. Sci. Solids 61, 113–141. doi: 10.1023/A:1011084330767
Nash, M. P., Mourad, A., Clayton, R. H., Sutton, P. M., Bradley, C. P., Hayward, M., et al. (2006). Evidence for multiple mechanisms in human ventricular fibrillation. Circulation 114, 536–542. doi: 10.1161/CIRCULATIONAHA.105.602870
Nash, M. P., and Panfilov, A. V. (2004). Electromechanical model of excitable tissue to study reentrant cardiac arrhythmias. Prog. Biophys. Mol. Biol. 85, 501–522. doi: 10.1016/j.pbiomolbio.2004.01.016
Nayak, A. R. (2013). Spiral-Wave Dynamics in Ionically Realistic Mathematical Models for Human Ventricular Tissue. Ph.D. thesis, Indian Institute of Science.
Nayak, A. R., Shajahan, T., Panfilov, A., and Pandit, R. (2013). Spiral-wave dynamics in a mathematical model of human ventricular tissue with myocytes and fibroblasts. PLoS ONE 8:9. doi: 10.1371/journal.pone.0072950
Noble, D. (2002). Modelling the heart: insights, failures and progress. Bioessays 24, 1155–1163. doi: 10.1002/bies.10186
Otani, N. F. (2002). A primary mechanism for spiral wave meandering. Chaos 12, 829–842. doi: 10.1063/1.1503921
Pandit, R., Pande, A., Sinha, S., and Sen, A. (2002). Spiral turbulence and spatiotemporal chaos: characterization and control in two excitable media. Physica A 306, 211–219. doi: 10.1016/S0378-4371(02)00499-5
Panfilov, A., Keldermann, R., and Nash, M. (2007). Drift and breakup of spiral waves in reaction–diffusion–mechanics systems. Proc. Natl. Acad. Sci. U.S.A. 104, 7922–7926. doi: 10.1073/pnas.0701895104
Panfilov, A. v., and Keener, J. (1995). Re-entry in an anatomical model of the heart. Chaos Solitons Fractals 5, 681–689. doi: 10.1016/0960-0779(93)E0050-L
Panfilov, A. V., Keldermann, R., and Nash, M. (2005). Self-organized pacemakers in a coupled reaction-diffusion-mechanics system. Phys. Rev. Lett. 95, 258104. doi: 10.1103/PhysRevLett.95.258104
Pang, Q. (2009). Design and Development of a Biostretch Apparatus for Tissue Engineering. Ph.D. thesis, University of Toronto.
Pathmanathan, P., and Whiteley, J. P. (2009). A numerical method for cardiac mechanoelectric simulations. Annal. Biomed. Eng. 37, 860–873. doi: 10.1007/s10439-009-9663-8
Pertsov, A. M., Davidenko, J. M., Salomonsz, R., Baxter, W. T., and Jalife, J. (1993). Spiral waves of excitation underlie reentrant activity in isolated cardiac muscle. Circ. Res. 72, 631–650. doi: 10.1161/01.RES.72.3.631
Potse, M., Dubé, B., Richer, J., Vinet, A., and Gulrajani, R. M. (2006). A comparison of monodomain and bidomain reaction-diffusion models for action potential propagation in the human heart. IEEE Trans. Biomed. Eng. 53, 2425–2435. doi: 10.1109/TBME.2006.880875
Qu, Z., Weiss, J. N., and Garfinkel, A. (1999). Cardiac electrical restitution properties and stability of reentrant spiral waves: a simulation study. Am. J. Physi. Heart Circ. Physiol. 276, H269–H283.
Qu, Z., Weiss, J. N., and Garfinkel, A. (2000a). From local to global spatiotemporal chaos in a cardiac tissue model. Phys. Rev. E 61, 727. doi: 10.1103/PhysRevE.61.727
Qu, Z., Xie, F., Garfinkel, A., and Weiss, J. N. (2000b). Origins of spiral wave meander and breakup in a two-dimensional cardiac tissue model. Annal. Biomed. Eng. 28, 755–771. doi: 10.1114/1.1289474
Rana, O. R., Zobel, C., Saygili, E., Brixius, K., Gramley, F., Schimpf, T., et al. (2008). A simple device to apply equibiaxial strain to cells cultured on flexible membranes. Am. J. Physiol. Heart Circ. Physiol. 294, H532–H540. doi: 10.1152/ajpheart.00649.2007
Roger, V. L., Go, A. S., Lloyd-Jones, D. M., Adams, R. J., Berry, J. D., Brown, T. M., et al. (2011). Heart disease and stroke statistics–2011 update a report from the american heart association. Circulation 123, e18–e209. doi: 10.1161/CIR.0b013e3182009701
Roger, V. L., Go, A. S., Lloyd-Jones, D. M., Benjamin, E. J., Berry, J. D., Borden, W. B., et al. (2012). Heart disease and stroke statistics–2012 update a report from the american heart association. Circulation 125, e2–e220. doi: 10.1161/CIR.0b013e31823ac046
Samie, F. H., and Jalife, J. (2001). Mechanisms underlying ventricular tachycardia and its transition to ventricular fibrillation in the structurally normal heart. Cardiovasc. Res. 50, 242–250. doi: 10.1016/S0008-6363(00)00289-3
Shajahan, T., Nayak, A. R., and Pandit, R. (2009). Spiral-wave turbulence and its control in the presence of inhomogeneities in four mathematical models of cardiac tissue. PLoS ONE 4:e4738. doi: 10.1371/journal.pone.0004738
Shajahan, T., Sinha, S., and Pandit, R. (2007). Spiral-wave dynamics depend sensitively on inhomogeneities in mathematical models of ventricular tissue. Phys. Rev. E 75, 011929. doi: 10.1103/PhysRevE.75.011929
Sinha, S., Pande, A., and Pandit, R. (2001). Defibrillation via the elimination of spiral turbulence in a model for ventricular fibrillation. Phys. Rev. Lett. 86, 3678–3681. doi: 10.1103/PhysRevLett.86.3678
Sinha, S., and Sridhar, S. (2007). “Controlling spatiotemporal chaos and spiral turbulence in excitable media,” in Handbook of Chaos Control, 2nd Edn., eds E. Schöll and H. G. Schuster (Weinheim: Wiley Online Library), 703–718. doi: 10.1002/9783527622313.ch32
Sotoudeh, M., Jalali, S., Usami, S., Shyy, J. Y., and Chien, S. (1998). A strain device imposing dynamic and uniform equi-biaxial strain to cultured cells. Annal. Biomed. Eng. 26, 181–189. doi: 10.1114/1.48
Sridhar, S., and Sinha, S. (2008). Controlling spatiotemporal chaos in excitable media using an array of control points. EPL (Europhys. Lett.) 81, 50002. doi: 10.1209/0295-5075/81/50002
Tang, G., Deng, M., Hu, B., and Hu, G. (2008). Active and passive control of spiral turbulence in excitable media. Phys. Rev. E 77, 046217. doi: 10.1103/PhysRevE.77.046217
Ten Tusscher, K., Noble, D., Noble, P., and Panfilov, A. (2004). A model for human ventricular tissue. Am. J. Physiol. Heart Circ. Physiol. 286, H1573–H1589. doi: 10.1152/ajpheart.00794.2003
Ten Tusscher, K., and Panfilov, A. (2003). Influence of nonexcitable cells on spiral breakup in two-dimensional and three-dimensional excitable media. Phys. Rev. E 68, 062902. doi: 10.1103/PhysRevE.68.062902
Ten Tusscher, K., and Panfilov, A. (2006). Alternans and spiral breakup in a human ventricular. Am. J. Physiol. Heart Circ. Physiol. 291, H1088–H1100. doi: 10.1152/ajpheart.00109.2006
Ter Keurs, H. E., and Boyden, P. A. (2007). Calcium and arrhythmogenesis. Physiol. Rev. 87, 457–506. doi: 10.1152/physrev.00011.2006
Thompson, S. A., Copeland, C. R., Reich, D. H., and Tung, L. (2011). Mechanical coupling between myofibroblasts and cardiomyocytes slows electric conduction in fibrotic cell monolayers. Circulation 123, 2083–2093. doi: 10.1161/CIRCULATIONAHA.110.015057
Trayanova, N. A., and Tice, B. M. (2009). Integrative computational models of cardiac arrhythmias–simulating the structurally realistic heart. Drug Discov. Today Dis. Models 6, 85–91. doi: 10.1016/j.ddmod.2009.08.001
Valderrábano, M., Kim, Y.-H., Yashima, M., Wu, T.-J., Karagueuzian, H. S., and Chen, P.-S. (2000). Obstacle-induced transition from ventricular fibrillation to tachycardia in isolated swine right ventriclesinsights into the transition dynamics and implications for the critical mass. J. Am. Coll. Cardiol. 36, 2000–2008. doi: 10.1016/S0735-1097(00)00941-4
Wang, D., Xie, Y., Yuan, B., Xu, J., Gong, P., and Jiang, X. (2010). A stretching device for imaging real-time molecular dynamics of live cells adhering to elastic membranes on inverted microscopes during the entire process of the stretch. Integr. Biol. 2, 288–293. doi: 10.1039/b920644b
Waters, C. M., Glucksberg, M. R., Lautenschlager, E. P., Lee, C.-W., Van Matre, R. M., Warp, R. J., et al. (2001). A system to impose prescribed homogenous strains on cultured cells. J. Appl. Physiol. 91, 1600–1610.
Weise, L. D., Nash, M. P., and Panfilov, A. V. (2011). A discrete model to study reaction-diffusion-mechanics systems. PLoS ONE 6:e21934. doi: 10.1371/journal.pone.0021934
Weise, L. D., and Panfilov, A. V. (2013). A discrete electromechanical model for human cardiac tissue: effects of stretch-activated currents and stretch conditions on restitution properties and spiral wave dynamics. PLoS ONE 8:e59317. doi: 10.1371/annotation/9ceadf50-eb8f-4051-9e41-772884d47385
Weiss, J. N., Qu, Z., Chen, P.-S., Lin, S.-F., Karagueuzian, H. S., Hayashi, H., et al. (2005). The dynamics of cardiac fibrillation. Circulation 112, 1232–1240. doi: 10.1161/CIRCULATIONAHA.104.529545
Winter, L. C., Gilbert, J. A., Elder, S. H., and Bumgardner, J. D. (2002). A device for imposing cyclic strain to cells growing on implant alloys. Annal. Biomed. Eng. 30, 1242–1250. doi: 10.1114/1.1529195
Witkowski, F. X., Leon, L. J., Penkoske, P. A., Giles, W. R., Spano, M. L., Ditto, W. L., et al. (1998). Spatiotemporal evolution of ventricular fibrillation. Nature 392, 78–82. doi: 10.1038/32170
Wu, T.-J., Lin, S.-F., Baher, A., Qu, Z., Garfinkel, A., Weiss, J. N., et al. (2004). Mother rotors and the mechanisms of d600-induced type 2 ventricular fibrillation. Circulation 110, 2110–2118. doi: 10.1161/01.CIR.0000143834.51102.91
Xie, F., Qu, Z., and Garfinkel, A. (1998). Dynamics of reentry around a circular obstacle in cardiac tissue. Phys. Rev. E 58, 6355. doi: 10.1103/PhysRevE.58.6355
Xie, F., Qu, Z., Weiss, J. N., and Garfinkel, A. (2001). Coexistence of multiple spiral waves with independent frequencies in a heterogeneous excitable medium. Phys. Rev. E 63, 031905. doi: 10.1103/PhysRevE.63.031905
Yashin, V. V., Kuksenok, O., Dayal, P., and Balazs, A. C. (2012a). Mechano-chemical oscillations and waves in reactive gels. Rep. Prog. Phys. 75, 066601. doi: 10.1088/0034-4885/75/6/066601
Yashin, V. V., Suzuki, S., Yoshida, R., and Balazs, A. C. (2012b). Controlling the dynamic behavior of heterogeneous self-oscillating gels. J. Mater. Chem. 22, 13625–13636. doi: 10.1039/c2jm32065g
Yoshida, R. (2010). Self-oscillating gels driven by the belousov–zhabotinsky reaction as novel smart materials. Adv. Mater. 22, 3463–3483. doi: 10.1002/adma.200904075
Yuan, G., Wang, G., and Chen, S. (2005). Control of spiral waves and spatiotemporal chaos by periodic perturbation near the boundary. EPL (Europhys. Lett.) 72, 908. doi: 10.1209/epl/i2004-10553-2
Zhang, H., Hu, B., and Hu, G. (2003). Suppression of spiral waves and spatiotemporal chaos by generating target waves in excitable media. Phys. Rev. E 68, 026134. doi: 10.1103/PhysRevE.68.026134
Zhang, H., Li, B.-W., Sheng, Z.-M., Cao, Z., and Hu, G. (2006). The effect of mechanical deformation on spiral turbulence. EPL (Europhys. Lett.) 76, 1109. doi: 10.1209/epl/i2006-10391-2
Zhang, H., Ruan, X.-S., Hu, B., and Ouyang, Q. (2004). Spiral breakup due to mechanical deformation in excitable media. Phys. Rev. E 70, 016212. doi: 10.1103/PhysRevE.70.016212
Zimmermann, M., and Kalusche, D. (2001). Fluctuation in autonomic tone is a major determinant of sustained atrial arrhythmias in patients with focal ectopy originating from the pulmonary veins. J. Cardiovasc. Electrophysiol. 12, 285–291. doi: 10.1046/j.1540-8167.2001.00285.x
Keywords: arrhythmias, fibrillation, ventricular model, wave-dynamics, spiral turbulence, periodic deformation, low-amplitude pulses
Citation: Nayak AR and Pandit R (2014) Spiral-wave dynamics in ionically realistic mathematical models for human ventricular tissue: the effects of periodic deformation. Front. Physiol. 5:207. doi: 10.3389/fphys.2014.00207
Received: 29 September 2013; Accepted: 14 May 2014;
Published online: 10 June 2014.
Edited by:
Zbigniew R. Struzik, The University of Tokyo, JapanReviewed by:
Mark Potse, Maastricht University, NetherlandsChristian Zemlin, Old Dominion University, USA
Copyright © 2014 Nayak and Pandit. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Rahul Pandit, Centre for Condensed Matter Theory, Department of Physics, Indian Institute of Science, Bangalore 560012, India e-mail:cmFodWxAcGh5c2ljcy5paXNjLmVybmV0Lmlu
 Alok R. Nayak
Alok R. Nayak Rahul Pandit
Rahul Pandit