- 1Clinic for Cardiac Surgery, Heart Center Leipzig, University Leipzig, Leipzig, Germany
- 2Nora Eccles Harrison Cardiovascular Research and Training Institute, University of Utah, Salt Lake City, UT, USA
- 3Clinic for Pediatric Cardiology, Heart Center Leipzig, University Leipzig, Leipzig, Germany
- 4Clinic for Cardiology, Heart Center Leipzig, University Leipzig, Leipzig, Germany
- 5Hospital for Children and Adolescents, University of Leipzig, Leipzig, Germany
Coordinated electrical activation of the heart is essential for the maintenance of a regular cardiac rhythm and effective contractions. Action potentials spread from one cell to the next via gap junction channels. Because of the elongated shape of cardiomyocytes, longitudinal resistivity is lower than transverse resistivity causing electrical anisotropy. Moreover, non-uniformity is created by clustering of gap junction channels at cell poles and by non-excitable structures such as collagenous strands, vessels or fibroblasts. Structural changes in cardiac disease often affect passive electrical properties by increasing non-uniformity and altering anisotropy. This disturbs normal electrical impulse propagation and is, consequently, a substrate for arrhythmia. However, to investigate how these structural changes lead to arrhythmias remains a challenge. One important mechanism, which may both cause and prevent arrhythmia, is the mismatch between current sources and sinks. Propagation of the electrical impulse requires a sufficient source of depolarizing current. In the case of a mismatch, the activated tissue (source) is not able to deliver enough depolarizing current to trigger an action potential in the non-activated tissue (sink). This eventually leads to conduction block. It has been suggested that in this situation a balanced geometrical distribution of gap junctions and reduced gap junction conductance may allow successful propagation. In contrast, source-sink mismatch can prevent spontaneous arrhythmogenic activity in a small number of cells from spreading over the ventricle, especially if gap junction conductance is enhanced. Beside gap junctions, cell geometry and non-cellular structures strongly modulate arrhythmogenic mechanisms. The present review elucidates these and other implications of passive electrical properties for cardiac rhythm and arrhythmogenesis.
Introduction
Although the heart can be considered as a simple mechanical pump, this pump is a highly complex system involving mechanical, electrical, active, passive, and endocrine factors. Many of these factors are subject to remodeling processes in cardiac disease and, thus, are not necessarily constant. This review focuses on remodeling of the passive electrical properties of the heart and its importance for arrhythmogenesis.
Passive electrical properties of cardiac tissue comprise the specific resistance of intracellular and extracellular spaces as well as membrane capacitance. These are strongly influenced by tissue structure. This involves size, shape and arrangement of cardiac cells, including myocytes and non-myocytes, as well as connective tissue, extracellular and intracellular volume conductors and gap junctions. Moreover, anisotropy and inhomogeneities in the spatial (or in some cases temporal) distribution of these factors are of importance.
Electrical anisotropy in the heart refers to differing specific resistances in longitudinal and transverse fiber direction. The elongated shape of myocytes and intercellular coupling mainly at cell poles result in lower longitudinal than transverse resistance. This applies both to the extra- and intracellular space. Spatial inhomogeneities in cardiac tissue, e.g., zones with enhanced deposition of collagen, (fibrosis, which increases with age), lead to a spatial variation of these resistances, which is referred to as non-uniformity. In consequence, cardiac tissue can be considered as non-uniform and anisotropic.
A simple model of the electrical equivalent circuit of cardiac tissue is a cable formed by cells coupled in series via Ohmic resistors. Each cell in this cable represents a resistor with a parallel capacitor (for review see Weidmann, 1990). The change in voltage is a function of distance (x) according to Vx = V0 exp(−x/λ) with the length constant λ = (rm/ri). The membrane resistance, rm, is expressed in Ωcm, the intracellular longitudinal resistance, ri, in Ω/cm. The input resistance at x = 0 can be described as rinput = V0/I = riλ. Due to the fiber geometry with radius a, the specific membrane resistance Rm equals 2 π arm [Ωcm2] and specific intracellular resistance Ri = πa2ri [Ωcm]. The specific membrane capacitance can be described as Cm = τ/Rm with the time constant τ. In a multicellular preparation with parallel running fibers the longitudinal resistance of the extracellular space ro also has to be considered. For these conditions λ is reflected by λ = (rm/(ri + ro)) and the conduction velocity θ depends on θ = (1/(τfootCm(ri + ro)). This cable theory was originally formulated for nerve axons (Hodgkin and Rushton, 1946) and later on for Purkinje fibers (Weidmann, 1952). It holds true for a continuous cable (Figure 1).
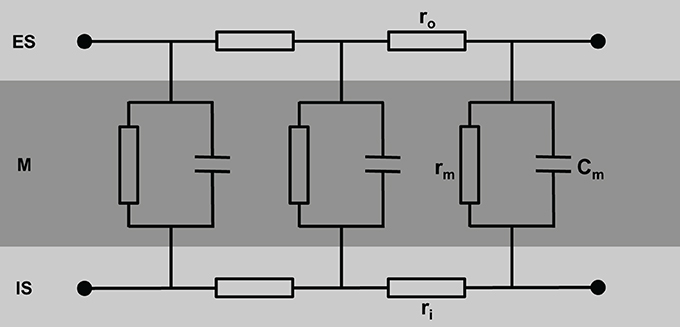
Figure 1. Schematic view of cardiac tissue modeled as a simple cable consisting of intracellular (ri) and extracellular (ro) resistors and capacitors (Cm). ES, extracellular space; M, cell membrane; IS, intracellular space.
However, this is oversimplifying, since the intracellular space of adjacent cells is connected via gap junction channels. A cluster of single gap junction channels forms a gap junction, which connects the cytoplasm of two adjacent cells by the resistance RGJ (see Figure 2). The gap junction resistance is higher than the resistance of the cytoplasm. Furthermore, the resistance ro of the extracellular space is not homogeneous. The resistance Rcleft of the extracellular cleft between two cells near intercalated disks (2–5 nm wide) can be assumed to differ significantly from the much wider clefts elsewhere (>20 nm) not only because of its small width, but also because it contains anchoring proteins and gap junction channels. Therefore, the cable necessarily becomes discontinuous (Figure 2).
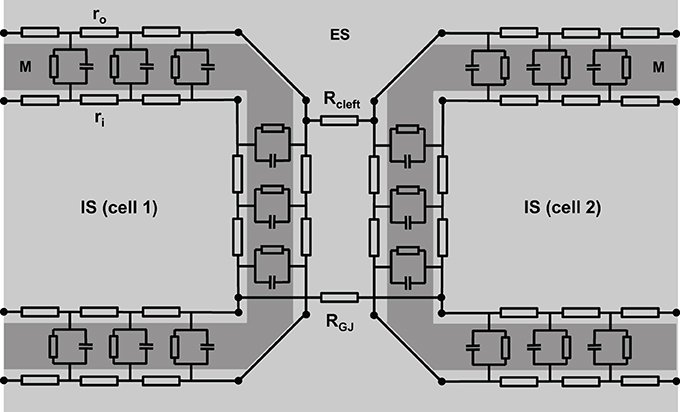
Figure 2. A more realistic scheme of coupled cardiac cells considering discontinuous properties. The cell membrane (M) is represented by a series of resistor-capacitor circuits, connecting the extracellular space (ES) with the intracellular space (IS). They are interconnected within one cell via extracellular (ro) and intracellular (ri) resistors. Gap junction resistance (RGJ) connects the intracellular spaces of adjacent cells, while extracellular coupling is realized via the resistance of the extracellular cleft (Rcleft).
Fast sodium channels are essential for impulse propagation. Opening of these channels at the beginning of an action potential generates a depolarizing current (INa), which is responsible for the fast voltage upstroke. Therefore, INa plays a key role in the propagation of action potentials from cell to cell. It has been shown that these sodium channels are clustered at cell-cell contact zones (Kucera et al., 2002; Maier et al., 2004). This further complicates a correct description of the electrophysiological behavior at cell poles. It also shows that modeling cardiac tissue as a continuum is only reasonable on a macroscopic scale.
Although the equivalent circuit of a discontinuous cable depicted in Figure 2 is more complex than the simple cable, it remains an oversimplification because it does not reflect the geometrical properties of cells and tissue. Cardiomyocytes are typically not shaped like bricks or regular cylinders—as often assumed in mathematical tissue models—but, instead, are of irregular shape with branches interdigitating at the cell poles (Spach et al., 2000). Additionally, cell size shows some variation.
In this regard, it is important to consider the ratio between the cell surface Am and the gap junction conductance gGJ (Seidel et al., 2010): increased diameter of the cell can enhance longitudinal propagation velocity θL if gGJ is enhanced proportionally to Am. If gGJ remains constant, however, increased diameter reduces θL. This becomes clear when considering that Am is linearly related to the cell capacitance Cm. Thus, it is important to analyze the ratio of gGJ/Am in order to understand whether a change in cell size will enhance or reduce θL. Furthermore, transverse gGJ may contribute to longitudinal propagation, which cannot be described by a one-dimensional model (Seidel et al., 2010).
Next, we need to consider the three-dimensional nature of the myocardium and the uneven distribution of fibrotic material, mostly collagen fibers, and fibroblasts. Initially, fibroblasts have been considered electrically silent, but research in the past two decades indicates that electrical propagation seems possible. It has been suggested that myofibroblasts can slow conduction (Rohr, 2004, 2012). Furthermore, it has been shown experimentally that impulse propagation along fibroblast inserts was successful over distances up to 300 μm (Gaudesius et al., 2003). However, it needs to be noted that these cells—although not capable of producing action potentials—were coupled via gap junction channels (see below), while HeLa cells without gap junctions did not enable propagation. Thus, it seems that communication-deficient zones will cause propagation failure.
How are Cardiac Cells Coupled?
Since the discovery of cardiac gap junctions, which form intercellular channels connecting the cytoplasm of adjacent myocytes, it is established that they represent a low-resistance pathway for electrical propagation (Page and Shibata, 1981). However, gap junction resistance is still higher than the cytoplasmic resistance. Accordingly, impulse propagation along the membrane of one cell is faster than over the intercellular gap junction. The time delay at gap junctions is about 0.21–0.27 ms, and ~0.05–0.1 ms at the cell membrane (Fast and Kléber, 1993; Hubbard et al., 2007).
Coupling Without Gap Junctions
If one considers neighbored cells as closely packed capacitors, ephaptic coupling via electrical fields might be possible (Sperelakis, 1979). Electrical field coupling (Sperelakis and Mann, 1977) or ephaptic coupling (Copene and Keener, 2008) refers to the initiation of an action potential in a non-activated downstream cell by the electrical field caused by an activated upstream cell. This kind of impulse propagation does not require cytoplasmic connections via gap junctions. It might occur at the intercalated disks, where the membranes of adjacent cells are only 2–5 nm apart.
Accumulation of K+ in the junctional extracellular cleft seems necessary to allow sodium channels at the intercalated disk of the upstream cell to fire some microseconds earlier than the channels in the remaining surface membrane. In a theoretical model, this was necessary for effective coupling (Sperelakis and Mann, 1977). However, at present it is unclear whether ephaptic coupling contributes to action potential propagation in normal tissue. Computer simulation studies indicate that, under certain conditions, ephaptic coupling may play a role, but strongly depends on parameters like sodium channel conductance and distribution, and the width of the extracellular cleft at the intercalated disk (Mori et al., 2008; Lin and Keener, 2010). Recent data show that in the perinexus Cx43 gap junctions interact with Na(v)1.5 channels (Rhett et al., 2012). The perinexus has therefore been suggested as the anatomical correlate for ephaptic coupling, the ephapse (Rhett et al., 2013; Veeraraghavan et al., 2014). Local accumulation and shifts of ions may alter local membrane potential. However, there is a lack of experimental evidence, because these local changes on a nanometer scale are difficult to measure. Hence, it remains unclear whether ephaptic coupling significantly contributes to cardiac impulse propagation, especially when considering that, according to the Guoy-Chapman theory, the electrical field near a charged membrane falls to zero within 2–3 nm (Carnie and McLaughlin, 1983).
Experimental evidence suggests that cells need to be coupled by gap junctions to allow the propagation of an electrical impulse: Weingart and Maurer (1988) showed that after manipulating two cells into intimate side-to-side contact, initially there was no transmission of electrotonic potentials or action potentials from one cell to the other. Action potential transfer became possible only after the cells had established new gap junctions. This experiment seems to rule out non-gap junctional mechanisms of intercellular action potential spreading. However, recent evidence was presented for another mechanism of electrical cell-to-cell coupling. Membrane-tunneling nanotubues were suggested as cytosolic bridges between cells (He et al., 2011). This theory, however, still needs further investigation.
Connexins and Gap Junctions
Cardiomyocytes and fibroblasts are homocellularly interconnected by gap junction channels (for review see Dhein, 1998, 2004). Heterocellular coupling between cardiomyocytes and fibroblasts, however, has only been shown in cell culture (Goshima and Tonomura, 1969; Gaudesius et al., 2003) or in the sinus node (Camelliti et al., 2004), but not in living ventricular myocardium. Cells can communicate via these gap junction channels. Each channel is about 150 Å long. The membranes of the two cells are separated in this area by a gap of nearly 20 Å, which is spanned by the channel subunits (Beyer et al., 1995). Cardiomyocytes are connected by intercalated disks, which contain three main structures: the fascia adherens, the desmosome (sometimes called macula adherens), and the nexus. While the fascia adherens is composed of two lipid bilayers separated by 200–300 Å, the desmosome is an almost laminated structure formed by the two membranes. At the nexus both cells are in most intimate contact. This zone contains the gap junction channels, which typically are clustered (Gourdie et al., 1990). A gap junction channel comprises of two hemichannels, which are provided by either cell. Each hemichannel is composed of 6 protein subunits, the connexins. Thus, a gap junction channel is a dodecameric channel with a pore in the center (Figure 3). Connexins belong to a large protein family with at least 21 isoforms in humans. The connexin protein is a four-transmembrane domain protein with an intracellular N- and C-terminal, 2 extracellular loops, and one intracellular loop. For details see Makowski et al. (1977); Chen et al. (1989); Perkins et al. (1997). The most variant part is the C-terminus, which also serves as binding partner for a number of protein kinases, which can control connexin trafficking, assembly, dis-assembly and single channel conductance by phosphorylation. Connexins are characterized by their molecular weight. For instance, Cx43 refers to the connexin with a molecular weight of 43 kDa. The family of connexins is divided with regard to the amino acid sequences and C-terminal length into five subgroups, i.e., α, β, γ, δ, and ε. The genetic names are composed of a “GJ” followed by the family and a number. Thus, Gjα1 means Cx43 which was the first connexin being characterized from the α-group (see http://www.genenames.org/genefamily/gj.php for reference). For a detailed overview on connexins (see Nielsen et al., 2012).
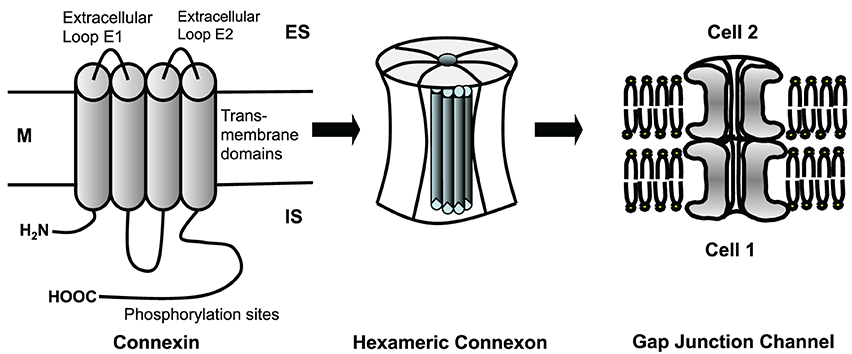
Figure 3. Connexins are four-transmembrane proteins with two extracellular loops and one intracellular loop. They build hexameric connexons (hemichannels), which dock to a connexon of an adjacent cell forming a complete, dodecameric gap junction channel. M, cell membrane; ES, extracellular space; IS, intracellular space.
In the heart the predominant connexin isoform is Cx43, which is found in ventricles and atria. Cx40 is mainly found in atrium and in the specific conduction system. Cx45 is mainly found in early developmental stages, in the conduction system, and between fibroblasts and cardiomyocytes. Connexins are synthesized in the rough endoplasmatic reticulum, folded and transported to the trans Golgi network, where they are oligomerized to hexameric hemichannels (connexons). These hexameres are then transported to the plasma membrane and inserted. It is assumed that they flow with lipid rafts within the membrane and accumulate in areas where N-cadherin and zonula occludens-1 protein (ZO-1) are present. At these sites they dock to other hexameres of the neighboring cell forming the gap junction channel. If the connexins are poly-phosphorylated at certain amino acids of the C-terminal, they can be ubiquitinylated and then degraded. Besides the classical proteosomal degradation lysosomal degradation also has been described.
Regulation of gap junction coupling can be realized by modulating the number of channels, i.e., by influencing synthesis, trafficking docking or degradation, or by changes of the single channel conductance. For a detailed review, see Dhein (2004); Salameh and Dhein (2005); Axelsen et al. (2013). Channel conductance depends on the connexin isoform, the phosphorylation state of the connexin, and on the connexin composition of the channel (e.g., homomeric, heteromeric) (Harris, 2001; Moreno, 2004). Interestingly, besides an open and a closed state a single channel can exhibit several conductance states (Harris, 2001; Bukauskas and Verselis, 2004). Moreover, heterotypic channels consisting of hemichannels of different connexin isoforms can show asymmetric voltage-dependent gating. Asymmetric gating refers to the observation that the conductance-to-voltage relationship depends on the polarity of the transjunctional voltage (see e.g., Bukauskas and Verselis, 2004; Schulte et al., 2008).
Anisotropy and Non-Uniformity (Inhomogeneity)
Anisotropy is defined as the property of being directionally dependent. With regard to cardiac tissue the term is mostly used to describe that specific longitudinal resistivity is lower than transverse resistivity. However, anisotropy values for extracellular and intracellular resistivity differ significantly. Further properties to be taken into account are discontinuity, which means that the fibers are separated by intercalated disks (in contrast to a continuous cable), and non-uniformity, which describes the spatial variation of anisotropy. The latter is due to variations in cellular morphology, cell types (myocytes and non-myocytes) and fibrotic material (collagen) or other non-conducting structures like connective tissue, fat, vessels etc. The difference between uniform and non-uniform anisotropy has many consequences for the pathophysiology of arrhythmia (Spach and Dolber, 1990).
Intracellular resistivity is higher in transverse than in longitudinal direction. Thus, anisotropy in the intracellular space ranges from ~5 to 10 (Clerc, 1976; Roberts and Scher, 1982; Stinstra et al., 2005) and mainly results from cardiomyocyte shape and cellular distribution of connexins. In many cardiac diseases the expression of connexins (Cx43, Cx40, Cx45) is altered. Enhanced levels of Cx43 have been found in cardiac hypertrophy, while in chronic infarction and severe heart failure Cx43 levels are reduced (Severs, 1994; Kostin et al., 2003; Severs et al., 2006). Alterations of Cx43 and Cx40 have been described in atrial fibrillation (Dupont et al., 2001; Polontchouk et al., 2001; Boldt et al., 2003). Since in atrial fibrillation both increased and decreased Cx43 levels have been found, it was suggested that the absolute level may depend not only on the type of arrhythmia but also on the concomitant cardiac pathology (Dhein et al., 2011). In many cardiac pathologies, e.g., chronic atrial fibrillation, cardiac hypertrophy, heart failure and after myocardial infarction, connexins were no longer restricted to cell poles but also expressed at the lateral cell membrane (Polontchouk et al., 2001; Kostin et al., 2002; Cabo et al., 2006). It remained unclear for years whether these lateral gap junctions are functional. In the case of atrial fibrillation, electrophysiological mapping together with immunohistology showed that the lateralization was accompanied by enhanced transverse conduction velocity θT (Dhein et al., 2011), suggesting that at least a fraction of these lateral gap junctions is functional.
The concept of electrical anisotropy also applies to resistivity of the extracellular space and, besides influencing impulse propagation, has a strong effect on the distribution of epicardial potentials (Roberts and Scher, 1982; Johnston et al., 2001; Stinstra et al., 2005; Schwab et al., 2013). Experimental and computational studies reported anisotropies in the extracellular space ranging from 1.5 to 3.5 (Clerc, 1976; Roberts et al., 1979; Stinstra et al., 2005; Hand et al., 2009). Schwab et al. (2013) distinguished between the two transverse directions (vertical or parallel to the epicardial surface) suggesting differences in anisotropy and pathological remodeling. Their results also indicate spatially non-uniform anisotropy in ventricular myocardium after infarction.
Evidence is growing that the extracellular space, including fibroblasts, plays an important role in cardiac disease and related electrophysiological changes for review see Pellman et al. (2010); Yue et al. (2011); Weber et al. (2013). This is also reflected in the use of bi-domain or multi-domain models for the simulation of cardiac impulse propagation, taking extracellular conductivity and fibroblasts into account (Jack et al., 1975; Peskoff, 1979; Geselowitz and Miller, 1983; Roberts et al., 2008; Sachse et al., 2009). The group of Veeraraghavan et al. (2012) suggested that the effect of gap junction conductance on impulse propagation is modulated by the fraction of extracellular space. They showed that the percentage of extracellular volume was inversely correlated to conduction velocity. This result is surprising because increased extracellular volume should result in lower extracellular resistivity and, according to cable theory, lead to faster propagation. They found that these effects were especially pronounced in transverse fiber direction. However, to increase extracellular volume they used mannitol, which also reduced cell width. A reduction in cell width, however, can strongly slow transverse velocity (Seidel et al., 2010; Toure and Cabo, 2010). Furthermore, with decreasing velocity the effect of gradual uncoupling (higher gap junction resistance) increases because of a switch from continuous to discontinuous propagation, preferably in transverse fiber direction (Seidel et al., 2010). These results show that effects of intra- and extracellular space on impulse propagation are complex and not easy to predict. It remains challenging to measure extracellular conductance and anisotropy in intact cardiac tissue because due to transmembrane channels the measured current between two electrodes will always contain an intracellular component.
As a result of non-uniformity and anisotropy in cardiac tissue fractionated waveforms develop. These have been interpreted as the reflection of discontinuous propagation where each of the multiple negative peaks represents the activation of a small group of fibers (Spach and Dolber, 1986, 1990). Interestingly, aging leads to a change in the tissue's biophysical properties and is associated with increased non-uniformity. This is due to the deposition of collagen fibers between the cells resulting in predominant uncoupling of side-to-side connections (Spach and Dolber, 1986, 1990; Dhein and Hammerath, 2001).
Source-Sink Problem
When an action potential propagates, the action potential upstroke velocity and amplitude are larger in the case of transverse propagation together with a shorter time constant of the foot potential τfoot. From a theoretical point of view this could mean that longitudinal propagation is more vulnerable to conduction block because of its lower upstroke velocity and amplitude. The increase in upstroke velocity in transverse propagation results from higher resistivity and reduced space constant in this direction. Thus, less current is lost to the neighboring cells (Delmar et al., 1987).
In order to elicit an action potential in a cell, it must receive a depolarizing current from an adjacent, activated cell. The activated cell acts as current source, while the non-activated cell is a current sink with the voltage difference being the driving force for this current. The current transfer is mainly realized via gap junction channels and, to some extent, via the extracellular space. Whether enough current can be transferred to activate a cell is a complex and geometric problem: if a small source (e.g., a tiny strand of activated cardiomyocytes) meets a large sink (e.g., a large area of non-activated cardiomyocytes) the current will flow radially from the activated site to many non-activated sites. Hence, the source current is distributed to many neighboring cells and in each of these the accumulated charge may be too low to trigger an action potential. This will cause conduction failure (Rohr et al., 1997; Rohr, 2004, 2012; Lee and Pogwizd, 2006). In this situation a paradoxical effect can occur: reducing gap junction conductance may preserve conduction by resolving the source-sink mismatch because less current is lost to adjacent sites (Rohr et al., 1997). This is, e.g., realized in the sinus node, where a small current source (sinus node) meets a large sink (atrium). At the sinus node/atrium border there is only little expression of connexins in interdigitating finger-like zones extending from the sinus node into the atrium (Joyner and van Capelle, 1986; Boyett et al., 2006). This reduces the sink because only a small current can flow to a small number of activation sites. In cable theory, this is represented by a smaller space constant leading to a lower capacitive load. On the other hand, if there is high gap junction coupling, the space constant increases leading to a high capacitive load (current sink) and a source-sink mismatch which can evoke conduction failure.
Shaw and Rudy (1997a,b) attempted to describe these phenomena mathematically by the safety factor (SF) of propagation as SF = Qc + Qout/Qin (=charge produced/charge consumed). If coupling is reduced gradually the safety factor first is enhanced as a result of the smaller space constant. However, if very low levels of coupling are reached, SF decreases until SF <1 and conduction failure occurs. This happens when gap junctions are almost closed or absent, because then not enough current can be transferred to an adjacent cell before the activated cell repolarizes. In contrast, if INa is reduced this will result in a progressive reduction of SF. However, propagation velocity will be reduced in both situations (Shaw and Rudy, 1997a,b).
Situations with source-sink problems generally occur when the curvature of the propagating wave front is high. Accordingly, they may be found at the end of Purkinje fibers, during propagation through small isthmuses, around obstacles, and during spiral wave re-entry. Furthermore, source-sink mismatch may occur at the border between normal cardiac tissue and an ischemic zone, when depolarizing current flows into the ischemic region. Since this region is usually non-excitable, it will act as a current sink and, consequently, reduce conduction velocity.
Arrhythmogenesis
Many definitions of arrhythmias are based on comparing a pathological with the normal heart rhythm. Bradyarrhythmia is a rhythm slower than normal, while tachyarrhythmia is faster than normal. Bradyarrhythmias are often caused by a block or delay of conduction within the specific conduction system, i.e., between sinus node and atrium, between atrioventricular node and bundle of His or within the bundles. If in these structures conduction is impaired, e.g., by a scar resulting from infarction, this will lead to delayed ventricular activation. However, the situation can be more complex involving source-sink problems. As described above, the propagation of an action potential from Purkinje fibers to the working myocardium represents a tissue expansion, which is generally prone to conduction block (Rohr et al., 1997). Both high sodium channel conductance and relatively low intercellular coupling increase conduction safety under these conditions. However, pathological changes like gap junction lateralization or cellular hypertrophy (increased sink), and reduced sodium channel availability (decreased source) can lead to unidirectional conduction block (Kléber and Rudy, 2004; Seidel et al., 2010). If unidirectional block occurs in a Purkinje fiber, this will slow ventricular activation and lead to an abnormal activation pattern. This is part of the reason why Purkinje fibers are considered key players in initiation and maintenance of ventricular arrhythmias (for review, see e.g., Boyden et al., 2010). Besides, unidirectional block can lead to reentry circles resulting in ventricular tachycardia or fibrillation. Thus, bradyarrhythmia can evolve into tachyarrhythmia.
Reentrant Activation
Reentry happens when the electrical activation follows a circular trajectory and is able to re-activate itself at the point of origin. It is a main cause of tachyarrhythmia. Several mechanisms for reentry are known. One common model is explained as follows: if at a bifurcation of the conducting system (e.g., the bifurcation in the anterior and posterior bundle branch) one branch acts as a unidirectional block, allowing conduction only from the periphery backwards, then activation may propagate along branch 2, thereafter across the ventricular muscle, and finally backwards via branch 1. The unidirectional block in this traditional consideration is thought to be caused by a prolonged refractory period in this area. Another classical example describes reentry as a wave which encircles an electrically inactive obstacle, e.g., a scar. This central zone can also be a permanently refractive area, steadily depolarized by the circulating wave, the “leading circle” (Allessie et al., 1977).
Detachment of the reentry wavefront from the obstacle can lead to spiral wave initiation. In this case, a usually non-stationary rotating source moves along a two- or three-dimensional trajectory. The waves initiated from this source show a typical spiral shape (Cabo et al., 1998). It has been shown that the trajectory of the spiral wave core and whether the wave is stable or not, depends strongly on tissue properties like excitability and non-uniformity (Pertsov et al., 1993).
A certain type of reentrant arrhythmia can originate from a situation in which two closely neighbored obstacles, e.g., collagenous strands or infarct scars, are located transverse to the direction of propagation, with only a small gap of low excitability in between. This structure forces the activation wave to circumvent the obstacles laterally. Behind, the tissue will be activated from both sides causing wavefront collision near the gap. The collision reduces the current sink and increases the source now allowing the activation to propagate through the gap and re-activate the area in front of the obstacles. This kind of reentry has been called “figure-of-eight” reentry mechanisms for ventricular arrhythmias. It may occur in particular when conduction velocity is low (el-Sherif et al., 1987; Lazzara, 1988). See Figure 4 for illustration.
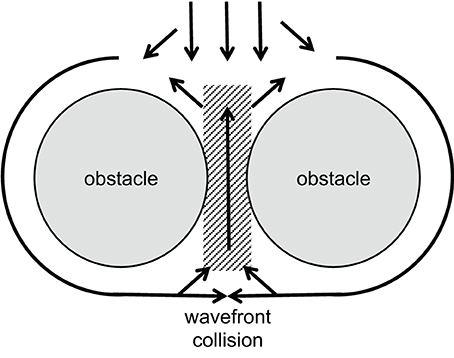
Figure 4. Schematic illustration of a figure-of-eight reentry. A wavefront approaches two obstacles separated by a small gap of low excitability (gray area). Conduction is blocked in front of this gap, separating the wavefront. Behind the obstacles, wavefront collision occurs. This increases the current source while reducing the sink and, thus, allows activation of the area between the obstacles. If conduction is slow enough, this leads to reentry in front of the obstacles as shown by el-Sherif et al. (1987).
These explanations illustrate very well the observed phenomena, although underlying mechanisms may be a bit more complicated (see below).
Calcium-Induced Depolarizations
Under certain pathological conditions like increased adrenergic stimulation or ischemia-reperfusion, cellular calcium overload occurs, leading to spontaneous diastolic calcium waves. These waves reflect spontaneous calcium release from the sarcoplasmic reticulum (Kimura et al., 1984; Marban et al., 1986). The sodium-calcium exchanger then operates in the forward mode generating a depolarizing current. The resulting increase of the membrane potential is often referred to as delayed afterdepolarization (DAD). DADs are considered as potential triggers for arrhythmia because, if big enough, they may initiate an action potential and, subsequently, arrhythmogenic ectopic extrasystoles (Lederer and Tsien, 1976; Xie et al., 2010). However, while it has been shown that a DAD can lead to an action potential in isolated cells (Capogrossi et al., 1987), it remains a matter of debate how a DAD in tissue can overcome the obvious source-sink mismatch (Xie et al., 2010; Tveito et al., 2012). A single cardiomyocyte is, on average, coupled to 4–6 adjacent cells. Under normal conditions, it is therefore impossible that an action potential is initiated. Here, the source-sink mismatch protects from arrhythmogenesis. To overcome the mismatch, there must be a reduced sink via uncoupling or an increased source via DAD synchronization between adjacent cells. Both mechanisms have been suggested to appear under conditions of gap-junctional remodeling (Morley et al., 2005) or adrenergic stimulation (Myles et al., 2012), respectively. Following this argumentation, enhanced coupling should increase the sink and may reduce the risk of arrhythmia. Interestingly, it was shown that the antiarrhythmic peptide AAP10 enhanced gap junction conductance and prevented from certain ventricular arrhythmia (Dhein et al., 1994; Müller et al., 1997; Jozwiak and Dhein, 2008; Hagen et al., 2009). This suggests that increasing gap junction conductance via drug therapy might be an effective strategy for certain forms of arrhythmia. Otherwise, closing of gap junctions could be a mechanism of cardiomyocytes to protect neighboring cells from further damage caused, e.g., by acidosis or calcium overload. It has been shown that gap-junction blockers like heptanol decrease the infarct size after myocardial ischemia (Miura et al., 2004). It is, therefore, surprising that the same effect was shown for gap junction openers like rotigaptide (Haugan et al., 2004), while other studies detected no influence on infarct size (lbye, Nielsen, Petersen, Harlow and Holstein-Rathlou, Xing et al., 2003). Further research is required in this field to better understand these effects and to develop novel anti-arrhythmic drug therapies.
Effects of Hypertrophy
Cardiac hypertrophy is associated with electrophysiological remodeling and an elevated risk of severe arrhythmia (Tomaselli and Marbán, 1999; Kozhevnikov et al., 2002). This is partly due to changes in cellular electrophysiology like remodeling of potassium channels leading to increased action potential duration and elongated QT intervals (Beuckelmann et al., 1993; Swynghedauw et al., 2003). Whether isolated cellular hypertrophy has pro-arrhythmic effects is, therefore, hard to assess experimentally. However, mathematical models have shown that increased cell capacitance increases capacitive load and the discontinuity of action potential propagation. This steepens the relationship between gap-junction conductance and conduction velocity elevating the risk of conduction block both due to uncoupling and source-sink mismatch (Seidel et al., 2010). Furthermore, hypertrophy leads to increased length or diameter of cardiomyocytes, which has both been shown to influence conduction (McIntyre and Fry, 1997; Spach et al., 2000; Seidel et al., 2010). This suggests that hypertrophy itself, in addition to the associated cardiac disease, can be an arrhythmogenic substrate.
Effects of Gap Junctions—Lateralization and Remodeling
Remodeling of the geometrical distribution of gap junctions occurs in a variety of cardiac diseases (Polontchouk et al., 2001; Kostin et al., 2004; Cabo et al., 2006; Salameh et al., 2009). In most cases the fraction of lateral connexins increases. Provided that these connexins form functional channels, they could contribute to arrhythmogenic alterations in impulse propagation (Cabo et al., 2006; Seidel et al., 2010). However, it is discussed controversially since years whether lateral connexins form fully functional gap junction channels. They might as well form hemichannels, which are assumed to be closed in normal physiological situations, or represent a pool of connexins/hemichannels floating in the membrane until they find anchoring site where they form a complete channel with the hemichannel of a neighboring cell. Pathophysiological situations with lateralized gap junctions comprise atrial fibrillation (Polontchouk et al., 2001; Kostin et al., 2002) cardiomyopathy (Kostin et al., 2003, 2004; Severs et al., 2006; Salameh et al., 2009) or myocardial infarction (Cabo et al., 2006). A study investigating atrial tissue from patients suffering from chronic atrial fibrillation found connexin lateralization accompanied by enhanced transverse conduction velocity. Moreover, in the same study metoprolol treatment led to a lower degree of lateralization and lower transverse conduction velocity (Dhein et al., 2011). This provides evidence that at least parts of these connexins form functional lateral gap junctions, although electrode spacing of 1 mm did not allow to precisely link an activation propagation to a certain cell shape. Direct proof needs (a) injection of dyes like Lucifer Yellow into cells within a vital layer of atrial tissue (metabolic coupling), and (b) microscopic mapping of electrical activation with a resolution <10 μm. This should be complemented with connexin immunohistology and electron microscopy of the mapped area and exact superimposition. Theoretical studies have shown potential effects of gap junction lateralization on action potential propagation and possible arrhythmogenic mechanisms. High side-to-side coupling of cardiomyocytes may favor conduction block due to source-sink mismatches (Seidel et al., 2010), while low side-to-side coupling has been suggested to unmask inhomogeneities (Müller and Dhein, 1993; Seidel et al., 2010).
Non-uniformity and anisotropy in cardiac tissue can cause fractionated waveforms. This is increased by a reduction in gap junction protein expression resulting in progression of irregular activation patterns as shown by de Bakker and van Rijen (2006).
Effects of Fibrosis and Anisotropic Inhomogeneity
Fibrosis is a very common process in cardiac remodeling. When cardiomyocytes are impaired by a pathological event and subsequently undergo apoptosis or necrosis, the remnants are eliminated in the context of an inflammatory process. Finally, the area formerly filled by cardiomyocytes is replaced with connective tissue. This includes fibroblasts and extracellular matrix, mainly collagen. This typical repair process helps to maintain cardiac shape and allows maintenance of intracardiac systolic pressures of about 120–150 mmHg. However, a disadvantage is that this replacement tissue is electrically silent, non-contractile and stiffer than normal myocardium. Fibrotic strands typically are between the cardiomyocytes, running parallel to their longitudinal axis (aligned to the fiber axis), thus separating laterally neighbored cardiomyocytes. Occasionally, there will be a remnant connection between cardiomyocytes, so that the activation pattern follows a zig-zag course with reduced transverse conduction velocity. In situations of a longitudinally propagating wavefront, this type of fibrosis will have only little effect. However, if the wavefronts travels transverse to the longitudinal axis, the fibrotic strand will form an obstacle causing “wavefront curvature” because the traveling wavefront will curve around this insulator (Fast and Kléber, 1997). A similar situation can occur at sudden changes in fiber direction (see “Texture of the Heart”).
The biophysical properties of the fibrotic cardiac tissue can be described as strongly anisotropic (longitudinal resistance << transverse resistance), discontinuous (cells are separated from each other) and non-uniform (local changes in the anisotropic properties) (de Bakker et al., 1993, 1996). The typical ECG under these conditions of highly discontinuous anisotropic tissue exhibits fractionated QRS complexes with reduced amplitude in the case of reduced myocardial mass (Spear et al., 1979; de Bakker et al., 1988).
Fibroblasts, although non-excitable, may allow electrotonic spread of activation, but with considerable delay. Gaudesius et al. (2003) showed in a strand of cardiomyocytes with an interponate of some fibroblasts successful propagation of the action potential, but with a clear delay at the fibroblast site. They showed that the activation can be successfully transmitted over a distance of up to 300 μm filled by fibroblasts. However, it needs to be mentioned that in pathophysiological situations these distances will not be filled with fibroblasts alone but also with a high fraction of collagen. Fibroblasts might couple via gap junctions to cardiomyocytes, which is presumably realized by Cx45 or Cx43, thereby connecting the low-resistance intracellular spaces of fibroblasts and cardiomyocytes. If there is a high fraction of collagen, however, continuous gap junction coupling between myocytes and fibroblasts over long distances becomes very unlikely. Additionally, the ohmic resistance of the extracellular space will be increased. This can lead to conduction failure. It is difficult to estimate the amount of collagenous tissue necessary for electrical isolation, but it will depend on the number of cells in relation to the mass of collagen. Furthermore, it remains unclear whether fibroblast-myocyte coupling occurs in-vivo (Kohl and Gourdie, 2014). So far, only one study provides convincing evidence for this possibility in the sinuatrial node (Camelliti et al., 2004), whereas other studies failed to identify heterocellular coupling in the ventricle (Baum et al., 2012).
Different types of fibrosis can be distinguished regarding the texture of collagen deposition: it may be diffuse with small, short, abundant collagenous strands or it may be patchy with larger areas of thick and long collagenous strands. It was shown that the latter type has a higher impact on activation propagation (Kawara et al., 2001). In a computer simulation, discontinuities could be minimized until they vanished when the fibrotic texture was progressively altered from a patchy type to a diffuse type (Pertsov, 1997).
Texture of the Heart
Of note, myocardial fiber direction changes from the endocardium to the epicardium by nearly 90° (Greenbaum et al., 1981). In a normal, non-diseased heart this is a gradual change. However, in diseased hearts, e.g., in cardiomyopathy, myocyte disarray has been observed which leads to zones with a sudden change in fiber direction within a short distance. This can result in a sudden change in resistance since a wavefront traveling along the fiber axis suddenly encounters transverse myocyte strands, so that the electrical resistance for the wave changes. This will cause delay of propagation or wavefront curvatures or discontinuities or unidirectional block (Spach et al., 1982). Interestingly, a similar situation of sudden changes in fiber direction was observed in canine and human pulmonary veins. In this area atrial fibrillation is usually initiated, and this structural particularity may contribute to the arrhythmogeneity of this region (Hocini et al., 2002; Arora et al., 2003).
Non-Excitable Regions
Beside myocardial fibers, non-excitable tissue components are present in the heart such as connective tissue (see above) or vessels or fat tissue. These non-excitable obstacles “may cause the formation of self-sustained vortices and uncontrolled high-frequency excitation in normal homogeneous myocardium” (Cabo et al., 1998). In this process the wavefront is thought to detach from the obstacle and form a vortex, i.e., spiral waves are initiated. This process of detachment and shedding of vortices is assumed to depend on wavefront curvature (Cabo et al., 1998).
However, there is another characteristic of non-excitable tissue regions: if a wavefront with low curvature propagates, current flows mainly along the potential gradient to the front. Hardly any current is lost to the sides or the area behind the wavefront, because there is no potential gradient. If the wave approaches a non-excitable, electrically insulated obstacle, current flowing to the front will decrease. Thus, in front of an obstacle less current is lost than during normal propagation. As a consequence, the action potential will be prolonged in this area due to the reduced current loss. In contrast, after the wave has surrounded the obstacle it meets unexcited tissue in front and lateral to the wavefront. Thus, current is lost to the sides and the front. As a result, action potential duration will be increased in front and shortened behind the obstacle. It has been shown by epicardial mapping around a coronary vessel that this is indeed the case (Gottwald et al., 1998). For illustration, see Figure 5. Interestingly, this study also showed that in ischemic tissue the difference in action potential duration before and behind an obstacle significantly increases due to slowed conduction. This is a consequence of the ischemic depolarization leading to reduced sodium channel availability, prolonging the time during which current can pass from the excited site to the non-excited sites. This will increase the current loss. Similarly, reduction in sodium channel conductance was shown to enhance local dispersion (variance in action potential duration) at zones of reduced gap junction coupling in a computer simulation (Müller and Dhein, 1993). It seems obvious that, in its extreme form, this phenomenon may lead to unidirectional block, which is a potential trigger of arrhythmia.
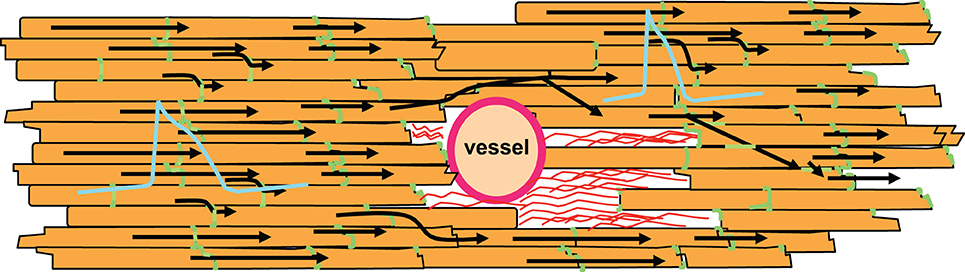
Figure 5. Non-excitable regions like coronary vessels or connective tissue (shown as red strands around the vessel) lead to changes in action potential duration. In front of the non-excitable area, current sink decreases leading to longer action potential duration. In contrast, behind this area current sink is increased, which shortens the action potential. Action potential shapes are illustrated in blue, gap junctions in green, cardiomyocytes in orange. Black arrows indicate impulse propagation.
Changes of the Biophysical Properties by Mechanical Forces
Mechanical stimuli will lead to local strain of cells, which means an alteration of cell length and length-to-width ratio. In computer simulations it has been shown that changes in cell geometry have an effect on conduction velocity (Spach et al., 2000; Seidel et al., 2010). A local stretch therefore can alter the local pathways of activation (Dhein et al., 2014). On the other hand, it has been shown that structural heterogeneities can affect stretch-induced ventricular arrhythmia (Seo et al., 2010). Wall thickness can be heterogeneously distributed over the ventricle, which will result in a regional modulation of a mechanical stimulus so that regional strain varies. This strain may activate stretch-activated ion channels thereby eliciting cardiac arrhythmia. It was recently shown that local left ventricular stretch leads to local delays in activation so that early and late activation occur closely beside each other (Dhein et al., 2014).
A sudden mechanical insult, an impact or blow by a small spheroid may induce ventricular fibrillation (Kalin et al., 2011). Such an insult is known as commotio cordis. The impact is thought to induce heterogeneity in repolarization within the wall together with a premature depolarization trigger.
Implications for the Clinics (Age)
In the daily clinic we also see the importance of the passive electrical properties as, in particular, elderly patients suffer from cardiac arrhythmia. Age has been described to be associated with cardiac fibrosis (Gottwald et al., 1997) and with disturbances of cardiac conduction velocity and enhanced dispersion of action potential duration (Dhein and Hammerath, 2001). According to the latter study, fibrotic strands aligned to the cardiac myocytes result in reduced transverse propagation velocity and thereby enhanced anisotropy. The authors concluded that reduced lateral gap junction coupling may be a typical feature of aged hearts. In accordance with this assumption, they could show that reduction of gap junction coupling in young hearts could mimic the situation found in aged hearts. They also observed that the extracellular potentials were fractionated in areas where activation spread was particularly inhomogeneous. Thus, age-related fibrosis and the resulting disturbances in activation spreading and repolarization indicate that the biophysical passive properties of the tissue are changed and may help to explain why in elderly patients arrhythmia is more frequent than in the young.
Fibrosis is a key characteristic in atrial fibrillation (Boldt et al., 2004), which can be reduced by angiotensin-converting enzyme inhibitors (Boldt et al., 2006). Fibrosis is, among others, considered a major determinant for the development of atrial fibrillation and may lead to structural uncoupling of fiber strands. Moreover, fibrosis enhances the complexity of atrial fibrillation (Verheule et al., 2013). Since according to the present knowledge fibrosis cannot be reversed, this marks a point of no return for atrial fibrillation. Clinical experience underlines that long-standing persistent atrial fibrillation with dilated atria and fibrotic tissue is unlikely to be successfully converted to sinus rhythm for a longer period.
Chronic pump failure leads to remodeling processes in the heart with hypertrophy of the fibers and lateralization of gap junctions. Clinically, it is known that patients suffering from heart failure, cardiomyopathy or cardiac hypertrophy often die from ventricular arrhythmia rather than from pump failure.
Passive electrical properties of cardiac tissue strongly influence myocardial activation, and thereby importantly contribute to the formation of arrhythmogenic substrates.
Final Remark
There are numerous excellent studies on passive electrical properties, gap junctions, arrhythmia, mechano-electrical feedback and related issues. We seriously apologize to those authors who could not be cited.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Allessie, M. A., Bonke, F. I., and Schopman, F. J. (1977). Circus movement in rabbit atrial muscle as a mechanism of tachycardia. III. The “leading circle” concept: a new model of circus movement in cardiac tissue without the involvement of an anatomical obstacle. Circ. Res. 41, 9–18. doi: 10.1161/01.RES.41.1.9
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Arora, R., Verheule, S., Scott, L., Navarrete, A., Katari, V., Wilson, E., et al. (2003). Arrhythmogenic substrate of the pulmonary veins assessed by high-resolution optical mapping. Circulation 107, 1816–1821. doi: 10.1161/01.CIR.0000058461.86339.7E
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Axelsen, L. N., Calloe, K., Holstein-Rathlou, N. H., and Nielsen, M. S. (2013). Managing the complexity of communication: regulation of gap junctions by post-translational modification. Front. Pharmacol. 4:130. doi: 10.3389/fphar.2013.00130
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Baum, J. R., Long, B., Cabo, C., and Duffy, H. S. (2012). Myofibroblasts cause heterogeneous Cx43 reduction and are unlikely to be coupled to myocytes in the healing canine infarct. Am. J. Physiol. Heart Circ. Physiol. 302, H790–H800. doi: 10.1152/ajpheart.00498.2011
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Beuckelmann, D. J., Näbauer, M., and Erdmann, E. (1993). Alterations of K+ currents in isolated human ventricular myocytes from patients with terminal heart failure. Circ. Res. 73, 379–385. doi: 10.1161/01.RES.73.2.379
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Beyer, E. C., Veenstra, R. D., Kanter, H. L., and Saffitz, J. E. (1995). “Molecular structure and patterns of expression of cardiac gap junction proteins,” in Cardiac Electrophysiology From cell to Bedside, 2nd Edn., eds D. Zipes and J. Jalife (Philadelphia: WB Saunders), 31–38.
Boldt, A., Scholl, A., Garbade, J., Resetar, ME., Mohr, F. W., Gummert, J. F., et al. (2006). ACE-inhibitor treatment attenuates atrial structural remodeling in patients with lone chronic atrial fibrillation. Basic Res. Cardiol. 101, 261–267. doi: 10.1007/s00395-005-0571-2
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Boldt, A., Wetzel, U., Lauschke, J., Weigl, J., Gummert, J., Hindricks, G., et al. (2004). Fibrosis in left atrial tissue of patients with atrial fibrillation with and without underlying mitral valve disease. Heart 90, 400–405. doi: 10.1136/hrt.2003.015347
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Boldt, A., Wetzel, U., Weigl, J., Garbade, J., Lauschke, J., Hindricks, G., et al. (2003). Expression of angiotensin II receptors in human left and right atrial tissue in atrial fibrillation with and without underlying mitral valve disease. J. Am. Coll. Cardiol. 42, 1785–1792. doi: 10.1016/j.jacc.2003.07.014
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Boyden, P. A., Hirose, M., and Dun, W. (2010). Cardiac Purkinje cells. Heart Rhythm 7, 127–135. doi: 10.1016/j.hrthm.2009.09.017
Boyett, M. R., Inada, S., Yoo, S., Li, J., Liu, J., Tellez, J., et al. (2006). Connexins in the sinoatrial and atrioventricular nodes. Adv. Cardiol. 42, 175–197. doi: 10.1159/000092569
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Bukauskas, F. F., and Verselis, V. K. (2004). Gap junction channel gating. Biochim. Biophys. Acta 1662, 42–60. doi: 10.1016/j.bbamem.2004.01.008
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Cabo, C., Pertsov, A. M., Davidenko, J. M., and Jalife, J. (1998). Electrical turbulence as a result of the critical curvature for propagation in cardiac tissue. Chaos 8, 116–126. doi: 10.1063/1.166292
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Cabo, C., Yao, J., Boyden, P. A., Chen, S., Hussain, W., Duffy, H. S., et al. (2006). Heterogeneous gap junction remodeling in reentrant circuits in the epicardial border zone of the healing canine infarct. Cardiovasc. Res. 72, 241–249. doi: 10.1016/j.cardiores.2006.07.005
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Camelliti, P., Green, C. R., LeGrice, I., and Kohl, P. (2004). Fibroblast network in rabbit sinoatrial node: structural and functional identification of homogeneous and heterogeneous cell coupling. Circ. Res. 94, 828–835. doi: 10.1161/01.RES.0000122382.19400.14
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Capogrossi, M. C., Houser, S. R., Bahinski, A., and Lakatta, E. G. (1987). Synchronous occurrence of spontaneous localized calcium release from the sarcoplasmic reticulum generates action potentials in rat cardiac ventricular myocytes at normal resting membrane potential. Circ. Res. 61, 498–503. doi: 10.1161/01.RES.61.4.498
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Carnie, S., and McLaughlin, S. (1983). Large divalent cations and electrostatic potentials adjacent to membranes. A theoretical calculation. Biophys. J. 44, 325–332. doi: 10.1016/S0006-3495(83)84306-9
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Chen, L., Goings, G. E., Upshaw-Earley, J., and Page, E. (1989). Cardiac gap junctions and gap junction-associated vesicles: ultrastructural comparison of in situ negative staining with conventional positive staining. Circ. Res. 64, 501–514. doi: 10.1161/01.RES.64.3.501
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Clerc, L. (1976). Directional differences of impulse spread in trabecular muscle from mammalian heart. J. Physiol. 255, 335–346.
Copene, E. D., and Keener, J. P. (2008). Ephaptic coupling of cardiac cells through the junctional electric potential. J. Math. Biol. 57, 265–284. doi: 10.1007/s00285-008-0157-3
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
de Bakker, J. M., van Capelle, F. J., Janse, M. J., Tasseron, S., Vermeulen, J. T., de Jonge, N., et al. (1993). Slow conduction in the infarcted human heart. ‘Zigzag’ course of activation. Circulation 88, 915–926. doi: 10.1161/01.CIR.88.3.915
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
de Bakker, J. M., van Capelle, F. J., Janse, M. J., Tasseron, S., Vermeulen, J. T., de Jonge, N., et al. (1996). Fractionated electrograms in dilated cardiomyopathy: origin and relation to abnormal conduction. J. Am. Coll. Cardiol. 27, 1071–1078. doi: 10.1016/0735-1097(95)00612-5
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
de Bakker, J. M., van Capelle, F. J., Janse, M. J., Wilde, A. A., Coronel, R., Becker, A. E., et al. (1988). Reentry as a cause of ventricular tachycardia in patients with chronic ischemic heart disease: electrophysiologic and anatomic correlation. Circulation 77, 589–606. doi: 10.1161/01.CIR.77.3.589
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
de Bakker, J. M., and van Rijen, H. M. (2006). Continuous and discontinuous propagation in heart muscle. J. Cardiovasc. Electrophysiol. 17, 567–573. doi: 10.1111/j.1540-8167.2006.00367.x
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Delmar, M., Michaels, D. C., Johnson, T., and Jalife, J. (1987). Effects of increasing intercellular resistance on transverse and longitudinal propagation in sheep epicardial muscle. Circ. Res. 60, 780–785. doi: 10.1161/01.RES.60.5.780
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Dhein, S. (1998). Gap junction channels in the cardiovascular system: pharmacological and physiological modulation. Trends Pharmacol. Sci. 19, 229–241. doi: 10.1016/S0165-6147(98)01192-4
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Dhein, S. (2004). Pharmacology of gap junctions in the cardiovascular system. Cardiovasc. Res. 62, 287–298. doi: 10.1016/j.cardiores.2004.01.019
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Dhein, S., Englert, C., Riethdorf, S., Kostelka, M., Dohmen, P. M., and Mohr, F. W. (2014). Arrhythmogenic effects by local left ventricular stretch: effects of flecainide and streptomycin. Naunyn Schmiedebergs. Arch. Pharmacol. 387, 763–775. doi: 10.1007/s00210-014-0988-y
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Dhein, S., and Hammerath, S. B. (2001). Aspects of the intercellular communication in aged hearts: effects of the gap junction uncoupler palmitoleic acid. Naunyn Schmiedebergs. Arch. Pharmacol. 364, 397–408. doi: 10.1007/s002100100462
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Dhein, S., Manicone, N., Müller, A., Gerwin, R., Ziskoven, U., Irankhahi, A., et al. (1994). A new synthetic antiarrhythmic peptide reduces dispersion of epicardial activation recovery interval and diminishes alterations of epicardial activation patterns induced by regional ischemia. A mapping study. Naunyn Schmiedebergs Arch. Pharmacol. 350, 174–184. doi: 10.1007/BF00241093
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Dhein, S., Rothe, S., Busch, A., Rojas Gomez, D. M., Boldt, A., Reutemann, A., et al. (2011). Effects of metoprolol therapy on cardiac gap junction remodelling and conduction in human chronic atrial fibrillation. Br. J. Pharmacol. 164, 607–616. doi: 10.1111/j.1476-5381.2011.01460.x
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Dupont, E., Ko, Y., Rothery, S., Coppen, S. R., Baghai, M., Haw, M., et al. (2001). The gap-junctional protein connexin40 is elevated in patients susceptible to postoperative atrial fibrillation. Circulation 103, 842–849. doi: 10.1161/01.CIR.103.6.842
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
el-Sherif, N., Gough, W. B., and Restivo, M. (1987). Reentrant ventricular arrhythmias in the late myocardial infarction period: 14. Mechanisms of resetting, entrainment, acceleration, or termination of reentrant tachycardia by programmed electrical stimulation. Pacing Clin. Electrophysiol. 10, 341–371. doi: 10.1111/j.1540-8159.1987.tb05974.x
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Fast, V. G., and Kléber, A. G. (1993). Microscopic conduction in cultured strands of neonatal rat heart cells measured with voltage-sensitive dyes. Circ. Res. 73, 914–925. doi: 10.1161/01.RES.73.5.914
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Fast, V. G., and Kléber, A. G. (1997). Role of wavefront curvature in propagation of cardiac impulse. Cardiovasc. Res. 33, 258–271. doi: 10.1016/S0008-6363(96)00216-7
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Gaudesius, G., Miragoli, M., Thomas, S. P., and Rohr, S. (2003). Coupling of cardiac electrical activity over extended distances by fibroblasts of cardiac origin. Circ. Res. 93, 421–428. doi: 10.1161/01.RES.0000089258.40661.0C
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Geselowitz, D. B., and Miller, W. T. (1983). A bidomain model for anisotropic cardiac muscle. Ann. Biomed. Eng. 11, 191–206. doi: 10.1007/BF02363286
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Goshima, K., and Tonomura, Y. (1969). Synchronized beating of embryonic mouse myocardial cells mediated by FL cells in monolayer culture. Exp. Cell. Res. 56, 387–392. doi: 10.1016/0014-4827(69)90029-9
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Gottwald, E., Gottwald, M., and Dhein, S. (1998). Enhanced dispersion of epicardial activation-recovery intervals at sites of histological inhomogeneity during regional cardiac ischaemia and reperfusion. Heart 79, 474–480.
Gottwald, M., Gottwald, E., and Dhein, S. (1997). Age-related electrophysiological and histological changes in rabbit hearts: age-related changes in electrophysiology. Int. J. Cardiol. 62, 97–106. doi: 10.1016/S0167-5273(97)00183-6
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Gourdie, R. G., Harfst, E., Severs, N. J., and Green, C. R. (1990). Cardiac gap junctions in rat ventricle: localization using site-directed antibodies and laser scanning confocal microscopy. Cardioscience 1, 75–82.
Greenbaum, R. A., Ho, S. Y., Gibson, D. G., Becker, A. E., and Anderson, R. H. (1981). Left ventricular fibre architecture in man. Br. Heart J. 45, 248–263. doi: 10.1136/hrt.45.3.248
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Hagen, A., Dietze, A., and Dhein, S. (2009). Human cardiac gap-junction coupling: effects of antiarrhythmic peptide AAP10. Cardiovasc. Res. 83, 405–415. doi: 10.1093/cvr/cvp028
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Hand, P. E., Griffith, B. E., and Peskin, C. S. (2009). Deriving macroscopic myocardial conductivities by homogenization of microscopic models. Bull. Math. Biol. 71, 1707–1726. doi: 10.1007/s11538-009-9421-y
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Harris, A. L. (2001). Emerging issues of connexin channels: biophysics fills the gap. Q. Rev. Biophys. 34, 325–472. doi: 10.1017/S0033583501003705
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Haugan, K., Marcussen, N., Kjølbye, A. L., Nielsen, M. S., Hennan, J. K., and Petersen, J. S. (2006). Treatment with the gap junction modifier rotigaptide (ZP123) reduces infarct size in rats with chronic myocardial infarction. J. Cardiovasc. Pharmacol. 47, 236–242. doi: 10.1097/01.fjc.0000200990.31611.6e
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
He, K., Shi, X., Zhang, X., Dang, S., Ma, X., Liu, F., et al. (2011). Long-distance intercellular connectivity between cardiomyocytes and cardiofibroblasts mediated by membrane nanotubes. Cardiovasc. Res. 92, 39–47. doi: 10.1093/cvr/cvr189
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Hocini, M., Ho, S. Y., Kawara, T., Linnenbank, A. C., Potse, M., Shah, D., et al. (2002). Electrical conduction in canine pulmonary veins: electrophysiological and anatomic correlation. Circulation 105, 2442–2448. doi: 10.1161/01.CIR.0000016062.80020.11
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Hodgkin, A. L., and Rushton, W. A. (1946). The electrical constants of a crustacean nerve fibre. Proc. R. Soc. Med. 134, 444–479. doi: 10.1098/rspb.1946.0024
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Hubbard, M. L., Ying, W., and Henriquez, C. S. (2007). Effect of gap junction distribution on impulse propagation in a monolayer of myocytes: a model study. Europace 9(Suppl. 6), vi20–vi28. doi: 10.1093/europace/eum203
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Jack, J., Noble, D., and Tsien, R. (1975). Electric Current Flow in Excitable Cells. Oxford: Clarendon.
Johnston, P. R., Kilpatrick, D., and Li, C. Y. (2001). The importance of anisotropy in modeling ST segment shift in subendocardial ischaemia. IEEE Trans. Biomed. Eng. 48, 1366–1376. doi: 10.1109/10.966596
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Joyner, R. W., and van Capelle, F. J. (1986). Propagation through electrically coupled cells. How a small SA node drives a large atrium. Biophys. J. 50, 1157–1164. doi: 10.1016/S0006-3495(86)83559-7
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Jozwiak, J., and Dhein, S. (2008). Local effects and mechanisms of antiarrhythmic peptide AAP10 in acute regional myocardial ischemia: electrophysiological and molecular findings. Naunyn Schmiedebergs. Arch. Pharmacol. 378, 459–470. doi: 10.1007/s00210-008-0317-4
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Kalin, J., Madias, C., Alsheikh-Ali, A. A., and Link, M. S. (2011). Reduced diameter spheres increases the risk of chest blow-induced ventricular fibrillation (commotio cordis). Heart Rhythm 8, 1578–1581. doi: 10.1016/j.hrthm.2011.05.009
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Kawara, T., Derksen, R., de Groot, J. R., Coronel, R., Tasseron, S., Linnenbank, A. C., et al. (2001). Activation delay after premature stimulation in chronically diseased human myocardium relates to the architecture of interstitial fibrosis. Circulation 104, 3069–3075. doi: 10.1161/hc5001.100833
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Kimura, S., Cameron, J. S., Kozlovskis, P. L., Bassett, A. L., and Myerburg, R. J. (1984). Delayed afterdepolarizations and triggered activity induced in feline Purkinje fibers by alpha-adrenergic stimulation in the presence of elevated calcium levels. Circulation 70, 1074–1082. doi: 10.1161/01.CIR.70.6.1074
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Kléber, A. G., and Rudy, Y. (2004). Basic mechanisms of cardiac impulse propagation and associated arrhythmias. Physiol. Rev. 84, 431–488. doi: 10.1152/physrev.00025.2003
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Kohl, P., and Gourdie, R. G. (2014). Fibroblast-myocyte electrotonic coupling: does it occur in native cardiac tissue? J. Mol. Cell. Cardiol. 70, 37–46. doi: 10.1016/j.yjmcc.2013.12.024
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Kostin, S., Dammer, S., Hein, S., Klovekorn, W. P., Bauer, E. P., and Schaper, J. (2004). Connexin 43 expression and distribution in compensated and decompensated cardiac hypertrophy in patients with aortic stenosis. Cardiovasc. Res. 62, 426–436. doi: 10.1016/j.cardiores.2003.12.010
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Kostin, S., Klein, G., Szalay, Z., Hein, S., Bauer, E. P., and Schaper, J. (2002). Structural correlate of atrial fibrillation in human patients. Cardiovasc. Res. 54, 361–379. doi: 10.1016/S0008-6363(02)00273-0
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Kostin, S., Rieger, M., Dammer, S., Hein, S., Richter, M., Klövekorn, W. P., et al. (2003). Gap junction remodeling and altered connexin43 expression in the failing human heart. Mol. Cell. Biochem. 242, 135–144. doi: 10.1023/A:1021154115673
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Kozhevnikov, D. O., Yamamoto, K., Robotis, D., Restivo, M., and El-Sherif, N. (2002). Electrophysiological mechanism of enhanced susceptibility of hypertrophied heart to acquired torsade de pointes arrhythmias: tridimensional mapping of activation and recovery patterns. Circulation 105, 1128–1134. doi: 10.1161/hc0902.104711
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Kucera, J. P., Rohr, S., and Rudy, Y. (2002). Localization of sodium channels in intercalated disks modulates cardiac conduction. Circ. Res. 91, 1176–1182. doi: 10.1161/01.RES.0000046237.54156.0A
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Lazzara, R. (1988). Electrophysiological mechanisms for ventricular arrhythmias. Clin. Cardiol. 11(3 Suppl. 2), II1–II4.
Lederer, W. J., and Tsien, R. W. (1976). Transient inward current underlying arrhythmogenic effects of cardiotonic steroids in Purkinje fibres. J. Physiol. 263, 73–100.
Lee, P. J., and Pogwizd, S. M. (2006). Micropatterns of propagation. Adv. Cardiol. 42, 86–106. doi: 10.1159/000092564
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Lin, J., and Keener, J. P. (2010). Modeling electrical activity of myocardial cells incorporating the effects of ephaptic coupling. Proc. Natl. Acad. Sci. U.S.A. 107, 20935–20940. doi: 10.1073/pnas.1010154107
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Maier, S. K., Westenbroek, R. E., McCormick, K. A., Curtis, R., Scheuer, T., and Catterall, W. A. (2004). Distinct subcellular localization of different sodium channel alpha and beta subunits in single ventricular myocytes from mouse heart. Circulation 109, 1421–1427. doi: 10.1161/01.CIR.0000121421.61896.24
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Makowski, L., Caspar, D. L., Phillips, W. C., and Goodenough, D. A. (1977). Gap junction structures. II. Analysis of the x-ray diffraction data. J. Cell. Biol. 74, 629–645. doi: 10.1083/jcb.74.2.629
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Marban, E., Robinson, S. W., and Wier, W. G. (1986). Mechanisms of arrhythmogenic delayed and early afterdepolarizations in ferret ventricular muscle. J. Clin. Invest. 78, 1185–1192. doi: 10.1172/JCI112701
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
McIntyre, H., and Fry, C. H. (1997). Abnormal action potential conduction in isolated human hypertrophied left ventricular myocardium. J. Cardiovasc. Electrophysiol. 8, 887–894. doi: 10.1111/j.1540-8167.1997.tb00850.x
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Miura, T., Ohnuma, Y., Kuno, A., Tanno, M., Ichikawa, Y., Nakamura, Y., et al. (2004). Protective role of gap junctions in preconditioning against myocardial infarction. Am. J. Physiol. Heart Circ. Physiol. 286, H214–H221. doi: 10.1152/ajpheart.00441.2003
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Moreno, A. P. (2004). Biophysical properties of homomeric and heteromultimeric channels formed by cardiac connexins. Cardiovasc. Res. 62, 276–286. doi: 10.1016/j.cardiores.2004.03.003
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Mori, Y., Fishman, G. I., and Peskin, C. S. (2008). Ephaptic conduction in a cardiac strand model with 3D electrodiffusion. Proc. Natl. Acad. Sci. U.S.A. 105, 6463–6468. doi: 10.1073/pnas.0801089105
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Morley, G. E., Danik, S. B., Bernstein, S., Sun, Y., Rosner, G., Gutstein, D. E., et al. (2005). Reduced intercellular coupling leads to paradoxical propagation across the Purkinje-ventricular junction and aberrant myocardial activation. Proc. Natl. Acad. Sci. U.S.A. 102, 4126–4129. doi: 10.1073/pnas.0500881102
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Müller, A., and Dhein, S. (1993). Sodium channel blockade enhances dispersion of the cardiac action potential duration. A computer simulation study. Basic Res. Cardiol. 88, 11–22.
Müller, A., Gottwald, M., Tudyka, T., Linke, W., Klaus, W., and Dhein, S. (1997). Increase in gap junction conductance by an antiarrhythmic peptide. Eur. J. Pharmacol. 327, 65–72. doi: 10.1016/S0014-2999(97)89679-3
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Myles, R. C., Wang, L., Kang, C., Bers, D. M., and Ripplinger, C. M. (2012). Local β-adrenergic stimulation overcomes source-sink mismatch to generate focal arrhythmia. Circ. Res. 110, 1454–1464. doi: 10.1161/CIRCRESAHA.111.262345
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Nielsen, M. S., Axelsen, L. N., Sorgen, P. L., Verma, V., Delmar, M., and Holstein-Rathlou, N. H. (2012). Gap junctions. Compr. Physiol. 2, 1981–2035. doi: 10.1002/cphy.c110051
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Page, E., and Shibata, Y. (1981). Permeable junctions between cardiac cells. Annu. Rev. Physiol. 43, 431–441. doi: 10.1146/annurev.ph.43.030181.002243
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Pellman, J., Lyon, R. C., and Sheikh, F. (2010). Extracellular matrix remodeling in atrial fibrosis: mechanisms and implications in atrial fibrillation. J. Mol. Cell. Cardiol. 48, 461–467. doi: 10.1016/j.yjmcc.2009.09.001
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Perkins, G., Goodenough, D., and Sosinsky, G. (1997). Three-dimensional structure of the gap junction connexon. Biophys. J. 72(2 Pt 1), 533–544. doi: 10.1016/S0006-3495(97)78693-4
Pertsov, A. (1997). “Scale of geometric structures responsible for discontinuous propagation in myocardial tissue,” in Discontinuous Conduction in the Heart, eds P. Spooner, R. Joyner, and J. Jalife (New York, NY: Futura Publishing Company Inc.), 273–293.
Pertsov, A. M., Davidenko, J. M., Salomonsz, R., Baxter, W. T., and Jalife, J. (1993). Spiral waves of excitation underlie reentrant activity in isolated cardiac muscle. Circ. Res. 72, 631–650. doi: 10.1161/01.RES.72.3.631
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Peskoff, A. (1979). Electric potential in three-dimensional electrically syncytial tissues. Bull. Math. Biol. 41, 163–181. doi: 10.1007/BF02460876
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Polontchouk, L., Haefliger, J. A., Ebelt, B., Schaefer, T., Stuhlmann, D., Mehlhorn, U., et al. (2001). Effects of chronic atrial fibrillation on gap junction distribution in human and rat atria. J. Am. Coll. Cardiol. 38, 883–891. doi: 10.1016/S0735-1097(01)01443-7
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Rhett, J. M., Ongstad, E. L., Jourdan, J., and Gourdie, R. G. (2012). Cx43 associates with Na(v)1.5 in the cardiomyocyte perinexus. J. Membr. Biol. 245, 411–422. doi: 10.1007/s00232-012-9465-z
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Rhett, J. M., Veeraraghavan, R., Poelzing, S., and Gourdie, R. G. (2013). The perinexus: sign-post on the path to a new model of cardiac conduction? Trends Cardiovasc. Med. 23, 222–228. doi: 10.1016/j.tcm.2012.12.005
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Roberts, D. E., Hersh, L. T., and Scher, A. M. (1979). Influence of cardiac fiber orientation on wavefront voltage, conduction velocity, and tissue resistivity in the dog. Circ. Res. 44, 701–712. doi: 10.1161/01.RES.44.5.701
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Roberts, D. E., and Scher, A. M. (1982). Effect of tissue anisotropy on extracellular potential fields in canine myocardium in situ. Circ. Res. 50, 342–351. doi: 10.1161/01.RES.50.3.342
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Roberts, S. F., Stinstra, J. G., and Henriquez, C. S. (2008). Effect of nonuniform interstitial space properties on impulse propagation: a discrete multidomain model. Biophys. J. 95, 3724–3737. doi: 10.1529/biophysj.108.137349
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Rohr, S. (2004). Role of gap junctions in the propagation of the cardiac action potential. Cardiovasc. Res. 62, 309–322. doi: 10.1016/j.cardiores.2003.11.035
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Rohr, S. (2012). Arrhythmogenic implications of fibroblast-myocyte interactions. Circ. Arrhythm. Electrophysiol. 5, 442–452. doi: 10.1161/CIRCEP.110.957647
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Rohr, S., Kucera, J. P., Fast, V. G., and Kléber, A. G. (1997). Paradoxical improvement of impulse conduction in cardiac tissue by partial cellular uncoupling. Science 275, 841–844. doi: 10.1126/science.275.5301.841
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Sachse, F. B., Moreno, A. P., Seemann, G., and Abildskov, J. A. (2009). A model of electrical conduction in cardiac tissue including fibroblasts. Ann. Biomed. Eng. 37, 874–889. doi: 10.1007/s10439-009-9667-4
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Salameh, A., and Dhein, S. (2005). Pharmacology of gap junctions. New pharmacological targets for treatment of arrhythmia, seizure and cancer? Biochim. Biophys. Acta 1719, 36–58. doi: 10.1016/j.bbamem.2005.09.007
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Salameh, A., Krautblatter, S., Karl, S., Blanke, K., Gomez, D. R., Dhein, S., et al. (2009). The signal transduction cascade regulating the expression of the gap junction protein connexin43 by beta-adrenoceptors. Br. J. Pharmacol. 158, 198–208. doi: 10.1111/j.1476-5381.2009.00344.x
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Schulte, J. S., Scheffler, A., Rojas-Gomez, D., Mohr, F. W., and Dhein, S. (2008). Neonatal rat cardiomyocytes show characteristics of nonhomotypic gap junction channels. Cell Commun. Adhes. 15, 13–25. doi: 10.1080/15419060802014404
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Schwab, B. C., Seemann, G., Lasher, R. A., Torres, N. S., Wulfers, E. M., Arp, M., et al. (2013). Quantitative analysis of cardiac tissue including fibroblasts using three-dimensional confocal microscopy and image reconstruction: towards a basis for electrophysiological modeling. IEEE Trans. Med. Imaging 32, 862–872. doi: 10.1109/TMI.2013.2240693
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Seidel, T., Salameh, A., and Dhein, S. (2010). A simulation study of cellular hypertrophy and connexin lateralization in cardiac tissue. Biophys. J. 99, 2821–2830. doi: 10.1016/j.bpj.2010.09.010
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Seo, K., Inagaki, M., Nishimura, S., Hidaka, I., Sugimachi, M., Hisada, T., et al. (2010). Structural heterogeneity in the ventricular wall plays a significant role in the initiation of stretch-induced arrhythmias in perfused rabbit right ventricular tissues and whole heart preparations. Circ. Res. 106, 176–184. doi: 10.1161/CIRCRESAHA.109.203828
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Severs, N. J. (1994). Pathophysiology of gap junctions in heart disease. J. Cardiovasc. Electrophysiol. 5, 462–475. doi: 10.1111/j.1540-8167.1994.tb01185.x
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Severs, N. J., Dupont, E., Thomas, N., Kaba, R., Rothery, S., Jain, R., et al. (2006). Alterations in cardiac connexin expression in cardiomyopathies. Adv. Cardiol. 42, 228–242. doi: 10.1159/000092572
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Shaw, R. M., and Rudy, Y. (1997a). Electrophysiologic effects of acute myocardial ischemia. A mechanistic investigation of action potential conduction and conduction failure. Circ. Res. 80, 124–138. doi: 10.1161/01.RES.80.1.124
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Shaw, R. M., and Rudy, Y. (1997b). Ionic mechanisms of propagation in cardiac tissue. Roles of the sodium and L-type calcium currents during reduced excitability and decreased gap junction coupling. Circ. Res. 81, 727–741. doi: 10.1161/01.RES.81.5.727
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Spach, M., and Dolber, P. (1990). “Discontinuous anisotropic propagation,” in Cardiac Electrophysiology: A textbook, eds M. Rosen, M. Janse, and A. Wit (Mount Kisco, NY: Futura Publishing Company Inc.), 517–534.
Spach, M. S., and Dolber, P. C. (1986). Relating extracellular potentials and their derivatives to anisotropic propagation at a microscopic level in human cardiac muscle. Evidence for electrical uncoupling of side-to-side fiber connections with increasing age. Circ. Res. 58, 356–371. doi: 10.1161/01.RES.58.3.356
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Spach, M. S., Heidlage, J. F., Dolber, P. C., and Barr, R. C. (2000). Electrophysiological effects of remodeling cardiac gap junctions and cell size: experimental and model studies of normal cardiac growth. Circ. Res. 86, 302–311. doi: 10.1161/01.RES.86.3.302
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Spach, M. S., Miller, W. T., Dolber, P. C., Kootsey, J. M., Sommer, J. R., and Mosher, C. E. (1982). The functional role of structural complexities in the propagation of depolarization in the atrium of the dog. Cardiac conduction disturbances due to discontinuities of effective axial resistivity. Circ. Res. 50, 175–191. doi: 10.1161/01.RES.50.2.175
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Spear, J. F., Horowitz, L. N., Hodess, A. B., MacVaugh, H., and Moore, E. N. (1979). Cellular electrophysiology of human myocardial infarction. 1. Abnormalities of cellular activation. Circulation 59, 247–256. doi: 10.1161/01.CIR.59.2.247
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Sperelakis, N. (1979). Propagation mechanisms in heart. Annu. Rev. Physiol. 41, 441–457. doi: 10.1146/annurev.ph.41.030179.002301
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Sperelakis, N., and Mann, J. E. (1977). Evaluation of electric field changes in the cleft between excitable cells. J. Theor. Biol. 64, 71–96. doi: 10.1016/0022-5193(77)90114-X
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Stinstra, J. G., Hopenfeld, B., and Macleod, R. S. (2005). On the passive cardiac conductivity. Ann. Biomed. Eng. 33, 1743–1751. doi: 10.1007/s10439-005-7257-7
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Swynghedauw, B., Baillard, C., and Milliez, P. (2003). The long QT interval is not only inherited but is also linked to cardiac hypertrophy. J. Mol. Med. 81, 336–345. doi: 10.1007/s00109-003-0437-8
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Tomaselli, G. F., and Marbán, E. (1999). Electrophysiological remodeling in hypertrophy and heart failure. Cardiovasc. Res. 42, 270–283. doi: 10.1016/S0008-6363(99)00017-6
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Toure, A., and Cabo, C. (2010). Effect of cell geometry on conduction velocity in a subcellular model of myocardium. IEEE Trans. Biomed. Eng. 57, 2107–2114. doi: 10.1109/TBME.2010.2050064
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Tveito, A., Lines, G. T., Edwards, A. G., Maleckar, M. M., Michailova, A., Hake, J., et al. (2012). Slow Calcium-Depolarization-Calcium waves may initiate fast local depolarization waves in ventricular tissue. Prog. Biophys. Mol. Biol. 110, 295–304. doi: 10.1016/j.pbiomolbio.2012.07.005
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Veeraraghavan, R., Gourdie, R. G., and Poelzing, S. (2014). Mechanisms of cardiac conduction: a history of revisions. Am. J. Physiol. Heart Circ. Physiol. 306, H619–H627. doi: 10.1152/ajpheart.00760.2013
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Veeraraghavan, R., Salama, M. E., and Poelzing, S. (2012). Interstitial volume modulates the conduction velocity-gap junction relationship. Am. J. Physiol. Heart Circ. Physiol. 302, H278–H286. doi: 10.1152/ajpheart.00868.2011
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Verheule, S., Tuyls, E., Gharaviri, A., Hulsmans, S., van Hunnik, A., Kuiper, M., et al. (2013). Loss of continuity in the thin epicardial layer because of endomysial fibrosis increases the complexity of atrial fibrillatory conduction. Circ. Arrhythm. Electrophysiol. 6, 202–211. doi: 10.1161/CIRCEP.112.975144
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Weber, K. T., Sun, Y., Bhattacharya, S. K., Ahokas, R. A., and Gerling, I. C. (2013). Myofibroblast-mediated mechanisms of pathological remodelling of the heart. Nat. Rev. Cardiol. 10, 15–26. doi: 10.1038/nrcardio.2012.158
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Weidmann, S. (1990). “Passive properties of cardiac fibers. A textbook,” in Cardiac Electrophysiology, eds M. Rosen, M. Janse, and A. Wit (Mount Kisco, NY: Futura Publishing Company Inc.), 29–35.
Weingart, R., and Maurer, P. (1988). Action potential transfer in cell pairs isolated from adult rat and guinea pig ventricles. Circ. Res. 63, 72–80. doi: 10.1161/01.RES.63.1.72
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Xie, Y., Sato, D., Garfinkel, A., Qu, Z., and Weiss, J. N. (2010). So little source, so much sink: requirements for afterdepolarizations to propagate in tissue. Biophys. J. 99, 1408–1415. doi: 10.1016/j.bpj.2010.06.042
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Xing, D., Kjølbye, A. L., Nielsen, M. S., Petersen, J. S., Harlow, K. W., Holstein-Rathlou, N. H., et al. (2003). ZP123 increases gap junctional conductance and prevents reentrant ventricular tachycardia during myocardial ischemia in open chest dogs. J. Cardiovasc. Electrophysiol. 14, 510–520. doi: 10.1046/j.1540-8167.2003.02329.x
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Yue, L., Xie, J., and Nattel, S. (2011). Molecular determinants of cardiac fibroblast electrical function and therapeutic implications for atrial fibrillation. Cardiovasc. Res. 89, 744–753. doi: 10.1093/cvr/cvq329
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Keywords: electrical propagation, passive electrical properties, cardiac tissue, gap junction, connexin, anisotropy, inhomogeneity, cable theory
Citation: Dhein S, Seidel T, Salameh A, Jozwiak J, Hagen A, Kostelka M, Hindricks G and Mohr F-W (2014) Remodeling of cardiac passive electrical properties and susceptibility to ventricular and atrial arrhythmias. Front. Physiol. 5:424. doi: 10.3389/fphys.2014.00424
Received: 21 August 2014; Accepted: 13 October 2014;
Published online: 03 November 2014.
Edited by:
George E. Billman, The Ohio State University, USAReviewed by:
Candido Cabo, City University of New York, USAHugh Clements-Jewery, West Virginia School of Osteopathic Medicine, USA
Copyright © 2014 Dhein, Seidel, Salameh, Jozwiak, Hagen, Kostelka, Hindricks and Mohr. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Stefan Dhein, Clinic for Cardiac Surgery, Heart Center Leipzig, University of Leipzig, Struempellstr. 39, 04289 Leipzig, Germany e-mail:c3RlZmFuLmRoZWluQG1lZGl6aW4udW5pLWxlaXB6aWcuZGU=
† These authors have contributed equally to this work.
 Stefan Dhein
Stefan Dhein Thomas Seidel
Thomas Seidel Aida Salameh
Aida Salameh Joanna Jozwiak
Joanna Jozwiak Anja Hagen
Anja Hagen Martin Kostelka1
Martin Kostelka1